Categorification of characteristic structures

1. Introduction

The problem of deciding when two algebraic structures are isomorphic is fundamental to algebra and computer science. It encompasses issues of decidability and complexity, and it tests the limits of our theories and algorithms. An initial tactic in deciding isomorphism is to identify substructures that are invariant under isomorphisms because doing so reduces the search space. We first discuss groups, where the literature is most developed (see, for example, \citelist[ELGO2002][BOW][Maglione2021][Wilson:filters]), but our results apply to monoids, loops, rings, and non-associative algebras.

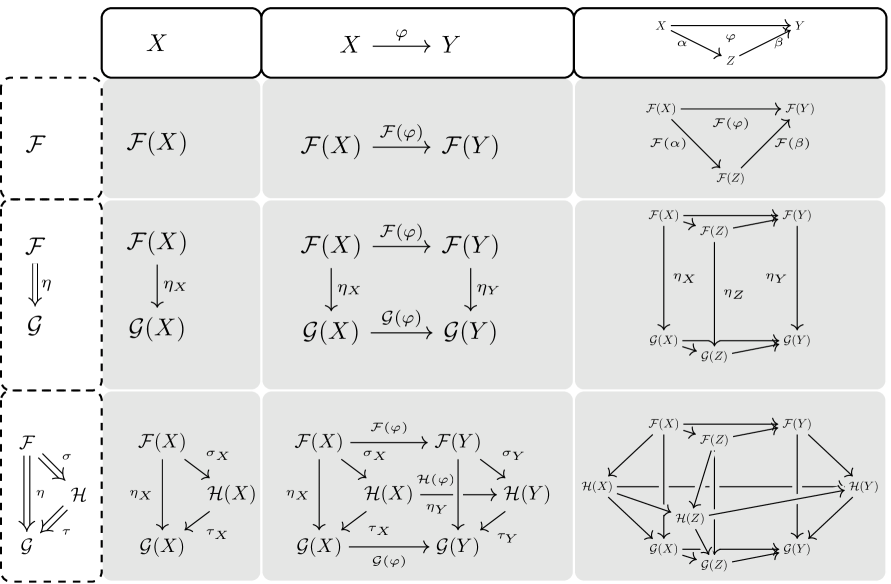
A subgroup $H$ of a group $G$ is characteristic if $\varphi(H)=H$ for every automorphism $\varphi:G\to G$ ; it is fully invariant if $\psi(H)\leqslant H$ for every homomorphism $\psi:G\to G$ . We use the language of categories, following [Riehl], and a type of natural transformation to describe our main results (details are given in Section 5.1).

Definition 1.1.

Let $\mathsf{A}$ be a category, and let $\mathsf{B}$ be a subcategory with inclusion functor $\mathcal{I}:\mathsf{B}\to\mathsf{A}$ . A counital is a natural transformation $\iota:\mathcal{C}\Rightarrow\mathcal{I}$ for some functor $\mathcal{C}:\mathsf{B}\to\mathsf{A}$ . The class of all such counitals is denoted $\text{Counital}(\mathsf{B},\mathsf{A})$ . For an object $X$ of $\mathsf{B}$ , the $X$ -component of $\iota$ is the morphism $\iota_{X}:\mathcal{C}(X)\to\mathcal{I}(X)$ in $\mathsf{A}$ .

A special case of our results, for the category of groups, can be stated as follows.

Theorem 1.

For the category $\mathsf{Grp}$ of groups and subcategory $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}$ of groups and their isomorphisms, the following equalities of sets hold:

$\{H\leqslant G~\|~H\text{ characteristic in }G\}$	$=$	$\left\{\mathrm{Im}(\iota_{G})~\middle\|~\iota\in\text{\rm Counital}\left(\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}},\mathsf{Grp}\right)\right\};$
$\{H\leqslant G~\|~H\text{ fully invariant in }G\}$	$=$	$\left\{\mathrm{Im}(\iota_{G})~\middle\|~\iota\in\text{\rm Counital}(\mathsf{Grp},\mathsf{Grp})\right\}$ .

Theorem 1 contrasts a “recognizable” description of characteristic (fully invariant) subgroups with a “constructive” one. For a fixed group $G$ , the sets on the left are of the form $\{H\mid P(G,H)\}$ , where $P$ is the appropriate logical predicate that allows us to recognize when a subgroup $H$ belongs to the set; those on the right are of the form $\{f(\iota)\mid\iota\in\text{Counital}(\ldots,\mathsf{Grp})\}$ , where $f(\iota)=\mathrm{Im}(\iota_{G})$ allows us to construct members of the subset by applying a function. Also, the descriptions on the left are “local” since they reference just a single parent group, whereas those on the right are “global” since they apply to the ambient categories.

The characterization of characteristic subgroups by natural transformations allows one to recast the lattice theory of characteristic subgroups into the globular compositions of natural transformations as explored in [Baez, Power]. We now explore other implications of Theorem 1.

1.1. Constraining isomorphism by characteristic subgroups

Characteristic subgroups constrain isomorphisms in the following sense:

Fact 1.2.

If $H$ is a characteristic subgroup of $G$ , and $\alpha,\beta:G\to\tilde{G}$ are isomorphisms, then $\alpha(H)=\beta(H)$ .

It is therefore useful for an isomorphism test to locate characteristic subgroups of a group $G$ : every hypothetical isomorphism from $G$ to $\tilde{G}$ must then assign such a subgroup $H$ to a unique corresponding subgroup $\tilde{H}$ of $\tilde{G}$ . This raises at least two issues. First, if the task is to construct isomorphisms, then we should assume that $\operatorname{Aut}(G)$ is not yet known. How then do we verify that $H$ is characteristic? Is there an alternative definition of the characteristic property that does not directly reference $\operatorname{Aut}(G)$ ? A second issue is how to determine the possible $\tilde{H}\leqslant\tilde{G}$ when we know only that $H$ is characteristic in $G$ . For familiar characteristic subgroups such as the center $\zeta(G)$ this is possible because the definition is already global to all groups. Hence, a hypothetical isomorphism $\alpha:G\to\tilde{G}$ must satisfy $\alpha(\zeta(G))=\zeta(\tilde{G})$ , and typically $\zeta(G)$ and $\zeta(\tilde{G})$ can be constructed without explicit knowledge of $\operatorname{Aut}(G)$ or $\operatorname{Aut}(\tilde{G})$ . However, the following family of examples, first explored by Rottlaender [Rottlander28], exhibits groups whose characteristic subgroups have no known global definition, so it is difficult to utilize Fact 1.2.

Example 1.3.

Let $p$ be a prime and $m<p$ a positive integer. Let $q\equiv 1\bmod{p}$ be a prime and denote by $\mathbb{F}_{q}$ the field with $q$ elements. Let $\theta\in\operatorname{GL}_{m}(\mathbb{F}_{q})$ , with $\theta^{p}=1$ , be diagonalizable with $m$ eigenvalues $a_{1},\ldots,a_{m}$ , each different from $1$ , satisfying the following property. If there exists $u\in\{1,\dots,p-1\}$ with $a_{i}^{u}=a_{j}$ for all $i\neq j$ , then $p\nmid(u^{k}-1)$ for $k\in\{1,\dots,m\}$ . For $m=2$ , this requires $a_{1}\neq a_{2}^{\pm 1}$ .

The cyclic group $C_{p}$ of order $p$ acts on the vector space $V=\mathbb{F}_{q}^{m}$ via $\theta$ . The condition on $\theta$ means that each eigenspace in $V$ is a characteristic subgroup of the semidirect product $G_{\theta}=C_{p}\ltimes_{\theta}V$ determined by $\theta$ , and exactly $m$ of the $1+q+q^{2}+\cdots+q^{m-1}$ order $q$ subgroups of $G_{\theta}$ are characteristic. Two such groups $G_{\theta}$ and $G_{\tau}$ may be isomorphic even if the eigenvalues of $\theta$ and $\tau$ are different. For example, this occurs when $\tau=\theta^{j}$ for some $j$ coprime to $p$ . Thus, the correspondence between characteristic subgroups of $G_{\theta}$ and $G_{\tau}$ is not a priori clear. $\square$

One of the goals of this work is to reinterpret the definition of a characteristic subgroup in a way that is independent of automorphisms and which is unambiguously defined for all groups. We do this by formulating the characteristic condition on the entire category of groups, thereby providing a categorification of the property of being characteristic. Moreover, our formulation pairs well with—and indeed is motivated by—the necessities of computation (see Section 1.3). To address this, we employ methods from theorem-checking, specifically type-theoretic techniques [Hindley-Seldin, Pierce:types, HoTT]; these have recently become accessible through systems such as Agda [Agda], Coq [Coq], and Lean [lean].

1.2. A local-to-global problem

Our approach is to transform the local characteristic property of subgroups into an equivalent global property of the category of all groups and their isomorphisms. Calculations now take place within the category instead of within individual groups, which opens up new ways to search for characteristic subgroups. Our approach also facilitates an a priori verification of the global characteristic property, rather than the usual a posteriori check that requires knowledge of automorphisms. The process is analogous to proving that $\zeta(G)$ is characteristic without employing specific properties of $G$ . Our methods extend to every characteristic subgroup, even those discovered via bespoke calculations.

The traditional model of a category $\mathsf{A}$ involves both objects and morphisms. By sometimes focusing only on morphisms, we work with categories as an algebraic structure with a partial binary associative product on $\mathsf{A}$ —given by composition of its morphisms—and $\mathbb{1}_{\mathsf{A}}=\{\operatorname{id}_{X}\mid X$ an object in $\mathsf{A}\}$ . It is partial because not every pair of morphisms is composable, in which case the product is undefined. This perspective yields a general algebraic framework for our computations.

The morphisms of a category can act on the morphisms of another category either on the left or the right. Although several interpretations of “category action” appear in the literature \citelist [Bergner-Hackney]*§2 [nlab:action] [FS]*1.271–274, there is no single established meaning. Let $\mathsf{A}$ , $\mathsf{B}$ , and $\mathsf{X}$ be categories. A left $\mathsf{A}$ -action on $\mathsf{X}$ is a partial-function, where $a\cdot x$ is defined for some morphisms $a$ of $\mathsf{A}$ and $x$ of $\mathsf{X}$ , that satisfies two conditions inspired by group actions. The first is that $(a\acute{a})\cdot x=a\cdot(\acute{a}\cdot x)$ , whenever defined, for all morphisms $a,\acute{a}$ of $\mathsf{A}$ and $x$ of $\mathsf{X}$ . The second is that $\mathbb{1}_{\mathsf{A}}\cdot x=\{x\}$ . To simplify notation, we write $\mathbb{1}_{\mathsf{A}}\cdot x=x$ . As in the theory of bimodules of rings, an $(\mathsf{A},\mathsf{B})$ -biaction on $\mathsf{X}$ is a left $\mathsf{A}$ -action and a right $\mathsf{B}$ -action on $\mathsf{X}$ such that for every morphism $a$ in $\mathsf{A}$ , $b$ in $\mathsf{B}$ , and $x$ in $\mathsf{X}$ ,

a\cdot(x\cdot b)=(a\cdot x)\cdot b

whenever both sides of the equation are defined. Suppose there are $(\mathsf{A},\mathsf{B})$ -biactions on categories $\mathsf{X}$ and $\mathsf{Y}$ . An $(\mathsf{A},\mathsf{B})$ -morphism is a partial-function, which we denote by $\mathcal{M}:{\mathsf{Y}}\to\mathsf{X}^{?}$ , such that

\mathcal{M}(a\cdot y\cdot b)=a\cdot\mathcal{M}(y)\cdot b

whenever $a\cdot y\cdot b$ is defined for morphisms $a$ in $\mathsf{A}$ , $b$ in $\mathsf{B}$ , and $y$ in $\mathsf{Y}$ .

We write $\mathsf{A}\leqslant\mathsf{B}$ to indicate that $\mathsf{A}$ is a subcategory of $\mathsf{B}$ , and denote the identity functor of $\mathsf{A}$ by $\operatorname{id}_{\mathsf{A}}:\mathsf{A}\to\mathsf{A}$ . A counit is a counital of the form $\eta:\mathcal{C}\Rightarrow\operatorname{id}_{\mathsf{A}}$ . The following specialization of one of our principal results to groups describes how characteristic subgroups relate to counits and morphisms of category biactions.

Theorem 2.

Let $G$ be a group and $H\leqslant G$ with inclusion $\iota_{G}:H\hookrightarrow G$ . There exist categories $\mathsf{A}$ and $\mathsf{B}$ , where $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}\;\leqslant\mathsf{A}\leqslant\mathsf{Grp}$ , such that the following are equivalent.

(1)

$H$ is characteristic in $G$ .
(2)

There is a functor $\mathcal{C}:\mathsf{A}\to\mathsf{A}$ and a counit $\eta:\mathcal{C}\Rightarrow\operatorname{id}_{\mathsf{A}}$ such that $H=\operatorname{Im}(\eta_{G})$ .
(3)

There is an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{M}:\mathsf{B}\to\mathsf{A}^{?}$ such that $\iota_{G}=\mathcal{M}(\operatorname{id}_{G}\cdot\mathbb{1}_{\mathsf{B}})$ .

We emphasize that the category $\mathsf{B}$ in Theorem 2 need not be a subcategory of $\mathsf{Grp}$ ; see Section 8 for an example. Moreover, our results apply to characteristic substructures of eastern algebras, which include monoids, loops, rings, and non-associative algebras. This generalization (Theorem 2-cat) and its dual version (2-dual) are proved in Section 6. We conclude this section with an example that illustrates how natural transformations arise from characteristic substructures.

Example 1.4.

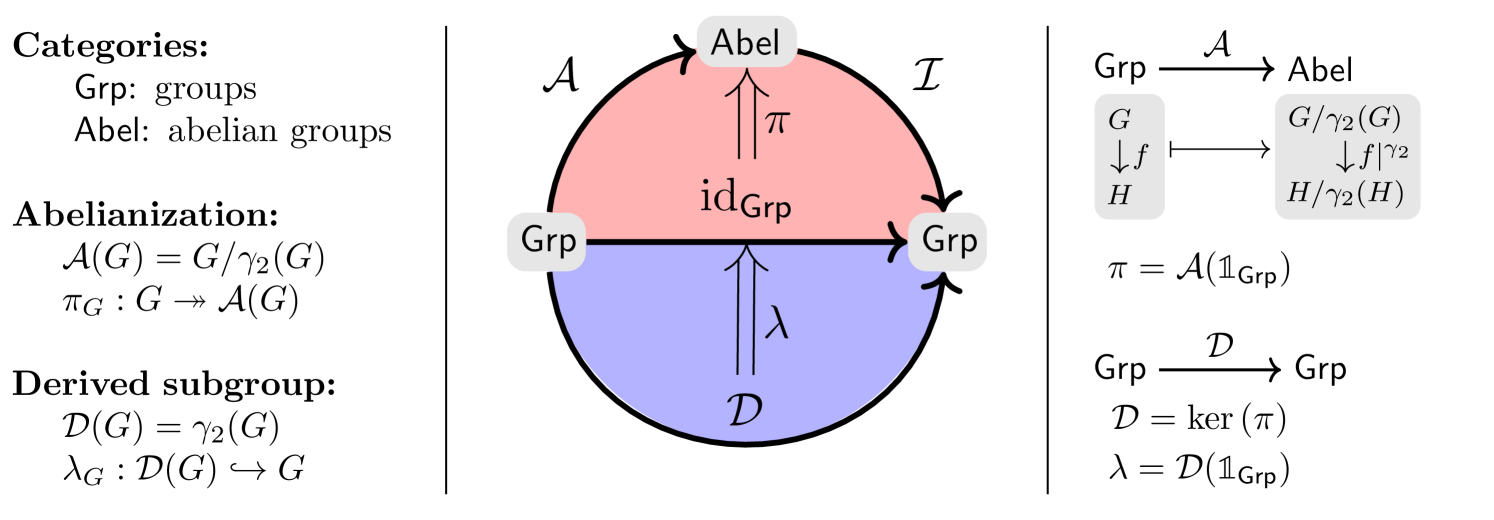
The derived subgroup $\gamma_{2}(G)$ of a group $G$ determines the inclusion homomorphism $\lambda_{G}:\gamma_{2}(G)\hookrightarrow G$ and a functor $\mathcal{D}:\mathsf{Grp}\to\mathsf{Grp}$ mapping groups to their derived subgroup and mapping homomorphisms to their restriction onto the derived subgroups. For every group homomorphism $\varphi:G\to H$ , observe that $\lambda_{H}\mathcal{D}(\varphi)=\operatorname{id}_{\mathsf{Grp}}(\varphi)\lambda_{G}$ , so $\lambda:\mathcal{D}\Rightarrow\operatorname{id}_{\mathsf{Grp}}$ is a natural transformation.

The center $\zeta(G)$ of $G$ determines the inclusion homomorphism $\rho_{G}:\zeta(G)\hookrightarrow G$ . To define a functor with object map $G\mapsto\zeta(G)$ , we must restrict the type of homomorphisms between groups since homomorphisms need not map centers to centers. (Consider, for example, an embedding $\mathbb{Z}/2\hookrightarrow\text{Sym}(3)$ .) Since every isomorphism maps center to center, we restrict to $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}$ , defining a functor $\mathcal{Z}:\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}\;\to\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}$ mapping $G\mapsto\zeta(G)$ and mapping each homomorphism to its restriction. If $\mathcal{I}:\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}\;\to\mathsf{Grp}$ is the inclusion functor, then $\rho:\mathcal{I}\mathcal{Z}\Rightarrow\mathcal{I}$ is a natural transformation. $\square$

1.3. Applications to computation

Part of the motivation for our work comes from computational challenges that arise in contemporary isomorphism tests in algebra. One of these is to develop new ways to discover characteristic subgroups. Standard constructions—such as the commutator subgroup, the center, and the Fitting subgroup—can be applied to any group. However, these subgroups often contribute little to resolving isomorphism. Many ideas have been introduced to search for new structures; see, for example, \citelist[BOW][ELGO2002][Maglione2021]. Often these involve very detailed computations with individual groups, and their application is ad hoc. Indeed, a primary motivation for this study is to systematize the disparate techniques currently used to search for characteristic subgroups.

Theorem 2 provides the framework for a systematic search for characteristic subgroups. Indeed, an $(\mathsf{A},\mathsf{B})$ -morphism generalizes the familiar and much studied category theory notion of adjoint functor pairs. We show in Section 4.6 that category actions offer a flexible way to implement the behavior of natural transformations in a computer algebra system. To exploit the full power of the categorical interpretation of characteristic subgroups, we work in a suitably general algebraic framework that allows a seamless transfer of information from one category to another. The familiar examples from Sections 7 and 8 demonstrate how to identify characteristic structure in a category and transfer it back to groups.

A second challenge concerns reproducibility and comparison of characteristic subgroups. Algorithms to decide isomorphism often, as a first step, generate a list of characteristic subgroups in a given group. For example, we could extract such a list for the family described in Example 1.3. An immediate question is: if we rerun this step for a different group, do we obtain the same list of corresponding characteristic subgroups (Fact 1.2)? It is not always clear that we do. For instance, some characteristic subgroup constructions employ randomization or make labelling choices that could change from one run to the next. Such shortcomings can compromise the utility of characteristic subgroup lists in deciding isomorphism.

Our proposed solution is to develop algorithms that return the natural transformation (or a morphism of biactions) from Theorem 2 instead of the characteristic subgroup itself. This will allow us, in principle, to extend the reach of a specific characteristic subgroup of a given group to an entire category, in much the same way that the commutator subgroup and center behave. The natural transformation can then be applied to a group $\tilde{G}$ to produce a characteristic subgroup $\tilde{H}$ that corresponds to $H$ in the sense of Fact 1.2: every isomorphism $G\to\tilde{G}$ necessarily maps $H$ to $\tilde{H}$ , so allowing a meaningful comparison of characteristic subgroups. The precise circumstances under which such extensions are possible are specified in Theorem 5.4.

A third challenge is verifiability: in a computer algebra system, subgroups are often given by monomorphisms which are defined on a given set of group generators. The construction of such a monomorphism usually invokes computations that prove the claimed properties (such as homomorphism, monic, characteristic image, and so on). We present our work in a framework that combines these computations, data, and proofs, by employing an intuitionistic Martin-Löf type theory; such a model also allows machine verification of proofs. In this setting, if a computer algebra system returns a counital $\iota$ , then this counital comes with a “type” that certifies that each morphism $\iota_{G}$ of $\iota$ yields a characteristic substructure.

1.4. Structure of this paper

In Section 2, we discuss the required background for our foundations (type theory). In Section 3, we introduce eastern algebras (essentially algebraic structures) and show how they can be viewed as abstract categories.

Section 4 studies category actions. In particular, we define capsules (category modules) and describe a computational model for natural transformations as category bimorphisms (Proposition 4.10). This also allows us to describe counitals (Theorem 4.11) and adjoint functor pairs (Theorem 4.13) in the language of bicapsules and bimorphisms.

In Section 5, we explain how characteristic structures can be described by counitals. The functors involved in this construction are defined on categories with one object, but Theorem 5.4—which we call the Extension Theorem—allows us to extend these functors to larger categories. This theorem is the essential ingredient for proving our main results. We also generalize Theorem 1 to eastern algebras (Theorem 1-cat).

In Section 6, we generalize Theorem 2 to eastern algebras (Theorem 2-cat). We show that characteristic substructures can be described as certain counits, and as bimorphism actions on capsules. We also prove the dual version of this result for characteristic quotients (Theorem 2-dual).

In Section 7, we use our framework to provide categorical descriptions of common characteristic subgroups, including verbal and marginal subgroups.

In Section 8, we describe a cross-category translation of counitals and explain, in categorical terms, how a counital for a category of groups can be constructed from a counital for a category of algebras.

Table 1 summarizes notation used throughout the paper.

Symbol	Description
$\mathsf{E}$	Eastern variety
$\mathsf{A},\mathsf{B},\mathsf{C},\mathsf{D}$	Abstract categories or categories that act
$\mathsf{X},\mathsf{Y},\mathsf{Z}$	Capsules
$\Delta,\Sigma$	Bicapsules
$\operatorname{id}_{X}$	Identity morphism of type $X$
$\mathbb{1}_{\mathsf{A}}$	Identity morphisms of $\mathsf{A}$
$\mathcal{F},\mathcal{G}$	Morphisms between categories
$\mathcal{I},\mathcal{J},\mathcal{K},\mathcal{L}$	Inclusion functors
$\mathcal{M},\mathcal{N},\mathcal{R},\mathcal{S}$	Capsule morphisms
$A^{X}$	Functions $X\to A$
$A^{n}$	Functions $\{1,\dots,n\}\to A$
$\Omega$	Signature
$\mathrm{East}_{\Omega}$	Type of $\Omega$ -eastern algebras
$\bot$	The void type
$B^{?}$	The type $B\sqcup\{\bot\}$
$f(a)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}b$	If $f(a)$ is defined, then $f(a)=b$
$f\asymp g$	Computable equality of functions
$f\mathbin{\blacktriangleleft},\mathbin{\blacktriangleleft}f$	Source and target of a morphism
$f\lhd,\lhd f$	Guards for a category action
$\mathrel{\mathop{\mathsf{A}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ , $\mathrel{\mathop{\mathsf{A}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\twoheadrightarrow$}\vss}}}$ , $\mathrel{\mathop{\mathsf{A}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\hookrightarrow$}\vss}}}$	The iso-, epi-, and mono-morphisms of $\mathsf{A}$ (resp.)

Table 1. A guide to notation

2. Type theory and certifying characteristic structure

To certify that a subgroup $H$ of a group $G$ , with inclusion $\iota$ , is characteristic, we must verify that

(2.1)

\begin{array}[]{llll}(\forall\varphi\in\operatorname{Aut}(G))&(\forall h\in H)&(\exists k\in H)&\varphi(\iota(h))=\iota(k).\end{array}

At face value, this a posteriori check requires knowledge of $\operatorname{Aut}(G)$ . To provide a certificate of being characteristic, we instead develop a constructive version of our main results using type theory language. Specifically, we use an intuitionistic Martin-Löf type theory (MLTT), a model of computation capable of expressing aspects of proofs that can be machine verified. In an MLTT, (2.1) can be expressed as

\displaystyle\prod_{\varphi:\operatorname{Aut}(G)}\prod_{h:H}\bigsqcup_{k:H}\mathrm{EQ}_{G}\left(\varphi(\iota(h)),\iota(k)\right);

this notation we explain below. An advantage of this approach is that certificate data can be verified by practical type-checkers. An MLTT employs the “propositions as types” paradigm (Curry–Howard Correspondence), where types correspond to propositions and terms are programs that correspond to proofs. The remainder of this section is a concise treatment of type theory from \citelist [Hindley-Seldin]*Chapters 10–13 [HoTT]*Chapter 3.

2.1. Types

Informally, types annotate data by signalling which syntax rules apply to the data. We write $a:A$ and say “ $a$ is a term of type $A$ ” or “ $a$ inhabits $A$ ”. For example, $a:\mathbb{N}$ signals that $a$ can only be used as a natural number. A type $A$ is inhabited if there exists at least one term $a:A$ and uninhabited if no term of type $A$ exists. The void type $\bot$ has no inhabitants by definition. Deciding whether a type is inhabited or not is computationally undecidable [Hindley-Seldin]*pp. 66–67. Therefore in computational settings types are permitted to be neither inhabited nor uninhabited. Type annotations enable us to use symbols according to their logical purpose; for example, $a:A$ is analogous to $a\in A$ , but type theories do not have the axioms of set theory.

Types are introduced from two sources. First, there is a context that defines a priori the types that we need: for example, $\mathbb{N}$ . Next, there are type-builders that construct new types from existing ones. We use both $A\to B$ and $B^{A}$ to denote the type of functions, and set $\operatorname{Dom}(A\to B)=A$ and $\operatorname{Codom}(A\to B)=B$ . If $n$ is a natural number, then an inhabitant of type $A^{n}$ can be interpreted as an $n$ -tuple $(a_{1},\ldots,a_{n})$ with each $a_{i}:A$ , or alternatively as a function $\{1,\ldots,n\}\to A$ . There is a unique function $\bot\to A$ (akin to the uniqueness of a function $\varnothing\to A$ ), so $A^{0}$ is a type with a single inhabitant—it is not void.

The notation $\prod_{i:I}A_{i}$ together with projection maps $\pi_{i}:\left(\prod_{i:I}A_{i}\right)\to A_{i}$ is used for Cartesian products, and $\bigsqcup_{i:I}A_{i}$ together with inclusion maps $\iota_{i}:A_{i}\to\bigsqcup_{i:I}A_{i}$ is used for disjoint unions. (The tradition in type theory is to use $\sum_{i:I}A_{i}$ instead of $\bigsqcup_{i:I}A_{i}$ , but this conflicts with algebraic uses of $\Sigma$ .)

2.2. Propositions as types

In set theory, propositions are part of the existing foundations. In type theory, propositions co-evolve with the theory as special types. A proposition $P$ in logic is associated to a type $\hat{P}:\mathrm{Type}$ . (Only in this section do we distinguish propositions $P$ in logic from propositions as types with the notation $\hat{P}$ .) If the type $\hat{P}$ is inhabited by data $p:\hat{P}$ , then the term $p$ is regarded as a proof that $P$ is true. For example, an implication $P\Rightarrow Q$ (here $\Rightarrow$ means “implies”) can be proved by means of a function $f:\hat{P}\to\hat{Q}$ , where $\hat{P}$ and $\hat{Q}$ are the respective types associated with $P$ and $Q$ , because it suffices to assume $P$ and derive a proof of $Q$ . Likewise, if we assume that there is a term $p:\hat{P}$ and apply the function $f$ , then it produces a term $f(p):\hat{Q}$ .

In classical logic, it is only the existence of a proof for a proposition that is relevant. Analogously, in type theory, $\hat{P}:\mathrm{Type}$ is a mere proposition, written $\hat{P}:\mathrm{Prop}$ , if it has at most one inhabitant.

Consider the function $\hat{P}:A\to\mathrm{Prop}$ . Now $(\forall a\in A)(P(a))$ is expressed by terms of type $\left(\prod_{a:A}\hat{P}_{a}\right):\mathrm{Prop}$ ; and $(\exists a\in A)(P(a))$ is expressed by terms of type $\bigsqcup_{a:A}P(a)$ (technically, the truncation of that type [HoTT]*§3.7). The negation of a proposition $P$ is $P\Rightarrow\textsc{False}$ , which accords with functions of type $\hat{P}\to\bot$ . For additional details, see [Hindley-Seldin]*Chapters 12–13 or [HoTT]*Chapter 3.

Martin-Löf developed a notion of equality that imitates the Leibniz Law [Feldman]:

(a=b)\iff\left[(\forall P(x))\;P(a)\Longleftrightarrow P(b)\right],

where $P(x)$ runs over all predicates of a single variable $x$ . Thus, for every type $A$ and terms $s,t:A$ , we define an auxiliary type $\text{EQ}_{A}(s,t)$ (where terms are proofs that $s=t$ ) with the rule that, given a function $f:A\to B$ , there is a function

(2.2)

\displaystyle\text{path}(f):\text{EQ}_{A}(s,t)\to\text{EQ}_{B}(f(s),f(t)).

2.3. Subtypes and inclusion functions

Sets are a special case of types: we write $S:\mathrm{Set}$ for a type $S$ if the type $\mathrm{EQ}_{S}(s,t)$ is a mere proposition for all $s,t:S$ . Let $A$ be a type. If $P:A\to\mathrm{Prop}$ , then

\{a:A\,|\,P(a)\}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{a:A}P(a),

is the subtype of $A$ defined by $P$ . We also write this as $B=\{a:A\,|\,P(a)\}\subset A$ . Terms of type $B$ have the form $\langle a,p\rangle$ for $a:A$ and $p:\mathrm{Prop}$ , where $p$ is a proof that $P(a)$ is inhabited. We sometimes use set theory notation to improve readability when describing a subtype. For more details, see [HoTT]*§3.5. For a typed function $f:A\to B$ , the image $\{f(a)\mid a:A\}$ is shorthand for $\{b:B\mid(\exists a:A)(f(a)=b)\}$ .

Subtypes have an associated inclusion function $\alpha:B\to A$ where $\alpha(\langle a,p\rangle)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}a$ . A subtlety is that if $C\subset B$ with inclusion map $\beta:C\to B$ , then the composition $\alpha\beta:C\to A$ is injective but does not show directly that $C\subset A$ . A term of type $C=\bigsqcup_{b:B}Q(b)$ , with $Q:B\to\mathrm{Prop}$ , has the form $\langle\langle a,p\rangle,q\rangle$ , which differs from those of type $B$ . A small modification addresses the fact that the relation $\subset$ is not strictly transitive. Define a subtype $C^{\prime}=\bigsqcup_{a:A}R(a)$ , where $R(a)=\bigsqcup_{p:P(a)}Q(a)$ , and inclusion $\gamma:C^{\prime}\to A$ . Now construct a map $\sigma:C\to C^{\prime}$ given by

\displaystyle\langle\langle a,p\rangle,q\rangle\mapsto\langle a,\langle p,q\rangle\rangle,

where $a:A$ and $\langle p,q\rangle:R(a)$ . Thus, $\alpha\beta=\gamma\sigma$ , and the composition $\alpha\beta$ is equivalent to $\gamma$ . Hence, $\subset$ is transitive up to this equivalence.

2.4. Partial-functions

For a type $B$ , we define

\displaystyle B^{?}

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}B\sqcup\{\bot\}.

A partial-function is a function is a term, $f$ , of type $A\to B^{?}$ . It is defined at $a:A$ if there is $b:B$ with $f(a)=\iota_{B}(b)$ , where $\iota_{B}:B\hookrightarrow B^{?}$ is the inclusion.

Given partial-functions $f,g:A\to B^{?}$ , the notion of equality as “ $f(a)=g(a)$ ” for every $a:A$ is too strict. We impose that condition only for those $a:A$ for which both $f(a)$ and $g(a)$ are defined. This motivates a notion of “directional equality”, where having one side defined implies that the other is also defined; only now do we decide whether the results are equal. Freyd and Scedrov [FS]*1.12 introduced the following venturi-tube $\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}$ relation on partial-functions.

Definition 2.1.

Given $f:A\to B^{?}$ , $a:A$ and $b:B$ , we write

\displaystyle f(a)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}b\text{ if }f\text{ is defined at }a:A\text{ and }f(a)=\iota_{B}(b).

For $f,g:A\to B^{?}$ we write $f\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}g$ if $f(a)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}g(a)$ for all $a:A$ , and we write $f\asymp g$ if $f\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}g$ and $g\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}f$ .

Note that $\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}$ is a pre-order (reflexive and transitive). If we compare $\asymp$ with (extensional) function equality

f=g\iff\left[(\forall a:A)\;f(a)=g(a)\right],

then $f=g$ implies that $f\asymp g$ . In classical logic (with the law of the excluded middle) the converse also holds because one can, by fiat, declare that $f$ is defined or undefined at $a:A$ . In some computational models such a separation is non-constructive, so computing $f(a)$ may not halt. Thus, we retain the $f\asymp g$ notation.

2.5. Certifying that the trivial group is characteristic

As an illustration, we present a type verifying the characteristic property of the trivial subgroup. Let $G:\mathrm{Group}$ be a group with identity $1:G$ . Let $H=\{x:G\mid\mathrm{EQ}_{G}(x,1)\}$ be the subtype of $G$ representing the trivial subgroup. Recall that terms of $H$ have the form $\langle x,p\rangle$ , where $x:G$ and $p:\mathrm{EQ}_{G}(x,1)$ , and there is a map $\iota:H\to G$ , $\langle x,p\rangle\mapsto x$ . If $h,k:H$ , then $\iota(h)=\iota(k)=1$ , and, by (2.2), for every $\varphi:\operatorname{Aut}(G)$ there is an invertible function of type

(2.3)

\displaystyle\text{EQ}_{G}(\varphi(1),1)\longleftrightarrow\text{EQ}_{G}(\varphi(\iota(h)),\iota(k)).

The latter function depends on $h$ and $k$ , but we suppress this dependency to simplify the exposition. Let $\mathrm{idLaw}(\varphi):\mathrm{EQ}_{G}(\varphi(1),1)$ be a proof that $\varphi:\operatorname{Aut}(G)$ fixes $1:G$ . Using (2.3), we define the term

\mathrm{idMap}(\varphi):\prod_{h:H}\bigsqcup_{k:H}\text{EQ}_{G}(\varphi(\iota(h)),\iota(k))

that takes as input $h:H$ and produces $\langle 1,\mathrm{idLaw}(\varphi)\rangle:\bigsqcup_{k:H}\text{EQ}_{G}(\varphi(\iota(h)),\iota(k))$ . Therefore we obtain the term

\displaystyle\mathrm{idMap}

\displaystyle:\prod_{\varphi:\operatorname{Aut}(G)}\prod_{h:H}\bigsqcup_{k:H}\text{EQ}_{G}(\varphi(\iota(h)),\iota(k)),

which certifies that $H$ is characteristic in $G$ ; compare to (2.1). Recall that in MLTT, types correspond to propositions, and terms are programs that correspond to proofs. Thus, the term $\mathrm{idMap}$ is not an exhaustive tuple listing $\operatorname{Aut}(G)$ , but a program (function) that takes as input $\varphi:\operatorname{Aut}(G)$ and $h:H$ , and produces $k:H$ and $p:\text{EQ}_{G}(\varphi(\iota(h)),\iota(k))$ .

3. Essentially algebraic structures

To interpret characteristic structure as computable categorical information, we treat categories as algebraic structures. (Computational categories should not be confused with categorical semantics of computation.) For our purpose, it suffices to use operations that may only be partially defined, so categories are important examples, as are monoids, groups, groupoids, rings, and non-associative algebras. We give an abridged account and refer to \citelist[Cohn]*§II.2 [AR1994:categories]*Chapter 3 for details.

3.1. Operators, grammars, and signatures

Informally, a grammar is a description of rules for formulas.

Definition 3.1.

An operator is a symbol with a grammar, which we describe using the Backus–Naur Form (BNF) [Pierce:types]*p. 24. The valence of an operator $\omega$ , written $|\omega|$ , is the number of parameters in its grammar. A set $\Omega$ of operators is a signature.

Example 3.2.

A signature for additive formulas specifies three operators:

<Add> ::= (<Add> + <Add>) | 0 | (-<Add>)

The bivalent addition $(+)$ depends on terms to the left and right; zero ( $0$ ) depends on nothing; and univalent negation ( $-$ ) is followed by a term. $\square$

It is easy to reject $+-+\,2\,3\,7$ since it is not meaningful. However, we might write $2+3-7$ intending $(2+3)+(-7)$ ; the BNF grammar <Add> accepts only the latter.

The purpose of the signature is to formulate important algebraic concepts such as homomorphisms. To declare that a function $f:A\to B$ is a homomorphism between additive groups, we use the signature of Example 3.2 as follows:

\displaystyle f((x+y))

\displaystyle=(f(x)+f(y)),

\displaystyle f(0)

\displaystyle=0,

\displaystyle f((-x))

\displaystyle=(-f(x)).

3.2. Algebraic structures

An algebra is a single type with a signature [Cohn]*§II.2.

Definition 3.3.

An algebraic structure with signature $\Omega$ is a type $A$ and a function $\omega\mapsto\omega_{A}$ , where $\omega:\Omega$ and $\omega_{A}:A^{|\omega|}\to A$ . A homomorphism of algebraic structures $A$ and $B$ , each having signature $\Omega$ , is a function $f:A\to B$ such that, for every $\omega:\Omega$ and $a_{1},\ldots,a_{|\omega|}:A$ ,

\displaystyle f(\omega_{A}(a_{1},\ldots,a_{|\omega|}))

\displaystyle=\omega_{B}(f(a_{1}),\ldots,f(a_{|\omega|})).

As in Section 2.2, we extend these propositions to types as follows:

	$\displaystyle\mathrm{Alge}_{\Omega}$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{A:\mathrm{Type}}~\prod_{\omega:\Omega}(A^{\|\omega\|}\to A)$
	$\displaystyle\mathrm{Hom}_{\Omega}(A,B)$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\!\bigsqcup_{f:A\to B}~\prod_{\omega:\Omega}~\prod_{a:A^{\|\omega\|}}\!\mathrm{EQ}_{B}\left(f(\omega_{A}(a_{1},\ldots,a_{\|\omega\|})),\omega_{B}(f(a_{1}),\ldots,f(a_{\|\omega\|}))\right).$

Terms of type $\mathrm{Alge}_{\Omega}$ are $\Omega$ -algebras.

For example, consider the additive group signature from Example 3.2. The underlying structure of an additive group can be described by a type (set) $A$ together with assignments of the operators in Add such as (<Add> + <Add>) to $+_{A}:A\times A\to A$ .

3.3. Free algebras and formulas

We now extend signatures to include variables that allow us to work with formulas.

Definition 3.4.

Let $\Omega$ be a signature and let $X$ be a type whose terms are variables. The free $\Omega$ -algebra in variables $X$ , denoted by $\Omega\langle X\rangle$ , is the type of every formula in $X$ constructed using the operators in $\Omega$ .

Example 3.5.

To describe formulas in variables $x,y$ and $z$ , we extend the additive signature $\Omega=\texttt{Add}$ of Example 3.2 as follows:

\begin{split}\texttt{<Add<X>>}\texttt{ ::= (<Add<X>> + <Add<X>>) | 0 | (-<Add<X>>) | x | y | z}.\end{split}

Here, $x+y$ and $(-x)+(0+z)$ have type $\texttt{Add}\langle X\rangle$ , but $x-$ and $x+7$ do not. The operations on the formulas $\Phi_{1}(X),\Phi_{2}(X):\texttt{Add}\langle X\rangle$ are:

	$\displaystyle\Phi_{1}(X)+_{\texttt{Add}\langle X\rangle}\Phi_{2}(X)$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}(\Phi_{1}(X)+\Phi_{2}(X))$
	$\displaystyle 0_{\texttt{Add}\langle X\rangle}$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}0$
	$\displaystyle-_{\texttt{Add}\langle X\rangle}\Phi_{1}(X)$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}(-\Phi_{1}(X)).$

Thus, $\texttt{Add}\langle X\rangle$ is the free additive algebra, but it lacks laws such as $x+y=y+x$ and $x+(-x)=0$ . We explain how to impose these laws in Section 3.4. $\square$

Fact 3.6.

Let $A$ be an $\Omega$ -algebra and $a:A^{X}$ , where $X$ is a type whose terms are variables. There is a unique homomorphism $\mathrm{eval}_{a}:\Omega\langle X\rangle\to A$ that satisfies $\mathrm{eval}_{a}(x)=a_{x}$ .

Consequently, we write $\Phi(a)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}{\rm eval}_{a}(\Phi)$ for formulas $\Phi:\Omega\langle X\rangle$ and $a:A^{X}$ .

Remark 3.7.

The construction in Fact 3.6 is categorical in nature, and we use it in Section 7 to construct characteristic subgroups. The category of $\Omega$ -algebras has objects of type $\mathrm{Alge}_{\Omega}$ together with homomorphisms. The pair of functors (given only by their object maps)

X\mapsto\Omega\langle X\rangle\quad\text{ and }\quad\langle A:\mathrm{Type},\ (\omega:\Omega)\mapsto(\omega_{A}:A^{|\omega|}\to A)\rangle\mapsto A

forms an adjoint functor pair between the categories of types and $\Omega$ -algebras; see Section 4.5 for related discussion.

3.4. Laws and varieties

Let ${A}$ be an $\Omega$ -algebra and let $X$ be a type for variables. We now describe the variety of algebraic structures whose operators satisfy a list of laws such as the axioms of a group. A law is a term of type $\Omega\langle X\rangle^{2}$ . We index laws by a type $L$ , so they are terms of type $L\to\Omega\langle X\rangle^{2}$ and are written $\ell\mapsto(\Lambda_{1,\ell},\Lambda_{2,\ell})$ . We say that ${A}$ is in the variety for the laws $L\to\Omega\langle X\rangle^{2}$ if

\displaystyle\begin{array}[]{lll}(\forall a:{A}^{X})&(\forall\ell:{L})&\Lambda_{1,\ell}(a)=\Lambda_{2,\ell}(a).\end{array}

Example 3.8.

The signature $\Omega$ for groups is the following:

\displaystyle\texttt{<G> ::= (<G><G>) | 1 | (<G>)${}^{-1}$}.

The variety of groups uses three laws, indexed by $L=\{{\tt asc},{\tt id},{\tt inv}\}$ with variables $X=\{x,y,z\}$ . If $\ell=\texttt{asc}$ , then $(\Lambda_{1,\ell},\Lambda_{2,\ell}):\Omega\langle X\rangle^{2}$ is

\Lambda_{1,\ell}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}x(yz)\quad\text{and}\quad\Lambda_{2,\ell}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}(xy)z,

so $\Lambda_{1,\ell}(g,h,k)=g(hk)$ and $\Lambda_{2,\ell}(g,h,k)=(gh)k$ . Hence, associativity is imposed on the $\Omega$ -algebra $G$ by requiring a term (“proof”) of type

\prod_{g:G}\prod_{h:G}\prod_{k:G}\text{EQ}_{G}(g(hk),(gh)k).

Encoding $1x=x$ and $x^{-1}x=1$ as additional laws gives a complete description of the variety of groups. Laws need not be algebraically independent: for example, $x1=x$ and $xx^{-1}=1$ are often also encoded. $\square$

For clarity, henceforth we write laws as propositions. For example, we write $g(hk)=(gh)k$ rather than terms of a mere proposition type.

3.5. Eastern algebras

We cannot always compose a pair of morphisms in a category: composition may be a partial-function. Hence, the morphisms need not form an algebraic structure under composition. We address this limitation by identifying precisely when the operators yield partial-functions.

Example 3.9.

The type of every function is given as

\mathrm{Fun}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{A:\mathrm{Type}}~\bigsqcup_{B:\mathrm{Type}}(A\to B).

Technically, to quantify over all types, we shift to a larger universe $\text{Type}_{1}$ ; see Remark 3.21. For $f:A\to B$ , define

\displaystyle f\mathbin{\blacktriangleleft}

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{id}_{A},

\displaystyle\mathbin{\blacktriangleleft}f

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{id}_{B},

\displaystyle(fg)(x)

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\begin{cases}f(g(x))&f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g,\\ \bot&\text{otherwise}.\end{cases}

The condition $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g$ guards against composing non-composable functions. (A helpful mnemonic for $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g$ is “What enters $f$ must match what exits $g$ ”.) This yields the composition signature:

\texttt{<Comp> ::= (<Comp><Comp>) | }(\mathbin{\blacktriangleleft}\texttt{<Comp>})\texttt{ | }(\texttt{<Comp>}\mathbin{\blacktriangleleft})

Note that $\mathbin{\blacktriangleleft}(f\mathbin{\blacktriangleleft})=\mathbin{\blacktriangleleft}\operatorname{id}_{A}=\operatorname{id}_{A}=f\mathbin{\blacktriangleleft}$ , and similarly $(\mathbin{\blacktriangleleft}f)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}f$ . $\square$

The composition signature defined in Example 3.9 is used throughout. Motivated by it, we make the following general definition.

Definition 3.10.

For a signature $\Omega$ , operator $\omega:\Omega$ , variables $X=\{x_{1},\dots,x_{|\omega|}\}$ , type $A$ , and formulas $\Phi_{1},\Phi_{2}:\Omega\langle X\rangle$ , the partial-function $\omega_{A}:A^{|\omega|}\to A^{?}$ is $(\Phi_{1},\Phi_{2})$ -guarded if

(3.1)

\left[(\forall a:A^{|\omega|})\;\;\Phi_{1}(a)=\Phi_{2}(a)\right]\iff\omega_{A}(a)\text{ is defined at $a$}.

The formulas $\Phi_{1},\Phi_{2}$ are the rails of $\omega$ . If $\Phi_{1}=\Phi_{2}$ , then the rails are trivial, so $\omega_{A}$ is everywhere defined and is total.

We define a type $\mathrm{Guard}(A,\omega,(\Phi_{1},\Phi_{2}))$ whose terms are pairs $\langle\omega_{A},p\rangle$ , where $p$ is a proof of (3.1). Fix a tuple of variables $X:\prod_{n:\mathbb{N}}\{x_{1},\dots,x_{n}\}$ . Define the type $\mathrm{Rails}(\Omega)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\prod_{\omega:\Omega}\Omega\langle X_{|\omega|}\rangle^{2}$ whose terms are the rails for the operators in $\Omega$ . Observe that the rails are everywhere defined.

We now define essentially algebraic structures, which we call eastern algebras; see [AR1994:categories]*§3.D.

Definition 3.11.

For a signature $\Omega$ , an $\Omega$ -eastern algebra is a type $A$ and an assignment $\omega\mapsto\langle\omega_{A},p\rangle$ of operators $\omega:\Omega$ to $\Phi_{\omega}$ -guarded partial-functions. Formally, $\Omega$ -eastern algebras are terms of the type

\displaystyle\mathrm{East}_{\Omega}

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{A:\mathrm{Type}}~\bigsqcup_{\Phi:\mathrm{Rails}(\Omega)}~\prod_{\omega:\Omega}\mathrm{Guard}(A,\omega,\Phi_{\omega}).

Every algebraic structure defines an eastern algebra by using trivial rails for each operator. In the next example, we observe that categories are eastern algebras. Recall that a category $\mathsf{C}$ has objects $U,V,\ldots$ of type $\mathsf{C}_{0}$ , morphisms $f$ of type $\mathsf{C}_{1}(U,V)$ , and a composition operation $\circ:\mathsf{C}_{1}(V,W)\times\mathsf{C}_{1}(U,V)\to\mathsf{C}_{1}(U,W)$ .

Example 3.12 (Categories as eastern algebras).

Let $\mathsf{C}$ be a category with object type $\mathsf{C}_{0}$ . Form the type of all morphisms of $\mathsf{C}$ :

(3.2)

\displaystyle\mathsf{C}_{1}

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{U:\mathsf{C}_{0}}\bigsqcup_{V:\mathsf{C}_{0}}\mathsf{C}_{1}(U,V).

For objects $U,V:\mathsf{C}_{0}$ , there is an inclusion map (see Section 2.1)

\displaystyle\iota_{UV}

\displaystyle:\mathsf{C}_{1}(U,V)\hookrightarrow\mathsf{C}_{1}.

Thus, for each $\varphi:\mathsf{C}_{1}$ , there exist unique $U,V:\mathsf{C}_{0}$ and $f:\mathsf{C}_{1}(U,V)$ such that $\varphi=\iota_{UV}(f)$ . The type $\mathsf{C}_{1}$ is an eastern algebra with the composition signature from Example 3.9, which is realized as follows. For $\varphi,\tau:\mathsf{C}_{1}$ , with $\varphi:U\to V$ and $\tau:U^{\prime}\to V^{\prime}$ ,

\displaystyle\varphi\mathbin{\blacktriangleleft}

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{id}_{U},

\displaystyle\mathbin{\blacktriangleleft}\varphi

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{id}_{V},

\displaystyle\tau\varphi

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\begin{cases}\tau\varphi&\tau\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}\varphi\quad(\textrm{i.e.}~U^{\prime}=V),\\ \bot&\text{otherwise}.\end{cases}

As before, $\varphi\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}\tau$ guards against composing incompatible morphisms. $\square$

3.6. Abstract categories

We consider categories as described in [FS]*1.11; their type differs from those of Example 3.12.

Definition 3.13.

Let $\Omega$ be the composition signature of Example 3.9. An abstract category is an $\Omega$ -eastern algebra satisfying the following laws in variables $f,g,h$ :

$\displaystyle\mathbin{\blacktriangleleft}(f\mathbin{\blacktriangleleft})$	$\displaystyle=f\mathbin{\blacktriangleleft}$	$\displaystyle(\mathbin{\blacktriangleleft}f)\mathbin{\blacktriangleleft}$	$\displaystyle=\mathbin{\blacktriangleleft}f$
$\displaystyle(\mathbin{\blacktriangleleft}f)f$	$\displaystyle=f$	$\displaystyle f(f\mathbin{\blacktriangleleft})$	$\displaystyle=f$
$\displaystyle\mathbin{\blacktriangleleft}(fg)$	$\displaystyle\asymp\mathbin{\blacktriangleleft}(f(\mathbin{\blacktriangleleft}g))$	$\displaystyle(fg)\mathbin{\blacktriangleleft}$	$\displaystyle\asymp((f\mathbin{\blacktriangleleft})g)\mathbin{\blacktriangleleft}$
$\displaystyle f(gh)$	$\displaystyle\asymp(fg)h.$

We sometimes refer to the operators $(-)\mathbin{\blacktriangleleft}$ and $\mathbin{\blacktriangleleft}(-)$ as guards.

A useful subtype of an abstract category $\mathsf{A}$ is the type of identities:

\mathbb{1}_{\mathsf{A}}=\{a\mathbin{\blacktriangleleft}\mid a:\mathsf{A}\}=\{\mathbin{\blacktriangleleft}a\mid a:\mathsf{A}\}.

Lemma 3.14.

The following hold in every abstract category.

(a)

The guards are idempotent, namely

\displaystyle((-)\mathbin{\blacktriangleleft})\mathbin{\blacktriangleleft}

\displaystyle=(-)\mathbin{\blacktriangleleft},

\displaystyle\mathbin{\blacktriangleleft}(\mathbin{\blacktriangleleft}(-))

\displaystyle=\mathbin{\blacktriangleleft}(-).

(b)

Terms $f$ and $g$ satisfy

\displaystyle\mathbin{\blacktriangleleft}(fg)

\displaystyle\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\mathbin{\blacktriangleleft}f,

\displaystyle(fg)\mathbin{\blacktriangleleft}\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}g\mathbin{\blacktriangleleft}.

Proof.

For a term $f$ in an abstract category,

\mathbin{\blacktriangleleft}(\mathbin{\blacktriangleleft}f)=\mathbin{\blacktriangleleft}((\mathbin{\blacktriangleleft}f)\mathbin{\blacktriangleleft})=(\mathbin{\blacktriangleleft}f)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}f.

A similar argument shows $(f\mathbin{\blacktriangleleft})\mathbin{\blacktriangleleft}=f\mathbin{\blacktriangleleft}$ , so (a) holds.

For (b), suppose $g$ is another term and $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g$ . Now $\mathbin{\blacktriangleleft}(fg)\asymp\mathbin{\blacktriangleleft}(f(\mathbin{\blacktriangleleft}g))$ is an equality: $\mathbin{\blacktriangleleft}(fg)=\mathbin{\blacktriangleleft}(f(\mathbin{\blacktriangleleft}g))$ . Since $f(f\mathbin{\blacktriangleleft})=f$ ,

\displaystyle\mathbin{\blacktriangleleft}(fg)=\mathbin{\blacktriangleleft}(f(\mathbin{\blacktriangleleft}g))=\mathbin{\blacktriangleleft}(f(f\mathbin{\blacktriangleleft}))=\mathbin{\blacktriangleleft}f.

Hence, $\mathbin{\blacktriangleleft}(fg)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\mathbin{\blacktriangleleft}f$ , and the other formula follows similarly. ∎

Proposition 3.15.

Let $\mathsf{C}$ be a category. The type $\mathsf{C}_{1}$ from (3.2) of all morphisms of $\mathsf{C}$ with the composition signature from Example 3.9 forms an abstract category.

Proof.

If $f:U\to V$ in $\mathsf{C}$ , then $\mathbin{\blacktriangleleft}(f\mathbin{\blacktriangleleft})=\operatorname{id}_{\text{Codom}\operatorname{id}_{U}}=\operatorname{id}_{U}=f\mathbin{\blacktriangleleft}.$ Similarly, $(\mathbin{\blacktriangleleft}f)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}f$ . Since the operators $(-)\mathbin{\blacktriangleleft}$ and $\mathbin{\blacktriangleleft}(-)$ have trivial rails, both of the equations $\mathbin{\blacktriangleleft}(f\mathbin{\blacktriangleleft})=f\mathbin{\blacktriangleleft}$ and $(\mathbin{\blacktriangleleft}f)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}f$ are everywhere defined.

Observe that $(\mathbin{\blacktriangleleft}f)f$ is defined and equals $\operatorname{id}_{V}f=f$ ; also $f(f\mathbin{\blacktriangleleft})$ is defined and equals $f\operatorname{id}_{U}=f$ . For $g:\mathsf{C}_{1}(U^{\prime},V^{\prime})$ , the expression $\mathbin{\blacktriangleleft}(fg)$ is defined whenever $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g$ , and $f(\mathbin{\blacktriangleleft}g)$ is defined whenever $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}(\mathbin{\blacktriangleleft}g)$ . Since $\mathbin{\blacktriangleleft}(-)$ is idempotent by Lemma 3.14 (a), both $\mathbin{\blacktriangleleft}(fg)$ and $f(\mathbin{\blacktriangleleft}g)$ are defined when $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g$ . Thus, $f\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}g$ implies

\mathbin{\blacktriangleleft}(fg)=\operatorname{id}_{V}=\mathbin{\blacktriangleleft}(f(f\mathbin{\blacktriangleleft}))=\mathbin{\blacktriangleleft}(f(\mathbin{\blacktriangleleft}g)),

so $\mathbin{\blacktriangleleft}(fg)\asymp\mathbin{\blacktriangleleft}(f(\mathbin{\blacktriangleleft}g))$ . A similar argument holds for $(fg)\mathbin{\blacktriangleleft}\asymp((f\mathbin{\blacktriangleleft})g)\mathbin{\blacktriangleleft}$ .

Lastly, composition is associative everywhere it is defined, so $f(gh)\asymp(fg)h$ . ∎

Example 3.16.

Let $\mathsf{A}$ be an abstract category with $\mathbb{1}_{\mathsf{A}}=\{e_{1},\ldots,e_{6}\}$ and additional morphisms $a_{12},a_{23},a_{13},\acute{a}_{13},b_{45},b_{54}$ , where $x_{ij}\mathbin{\blacktriangleleft}=e_{j}$ and $\mathbin{\blacktriangleleft}x_{ij}=e_{i}$ . Using the signature of Example 3.9, $\mathsf{A}$ is an eastern algebra with multiplication defined in Table 2 where every instance of $\bot$ is omitted. It is not easy to discern structure from this table, so two additional visualizations of $\mathsf{A}$ are given in Figure 1. The first is the Cayley graph of the multiplication with undefined products omitted. The second is the Peirce decomposition, which we now discuss. $\square$

\displaystyle\begin{array}[]{|c||ccccc|c|cccc|cc|}\hline\cr x&e_{1}&e_{2}&e_{3}&e_{4}&e_{5}&e_{6}&a_{12}&a_{23}&a_{13}&\acute{a}_{13}&b_{45}&b_{54}\\ \hline\cr\hline\cr x\mathbin{\blacktriangleleft}&e_{1}&e_{2}&e_{3}&e_{4}&e_{5}&e_{6}&e_{2}&e_{3}&e_{3}&e_{3}&e_{5}&e_{4}\\ \hline\cr\mathbin{\blacktriangleleft}x&e_{1}&e_{2}&e_{3}&e_{4}&e_{5}&e_{6}&e_{1}&e_{2}&e_{1}&e_{1}&e_{4}&e_{5}\\ \hline\cr\lx@intercol\hfil\hfil\lx@intercol\\ \hline\cr\cdot&e_{1}&e_{2}&e_{3}&e_{4}&e_{5}&e_{6}&a_{12}&a_{23}&a_{13}&\acute{a}_{13}&b_{45}&b_{54}\\ \hline\cr\hline\cr e_{1}&e_{1}&&&&&&a_{12}&&a_{13}&\acute{a}_{13}&&\\ e_{2}&&e_{2}&&&&&&a_{23}&&&&\\ e_{3}&&&e_{3}&&&&&&&&&\\ e_{4}&&&&e_{4}&&&&&&&b_{45}&\\ e_{5}&&&&&e_{5}&&&&&&&b_{54}\\ \hline\cr e_{6}&&&&&&e_{6}&&&&&&\\ \hline\cr a_{12}&&a_{12}&&&&&&a_{13}&&&&\\ a_{23}&&&a_{23}&&&&&&&&&\\ a_{13}&&&a_{13}&&&&&&&&&\\ \acute{a}_{13}&&&\acute{a}_{13}&&&&&&&&&\\ \hline\cr b_{45}&&&&&b_{45}&&&&&&&e_{4}\\ b_{54}&&&&b_{54}&&&&&&&e_{5}&\\ \hline\cr\end{array}

Table 2. The multiplication table for

\mathsf{A}

(a) Cayley graph

(b) Peirce decomposition

Figure 1. Visualizing the abstract category

\mathsf{A}

in Example 3.16

3.7. Peirce decomposition of abstract categories

Treating categories as algebraic structures allows us to frame aspects of category theory in algebraic terms. Our goal is an elementary representation theory of categories. In particular, we seek matrix-like structures—known as Peirce decompositions in ring theory—for abstract categories.

One can recover from an abstract category $\mathsf{A}$ notions of objects and morphisms by considering the identities $\mathbb{1}_{\mathsf{A}}$ . Using the laws in Definition 3.13,

(\forall e:\mathbb{1}_{\mathsf{A}})\;\;(\forall f:\mathbb{1}_{\mathsf{A}})\;\;\;ef=\begin{cases}e&\text{ if }f=e,\\ \bot&\text{ otherwise}.\end{cases}

In algebraic terms, the subtype $\mathbb{1}_{\mathsf{A}}$ is a type of pairwise orthogonal idempotents. For subtypes $X$ and $Y$ of $\mathsf{A}$ , define

XY=\{xy\mid x:X,y:Y,\ x\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}y\}.

Fact 3.17.

If $a:\mathsf{A}$ , then $\mathbb{1}_{\mathsf{A}}\{a\}=\{a\}=\{a\}\mathbb{1}_{\mathsf{A}}$ ; we write simply $\mathbb{1}_{\mathsf{A}}a=a=a\mathbb{1}_{\mathsf{A}}$ .

Given $e,f:\mathbb{1}_{\mathsf{A}}$ , we define three subtypes:

$\displaystyle(\text{left slice})$	$\displaystyle e\mathsf{A}$	$\displaystyle=\{a:\mathsf{A}\mid e=\mathbin{\blacktriangleleft}a\};$
$\displaystyle(\text{right slice})$	$\displaystyle\mathsf{A}f$	$\displaystyle=\{a:\mathsf{A}\mid a\mathbin{\blacktriangleleft}=f\};$
$\displaystyle(\text{hom-set})$	$\displaystyle e\mathsf{A}f$	$\displaystyle=\{a:\mathsf{A}\mid e=\mathbin{\blacktriangleleft}a,\ a\mathbin{\blacktriangleleft}=f\}.$

These subtypes appear in Figure 2 in the left, middle, and right images, respectively. If $e\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}a$ for $a:\mathsf{A}$ , then $ea=(e\mathbin{\blacktriangleleft})a=(\mathbin{\blacktriangleleft}a)a=a$ .

Figure 2. Visualizing the Peirce decomposition of

\mathsf{A}

If $a:\mathsf{A}$ , then $a:\mathsf{A}(a\mathbin{\blacktriangleleft})$ , and so on, from which we deduce the following.

Proposition 3.18.

If $\mathsf{A}$ is an abstract category, then $a\mapsto(\mathbin{\blacktriangleleft}a)a$ , $a\mapsto a(a\mathbin{\blacktriangleleft})$ , and $a\mapsto(\mathbin{\blacktriangleleft}a)a(a\mathbin{\blacktriangleleft})$ induce invertible functions $($ denoted by “ $\leftrightarrow$ ” $)$ of the following types:

\displaystyle\mathsf{A}

\displaystyle\longleftrightarrow\bigsqcup_{e:\mathbb{1}_{\mathsf{A}}}e\mathsf{A},

\displaystyle\mathsf{A}

\displaystyle\longleftrightarrow\bigsqcup_{f:\mathbb{1}_{\mathsf{A}}}\mathsf{A}f

\displaystyle\mathsf{A}

\displaystyle\longleftrightarrow\bigsqcup_{e:\mathbb{1}_{\mathsf{A}}}\bigsqcup_{f:\mathbb{1}_{\mathsf{A}}}e\mathsf{A}f.

Proposition 3.18, which we use to prove Theorem 5.4, allows us to draw upon intuition from matrix algebras. The morphisms of a category appear in its multiplication table, as in Table 2. Products of morphisms and slices are defined, as with matrix products, only when the inner indices agree. In this model, $\mathbb{1}_{\mathsf{A}}$ can be visualized as the identity matrix, where the entries on the diagonal are the individual identities $e:\mathbb{1}_{\mathsf{A}}$ . In Figure 1(b), that product is represented in a matrix-like form respecting the conditions of the Peirce decomposition.

Remark 3.19.

While there are differences between the types for categories and abstract categories, every theorem stated in one setting translates to a corresponding theorem in the other. More precisely, the translation is a model-theoretic definable interpretation [Marker:models]*§1.4: there is a prescribed formula that translates every theorem and its proof between the two theories. Example 3.16 shows how the model of categories with both objects and morphisms may be interpreted as definable types in the theory of categories with only morphisms (abstract categories). Conversely, if $\mathsf{A}$ is an abstract category, then we obtain a category $\mathsf{C}$ with object type $\mathsf{C}_{0}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathbb{1}_{\mathsf{A}}$ as follows. For objects $e,f:\mathsf{C}_{0}$ , we define

\mathsf{C}_{1}(e,f)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}f\mathsf{A}e,

where the identity morphisms of $\mathsf{C}$ are $e:\mathsf{C}_{1}(e,e)$ . To compose morphisms $fae:\mathsf{C}_{1}(e,f)$ with $gbf:\mathsf{C}_{1}(f,g)$ for objects $e,f,g:\mathsf{C}_{0}$ , we define

(gbf)(fae)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}gbae:\mathsf{C}_{1}(e,g).

Hence, we no longer distinguish between categories and abstract categories.

3.8. Eastern algebras as categories

Example 3.12 shows that a category is an eastern algebra. We now show that a variety of eastern algebras forms a category.

Definition 3.20.

Fix a signature $\Omega$ . Let $E_{1},E_{2}:\mathrm{East}_{\Omega}$ , where $E_{1}=\langle A,\Phi,\omega\mapsto\langle\omega_{A},p\rangle\rangle$ and $E_{2}=\langle B,\Gamma,\omega\mapsto\langle\omega_{B},q\rangle\rangle$ . A morphism from $E_{1}$ to $E_{2}$ is a partial-function $f:A\to B^{?}$ such that for every $\omega:\Omega$ and every $a_{1},\ldots,a_{|\omega|}:A$ ,

\displaystyle f(\omega_{A}(a_{1},\ldots,a_{|\omega|}))\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\omega_{B}(f(a_{1}),\ldots,f(a_{|\omega|})).

The type of morphisms from $E_{1}$ to $E_{2}$ is

\displaystyle\operatorname{Mor}_{\Omega}(E_{1},E_{2})

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{f:A\to B^{?}}~\prod_{\omega:\Omega}~\prod_{a:A^{|\omega|}}\left(f(\omega_{A}(a_{1},\ldots,a_{|\omega|}))\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\omega_{B}(f(a_{1}),\ldots,f(a_{|\omega|}))\right).

The object type $\mathrm{East}_{\Omega}$ and the morphism type $\operatorname{Mor}_{\Omega}$ form the category of $\Omega$ -eastern algebras. In particular, the $\Omega$ -morphisms of $\mathrm{East}_{\Omega}$ , namely the type

\operatorname{Mor}_{\Omega}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{E_{1}:\mathrm{East}_{\Omega}}~\bigsqcup_{E_{2}:\mathrm{East}_{\Omega}}\operatorname{Mor}_{\Omega}(E_{1},E_{2}),

can be viewed as an abstract category (see Proposition 3.15). Therefore, $\operatorname{Mor}_{\Omega}$ forms an eastern algebra with the composition signature.

We call a subcategory $\mathsf{E}$ of eastern algebras an eastern variety (with respect to signature $\Omega$ and laws $\mathcal{L}$ ) if it is full and its objects are those eastern $\Omega$ -algebras satisfying the laws $\mathcal{L}$ . We reserve $\mathsf{E}$ to denote an eastern variety.

Remark 3.21.

Regarding categories as eastern algebras could lead to a paradox of Russell type. The paradox is avoided either by limiting $\Pi$ -types to forbid some quantifications [Tucker] or by creating an increasing tower of universe types and pushing the larger categories into the next universe [HoTT]*§9.9. Both resolutions allow us to define categories and eastern algebras computationally.

Under the correspondence of Remark 3.19, morphisms between abstract categories are precisely functors between categories. This translation serves two of our goals. The first is an elementary representation theory for categories: by regarding categories as “monoids with partial-operators”, we mimic monoid actions. The second is to treat a category as a single data type with operations defined on it. This is considerably easier to implement as a computer program. Indeed, both GAP [GAP4] and Magma [magma] are designed for such algebras. There are benefits to the usual description of categories, but the translation to abstract categories is essential for our approach to computing with and within categories.

Next, we prove a generalization of Noether’s Isomorphism Theorem.

Theorem 3.22.

Let $\varphi:E_{1}\to E_{2}$ be a morphism between eastern algebras. There exist eastern algebras $\mathrm{Coim}(\varphi)$ and $\mathrm{Im}(\varphi)$ , an epimorphism $\mathrm{coim}(\varphi):E_{1}\twoheadrightarrow\mathrm{Coim}(\varphi)$ , a monomorphism $\mathrm{im}(\varphi):\mathrm{Im}(\varphi)\hookrightarrow E_{2}$ , and an isomorphism $\psi:\mathrm{Coim}(\varphi)\to\mathrm{Im}(\varphi)$ such that the following diagram commutes.

Proof.

Let $\Omega$ be a signature, and let $A$ be an $\Omega$ -eastern algebra. If every operation in $A$ is total, then we apply Noether’s Isomorphism Theorem [Cohn]*Theorem II.3.7. It is clear that the existence of the stated algebras and morphisms is constructive.

Otherwise, at least one operation is a partial-function. We define a new eastern algebra where all operations are total. Let $\Xi$ be a formal symbol, disjoint from $\Omega$ . Define a new type $E\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}A\sqcup\{\Xi\}$ with inclusion function $\iota_{A}:A\hookrightarrow E$ . By abuse of notation, we also apply $\iota_{A}$ to tuples over $A$ . Define a new signature $\Sigma$ , obtained from $\Omega$ by including $\Xi$ as a constant. We use trivial rails for every operator, and define $\omega_{E}:E^{|\omega|}\to E$ via

e\mapsto\begin{cases}\iota_{A}(\omega_{A}(a))&\text{if $e=\iota_{A}(a)$ for some $a:A^{|\omega|}$ with $\omega_{A}(a):A$,}\\ \Xi&\text{otherwise}.\end{cases}

Now every operation in $E$ is total, so the Isomorphism Theorem applies. Since every homomorphism of $\Sigma$ -eastern algebras fixes constants, the statement follows. ∎

The monomorphism $\mathrm{im}(\varphi)$ from Theorem 3.22 is the image of $\varphi$ , and the epimorphism $\mathrm{coim}(\varphi)$ is the coimage of $\varphi$ . Theorem 3.22 asserts, in particular, that categories of eastern algebras have images and coimages. These maps possess universal properties [Riehl]*§E.5.

3.9. Subobjects and images

We close with a list of facts about eastern varieties, which we use heavily in Section 5. We first define a pre-order that enables abbreviation of compositions of multiple morphisms. To motivate this, assume $\varphi:E_{1}\to E_{2}$ is a morphism of eastern algebras. Theorem 3.22 states there exists $\theta:E_{1}\to\mathrm{Im}(\varphi)$ such that $\varphi=\mathrm{im}(\varphi)\theta$ . We denote this by $\varphi\ll\mathrm{im}(\varphi)$ and make the following more general definition. For morphisms $a,b:\mathsf{E}$ ,

(3.3)		$\displaystyle a$	$\displaystyle\ll b\iff\left[(\exists c:\mathsf{E})\;\;a=bc\right],$
(3.4)		$\displaystyle a$	$\displaystyle\gg b\iff\left[(\exists d:\mathsf{E})\;\;a=db\right].$

Two monomorphisms $a,b:\mathsf{E}$ are equivalent if $a\ll b$ and $b\ll a$ . Similarly, epimorphisms $c,d:\mathsf{E}$ are equivalent if $c\gg d$ and $d\gg c$ .

Lemma 3.23.

Let $\mathsf{E}$ be an eastern variety. For morphisms $a,b:\mathsf{E}$ , if $a\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}b$ , then $a\,\mathrm{im}(b)\ll\mathrm{im}(ab)$ .

Proof.

By Theorem 3.22, there exist isomorphisms $\psi_{b},\psi_{ab}:\mathsf{E}$ such that

\displaystyle b

\displaystyle=\mathrm{im}(b)\psi_{b}\mathrm{coim}(b),

\displaystyle ab

\displaystyle=\mathrm{im}(ab)\psi_{ab}\mathrm{coim}(ab).

By the universal property of coimages, there exists a unique morphism $\pi:\mathsf{E}$ such that $\mathrm{coim}(ab)=\pi\,\mathrm{coim}(b)$ . Therefore,

\displaystyle a\,\mathrm{im}(b)\psi_{b}\mathrm{coim}(b)=ab=\mathrm{im}(ab)\psi_{ab}\mathrm{coim}(ab)=\mathrm{im}(ab)\psi_{ab}\pi\,\mathrm{coim}(b).

Since $\mathrm{coim}(b)$ is an epimorphism, $a\,\mathrm{im}(b)=\mathrm{im}(ab)\psi_{ab}\pi\psi_{b}^{-1}\ll\mathrm{im}(ab)$ . ∎

Lemma 3.24.

Let $\mathsf{E}$ be an eastern variety. For morphisms $a,b:\mathsf{E}$ , if $a\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}b$ , then $\mathrm{im}(ab)\ll\mathrm{im}(a)$ . If $a$ is also monic, then $\mathrm{im}(ab)\ll a\,\mathrm{im}(b)$ .

Proof.

The first claim follows from the universal property of images, so we assume $a$ is monic. By Theorem 3.22, there exists an isomorphism $\psi_{b}:\mathsf{E}$ such that

\displaystyle b

\displaystyle=\mathrm{im}(b)\psi_{b}\mathrm{coim}(b).

Since $a\,\mathrm{im}(b)$ is monic and $ab=(a\,\mathrm{im}(b))(\psi_{b}\mathrm{coim}(b))$ , by the universal property of images, there exists a morphism $\iota:\mathsf{E}$ such that $\mathrm{im}(ab)=a\,\mathrm{im}(b)\iota\ll a\,\mathrm{im}(b)$ . ∎

Eastern varieties have a coproduct [Riehl]*p. 81 given by the free product [Riehl]*p. 183. An example concerning groups is given in [Riehl]*Corollary 4.5.7. We list some facts concerning coproducts in eastern varieties.

Fact 3.25.

Let $I$ be a type. In an eastern variety $\mathsf{E}$ , the following hold for all $e:\mathbb{1}_{\mathsf{E}}$ and $a:I\to e\mathsf{E}$ .

(a)

There exists a coproduct morphism $\coprod_{i:I}a_{i}$ and morphisms $\iota:I\to\big{(}\coprod_{i:I}a_{i}\big{)}\mathsf{E}$ satisfying $\big{(}\coprod_{i:I}a_{i}\big{)}\iota_{j}=a_{j}$ for each $j:I$ .
(b)

If $I$ is uninhabited, then $f=\left(\coprod_{i:I}a_{i}\right)\mathbin{\blacktriangleleft}$ is the identity on the free algebra on the empty set. In particular, $\coprod_{i:I}a_{i}$ is the unique morphism inhabiting $e\mathsf{E}f$ .
(c)

If $b:\mathsf{E}$ such that $b\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}a_{i}$ for all $i:I$ , then $\coprod_{i:I}(ba_{i})=b\coprod_{i:I}a_{i}$ .
(d)

If $b:I\to\mathsf{E}$ with $a_{i}\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}b_{i}$ for all $i:I$ , then $\coprod_{i:I}(a_{i}b_{i})\ll\coprod_{i:I}a_{i}$ .
(e)

If $J\subset I$ , then $\coprod_{j:J}a_{j}\ll\coprod_{i:I}a_{i}$ .

Finally, if $a$ is monomorphism satisfying $\mathbin{\blacktriangleleft}a=e$ , for some identity $e$ , then $a\mathbin{\blacktriangleleft}$ can be regarded as a subobject of the object associated to $e$ . Given a collection $\{a_{i}\mid i:I\}$ of such monomorphisms, consider the smallest subobject containing all set-wise images of the $a_{i}\mathbin{\blacktriangleleft}$ . The coproduct allows us to effectively “glue” together all of the monomorphisms, but the result is not a monomorphism. To obtain a monomorphism, we take the image of the coproduct, namely

(3.5)

\displaystyle\text{im}\left(\coprod_{i:I}a_{i}\right).

4. Category actions, capsules, and counits

Theorem 2 asserts that characteristic subgroups arise from categories acting on other categories.

4.1. Category actions

Our formulation of category actions generalizes the familiar notion for groups and also actions of monoids and groupoids [MonoidsAC]*§I.4. The technical aspects of the definition concern the additional guards, denoted $\lhd$ , needed to express where products are defined. Their use is similar to the guards $\blacktriangleleft$ used for abstract categories (see Definition 3.13).

Definition 4.1.

Let $\mathsf{A}$ be an abstract category with guards denoted by $(-)\mathbin{\blacktriangleleft}$ and $\mathbin{\blacktriangleleft}(-)$ . Let $X$ be a type. A $($ left $)$ category action of $\mathsf{A}$ on $X$ consists of a type $\lhd X$ , functions $(-)\lhd:\mathsf{A}\to\lhd X$ and $\lhd(-):X\to\lhd X$ , and a partial-function $\cdot:\mathsf{A}\times X\to X^{?}$ that satisfies the following rules:
(1) ( $\forall a:\mathsf{A}$ ) ( $\forall x:X$ ) $\left[(a\lhd=\lhd x)\iff((\exists y:X)\;a\cdot x=y)\right]$ ; (2) ( $\forall a:\mathsf{A})$ ( $\forall x:X$ ) $\left[(a\mathbin{\blacktriangleleft})\lhd=a\lhd\text{ and }((a\mathbin{\blacktriangleleft})\cdot x)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}x\right]$ ; and (3) ( $\forall a,b:\mathsf{A}$ ) ( $\forall x:X$ ) $((ab)\cdot x)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}(a\cdot(b\cdot x))$ .

Given a left action of $\mathsf{A}$ on a type $Y$ , a partial-function $\mathcal{M}:X\to Y^{?}$ is an $\mathsf{A}$ -morphism if $\mathcal{M}(a\cdot x)=a\cdot\mathcal{M}(x)$ whenever $a:\mathsf{A}$ and $x:X$ with $a\lhd=\lhd x$ .

Right category actions are similarly defined. We unpack the symbolic expressions in Definition 4.1. Condition (1) states that the functions $(-)\lhd$ and $\lhd(-)$ serve as guards for the partial-function $\cdot:\mathsf{A}\times X\to X^{?}$ : namely, (1) characterizes precisely when $\cdot$ is defined. The first part of Condition (2) asserts that $(-)\lhd$ respects the $(-)\mathbin{\blacktriangleleft}$ identity of $\mathsf{A}$ ; the second part states that identity morphisms of $\mathsf{A}$ act as identities. Condition (3) is the familiar group action axiom in the setting of partial-functions.

For subtypes $S\subset\mathsf{A}$ and $Y\subset X$ , we write

\displaystyle S\cdot Y

\displaystyle=\{s\cdot y\mid s:S,\;y:Y,\;s\lhd=\lhd y\}.

From Definition 4.1, an $\mathsf{A}$ -morphism $\mathcal{M}:X\to Y^{?}$ is always defined on $\mathsf{A}\cdot X$ ; hence, we do not need guards for $\mathsf{A}$ -morphisms.

Definition 4.2.

The category action of $\mathsf{A}$ on $X$ is full if $e\cdot x\mapsto\lhd(e\cdot x)$ defines a bijection from $\mathbb{1}_{\mathsf{A}}\cdot X$ to $\mathsf{A}\lhd=\{a\lhd\mid a:\mathsf{A}\}$ .

Note that the category action of $\mathsf{A}$ on $X$ is full if and only if for every $a:\mathsf{A}$ there exists an $x:X$ such that $a\lhd=\lhd x$ .

Since we identify categories and abstract categories (Remark 3.19), we say that a category $\mathsf{C}$ acts on a type $X$ if its morphisms $\mathsf{C}_{1}$ act on $X$ .

Example 4.3.

Let $\mathsf{C}$ be a category with object type $\mathsf{C}_{0}$ and morphism type $\mathsf{C}_{1}$ . Set $X=\lhd X=\mathsf{C}_{0}$ . Define $(-)\lhd:\mathsf{C}_{1}\to\mathsf{C}_{0}$ via $f\lhd\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{Dom}f$ and define $\lhd(-):\mathsf{C}_{0}\to\mathsf{C}_{0}$ via $\lhd\,U\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}U$ . Let $\cdot:\mathsf{C}_{1}\times\mathsf{C}_{0}\to\mathsf{C}_{0}^{?}$ be the partial-function defined by

\displaystyle f\cdot U\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\begin{cases}\operatorname{Codom}f&\text{if }f\lhd=\lhd\,U,\\ \bot&\text{otherwise}.\end{cases}

This defines a full left action of $\mathsf{C}$ on $\mathsf{C}_{0}$ . A full right action is defined similarly. $\square$

Remark 4.4.

Let $\mathsf{C}$ be a category and let $X=\mathsf{C}_{1}$ . The definition of category action in [FS]*1.271–1.274 is similar to ours, but it requires $\lhd X=\mathbb{1}_{\mathsf{C}}=\{f\mathbin{\blacktriangleleft}\mid f:\mathsf{C}_{1}\}$ and $\lhd x=\mathbin{\blacktriangleleft}x$ and $f\lhd=f\mathbin{\blacktriangleleft}$ for every $x:X$ and $f:\mathsf{C}_{1}$ . Thus, for $f,g:\mathsf{C}_{1}$ and $x:X$ , both $f\cdot x$ and $g\cdot x$ are defined only when $f\mathbin{\blacktriangleleft}=\lhd x=g\mathbin{\blacktriangleleft}$ ; this is too restrictive for our purposes.

4.2. Capsules

As identified in Section 1.2, we focus on the action of one category $\mathsf{A}$ on another category $\mathsf{X}$ ; we call these “category modules” capsules. Note the change in notation from $X$ to $\mathsf{X}$ to emphasize this setting. In this case, $\mathsf{X}$ already has a candidate type for $\lhd\mathsf{X}$ , namely $\mathbin{\blacktriangleleft}\mathsf{X}=\mathbb{1}_{\mathsf{X}}$ . Furthermore, because a category has its own operation of composition, the action by $\mathsf{A}$ respects composition. For example, given a group homomorphism $\varphi:G\to H$ , we get an action $g\cdot h\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\varphi(g)h$ that satisfies $g\cdot(hh^{\prime})=(g\cdot h)h^{\prime}$ .

Definition 4.5.

A category $\mathsf{X}$ is a left $\mathsf{A}$ -capsule if there is a full left $\mathsf{A}$ -action on $\mathsf{X}$ with $\lhd\mathsf{X}=\mathbb{1}_{\mathsf{X}}$ such that the following hold:
(a) $(\forall x:\mathsf{X})$ $(\lhd x=\mathbin{\blacktriangleleft}x)$ ; (b) $(\forall a:\mathsf{A})$ $(\forall x,y:\mathsf{X})$ $a\cdot(xy)\asymp(a\cdot x)y$ .

A right $\mathsf{A}$ -capsule is similarly defined. We present our results below for left $\mathsf{A}$ -capsules, but they can be formulated for both.

Much of our intuition on actions draws on familiar themes in representation theory. A reader may be assisted by translating “ $\mathsf{A}$ -capsule” to “ $A$ -module” and considering the matching statement for modules. We write ${{}_{\mathsf{A}}{\mathsf{X}}}$ to indicate the presence of a left $\mathsf{A}$ -capsule action on $\mathsf{X}$ .

From now on, if a category $\mathsf{A}$ acts on itself, then we assume it is by the (left) regular action, where $\cdot:\mathsf{A}\times\mathsf{A}\to\mathsf{A}^{?}$ is given by composition in $\mathsf{A}$ . Moreover, a category action on another category is implicitly understood to be on the morphisms. We now show that capsules arise from morphisms between categories.

Proposition 4.6.

A category $\mathsf{X}$ is a left $\mathsf{A}$ -capsule of a category $\mathsf{A}$ if, and only if, there is a morphism $\mathcal{F}:\mathsf{A}\to\mathsf{X}$ such that $a\cdot x=\mathcal{F}(a)x$ . Furthermore, the morphism $\mathcal{F}$ is unique.

The following lemma proves one direction of Proposition 4.6.

Lemma 4.7.

Every morphism $\mathcal{F}:\mathsf{A}\to\mathsf{X}$ of categories makes $\mathsf{X}$ a left $\mathsf{A}$ -capsule, where for each $a:\mathsf{A}$ and $x:\mathsf{X}$ , the guard is defined by $a\lhd\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{F}(a)\mathbin{\blacktriangleleft}$ and the action is defined by $a\cdot x\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{F}(a)x$ .

Proof.

Condition (1) of Definition 4.1 is satisfied by the defined action.

For the first part of Condition (2), let $a:\mathsf{A}$ . Since $\mathcal{F}$ is a morphism and $(-)\mathbin{\blacktriangleleft}$ is everywhere defined, $\mathcal{F}(a\mathbin{\blacktriangleleft})=\mathcal{F}(a)\mathbin{\blacktriangleleft}$ . Hence, by Lemma 3.14 (a),

\displaystyle(a\mathbin{\blacktriangleleft})\lhd

\displaystyle=\mathcal{F}(a\mathbin{\blacktriangleleft})\mathbin{\blacktriangleleft}=(\mathcal{F}(a)\mathbin{\blacktriangleleft})\mathbin{\blacktriangleleft}=\mathcal{F}(a)\mathbin{\blacktriangleleft}=a\!\lhd.

For the second part of Condition (2), let $a:\mathsf{A}$ and $x:\mathsf{X}$ with $a\lhd=\lhd x$ , so $\mathcal{F}(a)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}x$ by definition. Thus,

(a\mathbin{\blacktriangleleft})\cdot x=\mathcal{F}(a\mathbin{\blacktriangleleft})x=(\mathcal{F}(a)\mathbin{\blacktriangleleft})x=(\mathbin{\blacktriangleleft}x)x=x,

so $(a\mathbin{\blacktriangleleft})\cdot x\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}x$ for every $a:\mathsf{A}$ and $x:\mathsf{X}$ .

For Condition (3), let $a,b:\mathsf{A}$ and $x:\mathsf{X}$ with $a\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}b$ and $(ab)\lhd=\lhd x$ , so $(ab)\cdot x$ is defined and $(ab)\mathbin{\blacktriangleleft}=b\mathbin{\blacktriangleleft}$ . We need to show that $(ab)\cdot x=a\cdot(b\cdot x)$ . Since $\mathcal{F}$ is a morphism,

(ab)\lhd=(\mathcal{F}(ab))\mathbin{\blacktriangleleft}=\mathcal{F}((ab)\mathbin{\blacktriangleleft})=\mathcal{F}(b\mathbin{\blacktriangleleft})=\mathcal{F}(b)\mathbin{\blacktriangleleft}=b\lhd.

Hence, $(ab)\lhd=\lhd x$ implies $b\lhd=\lhd x$ . Thus, $\mathcal{F}(b)x$ is defined. Also, $a\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}b$ implies $\mathcal{F}(a)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}(\mathcal{F}(b))$ , so

a\lhd=\mathcal{F}(a)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}(\mathcal{F}(b))=\mathbin{\blacktriangleleft}(\mathcal{F}(b)x)=\mathbin{\blacktriangleleft}(b\cdot x)=\lhd(b\cdot x).

It follows that $a\cdot(b\cdot x)$ is defined. Since $\mathcal{F}$ is a morphism,

a\cdot(b\cdot x)=\mathcal{F}(a)(\mathcal{F}(b)x)=\mathcal{F}(ab)x=(ab)\cdot x,

and therefore $(ab)\cdot x\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}a\cdot(b\cdot x)$ for every $a,b:\mathsf{A}$ and $x:\mathsf{X}$ .

To see that the action is full, consider $a:\mathsf{A}$ and define $x=\mathcal{F}(a)\mathbin{\blacktriangleleft}$ . By the laws of an abstract category, $a\lhd=\mathcal{F}(a)\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}({\mathcal{F}(a)\mathbin{\blacktriangleleft}})=\mathbin{\blacktriangleleft}x=\lhd x$ . Finally, $(a\cdot x)y=\mathcal{F}(a)xy\asymp a\cdot(xy)$ , so $\mathsf{X}$ is a left $\mathsf{A}$ -capsule. ∎

Our proof of the reverse direction of Proposition 4.6 uses the following result.

Lemma 4.8.

Let $\mathsf{X}$ be a left $\mathsf{A}$ -capsule. For every $a:\mathsf{A}$ , there is a unique $e:\mathbb{1}_{\mathsf{X}}$ such that $a\cdot e$ is the unique term of type $a\cdot\mathbb{1}_{\mathsf{X}}$ .

Proof.

Since the action is full, for each $a:\mathsf{A}$ there exists $x:\mathsf{X}$ such that $a\lhd=\lhd x$ , so $a\cdot x$ is defined. Since $\mathsf{X}$ is a left $\mathsf{A}$ -capsule, $a\lhd=\lhd x=\mathbin{\blacktriangleleft}x$ , so

\lhd(\mathbin{\blacktriangleleft}x)=\mathbin{\blacktriangleleft}(\mathbin{\blacktriangleleft}x)=\mathbin{\blacktriangleleft}x.

Hence, $a\cdot(\mathbin{\blacktriangleleft}x)$ is defined and has type $a\cdot\mathbb{1}_{\mathsf{X}}$ . Suppose $e,f:\mathbb{1}_{\mathsf{X}}$ and $a\lhd=\lhd e=\lhd f$ , so that $a\cdot e,a\cdot f:a\cdot\mathbb{1}_{\mathsf{X}}$ . Furthermore,

e=\mathbin{\blacktriangleleft}e=\lhd e=\lhd f=\mathbin{\blacktriangleleft}f=f.

Thus, $a\cdot e=a\cdot f$ , and there is exactly one term with type $a\cdot\mathbb{1}_{\mathsf{X}}$ . ∎

Under the assumptions of Lemma 4.8, we simplify notation and identify $a\cdot\mathbb{1}_{\mathsf{X}}$ with its unique term.

Proof of Proposition 4.6.

By Lemma 4.7, it remains to prove the forward direction and uniqueness. Suppose that $\mathsf{X}$ is a left $\mathsf{A}$ -capsule. By Lemma 4.8, for each $a:\mathsf{A}$ there is a unique $\mathcal{F}(a\mathbin{\blacktriangleleft}):\mathbb{1}_{\mathsf{X}}$ such that $(a\mathbin{\blacktriangleleft})\cdot\mathcal{F}(a\mathbin{\blacktriangleleft})$ is defined. Since $\mathsf{X}$ is a left $\mathsf{A}$ -capsule and $\mathcal{F}(a\mathbin{\blacktriangleleft})$ is an identity,

(a\mathbin{\blacktriangleleft})\lhd=a\lhd=\lhd\mathcal{F}(a\mathbin{\blacktriangleleft})=\mathbin{\blacktriangleleft}\mathcal{F}(a\mathbin{\blacktriangleleft})=\mathcal{F}(a\mathbin{\blacktriangleleft}).

Thus, $a\cdot\mathcal{F}(a\mathbin{\blacktriangleleft})$ is also defined. Put $\mathcal{F}(a)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}a\cdot\mathcal{F}(a\mathbin{\blacktriangleleft})$ . If $x:\mathsf{X}$ , then $a\cdot x$ is defined whenever

\mathbin{\blacktriangleleft}x=\lhd x=a\lhd=\mathcal{F}(a\mathbin{\blacktriangleleft})=\mathcal{F}(a\mathbin{\blacktriangleleft})\mathbin{\blacktriangleleft}.

Hence, $\mathcal{F}(a\mathbin{\blacktriangleleft})x$ is also defined in $\mathsf{X}$ . Because $\mathcal{F}(a\mathbin{\blacktriangleleft})$ is an identity, $\mathcal{F}(a\mathbin{\blacktriangleleft})x=x$ . Since $\mathsf{X}$ is a left $\mathsf{A}$ -capsule, $a\cdot x=a\cdot(\mathcal{F}(a\mathbin{\blacktriangleleft})x)=(a\cdot\mathcal{F}(a\mathbin{\blacktriangleleft}))x=\mathcal{F}(a)x$ . Hence, it remains to prove that $\mathcal{F}:\mathsf{A}\to\mathsf{X}$ is a morphism of categories.

For $a,b:\mathsf{A}$ , by the action laws

\displaystyle\mathcal{F}(ab)

\displaystyle\asymp(ab)\cdot\mathcal{F}((ab)\mathbin{\blacktriangleleft})\asymp(ab)\cdot\mathcal{F}(b\mathbin{\blacktriangleleft})\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}a\cdot(b\cdot\mathcal{F}(b\mathbin{\blacktriangleleft}))\asymp a\cdot\mathcal{F}(b).

Thus, $\mathcal{F}(ab)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}a\cdot\mathcal{F}(b)$ . But $\mathsf{X}$ is a left $\mathsf{A}$ -capsule, so Fact 3.17 implies that

(4.1)

\displaystyle a\cdot\mathcal{F}(b)

\displaystyle\asymp a\cdot(\mathbb{1}_{\mathsf{X}}\mathcal{F}(b))\asymp(a\cdot\mathbb{1}_{\mathsf{X}})\mathcal{F}(b)\asymp\mathcal{F}(a)\mathcal{F}(b).

Hence, $\mathcal{F}(ab)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\mathcal{F}(a)\mathcal{F}(b)$ . By Lemma 3.14 (b) and (4.1) for all $a:\mathsf{A}$ ,

\mathcal{F}(a)\mathbin{\blacktriangleleft}=(a\cdot\mathcal{F}(a\mathbin{\blacktriangleleft}))\mathbin{\blacktriangleleft}=(\mathcal{F}(a)\mathcal{F}(a\mathbin{\blacktriangleleft}))\mathbin{\blacktriangleleft}=\mathcal{F}(a\mathbin{\blacktriangleleft})\mathbin{\blacktriangleleft}=\mathcal{F}(a\mathbin{\blacktriangleleft}).

Similarly, $\mathcal{F}(\mathbin{\blacktriangleleft}a)=\mathbin{\blacktriangleleft}\mathcal{F}(a)$ . Hence, $\mathcal{F}$ is a morphism.

Lastly, we prove uniqueness of $\mathcal{F}$ . Suppose there exists $\mathcal{G}:\mathsf{A}\to\mathsf{X}$ such that $a\cdot x=\mathcal{G}(a)x$ for every $a:\mathsf{A}$ and $x:\mathsf{X}$ whenever $a\lhd=\lhd x$ . Since $a\lhd=\mathcal{F}(a\mathbin{\blacktriangleleft})$ , it follows that $\mathcal{G}(a)\mathbin{\blacktriangleleft}=\mathcal{F}(a\mathbin{\blacktriangleleft})$ , so $\mathcal{G}(a)=\mathcal{G}(a)\mathcal{F}(a\mathbin{\blacktriangleleft})=a\cdot\mathcal{F}(a\mathbin{\blacktriangleleft})=\mathcal{F}(a)$ . ∎

If $\mathsf{B}$ is a subcategory of $\mathsf{A}$ with inclusion $\mathcal{I}:\mathsf{B}\to\mathsf{A}$ , then the (left) regular action of $\mathsf{B}$ on $\mathsf{A}$ is defined to be the action given by $\mathcal{I}$ . In other words, the regular action of $\mathsf{B}$ on $\mathsf{A}$ is given by $b\cdot a=\mathcal{I}(b)a$ for $a:\mathsf{A}$ and $b:\mathsf{B}$ . By Lemma 4.7, each regular action defines a capsule. With regular actions we sometimes omit the “ $\cdot$ ”.

4.3. Category biactions and cyclic bicapsules

We now define the concepts appearing in Theorem 2(3).

Definition 4.9.

Let $\mathsf{A}$ and $\mathsf{B}$ be categories and let $X$ and $Y$ be types.

(a)

An $(\mathsf{A},\mathsf{B})$ -biaction on $X$ is a left $\mathsf{A}$ -action on $X$ and a right $\mathsf{B}$ -action on $X$ such that $a\cdot(x\cdot b)\asymp(a\cdot x)\cdot b$ for every $a:\mathsf{A}$ , $b:\mathsf{B}$ , and $x:X$ . Hence, writing $a\cdot x\cdot b$ is unambiguous. If, in addition, $\mathsf{X}$ is a left $\mathsf{A}$ -capsule and right $\mathsf{B}$ -capsule, then $\mathsf{X}$ is an $(\mathsf{A},\mathsf{B})$ -bicapsule.
(b)

Suppose there are $(\mathsf{A},\mathsf{B})$ -biactions on $X$ and $Y$ . An $(\mathsf{A},\mathsf{B})$ -morphism is a partial-function $\mathcal{M}:X\to Y^{?}$ such that $\mathcal{M}(a\cdot x\cdot b)=a\cdot\mathcal{M}(x)\cdot b$ , whenever $a:\mathsf{A}$ , $x:X$ , $b:\mathsf{B}$ with $a\lhd=\lhd x$ and $x\lhd=\lhd b$ .

We sometimes write ${{}_{\mathsf{A}}X_{\mathsf{B}}}$ for an $(\mathsf{A},\mathsf{B})$ -biaction on $X$ for clarity. Notice that an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{M}:X\to Y^{?}$ must be defined on $\mathsf{A}\cdot X\cdot\mathsf{B}$ . As with capsule morphisms, we do not need to establish guards. We abbreviate $(\mathsf{A},\mathsf{A})$ -bicapsule to $\mathsf{A}$ -bicapsule, $(\mathsf{A},\mathsf{A})$ -morphism to $\mathsf{A}$ -bimorphism, and $(\mathsf{A},\mathsf{A})$ -biaction to $\mathsf{A}$ -biaction. Note that $\mathsf{A}$ -bimorphisms are defined everywhere. Just as ring homomorphisms are not always linear maps, morphisms of capsules need not be morphisms of categories—morphisms of capsules do not in general send identities to identities.

Motivated by Proposition 4.6, we show that bicapsules provide a computationally useful perspective to record natural transformations of functors. If $\mathcal{F},\mathcal{G}:\mathsf{A}\to\mathsf{B}$ are functors and $\mu:\mathcal{G}\Rightarrow\mathcal{F}$ is a natural transformation, then, using Remark 3.19, the natural transformation property written with guards is

\mathcal{F}(a)\mu_{a\mathbin{\blacktriangleleft}}=\mu_{\mathbin{\blacktriangleleft}a}\mathcal{G}(a)

for every morphism $a$ in $\mathsf{A}$ .

Proposition 4.10.

In the following statements, the category $\mathsf{A}$ is also regarded as an $\mathsf{A}$ -bicapsule via its regular action.

(a)

For every natural transformation $\mu:\mathcal{G}\Rightarrow\mathcal{F}$ between functors $\mathcal{F},\mathcal{G}:\mathsf{A}\to\mathsf{X}$ , the assignment

\displaystyle a\cdot x\cdot a^{\prime}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{F}(a)x\mathcal{G}(a^{\prime})

\displaystyle(a,a^{\prime}:\mathsf{A},\;x:\mathsf{X})

makes $\mathsf{X}$ into an $\mathsf{A}$ -bicapsule, and the assignment $\mathcal{M}(a)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}a\cdot\mu_{a\mathbin{\blacktriangleleft}}$ defines an $\mathsf{A}$ -bimorphism $\mathcal{M}:\mathsf{A}\to\mathsf{X}^{?}$ .

(b)

Conversely, for every $\mathsf{A}$ -bimorphism $\mathcal{M}:\mathsf{A}\to\mathsf{X}^{?}$ , the assignments

\displaystyle\mathcal{F}(a)

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}a\cdot\mathbb{1}_{\mathsf{X}},

\displaystyle\mathcal{G}(a)

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathbb{1}_{\mathsf{X}}\cdot a

\displaystyle(a:\mathsf{A})

define functors $\mathcal{F},\mathcal{G}:\mathsf{A}\to\mathsf{X}$ , and the assignment

\displaystyle\mu_{a\mathbin{\blacktriangleleft}}

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{M}(a\mathbin{\blacktriangleleft})

\displaystyle(a:\mathsf{A})

defines a natural transformation $\mu:\mathcal{G}\Rightarrow\mathcal{F}$ .

Proof.

(a)

By Lemma 3.14 (b) for all $a,b,c:\mathsf{A}$ ,

\displaystyle\mathcal{M}(ab)

\displaystyle\asymp(ab)\cdot\mu_{(ab)\mathbin{\blacktriangleleft}}\asymp\mathcal{F}(ab)\mu_{(ab)\mathbin{\blacktriangleleft}}\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\mathcal{F}(a)\mathcal{F}(b)\mu_{b\mathbin{\blacktriangleleft}}\asymp a\cdot\mathcal{M}(b).

Since $\mu$ is a natural transformation,

\displaystyle\mathcal{M}(bc)

\displaystyle\asymp\mathcal{F}(bc)\mu_{(bc)\mathbin{\blacktriangleleft}}\asymp\mu_{\mathbin{\blacktriangleleft}(bc)}\mathcal{G}(bc)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\mu_{\mathbin{\blacktriangleleft}b}\mathcal{G}(b)\mathcal{G}(c)\asymp\mathcal{F}(b)\mu_{b\mathbin{\blacktriangleleft}}\mathcal{G}(c)\asymp\mathcal{M}(b)\cdot c.

Thus, $\mathcal{M}(abc)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}a\cdot\mathcal{M}(b)\cdot c$ , so $\mathcal{M}$ is an $\mathsf{A}$ -bimorphism.

(b)

We apply Proposition 4.6, so there are functors $\mathcal{F},\mathcal{G}:\mathsf{A}\to\mathsf{X}$ determined by the left and right actions, respectively. Let $a:\mathsf{A}$ and define $\mu_{e}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{M}(e)$ for $e:\mathbb{1}_{\mathsf{A}}$ . Now

	$\displaystyle\mathcal{F}(a)\mu_{a\mathbin{\blacktriangleleft}}$	$\displaystyle=\mathcal{F}(a)\mathcal{M}(a\mathbin{\blacktriangleleft})=a\cdot\mathcal{M}(a\mathbin{\blacktriangleleft})=\mathcal{M}(a(a\mathbin{\blacktriangleleft}))=\mathcal{M}(a)$
		$\displaystyle=\mathcal{M}((\mathbin{\blacktriangleleft}a)a)=\mathcal{M}(\mathbin{\blacktriangleleft}a)\cdot a=\mathcal{M}(\mathbin{\blacktriangleleft}a)\mathcal{G}(a)=\mu_{\mathbin{\blacktriangleleft}a}\mathcal{G}(a).$

Therefore, $\mu$ is a natural transformation, as required.∎

We summarize the conclusion in Proposition 4.10 (b), namely $\mu_{e}=\mathcal{M}(e)$ for every $e:\mathbb{1}_{\mathsf{A}}$ , by writing $\mu=\mathcal{M}(\mathbb{1}_{A})$ . While $\mathbb{1}_{\mathsf{A}}$ consists of many terms, $x\cdot\mathbb{1}_{\mathsf{A}}$ and $\mathbb{1}_{\mathsf{A}}\cdot x$ produce unique values, so $\mathbb{1}_{\mathsf{A}}$ plays a role similar to multiplying by $1$ . Since $\mathcal{M}:\mathsf{A}\to\mathsf{X}^{?}$ is an $\mathsf{A}$ -bimorphism, $\mathcal{M}(a)=a\cdot\mathcal{M}(\mathbin{\blacktriangleleft}a)=\mathcal{M}(a\mathbin{\blacktriangleleft})\cdot a$ for $a:\mathsf{A}$ , which shows that $\mathcal{M}$ is determined by $\mathcal{M}(\mathbb{1}_{\mathsf{A}})$ . We write

(4.2)

\displaystyle\mathsf{A}\cdot\mu\cdot\mathsf{A}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\left\{a\cdot\mu_{e}\cdot\acute{a}~\middle|~a,\acute{a}:\mathsf{A},e:\mathbb{1}_{\mathsf{A}},\ a\lhd=\lhd\mu_{e},\ \mu_{e}\lhd=\lhd\acute{a}\right\}.

The bicapsule in (4.2) is the cyclic $\mathsf{A}$ -bicapsule determined by $\mu=\mathcal{M}(\mathbb{1}_{\mathsf{A}})$ .

4.4. Units and counits

Given a category $\mathsf{A}$ and functor $\mathcal{H}:\mathsf{A}\to\mathsf{A}$ , a unit is a natural transformation $\mu:\operatorname{id}_{\mathsf{A}}\Rightarrow\mathcal{H}$ , and a counit is a natural transformation $\nu:\mathcal{H}\Rightarrow\operatorname{id}_{\mathsf{A}}$ . We will prove that units and counits are responsible for all characteristic structure. It therefore makes sense to translate these into capsule actions. We show that a unit $\mu$ is characterized as an $(\mathsf{A},\mathsf{B})$ -bimorphism $\mathcal{M}:\mathsf{A}\to\mathsf{B}^{?}$ and a counit $\nu$ by an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{N}:\mathsf{B}\to\mathsf{A}^{?}$ . As the relationship is dual, and we emphasize substructures instead of quotients, we state and prove this relationship only for counits.

Theorem 4.11.

Let $\mathsf{A}$ and $\mathsf{B}$ be categories.

(a)

If both $\mathsf{A}$ and $\mathsf{B}$ are $(\mathsf{A},\mathsf{B})$ -bicapsules and $\mathcal{N}:\mathsf{B}\to\mathsf{A}^{?}$ is an $(\mathsf{A},\mathsf{B})$ -morphism, then $\mathcal{F}(b)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathbb{1}_{\mathsf{A}}\cdot b$ and $\mathcal{G}(a)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}a\cdot\mathbb{1}_{\mathsf{B}}$ define functors $\mathcal{F}:\mathsf{B}\to\mathsf{A}$ and $\mathcal{G}:\mathsf{A}\to\mathsf{B}$ , and $\nu\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{N}\mathcal{G}(\mathbb{1}_{\mathsf{A}})$ is a counit $\nu:\mathcal{F}\mathcal{G}\Rightarrow\operatorname{id}_{\mathsf{A}}$ .
(b)

If $\mathcal{F}:\mathsf{B}\to\mathsf{A}$ and $\mathcal{G}:\mathsf{A}\to\mathsf{B}$ are functors and $\nu:\mathcal{F}\mathcal{G}\Rightarrow\operatorname{id}_{\mathsf{A}}$ is a counit, then $\mathsf{A}$ and $\mathsf{B}$ are $(\mathsf{A},\mathsf{B})$ -bicapsules, where $a\cdot y\cdot b\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{G}(a)yb$ and $a\cdot x\cdot b=\mathcal{F}\mathcal{G}(a)x\mathcal{F}\mathcal{G}\mathcal{F}(b)$ for $a,x:\mathsf{A}$ and $b,y:\mathsf{B}$ . Also, $\mathcal{N}^{\prime}(b)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{F}(b)\nu_{\mathcal{F}(b)\mathbin{\blacktriangleleft}}$ is an $(\mathsf{A},\mathsf{B})$ -morphism $\mathsf{B}\to\mathsf{A}$ such that $\mathcal{N}^{\prime}\mathcal{G}(e)=\nu_{\mathcal{F}\mathcal{G}(e)}$ for all $e:\mathbb{1}_{\mathsf{A}}$ .

Proof.

(a)

By Proposition 4.6, the maps $\mathcal{F}$ and $\mathcal{G}$ define functors where $x\cdot b\asymp x\mathcal{F}(b)$ and $a\cdot y\asymp\mathcal{G}(a)y$ , for $a,x:\mathsf{A}$ and $b,y:\mathsf{B}$ . Put $\nu=\mathcal{N}(\mathcal{G}(\mathbb{1}_{A}))$ . For $a:\mathsf{A}$ ,

\displaystyle a\nu_{a\mathbin{\blacktriangleleft}}

\displaystyle=a\mathcal{N}\mathcal{G}(a\mathbin{\blacktriangleleft})=a\mathcal{N}(\mathcal{G}(a)\mathbin{\blacktriangleleft})=\mathcal{N}(a\cdot(\mathcal{G}(a))\mathbin{\blacktriangleleft})=\mathcal{N}(\mathcal{G}(a)(\mathcal{G}(a))\mathbin{\blacktriangleleft})=\mathcal{N}\mathcal{G}(a),

and

\displaystyle\nu_{\mathbin{\blacktriangleleft}a}\mathcal{F}\mathcal{G}(a)

\displaystyle=\mathcal{N}\mathcal{G}(\mathbin{\blacktriangleleft}a)\cdot\mathcal{G}(a)=\mathcal{N}(\mathbin{\blacktriangleleft}\mathcal{G}(a))\cdot\mathcal{G}(a)=\mathcal{N}((\mathbin{\blacktriangleleft}\mathcal{G}(a))\mathcal{G}(a))=\mathcal{N}\mathcal{G}(a).

Hence, $a\nu_{a\mathbin{\blacktriangleleft}}=\nu_{\mathbin{\blacktriangleleft}a}\mathcal{F}\mathcal{G}(a)$ for all $a:\mathsf{A}$ , so $\nu:\mathcal{F}\mathcal{G}\Rightarrow\operatorname{id}_{\mathsf{A}}$ is a natural transformation.

We show that $\mathcal{N}^{\prime}(b)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{F}(b)\nu_{\mathcal{F}(b)\mathbin{\blacktriangleleft}}$ yields an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{N}^{\prime}:\mathsf{B}\to\mathsf{A}$ . First, if $a:\mathsf{A}$ and $y:\mathsf{B}$ with $a\lhd=\lhd y$ , then

	$\displaystyle\mathcal{N}^{\prime}(a\cdot y)$	$\displaystyle=\mathcal{N}^{\prime}(\mathcal{G}(a)y)$
		$\displaystyle=\mathcal{F}(\mathcal{G}(a)y)\nu_{\mathcal{F}(\mathcal{G}(a)y)\mathbin{\blacktriangleleft}}$
		$\displaystyle=\mathcal{F}\mathcal{G}(a)\mathcal{F}(y)\nu_{(\mathcal{F}\mathcal{G}(a)\mathcal{F}(y))\mathbin{\blacktriangleleft}}$
		$\displaystyle=\mathcal{F}\mathcal{G}(a)\mathcal{F}(y)\nu_{\mathcal{F}(y)\mathbin{\blacktriangleleft}}$
		$\displaystyle=\mathcal{F}\mathcal{G}(a)\mathcal{N}^{\prime}(y)$
		$\displaystyle=a\cdot\mathcal{N}^{\prime}(y).$

Next, if $b:\mathsf{B}$ such that $y\lhd=\lhd b$ , then

	$\displaystyle\mathcal{N}^{\prime}(yb)$	$\displaystyle=\mathcal{F}(yb)\nu_{\mathcal{F}(yb)\mathbin{\blacktriangleleft}}$
		$\displaystyle=\nu_{\mathbin{\blacktriangleleft}\mathcal{F}(yb)}\mathcal{F}\mathcal{G}\mathcal{F}(yb)$
		$\displaystyle=\nu_{\mathbin{\blacktriangleleft}(\mathcal{F}(y)\mathcal{F}(b))}\mathcal{F}\mathcal{G}\mathcal{F}(y)\mathcal{F}\mathcal{G}\mathcal{F}(b)$
		$\displaystyle=\nu_{\mathbin{\blacktriangleleft}\mathcal{F}(y)}\mathcal{F}\mathcal{G}\mathcal{F}(y)\mathcal{F}\mathcal{G}\mathcal{F}(b)$
		$\displaystyle=\mathcal{F}(y)\nu_{\mathcal{F}(y)\mathbin{\blacktriangleleft}}\mathcal{F}\mathcal{G}\mathcal{F}(b)$
		$\displaystyle=\mathcal{N}^{\prime}(y)\mathcal{F}\mathcal{G}\mathcal{F}(b)$
		$\displaystyle=\mathcal{N}^{\prime}(y)\cdot b.$

Finally, consider $e:\mathbb{1}_{\mathsf{A}}$ . Since functors map identities to identities, we deduce that

\displaystyle\mathcal{N}^{\prime}(\mathcal{G}(e))

\displaystyle=\mathcal{F}\mathcal{G}(e)\nu_{\mathcal{F}\mathcal{G}(e)\mathbin{\blacktriangleleft}}=\nu_{\mathcal{F}\mathcal{G}(e)}.\qed

4.5. Adjoint functor pairs

Adjoint functor pairs are an important special case of natural transformations. We give one of many equivalent definitions [Riehl]*§4.1.

Definition 4.12.

Let $\mathsf{A}$ and $\mathsf{B}$ be categories. An adjoint functor pair is a pair of functors $\mathcal{F}:\mathsf{B}\to\mathsf{A}$ and $\mathcal{G}:\mathsf{A}\to\mathsf{B}$ with the following property. For every object $U$ in $\mathsf{B}$ and $V$ in $\mathsf{A}$ , there is an invertible function

\Psi_{UV}:\mathsf{A}_{1}(\mathcal{F}(U),V)\to\mathsf{B}_{1}(U,\mathcal{G}(V))

that is natural in the following sense: if $b:\mathsf{B}_{1}(X,U)$ and $a:\mathsf{A}_{1}(V,Y)$ for objects $X$ in $\mathsf{B}$ and $Y$ in $\mathsf{B}$ then, for every $x\in\mathsf{A}_{1}(\mathcal{F}(U),V)$ ,

(4.3)

\Psi_{XY}(ax\mathcal{F}(b))=\mathcal{G}(a)\Psi_{UV}(x)b.

We say that $\mathcal{F}$ is left-adjoint to $\mathcal{G}$ and $\mathcal{G}$ is right-adjoint to $\mathcal{F}$ and write this as $\mathcal{F}:\mathsf{B}\dashv_{\Psi}\mathsf{A}:\mathcal{G}$ .

We now characterize adjoint functor pairs in terms of bicapsules. A reader may find it useful to review the translation between categories and abstract categories in Remark 3.19. The invertibility of $\Psi_{UV}$ in Definition 4.12 is equivalent to a pseudo-inverse property of morphisms of bicapsules.

For types $X$ and $Y$ , partial-functions $\mathcal{M}:X\to Y^{?}$ and $\mathcal{N}:Y\to X^{?}$ are pseudo-inverses if, for $x:X$ and $y:Y$ , $\mathcal{M}\mathcal{N}\mathcal{M}(x)\asymp\mathcal{M}(x)$ and $\mathcal{N}\mathcal{M}\mathcal{N}(y)\asymp\mathcal{N}(y)$ .

Theorem 4.13.

Let $\mathsf{A}$ and $\mathsf{B}$ be categories.

(a)

If $\mathsf{A}$ and $\mathsf{B}$ are $(\mathsf{A},\mathsf{B})$ -bicapsules and $\mathcal{M}:\mathsf{A}\to\mathsf{B}^{?}$ and $\mathcal{N}:\mathsf{B}\to\mathsf{A}^{?}$ are $(\mathsf{A},\mathsf{B})$ -morphisms that are pseudo-inverses, then $\mathcal{F}:\mathsf{B}\dashv_{\Psi}\mathsf{A}:\mathcal{G}$ where

	$\displaystyle\mathcal{F}$	$\displaystyle:\mathsf{B}\to\mathsf{A},\quad\mathcal{F}(b)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathbb{1}_{\mathsf{A}}\cdot b,$
	$\displaystyle\mathcal{G}$	$\displaystyle:\mathsf{A}\to\mathsf{B},\quad\mathcal{G}(a)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}a\cdot\mathbb{1}_{\mathsf{B}},$

and for $x:\mathsf{A}_{1}(\mathcal{F}(U),V)$ and $y:\mathsf{B}_{1}(U,\mathcal{G}(V))$ the bijections $\Psi_{UV}$ and $\Psi_{UV}^{-1}$ are given by

\displaystyle\Psi_{UV}(x)

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{M}(x)

\displaystyle\Psi_{UV}^{-1}(x)

\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{N}(y).

(b)

If $\mathcal{F}:\mathsf{B}\dashv_{\Psi}\mathsf{A}:\mathsf{G}$ is an adjoint functor pair, then $\mathsf{A}$ and $\mathsf{B}$ are $(\mathsf{A},\mathsf{B})$ -bicapsules with actions defined by

a\cdot y\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{G}(a)y\quad\text{and}\quad x\cdot b\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}x\mathcal{F}(b)

for $a,x:\mathsf{A}$ and $b,y:\mathsf{B}$ and $\Psi$ yields a pair of $(\mathsf{A},\mathsf{B})$ -morphisms $\mathcal{M}:\mathsf{A}\to\mathsf{B}^{?}$ and $\mathcal{N}:\mathsf{B}\to\mathsf{A}^{?}$ that are pseudo-inverses where

	$\displaystyle\mathcal{M}(x)$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\Psi_{UV}(x),$	$\displaystyle x:\mathsf{A}\cdot\mathbb{1}_{\mathsf{B}}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{\operatorname{id}_{V}:\mathbb{1}_{\mathsf{A}}}\bigsqcup_{\operatorname{id}_{U}:\mathbb{1}_{\mathsf{B}}}\mathsf{A}_{1}(\mathcal{F}(U),V),$
	$\displaystyle\mathcal{N}(y)$	$\displaystyle\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\Psi^{-1}_{UV}(y),$	$\displaystyle y:\mathbb{1}_{\mathsf{A}}\cdot\mathsf{B}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{\operatorname{id}_{V}:\mathbb{1}_{\mathsf{A}}}\bigsqcup_{\operatorname{id}_{U}:\mathbb{1}_{\mathsf{B}}}\mathsf{B}_{1}(U,\mathcal{G}(V)).$

Proof.

First we prove (a). Since $\mathsf{A}$ and $\mathsf{B}$ are $(\mathsf{A},\mathsf{B})$ -bicapsules, by Proposition 4.6 there are functors $\mathcal{F}:\mathsf{B}\to\mathsf{A}$ and $\mathcal{G}:\mathsf{A}\to\mathsf{B}$ defining the right $\mathsf{B}$ -capsule $\mathsf{A}_{\mathsf{B}}$ and the left $\mathsf{A}$ -capsule ${{}_{\mathsf{A}}\mathsf{B}}$ respectively. Since $\mathcal{M}$ and $\mathcal{N}$ are pseudo-inverses and capsule actions are full, $\mathcal{M}$ inverts $\mathcal{N}$ on $\mathsf{A}\cdot\mathbb{1}_{\mathsf{B}}$ and $\mathcal{N}$ inverts $\mathcal{M}$ on $\mathbb{1}_{\mathsf{A}}\cdot\mathsf{B}$ . For objects $U$ of $\mathsf{B}$ and $V$ of $\mathsf{A}$ , let $e=\operatorname{id}_{U}$ and $f=\operatorname{id}_{V}$ . For $x:\mathsf{A}_{1}(\mathcal{F}(U),V)=f\mathsf{A}\cdot e$ (see Remark 3.19), we define $\Psi_{UV}(x)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{M}(x)$ . Therefore, for $y:\mathsf{B}_{1}(U,\mathcal{G}(V))=f\cdot\mathsf{B}e$ , the map $y\mapsto\mathcal{N}(y)$ inverts $\Psi_{UV}$ , so the result follows.

Now we prove (b). By Proposition 4.6, we can exchange functors for capsules, so $\mathcal{F}:\mathsf{B}\to\mathsf{A}$ affords a right $\mathsf{B}$ -capsule $\mathsf{A}_{\mathsf{B}}$ . We enrich this action by adding the left regular action by $\mathsf{A}$ to produce an $(\mathsf{A},\mathsf{B})$ -bicapsule ${}_{\mathsf{A}}\mathsf{A}_{\mathsf{B}}$ . We do likewise with $\mathcal{G}:\mathsf{A}\to\mathsf{B}$ producing a second $(\mathsf{A},\mathsf{B})$ -capsule ${}_{\mathsf{A}}\mathsf{B}_{\mathsf{B}}$ .

To encode $\Psi$ , we define an $(\mathsf{A},\mathsf{B})$ -bimorphism $\mathcal{M}:\mathsf{A}\to\mathsf{B}^{?}$ by $\mathcal{M}(x)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\Psi_{UV}(x)$ for $x:A_{1}(\mathcal{F}(U),V)$ . This defines $\mathcal{M}$ on

\bigsqcup_{U:\mathsf{B}_{0}}\bigsqcup_{V:\mathsf{A}_{0}}\mathsf{A}_{1}(\mathcal{F}(U),V)=\bigsqcup_{e:\mathbb{1}_{\mathsf{B}}}\bigsqcup_{f:\mathbb{1}_{\mathsf{A}}}f\mathsf{A}\cdot e=\mathsf{A}\cdot\mathbb{1}_{\mathsf{B}}.

For all other values, $\mathcal{M}$ is undefined. Now (4.3) shows that on $\mathsf{A}\cdot\mathbb{1}_{\mathsf{B}}$ with $a:\mathsf{A}_{1}(V,Y)$ , $b:\mathsf{B}_{1}(X,U)$ , and $x:\mathsf{A}_{1}(\mathcal{F}(U),V)$ ,

\displaystyle\mathcal{M}(ax\cdot b)

\displaystyle=\Psi_{UV}(ax\mathcal{F}(b))=\mathcal{G}(a)\Psi_{XY}(x)b=a\cdot\mathcal{M}(x)b,

so $\mathcal{M}$ is an $(\mathsf{A},\mathsf{B})$ -bimorphism. We define $\mathcal{N}:\mathsf{B}\to\mathsf{A}^{?}$ analogously: if $y:\mathbb{1}_{\mathsf{A}}\cdot\mathsf{B}$ , then $\mathcal{N}(y)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\Psi^{-1}(y)$ (for suitable subscripts of $\Psi$ ), and otherwise $\mathcal{N}(y)$ is undefined. Therefore, for $x:\mathsf{A}\cdot\mathbb{1}_{\mathsf{B}}$ and $y:\mathbb{1}_{\mathsf{A}}\cdot\mathsf{B}$ ,

	$\displaystyle(\mathcal{M}\mathcal{N}\mathcal{M})(x)$	$\displaystyle=\Psi(\Psi^{-1}(\Psi(x)))=\Psi(x)=\mathcal{M}(x)$
	$\displaystyle(\mathcal{N}\mathcal{M}\mathcal{N})(y)$	$\displaystyle=\Psi^{-1}(\Psi(\Psi^{-1}(y)))=\Psi^{-1}(y)=\mathcal{N}(y).\qed$

4.6. A computational model for natural transformations

We use the algebraic perspective of Section 3.6 to discuss briefly a model for computing with natural transformations. The next definition formalizes how to treat morphisms of a category as functors between two other categories.

Definition 4.14.

Let $\mathsf{N}$ , $\mathsf{A}$ and $\mathsf{B}$ be abstract categories. A natural map of $\mathsf{N}$ from $\mathsf{A}$ to $\mathsf{B}$ consists of functions $\cdot:\mathbb{1}_{\mathsf{N}}\times\mathsf{A}\to\mathsf{B}$ and $\bullet:\mathsf{N}\times\mathbb{1}_{\mathsf{A}}\to\mathsf{B}$ that satisfy the following properties:
(1) $(\forall x,y:\mathsf{A})$ $(\forall e:\mathbb{1}_{\mathsf{N}})$ $e\cdot(xy)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}(e\cdot x)(e\cdot y)$ ; (2) $(\forall x:\mathsf{A})$ $(\forall e:\mathbb{1}_{\mathsf{N}})$ $e\cdot(x\mathbin{\blacktriangleleft})=(e\cdot x)\mathbin{\blacktriangleleft}$ and $e\cdot(\mathbin{\blacktriangleleft}x)=\mathbin{\blacktriangleleft}(e\cdot x)$ ; (3) $(\forall x:\mathsf{A})$ $(\forall s:\mathsf{N})$ $(s\bullet(\mathbin{\blacktriangleleft}x))((s\mathbin{\blacktriangleleft})\cdot x)=((\mathbin{\blacktriangleleft}s)\cdot x)(s\bullet(x\mathbin{\blacktriangleleft}))$ ; (4) $(\forall f:\mathbb{1}_{\mathsf{A}})$ $(\forall s,t:\mathsf{N})$ $(st)\bullet f\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}(s\bullet f)(t\bullet f)$ .

The use of $\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}$ in (1) and (4) depends only on $xy$ and $st$ , respectively, being defined. For the composition signature $\Omega$ from Example 3.9, the first two conditions of Definition 4.14 imply that there is a function $\mathbb{1}_{\mathsf{N}}\to\operatorname{Mor}_{\Omega}(\mathsf{A},\mathsf{B})$ given by $e\mapsto(x\mapsto e\cdot x)$ where $\operatorname{Mor}_{\Omega}(\mathsf{A},\mathsf{B})$ is the type of morphisms between abstract categories; see also Definition 3.20. This function $\mathbb{1}_{\mathsf{N}}\to\operatorname{Mor}_{\Omega}(\mathsf{A},\mathsf{B})$ enables us to treat the objects of $\mathsf{N}$ as functors from $\mathsf{A}$ to $\mathsf{B}$ . As illustrated in Example 4.15, conditions (3) and (4) are equivalent to the commutative diagrams in Figure 3 in the shaded $(2,2)$ and $(3,1)$ entries, respectively.

Refer to caption — Figure 3. A natural map of $\mathsf{N}$ (displayed in the left dotted column) from $\mathsf{A}$ (displayed in top row) to $\mathsf{B}$ (shaded gray)

Example 4.15.

We illustrate how the four conditions of Definition 4.14 translate to categories with objects and morphisms. Let $\mathsf{A}$ and $\mathsf{B}$ be two such categories, and let $\Omega$ be the composition signature from Example 3.9. Then $\operatorname{Mor}_{\Omega}(\mathsf{A},\mathsf{B})$ is the type functors from $\mathsf{A}$ to $\mathsf{B}$ . Let $\mathsf{N}$ be the category whose objects are the functors in $\operatorname{Mor}_{\Omega}(\mathsf{A},\mathsf{B})$ and whose morphisms are natural transformations. Let $\eta:\mathcal{F}\Rightarrow\mathcal{G}$ be a natural transformation between $\mathcal{F},\mathcal{G}:\operatorname{Mor}_{\Omega}(\mathsf{A},\mathsf{B})$ . Treating $\mathsf{N}$ as an abstract category, the guards are defined as follows: $\eta\mathbin{\blacktriangleleft}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{id}_{\mathcal{F}}:\mathcal{F}\Rightarrow\mathcal{F}$ and $\mathbin{\blacktriangleleft}\eta\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\operatorname{id}_{\mathcal{G}}:\mathcal{G}\Rightarrow\mathcal{G}$ . Define $\cdot:\mathbb{1}_{\mathsf{N}}\times\mathsf{A}\to\mathsf{B}$ by $(\operatorname{id}_{\mathcal{F}},\varphi)\longmapsto\mathcal{F}(\varphi)$ , and $\bullet:\mathsf{N}\times\mathbb{1}_{\mathsf{A}}\to\mathsf{B}$ by $(\eta,\operatorname{id}_{X})\longmapsto\eta_{X}$ . Now the conditions of Definition 4.14 become:
(1) $(\forall a,b:\mathsf{A})$ $(\forall\operatorname{id}_{\mathcal{F}}:\mathbb{1}_{\mathsf{N}})$ $\mathcal{F}(ab)\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\mathcal{F}(a)\mathcal{F}(b)$ ; (2) $(\forall a:\mathsf{A})$ $(\forall\operatorname{id}_{\mathcal{F}}:\mathbb{1}_{\mathsf{N}})$ $\mathcal{F}(a\mathbin{\blacktriangleleft})=(\mathcal{F}(a))\mathbin{\blacktriangleleft}$ and $\mathcal{F}(\mathbin{\blacktriangleleft}a)=\mathbin{\blacktriangleleft}(\mathcal{F}(a))$ ; (3) $(\forall(a:X\to Y):\mathsf{A})\quad(\forall(\eta:\mathcal{F}\Rightarrow\mathcal{G}):\mathsf{N})\quad\eta_{Y}\mathcal{F}(a)=\mathcal{G}(a)\eta_{X}$ ; (4) $(\forall\operatorname{id}_{X}:\mathbb{1}_{\mathsf{A}})$ $(\forall\eta,\epsilon:\mathsf{N})$ $(\eta\epsilon)_{X}\mathrel{\leavevmode\hbox to6.86pt{\vbox to4.92pt{\pgfpicture\makeatletter\hbox{\thinspace\lower 1.7375pt\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }\definecolor{pgfstrokecolor}{rgb}{0,0,0}\pgfsys@color@rgb@stroke{0}{0}{0}\pgfsys@invoke{ }\pgfsys@color@rgb@fill{0}{0}{0}\pgfsys@invoke{ }\pgfsys@setlinewidth{0.4pt}\pgfsys@invoke{ }\nullfont\pgfsys@beginscope\pgfsys@invoke{ }\pgfsys@invoke{ }\pgfsys@endscope\hbox to0.0pt{\pgfsys@beginscope\pgfsys@invoke{ }{{}}{{}} {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{6.45837pt}\pgfsys@lineto{2.15277pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{5.1667pt}\pgfsys@lineto{6.45831pt}{5.1667pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{0.0pt}{1.9375pt}\pgfsys@lineto{2.15277pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } {}{{}}{} {}{}{}\pgfsys@moveto{2.15277pt}{3.22919pt}\pgfsys@lineto{6.45831pt}{3.22919pt}\pgfsys@stroke\pgfsys@invoke{ } \pgfsys@invoke{ }\pgfsys@endscope{}{}{}\hss}\pgfsys@discardpath\pgfsys@invoke{ }\pgfsys@endscope\hss}}\endpgfpicture}}}\eta_{X}\epsilon_{X}$ . $\square$

The theory of functors and natural transformations is equivalent to that of natural maps on abstract categories, but the latter allows us to use multiple encodings of functors and natural transformations such as those available in computer algebra systems. If, for example, we compute the derived subgroup $\gamma_{2}(G)$ of a group $G$ in Magma, then the system may use an encoding for $\gamma_{2}(G)$ that differs from that supplied for $G$ . In such cases, Magma also returns an inclusion homomorphism $\lambda_{G}:\gamma_{2}(G)\hookrightarrow G$ .

5. The Extension Theorem

One of our goals is a categorification of characteristic subgroups and their analogues in eastern algebras. We start by translating the characteristic condition into the language of natural transformations.

5.1. Natural transformations express characteristic subgroups

Suppose that $H$ is a characteristic subgroup of a group $G$ . Hence, every automorphism $\varphi:G\to G$ restricts to an automorphism $\varphi|_{H}:H\to H$ of $H$ . In categorical terms, we now treat $\mathsf{A}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathsf{Aut}(G)$ as the subcategory of $\mathsf{Grp}$ consisting of a single object $G$ and all isomorphisms $G\to G$ . Likewise, we treat $\mathsf{B}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathsf{Aut}(H)$ as a subcategory of $\mathsf{Grp}$ . The restriction defines a functor $\mathcal{C}:\mathsf{A}\to\mathsf{B}$ . Of course, $\mathsf{Aut}(G)$ and $\mathsf{Aut}(H)$ are also groups and $\mathcal{C}$ is a group homomorphism, but the discussion below justifies the functor language.

Now we use the fact that $H$ is a subgroup of $G$ (by using the inclusion map $\rho_{G}:H\hookrightarrow G$ ). That $\varphi(H)$ is a subgroup of $H$ can be expressed as $\varphi\rho_{G}=\rho_{G}\varphi|_{H}=\rho_{G}\mathcal{C}(\varphi).$ Recognizing the different categories, we use the inclusion functors $\mathcal{I}:\mathsf{A}\to\mathsf{Grp}$ and $\mathcal{J}:\mathsf{B}\to\mathsf{Grp}$ to deduce the following:

\mathcal{I}(\varphi)\rho_{G}=\rho_{G}\mathcal{J}\mathcal{C}(\varphi).

Thus, a characteristic subgroup determines a natural transformation

\rho:\mathcal{J}\mathcal{C}\Rightarrow\mathcal{I}.

The next definition generalizes Definition 1.1.

Definition 5.1.

Fix an eastern variety $\mathsf{E}$ with subcategories $\mathsf{A}$ and $\mathsf{B}$ and inclusion functors $\mathcal{I}:\mathsf{A}\to\mathsf{E}$ and $\mathcal{J}:\mathsf{B}\to\mathsf{E}$ . A counital is a natural transformation $\rho:\mathcal{JC}\Rightarrow\mathcal{I}$ for some functor $\mathcal{C}:\mathsf{A}\to\mathsf{B}$ . The counital $\rho:\mathcal{JC}\Rightarrow\mathcal{I}$ is monic if $\rho_{X}$ is a monomorphism for all objects $X$ in $\mathsf{A}$ .

A common way to illustrate categories, functors, and natural transformations uses a 2-dimensional diagram where categories are vertices, functors are directed edges, and natural transformations are oriented 2-cells. The next diagram illustrates the counital discussed above.

We now generalize the notion of a characteristic subgroup to an arbitrary eastern algebra. Let $\mathsf{A}$ be a subcategory of an eastern variety $\mathsf{E}$ . For $G:\mathsf{E}$ , let $\mathsf{A}(G)$ be the category with a single object $G$ and morphisms $\mathsf{A}_{1}(G,G)$ , so $\mathsf{Aut}(G)=\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(G)$ . Observe that $\mathsf{A}(G)$ is a full subcategory of $\mathsf{A}$ .

Definition 5.2.

Let $G,H:\mathsf{E}$ , and let $\mathcal{I}:\mathsf{A}(G)\to\mathsf{A}$ and $\mathcal{J}:\mathsf{A}(H)\to\mathsf{A}$ be inclusions. A monomorphism $\iota:H\hookrightarrow G$ is $\mathsf{A}$ -invariant if there is a functor $\mathcal{C}:\mathsf{A}(G)\to\mathsf{A}(H)$ and a monic counital $\eta:\mathcal{JC}\Rightarrow\mathcal{I}$ such that $\eta_{G}$ is equivalent to $\iota$ (see Section 3.9 for the definition of equivalence).

Using the language of Definition 5.2, a characteristic subgroup $H$ of a group $G$ determines and is determined by a $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}$ -invariant monomorphism $H\hookrightarrow G$ . For fully invariant subgroups, the corresponding monomorphism is $\mathsf{Grp}$ -invariant.

5.2. The extension problem and representation theory

In Section 5.1, we observed that a characteristic subgroup $H$ of $G$ determines a functor $\mathcal{C}:\mathsf{A}\to\mathsf{B}$ and a natural transformation $\rho:\mathcal{JC}\Rightarrow\mathcal{I}$ , where $\mathsf{A}$ and $\mathsf{B}$ are categories with one object, namely $G$ and $H$ respectively. If a group $\acute{G}$ is isomorphic to $G$ , then by Fact 1.2 $\acute{G}$ has a characteristic subgroup corresponding to $H$ . It seems plausible that we may be able to extend the functor $\mathcal{C}$ to more groups and, hence, to larger categories. We now make this notion of extension precise and generalize it to the setting of eastern algebras.

Fix an eastern variety $\mathsf{E}$ . Let $\mathsf{A}$ , $\mathsf{B}$ , and $\mathsf{C}$ be subcategories of $\mathsf{E}$ where $\mathsf{A}\leqslant\mathsf{C}$ . We have inclusion functors $\mathcal{I}:\mathsf{A}\to\mathsf{E}$ , $\mathcal{J}:\mathsf{B}\to\mathsf{E}$ , $\mathcal{K}:\mathsf{C}\to\mathsf{E}$ and $\mathcal{L}:\mathsf{A}\to\mathsf{C}$ , where $\mathcal{I}=\mathcal{K}\mathcal{L}$ . Suppose that $\rho:\mathcal{J}\mathcal{C}\Rightarrow\mathcal{I}$ is a monic counital as depicted in Figure 4(a). The extension problem asks whether there is a functor $\mathcal{D}:\mathsf{C}\to\mathsf{E}$ and a natural transformation $\sigma:\mathcal{D}\Rightarrow\mathcal{K}$ such that

(5.1)

\displaystyle\rho_{X}=\sigma_{\mathcal{L}(X)}\tau_{X}

for some invertible morphism $\tau_{X}:\mathcal{JC}(X)\to\mathcal{DL}(X)$ for all objects $X$ of $\mathsf{A}$ . This is depicted in Figure 4(b).

(a) A diagram of a counital

(b) A diagram of an extension

Figure 4. Extending a counital

For now, we are concerned only with the existence and construction of such extensions. For use within an isomorphism test, it will be necessary to develop tools to compute efficiently with categories; the data types of Section 4.6 are designed for that purpose.

In light of Proposition 4.10, we can explore the natural transformations from Figure 4 through the lens of actions. Recall that concatenation always denotes regular actions. The natural transformation $\rho$ defined above is encoded as an $\mathsf{A}$ -bimorphism $\mathcal{R}:\mathsf{A}\to\mathsf{E}$ , where $\rho=\mathcal{R}(\mathbb{1}_{\mathsf{A}})$ , and this bimorphism defines a cyclic $\mathsf{A}$ -bicapsule $\Delta\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathsf{A}\rho\cdot\mathsf{A}$ via (4.2), which we fix throughout.

Our goal in part is to extend the cyclic $\mathsf{A}$ -bicapsule $\Delta$ to a cyclic $\mathsf{C}$ -bicapsule $\Sigma$ . Specifically, we will define $\Sigma\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathsf{C}\sigma\cdot\mathsf{C}$ , where $\sigma:\mathcal{D}\Rightarrow\mathcal{K}$ is depicted in Figure 4(b). This is the content of Theorem 5.4, but given in the general setting of eastern algebras. By construction (Proposition 4.10), the left actions on $\Delta$ and $\Sigma$ are regular; hence, we focus on right actions.

Example 5.3.

For the purposes of illustration, we consider a familiar construction that is similar to our context, namely Frobenius reciprocity and Morita condensation [Rowen, Theorem 25A.19]. Here $E$ is a ring, and $A$ and $C$ are subrings. Considering a Peirce decomposition of $E$ , let $\mathbb{1}_{A}$ and $\mathbb{1}_{C}$ be idempotents in $E$ such that $\mathbb{1}_{A}\mathbb{1}_{C}=\mathbb{1}_{A}=\mathbb{1}_{C}\mathbb{1}_{A}$ . Then $C=\mathbb{1}_{C}E\mathbb{1}_{C}$ is a (non-unital) subring of $E$ , and $A=\mathbb{1}_{A}E\mathbb{1}_{A}$ is a subring of both $C$ and $E$ . Furthermore, $\mathbb{1}_{A}E\mathbb{1}_{C}=\mathbb{1}_{A}C$ is an $(A,C)$ -bimodule and $C\mathbb{1}_{A}=\mathbb{1}_{C}E\mathbb{1}_{A}$ is a $(C,A)$ -bimodule. Suppose $\Delta$ is a right $A$ -module and $\Sigma$ a right $C$ -module. The theory of induction and restriction provides us, respectively, with a right $C$ -module and a right $A$ -module: namely,

\mathrm{Ind}^{C}_{A}(\Delta)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\Delta\otimes_{A}(\mathbb{1}_{A}C)\quad\text{and}\quad\mathrm{Res}^{C}_{A}(\Sigma)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\Sigma\otimes_{C}(C\mathbb{1}_{A}).

Thus, $A\to(\mathbb{1}_{A}C)\otimes_{C}(C\mathbb{1}_{A})$ yields a map $\Delta\cong\Delta\otimes_{A}A\to\mathrm{Res}_{A}^{C}(\mathrm{Ind}_{A}^{C}(\Delta))$ . If, for example, $C\mathbb{1}_{A}C=C$ , then $\Delta\cong\mathrm{Res}_{A}^{C}(\mathrm{Ind}_{A}^{C}(\Delta))$ . $\square$

Guided by the Peirce decomposition from Example 5.3, we seek similar constructions for categories and capsules. Recall that $\mathsf{E}$ contains a subcategory $\mathsf{C}$ that contains a subcategory $\mathsf{A}$ . This containment implies that $\mathbb{1}_{\mathsf{A}}$ is contained in (rather embeds under the inclusion functors into) $\mathbb{1}_{\mathsf{C}}$ . The bicapsule action of $\mathsf{A}$ on $\Delta$ induces a $\mathsf{C}$ -bicapsule, denoted $\mathrm{Ind}_{\mathsf{A}}^{\mathsf{C}}(\Delta)$ . By mimicking modules, we can consider a formal extension process. We form the type $\Delta\otimes_{\mathsf{A}}\mathsf{C}$ whose terms are pairs, denoted $\delta\otimes c$ for $\delta:\Delta$ and $c:\mathsf{C}$ , subject to the equivalence relation $(\delta\cdot a)\otimes c=\delta\otimes(ac)$ . Then we equip this type with the right $\mathsf{C}$ -action $(\delta\otimes c)\cdot c^{\prime}=\delta\otimes(cc^{\prime})$ . Defining $\mathsf{A}\backslash\mathsf{C}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\{\mathsf{A}c\mid c:\mathsf{C}\}$ , we write

\displaystyle\Delta\otimes_{\mathsf{A}}\mathsf{C}

\displaystyle=\coprod_{\mathsf{A}c:\mathsf{A}\backslash\mathsf{C}}\Delta\otimes_{\mathsf{A}}\mathsf{A}c.

We return to this construction in Section 8. Finally, since $\Delta=\mathsf{A}\rho\cdot\mathsf{A}$ and $\mathsf{C}$ are both subtypes of $\mathsf{E}$ , the product in $\mathsf{E}$ defines a map $\Delta\times\mathsf{C}\to\mathsf{E}$ that factors through $\Delta\otimes_{\mathsf{A}}\mathsf{C}$ . The image of the map is a cyclic $\mathsf{C}$ -bicapsule $\Sigma$ embedded in $\mathsf{E}$ , with corresponding $\mathsf{C}$ -bimorphism $\mathcal{S}:\mathsf{C}\to\mathsf{E}$ . The following theorem states that this is always possible if $\mathsf{A}$ is full in $\mathsf{C}$ . Table 3 summarizes some of the notation fixed throughout this section.

$\mathsf{E}$	eastern variety
$\mathsf{B},\mathsf{C}$	subcategories of $\mathsf{E}$
$\mathsf{A}$	full subcategory of $\mathsf{C}$

bimorphism	monic counital	cyclic bicapsule
$\mathcal{R}:\mathsf{A}\to\mathsf{E}$	$\rho=\mathcal{R}(\mathbb{1}_{\mathsf{A}})$	$\Delta=A\rho\cdot A$
$\mathcal{S}:\mathsf{C}\to\mathsf{E}$	$\sigma=\mathcal{S}(\mathbb{1}_{\mathsf{C}})$	$\Sigma=C\sigma\cdot C$

Table 3. Data for the proof of Theorem 5.4

Theorem 5.4 (Extension).

Let $\mathsf{E},\mathsf{C},\mathsf{A},\Delta$ be as in Table 3. If $\mathsf{A}$ is full in $\mathsf{C}$ , then there is a cyclic $\mathsf{C}$ -bicapsule $\mathsf{\Sigma}$ on $\mathsf{E}$ and unique cyclic $\mathsf{A}$ -bicapsules $\mathsf{\Upsilon}$ , $\mathsf{\Lambda}$ on $\mathsf{E}$ such that

\Delta=\mathrm{Res}_{\mathsf{A}}^{\mathsf{C}}(\Sigma)\otimes_{\mathsf{A}}\Upsilon\quad\text{and}\quad\mathrm{Res}_{\mathsf{A}}^{\mathsf{C}}(\Sigma)=\Delta\otimes_{\mathsf{A}}\Lambda.

We briefly describe the idea of the proof. We start with a cyclic $\mathsf{A}$ -bicapsule $\Delta$ with associated $\mathsf{A}$ -bimorphism $\mathcal{R}:\mathsf{A}\to\mathsf{E}$ . We seek an extension of $\mathcal{R}$ to a $\mathsf{C}$ -bimorphism $\mathcal{S}\colon\mathsf{C}\to\mathsf{E}$ that satisfies $\mathcal{S}\mathcal{L}=\mathcal{R}$ , where $\mathcal{L}\colon\mathsf{A}\to\mathsf{C}$ is the inclusion functor. If this holds, then, for every $e:\mathbb{1}_{\mathsf{A}}$ and every $c:\mathsf{C}$ with $c\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}\mathcal{R}(e)$ ,

c\cdot\mathcal{R}(e)=c\cdot\mathcal{S}\mathcal{L}(e)=\mathcal{S}(c\cdot e)=\mathcal{S}(c)=\mathcal{S}(\mathbin{\blacktriangleleft}c)\cdot c.

We now derive some necessary conditions for a putative $\mathcal{S}$ of this type. Recall from (3.3) that the notation $\alpha\ll\beta$ for morphisms $\alpha$ and $\beta$ implies that there is a morphism $\gamma$ such that $\alpha=\beta\gamma$ . Applying Lemma 3.24 to $c\cdot\mathcal{R}(e)=\mathcal{S}(c\mathbin{\blacktriangleleft})\cdot c$ yields $\mathrm{im}(c\cdot\mathcal{R}(e))\ll\mathrm{im}(\mathcal{S}(\mathbin{\blacktriangleleft}c))$ . For $f:\mathbb{1}_{\mathsf{C}}$ define

\displaystyle\mathbb{U}_{\mathsf{C}}(f)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{e:\mathbb{1}_{\mathsf{A}}}f\mathsf{C}\cdot e.

The left $\mathsf{A}$ -actions on $\mathsf{C}$ and $\mathsf{E}$ are regular, as is the left $\mathsf{C}$ -action on $\mathsf{E}$ . Hence, for $\langle e,c\rangle:\mathbb{U}_{\mathsf{C}}(f)$ ,

c\lhd=(c\cdot\mathbb{1}_{\mathsf{E}})\mathbin{\blacktriangleleft}=(c\mathbin{\blacktriangleleft})\cdot\mathbb{1}_{\mathsf{E}}=e\cdot\mathbb{1}_{\mathsf{E}}.

Therefore, $c\lhd=e\cdot\mathbb{1}_{\mathsf{E}}=\mathbin{\blacktriangleleft}(e\cdot\mathcal{R}(e))=\mathbin{\blacktriangleleft}\mathcal{R}(e)=\lhd\mathcal{R}(e)$ , so $c\cdot\mathcal{R}(e)$ is defined. Since $\mathrm{im}(c\cdot\mathcal{R}(e))\ll\mathrm{im}(\mathcal{S}(f))$ holds for every $\langle e,c\rangle:\mathbb{U}_{\mathsf{C}}(f)$ , we can make a single inclusion (see (3.5)):

(5.2)

\mathrm{im}\left(\coprod_{{\langle e,c\rangle\in\mathbb{U}_{\mathsf{C}}(f)}}\mathrm{im}(c\cdot\mathcal{R}(e))\right)\ll\mathrm{im}(\mathcal{S}(f)).

Observe that (5.2) also holds if, instead of $\mathcal{R}=\mathcal{SL}$ , we assume that there exists $\mathcal{T}:\mathsf{A}\to\mathsf{E}$ such that $\mathcal{R}(a)=\mathrm{Res}_{\mathsf{A}}^{\mathsf{C}}(\mathcal{S})(a)\mathcal{T}(a\mathbin{\blacktriangleleft})$ for all $a:\mathsf{A}$ ; here $\mathrm{Res}_{\mathsf{A}}^{\mathsf{C}}(\mathcal{S})(a)=\mathcal{S}(\mathbb{1}_{\mathsf{C}}\cdot a)$ denotes the restriction of $\mathcal{S}$ to $\mathsf{A}$ . This motivates us to choose $\mathcal{S}$ such that $\mathcal{S}(c)$ is defined as the left hand side of (5.2), and then solve for a suitable $\mathcal{T}$ .

In the language of bimorphisms, Theorem 5.4 asserts that there exists an $\mathsf{A}$ -bimorphism $\mathcal{T}\colon\mathsf{A}\to\mathsf{E}$ such that, for $a:\mathsf{A}$ ,

(5.3)

\displaystyle\mathcal{R}(a)

\displaystyle=\mathcal{S}(\mathbb{1}_{\mathsf{C}}\cdot(\mathbin{\blacktriangleleft}a))\mathcal{T}(a)=\mathcal{S}(\mathbb{1}_{\mathsf{C}}\cdot a)\mathcal{T}(a\mathbin{\blacktriangleleft})

where $\mathcal{S}$ is the $\mathsf{C}$ -bimorphism corresponding to $\Sigma$ ; we use this language in its proof. The second equality in (5.3) reflects the tensor product over $\mathsf{A}$ shown in Theorem 5.4.

5.3. Building blocks

We prove Theorem 5.4 in Section 5.4 using the three intermediate results presented in this section.

Lemma 5.5.

Let $\mathsf{C}$ and $\mathsf{E}$ be as in Table 3. For $\sigma:\prod_{f:\mathbb{1}_{\mathsf{C}}}(f~\cdot\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\hookrightarrow$}\vss}}})$ , the following are equivalent.

(1)

There is a $\mathsf{C}$ -bicapsule $\Sigma$ on $\mathsf{E}$ such that the function $\mathcal{S}:\mathsf{C}\to\Sigma$ given by $\mathcal{S}(c)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}c\cdot\sigma_{c\mathbin{\blacktriangleleft}}$ is a $\mathsf{C}$ -bimorphism.
(2)

For all $c:\mathsf{C}$ , $c\cdot\sigma_{c\mathbin{\blacktriangleleft}}\ll\sigma_{\mathbin{\blacktriangleleft}c}$ .

Proof.

We assume (1) holds and prove (2). By Proposition 4.10 (b), there exists a unique functor $\mathcal{G}:\mathsf{C}\to\mathsf{E}$ that induces the action of $\mathsf{C}$ on the right of $\mathsf{E}$ . Since $\mathcal{S}$ is a function and a $\mathsf{C}$ -bimorphism by assumption, $c\lhd=\lhd\sigma_{c\mathbin{\blacktriangleleft}}$ for all $c:\mathsf{C}$ , and

\displaystyle c\cdot\sigma_{c\mathbin{\blacktriangleleft}}

\displaystyle=\mathcal{S}(c)=\mathcal{S}((\mathbin{\blacktriangleleft}c)\cdot c)=\mathcal{S}(\mathbin{\blacktriangleleft}c)\cdot c=((\mathbin{\blacktriangleleft}c)\cdot\sigma_{(\mathbin{\blacktriangleleft}c)\mathbin{\blacktriangleleft}})\cdot c=\sigma_{\mathbin{\blacktriangleleft}c}\mathcal{G}(c).

Thus, (2) holds.

We now assume (2) holds and prove (1). First, we show that an $x:\mathsf{E}$ satisfying $c\cdot\sigma_{c\mathbin{\blacktriangleleft}}=\sigma_{\mathbin{\blacktriangleleft}c}x$ is unique. Suppose $y:\mathsf{E}$ satisfies $c\cdot\sigma_{c\mathbin{\blacktriangleleft}}=\sigma_{\mathbin{\blacktriangleleft}c}y$ , so $\sigma_{\mathbin{\blacktriangleleft}c}x=\sigma_{\mathbin{\blacktriangleleft}c}y$ . Since $\sigma_{\mathbin{\blacktriangleleft}c}$ is a monomorphism, $x=y$ . We denote this unique morphism by $u_{c}:\mathsf{E}$ . Since $\sigma_{\mathbin{\blacktriangleleft}c}u_{c}$ is defined for all $c:\mathsf{C}$ ,

\displaystyle\mathbin{\blacktriangleleft}u_{\mathbin{\blacktriangleleft}c}=(\sigma_{\mathbin{\blacktriangleleft}(\mathbin{\blacktriangleleft}c)})\mathbin{\blacktriangleleft}=(\sigma_{\mathbin{\blacktriangleleft}c})\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}u_{c}.

Next, we define a right $\mathsf{C}$ -capsule structure on $\mathsf{E}$ as follows. Let $\lhd(-):\mathsf{C}\to\mathbb{1}_{\mathsf{E}}$ be given by $\lhd c=\mathbin{\blacktriangleleft}u_{c}$ , and let $(-)\lhd:\mathsf{E}\to\mathbb{1}_{\mathsf{E}}$ be given by $x\lhd=x\mathbin{\blacktriangleleft}$ . For all $c:\mathsf{C}$ and $x:\mathsf{E}$ , let $x\cdot c=xu_{c}$ , which is defined if, and only if, $x\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}u_{c}$ . Condition (2) of Definition 4.1 follows from $\lhd(\mathbin{\blacktriangleleft}c)=\mathbin{\blacktriangleleft}u_{\mathbin{\blacktriangleleft}c}=\mathbin{\blacktriangleleft}u_{c}=\lhd c$ and $u_{e}:\mathbb{1}_{\mathsf{E}}$ for all $e:\mathbb{1}_{\mathsf{C}}$ since $\sigma_{e}$ is monic. Lastly, let $c,d:\mathsf{C}$ with $c\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}d$ . Then $(cd)\cdot\sigma_{(cd)\mathbin{\blacktriangleleft}}=\sigma_{\mathbin{\blacktriangleleft}(cd)}u_{cd}=\sigma_{\mathbin{\blacktriangleleft}c}u_{cd}$ and, since we have a regular left action,

\displaystyle(cd)\cdot\sigma_{(cd)\mathbin{\blacktriangleleft}}=c\cdot(d\cdot\sigma_{(cd)\mathbin{\blacktriangleleft}})=c\cdot(d\cdot\sigma_{d\mathbin{\blacktriangleleft}})=c\cdot\sigma_{\mathbin{\blacktriangleleft}d}u_{d}=\sigma_{\mathbin{\blacktriangleleft}c}u_{c}u_{d}.

Since $\sigma_{\mathbin{\blacktriangleleft}c}$ is a monomorphism, $u_{cd}=u_{c}u_{d}$ . Hence, this defines a right $\mathsf{C}$ -capsule on $\mathsf{E}$ since $\lhd c=\mathbin{\blacktriangleleft}u_{c}:\mathbb{1}_{\mathsf{E}}$ for all $c:\mathsf{C}$ . Since $\mathsf{C}$ acts regularly on $\mathsf{E}$ on the left, there exists a $\mathsf{C}$ -bicapsule $\Sigma$ on $\mathsf{E}$ by Proposition 4.6, with the regular left and right actions just defined. Finally, we prove that $\mathcal{S}$ is a $\mathsf{C}$ -bimorphism. For all $c,x,y:\mathsf{C}$ ,

\displaystyle\mathcal{S}(cx)

\displaystyle=(cx)\cdot\sigma_{(cx)\mathbin{\blacktriangleleft}}=(cx)\cdot\sigma_{x\mathbin{\blacktriangleleft}}=c\cdot(x\cdot\sigma_{x\mathbin{\blacktriangleleft}})=c\cdot\mathcal{S}(x),

provided $c\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}x$ . If $y\mathbin{\blacktriangleleft}=\mathbin{\blacktriangleleft}c$ , then

	$\displaystyle\mathcal{S}(yc)$	$\displaystyle=(yc)\cdot\sigma_{(yc)\mathbin{\blacktriangleleft}}=(yc)\cdot\sigma_{c\mathbin{\blacktriangleleft}}=y\cdot(c\cdot\sigma_{c\mathbin{\blacktriangleleft}})=y\cdot(\sigma_{\mathbin{\blacktriangleleft}c}u_{c})=(y\cdot\sigma_{y\mathbin{\blacktriangleleft}})u_{c}$
		$\displaystyle=\mathcal{S}(y)\cdot c.\qed$

Lemma 5.6.

For $\mathsf{E},\mathsf{C},\mathcal{R}$ as in Table 3, define $\sigma:\coprod_{f:\mathbb{1}_{\mathsf{C}}}(f~\cdot\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\hookrightarrow$}\vss}}})$ via

\sigma_{f}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathrm{im}\left(\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(f)}\mathrm{im}(x\cdot\mathcal{R}(e))\right).

For each $c:\mathsf{C}$ , there is a unique $y:\mathsf{E}$ satisfying $c\cdot\sigma_{c\mathbin{\blacktriangleleft}}=\sigma_{\mathbin{\blacktriangleleft}c}y$ .

Proof.

Let $c:\mathsf{C}$ , so $c\lhd=c\mathbin{\blacktriangleleft}$ , and $c\mathbin{\blacktriangleleft}=\lhd\sigma_{c\mathbin{\blacktriangleleft}}$ by definition of $\sigma$ . We show that $c\cdot\sigma_{c\mathbin{\blacktriangleleft}}\ll\sigma_{\mathbin{\blacktriangleleft}c}$ . By Lemma 3.23,

\displaystyle(\forall\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(f))

\displaystyle c\cdot\mathrm{im}(x\cdot\mathcal{R}(e))

\displaystyle\ll\mathrm{im}(c\cdot(x\cdot\mathcal{R}(e)))=\mathrm{im}((cx)\cdot\mathcal{R}(e)).

Thus, by Fact 3.25 (d),

(5.4)

\displaystyle\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(f)}\left(c\cdot\mathrm{im}(x\cdot\mathcal{R}(e))\right)

\displaystyle\ll\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(f)}\mathrm{im}((cx)\cdot\mathcal{R}(e)).

Therefore, using (3.5),

$\displaystyle c\cdot\mathrm{im}\left(\coprod_{\langle e,x\rangle}\mathrm{im}(x\cdot\mathcal{R}(e))\right)$	$\displaystyle\ll\mathrm{im}\left(c\cdot\coprod_{\langle e,x\rangle}\mathrm{im}(x\cdot\mathcal{R}(e))\right)$	$\displaystyle(\text{Lemma~\ref{lem:im}})$
	$\displaystyle=\mathrm{im}\left(\coprod_{\langle e,x\rangle}(c\cdot\mathrm{im}(x\cdot\mathcal{R}(e)))\right)$	$\displaystyle(\text{Fact~\ref{fact:coprod}\ref{factpart:factor-out}})$
	$\displaystyle\ll\mathrm{im}\left(\coprod_{\langle e,x\rangle}\mathrm{im}((cx)\cdot\mathcal{R}(e))\right)$	$\displaystyle(\text{Equation (\ref{eq:coprod-ineq})})$

where all of the coproducts are over $\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(c\mathbin{\blacktriangleleft})$ . By Fact 3.25 (e),

\mathrm{im}\left(\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(c\mathbin{\blacktriangleleft})}\mathrm{im}((cx)\cdot\mathcal{R}(e))\right)\ll\mathrm{im}\left(\coprod_{\langle e,z\rangle:\mathbb{U}_{\mathsf{C}}(\mathbin{\blacktriangleleft}c)}\mathrm{im}(z\cdot\mathcal{R}(e))\right).

Putting this together, we deduce that

\displaystyle c\cdot\sigma_{c\mathbin{\blacktriangleleft}}

\displaystyle=c\cdot\mathrm{im}\left(\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(c\mathbin{\blacktriangleleft})}\mathrm{im}(x\cdot\mathcal{R}(e))\right)\ll\mathrm{im}\left(\coprod_{\langle e,z\rangle:\mathbb{U}_{\mathsf{C}}(\mathbin{\blacktriangleleft}c)}\mathrm{im}(z\cdot\mathcal{R}(e))\right)=\sigma_{\mathbin{\blacktriangleleft}c},

so $c\cdot\sigma_{c\mathbin{\blacktriangleleft}}=\sigma_{c\mathbin{\blacktriangleleft}}y$ for some $y:\mathsf{E}$ . Since $\sigma_{\mathbin{\blacktriangleleft}c}$ is monic, $y$ is unique. ∎

Proposition 5.7.

Let $\mathsf{E},\mathsf{C},\mathsf{A},\mathcal{R}$ be as in Table 3. If $\mathsf{A}$ is full in $\mathsf{C}$ , then $\mathcal{S}:\mathsf{C}\to\mathsf{E}$ defined by

\mathcal{S}(c)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}c\cdot\mathrm{im}\left(\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}(c\mathbin{\blacktriangleleft})}\mathrm{im}(x\cdot\mathcal{R}(e))\right)

is a $\mathsf{C}$ -bimorphism, and there exists a unique $\lambda:\prod_{f:\mathbb{1}_{\mathsf{A}}}f\!\!\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\!\!f$ such that for all $a:\mathsf{A}$ ,

\mathcal{R}(a)=\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})\lambda_{a\mathbin{\blacktriangleleft}}\quad\text{and}\quad\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})=\mathcal{R}(a)\lambda_{a\mathbin{\blacktriangleleft}}^{-1}.

Proof.

Take $e,f:\mathbb{1}_{\mathsf{A}}$ , and recall that $\mathsf{A}$ acts regularly on both the left and right of $\mathsf{C}$ . Since $\mathsf{A}$ is full in $\mathsf{C}$ , these actions are full, so

f\cdot\mathsf{C}\cdot e=\mathbb{1}_{\mathsf{C}}\cdot(f\mathsf{A}e)=(f\mathsf{A}e)\cdot\mathbb{1}_{\mathsf{C}}.

Since the left actions of $\mathsf{A}$ on $\mathsf{C}$ and on $\mathsf{E}$ and the left action of $\mathsf{C}$ on $\mathsf{E}$ are regular, for each $a:\mathsf{A}$ and $x:\mathsf{E}$ with $a\lhd=\lhd x$ ,

(5.5)

\displaystyle(a\cdot\mathbb{1}_{\mathsf{C}})\cdot x

\displaystyle=a\cdot x.

Fix $a:\mathsf{A}$ . Set $c=a\cdot\mathbb{1}_{\mathsf{C}}$ , so $(c\mathbin{\blacktriangleleft})\mathsf{C}=(a\mathbin{\blacktriangleleft})\cdot\mathsf{C}$ . Thus, since the $\mathsf{A}$ -action on $\mathsf{C}$ is full,

(5.6)

\displaystyle\mathbb{U}_{\mathsf{C}}(c\mathbin{\blacktriangleleft})\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\bigsqcup_{e:\mathbb{1}_{\mathsf{A}}}\left((c\mathbin{\blacktriangleleft})\mathsf{C}\cdot e\right)

\displaystyle=\bigsqcup_{e:\mathbb{1}_{\mathsf{A}}}\left((a\mathbin{\blacktriangleleft})\cdot\mathsf{C}\cdot e\right)=((a\mathbin{\blacktriangleleft})\mathsf{A})\cdot\mathbb{1}_{\mathsf{C}},

where $(a\mathbin{\blacktriangleleft})\mathsf{A}$ acts on $\mathbb{1}_{\mathsf{C}}$ in the final expression. Therefore,

$\displaystyle\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})$	$\displaystyle=a\cdot\mathrm{im}\left(\coprod_{\langle e,x\rangle:\mathbb{U}_{\mathsf{C}}((a\mathbin{\blacktriangleleft})\cdot\mathbb{1}_{\mathsf{C}})}\mathrm{im}(x\cdot\mathcal{R}(e))\right)$	$\displaystyle(\text{Equation \eqref{eqn:C-to-A}})$
	$\displaystyle=a\cdot\mathrm{im}\left(\coprod_{a^{\prime}:(a\mathbin{\blacktriangleleft})\mathsf{A}}\mathrm{im}(a^{\prime}\cdot\mathcal{R}(a^{\prime}\mathbin{\blacktriangleleft}))\right)$	$\displaystyle(\text{Equation \eqref{eqn:subscripts}})$
	$\displaystyle=a\cdot\mathrm{im}\left(\coprod_{a^{\prime}:(a\mathbin{\blacktriangleleft})\mathsf{A}}\mathrm{im}(\mathcal{R}(a\mathbin{\blacktriangleleft})\cdot a^{\prime})\right)$	$\displaystyle(\text{$\mathsf{A}$-bimorphism, $\mathbin{\blacktriangleleft}a^{\prime}=a\mathbin{\blacktriangleleft}$})$
	$\displaystyle\ll a\cdot\mathcal{R}(a\mathbin{\blacktriangleleft})=\mathcal{R}(a).$	$\displaystyle(\text{Lemma~\ref{lem:im-monic}, Fact~\ref{fact:coprod}\ref{factpart:factor-out}})$

For the application of Lemma 3.24 in the last step, recall that $\mathcal{R}(e)$ is monic for $e:\mathsf{A}$ by our assumption (Table 3).

We establish the other direction as follows:

$\displaystyle\mathcal{R}(a\mathbin{\blacktriangleleft})$	$\displaystyle\ll\mathrm{im}(\mathcal{R}(a\mathbin{\blacktriangleleft}))=\mathrm{im}((a\mathbin{\blacktriangleleft})\cdot\mathcal{R}(a\mathbin{\blacktriangleleft}))$	$\displaystyle(\text{Theorem~\ref{thm:Noether}})$
	$\displaystyle\ll\coprod_{a^{\prime}:(a\mathbin{\blacktriangleleft})\mathsf{A}}\mathrm{im}(a^{\prime}\cdot\mathcal{R}(a^{\prime}\mathbin{\blacktriangleleft}))$	$\displaystyle(\text{Fact~\ref{fact:coprod}\ref{factpart:smaller-coprod}})$
	$\displaystyle\ll\mathrm{im}\left(\coprod_{a^{\prime}:(a\mathbin{\blacktriangleleft})\mathsf{A}}\mathrm{im}(a^{\prime}\cdot\mathcal{R}(a^{\prime}\mathbin{\blacktriangleleft}))\right).$	$\displaystyle(\text{Theorem~\ref{thm:Noether}})$

Acting with $a:\mathsf{A}$ from the left, we obtain $\mathcal{R}(a)\ll\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})$ .

From both computations, there exist $\lambda,\mu:\prod_{f:\mathbb{1}_{\mathsf{A}}}f\mathsf{E}f$ such that

\displaystyle\mathcal{R}(a)

\displaystyle=\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})\lambda_{a\mathbin{\blacktriangleleft}},

\displaystyle\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})

\displaystyle=\mathcal{R}(a)\mu_{a\mathbin{\blacktriangleleft}}.

It remains to show that $\mu_{a\mathbin{\blacktriangleleft}}=\lambda_{a\mathbin{\blacktriangleleft}}^{-1}$ for all $a:\mathsf{A}$ and $\lambda$ is unique. For all $e:\mathbb{1}_{\mathsf{A}}$ , $\mathcal{R}(e)$ is monic by the assumptions in Theorem 5.4, and $\mathcal{S}(e\cdot\mathbb{1}_{\mathsf{C}})$ is also monic by the definition of $\mathcal{S}$ . Since $\mathcal{R}(e)$ is monic,

\displaystyle\mathcal{R}(e)

\displaystyle=\mathcal{S}(e\cdot\mathbb{1}_{\mathsf{C}})\lambda_{e}=\mathcal{R}(e)\mu_{e}\lambda_{e}

implies $\mu_{e}\lambda_{e}:\mathbb{1}_{\mathsf{E}}$ . Similarly, $\lambda_{e}\mu_{e}:\mathbb{1}_{\mathsf{E}}$ because $\mathcal{S}(e\cdot\mathbb{1}_{\mathsf{C}})$ is monic and

\displaystyle\mathcal{S}(e\cdot\mathbb{1}_{\mathsf{C}})

\displaystyle=\mathcal{R}(e)\mu_{e}=\mathcal{S}(e\cdot\mathbb{1}_{\mathsf{C}})\lambda_{e}\mu_{e}.

The uniqueness of $\lambda$ follows since $\mathcal{R}(e)$ is monic. ∎

5.4. Proof of Theorem 5.4

Let $\mathcal{S}:\mathsf{C}\to\mathsf{E}$ be the $\mathsf{C}$ -bimorphism in Proposition 5.7. This proposition shows that there exists a unique $\lambda:\prod_{f:\mathbb{1}_{\mathsf{A}}}f\!\!\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\!\!f$ such that for all $a:\mathsf{A}$ ,

(5.7)

\displaystyle\mathcal{R}(a)

\displaystyle=\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})\lambda_{a\mathbin{\blacktriangleleft}}.

Since $\mathcal{R}$ is an $\mathsf{A}$ -bimorphism,

(5.8)

\displaystyle(a\cdot\mathbb{1}_{\mathsf{E}})\cdot\mathcal{R}(a\mathbin{\blacktriangleleft})

\displaystyle=\mathcal{R}(a)=\mathcal{R}(\mathbin{\blacktriangleleft}a)\cdot(\mathbb{1}_{\mathsf{E}}\cdot a).

Let $\Sigma$ be the $\mathsf{C}$ -bicapsule on $\mathsf{E}$ defined by the $\mathsf{C}$ -bimorphism $\mathcal{S}$ . Both $\Delta$ and $\Sigma$ are bicapsules, so applying (5.7) to (5.8) yields

(5.9)

\displaystyle(a\cdot\mathbb{1}_{\mathsf{E}})\mathcal{S}((a\mathbin{\blacktriangleleft})\cdot\mathbb{1}_{\mathsf{C}})\lambda_{a\mathbin{\blacktriangleleft}}

\displaystyle=\mathcal{S}((\mathbin{\blacktriangleleft}a)\cdot\mathbb{1}_{\mathsf{C}})\lambda_{\mathbin{\blacktriangleleft}a}(\mathbb{1}_{\mathsf{E}}\cdot a).

Since the left $\mathsf{C}$ -action on $\mathsf{E}$ and the left $\mathsf{A}$ -action on $\mathsf{C}$ are regular, $a\cdot\mathbb{1}_{\mathsf{E}}=(a\cdot\mathbb{1}_{\mathsf{C}})\cdot\mathbb{1}_{\mathsf{E}}$ . Thus, $(a\cdot\mathbb{1}_{\mathsf{E}})\mathcal{S}((a\mathbin{\blacktriangleleft})\cdot\mathbb{1}_{\mathsf{C}})=\mathcal{S}(a\cdot\mathbb{1}_{\mathsf{C}})=\mathcal{S}((\mathbin{\blacktriangleleft}a)\cdot\mathbb{1}_{\mathsf{C}})(\mathbb{1}_{\mathsf{E}}\cdot(\mathbb{1}_{\mathsf{C}}\cdot a))$ . Applying this to (5.9) and using the monic property of $\mathcal{S}((\mathbin{\blacktriangleleft}a)\cdot\mathbb{1}_{\mathsf{C}})$ , we deduce that

\displaystyle(\mathbb{1}_{\mathsf{E}}\cdot(\mathbb{1}_{\mathsf{C}}\cdot a))\lambda_{a\mathbin{\blacktriangleleft}}

\displaystyle=\lambda_{\mathbin{\blacktriangleleft}a}(\mathbb{1}_{\mathsf{E}}\cdot a).

Since the actions are capsules, $\lambda$ defines a natural transformation. By Proposition 4.10 (a), the function $a\mapsto(\mathbb{1}_{\mathsf{E}}\cdot(\mathbb{1}_{\mathsf{C}}\cdot a))\lambda_{a\mathbin{\blacktriangleleft}}$ defines an $\mathsf{A}$ -bimorphism $\mathcal{T}:\mathsf{A}\to\mathsf{E}$ . Thus, $\mathcal{T}(a\mathbin{\blacktriangleleft})=\lambda_{a\mathbin{\blacktriangleleft}}:\,\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ , and therefore

\displaystyle\mathcal{R}(a)

\displaystyle=\mathcal{S}(\mathbb{1}_{\mathsf{C}}\cdot a)\mathcal{T}(a\mathbin{\blacktriangleleft})=\mathcal{S}(\mathbb{1}_{\mathsf{C}}\cdot(\mathbin{\blacktriangleleft}a))(\mathbb{1}_{\mathsf{E}}\cdot(\mathbb{1}_{\mathsf{C}}\cdot a))\mathcal{T}(a\mathbin{\blacktriangleleft})=\mathcal{S}(\mathbb{1}_{\mathsf{C}}\cdot(\mathbin{\blacktriangleleft}a))\mathcal{T}(a).

The uniqueness of $\mathcal{T}$ follows from Proposition 4.10 (b) and the uniqueness of $\lambda$ . ∎

5.5. Proof of Theorem 1 for eastern varieties

Recall that $\text{Counital}(\mathsf{B},\mathsf{E})$ denotes the type of all counitals $\iota:\mathcal{K}\mathcal{C}\Rightarrow\mathcal{I}$ , where $\mathsf{B}\leqslant\mathsf{E}$ and $\mathsf{C}$ are categories, $\mathcal{C}:\mathsf{B}\to\mathsf{C}$ is a functor, and $\mathcal{I}:\mathsf{B}\to\mathsf{E}$ and $\mathcal{K}:\mathsf{C}\to\mathsf{E}$ are inclusion functors. Let $\text{Unital}(\mathsf{B},\mathsf{E})$ be the type of all unitals $\pi:\mathcal{I}\Rightarrow\mathcal{K}\mathcal{C}$ ; these are the duals of counitals. Recall from Theorem 3.22 that $\mathrm{im}$ and $\mathrm{coim}$ produce categorical morphisms, and from Section 3.9 the equivalence relations on monomorphisms and epimorphisms. Our use of set theory notation in the following generalization of Theorem 1 is justified because we compare subsets of a fixed algebra.

Theorem 1-cat.

Let $\mathsf{E}$ be an eastern variety. For every $G:\mathsf{E}$ , the following equalities of sets hold up to equivalence:

(1)	$\displaystyle\{\iota:H\hookrightarrow G\mid\iota\text{ is $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$-invariant}\}$	$\displaystyle=\left\{\text{\rm im}(\eta_{G})\mid\eta:\text{\rm Counital}\left(\mathrel{\mathop{\mathsf{\mathsf{E}}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}},\mathsf{E}\right)\right\};$
(2)	$\displaystyle\{\pi:G\twoheadrightarrow Q\mid\pi\text{ is $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$-invariant}\}$	$\displaystyle=\left\{\text{\rm coim}(\tau_{G})\mid\tau:\text{\rm Unital}\left(\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}},\mathsf{E}\right)\right\};$
(3)	$\displaystyle\{\iota:H\hookrightarrow G\mid\iota\text{ is $\mathsf{E}$-invariant}\}$	$\displaystyle=\left\{\text{\rm im}(\eta_{G})\mid\eta:\text{\rm Counital}(\mathsf{E},\mathsf{E})\right\};$
(4)	$\displaystyle\{\pi:G\twoheadrightarrow Q\mid\pi\text{ is $\mathsf{E}$-invariant}\}$	$\displaystyle=\left\{\text{\rm coim}(\tau_{G})\mid\tau:\text{\rm Unital}(\mathsf{E},\mathsf{E})\right\}.$

Proof.

We prove (1) in detail; the proof of (3) is analogous but requires replacing $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ with $\mathsf{E}$ . The proofs of (2) and (4) are dual to the proofs of (1) and (3), respectively.

Let $\iota:H\hookrightarrow G$ , which is a morphism in $\mathsf{E}$ . Recall that the single-object category $\mathsf{Aut}(G)$ consists of $G$ and all its automorphisms, and likewise for $\mathsf{Aut}(H)$ . Both are subcategories of $\mathsf{E}$ , and full subcategories of $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ . We denote the relevant inclusion functors by $\mathcal{I}:\mathsf{Aut}(G)\to\mathsf{E}$ , $\mathcal{J}:\mathsf{Aut}(H)\to\mathsf{E}$ , $\mathcal{L}:\mathsf{Aut}(G)\to\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ , and $\mathcal{K}:\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\;\to\mathsf{E}$ . As in Section 5.1, we obtain a natural transformation $\rho:\mathcal{J}\mathcal{C}\Rightarrow\mathcal{I}$ with (restriction) functor $\mathcal{C}:\mathsf{Aut}(G)\to\mathsf{Aut}(H)$ , so $\rho:\text{Counital}(\mathsf{Aut}(G),\mathsf{E})$ is a monic counital.

We now use Proposition 4.10 to pass to the associated cyclic $\mathsf{Aut}(G)$ -bicapsule $\Delta=\mathsf{Aut}(G)\cdot\rho\cdot\mathsf{Aut}(G)$ . Recall that the left action is defined by $\mathcal{I}$ , hence regular, and the right action is defined by $\mathcal{JC}$ . By construction, $\Delta$ satisfies the conditions of Theorem 5.4 since $\mathsf{Aut}(G)$ is full in $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ . We extend $\Delta$ to a cyclic $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ -bicapsule $\Sigma=\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\cdot\sigma\cdot\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ where $\sigma:\mathcal{K}\mathcal{D}\Rightarrow\mathcal{K}$ is a monic counital extending $\rho$ , namely, there exists an isomorphism $\tau_{G}:\mathcal{JC}(G)\to\mathcal{DL}(G)$ such that $\iota=\rho_{G}=\sigma_{\mathcal{L}(G)}\tau_{G}$ ; see (5.1). Since $\mathcal{L}$ is the inclusion functor, there exists an isomorphism $\tau^{\prime}:\mathsf{E}$ such that $\iota=\sigma_{G}\tau^{\prime}$ , so $\iota$ and $\sigma_{G}$ are equivalent. Hence, $\iota$ and $\mathrm{im}(\sigma_{G})$ are equivalent. Since $\sigma:\text{Counital}(\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}},\mathsf{E})$ , this proves the “ $\subseteq$ ” part of (1).

For the converse, consider $\eta:\text{Counital}(\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}},\mathsf{E})$ , say $\eta:\mathcal{HD}\Rightarrow\mathcal{K}$ for some functor $\mathcal{D}:\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\;\to\mathsf{C}$ , subcategory $\mathsf{C}\leqslant\mathsf{E}$ , and inclusion $\mathcal{H}:\mathsf{C}\to\mathsf{E}$ . If $\varphi:\mathsf{Aut}(G)$ , then $\mathcal{L}(\varphi):\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ , and so $\mathcal{K}\mathcal{L}(\varphi)\eta_{G}=\eta_{G}\mathcal{H}\mathcal{D}\mathcal{L}(\varphi)$ . Since $G=\mathcal{L}(G)=\mathcal{K}(G)$ , it follows that the morphism $\eta_{G}:\mathcal{HD}(G)\to G$ is characteristic, and therefore so is its monic image $\mathrm{im}(\eta_{G})$ . This proves the “ $\supseteq$ ” part of (1). ∎

6. Categorification of characteristic substructure

The final step in our work is to describe the source of all characteristic subgroups, and more generally characteristic substructures in eastern algebras. In Section 5, we showed that characteristic structure arises naturally from counitals. Now we demonstrate that all counitals are derived from counits. In particular, in Section 6.3, we prove the following generalization of Theorem 2 to eastern algebras.

Theorem 2-cat.

Fix an eastern variety $\mathsf{E}$ . Let $G$ be an object in $\mathsf{E}$ with subobject $H$ and inclusion $\iota:H\hookrightarrow G$ . There exist categories $\mathsf{A}$ and $\mathsf{B}$ , where $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\;\leqslant\mathsf{A}\leqslant\mathsf{E}$ , such that the following are equivalent.

(1)

$H$ is characteristic in $G$ .
(2)

There is a functor $\mathcal{C}:\mathsf{A}\to\mathsf{A}$ and a counit $\eta:\mathcal{C}\Rightarrow\operatorname{id}_{\mathsf{A}}$ such that $H=\operatorname{Im}(\eta_{G})$ .
(3)

There is an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{M}:\mathsf{B}\to\mathsf{A}$ such that $\iota=\mathcal{M}(\operatorname{id}_{G}\cdot\mathbb{1}_{\mathsf{B}})$ .

Our proof relies on the Extension Theorem 5.4 and further consideration of counitals.

Definition 6.1.

Fix a category $\mathsf{E}$ with subcategories $\mathsf{A}$ and $\mathsf{B}$ and inclusion functors $\mathcal{I}:\mathsf{A}\to\mathsf{E}$ and $\mathcal{J}:\mathsf{B}\to\mathsf{E}$ . A counital $\eta:\mathcal{JC}\Rightarrow\mathcal{I}$ is isosceles if $\mathsf{A}=\mathsf{B}$ and $\mathcal{I}=\mathcal{J}$ , and flat if, in addition, $\mathsf{A}=\mathsf{B}=\mathsf{E}$ and $\mathcal{I}=\mathcal{J}=\operatorname{id}_{\mathsf{E}}$ . Otherwise, it is scalene.

Example 6.2.

We mention three examples in $\mathsf{Grp}$ and illustrate their natural transformations in Figure 5. The first two are the derived subgroup and the centre of a group considered in Example 1.4. For the third example, we consider an arbitrary characteristic subgroup $H$ of a group $G$ . As discussed in Section 5.2, define $\mathsf{Aut}(G)$ to be the category with one object $G$ and its morphisms are the automorphisms of $G$ . Hence, $\mathsf{Aut}(G)$ and $\mathsf{Aut}(H)$ are subcategories of $\mathsf{Grp}$ with inclusion functors $\mathcal{J}$ and $\mathcal{K}$ , respectively. We define a functor $\mathcal{C}:\mathsf{Aut}(G)\to\mathsf{Aut}(H)$ by mapping $G$ to $H$ and automorphisms of $G$ to their restriction to $H$ , and so obtain a natural transformation $\iota:\mathcal{K}\mathcal{C}\Rightarrow\mathcal{J}$ . $\square$

(a) The derived subgroup

(b) The center

(c) A characteristic subgroup

Figure 5. Natural transformations from Example 6.2

In our study of characteristic structure we consider the three types of counitals. First, we use induced actions from Theorem 6.5 to pass from a scalene counital to one that is isosceles. Next, we work with isosceles counitals to determine an intermediate class of isosceles counitals known as internal counitals. Finally, we show that internal counitals are completely determined by a morphism of bicapsules.

Counits are common in many categorical contexts; for example, they occur for every adjoint functor pair. The case of flat counitals coincides precisely with the stricter class of fully-invariant substructures.

6.1. Composing counitals

In this section, we describe two ways to construct new counitals from given counitals by composing natural transformations and functors in different ways. These are two instances of a much larger theory; see [Baez, Power]. Figure 4 illustrates the usual composition of natural transformations. We now describe how to compose a functor with a natural transformation. Consider functors $\mathcal{F},\mathcal{G}:\mathsf{B}\to\mathsf{A}$ , $\mathcal{H}:\mathsf{C}\to\mathsf{B}$ , and $\mathcal{K}:\mathsf{A}\to\mathsf{D}$ for categories $\mathsf{A}$ , $\mathsf{B}$ , $\mathsf{C}$ , and $\mathsf{D}$ , and a natural transformation $\eta:\mathcal{F}\Rightarrow\mathcal{G}$ . Define $\eta\mathcal{H}:\mathcal{F}\mathcal{H}\Rightarrow\mathcal{G}\mathcal{H}$ by setting $(\eta\mathcal{H})_{X}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\eta_{\mathcal{H}(X)}$ for each object $X$ in $\mathsf{C}$ . Similarly, define $\mathcal{K}\eta:\mathcal{K}\mathcal{F}\Rightarrow\mathcal{K}\mathcal{G}$ by setting $(\mathcal{K}\eta)_{Y}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathcal{K}(\eta_{Y})$ for each $Y$ in $\mathsf{B}$ . The effects of $\eta\mathcal{H}$ and $\mathcal{K}\eta$ are displayed in Figure 6.

(a) A diagram for

\eta\mathcal{H}

(b) A diagram for

\mathcal{K}\eta

Figure 6. Composing natural transformations with functors

The composition we describe next is specific to natural transformations of a particular form, which include counitals. It composes two natural transformations that share a functor and reflects our expectation that the characteristic relation is transitive. In $\mathsf{Grp}$ , for example, given a counital describing a characteristic subgroup $H$ of $G$ , and a counital describing a characteristic subgroup $K$ of $H$ , we expect to have a counital that prescribes how $K$ is characteristic in $G$ .

To that end, suppose $\mathsf{E}$ is a category of eastern algebras with subcategories $\mathsf{A}$ , $\mathsf{B}$ , and $\mathsf{C}$ , and respective inclusions $\mathcal{I}$ , $\mathcal{J}$ , and $\mathcal{K}$ . Suppose $\eta:\mathcal{J}\mathcal{C}\Rightarrow\mathcal{I}$ and $\mu:\mathcal{K}\mathcal{D}\Rightarrow\mathcal{J}$ are natural transformations. Define $\mu\triangledown\eta:\mathcal{KDC}\Rightarrow\mathcal{I}$ by

\displaystyle(\mu\triangledown\eta)_{X}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\eta_{X}\mu_{\mathcal{C}(X)}

for all objects $X$ in $\mathsf{A}$ , see Figure 7. This construction reflects the fact that being a characteristic substructure is a transitive property.

Figure 7. The

\triangledown

-composition of counitals explains transitivity

6.2. Categorifying isosceles counitals

All extensions used in our proof of Theorem 1-cat lead to isosceles counitals. Counits—namely, counitals $\mathcal{J}\mathcal{C}\Rightarrow\mathcal{I}$ in which $\mathcal{J}=\mathcal{I}$ is the identity functor—are one source of isosceles counitals. This hints at a way to characterize characteristic subgroups.

We now prove that all counitals arising from characteristic subgroups extend to isosceles counitals, thereby proving Theorem 2-cat. The most direct proof might utilize Kan lifts, the dual of the better known Kan extensions [Riehl]*Chapter 6, but we give a self-contained proof.

Let $\mathcal{I}:\mathsf{A}\to\mathsf{C}$ be an inclusion functor of categories and let $\mathcal{C}:\mathsf{A}\to\mathsf{C}$ be a functor. If $\iota:\mathcal{C}\Rightarrow\mathcal{I}$ is a natural transformation, then, for every object $X$ in $\mathsf{A}$ , the morphism $\iota_{X}:\mathcal{C}(X)\to\mathcal{I}(X)$ is a morphism in $\mathsf{C}$ . We consider the special case when this morphism is also in $\mathsf{A}$ .

Definition 6.3.

A natural transformation $\iota:\mathcal{C}\Rightarrow\mathcal{I}$ is internal if, for every object $X$ in $\mathsf{A}$ , the morphism $\iota_{X}$ is a morphism in $\mathsf{A}$ .

The property of being internal is strong. Take, for example, $\mathsf{A}=\;\mathrel{\mathop{\mathsf{C}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ , so the morphisms are exclusively isomorphisms. If $\iota$ is internal, then $\iota_{X}:\mathcal{C}(X)\to X$ is an isomorphism. Such an $\iota$ does not identify a new substructure. In other words, $\mathsf{A}$ has too few morphisms for our purposes. By extending the types of morphisms, we prove in Proposition 6.4 that every monic isosceles counital lifts to an internal one, see Figure 8 for an illustration.

Figure 8. Extending an isosceles counital to an internal one

Proposition 6.4.

Let $\mathsf{E}$ be a category with subcategory $\mathsf{B}$ and inclusion $\mathcal{I}$ . Suppose every object in $\mathsf{E}$ is also an object in $\mathsf{B}$ . Let $\eta:\mathcal{I}\mathcal{E}\Rightarrow\mathcal{I}$ be a monic isosceles counital with $\mathcal{E}:\mathsf{B}\to\mathsf{B}$ . There exists a category $\mathsf{A}$ with inclusions $\mathcal{J}:\mathsf{B}\to\mathsf{A}$ and $\mathcal{K}:\mathsf{A}\to\mathsf{E}$ , a functor $\mathcal{D}:\mathsf{A}\to\mathsf{A}$ , and an internal monic isosceles counital $\hat{\eta}:\mathcal{K}\mathcal{D}\Rightarrow\mathcal{K}$ such that $\mathcal{JE}=\mathcal{DJ}$ , $\mathcal{I}=\mathcal{KJ}$ , and $\hat{\eta}\mathcal{J}=\eta$ .

Proof.

We define a subcategory $\mathsf{A}$ of $\mathsf{E}$ as follows: its objects are the objects of $\mathsf{E}$ ; its morphisms are given as finite compositions of morphisms $\mathcal{I}(\varphi):\mathsf{E}$ , where $\varphi$ is a morphism in $\mathsf{B}$ , and morphisms $\eta_{X}:\mathsf{E}$ , where $X$ an object in $\mathsf{B}$ . Hence, we have inclusions $\mathcal{J}:\mathsf{B}\to\mathsf{A}$ and $\mathcal{K}:\mathsf{A}\to\mathsf{E}$ such that $\mathcal{I}=\mathcal{KJ}$ . Since both $\mathsf{A}$ and $\mathsf{B}$ have the same objects as $\mathsf{E}$ , it follows that $\mathcal{I}$ , $\mathcal{J}$ , and $\mathcal{K}$ are the identities on objects. Moreover, $\mathcal{K}$ is the identity on morphisms.

We now construct a functor $\mathcal{D}:\mathsf{A}\to\mathsf{A}$ such that $\mathcal{J}\mathcal{E}=\mathcal{D}\mathcal{J}$ . It suffices to define $\mathcal{D}$ on morphisms and then verify that $\mathcal{D}$ is a functor. Set

\displaystyle\mathcal{D}(\varphi)

\displaystyle=\begin{cases}\mathcal{JE}(\varphi^{\prime})&\varphi=\mathcal{J}(\varphi^{\prime})\text{ for a morphism $\varphi^{\prime}$ in }\mathsf{B},\\ \eta_{\mathcal{E}(X)}&\varphi=\eta_{X}\text{ for some object $X$ in $\mathsf{B}$},\\ \mathcal{D}(\sigma)\mathcal{D}(\tau)&\varphi=\sigma\tau.\end{cases}

If $\mathcal{D}$ is well defined, then $\mathcal{D}(\varphi)$ is a morphism in $\mathsf{A}$ , and $\mathcal{J}\mathcal{E}=\mathcal{D}\mathcal{J}$ by construction. To verify that $\mathcal{D}$ is well defined, it suffices to consider the case where $\eta_{X}$ (with $X$ an object in $\mathsf{B}$ ) is also a morphism in $\mathsf{B}$ : specifically, there is a morphism $\beta:\mathsf{B}$ such that $\eta_{X}=\mathcal{I}(\beta)$ . Since $\mathcal{I}$ is the identity on objects, $\beta:\mathcal{E}(X)\to X$ . We will show that $\eta_{\mathcal{E}(X)}=\mathcal{K}\mathcal{D}(\eta_{X})=\mathcal{IE}(\beta)$ . To see this, we apply $\eta$ to the morphism $\beta:\mathcal{E}(X)\to X$ and obtain the following diagram (see shaded entry $(2,2)$ of Figure 3).

Since $\eta_{X}=\mathcal{I}(\beta)$ , the diagram implies that $\eta_{X}\eta_{\mathcal{E}(X)}=\eta_{X}\mathcal{IE}(\beta)$ . Since $\eta_{X}$ is monic by assumption, $\mathcal{IE}(\beta)=\eta_{\mathcal{E}(X)}$ . This proves that $\mathcal{D}$ is well defined.

We claim that there exists a natural transformation $\hat{\eta}:\mathcal{K}\mathcal{D}\Rightarrow\mathcal{K}$ such that $\hat{\eta}\mathcal{J}=\eta$ . Since the objects of $\mathsf{A}$ are those of $\mathsf{B}$ , we define $\hat{\eta}_{X}$ to be $\eta_{X}$ and show that this yields the required counital. First, we consider the case that $\varphi:X\to Y$ is a morphism in $\mathsf{B}$ . Then $\mathcal{K}\mathcal{D}\mathcal{J}(\varphi)=\mathcal{K}\mathcal{J}\mathcal{E}(\varphi)=\mathcal{I}\mathcal{E}(\varphi)$ , so

\displaystyle\hat{\eta}_{Y}\mathcal{K}\mathcal{D}(\mathcal{J}(\varphi))

\displaystyle=\eta_{Y}\mathcal{I}\mathcal{E}(\varphi)=\mathcal{I}(\varphi)\eta_{X}=\mathcal{K}(\mathcal{J}(\varphi))\hat{\eta}_{X}.

Now we assume $\varphi=\eta_{X}:\mathcal{IE}(X)\to\mathcal{I}(X)$ for some object $X$ in $\mathsf{B}$ . Since $\mathcal{I}$ is the identity on objects and $\mathcal{K}$ is the identity on morphisms,

\displaystyle\hat{\eta}_{\mathcal{I}(X)}\mathcal{K}\mathcal{D}(\eta_{X})

\displaystyle=\hat{\eta}_{X}\mathcal{KD}(\eta_{X})=\eta_{X}\mathcal{K}(\eta_{\mathcal{E}(X)})=\eta_{X}\eta_{\mathcal{E}(X)}=\mathcal{K}(\eta_{X})\hat{\eta}_{\mathcal{E}(X)}.

Lastly, we consider the case of an arbitrary finite composition $\varphi=\varphi_{1}\cdots\varphi_{n}$ where each $\varphi_{k}$ is either $\mathcal{J}(\varphi_{k}^{\prime})$ for some morphism $\varphi_{k}^{\prime}$ in $\mathsf{B}$ or a morphism $\eta_{X}$ for some object $X$ in $\mathsf{B}$ . It suffices to consider only the case where $n=2$ , say $\varphi=\varphi_{1}\varphi_{2}$ with $\varphi_{2}:X\to Z$ and $\varphi_{1}:Z\to Y$ . Now

	$\displaystyle\hat{\eta}_{Y}\mathcal{K}\mathcal{D}(\varphi)$	$\displaystyle=\hat{\eta}_{Y}\mathcal{K}\mathcal{D}(\varphi_{1})\mathcal{K}\mathcal{D}(\varphi_{2})$
		$\displaystyle=\mathcal{K}(\varphi_{1})\hat{\eta}_{Z}\mathcal{K}\mathcal{D}(\varphi_{2})$
		$\displaystyle=\mathcal{K}(\varphi_{1})\mathcal{K}(\varphi_{2})\hat{\eta}_{X}$
		$\displaystyle=\mathcal{K}(\varphi)\hat{\eta}_{X}.$

Thus, $\hat{\eta}:\mathcal{K}\mathcal{D}\Rightarrow\mathcal{K}$ . Since $\eta$ is monic, so is $\hat{\eta}$ . Also, $\hat{\eta}_{X}$ is a morphism in $\mathsf{A}$ for every object $X$ , so it is internal, as claimed. ∎

We now prove that every characteristic substructure of an eastern algebra is induced by a morphism of category biactions.

Theorem 6.5.

Let $X$ be an object in a category $\mathsf{E}$ of eastern algebras. Let $Y$ be characteristic in $X$ with inclusion $\iota:Y\to X$ . There exist subcategories $\mathsf{A}$ and $\mathsf{B}$ with $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\leqslant\mathsf{A},\mathsf{B}\leqslant\mathsf{E}$ , and an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{M}:\mathsf{B}\to\mathsf{A}$ such that $\mathcal{M}(\operatorname{id}_{X}\cdot\mathbb{1}_{\mathsf{B}})=\iota$ .

Proof.

Let $\mathcal{I}:\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\to\mathsf{E}$ be the inclusion functor. The proof of Theorem 1-cat shows that there exists a functor $\mathcal{E}:\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\;\to\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ and a monic counital $\eta:\mathcal{I}\mathcal{E}\Rightarrow\mathcal{I}$ such that $\eta_{X}=\iota$ . We use Proposition 6.4 (with $\mathsf{B}=\;\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ ) to create a category $\mathsf{A}$ generated from $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ and $\eta$ , an inclusion functor $\mathcal{K}:\mathsf{A}\to\mathsf{E}$ , a functor $\mathcal{D}:\mathsf{A}\to\mathsf{A}$ , and an internal monic counital $\hat{\eta}:\mathcal{K}\mathcal{D}\Rightarrow\mathcal{K}$ with $\hat{\eta}_{Z}=\eta_{Z}$ for all objects in $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}$ . Lastly, we apply Proposition 4.10(a) to $\hat{\eta}$ to obtain an $\mathsf{A}$ -bimorphism $\mathcal{N}:\mathsf{A}\to\mathsf{E}$ such that $\hat{\eta}=\mathcal{N}(\mathbb{1}_{\mathsf{A}})$ . Since $\hat{\eta}$ is internal, there exists an $\mathsf{A}$ -bimorphism $\mathcal{M}:\mathsf{A}\to\mathsf{A}$ such that $\mathcal{N}=\mathcal{KM}$ . Hence, $\hat{\eta}=\mathcal{K}\mathcal{M}(\mathbb{1}_{\mathsf{A}})$ . With $\mathsf{B}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathsf{A}$ , it follows that $\mathcal{M}(\operatorname{id}_{X}\cdot\mathbb{1}_{\mathsf{B}})=\hat{\eta}_{X}=\eta_{X}=\iota$ , as claimed. ∎

6.3. Proofs of main theorems

Having developed the required theory, we can now complete the proofs of our main results. Theorem 1 is a special case of Theorem 1-cat, which we proved in the previous section.

Proof of Theorem 2-cat. If (1) holds, then Theorem 6.5 yields (3). If (3) holds, then (2) follows from Theorem 4.11 (a) and the fact that $\iota=\mathcal{M}(\operatorname{id}_{G}\cdot\mathbb{1}_{\mathsf{B}})$ . If (2) holds, then (1) follows from Theorem 1-cat. ∎

Theorem 2 follows from Theorem 2-cat.

6.4. Duality

Recall from Section 5.5 that a natural transformation $\eta:\mathcal{I}\Rightarrow\mathcal{D}$ is a unital if $\mathcal{I}$ is an inclusion functor. If $\mathcal{I}=\operatorname{id}$ , then $\eta:\operatorname{id}\Rightarrow\mathcal{D}$ is a unit. A unital $\eta:\mathcal{I}\Rightarrow\mathcal{D}$ is epic if $\eta_{X}:\mathcal{I}(X)\to\mathcal{D}(X)$ is epic for all objects $X$ . Units and unitals are the duals of counits and counitals.

We state a dual analogue of Theorem 2-cat for characteristic quotients in eastern algebras; its proof follows mutatis mutandis from that of Theorem 2-cat.

Theorem 2-dual.

Let $\mathsf{E}$ be an eastern variety, and let $G$ be an object of $\mathsf{E}$ with quotient $Q$ and projection $\pi$ . There exist categories $\mathsf{A}$ and $\mathsf{B}$ , where $\mathrel{\mathop{\mathsf{E}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\leftrightarrow$}\vss}}}\;\leqslant\mathsf{A}\leqslant\mathsf{E}$ , such that the following are equivalent.

(1)

$Q$ is a characteristic quotient of $G$ .
(2)

There is a functor $\mathcal{U}:\mathsf{A}\to\mathsf{A}$ and a unit $\epsilon:\operatorname{id}_{\mathsf{A}}\Rightarrow\mathcal{U}$ such that $Q=\mathrm{Coim}(\epsilon_{G})$ .
(3)

There is an $(\mathsf{A},\mathsf{B})$ -morphism $\mathcal{M}:\mathsf{A}\to\mathsf{B}$ such that $\pi=\mathcal{M}(\mathbb{1}_{\mathsf{A}}\cdot\operatorname{id}_{G})$ .

Although a characteristic subgroup of a group $G$ is associated with a characteristic quotient of $G$ , and vice-versa, there are subtle differences in other categories of eastern algebras.

Example 6.6.

Let $\mathbb{Q}$ be the ring of rational numbers and $\mathbb{Z}$ its subring of integers. If $\varphi:\mathbb{Q}\to\mathbb{Q}$ is a homomorphism of unital rings, then $\varphi(1)=1$ . This forces $\varphi=\operatorname{id}_{\mathbb{Q}}$ , so $\mathbb{Z}$ is fully invariant in $\mathbb{Q}$ . Since $\mathbb{Q}$ is a field, its only quotients are itself and the trivial ring. Hence, $\mathbb{Q}$ has many fully-invariant substructures, but only two fully-invariant quotients. $\square$

In general, kernels of group homomorphisms are representable as subgroups (unlike ideals, which are not necessarily unital subrings). Conversely, every characteristic subgroup is normal and has an associated quotient. Formalizing these observations, we say that invariant structures of groups are self-dual up to equivalence of natural transformations in $\mathsf{Cat}$ , see [HoTT]*pp. 59–61. The next proposition provides a categorical description of this observation for $\mathsf{Grp}$ ; we use it in Section 7.

Proposition 6.7.

The following hold for categories $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}\;\leqslant\mathsf{A}\leqslant\mathsf{Grp}$ and $\mathsf{B}\leqslant\mathsf{Grp}$ with inclusion functors $\mathcal{I}:\mathsf{A}\to\mathsf{Grp}$ and $\mathcal{J}:\mathsf{B}\to\mathsf{Grp}$ .

(a)

Given a unital $\pi:\mathcal{I}\Rightarrow\mathcal{J}\mathcal{U}$ , there is a category $\mathsf{C}\leqslant\mathsf{Grp}$ , with inclusion $\mathcal{K}$ , and a functor $\mathcal{C}:\mathsf{A}\to\mathsf{C}$ such that ${\rm ker\,}(\pi):\mathcal{K}\mathcal{C}\Rightarrow\mathcal{I}$ is a counital where $\mathcal{C}(G)={\rm ker\,}(\pi_{G})$ and $({\rm ker\,}(\pi))_{G}:{\rm ker\,}(\pi_{G})\hookrightarrow G$ is the inclusion for every group $G$ .
(b)

Given a counital $\iota:\mathcal{J}\mathcal{C}\Rightarrow\mathcal{I}$ , there is a category $\mathsf{C}\leqslant\mathsf{Grp}$ , with inclusion $\mathcal{K}$ , and a functor $\mathcal{U}:\mathsf{A}\to\mathsf{C}$ such that ${\rm coker\,}(\iota):\mathcal{I}\Rightarrow\mathcal{K}\mathcal{U}$ is a unital where $\mathcal{U}(G)=G/\operatorname{Im}(\iota_{G})$ and $({\rm coker\,}(\iota))_{G}:G\twoheadrightarrow G/\operatorname{Im}(\iota_{G})$ for every group $G$ .
(c)

With the notation of (a) and (b), there are unique invertible $\mu,\tau:\mathsf{A}$ such that ${\rm coker\,}({\rm ker\,}(\pi))=\mu(\mathrm{im}(\pi))$ and ${\rm ker\,}({\rm coker\,}(\iota))=\iota\tau$ .

Proof.

(a)

For every morphism $\varphi:G\to H$ in $\mathsf{A}$ , there is an induced morphism $\varphi^{\prime}:\operatorname{Im}(\pi_{G})\to\operatorname{Im}(\pi_{H})$ such that $\varphi^{\prime}\pi_{G}=\pi_{H}\varphi$ , so

$\pi_{H}\varphi({\rm ker\,}(\pi_{G}))=\varphi^{\prime}\pi_{G}({\rm ker\,}(\pi_{G}))=1.$

Therefore $\varphi({\rm ker\,}(\pi_{G}))\leqslant{\rm ker\,}(\pi_{H})$ . In particular, the restriction

$\varphi|_{{\rm ker\,}(\pi_{G})}:{\rm ker\,}(\pi_{G})\to{\rm ker\,}(\pi_{H})$

is well defined. Let $\mathsf{C}$ be the category whose objects are ${\rm ker\,}(\pi_{G})$ for all groups $G$ and whose morphisms are $\varphi|_{{\rm ker\,}(\pi_{G})}$ for all morphisms $\varphi:G\to H$ in $\mathsf{A}$ . Let $\mathcal{K}:\mathsf{C}\to\mathsf{Grp}$ be the inclusion functor. Moreover, there is a functor $\mathcal{C}:\mathsf{A}\to\mathsf{C}$ given by $\mathcal{C}(G)={\rm ker\,}(\pi_{G})$ and $\mathcal{C}(\varphi)=\varphi|_{{\rm ker\,}(\pi_{G})}$ . If we define $\iota_{G}:{\rm ker\,}(\pi_{G})\hookrightarrow G$ to be the associated inclusion map for the kernel, then $\iota:\mathcal{K}\mathcal{C}\Rightarrow\mathcal{I}$ is the required counital.
(b)

The proof is dual to that of (a).
(c)

Consider the unital $\pi:\mathcal{I}\Rightarrow\mathcal{J}\mathcal{U}$ . By Theorem 3.22, for each group $G$ there is an isomorphism

$\mu:\mathcal{U}(G)=\mathrm{Im}\pi_{G}\to G/{\rm ker\,}\pi_{G}={\rm coker\,}({\rm ker\,}\pi_{G}).$

Thus, ${\rm coker\,}({\rm ker\,}(\pi))=\mu(\text{im}(\pi))$ ; likewise, for ${\rm ker\,}({\rm coker\,}(\iota))$ and $\iota$ . ∎

7. Categorification of standard characteristic subgroups

Theorem 2 states that every characteristic subgroup can be studied in three ways: as a group, as a natural transformation, and as a morphism of category biactions. In this section, we describe common characteristic subgroups using all three forms. In so doing, we reveal insights gained from the categorical perspective.

Throughout, we use the following notation for restriction and induction. Let $\varphi:G\to H$ be a homomorphism of groups, and let $\mathcal{C}(G)$ and $\mathcal{C}(H)$ be subgroups of $H$ and $G$ , respectively. If the restriction of $\varphi$ to $\mathcal{C}(G)$ maps into $\mathcal{C}(H)$ , then we denote it by

(7.1)

\displaystyle\varphi|_{\mathcal{C}}:\mathcal{C}(G)\to\mathcal{C}(H),\quad c\mapsto\varphi(c).

Similarly, if $\varphi$ maps a normal subgroup $\mathcal{Q}(G)$ of $G$ into a normal subgroup $\mathcal{Q}(H)$ of $H$ , then the induction of $\varphi$ via $\mathcal{Q}$ is

(7.2)

\displaystyle\varphi|^{\mathcal{Q}}:G/\mathcal{Q}(G)\to H/\mathcal{Q}(H),\quad g\mathcal{Q}(G)\mapsto\varphi(g)\mathcal{Q}(H).

7.1. Abelianization and derived subgroups

Figure 9 gives the three perspectives on the derived subgroup. We develop this example, so that we may also treat the lower central series and all verbal subgroups in Section 7.2.

The counital $\lambda:\mathcal{D}\Rightarrow\operatorname{id}_{\mathsf{Grp}}$ of Example 6.2 associated with the derived subgroup $\gamma_{2}(G)$ of a group $G$ can be constructed also as the kernel of the unital associated with abelianization. We explore the category biaction interpretation. Let $\mathsf{Abel}$ be the category of abelian groups, a subcategory of $\mathsf{Grp}$ with inclusion $\mathcal{I}:\mathsf{Abel}\to\mathsf{Grp}$ . We define a morphism $\mathcal{A}:\mathsf{Grp}\to\mathsf{Abel}$ given by $\varphi\mapsto\varphi|^{\gamma_{2}}$ . The functors $\mathcal{A}$ and $\mathcal{I}$ turn the categories $\mathsf{Grp}$ and $\mathsf{Abel}$ into $(\mathsf{Grp},\mathsf{Abel})$ -bicapsules.

We show that $\mathcal{A}:\mathsf{Grp}\to\mathsf{Abel}$ is a $(\mathsf{Grp},\mathsf{Abel})$ -morphism. Let $\varphi$ and $\tau$ be group homomorphisms, and let $\alpha$ be a homomorphism of abelian groups. Now

\displaystyle\mathcal{A}(\alpha\cdot\varphi\tau)

\displaystyle=(\mathcal{I}(\alpha)\varphi\tau)|^{\gamma_{2}}=\alpha\;\varphi|^{\gamma_{2}}\;\tau|^{\gamma_{2}}=\alpha\mathcal{A}(\varphi)\cdot\tau.

To obtain the counital associated with the derived subgroup, we apply Proposition 6.7 and take the kernel of $\mathcal{A}(\mathbb{1}_{\mathsf{Grp}})$ . Since the unital-counital pair obtained through this process is a unit-counit pair, we obtain the well-known observation that the derived subgroup is fully invariant.

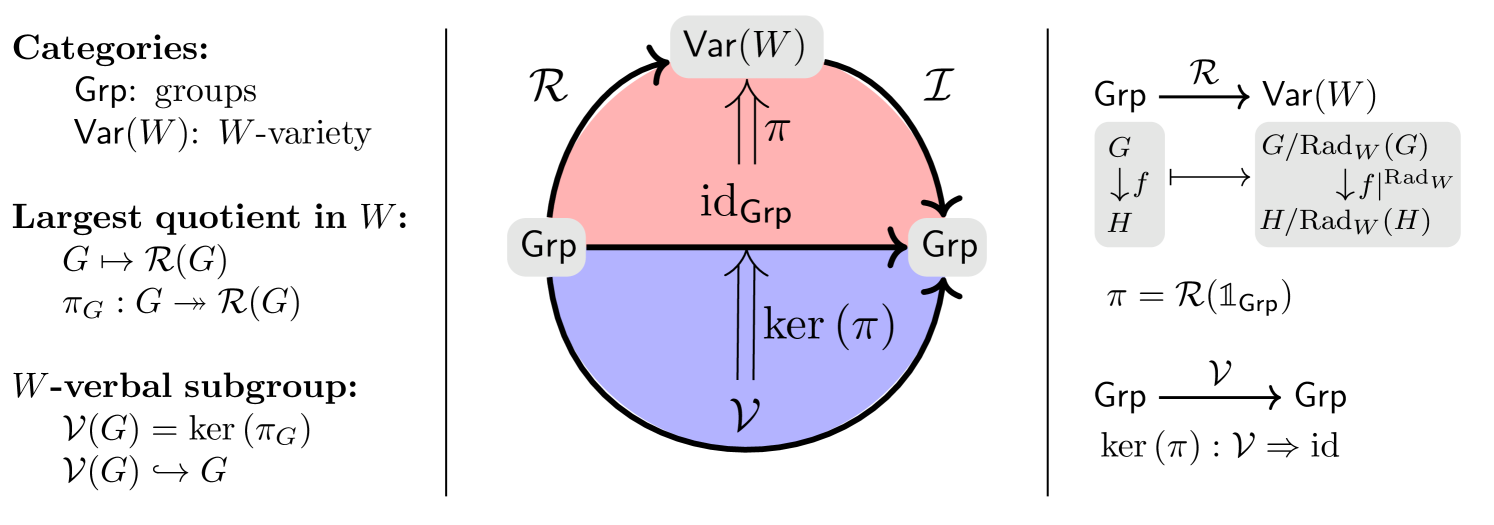
7.2. Verbal subgroups

We generalize the approach taken in Section 7.1. Let $\Omega$ be the group signature from Example 3.8. To each set $W$ of words from the free group $\Omega\langle X\rangle$ we associate a category $\mathsf{Var}(W)$ as follows (see Section 3.3). For each word $w:W$ , group $G$ , and $X$ -tuple $g:G^{X}$ , define $w_{G}:G^{X}\to G$ by $g\mapsto\mathrm{eval}_{g}(w)$ . Define $\mathsf{Var}(W)$ to be the full subcategory of $\mathsf{Grp}$ with objects

\{G:\mathsf{Grp}\mid(\forall g:G^{X})(\forall w:W)\;w_{G}(g)=1\}

with inclusion functor $\mathcal{I}:\mathsf{Var}(W)\to\mathsf{Grp}$ . The category $\mathsf{Var}(W)$ is the group variety with laws $W$ . Let $\mathrm{Rad}_{W}(G)$ be the minimal normal subgroup of a group $G$ such that $G/\mathrm{Rad}_{W}(G)$ is in $\mathsf{Var}(W)$ . Let $\mathcal{R}:\mathsf{Grp}\to\mathsf{Var}(W)$ be the functor such that $\mathcal{R}(G)$ is the largest quotient of $G$ contained in $\mathsf{Var}(W)$ , where the functor carries $G$ to $G/\mathrm{Rad}_{W}(G)$ , and morphisms $\varphi$ are sent to $\varphi|^{\mathrm{Rad}_{W}}$ .

Proposition 7.1.

The functors $\mathcal{R}$ and $\mathcal{I}$ form an adjoint functor pair: $\mathcal{R}:\mathsf{Grp}\dashv\mathsf{Var}(W):\mathcal{I}$ .

Proof.

By Proposition 4.6, the functors $\mathcal{R}$ and $\mathcal{I}$ turn both $\mathsf{Var}(W)$ and $\mathsf{Grp}$ into $(\mathsf{Var}(W),\mathsf{Grp})$ -bicapsules. The functor $\mathcal{R}$ is a $(\mathsf{Var}(W),\mathsf{Grp})$ -morphism: for morphisms $\alpha$ in $\mathsf{Var}(W)$ and $\varphi,\tau$ in $\mathsf{Grp}$ ,

\displaystyle\mathcal{R}(\alpha\varphi\cdot\tau)

\displaystyle=(\alpha\varphi\mathcal{I}(\tau))|^{\mathrm{Rad}_{W}}=\alpha|^{\mathrm{Rad}_{W}}\;\varphi|^{\mathrm{Rad}_{W}}\;\tau=\alpha\cdot\mathcal{R}(\varphi)\tau.

Since $\mathcal{R}$ and $\mathcal{I}$ are pseudo-inverses, the result follows from Theorem 4.13 (a). ∎

The adjoint functor pair in Proposition 7.1 categorifies verbal subgroups. The dual version of Theorem 4.11 describes how to obtain the unit $\pi:\operatorname{id}_{\mathsf{Grp}}\Rightarrow\mathcal{IR}$ from $\mathcal{R}$ . Applying Proposition 6.7, the kernel of $\pi$ yields a counit $\iota:\mathcal{V}\Rightarrow\operatorname{id}_{\mathsf{Grp}}$ for some functor $\mathcal{V}:\mathsf{Grp}\to\mathsf{Grp}$ . If $G$ is a group, then $\mathcal{V}(G)$ is the $W$ -verbal subgroup. We conclude that all verbal subgroups are fully invariant. Thus, from Proposition 7.1, we get an exact sequence of natural transformations

The corresponding diagram appears in Figure 10.

7.3. Marginal subgroups

Now we consider characteristic subgroups such as the center $\zeta(G)$ of a group $G$ . As seen in Example 1.4, there are group homomorphisms $\varphi:G\to H$ for which $\varphi(\zeta(G))\not\leqslant\zeta(H)$ , so, unlike verbal subgroups, the center is not fully invariant. This fact is revealed by the categorification of the center—it does not yield a counit between functors $\mathsf{Grp}\to\mathsf{Grp}$ , but rather a proper counital between functors of the form $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}\;\to\mathsf{Grp}$ , where $\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}$ is the category of groups whose morphisms are epimorphisms. We establish this fact more generally for the class of marginal subgroups introduced by P. Hall [Hall40].

Example 7.2 (Hall’s Isoclinism).

For an integer $n>0$ we write $G^{n}$ for the $n$ -fold direct product of a group $G$ . The commutator map $\kappa:G^{2}\to G$ is given by $(g,h)\mapsto[g,h]\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}g^{-1}h^{-1}gh$ . We define a congruence relation $\equiv$ on $G$ and write $x\equiv z$ if and only if $[x,z]=[y,z]$ for all $y:G$ . Factoring through this congruence relation and restricting the outputs to the verbal subgroups, we obtain a map $*:(G/\zeta(G))^{2}\to\gamma_{2}(G)$ such that the following diagram commutes.

Two groups are isoclinic if their commutator maps are equivalent. $\square$

For each group $G$ and each word $w$ , there is a unique minimal normal subgroup $w^{*}(G)$ such that the map $\overline{w}_{G}:(G/w^{*}(G))^{n}\to G$ given by

\displaystyle(g_{1}w^{*}(G),\dots,g_{n}w^{*}(G))

\displaystyle\longmapsto w_{G}(g_{1},\dots,g_{n})

is non-degenerate: namely, fixing any $n-1$ entries of the $n$ -tuple argument of $\overline{w}_{G}$ yields an injective map $G/w^{*}(G)\to G$ . Here $w_{G}$ is as defined in Section 7.2.

For a set $W$ of words, the associated marginal subgroup of a group $G$ is defined as $W^{*}(G)=\bigcap_{w:W}w^{*}(G)$ . Clearly, $W^{*}(G)$ is characteristic in $G$ . The image of $\overline{w}_{G}$ , and thus also $w_{G}$ , is the verbal subgroup associated with $w$ , written $w(G)$ .

Hall [Hall40] introduced the general notion of isologism for word-map equivalence. We extend this language to categories. Each word $w$ determines a category $\mathrel{\mathop{\mathsf{Log}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}_{w}$ with maps $\overline{w}_{G}:(G/w^{*}(G))^{n}\to w(G)$ as objects, where the morphisms are pairs $(\varphi_{1},\varphi_{2})$ of group epimorphisms such that the following diagram commutes.

We define two functors. The first is $\mathcal{L}:\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}\;\to\;\mathrel{\mathop{\mathsf{Log}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}_{w}$ given by $G\mapsto\overline{w}_{G}$ and $\varphi\mapsto(\varphi|^{w^{*}},\varphi|_{w})$ . The second is $\mathcal{P}:\;\mathrel{\mathop{\mathsf{Log}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}_{w}\;\to\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}$ given by $\overline{w}_{G}\mapsto G/w^{*}(G)$ and $(\varphi_{1},\varphi_{2})\mapsto\varphi_{1}$ . For a group $G$ , let $\pi_{G}:G\twoheadrightarrow G/w^{*}(G)$ be the usual projection homomorphism. Now $\pi:\operatorname{id}_{\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}}\Rightarrow\mathcal{PL}$ is a unit. Let $\mathcal{I}:\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}\;\to\mathsf{Grp}$ be the inclusion functor. Then the unital $\mathcal{I}\pi:\mathcal{I}\Rightarrow\mathcal{IPL}$ is a categorification of marginal quotients.

To categorify the marginal subgroup, we take the kernel of $\pi$ via Proposition 6.7 and compose with $\mathcal{I}$ : namely, $\mathcal{I}{\rm ker\,}(\pi):\mathcal{IC}\Rightarrow\mathcal{I}$ for some functor $\mathcal{C}:\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}\;\to\;\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\relbar\joinrel\twoheadrightarrow$}\vss}}}$ . Figure 11 displays the various morphisms and their relationships. This construction demonstrates that marginal subgroups are not just characteristic, but invariant under all epimorphisms.

The construction applies to other algebraic structures by simply involving formulas in the appropriate signature. However, the notion of congruence does not always yield a substructure, so the structures are more naturally expressed as characteristic quotients.

8. Composite characteristic structures

We now address one remaining powerful feature of our categorical description of characteristic structure. It relates to a comment we made after Theorem 2: a characteristic subgroup may arise from $(\mathsf{A},\mathsf{B})$ -morphisms $\mathsf{B}\to\mathsf{A}$ where $\mathsf{B}$ is not a category of groups. We give one illustration of how this “transferability” explains techniques currently used in isomorphism tests.

In [Wilson:filters]*§4, it is shown that a $p$ -group $G$ of class at most $2$ with exponent $p$ has a characteristic subgroup induced by the Jacobson radical of an algebra associated to the bilinear commutator map of $G$ . Here we construct that characteristic subgroup using a tensor product of capsules, as described in Section 5.2.

8.1. From groups to bimaps

Fix an odd prime $p$ , and let $\mathsf{G}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}_{2,p}$ be the category whose objects are $p$ -groups of class at most $2$ with exponent $p$ , and whose morphisms are isomorphisms. The objects of $\mathsf{G}$ are groups $G$ with exponent $p$ and central derived subgroup, so $\gamma_{2}(G)\leqslant\zeta(G)$ .

Let $\mathbb{F}_{p}$ be the field with $p$ elements, and let $\mathsf{B}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathrel{\mathop{\mathsf{Bi}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(\mathbb{F}_{p})$ be the category of alternating $\mathbb{F}_{p}$ -bilinear maps. The objects of $\mathsf{B}$ are bilinear maps $b:V\times V\to W$ , where $V$ and $W$ are $\mathbb{F}_{p}$ -spaces, such that $b(u,v)=-b(v,u)$ for all vectors $u,v$ . For objects $b:V\times V\to W$ and $b^{\prime}:V^{\prime}\times V^{\prime}\to W^{\prime}$ in $\mathsf{B}$ , a morphism $\varphi:b\to b^{\prime}$ is a pair of invertible linear maps $(\alpha:V\to V^{\prime},\beta:W\to W^{\prime})$ such that, for all $u,v\in V$ ,

b^{\prime}(\alpha u,\alpha v)=\beta b(u,v).

Define a functor $\mathcal{B}:\mathsf{G}\to\mathsf{B}$ that takes a group $G$ to

b_{G}:G/\gamma_{2}(G)\times G/\gamma_{2}(G)\to\gamma_{2}(G),\quad(x\gamma_{2}(G),y\gamma_{2}(G))\mapsto[x,y],

and a homomorphism $\varphi:G\to H$ to the pair $(\varphi|^{\gamma_{2}},\ \varphi|_{\gamma_{2}})$ , as defined in (7.1) and (7.2). Since $G$ has exponent $p$ and $\gamma_{2}(G)\leqslant\zeta(G)$ by assumption, $b_{G}$ is an alternating $\mathbb{F}_{p}$ -bilinear map.

Next, define a functor $\mathcal{G}:\mathsf{B}\to\mathsf{G}$ that takes an $\mathbb{F}_{p}$ -bilinear map $b:V\times V\to W$ to the group $G_{b}$ on $V\times W$ with binary operation

(v_{1},w_{1})\cdot(v_{2},w_{2})=\left(v_{1}+v_{2},w_{1}+w_{2}+\frac{1}{2}b(v_{1},v_{2})\right).

A morphism $(\alpha,\beta)$ from $b:V\times V\to W$ to $b^{\prime}:V^{\prime}\times V^{\prime}\to W^{\prime}$ in $\mathsf{B}$ induces a group isomorphism, denoted $\alpha\boxtimes\beta$ , mapping $G_{b}=V\times W$ to $G_{b^{\prime}}=V^{\prime}\times W^{\prime}$ by

(\alpha\boxtimes\beta)(v,w)\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}(\alpha u,\beta w).

Lemma 8.1.

The functor $\mathcal{B}:\mathsf{G}\to\mathsf{B}$ is a $(\mathsf{G},\mathsf{B})$ -morphism.

Proof.

The functor $\mathcal{B}$ induces a left $\mathsf{G}$ -action on (the morphisms of) $\mathsf{B}$ , and $\mathcal{G}$ induces a right $\mathsf{B}$ -action on $\mathsf{G}$ , so $\mathsf{B}$ and $\mathsf{G}$ are $(\mathsf{B},\mathsf{G})$ -bicapsules. Let $\lambda,\mu$ be morphisms of $\mathsf{G}$ and let $(\alpha,\beta)$ be a morphism of $\mathsf{B}$ such that $\lambda\mu\cdot(\alpha,\beta)=\lambda\mu(\alpha\boxtimes\beta)$ is defined. Now

	$\displaystyle\mathcal{B}(\lambda\mu\cdot(\alpha,\beta))$	$\displaystyle=\left((\lambda\mu(\alpha\boxtimes\beta))\|^{\gamma_{2}},\ (\lambda\mu(\alpha\boxtimes\beta))\|_{\gamma_{2}}\right)$
		$\displaystyle=\left(\lambda\|^{\gamma_{2}}\mu\|^{\gamma_{2}}\alpha,\ \lambda\|_{\gamma_{2}}\mu\|_{\gamma_{2}}\beta\right)$
		$\displaystyle=\lambda\cdot\mathcal{B}(\mu)(\alpha,\beta),$

so $\mathcal{B}$ is a $(\mathsf{G},\mathsf{B})$ -morphism. ∎

By applying the dual version of Theorem 4.11 (a), we obtain a unit $\operatorname{id}_{\mathsf{G}}\Rightarrow\mathcal{BG}$ . There is also a counit $\operatorname{id}_{\mathsf{G}}\Leftarrow\mathcal{BG}$ . Together these give a categorical interpretation of the Baer correspondence [Baer].

8.2. From bimaps to algebras

Let $\mathsf{A}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathrel{\mathop{\mathsf{Alge}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(\mathbb{F}_{p})$ be the category of $\mathbb{F}_{p}$ -matrix algebras with algebra isomorphisms. Using [Wilson:filters]*§4, define a functor $\mathcal{A}:\mathsf{B}\to\mathsf{A}$ by

\displaystyle\mathcal{A}(b)

\displaystyle=\left\{f\in\operatorname{End}(V)~\middle|~\exists f^{*}\in\operatorname{End}(V)^{op},\forall u,v\in V,\;b(fu,v)=b(u,f^{*}v)\right\}.

Invertible morphisms $(\alpha,\beta)$ in $\mathsf{B}$ from $b:V\times V\to W$ to $b^{\prime}:V^{\prime}\times V^{\prime}\to W^{\prime}$ are sent to

\mathcal{A}(\alpha,\beta):f\in\mathcal{A}(b)\mapsto f^{\alpha^{-1}}\in\mathcal{A}(b^{\prime}).

Fact 8.2.

The functor $\mathcal{A}$ is a $(\mathsf{B},\mathsf{A})$ -morphism.

8.3. From matrix algebras to semisimple algebras

Every matrix algebra $A$ over a field is Artinian, so the quotient of $A$ by its Jacobson radical $\mathrm{Jac}(A)$ is a semisimple algebra. The map $A\mapsto A/\mathrm{Jac}(A)$ is a functor from $\mathsf{A}$ to the category $\mathsf{S}\mathrel{\hstretch{.13}{=}\hskip 0.86108pt{=}}\mathrel{\mathop{\mathsf{SSAlge}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(\mathbb{F}_{p})$ of semisimple $\mathbb{F}_{p}$ -algebras. It is also an $(\mathsf{A},\mathsf{S})$ -morphism.

8.4. Combining capsules

Recall that

\displaystyle\mathsf{G}=\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}_{2,p},\qquad\mathsf{B}=\mathrel{\mathop{\mathsf{Bi}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(\mathbb{F}_{p}),\qquad\mathsf{A}=\mathrel{\mathop{\mathsf{Alge}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(\mathbb{F}_{p}),\qquad\mathsf{S}=\mathrel{\mathop{\mathsf{SSAlge}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}}(\mathbb{F}_{p}).

Denote by $\Delta$ the bicapsule associated to the $(\mathsf{G},\mathsf{B})$ -morphism in Lemma 8.1. Denote by $\Gamma$ and $\Upsilon$ , respectively, the bicapsules associated to the $(\mathsf{B},\mathsf{A})$ - and $(\mathsf{A},\mathsf{S})$ -morphisms in Fact 8.2 and Section 8.3. These three capsules can now be combined to produce the $(\mathsf{G},\mathsf{S})$ -capsule

\displaystyle\Delta\otimes_{\mathsf{B}}\Gamma\otimes_{\mathsf{A}}\Upsilon=\mathsf{G}\cdot\mu\cdot\mathsf{S}.

The resulting generator $\mu$ of this cyclic bicapsule is a unital. By Theorem 2-dual this provides the characteristic subgroup used in [Maglione:adjoints] and [Wilson:filters]*§4.

Acknowledgements

We thank Chris Liu for fruitful discussions and some proof-of-concept implementations. We thank John Power and Mima Stanojkovski for comments on a draft. Brooksbank was supported by NSF grant DMS-2319371. Maglione was supported by DFG grant VO 1248/4-1 (project number 373111162) and DFG-GRK 2297. O’Brien was supported by the Marsden Fund of New Zealand Grant 23-UOA-080 and by a Research Award of the Alexander von Humboldt Foundation. Wilson was supported by a Simons Foundation Grant identifier #636189 and by NSF grant DMS-2319370.

References

\ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry

$\{H\leqslant G~\|~H\text{ characteristic in }G\}$	$=$	$\left\{\mathrm{Im}(\iota_{G})~\middle\|~\iota\in\text{\rm Counital}\left(\mathrel{\mathop{\mathsf{Grp}}\limits^{\vbox to0.0pt{\kern-2.0pt\hbox{$\scriptstyle\longleftrightarrow$}\vss}}},\mathsf{Grp}\right)\right\};$
$\{H\leqslant G~\|~H\text{ fully invariant in }G\}$	$=$	$\left\{\mathrm{Im}(\iota_{G})~\middle\|~\iota\in\text{\rm Counital}(\mathsf{Grp},\mathsf{Grp})\right\}$ .

Categorification of characteristic structures

Abstract.

1. Introduction

Definition 1.1.

Theorem 1.

1.1. Constraining isomorphism by characteristic subgroups

Fact 1.2.

Example 1.3.

1.2. A local-to-global problem

Theorem 2.

Example 1.4.

1.3. Applications to computation

1.4. Structure of this paper

2. Type theory and certifying characteristic structure

2.1. Types

2.2. Propositions as types

2.3. Subtypes and inclusion functions

2.4. Partial-functions

Definition 2.1.

2.5. Certifying that the trivial group is characteristic

3. Essentially algebraic structures

3.1. Operators, grammars, and signatures

Definition 3.1.

Example 3.2.

3.2. Algebraic structures

Definition 3.3.

3.3. Free algebras and formulas

Definition 3.4.

Example 3.5.

Fact 3.6.

Remark 3.7.

3.4. Laws and varieties

Example 3.8.

3.5. Eastern algebras

Example 3.9.

Definition 3.10.

Definition 3.11.

Example 3.12 (Categories as eastern algebras).

3.6. Abstract categories

Definition 3.13.

Lemma 3.14.

Proof.

Proposition 3.15.

Proof.

Example 3.16.

3.7. Peirce decomposition of abstract categories

Fact 3.17.

Proposition 3.18.

Remark 3.19.

3.8. Eastern algebras as categories

Definition 3.20.

Remark 3.21.

Theorem 3.22.

Proof.

3.9. Subobjects and images

Lemma 3.23.

Proof.

Lemma 3.24.

Proof.

Fact 3.25.

4. Category actions, capsules, and counits

4.1. Category actions

Definition 4.1.

Definition 4.2.

Example 4.3.

Remark 4.4.

4.2. Capsules

Definition 4.5.

Proposition 4.6.

Lemma 4.7.

Proof.

Lemma 4.8.

Proof.

Proof of Proposition 4.6.

4.3. Category biactions and cyclic bicapsules

Definition 4.9.

Proposition 4.10.

Proof.

4.4. Units and counits

Theorem 4.11.