PHENIX Collaboration

Centrality dependence of Lévy-stable two-pion Bose-Einstein correlations in $\sqrt{s_{{}_{NN}}}=200$ GeV Au $+$ Au collisions.

N.J. Abdulameer Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary HUN-REN ATOMKI, H-4026 Debrecen, Bem tér 18/c, Hungary U. Acharya Georgia State University, Atlanta, Georgia 30303, USA A. Adare University of Colorado, Boulder, Colorado 80309, USA C. Aidala Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA Department of Physics, University of Michigan, Ann Arbor, Michigan 48109-1040, USA N.N. Ajitanand Deceased Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA Y. Akiba akiba@rcf.rhic.bnl.gov RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA R. Akimoto Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan H. Al-Ta’ani New Mexico State University, Las Cruces, New Mexico 88003, USA J. Alexander Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA A. Angerami Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA S. Antsupov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia K. Aoki KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan N. Apadula Iowa State University, Ames, Iowa 50011, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Y. Aramaki Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan H. Asano Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan E.C. Aschenauer Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA E.T. Atomssa Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA T.C. Awes Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA B. Azmoun Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Babintsev IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia M. Bai Collider-Accelerator Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA B. Bannier Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA E. Bannikov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia K.N. Barish University of California-Riverside, Riverside, California 92521, USA B. Bassalleck University of New Mexico, Albuquerque, New Mexico 87131, USA S. Bathe Baruch College, City University of New York, New York, New York, 10010 USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Baublis PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia S. Baumgart RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan A. Bazilevsky Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA R. Belmont University of Colorado, Boulder, Colorado 80309, USA Physics and Astronomy Department, University of North Carolina at Greensboro, Greensboro, North Carolina 27412, USA A. Berdnikov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia Y. Berdnikov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia L. Bichon Vanderbilt University, Nashville, Tennessee 37235, USA B. Blankenship Vanderbilt University, Nashville, Tennessee 37235, USA D.S. Blau National Research Center “Kurchatov Institute”, Moscow, 123098 Russia National Research Nuclear University, MEPhI, Moscow Engineering Physics Institute, Moscow, 115409, Russia J.S. Bok University of New Mexico, Albuquerque, New Mexico 87131, USA New Mexico State University, Las Cruces, New Mexico 88003, USA Yonsei University, IPAP, Seoul 120-749, Korea V. Borisov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia K. Boyle RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M.L. Brooks Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA H. Buesching Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Bumazhnov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia S. Butsyk University of New Mexico, Albuquerque, New Mexico 87131, USA S. Campbell Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA P. Castera Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA C.-H. Chen RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA D. Chen Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA M. Chiu Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA C.Y. Chi Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA I.J. Choi University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA J.B. Choi Deceased Jeonbuk National University, Jeonju, 54896, Korea S. Choi Department of Physics and Astronomy, Seoul National University, Seoul 151-742, Korea R.K. Choudhury Bhabha Atomic Research Centre, Bombay 400 085, India P. Christiansen Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden T. Chujo Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan O. Chvala University of California-Riverside, Riverside, California 92521, USA V. Cianciolo Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA Z. Citron Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Weizmann Institute, Rehovot 76100, Israel B.A. Cole Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA M. Connors Georgia State University, Atlanta, Georgia 30303, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA R. Corliss Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA M. Csanád ELTE, Eötvös Loránd University, H-1117 Budapest, Pázmány P. s. 1/A, Hungary T. Csörgő MATE, Institute of Technology, Laboratory of Femtoscopy, Károly Róbert Campus, H-3200 Gyöngyös, Mátrai út 36, Hungary Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary L. D’Orazio University of Maryland, College Park, Maryland 20742, USA S. Dairaku Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan A. Datta Department of Physics, University of Massachusetts, Amherst, Massachusetts 01003-9337, USA M.S. Daugherity Abilene Christian University, Abilene, Texas 79699, USA G. David Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA A. Denisov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia A. Deshpande RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA E.J. Desmond Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA K.V. Dharmawardane New Mexico State University, Las Cruces, New Mexico 88003, USA O. Dietzsch Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil L. Ding Iowa State University, Ames, Iowa 50011, USA A. Dion Iowa State University, Ames, Iowa 50011, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA M. Donadelli Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil V. Doomra Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA O. Drapier Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France A. Drees Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA K.A. Drees Collider-Accelerator Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA J.M. Durham Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA A. Durum IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia S. Edwards Collider-Accelerator Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y.V. Efremenko Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA T. Engelmore Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA A. Enokizono Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan R. Esha Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA K.O. Eyser Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA University of California-Riverside, Riverside, California 92521, USA B. Fadem Muhlenberg College, Allentown, Pennsylvania 18104-5586, USA D.E. Fields University of New Mexico, Albuquerque, New Mexico 87131, USA M. Finger, Jr Charles University, Faculty of Mathematics and Physics, 180 00 Troja, Prague, Czech Republic M. Finger Charles University, Faculty of Mathematics and Physics, 180 00 Troja, Prague, Czech Republic D. Firak Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA D. Fitzgerald Department of Physics, University of Michigan, Ann Arbor, Michigan 48109-1040, USA F. Fleuret Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France S.L. Fokin National Research Center “Kurchatov Institute”, Moscow, 123098 Russia J.E. Frantz Department of Physics and Astronomy, Ohio University, Athens, Ohio 45701, USA A. Franz Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.D. Frawley Florida State University, Tallahassee, Florida 32306, USA Y. Fukao RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan T. Fusayasu Nagasaki Institute of Applied Science, Nagasaki-shi, Nagasaki 851-0193, Japan K. Gainey Abilene Christian University, Abilene, Texas 79699, USA C. Gal Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA A. Garishvili University of Tennessee, Knoxville, Tennessee 37996, USA I. Garishvili Lawrence Livermore National Laboratory, Livermore, California 94550, USA A. Glenn Lawrence Livermore National Laboratory, Livermore, California 94550, USA X. Gong Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA M. Gonin Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France Y. Goto RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA R. Granier de Cassagnac Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France N. Grau Department of Physics, Augustana University, Sioux Falls, South Dakota 57197, USA S.V. Greene Vanderbilt University, Nashville, Tennessee 37235, USA M. Grosse Perdekamp University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA T. Gunji Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan L. Guo Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA T. Guo Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA H.-Å. Gustafsson Deceased Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden T. Hachiya RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA J.S. Haggerty Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA K.I. Hahn Ewha Womans University, Seoul 120-750, Korea H. Hamagaki Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan J. Hanks Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA K. Hashimoto RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan E. Haslum Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden R. Hayano Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan T.K. Hemmick Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA T. Hester University of California-Riverside, Riverside, California 92521, USA X. He Georgia State University, Atlanta, Georgia 30303, USA J.C. Hill Iowa State University, Ames, Iowa 50011, USA A. Hodges Georgia State University, Atlanta, Georgia 30303, USA University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA R.S. Hollis University of California-Riverside, Riverside, California 92521, USA K. Homma Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan B. Hong Korea University, Seoul 02841, Korea T. Horaguchi Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan Y. Hori Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan T. Ichihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA H. Iinuma KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan Y. Ikeda RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan J. Imrek Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary M. Inaba Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan A. Iordanova University of California-Riverside, Riverside, California 92521, USA D. Isenhower Abilene Christian University, Abilene, Texas 79699, USA M. Issah Vanderbilt University, Nashville, Tennessee 37235, USA D. Ivanishchev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia B.V. Jacak Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA M. Javani Georgia State University, Atlanta, Georgia 30303, USA X. Jiang Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA Z. Ji Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA B.M. Johnson Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Georgia State University, Atlanta, Georgia 30303, USA K.S. Joo Myongji University, Yongin, Kyonggido 449-728, Korea D. Jouan IPN-Orsay, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, BP1, F-91406, Orsay, France D.S. Jumper University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA J. Kamin Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA S. Kaneti Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA B.H. Kang Hanyang University, Seoul 133-792, Korea J.H. Kang Yonsei University, IPAP, Seoul 120-749, Korea J.S. Kang Hanyang University, Seoul 133-792, Korea J. Kapustinsky Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA K. Karatsu Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan M. Kasai RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan G. Kasza MATE, Institute of Technology, Laboratory of Femtoscopy, Károly Róbert Campus, H-3200 Gyöngyös, Mátrai út 36, Hungary Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary D. Kawall Department of Physics, University of Massachusetts, Amherst, Massachusetts 01003-9337, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.V. Kazantsev National Research Center “Kurchatov Institute”, Moscow, 123098 Russia T. Kempel Iowa State University, Ames, Iowa 50011, USA A. Khanzadeev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia K.M. Kijima Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan B.I. Kim Korea University, Seoul 02841, Korea C. Kim Korea University, Seoul 02841, Korea D.J. Kim Helsinki Institute of Physics and University of Jyväskylä, P.O.Box 35, FI-40014 Jyväskylä, Finland E.-J. Kim Jeonbuk National University, Jeonju, 54896, Korea H.J. Kim Yonsei University, IPAP, Seoul 120-749, Korea K.-B. Kim Jeonbuk National University, Jeonju, 54896, Korea Y.-J. Kim University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA Y.K. Kim Hanyang University, Seoul 133-792, Korea D. Kincses ELTE, Eötvös Loránd University, H-1117 Budapest, Pázmány P. s. 1/A, Hungary E. Kinney University of Colorado, Boulder, Colorado 80309, USA Á. Kiss ELTE, Eötvös Loránd University, H-1117 Budapest, Pázmány P. s. 1/A, Hungary E. Kistenev Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA J. Klatsky Florida State University, Tallahassee, Florida 32306, USA D. Kleinjan University of California-Riverside, Riverside, California 92521, USA P. Kline Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Y. Komatsu Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan B. Komkov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia J. Koster University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA D. Kotchetkov Department of Physics and Astronomy, Ohio University, Athens, Ohio 45701, USA D. Kotov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia L. Kovács ELTE, Eötvös Loránd University, H-1117 Budapest, Pázmány P. s. 1/A, Hungary F. Krizek Helsinki Institute of Physics and University of Jyväskylä, P.O.Box 35, FI-40014 Jyväskylä, Finland A. Král Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic G.J. Kunde Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA K. Kurita RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan M. Kurosawa RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y. Kwon Yonsei University, IPAP, Seoul 120-749, Korea G.S. Kyle New Mexico State University, Las Cruces, New Mexico 88003, USA Y.S. Lai Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA J.G. Lajoie Iowa State University, Ames, Iowa 50011, USA A. Lebedev Iowa State University, Ames, Iowa 50011, USA B. Lee Hanyang University, Seoul 133-792, Korea D.M. Lee Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA J. Lee Ewha Womans University, Seoul 120-750, Korea Sungkyunkwan University, Suwon, 440-746, Korea K.B. Lee Korea University, Seoul 02841, Korea K.S. Lee Korea University, Seoul 02841, Korea S.H. Lee Iowa State University, Ames, Iowa 50011, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA S.R. Lee Jeonbuk National University, Jeonju, 54896, Korea M.J. Leitch Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA M.A.L. Leite Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil M. Leitgab University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA B. Lewis Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA S.H. Lim Yonsei University, IPAP, Seoul 120-749, Korea L.A. Linden Levy University of Colorado, Boulder, Colorado 80309, USA M.X. Liu Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA S. Lökös MATE, Institute of Technology, Laboratory of Femtoscopy, Károly Róbert Campus, H-3200 Gyöngyös, Mátrai út 36, Hungary D.A. Loomis Department of Physics, University of Michigan, Ann Arbor, Michigan 48109-1040, USA B. Love Vanderbilt University, Nashville, Tennessee 37235, USA C.F. Maguire Vanderbilt University, Nashville, Tennessee 37235, USA Y.I. Makdisi Collider-Accelerator Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Makek Weizmann Institute, Rehovot 76100, Israel Department of Physics, Faculty of Science, University of Zagreb, Bijenička c. 32 HR-10002 Zagreb, Croatia A. Manion Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA V.I. Manko National Research Center “Kurchatov Institute”, Moscow, 123098 Russia E. Mannel Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA S. Masumoto Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan M. McCumber University of Colorado, Boulder, Colorado 80309, USA Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA P.L. McGaughey Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA D. McGlinchey University of Colorado, Boulder, Colorado 80309, USA Florida State University, Tallahassee, Florida 32306, USA Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA C. McKinney University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA M. Mendoza University of California-Riverside, Riverside, California 92521, USA B. Meredith University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA W.J. Metzger MATE, Institute of Technology, Laboratory of Femtoscopy, Károly Róbert Campus, H-3200 Gyöngyös, Mátrai út 36, Hungary Y. Miake Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan T. Mibe KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan A.C. Mignerey University of Maryland, College Park, Maryland 20742, USA A. Milov Weizmann Institute, Rehovot 76100, Israel D.K. Mishra Bhabha Atomic Research Centre, Bombay 400 085, India J.T. Mitchell Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Mitrankova Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Iu. Mitrankov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Y. Miyachi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan S. Miyasaka RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan A.K. Mohanty Bhabha Atomic Research Centre, Bombay 400 085, India S. Mohapatra Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA H.J. Moon Myongji University, Yongin, Kyonggido 449-728, Korea D.P. Morrison Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Motschwiller Muhlenberg College, Allentown, Pennsylvania 18104-5586, USA T.V. Moukhanova National Research Center “Kurchatov Institute”, Moscow, 123098 Russia B. Mulilo Korea University, Seoul 02841, Korea RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, School of Natural Sciences, University of Zambia, Great East Road Campus, Box 32379, Lusaka, Zambia T. Murakami Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan J. Murata RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan A. Mwai Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA T. Nagae Kyoto University, Kyoto 606-8502, Japan S. Nagamiya KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan J.L. Nagle University of Colorado, Boulder, Colorado 80309, USA M.I. Nagy ELTE, Eötvös Loránd University, H-1117 Budapest, Pázmány P. s. 1/A, Hungary Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary I. Nakagawa RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y. Nakamiya Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan K.R. Nakamura Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan T. Nakamura RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan K. Nakano RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan C. Nattrass University of Tennessee, Knoxville, Tennessee 37996, USA A. Nederlof Muhlenberg College, Allentown, Pennsylvania 18104-5586, USA M. Nihashi Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan R. Nouicer Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA T. Novák MATE, Institute of Technology, Laboratory of Femtoscopy, Károly Róbert Campus, H-3200 Gyöngyös, Mátrai út 36, Hungary Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary N. Novitzky Helsinki Institute of Physics and University of Jyväskylä, P.O.Box 35, FI-40014 Jyväskylä, Finland Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA G. Nukazuka RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.S. Nyanin National Research Center “Kurchatov Institute”, Moscow, 123098 Russia E. O’Brien Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA C.A. Ogilvie Iowa State University, Ames, Iowa 50011, USA K. Okada RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Orosz Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary HUN-REN ATOMKI, H-4026 Debrecen, Bem tér 18/c, Hungary A. Oskarsson Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden M. Ouchida Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan K. Ozawa Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan R. Pak Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Pantuev Institute for Nuclear Research of the Russian Academy of Sciences, prospekt 60-letiya Oktyabrya 7a, Moscow 117312, Russia V. Papavassiliou New Mexico State University, Las Cruces, New Mexico 88003, USA B.H. Park Hanyang University, Seoul 133-792, Korea I.H. Park Ewha Womans University, Seoul 120-750, Korea Sungkyunkwan University, Suwon, 440-746, Korea J.S. Park Department of Physics and Astronomy, Seoul National University, Seoul 151-742, Korea S. Park Mississippi State University, Mississippi State, Mississippi 39762, USA RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics and Astronomy, Seoul National University, Seoul 151-742, Korea Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA S.K. Park Korea University, Seoul 02841, Korea L. Patel Georgia State University, Atlanta, Georgia 30303, USA S.F. Pate New Mexico State University, Las Cruces, New Mexico 88003, USA H. Pei Iowa State University, Ames, Iowa 50011, USA J.-C. Peng University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA H. Pereira Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France D.Yu. Peressounko National Research Center “Kurchatov Institute”, Moscow, 123098 Russia R. Petti Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA C. Pinkenburg Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA R.P. Pisani Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Potekhin Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Proissl Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA M.L. Purschke Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA H. Qu Abilene Christian University, Abilene, Texas 79699, USA J. Rak Helsinki Institute of Physics and University of Jyväskylä, P.O.Box 35, FI-40014 Jyväskylä, Finland I. Ravinovich Weizmann Institute, Rehovot 76100, Israel K.F. Read Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA University of Tennessee, Knoxville, Tennessee 37996, USA D. Reynolds Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA V. Riabov National Research Nuclear University, MEPhI, Moscow Engineering Physics Institute, Moscow, 115409, Russia PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia Y. Riabov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia E. Richardson University of Maryland, College Park, Maryland 20742, USA D. Richford Baruch College, City University of New York, New York, New York, 10010 USA United States Merchant Marine Academy, Kings Point, New York 11024, USA D. Roach Vanderbilt University, Nashville, Tennessee 37235, USA G. Roche Deceased LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France S.D. Rolnick University of California-Riverside, Riverside, California 92521, USA M. Rosati Iowa State University, Ames, Iowa 50011, USA B. Sahlmueller Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA N. Saito KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan T. Sakaguchi Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Samsonov National Research Nuclear University, MEPhI, Moscow Engineering Physics Institute, Moscow, 115409, Russia PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia M. Sano Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan M. Sarsour Georgia State University, Atlanta, Georgia 30303, USA S. Sawada KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan K. Sedgwick University of California-Riverside, Riverside, California 92521, USA R. Seidl RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA A. Seleznev Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia A. Sen Georgia State University, Atlanta, Georgia 30303, USA Iowa State University, Ames, Iowa 50011, USA R. Seto University of California-Riverside, Riverside, California 92521, USA D. Sharma Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Weizmann Institute, Rehovot 76100, Israel I. Shein IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia T.-A. Shibata RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan K. Shigaki Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan M. Shimomura Iowa State University, Ames, Iowa 50011, USA Nara Women’s University, Kita-uoya Nishi-machi Nara 630-8506, Japan Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan K. Shoji Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan P. Shukla Bhabha Atomic Research Centre, Bombay 400 085, India A. Sickles Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA C.L. Silva Iowa State University, Ames, Iowa 50011, USA Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA D. Silvermyr Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA K.S. Sim Korea University, Seoul 02841, Korea B.K. Singh Department of Physics, Banaras Hindu University, Varanasi 221005, India C.P. Singh Deceased Department of Physics, Banaras Hindu University, Varanasi 221005, India V. Singh Department of Physics, Banaras Hindu University, Varanasi 221005, India M. Slunečka Charles University, Faculty of Mathematics and Physics, 180 00 Troja, Prague, Czech Republic K.L. Smith Florida State University, Tallahassee, Florida 32306, USA Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA R.A. Soltz Lawrence Livermore National Laboratory, Livermore, California 94550, USA W.E. Sondheim Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA S.P. Sorensen University of Tennessee, Knoxville, Tennessee 37996, USA I.V. Sourikova Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA P.W. Stankus Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA E. Stenlund Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden M. Stepanov Deceased Department of Physics, University of Massachusetts, Amherst, Massachusetts 01003-9337, USA A. Ster Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary S.P. Stoll Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA T. Sugitate Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan A. Sukhanov Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA J. Sun Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA Z. Sun Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary HUN-REN ATOMKI, H-4026 Debrecen, Bem tér 18/c, Hungary Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA J. Sziklai Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary E.M. Takagui Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil A. Takahara Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan A. Taketani RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y. Tanaka Nagasaki Institute of Applied Science, Nagasaki-shi, Nagasaki 851-0193, Japan S. Taneja Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA K. Tanida Advanced Science Research Center, Japan Atomic Energy Agency, 2-4 Shirakata Shirane, Tokai-mura, Naka-gun, Ibaraki-ken 319-1195, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Seoul National University, Seoul 151-742, Korea M.J. Tannenbaum Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Tarafdar Department of Physics, Banaras Hindu University, Varanasi 221005, India Vanderbilt University, Nashville, Tennessee 37235, USA A. Taranenko National Research Nuclear University, MEPhI, Moscow Engineering Physics Institute, Moscow, 115409, Russia Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA E. Tennant New Mexico State University, Las Cruces, New Mexico 88003, USA H. Themann Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA T. Todoroki RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan L. Tomášek Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic M. Tomášek Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic H. Torii Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan R.S. Towell Abilene Christian University, Abilene, Texas 79699, USA I. Tserruya Weizmann Institute, Rehovot 76100, Israel Y. Tsuchimoto Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan T. Tsuji Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan B. Ujvari Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary HUN-REN ATOMKI, H-4026 Debrecen, Bem tér 18/c, Hungary C. Vale Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA H.W. van Hecke Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA M. Vargyas ELTE, Eötvös Loránd University, H-1117 Budapest, Pázmány P. s. 1/A, Hungary Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary E. Vazquez-Zambrano Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA A. Veicht Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA J. Velkovska Vanderbilt University, Nashville, Tennessee 37235, USA M. Virius Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic A. Vossen University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA V. Vrba Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic E. Vznuzdaev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia R. Vértesi Institute for Particle and Nuclear Physics, HUN-REN Wigner Research Centre for Physics, (HUN-REN Wigner RCP, RMI), H-1525 Budapest 114, POBox 49, Budapest, Hungary X.R. Wang New Mexico State University, Las Cruces, New Mexico 88003, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA D. Watanabe Physics Program and International Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM²), Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan K. Watanabe Tomonaga Center for the History of the Universe, University of Tsukuba, Tsukuba, Ibaraki 305, Japan Y. Watanabe RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y.S. Watanabe Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan F. Wei Iowa State University, Ames, Iowa 50011, USA New Mexico State University, Las Cruces, New Mexico 88003, USA R. Wei Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA S.N. White Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA D. Winter Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA S. Wolin University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA C.L. Woody Physics Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Wysocki University of Colorado, Boulder, Colorado 80309, USA Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA B. Xia Department of Physics and Astronomy, Ohio University, Athens, Ohio 45701, USA Y.L. Yamaguchi Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3800, USA R. Yang University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA A. Yanovich IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia J. Ying Georgia State University, Atlanta, Georgia 30303, USA S. Yokkaichi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA I. Younus Physics Department, Lahore University of Management Sciences, Lahore 54792, Pakistan University of New Mexico, Albuquerque, New Mexico 87131, USA Z. You Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA I.E. Yushmanov National Research Center “Kurchatov Institute”, Moscow, 123098 Russia W.A. Zajc Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA A. Zelenski Collider-Accelerator Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA

(October 1, 2025)

Abstract

The PHENIX experiment measured the centrality dependence of two-pion Bose-Einstein correlation functions in $\sqrt{s_{{}_{NN}}}=200$ GeV Au $+$ Au collisions at the Relativistic Heavy Ion Collider at Brookhaven National Laboratory. The data are well represented by Lévy-stable source distributions. The extracted source parameters are the correlation-strength parameter $\lambda$ , the Lévy index of stability $\alpha$ , and the Lévy-scale parameter $R$ as a function of transverse mass $m_{T}$ and centrality. The $\lambda(m_{T})$ parameter is constant at larger values of $m_{T}$ , but decreases as $m_{T}$ decreases. The Lévy scale parameter $R(m_{T})$ decreases with $m_{T}$ and exhibits proportionality to the length scale of the nuclear overlap region. The Lévy exponent $\alpha(m_{T})$ is independent of $m_{T}$ within uncertainties in each investigated centrality bin, but shows a clear centrality dependence. At all centralities, the Lévy exponent $\alpha$ is significantly different from that of Gaussian ( $\alpha=2$ ) or Cauchy ( $\alpha=1$ ) source distributions. Comparisons to the predictions of Monte-Carlo simulations of resonance-decay chains show that in all but the most-peripheral centrality class (50%–60%), the obtained results are inconsistent with the measurements, unless a significant reduction of the in-medium mass of the $\eta^{\prime}$ meson is included. In each centrality class, the best value of the in-medium $\eta^{\prime}$ mass is compared to the mass of the $\eta$ meson, as well as to several theoretical predictions that consider restoration of $U_{A}(1)$ symmetry in hot hadronic matter.

I Introduction

In a previous paper [1] on Bose-Einstein Correlations (BECs)—also known as Hanbury Brown and Twiss (HBT) Correlations—the PHENIX Collaboration found that for 0%–30% centrality Au $+$ Au collisions at $\sqrt{s_{{}_{NN}}}$ =200 GeV, the two-particle BECs are well-described by a Lévy-stable source distribution. However, the traditional description of the same dataset, using a Gaussian source distribution was found to be inadequate [1]. A strong preference for the Lévy description had also been seen in e⁺+e^-collisions at the Large Electron-Positron Collider [2] and in $p$ $+$ $p$ , $p$ $+$ Pb , and Pb $+$ Pb collisions at the Large Hadron Collider [3, 4, 5, 6], in Be+Be and Ar+Sc collisions at the Super Proton Synchrotron [7, 8] and in Au $+$ Au collisions at the Relativistic Heavy Ion Collider (RHIC) [9].

Presented here is a precise measurement of the centrality and transverse-mass dependence of the two-pion BEC function in Au $+$ Au collisions at $\sqrt{s_{{}_{NN}}}$ = 200 GeV by the PHENIX experiment at RHIC. This data sample, recorded in 2010, allows a fine transverse-mass binning and inference of the shape of the correlation function more precisely than was possible with earlier data sets. For the first time, these results are presented as a function of centrality for six centrality classes in the range 0%–60%. As was done for the 0%–30% centrality class in Ref. [1], the source parameters of the Lévy distribution ( $\lambda$ , $R$ , $\alpha$ ) are measured.¹¹1Note that followed are the conventions introduced in Refs. [10] and [11, 12, 13], which is based on a book by P. J. Nolan [14] on univariate Lévy-stable source distributions, including also multivariate, but symmetric Lévy-stable distributions.. The centrality and the transverse-mass dependence of the Lévy-fit parameters are characterized with simple, theoretically and empirically motivated fit functions. The centrality dependence of the parameters of these functions is investigated in detail.

The structure of this paper is as follows: Sections II and III present the PHENIX experimental setup and the selection of the data sample, respectively. Section IV explores the procedure of measurement and fitting of the two-pion correlation function. Section V discusses the systematic uncertainties. Section VI presents the extracted Lévy parameters of the source as a function of centrality. Section VII discusses Monte Carlo simulations and some of the possible physics interpretations of these results, which have a strong exclusion power due to their high precision. Section VIII summarizes and concludes. Finally an Appendix details our Monte-Carlo simulations to interpret the PHENIX data.

In particular, PHENIX data on the transverse-mass and centrality dependence of the Lévy intercept parameter $\lambda(m_{T})$ are compared to centrality-dependent Monte-Carlo simulations of resonance decay chains. In all but the most-peripheral centrality class (50%–60%), the Monte-Carlo simulations are found to be inconsistent with the measurements unless a significant reduction of the in-medium mass of the $\eta^{\prime}$ meson is included. In each centrality class, the best value of the in-medium $\eta^{\prime}$ mass is determined from $\chi^{2}$ and confidence level (CL or p-value) maps, based on a comparison of PHENIX data and Monte-Carlo simulations. The resulting values of in-medium modified $\eta^{\prime}$ masses are compared to the mass of the $\eta$ meson as well as to several theoretical predictions that consider restoration of $U_{A}(1)$ symmetry in hot hadronic matter as discussed in Sections VII and VIII and then further detailed in the Appendix. Throughout this paper, units are used such that $\hbar=c=1$ . Also, the utilized fits represent the fitted data with CL in the statistically allowed 0.1% $\leq$ CL $\leq$ 99.9% interval.

II The PHENIX experiment

The data used in this analysis are the same, apart from the centrality selection, as in the previous PHENIX Lévy HBT analysis with a 0%–30% centrality selection [1]. The PHENIX experimental apparatus relevant to this analysis is thus also the same. Briefly, the PHENIX detector is subdivided into the central-arm spectrometer (covering 2 $\times$ 90^∘ azimuthal and $|\eta|\leq 0.35$ pseudorapidity acceptance), which is used here to focus mainly on hadron, electron, and photon identification and measurement. In the forward direction for each beam, two muon-arm spectrometers are used to focus mainly on identification and measurement of muons. There are also various event-characterization and triggering detectors in place. Of particular benefit here is good identification and measurement of charged pions. Ref. [1] provides further details.

III Data sample

The data sample used in this analysis comprises Au $+$ Au collisions recorded by the PHENIX detector at $\sqrt{s_{{}_{NN}}}$ = 200 GeV in 2010. The minimum-bias data sample contains $\approx$ 7.3 billion events which is reduced to $\approx$ 4.4 billion with the 0%–60% centrality selection. The centrality dependence of the transverse-mass trends is explored here in term of the numbers of participants ( $N_{\rm part}$ ), which was determined via Glauber-model calculations by the PHENIX experiment based on Ref. [15].

The present analysis shares almost all details with the previous analysis of Ref. [1], including using the word “cuts” to refer to selection criteria. The similarities and differences between the current and previous analyses are detailed below. In the present analysis, the Lévy fit parameters are determined in 23 bins of transverse mass from 0.248 GeV to 0.876 GeV and in six, 10% wide centrality bins in the range of 0%–60%. Well-measured tracks are selected using the same single-track cuts as in Ref. [1]. The event-selection criteria (except the centrality selection) and the particle-identification techniques are also the same as in Ref. [1]. The single-track cuts and their variations are considered as sources of systematic uncertainties, as described in Section V.

The particle identification (PID) of pions is based on time-of-flight information and the path length information given by the track model. As in Ref. [1], a general cut on transverse momentum, $p_{T}>0.16$ GeV, is applied to all pions. The cuts used in the PID are also considered as sources of systematic uncertainties.

In addition to the cuts on single tracks, pair cuts are imposed to minimize two-track effects: track merging, and splitting. Merging occurs when two tracks are so close to each other that the reconstruction algorithm considers them to be one track. Splitting is the opposite of the merging effect: one track is falsely reconstructed as two. These ambiguous pairs can be removed from the sample by geometrical cuts on their $\Delta\varphi$ – $\Delta z$ plane, where $\Delta\varphi$ denotes the azimuthal angle difference of the hit positions and $\Delta z$ is the difference of the $z$ coordinates of the pair, as determined by the drift chambers (DC), lead-scintillator electromagnetic calorimeter (PbSc), and time-of-flight (TOF) in the east and west arms of the PHENIX spectrometer.

These pair cuts were carefully investigated in the previous Lévy analysis [1]. However, due to the different centrality selections, the pair-cut settings here are slightly modified. The pair cuts are defined in the $\Delta\varphi$ – $\Delta z$ plane as:

	$\displaystyle\Delta\varphi>\Delta\varphi_{0}\left(1{-}\frac{\Delta z}{\Delta z_{0}}\right)\hskip 4.26773pt{\rm and}\hskip 4.26773pt\Delta\varphi>\Delta\varphi_{1}\hskip 5.69046pt\text{(DC and PbSc)},$		(1)
	$\displaystyle\Delta\varphi>\Delta\varphi_{0}\left(1{-}\frac{\Delta z}{\Delta z_{0}}\right)\hskip 5.69046pt\text{(TOF east)},$		(2)
	$\displaystyle\Delta\varphi>\Delta\varphi_{0}\hskip 4.26773pt{\rm and}\hskip 4.26773pt\Delta z>\Delta z_{0}\hskip 4.26773pt\text{(TOF west)}.$		(3)

The default values of the $\Delta\varphi_{0}$ , $\Delta\varphi_{1}$ , and $\Delta z_{0}$ can be found in Table 1, where also listed are the alternative values, which are used in Section V to determine the systematic uncertainties.

Table 1: The values of the coordinates for the pair-selection (cuts) criteria and the alternative values used to determine systematic uncertainties.

	DC				TOF east			TOF west			EM Cal
Pair cuts		$\Delta\varphi_{0}$	$\Delta z_{0}$	$\Delta\varphi_{1}$		$\Delta\varphi_{0}$	$\Delta z_{0}$		$\Delta\varphi_{0}$	$\Delta z_{0}$		$\Delta\varphi_{0}$	$\Delta z_{0}$	$\Delta\varphi_{1}$
		[rad]	[cm]	[rad]		[rad]	[cm]		[rad]	[cm]		[rad]	[cm]	[rad]
Default cut settings		0.12	8.	0.017		0.12	12		0.075	14.0		0.12	16	0.015
Loose drift chamber cut		0.11	7.	0.016		0.12	12		0.075	14.0		0.12	16	0.015
Strict drift chamber cut		0.13	9.	0.018		0.12	12		0.075	14.0		0.12	16	0.015
Loose ID detector cuts		0.12	8.	0.017		0.11	11		0.070	13.0		0.11	15	0.013
Strict ID detector cuts		0.12	8.	0.017		0.13	13		0.080	15.0		0.13	17	0.017

As in Ref. [1], in addition to these cuts, if multiple tracks are found that are associated with hits in the same tower of the PbSc slat of the TOF east, or strip of the TOF west detector, then all but one (randomly chosen) are removed. This ensures that no ghost tracks remain in the sample after the above-mentioned pair cuts.

Within statistical uncertainties of the fit parameters, using only positive pions gives results consistent with using only negative pions. Consequently, only the results from combined fits to both $(++)$ and $(--)$ charge combinations of identified pion pairs are presented here.

IV Measuring and fitting the two-particle correlation function

IV.1 Measuring the correlation function

In principle, a detailed shape analysis of the two-particle correlation functions could require three-dimensional measurements, but the lack of statistical precision could make such measurements impractical. The goal here is to obtain precise results in several transverse-mass and centrality bins. Thus, the correlation functions use a single variable $Q$ . PHENIX preliminary results on a multivariate Lévy analysis are also available [16], but go beyond the scope of the present paper.

Our relative momentum variable $Q$ is chosen as the modulus of the three-momentum difference in the longitudinal comoving system (LCMS) [17]. With the Bertsch-Pratt decomposition of the relative momentum to the “side, out, and long” components [18, 19] in the LCMS, the variable can be written as

\displaystyle Q

\displaystyle\equiv|\textbf{q}_{\rm LCMS}|=\sqrt{q^{2}_{\rm out,LCMS}+q^{2}_{\rm side,LCMS}+q^{2}_{\rm long,LCMS}}.

(4)

The motivation for this variable comes from the experimental observation [10] that in a Gaussian three-dimensional BEC analysis, a quadratic sum appearing in the BEC functions provided nearly equal BEC radius parameters, i.e, $R_{i}{\approx}R$ for $i={\rm side,out,long}$ . Thus, this quadratic sum can be simplified as

\displaystyle\sum_{i={\rm side,out,long}}R_{i}^{2}q_{i}^{2}{\approx}R^{2}\left(\sum_{i={\rm side,out,long}}q_{i}^{2}\right)=R^{2}Q^{2},

(5)

which depends on the relative momentum only through the one-dimensional variable $Q$ , the magnitude of the relative momentum of the pair in the LCMS. It was shown in Ref. [10] that the same quadratic sum appears in three-dimensional symmetric Lévy-stable distributions. So our choice for the relative momentum variable $Q$ actually includes, as a special case, the Lévy analysis of three-dimensional Bose-Einstein correlation functions under the condition that the HBT radii in all three spatial dimensions are equal within experimental uncertainties. An approximate equality of the transverse-mass and centrality-dependent BEC radii was found in several experiments, e.g., S $+$ Pb collisions at the CERN Super-Proton-Synchrotron energies by the NA44 Collaboration [20], and in $\sqrt{s_{NN}}=200$ GeV Au $+$ Au collisions at $\sqrt{s_{NN}}=200$ GeV by the PHENIX and STAR Collaborations in the Gaussian approximation in Refs. [21, 22]. PHENIX preliminary multivariate Lévy fits in Au $+$ Au collisions at $\sqrt{s_{NN}}=200$ GeV are also used in Ref. [16]. Especially note that the PHENIX preliminary three-dimensional Lévy-analysis for Au $+$ Au collisions at $\sqrt{s_{{}_{NN}}}$ =200 GeV finds that the three BEC radii in the LCMS are approximately equal (except perhaps at small transverse mass).

Furthermore, the radii are approximately equal to the radius found in a one-dimensional analysis [16], i.e., the Lévy source is indeed approximately spherical in the LCMS. Hence, this one-dimensional Lévy analysis, which focuses on the centrality and transverse-mass dependence, can be considered also as a reasonable approximation of a three-dimensional Lévy analysis. A detailed justification of this choice of $Q$ can also be found in Ref. [1], where the same variable is used.

Our choice of $Q$ can be written using the measured momenta of identified pions, $p_{i}^{\mu}=(E_{i},p_{i,x},p_{i,y},p_{i,z})$ . For $i=1,2$ :

\displaystyle Q

\displaystyle\equiv|\textbf{q}_{\rm LCMS}|=\sqrt{(p_{\rm 1,x}-p_{m2,x})^{2}+(p_{\rm 1,y}-p_{\rm 2,y})^{2}+\frac{4(p_{\rm 1,z}E_{2}-p_{\rm 2,z}E_{1})^{2}}{(E_{1}+E_{2})^{2}-(p_{1,z}+p_{2,z})^{2}}},

(6)

where the z axis coincides with the beam axis.

The correlation function is measured as:

\displaystyle C_{2}(Q)=\frac{A(Q)}{B(Q)}\cdot\frac{\int_{Q_{\rm int,min}}^{Q_{\rm int,max}}B(m_{T},Q)}{\int_{Q_{\rm int,min}}^{Q_{\rm int,max}}A(m_{T},Q)},

(7)

where $A(Q)$ is the actual $Q$ distribution of pairs of identical pions coming from the same event, $B(Q)$ is the corresponding distribution of pairs of identical pions from different events, and $Q_{\rm int,min}$ and $Q_{\rm int,max}$ denote the lower and upper bound of the integrals. Note that $A(Q)$ may contain correlations in addition to the quantum-statistical correlation due to the indistinguishability of the the measurement of identical bosons. Other correlations could be the consequence of conservation laws, resonance decays, kinematics, detector acceptance effects, etc.

Ideally, the background $B(Q)$ distribution, or reference sample, is identical to the sample of like-charged pion pairs in all respects, except for the Bose-Einstein interference effect itself [23]. As such a $B(Q)$ distribution does not exist in Nature; it has to be generated using approximation schemes. The choice here is explained below. Careful testing showed stability over the choice of the fit range and systematic variations of acceptance, PID, and other cuts detailed among the systematic uncertainties.

In choosing the background distribution $B(Q)$ , each member of the pairs are selected from different events. Hence, $B(Q)$ contains only trivial kinematic correlations between independent particles that are distributed with the same single-particle spectra and in the same kinematic range. The background distribution is affected by the centrality-selection cuts and detector-acceptance effects, rapidity, and transverse-mass cuts. In $A(Q)$ the pairs are correlated not only due to Bose-Einstein correlations, but also by other initial- or final-state interactions. Such effects from interactions include branching processes of jets, hadronization effects, resonance decays, energy, and momentum conservation laws, possible other kinematic effects, such as elastic scattering, Coulomb, and strong final-state interactions.

In general, $A(Q|MC)$ and $B(Q|MC)$ should be generated from Monte-Carlo simulations that describe these single-particle data and all other nonBEC correlation effects. These Monte-Carlo distributions are then used to correct $B(Q)$ for its lack of nonBEC correlations, as was done, for example in e⁺+e^- collisions by the L3 collaboration [2]. However, in high-energy heavy-ion physics there is a good reason why this complicated and Monte-Carlo-dependent procedure is not necessary. Namely, the presence of high-multiplicity events, with $\langle n\rangle\gg 1$ , where $\langle n\rangle$ is the mean charged-particle multiplicity at midrapidity. The usual kinematic correlations, which are due to resonance decays or conservation laws, are proportional to the mean multiplicity, $\langle n\rangle$ , while Bose-Einstein correlations grow with the mean number of pairs $\langle n(n-1)\rangle$ . Thus in high-multiplicity heavy ion collisions, Bose-Einstein correlations (together with Coulomb and strong final-state interactions that also grow proportionally with the number of pairs) outnumber all the other correlations. Hence, the MC approach can be safely abandoned. In the expression $A(Q)/B(Q)$ the Bose-Einstein, Coulomb, and strong final-state correlations dominate, and the other correlations are suppressed as $\langle n\rangle/\langle n(n-1)\rangle\propto 1/\langle n\rangle\ll 1$ .

In BEC measurements using charged particles, Coulomb repulsion modifies the correlation function at low $Q$ values creating the “Coulomb hole” [17]. To account for the final-state Coulomb interaction, the Coulomb wave function is integrated over the source of pions. Strong final-state interactions could also be taken into account using phase shifts that modify the Coulomb wave function. However, the strong final-state interaction of the pion pairs is small compared to the experimental precision [17, 24]. All the Lévy fits here (without corrections for the strong final-state interactions) are of good quality with CL $\gg 0.1$ %. The strong final-state interactions are found not to affect the quality of Lévy fits, nor to change the parameters significantly [17, 24]. Therefore, such corrections are not considered in this analysis. In contrast, the effect of Coulomb interactions is clearly visible as a Coulomb hole at small values of $Q$ . The fitting function is appropriately modified, as detailed Section IV.2.2.

IV.2 The fitting function

IV.2.1 The Lévy shape

For the shape of the correlation function, it is not possible to $a$ $priori$ assume or know, what is or what should be the shape-model of the Bose-Einstein correlation functions. Measurements of this quantity test the hypothesis of being consistent with a Lévy shape. Using the plane-wave approximation and assuming a spherically symmetric, Lévy-type source, the two-particle BEC function has the simple form

\displaystyle C_{2}(Q)=1+\lambda\exp{\left[-Q^{\alpha}R^{\alpha}\right]},

(8)

where $\lambda$ is the strength of the correlation, $R$ is the scale parameter in physical units, and $\alpha$ is the Lévy index of stability [10]. This hypothesis is tested not only by successful fits to the PHENIX data with CL $\gg 0.1$ %, which are stable and robust with systematic variations of particle identification, acceptance, and pair cuts, as detailed in Section V. The validity of the Lévy shape is also checked by employing a Lévy expansion technique [25, 12, 13]. This method utilizes a complete set of polynomials that are orthonormal with respect to a Lévy weight function [12]; so this method is able to characterize and model independently any deviation from a Lévy-stable source shape. To first order of the expansion, no significant deviation from the Lévy shape is found in any of the centrality and transverse-mass ranges investigated here.

The relevance of stable distributions to the analysis of (Coulomb-corrected) Bose-Einstein correlations was studied in Ref. [10], following the general mathematical ideas summarized in Ref. [14]. Univariate stable distributions are usually characterized by the Fourier transform of their density distributions that are called the characteristic functions. Following the convention of the previous analysis [1] and the theoretical paper where the idea first appeared [10], the $S(\alpha,\beta,\gamma,\delta;1)$ notation is used. The parameter $\alpha$ is the Lévy index of stability (or characteristic exponent) that is limited to the domain $0<\alpha\leq 2$ . The asymmetry parameter $\beta$ is limited to the domain $-1\leq\beta\leq 1$ . The scale parameter $\gamma$ is nonnegative and the location parameter $\delta$ can be any real number with $-\infty<\delta<\infty$ . The book by P. J. Nolan [14] details exhaustively the $\alpha=1$ special case and the ubiquitous nature of Lévy-stable source distributions. It provides illustrations of the stable densities in the $S(\alpha,\beta,\gamma,\delta;1)$ parameterization.

The asymmetric $\tau$ -model [26] was utilized successfully by the L3 Collaboration [2] to interpret two-jet data. Two of the experimentally testable predictions that are directly related to asymmetrical ( $\beta\neq 0$ ) source distributions were investigated. The first indication of such an asymmetry was related to a dip (an anticorrelated region) in the two-particle Bose-Einstein correlation function. Observance of such a dip in PHENIX data would be a strong experimental indication of the presence of an asymmetric source. However, such a dip is not observed in any of the investigated transverse-mass or centrality bins. Secondly, if the asymmetric $\tau$ -model has relevance in the present analysis, the BEC function would depend on any relative-momentum component only through the invariant momentum $q_{\rm inv}$ . In this case, the BEC functions increase with decreasing values of $q_{\rm inv}$ , even if $Q$ is kept constant. Such behavior is not observed here; on the contrary, the BEC function is seen to increase with decreasing $Q$ , even if $q_{\rm inv}$ is kept at constant values. Therefore, a vanishing asymmetry parameter, $\beta=0$ , is assumed.

The correlation function is thus based on the assumption of the simplest case of univariate and symmetric ( $\beta=0$ ) stable distributions. The scale parameter $\gamma$ is replaced by the physical parameter $R$ [10]. In the standardized notation of Nolan [14], this corresponds to the $(\alpha,\beta{=}0,\gamma{=}R/2^{\frac{1}{\alpha}},\delta;1)$ convention. The Fourier-transformed source-density distribution has a simple form, $f(q)=\exp(iq\delta-\frac{1}{2}|qR|^{\alpha})$ and its modulus square leads to the simple form of the BEC function of Eq. (8). Note that the correlation function does not depend on $\delta$ .

The relationship with the Gaussian source distribution is also apparent in Eq. (8) as it corresponds to the $\alpha=2$ special case. As detailed in Ref. [10], the physical scale parameter $R$ corresponds only in this $\alpha=2$ special case to the root-mean-square of the source. For all $0<\alpha<2$ , the root-mean-square is divergent, as is well known for the Cauchy or Lorentzian special case ( $\alpha=1$ ). In the $\alpha=1$ case the physical Lévy scale parameter $R$ corresponds to the half width at half maximum (HWHM) of the source distribution. In fact for all values of $\alpha$ , $R$ is proportional to the HWHM, the constant of proportionality depending on $\alpha$ . Another notable property of the Lévy stable source distributions is that in the $\alpha<1$ cases, even the first moment of the source distribution is divergent. In high energy particle and nuclear physics, the $R$ values correspond to a few femtometers [2, 1].

IV.2.2 The Coulomb interaction

As in Ref. [1], the Coulomb final-state interaction is characterized using the Sinyukov-Bowler method [27, 28]. This method corresponds to the integration of the two-particle Coulomb wave function [29] for a core-halo type of particle-emitting source [30, 31]. However, such a Coulomb wave-function integration cannot be performed analytically in the case of a Lévy source. Hence, numerical approaches are needed. The previous Lévy BEC analysis used an iterative method based on a numerical table which contains the values of the integral for a range of values in the parameters and in the variable. The details can be found in Ref. [1]. In this paper a parameterization [32, 33] is based on the aforementioned numerical table, which is considerably faster.

The momentum difference variable of the Coulomb correction is the invariant four-momentum difference $q_{\rm inv}$ rather than the variable $Q$ , which is used in the present analysis. Neglecting the difference between the two variables could introduce a systematic uncertainty of $\approx$ 5% [1]. In the present analysis, the difference is determined by measuring the actual pair distribution in both $Q$ and $q_{\rm inv}$ , $A(Q,q_{\rm inv})$ . Using this two-dimensional distribution, the Coulomb correction is incorporated with a weighted average.

The final form of the fitting function is then

$\displaystyle C_{2}(Q;\lambda,R,\alpha,N,\varepsilon)$	$\displaystyle=1-\lambda+\lambda\>C_{2}^{(0)}(Q;R,\alpha,N,\varepsilon)\>w(Q;R,\alpha)$
$\displaystyle{\rm with}\hskip 10.00002ptC_{2}^{(0)}(Q;R,\alpha,N,\varepsilon)$	$\displaystyle=(1+\exp(-R^{\alpha}Q^{\alpha}))N(1+\varepsilon Q)$
$\displaystyle{\rm and}\hskip 10.00002ptw(Q;R,\alpha)$	$\displaystyle=\frac{\sum_{k}A(Q,q_{{\rm inv,}k})K(q_{{\rm inv,}k};R,\alpha)}{\sum_{k}A(Q,q_{{\rm inv,}k})}$	(9)

where $K(q_{{\rm inv,}k};R,\alpha)$ is the Coulomb correction given by the parameterization [32, 33]. In the definition of the weight function $w(Q;R,\alpha)$ , the index of summation $k$ runs over those bins in $q_{\rm inv}$ for a given value of $Q$ , where the number of actual pairs after the two-track cuts is nonvanishing. This summation thus averages over the $q_{\rm inv}$ -dependent Coulomb correction for a Lévy-type source characterized by $R$ and $\alpha$ , in $q_{\rm inv}$ bins only where $A(Q,q_{{\rm inv,}k})$ is nonzero. This method generalizes on Eqs. (2) and (3) of Ref. [21] for a Lévy-shaped Bose-Einstein correlation function and also accounts for the $q_{\textmd{inv}}$ dependence of the Coulomb correction. The large $Q$ behavior was found to be consistent with a linear function, which is characterized with the functional form of $N(1+\varepsilon Q)$ .

V Systematic uncertainties

Nine sources of systematic uncertainties are investigated: the single track and the pair cuts, the choice of the arm of the PHENIX detector (because the arrangement is not symmetric), the fit range of the correlation functions, and the Coulomb-correction method. The systematic uncertainties of the results are estimated by varying one setting at a time, while keeping the others at their default values. For the cuts this means applying stricter or looser criteria. This is the same approach as used in Ref. [1], which see for details. For the pair cuts the values listed in Table 1 are used rather than those of Ref. [1]. For the choice of the arm of PHENIX the variation uses only one arm rather than both. The sensitivity of the results to the fit range was investigated by adding or leaving out one bin from the beginning ( $Q_{\rm min}$ ) or the end of the fit range ( $Q_{\rm max}$ ). The results do not vary significantly with the variation of $Q_{\rm max}$ , therefore this source does not contribute to the systematic uncertainty.

As a default Coulomb-correction method, the parameterization detailed in Refs. [32, 33] is used. A recent theoretical investigation [34] suggested several alternative methods. The systematic uncertainty of the Coulomb correction is taken as the difference between our approach and the most realistic variant of the Coulomb corrections mentioned in Section 3.2 of Ref. [34], namely the 6^th one in the enumeration. The total systematic uncertainty is estimated with a standard statistical approach. The individual contributions are summed quadratically, while both the statistical uncertainties $\sigma_{\rm stat}$ and the correlations between the uncertainties (denoted by $\rho$ ) are considered. Thus, the final systematic uncertainty ( $\sigma_{\rm syst}$ ) is expressed for a parameter, $p$ (default cut denoted by $p_{\rm def}$ and the $i$ th alternative cut by $p_{{\rm cut},i}$ ), with the following form:

\displaystyle\sigma_{\rm syst,tot}^{2}=\sum_{i}\left[(p_{\rm def}-p_{{\rm cut},i})^{2}-\sigma^{2}_{\rm stat}(p_{\rm def})-\sigma^{2}_{\rm stat}(p_{{\rm cut},i})+2\rho_{i}\sigma_{\rm stat}(p_{\rm def})\sigma_{\rm stat}(p_{{\rm cut},i})\right].

(10)

The $\rho_{i}$ correlation between the uncertainties can be estimated with a data-driven method by measuring the numbers of pairs yielded with the different settings

\displaystyle\rho_{i}=\begin{cases}\sqrt{\frac{N_{\rm def}}{N_{{\rm cut},i}}}&{\rm if}\hskip 14.22636ptN_{\rm def}<N_{{\rm cut},i}\\ \sqrt{\frac{N_{{\rm cut},i}}{N_{\rm def}}}&{\rm if}\hskip 14.22636ptN_{{\rm cut},i}<N_{\rm def}.\\ \end{cases}

(11)

The $\rho_{i}$ correlation coefficients typically are near unity, except for the third-pad-chamber matching cut and the arm settings, for which $\rho_{i}{\approx}0.6$ .

VI Centrality and transverse-mass-dependent results

The transverse-mass ( $m_{T}$ ) and centrality dependence (expressed in terms of the average number of participants, $N_{\rm part}$ ) of the Lévy parameters analyzed and are investigated along with their theoretically motivated combinations. The transverse mass is defined as $m_{T}~{=}~\sqrt{m_{\pi}^{2}+K_{T}^{2}}$ , where $K_{T}=\sqrt{K_{x}^{2}+K_{y}^{2}}$ is the transverse component of the average momentum of the pair $K=0.5(p_{1}+p_{2})$ and $m_{\pi}$ is the pion mass. The number of participants $N_{\rm part}$ was determined via Glauber-model calculations based on Ref. [15]. The centrality dependencies of the Lévy parameters are characterized by theoretically or empirically motivated functions. The fits are found to represent the data in each of the investigated centrality-class and transverse-mass bins, the confidence levels are in the statistically acceptable 0.1% $\leq$ CL $\leq$ 99.9% region. The fitted correlation functions are very similar to our results obtained in the 0%–30% centrality class. For example, a Lévy fit to our Bose-Einstein correlation data was published in Ref. [1].

VI.1 The centrality and transverse-mass dependence of the fit parameters

The dependence of the physical parameters $\lambda$ , $R$ , and $\alpha$ on centrality and transverse mass, $m_{T}$ is determined. The parameters of the linear background in Eq. (9) are found to be $N\approx 1$ and $\varepsilon\approx 0$ . In particular, the maximum of the modulus of the coefficient of linearity is found to be $\max(|\epsilon|)=0.085$ GeV^-1 and the average value is $\langle|\epsilon|\rangle=0.021\pm 0.001$ GeV^-1. The overall normalization coefficient $N$ has a maximal deviation from unity of $\max(|N-1|)=0.015$ , while its average deviation from unity is $\langle|N-1|\rangle=0.0050\pm 0.0001$ .

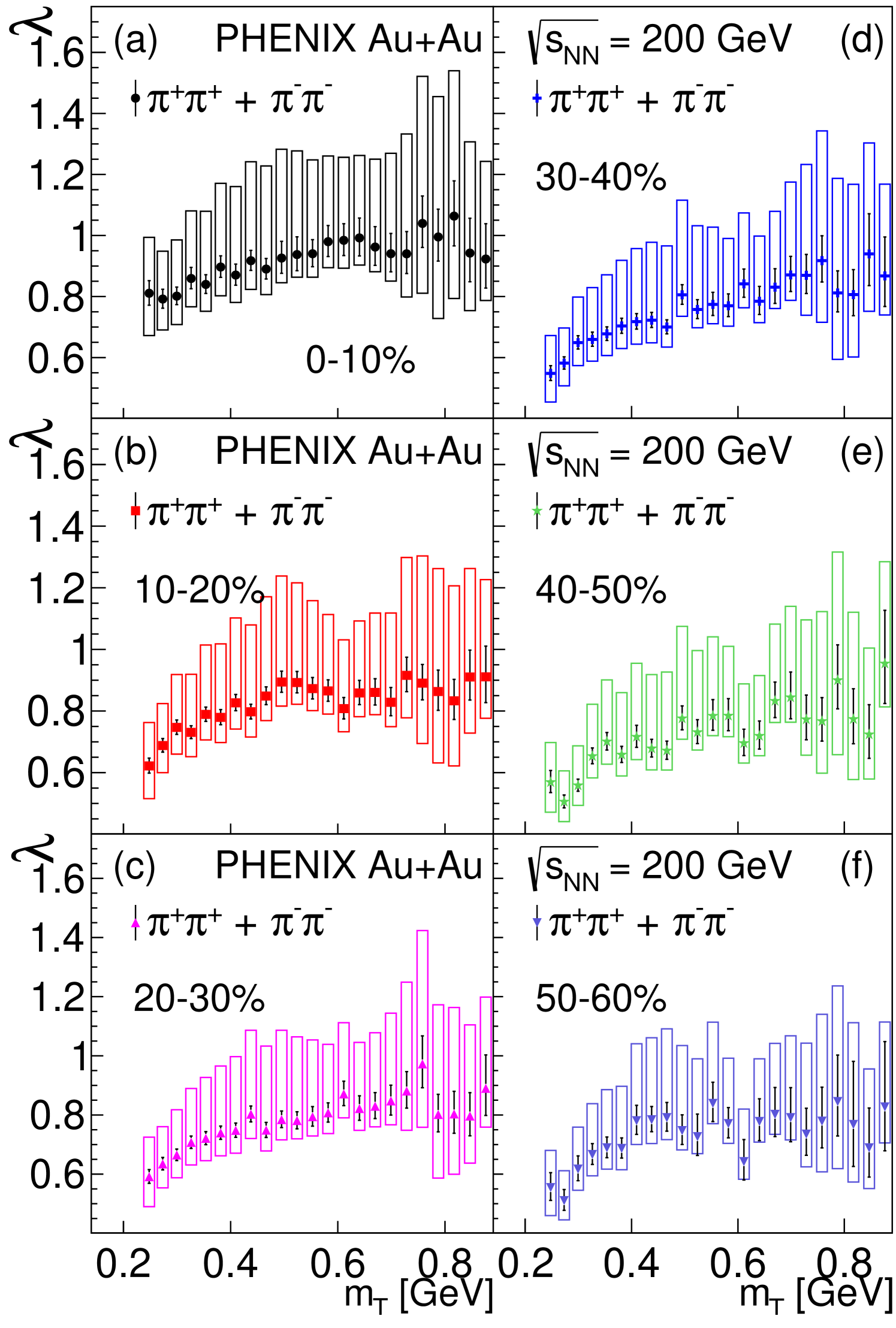
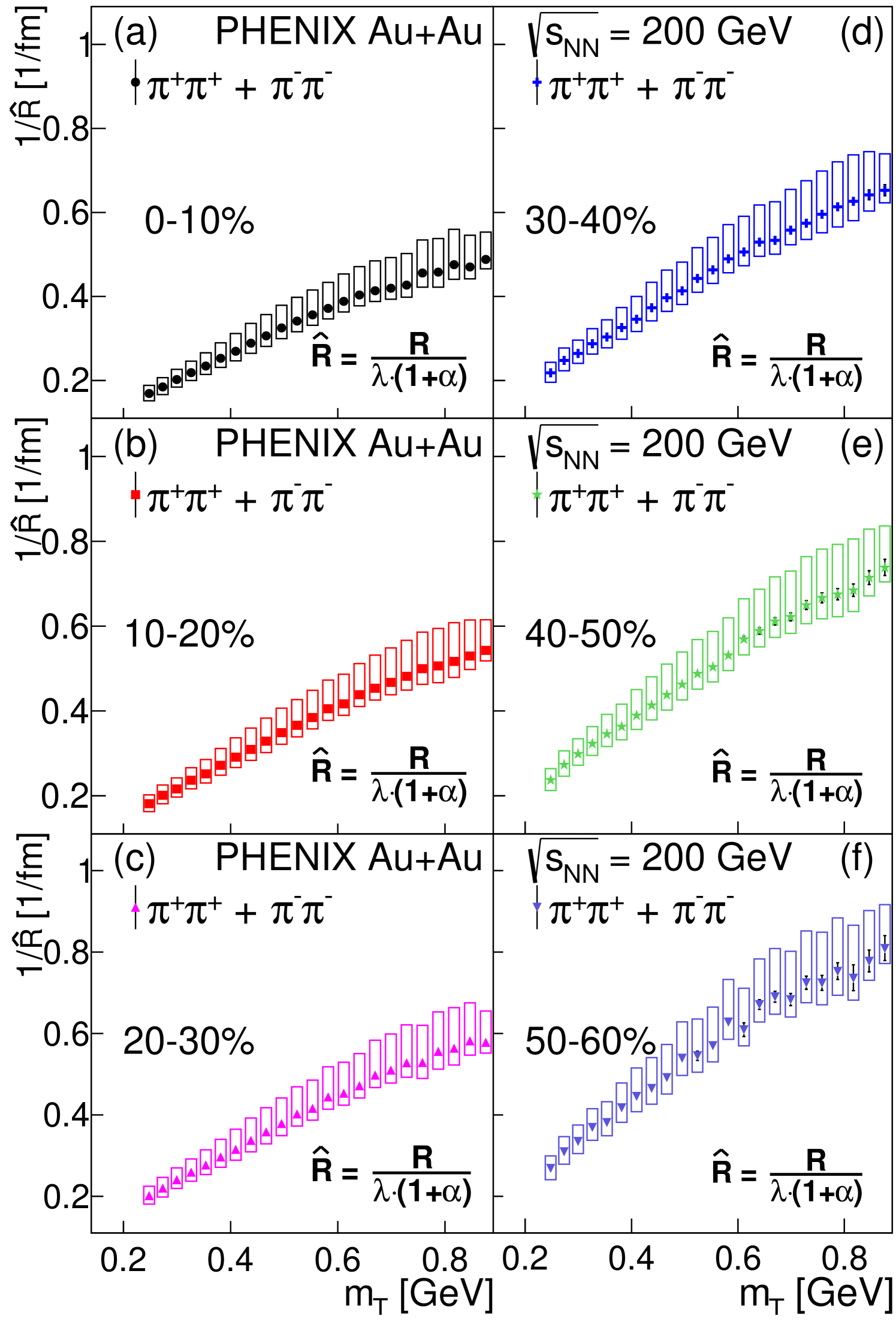
Refer to caption — Figure 1: The transverse-mass dependence of the correlation-strength parameter $\lambda$ in six centrality bins obtained from Lévy fits with Eq. (9). The central values are shown with dots, statistical uncertainties are indicated by vertical lines, while boxes are used to illustrate the systematic uncertainties.

The results of the fits for the 6 centrality and 23 $m_{T}$ bins are shown in Figs. 1–3. The intercept or the correlation-strength parameter $\lambda$ has a clearly observable suppression below $m_{T}\leq 0.5$ GeV average pair transverse mass. Above that it saturates at a centrality-dependent value. This low- $m_{T}$ suppression, which is characterized in more detail in Section VI.2 is observed in all centrality bins; however, in the most-peripheral (50%–60%) centrality class, this observation starts to be limited by statistics. This is one of the reasons that no data are shown for the most peripheral, 60%–95% centrality class.

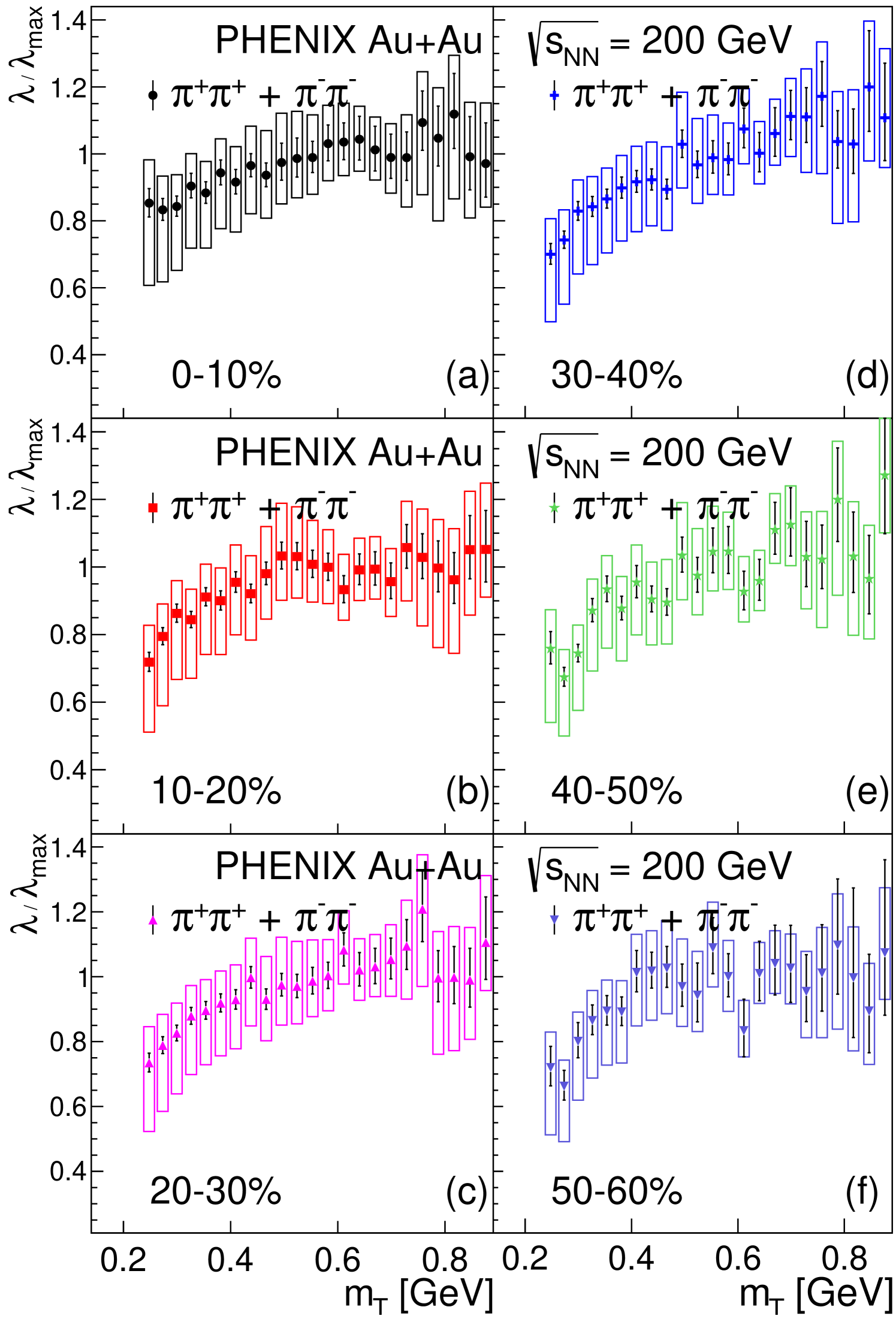
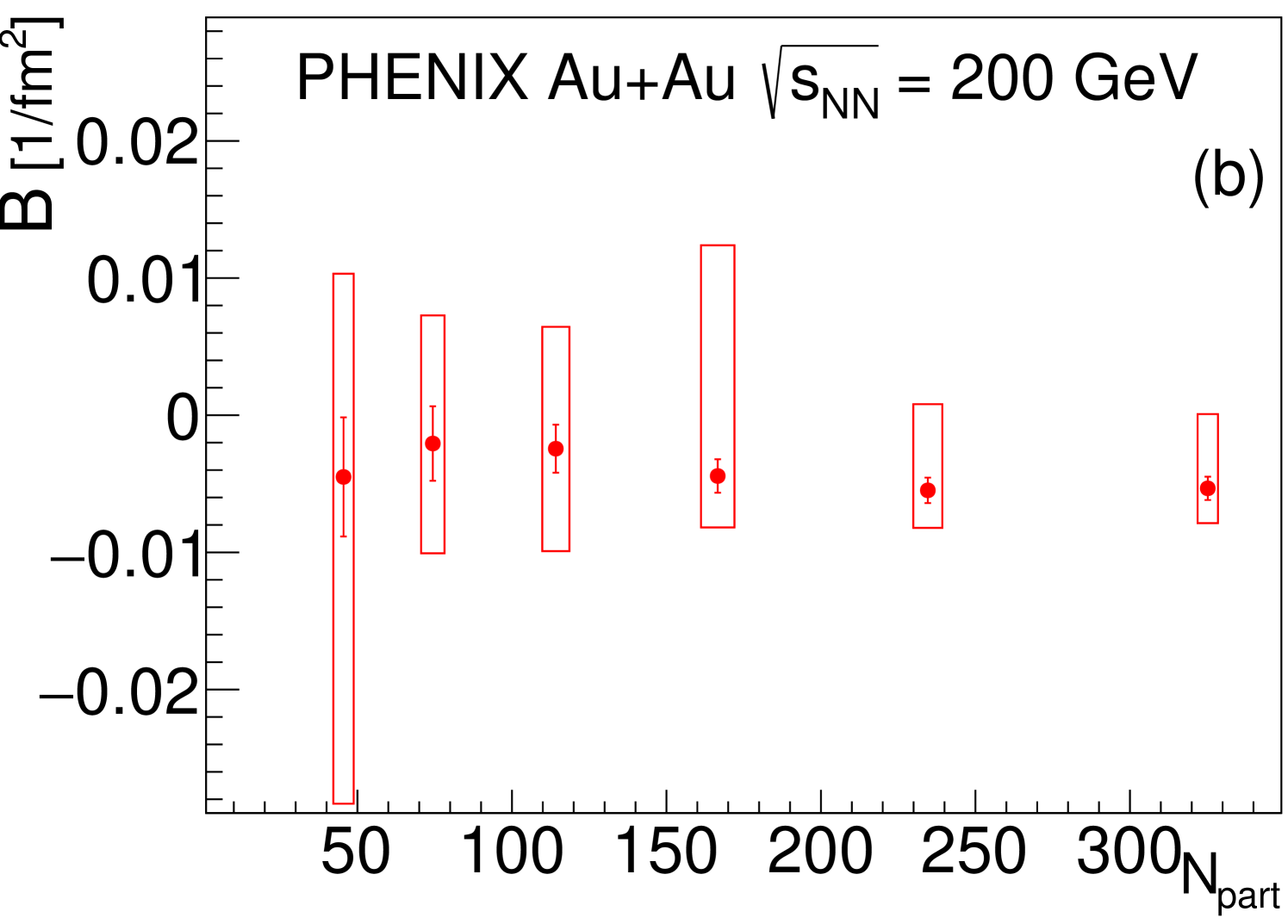
The saturation value of the intercept parameter could depend on background processes which are not in the scope of the present analysis. As was shown in Ref. [35], the value of the intercept parameter is lower for Gaussian, intermediate for an Edgeworth expansion [25], and higher for an exponential shape, which seems to be a systematic effect that depends on how the functional form of the Bose-Einstein correlation function extrapolates the data to the $Q=0$ limit. This systematic effect, an overall vertical uncertainty, can however be removed by normalizing to the saturation value of $\lambda(m_{T})$ at large $m_{T}$ , following Refs. [35, 1]. The saturation value is taken as the average value of $\lambda(m_{T})$ in the interval 0.45 GeV $\leq{m_{T}}\leq$ 0.9 GeV and is denoted by $\lambda_{\rm max}$ . This centrality-independent range is the same for each of the six centrality classes considered in this manuscript. However, from the similar range considered in Ref. [1] for the 0%–30% centrality selection, this range is slightly modified due to the different centrality classes considered. This range modification shifts the central values of $\lambda_{\textmd{max}}$ slightly, but the modification is within one standard deviation, which is within the uncertainties given in Ref. [1]. However, the value of $\lambda_{\rm max}$ does depend on centrality. The resulting $\lambda(m_{T})/\lambda_{\rm max}$ ratio is shown in Fig. 4.

Radial-flow effects are known to be strongly centrality dependent, and hence are expected to significantly influence both $\lambda(m_{T})$ and $\lambda_{\rm max}$ . Such an expectation is shown for example in Ref. [36]. If there is large radial flow, the decay products of $\eta^{\prime}$ are concentrated at high $m_{T}$ (compensating $p_{T}$ sharing between the several daughter pions, resulting in flat $\lambda(m_{T})/\lambda_{\rm max}(m_{T})$ ), while if the radial flow is low (such as in the peripheral event classes), then these decay products accumulate at low $m_{T}$ (resulting in a dip in $\lambda(m_{T})/\lambda_{\rm max}$ at low $m_{T}$ ). The two effects, the $p_{T}$ increasing radial flow and the $p_{T}$ sharing between the several pions from the $\eta^{\prime}\rightarrow\eta+\pi^{+}+\pi^{-}\rightarrow(\pi^{0}+\pi^{+}+\pi^{-})+\pi^{+}+\pi^{-}$ decay chain compensate one another at transverse velocity $\langle u_{T}\rangle{\approx}0.5$ , as shown in Ref. [36]. This expectation is cross-checked with the Monte-Carlo simulations detailed in the Appendix, where the simulation-based centrality dependence of $\lambda(m_{T})/\lambda_{\rm max}$ (without any in-medium $\eta^{\prime}$ mass modification) is also shown.

In Fig. 4, an approximate centrality independence of the characteristics of the suppression can be qualitatively observed. To test this observation quantitatively, a $\chi^{2}$ test was employed to obtain conservative values of the CL using only statistical uncertainties. For each of the 15 possible pairs of centrality classes, the $\chi^{2}$ is calculated under the hypothesis that their $\lambda/\lambda_{\rm max}$ distributions are identical. The resulting CL values are all in the range 0.15%–89.5%, which does not reject the hypothesis.

The experimental result on the centrality independence of $\lambda(m_{T})/\lambda_{\rm max}$ scaling is an unexpected, rather surprising observation. One possible explanation for such a scaling behavior is given in Section VII, based on the Monte-Carlo simulations detailed in the Appendix. A quantitative analysis of these $\lambda(m_{T})/\lambda_{\rm max}$ measurements is presented in Section VI.2.

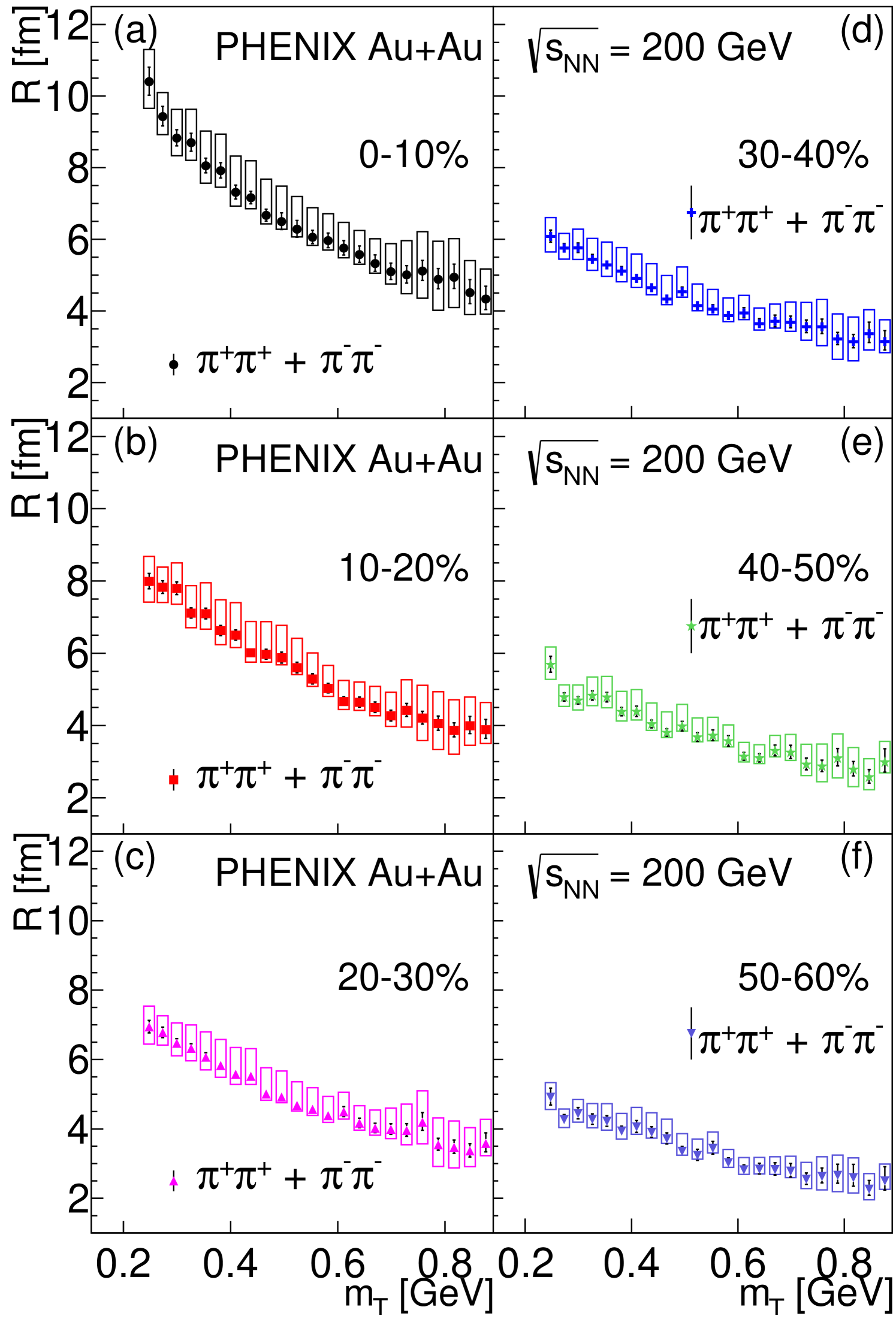
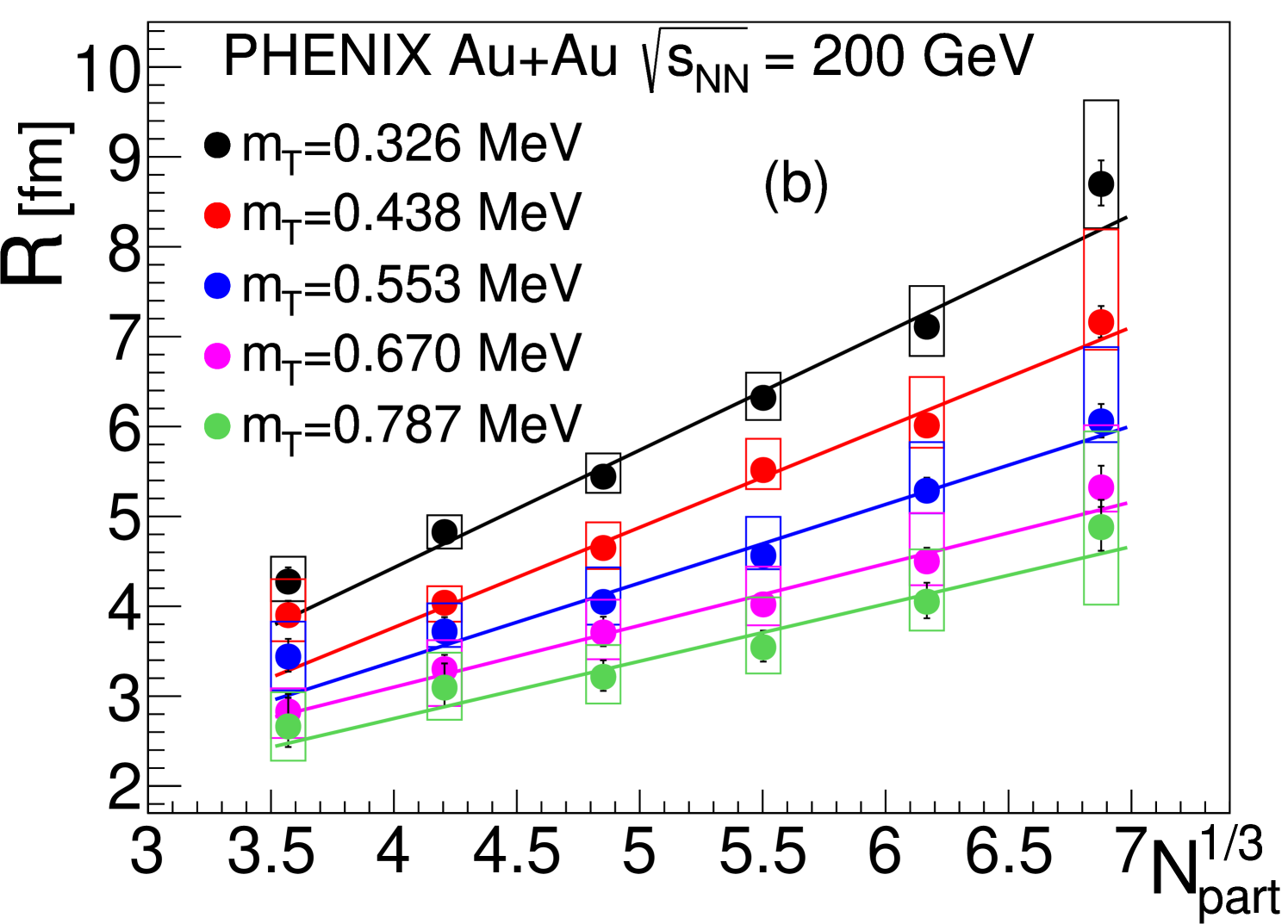
The Lévy-scale parameter, introduced in high-energy particle and nuclear physics as the physical-scale parameter $R$ in Ref. [10], decreases with $m_{T}$ for all centrality bins, as can be seen in Fig. 2. Analytic hydrodynamic calculations [27, 37, 38] predict that in the $\alpha=2$ special case, $R^{-2}(m_{T})$ depends linearly on $m_{T}$ , which can be parameterized as

\displaystyle\frac{1}{R^{2}}=Am_{T}+B

(12)

as shown in Fig. 5. The centrality dependence of the slope parameter $A$ and the intercept parameter $B$ is presented in Section VI.2.

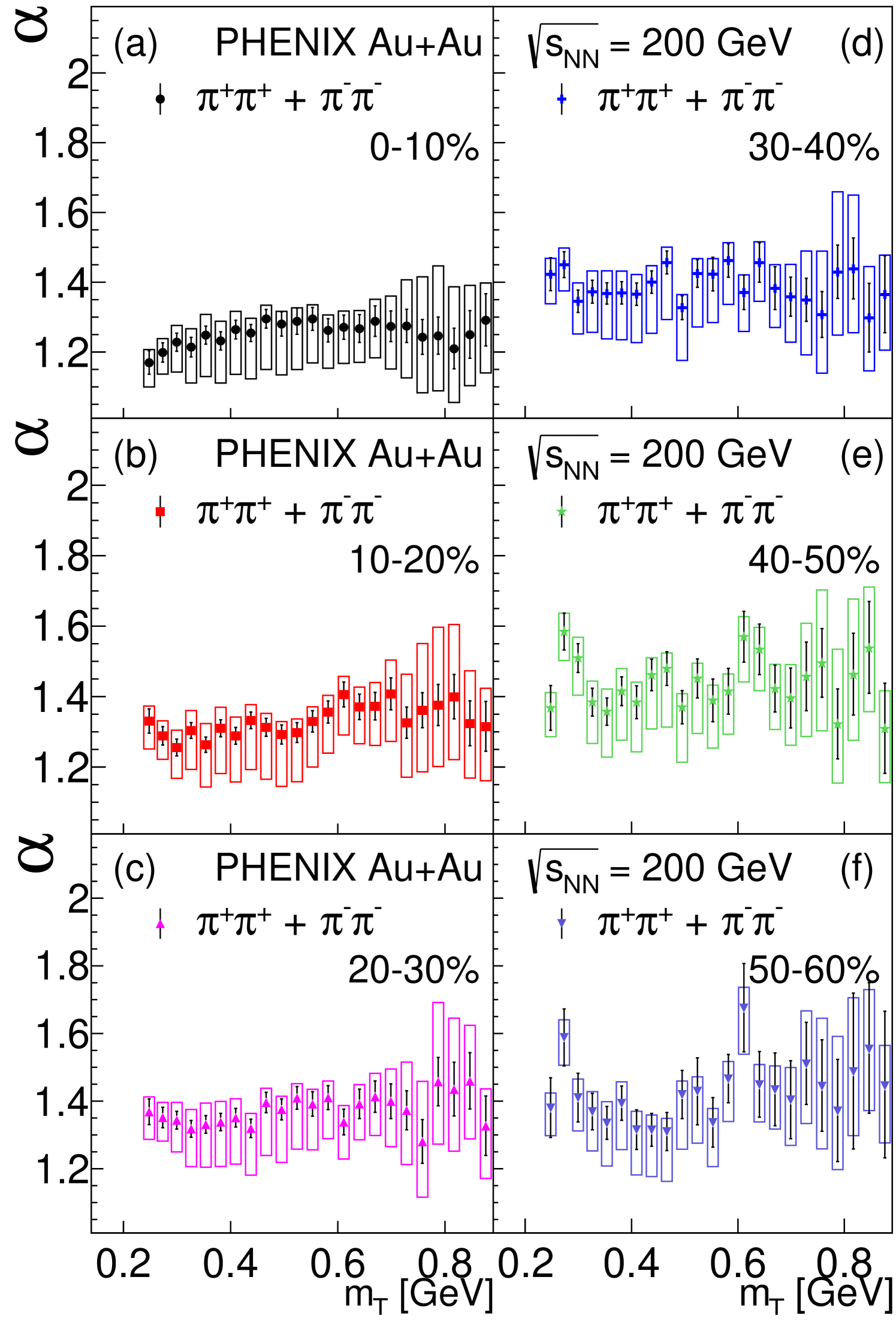
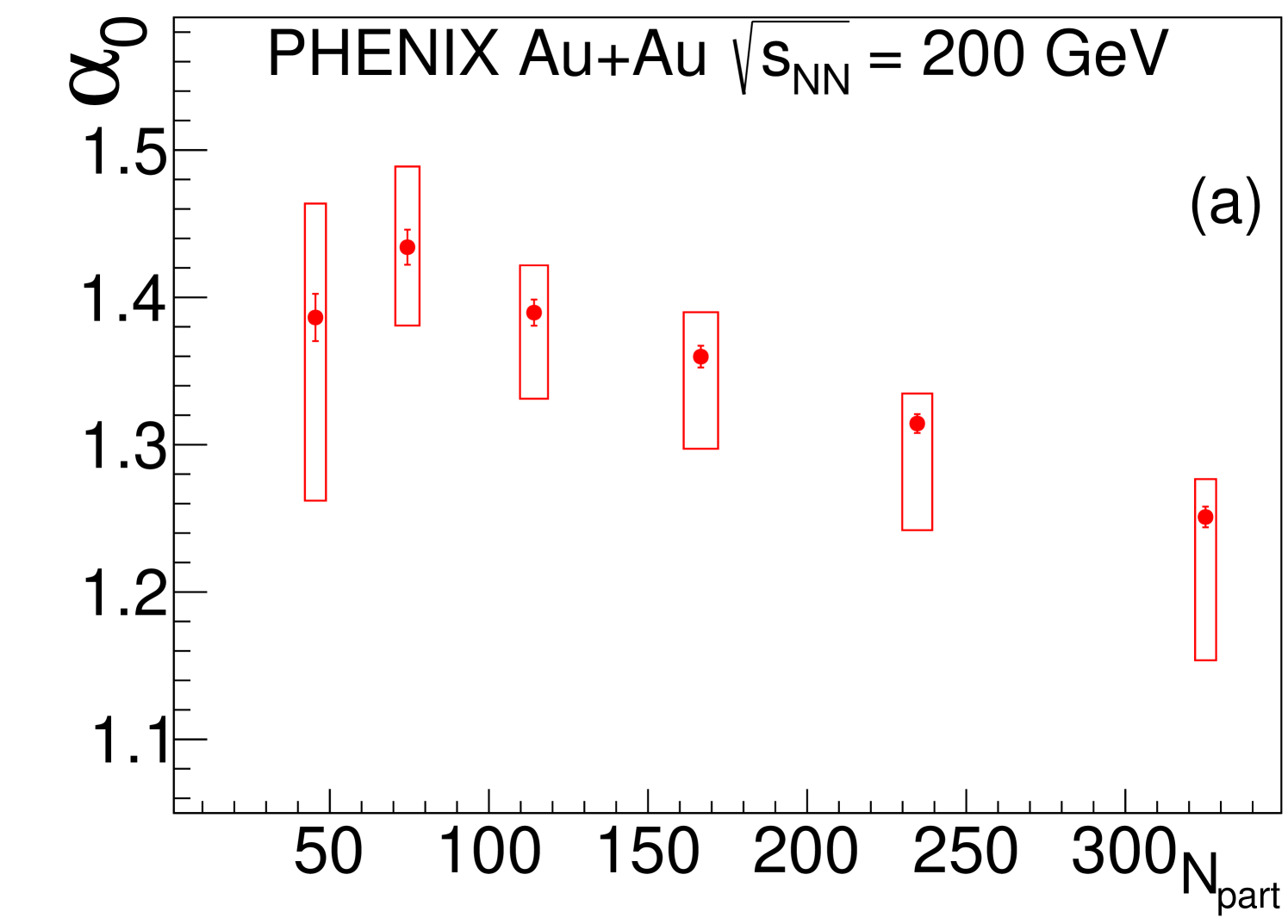
Figure 3 shows the measured values of the Lévy index $\alpha$ . In each centrality bin $\alpha$ appears to be independent of $m_{T}$ . In each centrality class, the data of Fig. 3 can be well represented by the $m_{T}$ -averaged values, $\alpha_{0}$ . As indicated in Fig. 10, these values are found to depend on centrality. The measured values of $\alpha$ are significantly lower than the Gaussian case of $\alpha=2$ , and are significantly higher than the exponential/Cauchy case of $\alpha=1$ . The centrality dependence of $\alpha_{0}$ is discussed in Section VI.2.

Similar to earlier PHENIX studies in the 0%–30% centrality-class range [1], strong correlations are observed between the parameters $\lambda$ , $R$ , and $\alpha$ . However, a specific combination of these three Lévy parameters, namely

\displaystyle\frac{1}{\widehat{R}}=\frac{\lambda(1+\alpha)}{R},

(13)

shown in Fig. 6, seems to be less correlated with the direct fit of Lévy parameters $\lambda$ , $R$ , $\alpha$ as compared to the correlations among them, which is very similar to the correlation plots published in Ref. [1] for the 0%–30% centrality class. The correlation coefficients between the parameters $\lambda$ , $R$ and $\alpha$ were determined in the Lévy fits and were considered when evaluating $\widehat{R}^{-1}$ .

In Ref. [1] $\widehat{R}^{-1}$ was found to depend approximately linearly on $m_{T}$ and was parameterized in the 0%–30% centrality class as

\displaystyle\frac{1}{\widehat{R}}=\widehat{A}m_{T}+\widehat{B}.

(14)

Figure 6 shows a more detailed centrality-dependent analysis. The centrality dependence of the $\widehat{A}$ slope parameter and $\widehat{B}$ intercept parameter is presented in Section VI.2. The linearity of $\widehat{R}^{-1}$ is broken at large $m_{T}$ , which is likely due to the saturation of the $\lambda$ parameter in that range. As noted in Ref. [1], the understanding of the approximate scaling properties of $\widehat{R}$ is another currently unsolved theoretical challenge.

VI.2 The centrality dependence of the physical parameters

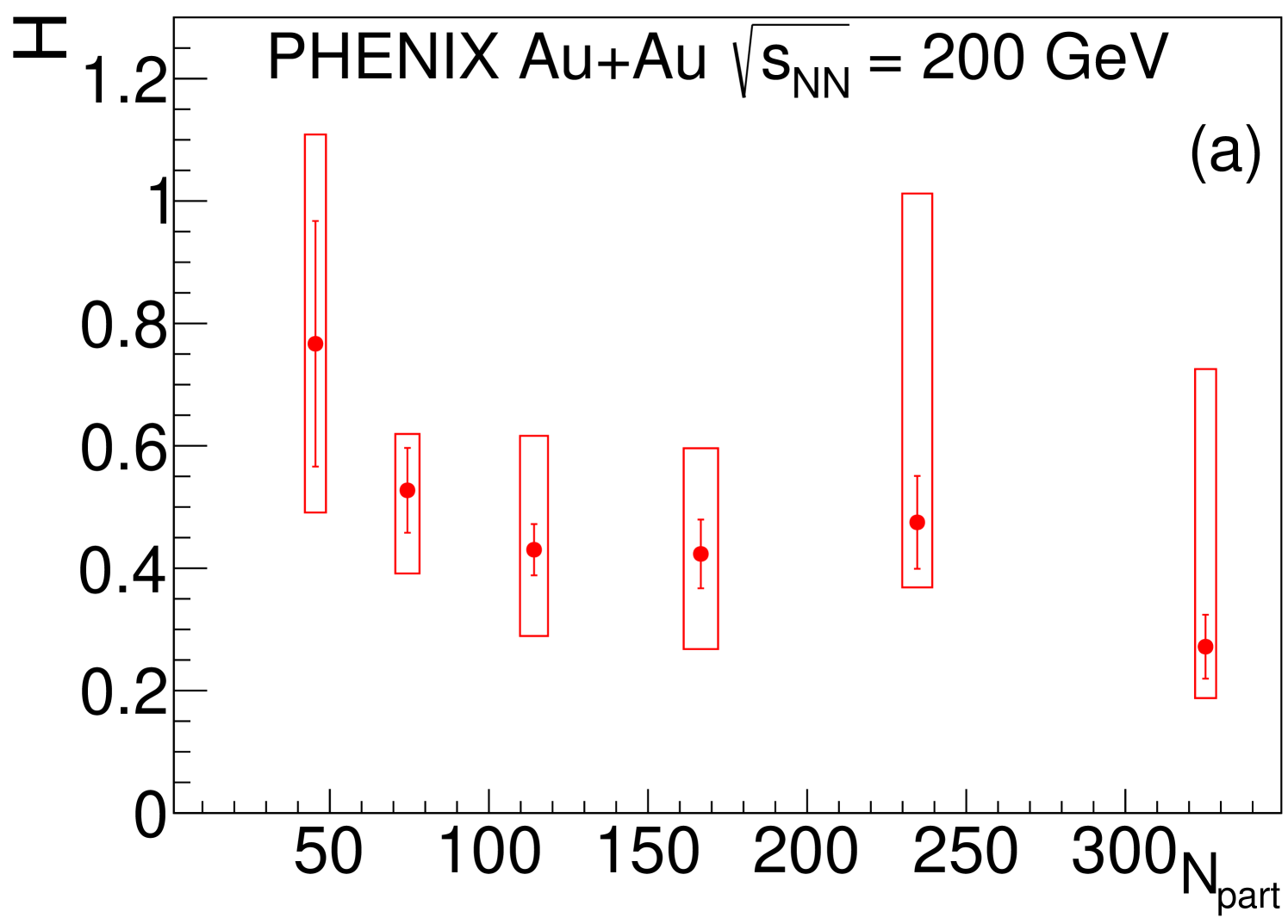
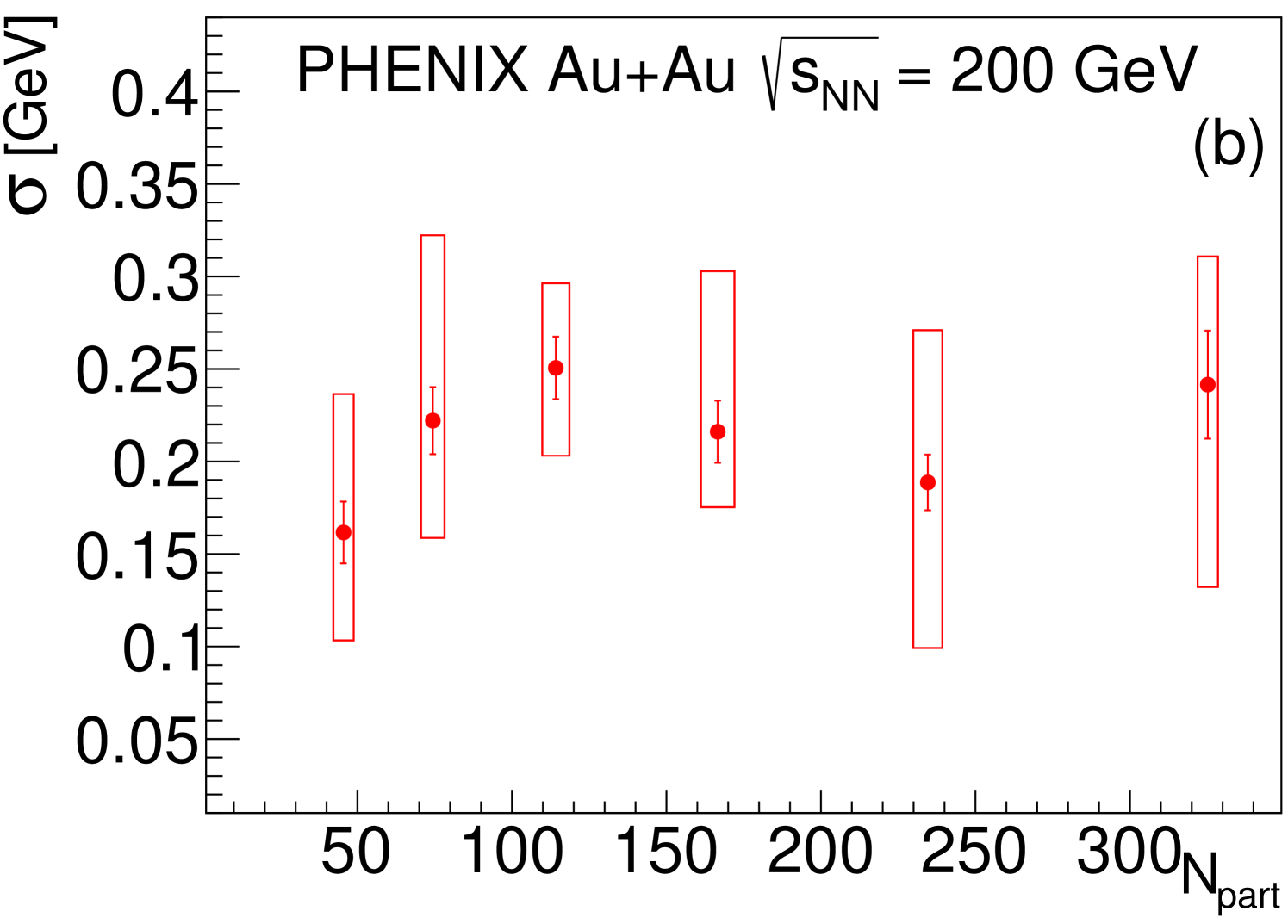
In this subsection, the centrality dependence of the physical parameters via theoretically or empirically motivated parameterizations are investigated. The centrality dependence of the parameters of these parameterizations is discussed here as a function of $N_{\rm part}$ . Quantitatively studying the suppression of $\lambda(m_{T})/\lambda_{\rm max}$ at low $m_{T}$ , uses fits of the phenomenological Gaussian parameterization, which was also used in Ref. [1],

\displaystyle\frac{\lambda}{\lambda_{\rm max}}=1-H\exp\left({-\frac{m_{T}^{2}-m_{\pi}^{2}}{2\sigma^{2}}}\right),

(15)

where the parameter $H=H(N_{\rm part})$ measures the depth of the suppression and parameter $\sigma=\sigma(N_{\rm part})$ measures the width of this suppression. In principle, both $H$ and $\sigma$ could have a centrality or $N_{\rm part}$ dependence.

From the experimentally observed, and rather surprising, centrality-independent scaling of $\lambda(m_{T})/\lambda_{\rm max}$ , the centrality independence of the $H$ and the $\sigma$ fit parameters is expected, as discussed in Section VI.1. Indeed, both obtained parameters are consistent with the hypothesis of centrality independent values $H_{0}$ and $\sigma_{0}$ , as indicated in Fig. 7.

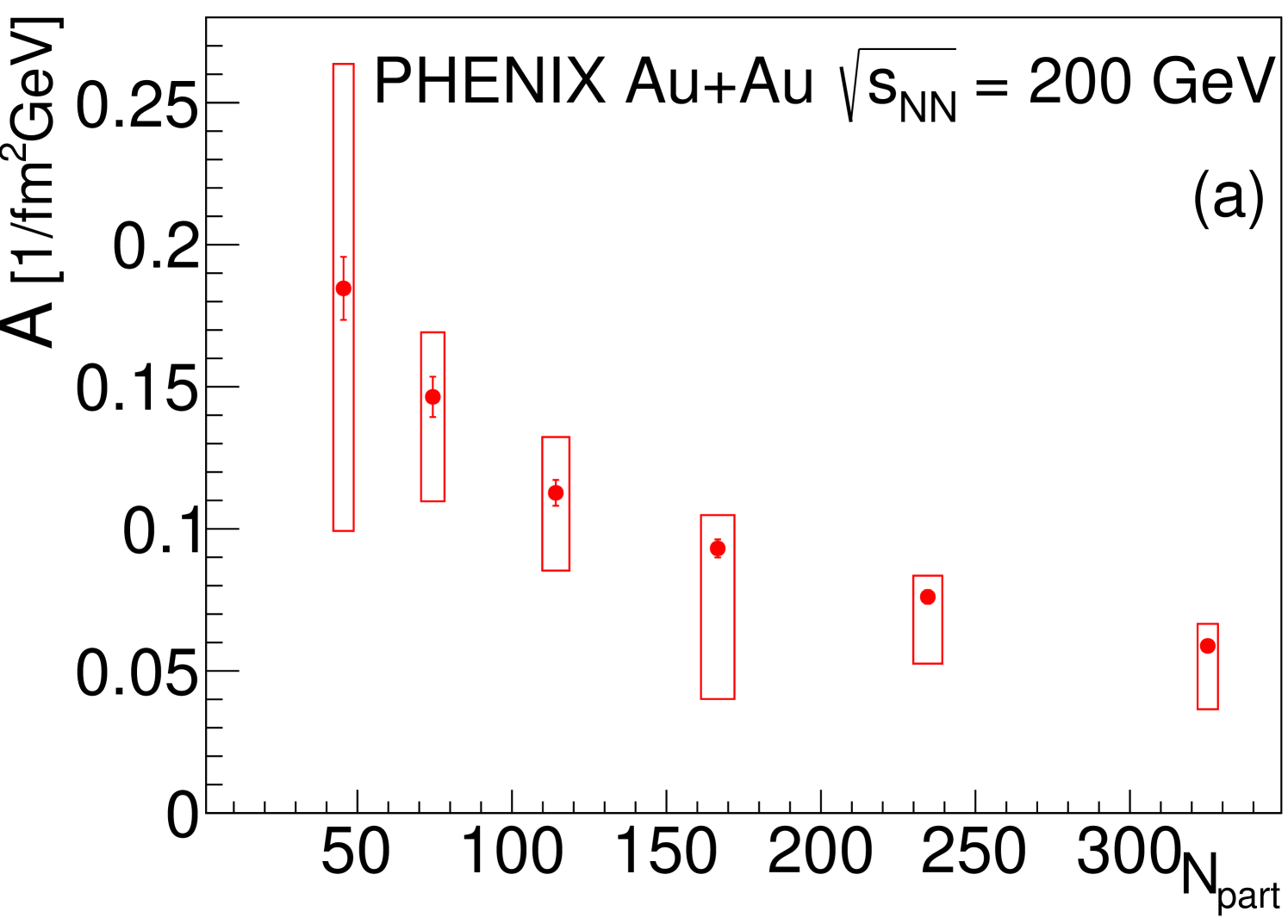
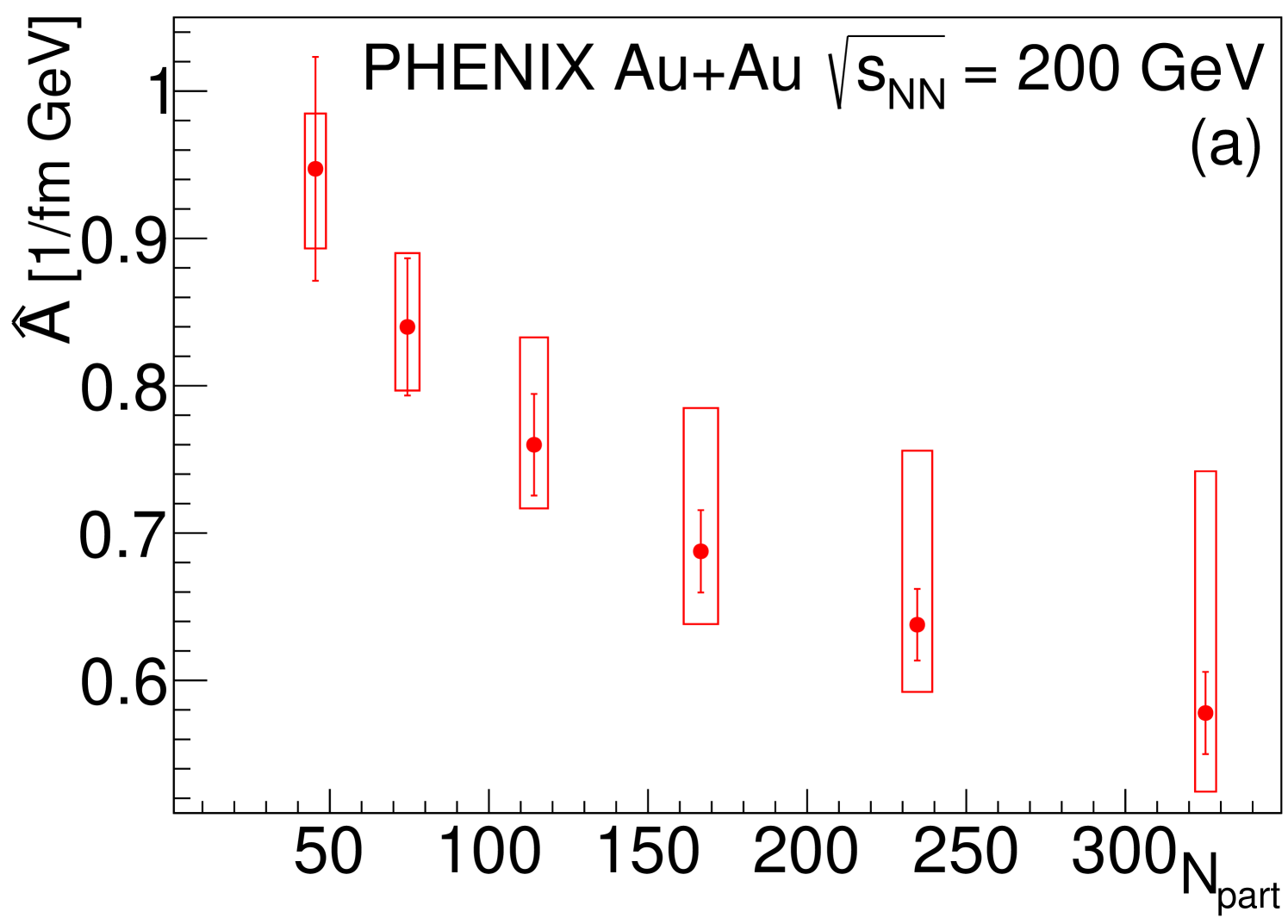
The affine linearity of the inverse square of the Lévy-scale parameter $R^{-2}(m_{T})$ , Eq. (12), is demonstrated in Fig. 5. The parameters of these fits as a function of $N_{\rm part}$ are shown in Fig. 8. The slope parameter $A$ decreases with $N_{\rm part}$ . The intercept parameter $B$ , which could be connected to the size of the source, is slightly negative within statistical uncertainties but is compatible with zero if systematic uncertainties are taken into account. Note that in hydrodynamical calculations with $\alpha=2$ , the parameter $B$ is dominated by the inverse of the squared geometrical size of the whole source: the smaller the value of B, the larger the geometrical size of the source, while parameter $A$ is dominated by radial flow effects [39, 38, 40].

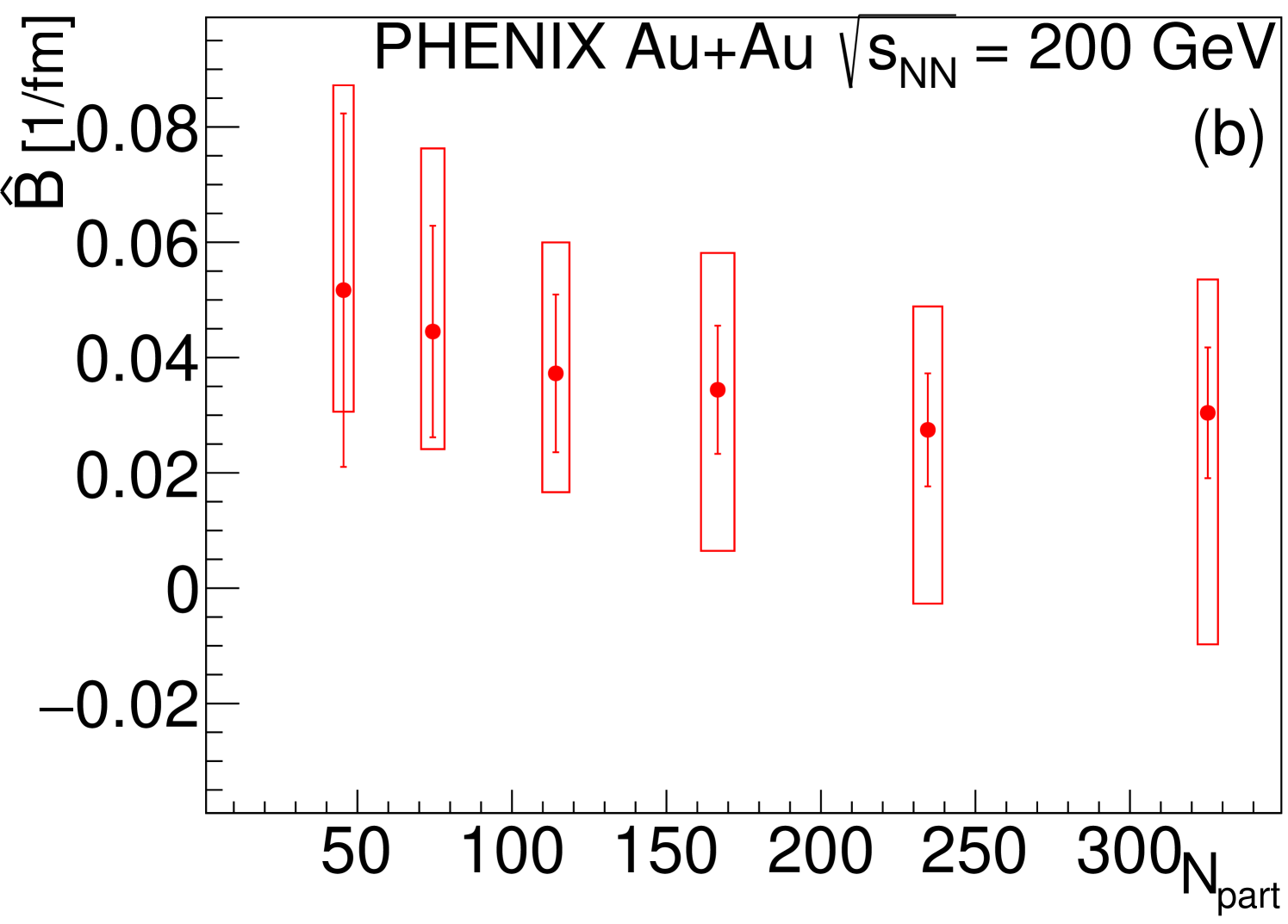
As mentioned in Section VI.1, the affine linearity of $\widehat{R}^{-1}(m_{T})$ , Eq. (14) is investigated, as a function of $N_{\rm part}$ . The centrality dependence of the slope and intercept parameters of these fits are shown in Fig. 9. The parameter $\widehat{A}$ exhibits a decreasing trend with increasing centrality similar to that seen for $A$ in the parameterization of $R^{-2}$ . Within statistical uncertainty, $\widehat{B}$ is compatible with a small positive number but both statistical and systematic uncertainties are too large to draw a strong conclusion from the present data.

As shown in Fig. 10(a), because the Lévy-exponent parameter $\alpha$ does not appear to depend on $m_{T}$ (see Fig. 3), the $m_{T}$ -averaged value, $\alpha_{0}$ , can be used to determine the centrality dependence of $\alpha$ . A significant centrality dependence of $\alpha_{0}$ is observed. The lowest value of $\alpha_{0}$ occurs for the most central collisions. As the collisions become more peripheral $\alpha_{0}$ saturates around $\approx$ 1.4.

The parameter $R$ is investigated in several $m_{T}$ bins as a function of $N_{\rm part}^{1/3}$ . The linearity of this dependence, shown in Fig. 10(b), suggests that the volume of the Lévy source, which is proportional to $R^{3}$ , is proportional to $N_{\rm part}$ . More detailed studies, investigating the centrality dependence in terms of constituent quark participants along the lines of Ref. [41] would be desirable but go beyond the scope of the present analysis.

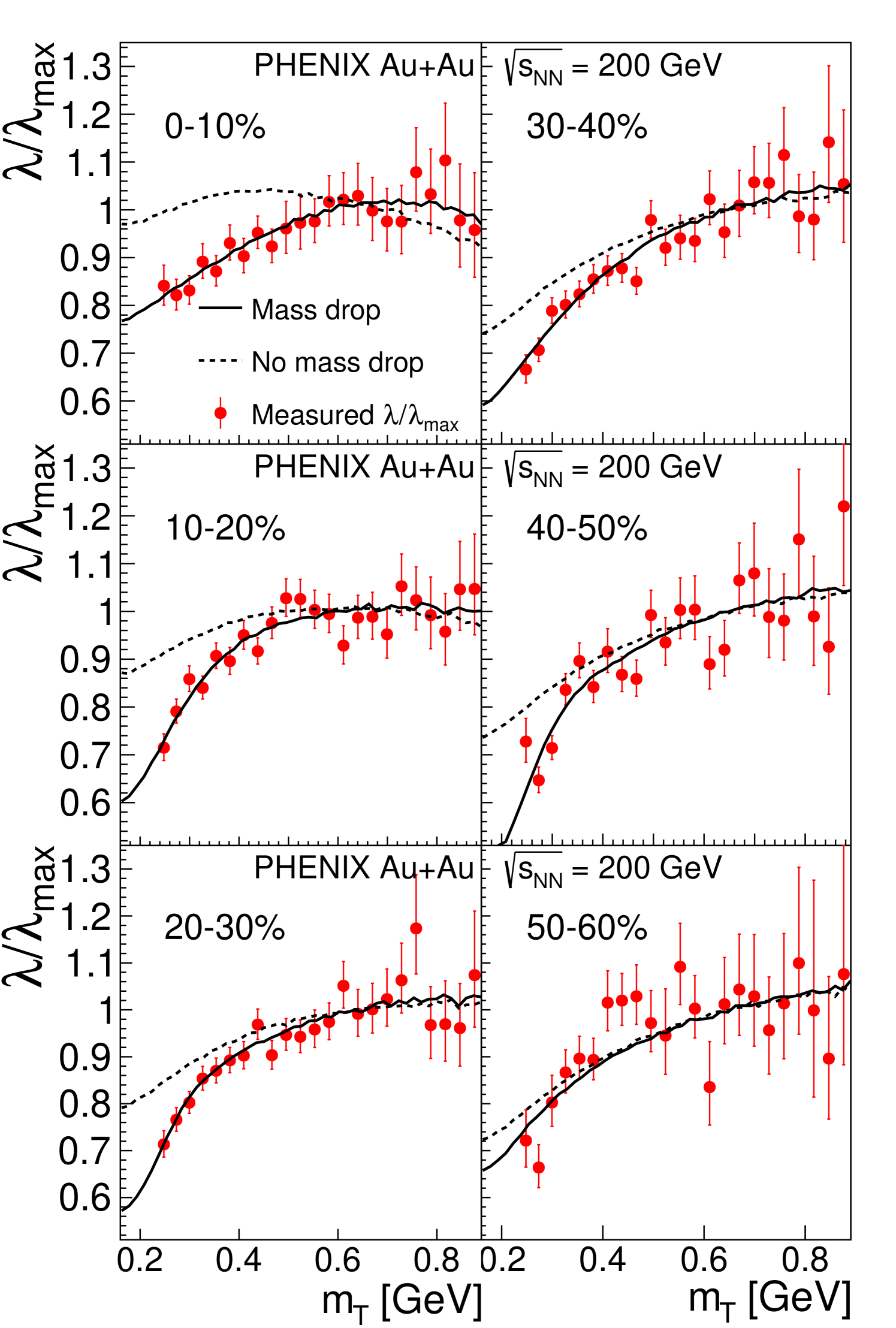
VII Comparison with Monte-Carlo simulations

The low- $m_{T}$ decrease of the $\lambda(m_{T})$ correlation-strength measurements [21, 42, 22] of charged pions is found in Ref. [36] to be an indirect signal of the in-medium mass reduction of the $\eta^{\prime}$ particles. The $\lambda(m_{T})$ suppression at low transverse mass ( $m_{T}$ ) has been investigated in Au $+$ Au collisions at $\sqrt{s_{NN}}$ = 200 GeV collisions by Monte-Carlo simulations [43, 44]. These calculations were also compared to the results of the previous PHENIX analysis of 0%–30% central Au $+$ Au collisions at $\sqrt{s_{NN}}=200$ GeV [1]. Although the measurements are performed in pair- $m_{T}$ (cf. Section VI) ranges while the simulations are in the single-particle transverse mass $\sqrt{m^{2}+p_{T}^{2}}$ , this difference can be neglected as $\lambda$ is a characteristic parameter of the two-particle correlation function at vanishing values of relative momentum, where $K{=}p$ and hence the single-particle transverse mass is equal to the pair $m_{T}$ . This property is also utilized in the core-halo picture, where the smoothness approximation is warranted and $\lambda$ is evaluated at $K{=}p$ [36].

The comparison of Monte-Carlo resonance-model simulations of $\lambda(m_{T})/\lambda_{\rm max}$ to the above presented data shows that, within systematic uncertainties, an in-medium mass drop of $\eta^{\prime}$ is not inconsistent with our measured data. Theoretically, the mass of the $\eta^{\prime}$ meson could be sensitive to the $U_{A}(1)$ symmetry restoration in hot and dense hadronic matter [45, 46]. The key point being that compared to the other pseudoscalar mesons, the $\eta^{\prime}$ is anomalously heavy, $\approx$ 958 MeV, although the $\eta^{\prime}$ quark content is similar to that of the $\eta$ meson. The $\eta$ meson mass, $m_{\eta}\approx$ 548 MeV, is closer to the mass of the charged kaons, $\approx{494}$ MeV while it is 410 MeV lighter than the mass of the $\eta^{\prime}$ meson, $m_{\eta}^{\prime}\approx{958}$ MeV, although the $\eta$ and the $\eta^{\prime}$ mesons have the same quark content [47]. The extra mass is explained in the Standard Model in terms of the $U_{A}(1)$ anomaly that couples the mass of the $\eta^{\prime}$ to the topological properties of the quantum-chromodynamics vacuum state. If at high temperatures the structure of this vacuum changes, the extra 410 MeV mass difference may vanish and the $\eta^{\prime}$ mesons may return to the mass scale of the other pseudoscalar mesons, with its mass becoming similar to that of the $\eta$ [46]. As the $\eta^{\prime}$ meson leaves the hot and dense matter, it regains its anomalously large mass at the expense of its kinetic energy and consequently this effect modifies the spectrum. See below for a discussion of how Monte-Carlo calculations are used to investigate the effect on $\lambda(m_{T})$ of this mass modification, along the lines of Ref. [1, 1, 36, 43, 44].

For each centrality class the SHAREv3 Monte-Carlo generator [48, 49] is used to evaluate the fraction of those short- and long-lived resonances that are the most important sources of pions. These fractions are used in our simulation. The input parameters to SHARE correspond to the STAR chemical freeze-out fits to the available experimental data on particle yields [50, 51, 52, 53, 54, 55, 56] and are available in the columns labeled grand-canonical-ensemble yields (GREY) of Table VIII in Ref. [57]. The results from SHARE serve as inputs to our simulations.

The two most important parameters in the simulations are the in-medium mass of $\eta^{\prime}$ (denoted by $m^{*}_{\eta^{\prime}}$ ) and the effective temperature of the $\eta^{\prime}$ condensate, the inverse-slope parameter (denoted by $B_{\eta^{\prime}}^{-1}$ ). The in-medium mass drives the depth, while the inverse slope controls the steepness of the “dip” of the $\lambda(m_{T})$ function. These two parameters are considered as fit parameters for the Monte-Carlo simulations. Further details of the simulation and the estimation of its systematic uncertainties are given in the Appendix and in Refs. [1, 36, 43, 44].

The $\chi^{2}$ scans are implemented by taking small steps in the in-medium $\eta^{\prime}$ mass and the inverse-slope parameter $B_{\eta^{\prime}}^{-1}$ , comparing the results to the data. From these scans are determined the optimal (minimum $\chi^{2}$ ) values and their uncertainties. The Appendix gives details of the simulation and the estimation of uncertainties.

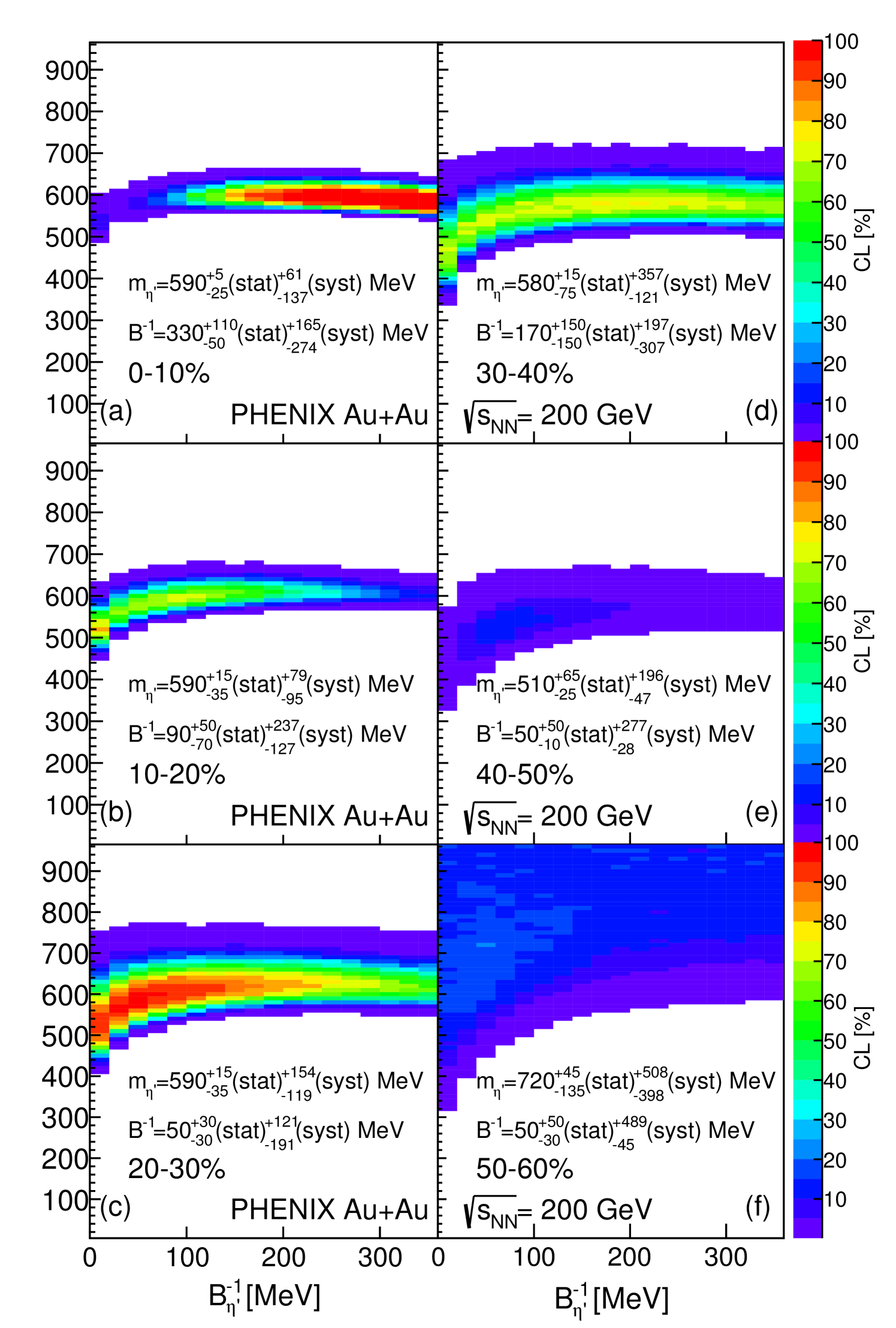
Figure 11 compares the data to both the optimal fits and the case that lacks the in-medium mass modification of the $\eta^{\prime}$ meson. For $m_{T}\,\hbox{\lower 1.72218pt\hbox{$\approx$}\hbox to0.0pt{\hss\raise 2.15277pt\hbox{$>$}}}\,500$ MeV there is no significant difference between the optimal fit and the assumption of no modification case. At low $m_{T}$ no modification is strongly disfavored.

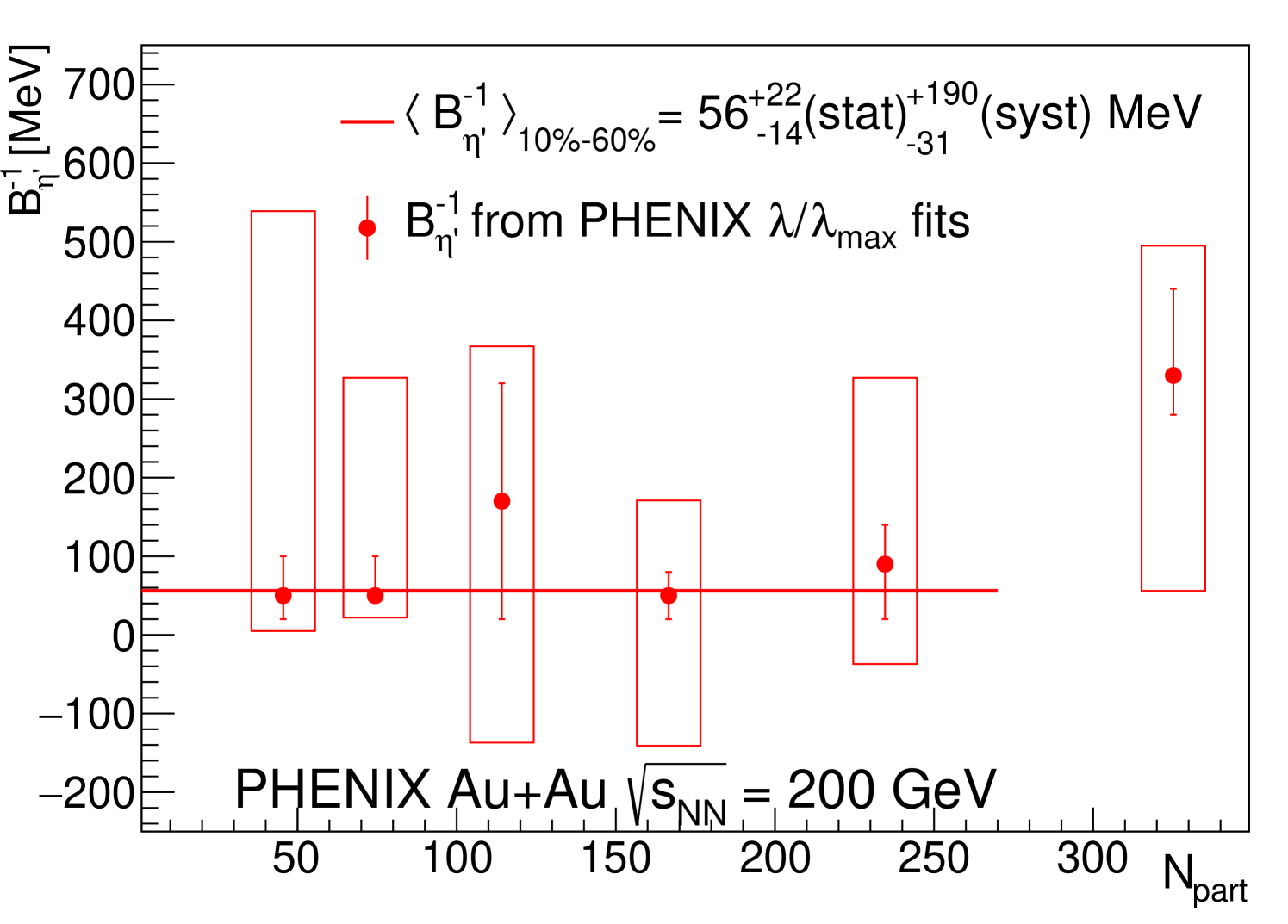
Our results suggest that a significant, centrality independent, in-medium mass drop of the $\eta^{\prime}$ is not inconsistent with the present measurements. In Figs. 12 and 13 the optimal values of $B^{-1}_{\eta^{\prime}}$ and $m^{*}_{\eta^{\prime}}$ , respectively, are shown as function of $N_{\rm part}$ . The average value of the modified $\eta^{\prime}$ mass is $m^{*}_{\eta^{\prime}}=581^{+12}_{-20}{\rm(stat)}^{+205}_{-91}{\rm(syst)}$ MeV. In the case of the inverse-slope parameter, the point corresponding to the 0%–10% centrality bin was omitted from the constant fit, i.e, the average value indicated in Fig. 12, represents the average value of the five remaining points, that is $B_{\eta^{\prime}}^{-1}=56^{+22}_{-14}{\rm(stat)}^{+190}_{-31}{\rm(syst)}$ MeV. In Fig. 12 the solid [black] line denotes this centrality-averaged value. In at least five centrality classes, from 0%–10% to 40%–50%, the measured $\lambda(m_{T})/\lambda_{\rm max}$ functions are found to be consistently described by considering the suppressed mass of the $\eta^{\prime}$ . However, in the most-peripheral centrality class (50%–60%) an unmodified $\eta^{\prime}$ mass cannot be excluded. In Fig. 13, the dashed [red] line indicates the centrality-averaged value of the in-medium modified mass of the $\eta^{\prime}$ meson. This observation of minimal mass modification can be interpreted as being due to the lack of enough hot and dense matter. The data are not inconsistent with Monte-Carlo simulations with vanishing differences between $m^{*}_{\eta^{\prime}}$ and $m_{\eta}{\approx}548$ MeV.

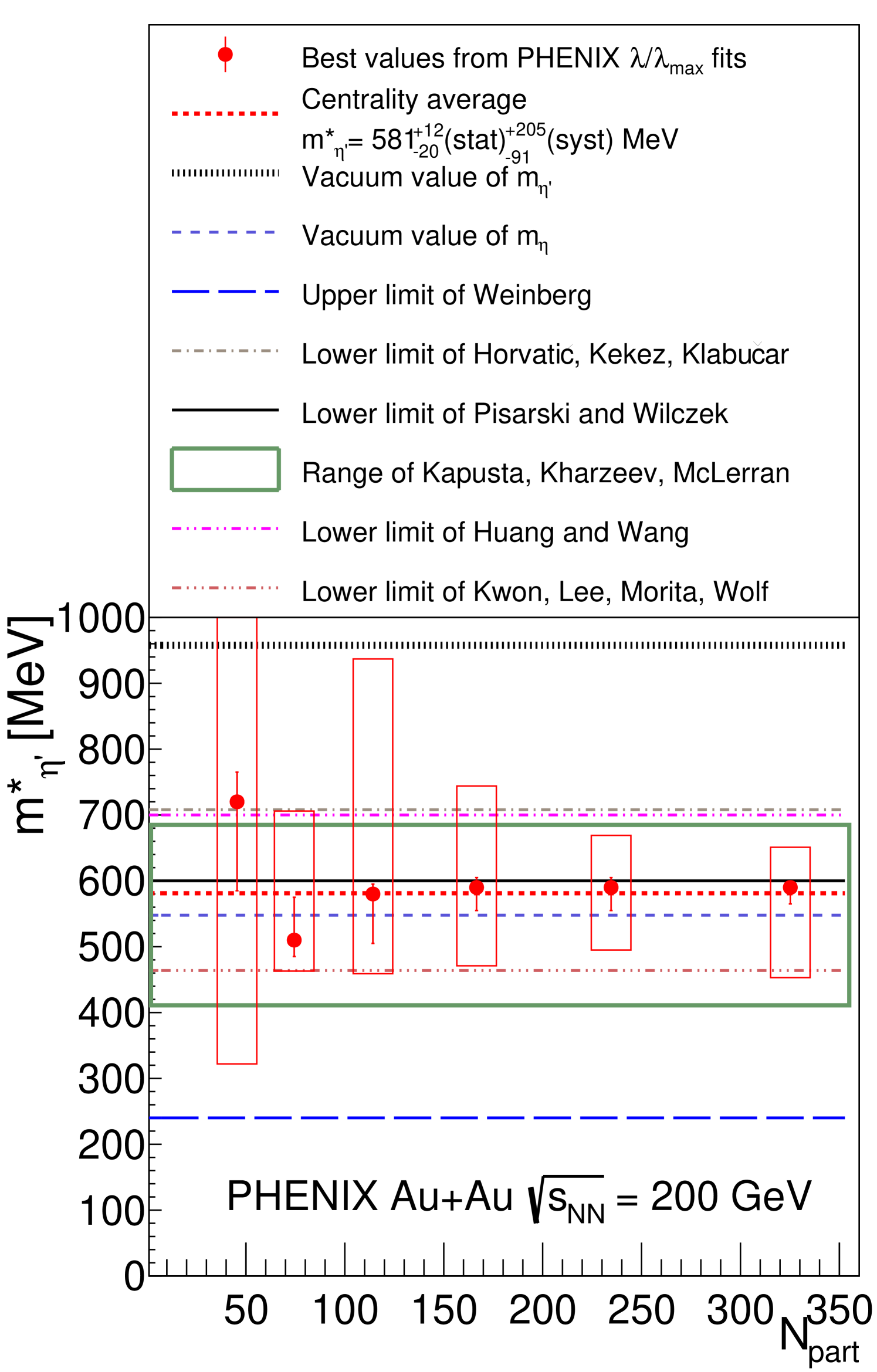
These are the first, centrality-dependent experimental results that suggest the suppression of the $\eta^{\prime}$ meson mass in a hot and dense medium. Figure 13 compares these results to some of the well-known theoretical predictions for the modified $\eta^{\prime}$ mass:

•

The Weinberg upper limit, $m^{*}_{\eta^{\prime}}\leq\sqrt{3}m_{\pi}$ , suggested in Ref. [58] clearly overestimates significantly, in each centrality bin, the possible in-medium mass drop of the $\eta^{\prime}$ particles.
•

Recent calculations by Horvatić, Kekez, and Klabučar (HKK) [59], based on the calculations of Witten-Veneziano equation and the generalization by Shore, evaluated the properties of the $\eta$ and $\eta^{\prime}$ mesons at high temperatures, when the $U_{A}(1)$ and the chiral symmetry breaking are considered together. A substantial decrease in the $\eta^{\prime}$ mass around the chiral transition temperature was obtained in Ref. [59], but there was no decrease in the $\eta$ mass. The new HKK results are an improvement on the earlier results of Ref. [43, 44]. The lower limits, which are shown by the [light-green] dashed-dotted line in Fig. 13, lie above our results except in the 50%–60% centrality class, where the uncertainty on our value of $m^{*}_{\eta^{\prime}}$ is particularly large. This is also true of the similar limit of Huang and Wang [60]. These models are in a modest tension with our results.
•

The Pisarski-Wilczek lower limit of 600 MeV, as determined from Fig. 1 of Ref. [45], is shown as a solid [black] line. It is, within uncertainty, consistent, with the fitted values.
•

The significant in-medium mass drop of the $\eta^{\prime}$ meson was related to the restoration of $U_{A}(1)$ symmetry and described as the return of a Goldstone-boson by Kapusta, Kharzeev and McLerran (KKM) Ref. [46]. They have given a broad range for the possible in-medium mass of the $\eta^{\prime}$ meson in case of a partial ${\rm U}_{A}(1)$ symmetry restoration, namely $411$ MeV $\leq m^{*}_{\eta^{\prime}}\leq 685$ MeV shown as a [green] box in Fig. 13. Our results lie within this range.
•

Kwon, Lee, Morita, and Wolf (KLMW) also utilized a temperature-dependent, generalized Witten-Veneziano relation to obtain a nearly 50% decrease in the mass of the $\eta^{\prime}$ meson in hot and dense hadronic medium, as a consequence of the restoration of $U_{A}(1)$ symmetry [61]. Their 2012 prediction of $m^{*}_{\eta^{\prime}}\geq 464$ MeV, shown as a triple dotted-dashed line in Fig. 13, is consistent with our results in each investigated centrality class.

VIII Summary and Conclusion

This paper presents measurements of the two-pion BEC function in Au $+$ Au collisions at $\sqrt{s_{{}_{NN}}}$ = 200 GeV using data recorded in 2010 by the PHENIX experiment. Lévy-stable distributions are utilized to characterize the data and determine the transverse-mass and centrality dependence of the Lévy parameters.

The Lévy parameterization is found to give a statistically acceptable description of the data with the Lévy exponent, $\alpha$ , significantly greater than 1 and less than 2. This exponent is determined in 23 $m_{T}$ and in 6 centrality bins and is observed to be well described with its $m_{T}$ -averaged value in every centrality bin. However, the transverse-mass-averaged values do depend on centrality.

The Lévy-scale parameter $R$ is proportional to the HWHM of the source distribution, with a coefficient of proportionality that depends on the Lévy exponent $\alpha$ . The behavior of its inverse square as function of $m_{T}$ that is observed can be described by an affine linear fit, whose parameters are examined as a function of centrality. The parameter $A$ , which can be related to the transverse velocity of the expansion, shows a trend similar to hydrodynamical predictions [39, 38]. However, the assumption of local thermalization results in the $\alpha=2$ special case (see, e.g., Refs. [39, 27, 38]), which is in significant contrast to our observations of $\alpha<2$ in each of the investigated centrality and transverse-mass bins.

Within statistical uncertainties, the parameter $B$ , is consistent with zero or with a slightly negative value. A negative value of $B$ is possible if the Cooper-Frye freeze-out terms are also taken into account [62]. This result may indicate a source that includes local thermalization with hydrodynamical expansion, followed by rescattering and decays of resonances. However, such nonequilibrium, scale-dependent features typically would result in deviations from the Lévy shape and from the applicability of generalized central-limit theorems. But first-order deviations from the Lévy-stable source distributions using the expansion method of Refs. [25, 12, 13] were found to be consistent with zero. It is theoretically challenging to explain simultaneously the measured value of $\alpha$ , which is found to be significantly less than the Gaussian value of 2, and the $m_{T}$ dependence of the Lévy scale parameter $R$ , which follows a hydrodynamically predicted scaling (see, e.g., Ref. [40]).

The connection to the initial geometry is supported by the linearity of the parameter $R$ as a function of $N_{\rm part}^{1/3}$ in any given $m_{T}$ bin. The precise characterization of the correlation functions and the prudent handling of the Coulomb final-state interaction make it possible to determine in detail the $m_{T}$ and centrality dependence of the $\lambda(m_{T})$ intercept parameter, as well as of its normalized form, $\lambda(m_{T})/\lambda_{\rm max}$ . In the trends of the latter it can be qualitatively observed that there is a low- $m_{T}$ suppression of $\lambda(m_{T})/\lambda_{\rm max}$ in every centrality bin and that the characteristics are more or less the same, i.e., the suppression is consistent with the hypothesis of centrality independence.

To quantify the suppression pattern, the Gaussian width and amplitude parameters, $\sigma$ and $H$ , were introduced. These parameters are observed to be centrality independent, except in the 50%–60% case, where the uncertainty on $H$ increases and does not allow a statistically significant conclusion. This independence is helpful to rule out or validate models with predictions about this behavior. The pion laser model, for example, predicts a strong centrality and multiplicity dependence [63, 37, 43].

In Ref. [36] it was observed that the amount of suppression of $\lambda(m_{T})$ and hence of $\lambda(m_{T})/\lambda_{\rm max}$ at low $m_{T}$ can be an experimentally observable signal of the (partial) restoration of $U_{A}(1)$ symmetry and a measure of in-medium reduction of the mass of the anomalously heavy $\eta^{\prime}$ mass. An approximately constant trend of the intercept parameter $\lambda$ as a function of $m_{T}$ was observed in small systems at lower energies, ( $E_{\rm LAB}=150$ AGeV [7, 20]), which is consistent with vanishing suppression ( $H=0$ ). These results are both qualitatively and quantitatively different from the presence of the suppression ( $H_{0}=0.42\pm 0.02$ (stat) ), which is within uncertainties independent of the centrality in $\sqrt{s_{NN}}=200$ GeV Au $+$ Au collisions at RHIC. This entirely experimental data-based, Monte-Carlo-independent observation suggests that the signal characterized by the value of $H$ is dependent on the energy and/or the system size. Further detailed measurements are needed to determine the energy and system size, where $H$ becomes nonvanishing for the first time, starting from zero in the small Be+Be collisions at the relatively low energy of $E_{\rm LAB}=150$ AGeV.

There could also be alternative or competing effects that could modify the correlation strength, see e.g. Ref. [64]. Further theoretical studies are needed to explain these data using other methods. However, one of the possible explanations relates the observations to restoration of $U_{A}(1)$ symmetry in a hot and dense hadronic matter as detailed in Refs. [36, 43, 44].

It is clear that our observed suppression of the $\lambda(m_{T})/\lambda_{\rm max}$ parameter at lower transverse mass is not inconsistent with the in-medium mass modification of the $\eta^{\prime}$ mesons, related to $U_{A}(1)$ symmetry restoration in hot hadronic matter. This relation was cross-checked with the help of detailed Monte-Carlo simulations, and creating $\chi^{2}$ and CL maps that compared simulations which allowed in-medium $\eta^{\prime}$ mass modification in hot and dense hadronic matter. As detailed in Section VII, and also in Table 2 of the Appendix it is shown that for each of the considered centrality classes the best value of the in-medium mass of the $\eta^{\prime}$ meson, $m_{\eta^{\prime}}^{*}=581^{+12}_{-20}{\rm(stat)}^{+205}_{-91}{\rm(syst)}$ MeV.

This mass is, within the uncertainties of this indirect measurement, the same as the Particle Data Group (PDG) value of the $\eta$ meson, $m_{\eta}=547.86\pm 0.02$ MeV [65]. This observation suggests that the return of the so-called prodigal Goldstone boson [46] and the restoration of the $U_{A}(1)$ symmetry is not inconsistent with our measurements.

However, our measurements are inconsistent with Monte-Carlo simulations that utilize the PDG value of the $\eta^{\prime}$ mass, $m_{\eta^{\prime}}=957.78\pm 0.06$ MeV, which does not allow for mass modification, except in the most peripheral, (50%–60%) centrality class. Several theoretical predictions from Refs. [58, 45, 46, 61, 59, 60] are compared to the results of our $\chi^{2}$ maps. These comparisons can be summarized as follows:

•

The Kapusta-Kharzeev-McLerran prediction [46] is in agreement with our measurements in each investigated centrality class.
•

The lower limit of Kwon, Lee, Morita, and Wolf [61] is also consistent with our measurement in each investigated centrality class.
•

Our measured centrality-average value of $m^{*}_{\eta^{\prime}}$ is slightly below, but consistent with, the lower limit predicted by Pisarski and Wilczek [45].
•

However, the upper limit of Weinberg [58] is several standard deviations below the central values obtained in each investigated centrality class.
•

The lower limit predictions of Horvatić, Kekez and Klabučar [59] and of Huang and Wang [60] are excluded except in the 50%–60% centrality class.
•

Our results also suggest that the prediction of Ref. [66] slightly underestimates the in-medium mass change of the $\eta^{\prime}$ .

However, the lack of in-medium $\eta^{\prime}$ mass modification is not consistent with our measurements, except in the 50%–60% centrality class, as discussed and detailed in the Appendix. Thus, these PHENIX results provide the most detailed, centrality-dependent constraints for future theoretical studies on $U_{A}(1)$ symmetry restoration in hot and dense hadronic matter. These results also exhibit an unprecedented selection power by excluding certain models in certain centrality classes. Thus these indirect PHENIX measurements provide important constraints and insights to future studies of (partial) $U_{A}(1)$ symmetry restoration in hot and dense hadronic matter.

For future experimental studies, these results emphasize the need for direct measurements of identified $\eta^{\prime}$ spectra in high-energy heavy-ion collisions at RHIC and at the Large Hadron Collider, in particular in the very soft, $p_{T}\ \leq 300$ MeV kinematic domain at midrapidity. Direct experimental observations of enhanced production of soft $\eta^{\prime}$ mesons seem to be particularly difficult, due to the expected backgrounds. Huge backgrounds, e.g. in the $\eta^{\prime}\rightarrow\gamma\gamma$ decay channel, are expected, e.g., from $\pi^{0}\rightarrow\gamma\gamma$ decays. Thus a direct observation of in-medium $\eta^{\prime}$ mass modification seems to be experimentally challenging, but based on the indirect results summarized here, are also expected to be particularly rewarding.

Acknowledgements.

We thank the staff of the Collider-Accelerator and Physics Departments at Brookhaven National Laboratory and the staff of the other PHENIX participating institutions for their vital contributions. We acknowledge clarifying and inspiring discussions with Sándor Hegyi, Dubravko Klabučar, Robert Pisarski and György Wolf concerning the interpretation of their published results. S.L. thanks IFJ PAN, Krakow, Poland for their encouragement to finish this work. We acknowledge support from the Office of Nuclear Physics in the Office of Science of the Department of Energy, the National Science Foundation, Abilene Christian University Research Council, Research Foundation of SUNY, and Dean of the College of Arts and Sciences, Vanderbilt University (U.S.A), Ministry of Education, Culture, Sports, Science, and Technology and the Japan Society for the Promotion of Science (Japan), Conselho Nacional de Desenvolvimento Científico e Tecnológico and Fundação de Amparo à Pesquisa do Estado de São Paulo (Brazil), Natural Science Foundation of China (People’s Republic of China), Croatian Science Foundation and Ministry of Science and Education (Croatia), Ministry of Education, Youth and Sports (Czech Republic), Centre National de la Recherche Scientifique, Commissariat à l’Énergie Atomique, and Institut National de Physique Nucléaire et de Physique des Particules (France), J. Bolyai Research Scholarship, EFOP, HUN-REN ATOMKI, NKFIH, MATE KKP and OTKA (Hungary), Department of Atomic Energy and Department of Science and Technology (India), Israel Science Foundation (Israel), Basic Science Research and SRC(CENuM) Programs through NRF funded by the Ministry of Education and the Ministry of Science and ICT (Korea). Ministry of Education and Science, Russian Academy of Sciences, Federal Agency of Atomic Energy (Russia), VR and Wallenberg Foundation (Sweden), University of Zambia, the Government of the Republic of Zambia (Zambia), the U.S. Civilian Research and Development Foundation for the Independent States of the Former Soviet Union, the Hungarian American Enterprise Scholarship Fund, the US-Hungarian Fulbright Foundation, and the US-Israel Binational Science Foundation.

Appendix: Details of the Monte-Carlo simulations

Monte-Carlo simulations with scenarios that allow for (or exclude) a possible in-medium mass modification of the $\eta^{\prime}$ meson and their comparisons to data were performed in Refs. [36, 43, 44] and in the previous PHENIX paper (Ref. [1]) by utilizing standard $\chi^{2}$ and CL maps. Similar, but now centrality-dependent simulations are summarized in this Appendix. These comparisons result in $\chi^{2}$ and CL maps that are utilized to determine the $\chi^{2}$ minimum (or CL maximum) yielding the best values, as well as the statistical and the systematic uncertainties of a possible in-medium mass-drop of the $\eta^{\prime}$ meson. Figure 14 shows an example of such a comparison, where each bin corresponds to a comparison of Monte-Carlo simulations of resonance decay chains with our data on $\lambda(m_{T})/\lambda_{{\rm max}}$ as a function of centrality, as detailed in Section VII.

Each panel of Fig. 14 contains the optimal values of $m^{*}_{\eta^{\prime}}$ and $B_{\eta^{\prime}}^{-1}$ in the scanned region. For our simulations, a unique $\chi^{2}$ minimum is found, in contrast to earlier studies in Refs. [43, 44]. By now, it is well known, that the dominant mechanism for soft-particle production is a thermal one in $\sqrt{s_{{}_{NN}}}$ = 200 GeV Au+Au collisions.

Earlier, a significantly broader class of models was considered in Refs. [43, 44] that resulted in two, characteristically different minima in the 0%–30% centrality class of the same reaction. Accordingly, Refs. [43, 44] evaluated the exclusion limits, focusing in particular on the smallest possible in-medium mass drop of the $\eta^{\prime}$ meson, which is required to describe the data with at least 0.1% CL in any of the considered Monte-Carlo simulations.

Our systematic investigations include an estimation of the exclusion limits for the lowest- and largest-possible values of the in-medium mass of the $\eta^{\prime}$ meson. The systematic variations are consistent, i.e. all the systematic variations result in essentially the same minimum. Thus, in contrast to Refs. [43, 44], our indirect observation of in-medium $\eta^{\prime}$ mass modification is used with the best value and its statistical and systematic uncertainties of $m^{*}_{\eta^{\prime}}$ , rather than exclusion limits.

Table 2 shows the centrality-dependent, fitted values of the in-medium $\eta^{\prime}$ mass $m^{*}_{\eta^{\prime}}$ and the inverse slope $B^{-1}_{\eta^{\prime}}$ with statistical and systematic uncertainties. The exclusion limits of these parameters were evaluated, but they do not result in statistically significant new ranges.

The $\eta^{\prime}$ spectrum has six parameters, which are considered as inputs to the $\lambda(m_{T})$ simulations. The two most important inputs are the in-medium mass of the $\eta^{\prime}$ , $m^{*}_{\eta^{\prime}}$ , and the characteristic-slope parameter, $B_{\eta^{\prime}}^{-1}$ , of the $\eta^{\prime}$ mesons that are emitted with PDG mass after the decay of the condensate. The second parameter characterizes a second component, a low- $p_{T}$ part of the $\eta^{\prime}$ spectrum and determines the slope of the suppression of the $\lambda$ parameter at low- $p_{T}$ [36, 43, 44]. These two parameters determine the shape of the observed dip in the low- $m_{T}$ region of the $\lambda(m_{T})$ function: a strongly reduced $\eta^{\prime}$ mass causes a dip in the low- $m_{T}$ part of the $\lambda(m_{T})$ function, while $B_{\eta^{\prime}}^{-1}$ controls the slope of this dip, see Refs. [43, 44]. These two parameters are considered as fit variables. The values of four nuisance parameters $\alpha_{\rm th}$ , $T_{f}$ , $\langle u_{T}\rangle$ , and $T_{\rm cond}$ , are treated as constants in the fit, but are varied to evaluate the systematic uncertainties of the fitted values.

The $\chi^{2}$ scans provide fine grids of CL in each centrality class. The in-medium mass is scanned with 10 MeV steps between 0 and 958 MeV (the vacuum mass of $\eta^{\prime}$ ) and $B_{\eta^{\prime}}^{-1}$ with 20 MeV steps between 0 and 360 MeV. The minimum value of $\chi^{2}$ (or maximum value of CL) is determined, which provides the most likely values of $m^{*}_{\eta^{\prime}}$ and $B_{\eta^{\prime}}^{-1}$ and their statistical uncertainties, as well as the CL of the fits to the data, which are compared to the data in Fig. 11. The values of the four “constant” parameters, $\alpha_{{\rm th}}$ , $T_{f}$ , $\langle u_{T}\rangle$ , and $T_{\rm cond}$ , are varied to evaluate the systematic uncertainties of the fitted values:

$\alpha_{{\rm th}}$

The centrality-dependent invariant single particle spectra of positively and negatively charged kaons as well as protons and antiprotons of Ref. [50] are fitted with the formula

\displaystyle N(m_{T})=C{m_{T}}^{\alpha_{{\rm th}}}\exp\left(-\frac{m_{T}}{T_{\rm eff}}\right)

(16)

where $C$ is a normalization constant. The polynomial exponent of the thermal spectrum is denoted by $\alpha_{{\rm th}}$ , to distinguish it from the Lévy-exponent $\alpha$ . Note that the parameter $\alpha_{{\rm th}}$ of this paper is the same, as the $\alpha$ parameter of Refs. [36, 43, 44]. The exponent $\alpha_{{\rm th}}=1-d/2$ , where $d$ is the number of spatial dimensions of the expansion; hence its allowed range is $1\leq d\leq 3$ . The value of $\alpha_{th}$ is fixed to $\alpha_{{\rm th}}=0$ , which corresponds to an effectively two-dimensional expansion [30, 39]. The same value was used in Ref. [50] by the PHENIX experiment when obtaining $T_{\rm eff}$ . Its value is assumed to be independent of centrality and is varied in the systematic studies between $1/2$ and $-1/2$ . Also similar to Ref. [50], good quality exponential fits are obtained, with CL $\geq 0.1$ %, in each centrality class for charged kaons, protons, and antiprotons in the transverse-mass range of $0.1\leq m_{T}-m\leq{1.0}$ GeV. Similar to Ref. [50], the mass dependence of the slopes is also well described with affine linear fits: $T_{\rm eff}(m)=T_{f}+m\langle u_{T}\rangle^{2}$ , but here these fits have a good CL with CL $\geq 0.1$ % in each centrality class.

$T_{f}$

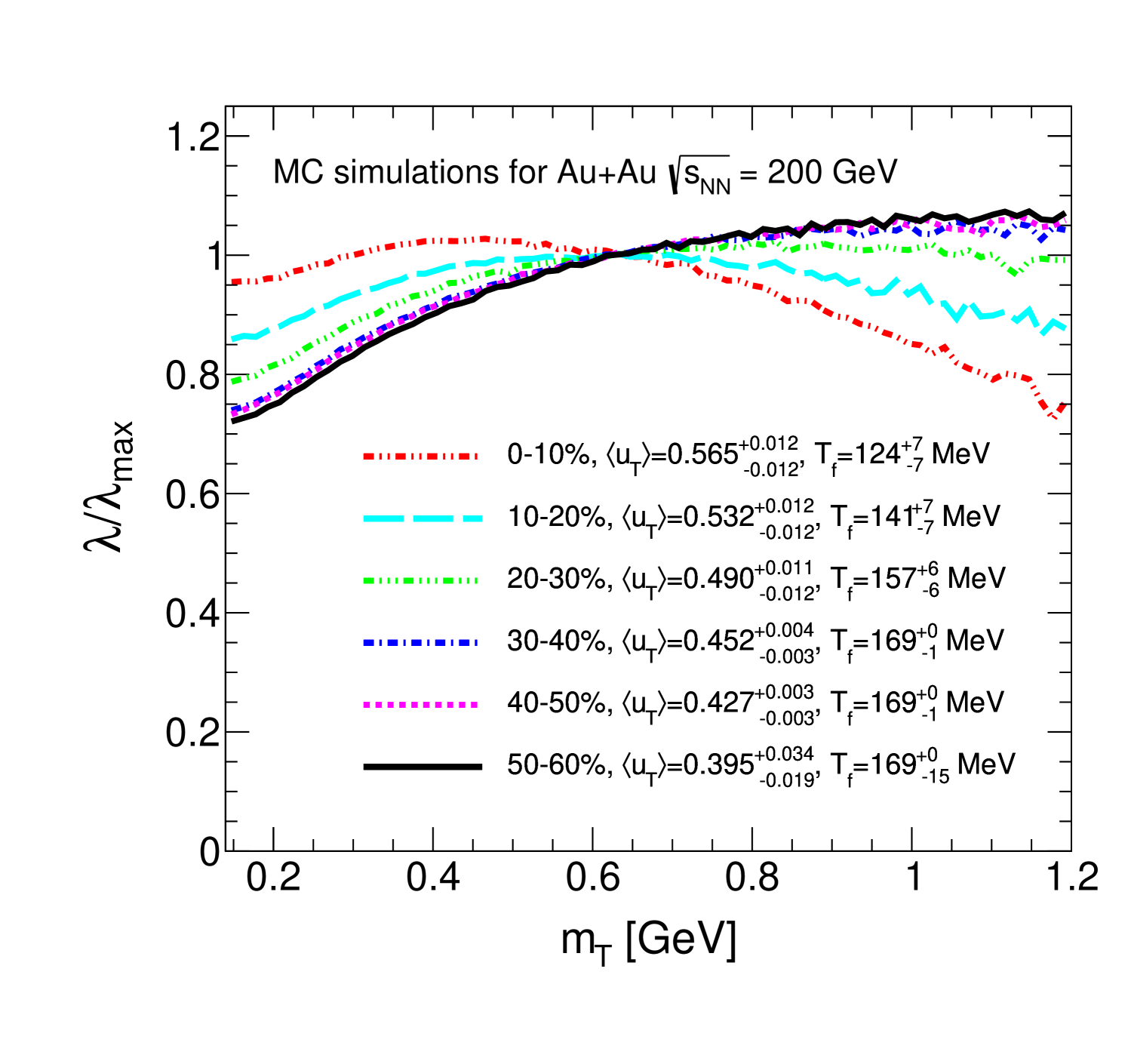
The kinetic freeze-out temperature is denoted by $T_{f}$ . Significant centrality dependent results for the kinetic freeze-out temperature are obtained here. In particular, the value of $T_{f}$ is significantly lower for the 0%–10% centrality class than for other centrality classes. For peripheral centrality classes, the value of $T_{f}$ increases, reaching its upper limit, the value of the chemical freeze-out temperature $T_{{\rm chem}}$ . Our results for the variations of $T_{f}$ and $\langle u_{T}\rangle$ with centrality are shown as inserted values in Fig. 15. Fixing $T_{f}$ to a centrality-independent constant, results in the above affine linear-mass-dependent coefficient fits, similar to Ref. [50], having CLs that are too small, well below the $0.1$ % $\leq{{\rm CL}}$ threshold values. A possible reason for a lower kinetic freeze-out temperatures $T_{f}$ in the 0%–10% centrality class is that a larger volume may cool remarkably longer and to a lower temperature, as noted by Hama and Navarra [67].

$\langle u_{T}\rangle$

The average radial flow is denoted by $\langle u_{T}\rangle$ . This parameter influences the overall slope of the $\lambda(m_{T})$ distribution at higher transverse mass and results in a centrality dependent expectation for $\lambda(m_{T})/\lambda_{\textmd{max}}$ . Note that the pion halo contains the decay products of long-lived resonances, which include the decay products of $\omega$ , $\eta$ , $\eta^{\prime}$ and $K_{s}^{0}$ mesons. It is thus important to simulate these decay chains precisely and in agreement with available experimental data. The best values of $T_{f}$ and $\langle u_{T}\rangle$ are obtained by simultaneous fits to the slope parameters of the positively and negatively charged kaons, protons, and antiprotons with the formula $T_{\rm eff}=T_{f}+m\langle u_{T}\rangle^{2}$ where $m$ is the mass of the meson or baryon. These parameters are systematically varied within the uncertainties allowed by these fits, shifting and fixing one of the $(T_{f},\langle u_{T}\rangle)$ pair by one standard deviation and refitting the other parameter to take into account their covariation. The invariant spectra of $K^{\pm}$ and those of protons and antiprotons are simulated using fits with good CL. The mass scaling of these spectra is then utilized. Nearly the same are the mass of the $\eta$ meson compared to charged kaons and the mass of the $\eta^{\prime}$ meson compared to protons and antiprotons. This gives a good basis to describe well the null effect, which is the no in-medium mass modification scenario of the $\eta$ and $\eta^{\prime}$ spectrum. This method has been tested and the test was published in Fig. 11 of Ref. [44]. Extrapolating the mass-scaled simulations to the PHENIX acceptance successfully reproduces the $\eta$ spectrum measured in $\sqrt{s_{{}_{NN}}}=200$ GeV Au $+$ Au collisions [68] in the $m_{T}-m_{\eta}\geq 1.75$ GeV range.

$T_{\rm cond}$

The effective temperature of the in-medium $\eta^{\prime}$ condensate is denoted by $T_{{\rm cond}}$ , as in Refs. [36, 43, 44]. This parameter, together with the in-medium mass of the $\eta^{\prime}$ mesons, controls the thermal enhancement of the $\eta^{\prime}$ mesons in the medium. The smaller this number, the smaller the $\eta^{\prime}$ mass drop for a given $\lambda(m_{T})/\lambda_{\rm max}$ measurement. Hence, the most conservative assumption is made for the default value, $T_{\rm cond}=T_{f}$ . As this temperature is inside the hot and dense, but already hadronic matter, part of our systematic studies is to vary $T_{\rm cond}$ within the allowed range of $T_{\rm chem}\geq T_{\rm cond}\geq T_{\rm f}$ . As the conservative default value lies at one of the edges of the allowed interval, this choice results in a more than usually asymmetric uncertainty distribution on the physical fit parameters, such as the in-medium mass of the $\eta^{\prime}$ and the slope parameter of the $\eta^{\prime}$ after the decay of the condensate, $m^{*}_{\eta^{\prime}}$ and $B_{\eta^{\prime}}^{-1}$ . From these systematic uncertainty studies, the in-medium $\eta^{\prime}$ mass is frequently observed to be smaller than our quoted best values, but cannot easily be larger than the best values because its upper uncertainties are much smaller than its lower uncertainties.

For each of the parameters $\alpha_{{\rm th}}$ , $T_{f}$ , $\langle u_{T}\rangle$ , and $T_{{\rm cond}}$ , the $\chi^{2}$ scans and the corresponding CL maps are redone for the variations. The relative difference between the default and the alternative setting is calculated. The final systematic uncertainty is the quadratic sum of these differences.

Additionally, several other cases are also investigated, including two special cases, $T_{f}=140$ MeV fixed, independent of centrality, and $T_{f}=177$ MeV fixed, also independent of centrality. The first case corresponds to Landau’s calculation of the freeze-out temperature (equal to the pion mass, mass of the lightest neutral quanta). The second case is consistent with the PHENIX publication on charged pion, kaon, and (anti)proton spectra [50]. The latter choice is found to be inconsistent with $T_{{\rm cond}}\geq T_{f}$ . The former gives results that are within the quoted systematic uncertainties.

Similarly to Ref. [1], the statistical uncertainty of $\lambda_{\rm max}$ is treated as a normalization uncertainty. Both this uncertainty ( $\approx{1}$ %) and the systematic uncertainty ( $\approx{1}$ %) caused by the choice of $m_{T}$ range when calculating $\lambda_{\rm max}$ are negligible compared to other uncertainties, except in the 50%–60% centrality case of $B_{\eta^{\prime}}^{-1}$ . In that case, no significant in-medium mass modification is found. Thus, $B_{\eta^{\prime}}^{-1}$ cancels from the results and cannot be precisely determined. Therefore, these three negligibly small sources of systematic errors are not included here.

The simulation does not include the PHENIX detector system; hence, the experimental systematic uncertainties are accounted for by propagating the total systematic uncertainties of the measured $\lambda/\lambda_{{\rm max}}$ . The values of the $m^{*}_{\eta^{\prime}}$ and $B_{\eta^{\prime}}^{-1}$ parameters with statistical and systematic uncertainties are shown in Fig. 13 and Fig. 12, respectively. The centrality-dependent results for the in-medium $\eta^{\prime}$ masses are shown on Fig. 13 and the corresponding numerical values are tabulated in Table 2.

Table 2: The centrality-dependent, fitted values, in [MeV], of the in-medium

\eta^{\prime}

mass

m^{*}_{\eta^{\prime}}

and the inverse slope

B^{-1}_{\eta^{\prime}}

. The statistical (stat) and systematic (syst) uncertainties are also presented.

Centrality	$m^{*}_{\eta^{\prime}}$	(stat)	(syst)	$B^{-1}_{\eta^{\prime}}$	(stat)	(syst)
0%–10%	590	${}^{+5}_{-25}$	${}^{+61}_{-137}$	330	${}^{+110}_{-50}$	${}^{+165}_{-274}$
10%–20%	590	${}^{+15}_{-35}$	${}^{+79}_{-95}$	90	${}^{+50}_{-70}$	${}^{+237}_{-127}$
20%–30%	590	${}^{+15}_{-35}$	${}^{+154}_{-119}$	50	${}^{+30}_{-30}$	${}^{+121}_{-191}$
30%–40%	580	${}^{+15}_{-75}$	${}^{+357}_{-121}$	170	${}^{+150}_{-150}$	${}^{+197}_{-307}$
40%–50%	510	${}^{+65}_{-25}$	${}^{+196}_{-47}$	50	${}^{+50}_{-10}$	${}^{+277}_{-28}$
50%–60%	720	${}^{+45}_{-135}$	${}^{+508}_{-398}$	50	${}^{+50}_{-30}$	${}^{+489}_{-45}$

As mentioned in Section VI.1, the normalized intercept parameter dependence on $m_{T}$ and centrality in are investigated in detail. An explanation of the dependence is given in terms of radial flow and $p_{T}$ sharing among the pions arising in $\eta^{\prime}$ decay. The simulations suggest a $\lambda(m_{T})/\lambda_{{\rm max}}$ curve, that changes monotonically with centrality. These changes appear related to the monotonic decrease of radial flow $\langle u_{T}\rangle$ , coupled to a monotonic increase of the kinetic freeze-out temperature $T_{f}$ as the collisions change from most central to more and more-peripheral collisions [36]. The values of $T_{f}$ and $\langle u_{T}\rangle$ are obtained from affine linear fits with $T_{\rm eff}=T_{f}+m\langle u_{T}\rangle^{2}$ to the slope parameters of the charged kaon, $K^{+}$ and $K^{-}$ , as well as to the proton and the antiproton single-particle spectra. Particular attention is paid to the requirement that the single exponential fit to the single-particle spectra have acceptable CLs with ${{\rm CL}}\geq 0.1\%$ , and that the affine linear fits with $T_{\rm eff}=T_{f}+m\langle u_{T}\rangle^{2}$ also reflect the slopes of the single-particle spectra $T_{\rm eff}$ with a CL $\geq 0.1$ %.

In addition to the systematic investigations detailed in this manuscript, several additional consistency checks were performed, such as including fit-range stability investigations and using three different methods of propagation of statistical, and systematic uncertainties. These were performed because the definition and the utilization of $\lambda_{\rm max}$ in this experimental manuscript, which has direct access to results within various experimental cuts, differs from the utilization of $\lambda_{\rm max}$ in Refs. [43, 44], which reported re-analysis of already published data. In those works, only the published systematic uncertainties were available to be propagated to the final results, while in the present paper every quantity up to the final results has been evaluated within each experimental cut.

The method of propagation of statistical and systematic uncertainties was cross checked though comparison with the less direct methods of Refs. [43, 44] as well as with the PHENIX method of Ref. [69]. These methods gave results that are consistent with (and typically have smaller uncertainties than) those presented in the body of this manuscript. Hence the central values, with statistical and systematic uncertainties, presented in the manuscript are obtained with the most conservative of the four different methods that were tested.

References

Adare et al. [2018] A. Adare et al. (PHENIX Collaboration), Lévy-stable two-pion Bose-Einstein correlations in $\sqrt{s_{NN}}$ =200 GeV Au $+$ Au collisions, Phys. Rev. C 97, 064911 (2018).
Achard et al. [2011] P. Achard et al. (L3 Collaboration), Test of the $\tau$ -Model of Bose-Einstein Correlations and Reconstruction of the Source Function in Hadronic Z-boson Decay at LEP, Eur. Phys. J. C 71, 1648 (2011).
Tumasyan et al. [2024] A. Tumasyan et al. (CMS Collaboration), Two-particle Bose-Einstein correlations and their Lévy parameters in PbPb collisions at $\sqrt{s_{\rm NN}}$ =5.02 TeV, Phys. Rev. C 109, 024914 (2024).
Khachatryan et al. [2011] V. Khachatryan et al. (CMS Collaboration), Measurement of Bose-Einstein Correlations in $pp$ Collisions at $\sqrt{s}=0.9$ and 7 TeV, J, High Energy Phys. 05, 029 (2011).
Siklér [2014] F. Siklér (CMS Collaboration), Femtoscopy with identified hadrons in $pp$ , $p$ Pb, and peripheral PbPb collisions in CMS (2014), CMS CR-2014/417, CMS-CR-2014-417, arXiv:1411.6609.
Aad et al. [2015] G. Aad et al. (ATLAS Collaboration), Two-particle Bose–Einstein correlations in $pp$ collisions at $\mathbf{\sqrt{s}=}$ 0. 9 and 7 TeV measured with the ATLAS detector, Eur. Phys. J. C 75, 466 (2015).
Adhikary et al. [2023] H. Adhikary et al. (NA61/SHINE Collaboration), Two-pion femtoscopic correlations in Be+Be collisions at $\sqrt{s_{\text{NN}}}=16.84$ GeV measured by the NA61/SHINE at CERN, Eur. Phys. J. C 83, 919 (2023).
Pórfy [2024] B. Pórfy (NA61/SHINE Collaboration), Femtoscopy at NA61/SHINE using symmetric Lévy sources in central ⁴⁰Ar+⁴⁵Sc from 40 $A$ GeV/ $c$ to 150 $A$ GeV/ $c$ , in 23rd Zimanyi School Winter Workshop (2024) arXiv:2406.02242.
Kincses [2024] D. Kincses (STAR Collaboration), Pion Interferometry with Lévy-Stable Sources in = 200 GeV Au + Au Collisions at STAR, Universe 10, 102 (2024).
Csörgő et al. [2004] T. Csörgő, S. Hegyi, and W. A. Zajc, Bose-Einstein correlations for Lévy stable source distributions, Eur. Phys. J. C 36, 67 (2004).
Csörgő et al. [2005] T. Csörgő, S. Hegyi, T. Novák, and W. A. Zajc, Bose-Einstein or HBT correlations and the anomalous dimension of QCD, Acta Phys. Polon. B 36, 329 (2005).
Novák et al. [2016] T. Novák, T. Csörgő, H. C. Eggers, and M. de Kock, Model independent analysis of nearly Lévy correlations, Acta Phys. Polon. Supp. 9, 289 (2016).
Csörgő et al. [2019] T. Csörgő, R. Pasechnik, and A. Ster, Odderon and proton substructure from a model-independent Lévy imaging of elastic $pp$ and $p\bar{p}$ collisions, Eur. Phys. J. C 79, 62 (2019).
Nolan [2020] P. J. Nolan, Univariate Stable Distributions: Models for Heavy Tailed Data, 1st ed. (Springer, Reading, Massachusetts, 2020) p. 333.
Miller et al. [2007] M. L. Miller, K. Reygers, S. J. Sanders, and P. Steinberg, Glauber modeling in high energy nuclear collisions, Ann. Rev. Nucl. Part. Sci. 57, 205 (2007).
Kurgyis [2018] B. Kurgyis (PHENIX Collaboration), Three dimensional Lévy HBT results from PHENIX, Acta Phys. Polon. Supp. 12, 477 (2018).
Pratt et al. [1990] S. Pratt, T. Csörgő, and J. Zimányi, Detailed predictions for two pion correlations in ultrarelativistic heavy ion collisions, Phys. Rev. C 42, 2646 (1990).
Bertsch et al. [1988] G. Bertsch, M. Gong, and M. Tohyama, Pion Interferometry in Ultrarelativistic Heavy Ion Collisions, Phys. Rev. C 37, 1896 (1988).
Pratt [1986] S. Pratt, Pion Interferometry of Quark-Gluon Plasma, Phys. Rev. D 33, 1314 (1986).
Bøggild et al. [1995] H. Bøggild et al. (NA44 Collaboration), Directional dependence of the pion source in high-energy heavy ion collisions, Phys. Lett. B 349, 386 (1995).
Adler et al. [2004a] S. S. Adler et al. (PHENIX Collaboration), Bose-Einstein correlations of charged pion pairs in Au $+$ Au collisions at $\sqrt{s_{NN}}=200$ GeV, Phys. Rev. Lett. 93, 152302 (2004a).
Adams et al. [2005a] J. Adams et al. (STAR Collaboration), Pion interferometry in Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV, Phys. Rev. C 71, 044906 (2005a).
Kittel and De Wolf [2005] W. Kittel and E. A. De Wolf, Soft multihadron dynamics (World Scientific Publishing, 2005) isbn: 978-981-256-295-1.
Kincses et al. [2020] D. Kincses, M. I. Nagy, and M. Csanád, Coulomb and strong interactions in the final state of Hanbury-Brown–Twiss correlations for Lévy-type source functions, Phys. Rev. C 102, 064912 (2020).
Csörgő and Hegyi [2000] T. Csörgő and S. Hegyi, Model independent shape analysis of correlations in one-dimension, two-dimensions or three-dimensions, Phys. Lett. B 489, 15 (2000).
Csörgő and Zimányi [1990] T. Csörgő and J. Zimányi, Pion interferometry for strongly correlated space-time and momentum space, Nucl. Phys. A 517, 588 (1990).
Akkelin and Sinyukov [1995] S. V. Akkelin and Yu. M. Sinyukov, The HBT interferometry of expanding sources, Phys. Lett. B , 525 (1995).
Bowler [1991] M. G. Bowler, Coulomb corrections to Bose-Einstein correlations have been greatly exaggerated, Phys. Lett. B 270, 69 (1991).
Alt et al. [2000] E. O. Alt, T. Csörgő, B. Lörstad, and J. Schmidt-Sorensen, Coulomb wave function corrections for n particle Bose-Einstein correlations, Eur. Phys. J. C 13, 663 (2000).
Csörgő et al. [1996] T. Csörgő, B. Lörstad, and J. Zimányi, Bose-Einstein correlations for systems with large halo, Z. Phys. C 71, 491 (1996).
Bolz et al. [1993] J. Bolz, U. Ornik, M. Plumer, B. R. Schlei, and R. M. Weiner, Resonance decays and partial coherence in Bose-Einstein correlations, Phys. Rev. D 47, 3860 (1993).
Csanád et al. [2019] M. Csanád, S. Lökös, and M. Nagy, Coulomb final state interaction in heavy ion collisions for Lévy sources, Universe 5, 133 (2019).
Csanád et al. [2020a] M. Csanád, S. Lökös, and M. Nagy, Expanded empirical formula for Coulomb final state interaction in the presence of Lévy sources, Phys. Part. Nucl. 51, 238 (2020a).
Kurgyis et al. [2023] B. Kurgyis, D. Kincses, M. Nagy, and M. Csanád, Coulomb Corrections for Bose–Einstein Correlations from One- and Three-Dimensional Lévy-Type Source Functions, Universe 9, 328 (2023).
Csanád [2006] M. Csanád (PHENIX Collaboration), Measurement and analysis of two- and three-particle correlations, Nucl. Phys. A 774, 611 (2006).
Vance et al. [1998] S. E. Vance, T. Csörgő, and D. Kharzeev, Observation of partial UA1 restoration from Bose-Einstein correlations, Phys. Rev. Lett. 81, 2205 (1998).
Csörgő and Zimányi [1998] T. Csörgő and J. Zimányi, Analytic solution of the pion-laser model, Phys. Rev. Lett. 80, 916 (1998).
Chapman et al. [1995] S. Chapman, P. Scotto, and U. W. Heinz, Model independent features of the two particle correlation function, Acta Phys. Hung. A 1, 1 (1995).
Csörgő and Lörstad [1996] T. Csörgő and B. Lörstad, Bose-Einstein correlations for three-dimensionally expanding, cylindrically symmetric, finite systems, Phys. Rev. C 54, 1390 (1996).
Kincses et al. [2022] D. Kincses, M. Stefaniak, and M. Csanád, Event-by-Event Investigation of the Two-Particle Source Function in Heavy-Ion Collisions with EPOS, Entropy 24, 308 (2022).
Adler et al. [2014] S. S. Adler et al. (PHENIX Collaboration), Transverse-energy distributions at midrapidity in p+p ,d+Au, and Au+Au collisions at $\sqrt{s_{NN}}=62.4$ –200 GeV and implications for particle-production models, Phys. Rev. C 89, 044905 (2014).
Abelev et al. [2009a] B. I. Abelev et al. (STAR Collaboration), Pion Interferometry in Au+Au and Cu+Cu Collisions at RHIC, Phys. Rev. C 80, 024905 (2009a).
Csörgő et al. [2010] T. Csörgő, R. Vértesi, and J. Sziklai, Indirect observation of an in-medium $\eta^{\prime}$ mass reduction in $\sqrt{s_{NN}}$ =200 GeV Au+Au collisions, Phys. Rev. Lett. 105, 182301 (2010).
Vértesi et al. [2011] R. Vértesi, T. Csörgő, and J. Sziklai, Significant in-medium $\eta$ ’ mass reduction in $\sqrt{s_{{}_{NN}}}$ =200 GeV Au+Au collisions at the BNL Relativistic Heavy Ion Collider, Phys. Rev. C 83, 054903 (2011).
Pisarski and Wilczek [1984] R. D. Pisarski and F. Wilczek, Remarks on the Chiral Phase Transition in Chromodynamics, Phys. Rev. D 29, 338 (1984).
Kapusta et al. [1996] J. I. Kapusta, D. Kharzeev, and L. D. McLerran, The Return of the prodigal Goldstone boson, Phys. Rev. D 53, 5028 (1996).
Workman and Others [2022] R. L. Workman and Others (Particle Data Group), Review of Particle Physics, Prog. Theo. Exp. Phys. 2022, 083C01 (2022).
Wheaton and Cleymans [2009] S. Wheaton and J. Cleymans, THERMUS: A Thermal model package for ROOT, Comput. Phys. Commun. 180, 84 (2009).
Petran et al. [2014] M. Petran, J. Letessier, J. Rafelski, and G. Torrieri, SHARE with CHARM, Comput. Phys. Commun. 185, 2056 (2014).
Adler et al. [2004b] S. S. Adler et al. (PHENIX Collaboration), Identified charged particle spectra and yields in Au+Au collisions at $\sqrt{s_{NN}}$ =200 GeV, Phys. Rev. C 69, 034909 (2004b).
Aggarwal et al. [2011] M. M. Aggarwal et al. (STAR Collaboration), $K^{*0}$ production in Cu+Cu and Au+Au collisions at $\sqrt{s_{{}_{NN}}}=62.4$ and 200 GeV, Phys. Rev. C 84, 034909 (2011).
Abelev et al. [2009b] B. I. Abelev et al. (STAR Collaboration), Systematic Measurements of Identified Particle Spectra in $p$ $+$ $p$ , $d$ $+$ Au, and Au $+$ Au Collisions from STAR, Phys. Rev. C 79, 034909 (2009b).
Bearden et al. [2003] I. G. Bearden et al. (BRAHMS Collaboration), Rapidity Dependence of Charged Antiparticle-to-Particle Ratios in Au+Au Collisions at $\sqrt{s_{NN}}=200$ GeV, Phys. Rev. Lett. 90, 102301 (2003).
Adams et al. [2005b] J. Adams et al. (STAR Collaboration), phi meson production in Au $+$ Au and $p$ $+$ $p$ collisions at $\sqrt{s_{NN}}=200$ GeV, Phys. Lett. B 612, 181 (2005b).
Gaudichet [2004] L. Gaudichet (STAR Collaboration), Lambda(1520) and Sigma(1385) resonance production in Au+Au and p+p collisions at RHIC $\sqrt{s_{NN}}=200$ GeV, J. Phys. G 30, S549 (2004).
Suire [2003] C. Suire (STAR Collaboration), Omega- and anti-Omega+ production in Au+Au collisions at $\sqrt{s_{NN}}=130$ and 200 GeV, Nucl. Phys. A 715, 470 (2003).
Adamczyk et al. [2017] L. Adamczyk et al. (STAR Collaboration), Bulk Properties of the Medium Produced in Relativistic Heavy-Ion Collisions from the Beam Energy Scan Program, Phys. Rev. C 96, 044904 (2017).
Weinberg [1975] S. Weinberg, The U(1) Problem, Phys. Rev. D 11, 3583 (1975).
Horvatić et al. [2019] D. Horvatić, D. Kekez, and D. Klabučar, $\eta^{\prime}$ and $\eta$ mesons at high T when the $U_{A}$ (1) and chiral symmetry breaking are tied, Phys. Rev. D 99, 014007 (2019).
Huang and Wang [1996] Z. Huang and X.-N. Wang, Partial U(1)A restoration and eta enhancement in high-energy heavy ion collisions, Phys. Rev. D 53, 5034 (1996).
Kwon et al. [2012] Y. Kwon, S. H. Lee, K. Morita, and G. Wolf, Renewed look at $\eta^{\prime}$ in medium, Phys. Rev. D 86, 034014 (2012).
Csörgő [2002] T. Csörgő, Particle interferometry from 40 MeV to 40 TeV, Acta Phys. Hung. A 15, 1 (2002).
Zimányi and Csörgő [1999] J. Zimányi and T. Csörgő, Multiboson correlations using wave packets, Acta Phys. Hung. A 9, 241 (1999).
Csanád et al. [2020b] M. Csanád, A. Jakovác, S. Lökös, A. Mukherjee, and S. K. Tripathy, Multiparticle quantum-statistical correlation functions in a Hubble-expanding hadron gas (2020b), arXiv:2007.07167.
Workman et al. [2022] R. L. Workman et al. (Particle Data Group), Review of Particle Physics, Prog. Theo. Exp. Phys. 2022, 083C01 (2022).
Kovács et al. [2021] G. Kovács, P. Kovács, and Z. Szép, One-loop constituent quark contributions to the vector and axial-vector meson curvature mass, Phys. Rev. D 104, 056013 (2021).
Hama and Navarra [1992] Y. Hama and F. S. Navarra, Energy and mass number dependence of the dissociation temperature in hydrodynamical models, Z. Phys. C 53, 501 (1992).
Adler et al. [2007] S. S. Adler et al. (PHENIX Collaboration), High transverse momentum $\eta$ meson production in $p^{+}p$ , $d^{+}$ Au and Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV, Phys. Rev. C 75, 024909 (2007).
Adare et al. [2008] A. Adare et al. (PHENIX Collaboration), Quantitative Constraints on the Opacity of Hot Partonic Matter from Semi-Inclusive Single High Transverse Momentum Pion Suppression in Au+Au collisions at $\sqrt{s_{NN}}$ =200 GeV, Phys. Rev. C 77, 064907 (2008).

Centrality dependence of Lévy-stable two-pion Bose-Einstein correlations in sN​N=200\sqrt{s_{{}_{NN}}}=200 GeV Au++Au collisions.