Channel Mapping Based on Interleaved Learning with Complex-Domain MLP-Mixer
Abstract
In multiple-input multiple-output (MIMO) orthogonal frequency division multiplexing (OFDM) systems, representing the whole channel only based on partial subchannels will significantly reduce the channel acquisition overhead. For such a channel mapping task, inspired by the intrinsic coupling across the space and frequency domains, this letter proposes to use interleaved learning with partial antenna and subcarrier characteristics to represent the whole MIMO-OFDM channel. Specifically, we design a complex-domain multilayer perceptron (MLP)-Mixer (CMixer), which utilizes two kinds of complex-domain MLP modules to learn the space and frequency characteristics respectively and then interleaves them to couple the learned properties. The complex-domain computation facilitates the learning on the complex-valued channel data, while the interleaving tightens the coupling of space and frequency domains. These two designs jointly reduce the learning burden, making the physics-inspired CMixer more effective on channel representation learning than existing data-driven approaches. Simulation shows that the proposed scheme brings 4.6~10dB gains in mapping accuracy compared to existing schemes under different settings. Besides, ablation studies show the necessity of complex-domain computation as well as the extent to which the interleaved learning matches the channel properties.
Index Terms:
Channel Mapping, Deep learning, Physics-inspired learning, MIMO, OFDM.I Introduction
Multiple-input multiple-output (MIMO) and orthogonal frequency division multiplexing (OFDM) modulation are two key enabling technologies in wireless communication systems, thanks to their ability in achieving high spectrum efficiency. Meanwhile, unleashing these potentials generally requires acquiring real-time channel state information (CSI). However, MIMO and OFDM techniques significantly increase the size of CSI data, resulting in significant signaling overhead [1].
To address this challenge, the work in [2] proposes the channel mapping over space and frequency, i.e., by leveraging the implicit correlations within the high-dimensional channel, obtaining the whole MIMO-OFDM channel from known subchannel at a partial set of antennas and subcarriers. In this way, the signaling overhead required for channel acquisition can be reduced from the entire high-dimensional channel to some specific subchannels. Specifically, the authors in [2] leverage the capabilities of deep learning (DL) techniques in mining implicit features and high-dimensional data representation, using a multi-layer perceptron (MLP) to learn the channel mapping function by fitting it from the training data. Moreover, there are some channel estimation works that use similar ideas to estimate the whole channel by mapping from only a small number of subchannels. In [3], the authors use DL learning techniques to map the information of partial subcarriers to whole subcarriers for channel estimation in OFDM systems. Further, the work in [4] improves the network structure in [3] with a residual convolutional neural network (Res_CNN) to enhance the performance of channel mapping and estimation.
Despite some preliminary attempts, existing channel mapping networks are still directly migrated from popular DL schemes and lack task-related design, which makes the learning mainly data-driven. However, data-driven learning is mediocre under limited training data, and the learned generalization is often weak. Therefore, it is necessary to design the network a priori according to the properties of the data and the task to improve the learning efficiency, such as the design of CNNs based on the translational equivalence and smoothness of images. This letter delves into the physical properties inside MIMO-OFDM channels and accordingly proposes a physics-inspired learning scheme for channel mapping. The main contributions of this letter are summarized as follows:
-
•
By revealing the intrinsic coupling between the space and frequency characteristics of an MIMO-OFDM channel, we propose an interleaved learning framework to investigate this cross-domain internal correlation.
-
•
To facilitate the learning process, we propose a novel complex-domain MLP-Mixer (CMixer) layer module for channel representation, and then construct a CMixer model for channel mapping by stacking multiple CMixer layers.
-
•
Through comparison experiments with existing methods, we demonstrate the superiority of the proposed scheme. Further ablation studies show the necessity and value of physics-inspired design for improving mapping performance.
II System Model
In this section, we introduce the system model, including the channel model and the channel mapping framework.
II-A Channel Model
We consider a massive MIMO system, where a base station (BS) with antennas serves multiple single-antenna users. Also, the considered system adopts OFDM modulation with subcarriers. The channel between one user and the BS is assumed to be composed of paths, which can be expressed as,
| (1) |
where is the carrier frequency, is the amplitude attenuation, is the propagation delay, and is the three-dimensional unit vector of departure direction of the -th path. Furthermore, is the array defined as,
| (2) |
where is the space vector array, represents the three-dimensional space vector between the -antenna and the first antenna, and is the speed of light. The transmission distance shift between the -th antenna and the first antenna on -th path can be written as . If the antenna array form is a uniform linear array, can be simplified as , where is the angle of departure (AoD) of the -th path and is the antenna space. This simplified case is equivalent to the channel model in the literature [5]. Further, the whole CSI matrix between the user and the BS can be expressed as,
| (3) |
where , is the -th subcarrier frequency, is the base frequency, and is the frequency shift between the -th subcarrier and the base frequency.
II-B Channel Mapping
As shown in the channel model, there are significant correlations within the CSI matrix, benefiting from the path-similarity of sub-channels. Further, channel mapping [2] aims at realizing such a task leveraging on this correlation: inputting sub-channels of some antennas and subcarriers to output the whole channel data, which can be written as,
| (4) |
where is the selected small subset in space and frequency, is also written as .
The channel mapping task has many potential applications. For example, in high-dimensional channel estimation, it is possible only to estimate the CSI of several antennas and subcarriers and then obtain the whole channel by channel mapping to decrease the pilot overhead. Furthermore, in the high-dimensional CSI feedback, it is possible only to upload partial downlink CSI, and the BS can still reconstruct the whole downlink CSI based on channel mapping, forming a user-friendly CSI feedback scheme without the additional encoder. In Eq. (4), for the subset , a typical selection is the whole channel of several certain antennas and subcarriers, i.e.,
| (6) |
where is the subset of the selected antennas, is the subset of the selected subcarriers, and represents that . Besides, the settings of A and B are often uniform distributions and as widely ranging as possible in space and frequency domains, respectively.
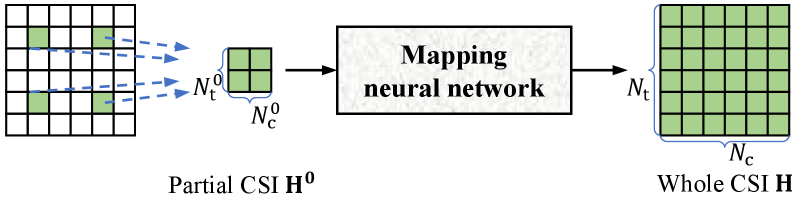
Since CSI is a complex coupling of multipath channel responses, the internal correlation in the CSI matrix is often implicit and, thus, is difficult to explore through traditional signal processing methods. Therefore, we use the DL technology with excellent implicit feature learning capabilities to realize efficient channel mapping. The overall DL-based channel mapping framework is shown in Fig. 1. This learning process mainly relies on the representation learning of channel data, i.e., representing implicit features from known channel information and then representing the whole channel based on the obtained features. For the mapping neural network, if some a priori design can be introduced according to the physical properties of the MIMO-OFDM channel, it will undoubtedly improve the representation learning and guide the network to learn more efficiently from the limited training data.
III Proposed Schemes and Related Analysis
This section details our proposed learning scheme and related analysis, including the revealed channel characteristic, the learning module inspired by this characteristic, and the proposed channel mapping scheme utilizing this module.
III-A Interlaced Space and Frequency Characteristics
This subsection presents that there is an unique interlaced space and frequency characteristic in MIMO-OFDM channel. Specifically, according to the channel model in Section II-A, we can define the following function,
| (7) |
where the parameters of , , are the shared large-scale features among all sub-channels. Therefore, is independent of the specific antennas and subcarriers. Then, leveraging , the CSI of the -th antenna and -th subcarrier can be written as , then the CSI matrix in Eq. (3) can be rewritten as,
| (12) |
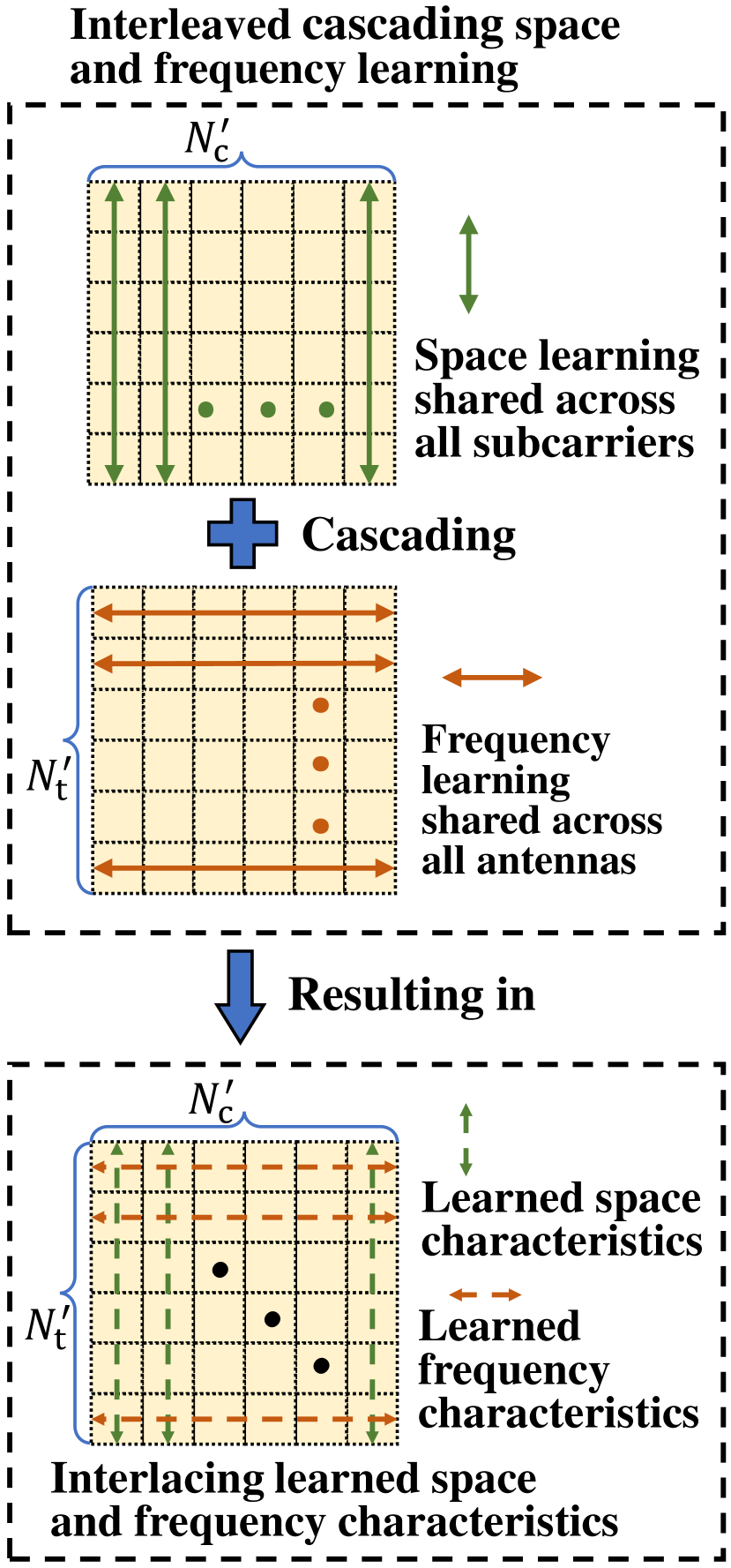
For any two columns of , all antennas’ CSI of different subcarriers, although have different frequency shifts , they still share the same space features and the same large-scale features . Similarly, for any two rows of , all subcarriers’ CSI of different antennas, although there exists different space shift , they still share the same frequency features and the same large-scale features . To summarize, based on the shared large-scale channel features , shared space features and shared frequency features interlaced couple, form the internal correlation of the whole CSI matrix.
III-B Interleaved Learning Module for Channel Representation
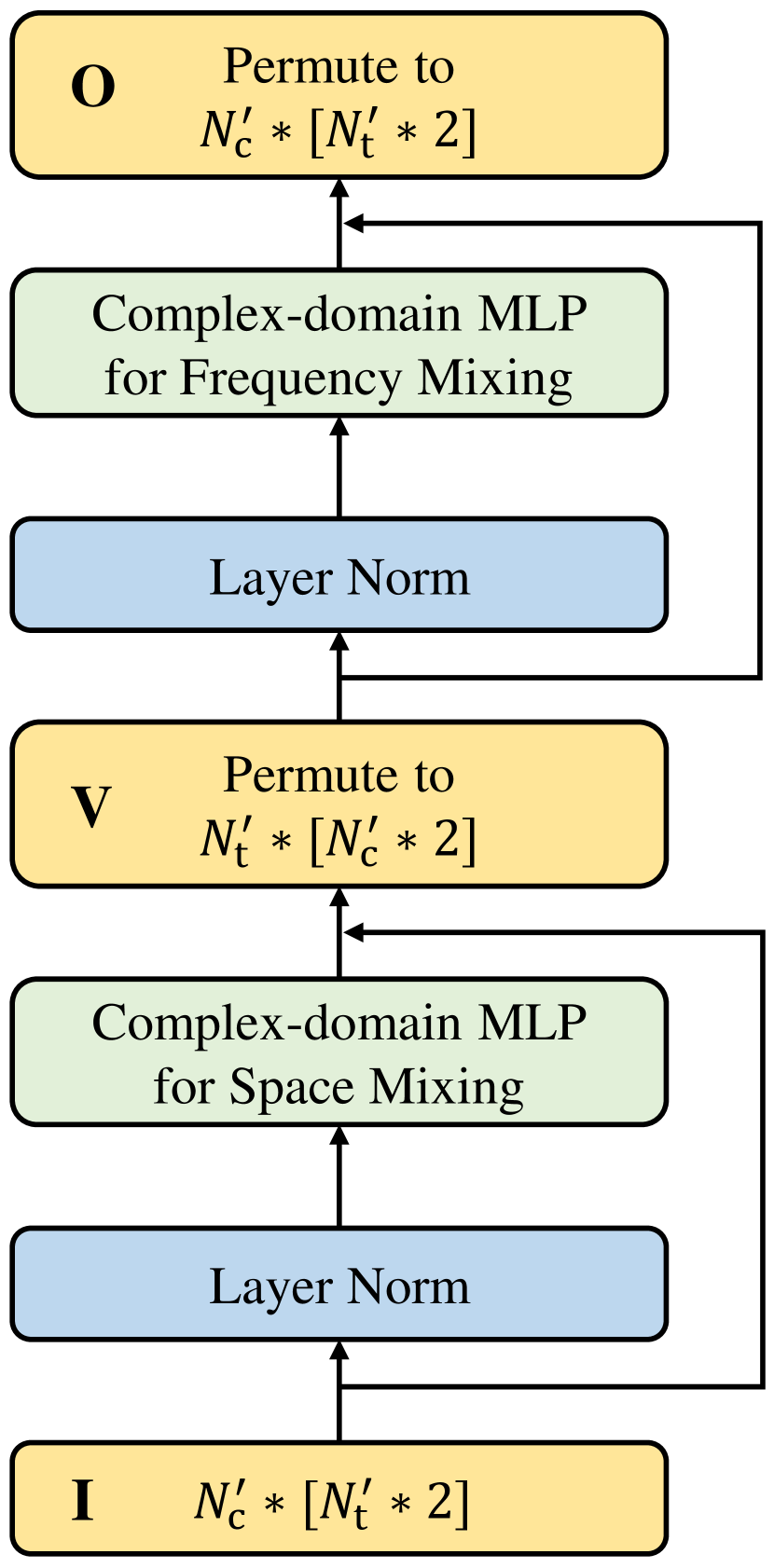
According to the revealed property, we propose an interleaved space and frequency learning approach for channel representation, as shown in Fig. 2(a). This approach first learns the space dimension, and this learning process is shared among all subcarriers, named as space mixing. This sharing of space learning process utilizes the sharing of space characteristics among all subcarriers. Then, the proposed approach learns the frequency dimension, and this learning process is also shared among all antennas, called frequency mixing. Similarly, this sharing of frequency learning process also utilizes the sharing of frequency characteristics among all antennas. The cascading of space mixing and frequency mixing interlaces the learned space and frequency characteristics, highly matching the revealed channel characteristics. In the neural network implement, similar to [6], we also introduce the residual connection and the layer normalization to keep the effectiveness and stability of training. Fig. 2(c) presents the specific learning module design, and the calculation process is as follows,
| (13a) | ||||
| (13b) | ||||
where is the input, is the output, is the intermediate variable matrix, are all of size, and , , and are the abbreviation of space mixing, frequency mixing, and layer normalization, respectively. The computation in Eq. (13) completes a nonlinear representation of the input through interleaved learning and yields an output of the same size as .
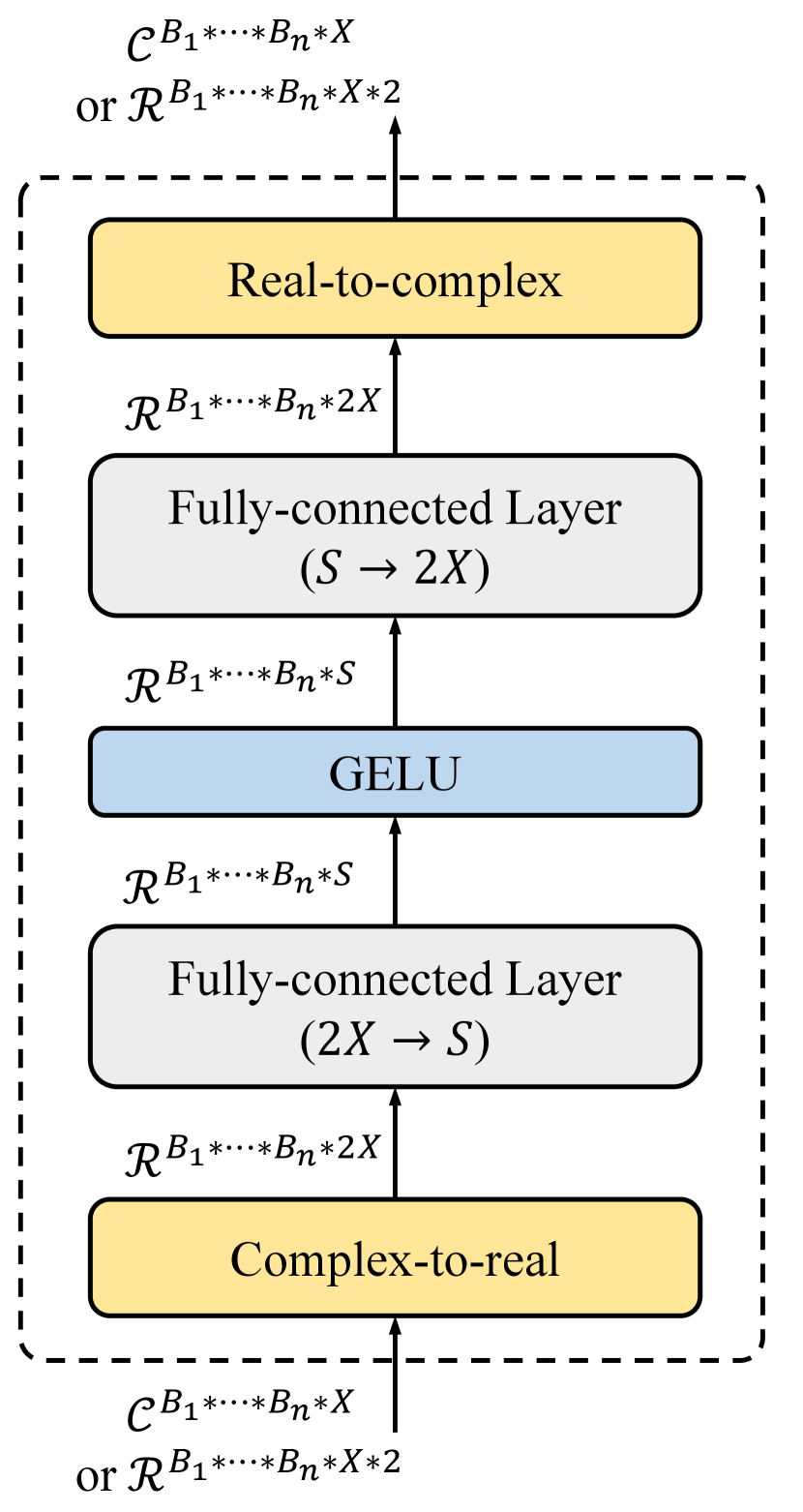
Considering that the channel characteristics are embodied in complex-valued data while the current mainstream DL platforms are based on real-valued operations, we design a complex-domain MLP (CMLP) module to specifically realize space mixing and frequency mixing. Fig. 2(d) shows the flowchart of CMLP, and the simplified calculation process can be written as follows,
| (14) |
where represents complex-valued data and represents real-valued data, refers to or . in Fig. 2(d) is constant multiples of . This method places the real and imaginary parts in the same neural layer for learning, which ensures the sufficient interaction of real and imaginary information better than treating the real and imaginary parts as separate channels. Moreover, this method recovers the complex dimension at the end to ensure that the next mixing can still be performed on the complex domain. Thus, the learning of the channel data can always remain in the complex domain, even if stacking multiple mixing layers. In summary, this subsection establishes an interleaved learning module, a CMixer layer, consisting of a cascade of a space-learning CMLP and a frequency-learning CMLP. It is suitable for channel representation learning since it is designed according to the channel’s physical properties.
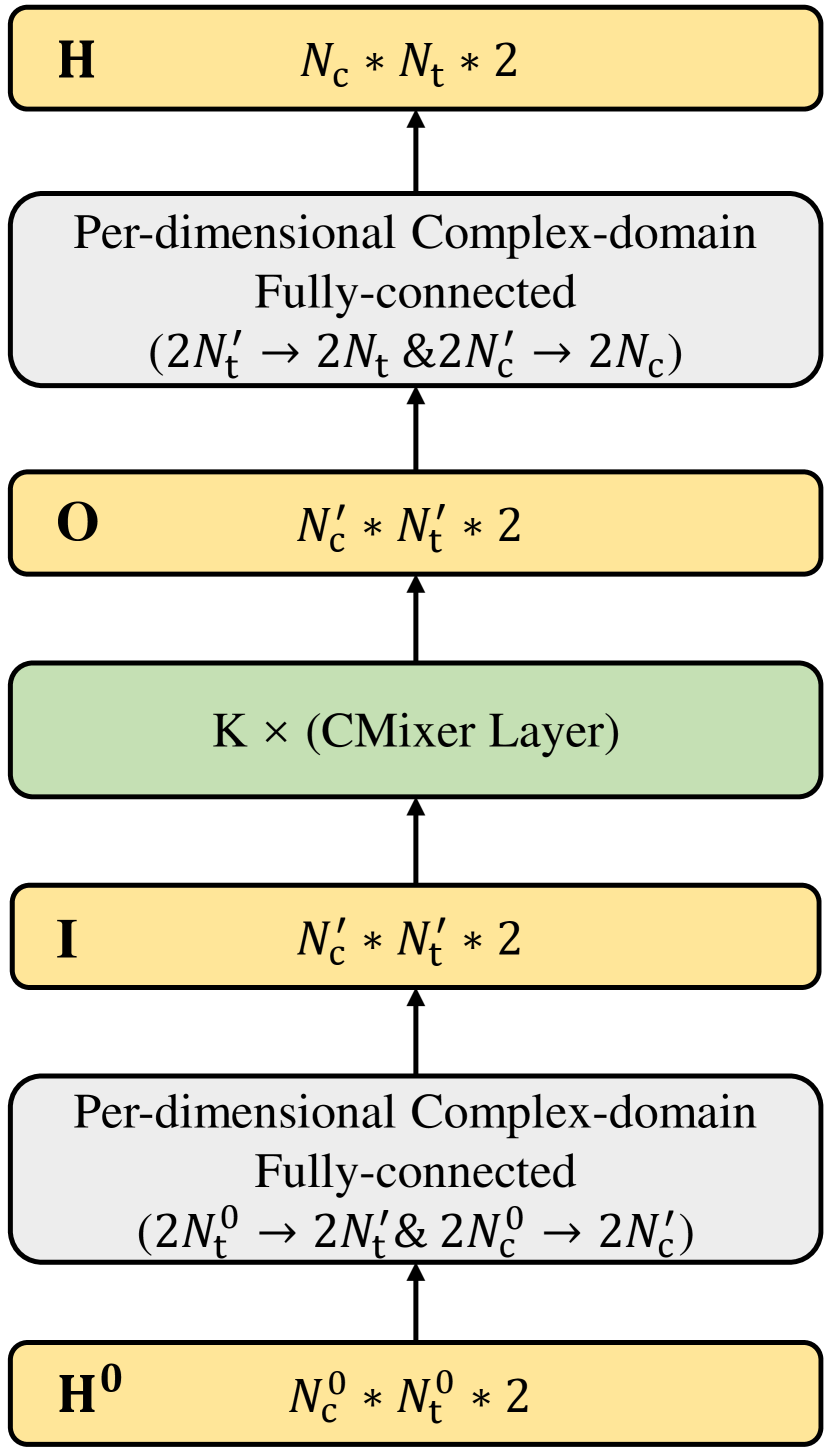
III-C CMixer Model for Channel Mapping
By stacking the above representation modules to enhance the nonlinearity and adding the necessary dimension mapping modules, the CMixer model is built for the channel mapping task. The network structure is shown in Fig. 2(b), and the calculation process is as follows. First, inputting the -size known channel to a MLP layer and a MLP layer to output a -size variable. This part yields parameters and computation complexity. Then, inputting the -size variable to stacked CMixer layers and the output variable is still of size. This part yields parameters and computation complexity. Finally, using a MLP layer and a MLP layer to mapping the previous output to -size variable, which is the whole MIMO-OFDM CSI. This part yields parameters and computation complexity. Since , and are constant multiples of , and are constant multiples of , the total parameter scale of this model is and the total computation complexity is . To train the model, mean square error (MSE) is used as the loss function, which can be written as
| (15) |
where is the parameter set of the proposed model, is the number of channel samples in the training set, and is the Euclidean norm. In addition, can be updated through the existing gradient descent-based optimizers, such as the adaptive momentum estimation (Adam) optimizer.
IV Simulation Experiments
In this section, we evaluate the performance and properties of the proposed CMixer through simulation experiments.
IV-A Experiment Settings
In this work, we use the open-source DeepMIMO dataset of ‘O1’ scenario at 3.5GHz [7] for the simulation experiment. The bandwidth is set as 40MHz and divided to 32 subcarriers, the BS is equipped with a uniform linear array (ULA) consisting of 32 antennas. The user area is chose as R701-R1400. 50000 channel samples are randomly sampled from the dataset and divided into the training set and testing set with a ratio of 4:1. In addition, for intuitive performance evaluation, we use two existing typical DL-based channel mapping schemes as benchmarks. One is the MLP method [2], using a pure MLP network to learn the mapping function. The other is the Res_CNN method [4], using a CNN with residual connection as the network structure. Also, the model and training settings are summarized in Table I.
| Parameters | Value |
| Batch size | 250 |
| Learning rate | (multiply by 0.2 every 500 epochs after the 500th epoch) |
| Model setting | |
| Subset | , , where |
| Number of model parameters | 0.176 million, the case of () |
| Floating-point operations (FLOPs) | 5.61 million, the case of () |
| Training epochs | 2000 |
| Optimizer | Adam |
Moreover, we use normalized MSE (NMSE) and cosine correlation [8] as the performance indices, which are defined as follows:
| (16) |
and
| (17) |
where the is the CSI of -th subcarrier, i.e. the -th columon of the CSI matrix .
IV-B Performance Evaluation
We first evaluate the mapping performance of the proposed CMixer and use various mapping settings to ensure the universality of evaluation results. The known channel size, the in Eq. (4), is set as 4×4, 5×5, 6×6 and 7×7 (antennas × subcarriers). Table II shows the mapping performance of proposed scheme and benchmarks. Compared with benchmarks, the proposed CMixer provides 4.6~10dB gains in NMSE and 5.7~9.6 percentage points gain in under same known channel size, or reduces required known channel size by up to under same and even better accuracy.
| Indexes | Schemes | Known channel size (antennas × subcarriers) | |||
| 4 × 4 | 5 × 5 | 6 × 6 | 7 × 7 | ||
| NMSE (dB) | CMixer | -10.49 | -14.11 | -15.38 | -19.24 |
| MLP | -5.85 | -6.88 | -7.53 | -9.22 | |
| Res_CNN | -3.37 | -4.49 | -7.23 | -8.94 | |
| CMixer | 0.9555 | 0.9807 | 0.9856 | 0.9940 | |
| MLP | 0.8589 | 0.8903 | 0.9071 | 0.9367 | |
| Res_CNN | 0.7394 | 0.8079 | 0.9017 | 0.9353 | |
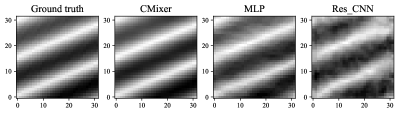
Further, Fig. 3 shows the mapping results of the different schemes on a random channel sample using grayscale visualization (Known channel size is 5 antennas × 5 subcarriers). It can be intuitively seen that the mapping channel based on CMixer is closer to the true channel than based on benchmarks. In summary, the above experimental results reflect the effectiveness and superiority of the proposed CMixer on the channel mapping task.
IV-C Ablation Studies
Complex-domain computation and interleaved learning are the two typical features of the proposed CMixer model. The performance evaluation in Section IV-B illustrates the superiority of the scheme as a whole, and this subsection evaluates the value of these sub-modules through ablation studies. These ablation experiments are all conducted under the known channel of 5 antennas × 5 subcarriers.
We first evaluate the necessity of using CMLPs. We replace the proposed CMLPs with vanilla MLPs. The specific ablation operation is changing the calculation (CMLP) to the calculation (MLP with real and imag parallelism), remaining the same computation complexity, , to ensure fairness. Table III shows the results of this ablation. Not using the CMLPs in either space mixing or frequency mixing leads to performance degradation. This phenomenon demonstrates the advantages of CMLPs in the representation learning of complex-valued channel data.
| Using MLP | Using CMLP | |
| Using MLP | -7.13 | -11.21 |
| Using CMLP | -12.38 | -14.11 |
Then, we also evaluate what leads to the effectiveness of the proposed interleaved learning and whether it exactly stems from the unique interlaced space and frequency characteristics in the channel. Specifically, we shuffle the element order in the channel matrix in a way that remains/loses interlaced space and frequency characteristics and use the CMixer to learn the new matrix as the representation output. The first shuffle mode is named as ‘interlaced shuffle’ and written as,
| (18) |
where each represents a permutation matrix. In this way, the new channel matrix has different space and frequency characteristics from the original channel , but its space and frequency characteristics are still interlaced coupled since its each row or column still respectively corresponds to certain antenna or subcarrier. The other shuffle mode is named as ‘non interlaced shuffle’ and written as,
| (19) |
where denotes the transposition of a matrix into a vector and is the reverse process of . In this shuffle mode, the row or column of does not necessarily correspond to certain antenna or subcarrier. Thus, the space and frequency characteristics are no longer coupled in an interlaced manner. Note that the above two kinds of new channel matrix and the original channel matrix are identical in element content and only differ on the data structure. We use various random permutation matrices for experiments, and the statistical results are shown in Table IV. The proposed CMixer can effectively represent with interlaced space and frequency characteristics while is severely degraded in representing without the interlaced characteristics. This phenomenon illustrates that the excellent performance of the proposed interleaved space and frequency learning indeed draws on the physical properties rather than relying exclusively on data fitting. The CMixer model’s performance gains come from the design inspired by channel characteristics.
| Shuffle mode | NMSE (dB) |
| Origin | |
| Interlaced | |
| Non-Interlaced |
V Conclusion
In this paper, we propose a CMixer model for channel mapping, achieving excellent performance. Modeling analysis and ablation studies state that the complex-domain computation and interleaved learning in this model are suitable for channel representation and, thus, are likely to be applicable in other channel-related tasks as well. We hope that our work can provide inspirations for using DL technologies to solve problems in wireless systems.
References
- [1] Z. Chen, Z. Zhang, and Z. Yang, “Big AI models for 6G wireless networks: Opportunities, challenges, and research directions,” arXiv preprint arXiv:2308.06250, 2023.
- [2] M. Alrabeiah and A. Alkhateeb, “Deep learning for TDD and FDD massive MIMO: Mapping channels in space and frequency,” in 2019 53rd Asilomar Conference on Signals, Systems, and Computers, 2019, pp. 1465–1470.
- [3] M. Soltani, V. Pourahmadi, A. Mirzaei, et al., “Deep learning-based channel estimation,” IEEE Communications Letters, vol. 23, no. 4, pp. 652–655, 2019.
- [4] L. Li, H. Chen, H.-H. Chang, et al., “Deep residual learning meets OFDM channel estimation,” IEEE Wireless Communications Letters, vol. 9, no. 5, pp. 615–618, 2020.
- [5] Z. Chen, Z. Zhang, Z. Xiao, et al., “Viewing channel as sequence rather than image: A 2-D Seq2Seq approach for efficient MIMO-OFDM CSI feedback,” IEEE Transactions on Wireless Communications, vol. 22, no. 11, pp. 7393–7407, 2023.
- [6] I.O. Tolstikhin, N. Houlsby, A. Kolesnikov, et al., “MLP-Mixer: An all-MLP architecture for vision,” Advances in Neural Information Processing Systems, vol. 34, pp. 24261–24272, Dec. 2021.
- [7] A. Alkhateeb, “DeepMIMO: A generic deep learning dataset for millimeter wave and massive MIMO applications,” arXiv preprint arXiv:1902.06435, 2019.
- [8] C.-K. Wen, W.-T. Shih, and S. Jin, “Deep learning for massive MIMO CSI feedback,” IEEE Wireless Communications Letters, vol. 7, no. 5, pp. 748–751, Oct. 2018.