Charge order induced Dirac pockets in the nonsymmorphic crystal TaTe₄

Since the discovery of Chern insulators Haldane1988 and topological insulators Kane2005 ; Kane2005_2 , fascinating physics about symmetry-protected topological phases has enormously expanded the research scope of quantum materials. The idea of defining bulk topological invariants was soon extended from gapped to gapless systems, featuring Dirac and Weyl semimetals Armitage2018 . Furthermore, due to the nonsymmorphic crystalline symmetries in solid state systems, low energy electronic excitations in crystals can achieve, in addition to Dirac and Weyl fermions, unconventional three,four,six,and eightfold fermions Wieder2016 ; Bradlyn2016 ; Tang2017 with no analog in the standard model. The experimental realization of ideal materials hosting these unconventional quasiparticles has been an ongoing task Lv2017 ; Ma2018 ; Takane2019 ; Li2019 ; Sanchez2019 ; Schroter2019 ; Schroter2020 ; Lv2019 ; Yang2020 ; Kumar2020 ; Ju2022 ; Rong2022 . In particular, experimental efforts on realizing eightfold fermions robust against spin-orbit coupling (SOC) have been hindered by the restricted number of space groups Wieder2016 and candidates strongly affected by electron-electron (e-e) interactions Sante2017 .

Beyond pristine lattices, charge orders (COs) and charge density wave (CDW) orders can further modify the crystalline symmetries. Originating from Peierl’s description of a one-dimensional (1D) chain Peierls1955 ; Frohlich1954 where all electrons at the Fermi level (E_F) can be connected with the same vector $q$=2$k_{\rm F}$ ($k_{\rm F}$ being the Fermi momentum), CDW order is the spontaneous translational symmetry breaking by the electronic degree of freedom, and can arise from Fermi surface nesting (FSN), electron-phonon coupling (EPC), and e-e interaction Zhu2015 , where a weak instability tendency of FSN has been pointed out beyond one dimension Johannes2008 ; Zhu2017 . CO shares the same phenomenology of modulated charge density upon a crystal lattice but differs in that the charge degree of freedom follows that of the lattice, which drives the translational symmetry breaking. More recently, CDWs and COs have received extensive attention due to their emergence in a series of correlated topological materials, including the possible axion physics in (TaSe₄)₂I Gooth2019 ; Shi2021 and the COs found in the kagome metals, both in non-magnetic AV₃Sb₅ (A = K, Rb, Cs) Li2020 ; Wu2022 ; Luo2022 ; Xie2022 and ScV₆Sn₆ Cheng2023 , as well as the magnetic kagome lattice FeGe Teng2022 ; Teng2022_2 ; Yin2022 . Therefore, investigating the interplay between CO and nontrivial topological band structure is of particular interest. Here, we focus on the scenario where the CO modifies the crystalline symmetries to produce new topological crossings and potential unconventional eightfold fermions, as probed in the quasi-1D material TaTe₄.

The subcell of TaTe₄ crystalizes in the P4/mcc space group (No. 124), with Ta chains aligned along the [001] direction. TaTe₄ with its isostructural analogs NbTe₄ Bjerkelund1964 ; Boswell1983 ; Mahy1983 ; Selte1964 and Ta_1-xNb_xTe₄ Eaglesham1985 ; Morelli1986 ; Boswell1986 ; Walker1988 ; Prodan1990 ; Bennett1992 ; Kusz1994 ; Kusz1995 form to a family of quasi-1D compounds that exhibit a series of incommensurate, commensurate, and discommensurate COs. In TaTe₄, a (2a$\times$2b$\times$3c) CO has been reported by single crystal x-ray and electron diffraction experiments Bjerkelund1964 ; Boswell1983 ; Mahy1983 ; Bronsema1987 ; Bennett1991 , with an onset temperature of T_CO = 450 K. Within the CO state, transport studies show a metallic behavior Tadaki1990 . Previous ARPES measurements, however, report a sizable gap at the Fermi level, E_F, contradictory to the metallic transport behavior Zwick1999 . Magnetotransport measurements have revealed a large magnetoresistance and quantum oscillations Tadaki1990 ; Sambongi1993 ; Luo2017 ; Gao2017 ; Zhang2020 . A nontrivial Berry phase was also suggested Luo2017 , although more rigorous analysis involving higher-order harmonics Alexandradinata2018 may be needed to pin down the Berry phase. Furthermore, recent scanning tunneling microscopy (STM) work revealed a (4a$\times$6c) surface CO Sun2020 and edge states Zhang2020 . The (4a$\times$6c) surface CO distinct from that of the bulk was attributed to the surface-enhanced e-e interaction, with EPC stabilizing CO states at high binding energies, while the 1D edge states were proposed to be evidence of the topological nature Zhang2020 of TaTe₄. Regarding the bulk CO, recent first-principles calculations designated EPC the dominant role for triggering the phase transition, rather than FSN Liu2021 ; Guster2022 . Microscopically, the CO was proposed to be induced by the tendency to maximize Ta-Ta bonding, while introducing minimum shrinkage in the Te-sublattice bondings Guster2022 . By using state-of-the-art ARPES, we first visualize the metallic band structure of TaTe₄, which resolves previous inconsistencies between ARPES spectra and optical measurements Zwick1999 . In particular, our results provide spectroscopic evidence of the CO induced Dirac points (DPs) respecting the (2a$\times$3c) periodicity near E_F. Such folded structure serves as the prerequisite for the nonsymmorphic symmetry-protected double Dirac fermions in the CO state of TaTe₄. Despite that the direct observation of the double Dirac points (DDPs) still awaits future efforts, our results provide a step towards identifying quantum materials where electronic orders can be utilized in introducing new symmetries to realize novel topological states.

Single crystals of TaTe₄ were grown using flux method. High-purity Ta powder (99.99%, Alfa Asear) and Te lumps (99.9995%, Alfa Asear) with molar ratio of 1:20 were placed into a quartz tube in a glove box with O₂ level and H₂O level $<$ 0.1 ppm. The quartz tube was flame sealed under vacuum. The quartz tube assembly was then heated in a box furnace from room temperature up to 1000 °C in 20 hours, stayed at 1000 °C for 24 hours and then slowly cooled to 550 °C at a rate of 3°C/h. Silver needle-like crystals with a typical size of 2$\times$0.2$\times$0.2 mm³ were obtained by decanting the flux with a centrifuge at 550 °C using quartz wool as a filter.

Single-crystal x-ray diffraction (XRD) was performed using a Bruker D8 Quest diffractometer equipped with a CMOS detector, and an Oxford Cryosystems 700 Series temperature controller. A hemisphere of frames was measured using a narrow-frame method with a scan width of 0.5° in $\varphi$ and $\omega$ and an exposure time of 12 s/frame with Mo K$\alpha$ radiation. The collected dataset was integrated using the Bruker Apex3 program, with the intensities corrected for the Lorentz factor, polarization, air absorption, and absorption due to variation in the path length through the detector faceplate. The data were scaled, and absorption correction was applied using SADABS Krause2015 . A starting model was obtained using the intrinsic method in SHELXT Sheldrick2015 , and atomic sites were refined anisotropically using SHELXL2014/7. Powder XRD was carried out at room temperature on a Rigaku Smartlab x-ray diffractometer with a monochromatic Cu K$\alpha$1 radiation. Electrical resistivity $\rho$(T,H) using a four probe configuration was measured down to 2 K and up to 9 T magnetic field in a quantum design physical property measurement system (PPMS). The composition and homogeneity of the single crystals were confirmed by scanning electron microscopy with energy dispersive x-ray spectroscopy (SEM-EDX) and mapping using Zeiss EVO LS 15 SEM with 20 kV.

ARPES measurements were performed at the Advanced Light Source, Beamlines 4.0.3 and 10.0.1, equipped with SCIENTA R8000 and R4000 analyzers, respectively, and at the Stanford Synchrotron Radiation Lightsource, BL 5-2, equipped with a DA30 electron analyzer. The single crystals were cleaved in-situ at 10 K and measured in ultra-high vacuum with a base pressure better than 5$\times$10^-11 Torr. Photon energy-dependent measurements cover from 30 to 200 eV. Energy and angular resolution were set to be better than 25 meV and 0.1°, respectively.

Charge self-consistent DFT calculations were performed with the experimental lattice constants by using the generalized gradient approximation (GGA) potential PBE1996 as implemented in the Vienna ab initio simulation package Kresse1996 ; Kresse1996_2 . A $k$ mesh of 7$\times$7$\times$7 for the non-CO phase and 2$\times$2$\times$1 for the CO phase was adopted. To better account for the interaction effect poorly approximated in GGA, we further employed the HSE06 functional to calculate the electronic structure along $\Gamma Z$ and $XR$ (see Fig. S5 in the Supplemental Material SM ). The CO electronic structure folds back to the BZ of the non-CO state via the vaspkit code Wang2021 .

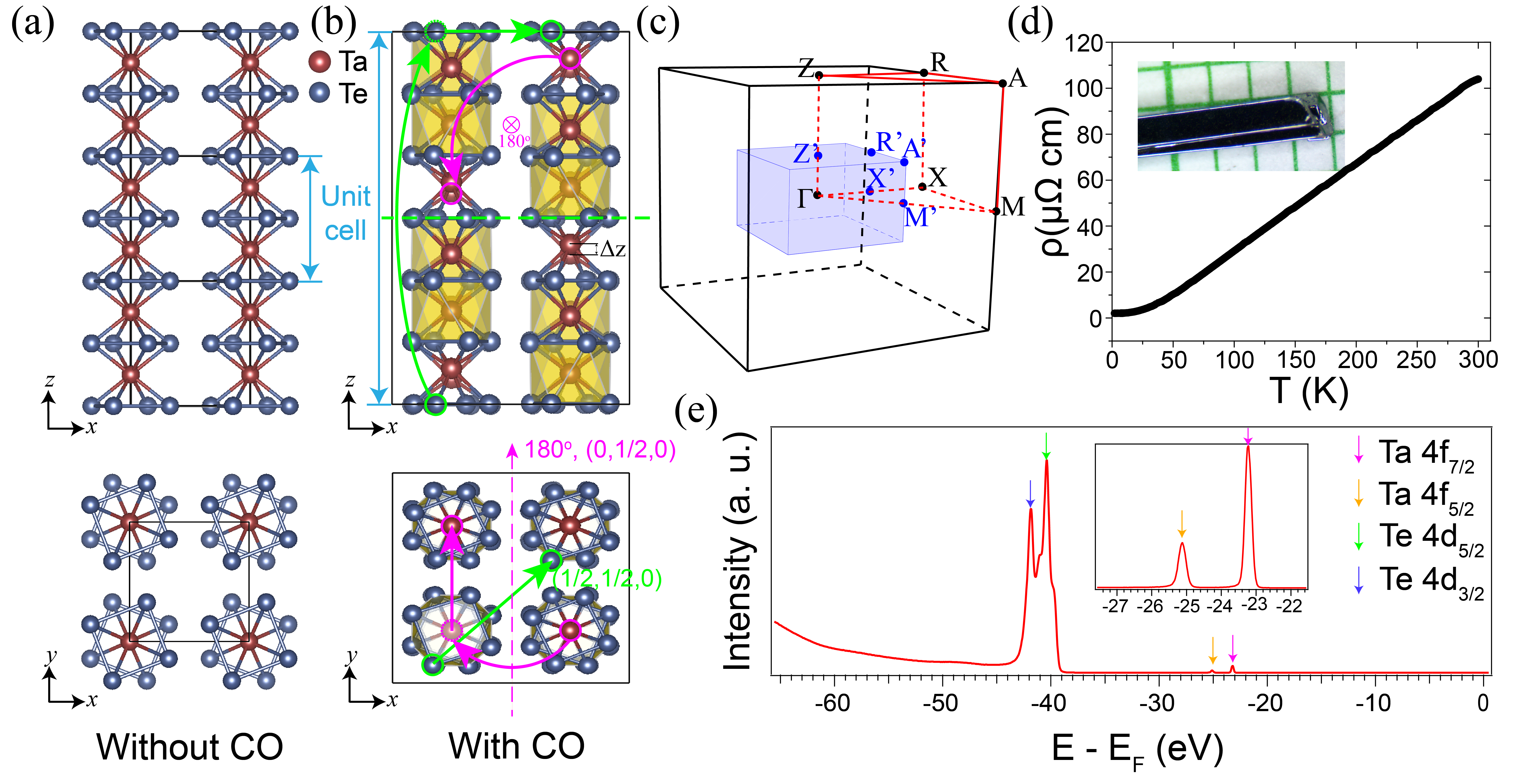
As the crystalline symmetries are important for the topological properties, we begin by discussing the crystal structure of the pristine and CO phases. The subcell crystal structure of non-CO TaTe₄ consists of tantalum chains surrounded by tellurium antiprisms [Fig. 1(a)]. In the CO phase (space group P4/ncc, No. 130), the distorted unit cell is tripled along $z$ and doubled along the two equivalent $x$ and $y$ directions [Fig. 1(b)]. The lattice parameters at T = 100 K in the CO phase identified from single crystal x-ray diffraction are: $a$ = $b$ = 12.996(3) Å and $c$ = 20.385(5) Å (See Table. S1 in the Supplemental Material SM ). The CO introduces new nonsymmorphic symmetries: for example, a twofold screw symmetry along $y$ and a glide mirror symmetry about the $xy$ plane. The two symmetry operations are illustrated by the magenta and green symbols in Fig. 1(b), respectively. When transforming to reciprocal space, the CO shrinks the pristine state BZ by a factor of (2$\times$2$\times$3), as depicted in Fig. 1(c). Throughout the paper, we label high symmetry points in the CO BZ in primed notation to distinguish them from their non-CO counterparts. TaTe₄ exhibits good metallic behavior, as indicated by the temperature-dependent resistivity with a relatively high residue resistivity ratio (RRR = 51) [Fig. 1(d)], indicating the good quality of grown single crystals. Further characterization of the single crystal magnetoresistance and homogeneity is presented in Fig. S1 and Fig. S2. In addition, core-level x-ray photoelectron spectrum identifies both Ta 4$f$ and Te 4$d$ peaks [Fig. 1(e)]. Since the natural cleaving plane for TaTe₄ is the (010) plane, $xz$ ($ac$) is the experimental in-plane direction, while the $y$ direction is the out-of-plane direction in the ARPES experiments. We also note that due to the equivalence of the $a$ and $b$ axes of the crystal, $k_{x}$ and $k_{y}$ are equivalent for the bulk crystal.

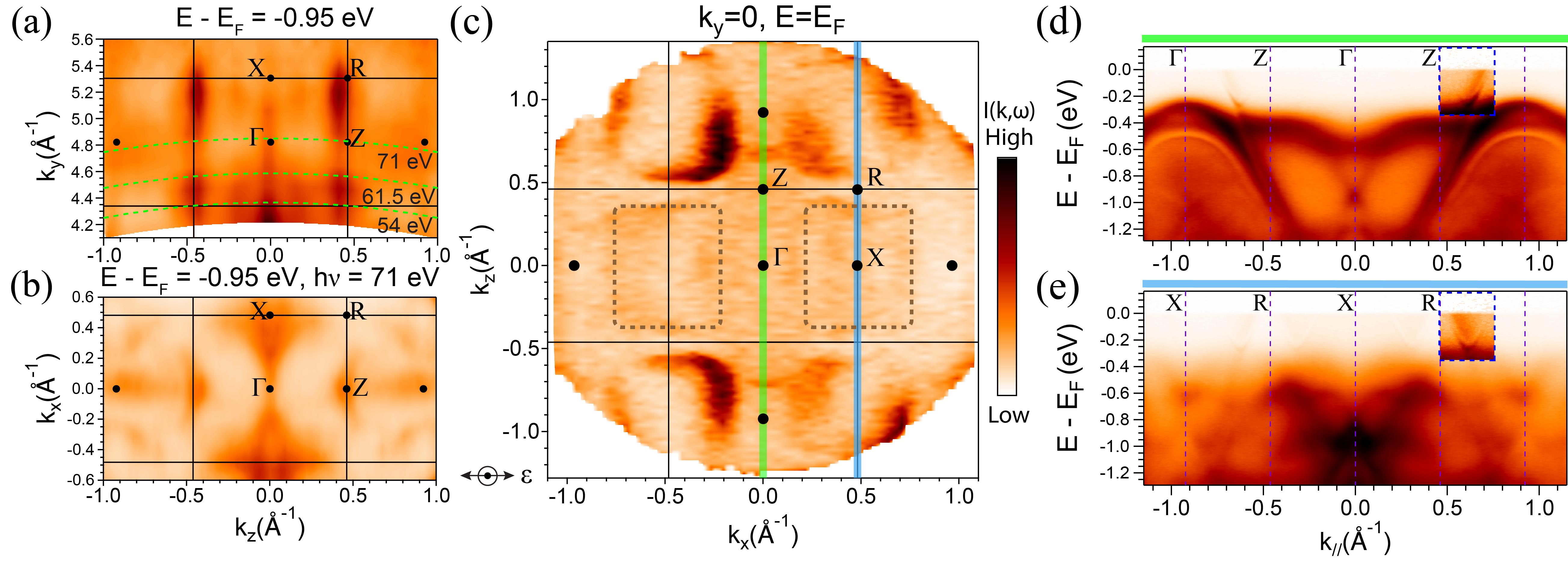
We first present the overall electronic structure measured by ARPES. To determine the inner potential, we compare the $k_{y}$-$k_{z}$ map measured in the out-of-plane direction by varying photon energy [Fig. 2(a)] and the equivalent $k_{x}$-$k_{z}$ map measured in the in-plane direction by varying angle at the same energy (E - E_F = -0.95 eV). The bulk states should be equivalent in these two maps, due to the equivalence of $k_{x}$ and $k_{y}$. From this comparison, we can identify the periodicity along $k_{y}$ from a dispersive feature along $\Gamma X$ where the narrowest (widest) part is located at $\Gamma$ ($X$), giving us an inner potential V₀ of 23 eV. From the Fermi surface (FS) measured at $k_{y}$ = 0 [Fig. 2(c)], we observe rectangular pockets centered around the $X$ points, with a periodicity compatible with the non-CO BZ, albeit strongly suppressed in the first BZ due to photoemission matrix element effects. Hence, these features must be associated with the band structure of the non-CO state. We also map out dispersions along the $\Gamma$-$Z$ and $X$-$R$ directions in Figs. 2(d) and (e). Spectral intensity is observed mostly beyond 0.2 eV of E_F, consistent with earlier identification of the CO gap in previous ARPES results Zwick1999 . However, in contrast to earlier reports where no dispersions were observed within the 0.2 eV gap, we clearly resolve the presence of dispersions up to E_F, reconciling the inconsistency with the metallic transport and optical conductivity behavior. From a more detailed view near E_F with an enhanced color scale, the near-E_F feature consists of a sharp outer electron pocket, with broadened intensity inside. In the following, we focus on these fine features near E_F.

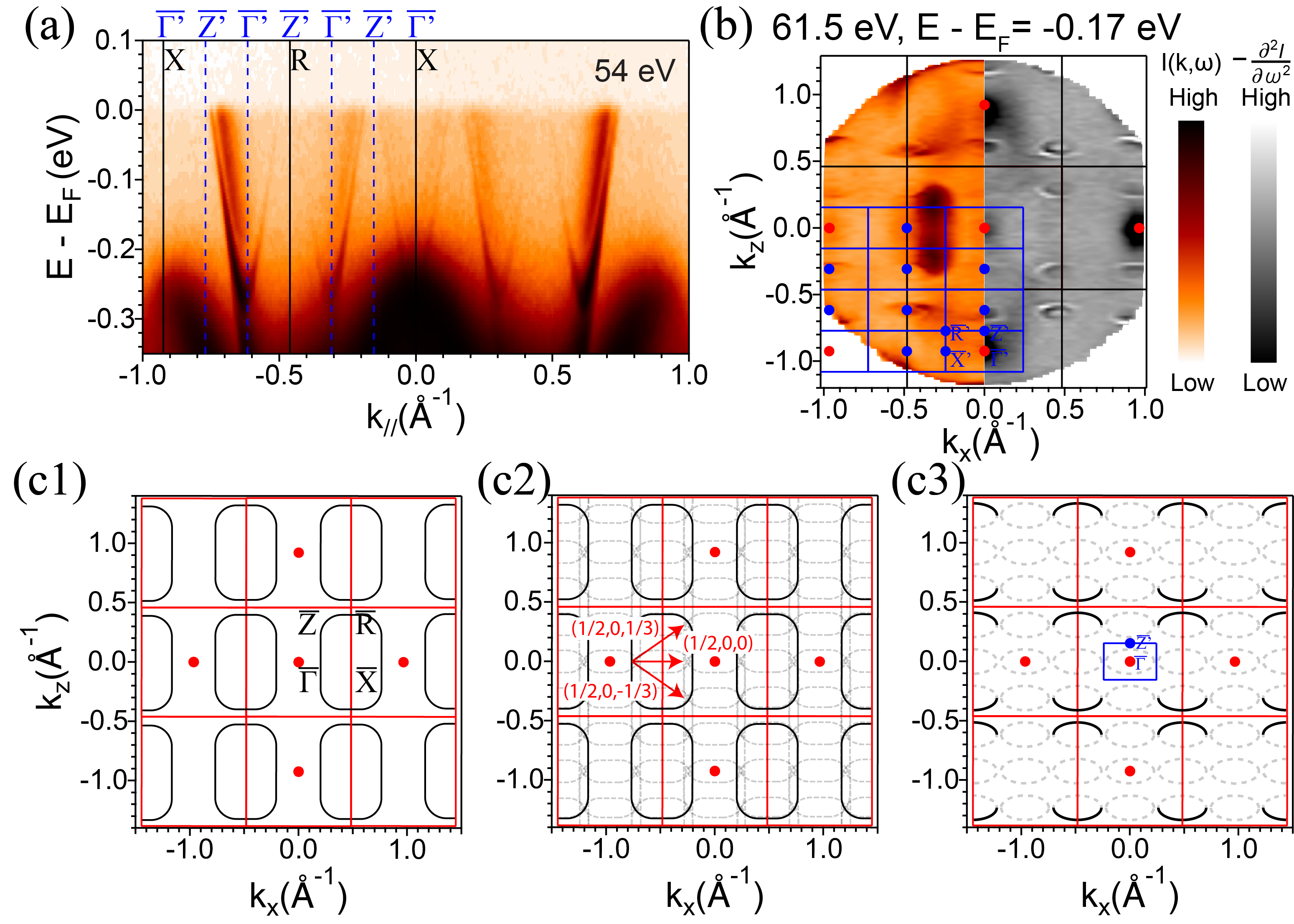
As shown in Fig. 3(a), the near-E_F electronic band structure probed by 54 eV photons shows multiple electronlike pockets which follow the folded BZ periodicity along $\overline{\Gamma^{\prime}}\overline{Z^{\prime}}$. They consist of two characteristic features: a sharp outer electron pocket and broadened inner electron pockets. To better illustrate the (2a$\times$3c) CO folding, we performed second derivative analysis (along the energy direction) on the constant energy contour at E - E_F = -0.17 eV, $h\nu$ = 61.5 eV, which nominally corresponds to the $k_{y}$ = $\pi$ plane ($X^{\prime}R^{\prime}A^{\prime}M^{\prime}$ plane) for the CO BZ. However, we note here that due to the low $k_{y}$ (out-of-plane) resolution (on the order of 0.1 $\text{\AA}^{-1}$) Sobota2021 in the vacuum ultraviolet (VUV) regime of ARPES, it is challenging to precisely distinguish the $k_{y}$ = 0 or $\pi$ planes separated by 0.15 $\text{\AA}^{-1}$ in the CO BZ. Therefore, we label the high symmetry plane as $\overline{\Gamma^{\prime}}\overline{Z^{\prime}}\overline{R^{\prime}}\overline{X^{\prime}}$ in Fig. 3(b). On the left half of Fig. 3(b), the mirrored raw intensity of the map shows both the rectangular Fermi pockets from the non-CO BZ similar to the ones marked in Fig. 2(c), and the small elliptical pockets near the boundaries of the rectangular pockets. These small elliptical pockets can be seen more clearly in the second derivative plot on the right half of the map, where they are centered at the $\overline{\Gamma^{\prime}}$ points of the CO folded BZ. Examining the ellipses in greater detail, one can see the small pockets to consist of two parts: the sharp outer components (white ellipses) and the broadened inner part (inner white intensities elongated along horizontal direction) corresponding to the features discussed in Fig. 3(a). Additionally, we do not observe any evidence of the (4a$\times$6c) surface CO suggested in a recent STM work Zhang2020 ; Sun2020 .

Next we illustrate the connection between the unfolded rectangular pockets and the folded elliptical pockets in the CO BZ [Figs. 3(c1)-(c3)]. If we start with the unfolded rectangular pockets as observed in the non-CO BZ [red BZ grids in Figs. 3(c1)-(c3)], we note that the folding of the pockets across $\bm{q}_{\rm CO}=(\pm\frac{1}{2},0,\pm\frac{1}{3})$ and its subset would indeed lead to the overlap of the rectangular pockets, as indicated by the interconnected dashed rectangles in Fig. 3(c2), the hybridization of which would produce elliptical pockets at the center of the CO-folded BZ, as shown in Fig. 3(c3). Here, we denote the ellipses from folding in dashed style, while the ones shared with original rectangular pockets in solid ellipses. Such band folding scheme provides a qualitative understanding of the relation between the observed unfolded rectangular pockets and the folded elliptical pockets, and confirms that the near-E_F electronic structure obeys the periodicity of the CO folding.

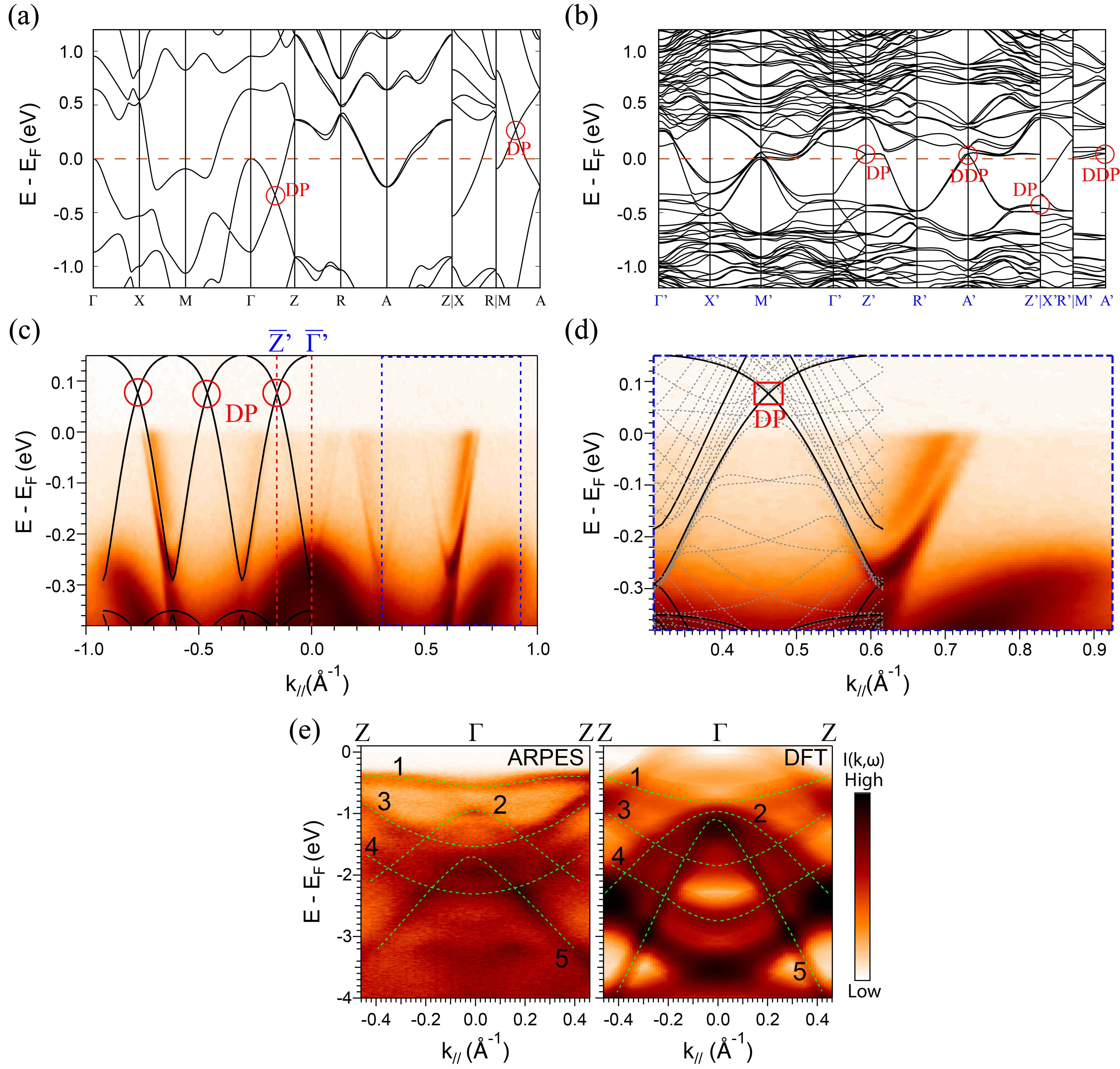
Since the CO introduces new nonsymmorphic symmetries to the crystal structure, we expect new topological features to arise due to the CO. In order to gain insights into the electronic structure from the theory perspective, we carried out DFT calculations with different exchange-correlation functionals. In Fig. 4, we present the main results from the generalized gradient approximation (GGA) by Perdew, Burke, and Ernzerhof (PBE) parameterization, while attempts on the HSE06 functional in comparison with ARPES data can be found in Fig. S5 SM . Regarding the PBE calculation, the electronic structure of both the non-CO (Fig. 4(a)) and CO [Fig. 4(b)] states shows clear metallic nature with both electron and hole pockets. The charge modulation in TaTe₄ does not lead to gap openings at the Fermi level, consistent with the experimental observations. As indicated by other calculations Zhang2020 ; Liu2021 ; Guster2022 , linear band crossings exist along $\Gamma Z$ and $MA$ in the non-CO phase, as circled in Fig. 4(a), leading to DPs. The presence of the CO modifies the band topology. In addition to DPs, the CO introduces double Dirac points (DDPs) pinned at the $A^{\prime}$ point Wieder2016 [Fig. 4(b)]. The symmetry protection mechanisms of DPs in the two phases of TaTe₄ are slightly different. In the non-CO phase, DPs appear along high-symmetry lines, while in the CO phase, DPs are pinned at the time-reversal invariant momentum (TRIM) points.

Finally, we report on the direct observation of the CO induced Dirac point (DP)-related bands near E_F, assisted by the comparison with DFT calculations. As shown in Fig. 4(c), the $\overline{\Gamma^{\prime}}$-$\overline{Z^{\prime}}$ dispersions of the near-E_F electron bands agree reasonably well with the bulk DFT calculations for the CO state after a 35 meV downshift of E_F. In particular, the periodicity of this band is consistent with the CO phase. Interestingly, DFT calculation shows these bands to cross in the form of DPs at about 75 meV above the Fermi level. Given that these are the dominant dispersions we observe near E_F, these DPs may potentially be the source of the nontrivial Berry phase, large magnetoresistance and resistivity plateau observed in recent transport measurements Luo2017 ; Gao2017 . To further analyze the details of the DP-related bands, we zoom in to the blue boxed region of Fig. 3(c) and overlay the $k_{y}$-broadened bulk DFT calculations between $\Gamma^{\prime}Z^{\prime}$ and $X^{\prime}R^{\prime}$ (see Fig. S4 SM for detailed contributions from different $k_{y}$ planes) on top of the ARPES spectra in Fig. 4(d), where the two separated features of the broadened inner and sharp outer pockets can be well explained by an out-of-plane momentum collapse of the photoemission data, reflecting the $k_{y}$ distribution of the DFT calculated bands. Considering the aforementioned out-of-plane momentum resolution of VUV ARPES, the explanation is further justified. However, the predicted DDPs at deeper binding energies are not directly observed (see Fig. S6 SM ). The underlying reason might be a combination of the following three factors. First, VUV ARPES may not have sufficient out-of-plane resolution to selectively probe the DDPs at $A^{\prime}$. Second, the CO folded bands, band hybridization, and band backfolding onto the non-CO BZ could cause further broadening effect on ARPES spectra, which hinders the task of resolving a high-fold band degeneracy up to eight. Third, we note that away from the near-E_F features, neither the non-CO nor the CO state DFT calculations show good agreement with ARPES spectra, as detailed in Fig. S6. Such mismatch impedes a directly experimental identification of the DDPs at deeper binding energies. The reason for such inconsistency is subject to future studies, while the recent STM work Sun2020 has suggested complicated surface reconstruction and possible enhanced surface e-e interactions, which are not captured by our current DFT calculations. Nonetheless, we find that by backfolding the CO state calculations to non-CO BZ, an overall better agreement between DFT and ARPES can be obtained, as exemplified in Fig. 4(e) for $\Gamma Z$. Specifically, one can observe a qualitative match for bands one to five as denoted, but unlike a good theoretical description for the near-E_F electron pockets, the positions and slopes of these bands at deeper binding energies do not coincide precisely.

In summary, we have presented ARPES measurements of the electronic structure on the CO compound TaTe₄. We clearly reveal the presence of low energy dispersions that reconcile the inconsistency between previous ARPES report and transport results. In particular, we directly visualize the CO-folded electron pockets near E_F, which are interpreted as the consequence of CO folding via the known CO wavevector $\bm{q}_{\rm CO}$ = ($\frac{1}{2}$, 0, $\frac{1}{3}$) from the original bands. Moreover, we present DFT calculations to understand the CO band structure and the role of topology in the nonsymmorphic crystal, where the DPs and DDPs are induced due to the emergent crystalline symmetries of the CO. The PBE calculations in the CO state with a $k_{y}$ stacking show good agreements for the near-E_F $\overline{\Gamma^{\prime}}$-$\overline{Z^{\prime}}$ electron pockets, indicating the direct observation of the lower branch of the symmetry-enforced DPs. Despite that the predicted DDPs remain elusive in terms of experimental visualization, TaTe₄ presents an interesting material platform where CO induces new crystalline symmetries that result in Dirac quasiparticles near the Fermi level.

This research used resources of the Advanced Light Source and the Stanford Synchrotron Radiation Lightsource, both U.S. DOE Office of Science User Facilities under Contract No. DE-AC02-05CH11231 and No. AC02-76SF00515, respectively. ARPES work at Rice University is supported by the Department of Defense, Air Force Office of Scientific Research under Grant No. FA9550-21-1-0343; and the Robert A. Welch Foundation grant no. C-2175. J.S.O. is supported by NSF Grant No. DMR-1921847 and No. DMR-1921798. Work at the University of California, Berkeley, is funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05-CH11231 (Quantum Materials program KC2202). Synthesis work at UT Dallas is supported by NSF under Grant No. DMR-1921581, AFOSR under Grant No. FA9550-19-1-0037 and ONR under Grant No. N00014-23-1-2020. X-ray structure determination and analysis is supported by Welch Foundation Welch AA-2056-20220101. G.L. acknowledges the National Key R&D Program of China (2022YFA1402703), National Natural Science Foundation of China (11874263), Shanghai 2021-Fundamental Research Aera (21JC1404700), Shanghai Technology Innovation Action Plan (20DZ1100605), and Sino-German Mobility program (M-0006). M.H. and D.L. acknowledge the support of the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Material Sciences and Engineering, under Contract No. DE-AC02-76SF00515.