Charmed-Bottom mesons from Lattice QCD
Abstract:
We present ground state spectra of mesons containing a charm and a bottom quark. For the charm quark we use overlap valence quarks while a non-relativistic formulation is utilized for the bottom quark on a background of 2+1+1 flavors HISQ gauge configurations generated by the MILC collaboration. The hyperfine splitting between states of mesons is found to be MeV. We also study the baryons containing only charm and bottom quarks and predict their ground state masses. Results are obtained at three lattice spacings.
1 Introduction
Lattice QCD methods provide a unique opportunity to study hadronic physics, particularly the energy spectra of hadrons. Substantial progress has been made to extract the ground and the excited states of charmed hadrons, particularly for charmonia. However, the study of bottom hadrons with relativistic actions and controlled discretizations is still prohibitively computer intensive though recent progress in relativistic heavy quark actions is promising. Most studies involving bottom quarks are based on the non-relativistic QCD (NRQCD) formulation, heavy quark effective theory (HQET) and the static quark formulation.
Study of heavy mesons plays a very important role in understanding the nature of strong interactions. Though heavy quarkonia and heavy light mesons have been investigated in great detail, not much is known about the heavy mesons containing only charm and bottom quarks. It is expected that the physics of charmed-bottom mesons involves multiple scales : (), (), and . It is interesting to investigate whether charmed-bottom mesons behave like heavy-light mesons or like quarkonia states. The information about hyperfine splittings and other spin splittings, in addition to the results on decay constants, can shed light on the structure of these states.
Experimentally only one state, , is established with mass at 6275(1) MeV [1]. Recently ATLAS observed another meson with mass MeV, which was interpreted as the excited state, [2]. However, this excitation has not been confirmed by other experiments yet. On the theoretical side, potential model predictions for these states vary widely. For example, the prediction for hyperfine splitting varies in the range 40-90 MeV [3, 4, 5, 6, 7]. This is due to various ways of tuning the heavy quark potentials with spin dependent terms and less clarity of the wavefunction at the origin [3, 4, 5, 6, 7]. On the other hand, using lattice QCD methods, though heavy-light or heavy-heavy mesons were studied extensively not many calculations were carried out for charmed-bottom mesons and baryons. Only two collaborations, HPQCD [8, 9] and Wurtz et al. [10], have studied charmed-bottom mesons recently. Similarly, there are very few recent results for charmed-bottom baryons [11, 12].
In this report, we present our preliminary results on charmed-bottom mesons and baryons. For the bottom quark we use an NRQCD action with non-perturbatively tuned coefficients with terms up to , whereas the overlap action is utilized for the valence charm quark. Hyperfine splitting between states as well as masses for other mesons are predicted. Moreover, ground state energy spectra of baryons with charm and bottom quarks are also predicted.
2 Simulation Details
We use three sets of dynamical 2+1+1 flavours HISQ gauge field ensambles generated by the MILC collaboration : , and lattices at gauge couplings and , respectively. The details of these gauge configurations are summarized in Ref. [13]. We use the unphysical pseudoscalar mass equal to 685 MeV to tune the strange quark mass while the baryon mass is used for calculating the lattice spacings as mentioned in Refs. [14, 15]. The measured lattice spacings, 0.1192(14), 0.0877(10) and 0.0582(5) fm, are consistent with 0.1207(11) 0.0888(8) and 0.0582(5) fm, respectively, measured by MILC collaboration with this set of ensembles using the parameter.
We have adopted an NRQCD formulation for the bottom quark. The non-relativistic action that we use is discussed in Ref. [16]. We have considered all terms up to and the leading term of the order of , where is the bare mass for bottom quark in lattice units. The NRQCD Hamiltonian is given by,
| (1) |
where is the kinetic term and is defined by,
| (2) |
whereas, contains interaction terms and is given by,
| (3) | |||||
The quantities with a tilde assume an corrected form of discretization. is the symmetric lattice derivative while and represent the lattice discretized versions of and , respectively. More details of this Hamiltonian can be found in Ref. [17]. This Hamiltonian is improved by including spin-independent terms through . For the coarser two ensembles, we use the values of the improvement coefficients, to , as estimated non-perturbatively by the HPQCD collaboration [18]. For the finer lattice, we use tree level coefficients. The NRQCD quark propagators are obtained by usual time evolution
| (4) |
A wall source is utilized as smearing function for calculating these quark propagators.
The bottom quark mass is tuned by equating the lattice spin-average mass of bottomonium to its experimental value. The lattice spin-average mass is obtained from the kinetic mass relation :
| (5) |
where the kinetic mass is calculated from the relativistic energy-momentum dispersion relation :
| (6) |
Here s are extracted from the energy difference between the mesons with momenta and zero. A momentum induced wall-source is utilized to obtain energy values from the correlators with finite momenta. This method was found to be very efficient compared to point or smeared sources [14] and helps to obtain kinetic masses precisely with significantly little statistics.
For valence charm quark propagators we use the overlap action as described in Refs. [14, 15]. The overlap action does not have errors, and it is chirally symmetric at finite lattice spacings. The charm mass is tuned by equating the spin-averaged kinetic mass of the charmonia states to its physical value. The tuned bare charm quark masses () are found to be 0.528, 0.425 and 0.29 on coarser to finer lattices respectively. Details of the charm tuning was described in Ref. [15].
3 Results
3.1 Charmed-bottom mesons
Lattice methods suffer from discretization errors, particularly for hadrons with heavy quarks. A good agreement of hyperfine splitting of the mesons on the lattice with the respective experimental value ensures good control over the discretization errors and hence a reliable estimation of the heavy meson spectra using lattice methods. Figure 1 shows our results for the hyperfine splittings in quarkonium for three different ensembles we use. Figure 1(a) is for charmonium showing our results with filled circles and experimental value with star symbol. An extrapolation with a form , including systematics, gives a fit value 115(3) MeV for this splitting which is consistent with the experimental value 113.9(6) MeV. We have excluded the disconnected diagrams which is shown to reduce the splittings by a few MeV [19]. Figure 1(b) is for bottomonium. Black circles are results from tree-level coefficients and blue are with improved coefficients in the NRQCD action (this color coding will be followed throughout). A naive fit combining the results from improved coefficients for coarser lattices and the result from unimproved coefficients at the finer lattice gives bottomonium hyperfine splitting as 64(3) MeV, whereas the experimental value is MeV. These results show that the discretization errors in our calculation for quarkonia are well within control.
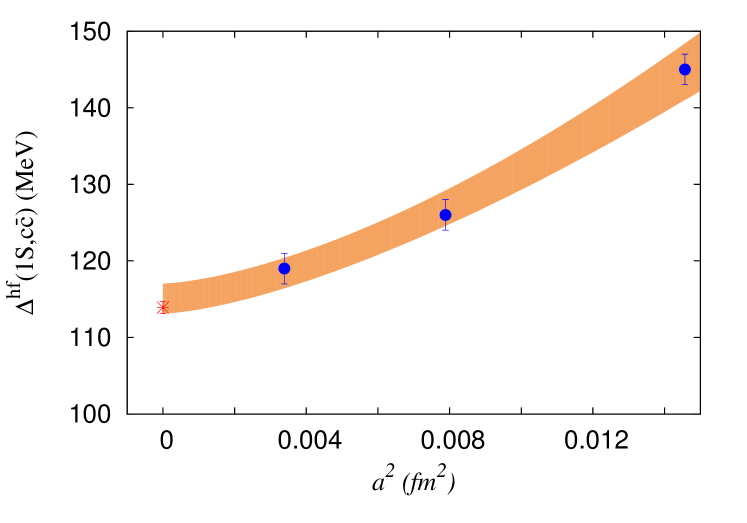
(a)
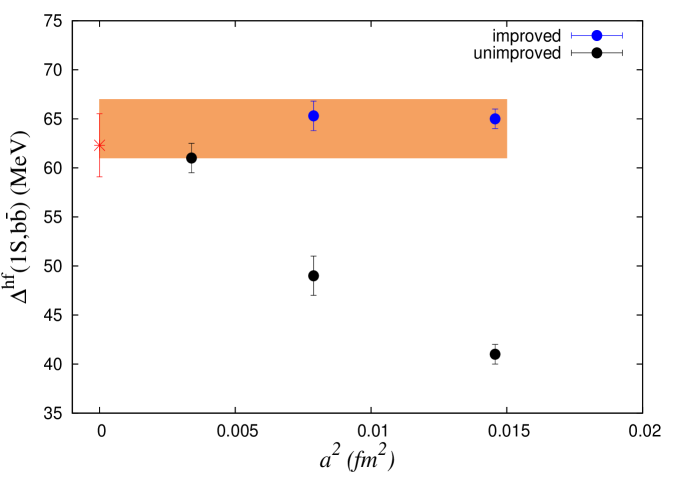
(b)
In figure 2(a), we show our main results on the hyperfine splittings of mesons : . Results from other lattice calculations are shown by red squares. A combined fit with results from improved and tree-level coefficients yields an estimate for this splitting as MeV (shown by blue star) which is consistent with predictions from other lattice calculations [9, 10]. With an NRQCD action the hyperfine splitting of quarkonia is proportional to the term, which is in our case, and it also depends on higher order () operators. These higher order corrections would also be present in the mesons, which could be reduced in the ratio of such hyperfine splittings, e.g. between and mesons [9]. Similar to HPQCD [9] we have constructed the following ratio,
| (7) |
In figure 2(b) we show this ratio at three lattice spacings.
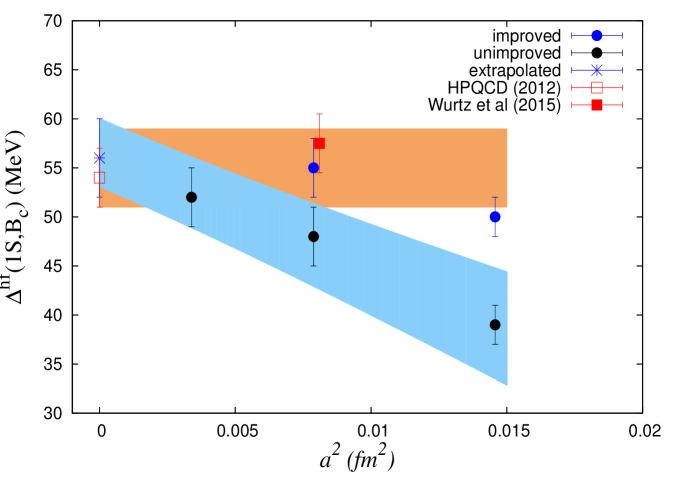
(a)
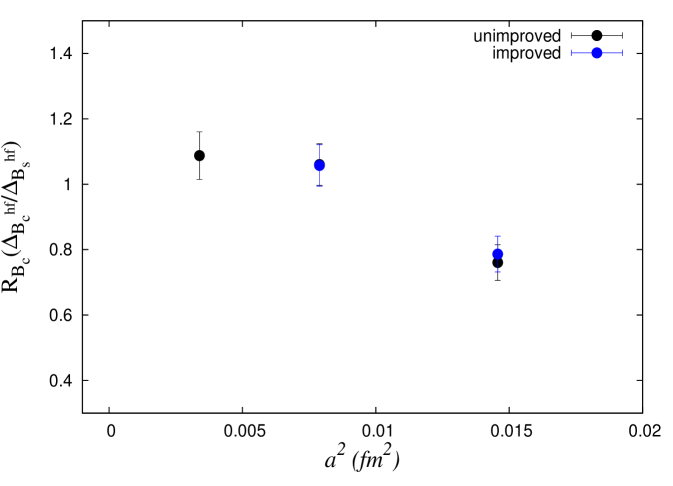
(b)
We also calculate the ground state masses of the axial-vector and scalar mesons. In figure 3(a) we plot the splitting between scalar and pseudoscalar states () while in figure 3(b) the splitting between axial vector and vector states () is shown. HPQCD results are shown with open square. After extrapolation with a form to the data from unimproved coefficients we obtain MeV and MeV (shown by blue star). Taking the experimental value of , the ground state masses for the scalar and axial-vector mesons are = 6690(17) MeV and = 6726(16) MeV respectively.
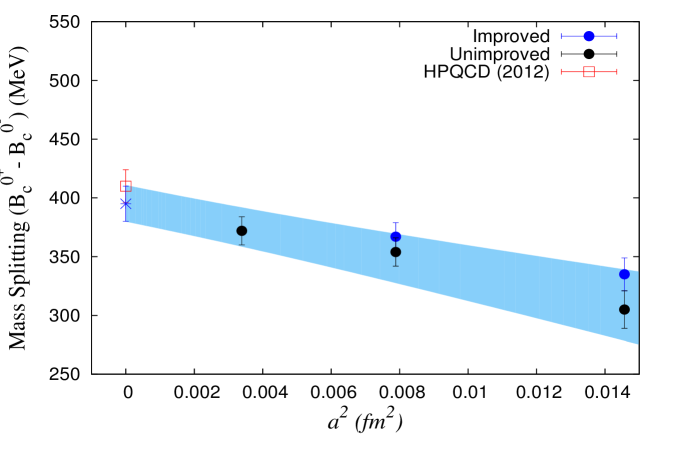
(a)
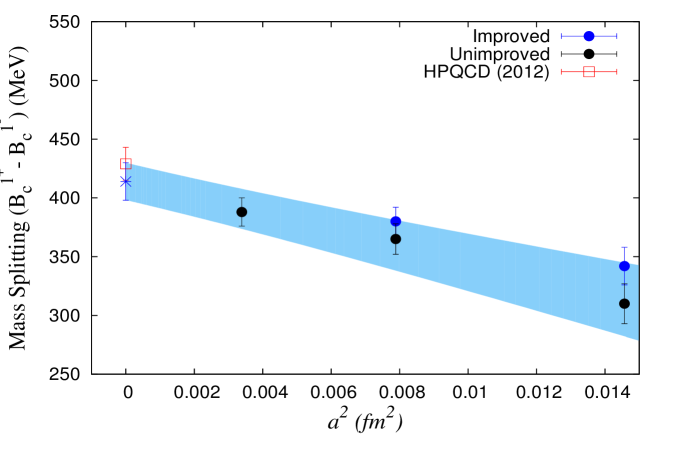
(b)
3.2 Charmed-bottom baryons
Baryons with three heavy quarks are interesting systems as they can provide important information about the potential between three heavy quarks and they can also be a study ground for effective field theories as well as perturbative QCD. Here we present the ground state masses of baryons containing only charm and bottom quarks, namely and . Very similar to mesons, the hyperfine splittings between these baryons can provide important information about the spin dependent interactions in heavy quark systems. In figure 4 we plot these splittings along with other lattice results [11, 12] and quark model predictions [20].
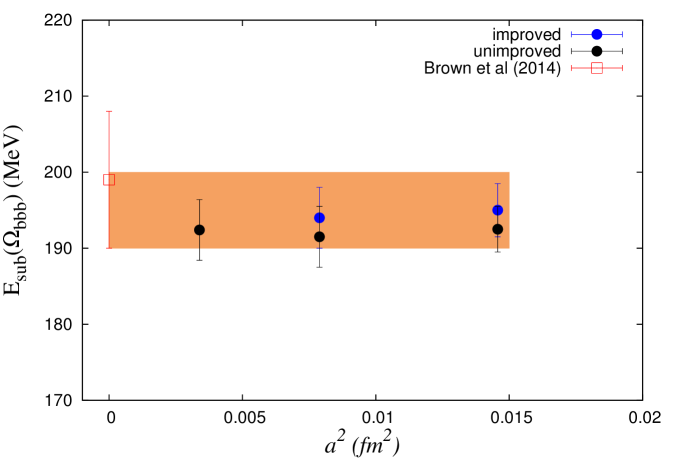
Finally, we present results for the triply bottom baryon , which may be viewed as baryonic analogues of bottomonium. Being heavier with three bottom quarks it provides a good arena to test the discretization error in a lattice calculation with bottom quarks. For the relative removal of discretization error due to the bottom quark we calculate the subtracted energy defined as , where is the lattice estimate of the spin average bottomonium mass. Figure 5 shows our results for this subtracted energy at different lattice spacings with improved and tree-level coefficients along with the result from another lattice calculation [12]. Flatness of the plot shows that discretization errors due to bottom quarks after subtraction are well within control. Combining data from improved coefficients, the prediction for the ground state spin-3/2 triply bottom baryon is following : MeV, and taking the PDG spin average mass for bottomonium as 9445(3) MeV, MeV.
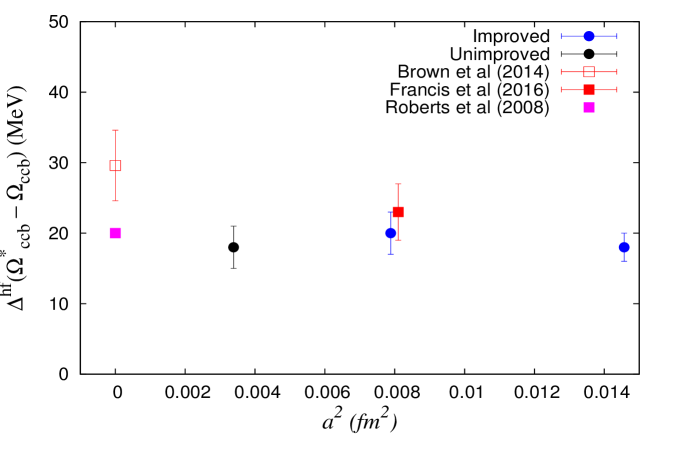
(a)
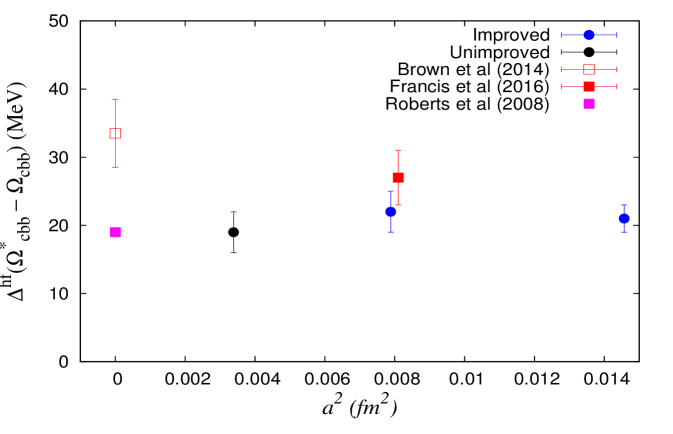
(b)
4 Conclusions
We report the ground state energy spectra of charmed-bottom mesons. An NRQCD Hamiltonian with non-perturbatively improved coefficients is used for bottom quarks while a relativistic overlap action is adopted for charm quarks on a background of 2+1+1 flavours HISQ gauge configurations generated by the MILC collaboration. Results are obtained at three lattice spacings with physical volume of about 3 fm. We tune the bottom and the charm quark masses by equating the lattice spin-averaged kinetic masses of states in bottomonia and charmonia with their experimental values. The hyperfine splittings between these states are found to be 64(3) and MeV for bottomonia and charmonia, respectively, which are quite consistent with their experimental values. Our result on hyperfine splitting between states of mesons is MeV. This result is consistent with HPQCD [9] as well as Wurtz et al. [10] who found this splitting to be 54(3) and 57.5(3) MeV, respectively. It is interesting to note that all lattice results are inconsistent with many quark model results which vary in the range between 40-90 MeV [3, 4, 5, 6, 7]. Due to this rather small splitting, detection of from its decay may turn out to be challenging in experiments. Taking the PDG value of state as 6275(1) MeV, our prediction for the ground state mass of is MeV. We also calculate the ground state energy of other mesons, namely, and . Our preliminary results on the splittings between and states are found to be 411(16) MeV and 395(15) MeV, respectively. The ground state masses of baryons containing only charm and bottom quarks are also extracted. The hyperfine splittings between spin-3/2 and spin-1/2 and states are found to be 20(5) MeV and 21(5) MeV, respectively. Our prediction for the ground state spin-3/2 triply bottom baryon is MeV.
5 Acknowledgement
Computations were carried out on the Blue Gene/P of the Indian Lattice Gauge Theory Initiative, and on the Gaggle cluster of the Department of Theoretical Physics, TIFR. We thank A. Salve and K. Ghadiali for technical support. M. P. acknowledges support from the Austrian Science Fund FWF:I1313-N27 and the Deutsche and Forschungsgemeinschaft Grant No. SFB/TRR 55. R.L. is supported in part by NSERC of Canada. We are grateful to the MILC collaboration and in particular to S. Gottlieb for providing us with the HISQ lattices.
References
- [1] C. Patrignani et al. [Particle Data Group], Chin. Phys. C, 40, 100001 (2016).
- [2] G. Aad et al. [ATLAS Collaboration], Phys. Rev. Lett. 113, no. 21, 212004 (2014).
- [3] W. Kwong and J. Rosner, Phys. Rev. D 44, 212 (1991).
- [4] E. Eichten and C. Quigg, Phys. Rev. D 49, 5845 (1994).
- [5] V. V. Kiselev et al., Phys. Rev. D 51, 3613 (1995).
- [6] D. Ebert et al., Phys. Rev. D 67, 014027 (2003).
- [7] S. Godfrey, Phys. Rev. D 70, 054017 (2004).
- [8] E. B. Gregory et al. [HPQCD], Phys. Rev. Lett. 104, 022001 (2010).
- [9] R. J. Dowdall et al. [HPQCD], Phys. Rev. D 86, 094510 (2012).
- [10] M. Wurtz, R. Lewis and R. M. Woloshyn, Phys. Rev. D 92, no. 5, 054504 (2015).
- [11] A. Francis et al., PoS LATTICE 2016, 133 (2016).
- [12] Z. S. Brown et al., Phys. Rev. D 90, no. 9, 094507 (2014).
- [13] A. Bazavov et al. [MILC Collaboration], Phys. Rev. D 87, no. 5, 054505 (2013).
- [14] S. Basak et al., PoS LATTICE 2012, 141 (2012).
- [15] S. Basak et al., PoS LATTICE 2013, 243 (2014).
- [16] G. P. Lepage et al., Phys. Rev. D 46, 4052 (1992).
- [17] R. Lewis and R. M. Woloshyn, Phys. Rev. D 79, 014502 (2009).
- [18] R. J. Dowdall et al. [HPQCD Collaboration], Phys. Rev. D 85, 054509 (2012).
- [19] L. Levkova and C. DeTar, Phys. Rev. D 83, 074504 (2011).
- [20] W. Roberts and M. Pervin, Int. J. Mod. Phys. A 23, 2817 (2008).