Chiral Altermagnon in MnTe

Chiral magnons - collective modes which exhibit a definite handedness - are an emerging frontier, offering exciting opportunities to enable spintronic devices and spin-based information processing Šmejkal et al. (2018); Tokura et al. (2019); Dieterle et al. (2019); Yu et al. (2019); Wang et al. (2020); Yang (2020); Yang et al. (2021). Traditionally, such excitations have been associated with magnets exhibiting either net magnetization or complex spin textures Fert et al. (2017); Zhou et al. (2024). However, recent theoretical advances suggest that chiral magnons Nambu et al. (2020); Cheong and Xu (2022) may also arise in so called altermagnets Šmejkal et al. (2020, 2022a, 2022b) which have a net-zero magnetization.

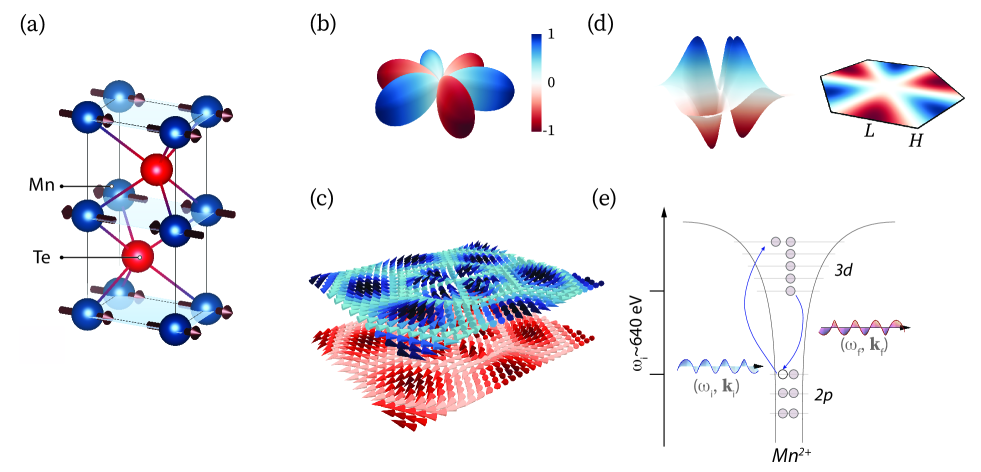
A proposed altermagnet, manganese telluride (MnTe) Juza et al. (1956) represents an ideal platform to explore this notion. While hosting robust $A-$type anti-ferromagnetic order [Figure 1(a)] Kunitomi, Nobuhiko et al. (1964); Efrem D’Sa et al. (2005); Kriegner et al. (2017), it displays electronic and magnetic properties Krempaský et al. (2024); Lee et al. (2024); Osumi et al. (2024); Hajlaoui et al. (2024); Liu et al. (2024); Amin et al. (2024) unexpected for an anti-ferromagnet Nagaosa et al. (2010); Šmejkal et al. (2022). More fundamentally, its crystalline structure breaks inversion and translation symmetry which are key ingredients for altermagnetism Šmejkal et al. (2022a, b). As a consequence, anisotropies imprint on the spin structure and shape the symmetry of the altermagnetic order parameter in MnTe, characterized by a predicted $g-$wave-like spin polarization [Figure 1(b)] Šmejkal et al. (2022a). This $g-$wave symmetry captures the effect of broken inversion and translational symmetries, thereby enforcing a momentum-dependent splitting of the electronic band structure, recently confirmed in photo-emission experiments Krempaský et al. (2024); Lee et al. (2024); Osumi et al. (2024); Hajlaoui et al. (2024). Similarly, collective magnetic excitations (i.e. magnons) which would nominally remain degenerate in anti-ferromagnets are expected to split in certain momentum-space regions Šmejkal et al. (2023). Initial observations suggest that such a splitting indeed occurs Liu et al. (2024). Taken together, these results provide strong evidence that MnTe realizes altermagnetism and presents a compelling arena to reveal the chiral magnetic excitations foreseen to emerge in altermagnets Šmejkal et al. (2022b).

In real space, these magnons can be visualized as spin rotations which precess out of phase with neighbors in adjacent sublattice planes, preserving net-zero magnetization [Figure 1(c), see Movie S1 for details]. As the degeneracy of the magnetic branches is lifted, the sublattice excitations are decoupled and the spin polarization expresses a spatial dependence. In a momentum-space perspective, as schematically shown in Figure 1(d), the spin polarization varies across the Brillouin zone (BZ), consistent with $g-$wave symmetry. These symmetry constraints enforce nodal lines and promote chiral magnetic excitations in distinct sectors of the BZ.

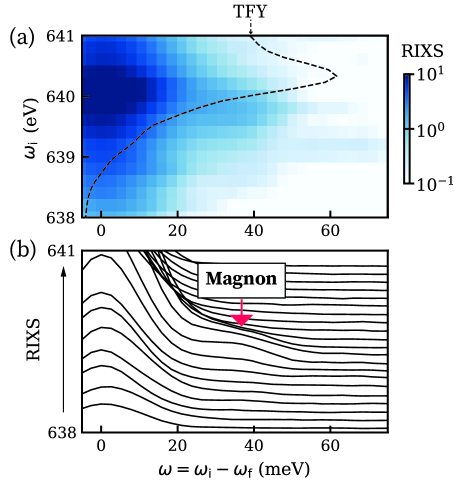
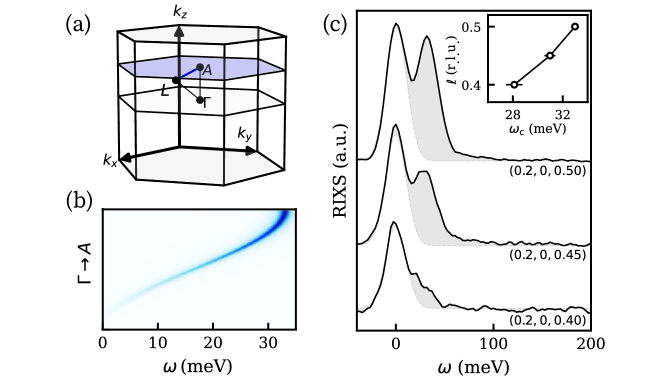
To capture chiral excitations experimentally, circular dichroism resonant inelastic X-ray scattering (CD-RIXS) has developed into a promising tool Schüler et al. (2023); Ueda et al. (2023). In this work, circularly polarized photons were used to excite electrons from the Mn $2p$ core levels to its half-filled $3d$ orbitals [Figure 1(e)]. Within the lifetime of this intermediate state, energy transferred from the incident photons can create magnetic excitations which manifest as red-shifted, i.e. inelastic, features upon spectrally resolving the scattered photon energy Ament et al. (2011). To locate a clean resonance condition of the magnetic excitation, we tuned the incident photon energy $\omega_{\mathrm{i}}$ across the Mn $L_{3}$ absorption edge. Indeed, such an incident photon energy dependence revealed a feature in the inelastic spectrum appearing just below the fluorescence main peak energy [Figure 2(a)]. This excitation is located at an energy transfer of $\omega\sim 35\,\mathrm{meV}$ [Figure 2(b)], an energy scale that aligns with the previously reported magnon band in MnTe Szuszkiewicz et al. (2005); Liu et al. (2024).

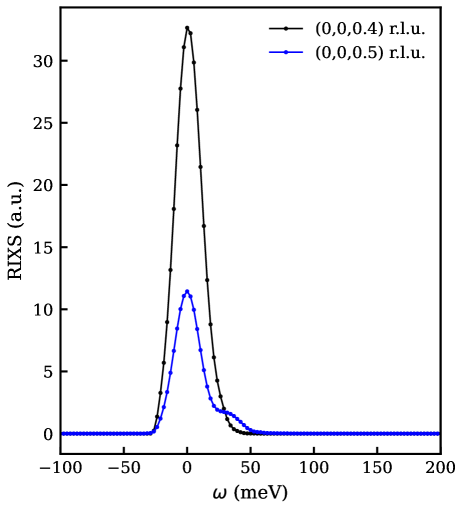
To further corroborate the magnetic origin, we measured its momentum dependence along a trajectory in the Brillouin zone (BZ) [Figure 3(a)]. In hexagonal anti-ferromagnets with anti-parallel spins aligned along the $c-$axis, the magnon dispersion typically exhibits its maximum bandwidth at (0,0,0.5) reciprocal lattice units (r.l.u.) at the $A-$point [Figure 3(b)], as is the case for MnTe Szuszkiewicz et al. (2005); Liu et al. (2024). Conversely, the magnon mode disperses to zero as it approaches the $\Gamma$ point [Figure 3(b)], reflecting the broken spin-rotational symmetry Goldstone et al. (1962). This behavior also holds for MnTe where the magnon shifts away from the elastic line as the out-of-plane momentum component is tuned towards the $A-L$ plane [see Figure 3(c) and figure S1].

Having confirmed its magnetic origin, we focused on probing its chirality. The spin polarization in momentum space representation [Figure 1 (d)] indicates a significant anisotropy in chiral magnon intensity. In this picture, a lifted degeneracy manifests as a dichroic signal in a region of the BZ exhibiting a non-zero spin polarization. Conversely, along nodal directions, the dichroism is expected to vanish, as the spin polarization is suppressed.

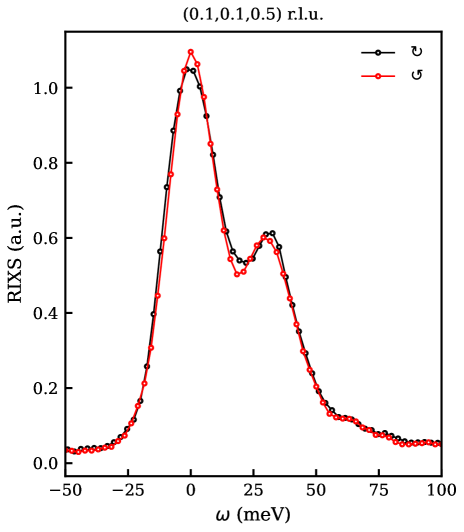
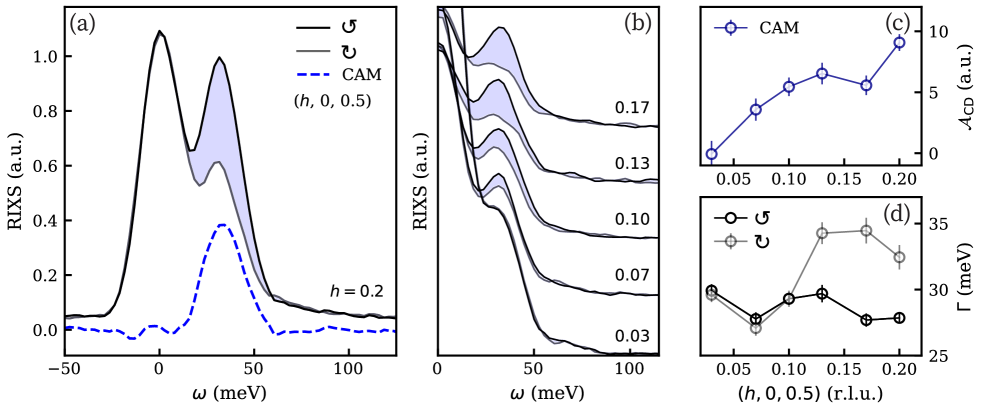
Towards the $A-L$ direction at (0.2, 0, 0.5) r.l.u., a pronounced difference of the magnon intensity is seen for the two polarization channels, as depicted in Figure 4(a). This difference in intensity reflects the orbital angular momentum transfer associated with the excitation, providing a direct measure of the magnon chirality. In other words, as altermagnets exhibit a momentum-dependent spin-polarization Šmejkal et al. (2022b), the sub-lattice decoupling manifests as selective sensitivity to one circular polarization, a hallmark of their fundamentally broken inversion and translational symmetry.

Subtracting these two spectra yields a peak-like signature that encapsulates the chiral portion of the magnetic excitations. We term this excitation a chiral altermagnon (CAM). Modulating the momentum transfer from (0.2, 0, 0.5) r.l.u. towards the $A-$point decreases the CAM intensity systematically [Figure 4(b),(c)], consistent with the picture drawn in Figure 1(d). This intensity dispersion, along with a vanishingly small circular dichroism along the nodal direction [see figure S2] is consistent with an altermagnetic spin polarization.

We note that along the $A-L$ direction, an energy splitting was not observed in a prior neutron scattering study Liu et al. (2024). However, in this work, the CAM width obtained from CD-RIXS differs between the two polarization channels [Figure 4(d)], indicating distinct lower bounds for the magnon lifetimes. The subdominant branch exhibits a broader peak (shorter lifetime), whereas the width of the dominant branch remains essentially constant and is near the instrumental resolution limit. These observations could imply that any lifting of degeneracy is governed more by damping than by a resolvable energy gap. Consequently, a conventional inelastic neutron scattering probe might not detect a splitting precisely where CD-RIXS reveals strong dichroism. However, future experiments at higher resolution - both RIXS and polarized inelastic neutron scattering - will be essential to resolve this apparent discrepancy. With these, it may be possible to clarify whether a small energy splitting or purely lifetime-based effects (or both) underlie the observed CAM response.

We have demonstrated that chiral altermagnons arise in MnTe, an anti-ferromagnet that displays characteristics canonically associated with finite magnetization. The pronounced dichroic signal whose momentum-dependence aligns with the altermagnetic $g-$wave symmetry underscores how broken spatial symmetries may foster chirality in otherwise collinear spin systems. Moreover, our results complete a crucial triad in the rapidly developing field of altermagnetism: the observations of spin-split electronic band structures Krempaský et al. (2024); Lee et al. (2024); Osumi et al. (2024); Hajlaoui et al. (2024), the splitting of magnon bands Liu et al. (2024), and now, the direct experimental observation of chirality in magnetic excitations, which positions MnTe as the archetypal altermagnet.

Future investigations will need to address the role of chiral magnons in shaping both transport and spectroscopic properties of altermagnetic materials. Advancing this field further will require a robust theoretical framework that captures the momentum-resolved nature of these excitations and their interaction with electronic and magnetic degrees of freedom, including damping-driven effects.

Lastly, as altermagnets lack stray magnetic fields, they are ideal for compact and interference-free device integration. By demonstrating that altermagnets host chiral excitations, our work paves the way for novel spin-based applications in which chiral altermagnons take center stage.