Chirality memory stored in magnetic domain walls in the ferromagnetic state of MnP

Chirality is a lack of mirror symmetry in matter. If a molecule has chirality, its mirror image is different from the original structure. In other words, the molecule has two distinguishable states (enantiomer) with different chiralities. In the human body, some molecules, such as amino acids, are homo-chiral, meaning that they show only one certain chiral state. In biology, it is important to elucidate how chiral information is transferred and memorized.[1, 2].

Chirality also appears in magnetic structures. One example is a helical magnetic structure, in which the ordered direction of the magnetic moment spatially rotates in a plane perpendicular to the propagation vector (Fig. 1 (a)). The sense of rotation is reversed by any mirror operation and therefore determines the chiral state. Similar magnetic chirality shows up in a Bloch-type domain wall (DW) in ferromagnets (Fig. 1 (a)). The magnetic moment rotates on the domain wall, and the sense of rotation is responsible for the chirality, similarly to helimagnets. In this paper, we report the transfer of chiral information from a helical magnetic structure to a ferromagnetic DW during a helimagnetic to ferromagnetic phase transition in an itinerant helimagnet MnP.

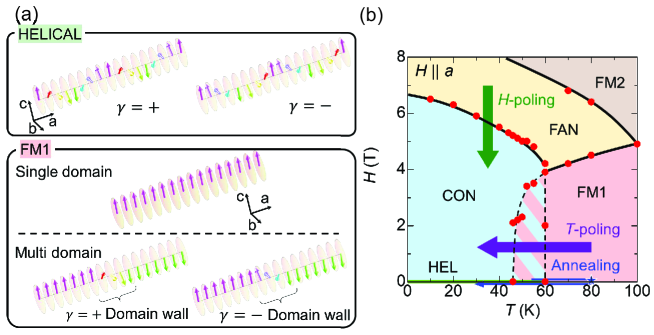
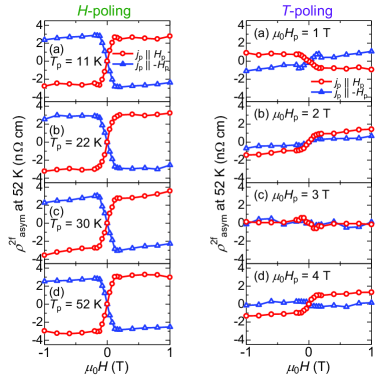
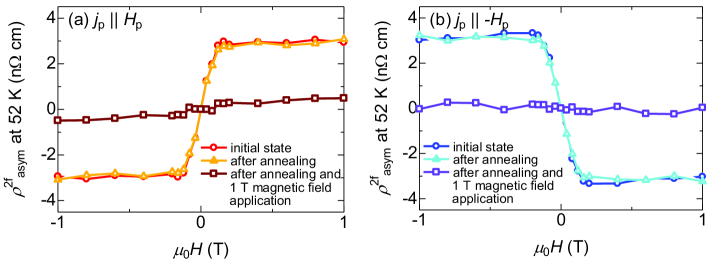
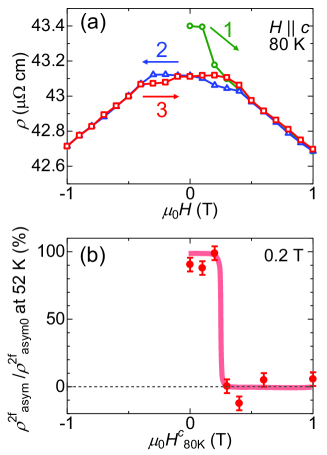
Fig. 1(b) shows the phase diagram of MnP[4, 5, 6, 7, 8, 9, 10, 11, 12], which was constructed based on magnetoresistance measurements of a microscale sample ($10\times 20\times 1$ $\rm\mu m^{3}$) fabricated for the present study by using the focused ion beam technique [3]. It is quite similar to that of a bulk sample reported in a previous study[11]. The ferromagnetically ordered phase (FM1) was stable even at zero magnetic field above 60 K, and the magnetic moments aligned along the $c$-axis. In this magnetic state, Bloch-type magnetic domain walls were observed by Lorentz transmission electron microscopy[12]. On the other hand, in the helimagnetic state (HEL), which showed up below 44 K, the helical plane was normal to the propagation vector along the $a$-axis[7]. The intermediate hatched region indicates the metastable region typical of the first-order phase transition. When the magnetic field was applied parallel to the $a$-axis in the helimagnetic state, the magnetic moments were tilted, forming a conical magnetic state (CON). As the magnetic field increased further before the magnetic moments became completely aligned along the $a$-axis (FM2), there emerged a fan structure (FAN), in which the magnetic moments were within the $ac$ plane, and the angle between the magnetic moment and the propagation vector spatially oscillated along the propagation vector. In our previous work[13], we controlled the chirality of the helimagnetic structure by the simultaneous application of a magnetic field and a dc electric current and probed the controlled chirality by the nonreciprocal electronic transport, which is the field asymmetric component of 2nd harmonic resistivity[14, 15, 16, 17]. The controlled chirality was shown to be dependent on whether the applied magnetic field and the dc electric current are parallel or antiparallel to each other. In this paper, we show how the controlled chirality in the helimagnetic state was preserved or disappeared in the high-temperature ferromagnetic state.

To reveal how the chirality information is affected by external stimuli in the course of phase transitions, we show the field-asymmetric 2nd harmonic resistivity after the simultaneous application of a magnetic field and a dc electric current in the course of FAN-to-CON and FM1-to-CON phase transitions. For the FAN-to-CON transition, we applied a dc electric current $j_{\rm p}$ parallel or antiparallel to the magnetic field $H_{\rm p}$ along the propagation vector ($a$-axis) when the FAN-to-CON transition field was traversed. The magnitude of $\mu_{\rm 0}H_{\rm p}$ was slowly decreased from 7 T to 4 T at a rate of 0.6 $\rm Tmin^{-1}$. Then, we removed the dc electric current $j_{\rm p}$. We call the series of these processes the “$H$-poling procedure”(Fig. 1 (b)). In our previous paper[13], we performed the $H$-poling procedure at 51 K and measured the 2nd harmonic resistivity to show the chirality control. Here we performed the $H$-poling procedure at various temperatures and measured the 2nd harmonic resistivity at the same temperature, 52 K. Figures 2 (a)-(d) show the asymmetric component of the 2nd harmonic resistivity $\rho^{\rm 2f}_{\rm asym}=(\rho^{\rm 2f}(H$) $-$ $\rho^{\rm 2f}(-H$))/2 at 52 K after the $H$-poling at various temperatures $T_{\rm p}$. Here $\rho^{\rm 2f}$ is the observed 2nd harmonic resistivity. As discussed in the previous paper[13], $\rho^{\rm 2f}_{\rm asym}$ is sensitive to the breaking of chiral symmetry, whereas the symmetric component seems to be due to sample nonuniformity and/or electrode contact. Notable $\rho^{\rm 2f}_{\rm asym}$ was discerned for all the poling conditions. The signal was reversed by the reversal of the dc poling electric current. These features indicate that the chirality is effectively controlled by the application of the electric current and the magnetic field in the course of the FAN-CON transition, irrespective of temperature.

While the FAN-CON transition is a second-order phase transition, the FM1-CON transition is a first order one. For this reason, the chirality responses in the course of these phase transitions were quite different. We tried to control the chirality by a similar poling procedure via the FM1-CON transition (Fig. 1 (b)). We applied $j_{\rm p}$ parallel or antiparallel to $H_{\rm p}$ along the $a$-axis when the transition temperature was traversed. The temperature was slowly decreased from 80 K to 30 K at a rate of 0.5 $\rm Kmin^{-1}$ with a constant magnitude of $H_{\rm p}$. Then, we removed $j_{\rm p}$. We call the series of these processes the “$T$-poling procedure”. Figures 2 (e)-(h) show $\rho^{\rm 2f}_{\rm asym}$ at 52 K after $T$-poling procedures at various $H_{\rm p}$. The magnitude was much smaller than the case of the $H$-poling. It should be noted that the signal was not reproducible[3]. These features indicate that the $T$-poling is not effective for chirality control.

Thus, the chirality was insensitive to the external stimuli when traversing the first-order FM1-CON transition. We also found that the chiral information was preserved through this phase transition at zero magnetic field, as shown below. In Figs. 3 (a) and (b), we show $\rho^{\rm 2f}_{\rm asym}$ just after the $H$-poling and after the $H$-poling and the subsequent annealing process (heating up to 80 K, cooing down to 30 K, and going back to the original measuring temperature of 52 K, as shown in Fig. 1 (b)). The $\rho^{\rm 2f}_{\rm asym}$ signal was almost unchanged even after the annealing process, irrespective of the sign of $\rho^{\rm 2f}_{\rm asym}$. This observation suggests that the chiral information is preserved even in the FM1 phase at zero field. Then, the question is how the chiral information is preserved in the collinear ferromagnet. This can be answered by considering the effect of magnetic field application along the magnetic easy axis ($c$-axis) at 80 K. After heating the sample up to 80 K, we rotated the sample device in the superconducting magnet and applied a magnetic field $\mu_{0}H^{c}_{\rm 80K}$ as large as 1 T along the $c$-axis. Then, we decreased the temperature to 30 K at 0 T and increased it again to the original measuring temperature of 52 K. Figures 3 (a) and (b) also show $\rho^{\rm 2f}_{\rm asym}$ at 52 K after this annealing process with the application of a magnetic field $H^{c}_{\rm 80K}$. It is clear from this figure that the $\rho^{\rm 2f}_{\rm asym}$ signal was quenched by the application of $H^{c}_{\rm 80K}$. This result implies that it is the ferromagnetic domain walls that memorize the chiral information.

To confirm the chirality memory effect of the ferromagnetic domain walls, we investigated the $H^{c}_{\rm 80K}$ dependence of $\rho^{\rm 2f}_{\rm asym}$. We measured $\rho^{\rm 2f}_{\rm asym}$ just after $H$-poling and after $H$-poling and the subsequent annealing process with the application of various magnetic fields $H^{c}_{\rm 80K}$. In Fig. 4(b), we plot $\rho^{\rm 2f}_{\rm asym}$ measured after the annealing process normalized by that before the annealing process ($\rho^{\rm 2f}_{\rm asym0}$) as a function of $H^{c}_{\rm 80K}$, compared with the linear resistivity in magnetic fields parallel to the $c$-axis. The linear resistivity showed hysteretic behavior. The initial state of the measurement was zero magnetic field just after heating from the helimagnetic state. The resistivity was relatively large at the initial state and decreased with the magnetic field (circles). After the application of a large magnetic field, the resistivity showed a butterfly type hysteresis loop (triangles and squares) and was smaller than the initial resistivity. These features indicate that the magnetic domain walls present at the initial state increased the resistivity, which disappeared above 0.4 T. Importantly, $\rho^{\rm 2f}_{\rm asym}/\rho^{\rm 2f}_{\rm asym0}$ was quenched at almost the same magnetic field as shown in Fig. 4 (b). This strongly supports the scenario that the magnetic domain walls memorized the chiral information in the FM1 phase.

In conclusion, we have demonstrated a chirality memory effect of ferromagnetic domain walls. The chirality of the helical magnetic structure is preserved even after annealing in the high-temperature ferromagnetic state at zero field. The origin of this memory effect is ascribed to the Bloch-type domain walls in the ferromagnetic state. Previously, similar memory effects have been observed in multiferroic helimagnets[18, 19, 20, 21, 22, 23, 24, 25]. Some of these effects are suggested to be caused by the so-called polar nanoregion[18, 19, 20, 21]. In other cases, the charge degree of freedom seems to be responsible for the memory effect[22, 23, 24]. Beilsten-Edmands $et$ $al$. speculated, based on Monte Carlo simulation, that the antiferromagentic domain wall is responsible for the memory effect in the case of $\rm CuFeO_{\rm 2}$[25]. The present result unambiguously shows, based on the experimental result of magnetic field application along the easy axis, that the Bloch-type domain walls are responsible for the memory effect in the case of MnP. This suggests that the magnetic domain walls work as small chiral nuclei in the nonchiral phase, which are important in determining the chirality after the first order nonchiral-chiral phase transition.

The authors thank G.E.W. Bauer, Y. Shimamoto, Y. Togawa, and J. Ohe for fruitful discussions. The crystal growth was carried out by joint research in the Institute for Solid State Physics, The University of Tokyo with the help of R. Ishii and Z. Hiroi. The fabrication of the sample device was carried out partly by collaborative research in the Cooperative Research and Development Center for Advanced Materials, Institute of Materials Research, Tohoku University with the help of K. Takanashi and T. Seki. This work was supported in part by JSPS KAKENHI grant numbers JP16H04008, JP17H05176, JP18K13494, JP19H05600, and JP20K03828, the JST ERATO Spin Quantum Rectification Project (JPMJER1402), PRESTO grant number JPMJPR19L6, and the Mitsubishi foundation. N.J. is supported by a JSPS fellowship (No. JP19J11151).