Chirally Cosmetic Surgeries on Kinoshita-Terasaka and Conway knot families

Xiliu Yang LMAM, School of Mathematics Sciences, Peking University, Beijing, P.R. China 1801110020@pku.edu.cn

Abstract.

In this note, we prove that a nontrivial Kinoshita-Terasaka or Conway knot does not admit chirally cosmetic surgeries, by calculating the finite type invariant of order 3.

1. Introduction

Let $K$ be a knot in $S^{3}$ and $r$ be a number in $\mathbb{Q}\cup\{\infty\}$ , we denote by $S^{3}_{r}(K)$ the manifold obtained by the Dehn surgery along $K$ with slope $r$ . Two surgeries along $K$ with distinct slopes $r$ and $s$ are called purely cosmetic if $S^{3}_{r}(K)\cong S^{3}_{s}(K)$ , and called chirally cosmetic if $S^{3}_{r}(K)\cong-S^{3}_{s}(K)$ . Here $M\cong N$ means that $M$ and $N$ are homeomorphic as oriented manifolds, and $-M$ represents the manifold $M$ with opposite orientation.

The (purely) Cosmetic Surgery Conjecture [17, Problem 1.81(A)], [4, Conjecture 6.1] asserts that if a knot $K$ is nontrivial, then it does not admit purely cosmetic surgeries. This conjecture has been studied in many cases using different obstructions. For instance, if $K$ admits purely cosmetic surgeries, then the surgery slope cannot be $\infty$ [5], the normalized Alexander polynomial $\Delta_{K}(t)$ of $K$ satisfies $\Delta_{K}^{\prime\prime}(1)=0$ [2], the Jones polynomial $V_{K}(t)$ satisfies $V^{\prime\prime}_{K}(1)=V^{\prime\prime\prime}_{K}(1)=0$ [8], and the finite type invariants satisfies $v_{2}(K)=v_{3}(K)=0$ [8]. Some other constraints are given, for example, by using the LMO invariants [12], the quantum $SO(3)$ -invariant [3]. Besides the above criteria, Heegaard Floer homology, as well as its immersed curve version, has been particularly effective for this conjecture. Combining the work of Ozsváth and Szabó [22], Ni and Wu [21], and Hanselman [6], we know that if two distinct slopes $r$ and $s$ are purely cosmetic, then $r=-s$ , and the set $\{r,s\}$ can only be $\{\pm 2\}$ or $\{\pm 1/p\}$ for some integer $p$ . This conjecture has been verified for many knots, including, Seifert genus one knots [28], cable knots [24], composite knots [25], 2-bridge knots [11], 3-braid knots [27], pretzel knots [23], and knots with at most 17 crossings [6, 3]. Indeed, the purely cosmetic surgeries are really rare. Specifically, given $b>0$ , there are only finitely many knots with braid index $b$ that possibly admit purely cosmetic surgeries [14].

On the other hand, the chirally case is rather complicated since there are two known families of chirally cosmetic surgeries for knots in $S^{3}$ :

(A).

For an amphicheiral knot $K$ and a slope $r$ , we have $S^{3}_{r}(K)\cong-S^{3}_{-r}(K)$ .
(B).

For a $(2,k)$ -torus knot $K$ , we have $S^{3}_{r}(K)\cong-S^{3}_{s}(K)$ , where $\{r,s\}=\{\frac{2k^{2}(2m+1)}{k(2m+1)+1},\frac{2k^{2}(2m+1)}{k(2m+1)-1}\}$ for some integer $m$ [20].

With the exception of the above two cases, no knot was found to have chirally cosmetic surgeries. The conjecture for chirally case states as follows:

Conjecture 1.

[10, Conjecture 1] Suppose $K$ is not amphichiral and is not a $(2,k)$ -torus knot, then $K$ does not admit chirally cosmetic surgeries.

The conjecture has been verified for alternating genus one knots [9], alternating odd pretzel knots [27, 26], a certain family of the positive Whitehead doubles [26], and cable knots with some additional assumptions [13]. In this short note, we prove the following:

Theorem 1.1.

Any nontrivial Kinoshita-Terasaka and Conway knot does not admit chirally cosmetic surgeries.

The purely cosmetic surgeries on knots of both two families are ruled out in [1], and we provide an alternative proof. Our proof is based on the calculation of the constraint $O(K)$ defined in [10]. Let $a_{2i}(K)$ be the coefficient of the $z^{2i}$ -term of the Conway polynomial $\nabla_{K}(z)$ , and $v_{3}(K)$ be the finite type invariant of order 3, $O(K)$ is defined as:

O(K)\triangleq\left\{\begin{aligned} &\left|\frac{7a_{2}(K)^{2}-a_{2}(K)-10a_{4}(K)}{4v_{3}(K)}\right|,&v_{3}(K)\neq 0;\\ &\infty,&\text{otherwise}.\end{aligned}\right.

We appeals the following obstruction theorem:

Theorem 1.2.

[10, Theorem 1.10] A knot $K$ has no chirally cosmetic surgeries if $O(K)\leq 2$ .

Acknowledgements.

The author would like to thank Professor Jiajun Wang for helpful discussions. The author also thanks Zhujun Cao and Cheng Chang for corrections.

2. Prove of the main result

In [16], Kinoshita and Terasaka constructed a family of knots $KT_{r,n}$ parametrized by integers $r$ and $n$ . These knots are obtained from a diagram of the four-stranded pretzel links $P(r+1,-r,r,-r-1)$ by introducing $2n$ twists, as shows in Figure 1. There are some redundancies in these knots. Specifically, $KT_{r,n}$ is isotopic to the unknot if and only if $r\in\{0,\pm 1,-2\}$ or $n=0$ . By turning the knot inside out, one can observe a symmetry which identifies $KT_{r,n}$ and $KT_{-r-1,n}$ . Finally, we note that the mirror image of $KT_{r,n}$ is $KT_{r,-n}$ .

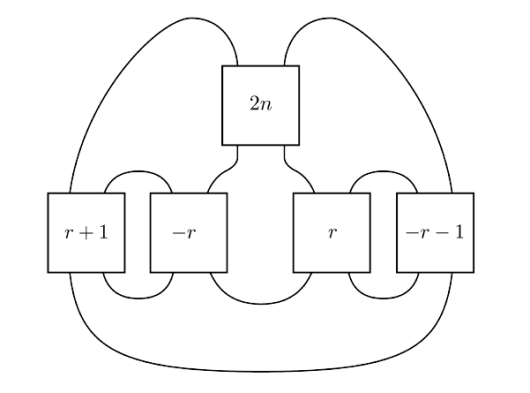
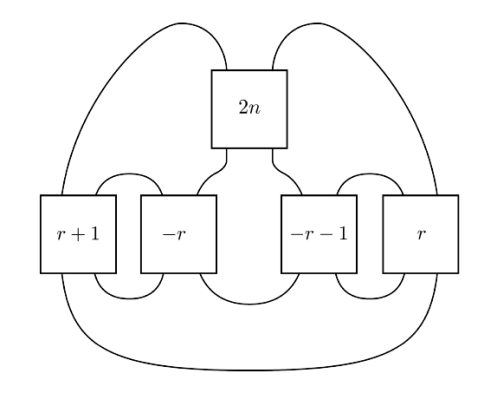
Refer to caption — Figure 1. The diagram of Kinoshita-Terasaka knots $KT_{r,n}$ (left) and Conway knots $C_{r,n}$ (right). The number $r$ in the boxes means $r$ -times half twists.

The Conway knot $C_{r,n}$ shows in Figure 1, is obtained from $KT_{r,n}$ by a mutation. These knots also have a similar construction as $KT_{r,n}$ , only using the four-stranded pretzel links $P(r+1,-r,-r-1,r)$ instead of $P(r+1,-r,r,-r-1)$ . Therefore, Conway and Kinoshita-Terasaka knots satisfy many of the same relations. In particular, $C_{r,n}$ is isotopic to the unknot iff $r\in\{0,\pm 1,-2\}$ or $n=0$ , $C_{r,n}=C_{-r-1,n}$ , and $C^{*}_{r,n}=C_{r,-n}$ .

What makes these two families special is that they have trivial Alexander polynomials $\Delta_{K}(t)$ , as well as Conway polynomials $\nabla_{K}(z)$ , since $\Delta_{K}(t)=\nabla_{K}(t^{1/2}-t^{-1/2})$ . We note that their Conway polynomials can be computed directly by skein relation at $2n$ -twist part from those of pretzel link computed in [15, Theorem 3.2]. By definition, $a_{2}(K)=a_{4}(K)=0$ . It remains to find $v_{3}(K)$ .

Lemma 2.1.

$v_{3}(KT_{r,n})=v_{3}(C_{r,n})=-\frac{nk(k+1)}{4}$ , here $k=\lfloor\frac{r}{2}\rfloor$ .

Proof.

By the symmetry identifying, there is no loss of generality in assuming $r\geq 0$ and $n\geq 0$ . We compute for Conway knot $C_{r,n}$ first.

Note that

v_{3}(K)=-\frac{1}{144}V_{K}^{\prime\prime\prime}(1)-\frac{1}{48}V_{K}^{\prime\prime}(1)=-\frac{1}{24}j_{3}(K),

where $V_{K}(t)$ is the Jones polynomial, and $j_{n}(K)$ is the coefficient of $h^{n}$ in $V_{K}(e^{h})$ of $K$ , by putting $t=e^{h}$ . Here we use another knot invariant $w_{3}(K)$ defined by Lescop in [19]. The advantage is $w_{3}$ satisfies a crossing change formula

(1)

w_{3}(K_{+})-w_{3}(K_{-})=\frac{a_{2}(K^{\prime})+a_{2}(K^{\prime\prime})}{2}-\frac{a_{2}(K_{+})+a_{2}(K_{-})+{\rm lk}^{2}(K^{\prime},K^{\prime\prime})}{4},

where $(K_{+},K_{-},K^{\prime}\cup K^{\prime\prime})$ is a skein triple consisting of two knots $K_{\pm}$ and a two-component link $K^{\prime}\cup K^{\prime\prime}$ , cf. [19, Proposition 7.2] and [8]. On the other hand, a formula from Hoste [7, Theorem 1] states that

(2)

{\rm lk}(K^{\prime},K^{\prime\prime})=a_{2}(K_{+})-a_{2}(K_{-}).

In our case, by smoothing at $2n$ -twist part, $K_{+}$ is $C_{r,n}$ and $K_{-}$ is $C_{r,n-1}$ , both of which have trivial Conway polynomial; and $K^{\prime},K^{\prime\prime}$ are two components of pretzel link $P(r+1,-r,-r-1,r)$ . If $r$ is even, the two components $K^{\prime}$ and $K^{\prime\prime}$ are torus knots $T_{2,r+1}$ and $T_{2,-r-1}$ , respectively; when $r$ is odd, they are $T_{2,r}$ and $T_{2,-r}$ . We compute $a_{2}(T_{2,r})$ when $T_{2,r}$ is a knot, i.e., $r=2k+1$ is odd. By equation (2) again,

a_{2}(T_{2,2k+1})-a_{2}(T_{2,2k-1})={\rm lk}(K_{1},K_{2}),

here $K_{1}$ and $K_{2}$ are two components of the torus link $T_{2,2k}$ , thus with linking number $k$ . Notice that $T_{2,1}$ is the unknot, so that $a_{2}(T_{2,1})=0$ . Therefore, it is easy to see

a_{2}(T_{2,2k+1})=\frac{k(k+1)}{2}.

Since $\nabla_{K}(z)=\nabla_{K^{*}}(z)$ holds for knot $K$ and its mirror $K^{*}$ , we can obtain

w_{3}(C_{r,n})-w_{3}(C_{r,n-1})=\frac{a_{2}(K^{\prime})+a_{2}(K^{\prime\prime})}{2}=a_{2}(K^{\prime})=\left\{\begin{aligned} &\frac{k(k+1)}{2},&r=2k;\\ &\frac{k(k+1)}{2},&r=2k+1.\end{aligned}\right.

Note that $w_{3}(K)=\frac{1}{72}V^{\prime\prime\prime}_{K}(1)+\frac{1}{24}V^{\prime\prime}_{K}(1)=-2v_{3}(K)$ , cf. [8, Lemma 2.2]. When $n=0$ , $C_{r,0}$ is the unknot, so that $w_{3}(C_{r,n-1})=-2v_{3}(\text{unknot})=0$ . Therefore,

v_{3}(C_{r,n})=-\frac{1}{2}w_{3}(C_{r,n})=-\frac{nk(k+1)}{4}.

For the case that $r<0$ or $n<0$ , the formula can also be verified due to the facts that $C_{r,n}=C_{-r-1,n}$ , $C_{r,n}^{*}=C_{r,-n}$ and $v_{3}(K)=-v_{3}(K^{*})$ .

For the knot $KT_{r,n}$ , since $v_{3}(K)$ is determined by its Jones polynomial, which is invariant under mutation, $v_{3}(KT_{r,n})=v_{3}(C_{r,n})$ for all $r,n$ . ∎

Remark 2.2.

One can also compute $w_{3}(KT_{r,n})$ directly in the same way. The only difference is the two components of pretzel link $P(r+1,-r,r,-r-1)$ are a unknot and a connected sum $T_{2,r+1}\#T_{2,-r-1}$ or $T_{2,r}\#T_{2,-r}$ , depending on the parity of $r$ . And then, $a_{2}(K\#K^{\prime})=a_{2}(K)+a_{2}(K^{\prime})$ follows the fact that $\nabla_{K\#K^{\prime}}(z)=\nabla_{K}(z)\cdot\nabla_{K^{\prime}}(z)$ .

Example 2.1.

The knot $K11n34$ in Hoste-Thistlethwaite table [18] is the mirror of the original Conway knot $C_{2,1}$ , that is, $K11n34=C_{2,-1}$ . The Jones polynomial is

V(q)=-q^{4}+2q^{3}-2q^{2}+2q+q^{-2}-2q^{-3}+2q^{-4}-2q^{-5}+q^{-6}.

Direct calculation of the derivatives of $V$ at $q=1$ gives that $V^{\prime\prime}(1)=0$ and $V^{\prime\prime\prime}(1)=-72$ . So, we have

v_{3}=-\frac{1}{48}V^{\prime\prime}(1)-\frac{1}{144}V^{\prime\prime\prime}(1)=\frac{1}{2}.

Note that $\lfloor\frac{r}{2}\rfloor=0$ iff $r=0$ or $1$ , and $\lfloor\frac{r}{2}\rfloor=-1$ iff $r=-1$ or $-2$ . We have the following corollary immediately.

Corollary 2.3.

Let $K$ belong to one of the families $KT_{r,n}$ and $C_{r,n}$ . $v_{3}(K)=0$ if and only if $K$ is isotopic to the unknot, i.e., $r\in\{0,\pm 1,-2\}$ or $n=0$ .

Now we can verify the purely and chirally cosmetic surgeries on these knots.

Corollary 2.4.

[1, Theorem 2.] The purely cosmetic surgery conjecture is true for all nontrivial Kinoshita-Terasaka and Conway knots.

Proof.

This is a direct consequence of Corollary 2.3 and the following theorem. ∎

Theorem 2.5.

[8, Theorem 3.5.] If a knot $K$ has the finite type invariant $v_{2}(K)\neq 0$ or $v_{3}(K)\neq 0$ , then $S^{3}_{r}(K)\not\cong S^{3}_{s}(K)$ when $r\neq s$ .

Proof of Theorem 1.1.

Suppose $K$ be a nontrivial member of $KT_{r,n}$ or $C_{r,n}$ . From Corollary 2.3, we have $v_{3}(K)\neq 0$ . By definition,

O(K)=\left|\frac{7a_{2}(K)^{2}-a_{2}(K)-10a_{4}(K)}{4v_{3}(K)}\right|=0.

As a consequence of Theorem 1.2 ([10, Theorem 1.10.]), $K$ has no chirally cosmetic surgeries. ∎

References

[1] B. Boehnke, C. Gillis, H. Liu, and S. Xue, The purely cosmetic surgery conjecture is true for the Kinoshita-Terasaka and Conway knot families, arXiv:2009.00522v1 [math.GT].
[2] S. Boyer and D. Lines, Surgery formulae for Casson’s invariant and extensions to homology lens spaces, J. Reine Angew. Math. 405 (1990), 181-220.
[3] R. Detcherry, A quantum obstruction to purely cosmetic surgeries, arXiv:2102.11323v2 [math.GT].
[4] C. Gordon, Dehn surgery on knots, Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), 631-642, Math. Soc. Japan, Tokyo.
[5] C.Gordon and J.Luecke, Knots are determined by their complements, J. Amer. Math. Soc. 2 (1989), no. 2, 371-415.
[6] J. Hanselman, Heegaard Floer homology and cosmetic surgeries in $S^{3}$ , J. Eur. Math. Soc. (2022), published online first.
[7] J. Hoste, The first coeffcient of the Conway polynomial, Proc. Amer. Math. Soc. 95 (1985), no. 2, 299-302.
[8] K. Ichihara and Z. Wu, A note on Jones polynomial and cosmetic surgery, Comm. Anal. Geom. 27(2019), no. 5, 1087-1104.
[9] K. Ichihara, T. Ito, and T. Saito, Chirally cosmetic surgeries and Casson invariants, Tokyo J. Math. 44 (2021), no. 1, 1-24.
[10] K. Ichihara, T. Ito, and T. Saito, On constraints for knots to admit chirally cosmetic surgeries and their calculations, arXiv:2112.04156v2 [math.GT].
[11] K. Ichihara, I. Jong, T. Mattman, and T. Saito, Two-bridge knots admit no purely cosmetic surgeries, Algebr. Goem. Topol. 21 (2021), no. 5, 2411-2424.
[12] T. Ito, On LMO invariant constraints for cosmetic surgery and other surgery problems for knots in $S^{3}$ , Comm. Anal. Geom. 28 (2020), no. 2, 321-349.
[13] T. Ito, A note on chirally cosmetic surgery on cable knots, Canad. Math. Bull. 64 (2021), no. 1, 163-173.
[14] T. Ito, A remark on a finiteness of purely cosmetic surgeries, arXiv:2104.07922v1 [math.GT].
[15] D. Kim and J. Lee, Some invariants of pretzel links, Bull. Austral. Math. Soc. 75 (2007), no. 2, 253-271.
[16] S. Kinoshita and H. Terasaka, On unions of knots, Osaka Math. J. 9 (1957), 131-153.
[17] R. Kirby, Problems in low-dimensional topology, Geometric topology (Athens, GA, 1993), 35-473, AMS/IP Stud. Adv. Math., 2.2, Amer. Math. Soc., Providence, RI.
[18] The Knot Atlas, http://katlas.org/.
[19] C. Lescop, Surgery formulae for finite type invariants of rational homology 3-spheres, Algebr. Geom. Topol. 9 (2009), no. 2, 979-1047.
[20] Y. Mathieu, Closed 3-manifolds unchanged by Dehn surgery, J. Knot Theory Ramifications 1 (1992), no. 3, 279-296.
[21] Y. Ni and Z. Wu, Cosmetic surgeries on knots in $S^{3}$ , J. Reine Angew. Math. 706 (2015), 1-17.
[22] P. Ozsváth and Z. Szabó, Knot Floer homology and rational surgeries, Algebr. Geom. Topol. 11 (2011), no. 1, 1-68.
[23] A. Stipsicz and Z Szabó, Purely cosmetic surgeries and pretzel knots, Pacific J. Math. 313 (2021), no. 1, 195-211.
[24] R. Tao, Cable knots do not admit cosmetic surgeries, J. Knot Theory Ramifications 28 (2019), no. 4, 1950034, 11 pp.
[25] R. Tao, Connected sums of knots do not admit purely cosmetic surgeries, arXiv:1909.05048v1 [math.GT].
[26] K. Varvarezos, Heegaard Floer homology and chirally cosmetic surgeries, arXiv:2003.08442v1 [math.GT].
[27] K. Varvarezos, Alternating odd pretzel knots and chirally cosmetic surgeries, J. Knot Theory Ramifications 31 (2022), no. 6, Paper No. 2250045, 20 pp.
[28] J. Wang, Cosmetic surgeries on genus one knots, Algebr. Geom. Topol. 6 (2006), 1491-1517.