Chromatic numbers of Cayley graphs of abelian groups: Cases of small dimension and rank

The case $m=1$ can be dealt with immediately.

If $y_{1}=\cdots=y_{r}=0$, then $\chi(X)=2$, by [1, Lemma LABEL:general-lemma-bipartite].

Recall that a diamond is a graph with $4$ vertices, exactly one pair of which consists of nonadjacent vertices. In other words, a diamond is a $K_{4}$ (complete graph on $4$ vertices) with one edge deleted. The two vertices not adjacent to one another are the endpoints of the diamond.

Def. 2.2 does not preclude the possibiity of the diamonds in the lanyard having edges in common. For example, Let $X=\text{Cay}(\mathbb{Z}_{5},\{\pm 1,\pm 2\})$. Then $X$ is a $K_{5}$ graph with vertex set $\{0,1,2,3,4\}$. We write an edge in $X$ as a string of two vertices. So $X$ contains as a subgraph a diamond with edges $01,02,12,13,23$ and endpoints $0$ and $3$. It also contains as a subgraph a diamond with edges $41,42,12,13,23$ and endpoints $4$ and $3$. The edge sets of these two diamonds are non-disjoint. Taking the union of these two diamonds produces an unclasped diamond lanyard of length two with endpoints $0$ and $4$. Observing that $04$ is also an edge in $X$, indeed $X$ contains a clasped diamond lanyard as a subgraph.

We sometimes refer to a clapsed diamond lanyard simply as a diamond lanyard. A diamond lanyard of length $1$ is a $K_{4}$, and a diamond lanyard of length $2$ where the two diamonds have disjoint edges is called a Mosers’ spindle [7]. Figure 1 illustrates a diamond lanyard of length $4$.

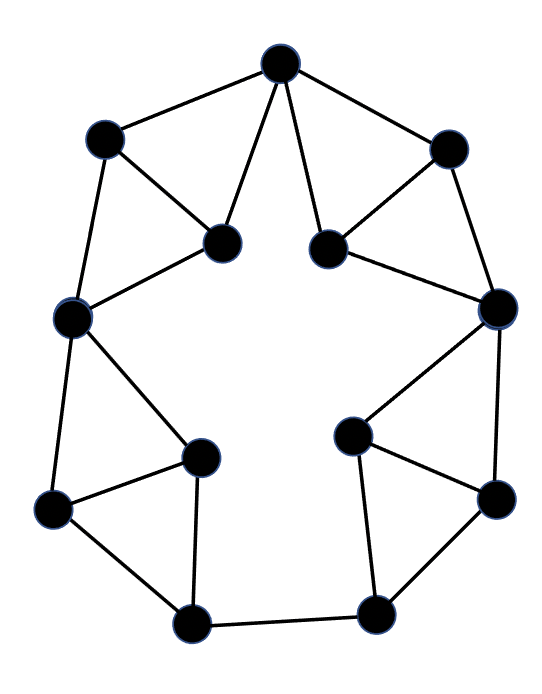
(We would have preferred to have dubbed these “diamond chain necklaces,” but the term “necklace graph” already has a standard meaning.)

We observe that diamond lanyards are not $3$-colorable. For suppose we have a proper $3$-coloring. Note that in any proper $3$-coloring of a diamond, its endpoints must have the same color. Hence the endpoints of the diamond lanyard must have the same color, but they are adjacent, which is a contradiction. Thus, we have the following lemma.

We remark that a diamond lanyard of length $\geq 2$, where the defining diamonds have mutually disjoint edge sets, is a unit-distance graph; hence the chromatic number of the plane is at least $4$. (Indeed, as discussed in the introduction of [1], it is now known to be at least $5$.)

We now turn our attention to the other object that can stand in the way of $3$-colorability for our graphs. Let $C_{13}(1,5)$ be the circulant graph $\text{Cay}(\mathbb{Z}_{13},\{\pm 1,\pm 5\})$. (For more about this notation, see Def. 2.5.) Heuberger proves the following lemma in [4] using a “vertex-chasing” argument. Here we prove it by showing that the independence number is $4$. We include this proof so that it might suggest generalizations.

In this subsection, we completely determine $\chi(X)$ when $X$ has a $2\times 2$ matrix as an associated Heuberger matrix. (Note that if the number of columns exceeds the number of rows, we can perform column operations as in [1, Lemma LABEL:general-lemma-isomorphisms] to get a zero column, and then delete it. So the results of this section, together with the Tomato Cage Theorem, completely take care of all dimension $2$ cases.)

Suppose $X$ is a standardized abelian Cayley graph with a $2\times 2$ Heuberger matrix. By performing row and column operations as in Lemma [1, Lemma LABEL:general-lemma-isomorphisms], one can show that $X$ is isomorphic to a standardized abelian Cayley graph $X^{\prime}$ with an associated matrix $M_{X^{\prime}}$ that is lower-triangular, and such that the diagonal entries of $M_{X^{\prime}}$ are non-negative. Hence we may restrict our attention to the case where $M_{X}$ is a $2\times 2$ lower-triangular matrix with nonnegative diagonal entries.

Next we delve into a class of graphs that play a crucial role in the main theorem for this subsection.

The condition $\gcd(a,b,n)=1$ is equivalent to the connectedness of $C_{n}(a,b)$, and the condition that $n\nmid a$ and $n\nmid b$ is equivalent to the absence of loops.

In [4], Heuberger completely determines the chromatic number of all Heuberger circulants, as follows.

We note that [4] excludes the case $a\equiv\pm b\;(\textup{mod}\;n)$, in which event $C_{n}(a,b)$ is an $n$-cycle. However, the theorem as stated here includes this possibility as well.

Observe that the third case in Theorem 2.6 is precisely Lemma 2.4. Moreover, for the fourth case, Lemma 2.3 shows that $\chi(C_{n}(a,b))\geq 4$, for the following reason. First suppose that $a\equiv 2b\;(\textup{mod}\;n)$. Observe that for all $x\in\mathbb{Z}_{n}$, there is a diamond in $C_{n}(a,b)$ with vertex set $\{x,x+a,x+2a,x+3a\}$, where the endpoints are $x$ and $x+3a$. Because $a\equiv 2b\;(\textup{mod}\;n)$ and $\gcd(a,b,n)=1$, we must have that $\gcd(a,n)=1$. Moreover, because $3\nmid n$, we have that $\gcd(3a,n)=1$. Let $m$ be a positive integer such that $3am\equiv 1\;(\textup{mod}\;n)$. Then $C_{n}(a,b)$ contains a diamond lanyard with vertex set $\{ja\;|\;0\leq j\leq m\}$, so by Lemma 2.3, we have that $\chi(C_{n}(a,b))\geq 4$. A similar argument works when $a\equiv-2b\;(\textup{mod}\;n)$ or when $b\equiv\pm 2a\;(\textup{mod}\;n)$. This is essentially the reasoning in [4] for the lower bounds in these cases. Hence a Heuberger circulant is $4$-colorable unless it is $K_{5}$; and it is $3$-colorable unless it contains as a subgraph either a diamond lanyard or it equals $C_{13}(1,5)$. (Recall that $K_{5}$ contains a diamond lanyard, so we needn’t include it in the list of obstructions to $3$-colorability.)

Next, we show that when the entries of the first column of $M_{X}$ are relatively prime, then with some mild additional conditions imposed, $X$ is isomorphic to a Heuberger circulant.

Note that after switching the columns of the matrix, Lemma 2.7 becomes a special case of [1, Example LABEL:general-example-arbitrary-circulant-graph]. We have included it here separately so as to give a more elementary proof for $2\times 2$ matrices.

We remark that not every graph with an associated $2\times 2$ Heuberger matrix is isomorphic to a circulant. The graph $\begin{pmatrix}4&0\\ 2&4\end{pmatrix}_{X}^{\text{SACG}}$, for instance, provides a counterexample. One computes that $X$ must have order $16$ and so, if circulant, would be of the form $\text{Cay}(\mathbb{Z}_{16},S)$ for some $S$. Because $X$ is connected and bipartite, and has degree $4$, we see that up to isomorphism, we can assume $S=\{\pm 1,\pm 3\}$ or $S=\{\pm 1,\pm 7\}$. Direct arguments (for example, counting the number of paths of length $2$ between various vertices) show that neither choice of $S$ produces a circulant graph isomorphic to $X$.

The following lemma characterizes $2\times 2$ matrices whose associated graphs have loops. This occurs either when the determinant is nonzero and divides a row, or else when one row is zero and the other has relatively prime entries.

We now have all the pieces in place needed to find $\chi(X)$ whenever $X$ has an associated $2\times 2$ matrix.

It follows from Thm. 2.9 and our previous observations about Heuberger circulants that for a standardized abelian Cayley graph $X$ with an associated $2\times 2$ Heuberger matrix, if $X$ does not have loops, then $X$ is $4$-colorable unless it contains $K_{5}$ as a subgraph; and it is $3$-colorable unless it contains as a subgraph either a diamond lanyard or $C_{13}(1,5)$. We will see in §2.5 that this statement holds for the $3\times 2$ case as well.

When $M_{X}$ is a $2\times 2$ matrix, we perform row and column operations to create a $2\times 2$ lower triangular matrix $M_{X^{\prime}}$ for which $X^{\prime}$ is isomorphic to $X$. Observing the effect of these operations on the determinant, we find that $|\det\;M_{X}|=|\det\;M_{X^{\prime}}|$. Note that in Theorem 2.9, whenever $X$ has no loops and $\chi(X)>3$, we have that $|\det\;M_{X}|$ is not divisible by $3$. Thus we have the following corollary, which provides an easily checked sufficient condition for $3$-colorability.

We note that Cor. 2.10 fails in general for larger matrices. For example, we have by Thm. 2.9, Thm. 2.6, [1, Lemma LABEL:general-lemma-block-structure], and Example [1, LABEL:general-example-cycle] that

However, observe that not every $2\times 2$ minor of the matrix above has determinant divisible by $3$. As mentioned in the introduction, we conjecture that if this stronger condition holds, and $X$ does not have loops, then $X$ is $3$-colorable.

In Subsection 2.3, we saw that it was useful to deal only with $2\times 2$ Heuberger matrices in a certain convenient format. The same goes for $3\times 2$ Heuberger matrices. The crux of this idea is drawn from [4], where Hermite normal form is used. For $3\times 2$ matrices, we refine the requirements slightly for our purposes, so as to further reduce the number of exceptional cases. The purpose of the present subsection is to define this “modified Hermite normal form” for $3\times 2$ matrices and to show that with very few exceptions every standardized abelian Cayley graph with an associated $3\times 2$ Heuberger matrix is isomorphic to one with a matrix in this form. We do not attempt here to generalize these definitions to matrices of arbitrary size, as we do not know yet what restrictions will prove to be most useful when the rank or dimension is larger.

There are some departures here from the usual Hermite normal form. For example, $|y_{21}|$ cannot be more than half of $y_{22}$, a more stringent requirement than being less than $y_{22}$, as in ordinary Hermite normal form. As we shall see, we can impose this narrower condition because we have both row and column operations at our disposal, not just column operations. Moreover, this form may be the transpose of what some readers are accustomed to, but we have adopted this convention so as to be consistent with [4]. The third condition has no analogue with Hermite normal form but will turn out to be rather useful in the succeeding subsection.

We next show that every standardized abelian Cayley graph with a $3\times 2$ Heuberger matrix of rank 2 without zero rows is isomorphic to one with a Heuberger matrix in modified Hermite normal form.

Suppose we have a $3\times 2$ Heuberger matrix $M_{X}$. If $M_{X}$ has a zero row, then by [1, Lemma LABEL:general-lemma-delete-row-all-zeroes], we can delete it without affecting the chromatic number $\chi$, whereupon Thm. 2.9 can be used to find $\chi$. If the columns of $M_{X}$ are linearly dependent over $\mathbb{Q}$, then as per [1, Lemma LABEL:general-lemma-isomorphisms] appropriate column operations that do not change $X$ will produce a zero column, which can be deleted without changing $X$. [1, Thm. LABEL:general-theorem-tree-guard] can then be used to find $\chi(X)$. Otherwise, in light of Lemma 2.12, we lose no generality by assuming that $M_{X}$ is in modified Hermite normal form.

We next show that when $M_{X}$ is in modified Hermite normal form, we can determine immediately whether $X$ has loops. Recall that $e_{j}$ is the $j$th standard basis vector, with a $1$ as its $j$th entry and $0$ for every other entry.

In this section we prove the following theorem, which completely determines the chromatic number of an arbitrary standardized abelian Cayley graph with a $3\times 2$ Heuberger matrix in modified Hermite normal form.

The main idea behind the proof of Theorem 2.14 is to add or subtract two rows as per [1, Lemma LABEL:general-lemma-homomorphisms] to obtain a homomorphism from $X$ to a graph with a $2\times 2$ Heuberger matrix. Theorem 2.9 and its corollary provide conditions under which this latter graph (and hence $X$) is $3$-colorable. If those conditions are not met, then we get information about $M_{X}$. In this case we can repeat the procedure using some other homomorphism to further narrow down the possibilities for those $M_{X}$ for which $\chi(X)>3$. In particular, we are led in this way to consider three special types of matrices $M_{X}$: those with $y_{22}=0$ (we call these “L-shaped” matrices); those with $y_{11}=y_{22}=1$ and $y_{21}=0$ (we call these “$I$ on top” matrices); and those with $y_{11}=y_{21}=y_{31}=1$ (we call these “first column all ones” matrices). Every exceptional case traces back ultimately to one of these three. Hence, to lay the groundwork for the proof of Theorem 2.14, we first prove three technical lemmas which compute the chromatic numbers in these three circumstances. The proofs of all three use the same main idea: Add or subtract rows to map to a graph with a $2\times 2$ matrix. If such maps fail to produce a $3$-coloring, then show that $X$ contains a diamond lanyard.

We begin with “first column all ones” matrices.