Classical features, Anderson-Higgs mechanism, and unitarity in Lee-Wick pseudo-electrodynamics
Abstract
In this paper, the dimensional reduction is applied to the Lee-Wick electrodynamics in which the classical sources are confined on a spatial plane. As result, the Lee-Wick pseudo-electrodynamics is achieved as a non-local electromagnetism defined in dimensions. The abelian Anderson-Higgs mechanism is so introduced in the Lee-Wick pseudo-electrodynamics through a complex scalar sector in dimensions, breaking spontaneously the -gauge symmetry of the non-local theory. As consequence, the pseudo-Lee-Wick field acquires a light mass, beyond the usual heavy Lee-Wick mass, that is a natural mass parameter of the theory. After the spontaneous symmetry breaking takes place, classical features of the theory are discussed, as the Proca-Lee-Wick pseudo-electrodynamics, with the field equations and conservation laws. The introduction of Lee-Wick fermions also is proposed, in which it opens the discussion of a viable Proca-Lee-Wick pseudo-quantum electrodynamics in dimensions. The unitarity at the tree level of the Lee-Wick pseudo-electrodynamics is discussed through the Optical theorem.
I Introduction
Quantum field theories (QFTs) in two spatial dimensions have gained relevance with several applications in condensed matter physics in the last years. As examples, the quantum Hall effect [1, 2, 3, 4], topological planar materials [5, 6, 7, 8, 9], the study of transport in graphene [10, 11, 12, 13], superconductivity in layered materials [14, 15, 16, 17, 18], and among others show that field theories in low dimensions are excellent theoretical approach to explain experimental results in material physics. In special, Dirac materials are systems that exhibit a semi-relativistic dynamics for massless or massive particles with Fermi velocity and that are good tests for QFTs [19]. The interaction electron-electron in planar materials must so be mediated by a gauge field defined in dimensions, following the basic principle from quantum electrodynamics (QED). The gauge theory that describe the interactions of fermions in a planar QED is known as pseudo-electrodynamics (PED) [20]. Basically, the PED is obtained from usual Maxwell ED when the classical sources of charges and currents are confined on a spatial plane, reducing the space-time from to dimensions in the generating functional of the Abelian gauge theory. As consequence of the reduced dimension, the PED is a non-local ED with derivatives of infinity order in the D’Alembertian operator. The PED preserves the gauge symmetry and the continuity equation for the current. As fundamental ingredients of a QFT, the PED also preserves the properties of causality [21], and unitarity [22]. Extensions of the PED has been investigated in the literature, as the addition of topological Chern-Simons term [23, 24], the dimensional reduction of the Proca ED that leads to Pseudo-Proca ED [25, 26, 27], and the dimensional reduced QED applied to planes and fermion gap generation [28]. In brane physics, the dynamical chiral symmetry breaking was studied through the dimensional reduction of the QED [29]. The dimensional reduction in connection with boundary conditions were studied for scalar and abelian gauge theories [30].
However, the Proca theory breaks the gauge invariance, and others extensions of the Maxwell, that preserve the gauge invariance can be the good source of investigation to include a massive gauge field in planar materials. One of these possibilities is in the Lee-Wick ED [31, 32], that also is known as Podolsky ED [33, 34]. The Lee-Wick theory is a ED with higher derivative in the kinetic term, that introduces naturally a massive degree of freedom called Lee-Wick mass, preserves the gauge invariance. The Lee-Wick static potential is the subtraction of Coulombian by the Yukawa potential, and as consequence, it is finite at the origin. The Maxwell ED is recovered when the Lee-Wick mass is infinity, and induces the idea that the particle associated with the Lee-Wick field is heavy. From point of view of QFT, the motivation to study the Lee-Wick ED is in the fact of the propagator to have a better behaviour in the ultraviolet regime, and that helps in the renormalizability of the theory in 4D. Therefore, many investigations were studied in literature [35, 36, 37, 38, 39, 40], including the construction of a Standard Model for elementary particles based on Lee-Wick approach [41]. Thus, in low dimensions, the Lee-Wick ED can be a super-renormalizable or finite in the first orders of the perturbation theory. This is the main motivation to investigate the aspects of the Lee-Wick ED when applied to the planar materials.
In this paper, we show the dimensional reduction to dimensions in the Lee-Wick ED, where the sources are constraint on a spatial plane. Thereby, the non-local theory called Lee-Wick pseudo-electrodynamics is obtained and defined in two spatial dimensions and one time-coordinate [42]. The known pseudo-ED is so recovered when the Lee-Wick mass (that is a natural mass parameter of the theory) goes to infinity. Motivated by the Abelian Chern-Simons model applied to planar superconductors [43], we propose a Higgs-Anderson mechanism to break spontaneously the -gauge symmetry via a complex scalar field in dimensions, whose vacuum expected value yields a mass to the Lee-Wick pseudo-electrodynamics, beyond the Lee-Wick mass parameter. For simplification, it is considered that the mass acquired via spontaneous symmetry breaking (SSB) is lighter in relation to Lee-Wick mass. The scalar sector after the SSB also is showed as a toy model that is super-renormalizable in -dimensions. It is discussed some classical features of the Proca-Lee-Wick pseudo-ED, as the field equations and the correspondent conservations laws. Posteriorly, the fermion sector is introduced as a starting point for discussion of the viable pseudo-quantum electrodynamics in the presence of a Proca mass for the Lee-Wick field in dimensions. As important consistency of a quantum field theory, the conditions for the unitarity of the Lee-Wick pseudo-electrodynamics are showed through the Optical theorem [44].
The paper is organized as follows : In the section II, the dimensional reduction of the Lee-Wick is showed to yield the Lee-Wick pseudo-ED. The section III is dedicated to the Anderson-Higgs mechanism applied to Lee-Wick pseudo-ED. Some classical properties of the Proca-Lee-Wick pseudo-ED are showed in the section IV. In the section V is proposed the fermion sector coupled to the Proca-Lee-Wick field in dimensions. The section VI is dedicated to discussion of the unitarity in Lee-Wick pseudo-ED at three level. For end, the conclusions are highlighted in the section VII.
The natural units system are used throughout the paper. The signature of the metric is for the theory in dimensions. In the theory dimensionally reduced to dimensions, we use the bar index for vectors and tensors, with the metric .
II The dimensional reduction in Lee-Wick electrodynamics
The well-known Lee-Wick ED is set by the lagrangian density in the presence of a gauge fixing term
| (1) | |||||
where is the strength field tensor of the -potential, is the Lee-Wick mass for , is a real gauge fixing parameter, and is a external classical source. The limit recovers the usual Maxwell ED with a covariant gauge fixing term. Thereby, the Lee-Wick mass represents degree freedom of a heavy gauge boson. The action principle applied to the lagrangian (1) yields the field equation for the -potential
| (2) |
in which is the operator
| (3) |
The solution for the equation (2) is expressed by
| (4) |
where is the solution of the homogeneous equation , and is the Green function associated with the operator (II) that satisfies the equation
| (5) |
After integrations by parts, the functional action can be written as
| (6) |
that substituting the solution (4), it is reduced to the functional of the external source
| (7) |
For convenience, the dimensional reduction is realized with the action written in the euclidian space, with and , in which the operator (II) is given by
| (8) |
The projectors in the euclidian space are defined by
| (9) |
that satisfy the relations
| (10) |
Using the Fourier transform in the momentum space (euclidian), the Green function that satisfies (5) is read below
| (11) |
where is the -momentum in the euclidian space, and is positive. Consequently, the effective action in the euclidian space is
| (12) |
The dimensional reduction is so introduced constraint the external sources on the 2D spatial plane
| (13a) | |||||
| (13b) | |||||
where sets the coordinates on the 3D euclidian space-time. Substituting these conditions in (12), the euclidian action is reduced to a 3D space-time as
| (14) |
where the new Green function in 3D is
| (15) |
in which we have used the conserved current in the momentum space. The -integration yields the result
| (16) |
where . Calculating the integrals in (II), the Green function in the euclidian space is
| (17) |
where is a Bessel function of second kind, and the effective action (14) is
| (18) |
Thereby, we seek now the Lagrangian density defined in the space-time that leads to the Green function (II). The proposed Lagrangian must be in the form
| (19) | |||||
where is the D’Alembertian operator in dimensions, is a operator that depends on , is the EM tensor defined on the space-time, and is the correspondent potential. The space-time derivatives acts on the fields of the theory. If we repeat the same steps for the Lagrangian (19), the correspondent Green function in is given by
| (20) |
and comparing it with (II), the -function is
| (21) |
Using the representation of as , the -operator is
| (22) |
and the lagrangian (19) can be written as
| (23) | |||||
where we have defined the -operador as
| (24) |
The kinetic term in (23) can be written in form of field-operator-field as
| (25) |
and show that the dimensional reduction leads to a non-local electrodynamics of infinity order in the D’Alembertian operator . The theory (23) can be called pseudo-Lee-Wick electrodynamics, in which the limit recovers the pseudo-electrodynamics discussed in the refs. [20, 22]. The lagrangian (23) (up to gauge fixing term) is gauge invariant under the transformation , if the current density is conserved, i.e., it obeys the continuity equation on the plane. Substituting the result of the -function (21) in (II), the Green function in the -gauge fixing is
| (26) |
Notice that the expression Green function in the momentum space has two poles : and . Thus, the theory shows one massless degree freedom, and another massive degree freedom described by the Lee-Wick mass. The case of two like-point charged particles at rest, the current density is , and the effective action reduces to energy of interaction between these two particles :
| (27) |
whose result is well known in the literature
| (28) |
where is the distance that separate the charges. The energy (28) is the same of the usual Lee-Wick ED that is the difference of the Coulomb by the Yukawa potential with the Lee-Wick mass.
It is worth to clarify that the Pseudo-Lee-Wick ED is a causal theory. As obtained in the ref. [42], the retarded and advanced Green functions associated with the equation (2) when in the prescription of are given by
| (29) |
where the signs indicate the retarded and advanced , , is the Heaviside function, and is Bessel function of first kind. The result shows that the retarded Green function is null outside the light-cone, for . The Feynman Green function is obtained with the prescription of , such that the result is [42]
| (30) |
in which is a Hankel function of first kind.
III The Anderson–Higgs mechanism in the pseudo-Lee Wick ED
The sector of a complex scalar field -gauge invariant is governed by the Lagrangian
| (31) |
where is the scalar potential, and are two real parameters, and is the Lee-Wick mass for the scalar field. The covariant derivative operator is , in which is a real coupling constant. The complex scalar field under a local transformation keeps the lagrangian (31) -gauge invariant in dimensions. As in the usual mechanism, the scalar potential acquires the vacuum expected value (VEV) , with , and therefore, the scalar field can be written as the perturbation in the unitary gauge
| (32) |
Notice that has dimension of mass elevated to in three dimensions, such that the combination (32) is dimensionally satisfied in 3D. After the SSB mechanism, the free sector of (31) is
| (33) |
where the term is a mass acquired by the gauge field due to VEV scale, and is a mass acquired by the scalar field . We consider in this paper the condition in that , and consequently, the Lee-Wick masses and are heavier in relation to masses and .
The pure scalar sector of -field is read below
| (34) |
that sets a toy model in 3D with self-interactions of and of coupling constants and , respectively. The free sector in (34) yields the scalar propagator in the momentum space
| (35) | |||||
that constraints the condition , and , are the mass eigenstates :
| (36a) | |||||
| (36b) | |||||
In the case of , these eigenstates are reduced to and , respectively, and simplifies (35) as
| (37) |
which it is clearly the composition of a scalar propagator with mass summed to scalar propagator with a minus sign and mass . Thereby, the toy model (34) can be interpreted as one scalar theory of mass subtracted of another scalar theory with heavy mass of . To check it explicitly, it is introduced the auxiliary scalar field , such that the modified lagrangian is
| (38) |
The variation of (III) in relation to yields the relation
| (39) |
that when substituted in (III), we recover the original lagrangian (34). We make the transformation in (III) to obtain the scalar lagrangian in terms of and
| (40) | |||||
The previous lagrangian can be diagonalized by the transformation
| (41a) | |||
| (41b) | |||
in which the -mixing angle satisfies the relation
| (42) |
For , the mixing angle is very small, and the lagrangian (40) in the basis of and is given by
| (43) | |||||
In (43), we have two pseudo-scalars theories, the -field sets a light scalar particle with mass , and is a heavy scalar particle (that is the Lee-Wick scalar particle) with signs exchanged in the kinetic terms in relation to the terms of . As consequence, the propagator of the -field is
| (44) |
that confirms the second term in the propagator (37). The propagator (35) behaves like in the ultraviolet regime, that leads to finite loop integrals for the scalar toy model (34) in dimensions. Thus, this scalar sector has finite contributions at the one-loop.
In the gauge sector, the massive term of added to the gauge kinetic term of (23) composes the pseudo Proca-Lee-Wick ED in 3D
| (45) | |||||
The propagator of the gauge sector after the SSB is
| (46) | |||||
that in the ultraviolet range in which , with , the expression (46) goes to zero, and consequently, this behaviour corroborates to the renormalizability of the model in the perturbative analysis of a quantum field theory. Contracting (46) with the external conserved current , we obtain the amplitude :
| (47) | |||||
in which the poles are defined by the solution of the equation
| (48) |
whose roots are at and , if . Taking into account that is space-like (), see the refs. [35, 36, 37], we have the residues
| (49) |
The above residues show that the model carries two spin-1 modes, one with a light mass at , and the other one with a heavier mass at . The positive residue corresponds to the Proca pseudo-electrodynamics, that describes a massive vector mode propagating non-locally on the plane. The negative residue is associated with the mode of a unstable heavy particle of mass .
IV Some properties of the pseudo Proca-Lee-Wick electrodynamics
In this section, we study some classical features of the pseudo Proca-Lee-Wick electrodynamics. The Proca-Lee-Wick action associated with the lagrangian (45) defined in the space-time in the presence of an external source is
| (50) |
in which the action principle yields the field equations
| (51) |
In our analysis here, we consider , such that the gauge fixing term can be removed. The equations without sources are set by the Bianchi identity
| (52) |
that alternatively also can be represented by the divergence , where is the dual tensor of in dimensions. The conservation current leads to subsidiary condition for the -potential in (51). The components of the EM tensor provides the electric field on the spatial plane, and the magnetic field perpendicular to this plane that we consider the -direction, , . The matrix representation of is
| (56) |
In vector notation, the equations of the pseudo-Proca-Lee-Wick electrodynamics are
| (57a) | |||||
| (57b) | |||||
| (57c) | |||||
Using the subsidiary condition, the -potential satisfies the equation
| (58) |
The conservation laws can be obtained directly from the field equations. Multiplying the equation (51) by , and using the Bianchi identity, we obtain the relation
| (59) |
The subsidiary condition allows to write the expression (IV) as the total derivative
| (60) |
where the energy-momentum tensor is given by
| (61) |
As we expect, the energy-momentum tensor is not gauge invariant when . The case without sources in (60) leads to conservation law , in which the conserved momentum for the Proca-Lee-Wick field is the integral of the - component over the spatial plane
| (62) |
The components yield the energy and the linear momentum densities stored in the Proca-Lee-Wick field, respectively,
| (63a) | |||
| (63b) | |||
For a static like point charge distribution, the current density is , and the effective action (14) yields the static energy potential between two identical charges separated by a distance
| (64) |
that can be reduced to integral
| (65) |
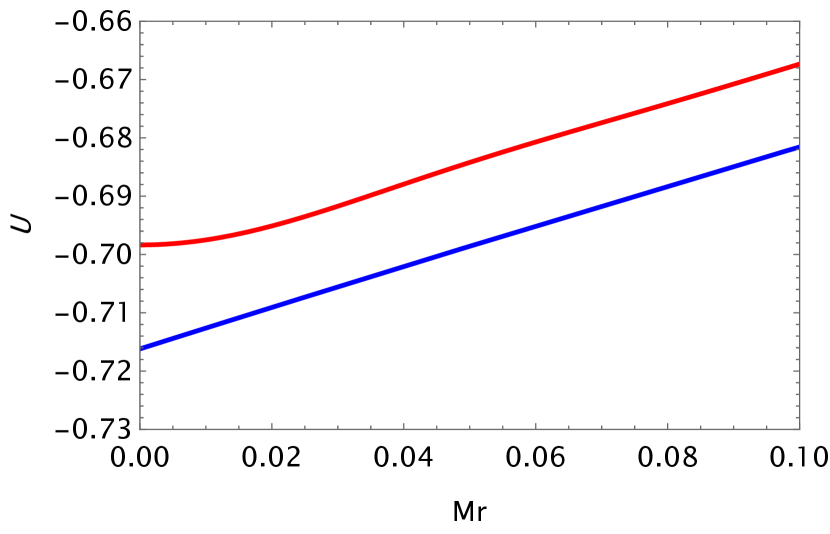
in which . This potential is plotted numerically as function of in comparison with the Lee-Wick potential (28) in the figure (1). We choose and . The red line is the numerical solution of (65) in that the potential is finite at origin with in energy units.
V The pseudo Proca-Lee-Wick quantum electrodynamics
The addition of fermions to the Lagrangian density (45) sets the Proca-Lee-Wick pseudo-quantum electrodynamics
| (66) |
where is the covariant derivative operator contracted with the Dirac matrices, is a Dirac spinor (electron field) in dimensions, is the electron mass, is the Lee-Wick mass for the fermion, are the Dirac matrices in which the spatial component includes the Fermi velocity , that satisfy the relation , and is the adjunct field. In the Dirac basis, the and -matrices are represented by
| (71) | |||||
| (74) |
in which are the Pauli matrices. The covariant derivative operator couples the gauge field to the fermions as , in that the coupling constant is dimensionless in three dimensions (in the case of natural units ). Taking the limits and , the Lagrangian is reduced to the case of the pseudo-quantum ED in the presence of the mass [45].
The Dirac equation from (V) coupled to the EM-field is
| (75) |
In free sector of (V), the fermion has the propagator in the momentum space
| (76) |
in which for fermions in the momentum space. The poles of (V) are determinate by the equation
| (77) |
whose roots of are given by and , if . Therefore, the propagator (V) can be written as the combination
| (78) |
The result (78) shows the combination of one propagator for a light fermion of mass subtracted of a propagator for the heavy Lee-Wick fermion of mass . To see it explicitly in the lagrangian (V), we introduce the auxiliaries fermion fields and such that the modified fermion lagrangian is
| (79) | |||||
in which the action principle associated with and yield the relations, respectively,
| (80) |
that when substituted in (79), we recover the original fermion lagrangian from (V). Making in (79), the fermion lagrangian in terms of , and is
| (81) | |||||
If we write and as the quiral components of a fermion , and , where and are the left- and right-handed projectors, in which , the second line in (81) reduces to the Lagrangian of the -fermion with the Lee-Wick mass and the global minus sign, in which the mixed lagrangian with is
| (82) |
The lagrangian can be written in the matrix form
| (83) |
where , and the kinetic matrix is , and the mass matrix is
| (87) |
The mass matrix in (83) can be diagonalized by the transformation , in which is an unitary matrix, and is the diagonal mass matrix with eigenvalues and , respectively. In the basis of and , we obtain finally
| (88) |
Physically, is a light fermion of mass , and is the heavy Lee-Wick with mass . The propagator of is
| (89) |
that explain the last term in (78). Therefore, the propagators of the fermion and of the Proca-Lee-Wick pseudo ED can help in renormalizability of the lagrangian (V). Even if new couplings emerge from (V), the investigation of the renormalization, or if the theory is finite in dimensions, is an important step for the consistency of a viable QFT.
VI Unitarity in pseudo-Lee-Wick electrodynamics
Unitarity is an important requirement for a quantum field theory. For systems in which the Hamiltonian operator does not depend on time explicitly, the operator governs the time evolution of a state vector in quantum mechanics, where the unitarity imposes the condition . The state vector is normalized in any time, and consequently, the probability is conserved. The unitarity of the -operator implies the -matrix is unitary, whose the elements are defined by
| (90) |
where and are a complete set of free asymptotic states. The -operator is written as , in which the unitarity leads to relation , and defining the element , the previous relation yields the result
| (91) |
that is known as the Optical theorem. Writing , in which is the Feynman propagator for a scalar field, and the unitarity condition yields the relation
| (92) |
where is a phase factor needed to dimensional analysis that guarantee the sum over the intermediate states leads to identity. Using the Fourier transform in (VI), this relation in the momentum space is
| (93) |
where is the characteristic time of the system, that appears by the phase factor
| (94) |
Since we are interested in the unitarity of a gauge theory at tree level, the relation (93) for a gauge field is modified by
| (95) |
Therefore, the unitarity analysis starts with the Feynman propagator for the pseudo Lee-Wick electrodynamics (23). The feynman propagator in the momentum space for (23) in terms of the projectors and is
| (96) |
where
| (97a) | |||||
| (97b) | |||||
The term in can be discarded by the gauge choice, or by the fact of the contraction with the conserved current, such that . Thus, the Optical theorem (96) leads to relation
| (98) |
Notice that can be written as
| (99) |
where the numerators are complex functions of , that are written in the polar form : and , in which , , with the arguments and , respectively. Substituting (99) in (98), we obtain the relation
| (100) |
Squaring the equation (100) and multiplying it by , we use the identities
| (101a) | |||||
| (101b) | |||||
we obtain this relation evaluated at and
| (102) |
Using the imaginary parts and the previous definitions, the expression (VI) yields relation of , and
| (103) |
where
| (104) |
For a small -parameter, such that , and , that leads to relation
| (105) |
This result is very similar to that obtained in ref. [22] for the case of pseudo-quantum electrodynamics in the presence of radiative corrections at one-loop for the vacuum polarization. Therefore, we can confirm that the pseudo-Lee-Wick ED is unitary at tree level.
VII Conclusions
In this paper, we study the dimensional reduction of the Lee-Wick electrodynamics that leads to non-local pseudo-Lee-Wick electrodynamics in dimensions, when the classical sources are confined on a spatial plane. The theory is a planar electrodynamics with derivatives of infinity order that is gauge invariant, and depends on the Lee-Wick mass parameter , where the known Maxwell pseudo-electrodynamics is recovered in the limit . Thereby, this extend planar ED can mediate the interaction of electrons in a bidimensional material, in the presence of a massive gauge field that maintain the gauge invariance principle. As it is known, the Lee-Wick ED also present massless degree of freedom with propagation in the space-time, that similarly, keeps in the pseudo-Lee-Wick ED. Motived by planar superconductors models, a Higgs complex scalar field is introduced to yield mass like Proca to the massless sector of the pseudo-Lee-Wick ED, in which the gauge symmetry is spontaneously broken in dimensions. Thus, one theory with a light massive degree freedom is obtained, beyond the heavy Lee-Wick mass. In this stage, the limit of leads to a pseudo-Proca ED, where the Proca mass is acquired by a vacuum expected value scale. Some results, like the field equations and conservation laws are discussed on the classical pseudo-Proca-Lee-Wick ED. The sector of fermions in the Lee-Wick approach is introduced coupled to the Proca-Lee-Wick field. Thereby, the free sector contains a massive partner fermion that has a heavier mass in relation to the usual Dirac mass. After some transformations, it is showed that the fermion Lagrangian is composite by a light Dirac fermion subtracted of a heavy Dirac fermion, both coupled to the Proca-Lee-Wick field. Posteriorly, the unitarity of the Lee-Wick pseudo ED is investigated through the Optical theorem at tree level. The non-local shape of the propagator shows that the theory is unitary in which the characteristic time is related to -parameter from the Feynman propagator prescription. This result is similar to the case of the pure pseudo-ED.
The proposal of the pseudo-Proca-Lee-Wick quantum electrodynamics opens the possibility of investigation for the unitarity of the theory in the presence of fermions, and taking account the radiative corrections. The renormalization of this theory also is an interesting investigation in dimensions since that the Proca-Lee-Wick and the fermion propagators have a good behavior in the ultraviolet regime. Furthermore, the loop integrals can have an improved divergency degree or finite by power counting in dimensions. Other perspective is studying the effects of the extended pseudo-QED in the presence of a topological Chern-Simons Lagrangian, that is like
| (106) |
where is the dimensionless parameter, see the ref. [23]. The radiative corrections can be calculated in one-loop approximation such that the electron self-energy, vacuum polarization and the vertex correction must be finite. The form factors and the electron anomalous magnetic moment can give a limit for the Lee-Wick mass parameter in the planar theory. These investigations are perspectives for a forthcoming project.
References
- [1] T. Ando, Y. Matsumoto and Y. Uemura, Theory of Hall Effect in a Two-Dimensional Electron System, Journ. of the Phys. Soc. of Japan 39, 279 (1975).
- [2] D. C. Tsui, H.L. Stormer, A.C. Gossard, Two Dimensional Magnetotransport in the Extreme Quantum Limit, Phys. Rev. Lett. 48, 1559 (1982).
- [3] R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations, Phys. Rev. Lett. 50, 1395 (1983).
- [4] C. C. Chamon, E. Fradkin, Distinct universal conductances in tunneling to quantum Hall states: The role of contacts, Phys. Rev. B 56, 2012 (1997).
- [5] X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Erratum: Topological field theory of time-reversal invariant insulators, Phys. Rev. B 81, 159901(E) (2010).
- [6] M. Z. Hasan and C. L. Kane, Colloquium: Topological insulators Rev. Mod. Phys. 82, 3045 (2010).
- [7] C.-K. Chiu, J. C. Y. Teo, A. P. Schnyder, and S. Ryu, Classification of topological quantum matter with symmetries, Rev. Mod. Phys. 88, 035005 (2016).
- [8] P.-L. Zhao, X.-B. Qiang, H.-Z. Lu, and X. C. Xie, Coulomb Instabilities of a Three-Dimensional Higher-Order Topological Insulator, Phys. Rev. Lett. 127, 176601 (2021).
- [9] X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Topological field theory of time-reversal invariant insulators, Phys. Rev. B 78, 195424 (2008).
- [10] E. V. Gorbar, V. P. Gusynin, V. A. Miransky, and I. A. Shovkovy, Coulomb interaction and magnetic catalysis in the quantum Hall effect in graphene, Phys. Scr. T 146, 014018 (2012).
- [11] I. F. Herbut, Interactions and Phase Transitions on Graphene’s Honeycomb Lattice, Phys. Rev. Lett. 97, 146401 (2006).
- [12] V. P. Gusynin, V. A. Miransky, S. G. Sharapov, and I. A. Shovkovy, Excitonic gap, phase transition, and quantum Hall effect in graphene, Phys. Rev. B 74, 195429 (2006).
- [13] I. F. Herbut, V. Juricic, and O. Vafek, Coulomb Interaction, Ripples, and the Minimal Conductivity of Graphene, Phys. Rev. Lett. 100, 046403 (2008).
- [14] Z. Tesanovic, L. Xing, L. Bulaevskii, Q. Li, and M. Suenaga, Critical Fluctuations in the Thermodynamics of Quasi-Two-Dimensional Type-II Superconductors, Phys. Rev. Lett. 69, 3563 (1992).
- [15] S.-C. Zhang, quantum nonlinear sigma model theory of the high superconductivity, Science 275, 1089 (1997).
- [16] M. Franz, Z. Tesanovic, and O. Vafek, QED3 theory of pairing pseudogap in cuprates: From -wave superconductor to antiferromagnet via an algebraic Fermi liquid, Phys. Rev. B 66, 054535 (2002).
- [17] S. A. Kivelson, I. P. Bindloss, E. Fradkin, V. Oganesyan, J. M. Tranquada, A. Kapitulnik, and C. Howald, How to detect fluctuating stripes in the high-temperature superconductors, Rev. Mod. Phys. 75, 1201 (2003).
- [18] E. C. Marino, D. Niemeyer, V. S. Alves, T. Hansson, and S. Moroz, Screening and topological order in thin superconducting films, New J. Phys. 20, 083049 (2018).
- [19] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys. 81, 109 (2009).
- [20] E. C. Marino, Quantum electrodynamics of particles on a plane and the Chern-Simons theory, Nucl. Phys. B 408, 551 (1993).
- [21] R. L. P. G. do Amaral and E. C. Marino, Canonical quantization of theories containing fractional powers of the d’Alembertian operator, J. of Physics : Mathematical and General 25, 5183 (1992).
- [22] E. C. Marino, Leandro O. Nascimento, Van Sérgio Alves, and C. Morais Smith, Unitarity of theories containing fractional powers of the d’Alembertian operator, Phys. Rev. D 90, 105003 (2014).
- [23] V. S. Alves, E. Marino, L. O. Nascimento, J. Medeiros Neto, R. F. Ozela, and R. O. Ramos, Bounded particle interactions driven by a nonlocal dual Chern-Simons model, Phys. Lett. B 797, 134860 (2019).
- [24] Gabriel C. Magalhães, Van Sérgio Alves, E. C. Marino, and Leandro O. Nascimento, Pseudo quantum electrodynamics and Chern-Simons theory coupled to two-dimensional electrons, Phys. Rev. D 101, 116005 (2020).
- [25] R. F. Ozela, Van Sérgio Alves, E. C. Marino, Leandro O. Nascimento, J. F. Medeiros Neto, Rudnei O. Ramos and C. Morais Smith, Projected Proca Field Theory: a One-Loop Study, arXiv:1907.11339v2 [hep-th].
- [26] Rodrigo F. Ozela, Van Sérgio Alves, Leandro O. Nascimento, E. C. Marino, C. Morais Smith, R. O. Ramos and J. F. Medeiros Neto, Effective mass in mixed-dimensionality pseudo-Proca systems, g-factor corrections, and the radiative effects to the interaction potential, Phys. Rev. D 108, 056017 (2023).
- [27] Van Sérgio Alves, Tommaso Macrì, Gabriel C. Magalhães, E. C. Marino, and Leandro O. Nascimento, Two-dimensional Yukawa interactions from nonlocal Proca quantum electrodynamics, Phys. Rev. D 97, 096003 (2018).
- [28] E. V. Gorbar, V. P. Gusynin, and M. R. Parymuda, Reduced QED with Few Planes and Fermion Gap Generation, Entropy 25, 1317 (2023).
- [29] E. V. Gorbar, V. P. Gusynin, and V. A. Miransky, Dynamical chiral symmetry breaking on a brane in reduced QED, Phys. Rev. D 64, 105028 (2001).
- [30] A. Edery, N. Graham and I. MacDonald, 3D scalar model as a 4D perfect conductor limit : dimensional reduction and variational boundary conditions, Phys. Rev.D 79, 125018 (2009).
- [31] T. Lee and G. Wick, Negative metric and the unitarity of the S-matrix, Nucl. Phys. B9, 209 (1969).
- [32] T. Lee and G. Wick, Finite Theory of Quantum Electrodynamics, Phys. Rev. D 2, 1033 (1970).
- [33] B. Podolsky, A Generalized Electrodynamics Part I—Non-Quantum, Phys. Rev. 62, 68 (1942).
- [34] B. Podolsky and C. Kikuchi, A Generalized Electrodynamics Part II—Quantum, Phys. Rev. 65, 228 (1944).
- [35] A. Accioly, Quadratic gravity theories in 2+1 dimensions and the topological Chern-Simons term, Phys. Rev. D 67, 127502 (2003).
- [36] A. Accioly, Nucl. Phys. B (Proc. Suppl.) 127, 100 (2004).
- [37] A. Accioly and M. Dias, Algorithm for Probing the Unitarity of Topologically Massive Models, Int. J. Theor. Phys. 44, 1123 (2005).
- [38] A. Accioly, P. Gaete, J. A. Helayël-Neto, E. Scatena and R. Turcati, Investigations in the Lee-wick electrodynamics, Mod. Phys. Lett. A 26, 1985 (2011).
- [39] R. Turcati and M. J. Neves, Probing Features of the Lee-Wick Quantum Electrodynamics, Advances in High Energy Physics, 2014, 153953 (2014).
- [40] R. Turcati and M. J. Neves, Complex-mass shell renormalization of the higher-derivative electrodynamics, Eur. Phys. J. C 76, 456 (2016).
- [41] Benjamín Grinstein, Donal O’Connell, and Mark B. Wise, The Lee-Wick standard model, Phys. Rev. D 77, 025012 (2008).
- [42] Pedro Henrique Ortega, A pseudo-eletrodinâmica de Podolsky, PhD Thesis, Federal University of Rio de Janeiro (2018).
- [43] Yi-Hui Xing, Lin Zhuang, E. C. Marino, and Wu-Ming Liu, Critical behavior and duality in dimensionally reduced planar Chern-Simons superconductors, Phys. Rev. B 108, L220504 (2023).
- [44] M. E. Peskin and D. V. Schroeder, An introduction to quantum field theory, Westview press (1995).
- [45] Eduardo C. Marino, Quantum field theory approach to condensed matter physics, Cambridge university press (2017).