Clique-factors in graphs with sublinear -independence number
Abstract
Given a graph and an integer , we denote by the maximum size of a -free subset of vertices in . A recent question of Nenadov and Pehova asks for determining the best possible minimum degree conditions forcing clique-factors in -vertex graphs with , which can be seen as a Ramsey–Turán variant of the celebrated Hajnal–Szemerédi theorem. In this paper we find the asymptotical sharp minimum degree threshold for -factors in -vertex graphs with for all .
1 Introduction
Let be an -vertex graph and be an -vertex graph. An -tiling is a collection of vertex-disjoint copies of in . An -factor is an -tiling which covers all vertices of . The celebrated Hajnal–Szemerédi theorem [18] states that for all integers with and , any -vertex graph with contains a -factor. Since then there have been many developments in several directions. From the insight of equitable coloring, Kierstead and Kostochka proved the Hajnal–Szemerédi theorem with an Ore-type degree condition [23]. For a general graph , Alon and Yuster [2] first gave an asymptotic result by showing that if , then contains an -factor, where is the chromatic number of . Later, Kühn and Osthus [30] managed to characterise, up to an additive constant, the minimum degree condition that forces an -factor. There are also several significant generalisations in the setting of partite graphs [22], directed graphs [39] and hypergraphs [36].
1.1 Motivation
Erdős and Sós [14] initiated the study of a variant of Turán problem which excludes all graphs with large independence number. More generally, for an integer and a graph , the -independence number of , denoted by , is the maximum size of a -free subset of vertices. Given integers and a function , we use to denote the maximum number of edges of an -vertex -free graph with . In particular, the Ramsey–Turán density of is defined as . Szemerédi [38] first showed that . This turned out to be sharp as Bollobás and Erdős [7] provided a matching lower bound using an ingenious geometric construction. There are some recent exciting developments in this area [3, 4, 16, 24, 31, 33]. For further information on Ramsey–Turán theory the reader is referred to a comprehensive survey [37] by Simonovits and Sós.
Note that the extremal example that achieves the optimality of the bound on in the Hajnal–Szemerédi theorem also has large independence number [6], which makes it far from being typical. Following the spirit of the Ramsey–Turán theory, a natural question on the Hajnal–Szemerédi theorem is whether the minimum degree condition can be weakened when the host graph has sublinear independence number. The following Ramsey–Turán type problem was proposed by Balogh, Molla and Sharifzadeh [6].
Problem 1.1.
[6] Let be an integer and be an -vertex graph with . What is the minimum degree condition on that guarantees a -factor?
Balogh, Molla and Sharifzadeh [6] studied -factors and showed that if the independence number of an -vertex graph is and for any , then contains a triangle factor. Recently Knierim and Su [26] resolved the case by determining the asymptotically tight minimum degree bound .
The following problem was proposed by Nenadov and Pehova [35].
Problem 1.2.
For all with , let be an -vertex graph with and . What is the best possible minimum degree condition on that guarantees a -factor?
Nenadov and Pehova [35] also provided upper and lower bounds on the minimum degree condition. In particular, they solved Problem 1.2 for and proved that is the correct minimum degree threshold. Knierim and Su [26] reiterated Problem 1.2 in their paper and proposed a minimum degree condition as follows.
Problem 1.3.
Very recently, Chang, Han, Kim, Wang and Yang [8] determines the asymptotically optimal minimum degree condition for , which solves Problem 1.2 for this range, and indeed provides a negative answer to Problem 1.3.
Theorem 1.4.
[8] Let such that . For any , there exists such that for sufficiently large , every -vertex graph with
contains a -factor. Moreover, the minimum degree condition is asymptotically best possible.
Based on this result, Problem 1.3 should be revised as follows.
Problem 1.5.
Is it true that suffices in Problem 1.3?
1.2 Main results and discussions
By the aformentioned results, Problem 1.5 is solved for [26] and for [8], both done by quite involved proofs. It seems to us that a complete resolution of Problem 1.5 is a quite challenging task.
The purpose of this paper is to extend the discussion on the problem to sublinear -independence numbers. We first state a simplified version of our main result which says that the answer to Problem 1.5 is yes if we assume a slightly stronger assumption .
Theorem 1.6.
For , such that , the following holds for sufficiently large . Every -vertex graph with and contains a -factor.
To state our main result, we define more general versions of the Ramsey–Turán densities as follows.
Definition 1.7.
Let be a monotone increasing function, and .
-
()
Let be the maximum integer for which there exists an -vertex -free graph with and . Then let
-
()
Let be the maximum integer for which there exists an -vertex -free graph with and . Then let
By definition trivially it holds that . It is proved in [8] that if there exists such that for every and .
The full version of our result is stated as follows.
Theorem 1.8.
For , such that , there exists such that the following holds for sufficiently large . Let and be a monotone increasing function, where slowly.111The strange-looking function satisfies for any constant . Then every -vertex graph with
contains a -factor.
In fact, Theorem 1.8 implies Theorem 1.6 by the observation that holds for any function with . We shall supply lower bound constructions (see next subsection) which show that the minimum degree condition in Theorem 1.8 is asymptotically best possible for , for any and any . This can be seen as a stepping stone towards a full understanding of the Ramsey–Turán tiling thresholds for cliques where .
Here we also provide some concrete thresholds that we could spell out from Theorem 1.8. Recall that Nenadov and Pehova [35] solved Problem 1.2 for whilst Knierim and Su [26] solved the case . Now we consider the first open case . Note that . Then Theorem 1.4 says that for (that is, ) and , is the minimum degree threshold forcing a -factor. For the remaining cases , Theorem 1.8 implies that the minimum degree threshold is under a stronger condition for any fixed .
Our proof of Theorem 1.8 uses the absorption method and the regularity method. In particular, we use dependent random choice for embedding cliques in regular tuples with sublinear independence number, which is closely related to the Ramsey–Turán problem.
1.3 Sharpness of the minimum degree condition
We note that both terms in the minimum degree condition in Theorem 1.8 are asymptotically best possible. First, we show that the first term cannot be weakened when for some constant as follows.
Proposition 1.9.
Given integers with and constants with , , the following holds for all sufficiently large and constant . There exists an -vertex graph with and such that every -tiling in covers at most vertices.
Indeed, Proposition 1.9 also gives, in the setting that , a lower bound construction for the minimum degree condition forcing an almost -tiling that leaves a constant number of vertices uncovered. More results on almost graph tilings can be found in a recent comprehensive paper [19].
The second term is also asymptotically tight, which is given by a cover threshold construction as follows.
Cover Threshold.
To have a -factor in , a naive necessary condition is that every vertex is covered by a copy of in . The cover threshold has been first discussed in [20] and appeared in a few different contexts [8, 9, 12].
Now we give a construction that shows the optimality of the term for the function as in Theorem 1.8. A similar construction can be found in [8]. Given integers and constants , we construct (for large ) an -vertex graph by
-
first fixing a vertex such that and is a -free subgraph with and ;
-
and then adding a clique of size that is complete to .
There exists no copy of covering and thus contains no -factor; moreover, by choosing , we obtain and .
Notation. Throughout the paper we follow standard graph-theoretic notation [11]. For a graph , let and . For , denotes the induced subgraph of on . The notation is used to denote the induced subgraph after removing , that is, . For two subsets , we use to denote the number of edges joining and . Given a vertex and , denote by the set of neighbors of in and let . In particular, we write for the set of neighbors of in . We omit the index if the graph is clear from the context. Given a set and an integer , we write for the family of all -subsets of . For all integers with , let and .
When we write , we always mean that are constants in , and means that there exists such that the subsequent arguments hold for all . Hierarchies of other lengths are defined analogously. In the remaining proofs, we always take and unless otherwise stated.
2 Proof strategy and Preliminaries
Our proof uses the absorption method, pioneered by the work of Rödl, Ruciński and Szemerédi [36] on perfect matchings in hypergraphs, though similar ideas already appeared implicitly in previous works, e.g. Krivelevich [29]. A key step in the absorption method for -factor problem is to show that for every set of vertices, the host graph contains -vertex absorbers (to be defined shortly). However, as pointed out in [6], in our setting this is usually impossible because when we construct the absorbers using the independence number condition, it does not give such a strong counting. Instead, a much weaker notion has been used in this series of works, that is, we aim to show that for (almost) every set of vertices, the host graph contains vertex-disjoint absorbers. Note that this weak notion of absorbers have been successfully used in our setting [35, 26] and the randomly perturbed setting [9].
2.1 The absorption method
Following typical absorption strategies, our main work is to establish an absorbing set (see Lemma 2.2) and find an almost-perfect tiling (see Lemma 2.3). We first introduce the following notions of absorbers and absorbing sets from [35].
Definition 2.1.
Let be a graph with vertices and be a graph with vertices.
-
1.
We say that a subset is a -absorbing set for some if for every subset with and , contains an -factor.
-
2.
Given a subset of size and an integer , we say that a subset is an -absorber if and both and contain an -factor.
Now we are ready to state our first crucial lemma, whose proof can be found in Section 4.
Lemma 2.2 (Absorbing Lemma).
Given positive integers with and constants with , there exist such that the following holds for sufficiently large . Let be an -vertex graph with and . Then contains a -absorbing set of size at most .
Our second crucial lemma is on almost -factor as follows, whose proof will be given in Section 3.
Lemma 2.3 (Almost perfect tiling).
Given positive integers such that and positive constants , the following statement holds for sufficiently large . Every -vertex graph with and contains a -tiling that leaves at most vertices in uncovered.
Proof of Theorem 1.8.
Given any positive integers with and a constant . Choose . Let be an -vertex graph with
By Lemma 2.2 with , we find a -absorbing set of size at most for some . Let . Then we have . Therefore by applying Lemma 2.3 on with , we obtain a -tiling that covers all but a set of at most vertices in . Since , the absorbing property of implies that contains a -factor , which together with forms a -factor in . ∎
3 Finding almost perfect tilings
In this section we address Lemma 2.3. The proof of Lemma 2.3 uses the regularity method, a tiling result of Komlós (Theorem 3.5), and dependent random choice (Lemma 3.6). We shall first give the crucial notion of regularity and then introduce the powerful Szemerédi’s Regularity Lemma.
3.1 Regularity
Given a graph and a pair of vertex-disjoint subsets in , the density of is defined as
For constants , we say that is an -regular pair with density at least (or is -regular) if and for all , with , , we have
Moreover, a pair is called -- if is -regular, for all and for all . The following fact is an easy consequence of the definition of regularity.
Fact 3.1.
Given constants and a bipartite graph , if is -regular, then for all and with and , we have that is -regular in for any .
Given a family of vertex-disjoint sets in which are pairwise -regular, we can find in each set a large subset such that every pair of resulting subsets is super-regular.
Proposition 3.2 (see Proposition 2.6 in [8]).
Given a constant and integers with , let be an -vertex graph and be vertex-disjoint subsets each of size in such that every pair is -regular with density . Then there exists for each a subset of size at least such that every pair is -super-regular.
We now state a degree form of the regularity lemma (see [27, Theorem 1.10]).
Lemma 3.3 (Degree form of the Regularity Lemma [27]).
For every there is an such that the following holds for any real number and . Let be a graph with vertices. Then there exists a partition of and a spanning subgraph with the following properties:
-
;
-
for and for some ;
-
for every ;
-
every is an independent set in ;
-
each pair , is -regular in with density 0 or at least .
A widely-used auxiliary graph accompanied with the regular partition is the reduced graph. The -reduced graph of is a graph defined on the vertex set such that is connected to by an edge if has density at least in . So if is not connected to , then has density by property above. To ease the notation, we use to denote the degree of in for each . Note that also can be regarded as a weighted graph in which the weight for each edge , denoted by for simplicity, is exactly the density of the pair in .
Fact 3.4.
For positive constants and , let be a graph on vertices with . Let and be obtained by applying Lemma 3.3 on with constants and . Let be the -reduced graph as given above. Then for every we have
Proof.
Note that and for each . Thus we have
which implies
∎
To find an almost perfect -tiling, we shall also make use of the following result of Komlós [28] on graph tilings. Given a graph on vertices, the critical chromatic number of is defined as where and denotes the smallest size of a color class over all -colorings of .
Theorem 3.5 (Komlós [28]).
Given any graph and a constant , there exists an integer such that every graph of order with contains an -tiling covering all but at most vertices.
Based on this result, we will first apply the regularity lemma to to get a reduced graph for a constant , and then apply Theorem 3.5 to get an -tiling of covering almost all vertices for a suitably-chosen auxiliary graph . To get an almost -tiling of from this almost -tiling of , we will use the following lemma which says if we can find a in a copy of in , then we can find a in under certain conditions on . Its proof follows from that of Claim 6.1 in [5], where a similar assumption on (instead of ) is used. For completeness we include a proof of Lemma 3.6 in the appendix.
Lemma 3.6.
Given a constant and integers , there exist such that for any constant the following holds for every sufficiently large and . Let be an -vertex graph with and be pairwise vertex-disjoint sets of vertices in with for each and every pair being -regular. Then there exists a copy of in which contains exactly vertices in each for .
3.2 Proof of Lemma 2.3
Proof of Lemma 2.3.
Given such that and , we choose
Let be an -vertex graph with and . By applying Lemma 3.3 on with constants and , we obtain a partition for some and a spanning subgraph with properties (a)-(e) as stated. Let for all and be the corresponding -reduced graph of . Then it follows from Fact 3.4 that .
Let for some integers with . Note that the complete -partite graph has . Now we apply Theorem 3.5 on with and to obtain a family of vertex-disjoint copies of that cover all but at most vertices of .
Given a copy of in , without loss of generality, we may assume that its vertex set is together with the parts denoted by
Note that every pair of clusters from distinct parts forms an -regular pair with density at least .
We shall greedily embed in the original graph vertex-disjoint copies of that together cover almost all the vertices in . Now for each we divide arbitrarily into subclusters of (almost) equal size. For each we divide into subclusters of (almost) equal size. Here for simplicity we may further assume that for and for every . We call a family of subclusters legal if for each , i.e., forms a copy of in . Note that each () contains exactly subclusters in total. Therefore we can greedily partition the set of all subclusters into pairwise disjoint legal families.
Now if we have a -tiling in for every legal family , that covers all but at most vertices of , then we can find a -tiling covering all but at most vertices of . Applying this to all copies of from would give us a -tiling in covering all but at most
vertices. So to complete the proof of Lemma 2.3, it is sufficient to prove the following claim.
Claim 3.7.
Given any legal family , admits a -tiling covering all but at most vertices of .
Proof of claim.
For convenience, we write with . Recall that and for . If we can greedily pick vertex-disjoint copies of such that each contains exactly vertices in and vertices in for each , then almost all vertices in can be covered in this way. Now it suffices to show that for any with , each of size at least , there exists a copy of with exactly vertices inside and vertices inside each .
For any distinct , the pair is -regular with density at least . Then Fact 3.1 implies that every two sets from form an -regular pair with density at least , where . Therefore as , by applying Lemma 3.6 on with and the fact that , we obtain a copy of which contains exactly vertices in each for . Thus we obtain a desired copy of by discarding arbitrary vertices from from the clique above. ∎
∎
4 Building an absorbing set
The construction of an absorbing set is now known via a novel idea of Montgomery [34], provided that (almost) every set of vertices has linearly many vertex-disjoint absorbers as aforementioned. Such an approach is summarized as the following result by Nenadov and Pehova [35].
Lemma 4.1.
[35] Let be a graph with vertices and let and be constants. Then there exist and such that the following statement holds. Suppose that is a graph with vertices such that every has a family of at least vertex-disjoint -absorbers. Then contains a -absorbing set of size at most .
4.1 Finding absorbers
In order to find linearly many vertex-disjoint absorbers for (almost) every -subset, we shall use a notion of reachability introduced by Lo and Markström [32]. Here we introduce a slightly different version in our setup. Let be a graph of vertices and be a graph of vertices. For any two vertices , a set is called an -reachable set for if both and have -factors. For and , we say that two vertices and are -reachable (in ) if there are vertex-disjoint -reachable sets in , each of size at most . Moreover, we say that a vertex set is -closed if any two vertices in are -reachable in . Note that the corresponding -reachable sets for may not be included in . We say is -inner-closed if is -closed and additionally the corresponding -reachable sets for every pair also lie inside .
The following result from [19] builds a sufficient condition to ensure that every -subset has linearly many vertex-disjoint absorbers.
Lemma 4.2 ([19]).
Given with and , the following holds for any -vertex graph and sufficiently large . Let be an -vertex graph such that is -closed. Then every has a family of at least vertex-disjoint -absorbers.
Based on this lemma, it suffices to show that is closed. However, we shall show a slightly weaker result, namely, there exists a small vertex set such that the induced subgraph is inner-closed. The proof of Lemma 4.3 can be found in Section 4.2.
Lemma 4.3.
Given with and with , there exist such that the following holds for sufficiently large . Let be an -vertex graph with
Then admits a partition such that and is -inner-closed.
Then by Lemma 4.2 applied on , we can easily get the following corollary.
Corollary 4.4.
Given positive integers with and with , there exist such that the following holds for sufficiently large . Let be an -vertex graph with and . Then admits a partition such that and every has a family of at least vertex-disjoint -absorbers in .
To deal with the exceptional vertex set , we shall pick mutually vertex-disjoint copies of each containing a vertex in . To achieve this, one has to make sure that every vertex is covered by many copies of in (the aforementioned cover threshold). The following result enables us to find linearly many copies of covering any given vertex.
Proposition 4.5.
Given and a constant , there exists such that for all sufficiently large the following holds. Let be an -vertex graph with and . If is a subset of with , then for each vertex , contains a copy of covering .
Proof.
We choose and let . It suffices to show that for each vertex , there is a copy of in . Note that for every vertex in , we have . Given any vertex with , we have
Thus . Therefore by the definition of and the choice that , contains a copy of , which together with yields a copy of in . ∎
Proof of Lemma 2.2.
Given positive integers with and with , we choose . Let be an -vertex graph with , and . Then Corollary 4.4 implies that admits a partition such that and every has a family of at least vertex-disjoint -absorbers in . Let . Then by applying Lemma 4.1 on , we obtain in a -absorbing subset of size at most .
Now, we shall iteratively pick vertex-disjoint copies of each covering at least a vertex in whilst avoiding using any vertex in , and we claim that every vertex in can be covered in this way.
Let . For , we apply Proposition 4.5 iteratively to find a copy of covering in , while avoiding and all copies of found so far. Because of the fact that , this is possible as during the process, the number of vertices that we need to avoid is at most . Let be the union of the vertex sets over all copies of covering and . Recall that is a -absorbing set for , and . Then it is easy to check that is a -absorbing set for and
where the last inequality follows since . ∎
Now it remains to prove Lemma 4.3, which is done in the next subsection.
4.2 Proof of Lemma 4.3
Lemma 4.6.
[8, Lemma 5.1] Given with and a monotone increasing function , for all with , there exist positive constants and such that the following holds for sufficiently large . Let be an -vertex graph with and . Then admits a partition such that and every vertex in is -reachable to at least other vertices in with all the corresponding -reachable sets belonging to .
Proof of Lemma 4.3.
Given with and with , we choose constants
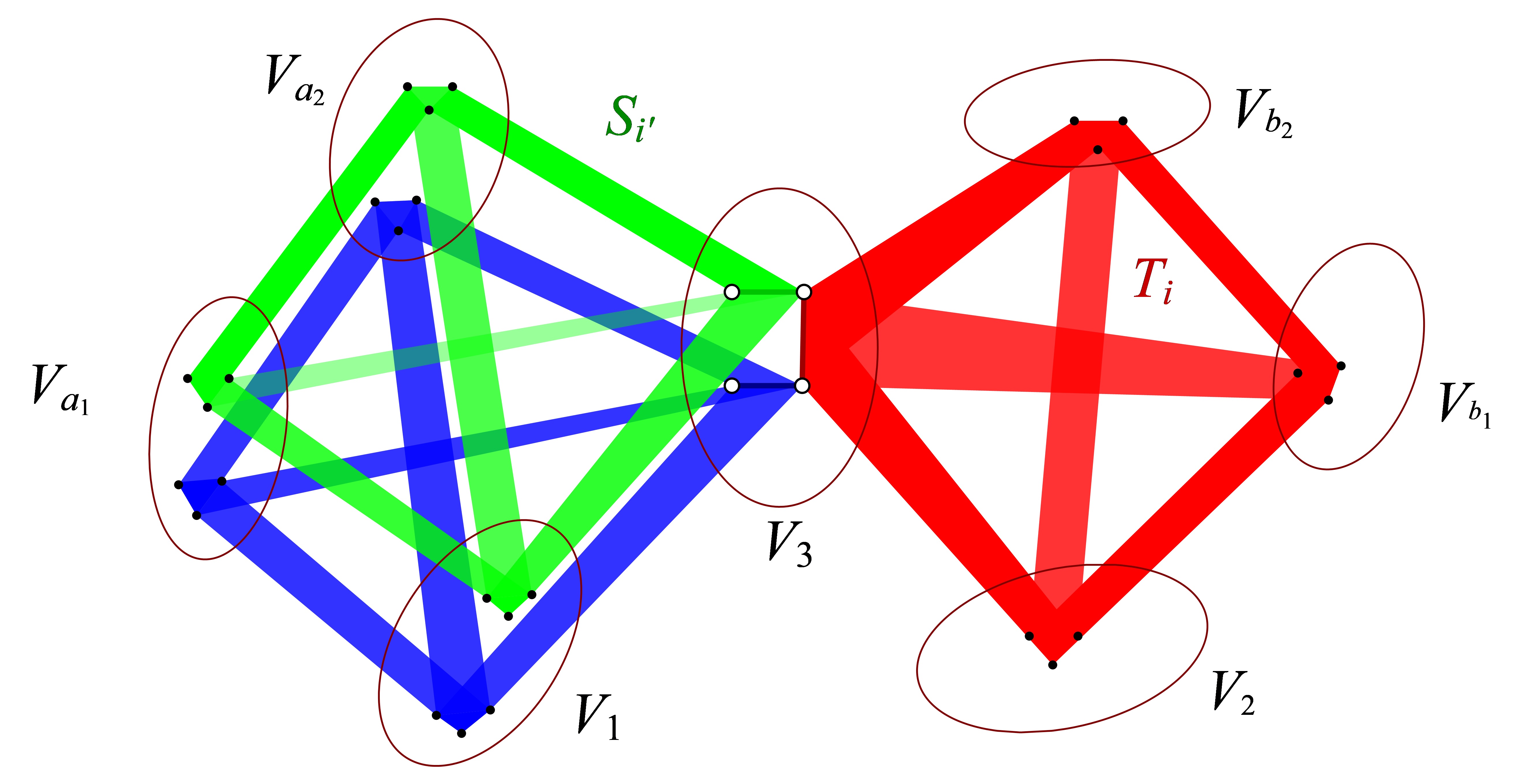
and let be an -vertex graph with and . Then by applying Lemma 4.6, we obtain a partition such that and every vertex in is -reachable to at least other vertices in . For any two vertices , we shall prove in that are -reachable.
Let and be the sets of vertices that are -reachable to and , respectively. By taking subsets from them and renaming if necessary, we may further assume that and . Then by applying Lemma 3.3 on with positive constants and , we obtain a refinement of the original partition and a spanning subgraph with properties (a)-(e), where we let for all and be the corresponding -reduced graph. Without loss of generality, we may assume that and . Note that by Fact 3.4, we can observe that . Let be a common neighbor of and in .
Now we shall show that and are -reachable. We write for some integers with . Note that . Thus every vertices in have at least common neighbors and we can greedily pick two copies of in that contain the edge and respectively and overlap only on the vertex . We use and to denote the two family of clusters related to the two copies of in . Applying Lemma 3.6 on with and playing the role of , we can iteratively take vertex-disjoint copies of (since ) which are denoted by , such that each has exactly vertices in , vertices in and , . Let be a subset obtained by taking exactly one vertex from each such . Then and again by applying Lemma 3.6 on with and playing the role of , we can greedily pick vertex-disjoint copies of , denoted by , such that each has exactly vertices in , vertices in and , .
Now it remains to show the following statement with . Recall that .
Claim 4.7.
There exist vertex-disjoint -reachable sets for , each of size .
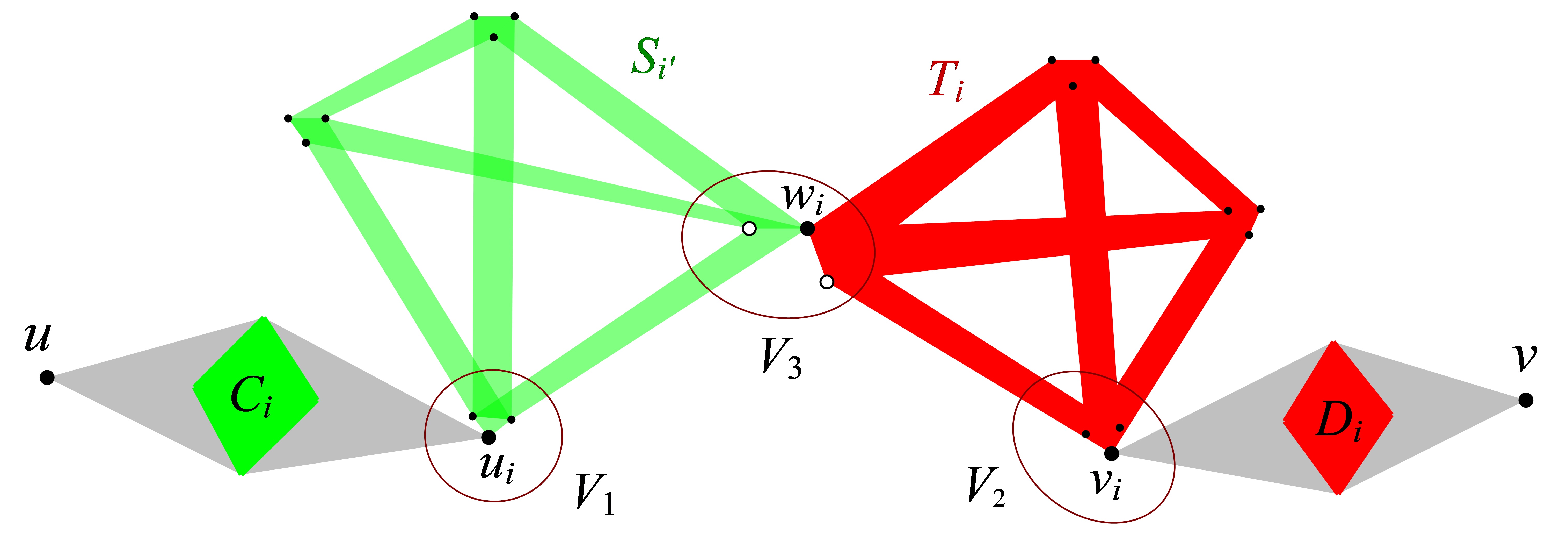
Proof of claim.
Here the main idea is to extend all such ’s to pairwise vertex-disjoint -reachable sets. Note that for each , there exists such that the two copies of intersect on exactly one vertex in , denoted by . Let be an arbitray vertex chosen from that lies in , and be chosen from that lies in . Then by the assumption that is -reachable to , there exist at least vertex-disjoint -reachable sets for and (resp. and ). Therefore by the fact that , we can greedily choose two vertex-disjoint -reachable sets, say and , for and , respectively, which are also disjoint from all cliques or for . It is easy to check that the set
has size and (similarly for ) contains copies of , which are induced on the sets and , respectively. Thus by definition is a -reachable set for and . A desired number of mutually disjoint -reachable set can be chosen by extending each as above. ∎
∎
5 A construction
In this section, we shall use a construction of -free graphs with small to prove Proposition 1.9. An explicit construction was firstly obtained by Erdős and Rogers [13] in the setting that . Here we give a probabilistic construction as follows, whose proof is very similar to that of a result of Nenadov and Pehova (see Proposition 4.1 in [35]).
Lemma 5.1.
For any with , a constant and sufficiently large integer , there exists an -vertex -free graph such that .
Now we firstly give a short proof of Proposition 1.9, and then present the proof of Lemma 5.1 at the end of this section.
Proof of Proposition 1.9.
Fix and constants as in the statement. Let be sufficiently large and define . Then by Lemma 5.1, we choose to be a -vertex -free graph with .
Let be an -vertex graph with vertex partition such that
-
(i)
is a clique with ;
-
(ii)
is a complete bipartite graph;
-
(iii)
induces a copy of .
Now we claim that has the desired properties. Indeed it is easy to see that and . Since is -free, every copy of must intersect on at least vertices. Thus every -tiling in contains at most vertex-disjoint copies of , which together cover at most vertices. ∎
Proof of Lemma 5.1.
We only consider as the case follows from a celebrated result on Ramsey number that [25]. We choose and let . Considering the random graph with , we shall verify that with positive probability, is -free and . By applying the FKG inequality [15], we have that
where we bound for . Now it remains to determine the probability of the event that .
Let be the random variable counting all sets such that and is -free. Then
Here we shall use a powerful inequality of Janson [21], where for each -set we denote by the indicator variable for the event that . Let . Then by Janson’s inequality, we obtain that
where and . Note that
where the last equality follows because and thus holds for any . Therefore and by Markov’s inequality, with probability at least , we have , that is, .
By the inclusive-exclusive principle, the probability of the event that is -free and is at least
and it is positive for sufficiently large as long as
which follows easily as . ∎
6 Concluding remarks
In this paper we study the minimum degree condition for -factors in graphs with sublinear -independence number. Our result is asymptotically sharp when for any constant .
This leads to the following question: What is the general behavior of the minimum degree condition forcing a clique factor when the condition of -independence number is imposed within the range ? We formulate this as follows. Given integers with , a constant and a monotone increasing function , we denote by the maximum integer such that there exists an -vertex graph with and which does not contain a -factor. Here we try to understand when and how the value changes sharply when the magnitude of varies. This can be seen as a degree version of the well-known phase transition problem for in Ramsey–Turán theory (see [5, 3, 24]). It is worth noting that many open questions on the phase transition problem of are essentially related to Ramsey theory.
Here we consider the basic case . Recall that Knierim and Su [26] resolved Problem 1.1 for by giving an asymptotically tight minimum degree bound . In our context of , this can be roughly reformulated as
Also, for integers with , Theorem 1.4 can be stated as
In this paper, our main theorem combined with Proposition 1.9 and the cover threshold implies that for and ,
This provides an insight into the general behavior of but the asymptotic behavior of for a general seems to be out of reach. It will be interesting to study the case for any constant .
References
- [1] Noga Alon, Michael Krivelevich, and Benny Sudakov. Turán numbers of bipartite graphs and related Ramsey-type questions. volume 12, pages 477–494. 2003. Special issue on Ramsey theory.
- [2] Noga Alon and Raphael Yuster. -factors in dense graphs. Journal of Combinatorial Theory, Series B, 66(2):269–282, 1996.
- [3] J. Balogh and J. Lenz. Some Exact Ramsey–Turán Numbers. Bulletin of the London Mathematical Society, 44:1251–1258, 2012.
- [4] J. Balogh and J. Lenz. On Ramsey–Turán numbers of graphs and hypergraphs. Israel Journal of Mathematics, 194:45–68, 2013.
- [5] József Balogh, Ping Hu, and Miklós Simonovits. Phase transitions in Ramsey–Turán theory. Journal of Combinatorial Theory, Series B, 114:148–169, 2015.
- [6] József Balogh, Theodore Molla, and Maryam Sharifzadeh. Triangle factors of graphs without large independent sets and of weighted graphs. Random Structures and Algorithms, 49(4):669–693, 2016.
- [7] B. Bollobás and P. Erdős. On a Ramsey–Turán type problem. Journal of Combinatorial Theory, Series B, 21(2):166–168, 1976.
- [8] Fan Chang, Jie Han, Jaehoon Kim, Guanghui Wang, and Donglei Yang. Embedding clique-factors in graphs with low -independence number. arXiv preprint arXiv:2111.10512, 2021.
- [9] Yulin Chang, Jie Han, Yoshiharu Kohayakawa, Patrick Morris, and Guilherme Oliveira Mota. Factors in randomly perturbed hypergraphs. Random Structures and Algorithms, 60(2):153–165, 2022.
- [10] David Conlon, Jacob Fox, and Benny Sudakov. Ramsey numbers of sparse hypergraphs. Random Structures and Algorithms, 35(1):1–14, 2009.
- [11] R. Diestel. Graph Theory, volume 173 of. Graduate texts in mathematics, 2017.
- [12] Laihao Ding, Jie Han, Shumin Sun, Guanghui Wang, and Wenling Zhou. -factors in quasi-random hypergraphs. Journal of the London Mathematical Society, 106(3):1810–1843, 2022.
- [13] P. Erdős and C. A. Rogers. The construction of certain graphs. Canadian Journal of Mathematics. Journal Canadien de Mathématiques, 14:702–707, 1962.
- [14] P. Erdős and Vera T. Sós. Some remarks on Ramsey’s and Turán’s theorem. In Combinatorial theory and its applications, II (Proc. Colloq., Balatonfüred, 1969), pages 395–404, 1970.
- [15] C. M. Fortuin, P. W. Kasteleyn, and J. Ginibre. Correlation inequalities on some partially ordered sets. Communications in Mathematical Physics, 22:89–103, 1971.
- [16] Jacob Fox, Po-Shen Loh, and Yufei Zhao. The critical window for the classical Ramsey-Turán problem. Combinatorica, 35(4):435–476, 2015.
- [17] Jacob Fox and Benny Sudakov. Dependent random choice. Random Structures and Algorithms, 38(1-2):68–99, 2011.
- [18] András Hajnal and Endre Szemerédi. Proof of a conjecture of P. Erdős. Combinatorial theory and its applications, 2(4):601–623, 1970.
- [19] J. Han, Patrick Morris, Guanghui Wang, and Donglei Yang. A Ramsey–Turán theory for tilings in graphs. arXiv preprint arXiv:2106.09688, 2021.
- [20] J. Han, C. Zang, and Y. Zhao. Minimum vertex degree thresholds for tiling complete 3-partite 3-graphs. Journal of Combinatorial Theory, Series A, 149:115–147, 2017.
- [21] Svante Janson, Tomasz Łuczak, and Andrzej Ruciński. An exponential bound for the probability of nonexistence of a specified subgraph in a random graph. In Random graphs ’87 (Poznań, 1987), pages 73–87. Wiley, Chichester, 1990.
- [22] Peter Keevash and Richard Mycroft. A multipartite Hajnal–Szemerédi theorem. Journal of Combinatorial Theory, Series B, 114:187–236, 2015.
- [23] H. A. Kierstead and A. V. Kostochka. An Ore-type theorem on equitable coloring. Journal of Combinatorial Theory, Series B, 98(1):226–234, 2008.
- [24] Jaehoon Kim, Younjin Kim, and Hong Liu. Two conjectures in Ramsey-Turán theory. SIAM Journal on Discrete Mathematics, 33(1):564–586, 2019.
- [25] Jeong Han Kim. The Ramsey number has order of magnitude . Random Structures and Algorithms, 7(3):173–207, 1995.
- [26] Charlotte Knierim and Pascal Su. -factors in graphs with low independence number. Journal of Combinatorial Theory, Series B, 148:60–83, 2021.
- [27] J. Komlós and M. Simonovits. Szemerédi’s Regularity Lemma and its applications in graph theory. Combinatorics, Paul Erdős is eighty, Vol. 2 (Keszthely, 1993), 1996.
- [28] János Komlós. Tiling Turán theorems. Combinatorica, 20(2):203–218, 2000.
- [29] M. Krivelevich. Triangle factors in random graphs. Combinatorics, Probability and Computing, 6:337–347, 1997.
- [30] D Kühn and D. Osthus. The minimum degree threshold for perfect graph packings. Combinatorica, 29(1):65–107, 2009.
- [31] Hong Liu, Christian Reiher, Maryam Sharifzadeh, and Katherine Staden. Geometric constructions for Ramsey–Turán theory. arXiv preprint arXiv:2103.10423, 2021.
- [32] Allan Lo and Klas Markström. -factors in hypergraphs via absorption. Graphs and Combinatorics, 31(3):679–712, 2015.
- [33] Clara Marie Lüders and Christian Reiher. The Ramsey-Turán problem for cliques. Israel Journal of Mathematics, 230(2):613–652, 2019.
- [34] Richard Montgomery. Spanning trees in random graphs. Advances in Mathematics, 356:106–793, 2019.
- [35] R. Nenadov and Y. Pehova. On a Ramsey–Turán variant of the Hajnal–Szemerédi theorem. SIAM Journal on Discrete Mathematics, 34(2):1001–1010, 2020.
- [36] Vojtech Rödl, Andrzej Ruciński, and Endre Szemerédi. Perfect matchings in large uniform hypergraphs with large minimum collective degree. Journal of Combinatorial Theory, Series A, 116(3):613–636, 2009.
- [37] M. Simonovits and V. T. Sós. Ramsey–Turán theory. Discrete Mathematics, 229(1-3):293–340, 2001.
- [38] E. Szemerédi. On graphs containing no complete subgraphs with 4 vertices. Matematikai Lapok. Bolyai János Matematikai Társulat, 23:113–116, 1972.
- [39] A. Treglown. On directed versions of the Hajnal–Szemerédi theorem. Combinatorics, Probability and Computing, 24:873–928, 2015.
Appendix A Proof of Lemma 3.6
We use the method of dependent random choice to prove Lemma 3.6. The method was developed by Füredi, Gowers, Kostochka, Rödl, Sudakov, and possibly many others. The next lemma is taken from Alon, Krivelevich and Sudakov [1]. Interested readers may check the survey paper on this method by Fox and Sudakov [17].
Lemma A.1 (Dependent Random Choice).
[1] Let be positive integers. Let be a graph with vertices and average degree . If there is a positive integer such that
| (1) |
then contains a subset of at least vertices such that every vertices in have at least common neighbors.
Conlon, Fox, and Sudakov [10] extended Lemma A.1 to hypergraphs. The weight of a set of edges in a hypergraph is the number of vertices in the union of these edges.
Lemma A.2 (Hypergraph Dependent Random Choice).
[10] Suppose are positive integers, , and is an -uniform -partite hypergraph with and at least edges. Then there exists an -uniform -partite hypergraph on the vertex sets which has at least edges and such that for each nonnegative integer , there are at most dangerous sets of edges of with weight , where a set of edges of is dangerous if and the number of vertices such that for every edge is less than .
Proof of Lemma 3.6.
Given a constant and integers , we choose
Let be an -vertex graph with , where
Let be given such that , and every pair is -regular with density at least . We define a -uniform -partite hypergraph whose vertex set is and edge set is the family of -sets that span -cliques in and contain one vertex from each of . We may assume , then by the counting lemma, , where . Let
We start from . For we apply Lemma A.2 to with and to get . Note that are all constants and . It is easy to check that for , we have
Then by Lemma A.2 there exists an -uniform -partite hypergraph on the vertex sets that contains at least edges and contains no dangerous sets of edges on vertices. (Recall that a set of edges on vertices is dangerous if the number of vertices for which for every edge is less than ). Now we have a hypergraph sequence . We will prove by induction on that there is a -set for such that and is complete -partite. Note that if a vertex set is an edge of , then is a -clique. So , which will prove Lemma 3.6.
We first show that the induction hypothesis holds for . Note that = 2, so is a bipartite graph on vertices with at least edges. We now apply Lemma A.1 to with
We check condition (1):
where the last equality and inequality follow as long as . Therefore we have a subset of with such that every vertices in have at least common neighbors in . Either or contains at least half of the vertices of , so w.l.o.g. we may assume that contains at least vertices. Because , the vertex set contains a -vertex set such that . The vertices of have at least common neighbors in , so their common neighborhood also contains a -vertex subset of such that . Now is complete bipartite. We are done with the base case .
For the induction step, assume that the induction hypothesis holds for , then we can find a complete -partite subhypergraph of spanned by , where for every . The hypergraph has no dangerous set of edges on vertices, and contains vertices and edges, so is not dangerous. Then we can find a set of vertices in such that for every edge and every vertex , , which means that is complete -partite. Then, because , we can find a -vertex subset of such that . ∎