Cluster-shell competition and effect of adding hyperons

In our framework, every single particle is described in a Gaussian form as in many traditional cluster models, including the Brink model [9],

where the Gaussian center parameter $\bm{\zeta}$ is related to the expectation value of the position of the nucleon, and $\chi^{\tau,\sigma}$ is the spin-isospin part of the wave function. The $\alpha$ cluster is expressed by four nucleons with different spin and isospin sharing the same $\bm{\zeta}$ value. For the size parameter $\nu$, here we use $\nu=1/2b^{2}$ and $b=1.46$ fm. The Slater determinant is constructed from these single-particle wave functions by antisymmetrizing them. The $\Lambda$ particle is represented by the same local Gaussian-type wave function.

This traditional $\alpha$ cluster wave function cannot take into account the effect of non-central interactions including the spin-orbit interaction. We can extend the model based on the AQCM, by which the contribution of the spin-orbit interaction due to the breaking of $\alpha$ clusters is included. Here the $\bm{\zeta}$ values in Eq. (1) are changed to complex numbers. When the original value of the Gaussian center parameter $\bm{\zeta}$ is $\bm{R}$, which is real and related to the spatial position of this nucleon, it is transformed by adding the imaginary part as

where $\bm{e}^{\text{spin}}$ is a unit vector for the intrinsic-spin orientation of this nucleon. The control parameter $\lambda$ is associated with the breaking of the cluster. After this transformation, the $\alpha$ clusters are called quasi-clusters. The two nucleons in the same quasi-cluster with opposite spin orientation have $\bm{\zeta}$ values that are complex conjugate to each other. This situation corresponds to the time-reversal motion of two nucleons.

In our previous analysis on ${}^{12}\mathrm{C}$ [10], we have introduced two parameters representing the distances between quasi-clusters and their breaking ($\lambda$). The subclosure configuration of $\left(s_{1/2}\right)^{4}\,\left(p_{3/2}\right)^{8}$ of the $jj$-coupling shell model can be obtained at the limit of small relative distances and $\lambda=1$.

Each AQCM Slater determinant is projected to the eigenstates of parity and angular momentum by using the projection operator $P_{J^{\pi}}^{K}$,

Here ${D_{MK}^{J}}$ is the Wigner $D$-function and $R\left(\Omega\right)$ is the rotation operator for the spatial and spin parts of the wave function. This integration over the Euler angle $\Omega$ is numerically performed. The operator $P^{\pi}$ is for the parity projection ($P^{\pi}=\left(1+P^{r}\right)/\sqrt{2}$ for the positive-parity states, where $P^{r}$ is the parity-inversion operator), which is also performed numerically.

The AQCM basis states with different distances between quasi-clusters and $\lambda$ values are superposed based on GCM. We also generate Gaussian centers for the $\Lambda$ particles using random numbers, and the basis states with different positions are superposed. The coefficients $\left\{c^{K}_{i}\right\}$ for the linear combination of the Slater determinants are obtained together with the energy eigenvalue $E$ when we diagonalize the norm and Hamiltonian matrices, namely by solving the Hill-Wheeler equation.

The Hamiltonian consists of kinetic energy and potential energy terms. For the potential part, the interaction consists of the central, spin-orbit, and Coulomb terms. The nucleon-nucleon interaction is Volkov No.2 [32] with the Majorana exchange parameter of $M=0.6$, which has been known to reproduce the scattering phase shift of ⁴He–⁴He [33]. For the spin-orbit part, we use the spin-orbit term of the G3RS interaction [34], which is a realistic interaction originally developed to reproduce the nucleon-nucleon scattering phase shifts. The strength of the spin-orbit interactions [10] is set to $V_{ls}^{1}=V_{ls}^{2}=1450\,\mathrm{MeV}$, which reproduces the binding energy of ¹²C from the three-$\alpha$ threshold. For the nucleon-$\Lambda$ interaction, we employ only the central part; YNG-ND interaction [35]. The $k_{F}$ value for ${}^{9}_{\Lambda}$Be and ${}^{10}_{\Lambda\Lambda}$Be is 0.962 fm^-1 as in Ref. [14] and 1.17 fm^-1 for ${}^{13}_{\Lambda}$C and ${}^{14}_{\Lambda\Lambda}$C as in Ref. [17]. For the $\Lambda$-$\Lambda$ interaction, we adopt the one called “NS” in Ref. [35], which allows the reproduction of the binding energy of ${}^{6}_{\Lambda\Lambda}$He.

We start the discussion with ${}^{8}\mathrm{Be}$. Our Hamiltonian gives the energy of $-27.57$ MeV for the $\alpha$ cluster, and thus, $-55.1$ MeV is the two-$\alpha$ threshold energy (experimentally $-56.6$ MeV, to which our theoretical value does not contradict). Figure 1 (a) shows the energy curves of the $0^{+}$ state of ${}^{8}\mathrm{Be}$ as a function of the distance between two ${}^{4}\mathrm{He}$ clusters. The solid line is for $\lambda=0$ (pure two $\alpha$’s), and the dotted and dashed line are for two quasi-clusters with $\lambda=0.1$ and 0.2, respectively. The energy minimum point appears around the relative distance of $\sim$3.5 fm. This distance is quite large, and this is outside of the interaction range of the spin-orbit interaction. Therefore, the $\lambda$ value that gives the minimum energy is zero (solid line), which means that the $\alpha$ clusters are not broken. The $\alpha$ breaking effect can be seen in more inner regions, where the energies of dotted and dashed lines are lower than the solid line. The $\alpha$ clusters are surely broken there. However, at short relative distances, the energy itself is high enough, and the spin-orbit interaction only plays a role in reducing the increase of the excitation energy to some extent when two clusters get closer.

The situation is slightly different in Figure 1 (b), which is for the $1/2^{+}$ of ${}^{9}_{\Lambda}$Be, where one $\Lambda$ particle is added. We superpose 50 Slater determinants with different positions for the $\Lambda$ particle and diagonalize the Hamiltonian based on the GCM for each cluster-cluster distance and $\lambda$. Owing to the $\Lambda$ particle added, the attractive effect is increased, and the optimal distance between the two ${}^{4}\mathrm{He}$ nuclei (lowest energy point) is around 3 fm, slightly shorter than the ${}^{8}\mathrm{Be}$ case. Here, the solid line ($\lambda=0$) and the dotted line ($\lambda=0.1$) almost degenerate, and thus, the $\alpha$ clusters are slightly broken due to the spin-orbit effect. The tendency is a bit enhanced in ${}^{10}_{\Lambda\Lambda}$Be shown in Fig 1 (c). The optimal cluster-cluster distance is less than 3 fm, where the dotted line ($\lambda=0.1$) is slightly lower than the solid line ($\lambda=0$). The number of Slater determinants with different positions for the $\Lambda$ particles is increased to 100 for each ⁴He–⁴He distance and $\lambda$. In this way, since the ⁴He–⁴He distances are large in ${}^{9}_{\Lambda}$Be and ${}^{10}_{\Lambda\Lambda}$Be, we find that the $\alpha$-cluster braking effect is rather small.

Next we discuss ${}^{12}\mathrm{C}$ and ${}^{13}_{\Lambda}$C, and ${}^{14}_{\Lambda\Lambda}$C. The three-$\alpha$ threshold energy is $-82.7$ MeV in our calculation compared with the experimental value of $-84.9$ MeV. Figure 2 (a) shows the energy curves of $0^{+}$ state of ${}^{12}\mathrm{C}$ with an equilateral triangular configuration as a function of the distance between two ${}^{4}\mathrm{He}$ clusters. The solid line is for $\lambda=0$ (pure three $\alpha$’s). Since one ${}^{4}\mathrm{He}$ is added to ${}^{8}\mathrm{Be}$, the energy minimum point appears around the relative distance of 2.5–3.0 fm, shorter by 1 fm than the previous ${}^{8}\mathrm{Be}$ case before allowing the breaking of $\alpha$ clusters. Therefore, it is considered that the three $\alpha$ clusters step in the interaction range of the spin-orbit interaction. The dotted line ($\lambda=0.1$) and dashed line ($\lambda=0.2$) almost degenerate at the region of the lowest energy (the relative cluster-cluster distance shrinks to 2 fm there).

This tendency is enhanced in Fig. 2 (b), which is for the $1/2^{+}$ of ${}^{13}_{\Lambda}$C, where one $\Lambda$ particle is added. Owing to the $\Lambda$ particle added, the attractive effect is increased, and the optimal distance between the ${}^{4}\mathrm{He}$ nuclei is around 2.5 fm (solid line) before breaking the $\alpha$ clusters. When we allow the breaking, the energy curves become almost flat inside the relative ⁴He–⁴He distance of 2 fm. The energy minimum points of the dotted ($\lambda=0.1$) and dashed ($\lambda=0.2$) lines are lower than that of the solid line ($\lambda=0$).

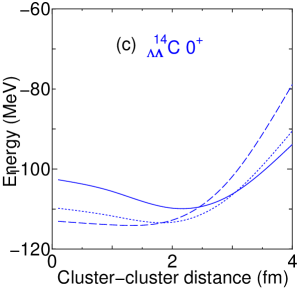
The attractive effect of the $\Lambda$ particles is much more enhanced in Fig. 2 (c), which is for the $0^{+}$ state of ${}^{14}_{\Lambda\Lambda}$C. The optimal distance between the ${}^{4}\mathrm{He}$ nuclei (energy minimum point) is around 2.2 fm before breaking the $\alpha$ clusters (solid line). When we allow the breaking, the energy minimum point appears at the relative cluster–cluster distance of $\sim$1.4 fm, where the dashed line ($\lambda$=0.2) gives the lowest energy, and $\alpha$ clusters are significantly broken. We can confirm that the optimal cluster distance gets shorter, and the breaking of $\alpha$ clusters becomes larger with the increasing number of $\Lambda$ particles added to the system.

To demonstrate the relation between the effect of $\alpha$ breaking and spin-orbit interaction, we calculate the ground state energies of ⁸Be, ${}^{9}_{\Lambda}$Be, ${}^{10}_{\Lambda\Lambda}$Be (Table 1) and those of ¹²C, ${}^{13}_{\Lambda}$C, ${}^{14}_{\Lambda\Lambda}$C (Table 2) with two models: “AQCM”’ which explicitly takes account of the breaking effect of $\alpha$, and “Brink model” which does not involve the $\alpha$ breaking effect ($\lambda=0$). We superpose Slater determinants with different positions of the $\Lambda$ particle(s), ⁴He–⁴He cluster distances, and $\alpha$-breaking parameter $\lambda$ and diagonalize the Hamiltonian based on the GCM.

For the Be case (Table 1), the energy difference between Brink and AQCM is less than 0.2 MeV in ${}^{8}\mathrm{Be}$, which means that the spin-orbit interaction does not break the $\alpha$ clusters since they are separated by a certain distance. The situation is basically the same when $\Lambda$ particle(s) is added. The difference is about 0.5-0.6 MeV in ${}^{9}_{\Lambda}$Be and ${}^{10}_{\Lambda\Lambda}$Be. Concerning the ground state energy of ${}^{10}_{\Lambda\Lambda}$Be, the binding energy ($B_{\Lambda\Lambda}$) of $17.5\pm 0.4$ MeV from ⁸Be has been reported in Ref. [36], which has been revised to $14.7\pm 0.4$ MeV in Ref. [37] (see the discussions in Refs. [38, 39]), and the present result (15.23 MeV) is almost consistent with the latter case.

For the C case (Table 2), the energy difference between Brink and AQCM is about 3.3 MeV in ${}^{12}\mathrm{C}$, and this is much enhanced with the increasing number of the $\Lambda$ particles added. The difference increases to 5.2 MeV in ${}^{14}_{\Lambda\Lambda}$C. This is because the spin-orbit interaction works in the inner region of the nuclear systems; the glue-like effect of $\Lambda$ particles shrinks the system and induces more contribution of the spin-orbit interaction.

To clarify the mixing of the $jj$-coupling shell model components in each state, we utilize the expectation value of the one-body spin-orbit operator,

where $\bm{l}_{i}$ and $\bm{s}_{i}$ are the orbital angular momentum and the spin operators for the $i$th nucleon. The sum runs over the nucleons. The expectation value is zero for the pure $\alpha$ cluster state owing to the antisymmetrization effect. Also, the $\bm{l}_{i}\cdot\bm{s}_{i}/\hbar^{2}$ value is $0.5$ for one nucleon in the $p_{3/2}$ orbit, and the eigen value is $4$ for the subclosure configuration of the $jj$-coupling shell model $(\left(s_{1/2}\right)^{4}\,\left(p_{3/2}\right)^{8})$ in ¹²C.

The expectation values of the one-body spin-orbit operator for the ground states of ${}^{8}\mathrm{Be}$, ${}^{9}_{\Lambda}$Be, and ${}^{10}_{\Lambda\Lambda}$Be are listed in the column “one-body LS” in Table 1. Although the value increases with the number of $\Lambda$ particles added, it is rather small and cluster structure is considered to be not broken. However, this is completely different in the C case. The expectation values of the one-body spin-orbit operator for the ground states of ${}^{12}\mathrm{C}$, ${}^{13}_{\Lambda}$C, and ${}^{14}_{\Lambda\Lambda}$C are listed in the column “one-body LS” in Table 2. The value is $1.55$ for ${}^{12}\mathrm{C}$, and we can reconfirm that the ground state has mixed configurations of shell and cluster aspects. As the number of the $\Lambda$ particles added increases, we can see that the ground states approach the $jj$-coupling shell model side. The values for ${}^{13}_{\Lambda}$C and ${}^{14}_{\Lambda\Lambda}$C are 1.86 and 2.05, respectively.

We have discussed that the ground states shift to the $jj$-coupling shell model side by adding $\Lambda$ particles, and the final question is where the “pure” three-$\alpha$ cluster state appears in ${}^{14}_{\Lambda\Lambda}$C. We can discuss it by preparing the pure three-$\alpha$ cluster states and orthogonalizing them to the ground state. The shift of the ground state to the $jj$-coupling shell-model-side after allowing the breaking of $\alpha$ clusters is found to play a crucial role.

The solid line in Fig. 3 (a) shows the excited $0^{+}$ state with equilateral triangular configurations of pure three-$\alpha$ clusters as a function of the relative distances between the $\alpha$ clusters. At each $\alpha$–$\alpha$ distance, the wave function is orthogonalized to the ground state. Here the ground state is represented by the optimal AQCM basis state (⁴He–⁴He distance of $1.4$ fm and $\Lambda=0.2$) shown by the solid circle. Therefore, the two-by-two matrix is diagonalized at every point on the horizontal axis. It is found that the pure cluster state appears around the excitation energy of $E_{x}=15$ MeV with the relative $\alpha$–$\alpha$ distance of $\sim$2.5 fm. To simplify the discussion, the positions for the Gaussian center parameters for the $\Lambda$ particles are set to origin only in Figs. 3 (a) and (b).

This situation is quite different if the $\alpha$ cluster is assumed to be not broken due to the spin-orbit interaction in the ground state. This is an artificial calculation, but we can clearly see the influence of the cluster-shell competition in the excited state; Fig. 3 (b) shows the result when the ground state is represented by the Brink model, which is prepared by changing the $\lambda$ value to zero and the ⁴He–⁴He distance to 2.2 fm. The excited $0^{+}$ state is quite influenced by this change of the ground state. The energy is pushed up by more than 10 MeV, and the optimal $\alpha$–$\alpha$ distance is increased to $\sim$3 fm. This is because if the ground state is a pure three-$\alpha$ cluster state, the excited states need to be more clusterized to satisfy the orthogonal condition. On the other hand, if the ground state has different components other than the cluster structure, it is easier for the pure cluster state to be orthogonal to the ground state. This effect has been known in ${}^{12}\mathrm{C}$ and called the “shrink effect” of the second $0^{+}$ state; when the $\alpha$ breaking component is mixed in the ground state, the second $0^{+}$ state orthogonal to the ground state shrinks. We found that this shrinking effect is much more enhanced in ${}^{14}_{\Lambda\Lambda}$C.