Clustering of Extremely Red Objects in Elais-N1 from the UKIDSS DXS with optical photometry from Pan-STARRS 1 and Subaru
Abstract
We measure the angular clustering of 33 415 extremely red objects (EROs) in the Elais-N1 field covering 5.33 deg2, which cover the redshift range to . This sample was made by merging the UKIDSS Deep eXtragalactic Survey (DXS) with the optical Subaru and Pan-STARRS PS1 datasets. We confirm the existence of a clear break in the angular correlation function at corresponding to Mpc at . We find that redder or brighter EROs are more clustered than bluer or fainter ones. Halo Occupation Distribution (HOD) model fits imply that the average mass of dark matter haloes which host EROs is over and that EROs have a bias ranging from 2.7 to 3.5. Compared to EROs at , at EROs have a higher bias and fewer are expected to be satellite galaxies. Furthermore, EROs reside in similar dark matter haloes to those that host galaxies. We compare our new measurement and HOD fits with the predictions of the GALFORM semi-analytical galaxy formation model. Overall, the clustering predicted by GALFORM gives an encouraging match to our results. However, compared to our deductions from the measurements, GALFORM puts EROs into lower mass haloes and predicts that a larger fraction of EROs are satellite galaxies. This suggests that the treatment of gas cooling may need to be revised in the model. Our analysis illustrates the potential of clustering analyses to provide observational constraints on theoretical models of galaxy formation.
keywords:
surveys-galaxies: evolution - galaxies: photometry - cosmology: observations - infrared: galaxies.1 Introduction
In the Lambda Cold Dark Matter (CDM) paradigm, small fluctuations in the primordial density field grow through gravitational instability and merge to form more massive structures. In this scenario, small haloes in general form first and become the seeds for larger haloes; galaxies form at the centres of these dark matter haloes, as the baryons collapse, cool and form stars (White & Rees 1978). Therefore the formation and evolution of galaxies depends critically on the properties of dark matter haloes (e.g., Eke et al. 2004; Baugh 2006). In addition, the spatial distribution of galaxies must be related to that of the underlying dark matter haloes.
In this context, the measurement of the clustering of galaxies makes it possible to link galaxy properties with halo properties, since the clustering of galaxies is determined by the clustering of their host haloes, with more massive haloes showing higher clustering amplitudes than lower mass haloes (e.g., Mo & White 1996). The most popular methods linking them are the two-point correlation function of galaxies (Peebles 1980) and the halo model with the Halo Occupation Distribution (HOD) framework (Jing, Mo & Boerner 1998; Benson et al. 2000; Ma & Fry 2000; Peacock & Smith 2000; Seljak 2000; Scoccimarro et al. 2001; Berlind & Weinberg 2002; for a review see Cooray & Sheth 2002). The two-point correlation function describes the excess probability over random of the existence of a galaxy pair at a specific separation. The HOD quantifies the probability that a certain type of galaxy is hosted by a halo of a given mass. Given a cosmology and the HOD, the galaxy correlation function can be generated.
Recently, wide area surveys have provided an opportunity to measure the clustering of different galaxies accurately. From optical imaging and spectroscopic surveys, the correlation function of low redshift galaxies selected by their luminosity or colour has been measured (Norberg et al. 2001, 2002; Zehavi et al. 2002, 2005; Coil et al. 2008; Ross & Brunner 2009; Ross, Percival & Brunner 2010; Zehavi et al. 2011). In addition, the halo properties of luminous red galaxies (LRGs) at were estimated using redshift information by Blake, Collister & Lahav (2008), Wake et al. (2008a) and Sawangwit et al. (2011). The correlation function has also been used to study the properties of radio galaxies, quasars and Active Galactic Nuclei (AGN) (Wake et al. 2008b; Croom et al. 2005; Coil et al. 2009; Ross et al. 2009; Hickox et al. 2011).
Extracting galaxies at , especially red galaxies, is difficult since the bulk of their stellar emission is redshifted to IR wavelengths. Thus a near-IR dataset is required to select red, passive galaxies at . There are several colour criteria known to be successful at selecting galaxies at . Firstly, Extremely Red Objects (EROs, Elston, Rieke & Rieke 1988) can be selected by their red optical/near-IR colour (e.g. ). This selection is efficient in detecting massive galaxies, , at (Conselice et al. 2008). Moreover, it is known that EROs are strongly clustered (Daddi et al. 2000; Roche et al. 2002, 2003; Brown et al. 2005; Kong et al. 2006, 2009; Kim et al. 2011a) and so are expected to reside in massive dark matter haloes (Moustakas & Somerville 2002; Gonzalez-Perez et al. 2009; Palamara et al. 2013). However, EROs selected with a simple colour cut are contaminated by dusty, star-forming galaxies (Pozzetti & Mannucci 2000; Smail et al. 2002; Roche et al. 2002; Cimatti et al. 2002, 2003; Moustakas et al. 2004; Sawicki et al. 2005; Simpson et al. 2006; Conselice et al. 2008; Kong et al. 2009). Alternatively, a red near-IR colour, , is useful to select Distant Red Galaxies (DRGs) which are predominantly intrinsically red galaxies at (Franx et al. 2003). Like EROs, DRGs are also strongly clustered (Grazian et al. 2006; Foucaud et al. 2007; Quadri et al. 2008; Guo & White 2009). For both populations, recent results by Quadri et al. (2008) for DRGs and Kim et al. (2011a) for EROs showed that their angular correlation functions cannot be described by a single power-law. This means that the correlation functions of both populations can be separated into the contributions from the one-halo term (the clustering of objects in the same halo) and the two-halo term (the clustering of galaxies in different haloes). Another intermediate redshift selection successfully defined by optical/near-IR colours is the selection (Daddi et al. 2004). This population can be easily split into star-forming () and passive () galaxies at , and are also strongly clustered (Kong et al. 2006; Hartley et al. 2008; McCracken et al. 2010; Merson et al. 2013).
Despite the successful colour criteria for selecting high redshift galaxies, previous measurements of the correlation function have suffered from the small areas surveyed. In particular, the lack of wide-field near-IR imaging data has prevented the detection of sufficiently large samples of high redshift galaxies. However, this has now been overcome with recent wide and deep near-IR surveys using the latest wide field cameras such as the Wide Field Camera (WFCAM, Casali et al. 2007). The UKIRT Infrared Deep Sky Survey (UKIDSS, Lawrence et al. 2007) is the most comprehensive near-IR survey to date. In this paper, we use near-IR images of a wide, contiguous field from the 7th and 8th Data Release (DR7 & DR8) of the Deep eXtragalactic Survey (DXS), a sub-survey of UKIDSS, in combination with additional optical datasets. From the merged optical to near-IR catalogue, the clustering and halo properties of EROs have been measured and are discussed.
In § 2, we describe data analysis methods such as the compilation of multi-wavelength datasets, ERO selection method and photometric redshift determination. Then the analysis methods used to determine the clustering and halo modeling are described in § 3. We present the results in § 4, and discuss them in comparison with theoretical models in § 5. Unless otherwise noted, the photometry is quoted in the AB system. Throughout the bulk of the paper we assume the following cosmology : 0.27, 0.73, and 100 km s-1 Mpc-1 with 0.73; the exception is in § 5 in which we adopt a slightly different set of cosmological parameters to match those used in a galaxy formation simulation which we test against our new measurements.
2 Data
In this section we first describe the near-IR photometry (§ 2.1) and supplementary optical photometry (§ 2.2) before discussing the selection of EROs (§ 2.3) and the estimation of their photometric redshifts (§ 2.4).
2.1 UKIDSS
The UKIRT Infrared Deep Sky Survey (UKIDSS) began in 2005 and consists of 5 sub-surveys (Lawrence et al. 2007). The Wide Field Camera (WFCAM, Casali et al. 2007) mounted on the UK Infrared Telescope (UKIRT) has been used to obtain UKIDSS images. The Deep eXtragalactic Survey (DXS) is a deep, wide survey mapping 35 deg2 with a 5 point-source sensitivity of and as one of the sub-surveys. It covers 4 different fields and aims to detect photometric samples of galaxies.
WFCAM is composed of four Rockwell Hawaii-II 2K2K array detectors (Casali et al. 2007). The sky coverage of each detector is 13.713.7 arcmin2 with 0.4 arcsec/pixel. In order to avoid an undersampled point spread function caused by the relatively large pixel scale, a microstepping technique is applied, i.e. 0.2 arcsec/pixel for the final science image. Since there are gaps between each detector, 4 exposures are necessary to generate a contiguous image covering 0.8 deg2.
In this study we deal with the Elais-N1 field centred on 16h 11m 09.7s, +55d 0m 47.0s (J2000). The datasets from UKIDSS data releases 7 and 8 were used for this work111http://surveys.roe.ac.uk/wsa/. In these releases, -band data covers the whole region but -band coverage is currently only 56 per cent. The typical seeing is at and at . Although the -band dataset has mapped 6.5 deg2 after masking unreliable regions, the actual area for this work depends on the optical datasets (see next subsection).
There are some known issues about the WFCAM images and database catalogues, such as cross-talk and non-optimal galaxy photometry (Dye et al. 2006). To avoid these, we therefore created our own photometric catalogues from the stacked images. Full details are described in Kim et al. (2011a) so we simply summarise the main steps in this paper. Stacked images from the UKIDSS standard pipeline were combined into individual images for each pointing using the Swarp software package (Bertin et al. 2002). Then astronomical objects were extracted with SExtractor (Bertin & Arnouts 1996) and a 2-arcsec aperture magnitude for colour and the AUTO magnitude for total magnitude were also measured. Finally spurious objects such as cross-talk images, diffraction spikes and duplicated objects in overlapping regions were removed. We found 670 214 objects and determined the completeness from an artificial star test to be per cent at the DXS magnitude goals of and . The Vega-AB offsets for these bands are: mag. for and mag. for .
2.2 Other datasets
In order to identify EROs we require deep optical imaging. We use two different datasets for this paper, one that best matches the DXS area (Pan-STARRS) and one that is deeper but over a smaller area (Subaru). The combination of the two allows us to determine the clustering properties of EROs as a function of depth and area.
2.2.1 Pan-STARRS
The Panoramic Survey Telescope and Rapid Response System (Pan-STARRS, Kaiser & Pan-STARRS team 2002) is a large optical survey scanning the whole sky visible from Hawaii with filters (Tonry et al. 2012). The science objectives are various, from the Solar system astronomy to the distant Universe. The Pan-STARRS prototype telescope (PS1) is a 3-year science mission performed by the PS1 Science Consortium222 http://ps1sc.org/. The 1.8m PS1 telescope feeds a 1.4 gigapixel camera covering a 3.2 degree diameter field of view with filters.
We use the Medium Deep Survey (MDS) data which comprises ten separate fields. The data for the Elais-N1 field (MD08) presented here are from observations between 2009 and 2010. The stacked images were generated by the Pan-STARRS Image Processing Pipeline (IPP). The stack IDs of PS1 ranges from 129692 to 129259, with the data label “MD08.refstack.20100713”. The number of stacked images are more than 80, and the shortest mean exposure time is 3 hours at -band. The objects were detected by running SExtractor (Bertin & Arnouts 1996). The flux calibration was performed with the IPP synthetic photometry database. The PS1 catalogue is derived from a single Medium Deep Survey pointing where the photometric uniformity across the field is very well calibrated. The rotation of the camera minimises differences in chip sensitivity as each area of sky is observed by many different chips so our image depth is homogeneous and well understood. The magnitude for the 50 per cent detection limit was found to be by matching sources with the deeper Subaru catalogue (see below for the Subaru data). The PS1 catalogue was merged with the DXS near-IR catalogue (DXS/PS1) by finding the closest object within 1-arcsec. In order to calculate the colour of matched objects, a 3-arcsec aperture magnitude from PS1 was used, since the typical seeing of PS1 MDS for this field is which is worse than the value at for DXS. The area covered by the DXS/PS1 combination is 5.33 deg2. Galactic extinction was corrected for using the dust map of Schlegel, Finkbeiner & Davis (1998).
2.2.2 Subaru
Time was obtained on Subaru to provide a deep comparison for the UKIDSS DXS dataset in the -band with Suprime-Cam (Miyazaki et al. 2002) and a joint catalogue was also produced (DXS/Subaru). The Suprime-Cam imaging (PI Yamada) covers part of the DXS Elais-N1 field. The images were taken in April 2004 and March 2005. The data reduction was made by using SDFRED (Yagi et al. 2002; Ouchi 2004) as well as local IDL programs. The standard star of P177D ( 15h 59m 13.6s, +47d 36m 41.8s) was used for the photometric calibration. The 5 point-source limit is (Sato et al., in preparation). However, we cut samples at , because there are field-to-field variations below this level. We determined this limit by splitting the area into 63 sub-areas of 0.40.4 deg2 to establish the variation in the number of objects detected on a scale smaller than the Suprime-Cam field of view. For objects in the ranges and , the field-to-field variation in counts are 6 and 8 per cent respectively indicating that the counts are consistent over this 2 magnitude range. However, for objects with the field-to-field variation rises to 23 per cent which could significantly affect our clustering on these scales so we limit our analysis to . For colour calculations a 2-arcsec aperture magnitude was used since the seeing of the Subaru data is similar to that of the UKIDSS DXS. The area covered by DXS/Subaru is 3.88 deg2 located on the central region of DXS/PS1. As for DXS/PS1, Galactic extinction was also corrected for using the dust map of Schlegel et al. (1998). The Vega-AB offsets for these bands are: mag. for .
2.2.3 SWIRE
The Elais-N1 field was also mapped by the Spitzer Wide-area InfraRed Extragalactic (SWIRE) survey (Lonsdale et al. 2003). SWIRE imaged 49 deg2 split over 6 fields at mid-IR wavelengths. In this work, a 1.9-arcsec aperture magnitude of IRAC band data from DR2 (Surace et al. 2005) was merged with the other datasets by the same scheme mentioned above. However only and m catalogues were used to measure photometric redshifts for the DXS/PS1 dataset, since the shallower depth in the longer wavelength regime. These bands are labeled as and respectively. The Vega-AB offsets for these bands are mag. for and mag. for .
2.3 ERO selection
In this study EROs are selected using the colour from DXS/PS1 and DXS/Subaru. Firstly, Galactic stars must be removed to avoid contamination. In the case of DXS/PS1 various schemes were applied. Bright stars () were removed using the magnitude difference between -band aperture and total magnitudes. Then stellar sequences in vs. and vs. colour-colour diagrams were extracted. These criteria are and . Stars in the DXS/Subaru data were selected by comparing with those in the DXS/PS1. The faintest candidate stars in DXS/Subaru were not removed, but this does not affect our analysis because very few of these objects meet the ERO colour cut. We note that the fraction of faint stars () selected as EROs is less than 1 per cent, based on the UKIDSS Ultra Deep Survey DR3 catalogue (Simpson et al. 2006).
From the catalogues with Galactic stars removed, colour criteria were applied to select EROs. For DXS/PS1 , and limits were applied to satisfy the classical colour cut () for EROs and match the observed magnitudes. For the DXS/Subaru dataset, , and limits were used. The magnitude limits applied for each band are set to ensure we detect objects uniformly across the whole area (see the previous section). The difference in the applied colour cuts between the two catalogues arises purely from the magnitude difference between PS1 -band and Subaru -band, derived by comparing common objects in both catalogues. Hereafter we quote and for EROs from both datasets instead of and . Using these criteria we selected 17 250 and 23 916 EROs with and 5 039 and 7 959 with from the DXS/PS1 and DXS/Subaru datasets respectively.
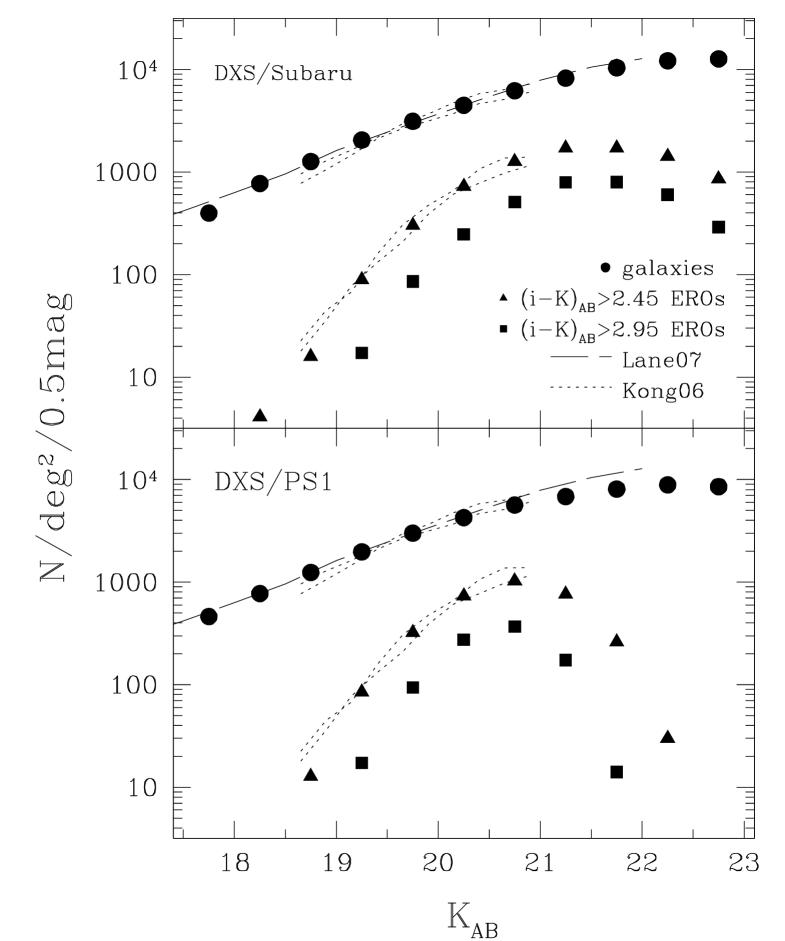
Fig. 1 shows the number counts for all galaxies and for just EROs. The circles indicate the number counts of all galaxies, and triangles and squares are for EROs with bluer ( for DXS/Subaru and for DXS/PS1) and redder ( for DXS/PS1 and for DXS/PS1) cuts from this work, respectively. The number counts of galaxies in Lane et al. (2007, dashed line) and Kong et al. (2006, upper dotted line), and EROs in Kong et al. (2006, lower dotted lines) are also displayed. The counts from this work are consistent with previous studies. However the number counts decrease at fainter magnitudes () due to the depth of the optical datasets. The shallow depth of the optical datasets prevents the detection of the reddest galaxies. This effect is more significant for the DXS/PS1 sample than DXS/Subaru because of the more restricted depth of the PS1 dataset.
2.4 Photometric redshift
The main purpose of this paper is to compare the properties of haloes which host EROs at different redshifts by measuring their angular clustering. For this purpose the photometric redshifts of EROs were measured using the , , , , , , and m photometric data from DXS-PS1-SWIRE. The EAZY photometric redshift code (Brammer, van Dokkum & Coppi 2008) was run to measure the photometric redshift of all objects using the default parameters of the EAZY code. To test the redshift accuracy of this method we used spectroscopic redshifts from Rowan-Robinson et al. (2008), which included those in Berta et al. (2007) and Trichas et al. (2010). The normalised median absolute deviation (NMAD) in was found to be .
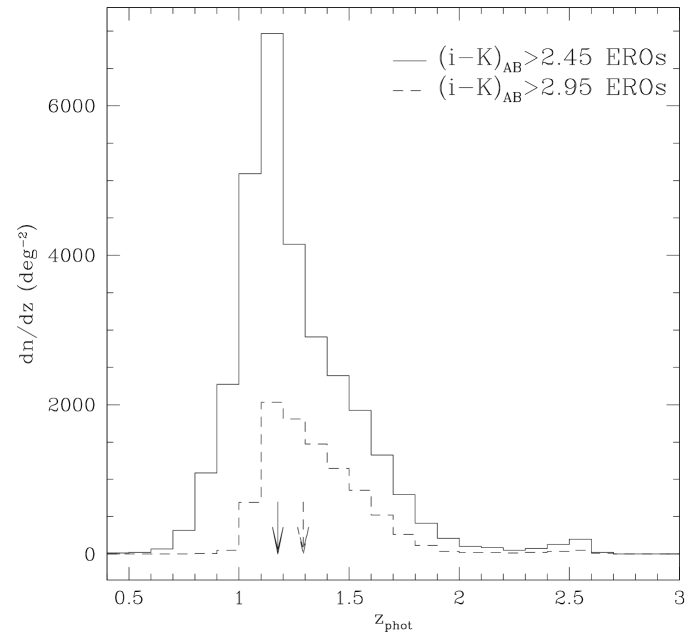
However, there are only a small number of spectroscopic redshifts at , where most EROs are located. Therefore we also applied the empirical method of Quadri & Williams (2010) to constrain the photometric redshift uncertainty for EROs. This method assumes that close pairs of galaxies should show a significant probability of being located at the same redshift. We counted pairs of EROs having an angular separations and those with randomised positions. Then, the difference between the two sets in was used to measure the photometric redshift uncertainty of EROs. This gave a dispersion of which is consistent with the NMAD value from spectroscopic samples. Fig. 2 shows the redshift distributions of EROs in DXS/PS1 using a best-fit photometric redshift. The solid histogram is for EROs, and the dashed one is for EROs. It is apparent that most EROs are located at . However, the ERO selection also contains galaxies at . The median redshifts are 1.176 and 1.291 for and EROs respectively, and displayed in Fig. 2 as arrows. The trend that redder EROs are to be found at higher redshift was also predicted by Gonzalez-Perez et al. (2009).
3 Analysis methods
3.1 Angular correlation function
The angular two-point correlation function is the excess probability of finding a galaxy pair at a given angular separation compared to a random distribution (Peebles 1980). We used the estimator from Landy & Szalay (1993) to estimate the angular two-point correlation function:
| (1) |
where DD is the number of observed ERO pairs with separations . For this study we used 0.15. DR and RR are data-random and random-random pairs in the same interval, respectively. The random catalogue was generated with 30 times more unclustered points than the observed EROs, and had the same angular mask as the EROs. All pair counts were normalised to have the same total numbers.
One of the aims of this study is to investigate the properties of haloes hosting EROs at different redshifts. However, our photometric redshift measurement may not be accurate enough to split samples cleanly into redshift bins. Therefore we used the probability distribution function of our photometric redshifts to measure the angular correlation function of EROs in different redshift bins and estimate the redshift distribution function of EROs for the halo modeling. The details are described in Wake et al. (2011). Briefly, the weight of each ERO is defined as the fractional probability of a particular ERO being within a given redshift interval, using the probability distribution function from the EAZY code. For the angular correlation function this weight was used to count pairs. Also, the weighted probability distribution function of photometric redshifts was used to estimate the redshift distribution. This strategy is similar to that introduced by Myers et al. (2009). In addition, the estimated redshift distribution was also used to measure the number density of EROs in each redshift bin using the same scheme as Ross & Brunner (2009).
The error on the correlation function was estimated using the Jackknife resampling method to compute the deviation of the correlation functions between subfields (for a description see Norberg et al. 2009). We divided the whole area into 25 subfields for DXS/Subaru and 30 subfields for DXS/PS1, then repeated the measurement of the correlation function. From each set of resamplings we can estimate the error using
| (2) |
where and DRi are the correlation function and data-random pairs excluding the subfield, and is the total number of times that the data is resampled. In the Jackknife, corresponds to the number of subfields into which the dataset is divided. Then the covariance matrix is calculated with
| (3) |
where is the mean correlation function of jackknife subsamples in the th bin. The covariance matrix was used to fit the halo model.
The restricted survey area leads to a negative offset of the observed correlation function from the actual one, which is known as the integral constraint (IC, Groth & Peebles 1977). In order to correct for this bias, we applied the same method as Kim et al. (2011a) using the equation in Roche et al. (1999),
| (4) |
Since it is known that the correlation function of EROs is not well described by a single power-law (Gonzalez-Perez et al. 2011; Kim et al. 2011a), the functional form of was used to describe the correlation function. This form is a close match to the angular correlation function measured for ERO samples defined by magnitude and colour cut, and is adopted as the true underlying correlation function to compute the integral constraint in Eq. 4. Then Eq. 4 was used to estimate the integral constraint, which is then added to our estimate of the angular correlation function. Another approach is to use the correlation function obtained from the halo model as the actual correlation function in Eq. 4 (Wake et al. 2011). For the redshift limited samples of EROs, we use the HOD modeled correlation function to calculate the integral constraint with the Eq. 4. We note that the integral constraint ranges from 0.004 to 0.008 with the functional form of the correlation function for magnitude or colour limited EROs, and that brighter or redder EROs have larger integral constraints due to their enhanced clustering strength. Similarly the value obtained from the halo model for redshift limited samples is between 0.004 and 0.007. We are now probing sufficient area that the integral constraint does not have a major effect on our results.
3.2 Halo modeling
The halo model (see Cooray & Sheth 2002 for a review) is widely used to estimate the mass of the host dark matter haloes of observed galaxies (Blake et al. 2008; Wake et al. 2008a; Ross & Brunner 2009; Zehavi et al. 2011). We apply it to describe the angular correlation functions of EROs and hence to measure the properties of the dark matter haloes which host EROs.
The halo occupation distribution (HOD) describes the mean number of galaxies being hosted by a halo of a given mass (). In the halo model, galaxies are separated into centrals and satellites. The mean number of galaxies, , is the combination of the mean number of central galaxies, , and satellites, (Zheng et al. 2005; Blake et al. 2008; Wake et al. 2008a; Ross & Brunner 2009), i.e.
| (5) |
where the mean number of the central galaxies and satellites are assumed to be described by
| (6) |
and
| (7) |
where , , and are parameters defining the shape of HOD. If is smaller than , is set to 0.
In order to generate the real-space correlation function we followed the scheme set out in Ross & Brunner (2009). Firstly, we modeled the power spectrum contributed by galaxies in a single halo (1-halo term) and those in separate haloes (2-halo term, ). Also the power spectrum for the 1-halo term is split into that of central-satellite pairs () and satellite-satellite pairs (). The equations for each term are
| (8) |
| (9) |
and
| (10) | |||||
where is the halo mass function as parameterised in Tinker et al. (2010), is the Fourier transform of the halo density profile of Navarro, Frenk & White (1997) and indicates the matter power spectrum at the redshift of the sample. The term can be thought of as an asymptotic bias. The dependence on arises because only haloes with virial radii less than half of the pair separation of interest are considered; more massive haloes would experience an exclusion effect at separation (see the discussion in Appendix B of Tinker et al. 2005). In addition the virial mass () is defined as
where is the mean comoving background density. To generate we used the ‘CAMB’ software package (Lewis, Challinor & Lasenby 2000) including the fitting formulae of Smith et al. (2003) to model non-linear growth. The average number density of galaxies () is expressed as
| (11) |
, and the scale-dependent bias () are determined using the scheme from Tinker et al. (2005). The halo bias function () in Tinker et al. (2010) is used to calculate the scale-dependent bias. The calculated power-spectra were converted into real-space correlation functions using Fourier transformations
A halo model with three free parameters ( and ) was used to produce the angular correlation function. In this case, was fixed by matching the observed number density using the other given parameters, and was set as which was found to be suitable in previous studies (Zehavi et al. 2011). The modeled correlation function was projected to angular space using the Limber equation (Limber 1954). Then the covariance matrix was used to find the best fitting parameters having the minimum value. The fitting range used was , where the influence of the integral constraint is minimal.
From the fitted parameters, the effective mass (), the effective bias () and the satellite fraction can be estimated using
| (12) |
| (13) |
and
| (14) |
In order to determine the properties of haloes hosting EROs at different redshifts, we compare all the fitted and estimated values for EROs in three redshift bins (see § 4.3).
4 Results
4.1 Angular correlation function
| Criteria | slopesmall | slopelarge | Num. | |||
|---|---|---|---|---|---|---|
| 1.630.6 | 9.663.5 | 1.100.07 | 0.680.12 | 0.5, 0.3 | 6159 | |
| 1.420.4 | 7.352.3 | 1.080.05 | 0.690.10 | 1.0, 0.4 | 11726 | |
| 2.742.2 | 14.456.5 | 1.050.15 | 0.720.15 | 0.6, 0.8 | 2012 | |
| 3.071.4 | 11.894.2 | 0.980.09 | 0.620.12 | 0.8, 0.3 | 4343 | |
| 1.930.9 | 10.874.2 | 1.130.09 | 0.700.13 | 0.9, 0.4 | 2272.9 | |
| 1.630.5 | 7.812.5 | 1.110.06 | 0.730.10 | 0.9, 0.4 | 3712.5 | |
| 3.501.9 | 15.594.6 | 0.910.11 | 0.500.11 | 0.3, 0.4 | 2663.2 |
It is known that the clustering properties of EROs depend on magnitude and colour (Daddi et al. 2000; Roche et al. 2002, 2003; Brown et al. 2005; Georgakakis et al. 2005; Kong et al. 2006, 2009; Gonzalez-Perez et al. 2011; Kim et al. 2011a). In this section we discuss the properties of the angular two-point correlation function of EROs from the DXS/Subaru and the DXS/PS1 samples.
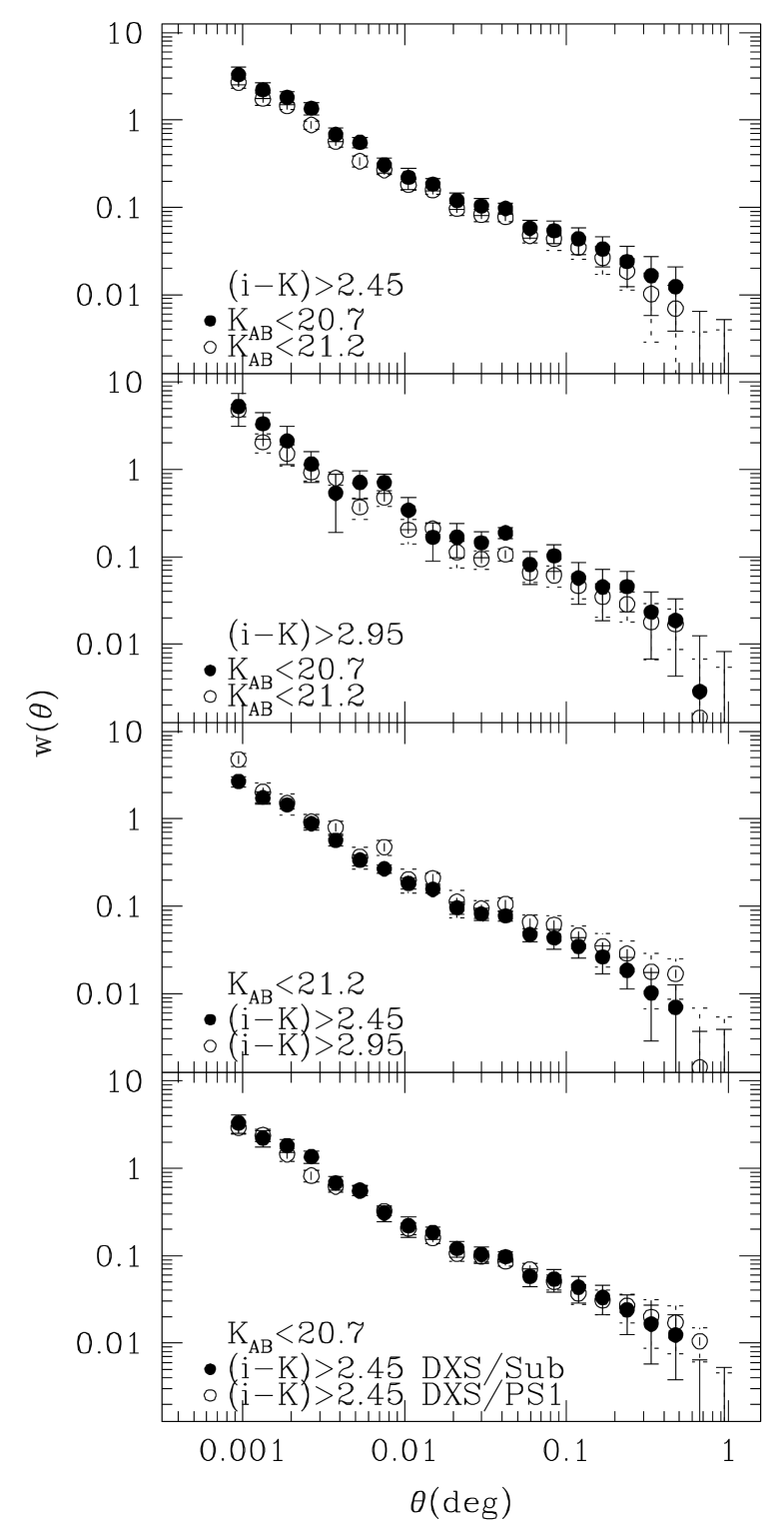
Fig. 3 shows the correlation functions of EROs selected using various criteria. All correlation functions in this plot show a clear break at , which corresponds to Mpc at in comoving coordinates. This break was already reported in Kim et al. (2011a) and implies that a single power-law cannot properly describe the correlation function of EROs. The presence of significant larger scale clustering was confirmed by Kim et al. (2011a) with a detailed analysis of multiple sub-areas of the field and over different ranges in magnitude. Therefore we tried to fit a power-law () to these correlation functions on small, , and large, , scales separately. The boundaries for this fitting were selected to minimise the influence of the integral constraint on the largest scales. The values measured are listed in the top four rows of Table 1. The amplitudes measured for redder or brighter EROs are larger than found for bluer or fainter samples. These features can also be seen in Fig. 3. The top two panels display the dependence of clustering on limiting magnitude, and the third panel from the top shows the colour dependence, which are based on the DXS/Subaru dataset.
In order to check the consistency of these measurements we compared the results with those from the DXS SA22 field in Kim et al. (2011a) which showed good agreement with previously published results. The slopes () in Kim et al. were () for EROs and () for EROs. The values using the same criteria in this work are () and (). On small scales these values are in agreement within the uncertainty range. However, the correlation functions measured in this work are slightly steeper than previous results, particularly on the largest scales. Since Kim et al. used a smaller area, these results might be more affected by cosmic variance, explaining the differences on the large scales. The most pertinent point is that the correlation function is steeper on small scales and flatter on large scales than the single power-law with assumed in most previous studies. Furthermore, to compare amplitudes directly, we measured the amplitudes again with fixed slopes of and for small and large scales respectively. For EROs, the amplitudes () were () in Kim et al., and () in this work. These are also consistent on small scales but not on the largest scales. The reason why the uncertainty is larger in this work than the previous one is that we used the Jackknife resampling method in this study. It is known that the Poissonian error underestimates the uncertainty on the correlation function, especially on the largest scales (Ross et al. 2007; Sawangwit et al. 2011; Nikoloudakis, Shanks & Sawangwit 2013). We also note that the Jackknife resampling method works well on large scales (Scranton et al. 2002; Zehavi et al. 2005). Based on the scale of inflection and the values of amplitude and slope, we conclude that our measurements are consistent with previous results and improve upon them by studying a larger area of sky.
In the bottom panel of Fig. 3, we compare the angular correlation functions from the DXS/Subaru and the DXS/PS1 samples. As mentioned above the area for DXS/PS1 is larger than that of DXS/Subaru, but DXS/Subaru is deeper. The correlation functions of EROs from different optical datasets are well matched, suggesting that there is no significant bias for DXS/PS1 caused by the optical dataset. We use DXS/PS1 EROs to constrain the halo properties in the next sections. Overall, the measurements in this work are consistent with previous work, although even wider data are necessary to measure the angular clustering on large scales more accurately and to test for field to field variations due to cosmic variance. In the near future, PS1 will cover a deeper magnitude range and provide more reliable measurements for the clustering of high redshift galaxies in all four DXS fields.
4.2 Clustering of EROs in redshift bins
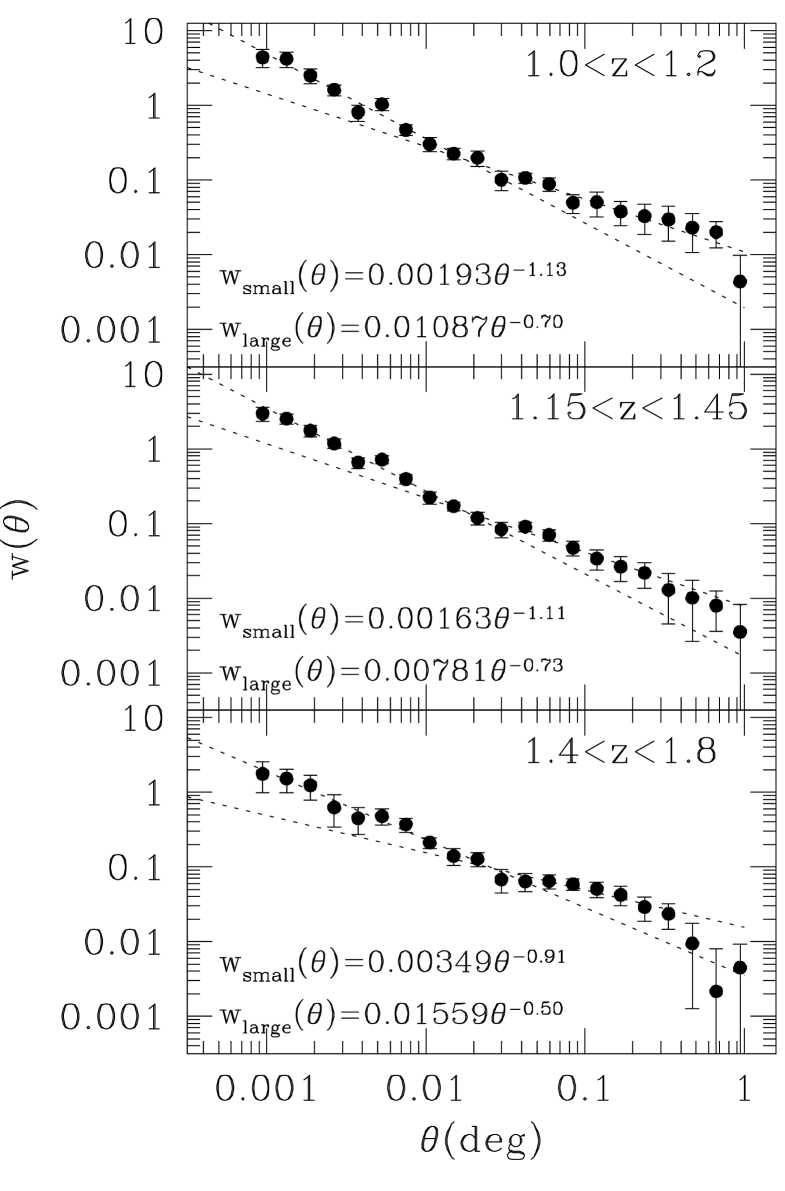
Photometric redshifts provide an opportunity to compare the clustering properties of EROs in different redshift bins. From the DXS/PS1 catalogue we classified EROs based on their redshift and absolute magnitude. Firstly, we applied a -band absolute magnitude cut () with to select EROs with a similar -band luminosity in different redshift bins. The -band absolute magnitude was calculated using the k-correction value obtained from the Bruzual & Charlot (2003) GALAXEV code and a luminosity distance calculated using the Javascript Cosmology Calculator (Wright 2006). We assumed a formation redshift of and considered a range of metallicities around solar to find a best fit to colours of the ERO. The simple stellar population templates with a Chabrier (2003) initial mass function were used. Then, the EROs were split into three redshift bins : and . The bin size was chosen to select sufficiently large samples to enable accurate clustering measurements. The angular two-point correlation functions for each sample were measured using the probability distribution function of photometric redshift as described in § 3.1. Finally a power-law fit was performed on small and large scales separately. The same fitting range as above was used. Fig. 4 shows the angular two-point correlation functions of DXS/PS1 EROs at (top), (middle) and (bottom). Dotted lines indicate the power-law fits on small and large scales separately. The bottom three rows in Table 1 list the fitted results. The number of EROs in each bin is the sum of the weights estimated from the probability distribution function of photometric redshift. Although the correlation function shows a slightly flatter shape in the highest redshift bin than the others, all the estimated power-law slopes have similar values within the uncertainty range.
We also note that the amplitudes on large scales with a fixed power-law slope () are 0.0080.0007 at and 0.0090.0008 at . The power-law slope of was derived for EROs at . These similar amplitudes on large scales indicate a higher bias at higher redshift. This will be discussed in the next section.
4.3 Halo modeling
In this section we study the properties of those haloes hosting EROs at different redshifts. The angular correlation functions for DXS/PS1 EROs in different redshift bins with and were used for the halo modeling. The halo models were generated at the median redshift of the bins, and . The halo model with the three free parameters (, and ) mentioned in § 3.2 was applied at each redshift. We note that this assumed HOD frame work is basically appropriate for mass or luminosity limited samples. In fact EROs are not mass limited samples. Therefore some central or satellite galaxies may be missed, which affects the shape of HODs. In this section, we simply apply the standard HOD model to the clustering of EROs. Then a modified HOD will be discussed in the next section.
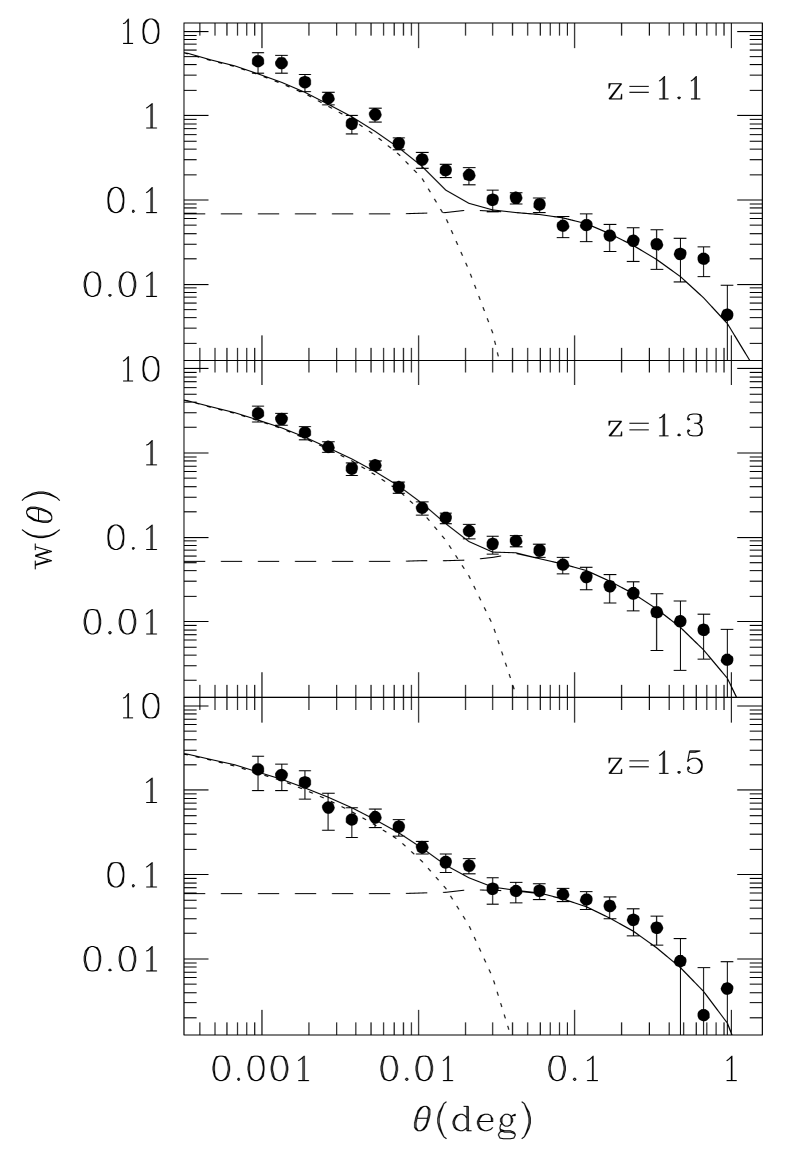
Fig. 5 shows the angular correlation function estimated from the observed EROs, brighter than in the different redshift bins (circles), and the best fit halo models (lines). The dotted and dashed lines represent the 1- and 2-halo terms, respectively. The features of the correlation functions of all ERO subsets are relatively well fitted by the standard halo model. The HOD fit parameters are listed in Table 2. The errors on the HOD parameters in the fits were by determined finding the minimum and maximum parameter values with from the best fit solution. For other derived parameters (, and ), was used.
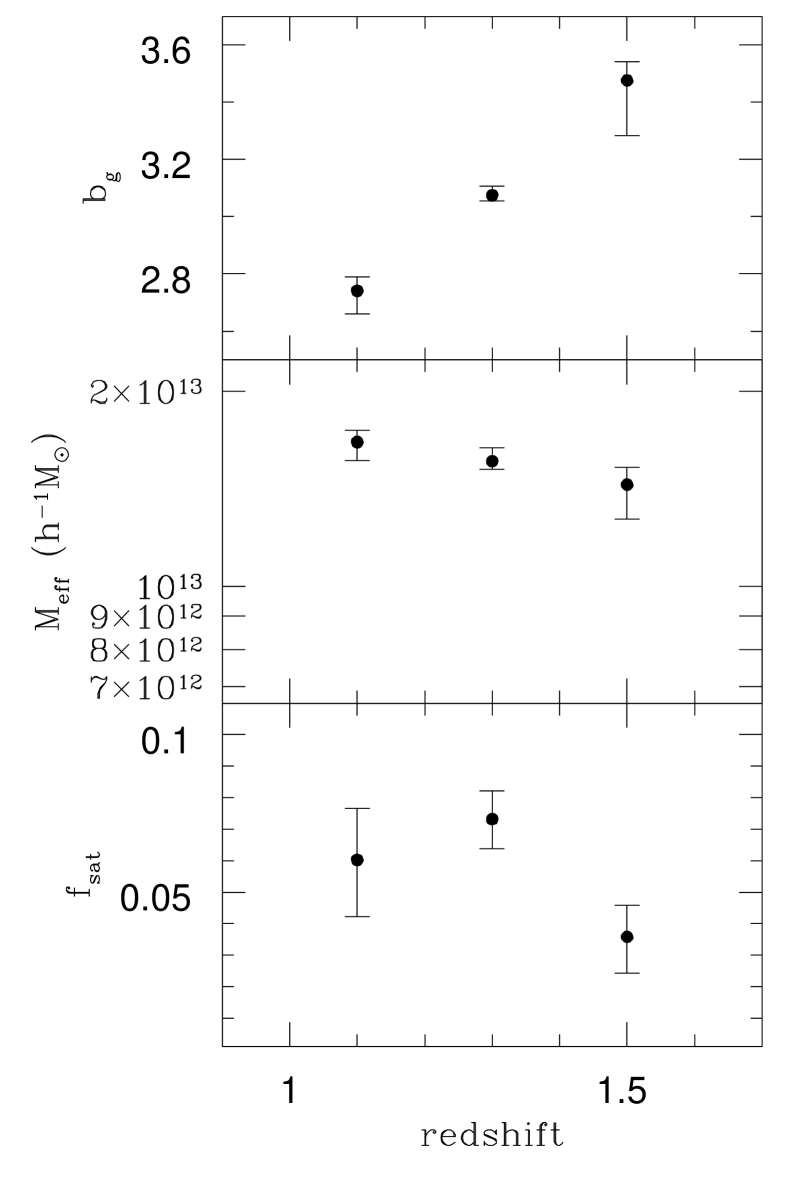
The top panel in Fig. 6 displays the effective bias which is estimated using the equation in § 3.2. The EROs at higher redshift show a higher bias which is similar to the trend found in previous studies of various populations (Blake et al. 2008; Wake et al. 2008a; Sawangwit et al. 2011 for Luminous Red Galaxies (LRG), Matsuoka et al. 2011; Wake et al. 2011 for stellar mass limited samples and Ross, Percival & Brunner 2010 for absolute magnitude cut samples). The biases of EROs reported previously were at for and EROs from the semi-analytical model in Gonzalez-Perez et al. (2011) and in Moustakas & Somerville (2002), which are similar to our measurements, although Moustakas & Somerville (2002) applied a single power-law and used a different criteria, and , for the Las Campanas Infrared Survey data (McCarthy et al. 2001; Firth et al. 2002). These values are similar to those for low redshift LRGs which have (Blake et al. 2008; Wake et al. 2008a; Sawangwit et al. 2011). If EROs have similar stellar masses to LRGs, EROs should be more biased than the lower redshift LRGs. However, we note that the median stellar mass of an SDSS LRG is with a narrow distribution (Barber, Meiksin & Murphy 2007), but in the case of EROs at , the distribution shows a peak at and a sharp cut-off at (Conselice et al. 2008). Therefore our samples are probably marginally less massive than LRGs at lower redshifts.
The middle panel in Fig. 6 shows the effective mass of dark matter haloes hosting EROs. We found that the average halo mass hosting EROs is over and that EROs at higher redshift are in slightly less massive haloes than those at lower redshift. Gonzalez-Perez et al. (2011) reported that the median mass of haloes hosting and EROs at is from a semi-analytical model, and Moustakas & Somerville (2002) estimated the average halo mass hosting EROs as at . Recently Palamara et al. (2013) published the halo mass of EROs as based on the clustering strength with a power law slope of 1.73. Since we have dealt with a full halo model in this work rather than a simplified conversion, the result may be the better measurement than previous work for EROs.
Other studies use a variety of definitions of “passive” galaxies at , which have differing degrees of overlap with the ERO sample considered in this paper. Hartley et al. (2010) used star formation history modelling to define galaxies as passive, selecting those in which they inferred that the current star formation rate is less than 10% of the initial star formation rate and using a red cut on the rest-frame colour. These authors estimated that passive galaxies defined in this way with at are located in haloes ranging from to . We infer a host halo mass that is slightly higher than the prediction of Gonzalez-Perez et al. (2011), but slightly lower than that for the passive galaxies as defined by Hartley et al. (2010). The comparison with the theoretical work is discussed further in § 5. However, overall, EROs may reside in slightly less massive haloes than passive galaxies of comparable luminosity. It is known that EROs can be split on the basis of their colours into passive galaxies with old stellar populations or dusty, star-forming galaxies (Pozzetti & Mannucci 2000; Smail et al. 2002; Roche et al. 2002; Cimatti et al. 2002, 2003; Moustakas et al. 2004; Sawicki et al. 2005; Simpson et al. 2006; Conselice et al. 2008; Kong et al. 2009). In Kim et al. (2011a), the fraction of old, passive EROs defined in this way was found to be more than per cent. In this work it is not possible to split the whole sample into these two sub-populations by using and colours due to the lack of -band imaging over the full area. So, we simply apply the criterion to the two-colour diagram for the region where -band imaging exists. The fraction of old, passive EROs is 45.4 per cent at and 54.4 per cent at . The significant fraction of dusty, star-forming galaxies may dilute the clustering of EROs which might explain why we find lower halo masses than pure passive galaxy samples would predict.
The bottom panel in Fig. 6 shows the evolution of the satellite fraction with redshift derived from the HOD model. EROs are made up of a larger fraction of satellite galaxies at lower redshifts, although the best fitting power-law slope of satellites () at is much larger than unity, which is the value typically seen in simulations of galaxy formation (e.g. Almeida et al. 2008) and as recovered in many previous analyses of observational measurements of clustering. However, in Wake et al. (2008a), the slope for satellite LRGs at was 2.0, and Matsuoka et al. (2011) also reported a similar value for massive galaxies at . So this is not the first result showing a large slope. However, we also note there are other components of the HOD that could lead to a low satellite fraction other than a steep satellite slope. The mass thresholds ( and ) for the HOD may be factors causing the result. The threshold for the HOD of central EROs () is smaller than that for LRGs or massive galaxies, which are a few times . Moreover, is larger than SDSS galaxies at (Ross et al. 2010). This means that EROs are in less massive haloes than LRGs when they are the central galaxy and in more massive haloes than typical galaxies when they are a satellite. Therefore, these effects may lead to the lower satellite fraction than the previous results for ordinary galaxies.
As mentioned above, EROs can be split into old, passive galaxies (OG) or dusty, star-forming galaxies (DG) on the basis of their and colours. Kim et al. (2011a) show that these two sub-populations have very different clustering properties with OGs being more strongly clustered than DGs. Unfortunately, the -band coverage of the EN1 field is not complete so we cannot perform the same analysis as Kim et al. (2011a). Gonzalez-Perez et al. (2011) determine the difference in clustering of these sub-populations in semi-analytical simulations and find a comparable difference in the clustering to that in Kim et al. (2011a). Therefore it is likely that OGs are more biased and/or in more massive haloes than DGs but the clustering of DGs is sufficiently similar to that of OGs that any halo modeling of the combined population is representative. We will perform a more detailed halo modeling of each sub-population with the full DXS dataset in a future paper.
Additionally we note the results of halo modeling for stellar mass limited samples. Wake et al. (2011) used data from the NEWFIRM medium band survey (NMBS; van Dokkum et al. 2009; Brammer et al. 2009; van Dokkum et al. 2010; Whitaker et al. 2011) to measure the clustering of stellar mass limited samples of galaxies at . The highest mass limits of their samples were at and at . Comparing our results to theirs, the effective mass and bias for EROs are higher than those in Wake et al.(2011). This can be easily explained by the higher stellar mass of EROs, as more massive or brighter galaxies reside in more massive haloes (Zehavi et al. 2005, 2011; Foucaud et al. 2010; Hartley et al. 2010; Matsuoka et al. 2011; Furusawa et al. 2011) and show a higher bias (Coil et al. 2006; Ross & Brunner 2009; Zehavi 2011), if we assume EROs have stellar masses greater than .
Foucaud et al. (2010) measured the mass of haloes hosting Palomar/DEEP2 galaxies at based on the model in Mo & White (2002). They reported the halo mass and bias as and 2.80.6, which are similar to our result for EROs at . Therefore EROs may have similar properties with those galaxies.
| median | log | log | log | dof | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1.1 | 2.87 | ||||||||
| 1.3 | 2.71 | ||||||||
| 1.5 | 0.93 |
5 Comparison with galaxy formation models
EROs are massive galaxies, possibly with old stellar populations, observed at substantial lookback times, and so one might expect it to be difficult to explain such galaxies in a cosmological model in which structure grows in a bottom-up fashion through gravitational instability. Indeed, reproducing the observed abundance of EROs posed a long standing challenge to hierarchical galaxy formation models (Smith et al. 2002). Recent theoretical studies have related this problem to the modelling of the suppression of gas cooling in massive haloes as a result of AGN heating (Gonzalez-Perez et al. 2009) and the need for including the contribution of stars in the thermally-pulsating asymptotic giant branch phase (Fontanot & Monaco 2010; Henriques et al. 2011).
Using the GALFORM semi-analytical model of galaxy formation introduced by Cole et al. (2000), Gonzalez-Perez et al. (2009) examined the predictions for EROs in two published models, those of Baugh et al. (2005) and Bower et al. (2006).
The Baugh et al (2005). model underpredicts the abundance of EROs by more than an order of magnitude. This is due in part to the long timescale adopted for merger-driven starbursts in this model, which means that some residual star formation may be ongoing at a significant time after the start of the burst, and because of the top-heavy stellar initial mass function (IMF) assumed in starbursts, which, for an old stellar population, leads to less K-band light per unit mass of stars formed compared with a solar neighbourhood IMF. Both of these effects will lead to galaxies having bluer optical - near infrared colours, which will tend to move them out of the ERO colour selection.
The Bower et al. (2006) model, as Gonzalez-Perez et al. (2009) demonstrated for the first time, gives a very good match to the observed ERO counts. The inclusion of AGN feedback in the Bower et al. (2006) model was one of the main reasons behind this success. Overall, the properties of EROs predicted in the Bower et al. (2006) model show good agreement with observations. Most GALFORM EROs are quiescent galaxies rather than dusty starbursts, and have stellar masses at (Gonzalez-Perez et al. 2009). Gonzalez-Perez et al. (2011) broadened the examination of the properties of EROs in the Bower et al. (2006) model to include their clustering.
In this section, we return to the testing of the predicted clustering of EROs in GALFORM started by Gonzalez-Perez et al. (2011). We begin by comparing the predicted angular clustering of EROs with the new observational measurements presented in this paper (§ 5.1). We then discuss the interpretation of this clustering in terms of fitted HODs, using the parametric form for the HOD given in Eqs. 5, 6, 7 (§ 5.2). GALFORM makes a direct prediction of the form of the HOD, and we compare this intrinsic HOD with the fitted HOD in § 5.3. The comparison of the model predictions with the observational results is discussed in § 5.4.
5.1 Galaxy angular clustering comparison
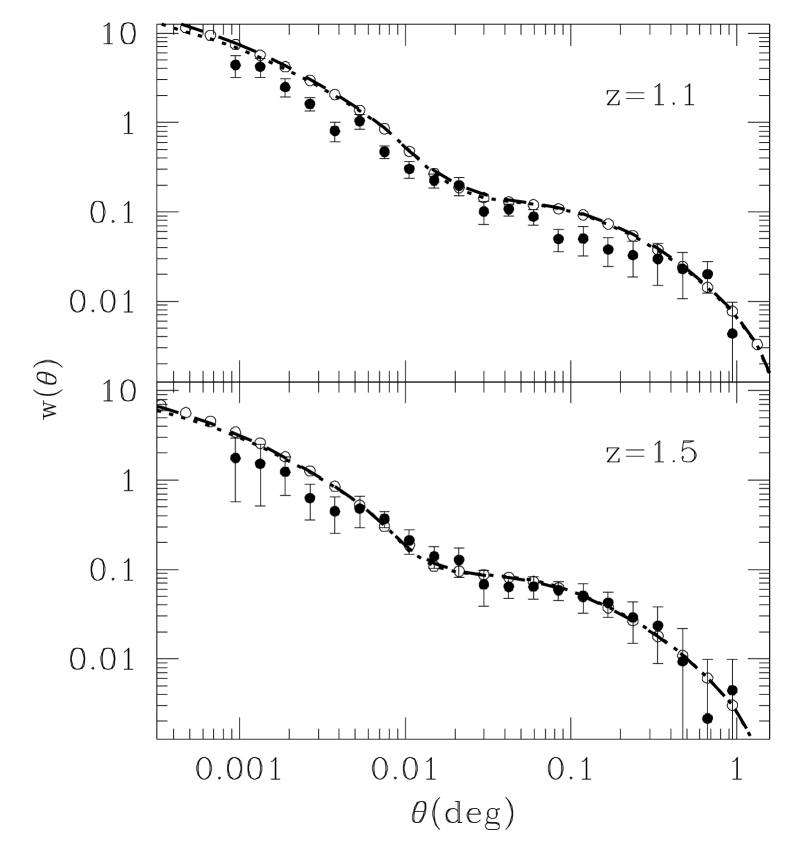
We start with Fig. 7 in which we compare our new observational estimate of the angular correlation function of EROs with and (filled circles) with the clustering predicted by GALFORM for such galaxies (open circles). The model galaxies were extracted with the same colour cut and an apparent magnitude333The magnitudes are and for and , respectively. corresponding at and 1.5. The theoretical clustering is obtained from the ERO HOD output directly by GALFORM at a given redshift, along with the predicted redshift distributions. We note that this may be different from previous works about the clustering based on GALFORM and Gonzalez-Perez et al. (2011). The lines in Fig. 7 show the angular correlation function obtained by fitting different parametric forms for the HOD to the clustering predicted by GALFORM and will be discussed further in § 5.3.
This method of deriving the angular correlation function from GALFORM does not readily yield an appropriate estimate of the error on the angular clustering, as the effective volume considered, the volume of the Millennium N-body simulation, is much larger than that covered by the observational data. Instead, we take the fractional errors inferred on the observational estimate of the correlation function, and apply these to the GALFORM predictions (note this are not plotted in Fig. 7). In the future it will be possible to extract exactly the same volume sample from the models, using the lightcone mock catalogue building capability developed by Merson et al. (2013).
The upper panel of Fig. 7 shows that at the GALFORM predictions show slightly stronger angular clustering than is observed, with some tension at the 2–3 level (see § 5.2). On large scales, the observational estimate may be affected by sampling variance. On the other hand, the discrepancy at small angular separations () can be interpreted as the model predicting a larger 1-halo term than is suggested by the observations. This in turn implies that the model predicts that too many EROs are satellite galaxies at this redshift.
The lower panel of Fig. 7 shows the angular clustering at . In this case, the predictions agree remarkably well with the new observational estimate on large scales. The larger volume covered at than at reduces the effect of cosmic variance. However, the discrepancy on small scales also implies a larger satellite fraction in the models compared with the observations, in the same sense as that suggested at .
There are several factors which could be responsible for the discrepancy between the observed and predicted clustering. Firstly, as EROs are unusual objects drawn from the tail of luminosity and colour distributions, the precise colour criterion applied to construct the ERO samples can have a substantial impact on the predictions. Small differences between the predicted and observed colour distributions can result in large variations in the number of galaxies selected and their clustering. Gonzalez-Perez et al. (2011) noted that the agreement between theory and observations was greatly improved on perturbing the colour cut used to select EROs in the model. Secondly, the semi-analytical modeling predicts too many red satellites resulting in a higher clustering amplitude in the 1-halo term. As already mentioned, most EROs predicted by GALFORM are quiescent galaxies (Gonzalez-Perez et al. 2009). In addition, the clustering amplitude of quiescent EROs is signicantly higher than dusty, star-forming EROs on small scales in the model (Gonzalez-Perez et al. 2011). However observational results show a smaller discrepancy than this model prediction (Miyazaki et al. 2003; Kim et al. 2011a). Hence, it may be necessary to amend the prescription for satellite formation in the models (Kim et al. 2009; Kimm et al. 2009). This issue will be addressed in more detail in § 5.4. Thirdly, even for the large number of EROs used in our analysis, the relatively small area of the fields (a combined areas of just over square degrees) means that the clustering estimates are susceptible to sampling variance. This effect is taken into account to some extent in the Jackkinfe errors plotted on our measurements. However, Norberg et al. (2009) demonstrate that an internal estimate of the error such as that obtained using Jackknife resampling can still vary in amplitude between different realisations of the data, particularly if the intrinsic clustering is strong, as is the case with EROs.
5.2 Comparison of HODs fitted to observations and GALFORM
| median | log | log | log | ||||
|---|---|---|---|---|---|---|---|
| fit to observations | |||||||
| 1.1 | |||||||
| 1.5 | |||||||
| fit to GALFORM | |||||||
| 1.1 | |||||||
| 1.5 |
We now compare the HODs derived by fitting the parametric form of Zheng et al. (2005) to the observed clustering and to the clustering predicted by the model. To allow a meaningful comparison, we perform the HOD analysis of the observed clustering again adopting the background cosmology used in the Bower et al. (2006) model, which matches that used in the Millennium N-body simulation of Springel et al. (2005)444The cosmological parameters used in the Millennium Simulation are 0.25, 0.75, and 73 km s-1 Mpc-1..
The results of this exercise are shown by the dotted lines in Fig. 7, which show the angular clustering obtained using the parametric form for the HOD given by Eqs. 5, 6 & 7, with parameters chosen to give the best fit to the theoretical angular clustering obtained from the GALFORM predicted HOD. Table 3 lists the best fitting HOD parameters and some derived quantities. The effective bias factors and host halo masses deduced from the best fitting HOD to the observed clustering are higher than those derived from the fits to the predicted clustering. The effective masses are a factor of higher at and a factor higher at in the fits to the observations compared with the fits to the model. Another discrepancy between models and observations regards the fraction of EROs that are satellites, which is times higher in the model fits than in the fits to the measured clustering.
The main panels of Fig. 8 display the best fit central HODs to the angular clustering of EROs in the observations (solid line) and the GALFORM predictions (dotted line) at (upper) and (lower). The insets of Fig. 8 show the HODs for all galaxies, combining the HODs of central and satellite EROs. The best fit HOD to the predicted clustering extends to lower mass haloes than the fit to the observed clustering. In addition, satellites in the model also reside in less massive haloes than the observations. These departures may explain the higher halo masses and lower satellite fractions in the observations than in the model. The form of the HOD output by GALFORM will be discussed in next subsection.
5.3 The intrinsic form of the HOD predicted by GALFORM
| redshift | ||||||
|---|---|---|---|---|---|---|
| 1.1 | 11.8 | 12.572 | 11.918 | 13.523 | 13.105 | 0.25 |
| 1.5 | 8.8 | 12.320 | 11.784 | 13.199 | 12.903 | 0.19 |
The galaxy HOD is a prediction of GALFORM and not an input. GALFORM models the physics of the baryonic component of the Universe to predict the number of galaxies per halo and their properties. The HOD is extracted by applying the observational selection to the model output and simply counting the number of galaxies which are retained in each dark matter halo, distinguishing between the central galaxy and its satellites. The HOD and the quantities derived from it can be extracted directly from the model, without having to go through the intermediate step of fitting a parametric form for the HOD to the predicted clustering. As we will see later on in this subsection, the form of the actual HOD output by GALFORM can be different from the standard parametrization we have adopted so far.
We begin by listing in Table 4 some basic properties predicted by GALFORM for the EROs and their host haloes. The effective host halo mass defined by Eq. 12 with the direct output HOD of GALFORM is in very close agreement with that derived from the HOD fit to the predicted angular clustering listed in Table 3. This means that EROs predicted by GALFORM are in less massive haloes than the observations. The major differences between the model prediction and observations are number density and satellite fraction. The predicted number density of EROs is much larger than the observational estimate in the previous section. Also the fraction of EROs that are satellites from the direct model prediction is around 4–5 times higher than the fraction obtained from the best fitting HOD to the observation.
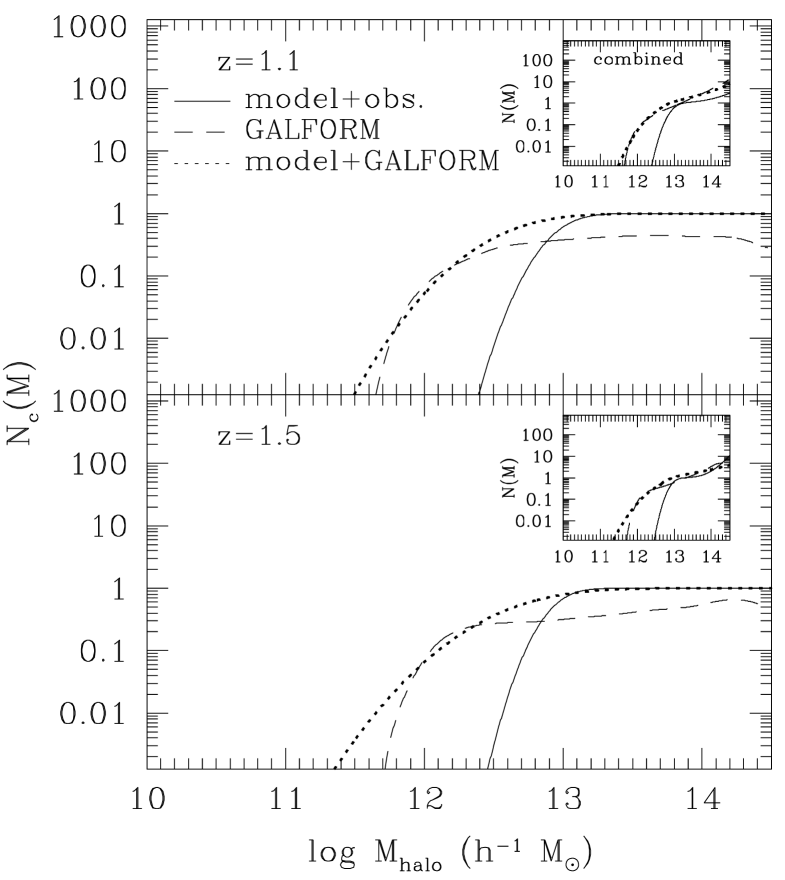
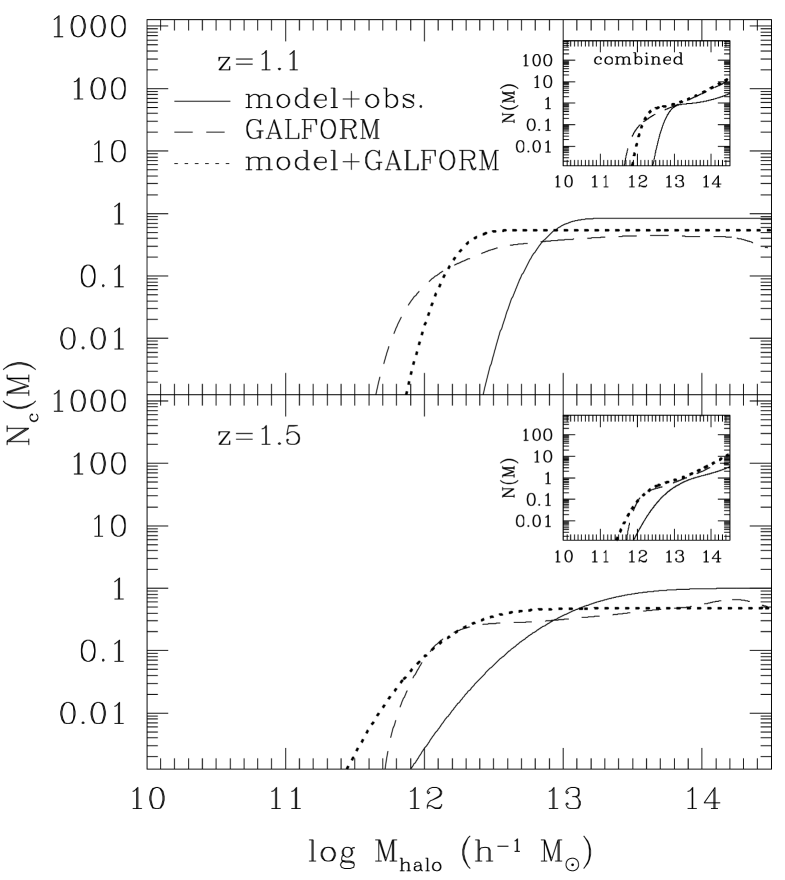
We plot the HOD predicted directly by GALFORM in Fig. 8 (dashed line). We compare this with the parameterised form for the HOD proposed by Zheng et al. (2005), which was motivated by earlier simulations of galaxy formation which did not include AGN feedback. In the Zheng et al. (2005) framework, the HOD of central galaxies is assumed to reach unity, i.e. above some halo mass, every central galaxy is assumed to meet the selection criteria of the sample. The parametric HOD (dotted line) plotted in Fig. 8 is the best fit to the angular clustering predicted by GALFORM.
The predicted HOD can differ substantially from the canonical form typically assumed for the HOD as shown in Fig. 8 and remarked upon by Contreras et al. (2013) in their comparison of the HOD predicted in different semi-analytical models. The deviation is largely driven by AGN feedback, which shuts down gas cooling in massive haloes in GALFORM. In general, the onset of AGN feedback above some halo mass alters how galaxy properties vary with halo mass. This could be manifest as a dramatic break in the relation between the galaxy property and halo mass, as in the case of cold gas mass (Kim et al. 2011b), or as a change in the slope and scatter of the relation, as in the case of -band luminosity (Gonzalez-Perez et al. 2011). With AGN feedback, the most massive galaxy in a sample may no longer be in the most massive dark matter halo due to the increased scatter in the correlation between galaxy properties and halo mass.
Fig. 8 shows the HOD of central galaxies that are EROs at (upper) and (lower), respectively. The predicted HOD of central EROs differs from the observationally inferred in terms of the transition from zero galaxies per halo and also in the number of central galaxies which are EROs. At both redshifts, the mean number of centrals is below unity for the predicted HOD. In addition the fitted HOD shows a smoother shape than the GALFORM prediction. These features emphasize the importance of the form adopted for the HOD when interpreting the results of halo modeling.
Motivated by the comparison between the predicted and fitted HODs in Fig. 8, we explore fitting a modified parametric form for the HOD to the angular clustering predicted by GALFORM. The new form allows the mean number of central galaxies as a function of halo mass, , to vary rather than forcing it to be unity:
| (15) |
where sets the maximum mean number of central EROs and is allowed to take on values . Since we have introduced an additional free parameter with this formulation of the HOD, we fix the exponent of the power-law slope () for satellites to unity, as derived in previous work for SDSS galaxies (Zehavi et al. 2011) and the GALFORM prediction. The best fit angular correlation function using this revised parametric form for the HOD is shown in Fig. 7 by the dashed lines. Fig. 9 shows the best fitting HODs to the measured and predicted angular clustering using this modified form. The line styles are the same as used in Fig. 8. The parametric HOD of central EROs which gives the best fit to the predicted clustering is now closer to the direct HOD prediction of GALFORM. However, the best fit HOD to the GALFORM clustering predictions still extends to lower halo masses than the best fit to the observed angular clustering. It is interesting to note when fitted to the observed ERO clustering (solid lines) at may be possible to be below unity, with a best fitting value of , but does so at , with . These values may indicate the onset of AGN feedback between these two redshifts. However, this interpretation is complicated by the fact that EROs do not correspond readily to a mass limited sample, which may lead to some central galaxies being omitted as they have the different colours, offering an alternative explanation for a mean number of central galaxies that is less than unity. All deduced parameters are listed in Table 5.
The modified HOD fits the HOD of central EROs in GALFORM much better at both redshifts than was possible using the Zheng et al. (2005) HOD. This emphasizes the importance of using a realistic form for the HOD form to derive robust halo properties from the galaxy distribution.
| median | log | log | log | ||||
|---|---|---|---|---|---|---|---|
| fit to observations | |||||||
| 1.1 | |||||||
| 1.5 | |||||||
| fit to GALFORM | |||||||
| 1.1 | |||||||
| 1.5 |
5.4 What went wrong?
The comparisons above point to GALFORM predicting that, overall, EROs are found in less massive haloes and that more EROs are satellites compared with the conclusions reached by fitting HOD models to the observed clustering.
Both problems could be solved by changing the treatment of cooling gas in GALFORM. Gonzalez-Perez et al. (2011) looked at the predictions of a different semi-analytical model, that of Font et al. (2008). The Font et al. model includes partial stripping of the hot gas halo from satellite galaxies, whereas the default assumption is that all of the hot gas is stripped from a galaxy once it becomes a satellite within a larger halo. In the Font et al. model, depending on the orbit of the satellite and the ram pressure that it experiences, some hot gas may be retained and can cool onto the galaxy even after it has become a satellite. This change to the model makes satellites bluer, by permitting more star formation to take place. However, Font et al. also invoked a factor of two increase in the stellar yield without changing the IMF, which leads to redder galaxy colours. Gonzalez-Perez et al. report that the Font et al model produces stronger clustering for EROs than the model of Bower et al. but also leads to more EROs than are observed.
Additionally, Gonzalez-Perez et al. (2009) mentioned that the Bower et al. (2006) model quenched the star formation of massive galaxies too efficiently by the AGN feedback, based on the predicted redshift distribution of passive galaxies. Zheng et al. (2009) also pointed out that this model predicts more red galaxies in a few times haloes than observations but less in more massive haloes, comparing the HODs of observed and predicted LRGs. Therefore it may be possible that GALFORM predicts more red central galaxies such as EROs and LRGs in lower mass haloes.
These comparison illustrate the potential of our new clustering results to constrain the modeling of different elements of the physics of galaxy formation.
6 Conclusion
Recently wide and deep near-IR surveys have made it possible to select galaxies effectively. In this study we have used a near-IR dataset from the UKIDSS DXS and optical datasets from Pan-STARRS PS1 and Subaru to investigate the clustering of EROs and the halo properties hosting them. The main results can be summarised as follows;
-
1.
colour cuts were applied to extract EROs from the 3.88 deg2 DXS/Subaru and the 5.33 deg2 DXS/PS1 catalogues, respectively. We detected 17 250 EROs from DXS/PS1 and 23 916 EROs from DXS/Subaru. The number counts of EROs agree well with previous studies. The photometric redshifts of galaxies in DXS/PS1 were measured from and SWIRE IRAC colours. These EROs were split into subsamples of different photometric redshift and brighter than a fixed absolute magnitude ().
-
2.
The angular correlation functions of EROs were measured with several colour and magnitude thresholds from the DXS/Subaru sample. All these correlation functions showed a clear break at which implies that the angular correlation function of EROs cannot be described by a single power-law. Furthermore, redder or brighter EROs showed higher amplitudes than bluer or fainter ones. The correlation functions from the DXS/PS1 and the DXS/Subaru samples with the same criteria also showed good agreement. The correlation functions at different redshifts had similar amplitudes on large scales, indicating a higher bias at higher redshift.
-
3.
A standard halo model was fitted to the observed angular correlation of EROs and matches well. The biases for EROs range between 2.7 and 3.5, and the average dark matter halo mass hosting EROs is over . EROs at higher redshifts are more biased and located in slightly less massive dark matter haloes than at lower redshift. Also the ERO satellite fraction decreases with increasing redshift. The different fraction of old, passive EROs at different redshifts may affect the properties. In addition, the overall halo properties for EROs are consistent with galaxies.
-
4.
The predicted angular correlation function of EROs from the GALFORM semi-analytic model showed good agreement with the observed correlation function. Comparing the halo model for observed EROs to the GALFORM predictions, we found that the EROs predicted by GALFORM present too high a fraction of satellite galaxies or too many galaxies in less massive haloes. Finally, we stress that the results from the HOD frame work must be interpreted with care due to the effect of AGN feedback and that additional refinements are necessary in future semi-analytical models to improve the modelling of the physics of galaxy formation.
Our clustering results are derived from the large solid angle survey currently available. Nevertheless, the effects of cosmic variance dominate at large scales, so substantial improvements could be obtained in the measurements from even larger surveys. In the near future, the completed UKIDSS and VISTA surveys will be important for making further progress on studying galaxy evolution at . Moreover the combination of near-IR surveys and improved optical surveys such as Pan-STARRS, Hyper Suprime Camera on Subaru and LSST will have a dramatic impact.
Acknowledgments
Authors thank referee for comments improving the paper. This work is based on the data from UKIRT Infrared Deep Sky Survey. We are grateful to UKIDSS team, the staff in UKIRT, Cambridge Astronomical Survey Unit and Wide Field Astronomy Unit in Edinburgh. The United Kingdom Infrared Telescope is run by the Joint Astronomy Centre on behalf of the Science and Technology Facilities Council of the U.K. The PS1 Surveys have been made possible through contributions of the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max-Planck Institute for Astronomy, Heidelberg and the Max-Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network, Incorporated, the National Central University of Taiwan, and the National Aeronautics and Space Administration under grant no. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate. This work is also partially based on data collected at Subaru Telescope, which is operated by the National Astronomical Observatory of Japan. GALFORM was run on the ICC Cosmological machine, which is part of the DiRAC Facility jointly funded by STFC, the Large Facilities Capital Fund of BIS, and Durham University. JWK acknowledges the support from the Creative Research Initiative program, No. 2008-0060544, of the National Research Foundation of Korea (NRF) funded by the Korea government (MSIP). ACE acknowledges support from STFC grant ST/I001573/1. VGP, CMB and CGL acknowledge support from STFC grant ST/F001166/1.
References
- [\citeauthoryearAlmeidaetal2008] Almeida C., Baugh C. M., Wake D. A., Lacey C. G., Benson A. J., Bower R. G., Pimbblet K., 2008, MNRAS, 386, 2145
- [\citeauthoryearBarberetal2007] Barber T., Meiksin A., Murphy T., 2007, MNRAS, 377, 787
- [\citeauthoryearBaugh2006] Baugh C. M., 2006, Reports on Progress in Physics, 69, 3101
- [\citeauthoryearBaughetal2005] Baugh C. M., Lacey C. G., Frenk C. S., Granato G. L., Silva L., Bressan A., Benson A. J., Cole S., 2005, MNRAS, 356, 1191
- [\citeauthoryearBensonetal2000] Benson A. J., Cole S., Frenk C. S., Baugh C. M., Lacey C. G., 2000, MNRAS, 311, 793
- [\citeauthoryearBerlindandWeiberg2002] Berlind A. A., Weinberg D. H., 2002, ApJ, 575, 587
- [\citeauthoryearBertaetal2007] Berta S. et al., 2007, A&A, 467, 565
- [\citeauthoryearBertin & Arnouts1996] Bertin E., Arnouts S., 1996, A&AS, 117, 393
- [\citeauthoryearBertinetal1996] Bertin E., Mellier Y., Radovich M., Missonier G., Didelon P., Morin B., 2002, in Bohlender D. A., Durand, D., Handley T. H., eds, ASP Conf. Ser., Vol. 281, Astronomical Data Analysis Software and Systems XI. Astron. Soc. Pac., San Francisco, p. 228
- [\citeauthoryearBlakeetal2008] Blake C., Collister A., Lahav O., 2008, MNRAS, 385, 1257
- [\citeauthoryearBoweretal2006] Bower R. G., Benson A. J., Malbon R., Helly J. C., Frenk C. S., Baugh C. M., Cole S., Lacey C. G., 2006, MNRAS, 370, 645
- [\citeauthoryearBrammeretal2008] Brammer G. B., van Dokkum P. G., Coppi P., 2008, ApJ, 686, 1503
- [\citeauthoryearBrammeretal2009] Brammer G. B. et al., 2009, ApJ, 706, 173
- [\citeauthoryearBrownetal2005] Brown M. J. I., Jannuzi B. T., Dey A., Tiede G. P., 2005, ApJ, 621, 41
- [\citeauthoryearBruzual2003] Bruzual G., Charlot S., 2003, MNRAS, 344, 1000
- [\citeauthoryearCasalietal2007] Casali M. et al., 2007, A&A, 467, 777
- [\citeauthoryearChabrier2003] Chabrier, G. 2003, PASP, 115, 763
- [\citeauthoryearCimattietal2002] Cimatti A. et al., 2002, A&A, 381, L68
- [\citeauthoryearCimattietal2003] Cimatti A. et al., 2003, A&A, 412, L1
- [\citeauthoryearCoiletal2006] Coil A. L., Newman J. A., Cooper M. C., Davis M., Faber S. M., Koo D. C., Willmer C. N. A., 2006, ApJ, 644, 671
- [\citeauthoryearCoiletal2008] Coil A. L. et al., 2008, ApJ, 672, 153
- [\citeauthoryearCoiletal2009] Coil A. L. et al., 2009, ApJ, 701, 1484
- [\citeauthoryearColeetal2000] Cole S., Lacey C. G., Baugh C. M., Frenk C. S., 2000, MNRAS, 319, 168
- [\citeauthoryearConseliceetal2008] Conselice C. J., Bundy K., U V., Eisenhardt P., Lotz J., Newman J., 2008, MNRAS, 383, 1366
- [\citeauthoryearContrerasetal2013] Contreras S., Baugh C., Norberg P., Padilla N., 2013, MNRAS, 432, 2717
- [\citeauthoryearCooraySheth2002] Cooray A., Sheth R., 2002, Physics Reports, 372, 1
- [\citeauthoryearCroom052005] Croom, S. M., Boyle, B. J., Shanks, T., Smith, R. J., Miller, L., Outram, P. J., Loaring, N. S., Hoyle, F. da Angela, J., 2005, MNRAS, 356, 415
- [\citeauthoryearDaddietal2000] Daddi E., Cimatti A., Pozzetti L., Hoekstra H., Röttgering H. J., Renzini A., Zamorani G., Mannucci F., 2000, A&A, 361, 535
- [\citeauthoryearDaddietal2004] Daddi E., Cimatti A., Renzini A., Fontana A., Mignoli M., Pozzetti L., Tozzi P., Zamorani G., 2004, ApJ, 617, 746
- [\citeauthoryearDyeetal2006] Dye S. et al., 2006, MNRAS, 372, 1227
- [\citeauthoryearEkeetal2004] Eke V. R. et al., 2004, MNRAS, 355, 769
- [\citeauthoryearElstonetal1988] Elston R., Rieke G. H., Rieke M. J., 1988, ApJ, 331, 77
- [\citeauthoryearFirthetal2002] Firth A. E. et al., 2002, MNRAS, 332, 617
- [\citeauthoryearFontetal2008] Font A. S. et al., 2008, MNRAS, 389, 1619
- [\citeauthoryearFontanotMonaco2010] Fontanot F., Monaco P., 2010, MNRAS, 405, 705
- [\citeauthoryearFoucaudetal2007] Foucaud S. et al., 2007, MNRAS, 376, L20
- [\citeauthoryearFoucaudetal2010] Foucaud S., Conselice C. J., Hartley W. G., Lane K. P., Bamford S. P., Almaini O., Bundy K., 2010, MNRAS, 406, 147
- [\citeauthoryearFranxetal2003] Franx M. et al., 2003, ApJ, 587, L79
- [\citeauthoryearFurusawaetal2011] Furusawa J., Sekiguchi K., Takata T., Furusawa H., Shimasaku K., Simpson C., Akiyama M., 2011, ApJ, 727, 111
- [\citeauthoryearGeorgakakisetal2005] Georgakakis A., Afonso J., Hopkins A. M., Sullivan M., Mobasher B., Cram L. E., 2005, ApJ, 620, 584
- [\citeauthoryearGonzalez-perezatal2009] Gonzalez-Perez V., Baugh C. M., Lacey C. G., Almeida, C., 2009, MNRAS, 398, 497
- [\citeauthoryearGonzalez-perezatal2011] Gonzalez-Perez V., Baugh C. M., Lacey C. G., Kim J. -W., 2011, MNRAS, 417, 517
- [\citeauthoryearGrazianetal2006] Grazian A. et al., 2006, A&A, 453, 507
- [\citeauthoryearGrothPeebles1977] Groth E. J., Peebles, P. J. E., 1977, ApJ, 217, 385
- [\citeauthoryearGuoWhite2009] Guo Q., White S. D. M., 2009, MNRAS, 396, 39
- [\citeauthoryearHartleyetal2008] Hartley W. G. et al., 2008, MNRAS, 391, 1301
- [\citeauthoryearHartleyetal2010] Hartley W. G. et al., 2010, MNRAS, 407, 1212
- [\citeauthoryearHenriquesetal2011] Henriques B., Maraston C., Monaco P., Fontanot F., Menci N., De Lucia G., Tonini C., 2011, MNRAS, 415, 3571
- [\citeauthoryearHickoxetal2011] Hickox R. C. et al., 2011, ApJ, 731, 117
- [\citeauthoryearJingetal1998] Jing Y. P., Mo H. J., Boerner G., 1998, ApJ, 494, 1
- [\citeauthoryearKaiser2002] Kaiser N., Pan-STARRS team, 2002, BAAS, 34, 1304
- [\citeauthoryearKimetal2011] Kim H. -S., Baugh C. M., Benson A. J., Cole S., Frenk C. S., Lacey C. G., Power C., Schneider M., 2011b, MNRAS, 414, 2367
- [\citeauthoryearKimetal2009] Kim H. -S., Baugh C. M., Cole S., Frenk C. S., Benson A. J., 2009, MNRAS, 400, 1527
- [\citeauthoryearKimetal2011] Kim J. -W., Edge A. C., Wake D. A., Stott, J. P., 2011a, MNRAS, 410, 241
- [\citeauthoryearKimmetal2009] Kimm T. et al. 2009, MNRAS, 394, 1131
- [\citeauthoryearKongetal2006] Kong X. et al., 2006, ApJ, 638, 72
- [\citeauthoryearKongetal2009] Kong X., Fang G., Arimoto N., Wang M., 2009, ApJ, 702, 1458
- [\citeauthoryearLandy & Szalay1993] Landy S. D., Szalay A. S., 1993, ApJ, 412, 64
- [\citeauthoryearLaneetal2007] Lane K. P. et al., 2007, MNRAS, 379, L25
- [\citeauthoryearLawrenceetal2007] Lawrence A. et al., 2007, MNRAS, 379, 1599
- [\citeauthoryearLewisetal2000] Lewis A., Challinor A., Lasenby A., 2000, ApJ, 538, 473
- [\citeauthoryearLimber1954] Limber D. N., 1954, ApJ, 119, 655
- [\citeauthoryearLonsdaleetal2003] Lonsdale C. J. et al., 2003, PASP, 115, 897
- [\citeauthoryearMaanFry2000] Ma C. -P., Fry J. N., 2000, ApJ, 543, 503
- [\citeauthoryearMatsuokaetal2011] Matsuoka Y., Masaki S., Kawara K., Sugiyama N., 2011, MNRAS, 410, 548
- [\citeauthoryearMcCarthyetal2001] McCarthy P. J. et al., 2001, ApJ, 560, L131
- [\citeauthoryearMcCrackenetal2010] McCracken T. M. et al., 2010, ApJ, 708, 202
- [\citeauthoryearMersonetal2013] Merson A. I. et al., 2013, MNRAS, 429, 556
- [\citeauthoryearMiyazakietal2003] Miyazaki M. et al., 2003, PASJ, 55, 1079
- [\citeauthoryearMiyazakietal2002] Miyazaki S. et al., 2002, PASJ, 54, 833
- [\citeauthoryearMoandWhite1996] Mo H. J., White S. D. M., 1996, MNRAS, 282, 347
- [\citeauthoryearMoandWhite2002] Mo H. J., White S. D. M., 2002, MNRAS, 336, 112
- [\citeauthoryearMoustakasSomerville2002] Moustakas L. A., Somerville R. S., 2002, ApJ, 577, 1
- [\citeauthoryearMoustakasetal2004] Moustakas L. A. et al., 2004, ApJ, 600, L131
- [\citeauthoryearMyersetal2009] Myers A. D., White M., Ball N. M., 2009, MNRAS, 399, 2279
- [\citeauthoryearNavarroetal1997] Navarro J. F., Frenk C. S., White S. D. M., 1997, ApJ, 490, 493
- [\citeauthoryearNikoloudakisetal2013] Nikoloudakis N., Shanks T., Sawangwit U., 2013, MNRAS, 429, 2032
- [\citeauthoryearNorbergetal2001] Norberg P. Baugh C. M., Gaztañaga E., Croton D. J., 2009, MNRAS, 396, 19
- [\citeauthoryearNorbergetal2001] Norberg P. et al., 2001, MNRAS, 328, 64
- [\citeauthoryearNorbergetal2002] Norberg P. et al., 2002, MNRAS, 332, 827
- [\citeauthoryearOuchi2004] Ouchi M., 2004, ApJ, 611, 660
- [\citeauthoryearPalamaraetal2013] Palamara D. P. et al., 2013, ApJ, 764, 31
- [\citeauthoryearPeacockandSmith2000] Peacock J. A., Smith R. E., 2000, MNRAS, 318, 1144
- [\citeauthoryearPeebles1980] Peebles P. J. E., 1980, The Large-Scale Structure of the Universe. Princeton Univ, Press, Princeton, NJ.
- [\citeauthoryearPozzetti & Mannucci2000] Pozzetti L., Mannucci F., 2000, MNRAS, 317, L17
- [\citeauthoryearQuadriWilliams2010] Quadri R. F., Williams R. J., 2010, ApJ, 725, 794
- [\citeauthoryearQuadrietal2008] Quadri R. F., Williams R. J., Lee K., Franx M., van Dokkum P., Brammer G. B., 2008, ApJ, 685, L1
- [\citeauthoryearRocheetal2002] Roche N. D., Almaini O., Dunlop J., Ivison R. J., Willott C. J., 2002, MNRAS, 337, 1282
- [\citeauthoryearRocheetal2003] Roche N. D., Dunlop J., Almaini O., 2003, MNRAS, 346, 803
- [\citeauthoryearRocheetal1999] Roche N., Eales S. A., Hippelein H., Willott C. J., 1999, MNRAS, 306, 538
- [\citeauthoryearRossetal2007] Ross N. P. et al., 2007, MNRAS, 381, 573
- [\citeauthoryearRossN20092009] Ross N. P. et al., 2009, ApJ, 697, 1634
- [\citeauthoryearRossetal2009] Ross A. J., Brunner R. J., 2009, MNRAS, 399, 878
- [\citeauthoryearRossetal2010] Ross A. J., Percival W. J., Brunner R. J., 2010, MNRAS, 407, 420
- [\citeauthoryearRowanRobinsonetal2008] Rowan-Robinson M. et al., 2008, MNRAS, 386, 697
- [\citeauthoryearSawangwitetal2009] Sawangwit U., Shanks T., Abdalla F. B., Cannon R. D., Croom S. M., Edge A. C., Ross N. P., Wake D. A., 2011, MNRAS, 416, 3033
- [\citeauthoryearSawickietal2005] Sawicki M., Stevenson M., Barrientos L. F., Gladman B., Mallén-Ornelas G., van den Bergh S., 2005, ApJ, 627, 621
- [\citeauthoryearSchlegeletal1998] Schlegel D. J., Finkbeiner D. P., David, M., 1998, ApJ, 500, 525
- [\citeauthoryearScoccimarroetal2001] Scoccimarro R., Sheth R. K., Hui L., Jain B., 2001, ApJ, 546, 20
- [\citeauthoryearScrantonetal2002] Scranton R. et al., 2002, ApJ, 579, 48
- [\citeauthoryearSeljak2000] Seljak U., 2000, MNRAS, 318, 203
- [\citeauthoryearSimpsonetal2006] Simpson C. et al., 2006, MNRAS, 373, L21
- [\citeauthoryearSmailetal2002] Smail I., Owen F. N., Morrison G. E., Keel W. C., Ivison R. J., Ledlow M. J., 2002, ApJ, 581, 844
- [\citeauthoryearSmithetal2002] Smith G. P. et al., 2002, MNRAS, 330, 1
- [\citeauthoryearSmithetal2003] Smith R. E. et al., 2003, MNRAS, 341, 1311
- [\citeauthoryearSpringel2005] Springel, V. et al. 2005, Nature, 435, 629
- [\citeauthoryearSuraceetal2005] Surace J., Shupe D. L., Fang F., Lonsdale C. J., Gonzalez-Solares E., 2005, SSC Web site Release: The SWIRE Data Release 2 (Pasadena, CA: CalTech)
- [\citeauthoryearTinkeretal2010] Tinker J. L., Robertson B. E., Kravtsov A. V., Klypin A., Warren M. S., Yepes G., Gottlöber S., 2010, ApJ, 724, 878
- [\citeauthoryearTinkeretal2010] Tinker J. L., Weinberg D. H., Zheng Z., Zehavi I., 2005, ApJ, 631, 41
- [\citeauthoryearTrichasetal2010] Trichas M. et al., 2010, MNRAS, 405, 2243
- [\citeauthoryearTonryetal2012] Tonry J. L. et al., 2012, ApJ, 750, 99
- [\citeauthoryearvanDokkumetal2009] van Dokkum P. G. et al., 2009, PASP, 121, 2
- [\citeauthoryearvanDokkumetal2010] van Dokkum P. G. et al., 2010, ApJ, 709, 1018
- [\citeauthoryearWakeetal2008a] Wake D. A. et al., 2008a, MNRAS, 387, 1045
- [\citeauthoryearWakeetal2008b] Wake, D. A., Croom, S. M., Sadler, E. M., Johnston, H. M., 2008b, MNRAS, 391, 1674
- [\citeauthoryearWakeetal2011] Wake D. A. et al., 2011, ApJ, 728, 46
- [\citeauthoryearWhitakeretal2011] Whitaker K. E. et al., 2011, ApJ, 735, 86
- [\citeauthoryearWhiteandRees1978] White S. D.M., Rees M. J., 1978, MNRAS, 183, 341
- [\citeauthoryearWright2006] Wright E. L., 2006, PASP, 118, 1711
- [\citeauthoryearYagietal2002] Yagi M., Kashikawa N., Sekiguchi M., Doi M., Yasuda N., Shimasaku K., Okamura S., 2002, AJ, 123, 66
- [\citeauthoryearZehavietal2002] Zehavi I. et al., 2002, ApJ, 571, 172
- [\citeauthoryearZehavietal2005] Zehavi I. et al., 2005, ApJ, 630, 1
- [\citeauthoryearZehavietal2011] Zehavi I. et al., 2011, ApJ, 736, 59
- [\citeauthoryearZhengetal2005] Zheng Z. et al., 2005, ApJ, 633, 791
- [\citeauthoryearZhengetal2009] Zheng Z., Zehavi I., Eisenstein D. J., Weinberg D. H., Jing Y. P., 2009, ApJ, 707, 554