CNLL: A Semi-supervised Approach For Continual Noisy Label Learning

Nazmul Karim, Umar Khalid, Ashkan Esmaeili, and Nazanin Rahnavard
Department of Electrical and Computer Engineering
University of Central Florida, USA
{nazmul.karim18, umarkhalid, ashkan.esmaeili} @knights.ucf.edu
nazanin.rahnavard@ucf.edu

Abstract

The task of continual learning requires careful design of algorithms that can tackle catastrophic forgetting. However, the noisy label, which is inevitable in a real-world scenario, seems to exacerbate the situation. While very few studies have addressed the issue of continual learning under noisy labels, long training time and complicated training schemes limit their applications in most cases. In contrast, we propose a simple purification technique to effectively cleanse the online data stream that is both cost-effective and more accurate. After purification, we perform fine-tuning in a semi-supervised fashion that ensures the participation of all available samples. Training in this fashion helps us learn a better representation that results in state-of-the-art (SOTA) performance. Through extensive experimentation on 3 benchmark datasets, MNIST, CIFAR10 and CIFAR100, we show the effectiveness of our proposed approach. We achieve a 24.8% performance gain for CIFAR10 with 20% noise over previous SOTA methods. Our code is publicly available.¹¹1https://github.com/nazmul-karim170/CNLL

1 Introduction

Deep learning models exhibit impressive performance on numerous tasks in computer vision, machine intelligence, and natural language processing [15, 76, 25, 24]. However, deep neural networks (DNNs) struggle to continually learn new tasks, where the model is desired to learn sequential tasks without forgetting their previous knowledge [40, 45, 57]. Although several studies have addressed the issue of continual learning, the problem of continual learning and noisy label classification in one framework is relatively less explored. As continual learning and noisy label tasks are inevitable in real world scenarios; therefore, it is highly probable that they both emerge concurrently [27]. Hence, this study explores the development of a tangible and viable deep learning approach that can overcome both catastrophic forgetting and noisy label data challenges.

We leverage the replay-based approach to handle the continual learning tasks. However, replaying a noisy buffer degrades the performance further [27] due to flawed mapping of the previously learned knowledge. Furthermore, existing noisy labels strategies in the literature exhibit performance limitations in the online task-free setting [27, 3, 47, 26]. In their original framework, these methods operate on the assumption that entire dataset is provided to eliminate the noise and are thus adversely affected by a small amount of buffered data. To counter these limitations, SPR [27] argue that if a pure replay buffer is maintained, the significant performance gains can be achieved. While SPR [27] employs self-supervised learning in order to create a purified buffer, this type of learning demands a long training time with high computations which limits its application in practical scenario. We aim to alleviate this issue through a masking-based purification technique that is suitable for online continual learning. Furthermore, [27] only relies on clean samples and discards the potential noisy samples. While having a purified buffer offers a better learning scenario, one can still utilize the noisy samples for unsupervised feature learning.

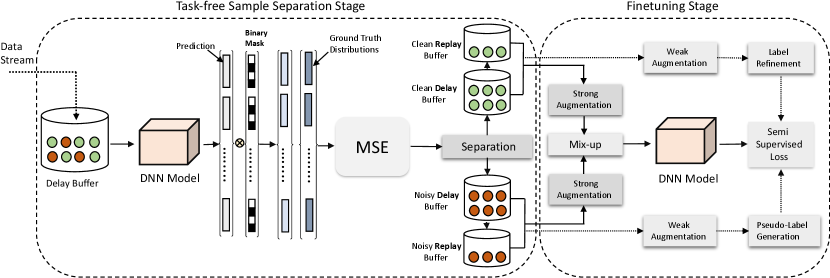
Refer to caption — Figure 1: Our proposed CNLL framework. As the data streaming continues, we warm up the model using the samples from delay buffer $\mathcal{D}$ . After the warm-up, we use the mean square error ( $MSE$ ) loss to measure the distance between predictions and ground-truth distributions. The loss distribution helps us creating the clean and noisy *delay* buffers ( $\mathcal{C}$ and $\mathcal{N}$ ). We update clean and noisy *replay* buffers ( $\mathcal{B_{C}}$ and $\mathcal{B_{N}}$ ) with samples from delay buffers. A few highly confident samples (low loss values) from $\mathcal{C}$ are stored in $\mathcal{B_{C}}$ while samples with low confidence are stored in $\mathcal{B_{N}}$ . Using these buffers ( $\mathcal{C}$ , $\mathcal{N}$ , $\mathcal{B_{C}}$ and $\mathcal{B_{N}}$ ), we perform an SSL-based fine-tuning that results in SOTA performance across 3 different datasets with various noise rates and types.

To this end, we propose a novel sample separation mechanism suitable for online task-free continual learning. We aim to circumvent the limitation of [27] by conventional supervised learning and a masking-based distance metric to separate the incoming data stream into two different buffers: clean and noisy buffers. Later, we employ clean buffer for supervised fine-tuning and noisy buffer for unsupervised feature learning in a semi-supervised learning (SSL) fashion. Our carefully designed separation technique with SSL-based fine-tuning achieves state-of-the-art performance. We verify our claims through extensive experimental evaluation.

In summary, the contributions of this study can be listed as follows-

•

We propose a novel purifying technique to tackle the noisy label problem in the realm of continual learning. We employ masking-based loss metric to accurately filter out clean samples from the noisy data stream.
•

Instead of discarding the noisy samples, we propose to utilize them for unsupervised feature learning which improves the overall performance significantly.
•

Our proposed technique Continual Noisy Label Leaning (CNLL) outperforms current SOTA on three synthetic noise benchmarks of MNIST [32], CIFAR-10 [31], and CIFAR-100 [31].

The rest of the paper is ordered as follows. Related study is discussed in Section 2. Section 3 highlights the background of the study, and Section 4 presents the approach of the proposed noisy continual learning framework. Experimental results are illustrated in Section 5. We discuss the scope of future work in Section 6. Finally, the paper is concluded in Section 7.

2 Related Work

The fundamental challenge of continual learning is to address the catastrophic forgetting, where the model is trained on multiple tasks sequentially [5, 4, 47, 8]. In recent studies, the problem of continual learning has been addressed mainly with four representative approaches [27]. These include regularization[30, 77, 5], replay [18, 27, 53], distillation [36] and expansion techniques [74, 54]. The regularization based technique is designed to penalize any changes in the network parameters while learning the current task to prevent the catastrophic forgetting. EWC [29] , MAS [2], SI [77], NPC [43] and RWalk [10] are among continual learning methods in the literature that impose regularization on the network parameters. The reply memory based methods train the model using the replayed data of the previous tasks in addition to the data for a new task. Some of the replay-based techniques use a subset of data from the old task [69, 82], while some others generate synthetic data to replace the original data from the previous tasks [56, 22, 42]. The distillation-based continual learning approaches are inspired by the knowledge-distillation [21, 12] technique, where the model trained on the previous tasks is regarded as a teacher, and the model being trained on the new task is taken as a student. Here, the distillation loss is utilized to eliminate any performance deterioration on the previous tasks. LwF [36], LwM [14], MCIL [38] and lifelong GAN [78] are some of the popular distillation-based continual learning methods. These methods do not rely on the data from the previous tasks. They either use only the training data of the current task [36] or may generate the synthetic data [78] in addition to the training samples of the current task to train the network. In the expansion-based strategy, the model architecture is dynamically altered by expansion when new tasks are encountered. The expansion is achieved either by increasing the width or depth of the model [23, 35, 73]. As such methods may introduce computational and memory cost, an alternative technique is to employ masking the weights or neurons to break the original network into multiple sub-networks [1, 55, 48]. In this scenario, each sub-network has to be trained separately for the corresponding task, and masked weights are then used, for inference.
In addition, learning from data with noisy labels is another challenging task that deep learning models often encounter during training[50, 59, 41, 36]. Recent researches try to overcome such training scenarios by proposing approaches such as label cleaning [75, 28] and loss regularization[81, 67, 20] etc. Zhang et al. [79] explain that deep neural networks can be efficiently trained with any ratio of noisy labels, but may generalize poorly on test samples. The established regularization methods such as weight decay, data augmentation and batch normalization have failed to overcome this overfitting issue [59]. Numerous methods, such as k-Nearest Neighbor, Anomaly Detection, and Outlier Detection have been recently studied for label cleaning that eliminate the false-labeled samples from the noisy training dataset [16, 13, 63]. However, these methods tend to remove the clean samples from the training data and henceforth, deteriorate the overall performance of the model. Loss regularization is another technique to address the noisy label challenge that focus on designing the noise correction loss to effectively optimize the objective function only on the clean samples. Noise transition matrix has been proposed in [44] for loss correction. [33] introduces meta-loss to optimally find parameters which are robust to noise. Bootstrapping loss has been introduced in [6], while [17] proposes an information theory-based loss for loss regularization. Early learning regularization [37], JoCoR [68], Jo-SRC [71] and sparse regularization [83] are some of the most recent regularization approaches to combat noisy label issue. However, these methods require a lot of samples to achieve a satisfactory performance, while this may not be the case in online continual learning scenario.

3 Background

In this work, we focus on the online task-free continual learning problem. In the online case, one does not have the knowledge of a particular task’s start or end times. At any time $t$ , the system receives the data stream $(\mathbf{x}_{t},y_{t})$ drawn from a current distribution $d_{k}$ . Here, $k$ indicates the task number. The distribution $d_{k}$ can experience a sudden or gradual change in $d_{k+1}$ . Since the system is unaware of the occurrence of the distribution shift, it becomes challenging to prevent the catastrophic forgetting phenomenon in the online continual learning settings. Our aim is to continually learn and update a DNN model $\mathbf{f}(.;\Theta)$ such that it minimizes error on the already seen and upcoming data streams. The continuous process of accumulating and updating knowledge needs careful design of the optimization function. Given a DNN model $\mathbf{f}(.;\Theta)$ with parameters $\Theta$ , the objective function we set to minimize is

\min_{\Theta}\mathcal{L}(\mathbf{f}(X_{\mathcal{D}};\Theta),Y_{\mathcal{D}})+\mathcal{L}(\mathbf{f}(X_{\mathcal{B}};\Theta),Y_{\mathcal{B}}).

(1)

Here, $\mathcal{L}$ is a suitable loss function. Moreover, $\{X_{\mathcal{D}},Y_{\mathcal{D}}\}$ and $\{X_{\mathcal{B}},Y_{\mathcal{B}}\}$ are the data stream sets in the current buffer $\mathcal{D}$ and a replay buffer $\mathcal{B}$ . The replay buffer $\mathcal{B}$ contains a small number of selected samples from already seen data streams. Now, consider the data stream $(\mathbf{x}_{t},y_{t})$ to contain label noise, where $y_{t}$ may have been mislabelled. Therefore, both $\mathcal{D}$ and $\mathcal{B}$ may contain label noise that have adverse effect on the generalization performance of the model. It has been shown in [27] that the presence of noisy label deteriorates the performance of continual learning, mirroring the effect of retrograde amnesia [60]. The effect of catastrophic forgetting [39, 49] is much worse under the effect of noisy labels. The reason for this is assumed to be the corrupted buffer/memory that hinders the subsequent learning. Previous study [27] shows that having a clean buffer helps in improving the performance significantly.

Algorithm 1 Task-free Sample Separation for CNLL

Input: Training data

(\mathbf{x}_{t},y_{t}),...,(\mathbf{x}_{T_{train}},y_{T_{train}})

, Warmup Period

E

, and network parameters

\Theta

\mathcal{C}=\mathcal{N}=\{\}

// Initialize Clean and Noisy Delay Buffer

\mathcal{B_{C}}=\mathcal{B_{N}}=\{\}

// Initialize Clean and Noisy Replay Buffer

\mathcal{D}=\{\}

// Initialize Delay buffer

for

t=1

T_{train}

\mathcal{D}

is full then

\Theta\leftarrow

\textsc{WarmUp}(\Theta,\mathcal{D},E)

for

i=1

|\mathcal{D}|

\mathbf{\mathbf{p}}_{i}=\mathbf{f}(\mathbf{x}_{i};\Theta)

Initialize binary mask

\mathbf{m}_{i}

l_{i}=MSE(\mathbf{y}_{i},\mathbf{m}_{i}\odot\mathbf{p}_{i})

end for

Calculate

l_{threshold}

using Eq. 3

\mathcal{D}_{clean}\leftarrow\{(x_{i},y_{i}):\forall\hskip 5.69046ptl_{i}<l_{threshold}\}

\mathcal{C}\leftarrow\mathcal{C}\ \cup\mathcal{D}_{clean}

\mathcal{D}_{noisy}\leftarrow\mathcal{D}\setminus\mathcal{D}_{clean}

\mathcal{N}\leftarrow\mathcal{N}\ \cup\mathcal{D}_{noisy}

Reset

\mathcal{D}

else

update

\mathcal{D}

with

(\mathbf{x}_{t},y_{t})

end if

\mathcal{C}

is full then

Update

\mathcal{B_{C}}

using eq. 4

Reset

\mathcal{C}

end if

\mathcal{N}

is full then

Update

\mathcal{B_{N}}

using eq. 5

Reset

\mathcal{N}

end if

\mathcal{C}

and

\mathcal{N}

is full then

Fine-tune and Inference Phase for

\Theta

end if

end for

4 Proposed Method

Figure 1 shows the our proposed framework where a delay/current buffer $\mathcal{D}$ of limited size stores the incoming data stream. Our objective is to separate this buffer into a clean buffer $\mathcal{C}$ and a noisy buffer $\mathcal{N}$ . The former will hold the clean samples where noisy samples will be in the later. In contrast to SPR [27], we aim to learn better representations utilizing not only pure samples but also the noisy ones. We can use unsupervised feature learning for the noisy data that eventually improves the overall performance. Furthermore, SPR [27] employs a self-supervised learning based purifying technique that requires complicated formulation and long training time. Instead, we use a much simpler, faster and effective purifying technique that seems to outperform [27] in all benchmark datasets.

4.1 Sample Separation

Whenever $\mathcal{D}$ is full, we perform a warm-up of the model $\mathbf{f}(.;\Theta)$ . In general, warm-up indicates a brief period of fully supervised training on $\mathcal{D}$ . In this period, we minimize standard cross-entropy (CE) loss with a very low learning rate to perform warm-up. It has been shown in [7] that DNN learns the simple pattern first before memorizing the noisy labels over the exposure of long training. Due to this fact, clean samples tends to have low loss compared to noisy samples after the warm-up. One should be able to separate $\mathcal{D}$ into clean ( $\mathcal{C}$ ) and noisy ( $\mathcal{N}$ ) buffers by putting a threshold on the loss values.

For $\mathbf{x}_{i}$ , the average prediction probabilities can be denoted as $\mathbf{p}_{i}=[\mathbf{p}_{i}^{1},\mathbf{p}_{i}^{2},......,\mathbf{p}_{i}^{c}]$ and $\mathbf{y}_{i}=[\mathbf{y}_{i}^{1},\mathbf{y}_{i}^{2},......,\mathbf{y}_{i}^{c}]$ is the given ground-truth label distribution. Here, $c$ is the number of total classes in all tasks combined. To measure the differences between $\mathbf{y}_{i}$ and $\mathbf{p}_{i}$ , we use mean square error ( $MSE$ ) loss, $l_{i}$ , which can be defined as,

\begin{split}l_{i}&=MSE(\mathbf{y}_{i},\mathbf{m}\odot\mathbf{p}_{i})\\ &=\sum_{j=1}^{c}(\mathbf{y}^{j}_{i}-\mathbf{m}^{j}_{i}\odot\mathbf{p}^{j}_{i}))^{2}.\end{split}

(2)

Here, $\mathbf{m}_{i}\in[0,1]^{c}$ is the class-specific binary mask that contains 1 for classes that are currently present in the delay buffer and 0 for rest of the classes. Note that $\mathcal{D}$ may not contain samples from all classes at any given time and the number of classes present in $\mathcal{D}$ , $c_{\mathcal{D}}$ , may vary over time. Therefore, considering prediction probabilities ( $\mathbf{p}_{i}$ ) for all possible classes may result in losses that are misguided. As $c_{\mathcal{D}}\leq c$ , dynamically adjusting the binary mask according to the present classes is justified and seems to alleviate this issue. After measuring $\mathbf{l}=\{l_{i}:i\in(1,\dots,N)\}$ , we estimate the separation threshold $l_{threshold}$ as,

l_{threshold}=l_{mean},

(3)

where $l_{mean}$ is the mean of the loss distribution $\mathbf{l}$ and $N$ is the number of samples in delay buffer $\mathcal{D}$ .

Algorithm 2 Fine-tuning and Inference Stage of CNLL

Input: Test data

(\mathbf{x}_{t},y_{t}),...,(\mathbf{x}_{T_{test}},y_{T_{test}})

, network parameters

\Theta

, clean and noisy delay buffers

\mathcal{C}

and

\mathcal{N}

, clean and noisy replay buffers

\mathcal{B_{C}}

and

\mathcal{B_{N}}

\Psi\leftarrow\Theta

//Copy parameters

Get

\mathcal{S}

and

\mathcal{U}

sets using eq. 6

\Psi\leftarrow

FixMatch(

\mathcal{S}

\mathcal{U}

\Psi

) //SSL Fine-tuning Phase

for

t=1

T_{test}

Classification of

x_{t}

using

\Psi

//Inference Phase

end for

Our proposed thresholding method neither depends on any type of training hyper-parameters, nor needs to be adjusted for different noise type, rate, or even datasets. We empirically validate that taking $l_{mean}$ as the threshold gives us the best separation of clean and noisy samples. Furthermore, whenever $\mathcal{C}$ is full, we hold $N_{1}$ number of highly confident (with low loss values) clean samples from $C$ in the clean replay buffer $\mathcal{B_{C}}$ . On the contrary, $N_{2}$ number of noisy samples with high loss values are stored in the noisy replay buffer $\mathcal{B_{N}}$ . Considering $\mathbf{l}_{\mathcal{C}}$ and $\mathbf{l}_{\mathcal{N}}$ are loss vectors containing loss values for samples in $\mathcal{C}$ and $\mathcal{N}$ . The update rule for the clean replay buffer $\mathcal{B_{C}}$ can be expressed as,

\begin{split}\mathbf{l}_{\mathcal{C}}^{(low)}\leftarrow\text{Lowest}\hskip 2.84544ptN_{1}\hskip 2.84544pt\text{values in}\hskip 2.84544pt\mathbf{l}_{\mathcal{C}}\\ \mathcal{B_{C}}\leftarrow\{(x_{i},y_{i}):\forall\hskip 5.69046ptl_{i}\in\mathbf{l}_{\mathcal{C}}^{(low)}\}\end{split}

(4)

Similarly for the noisy replay buffer $\mathcal{B_{N}}$ , we set the update rule as

\begin{split}\mathbf{l}_{\mathcal{N}}^{(high)}\leftarrow\text{Highest}\hskip 2.84544ptN_{2}\hskip 2.84544pt\text{values in}\hskip 2.84544pt\mathbf{l}_{\mathcal{N}}\\ \mathcal{B_{N}}\leftarrow\{(x_{i},y_{i}):\forall\hskip 5.69046ptl_{i}\in\mathbf{l}_{\mathcal{N}}^{(high)}\}\end{split}

(5)

Algorithm 1 summarizes the proposed sample separation approach.

4.2 Fine-tuning Stage

Figure 1 also shows the fine-tuning stage after separation. Since the labels of the noisy buffers ( $\mathcal{N}$ and $\mathcal{B_{N}}$ ) cannot be trusted, we consider them as the unlabeled data. On the other hand, clean buffers ( $\mathcal{C}$ and $\mathcal{B_{C}}$ ) contain data with reliable labels. Therefore, these buffers can be considered as the source of labeled data. To this end, we can define the labelled and unlabelled sets, $\mathcal{S}$ and $\mathcal{U}$ for the SSL-based fine-tuning as

\begin{split}\mathcal{S}&=\mathcal{C}\cup\mathcal{B_{C}}\\ \mathcal{U}&=\mathcal{N}\cup\mathcal{B_{N}}\end{split}

(6)

We consider SSL-based training utilizing both labeled and unlabeled data. We follow the FixMatch [58] for SSL training. At first, we generate two weakly augmented copies of samples from $\mathcal{S}$ and $\mathcal{U}$ . The model generated predictions for both these copies are $\mathbf{q}_{t}$ and $\mathbf{r}_{t}$ . For labeled data, we refine their labels $\mathbf{y}_{t}$ using the model prediction $\mathbf{q}_{t}$ as,

\bar{\mathbf{y}}_{t}=w_{t}\mathbf{y}_{t}+(1-w_{t})\mathbf{q}_{t},

(7)

where $w_{t}$ is the label refinement coefficient. The pseudo-label $\mathbf{r}_{t}$ for each of the samples in $\mathcal{U}$ are produced solely through model’s prediction.

	MNIST					CIFAR-10
	symmetric			asymmetric		symmetric			asymmetric
Noise rate (%)	20	40	60	20	40	20	40	60	20	40
Multitask 0% noise [9]	98.6					84.7
Finetune	19.3	19.0	18.7	21.1	21.1	18.5	18.1	17.0	15.3	12.4
EWC [30]	19.2	19.2	19.0	21.6	21.1	18.4	17.9	15.7	13.9	11.0
CRS [66]	58.6	41.8	27.2	72.3	64.2	19.6	18.5	16.8	28.9	25.2
CRS + L2R [51]	80.6	72.9	60.3	83.8	77.5	29.3	22.7	16.5	39.2	35.2
CRS + Pencil [72]	67.4	46.0	23.6	72.4	66.6	23.0	19.3	17.5	36.2	29.7
CRS + SL [67]	69.0	54.0	30.9	72.4	64.7	20.0	18.8	17.5	32.4	26.4
CRS + JoCoR [68]	58.9	42.1	30.2	73.0	63.2	19.4	18.6	21.1	30.2	25.1
PRS [26]	55.5	40.2	28.5	71.5	65.6	19.1	18.5	16.7	25.6	21.6
PRS + L2R [51]	79.4	67.2	52.8	82.0	77.8	30.1	21.9	16.2	35.9	32.6
PRS + Pencil [72]	62.2	33.2	21.0	68.6	61.9	19.8	18.3	17.6	29.0	26.7
PRS + SL [67]	66.7	45.9	29.8	73.4	63.3	20.1	18.8	17.0	29.6	24.0
PRS + JoCoR [68]	56.0	38.5	27.2	72.7	65.5	19.9	18.6	16.9	28.4	21.9
MIR [2]	57.9	45.6	30.9	73.1	65.7	19.6	18.6	16.4	26.4	22.1
MIR + L2R [51]	78.1	69.7	49.3	79.4	73.4	28.2	20.0	15.6	35.1	34.2
MIR + Pencil [72]	70.7	34.3	19.8	79.0	58.6	22.9	20.4	17.7	35.0	30.8
MIR + SL [67]	67.3	55.5	38.5	74.3	66.5	20.7	19.0	16.8	28.1	22.9
MIR + JoCoR [68]	60.5	45.0	32.8	72.6	64.2	19.6	18.4	17.0	27.6	23.5
GDumb [47]	70.0	51.5	36.0	78.3	71.7	29.2	22.0	16.2	33.0	32.5
GDumb + L2R [51]	65.2	57.7	42.3	67.0	62.3	28.2	25.5	18.8	30.5	30.4
GDumb + Pencil [72]	68.3	51.6	36.7	78.2	70.0	26.9	22.3	16.5	32.5	29.7
GDumb + SL [67]	66.7	48.6	27.7	73.4	68.1	28.1	21.4	16.3	32.7	31.8
GDumb + JoCoR [68]	70.1	56.9	37.4	77.8	70.8	26.3	20.9	15.0	33.1	32.2
SPR [27]	85.4	86.7	84.8	86.8	86.0	43.9	43.0	40.0	44.5	43.9
CNLL(ours)	92.8	90.1	88.8	91.5	89.4	68.7	65.1	52.8	67.2	59.3

Table 1: Overall accuracy for MNIST and CIFAR-10 datasets. Results are generated after noisy labeled continual learning for all tasks as explained in 4. Here, the delay buffer size is 500 for both datasets. The results reported here are the average of five experiments conducted with unique random seed. Results for other methods are presented according to [27].

	random symmetric			superclass symmetric
noise rate (%)	20	40	60	20	40	60
GDumb + L2R [51]	15.7	11.3	9.1	16.3	12.1	10.9
GDumb + Pencil [72]	16.7	12.5	4.1	17.5	11.6	6.8
GDumb + SL [67]	19.3	13.8	8.8	18.6	13.9	9.4
GDumb + JoCoR [68]	16.1	8.9	6.1	15.0	9.5	5.9
SPR [27]	21.5	21.1	18.1	20.5	19.8	16.5
CNLL(ours)	38.7	32.1	26.2	39.0	32.6	27.5

Table 2: Results reported here are obtained after noisy labeled continual learning on CIFAR-100. The results reported here are the average of five experiments conducted with unique random seed. Results for other methods are presented according to [27].

	MNIST					CIFAR-10
	symmetric			asymmetric		symmetric			asymmetric
noise rate (%)	20	40	60	20	40	20	40	60	20	40
AUM [46]	7.0	16.0	11.7	30.0	29.5	36.0	24.0	11.7	46.0	30.0
INCV [11]	23.0	22.5	14.3	37.0	31.5	22.0	18.5	9.3	37.0	30.0
SPR [27]	96.0	96.5	93.0	100	96.5	75.5	70.5	54.3	69.0	60.0
CNLL(ours)	98.1	98.0	96.8	100	98.6	82.6	80.1	66.0	81.3	73.5

Table 3: Filtered noisy label percentage in the clean buffer. CNLL is significantly better at separating the clean samples from the noisy samples.

To this end, we apply label-preserving augmentation technique, Mixup [80], to strongly augmented copies of $\mathcal{S}$ and $\mathcal{U}$ . Finally, the semi-supervised loss function we minimize is

\mathcal{L}=\mathcal{L}_{\mathcal{X}}+\lambda_{\mathcal{U}}\mathcal{L}_{\mathcal{U}}+\lambda_{r}\mathcal{L}_{\mathrm{reg}}.

(8)

Here, $\mathcal{L}_{\mathcal{X}}$ and $\mathcal{L}_{\mathcal{U}}$ are the loss functions for labelled and unlabelled data. Moreover, $\lambda_{\mathcal{U}}$ and $\lambda_{r}$ are unsupervised loss coefficient and regularization coefficient, respectively. We employ the regularization loss $\mathcal{L}_{\mathrm{reg}}$ is to prevent single-class assignment of all samples. We define it based on a prior uniform distribution $(\pi_{c}=1/c)$ to regularize the network’s output across all samples in the mini-batch similar to Tanaka et al. [61] ,

\mathcal{L}_{reg}=\sum_{c}{\pi_{c}log\big{(}\frac{\pi_{c}}{\frac{1}{|\mathcal{S}+\mathcal{U}|}\sum_{\mathbf{x}\in|\mathcal{S}+\mathcal{U}|}\mathbf{f}(\mathbf{x};\Theta))}\big{)}}

(9)

We describe the fine-tuning and testing stages in Algorithm 2.

5 Experiments

In this section, we draw comparison between CNLL and other SOTA models in the settings proposed in SPR [27]. The proposed method is evaluated on three benchmarks datasets MNIST [32], CIFAR-10 [31], and CIFAR-100 [31].

5.1 Experimental Design

We design our experiments based on the recent works for robust evaluation in continual learning [27, 5, 64]. We consider five tasks on CIFAR-10 [31] and MNIST [32], and 2 random classes for each task. On the other hand, 20 tasks are considered on CIFAR-100, where each task has 5 classes chosen in 2 different ways: a) according to super-classes, and b) randomly. For CIFAR10 and MNIST, we use two noise models to create the synthetic noise dataset. First, we employ symmetric label noise where some portion of samples from a particular class are uniformly distributed over other classes. Five tasks are then formed by picking class pairs randomly without replacement. Secondly, the asymmetric label noise is introduced by allocating other similar class labels [33]. For symmetric noise, we consider 3 different noise rates of 20%, 40%, and 60%. We consider only 20%, 40% rates for aysmmetric case. The warmup period lasts for 30 epochs whereas we perform fine-tuning for 60 epochs. During warmup, we employ a learning rate of 0.001 with a batch size of 64. As there is noise in the data stream, higher learning rate may result in memorization of the noisy samples. Which in turn will create faulty separation of samples leading to poor generalization performance. Whereas, we amplify the learning rate to 0.1 for the fine-tuning stage. As for buffers size, we make the $\mathcal{B_{C}}$ and $\mathcal{B_{N}}$ variable length buffers. The values of $T_{train}$ and $T_{test}$ are also variables and depends on the duration of the training and inference period. For CIFAR10, we consider a pair of values of $50,000$ and $10,000$ for $T_{train}$ and $T_{test}$ . Details of other hyper-parameters can be found in Table 4.

Hyper-Parameter	Value
Size of $\mathcal{D}$	500
Size of $\mathcal{C}$	500
Size of $\mathcal{N}$	1000
$N_{1}$	25
$N_{2}$	50
SGD Momentum	0.9
Weight Decay	$5e^{-4}$

Table 4: Hyper-parameters used for training.

As for model architectures, MLP [62] with two hidden layers is used for all MNIST experiments, and ResNet-18 [19] architecture is used for CIFAR-10, CIFAR-100 experiments.

5.2 Baseline Methods

As mentioned earlier, this study explores continual learning scenario with noisy labeled data. Therefore, the baseline is designed by incorporating SOTA methods proposed for noisy labels learning and continual learning. For continual learning, we choose CRS [52], MIR [3], PRS [26] and Gdumb [47]. Six approaches are selected from the literature for the noisy label learning that are SL [67],JoCoR [68], L2R [51], Pencil [72], AUM [46], and INCV [11]. Furthermore, CNLL is evaluated against SPR [27] which in our knowledge is the only study that has addressed continual learning and noisy labels concurrently.

The hyperparameters for the baselines are as follows.

•

Multitask [9]: We perform i.i.d offline training for 50 epochs with uniformly sampled mini-batches.
•

Finetune: We run online training through the sequence of tasks.
•

GDumb [47] : As an advantage to GDumb, we allow CutMix with $p=0.5$ and $\alpha=1.0$ . We use the SGDR schedule with $T_{0}=1$ and $T_{mult}=2$ . Since access to a validation data in task-free continual learning is not natural, the number of epochs is set to 100 for MNIST and CIFAR-10 and 500 for WebVision.
•

PRS [26]: We set $\rho=0$ .
•

L2R [51]: We use meta update with $\alpha=1$ , and set the number of clean data per class as 100 and the clean update batch size as 100.
•

Pencil [72]: We use $\alpha=0.4,\beta=0.1$ , stage1 = 70, stage2 = 200, $\lambda=600$ .
•

SL [67]: We use $\alpha=1.0,\beta=1.0$ .
•

JoCoR [68]: We set $\lambda=0.1$ .
•

AUM [46]: We set the learning rate to 0.1, momentum to 0.9, weight decay to 0.0001 with a batch size of 64 for 150 epochs. We apply random crop and random horizontal flip for input augmentation.
•

INCV [11]: We set the learning rate to 0.001, weight decay to 0.0001, a batch size 128 with 4 iterations for 200 epochs. We apply random crop and random horizontal flip for input augmentation.
•

SPR [27]: Self-supervised batch size is 300 for MNIST and 500 for CIFAR-10. Among other parameters, we set $\beta_{1}=0.9,\beta_{2}=0.999,\epsilon=0.0002,E_{max}=5$ .

5.3 Results

For CIFAR-10 and MNIST, the performance of CNLL has been compared with baselines in Table 1. CNLL outperforms other methods for both symmetric and asymmetric noise types. We set the upper bound using Multitask [9] which is trained under an optimal setting with perfectly clean data (i.e., the 0% noise rate) and offline training. For 20 $\%$ symmetric noise , CNLL achieves an performanc gain of 7.4% for MNIST and 24.8% for CIFAR-10 over SPR [27]. We achieve same type of improvement for a more realistic scenario of asymmetric noise. These performance improvements can be attributed to our well-designed separation mechanism that can filter out noisy samples with high success rate. We show this in Table 3. Furthermore, keeping the noisy samples rather than discarding them creates the scope of SSL training. The SSL training with strong augmentations helps learning better representations/features than the conventional fully supervised fine-tuning.

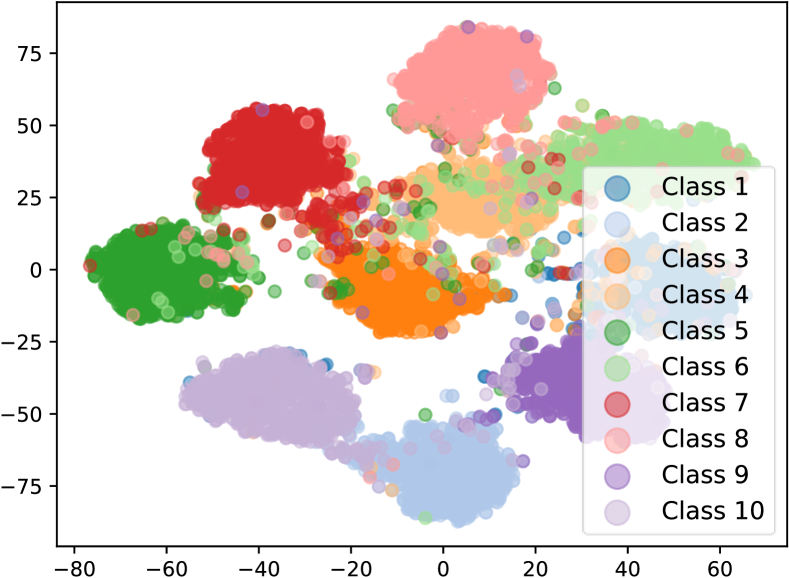
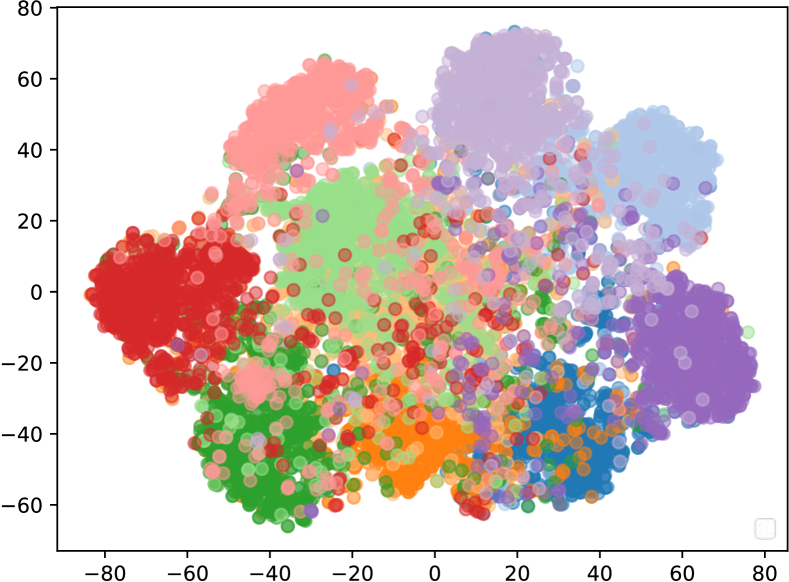
In addition, Table 2 shows the comparison of CNLL with other SOTA methods on CIFAR-100 dataset with random symmetric and super-class symmetric noise. As presented in Table 2, CNLL outperforms the next best method by 17.2% for 20% random symmetric noise. This result is consistent for super-class symmetric noise. Figure 2 also resonates our claims as our method obtains a satisfactory separation of test samples from all classes. To obtain this clustering, we feed all test images to the trained DNN model only to get the output features. We get this output features from the CNN backbone of DNN. Then a technique named t-Distributed Stochastic Neighbour Embedding (t-SNE) [65] has been used to visualize these high dimensional features in a 2D map. The more separation and compactness of these clusters indicate the generalization performance of the DNN model. In both clean and noisy label cases, CNLL performs well in separating the test samples.

6 Scope of Future Work

While we only considered noisy label in online task-free continual learning settings, there are other forms of continual learning that still needs to be explored. Furthermore, CNLL deals with symmetric and asymmetric cases, future studies can focus on the instance/part dependent label noise. To address this, SPR [27] experiements with WebVision benchmark dataset [34]. However, there are other real-world noisy label datasets such as CLothing1M [70] that contains a higher percentage of noisy labels. In future, we will focus on developing sophisticated algorithm for such noise scenarios.

7 Conclusion

We propose a novel training scheme that consists of two phases: task-free sample separation and fine-tuning. By dynamically adjusting a class-specific binary mask, we apply a distance metric to separate the incoming data-stream into clean and noisy sets or buffers. The separation we proposed are dynamic and hyper-parameter independent. Next, we use semi-supervised fine-tuning instead of traditional fully supervised training. Due to the better design of noise cleansing mechanism and superior training scheme, CNLL merits over SOTA in 3 benchmark datasets. Through extensive experimentation, we show the effectiveness of our method as it achieves a 17.2% accuracy improvement, for CIFAR100 with 20 tasks and 20% noise, over the next best method.
Acknowledgement: This work was partly supported by the National Science Foundation under Grant No. CCF-1718195.

References

[1] Davide Abati, Jakub Tomczak, Tijmen Blankevoort, Simone Calderara, Rita Cucchiara, and Babak Ehteshami Bejnordi. Conditional channel gated networks for task-aware continual learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 3931–3940, 2020.
[2] Rahaf Aljundi, Francesca Babiloni, Mohamed Elhoseiny, Marcus Rohrbach, and Tinne Tuytelaars. Memory aware synapses: Learning what (not) to forget. In Proceedings of the European Conference on Computer Vision (ECCV), pages 139–154, 2018.
[3] Rahaf Aljundi, Eugene Belilovsky, Tinne Tuytelaars, Laurent Charlin, Massimo Caccia, Min Lin, and Lucas Page-Caccia. Online continual learning with maximal interfered retrieval. Advances in neural information processing systems, 32, 2019.
[4] Rahaf Aljundi, Min Lin, Baptiste Goujaud, and Yoshua Bengio. Gradient based sample selection for online continual learning. Advances in neural information processing systems, 32, 2019.
[5] Rahaf Aljundi, Marcus Rohrbach, and Tinne Tuytelaars. Selfless sequential learning. arXiv preprint arXiv:1806.05421, 2018.
[6] Eric Arazo, Diego Ortego, Paul Albert, Noel O’Connor, and Kevin McGuinness. Unsupervised label noise modeling and loss correction. In International conference on machine learning, pages 312–321. PMLR, 2019.
[7] Devansh Arpit, Stanislaw Jastrzkebski, Nicolas Ballas, David Krueger, Emmanuel Bengio, Maxinder S Kanwal, Tegan Maharaj, Asja Fischer, Aaron Courville, Yoshua Bengio, et al. A closer look at memorization in deep networks. In International Conference on Machine Learning, pages 233–242. PMLR, 2017.
[8] Lucas Caccia, Eugene Belilovsky, Massimo Caccia, and Joelle Pineau. Online learned continual compression with adaptive quantization modules. In International Conference on Machine Learning, pages 1240–1250. PMLR, 2020.
[9] Rich Caruana. Multitask learning. Machine learning, 28(1):41–75, 1997.
[10] Arslan Chaudhry, Puneet K Dokania, Thalaiyasingam Ajanthan, and Philip HS Torr. Riemannian walk for incremental learning: Understanding forgetting and intransigence. In Proceedings of the European Conference on Computer Vision (ECCV), pages 532–547, 2018.
[11] Pengfei Chen, Ben Ben Liao, Guangyong Chen, and Shengyu Zhang. Understanding and utilizing deep neural networks trained with noisy labels. In International Conference on Machine Learning, pages 1062–1070. PMLR, 2019.
[12] Jang Hyun Cho and Bharath Hariharan. On the efficacy of knowledge distillation. In Proceedings of the IEEE/CVF international conference on computer vision, pages 4794–4802, 2019.
[13] Sarah Jane Delany, Nicola Segata, and Brian Mac Namee. Profiling instances in noise reduction. Knowledge-Based Systems, 31:28–40, 2012.
[14] Prithviraj Dhar, Rajat Vikram Singh, Kuan-Chuan Peng, Ziyan Wu, and Rama Chellappa. Learning without memorizing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 5138–5146, 2019.
[15] Ashkan Esmaeili, Mohsen Joneidi, Mehrdad Salimitari, Umar Khalid, and Nazanin Rahnavard. Two-way spectrum pursuit for cur decomposition and its application in joint column/row subset selection. In 2021 IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), pages 1–6, 2021.
[16] Dragan Gamberger, Nada Lavrac, and Saso Dzeroski. Noise detection and elimination in data preprocessing: experiments in medical domains. Applied artificial intelligence, 14(2):205–223, 2000.
[17] Hrayr Harutyunyan, Kyle Reing, Greg Ver Steeg, and Aram Galstyan. Improving generalization by controlling label-noise information in neural network weights. In International Conference on Machine Learning, pages 4071–4081. PMLR, 2020.
[18] Tyler L. Hayes, Nathan D. Cahill, and Christopher Kanan. Memory efficient experience replay for streaming learning. In 2019 International Conference on Robotics and Automation (ICRA), pages 9769–9776, 2019.
[19] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Identity mappings in deep residual networks. In European conference on computer vision, pages 630–645. Springer, 2016.
[20] Dan Hendrycks, Mantas Mazeika, Duncan Wilson, and Kevin Gimpel. Using trusted data to train deep networks on labels corrupted by severe noise. Advances in neural information processing systems, 31, 2018.
[21] Geoffrey Hinton, Oriol Vinyals, Jeff Dean, et al. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2(7), 2015.
[22] Wenpeng Hu, Zhou Lin, Bing Liu, Chongyang Tao, Zhengwei Tao, Jinwen Ma, Dongyan Zhao, and Rui Yan. Overcoming catastrophic forgetting for continual learning via model adaptation. In International conference on learning representations, 2018.
[23] Ching-Yi Hung, Cheng-Hao Tu, Cheng-En Wu, Chien-Hung Chen, Yi-Ming Chan, and Chu-Song Chen. Compacting, picking and growing for unforgetting continual learning. Advances in Neural Information Processing Systems, 32, 2019.
[24] Umar Khalid, Ashkan Esmaeili, Nazmul Karim, and Nazanin Rahnavard. Rodd: A self-supervised approach for robust out-of-distribution detection. arXiv preprint arXiv:2204.02553, 2022.
[25] Umar Khalid, Nazmul Karim, and Nazanin Rahnavard. Rf signal transformation and classification using deep neural networks. arXiv preprint arXiv:2204.03564, 2022.
[26] Chris Dongjoo Kim, Jinseo Jeong, and Gunhee Kim. Imbalanced continual learning with partitioning reservoir sampling. In European Conference on Computer Vision, pages 411–428. Springer, 2020.
[27] Chris Dongjoo Kim, Jinseo Jeong, Sangwoo Moon, and Gunhee Kim. Continual learning on noisy data streams via self-purified replay. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 537–547, 2021.
[28] Youngdong Kim, Junho Yim, Juseung Yun, and Junmo Kim. Nlnl: Negative learning for noisy labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 101–110, 2019.
[29] James Kirkpatrick, Razvan Pascanu, Neil Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka Grabska-Barwinska, et al. Overcoming catastrophic forgetting in neural networks. Proceedings of the national academy of sciences, 114(13):3521–3526, 2017.
[30] James Kirkpatrick, Razvan Pascanu, Neil C. Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A. Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka Grabska-Barwinska, Demis Hassabis, Claudia Clopath, Dharshan Kumaran, and Raia Hadsell. Overcoming catastrophic forgetting in neural networks. CoRR, abs/1612.00796, 2016.
[31] Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
[32] Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
[33] Junnan Li, Yongkang Wong, Qi Zhao, and Mohan Kankanhalli. Learning to learn from noisy labeled data, 2019.
[34] Wen Li, Limin Wang, Wei Li, Eirikur Agustsson, and Luc Van Gool. Webvision database: Visual learning and understanding from web data. arXiv preprint arXiv:1708.02862, 2017.
[35] Xilai Li, Yingbo Zhou, Tianfu Wu, Richard Socher, and Caiming Xiong. Learn to grow: A continual structure learning framework for overcoming catastrophic forgetting. In International Conference on Machine Learning, pages 3925–3934. PMLR, 2019.
[36] Yuncheng Li, Jianchao Yang, Yale Song, Liangliang Cao, Jiebo Luo, and Li-Jia Li. Learning from noisy labels with distillation. In Proceedings of the IEEE International Conference on Computer Vision, pages 1910–1918, 2017.
[37] Sheng Liu, Jonathan Niles-Weed, Narges Razavian, and Carlos Fernandez-Granda. Early-learning regularization prevents memorization of noisy labels. Advances in neural information processing systems, 33:20331–20342, 2020.
[38] Yaoyao Liu, Yuting Su, An-An Liu, Bernt Schiele, and Qianru Sun. Mnemonics training: Multi-class incremental learning without forgetting. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition, pages 12245–12254, 2020.
[39] Michael McCloskey and Neal J Cohen. Catastrophic interference in connectionist networks: The sequential learning problem. In Psychology of learning and motivation, volume 24, pages 109–165. Elsevier, 1989.
[40] Sudhanshu Mittal, Silvio Galesso, and Thomas Brox. Essentials for class incremental learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 3513–3522, 2021.
[41] Nagarajan Natarajan, Inderjit S Dhillon, Pradeep K Ravikumar, and Ambuj Tewari. Learning with noisy labels. Advances in neural information processing systems, 26, 2013.
[42] Oleksiy Ostapenko, Mihai Puscas, Tassilo Klein, Patrick Jahnichen, and Moin Nabi. Learning to remember: A synaptic plasticity driven framework for continual learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11321–11329, 2019.
[43] Inyoung Paik, Sangjun Oh, Taeyeong Kwak, and Injung Kim. Overcoming catastrophic forgetting by neuron-level plasticity control. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 5339–5346, 2020.
[44] Giorgio Patrini, Alessandro Rozza, Aditya Krishna Menon, Richard Nock, and Lizhen Qu. Making deep neural networks robust to label noise: A loss correction approach. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1944–1952, 2017.
[45] YUN Peng, LIU Yuxuan, and LIU Ming. In defense of knowledge distillation for task incremental learning and its application in 3d object detection. IEEE Robotics and Automation Letters, 6(2):2012–2019, 2021.
[46] Geoff Pleiss, Tianyi Zhang, Ethan Elenberg, and Kilian Q Weinberger. Identifying mislabeled data using the area under the margin ranking. Advances in Neural Information Processing Systems, 33:17044–17056, 2020.
[47] Ameya Prabhu, Philip HS Torr, and Puneet K Dokania. Gdumb: A simple approach that questions our progress in continual learning. In European conference on computer vision, pages 524–540. Springer, 2020.
[48] Jathushan Rajasegaran, Munawar Hayat, Salman H Khan, Fahad Shahbaz Khan, and Ling Shao. Random path selection for continual learning. Advances in Neural Information Processing Systems, 32, 2019.
[49] Roger Ratcliff. Connectionist models of recognition memory: constraints imposed by learning and forgetting functions. Psychological review, 97(2):285, 1990.
[50] Scott Reed, Honglak Lee, Dragomir Anguelov, Christian Szegedy, Dumitru Erhan, and Andrew Rabinovich. Training deep neural networks on noisy labels with bootstrapping. arXiv preprint arXiv:1412.6596, 2014.
[51] Mengye Ren, Wenyuan Zeng, Bin Yang, and Raquel Urtasun. Learning to reweight examples for robust deep learning. In International conference on machine learning, pages 4334–4343. PMLR, 2018.
[52] Matthew Riemer, Ignacio Cases, Robert Ajemian, Miao Liu, Irina Rish, Yuhai Tu, and Gerald Tesauro. Learning to learn without forgetting by maximizing transfer and minimizing interference. arXiv preprint arXiv:1810.11910, 2018.
[53] David Rolnick, Arun Ahuja, Jonathan Schwarz, Timothy Lillicrap, and Gregory Wayne. Experience replay for continual learning. Advances in Neural Information Processing Systems, 32, 2019.
[54] Andrei A Rusu, Neil C Rabinowitz, Guillaume Desjardins, Hubert Soyer, James Kirkpatrick, Koray Kavukcuoglu, Razvan Pascanu, and Raia Hadsell. Progressive neural networks. arXiv preprint arXiv:1606.04671, 2016.
[55] Joan Serra, Didac Suris, Marius Miron, and Alexandros Karatzoglou. Overcoming catastrophic forgetting with hard attention to the task. In International Conference on Machine Learning, pages 4548–4557. PMLR, 2018.
[56] Hanul Shin, Jung Kwon Lee, Jaehong Kim, and Jiwon Kim. Continual learning with deep generative replay. Advances in neural information processing systems, 30, 2017.
[57] James Smith, Yen-Chang Hsu, Jonathan Balloch, Yilin Shen, Hongxia Jin, and Zsolt Kira. Always be dreaming: A new approach for data-free class-incremental learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 9374–9384, 2021.
[58] Kihyuk Sohn, David Berthelot, Nicholas Carlini, Zizhao Zhang, Han Zhang, Colin A Raffel, Ekin Dogus Cubuk, Alexey Kurakin, and Chun-Liang Li. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. Advances in Neural Information Processing Systems, 33:596–608, 2020.
[59] Hwanjun Song, Minseok Kim, Dongmin Park, Yooju Shin, and Jae-Gil Lee. Learning from noisy labels with deep neural networks: A survey. IEEE Transactions on Neural Networks and Learning Systems, 2022.
[60] LARRY R Squire. Two forms of human amnesia: An analysis of forgetting. Journal of Neuroscience, 1(6):635–640, 1981.
[61] Daiki Tanaka, Daiki Ikami, Toshihiko Yamasaki, and Kiyoharu Aizawa. Joint optimization framework for learning with noisy labels, 2018.
[62] Jiexiong Tang, Chenwei Deng, and Guang-Bin Huang. Extreme learning machine for multilayer perceptron. IEEE transactions on neural networks and learning systems, 27(4):809–821, 2015.
[63] Jaree Thongkam, Guandong Xu, Yanchun Zhang, and Fuchun Huang. Support vector machine for outlier detection in breast cancer survivability prediction. In Asia-Pacific Web Conference, pages 99–109. Springer, 2008.
[64] Gido M Van de Ven and Andreas S Tolias. Three scenarios for continual learning. arXiv preprint arXiv:1904.07734, 2019.
[65] Laurens Van der Maaten and Geoffrey Hinton. Visualizing data using t-sne. Journal of machine learning research, 9(11), 2008.
[66] Jeffrey S Vitter. Random sampling with a reservoir. ACM Transactions on Mathematical Software (TOMS), 11(1):37–57, 1985.
[67] Yisen Wang, Xingjun Ma, Zaiyi Chen, Yuan Luo, Jinfeng Yi, and James Bailey. Symmetric cross entropy for robust learning with noisy labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 322–330, 2019.
[68] Hongxin Wei, Lei Feng, Xiangyu Chen, and Bo An. Combating noisy labels by agreement: A joint training method with co-regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13726–13735, 2020.
[69] Yue Wu, Yinpeng Chen, Lijuan Wang, Yuancheng Ye, Zicheng Liu, Yandong Guo, and Yun Fu. Large scale incremental learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 374–382, 2019.
[70] Tong Xiao, Tian Xia, Yi Yang, Chang Huang, and Xiaogang Wang. Learning from massive noisy labeled data for image classification. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2691–2699, 2015.
[71] Yazhou Yao, Zeren Sun, Chuanyi Zhang, Fumin Shen, Qi Wu, Jian Zhang, and Zhenmin Tang. Jo-src: A contrastive approach for combating noisy labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 5192–5201, 2021.
[72] Kun Yi and Jianxin Wu. Probabilistic end-to-end noise correction for learning with noisy labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 7017–7025, 2019.
[73] Jaehong Yoon, Eunho Yang, Jeongtae Lee, and Sung Ju Hwang. Lifelong learning with dynamically expandable networks. arXiv preprint arXiv:1708.01547, 2017.
[74] Jaehong Yoon, Eunho Yang, Jeongtae Lee, and Sung Ju Hwang. Lifelong learning with dynamically expandable networks. ArXiv, abs/1708.01547, 2018.
[75] Qing Yu and Kiyoharu Aizawa. Unknown class label cleaning for learning with open-set noisy labels. In 2020 IEEE International Conference on Image Processing (ICIP), pages 1731–1735, 2020.
[76] Zafar, Adeel and Khalid, Umar. Detect-and-describe: Joint learning framework for detection and description of objects. MATEC Web Conf., 277:02028, 2019.
[77] Friedemann Zenke, Ben Poole, and Surya Ganguli. Continual learning through synaptic intelligence. In International Conference on Machine Learning, pages 3987–3995. PMLR, 2017.
[78] Mengyao Zhai, Lei Chen, Frederick Tung, Jiawei He, Megha Nawhal, and Greg Mori. Lifelong gan: Continual learning for conditional image generation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 2759–2768, 2019.
[79] Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning (still) requires rethinking generalization. Communications of the ACM, 64(3):107–115, 2021.
[80] Hongyi Zhang, Moustapha Cisse, Yann N Dauphin, and David Lopez-Paz. mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412, 2017.
[81] Zhilu Zhang and Mert Sabuncu. Generalized cross entropy loss for training deep neural networks with noisy labels. Advances in neural information processing systems, 31, 2018.
[82] Bowen Zhao, Xi Xiao, Guojun Gan, Bin Zhang, and Shu-Tao Xia. Maintaining discrimination and fairness in class incremental learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13208–13217, 2020.
[83] Xiong Zhou, Xianming Liu, Chenyang Wang, Deming Zhai, Junjun Jiang, and Xiangyang Ji. Learning with noisy labels via sparse regularization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 72–81, 2021.