Collective-motion-enhanced acceleration sensing via an optically levitated microsphere array
Abstract
Optically levitated microspheres are an excellent candidate for force and acceleration sensing. Here, we propose an acceleration sensing protocol based on an optically levitated microsphere array (MSA). The system consists of an -microsphere array levitated in a driven optical cavity via holographic optical tweezers. By positioning the microspheres suitably relative to the cavity, only one of the collective modes of the MSA is coupled to the cavity mode. The optomechanical interaction encodes the information of acceleration acting on the MSA onto the intracavity photons, which can then be detected directly at the output of the cavity. The optically levitated MSA forms an effective large mass-distributed particle, which not only circumvents the problem of levitating a large mass microsphere but also results in a significant improvement of sensitivity. Compared with the traditional single-microsphere measurement scheme, our method presents an improvement in sensitivity by a factor of .
I Introduction
Optomechanics is a fascinating field that explores the interaction between optical and mechanical degrees of freedom, and it has a wide range of applications in various scientific domains [1]. One of the most promising applications of optomechanics is in precision measurement, where optomechanical sensors enable the ultra-sensitive detection of forces and accelerations.[2, 3, 4, 5, 6, 7].
Levitated optomechanics [8], where nano- and micro-objects are levitated in vacuum by optical tweezers [9, 10, 11], has emerged as a particularly promising area of research that has gained significant attention [12, 13, 14, 15, 16, 17]. Optically levitated sensors provide high isolation from thermal and environmental sources of noise in high-vacuum, enabling exceptional displacement, force, and acceleration sensitivity [18, 19, 20, 21]. Experimental results have demonstrated force sensitivity as low as [22, 23] and acceleration sensitivity below sub- () [24, 25, 26]. Levitated optomechanical systems offer precise control of the nanoparticle’s translation and rotational degrees of freedom [27, 28, 29, 30, 31, 32, 33], making them an ideal platform for fundamental scientific research [34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44], such as the detection of high-frequency gravitational wave [45, 46], the search for dark matter [47], and the exploration of macroscopic quantum superposition with mesoscopic particles [48, 49, 50, 51, 52]. Additionally, electrostatic and magnetic levitation [8, 53], as well as coupling to solid-state spin systems [54, 55] have extended the capabilities of levitated optomechanics and open up new opportunities for both scientific research and technological applications.
In the fields of precision measurements and searching for new physics, detecting forces and accelerations with increasing sensitivity is crucial [44, 8]. When it comes to acceleration sensing, a large mass nanoparticle is advantageous because the acceleration sensitivity is inversely proportional to its mass [56], i.e.,
| (1) |
where is the damping rate, the Boltzmann constant, and the temperature of the surrounding environment. However, optically levitating a large mass nanoparticle experimentally is a huge challenge because laser heating constrains the maximum size of particles that can be levitated [24]. Another approach to improve sensitivity is by reducing the pressure in the surrounding environment. Levitated optomechanical experiments have been conducted at a pressure level of around mbar [51, 52]. However, a further reduction in pressure is still a formidable challenge.
Here, we present a novel acceleration sensing method based on an optically levitated MSA. By employing the holographic optical tweezers [57] which can generate multiple controllable optical traps, an array of small mass microspheres is levitated in vacuum forming an effective large mass sphere. The mass of the effective sphere is distributed in multiple optical traps, thus circumventing the problem of the maximum size of spheres that can be levitated in a single optical trap. Moreover, the effective large mass sphere will lead to a significant improvement in acceleration sensitivity when its motion of the center of mass (COM) is used for acceleration sensing. For reading out the motion of the MSA that contains the acceleration information, we introduce a driven Fabry-Perot (FP) cavity that couples with all the microspheres. The optomechanical interaction between the cavity field and microspheres imprints the collective motion of the spheres on the optical field, and thus the acceleration information can be obtained by measuring the cavity field.
A simplified schematic of the experimental setup is shown in Fig. 1, where an MSA is trapped and levitated in an FP cavity by a holographic optical tweezer. An external laser drives the cavity and excites a standing wave mode. By placing the microspheres at suitable positions relative to the cavity, the cavity mode only couples to one of the collective modes of the MSA which takes the information of the acceleration acting on the MSA. Then by measuring the correlation function of photons leaking from the cavity via optical methods such as homodyne or heterodyne detection at the output, we can acquire the acceleration information.
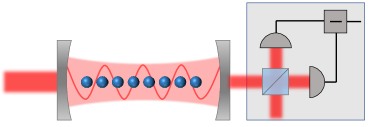
II The scheme of acceleration sensing
The physical model - As introduced above, we consider an optically levitated MSA where dielectric microspheres with mass respectively are trapped and levitated in an FP cavity which is driven by a laser, forming a multi-oscillator cavity optomechanical system (see Fig. 1). The Hamiltonian of the whole system in a frame rotating at pumping frequency reads
| (2) | ||||
where is the annihilation operator of the cavity mode, is the detuning of the cavity mode with frequency from the pumping laser, and is the strength of the pump. and denote respectively the dimensionless position and momentum operators of the mechanical oscillators, and is the frequencies of the mechanical oscillators. is the external force acting on each mechanical oscillator, which induces the inertial acceleration via
| (3) |
accounts for the linear coupling between the cavity mode and the mechanical oscillators. In the case that the radii of spheres are much smaller than the cavity mode wavelength , the dipole force potential created by the cavity mode can be approximated as [58]
| (4) |
where denotes the wave number of cavity field, is the equilibrium position of the th oscillator, and is the single photon optomechanical coupling strength with and the volumes of the mircospheres and the cavity respectively and the electric permittivity. Assuming the oscillation of the sphere around its equilibrium position is small, one can expand the dipole force potential to first order and obtain a linear-coupling interaction Hamiltonian
| (5) |
where is the linear-coupling strength, whose value can be adjusted by shifting the equilibrium positions .
The dynamical equations and solutions - In strong driving regime, we can rewrite each operator as the sum of its classical steady-state mean value and a small quantum fluctuation operator, i.e., , and . Employing the standard linearization procedure [59], we obtain the quantum Langevin equations (QLEs) in terms of the quantum fluctuating operators
| (6) | |||||
where we have phenomenologically introduced and accounting for the dissipation of the cavity field and the mechanical oscillators, respectively. At the same time, we also obtain a set of classical Langevin equations (CLEs) from which the steady-state values can be figured out (see the Appendix for details). and are effective detuning and coupling strength, depending on the steady-state values obtained from the CLEs. The operator in Eqs. (II) accounts for the input noise of the cavity field, which has zero mean value and the correlation function
| (7) |
where we have assumed the equilibrium mean photon number of the thermal bath
due to the high optical frequency . is the input noise of the Brownian force acting on the th mechanical oscillator, whose correlation function is given by
| (8) | ||||
with the Kroneker symbol. The involved mechanical frequencies are never larger than hundreds of MHz and therefore one can make the approximation with the mean thermal phonon number. As a result, the correlation function of Brownian noise can be safely considered Markovian [59, 60], i.e.,
| (9) |
The Eqs. (II) show that if the couplings between each oscillator and the cavity field are the same, that is , only the collective mode couples to the cavity field. Meanwhile, considering that one can choose the microspheres with the (almost) identical size, the environments around these closely positioned microspheres () are the same, and the mechanical resonance frequency can be precisely controlled by tuning the trapping laser power, we reasonably assume that , , and . The QLEs are therefore rewritten in a closed form as
| (10) | ||||
where and are the total Brownian noise operator and the total external force, respectively. Without loss of generality, we assume each mechanical oscillator undergoes the same acceleration and the total external force can be rewritten as
| (11) |
For convenience, we have introduced here the amplitude and phase quadratures of the cavity field as
| (12) |
The QLEs. (10) clearly show that the information of acceleration is encoded into the cavity field mediated through the collective mode . As mentioned above, the optomechanical coupling strengths need to meet the condition , which can be achieved by adjusting the trapping equilibrium positions of the microspheres so that they satisfy
| (13) |
where and is an integer. In state-of-the-art optomechanical experiments with levitated nano-particles, the manipulation of the trapping particle position with a step size of nm has been achieved [50], which is less than compared to the standing wavelength. The position manipulation precision can be further improved by using better nano-positioners.
By Fourier transforming the QLEs. (10) into the frequency domain and using the standard input-output relations , one can solve the equations and obtain the power spectral density (PSD) of the output optical field in amplitude quadrature for instance in terms of the PSDs of acceleration and the input noise as follows
| (14) | ||||
from which, one can solve eventually the PSD of the acceleration in terms of the PSDs of the output optical field in amplitude quadrature and input noises as
| (15) | ||||
where the symbol denotes the response function (whose concrete form can be found in the Appendix) from the external noise or signal source to the detectable quadrature , and the PSD for quantity is defined as . It is noteworthy that the area under the experimentally measured PSD yields the variance of the acceleration [61], i.e.,
| (16) |
Thus one can acquire both the frequency and amplitude information of the acceleration from its PSD. The Brownian noise can be calculated from Eq. (9) as and the optical input noisy PSDs are simply for the vacuum optical reservoir. After measuring the PSD in amplitude quadrature (or in phase quadrature) that can be done directly with the homodyne or heterodyne detection [32, 50, 51] we will eventually be able to carry out the PSD of acceleration.
III The improvement of acceleration sensitivity through the collective motion
To estimate the acceleration , we invert the measured PSD of the output optical field in Eq. (14) and obtain
| (17) |
where the optical input noise
| (18) | ||||
Therefore the signal-to-noise ratio () turns out to be
| (19) |
By setting as the condition that defines sensitivity, we obtain the acceleration sensitivity as
| (20) |
The Brownian noise acting on each mechanical oscillator is independent and uncorrelated, thus the PSD of the total Brownian noise is the sum of the PSD of the Brownian noise acting on every single mechanical oscillator , which is given by
| (21) |
where is the PSD of the Brownian noise acting on a single mechanical oscillator. Therefore the acceleration sensitivity is simplified as
| (22) |
This equation clearly shows that the acceleration sensitivity improves in increasing the number of oscillators . In the limit of , i.e., the dissipative dynamics of the system are dominated solely by the thermal noise, the optical input noise can be omitted. As a result, we find a -times improvement in sensitivity compared with the standard single-oscillator acceleration sensing scheme (see Eq. (1)),
| (23) |
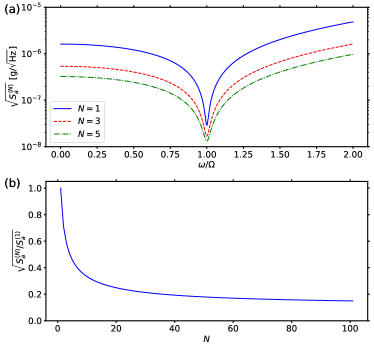
Figure 2(a) shows the acceleration sensitivity as a function of frequency for different numbers of the oscillators . The results indicate that the acceleration sensitivity improves with the increase of the oscillator number . The acceleration sensitivity drops at the mechanical resonance frequency due to the Lorentzian-like line shape response function. Figure 2(b) shows the acceleration sensitivity at the mechanical resonance frequency (normalized with the sensitivity for ) as a function of the number of oscillators . The sensitivity represents a significant improvement in increasing the oscillator number. The higher sensitivity can be achieved by using more oscillators.
IV The numerical simulation
We numerically simulate the dynamics of the whole optomechanical system via the following Markovian Master equation
| (24) |
where is the density operator of the optomechanical system, is the linearized Hamiltonian, and is the time-dependent external force acting on each mechanical oscillator which induces an acceleration via the relation in Eq. (3), i.e., one can obtain the acceleration through . The Lindblad superoperator describing the system dissipation reads
| (25) | ||||
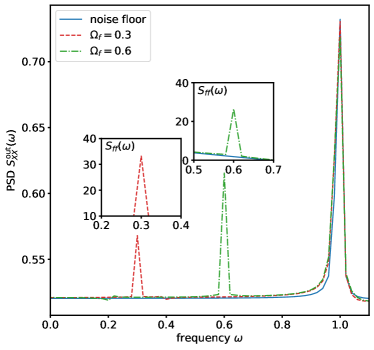
where is the mechanical annihilation operator of the th sphere. In the simulation, we assume the external forces acting on each oscillator are identical and in the form of with the amplitude and the frequency . We simulate the dynamical evolution of a three-microsphere array optomechanical system and plot the PSDs of the output optical field in amplitude quadrature and the total force (insets) for different frequencies in Fig. 3. Two peaks at the frequencies corresponding to that of the external force are observed, which confirms that the optomechanical interaction encodes the information of the collective motion induced by the external acceleration into the cavity field. We also note that the height of the peaks corresponding to the external force in the optical PSD increases along with the frequency of the acceleration approaching the mechanical resonance frequency due to the Lorentzian-like line shape response functions. In the insets, the two PSDs of the forces corresponding to the frequencies and have almost equal height (filled area) because of the same amplitude . According to the connection between the amplitude and the PSD in Eq. (16), we integrate the PSD around the peak and over the noise floor in the insets and obtain the variance and . This result is well consistent with the variance obtained from the analytical expression with .
V The experimental realization.
We can employ holographic optical tweezers to levitate many nano-particles inside an optical cavity to realize our acceleration sensing scheme. Following the Ref. [63], a one/two-dimensional array can be created by a pair of orthogonal acousto-optic deflectors (AOD). The resulting beams are focused by an objective lens to create an array of optical tweezers in an optical cavity, which is driven by a laser beam. An auxiliary trapping beam is used to rearrange the pattern of an array and therefore adjust the positions of the nano-particles so that only their collective mode is coupled to the cavity mode. The transmission field of the cavity is measured by a homodyne detection scheme.
Here, the adjacent distance of two particles (equilibrium positions) should satisfy the condition in Eq. (13), which can be adjusted by the integer . Since the distance between two adjacent optical traps created by holographic optical tweezers is several microns in experiments, the integer should be larger than at least. However, this has no effect on the coupling between the collective mode and cavity mode.
VI Summary and outlook
In conclusion, we have proposed a protocol for acceleration sensing by using an optically levitated MSA. With the help of holographic optical tweezers, small mass microspheres are trapped and levitated in a driven FP cavity. These small mass spheres form an effective large mass sphere whose mass is distributed in multiple different optical traps, which circumvents the difficulty of levitating a large mass microsphere in a single optical trap. Moreover, the collective motion of the MSA leads to a measurement enhancement effect that can greatly improve acceleration sensitivity. The FP cavity coupled with the MSA is used for the readout of the acceleration information: By suitably adjusting the positions of the microspheres in the cavity, the optomechanical interaction encodes the acceleration information acting on the MSA onto the intracavity photons, which can be measured at the cavity output via the homodyne or heterodyne detection. The results of analytical derivations and numerical simulations show that, compared to the traditional single-microsphere measurement protocol, our scheme presents a -times improvement in sensitivity.
In the future, along with the development of holographic optical tweezers technique [57] in high vacuum and optical measurement methods, our protocol may be extended to a large 3D sensing array which possibly enables full-profile imaging and dynamical evolution monitoring of a force field in real-time. In addition, the optically levitated MSA itself provides a platform to investigate quantum entanglement and quantum correlation [64, 65].
*
Appendix A The derivation of the PSD of acceleration
Here we describe the detailed derivation of the PSD of the acceleration in Eq. (15) in the main text. From the Hamiltonian (2) and the standard linearization procedure [59], we obtain the quantum Langevin equations QLEs. (II) in terms of the quantum fluctuation operators, together with a set of classical Langevin equations (CLEs) in terms of the classical mean values,
| (26) | ||||
By setting the time derivatives to zero in Eqs. (26), one obtains the steady-state mean values as
| (27) | ||||
which are used to determine the effective detuning and coupling strengths in QLEs (II). To solve the QLEs in Eqs. (10) in the main text, we transform them into the frequency domain via the Fourier transformation , where the operator with and without tilde denote the same quantity in time and frequency domain, respectively. The QLEs in the frequency domain reads
| (28) | ||||
where is the bare mechanical response function (susceptibility). By solving Eqs. (28), we obtain the amplitude and phase quadratures of the cavity field as
| (29a) | |||||
| (29b) | |||||
with the corresponding response functions
| (30a) | |||
| (30b) | |||
| (30c) | |||
| (30d) | |||
| (30e) | |||
| (30f) | |||
| (30g) | |||
where
| (31) |
With the solutions of and , the PSDs of the cavity field quadratures are given by
| (32a) | |||||
| (32b) | |||||
from which, we can therefore solve the PSD of the external force in terms of PSD of cavity field in the amplitude or phase quadrature
| (33) | |||||
The power spectral densities of the input noise can be calculated via the correlation functions in Eqs. (7) and (9), and the exact results are given by
| (34) | ||||
To establish the connection between and quantities measurable directly in experiments, we need to further consult quantum input-output theory. By substituting the input-output relations and into Eqs. (29), we obtain the amplitude and phase quadratures of the output optical field as
| (35) | |||||
| (36) |
By using the relation between the force and acceleration in Eq. (3), one can obtain the PSD of the output optical field in amplitude and phase in terms of the PSD of the acceleration as
| (37a) | |||||
| (37b) | |||||
By solving equations above, we obtain the eventual expression of PSD of the acceleration determined by the output optical field and the input noises as follows
| (38) | |||||
In experiments, the output optical field PSD in amplitude quadrature or in phase quadrature can be obtained directly by the optical homodyne and heterodyne detection.
Acknowledgements.
We thank Peitong He, Tao Liang, Xiaowen Gao, and Zhenhai Fu for useful discussions. This work is supported by Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ22A040010) and the Major Scientific Research Project of Zhejiang Lab (2019 MB0AD01).References
- Aspelmeyer et al. [2014a] M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, Cavity optomechanics, Reviews of Modern Physics 86, 1391 (2014a).
- Anetsberger et al. [2009] G. Anetsberger, O. Arcizet, Q. P. Unterreithmeier, R. Rivière, A. Schliesser, E. M. Weig, J. P. Kotthaus, and T. J. Kippenberg, Near-field cavity optomechanics with nanomechanical oscillators, Nature Physics 5, 909 (2009).
- Gavartin et al. [2012] E. Gavartin, P. Verlot, and T. J. Kippenberg, A hybrid on-chip optomechanical transducer for ultrasensitive force measurements, Nature nanotechnology 7, 509 (2012).
- Krause et al. [2012] A. G. Krause, M. Winger, T. D. Blasius, Q. Lin, and O. Painter, A high-resolution microchip optomechanical accelerometer, Nature Photonics 6, 768 (2012).
- Guzmán Cervantes et al. [2014] F. Guzmán Cervantes, L. Kumanchik, J. Pratt, and J. M. Taylor, High sensitivity optomechanical reference accelerometer over 10 khz, Applied Physics Letters 104, 221111 (2014).
- Mason et al. [2019] D. Mason, J. Chen, M. Rossi, Y. Tsaturyan, and A. Schliesser, Continuous force and displacement measurement below the standard quantum limit, Nature Physics 15, 745 (2019).
- Zhao et al. [2020] W. Zhao, S.-D. Zhang, A. Miranowicz, and H. Jing, Weak-force sensing with squeezed optomechanics, Science China Physics, Mechanics & Astronomy 63, 224211 (2020).
- Gonzalez-Ballestero et al. [2021] C. Gonzalez-Ballestero, M. Aspelmeyer, L. Novotny, R. Quidant, and O. Romero-Isart, Levitodynamics: Levitation and control of microscopic objects in vacuum, Science 374, eabg3027 (2021).
- Ashkin and Dziedzic [1971] A. Ashkin and J. Dziedzic, Optical levitation by radiation pressure, Applied Physics Letters 19, 283 (1971).
- Ashkin and Dziedzic [1976] A. Ashkin and J. Dziedzic, Optical levitation in high vacuum, Applied Physics Letters 28, 333 (1976).
- Ashkin and Dziedzic [1977] A. Ashkin and J. Dziedzic, Feedback stabilization of optically levitated particles, Applied Physics Letters 30, 202 (1977).
- Ashkin et al. [1987] A. Ashkin, J. M. Dziedzic, and T. Yamane, Optical trapping and manipulation of single cells using infrared laser beams, Nature 330, 769 (1987).
- Ashkin and Dziedzic [1987] A. Ashkin and J. M. Dziedzic, Optical trapping and manipulation of viruses and bacteria, Science 235, 1517 (1987).
- Fazal and Block [2011] F. M. Fazal and S. M. Block, Optical tweezers study life under tension, Nature photonics 5, 318 (2011).
- Dholakia and Čižmár [2011] K. Dholakia and T. Čižmár, Shaping the future of manipulation, Nature photonics 5, 335 (2011).
- Padgett and Bowman [2011] M. Padgett and R. Bowman, Tweezers with a twist, Nature photonics 5, 343 (2011).
- Maragò et al. [2013] O. M. Maragò, P. H. Jones, P. G. Gucciardi, G. Volpe, and A. C. Ferrari, Optical trapping and manipulation of nanostructures, Nature nanotechnology 8, 807 (2013).
- Ranjit et al. [2015] G. Ranjit, D. P. Atherton, J. H. Stutz, M. Cunningham, and A. A. Geraci, Attonewton force detection using microspheres in a dual-beam optical trap in high vacuum, Physical Review A 91, 051805 (2015).
- Ranjit et al. [2016] G. Ranjit, M. Cunningham, K. Casey, and A. A. Geraci, Zeptonewton force sensing with nanospheres in an optical lattice, Physical Review A 93, 053801 (2016).
- Hempston et al. [2017] D. Hempston, J. Vovrosh, M. Toroš, G. Winstone, M. Rashid, and H. Ulbricht, Force sensing with an optically levitated charged nanoparticle, Applied Physics Letters 111, 133111 (2017).
- Blakemore et al. [2019] C. P. Blakemore, A. D. Rider, S. Roy, Q. Wang, A. Kawasaki, and G. Gratta, Three-dimensional force-field microscopy with optically levitated microspheres, Physical Review A 99, 023816 (2019).
- Tebbenjohanns et al. [2019] F. Tebbenjohanns, M. Frimmer, A. Militaru, V. Jain, and L. Novotny, Cold damping of an optically levitated nanoparticle to microkelvin temperatures, Physical review letters 122, 223601 (2019).
- Tebbenjohanns et al. [2020] F. Tebbenjohanns, M. Frimmer, V. Jain, D. Windey, and L. Novotny, Motional sideband asymmetry of a nanoparticle optically levitated in free space, Physical Review Letters 124, 013603 (2020).
- Monteiro et al. [2017] F. Monteiro, S. Ghosh, A. G. Fine, and D. C. Moore, Optical levitation of 10-ng spheres with nano-g acceleration sensitivity, Physical Review A 96, 063841 (2017).
- Rider et al. [2018] A. D. Rider, C. P. Blakemore, G. Gratta, and D. C. Moore, Single-beam dielectric-microsphere trapping with optical heterodyne detection, Physical Review A 97, 013842 (2018).
- Monteiro et al. [2020a] F. Monteiro, W. Li, G. Afek, C.-l. Li, M. Mossman, and D. C. Moore, Force and acceleration sensing with optically levitated nanogram masses at microkelvin temperatures, Physical Review A 101, 053835 (2020a).
- Barker [2010] P. Barker, Doppler cooling a microsphere, Physical review letters 105, 073002 (2010).
- Gieseler et al. [2012] J. Gieseler, B. Deutsch, R. Quidant, and L. Novotny, Subkelvin parametric feedback cooling of a laser-trapped nanoparticle, Physical review letters 109, 103603 (2012).
- Kiesel et al. [2013] N. Kiesel, F. Blaser, U. Delić, D. Grass, R. Kaltenbaek, and M. Aspelmeyer, Cavity cooling of an optically levitated submicron particle, Proceedings of the National Academy of Sciences 110, 14180 (2013).
- Millen et al. [2015] J. Millen, P. Fonseca, T. Mavrogordatos, T. Monteiro, and P. Barker, Cavity cooling a single charged levitated nanosphere, Physical review letters 114, 123602 (2015).
- Hebestreit et al. [2018] E. Hebestreit, M. Frimmer, R. Reimann, and L. Novotny, Sensing static forces with free-falling nanoparticles, Physical review letters 121, 063602 (2018).
- Delić et al. [2019] U. Delić, M. Reisenbauer, D. Grass, N. Kiesel, V. Vuletić, and M. Aspelmeyer, Cavity cooling of a levitated nanosphere by coherent scattering, Physical review letters 122, 123602 (2019).
- Hoang et al. [2016a] T. M. Hoang, Y. Ma, J. Ahn, J. Bang, F. Robicheaux, Z.-Q. Yin, and T. Li, Torsional optomechanics of a levitated nonspherical nanoparticle, Physical review letters 117, 123604 (2016a).
- Li et al. [2010] T. Li, S. Kheifets, D. Medellin, and M. G. Raizen, Measurement of the instantaneous velocity of a brownian particle, Science 328, 1673 (2010).
- Li and Raizen [2013] T. Li and M. G. Raizen, Brownian motion at short time scales, Annalen der Physik 525, 281 (2013).
- Gieseler et al. [2013] J. Gieseler, L. Novotny, and R. Quidant, Thermal nonlinearities in a nanomechanical oscillator, Nature physics 9, 806 (2013).
- Moore et al. [2014] D. C. Moore, A. D. Rider, and G. Gratta, Search for millicharged particles using optically levitated microspheres, Physical review letters 113, 251801 (2014).
- Gieseler et al. [2014] J. Gieseler, R. Quidant, C. Dellago, and L. Novotny, Dynamic relaxation of a levitated nanoparticle from a non-equilibrium steady state, Nature nanotechnology 9, 358 (2014).
- Jain et al. [2016] V. Jain, J. Gieseler, C. Moritz, C. Dellago, R. Quidant, and L. Novotny, Direct measurement of photon recoil from a levitated nanoparticle, Physical review letters 116, 243601 (2016).
- Rider et al. [2016] A. D. Rider, D. C. Moore, C. P. Blakemore, M. Louis, M. Lu, and G. Gratta, Search for screened interactions associated with dark energy below the 100 m length scale, Physical review letters 117, 101101 (2016).
- Rondin et al. [2017] L. Rondin, J. Gieseler, F. Ricci, R. Quidant, C. Dellago, and L. Novotny, Direct measurement of kramers turnover with a levitated nanoparticle, Nature nanotechnology 12, 1130 (2017).
- Nie et al. [2014] W. Nie, Y. Lan, Y. Li, and S. Zhu, Generating large steady-state optomechanical entanglement by the action of casimir force, SCIENCE CHINA Physics, Mechanics & Astronomy 57, 2276 (2014).
- Carney et al. [2021] D. Carney, G. Krnjaic, D. C. Moore, C. A. Regal, G. Afek, S. Bhave, B. Brubaker, T. Corbitt, J. Cripe, N. Crisosto, et al., Mechanical quantum sensing in the search for dark matter, Quantum Science and Technology 6, 024002 (2021).
- Moore and Geraci [2021] D. C. Moore and A. A. Geraci, Searching for new physics using optically levitated sensors, Quantum Science and Technology 6, 014008 (2021).
- Arvanitaki and Geraci [2013] A. Arvanitaki and A. A. Geraci, Detecting high-frequency gravitational waves with optically levitated sensors, Physical review letters 110, 071105 (2013).
- Winstone et al. [2022] G. Winstone, Z. Wang, S. Klomp, G. R. Felsted, A. Laeuger, C. Gupta, D. Grass, N. Aggarwal, J. Sprague, P. J. Pauzauskie, et al., Optical trapping of high-aspect-ratio nayf hexagonal prisms for khz-mhz gravitational wave detectors, Physical review letters 129, 053604 (2022).
- Monteiro et al. [2020b] F. Monteiro, G. Afek, D. Carney, G. Krnjaic, J. Wang, and D. C. Moore, Search for composite dark matter with optically levitated sensors, Physical Review Letters 125, 181102 (2020b).
- Romero-Isart et al. [2010] O. Romero-Isart, M. L. Juan, R. Quidant, and J. I. Cirac, Toward quantum superposition of living organisms, New Journal of Physics 12, 033015 (2010).
- Romero-Isart et al. [2011] O. Romero-Isart, A. C. Pflanzer, F. Blaser, R. Kaltenbaek, N. Kiesel, M. Aspelmeyer, and J. I. Cirac, Large quantum superpositions and interference of massive nanometer-sized objects, Physical review letters 107, 020405 (2011).
- Delić et al. [2020] U. Delić, M. Reisenbauer, K. Dare, D. Grass, V. Vuletić, N. Kiesel, and M. Aspelmeyer, Cooling of a levitated nanoparticle to the motional quantum ground state, Science 367, 892 (2020).
- Magrini et al. [2021] L. Magrini, P. Rosenzweig, C. Bach, A. Deutschmann-Olek, S. G. Hofer, S. Hong, N. Kiesel, A. Kugi, and M. Aspelmeyer, Real-time optimal quantum control of mechanical motion at room temperature, Nature 595, 373 (2021).
- Tebbenjohanns et al. [2021] F. Tebbenjohanns, M. L. Mattana, M. Rossi, M. Frimmer, and L. Novotny, Quantum control of a nanoparticle optically levitated in cryogenic free space, Nature 595, 378 (2021).
- Lewandowski et al. [2021] C. W. Lewandowski, T. D. Knowles, Z. B. Etienne, and B. D’Urso, High-sensitivity accelerometry with a feedback-cooled magnetically levitated microsphere, Physical Review Applied 15, 014050 (2021).
- Hoang et al. [2016b] T. M. Hoang, J. Ahn, J. Bang, and T. Li, Electron spin control of optically levitated nanodiamonds in vacuum, Nature communications 7, 12250 (2016b).
- Gieseler et al. [2020] J. Gieseler, A. Kabcenell, E. Rosenfeld, J. Schaefer, A. Safira, M. J. Schuetz, C. Gonzalez-Ballestero, C. C. Rusconi, O. Romero-Isart, and M. D. Lukin, Single-spin magnetomechanics with levitated micromagnets, Physical review letters 124, 163604 (2020).
- Millen et al. [2020] J. Millen, T. S. Monteiro, R. Pettit, and A. N. Vamivakas, Optomechanics with levitated particles, Reports on Progress in Physics 83, 026401 (2020).
- Yang et al. [2021] Y. Yang, Y. Ren, M. Chen, Y. Arita, and C. Rosales-Guzmán, Optical trapping with structured light: a review, Advanced Photonics 3, 034001 (2021).
- Chang et al. [2010] D. E. Chang, C. Regal, S. Papp, D. Wilson, J. Ye, O. Painter, H. J. Kimble, and P. Zoller, Cavity opto-mechanics using an optically levitated nanosphere, Proceedings of the National Academy of Sciences 107, 1005 (2010).
- Genes et al. [2008a] C. Genes, D. Vitali, P. Tombesi, S. Gigan, and M. Aspelmeyer, Ground-state cooling of a micromechanical oscillator: Comparing cold damping and cavity-assisted cooling schemes, Physical Review A 77, 033804 (2008a).
- Genes et al. [2008b] C. Genes, D. Vitali, and P. Tombesi, Simultaneous cooling and entanglement of mechanical modes of a micromirror in an optical cavity, New Journal of Physics 10, 095009 (2008b).
- Aspelmeyer et al. [2014b] M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, Cavity optomechanics, Reviews of Modern Physics 86, 1391 (2014b).
- Martinetz et al. [2018] L. Martinetz, K. Hornberger, and B. A. Stickler, Gas-induced friction and diffusion of rigid rotors, Physical Review E 97, 052112 (2018).
- Yan et al. [2022] J. Yan, X. Yu, Z. V. Han, T. Li, and J. Zhang, On-demand assembly of optically-levitated nanoparticle arrays in vacuum, arXiv preprint arXiv:2207.03641 (2022).
- Rudolph et al. [2022] H. Rudolph, U. Delić, M. Aspelmeyer, K. Hornberger, and B. A. Stickler, Force-gradient sensing and entanglement via feedback cooling of interacting nanoparticles, arXiv preprint arXiv:2204.13684 (2022).
- Rieser et al. [2022] J. Rieser, M. A. Ciampini, H. Rudolph, N. Kiesel, K. Hornberger, B. A. Stickler, M. Aspelmeyer, and U. Delić, Tunable light-induced dipole-dipole interaction between optically levitated nanoparticles, Science 377, 987 (2022).