Collision centrality and system size dependences of light nuclei production via dynamical coalescence mechanism
Abstract
Light (anti-)nuclei in relativistic heavy-ion collisions are considered to be formed by the coalescence mechanism of (anti-)nucleons in the present work. Using a dynamical phase-space coalescence model coupled with a multi-phase transport (AMPT) model, we explore the formation of light clusters such as deuteron, triton and their anti-particles in different centralities for 197Au + 197Au collisions at GeV. The calculated transverse momentum spectra of protons, deuterons, and tritons are comparable to those of experimental data from the RHIC-STAR collaboration. Both coalescence parameters for (anti-)deuteron and for triton increase with the transverse momentum as well as the collision centrality, and they are comparable with the measured values in experiments. The effect of system size on the production of light nuclei is also investigated by 10B + 10B, 16O + 16O, 40Ca + 40Ca, and 197Au + 197Au systems in central collisions. The results show that yields of light nuclei increase with system size, while the values of coalescence parameters present an opposite trend. It is interesting to see that the system size, as well as the centrality dependence of ( = 2, 3), falls into the same group, which further demonstrates production probability of light nuclei is proportional to the size of the fireball. Furthermore, we compare our coalescence results with other models, such as the thermal model and analytic coalescence model, it seems that the description of light nuclei production is consistent with each other.
I Introduction
Quantum Chromodynamics (QCD) predicts that a new state of matter, namely the quark-gluon plasma (QGP), is likely to be formed in an extremely high temperature or density environment Karsch (2002), which could be existed in the microseconds after the big bang. Studying this new matter is of great significance for us to have a comprehensive understanding not only of the basic composition and interaction of matter but also the information of the early evolution of the universe. Relativistic heavy-ion collision is currently considered as a unique way in the laboratory to detect such extremely high-temperature and -density QCD matter and then explore the QGP phase structure. However, the QGP state can only survive at a relatively short stage in the collision process, and it is soon hadronized as the system’s temperature and density rapidly decrease, then hadrons will interact with each other. While hadronic interaction ceases, the particle approaches a kinetic freeze-out stage. Experimentally one can infer the properties of the early QGP by exploring the kinetic freeze-out particles. Therefore, exploring the properties of QGP and QCD critical point from the regular hadronic matter to the QGP phase remains of great interest to the field Wong (1994); Shuryak (2017); Braun-Munzinger et al. (2016); Chen et al. (2018); Wu et al. (2021); Shen and Li (2020); Fukushima and Sasaki (2013); Bzdak et al. (2020).
Considering the light nuclei have small binding energy, it is also an open question of how they can survive from the hot nuclear matter. They might be disintegrated and regenerated through the coalescence of nucleons which are de-coupled from the hot and dense system, so the production of light nuclei can be used to extract the information of freeze-out nucleon distributions Adam et al. (2019) and to understand how the QGP expands, cools and hadronizes. These pieces of information provide crucial insights for dynamical mechanism and space-time evolution of heavy-ion collisions Gao et al. (2020); Tang et al. (2020); Han et al. (2020); Wang et al. (2019); Liu and Huang (2020). Recently the light nucleus also demonstrates its significance to search for the possible critical point in the phase diagram of strongly interacting quark matter Sun et al. (2018); Yu et al. (2020); Deng and Ma (2020); Liu et al. (2020); Sun et al. (2017); Shuryak and Torres-Rincon (2019). Theoretical study about the light clusters has been undertaken for a long time and several models or methods are used to explore the production of light nuclei. Thermal models Shuryak and Torres-Rincon (2020); Andronic et al. (2021); Wang et al. (2020); Abelev et al. (2009) have successfully described the yields of hadrons and nuclei. Besides, the coalescence model has been used to describe the production of light nuclei for many years Mattiello et al. (1997); Yan et al. (2006); Zhang et al. (2010); Cho et al. (2017); Wang and Ma (2019); Zhao et al. (2020); Sun et al. (2019). These calculations by using a similar coalescence mechanism coupled with phase-space distribution from different models, such as blast-wave model and transport model, seem to resemble each other of description for light nuclei production at RHIC and LHC energies. The production of light nuclei can be also described by the kinetic equations Danielewicz and Bertsch (1991); Oliinychenko et al. (2019). Especially recently, the relativistic kinetic equations with their nonlocal collision integrals were also solved for successfully describing light (anti-)nuclei production from the many-body scatterings in high-energy nuclear collisions Sun et al. (2021).
In the present work, the system size dependence (centrality and collision system) are payed more attention. We investigate the production of deuteron and triton in relativistic heavy-ion collision by means of A Multi-Phase Transport (AMPT) model Lin et al. (2005) followed by a dynamical coalescence model for 197Au + 197Au collisions at different centralities as well as for the central collisions of 10B + 10B, 16O + 16O, and 40Ca + 40Ca at GeV. The coalescence factor extracted from the transverse momentum spectra of light nuclei and proton represents the coalescence probability, and it is related to the source volume that decreases with the increasing of constituent momentum of coalesced nucleons Bellini and Kalweit (2019). The transverse momentum () distribution and the coalescence parameters () of light nuclei are comparable to the experimental data. On the other hand, the properties of QGP are sensitive to the initial geometry and the dynamical fluctuations in heavy-ion collisions, and the system size scan experiment has been proposed at RHIC energies recently Huang et al. (2020). These experiments will provide us more information of the initial geometry distribution and fluctuation effects on momentum distribution at the final stage, and some related theoretical analytical works have been performed Sievert and Noronha-Hostler (2019); Nagle et al. (2014); Lim et al. (2019); Katz et al. (2020); Zhang et al. (2020); Wang et al. (2020); Liu et al. (2017). Along this direction, a system scan of the coalescence parameters is undertaken in the present work and it is found that falls into the same group for its centrality dependence when both the system size and centrality are expressed by charged particle multiplicity(),including , , , , which indicates that light nuclei production essentially depends on the size of the fireball.
The paper is arranged as follows: In Section II, a brief description of the AMPT model which is used to generate the nucleon phase-space distribution at the freeze-out stage is presented. Also,the coalescence model for the light cluster is described, including the Wigner phase space density functions for the (anti)deuteron and (anti)triton. In section III, the results of distribution and the coalescence parameters of (anti)deuteron and triton from 10B + 10B, 16O + 16O and 40Ca + 40Ca in central collisions as well as 197Au + 197Au collisions at different centralities are compared to the available experimental data. Finally, a conclusion is presented in Section IV.
II MODEL and ALGORITHMS
II.1 AMPT model
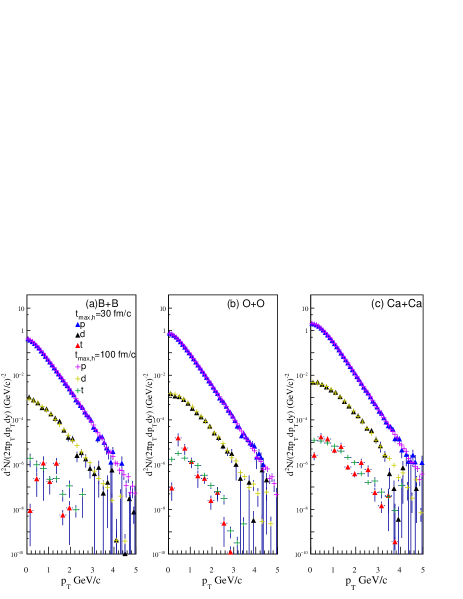
A multi-phase transport model Lin et al. (2005) was used to provide the phase-space of nucleons in this work. The model is composed of four parts: the HIJING model Wang and Gyulassy (1991); Gyulassy and Wang (1994) is used to simulate the initial conditions, the Zhang’s Parton Cascade (ZPC) model Zhang (1998) is employed to describe partonic interaction, the Lund string fragmentation or coalescence model is used for the hadronization process, and A Relativistic Transport (ART) model Li and Ko (1995) is applied to describe the hadronic rescattering process. As an event generator used in this work, the AMPT model outputs the phase-space distribution at the final stage in the hadronic rescattering process (ART model Li and Ko (1995)) with considering baryon-baryon, baryon-meson, and meson-meson elastic and inelastic scatterings, as well as resonance decay or week decay. In Refs. Li and Ko (1995); Lin et al. (2005) the interaction cross section was presented and extended. The hadronic rescattering time would affect light nuclei spectra and yield which are based on the phase-space information of nucleons from the AMPT model. Refs. Lin et al. (2005); Ma and Lin (2016) suggest the maximum hadronic rescattering time (), which means to cease a hadron interacting with others if it still dose not reach freeze-out state at that time, 30 for the RHIC energy region and 200 for the LHC energy region. Here the spectra of , and with the cutoff of the maximum hadronic rescattering time of 30 and 100 are checked. Fig. 1 shows the spectra of proton, deuteron and triton of 197Au + 197Au collisions at mid-rapidity for different centralities at GeV, and Fig. 2 presents the results for the 010% central collisions of 10B + 10B, 16O + 16O, 40Ca + 40Ca at GeV and mid-rapidity . We can find that these two cases are very close to each other. Afterwords we choose the case of = 100 for the following calculations. We would mention that the AMPT model has been successfully used to simulate physics in heavy-ion collisions at the RHIC and LHC energies Lin et al. (2005); Ma and Lin (2016); Lin and Zheng (2021) and the detailed parameter configurations can be found therein.
II.2 Dynamical coalescence model
In the coalescence model Csernai and Kapusta (1986), the invariant yields of light nuclei with charge number and atomic mass number can be described by the yields of cluster constituents (protons and neutrons) multiplying by a coalescence parameter ,
| (1) |
where and are the momenta of proton and neutron, respectively, and is the momentum of the nucleus with the mass number which is approximate times of proton momentum, i.e. , assuming that the distributions of neutrons and protons are the same. The coalescence parameter related to the local nucleon density reflects the probability of nucleon coalescence. The coalescence parameter is also related to the effective volume of the nuclear matter at the time of coalescence of nucleons into light nuclei, called nucleon correlation volume Csernai and Kapusta (1986), i.e. .
The dynamical coalescence model can give the probability of light nuclei (-nucleon cluster) by the overlap of the cluster Wigner phase-space density with the nucleon phase-space distributions at an equal time in the -nucleon rest frame at the freeze-out stage Chen et al. (2003). The momentum distribution of a cluster in a system containing nucleons can be expressed by,
| (2) |
where and are the number of the nucleon and proton of the cluster, respectively; and are the neutron and proton phase-space distribution functions at freeze-out, respectively; is the Wigner density function; and are the relative coordinates and momentum in the -nucleon rest frame; the spin-isospin statistical factor is 3/8 for deuteron and 1/3 for triton Chen et al. (2003), note whether to consider the isospin effect is still an unresolved problem, neglecting the isospin effect can be found in Zhao et al. (2018); Sun et al. (2021). While the neutron and proton phase-space distribution comes from the transport model simulations, the multiplicity of a -nucleon cluster is then given by,
| (3) |
where the denotes the event averaging.
II.3 Wigner phase-space density
The Wigner phase-space density of (anti)deuteron is assumed as Chen et al. (2003),
| (4) |
where the Gaussian fit coefficient and are given in Ref. Chen et al. (2003). = (-)/2 is the relative momentum and = (-) is the relative coordinate of proton and neutron inside deuteron.
The Wigner phase-space density of triton is obtained from a spherical harmonic oscillator Chen et al. (2003); Zhang et al. (2010); Sun and Chen (2015),
| (5) |
where and are relative coordinates, and are the relative momenta in the Jacobi coordinate, the parameter is obtained from the root-mean-square radius, 1.61 for triton Chen et al. (2003).
In practice, the coalescence procedure by using Eq. (3) can not guarantee the energy conservation, such as for the formation of dueteron . If a proton and a neutron with momentum-energy and coalesces a deuteron with , and then the lost energy is . From Eq. (4), it can be seen that the lost energy is ignorable since the Wigner density is suppressed exponentially at the large relative momentum. For the three-body case, a similar derivation can be obtained. Actually, we made a numerical check for the effect of lost energy, it is found that it is negligible for the yield and spectra of the light nuclei production.
In this calculation, the AMPT model provides the phase-space of nucleons at the freeze-out stage in heavy-ion collisions and the followed coalescence model is coupled to give the transverse momentum spectra of deuterons () and tritons (). Based on the obtained spectra, the yields of and , as well as the coalescence parameters, are discussed.
III Results and Discussion
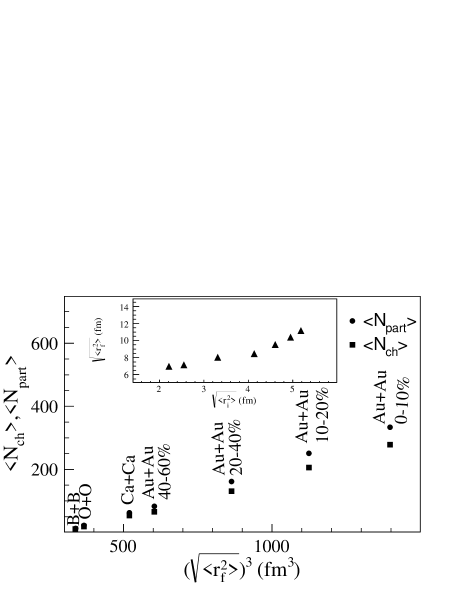
To discuss the system size dependence of light nuclei production, some quantities of the collision systems are shown in figure 3, such as representing the average number of participants, and denoting the average number of charged hadrons (, , , ) with a kinetic window of GeV and rapidity (mid-rapidity), representing the averaged radius of the initial collision zone which is calculated through the participants, representing the averaged radius of the collision system at freeze-out stage which is calculated through the charged hadrons. It is seen that and are all proportional to collision system size at final stage, namely , for different collision systems. In the insert, the freeze-out radius of the collision system increases with the initial radius of the collision zone, namely . So both and can characterise the collision system size, and it is therefore convenient to discuss system size dependence of observables by comparing the -dependent results with experimental data in the following.
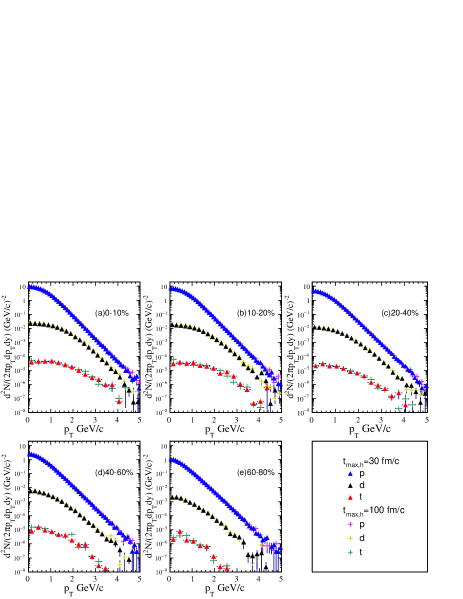
III.1 spectra of (), () and ()
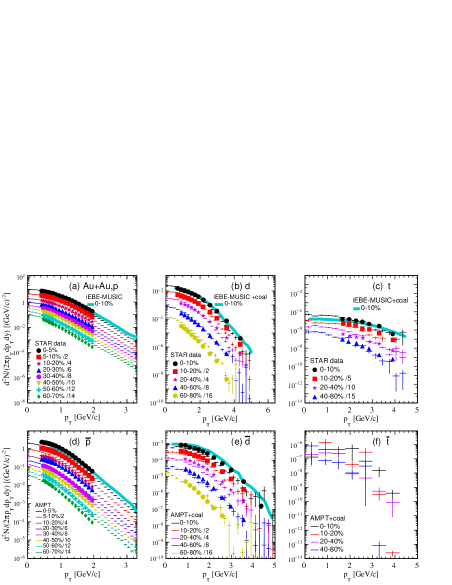
Figure 4 presents the transverse momentum spectra of (), () and () calculated by the AMPT model coupling with the coalescence model in Au + Au collisions at GeV. The results are shown for the collision centrality classes of 05%, 510%, 1020%, 2030%, 3040%, 4050%, 5060%, and 6070% for () in Fig. 4(a) and (d), 010%, 1020%, 2040%, 4060%, and 6080% for () in Fig. 4 (b) and (e), 010%, 1020%, 2040%, and 4080% for () in Fig. 4(c) and (f). It is found that the results can well describe the experimental data for Adamczyk et al. (2017a), Adam et al. (2019) and Zhang (2021) spectra from the STAR collaboration, especially in central collisions. Besides, we compared the transverse momentum spectra of (), () and with the results from the iEBE-MUSIC hybrid model plus coalescence model Zhao et al. (2020). Note that the isospin effect in the statistical factor in Eq. (2) can result in a constant factor among the results Zhao et al. (2020); Sun et al. (2021) and does not affect the shape of the spectra. It is interesting to see that two models are consistent, which implies that the phase-space of the two models have similar properties or distributions.
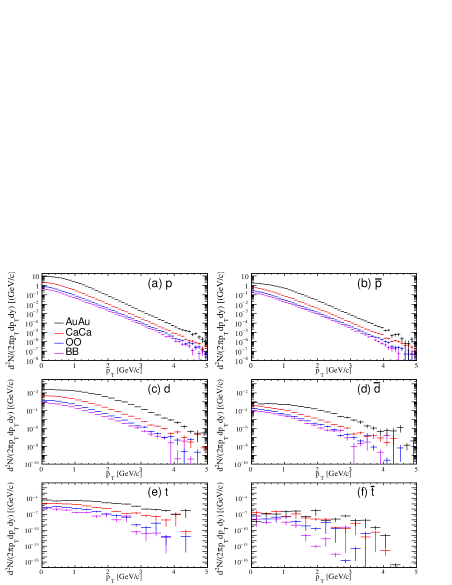
Figure 5 shows the calculated transverse momentum spectra for () ((a) and (b)), () ((c) and (d)) and () ((e) and (f)) in 10B + 10B, 16O + 16O, 40Ca + 40Ca, and 197Au + 197Au in 010% central collisions at = 39 GeV. The spectra present an obvious collision system dependence in central collisions and drop with the decreasing of the collision system size Zhang et al. (2011).
III.2 of (), () and ()
The rapidity densities () of (), () and () are calculated in mid-rapidity as a function of in 10B + 10B, 16O + 16O, 40Ca + 40Ca, and 197Au + 197Au collisions at = 39 GeV, as shown in Fig. 6. It is found that of as a function of (Fig. 6(a)) can well describe the data Adamczyk et al. (2017a) but underestimate data in Au + Au collisions at = 39 GeV. For and (Fig. 6(b)), it presents the similar description quality to the data Adam et al. (2019). of and as a function of is presented in Fig. 6(c). As shown in Fig. 6(a) and (b), of and are comparable to those from the iEBE-MUSIC hybrid model plus coalescence model Zhao et al. (2020) in central collisions, and little difference for anti-matter partners. In addition, the yields of these light (anti)nuclei for the 0-10% central collisions of 10B + 10B, 16O + 16O, and 40Ca + 40Ca systems at = 39 GeV are also shown in Fig. 6, and it seems that they follow the similar systematics. In general, it is reasonably speculated that of (anti)proton, (anti)deuteron and triton present an increasing trend with (collision system size) in different collision centralities as well as collision systems.
Furthermore, we calculate the dependence of ratios of and by using a thermal model Braun-Munzinger et al. (2004),
| (6) |
where , , and are the baryon number, strangeness number and charge number, , and , are their corresponding chemical potentials of particle , is the modified Bessel function and the upper sign is for bosons and lower for fermions, is the spinisospin degeneracy factor. We use the parameters such as the chemical freeze-out temperature as well as the baryon chemical potential from Ref. Adamczyk et al. (2017a). As shown in Fig. 6(d), the and ratios of AMPT + coalescence model are bigger than STAR data Adamczyk et al. (2017a); Adam et al. (2019); Zhang (2019). And the ratio from the thermal model can describe the STAR data Adamczyk et al. (2017a); Adam et al. (2019); Zhang (2019) but overestimates the ratio, which is consistent with the results in references Zhang (2019); Yu and Luo (2019); Vovchenko et al. (2020).
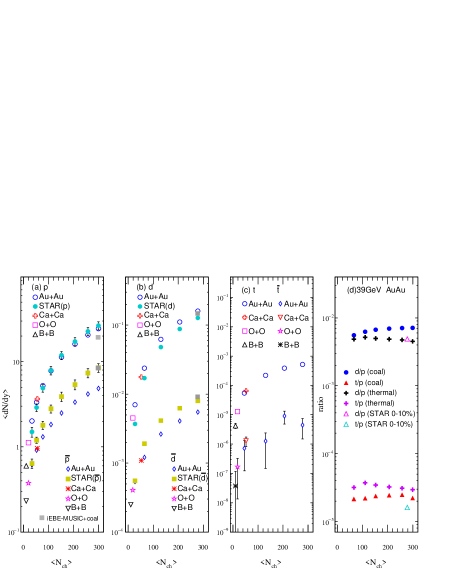
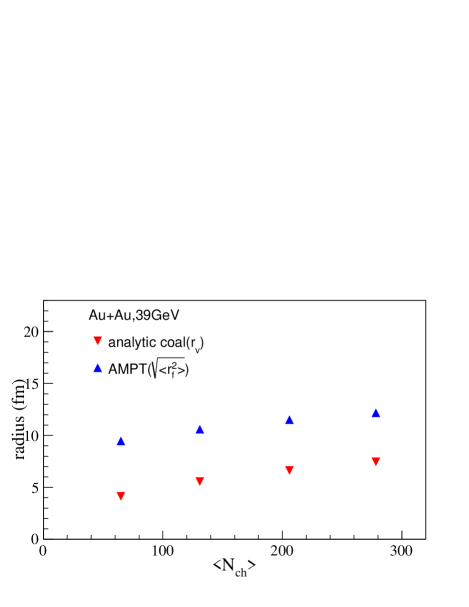
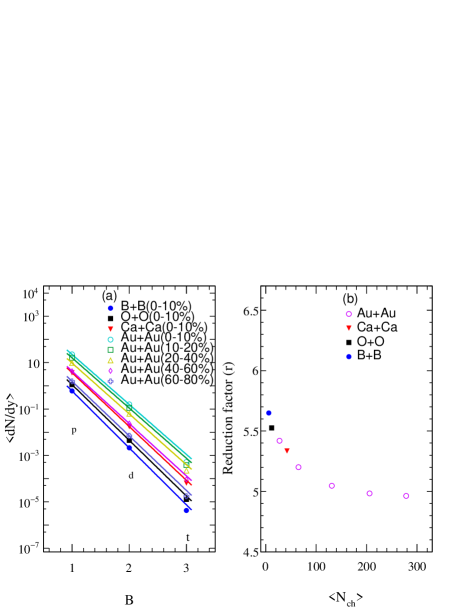
Figure 7 presents a comparison between dependence of the fireball radius () calculated directly by the coordinates from the AMPT model and that from the analytic coalescence model Sun and Chen (2017) in 197Au + 197Au collisions at GeV. In analytic coalescence model Sun and Chen (2017), a blast-wave-like parametrization is used for the phase-space configuration of constituent particles at freeze-out. We extract the effective volume by equation (25) in Ref. Sun and Chen (2017), then the fireball radius can be calculated by assuming a spherical fireball. We find that the both radii ( and ) present a similar dependence, i.e. increasing as . Of course, we notice that the values of size have model or calculation method dependence.
Figure 8(a) shows the of proton, deuteron and triton as a function of baryon number from the coalescence model in 010% 10B + 10B, 16O + 16O, and 40Ca + 40Ca collisions, as well as the 010%, 1020%, 2040%, 4060%, and 6080% 197Au + 197Au collisions at GeV. The lines are the fits to the calculated results by a function of , here denotes amplitude, is the baryon number and is the reduction factor. It is found that the yields of proton, deuteron ,and triton in each collision system exhibit a decreasing exponential trend with the baryon number. The reduction factor Shah et al. (2016); Sun and Chen (2015) by fitting the yields of proton, deuteron and triton as a function of is shown in Fig. 8(b). While the system size is expressed by , the reduction factor decreases sharply with the increasing of and then saturate at large . This implies that light nuclei production becomes more difficult in small systems, especially for that with baryon number 3 in the relativistic heavy-ion collisions.
III.3 Coalescence parameters and
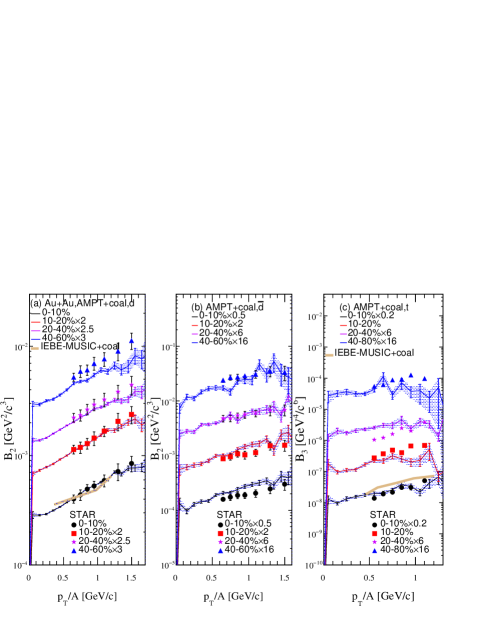
.
To further characterize the system size dependence of light nuclei production, the coalescence probability of forming light clusters is investigated by the coalescence parameters ( = 2 and 3) as defined in Eq. (1). In panel (a) and (b) of Fig. 9, the calculated coalescence parameter are compared with the data measured by the STAR collaboration Adam et al. (2019) in 197Au + 197Au collisions at RHIC energy of 39 GeV in 010%, 1020%, 2040%, and 4060% (4080% for triton) centralities. The calculated results present a similar trend with the experimental data,the coalescence parameters in panel (a), (b) and in panel (c) as a function of in different collision centralities always present an increasing trend, this might be due to the increasing correlation volume with the decreasing of , leading to a higher coalescence probability for larger values. In addition, the values of and decrease with collision centrality (i.e. the more central collisions the less ), which suggests that source volume being larger in central collisions. From the viewpoint of the coalescence probability of nucleons to form these light clusters, it is reasonable to have a bigger coalescence probability while the distance between the protons and neutrons is smaller. On the other hand, we note that the values of for deuterons are systematically larger than those of anti-deuterons in the same centrality, it is consistent with the experimental observation Adam et al. (2019), indicating that the correlated volume of baryons is smaller than that of anti-baryons. Besides, the comparison of our results of and with the iEBE-MUSIC hybrid model plus coalescence model Zhao et al. (2020) is also shown in this figure, and the trend remains similar.
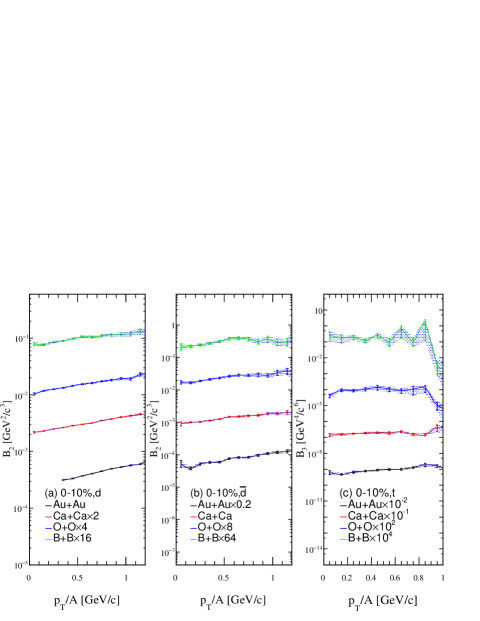
Furthermore, the coalescence parameter for (anti)deuterons as a function of is also calculated for 10B + 10B, 16O + 16O, and 40Ca + 40Ca collisions at 010% centrality at = 39 GeV, and the results are presented in Fig. 10 (a) and (b). It is found that the coalescence parameter presents a system size dependence, i.e. decreases as the system size increases. This result is consistent with the centrality dependence in the same system such as Au + Au collisions. The dependence of also presents an upward trend as shown in Fig. 9. The coalescence parameter is presented as a function of for the 010% central collisions of 10B + 10B, 16O + 16O, 40Ca + 40Ca, and 197Au + 197Au systems at = 39 GeV in Fig. 10(c), it shows the similar trend with even though the error remains larger.
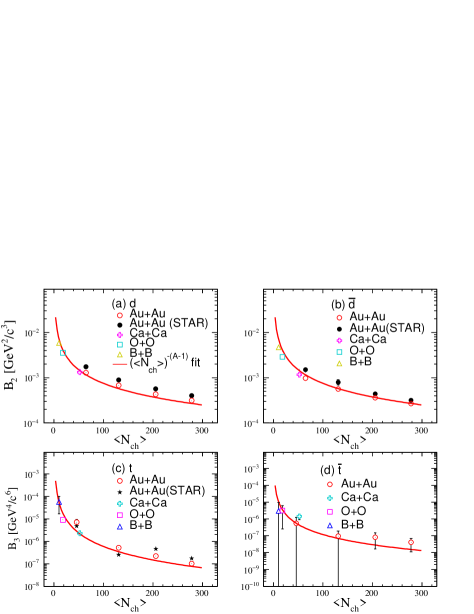
Figure 11 shows the dependence of coalescence parameters and of () (a, b), () (c, d) in 197Au+197Au collisions at 010%, 1020%, 2040%, and 4060% (4080% for ) centralities as well as 010% central collisions of 10B + 10B, 16O + 16O, 40Ca + 40Ca systems at GeV. It is observed that the coalescence parameters and present an obvious collision centrality dependence, the values of for deuteron and anti-deuteron decrease with the increasing of . The dependence of for triton in 197Au + 197Au collisions at 010%, 1020%, 2040%, and 4080% centralities at GeV is also shown in this figure. also shows a decreasing trend with . Besides, it is observed that the values of and present an obvious collision system dependence in 0-10% central collisions of 10B + 10B, 16O + 16O, 40Ca + 40Ca, and 197Au + 197Au systems, the values of and for deuteron and anti-deuteron drop with the increasing of system size, the value of also shows a decreasing trend with . Considering the properties of system size dependence from figure 3 as well as the relationship between coalescence parameter and nucleon correlation volume, i.e. Csernai and Kapusta (1986), we found that can be expressed by a simple function, (here = 2 or 3). From the viewpoint of light nuclei production by coalescence mechanism, it is concluded that the coalescence parameter can reflect the collision system size when the system is at kinetic freeze-out stage.
The thermal model has been successfully used to describe the multiplicities or particle ratios of hadrons and light nuclei Andronic et al. (2018) in relativistic heavy-ion collisions, while the coalescence model basing on phase space data is another useful tool to treat light nuclei production. In practice, the phase-space data can be generated from various models, such as blast-wave model Sun and Chen (2016), hydrodynamics Zhao et al. (2020), transport model Sombun et al. (2019) or pure analytical calculation Sun and Chen (2017). In our work, the coalescence model basing on the AMPT phase space data is used to study the light nuclei production at RHIC lower energy in the Beam Energy Scan project Aggarwal et al. (2010); Adamczyk et al. (2017b), the results are consistent with the previous calculations and provide a more comprehensive understanding of the experiment data. Therefore we argue that these models could approach an equivalent simulation of the production of light nuclei assuming the thermal or kinetic freeze-out properties of the collision systems, respectively.
IV Summary
In summary, based on the AMPT model coupled with the dynamic coalescence model, the collision system size dependence of light nuclei production was investigated for the 010%, 1020%, 2040%, 4060%, and 6080% 197Au + 197Au collisions at GeV. The calculated transverse momentum spectra can well describe the experimental data from the STAR collaboration and the extracted coalescence parameters of and fitted the data well. In the same way, the production of light nuclei is also calculated for the 010% central collisions of 10B + 10B, 16O + 16O, and 40Ca + 40Ca systems at GeV. As the system size is denoted by for different centralities and collision systems, the yields of light nuclei present an obvious system size dependence, namely increases with the system size (). The reduction factor for light nuclei production is also presented for the system size dependence, which indicates that light nuclei production becomes more difficult in small systems. And the coalescence parameters ( = 2, 3) as a function of fall into the same group regardless for different centralities in a fixed collision system or different systems at a fixed centrality. Coalescence parameters ( = 2, 3) present a decreasing trend with the increasing of , i.e. follow a proportional dependence on . We can conclude that the light nucleus production essentially depends on the fireball volume, reflected in the system size or centralities. These results shed light on further experimental system scan project at RHIC or LHC.
Acknowledgements.
This work was supported in part by the National Natural Science Foundation of China under contract Nos. 11875066, 11890710, 11890714, 11925502, 11961141003, National Key R&D Program of China under Grant No. 2018YFE0104600 and 2016YFE0100900, the Strategic Priority Research Program of CAS under Grant No. XDB34000000, the Key Research Program of Frontier Sciences of the CAS under Grant No. QYZDJ-SSW- SLH002, and the Guangdong Major Project of Basic and Applied Basic Research No. 2020B0301030008.References
- Karsch (2002) F. Karsch, Nuclear Physics A 698, 199 (2002).
- Wong (1994) C.-Y. Wong, Introduction to High-Energy Heavy-Ion Collisions (WORLD SCIENTIFIC, 1994).
- Shuryak (2017) E. Shuryak, Rev. Mod. Phys. 89, 035001 (2017).
- Braun-Munzinger et al. (2016) P. Braun-Munzinger, V. Koch, T. Schäfer, and J. Stachel, Physics Reports 621, 76 (2016).
- Chen et al. (2018) J. Chen, D. Keane, Y.-G. Ma, A. Tang, and Z. Xu, Physics Reports 760, 1 (2018).
- Wu et al. (2021) S. Wu, C. Shen, and H. Song, Chinese Physics Letters 38, 081201 (2021).
- Shen and Li (2020) C. Shen and Y. Li, Nucl. Sci. Tech. 31, 122 (2020).
- Fukushima and Sasaki (2013) K. Fukushima and C. Sasaki, Progress in Particle and Nuclear Physics 72, 99 (2013).
- Bzdak et al. (2020) A. Bzdak, S. Esumi, V. Koch, J. Liao, M. Stephanov, and N. Xu, Physics Reports 853, 1 (2020).
- Adam et al. (2019) J. Adam et al. (STAR Collaboration), Phys. Rev. C 99, 064905 (2019).
- Gao et al. (2020) J.-H. Gao, G.-L. Ma, S. Pu, and Q. Wang, Nucl. Sci. Tech. 31, 90 (2020).
- Tang et al. (2020) Z.-B. Tang, W.-M. Zha, and Y.-F. Zhang, Nucl. Sci. Tech. 31, 81 (2020).
- Han et al. (2020) Z. Han, B. Chen, and Y. Liu, Chinese Physics Letters 37, 112501 (2020).
- Wang et al. (2019) H. Wang, J. H. Chen, Y. G. Ma, et al., Nucl. Sci. Tech. 30, 185 (2019).
- Liu and Huang (2020) Y.-C. Liu and X.-G. Huang, Nucl. Sci. Tech. 31, 56 (2020).
- Sun et al. (2018) K.-J. Sun, L.-W. Chen, C. M. Ko, J. Pu, and Z. Xu, Physics Letters B 781, 499 (2018).
- Yu et al. (2020) N. Yu, D. Zhang, and X. Luo, Chinese Physics C 44, 014002 (2020).
- Deng and Ma (2020) X. G. Deng and Y. G. Ma, Phys. Lett. B 808, 135668 (2020).
- Liu et al. (2020) H. Liu, D. Zhang, S. He, K.-J. Sun, N. Yu, and X. Luo, Physics Letters B 805, 135452 (2020).
- Sun et al. (2017) K.-J. Sun, L.-W. Chen, C. M. Ko, and Z. Xu, Physics Letters B 774, 103 (2017).
- Shuryak and Torres-Rincon (2019) E. Shuryak and J. M. Torres-Rincon, Phys. Rev. C 100, 024903 (2019).
- Shuryak and Torres-Rincon (2020) E. Shuryak and J. M. Torres-Rincon, European Physical Journal A 56, 241 (2020).
- Andronic et al. (2021) A. Andronic, P. Braun-Munzinger, D. Gündüz, Y. Kirchhoff, M. Köhler, J. Stachel, and M. Winn, Nuclear Physics A 1010, 122176 (2021).
- Wang et al. (2020) D.-F. Wang, S. Zhang, and Y.-G. Ma, Phys. Rev. C 101, 034906 (2020).
- Abelev et al. (2009) B. I. Abelev et al. (STAR Collaboration), Phys. Rev. C 79, 034909 (2009).
- Mattiello et al. (1997) R. Mattiello, H. Sorge, H. Stöcker, and W. Greiner, Phys. Rev. C 55, 1443 (1997).
- Yan et al. (2006) T. Z. Yan, Y. G. Ma, X. Z. Cai, et al., Physics Letters B 638, 50 (2006).
- Zhang et al. (2010) S. Zhang, J. H. Chen, H. Crawford, D. Keane, Y. G. Ma, and Z. Xu, Physics Letters B 684, 224 (2010).
- Cho et al. (2017) S. Cho, T. Hyodo, D. Jido, et al., Progress in Particle and Nuclear Physics 95, 279 (2017).
- Wang and Ma (2019) T. T. Wang and Y. G. Ma, Eur. Phys. J. A 55, 102 (2019).
- Zhao et al. (2020) W. Zhao, C. Shen, C. M. Ko, Q. Liu, and H. Song, Phys. Rev. C 102, 044912 (2020).
- Sun et al. (2019) K.-J. Sun, C. M. Ko, and B. Dönigus, Physics Letters B 792, 132 (2019).
- Danielewicz and Bertsch (1991) P. Danielewicz and G. Bertsch, Nuclear Physics A 533, 712 (1991).
- Oliinychenko et al. (2019) D. Oliinychenko, L.-G. Pang, H. Elfner, and V. Koch, Phys. Rev. C 99, 044907 (2019).
- Sun et al. (2021) K.-J. Sun, R. Wang, C. M. Ko, Y.-G. Ma, and C. Shen, arXiv e-prints , arXiv:2106.12742 (2021).
- Lin et al. (2005) Z.-W. Lin, C. M. Ko, B.-A. Li, B. Zhang, and S. Pal, Phys. Rev. C 72, 064901 (2005).
- Bellini and Kalweit (2019) F. Bellini and A. P. Kalweit, Phys. Rev. C 99, 054905 (2019).
- Huang et al. (2020) S. Huang, Z. Chen, W. Li, and J. Jia, Phys. Rev. C 101, 021901 (2020).
- Sievert and Noronha-Hostler (2019) M. Sievert and J. Noronha-Hostler, Phys. Rev. C 100, 024904 (2019).
- Nagle et al. (2014) J. L. Nagle, A. Adare, S. Beckman, T. Koblesky, J. O. Koop, D. McGlinchey, P. Romatschke, J. Carlson, J. E. Lynn, and M. McCumber, Phys. Rev. Lett. 113, 112301 (2014).
- Lim et al. (2019) S. H. Lim, J. Carlson, C. Loizides, D. Lonardoni, J. E. Lynn, J. L. Nagle, J. D. Orjuela Koop, and J. Ouellette, Phys. Rev. C 99, 044904 (2019).
- Katz et al. (2020) R. Katz, C. A. G. Prado, J. Noronha-Hostler, and A. A. P. Suaide, Phys. Rev. C 102, 041901 (2020).
- Zhang et al. (2020) S. Zhang, Y. G. Ma, G. L. Ma, J. H. Chen, Q. Y. Shou, W. B. He, and C. Zhong, Physics Letters B 804, 135366 (2020).
- Liu et al. (2017) P. Liu, J.-H. Chen, Y.-G. Ma, et al., Nucl. Sci. Tech. 28, 55 (2017).
- Wang and Gyulassy (1991) X.-N. Wang and M. Gyulassy, Phys. Rev. D 44, 3501 (1991).
- Gyulassy and Wang (1994) M. Gyulassy and X.-N. Wang, Computer Physics Communications 83, 307 (1994).
- Zhang (1998) B. Zhang, Computer Physics Communications 109, 193 (1998).
- Li and Ko (1995) B.-A. Li and C. M. Ko, Phys. Rev. C 52, 2037 (1995).
- Ma and Lin (2016) G.-L. Ma and Z.-W. Lin, Phys. Rev. C 93, 054911 (2016).
- Lin and Zheng (2021) Z.-W. Lin and L. Zheng, Nucl. Sci. Tech. 32, 113 (2021).
- Csernai and Kapusta (1986) L. Csernai and J. I. Kapusta, Physics Reports 131, 223 (1986).
- Chen et al. (2003) L.-W. Chen, C. Ko, and B.-A. Li, Nuclear Physics A 729, 809 (2003).
- Zhao et al. (2018) W. Zhao, L. Zhu, H. Zheng, C. M. Ko, and H. Song, Phys. Rev. C 98, 054905 (2018).
- Sun et al. (2021) K.-J. Sun, C. M. Ko, and Z.-W. Lin, Phys. Rev. C 103, 064909 (2021).
- Sun and Chen (2015) K.-J. Sun and L.-W. Chen, Physics Letters B 751, 272 (2015).
- Adamczyk et al. (2017a) L. Adamczyk et al. (STAR Collaboration), Phys. Rev. C 96, 044904 (2017a).
- Zhang (2021) D. Zhang, Nuclear Physics A 1005, 121825 (2021).
- Zhang et al. (2011) S. Zhang, Y. H. Zhu, G. L. Ma, Y. G. Ma, X. Z. Cai, J. H. Chen, and C. Zhong, Nuclear Physics A 860, 76 (2011).
- Braun-Munzinger et al. (2004) P. Braun-Munzinger, K. Redlich, and J. Stachel, “Particle production in heavy ion collisions,” in Quark-Gluon Plasma 3 (World Scientific Publishing Co Pte Ltd, 2004) pp. 491–599.
- Zhang (2019) D. Zhang (for the STAR Collaboration), JPS Conf. Proc. 32, 010069 (2019).
- Yu and Luo (2019) N. Yu and X. Luo, Eur. Phys. J. A 55, 26 (2019).
- Vovchenko et al. (2020) V. Vovchenko, B. Dönigus, B. Kardan, M. Lorenz, and H. Stoecker, Physics Letters B 809, 135746 (2020).
- Sun and Chen (2017) K.-J. Sun and L.-W. Chen, Phys. Rev. C 95, 044905 (2017).
- Shah et al. (2016) N. Shah, Y. G. Ma, J. H. Chen, and S. Zhang, Physics Letters B 754, 6 (2016).
- Andronic et al. (2018) A. Andronic, P. Braun-Munzinger, K. Redlich, and J. Stachel, Nature 561, 321 (2018).
- Sun and Chen (2016) K.-J. Sun and L.-W. Chen, Phys. Rev. C 93, 064909 (2016).
- Sombun et al. (2019) S. Sombun, K. Tomuang, A. Limphirat, P. Hillmann, C. Herold, J. Steinheimer, Y. Yan, and M. Bleicher, Phys. Rev. C 99, 014901 (2019).
- Aggarwal et al. (2010) M. Aggarwal et al. (STAR collaboration), arXiv e-prints , arXiv:1007.2613 (2010).
- Adamczyk et al. (2017b) L. Adamczyk et al. (STAR Collaboration), Phys. Rev. C 96, 044904 (2017b).