This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

1]Department of Physics, PSG College of Arts & Science, Coimbatore-641 014, Tamilnadu, India.
Email:apsvinayagam11@gmail.com 2]Centre for Nonlinear Science (CeNSc), PG and Research Department of Physics,
Government college for Women, Kumbakonam, Tamilnadu, India.
Email:b vittal.cnls@gmail.com

Collisional Dynamics of Solitons and Pattern Formation in an Integrable Cross Coupled Nonlinear Schrödinger equation with constant background

P. S. Vinayagam    D. Aravindha Krishnan    R. V. Kamaleshwaran    R. Radha [ [
Abstract

We investigate the dynamics arising out of the propagation of light pulses with different polarizations through a condensate (referred to as a constant background field) with cross coupling described by a coupled nonlinear Schrödinger equation(NLSE) type equation. We then employ Gauge and Darboux transformation approach to bring out the rich dynamics arising out of the background field and cross coupling. The collisional dynamics of bright solitons is found to be inelastic. The constant background field is found to facilitate the periodic localization of light pulses during propagation. We have also unearthed breathers, bright-bright, bright-dark and dark-bright solitons of the coupled NLSE. While the amplitude of breathers oscillate with time as predicted, their maximum(or minimum) amplitude is found to remain a constant and the addition of cross coupling only contributes to the rapid fluctuations in its amplitude over a period of time. In addition, the reinforcement of cross coupling in the presence of constant wave field facilitates the interference of light pulses leading to interesting pattern formation among bright-bright, bright-dark and dark-bright solitons. The highlight of the results is that one obtains various localized excitations like breathers, bright and dark solitons by simply manipulating the amplitude of the constant wave field.

keywords:
Coupled nonlinear Schrödinger equation, Gauge transformation, Darboux transformation, Lax pair, Breathers, Solitons
pacs:
03.75.Lm, 03.75.-b, 05.45.Yv

1 Introduction

The exploration of nonlinear phenomena in physical systems has been a cornerstone of modern physics, revealing intricate behaviors that defy conventional understanding. To unearth these unconventional phenomena, the nonlinear Schrödinger equation (NLSE) stands out as a fundamental mathematical framework for describing wave propagation in various fields, such as optics [1, 2] and plasma physics [3] to condensed matter systems [4] and beyond. However, when coupled with a background wave field that exhibits instability, the dynamics become significantly more complex, offering intriguing avenues for investigation [5, 6].

Recently, the study of localized structures in various physical settings described by nonlinear partial differentials equations such as discrete Kadomtsev-Petviashvili (KP) equation [7], nonlocal NLSE [8], higher order integrable models and their bi-hamilton formulations [9], fractional differential equations [10], Parity-Time symmetric nonlocal equations [11], Gross-Pitaevskii equation [12, 13], space shifted nonlocal NLSE [14], and more [15, 16, 17, 18, 19, 20] has attracted the attention due to their real world applications in the respective domains.

We explore the intriguing realm of the coupled focusing nonlinear Schrödinger equation (CFNLSE) amidst an unstable background wave field. This scenario represents a fascinating intersection of nonlinear dynamics and instability, with profound implications across multiple disciplines [21]. Understanding the intricate interplay between nonlinear effects and unstable backgrounds is crucial for elucidating phenomena such as wave turbulence [22], soliton dynamics [23], and pattern formation [23], all of which find applications in diverse fields including optical communications [24], Bose-Einstein condensates [25], and plasma physics [26].

When coupled focusing NLSEs evolve in an unstable background wave field like a condensate, the interplay between nonlinearity and instability introduces a myriad of intriguing phenomena. Instabilities can arise from various sources, including the presence of noise, external perturbations, or inherent instability in the system parameters. Understanding the dynamics of coupled NLSEs in such environments is crucial for predicting and controlling the behavior of nonlinear waves in practical applications.

In this paper, we focus on the dynamics of the propagation of cross coupled light pulses through a condensate described by the cross coupled NLS type equation. We transform it to an extended Manakov system through a similarity transformation and generate bright, dark solitons and breathers. We then bring out the impact of constant wave back ground (condensates) and cross coupling on the soliton dynamics.

The plan of the paper is as follows. In section II, we derive the mathematical (integrable) model governing the propagation of cross coupled light pulses through a constant background field. We then employ a similarity transformation to convert the cross coupled NLS type equation into an extended Manakov system in section II. We then harness the Lax pair of the extended Manakov system to generate soliton solutions employing both Gauge (vacuum seed) and Darboux transformation(nonzero seed) in section III . We then analyze the collisional dynamics of solitons under the combined impact of constant wave field and cross coupling. We also dwell upon the impact of cross coupling on breathers, bright-bright, bright-dark and dark-bright soliton solutions in the presence of constant background wave to bring about interesting pattern formation in Section IV. The results are then summarized at the end in section V.

2 Model equation and Similarity transformation

The dimensionless form of the coupled nonlinear Schrödinger equation (CNLSE) with a constant background field and a cross coupling is given by:

i​q1​t​(x,t)+12​q1​x​x​(x,t)+(|q1​(x,t)|2+|q2​(x,t)|2−A2)​q1​(x,t)+Ω​q2​(x,t)\displaystyle iq_{1t}(x,t)+\frac{1}{2}q_{1xx}(x,t)+\left(|q_{1}(x,t)|^{2}+|q_{2}(x,t)|^{2}-A^{2}\right)q_{1}(x,t)+\Omega q_{2}(x,t) =\displaystyle= 0\displaystyle 0
i​q2​t​(x,t)+12​q2​x​x​(x,t)+(|q1​(x,t)|2+|q2​(x,t)|2−A2)​q2​(x,t)+Ω​q1​(x,t)\displaystyle iq_{2t}(x,t)+\frac{1}{2}q_{2xx}(x,t)+\left(|q_{1}(x,t)|^{2}+|q_{2}(x,t)|^{2}-A^{2}\right)q_{2}(x,t)+\Omega q_{1}(x,t) =\displaystyle= 0\displaystyle 0

where x and t denote the spatial and temporal coordinates and q1,2q_{1,2} represent the two complex field variables while A represents the constant amplitude of the background field and Ω\Omega the cross coupling. The above model represents the propagation of two light pulses with different polarizations with cross coupling through a condensate (back ground field) and has been investigated recently [21] for (Ω=0\Omega=0). We plan to establish the integrability of the model with both constant background wave and cross coupling.

We now introduce the following similarity transformation [27] to remove the cross coupling

(q1​(x,t)q2​(x,t))=(a​cos⁡(Ω​t)b​sin⁡(Ω​t)b​sin⁡(Ω​t)a​cos⁡(Ω​t)).(ψ1​(x,t)ψ2​(x,t))\displaystyle\left(\begin{array}[]{c}q_{1}(x,t)\\ q_{2}(x,t)\\ \end{array}\right)=\left(\begin{array}[]{cc}a\cos(\Omega t)&b\sin(\Omega t)\\ b\sin(\Omega t)&a\cos(\Omega t)\\ \end{array}\right).\left(\begin{array}[]{c}\psi_{1}(x,t)\\ \psi_{2}(x,t)\\ \end{array}\right) (8)

where the constants are a=1a=1 &\& b=−ib=-i so that equation (1) gets transformed into an extended Manakov model of the following form

i​ψ1​t​(x,t)+12​ψ1​x​x​(x,t)+(|ψ1​(x,t)|2+|ψ2​(x,t)|2−A2)​ψ1​(x,t)\displaystyle i\psi_{1t}(x,t)+\frac{1}{2}\psi_{1xx}(x,t)+\left(|\psi_{1}(x,t)|^{2}+|\psi_{2}(x,t)|^{2}-A^{2}\right)\psi_{1}(x,t) =\displaystyle= 0\displaystyle 0 (9a)
i​ψ2​t​(x,t)+12​ψ2​x​x​(x,t)+(|ψ1​(x,t)|2+|ψ2​(x,t)|2−A2)​ψ2​(x,t)\displaystyle i\psi_{2t}(x,t)+\frac{1}{2}\psi_{2xx}(x,t)+\left(|\psi_{1}(x,t)|^{2}+|\psi_{2}(x,t)|^{2}-A^{2}\right)\psi_{2}(x,t) =\displaystyle= 0\displaystyle 0 (9b)

In the next section, we exploit the corresponding Lax pair of the above equation (9) and employ Gauge and Darboux Transformation (DT) using trivial and nontrivial seed solutions respectively to obtain explicit soliton solutions.

3 Lax pair, Gauge and Darboux transformations

3.1 Lax pair

Equation (9) admits the following Lax pair [21] which can be written in a compact form in terms of a pair of matrices as

𝚽X\displaystyle{\bf\Phi}_{X} =\displaystyle= 𝐔​𝚽,\displaystyle{\bf U\Phi}, (10a)
𝚽T\displaystyle{\bf\Phi}_{T} =\displaystyle= 𝐕​𝚽,\displaystyle{\bf V\Phi}, (10b)

where 𝐔{\bf U} and 𝐕{\bf V} are the 3×\times3 matrices known as the Lax pair matrices, which assume the following form:

𝐔=(−i​λψ1​(x,t)ψ2​(x,t)−ψ1(x,t)∗i​λ0−ψ2(x,t)∗0i​λ)\displaystyle{\bf U}=\left(\begin{array}[]{ccc}-i\lambda&\psi_{1}(x,t)&\psi_{2}(x,t)\\ -\psi_{1}{}^{*}(x,t)&i\lambda&0\\ -\psi_{2}{}^{*}(x,t)&0&i\lambda\\ \end{array}\right) (14)
𝐕=(V11V12V13V21V22V23V31V32V33)\displaystyle{\bf V}=\left(\begin{array}[]{ccc}V_{11}&V_{12}&V_{13}\\ V_{21}&V_{22}&V_{23}\\ V_{31}&V_{32}&V_{33}\\ \end{array}\right) (18)
V11\displaystyle V_{11} =iλ2−12i(ψ1(x,t)ψ1(x,t)∗+ψ2(x,t)ψ2(x,t)∗−A2)\displaystyle=i\lambda^{2}-\frac{1}{2}i\left(\psi_{1}(x,t)\psi_{1}{}^{*}(x,t)+\psi_{2}(x,t)\psi_{2}{}^{*}(x,t)-A^{2}\right)
V12\displaystyle V_{12} =iλ2−12iψ1(x,t)ψ1(x,t)∗+ψ2(x,t)ψ2(x,t)∗−A2\displaystyle=i\lambda^{2}-\frac{1}{2}i\psi_{1}(x,t)\psi_{1}{}^{*}(x,t)+\psi_{2}(x,t)\psi_{2}{}^{*}(x,t)-A^{2}
V13\displaystyle V_{13} =−λ​ψ2​(x,t)−12​i​ψ2​x​(x,t)\displaystyle=-\lambda\psi_{2}(x,t)-\frac{1}{2}i\psi_{2x}(x,t)
V21\displaystyle V_{21} =λψ1(x,t)∗−12iψ1​x(x,t)∗\displaystyle=\lambda\psi_{1}{}^{*}(x,t)-\frac{1}{2}i\psi_{1x}{}^{*}(x,t)
V22\displaystyle V_{22} =−12i(A2−ψ1(x,t)ψ1(x,t)∗)−iλ2\displaystyle=-\frac{1}{2}i\left(A^{2}-\psi_{1}(x,t)\psi_{1}{}^{*}(x,t)\right)-i\lambda^{2}
V23\displaystyle V_{23} =12iψ2(x,t)ψ1(x,t)∗\displaystyle=\frac{1}{2}i\psi_{2}(x,t)\psi_{1}{}^{*}(x,t)
V31\displaystyle V_{31} =λψ2(x,t)∗−12iψ2​x(x,t)∗\displaystyle=\lambda\psi_{2}{}^{*}(x,t)-\frac{1}{2}i\psi_{2x}{}^{*}(x,t)
V32\displaystyle V_{32} =12iψ1(x,t)ψ2(x,t)∗\displaystyle=\frac{1}{2}i\psi_{1}(x,t)\psi_{2}{}^{*}(x,t)
V33\displaystyle V_{33} =−12i(A2−ψ2(x,t)ψ2(x,t)∗)−iλ2\displaystyle=-\frac{1}{2}i\left(A^{2}-\psi_{2}(x,t)\psi_{2}{}^{*}(x,t)\right)-i\lambda^{2}

where λ\lambda is the complex spectral parameter. The consistency condition 𝚽x​t=𝚽t​x{\bf\Phi}_{xt}={\bf\Phi}_{tx} leads to 𝐔t−𝐕x+[𝐔,𝐕]=𝟎{\bf U}_{t}-{\bf V}_{x}+[{\bf U},{\bf V}]={\bf 0} which generates the extended Manakov model given by eq. (9).

3.2 Gauge transformation and Soliton Solutions

In this subsection, starting from a trivial seed solution, we construct bright soliton solutions and analyze the impact of constant wave field.

So, we start from the trivial seed as ψ1​(x,t)=ψ2​(x,t)=0\psi_{1}(x,t)=\psi_{2}(x,t)=0 and employ Gauge transformation approach [28] to construct bright soliton solutions of the following form

ψ1​(x,t)\displaystyle\psi_{1}(x,t) =\displaystyle= −ϵ1​exp⁡[i​(−2​α​x+A2​t+2​(α2−β2)​t+2​χ1)]​Sech​(2​β​x−4​α​β​t−2​δ1)2​2\displaystyle-\frac{\epsilon_{1}\exp\left[i\left(-2\alpha x+A^{2}t+2(\alpha^{2}-\beta^{2})t+2\chi_{1}\right)\right]\text{Sech}\left(2\beta x-4\alpha\beta t-2\delta_{1}\right)}{2\sqrt{2}}
ψ2​(x,t)\displaystyle\psi_{2}(x,t) =\displaystyle= −ϵ2​exp⁡[i​(−2​α​x+A2​t+2​(α2−β2)​t+2​χ1)]​Sech​(2​β​x−4​α​β​t−2​δ1)2​2\displaystyle-\frac{\epsilon_{2}\exp\left[i\left(-2\alpha x+A^{2}t+2(\alpha^{2}-\beta^{2})t+2\chi_{1}\right)\right]\text{Sech}\left(2\beta x-4\alpha\beta t-2\delta_{1}\right)}{2\sqrt{2}}

where, δ1\delta_{1} and χ1\chi_{1} are arbitrary real parameters, ϵ1\epsilon_{1} and ϵ2\epsilon_{2} are coupling constants which are complex in nature subject to the constraint

β=−ϵ1​ϵ11+ϵ2​ϵ214​2\displaystyle\beta=-\frac{\sqrt{\epsilon_{1}\epsilon_{11}+\epsilon_{2}\epsilon_{21}}}{4\sqrt{2}} (20)

where, ϵ11\epsilon_{11} and ϵ21\epsilon_{21} are conjugates of ϵ1\epsilon_{1}, ϵ2\epsilon_{2} respectively with λ\lambda=α\alpha+iβ\beta, where α\alpha,and β\beta are arbitrary constants. Bright solitons of the extended Manakov system with constant wave field along with cross coupling given by eq. (1) can be straightforwardly written using the transformation given by eq.(8). From the above, we understand that one can not bring out the impact of constant wave field on the density of the solitons driving the light pulses as it is present only in the phase term. The Gauge transformation approach [28] can be extended to generate multisoliton solutions. For example, the two-soliton solution ψ1,2(2)\psi_{1,2}^{(2)} for the two modes can be expressed as

ψ1(2)=2​i​A​1B,\displaystyle\psi_{1}^{(2)}=2i\frac{A1}{B}, (21a)
ψ2(2)=2​i​A​2B,\displaystyle\psi_{2}^{(2)}=2i\frac{A2}{B}, (21b)

where

A​1\displaystyle A1 =(λ2−λ1)​M121​M222​(λ1−μ1)​(λ2−μ2)+M122​M221​(λ2−μ1)​(μ2−λ1)​(λ2−μ2)\displaystyle=\left(\lambda_{2}-\lambda_{1}\right)M_{121}M_{222}\left(\lambda_{1}-\mu_{1}\right)\left(\lambda_{2}-\mu_{2}\right)+M_{122}M_{221}\left(\lambda_{2}-\mu_{1}\right)\left(\mu_{2}-\lambda_{1}\right)\left(\lambda_{2}-\mu_{2}\right)
+(μ2−μ1)​M111​M122​(λ2−μ1)​(λ2−μ2)+(μ2−μ1)​M112​M121​(λ1−μ1)​(μ2−λ1),\displaystyle+\left(\mu_{2}-\mu_{1}\right)M_{111}M_{122}\left(\lambda_{2}-\mu_{1}\right)\left(\lambda_{2}-\mu_{2}\right)+\left(\mu_{2}-\mu_{1}\right)M_{112}M_{121}\left(\lambda_{1}-\mu_{1}\right)\left(\mu_{2}-\lambda_{1}\right),
A​2\displaystyle A2 =(λ2−λ1)​M112​M211​(λ1−μ1)​(λ2−μ2)+M111​M212​(λ2−μ1)​(μ2−λ1)​(λ2−μ2)\displaystyle=\left(\lambda_{2}-\lambda_{1}\right)M_{112}M_{211}\left(\lambda_{1}-\mu_{1}\right)\left(\lambda_{2}-\mu_{2}\right)+M_{111}M_{212}\left(\lambda_{2}-\mu_{1}\right)\left(\mu_{2}-\lambda_{1}\right)\left(\lambda_{2}-\mu_{2}\right)
+(μ2−μ1)​M212​M221​(λ2−μ1)​(λ2−μ2)+(μ2−μ1)​M211​M222​(λ1−μ1)​(μ2−λ1),\displaystyle+\left(\mu_{2}-\mu_{1}\right)M_{212}M_{221}\left(\lambda_{2}-\mu_{1}\right)\left(\lambda_{2}-\mu_{2}\right)+\left(\mu_{2}-\mu_{1}\right)M_{211}M_{222}\left(\lambda_{1}-\mu_{1}\right)\left(\mu_{2}-\lambda_{1}\right),
B\displaystyle B =(M122​M211+M121​M212)​(λ1−μ1)​(λ2−μ2)+(M112​M221+M111​M222)​(λ2−μ1)​(μ2−λ1)\displaystyle=\left(M_{122}M_{211}+M_{121}M_{212}\right)\left(\lambda_{1}-\mu_{1}\right)\left(\lambda_{2}-\mu_{2}\right)+\left(M_{112}M_{221}+M_{111}M_{222}\right)\left(\lambda_{2}-\mu_{1}\right)\left(\mu_{2}-\lambda_{1}\right)
+(λ2−λ1)​(μ2−μ1)​(M111​M112+M221​M222)\displaystyle+\left(\lambda_{2}-\lambda_{1}\right)\left(\mu_{2}-\mu_{1}\right)\left(M_{111}M_{112}+M_{221}M_{222}\right)

with λj=λj¯∗=αj+i​βj\lambda_{j}=\bar{\lambda_{j}}^{*}=\alpha_{j}+i\beta_{j} ,

M11​j\displaystyle M_{11j} =e−θj​2;M12​j=e−i​ξj​ε1(j);M13​j=e−i​ξj​ε2(j);\displaystyle=e^{-\theta_{j}}\sqrt{2};\quad M_{12j}=e^{-i\xi_{j}}\varepsilon_{1}^{(j)};\quad M_{13j}=e^{-i\xi_{j}}\varepsilon_{2}^{(j)};
M21​j\displaystyle M_{21j} =ei​ξj​ε1∗(j);M22​j=eθj/2;M23​j=0;\displaystyle=e^{i\xi_{j}}\varepsilon_{1}^{*(j)};\quad M_{22j}=e^{\theta_{j}}/\sqrt{2};\quad M_{23j}=0;
M31​j\displaystyle M_{31j} =ei​ξj​ε2∗(j);M32​j=0;M33​j=eθj/2,\displaystyle=e^{i\xi_{j}}\varepsilon_{2}^{*(j)};\quad M_{32j}=0;\quad M_{33j}=e^{\theta_{j}}/\sqrt{2},

where

θj\displaystyle\theta_{j} =2​βj​x−4​∫(αj​βj)​𝑑t+2​δj,\displaystyle=2\beta_{j}x-4\int(\alpha_{j}\beta_{j})dt+2\delta_{j},
ξj\displaystyle\xi_{j} =A2​t−2​αj​x−2​∫(αj2−βj2)​𝑑t−2​χj,\displaystyle=A^{2}t-2\alpha_{j}x-2\int(\alpha_{j}^{2}-\beta_{j}^{2})dt-2\chi_{j},
βj\displaystyle\beta_{j} =−ϵ1​j​ϵ1​j∗+ϵ2​j​ϵ2​j∗4​2\displaystyle=-\frac{\sqrt{\epsilon_{1j}\epsilon_{1j}^{\ast}+\epsilon_{2j}\epsilon_{2j}^{\ast}}}{4\sqrt{2}} (22)

where j=1,2j=1,2 and, ∗ describes the conjugate of the respective term.

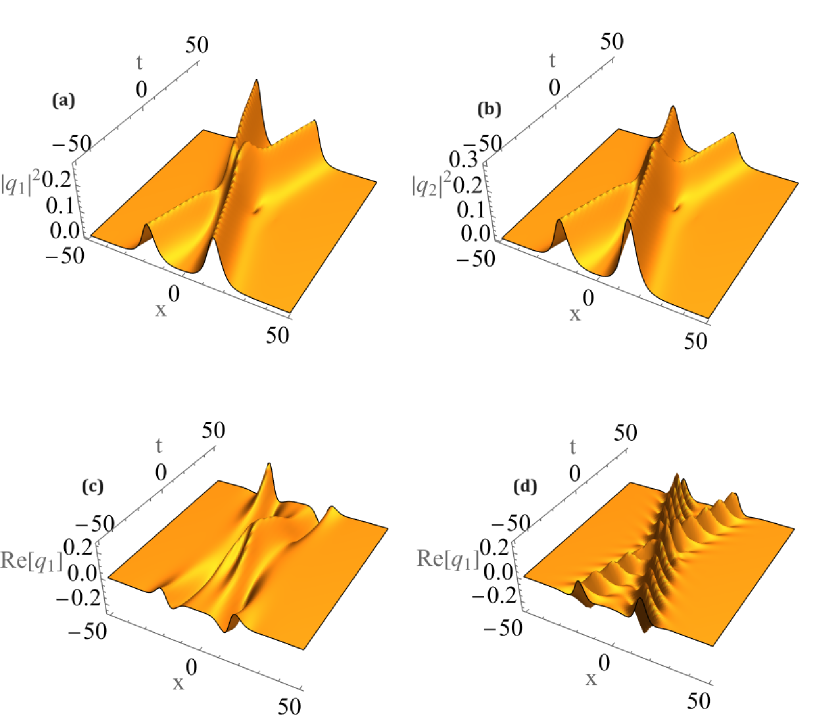
Refer to caption
Figure 1: Inelatic collision of light pulses without cross coupling (Ω=0\Omega=0) shown in panels (a,b) for the parametric choice α1\alpha_{1}=0.15, α2\alpha_{2}=-0.15, δi\delta_{i}=χi\chi_{i}=0.1 ϵ1​j\epsilon_{1j}=0.5 where j=1,2j=1,2 for A=0A=0. Panel (c) represents the real part of q1q_{1} for A=0A=0 while panel (d) describes the real part of q1q_{1} for non zero AA

The two soliton density profile is plotted in panels (a,b) of fig.1. From fig.1 (a,b), we observe that the light pulses of the extended Manakov model exchange energy among themselves undergoing inelastic collision [29, 30] in the absence of constant wave field. From fig.1(d), it is obvious that the constant wave field (or a condensate) interacts with light pulses thereby enhancing its amplitude at periodic intervals of time while the light-matter interaction is missing in fig.1(c) for A=0A=0. The behaviour of the constant wave field is similar to a reservoir feeding mater wave energy into the light pulses.

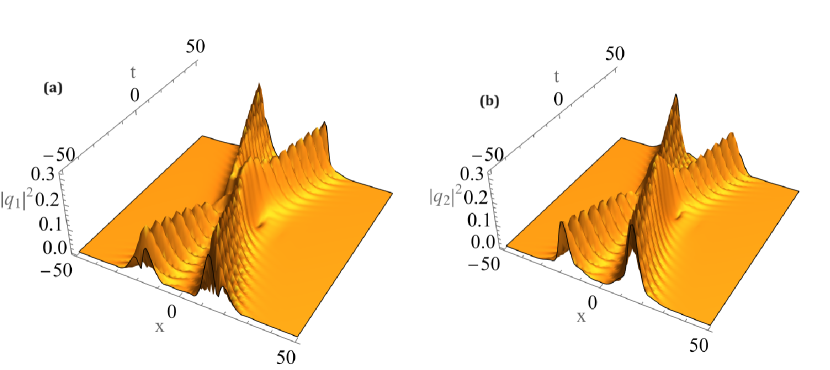
Refer to caption
Figure 2: Inelastic Bright-Bright solitons with oscillating amplitude for cross coupling parameter Ω=0.5\Omega=0.5 with the rest of the parameters being the same as shown in fig.1

It is quite obvious that the addition of cross coupling only adds to the oscillation in the amplitude or the density of the solitons driving the light pulses as shown in fig.2.

3.3 Darboux Transformation

Since the impact of the constant wave field (or a condensate) has been witnessed only in the real or imaginary part of the wave function and not in the density of the soliton solutions generated by means of Gauge transformation approach, it is better exploit an approach to generate the soliton solutions with a nontrivial seed solutions employing ”Darboux transformation” [31]. We choose the following non-trivial seed solution

ψ1(0)\displaystyle\psi_{1}^{(0)} =a​ei​A​t&ψ2(0)=0\displaystyle=ae^{iAt}\;\;\&\;\;\psi_{2}^{(0)}=0 (23)

which leads to the constraint relating the amplitude of the solitons with the constant wave field as

a=A2+1.\displaystyle a=\sqrt{A^{2}+1}. (24)

With the above nontrivial seed, the iteration employing Darboux transformation can be extended to generate soliton solutions of the second order of the following form:

ψ1(2)\displaystyle\psi_{1}^{(2)} =ψ1(0)+2​i​|N1||R2|\displaystyle=\psi_{1}^{(0)}+\frac{2i\left|N_{1}\right|}{\left|R_{2}\right|} (25a)
ψ1(2)\displaystyle\psi_{1}^{(2)} =ψ2(0)+2​i​|N2||R2|\displaystyle=\psi_{2}^{(0)}+\frac{2i\left|N_{2}\right|}{\left|R_{2}\right|} (25b)

where

N1\displaystyle N_{1} =(A2+1​λ1​ei​tA2+1​λ2​ei​tλ1∗φ1∗λ2∗φ2∗00A2+1​ei​tA2+1​ei​tφ1∗φ2∗00λ1ϕ1λ2ϕ200λ1∗φ1∗λ2∗φ2∗ϕ1ϕ200φ1∗φ2∗A2+1​λ12​ei​tA2+1​λ22​ei​tλ12​φ1∗λ22​φ2∗00φ1φ2−A2+1​e−i​t−Ψ2∗−ϕ1∗−ϕ2∗)\displaystyle=\left(\begin{array}[]{cccccc}\sqrt{A^{2}+1}\text{$\lambda_{1}$}e^{it}&\sqrt{A^{2}+1}\text{$\lambda_{2}$}e^{it}&\text{$\lambda_{1}^{\ast}$}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}^{\ast}$}\text{$\varphi_{2}^{\ast}$}&0&0\\ \sqrt{A^{2}+1}e^{it}&\sqrt{A^{2}+1}e^{it}&\text{$\varphi_{1}^{\ast}$}&\text{$\varphi_{2}^{\ast}$}&0&0\\ \text{$\lambda_{1}$}\text{$\phi_{1}$}&\text{$\lambda_{2}$}\text{$\phi_{2}$}&0&0&\text{$\lambda_{1}^{\ast}$}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}^{\ast}$}\text{$\varphi_{2}^{\ast}$}\\ \text{$\phi_{1}$}&\text{$\phi_{2}$}&0&0&\text{$\varphi_{1}^{\ast}$}&\text{$\varphi_{2}^{\ast}$}\\ \sqrt{A^{2}+1}\text{$\lambda_{1}$}^{2}e^{it}&\sqrt{A^{2}+1}\text{$\lambda_{2}$}^{2}e^{it}&\text{$\lambda_{1}$}^{2}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}$}^{2}\text{$\varphi_{2}^{\ast}$}&0&0\\ \text{$\varphi_{1}$}&\text{$\varphi_{2}$}&-\sqrt{A^{2}+1}e^{-it}&-\text{$\Psi_{2}^{\ast}$}&-\text{$\phi_{1}^{\ast}$}&-\text{$\phi_{2}^{\ast}$}\\ \end{array}\right) (32)
N2\displaystyle N_{2} =(A2+1​λ1​ei​tA2+1​λ2​ei​tλ1∗φ1∗λ2∗φ2∗00A2+1​ei​tA2+1​ei​tφ1∗φ2∗00λ1ϕ1λ2ϕ200λ1∗φ1∗λ2∗φ2∗ϕ1ϕ200φ1∗φ2∗λ12​ϕ1λ22​ϕ200λ12​φ1∗λ22​φ2∗φ1φ2−A2+1​e−i​t−Ψ2∗−ϕ1∗−ϕ2∗)\displaystyle=\left(\begin{array}[]{cccccc}\sqrt{A^{2}+1}\text{$\lambda_{1}$}e^{it}&\sqrt{A^{2}+1}\text{$\lambda_{2}$}e^{it}&\text{$\lambda_{1}^{\ast}$}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}^{\ast}$}\text{$\varphi_{2}^{\ast}$}&0&0\\ \sqrt{A^{2}+1}e^{it}&\sqrt{A^{2}+1}e^{it}&\text{$\varphi_{1}^{\ast}$}&\text{$\varphi_{2}^{\ast}$}&0&0\\ \text{$\lambda_{1}$}\text{$\phi_{1}$}&\text{$\lambda_{2}$}\text{$\phi_{2}$}&0&0&\text{$\lambda_{1}^{\ast}$}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}^{\ast}$}\text{$\varphi_{2}^{\ast}$}\\ \text{$\phi_{1}$}&\text{$\phi_{2}$}&0&0&\text{$\varphi_{1}^{\ast}$}&\text{$\varphi_{2}^{\ast}$}\\ \text{$\lambda_{1}$}^{2}\text{$\phi_{1}$}&\text{$\lambda_{2}$}^{2}\text{$\phi_{2}$}&0&0&\text{$\lambda_{1}$}^{2}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}$}^{2}\text{$\varphi_{2}^{\ast}$}\\ \text{$\varphi_{1}$}&\text{$\varphi_{2}$}&-\sqrt{A^{2}+1}e^{-it}&-\text{$\Psi_{2}^{\ast}$}&-\text{$\phi_{1}^{\ast}$}&-\text{$\phi_{2}^{\ast}$}\\ \end{array}\right) (39)
R2\displaystyle R_{2} =(A2+1​λ1​ei​tA2+1​λ2​ei​tλ1∗φ1∗λ2∗φ2∗00A2+1​ei​tA2+1​ei​tφ1∗φ2∗00λ1ϕ1λ2ϕ200λ1∗φ1∗λ2∗φ2∗ϕ1ϕ200φ1∗φ2∗λ1φ1λ2φ2−A2+1​λ1∗​e−i​t−λ2∗Ψ2∗−λ1∗ϕ1∗−λ2∗ϕ2∗φ1φ2−A2+1​e−i​t−Ψ2∗−ϕ1∗−ϕ2∗)\displaystyle=\left(\begin{array}[]{cccccc}\sqrt{A^{2}+1}\text{$\lambda_{1}$}e^{it}&\sqrt{A^{2}+1}\text{$\lambda_{2}$}e^{it}&\text{$\lambda_{1}^{\ast}$}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}^{\ast}$}\text{$\varphi_{2}^{\ast}$}&0&0\\ \sqrt{A^{2}+1}e^{it}&\sqrt{A^{2}+1}e^{it}&\text{$\varphi_{1}^{\ast}$}&\text{$\varphi_{2}^{\ast}$}&0&0\\ \text{$\lambda_{1}$}\text{$\phi_{1}$}&\text{$\lambda_{2}$}\text{$\phi_{2}$}&0&0&\text{$\lambda_{1}^{\ast}$}\text{$\varphi_{1}^{\ast}$}&\text{$\lambda_{2}^{\ast}$}\text{$\varphi_{2}^{\ast}$}\\ \text{$\phi_{1}$}&\text{$\phi_{2}$}&0&0&\text{$\varphi_{1}^{\ast}$}&\text{$\varphi_{2}^{\ast}$}\\ \text{$\lambda_{1}$}\text{$\varphi_{1}$}&\text{$\lambda_{2}$}\text{$\varphi_{2}$}&-\sqrt{A^{2}+1}\text{$\lambda_{1}^{\ast}$}e^{-it}&-\text{$\lambda_{2}^{\ast}$}\text{$\Psi_{2}^{\ast}$}&-\text{$\lambda_{1}^{\ast}$}\text{$\phi_{1}^{\ast}$}&-\text{$\lambda_{2}^{\ast}$}\text{$\phi_{2}^{\ast}$}\\ \text{$\varphi_{1}$}&\text{$\varphi_{2}$}&-\sqrt{A^{2}+1}e^{-it}&-\text{$\Psi_{2}^{\ast}$}&-\text{$\phi_{1}^{\ast}$}&-\text{$\phi_{2}^{\ast}$}\\ \end{array}\right) (46)
Ψj\displaystyle\Psi_{j} =a​ϵj​e12​i​t​(A2+2​λj2)−i​λj​x\displaystyle=a\;\epsilon_{j}e^{\frac{1}{2}it\left(A^{2}+2\text{$\lambda_{j}$}^{2}\right)-i\text{$\lambda_{j}$}x}
ϕj\displaystyle\phi_{j} =b​ϵj​ei​λj​x−12​i​t​(A2+2​λj2)\displaystyle=b\;\epsilon_{j}e^{i\text{$\lambda_{j}$}x-\frac{1}{2}it\left(A^{2}+2\text{$\lambda_{j}$}^{2}\right)}
φj\displaystyle\varphi_{j} =d​ϵj​ei​λj​x−12​i​t​(A2+2​λj2)\displaystyle=d\;\epsilon_{j}e^{i\text{$\lambda_{j}$}x-\frac{1}{2}it\left(A^{2}+2\text{$\lambda_{j}$}^{2}\right)}

j=1,2j=1,2 and, ∗ describes the conjugate of respective term and λj=λj​R+i​λj​I\lambda_{j}=\lambda_{jR}+i\lambda_{jI}.

3.4 Host of Breather, Bright and Dark solutions

Rewriting the above more general DT soliton solution given by Eq.(25) in a compact form, we arrive at the following expression:

ψj(2)\displaystyle\psi_{j}^{(2)} =αk​[c​o​s​h​(λ1)​c​o​s​h​(B1−2​i​λ2)+c​o​s​h​(λ2)​c​o​s​h​(B2−2​i​λ1)c​o​s​h​(λ1)​c​o​s​h​(B1)+c​o​s​h​(λ2)​c​o​s​h​(B2)]\displaystyle=\alpha_{k}\Big{[}\frac{cosh(\lambda_{1})cosh(B_{1}-2i\lambda_{2})+cosh(\lambda_{2})cosh(B_{2}-2i\lambda_{1})}{cosh(\lambda_{1})cosh(B_{1})+cosh(\lambda_{2})cosh(B_{2})}\Big{]} (47)

where,

B1\displaystyle B_{1} =X1+X2−λ1+a1,\displaystyle=X_{1}+X_{2}-\lambda_{1}+a_{1},
B2\displaystyle B_{2} =−X1+X2+i​λ2−i​A\displaystyle=-X_{1}+X_{2}+i\lambda_{2}-iA
X1\displaystyle X_{1} =i​J1​S​i​n​h​(λ1+i​λ2)​(x+J1​C​o​s​h​(λ1+i​λ2)​t)​ϵ1​j\displaystyle=i\sqrt{J_{1}}Sinh(\lambda_{1}+i\lambda_{2})\Big{(}x+\sqrt{J_{1}}Cosh(\lambda_{1}+i\lambda_{2})t\Big{)}\epsilon_{1j}
X2\displaystyle X_{2} =−i​J1​S​i​n​h​(λ1−i​λ2)​(−x+J1​C​o​s​h​(λ1−i​λ2)​t)​ϵ1​j\displaystyle=-i\sqrt{J_{1}}Sinh(\lambda_{1}-i\lambda_{2})\Big{(}-x+\sqrt{J_{1}}Cosh(\lambda_{1}-i\lambda_{2})t\Big{)}\epsilon_{1j}
J1\displaystyle J_{1} =−(a​α12+2​b​α1​α2+d​α22)\displaystyle=-(a\alpha_{1}^{2}+2b\alpha_{1}\alpha_{2}+d\alpha_{2}^{2})

where, αj\alpha_{j}, βj\beta_{j}, a, b, and d are arbitrary real parameters.

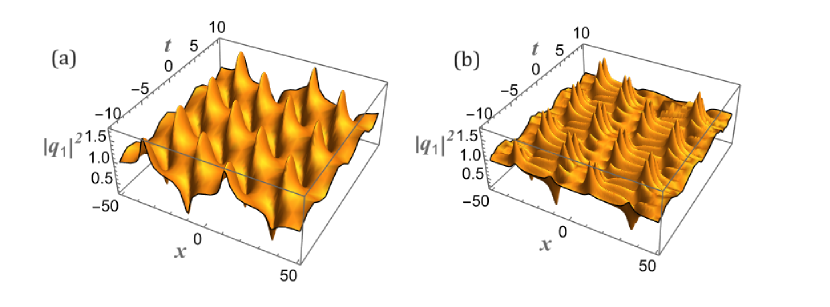
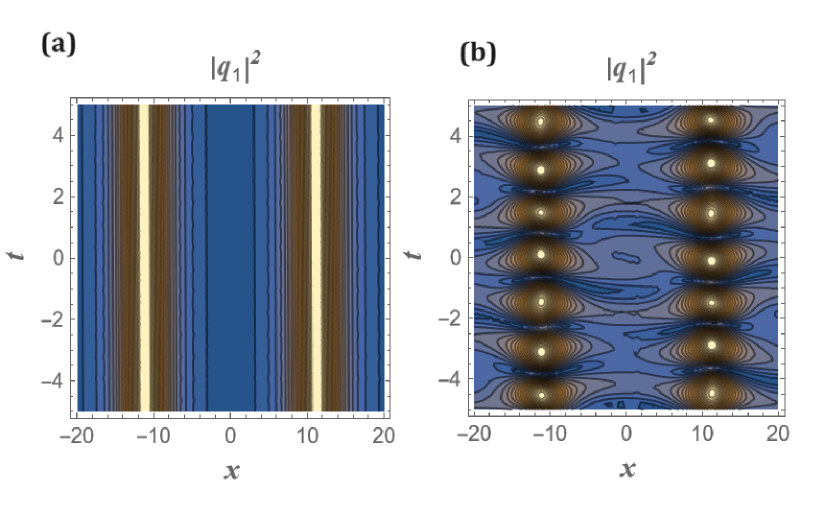
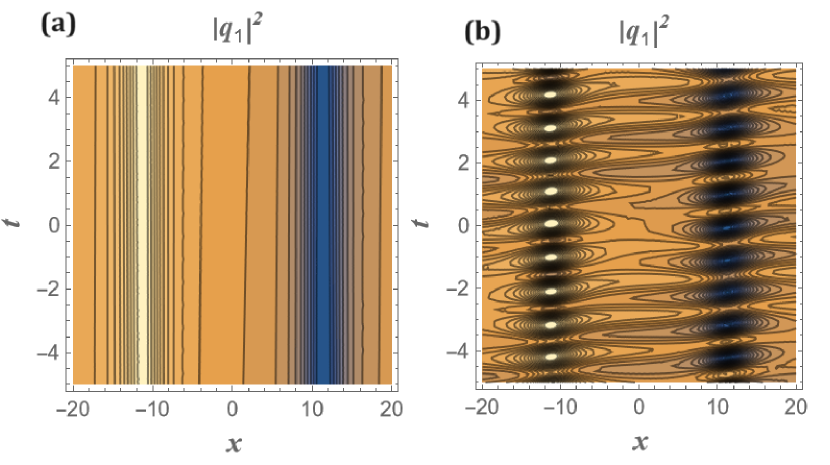
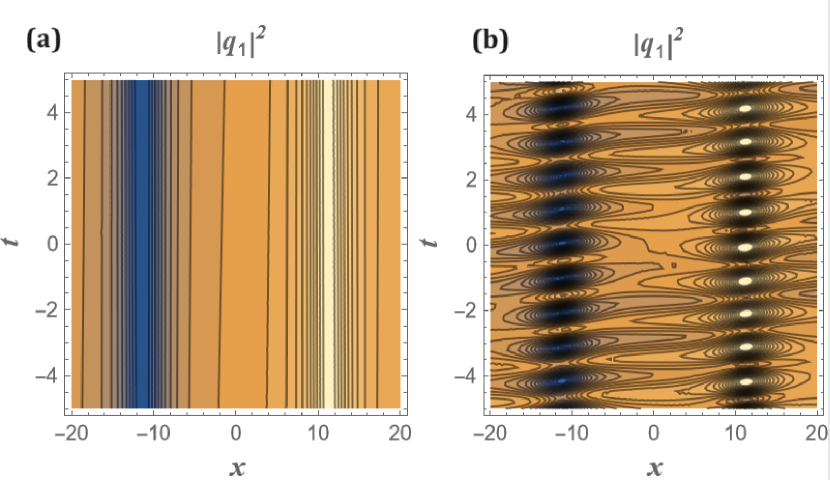
A host of soliton pairs is associated with Eq.(47). Upon examination, we observe that the soliton solutions comprise (i) a pair of solitons such as BB, BD, and DB, as well as (ii) an oscillating soliton wave. These solutions are all present on a constant background. We have presented an oscillatory solution for J1<0J_{1}<0, which is the breather soliton [32, 33, 13], as illustrated in Fig.3, in addition to the pair of solitons (BB, BD, and DB) displayed in Figs.4, 5, and 6. A thorough explanation of how to generate these solutions is provided in the following section.

Refer to caption
Refer to caption
Figure 3: Density profile of Breather solitons without Ω=0\Omega=0 (a) and with cross coupling (b) Ω=0.5\Omega=0.5 for the choice of parameters λ1\lambda_{1}=0.008+0.07 ii, λ2\lambda_{2}=0.07+0.008 ii, ϵj=1\epsilon_{j}=1, where j=1,2j=1,2 and A=0.05A=0.05. Panels (c) and (d) represent the corresponding time evolution of breathers shown in panels (a) and (b)
Refer to caption
Figure 4: Collisional dynamics of bright-bright solitons without cross (Ω=0\Omega=0) (a) and with cross (Ω=0.5\Omega=0.5) coupling (b) for A=0.5A=0.5 with the other parameters being the same as in fig.3
Refer to caption
Figure 5: Collisional dynamics of bright-dark solitons without cross (Ω=0\Omega=0) (a) and with cross (Ω=0.5\Omega=0.5) coupling (b) for the choice of parameters A=0.9A=0.9 with the other parameters being the same as in fig.4
Refer to caption
Figure 6: Collisional dynamics of dark-bright solitons without cross (Ω=0\Omega=0) (a) and with cross (Ω=0.5\Omega=0.5) coupling (b) for the choice of parameters A=−0.9A=-0.9 with the other parameters being the same as in fig.5

3.5 Impact of Constant Wave field and Cross Coupling on the Soliton Dynamics

As discussed earlier, the impact of constant wave field on the soliton solutions generated by Gauge transformation method is reflected only in the real or imaginary parts of the solution and not on the density of the solutions. To bring out the impact of constant wave field explicitly, Darboux tranformation [31] has been employed to generate breathers, bright-bright, bright-dark and dark-bright solutions.

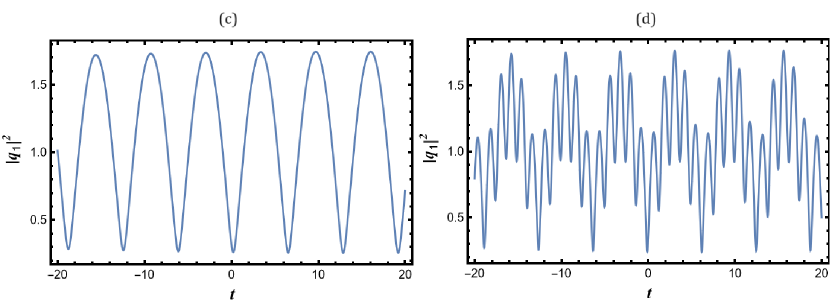
The density profile of breather solutions without and with cross coupling is shown in panels (a) and (b) of fig.3 while panels (c) and (d) show the corresponding time evolution of breathers. From fig.3, we understand that the amplitude (density) of the breather solitons fluctuates with time with the minima and maxima remaining constant over a period of time. The addition of cross coupling only contributes to rapid oscillations in the amplitude of the breather solutions in a given cycle with the maxima and minima again remaining constant as shown in panel (d) of fig.3. The breathers are found to be stable and are completely different from the one reported in ref[21]. In the case of bright-bright solitons, the presence of constant wave field (or a condensate) ensures that the amplitude of the solitons stays constant (shown in panel (a) of fig.4) while the addition of cross coupling generates an interference pattern with bright fringes appearing at periodic intervals shown in panel (b) of fig.4. This behaviour is repeated in the case of bright-dark and dark- bright soliton solutions shown in figs.5 and 6 where again the constant wave field ensures the amplitude of bright (dark) solitons remains constant while the reinforcement of cross coupling in addition to the constant wave field contributes to the fluctuations in the amplitudes where the density of bright (or dark) solitons becomes maximum at periodic intervals of time thereby generating interesting interference patterns in the process. The highlight of the results is that by simply manipulating the amplitude of the constant wave field, one obtains various localized excitations like breathers, bright and dark solitons and the two bound state counterparts.

4 Conclusion

In this paper, we have investigated the propagation of cross coupled light pulses through a constant wave field (or a condensate) described by a coupled NLS type equation and brought out the collisional dynamics of solitons. We have employed both Gauge and Darboux transformation approach to generate bright/dark solitons and breathers to bring out the impact of constant wave field and cross coupling. While cross coupling contributes to the fluctuations in the amplitude of the solutions, the constant wave field ensures that the density or the amplitude of the solitons remains constant. The fact that the amplitude of the solitons driving the light pulses can be maintained constant by propagating through a condensate means that the results can have interesting ramifications in quantum information processing.

5 Declaration of Competing Interest

The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

6 Acknowledgments

PSV wishes to express his deepest gratitude to the Principal and the Management of PSG College of Arts and Science for their moral support, encouragement throughout the tenure of this project. RR wishes thank DST-CRG (File number:CRG/2023/008153 dt. 30th January,2024) and DST-CURIE (DST/CURIE -PG/
2022/54 dt 21/11/2022) for financial support.

References

  • [1] Y.S.Kivshar and G.P.Agrawal, Optical Solitons(Academic, San Diego, 2003).
  • [2] A.Hasegawa and Y.Kodama. Solitons in Optical Communications (Oxford University Press, New York, 1995).
  • [3] E.A. Kuznetsov, A.M.Rubenchik and V.E.Zakharov. Phys. Reports. 142, 3 (1986).
  • [4] P.G. Kevrekidis, D.J. Frantzeskakis, and R.Carretero-González. Emergent Nonlinear Phenomena in Bose-Einstein Condensates (Springer, Berlin, 2008).
  • [5] R. Radha R and P.S. Vinayagam. Phys. Lett. A 376 977 (2012).
  • [6] R. Radha and P.S.Vinayagam. Rom. Rep. Phys. 67(1) 89, (2015).
  • [7] Kelei Tian et al., Rom. Rep. Phys. 76, 103 (2024).
  • [8] Yan Wang and Yang-Yang Xi, Rom. Rep. Phys. 76, 101 (2024).
  • [9] Jin-Yun Yang and Wen-Xiu Ma, Rom. J. Phys. 69, 101 (2024).
  • [10] Guo-Qing Liu and Guo-Cheng Wu, Rom. J. Phys. 69, 107 (2024).
  • [11] N. Liang, D. Mihalache, M. Ma, J. Rao, and Y. Liu, Rom. Rep. Phys. 76, 106 (2024).
  • [12] D. Mihalache, Rom. Rep. Phys. 76, 402 (2024).
  • [13] H.C. Sameut, P. Sakthivinayagam, U. Khawaja, M. Benarous, and H. Belkroukra. Phys.Wave. Phen. 28, 305 (2021).
  • [14] S. Chen, D. Mihalache, K. Jin, J. Li, and J. Rao, Rom. Rep. Phys. 75, 108 (2023).
  • [15] Wen-Xiu Ma, Rom. J. Phys. 68, 116 (2023).
  • [16] Wen-Xiu Ma, Rom. Rep. Phys. 75, 115 (2023).
  • [17] W. Alhejaili, A.-M. Wazwaz, and S. A. El-Tantawy, Rom. J. Phys. 68, 113 (2023).
  • [18] S.N. Nikolic, N.B. Aleksic, W. Krolikowski, M.R. Belic, and N. Akhmediev, Rom. J. Phys. 68, 115 (2023).
  • [19] I. Bakirtas, N. Antar, T.P. Horikis, and D.J. Frantzeskakis, Rom. Rep. Phys. 75, 118 (2023).
  • [20] A. Ankiewicz, Rom. Rep. Phys. 75, 109 (2023).
  • [21] Andrey Gelash, and Anton Raskovalov. Stud. App. Math. 150 841, (2022).
  • [22] G. Josselin, L.Mietek, and P.Antonio. J. Opt. Soc. Am. B. 29(8) 2229, (2012).
  • [23] Boris Malamed. Multidimensional solitons (AIP Publishers, 2022)
  • [24] A.Hasegawa and F.Tappert. Appl. Phys. Lett. 23 142, (1973); 23 171, (1973).
  • [25] A. Osborne. Nonlinear ocean waves (Academic Press, 2010).
  • [26] A. I. Maimistov and A. M. Basharov. Nonlinear optical waves, (Springer Science & Business Media, 2013).
  • [27] B. Deconinck, P. G.Kevrekidis, H. E. Nistazakis, and D.J. Frantzeskakis. Phys. Rev. A 70 063605, (2004).
  • [28] L. L. Chau, J . C. Shaw, H.C. Yen. J. Math. Phys. 32 1737, (1991).
  • [29] R. Radha, P.S. Vinayagam, H. J. Shin and K. Porsezian. Chi. Phys. B. 23(3) 034214, (2014).
  • [30] R. Radhakrishnan, M. Lakshmanan and J. Hietarinta. Phys.Rev.E. 56 2213, (1997).
  • [31] V. B. Matveev, M. A. Salle, Darboux Transformations and Solitons (Springer-Verlag; Berlin: 1991.)
  • [32] B. Kibler, J. Fatome, C. Finot, G. Millot, F. Dias, G. Genty, et al. Nature 6 790, (2010).
  • [33] B. Kibler, J. Fatome, C.Finot, G. Millot, G. Genty, B. Wetzel, et al. Sci. Rep. 2 463, (2012).