Colossal room-temperature electrocaloric strength aided by hydrostatic pressure in lead-free multiferroic solid solutions
Abstract
Solid-state cooling applications based on the electrocaloric (EC) effect are particularly promising from a technological point of view due to their downsize scalability and natural implementation in circuitry. However, EC effects typically occur far from room temperature, involve materials that contain toxic substances and require relatively large electric fields (– kV cm-1) that cause fateful leakage current and dielectric loss problems. Here, we propose a possible solution to these practical issues that consists in concertedly applying hydrostatic pressure and electric fields on lead-free multiferroic materials. We theoretically demonstrate this strategy by performing first-principles simulations on supertetragonal BiFe1-xCoxO3 solid solutions (BFCO). It is shown that hydrostatic pressure, besides adjusting the occurrence of EC effects to near room temperature, can reduce enormously the intensity of the driving electric fields. For pressurized BFCO, we estimate a colossal room-temperature EC strength, defined like the ratio of the adiabatic EC temperature change by the applied electric field, of K cm kV-1, a value that is several orders of magnitude larger than those routinely measured in uncompressed ferroelectrics.
One of the limiting factors of modern microelectronic devices is their tremendous heat dissipation density, which needs to be mitigated through cooling in order to ensure proper performance. Current refrigeration technologies, however, rely on compression cycles of environmentally harmful gases and cannot be scaled down to microchip dimensions. Electrocaloric (EC) cooling is a highly promising solid-state refrigeration technology for thermal management of chips and microcircuitry owing to its high efficiency, environmental friendliness, and easy miniaturization liu16 . EC refrigeration exploits the reversible thermal change of ferroelectric materials resulting from phase transitions induced by external electric field variations. Large EC isothermal entropy changes, , of J K-1kg-1 and adiabatic temperature changes, , of K have been measured in ferroelectric materials like BaTiO3 bto1 ; bto2 , Pb(Zr,Ti)O3 ec1 and HfO2 ec0 , to cite few examples.
Nonetheless, unfortunately, the largest EC effects observed to date normally occur at temperatures far from room temperature problem1 , involve materials that contain toxic substances like lead and require large electric fields that are energetically costly and produce adverse leakage currents and dielectric losses problem2 ; problem3 . Recently, several materials design strategies have been proposed to overcome these common EC problems. For instance, by exploiting electrostatic coupling and interface effects in lead-free ferroelectric relaxor heterostructures, an unprecedentedly large EC adiabatic temperature shift of K has been realized near room temperature for moderate electric bias ( kV cm-1) ec6 . Nevertheless, the magnitude of such EC effects can be strongly influenced by the specific details of the heterostructure synthesis process and thus in practice may strongly fluctuate from one sample to another. Another recent EC advancement has been reported for the layered hybrid perovskite ferroelectric [(CH3)2CHCH2NH3]2PbCl4 ec7 , in which a sharp first-order ferroelectric phase transition associated to a high-entropy change occurs instead of the continuous phase transformation associated to a low-entropy change that is characteristic of inorganic ferroelectric perovskites cohen92 . In this case, a giant of K has been measured at room temperature for a small electric field of kV cm-1. However, the implicated material still contains lead and the degree of reversibility associated to such giant EC effects appears to be quite limited.
In this work, we propose a completely different approach for the enhancement of EC effects that consists in the application of multiple external fields on lead-free multiferroic materials able to undergo sharp first-order phase transitions. In particular, we demonstrate by means of computational first-principles methods that the sequential operation of hydrostatic pressure and electric fields in BiFe1-xCoxO3 solid solutions (BFCO) can trigger large and inverse EC effects of J K-1kg-1 and K at room temperature. Moreover, aided by pressure BFCO displays a colossal EC strength of K cm kV-1, defined like /, which surpasses by several orders of magnitude the typical values reported for uncompressed ferroelectrics.
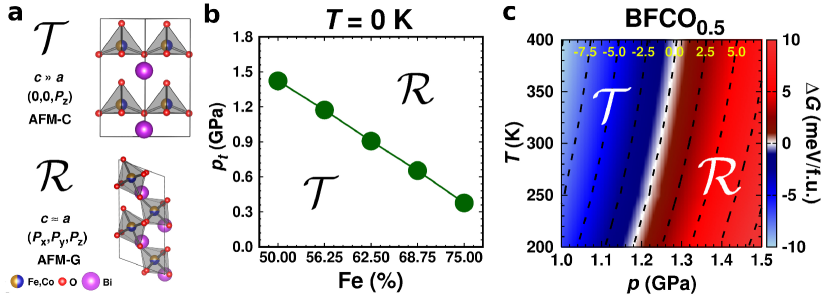
Results
Phase competition in BFCO under pressure. At room temperature and zero pressure, BiFe1-xCoxO3 solid solutions (BFCO) can be stabilized in two different polymorphs, depending on the relative content of Fe/Co atoms, exhibiting rhombohedral () and tetragonal () symmetries bfco1 ; bfco2 ; menendez20 . For relative cobalt contents of , the BFCO ground state is the phase, which is analogous to the ground state of bulk BiFeO3 bfco1 ; bfco2 ; menendez20 ; cazorla13 . This rhombohedral phase presents an electric polarization of – C cm-2 that is oriented along the pseudocubic direction (Fig. 1a) and G-type antiferromagnetic spin ordering (AFM-G, the net magnetic moment of each transition metal ion is antiparallel to those of its six first nearest neighbours). For larger relative cobalt contents, , the BFCO ground state corresponds to the phase, which is analogous to the ground state of bulk BiCoO3 bfco1 ; bfco2 ; menendez20 ; cazorla17 ; cazorla18 . This tetragonal phase presents a giant electric polarization of – C/cm2 oriented along the pseudocubic direction (Fig. 1a), hence sometimes it is referred to as “supertetragonal”, and C-type antiferromagnetic spin ordering (AFM-C, the net magnetic moment of each transition metal ion is parallel to those of its two first nearest neighbours located along the polar axis and antiparallel to those of its other four first nearest neighbours).
Under increasing temperature and for relative cobalt contents of , the supertetragonal phase can be stabilized over the phase owing to its larger vibrational entropy bfco1 ; bfco2 ; menendez20 . Such a -induced phase transition clearly is of first-order type (or discontinuous) since the volume change associated to it is huge (%). To the best of our knowledge, there are not experimental studies on BFCO under pressure. Here, we amend for such a lack of information by carrying out accurate first-principles calculations based on density functional theory (DFT, Methods) menendez20 ; cazorla17d . Figure 1b shows the estimated hydrostatic pressure that is necessary to drive the phase transition at low temperatures (i.e., disregarding entropy and also likely quantum nuclear effects) and for compositions in the interval . This transition pressure is found to steadily, and significantly, decrease under increasing Fe content. For instance, amounts to GPa at and to GPa at . As expected, the closer the cobalt content is to the – morphotropic phase boundary (), the easier results to switch from the supertetragonal to the rhombohedral phase with pressure.
Simulating temperature effects in materials with first-principles methods is computationally very intensive and laborious. However, temperature effects are critical for the assessment of possible caloric phenomena hence cannot be neglected in the present study. We employed the quasi-harmonic approximation (QHA) menendez20 ; cazorla17d to calculate ab initio Gibbs free energies for BFCO in the and phases over broad pressure, temperature and electric field conditions, thus allowing for the estimation of barocaloric and electrocaloric effects (Methods).
Figure 1c shows the – phase diagram calculated for BFCO at a composition of , hereafter referred
to as BFCO0.5. Therein, it is appreciated that consistenly increases under raising temperature, reaching a value
of GPa at room temperature. In spite of such a relatively large pressure, in what follows we present multicaloric results
obtained for bulk BFCO0.5 at and near room temperature since from a computational point of view this solid solution is highly
affordable (i.e., the size of the corresponding simulation cells are among the smallest thus making the QHA free energy calculations
feasible). In practice, much smaller pressures of the order of GPa can be attained by reducing the relative content of Co
ions (Fig. 1b) without significantly affecting the main conclusions presented in the next sections.
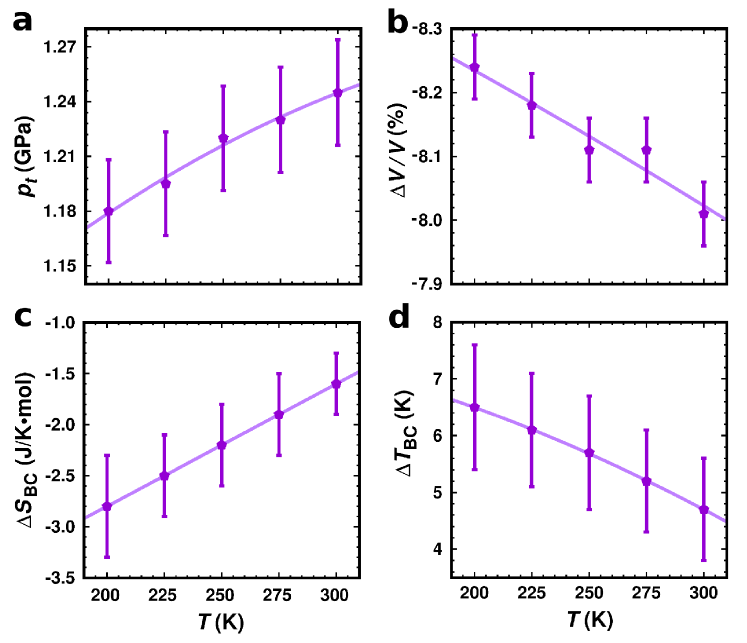
Barocaloric performance of BFCO0.5. We start by analyzing the barocaloric effects induced by hydrostatic pressure in bulk BFCO0.5 in the absence of electric fields. Figures 2a-b show the compression required to induce the phase transition as a function of temperature, , and the accompanying relative volume change. The estimated phase transition volume change is negative and very large as it amounts to % in absolute value. Such a huge relative volume change augurs a large phase transition entropy change, as it can be inferred from the Clausius-Clapeyron relation . However, after doing the calculations and assuming that (Methods), it was found that the ensuing barocaloric isothermal entropy shifts were actually quite modest (Fig. 2c). For instance, at room temperature we obtained J K-1 mol-1 ( J K-1 kg-1), which is about one order of magnitude smaller than the giant barocaloric entropy changes found in superionic and plastic crystals ( J K-1 kg-1) aznar17 ; cazorla16 ; cazorla17b ; cazorla18b ; lloveras19 ; li19 ; cazorla19b ; sau21 ; cazorla19 . Under decreasing temperature, slightly increases (e.g., J K-1 mol-1 at K) however the estimated values still are quite reduced. The reason for these outcomes is that barely changes with temperature in the explored thermodynamic range (i.e., the temperature derivative of the phase transition pressure amounts only to GPa K-1, Fig. 2a).
The revealed minute -induced variation, on the other hand, implies sizeable changes in the phase transition temperature, , induced by small pressure shifts (since ), thus suggesting possibly large barocaloric thermal shifts in bulk BFCO0.5. Figure 2d shows the barocaloric adiabatic temperature changes, , estimated as a function of temperature (Methods). At room temperature ( K), was found to amount to K ( K) which, although it cannot rival with the barocaloric adiabatic temperature changes reported for superionic and plastic crystals ( K) aznar17 ; cazorla16 ; cazorla17b ; cazorla18b ; lloveras19 ; li19 ; cazorla19b ; sau21 ; cazorla19 , it shows promise in the context of electrocaloric effects (– K).
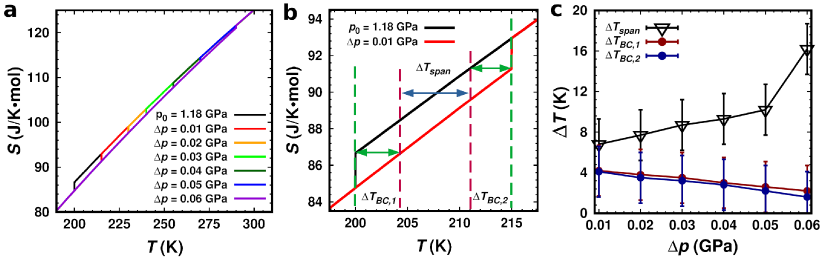
The barocaloric results presented above were obtained with the indirect Clausius-Clayperon (CC) method, which is not exact aznar17 . Aimed to assess the extent of the employed approximations, we mimicked with theory quasi-direct barocaloric experiments aznar17 ; lloveras19 in which entropy curves are estimated as a function of pressure and temperature and from which and can be straightforwardly determined (Figs. 3a-b) cazorla19 . Moreover, with this quasi-direct estimation approach is also possible to determine for a given pressure shift, , the temperature span, , over which barocaloric effects can be operated (Fig. 3b). In view of the huge of K GPa-1 estimated for BFCO0.5, giant values are anticipated li20 .
Figure 3c shows the results of our quasi-direct barocaloric descriptor estimations. At room temperature and K,
we obtained adiabatic temperature changes of and K, respectively. Within the numerical uncertainties,
these results are compatible with our previous estimations obtained with the CC method; however, it goes without saying that the
reported error bars are unacceptably too large. The reasons for the relatively huge numerical uncertainties on
are the small and great -induced shifts involved in its quasi-direct estimation (Fig. 3a). Thus,
unfortunately, in the present case it is not possible to discern the actual precision of the barocaloric adiabatic temperature
changes obtained with the approximate CC method. Nevertheless, the estimation of is still possible given its noticeably
large size (Figs. 3a-b). By considering an outset compression of GPa, we obtained K for a
small pressure shift of GPa (calculated by adding up all the increments shown in Fig. 3c).
This result is very encouraging since it indicates that, in spite of the relative smallness of and ,
barocaloric effects in BFCO0.5 could be operated over unusually ample temperature ranges.
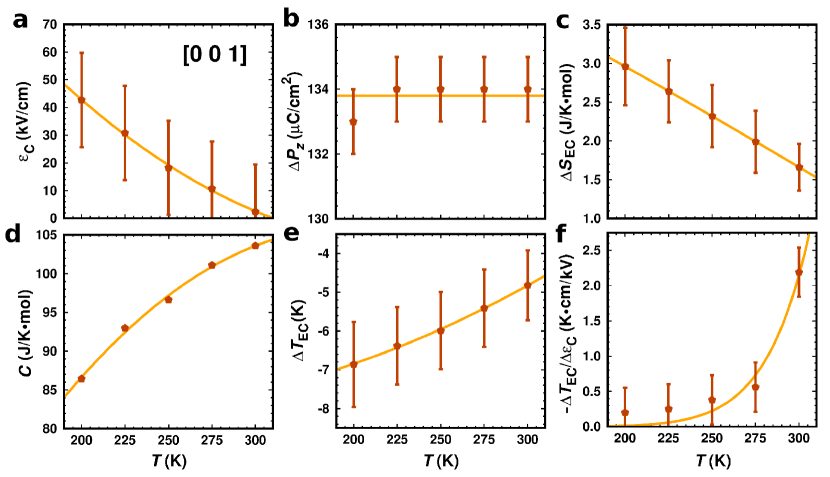
Electrocaloric performance of pressurized BFCO0.5. The electric polarization, , of BFCO0.5 in the and phases are significantly different; for instance, in the supertetragonal phase is more than two times larger than that in the rhombohedral phase menendez20 , adding up to polarization module differences of C cm-2 (Fig. 4b). Such a huge electric polarization disparity seems very promising from an electrocaloric (EC) point of view, as it can be inferred from the electric Clausius-Clapeyron relation , where represents the entropy change associated to the field-induced phase transition and the necessary electric field to switch from the to the phase. Figure 4a shows the estimated for a fixed pressure of GPa as a function of temperature (Methods), which has been selected to ensure proper stabilization of the phase under conditions K. As clearly appreciated therein, the critical electric field steadily decreases under increasing temperature, ranging from kV cm-1 at K to kV cm-1 at room temperature.
Figures 4c-e show the electrocaloric isothermal entropy and adiabatic temperature changes, and , estimated for compressed BFCO0.5 using the indirect CC approach (Methods). In this case, the sign of the EC descriptors indicate that the caloric effect is inverse (i.e., ), which follows from the fact that the high-entropy phase presenting the largest electric polarization is stabilized via application of the external electric bias. As expected, the size and temperature dependence of and , which are directly related through the temperature and heat capacity (Fig. 4d, Methods), are very much similar to those of and since the underlying phase transitions are equivalent. For instance, at K we estimated an electrocaloric adiabatic temperature change of K and at room temperature of K, to be compared with the analogous barocaloric shifts of and K. These values are very much promising, specially when considering the small size of the required driving electric fields (that is, – kV cm-1).
Figure 4f encloses results for the electrocaloric strength of BFCO0.5, , expressed as a
function of temperature; this quantity is defined like the ratio of by the corresponding electric bias.
At K, the attained adiabatic temperature change is highest however the required switching electric field is
also largest, thus the resulting electrocaloric strength is smaller than obtained at higher temperatures. Still, the
calculated amounting to K cm kV-1 is already comparable to the record experimental values
reported for oxide and hybrid organic-inorganic perovskites bto1 ; bto2 ; ec7 . Remarkably, under increasing temperature
the electrocaloric strength of BFCO0.5 noticeably increases reaching a maximum, and colossal, value of K cm kV-1
at K. These figures will be put into context in a next section; in what follows, we explain how the dual
response of BFCO0.5 to mechanical and electric stimuli may be exploited in practical solid-state cooling cycles.
| Y-HfO2 | 358 | 3500 | 24.8 | 0.01 | [ec0, ] |
| 0.93PMN-0.07PT | 298 | 723 | 9.0 | 0.01 | [ec2, ] |
| (NH4)2SO4 | 220 | 400 | 4.5 | 0.01 | [as2, ] |
| Terpolymer/PMN-PT | 303 | 1800 | 31.0 | 0.02 | [ec3, ] |
| Ba0.65Sr0.35TiO3 | 293 | 130 | 3.1 | 0.02 | [ec5, ] |
| BaZr0.2Ti0.8O3 | 313 | 145 | 4.5 | 0.03 | [ec4, ] |
| BNBT-BCZT | 370 | 620 | 23.0 | 0.04 | [ec6, ] |
| PbZr0.46Sn0.46Ti0.08O3 | 317 | 30 | 1.6 | 0.05 | [ec1, ] |
| BaTiO3 | 400 | 4.0 | 0.9 | 0.23 | [bto1, ] [bto2, ] |
| ((CH3)2CHCH2NH3)2PbCl4 | 302 | 30 | 11.1 | 0.37 | [ec7, ] |
| BFCO0.5 (pressurized) | 300 | 2.2 | -4.8 | 2.18 | This work |
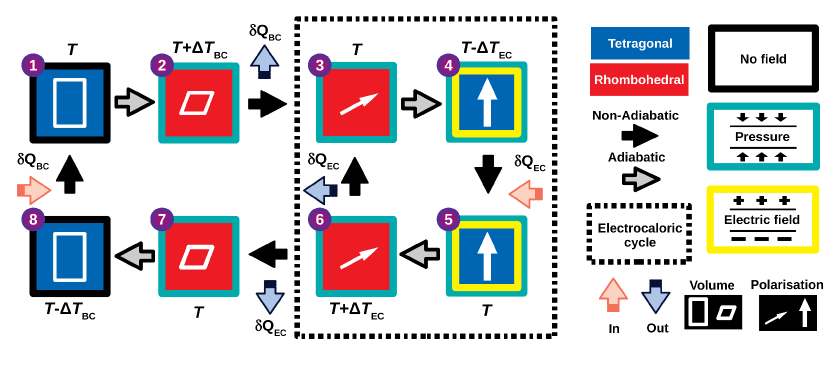
Proposed – multicaloric cycle. Single stimulus solid-state cooling cycles typically consists of four thermodynamic steps, two involving the adiabatic switching on and off of the applied external field and the other two constant-field heat transfer processes with the environment and the system to be refrigerated cazorla19 . In the present work, we propose an original multi-stimuli solid-state cooling cycle consisting of eight thermodynamic steps that has been designed to minimize the applied electric field, thus maximizing , and with a cumulative multicaloric performance of and .
Figure 5 sketches the envisaged multi-stimuli solid-state cooling cycle comprising hydrostatic pressure and electric fields being applied on multiferroic lead-free BFCO solid solutions near room temperature. The cycle starts with multiferroic BFCO in the supertetragonal phase at temperature . Subsequently, hydrostatic pressure is adiabatically applied on BFCO so that it transforms into the phase and experiences a temperature increase of . In the third step, heat is released to the ambient, , and the initial temperature of the cycle is restored; compressed BFCO still remains in the phase. Next, an electric field is adiabatically applied on compressed BFCO so that it transforms into the phase, thus experiencing a temperature decrease of . In the fifth step, heat is absorbed by the system, , and the initial temperature of the cycle is restored; compressed and electrically biased BFCO remains in the phase. Subsequently, the electric field is adiabatically removed thus BFCO transforms into the phase and experiences a temperature increase of . In the seventh step, heat is released to the ambient, , and the initial temperature of the cycle is restored; compressed BFCO remains in the phase. Finally, hydrostatic pressure is adiabatically released so that BFCO transforms back into the phase and experiences a temperature decrease of . Heat then is absorbed by the system, , and the initial temperature of the cycle is restored, thus completing an entire multi-stimuli cycle.
Upon completion of a multi-stimuli cycle, multiferroic BFCO is able to remove an amount of heat equal to , or equivalently, , from the targeted system to be refrigerated and release it to the ambient (thus cooling it down). The described multi-stimuli cycle lends itself to several useful variations. For instance, the state reached in the seventh step is thermodynamically equivalent to that attained in the third; therefore, one could recursively perform the electrocaloric subcycle consisting of steps (3)–(4)–(5)–(6) which entails application and removal of an electric bias under fixed hydrostatic pressure (dashed lines in Fig. 5). Likewise, if the multi-stimuli cooling cycle starts with multiferroic BFCO in the rhombohedral phase instead of the phase, due to some composition synthesis constraints, for example, then the sequential application of hydrostatic pressure and electric field explained above needs to be swapped.
Discussion
Table I summarizes some representative materials for which EC effects occurring at or near room temperature have been experimentally measured and reported in the literature. The selected compounds belong to three different families of ferroelectric materials, namely, oxides (e.g., HfO2 and BaTiO3), hybrid organic-inorganic perovskites ([(CH3)2CHCH2NH3]2PbCl4) and polymers (Terpolymer). In terms of largest , the oxides Y-HfO2 ec0 and BNBT-BCZT ec6 and the elastomer Terpolymer/PMN-PT ec3 emerge as the most promising since they display colossal values of – K. Nevertheless, these record materials require of quite large electric fields to realize their full EC potential ( kV cm-1), hence with no exception their associated electrocaloric strengths turn out to be quite mediocre, namely, K cm kV-1.
Ferroelectric materials exhibiting moderate or even small but attained under smaller electric fields ( kV cm-1), on the other hand, become the clear winners in terms of largest . For instance, the archetypal perovskite oxide BaTiO3 renders an adiabatic temperature change of roughly K driven by a minute electric field of kV cm-1, thus leading to a huge electrocaloric strength of K cm kV-1 bto1 ; bto2 . Likewise, the hybrid organic-inorganic perovskite [(CH3)2CHCH2NH3]2PbCl4 holds the record value of K cm kV-1, which results from a small electric field of kV cm-1 and an adiabatic temperature change of K ec7 . It is worth noting that all these figures correspond to experimental data.
Table I encloses also the EC results that we have theoretically estimated in this study for pressurized BFCO0.5 at room temperature. According to our QHA-DFT calculations, compressed multiferroic BFCO solid solutions have the potential to surpass all previously known EC materials in terms of largest . In particular, we predict an outstanding electrocaloric strength of K cm kV-1 that arises from an adiabatic temperature change of K and an electric bias of kV cm-1. This theoretically estimated value is from one to two orders of magnitude larger than those experimentally measured in uncompressed ferroelectrics. The key mechanism in achieving such a colossal figure is to employ an ancillary field, in our case hydrostatic pressure, to bring the system towards the verge of a ferroelectric phase transition so that it is possible to drive it with a minuscule electric field.
In the specific case considered here, the pressure required to achieve the colossal value of
K cm kV-1 is higher than GPa. Obviously, this compression is too large to be considered for practical
applications. Nevertheless, as it was argued at the begining of the Results section, it is possible to significantly
reduce the size of this ancillary pressure to the order of GPa by decreasing the relative content of
cobalt ions down to the critical composition of . Moreover, the enhancement approach
proposed in this study, and theoretically demonstrated for BFCO0.5, in principle should be generalizable to
many other well-known EC materials since most of them are responsive to pressure as well (even though the magnitude of
the resulting BC effects may be quite small in comparison to those achieved in state-of-the-art barocaloric materials). Take
the archetypal ferroelectric compound BaTiO3 as an example. The ferro- to paraelectric phase transition temperature
in this material can be effectively shifted with pressure, namely, K GPa-1 hayward02 ,
thus its room-temperature EC performance could be potentially improved with our proposed strategy. Finally, to mention that
recent developments in the synthesis of ferroelectric membranes and thin films may also allow for the enhancement of
the figure-of-merit by combining electric fields with other types of mechanical stimuli like uniaxial
zang22 and biaxial liu16b stress.
In conclusion, we have proposed a new strategy for the enhancement of the electrocaloric strength of ferroelectric materials that consists in concertedly applying pressure and electric fields. We have theoretically proved our new concept on multifunctional BFCO solid solutions, an intriguing family of compounds displaying a discontinuous phase transition between two multiferroic states. In particular, for compressed BFCO0.5 we estimated a record parameter of K cm kV-1 at room temperature resulting from an adiabatic temperature change of K and an electric bias of kV cm-1. This electrocaloric strength turns out to be colossal since it is from one to two orders of magnitude larger than those experimentally measured in uncompressed ferroelectrics. The demonstrated enhancement strategy can be applied to other types of ferroelectric materials, not necessarily magnetic, and be modified at convenience on the mechanical component. Thus, the combination of multiple stimuli opens new horizons in the field of caloric materials and solid-state refrigeration by expanding the design of possible cooling cycles and boosting current caloric performances. We hope that the present theoretical study will motivate new experimental works on the engineering of original and environmentally friendly solid-state cooling devices.
Methods
Spin-polarized DFT calculations were performed with the generalized gradient approximation proposed by Perdew, Burke and Ernzerhof (PBE) as it is implemented in the VASP package vasp ; pbe96 . The “Hubbard-” scheme due to Dudarev et al. was employed in the PBE calculations for treating better the Co (Fe) electrons, adopting a value of () eV menendez20 ; menendez20b ; cazorla17 ; cazorla18 ; cazorla13 . The “projected augmented wave” method bloch94 was used to represent the ionic cores considering the following electronic states as valence: Co , Fe , Bi , and O . An energy cut-off of eV and a -centered -point grid of were employed for a simulation cell containing atoms cazorla15 , thus obtaining zero-temperature energies converged to within meV/f.u. Geometry relaxations were performed for an atomic force threshold of eVÅ-1. Electric polarizations were accurately estimated with the hybrid HSE06 functional hse06 and the Berry phase formalism king93 ; resta94 ; bellaiche99 .
Ab initio free energies were estimated within the quasi-harmonic approximation (QHA) cazorla13 ; cazorla17d ; phonopy as a function of and . Phonon frequencies were calculated with the small displacement method phonopy . The following technical parameters provided QHA free energies converged to within meV per formula unit: -atom supercells, atomic displacements of Å, and -point grids of for integration within the first Brillouin zone. The effects of chemical disorder were addressed by generating all possible atomic Co–Fe and magnetic spin arrangements (ferromagnetic –FM– and antiferromagnetic –AFM– of type A, C, and G) for a supercell containing atoms. Quasi-harmonic free energies were calculated only for the lowest-energy configurations. Our spin-polarized DFT calculations were performed for bulk BiFe0.5Co0.5O3.
Within the QHA cazorla13 ; cazorla17d ; phonopy , the Gibbs free energy of a given crystal phase, , is expressed as:
| (1) |
where is the static energy of the system (i.e., as directly obtained from zero-temperature DFT calculations), the pressure, the volume, and the lattice Helmholtz free energy. (The dependence of the different energy terms on and have been explicitly noted.) For given and , can be determined with the formula:
| (2) | |||||
where are the phonon frequencies obtained at the reciprocal lattice vector and phonon branch , the total number of wave vectors used for integration in the Brillouin zone, and the Boltzmann constant. Meanwhile, the hydrostatic pressure is calculated via the expression:
| (3) |
which numerically allows to determine . Thus, by performing and DFT calculations for a set of points, over which interpolation is applied to describe and continuously, and by using Eqs. (1)–(3), it is possible to estimate . To quantify the temperature at which the phase transition occurs at a given pressure, , the condition was employed.
Likewise, the entropy of the crystal can be obtained through the expression:
| (4) |
and the heat capacity like:
| (5) | |||||
Through the knowledge of and Eqs. (2)–(5), then it is possible to determine and .
In the absence of electric fields, the isothermal entropy change associated to barocaloric effects was approximately estimated with the Clausius-Clapeyron (CC) method like sau21 :
| (6) |
where is the change in volume occurring during the phase transition and the critical pressure. Likewise, the corresponding adiabatic temperature change can be approximated with the expression manosa17 :
| (7) |
where is the heat capacity of the system at zero pressure.
In the presence of electric fields, and assuming zero pressure, the thermodynamic potential that describes a particular phase is the Gibbs free energy defined as , where and are the same terms that appear in Eq. (1), the electric polarization and the applied electric field. In this case, the thermodynamic condition that determines a –induced phase transition is . The value of the corresponding critical electric field then can be estimated like:
| (8) |
where is the Helmholtz free energy difference between the two phases, and the resulting change in the electric polarization along the electric field direction. For conditions, an additional term should appear in the right-hand side of Eq. (8).
Once the value of and its dependence on temperature are determined through Eq. (8), the isothermal entropy change associated to electrocaloric effects can be approximately estimated with the CC method like cazorla18 :
| (9) |
Likewise, the corresponding adiabatic temperature change was approximated with the expression manosa17 :
| (10) |
where is the heat capacity of the system at zero electric field.
References
- (1) Liu, Y., Scott, J. F. and Dkhil, B. Direct and indirect measurements on electrocaloric effect: Recent developments and perspectives. Appl. Phys. Rev. 3, 031102 (2016).
- (2) Stern-Taulats, E., Lloveras, P., Barrio, M., Defay, E., Egilmez, M., Planes, A., Tamarit, J. Ll., Mañosa, Ll., Mathur, N. D. and Moya, X. Inverse barocaloric effects in ferroelectric BaTiO3 ceramics. APL Mater. 4, 091102 (2016).
- (3) Moya, X., Stern-Taulats, E., Crossley, S., González-Alonso, D., Kar-Narayan, S., Planes, A., Mañosa, Ll. and Mathur, N. D. Giant electrocaloric strength in single-crystal BaTiO3. Adv. Mater. 25, 1360 (2013).
- (4) Thacher, P. D. Electrocaloric effects in some ferroelectric and antiferroelectric Pb(Zr,Ti)O3 compounds. J. Appl. Phys. 39, 1996 (1968).
- (5) Samanta, S., Anoop, G., Seol, W., Park, S. M., Joh, H., Choi, J. O., Ahn, D., Unithrattil, S., Kim, H., Yeom, J., Hong, S. and Jo, J. Y. Large electrocaloric effect with high thermal and electric field cycling stability in solution-processed Y:HfO2 thin films. J. Mater. Chem. A 10, 9960 (2022).
- (6) Mischenko, A. S., Zhang, Q., Scott, J. F., Whatmore, R. W., and Mathur, N. D. Giant electrocaloric effect in thin-film PbZr0.95Ti0.05O3. Science 311, 1270 (2006).
- (7) Neese, B., Chu, B., Lu, S.-G., Wang, Y., Furman, E., and Zhang, Q. Large electrocaloric effect in ferroelectric polymers near room temperature. Science 321, 821 (2008).
- (8) Asbani, B., Gagou, Y., Dellis, J.-L., Trcek, M., Kutnjak, Z., Amjoud, M., Lahmar, A., Mezzane, D., and El Marssi, M. Lead-free Ba0.8Ca0.2TexTi1-xO3 ferroelectric ceramics exhibiting high electrocaloric properties. J. Appl. Phys. 121, 064103 (2017).
- (9) Shirsath, S. E., Cazorla, C., Lu, T., Zhang, L., Tay, Y. Y., Lou, X., Liu, Y., Li, S. and Wang, D. Interface-charge induced giant electrocaloric effect in lead free ferroelectric thin-film bilayers. Nano Lett. 20, 1262 (2020).
- (10) Liu, X., Wu, Z., Guan, T., Jiang, H., Long, P., Li, X., Ji, C., Chen, S., Sun, Z. and Luo, J. Giant room temperature electrocaloric effect in a layered hybrid perovskite ferroelectric: [(CH3)2CHCH2NH3]2PbCl4. Nat. Commun. 12, 5502 (2021).
- (11) Cohen, R. E. Origin of ferroelectricity in perovskite oxides. Nature 358, 136 (1992).
- (12) Azuma, M., Niitaka, S., Hayashi, N., Oka, K., Takano, M., Funakubo, H. and Shimakawa, Y. Rhombohedral-tetragonal phase boundary with high Curie temperature in (1-x)BiCoO3-xBiFeO3 solid solution. Jpn. J. Appl. Phys. 47, 7579 (2008).
- (13) Hojo, H., Oka, K., Shimizu, K., Yamamoto, H., Kawabe, R. and Azuma, M. Development of bismuth ferrite as a piezoelectric and multiferroic material by cobalt substitution. Adv. Mater. 30, 1705665 (2018).
- (14) Menéndez, C. and Cazorla, C. Giant thermal enhancement of the electric polarization in ferrimagnetic BiFe1-xCoxO3 solid solutions near room temperature. Phys. Rev. Lett. 125, 117601 (2020).
- (15) Cazorla, C. and Íñiguez, J. Insights into the phase diagram of bismuth ferrite from quasiharmonic free-energy calculations. Phys. Rev. B 88, 214430 (2013).
- (16) Cazorla, C., Diéguez, O. and Íñiguez, J. Multiple structural transitions driven by spin-phonon couplings in a perovskite oxide. Sci. Adv. 3, e1700288 (2017).
- (17) Cazorla, C. and Íñiguez, J. Giant direct and inverse electrocaloric effects in multiferroic thin films. Phys. Rev. B 98, 174105 (2018).
- (18) Cazorla, C. and Boronat, J. Simulation and understanding of atomic and molecular quantum crystals. Rev. Mod. Phys. 89, 035003 (2017).
- (19) Aznar, A., Lloveras, P., Romanini, M. et al. Giant barocaloric effects over a wide temperature range in superionic conductor AgI. Nat. Commun. 8, 1851 (2017).
- (20) Cazorla, C. and Errandonea, D. Giant mechanocaloric effects in fluorite-structured superionic materials. Nano Lett. 16, 3124 (2016).
- (21) Sagotra, A. K., Errandonea, D. and Cazorla, C. Mechanocaloric effects in superionic thin films from atomistic simulations. Nat. Commun. 8, 963 (2017).
- (22) Sagotra, A.K., Chu, D. and Cazorla, C. Room-temperature mechanocaloric effects in lithium-based superionic materials. Nat. Commun. 9, 3337 (2018).
- (23) Lloveras, P., Aznar, A., Barrio, M. et al. Colossal barocaloric effects near room temperature in plastic crystals of neopentylglycol. Nat. Commun. 10, 1803 (2019).
- (24) Li, B., Kawakita, Y., Ohira-Kawamura, S. et al. Colossal barocaloric effects in plastic crystals. Nature 567, 506 (2019).
- (25) Cazorla, C. Refrigeration based on plastic crystals. Nature 567, 470 (2019).
- (26) Sau, K., Ikeshoji, T., Takagi, S., Orimo, S.-I., Errandonea, D., Chu, D. and Cazorla, C. Colossal barocaloric efects in the complex hydride Li2B12H12. Sci. Rep. 11, 11915 (2021).
- (27) Cazorla, C. Novel mechanocaloric materials for solid-state cooling applications. Appl. Phys. Rev. 6, 041316 (2019).
- (28) Li, J., Dunstan, D., Lou, X., Planes, A., Mañosa, Ll., Barrio, M., Tamarit, J.-Ll. and Lloveras, P. Reversible barocaloric effects over a large temperature span in fullerite C60. J. Mater. Chem. A 8, 20354 (2020).
- (29) Correia, T. M., Young, J. S., Whatmore, R. W., Scott, J. F., Mathur, N. D. and Zhang, Q. Investigation of the electrocaloric effect in a PbMg1/3Nb2/3O3-PbTiO3 relaxor thin film. Appl. Phys. Lett. 95, 182904 (2009).
- (30) Huang, C., Yang, H.-B. and Gao, C.-F. Giant electrocaloric effect in cracked ferroelectrics. J. Appl. Phys. 123, 154102 (2018).
- (31) Qian, X.-S., Ye, H. J., Zhang, Y. T., Gu, H., Li, X., Randall, C. A. and Zhang, Q. M. Giant electrocaloric response over a broad temperature range in modified BaTiO3 ceramics. Adv. Funct. Mater. 24, 1300 (2014).
- (32) Liu, X. Q., Chen, T. T., Wu, Y. J. and Chen, X. M. Enhanced electrocaloric effects in spark plasma-sintered Ba0.65Sr0.35TiO3-based ceramics at room temperature. J. Am. Ceram. Soc. 96, 1021 (2013).
- (33) Crossley, S., Li, W., Moya, X. and Mathur, N. D. Large electrocaloric effects in single-crystal ammonium sulfate. Phil. Trans. R. Soc. A 374, 20150313 (2016).
- (34) Hayward, S. A. and Salje, E. K. H. The pressure-temperature phase diagram of BaTiO3: a macroscopic description of the low-temperature behaviour. J. Phys.: Condens. Matter 14, L599 (2002).
- (35) Zang, Y., Di, C., Geng, Z. et al. Giant thermal transport tuning at a metal/ferroelectric interface. Adv. Mater. 34, 2105778 (2022).
- (36) Liu, Y., Phillips, L. C., Mattana, R., Bibes, M., Barthélémy, A. and Dkhil, B. Large reversible caloric effect in FeRh thin films via a dual-stimulus multicaloric cycle. Nat. Commun. 7, 11614 (2016).
- (37) Kresse, G. and Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
- (38) Perdew, J. P., Burke, K. and Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
- (39) Menéndez, C., Chu, D. and Cazorla, C. Oxygen-vacancy induced magnetic phase transitions in multiferroic thin films. npj Comput. Mater. 6, 76 (2020).
- (40) Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
- (41) Cazorla, C. and Stengel, M. Electrostatic engineering of strained ferroelectric perovskites from first principles. Phys. Rev. B 92, 214108 (2015).
- (42) Heyd, J., Scuseria, G. E. and Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003).
- (43) King-Smith, R. D. and Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651 (1993).
- (44) Resta, R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66, 899 (1994).
- (45) Bellaiche, L. and Vanderbilt, D. Intrinsic piezoelectric response in perovskite alloys: PMN-PT versus PZT. Phys. Rev. Lett. 83, 1347 (1999).
- (46) Togo, A. and Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1 (2015).
- (47) Maosa, L. and Planes, A. Materials with giant mechanocaloric effects: Cooling by strength. Adv. Mater. 29, 1603607 (2017).
ACKNOWLEDGEMENTS
The authors thank Riccardo Rurali for insightful discussions on the calculation of phonon properties of BFCO solid solutions. C.C. acknowledges financial support from the Spanish Ministry of Science, Innovation and Universities under the “Ramón y Cajal” fellowship RYC2018-024947-I and TED2021-130265B-C22 project. Computational support was provided by the Red Española de Supercomputación (RES) under the grants FI-2022-1-0006, FI-2022-2-0003 and FI-2022-3-0014.