Comment on “Length-dependent translation of messenger RNA by ribosomes”

In recent paper Valleriani2011 , Valleriani et al presented a simple model to describe the length-dependent translation properties of messager RNA (mRNA). In their model, the mRNA degradation process is assumed to be governed by rate $\omega_{r}$, i.e. the probability density of lifetime $t$ of an intact mRNA is

Meanwhile, the rate of ribosome entering the coding region of mRNA is assumed to be $\omega_{\rm on}$, and the degradation rate of protein is denoted by $\omega_{p}$.

To discuss the mRNA length-dependent properties of the translation to protein by ribosomes, in Valleriani2011 the expression of translational ratio, defined as

is obtained for translations in both prokaryotic and eukaryotic cells. Where $\omega_{\rm tl}$ is the translation rate from mRNA to protein by ribosomes. Since the protein degradation rate $\omega_{p}$ is independent of mRNA, the essential point to analyze the mRNA length-dependent properties of the translational ratio $r$, is to get the expression of translation rate $\omega_{\rm tl}$. Experimentally, there might be three methods to get $\omega_{\rm tl}$:

One can easily show that, for the mRNA translation problem discussed in Valleriani2011 , $T(t)=t$, $N(t)=\theta(t-t_{L}^{\rm pro})\omega_{\rm on}(t-t_{L}^{\rm pro})$ for translation in prokaryotic cells, and $T(t)=t+t_{L}^{\rm eu}$, $N(t)=\omega_{\rm on}t$ for translation in eukaryotic cells. Where $\theta(t)$ is Heaviside function, i.e. $\theta(t)=1$ for $t>0$ and $\theta(t)=0$ for $t<0$, $t_{L}^{\rm pro}=L/v^{\rm pro}$ and $t_{L}^{\rm eu}=L/v^{\rm eu}$ are the time taken by ribosomes to reach the end of mRNA, $L$ is the length of mRNA, $v^{\rm pro}$ and $v^{\rm eu}$ are the average velocities of ribosome along mRNA in prokaryotic and eukaryotic cells respectively.

Intuitively, method (I) is reasonable, and actually this method is used in Valleriani2011 . On the other hand, method (III) is usually employed for some mathematical problems. For example, to get the mean translation rate $\omega$ of a process which includes two sub-processes with rate $\omega_{1}$ and $\omega_{2}$, one usually does the following calculations

It should be pointed out that, if the method (III) is employed to get $\omega_{\rm tl}$, the experimental samples with no protein synthesized, i.e. samples for $N(t)=0$, should be discarded to avoid the infinite waiting time cases. Correspondingly, in the theoretical calculation in Eq. (5), the average $\langle T(t)/N(t)\rangle$ should be done for only large enough time $t\geq t_{\rm lim}$ which satisfies $N(t)\geq 1$, and the probability density $\phi_{U}$ should be changed accordingly, $\hat{\phi}_{U}(t)=\phi_{U}(t)/\int_{t_{\rm lim}}^{\infty}\phi_{U}(t)dt=\omega_{r}\exp[-\omega_{r}(t-t_{\rm lim})]$ for $t\geq t_{\rm lim}$. In our numerical calculations, we use $t_{\rm lim}^{\rm pro}=t_{L}^{\rm pro}+1/\omega_{\rm on}$ for translation in prokaryotic cells, and $t_{\rm lim}^{\rm eu}=1/\omega_{\rm on}$ for translation in eukaryotic cells.

Meanwhile, the simple method (II) is often used in the experimental data statistics. For this mRNA translation problem, one can easily get the following results by method (II). For mRNA translation in prokaryotic cells,

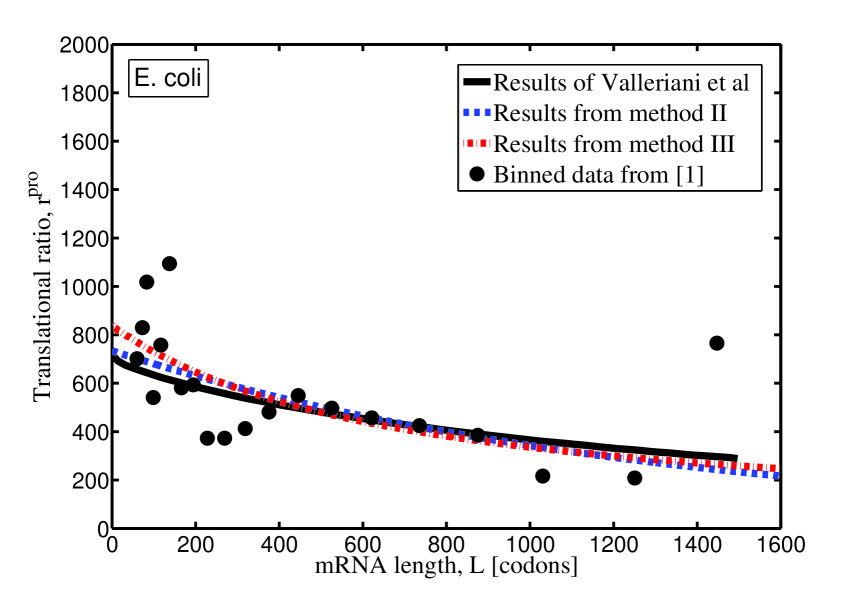
So the translational ratio $r^{\rm pro}=\omega_{\rm tl}^{\rm pro}/\omega_{p}$ decays exponentially with the length $L^{\rm pro}$ of mRNA. Meanwhile, for the mRNA translation in eukaryotic cells,

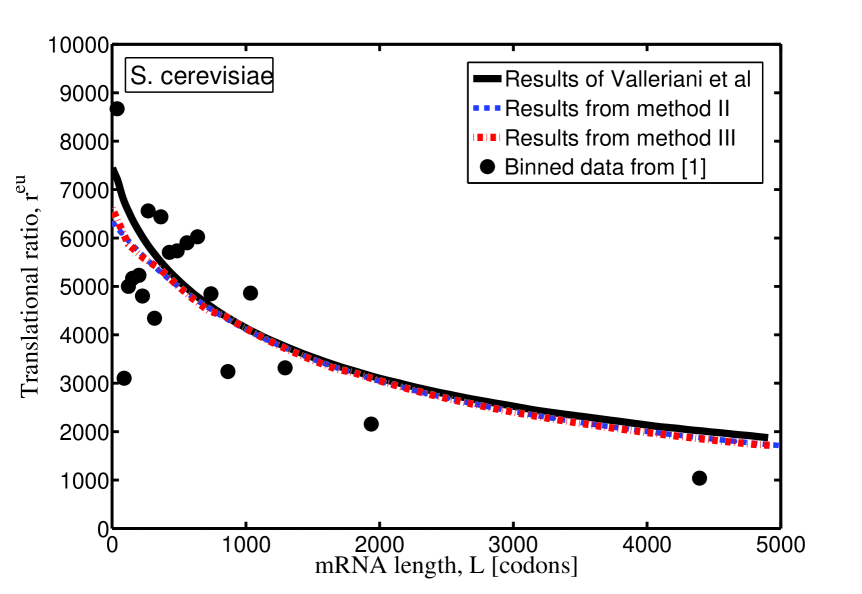
So, roughly speaking, the translational ratio $r^{\rm eu}=\omega_{\rm tl}^{\rm eu}/\omega_{p}$ decays reciprocally with the length of mRNA. Note: similar as the above discussion about the calculation of translation rate $\omega_{\rm tl}$ in prokaryotic cells by method III, if the samples with $N(t)=0$ are discarded in experimental measurements, the methods I and II should also be changed correspondingly, with a modified probability density $\hat{\phi}_{U}(t)$ for $t\geq t_{\rm lim}$ only.

For the sake of comparison, the theoretical results of translational ratio $r$ of E. coli and S. cerevisiae, obtained by the three methods, are plotted in Fig. 1, with model parameters listed in Tab. 1. Since method I is used by Valleriani et al. in Valleriani2011 , the curves in Fig. 1 (and the corresponding model parameters in Tab. 1) are copied from Valleriani2011 . One can see that, compared with the experimental data, these three methods all work reasonably well, but with slightly different model parameter (see Tab. 1). The most reasonable parameters should be the ones which are obtained by the same method as that used in the experimental measurements.

In conclusion, when one tries to apply the model presented in Valleriani2011 to real experimental data, the method used to get the translation rate $\omega_{\rm tl}$ should be chosen properly to be consist with experiments.