junginger@uvic.ca

In a recent Letter by Romanenko et al. [1], the authors used low-energy muon spin rotation (LE-$\mu$SR) [2, 3] to measure the Meissner screening profile in cutouts from \chNb superconducting radio frequency (SRF) cavities, systematically comparing how different surface treatments affect the screening properties of the elemental type-II superconductor. They reported a “strong” modification to the character of the screening profile upon mild baking at $120\text{\,}\mathrm{\SIUnitSymbolCelsius}$ for $48\text{\,}\mathrm{h}$ [4], which was interpreted as a depth-dependent carrier mean-free-path resulting from a “gradient in vacancy concentration” near the surface [1]. While this observation led to speculation that this surface treatment yields an “effective” superconducting bilayer (see e.g., [5]), we suggest that its likeness to such [6] is accidental and that the behavior is an artifact from the analysis.

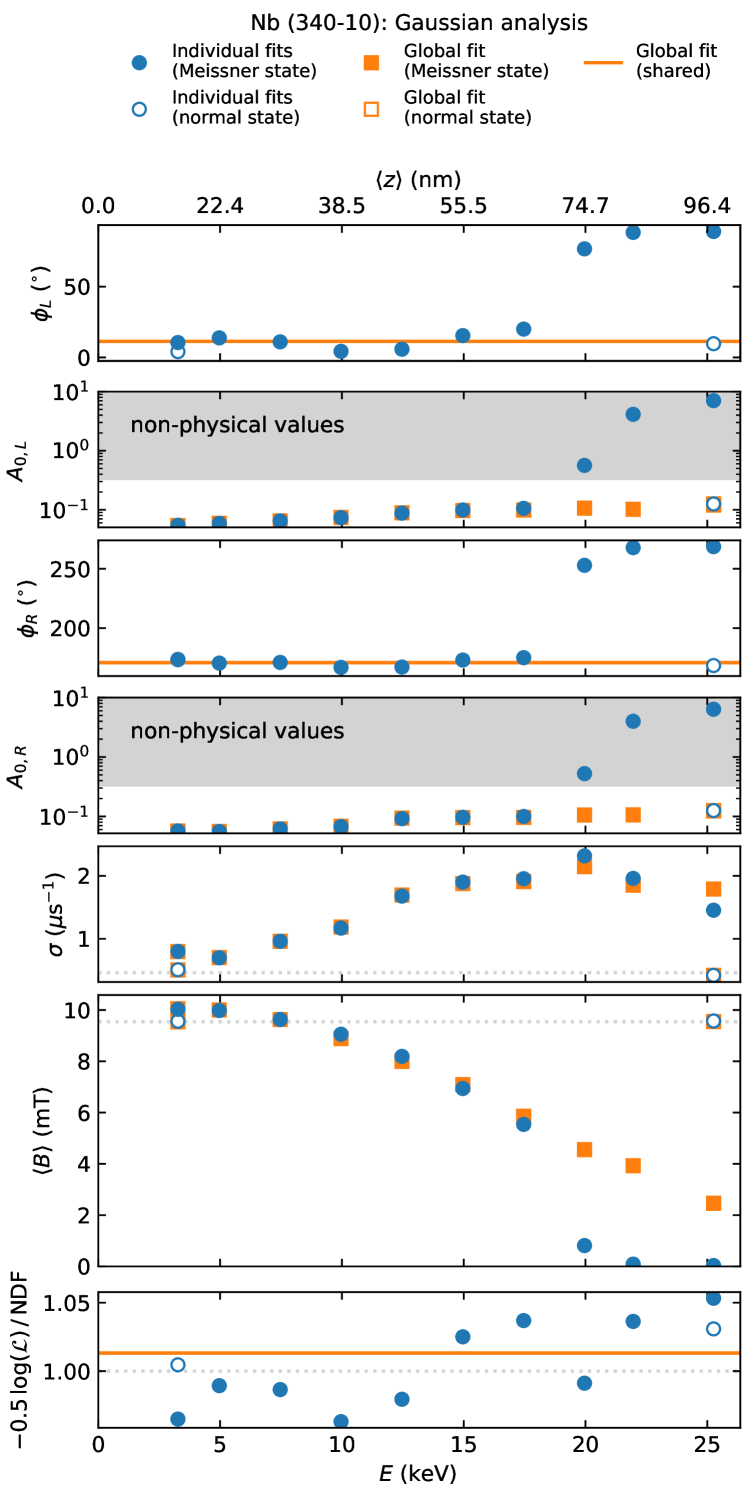
Issues with the reported analysis are apparent upon scrupulous inspection of Figures 3 and 4 in the Letter [1], where the mean field $\langle B\rangle$ below the sample surface (obtained through different analysis models) is plotted against the mean muon stopping depth $\langle z\rangle$. In Figure 3, where $\langle B\rangle$ was determined from fits to a Gaussian model (i.e., a Gaussian-damped cosine function), ¹¹1We also note that the assignment of the plotted symbols ($\blacksquare$, $\blacktriangle$, and $\bullet$) in Figure 3’s caption [1] are inconsistent with the legend in the inset. Additionally, in both Figures 3 and 4 [1], several points appear at $\langle z\rangle=$0\text{\,}\mathrm{nm}$$, but without explanation. Clearly, these cannot originate from an actual measurement by LE-$\mu$SR where “muon implantation energies of $3.3\leq E\leq$25.3\text{\,}\mathrm{keV}$$ were used”. Romanenko et al. [1] correctly draw attention to the strikingly different $\langle B\rangle(\langle z\rangle)$ dependence found upon mild baking [4]; however, no mention is made as to why the data deviate from exponential decay (i.e., the well-known form of Meissner screening profiles for thick slabs [8]) for all surface treatments. Instead, the discussion shifts to accounting for non-local electrodynamics [9, 10] and strong electron-phonon coupling [11] in the formulation of $B(z)$. While the former can cause $B(z)$ to decay non-exponentially, its effect is known to be subtle for \chNb [12], and it’s unclear how such corrections could account for the abrupt discontinuity observed at $\langle z\rangle\approx$60\text{\,}\mathrm{nm}$$.

This “step” in $\langle B\rangle$ vs. $\langle z\rangle$ persists in Figure 4 [1], where $\langle B\rangle$ was determined from fits to Pippard’s non-local model [9, 12], including results from treating the LE-$\mu$SR data individually or as part of a global analysis. Surprisingly, the $\langle z\rangle$ dependence of the other two cutouts (100-6 and 30-6) appear drastically different from Figure 3, with their field attenuation now resembling an exponential. While this might suggest that the Gaussian analysis is too crude an approach, such a conclusion is inconsistent with earlier LE-$\mu$SR measurements on a \chNb thin film [12]. The persistence of the baked sample’s sudden drop in $\langle B\rangle$ is both conspicuous and non-physical, especially considering that it implies an unrealistically large current density $J(z)\equiv-[\mathrm{d}B(z)/\mathrm{d}z]/\mu_{0}$ (where $\mu_{0}$ is the permeability constant) at the depth of the discontinuity (see e.g., [5, 13]).

Motivated by results from our own investigation into how SRF cavity treatments affect Meissner screening in \chNb (which showed exponential screening profiles for all treatments studied) [14], we revisited the original LE-$\mu$SR data reported in the Letter [1]. In general, we find that the “step” near $\langle z\rangle\approx$60\text{\,}\mathrm{nm}$$ is only reproduced when fits adopt parameters with non-physical values. For example, following the Gaussian analysis described in the Letter [1], we obtain the fit parameters shown in Figure˜1, illustrating that the sudden drop in $\langle B\rangle$ is coincident with a divergence in both the phase $\phi_{i}$ and initial asymmetry $A_{0,i}$, neither of which is realistic ²²2The phase $\phi_{i}$ of the spin-precession signal is determined by the $\mu^{+}$ beam properties and should be unchanged across a series of related measurements (e.g., at different implantation energies). Similarly, the initial asymmetry $A_{0,i}$ is determined by the properties of $\mu^{+}$ decay and the detector setup, with values rarely exceeding $\sim 1/3$ (i.e., the value obtained following averaging over all decay positron energies).. This situation is easily rectified by constraining the fit (e.g., through treating the phase as a shared parameter), upon which the “step” vanishes without any meaningful penalty to the overall goodness-of-fit.

To provide a refined assessment of the Meissner screening in the 340-10 cavity cutout, we also re-analyzed the LE-$\mu$SR data using the approach described in Ref. 14, wherein a skewed Gaussian is used to approximate the local field distribution along with an improved simulation of $\mu^{+}$ stopping in \chNb. ³³3At this juncture, we emphasize that there is no “intrinsic” flaw in the analysis approaches described in the Letter [1] and that both should work well when applied diligently. In fact, the workflow outlined in Ref. 14 can be considered as further refinement to the methodology used to characterize \chNb SRF materials using LE-$\mu$SR. Screening profiles determined from this procedure are shown in Figure˜2, where any discontinuity in $\langle B\rangle$ is notably absent. Moreover, we find that the profiles are well-described by an exponential $B(z)$, as expected for a “dirty” superconductor [8] and consistent with our other results [14]. Note that we also included an effective demagnetization factor $\tilde{N}$ in this analysis, which accounts for the (geometric) enhancement of the applied field $B_{\mathrm{applied}}$ well-into the Meissner state. ⁴⁴4That is, for certain combinations of material geometries and field directions (e.g., a thick slab with the field applied parallel to its surface), the expelled magnetic flux that closely contours the sample’s dimensions can be “squeezed” along certain areas of the material’s surface, leading to the appearance that the applied field has been enhanced (see e.g., Ref. 19). The manifestation of this phenomenon is evident in Figure 1, where at low $E$ the $\langle B\rangle$ in the Meissner state exceeds that in the normal state. We stress that incorporating this detail was necessary to correctly describe the data. ⁵⁵5The omission of this detail in the Letter [1] is likely because of it’s seldom use in the literature. For example, most LE-$\mu$SR experiments at the time focussed on thin film samples, whose dimensions ensure that $\tilde{N}\rightarrow 0$.

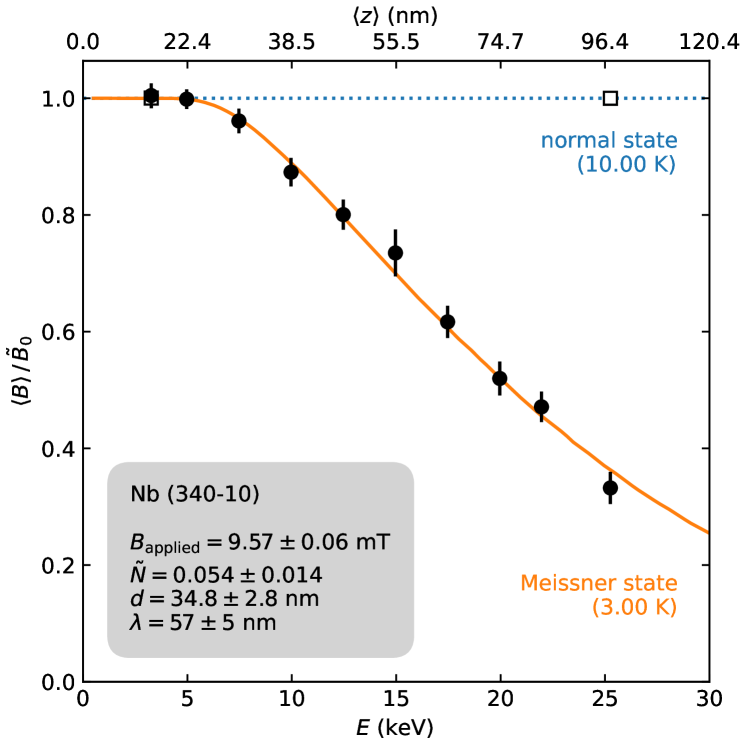
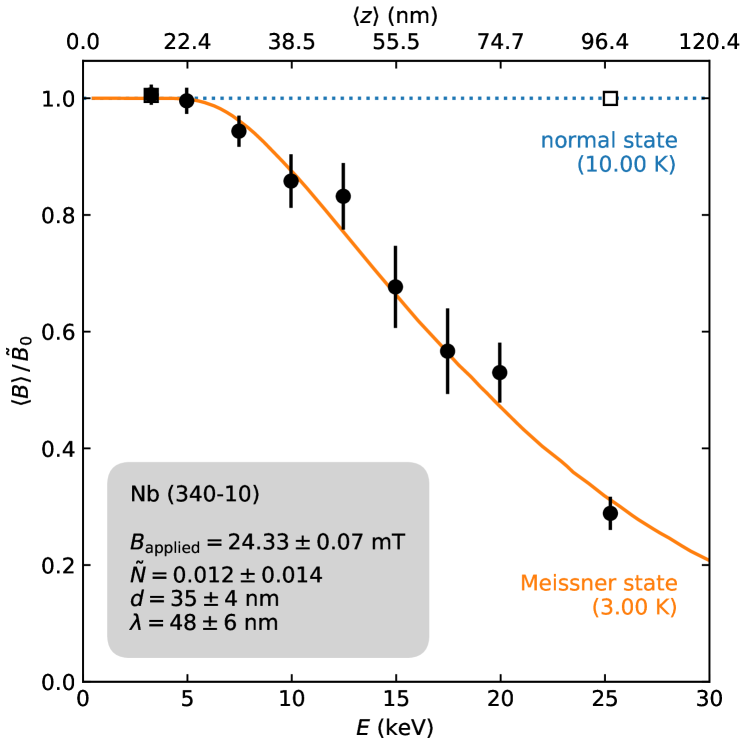
Lastly, we note that our re-analysis also finds an unusually large non-superconducting “dead layer” $d$ at the surface of the 340-10 cutout. This is easily identified by $\langle B\rangle$’s asymptotic approach to the “effective” applied field $\tilde{B}_{0}=B_{\mathrm{applied}}/(1-\tilde{N})$ with decreasing implantation energy $E$ (i.e., $\langle z\rangle$). We find that $d\approx$35\text{\,}\mathrm{nm}$$ (see Figure˜2), which is significantly larger than the $\sim 20\text{\,}\mathrm{nm}$ implied in the Letter [1], as well as those given in other reports [14, 12]. While $d$ is a sample-dependent (rather than an intrinsic material-dependent) property, this value is exceptionally large and is unlikely a result of surface roughness alone (see e.g., [20, 21]). An intriguing alterative (in line with the ideas presented by Romanenko et al. [1]) is that there may be a near-surface region where the magnetic penetration depth $\lambda$ is spatially inhomogeneous. This idea has been considered theoretically on general grounds [22] and more recently in the context of SRF cavities [23, 24]. The impact of such an effect, however, is likely subtle and beyond the resolution of the current measurements.

In summary, we re-analyzed the LE-$\mu$SR data originally reported in the Letter by Romanenko et al. [1], revealing the absence of any “strong” changes to the Meissner screening profile of \chNb upon mild baking [4], with the field screening well-described by an exponential London model [8]. Interestingly, the re-analysis also uncovered an unusually large “dead layer”, which may suggest the presence of spatial inhomogeneities in the screening properties close to the surface (e.g., from a depth-dependent penetration depth) [22, 23, 24]. The data suggests that their effect on $B(z)$ is likely subtle, necessitating high-resolution measurements probing the near-surface region ($z\lesssim$40\text{\,}\mathrm{nm}$$) to be conclusive. We hope that this Comment will stimulate further investigation into the matter.