Common tangents to convex bodies

Federico Castillo Departamento de Matemáticas, Pontificia Universidad Católica de Chile, Santiago, Chile federico.castillo@mat.uc.cl , Joseph Doolittle Institut für Geometrie, Technische Universität Graz, Austria jdoolittle@tugraz.at and José A. Samper Departamento de Matemáticas, Pontificia Universidad Católica de Chile, Santiago, Chile jsamper@mat.uc.cl

Abstract.

It is well-known since the time of the Greeks that two disjoint circles in the plane have four common tangent lines. Cappell et al. proved a generalization of this fact for properly separated strictly convex bodies in higher dimensions. We have shown that the same generalization applies for arbitrary convex bodies. When the number of convex sets involved is equal to the dimension, we obtain an alternative combinatorial proof of Bisztriczky’s theorem on the number of common tangents to $d$ separated convex bodies in $\mathbb{R}^{d}$ .

1. Introduction

It a known since the times of Euclid and Apollonius that two disjoint circles have four common tangents. In fact they had explicit constructions with straightedge and compass to describe these lines.

Figure 1. Four tangents to two circles.

Note that the circles need to be disjoint for these four tangents to exist; the number of common tangents can be any integer less than four depending on whether the circles are internally/externally tangent, intersecting, or nested. This paper is a generalization of this result in the realm of convex geometry; we describe the set of common tangent hyperplanes to suitably separated convex bodies.

In order to properly state our main theorem, we first define the separation we use. Let $\mathcal{K}^{d}$ be the set of convex bodies (compact, convex, with non-empty interior) in $\mathbb{R}^{d}$ . We say that a family $\mathbf{S}=\{\mathrm{S}_{1},\dots,\mathrm{S}_{m}\}\subset\mathcal{K}^{d}$ is strongly separated if for every subset $I\subseteq[m]$ there exists an affine hyperplane $\mathrm{H}$ such that $\bigcup_{i\in I}\mathrm{S}_{i}\subseteq\mathrm{H}^{-}$ and $\bigcup_{i\notin I}\mathrm{S}_{i}\subseteq\mathrm{H}^{+}$ . The set $\mathcal{H}^{d}$ of all hyperplanes in $\mathbb{R}^{d}$ is parametrized by the real projective space $\mathbb{RP}^{d}$ . Let $\mathcal{T}(\mathbf{S})\subset\mathcal{H}^{d}$ be the set of hyperplanes that are tangent to a family $\mathbf{S}$ and contain the entire family on the same side. Our main theorem is the following.

Theorem A.

Let $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{m}\}\subset\mathcal{K}^{d}$ be a family of strongly separated convex bodies in $\mathbb{R}^{d}$ where $m\leq d$ . The set $\mathcal{T}(\mathbf{K})$ is homeomorphic to the sphere $\mathbb{S}^{d-m}$ .

This is a generalization of a theorem of Cappell, Goodman, Pach, Pollack, Sharir and Wenger [5, Theorem 2]. They proved Theorem A in the case where every convex body is strictly convex. We remark that our proof strategy is different to the original technique in [5]. There, the strict convexity is used in an essential way to show that the geometric locus of the tangent hyperplanes form a manifold with boundary as the bodies are appropriately deformed. We instead build on intuition from polytope theory and Bruggeser and Mani’s approach to shellability [4, Section 4] to provide an inductive argument. We consider the convex hull of all the bodies and interpret the separation conditions as visibility conditions in the polar convex body. This idea allows us to formulate a dual problem that implies our theorem and which allows us to reduce dimension properly.

Our theorem applies to arbitrary convex bodies and in particular to polytopes, in this case the set of tangent hyperplanes is a polyhedral complex (Theorem 3.13) combinatorially equivalent to the boundary of a polytope. We also remark that our results give an alternative proof of Bisztricksky’s theorem [2] that there are exactly $2^{d}$ tangent hyperplanes to $d$ strongly separated convex bodies in $\mathbb{R}^{d}$ . This generalizes the result mention at the beginning, see Figure 1. The core of this proof, as explained in [2], is to show that there exist exactly two common tangents to the $d$ strongly separated convex bodies in $\mathbb{R}^{d}$ with every body on the same side of both tangents, so that these hyperplanes sandwich the whole family. This is the case $m=d$ of Theorem A. We remark that [5] generalizes their version of Theorem A to arbitrary convex bodies when $m=d$ in order to prove Bisztricksky’s theorem.

It may be worth to note that there is another topological proof of Bisztricksky’s theorem by Lewis, von Hohenbalken, and Klee [15] using Kakutani’s extension of Brouwer’s fixed point theorem. Our proof is elementary, but the arguments are subtle: in the introduction of [15], the authors mention that Bisztriczky had announced that his original proof of the Theorem was insufficient. In any case, there are at least different proofs and also several generalizations of this theorem, see e.g. [1], [9], [10], and [11].

Finally, the subject of common tangents to multiple objects has been considered from an algebraic point of view; the circles in the original Greek problem have been replaced by real quadrics or convex semialgebraic sets, and the lines have been replaced by $k$ -planes. See for example [3], [14], [19], and [20]. It would be interesting to know if the algebraic results for general $k$ -planes also extend to convex bodies.

Acknowledgements

We thank Mauricio Bustamante, Florian Frick, Frank Sottile, and Giancarlo Urzúa for helpful discussions. This project began in the Max Planck Institute for Mathematics in the Sciences, Leipzig. The first author thanks the Institut für Mathematik, Arbeitsgruppe Diskrete Geometrie at FU Berlin for their hospitality. The first-named author was partially supported by the FONDECYT Regular grant 1221133. The second-named author was supported by the Austrian Science Fund FWF, grant P 33278. The third-named author was partially supported by the FONDECYT Iniciación grant 11221076.

2. Preliminaries and notation

An (affine) hyperplane in $\mathbb{R}^{d}$ can be written as $\mathrm{H}_{\mathbf{u},\alpha}:=\{\mathbf{x}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{x},\mathbf{u}\rangle=\alpha\}$ , where $\mathbf{u}\in\mathbb{R}^{d}$ is a nonzero vector and $\alpha\in\mathbb{R}$ is any real scalar. Every affine hyperplane defines two open halfspaces (we informally call them sides):

\mathrm{H}^{+}_{\mathbf{u},\alpha}:=\{\mathbf{x}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{x},\mathbf{u}\rangle>\alpha\},\text{ and}\quad\mathrm{H}^{-}_{\mathbf{u},\alpha}:=\{\mathbf{x}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{x},\mathbf{u}\rangle<\alpha\}.

The positive and negative parts are exchanged if we replace $\mathbf{u}$ by $-\mathbf{u}$ and $\alpha$ by $-\alpha$ . We denote their closures $\mathrm{H}^{\geq}_{\mathbf{u},\alpha}=\mathrm{H}^{+}_{\mathbf{u},\alpha}\cup\mathrm{H}_{\mathbf{u},\alpha}$ and $\mathrm{H}^{\leq}_{\mathbf{u},\alpha}=\mathrm{H}^{-}_{\mathbf{u},\alpha}\cup\mathrm{H}_{\mathbf{u},\alpha}$ , and we often omit the subscripts $\mathbf{u},\alpha$ . We say a hyperplane $\mathrm{H}$ is tangent to (or supporting of) a set $S\subset\mathbb{R}^{d}$ if $S\cap\mathrm{H}$ is nonempty and $S$ is contained in one of the two closed halfspaces defined by $\mathrm{H}$ .

An affine linear subspace $\mathrm{L}$ of dimension $k$ is called a $k-$ flat. Notice that there is a unique $d-$ flat in $\mathbb{R}^{d}$ which is the whole space. For $k<d$ a $k-$ flat $\mathrm{L}$ is tangent at $\mathrm{K}$ if $\mathrm{L}$ is contained in a tangent hyperplane to $\mathrm{K}$ and $\mathrm{L}\cap\mathrm{K}$ is nonempty. By convention, the ambient space $\mathbb{R}^{d}$ , the unique $d-$ flat, is tangent to every convex body.

We denote the topological interior of a set $S$ by $\operatorname{int}(S)$ and its closure by $\operatorname{cl}(S)$ . A convex body $\mathrm{K}\subseteq\mathbb{R}^{d}$ is a compact convex set with $\operatorname{int}(\mathrm{K})\neq\emptyset$ . The set of all convex bodies in $\mathbb{R}^{d}$ is denoted $\mathcal{K}^{d}$ . Two convex bodies $\mathrm{K}_{1}$ and $\mathrm{K}_{2}$ are separated if there exists a hyperplane $\mathrm{H}$ such that $\mathrm{K}_{1}\subseteq\mathrm{H}^{\geq}$ and $\mathrm{K}_{2}\subseteq\mathrm{H}^{\leq}$ . If $\geq,\leq$ can be replaced by $+,-$ , then the separation is called strict. A convex body $\mathrm{K}$ is said to be strictly convex if its intersection with each of its tangent hyperplanes is a singleton. Unit closed balls are strictly convex, polytopes are not.

In [2] and [5]; they used a different definition of separated, they call a family of subsets $\mathbf{S}=\{\mathrm{S}_{1},\dots,\mathrm{S}_{m}\}\subseteq\mathcal{K}^{d}$ separated if for every $n$ -dimensional affine subspace, with $1\leq n\leq d-2$ , intersects at most $n+1$ members of $\mathbf{S}$ . This notion of separation is equivalent to what we define as strong separation (see [2, Lemma 1] for one direction).

Sometimes it is more useful to use cones instead of convex bodies A family of cones $\mathbf{C}=\{\mathrm{C}_{1},\dots,\mathrm{C}_{k}\}$ in $\mathbb{R}^{d}$ is said to be acyclic if there is no linear dependence on $\operatorname{cone}(\mathbf{C})$ with all coefficients positive. See [22, Chapter 6.2] for more information.

Any family of convex bodies $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{k}\}$ in $\mathbb{R}^{d}$ can be turned into an acyclic family of cones in $\mathbb{R}^{d+1}$ by defining $\mathrm{C}_{i}:=\operatorname{cone}(\mathrm{K}_{i},1)$ over each convex body. We call this construction the linearization of $\mathbf{K}$ . Conversely, for any acyclic family of cones $\mathbf{C}=\{\mathrm{C}_{1},\dots,\mathrm{C}_{k}\}$ in $\mathbb{R}^{d+1}$ , there exists some hyperplane $\mathrm{H}$ that intersects the interior of each $\mathrm{C}_{i}$ . The family defined by $\mathrm{K}_{i}:=\mathrm{C}_{i}\cap\mathrm{H}$ consists of convex bodies in $\mathrm{H}\cong\mathbb{R}^{d}$ .

2.1. Polarity

We always assume that the origin is in the interior of the convex body under consideration. We define the polar of the body $\mathrm{K}$ to be

\mathrm{K}^{\circ}:=\{\mathbf{y}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{y},\mathbf{x}\rangle\leq 1\,\text{for every }\mathbf{x}\in\mathrm{K}\}.

Intuitively, the polar is the set of valid inequalities. Polarity allow us to exchange boundary points and supporting hyperplanes.

•

We have $\mathbf{y}\in\partial\mathrm{K}^{\circ}$ if and only if there exists an $\mathbf{x}\in\mathrm{K}$ with $\langle\mathbf{y},\mathbf{x}\rangle=1$ .
•

The hyperplane $\{\mathbf{y}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{y},\mathbf{x}\rangle\leq 1\}$ is supporting for $\mathrm{K}^{\circ}$ if and only if $\mathbf{x}\in\partial\mathrm{K}$ .

2.2. Visibility

Let $\mathrm{H}\subset\mathbb{R}^{d}$ be a hyperplane and $\mathbf{a}\notin\mathrm{H}$ . We define the projection away from $\mathbf{a}$ to $\mathrm{H}$ as the function

\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\cdot):\mathbb{R}^{d}\to\mathrm{H}\cong\mathbb{R}^{d-1},\quad\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathbf{x})=\textrm{aff. span}(\mathbf{a},\mathbf{x})\cap\mathrm{H}.

(2.1)

The range of this function is equal to $\mathrm{H}$ which can be identified with $\mathbb{R}^{d-1}$ . Its domain is $\mathbb{R}^{d}\backslash\mathrm{H}_{\mathbf{a}}$ where $\mathrm{H}_{\mathbf{a}}$ is the hyperplane parallel to $\mathrm{H}$ passing through $\mathbf{a}$ .

Definition 2.1.

Let $\mathrm{K}\subseteq\mathcal{K}^{d}$ and $\mathbf{a}\notin\mathrm{K}$ . We say that $\mathbf{q}\in\mathrm{K}$ is visible from $\mathbf{a}$ if $\mathrm{K}\cap[\mathbf{q},\mathbf{a}]=\{\mathbf{q}\}$ , otherwise we say $\mathbf{q}$ is covisible from $\mathbf{a}$ . The set of visible points in $\mathrm{K}$ from $\mathbf{a}$ is denoted $\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ . We call a subset $S$ of $\mathrm{K}$ visible if there exists $\mathbf{a}$ such that $\operatorname{V}_{\mathbf{a}}(\mathrm{K})=S$ . The closure of the complement of a visible set is called a covisible set.

Remark 2.2.

It is often convenient to not concern ourselves with the difference between visibility and covisibility and treat them on equal footing. Any visible (resp. covisible) set can be transformed into a covisible (resp. visible) set by a projective transformation.

Most of the time we can check visibility by the existence of certain tangent hyperplanes.

Lemma 2.3.

Let $\mathrm{K}\subseteq\mathcal{K}^{d}$ and $\mathbf{a}\notin\mathrm{K}$ . We have that if $\mathbf{q}\in\operatorname{int}(\operatorname{V}_{\mathbf{a}}(\mathrm{K}))$ then there exists a hyperplane $\mathrm{H}$ tangent at $\mathbf{q}$ strictly separating $\operatorname{int}(\mathrm{K})$ and $\mathbf{a}$ .

Proof.

Assume $\mathbf{q}$ is visible from $\mathbf{a}$ then the convex half-open segment $[\mathbf{a},\mathbf{q})$ is disjoint from $\mathrm{K}$ . By the Separation Theorem [16, Theorem 1.3.7] there exists a hyperplane $\mathrm{H}$ separating $\mathrm{K}$ and $[\mathbf{a},\mathbf{q})$ which contains $\mathbf{q}$ by construction. Note that $\mathbf{a}\notin\mathrm{H}$ since otherwise $\mathbf{q}\in\partial\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ . So $\mathrm{H}$ is the desired hyperplane. ∎

Remark 2.4.

The converse of Lemma 2.3 is not true. If $\mathrm{K}$ is a triangle in the plane and $\mathbf{a}$ is a point that sees a single edge $[\mathbf{q}_{1},\mathbf{q}_{2}]$ then both $\mathbf{q}_{1},\mathbf{q}_{2}$ are not in the interior of the visibility region but the span of the segment is a hyperplane satisfying the conditions of the Lemma.

We define the witness set for $\mathrm{K}\in\mathcal{K}^{d}$ and $S\subset\partial\mathrm{K}$ :

\operatorname{Wit}_{\mathrm{K}}(S):=\{\mathbf{a}\in\mathbb{R}^{d}~{}:~{}\operatorname{V}_{\mathbf{a}}(\mathrm{K})=S\}.

(2.2)

Lemma 2.3 allow us to describe witness sets.

Lemma 2.5.

Let $\mathrm{K}\in\mathcal{K}^{d}$ and $S\subset\partial\mathrm{K}$ . We define a collection of halfspaces $\mathcal{H}$ as follows:

(1)

It contains $\mathrm{H}^{>}$ for every hyperplane $\mathrm{H}$ tangent to $\mathrm{K}$ at $\mathbf{q}\in\operatorname{int}(S)$ and such that $\mathrm{K}\subset\mathrm{H}^{\leq}$ .
(2)

It contains $\mathrm{H}^{\leq}$ for every hyperplane $\mathrm{H}$ tangent to $\mathrm{K}$ at $\mathbf{q}\in\partial\mathrm{K}\backslash\operatorname{int}(S)$ and such that $\mathrm{K}\subset\mathrm{H}^{\leq}$ .

We have that $\bigcap\mathcal{H}=\operatorname{Wit}_{\mathrm{K}}(S)$ . In particular, witness sets are convex.

Proof.

Let $\mathbf{a}\in\bigcap\mathcal{H}$ then the first condition one ensures that $\operatorname{int}(S)\subseteq\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ . Lemma 2.3 implies that $\partial\mathrm{K}\backslash\operatorname{int}(S)$ is disjoint from $\operatorname{int}(\operatorname{V}_{\mathbf{a}}(\mathrm{K})))$ . Since $\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ is always closed these conditions imply that it is equal to $S$ , so that $\bigcap\mathcal{H}\subseteq\operatorname{Wit}_{\mathrm{K}}(S)$ .

Conversely for any $\mathbf{a}\in\operatorname{Wit}_{sK}(S)$ we have by Lemma 2.3 that $\mathbf{a}$ is in all halfspaces of $\mathcal{H}$ , and so $\operatorname{Wit}_{\mathrm{K}}(S)\subseteq\bigcap\mathcal{H}$ . ∎

We shall use the following result due to Ewald, Larman, Rogers [7] (see also [16, Section 2.3]) that was later generalized by Zalgaller [21].

Theorem 2.6 (Ewald, Larman, Rogers ).

Let $\mathrm{K}\in\mathcal{K}^{d}$ . The set of vectors $\mathbf{u}\in\mathbb{S}^{d-1}$ such that there is a $1-$ flat parallel to $\mathbf{u}$ tangent to $\mathrm{K}$ at more than one point has measure zero in the unit sphere $\mathbb{S}^{d-1}$ . As a consequence, a generic orthogonal projection $\pi$ into a hyperplane $\mathrm{H}$ induces an homeomorphism between $\partial\pi(\mathrm{K})$ and its preimage.

The following Lemma is the key tool for our proof of Theorem A.

Proposition 2.7.

Let $\mathbf{a}\notin\mathrm{K}$ be a generic point and $\mathrm{H}$ hyperplane strictly separating $\mathbf{a}$ from $\mathrm{K}$ , then $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\cdot)$ maps $\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ into a convex set $\mathrm{M}\subset\mathrm{H}$ and induces an homeomorphism between $\partial\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ and $\partial\mathrm{M}$ .

Let $\mathbf{b}\in\mathbb{R}^{d}$ be another point such that $\operatorname{V}_{\mathbf{a}}(\mathrm{K})\subset\operatorname{V}_{\mathbf{b}}(\mathrm{K})$ and $\mathbf{b}^{\prime}=\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathbf{b})\notin\mathrm{M}$ . Let $\mathrm{H}_{\mathbf{a}}$ be the hyperplane parallel to $\mathrm{H}$ passing through $\mathbf{a}$ . If $\mathbf{b}$ is in the same side as $\mathrm{K}$ with respect to $\mathrm{H}_{\mathbf{a}}$ , then

\mathbf{q}\in\partial\bigg{(}\operatorname{V}_{\mathbf{b}}(\mathrm{K})\backslash\operatorname{V}_{\mathbf{a}}(\mathrm{K})\bigg{)}\cap\partial\operatorname{V}_{\mathbf{a}}(\mathrm{K})\Longrightarrow\mathbf{q}^{\prime}\in\operatorname{V}_{\mathbf{b}^{\prime}}(\mathrm{M}),

(2.3)

where $\mathbf{q}^{\prime}=\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathbf{q})$ . On the other hand, if $\mathbf{b}$ is in the opposite side as $\mathrm{K}$ with respect to $\mathrm{H}_{\mathbf{a}}$ , then

\mathbf{q}\in\partial\bigg{(}\operatorname{V}_{\mathbf{b}}(\mathrm{K})\backslash\operatorname{V}_{\mathbf{a}}(\mathrm{K})\bigg{)}\cap\partial\operatorname{V}_{\mathbf{a}}(\mathrm{K})\Longrightarrow\mathbf{q}^{\prime}\in\mathrm{M}\backslash\operatorname{V}_{\mathbf{b}^{\prime}}(\mathrm{M}).

(2.4)

Proof.

For the first part we apply a projective transformation sending $\mathbf{a}$ to a point at infinity. In this case $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}$ is an orthogonal projection to a generic $\mathrm{H}$ . Theorem 2.6 implies the first part of the statement. In particular we can assume that for every $\mathbf{q}\in\partial\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ the line $\mathrm{L}$ spanned by $\mathbf{a}$ and $\mathbf{q}$ is tangent at $\mathrm{K}$ only at $\mathbf{q}$ . Now we prove the second part.

We reduce to a two dimensional case. If $\mathbf{b}\in\mathrm{L}$ , consider any $2-$ flat $\mathrm{F}$ containing $\mathrm{L}$ intersecting the interior of $\mathrm{K}$ If $\mathbf{b}\notin\mathrm{L}$ , consider the $2-$ flat $\mathrm{F}$ spanned by $\mathrm{L}$ and $\mathbf{b}$ . We restrict to $\mathrm{F}\cong\mathbb{R}^{2}$ which we identify with the xy-plane. We obtain a convex body $\mathrm{K}^{\prime}=\mathrm{K}\cap\mathrm{F}$ with a point $\mathbf{q}$ in the boundary and the line $\mathrm{L}$ that we can assume to be the y-axis. If a point $\mathbf{p}\in\mathrm{K}\cap\mathrm{L}$ is visible from $\mathbf{b}$ in $\mathbb{R}^{d}$ , then it is also visible when restricted to $\mathrm{F}$ . The condition of Equation (2.3) implies that for every open ball $\mathrm{B}$ centered in $\mathbf{q}$ the sets $\mathrm{B}\cap\operatorname{V}_{\mathbf{a}}(\mathrm{K})$ and $\mathrm{B}\cap(\operatorname{V}_{\mathbf{b}}(\mathrm{K})\backslash\operatorname{V}_{\mathbf{a}}(\mathrm{K}))$ are both nonempty and are contained in $\mathrm{B}\cap\operatorname{V}_{\mathbf{b}}(\mathrm{K})$ . When restricting to $\mathbb{R}^{2}$ these conditions imply that $\mathbf{b}$ sees points arbitrarily close to $\mathbf{q}$ from both directions (up and down). It follows that that $\mathbf{b}$ must be strictly to the right side of $\mathrm{L}$ , see Figure 2 (in particular, it follows that $\mathbf{b}$ cannot be in $\mathrm{L}$ ).

Note that supporting hyperplanes at $\mathbf{q}^{\prime}$ in the projection are in bijection with supporting hyperplanes in $\mathbb{R}^{d}$ containing $\mathrm{L}$ . Since $\operatorname{V}_{\mathbf{b}}(\mathrm{K})$ is closed it is enough to assume that $\mathbf{q}\in\operatorname{int}(\operatorname{V}_{\mathbf{b}}(\mathrm{K}))$ on the left hand side of Equations (2.3)–(2.4). This implies that any hyperplane $\mathrm{H}^{\prime}$ containing $\mathrm{L}$ will not contain $\mathbf{b}$ , and there are two cases:

(1)

If $\mathbf{b}$ is and $\mathrm{K}$ are on the same side relative to $\mathrm{H}_{\mathbf{a}}$ , then in the projection $\mathbf{q}^{\prime}$ is visible from $\mathbf{b}^{\prime}$ .
(2)

If $\mathbf{b}$ is and $\mathrm{K}$ are on opposite sides relative to $\mathrm{H}_{\mathbf{a}}$ , then $\mathbf{q}^{\prime}$ is covisible from $\mathbf{b}^{\prime}$ .

∎

Figure 2. A reduction to the two dimensional case. The hyperplanes

\mathrm{H}

and

\mathrm{H}_{\mathbf{a}}

are dotted in the figure. There are two points

\mathbf{b}

representing the two cases in the proof.

3. Proof of Theorem A

We first use polarity to transform the problem.

Definition 3.1.

Let $m>1$ be an integer. A convex body $\mathrm{Q}$ has a proper $m-$ coloring if $\partial\mathrm{Q}$ can be covered with sets $\mathcal{C}_{1},\dots,\mathcal{C}_{m}$ such that

(1)

$\operatorname{int}(\mathcal{C}_{i})\cap\operatorname{int}(\mathcal{C}_{j})=\emptyset$ for each $1\leq i<j\leq m$ .
(2)

For every subset $\emptyset\subsetneq S\subsetneq[m]$ the set $\bigcup_{j\in S}\mathcal{C}_{j}$ is either visible or covisible. If visible, then the set of witness points has nonempty interior.

Remark 3.2.

Notice that in particular each set $\mathcal{C}_{i}$ is visible/covisible. It follows that $\mathcal{C}_{i}$ is homeomorphic to a $(d-1)$ -dimensional ball.

Given a properly colored convex body $\mathrm{Q}$ we call the set $\textrm{Rainbow}(\mathrm{Q})=\bigcap_{[m]}\mathcal{C}_{i}$ its rainbow set. Recall that $\mathcal{T}(\mathbf{K})$ is the set of all hyperplanes tangent to $\mathbf{K}$ and with all bodies on the same side.

Proposition 3.3.

Let $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{m}\}\subset\mathcal{K}^{d}$ be a strictly separated family of convex bodies. There exists a $d$ -dimensional convex body $\mathrm{Q}$ with a proper $m-$ coloring such that $\mathcal{T}(\mathbf{K})$ is homeomorphic to $\textrm{Rainbow}(\mathrm{Q})$ .

Proof.

Given a family $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{m}\}\subset\mathcal{K}^{d}$ of strongly separated convex bodies in $\mathbb{R}^{d}$ , we consider its convex hull $\mathrm{K}=\operatorname{conv}(\mathbf{K})$ which has nonempty interior. By translating if necessary we assume that $\mathbf{0}$ is in the interior of $\mathrm{K}$ . We consider the polar body $\mathrm{Q}:=\mathrm{K}^{\circ}$ .

Every point $\mathbf{x}\in\partial\mathrm{K}$ induces the supporting hyperplane $\{\mathbf{y}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{y},\mathbf{x}\rangle=1\}$ on $\mathrm{Q}$ . We define $\mathcal{C}_{i}\subset\partial\mathrm{Q}$ to be the union of the intersections of $\mathrm{Q}$ with all supporting hyperplanes induced points in $\mathrm{K}_{i}$ .

Figure 3. Illustration of the polarity in Proposition 3.3.

We claim that the strong separation for $\mathbf{K}$ implies that the union of $\mathcal{C}_{i}$ for $i\in I$ is either visible or covisible: Let $\mathbf{z}$ be a vector such that the hyperplane $\{\mathbf{x}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{z},\mathbf{x}\rangle=1\}$ strictly separates colors $I$ from the complement. We have that

\langle\mathbf{z},\mathbf{x}\rangle<1,\forall\mathbf{x}\in\bigcup_{I^{c}}\mathrm{K}_{i},\quad\langle\mathbf{z},\mathbf{x}\rangle>1,\forall\mathbf{x}\in\bigcup_{I}\mathrm{K}_{i}.

(3.1)

(1)

Let $\mathbf{q}\in\mathcal{C}_{i}\subset\mathrm{Q}$ with $i\in I$ . By definition there exists $\mathbf{x}\in\mathrm{K}_{i}$ , such that $\langle\mathbf{q},\mathbf{x}\rangle=1$ . Since $\langle\mathbf{p},\mathbf{x}\rangle\leq 1$ for all $\mathbf{p}\in\mathrm{Q}$ but $\langle\mathbf{z},\mathbf{x}\rangle>1$ , the hyperplane $\{\mathbf{y}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{y},\mathbf{x}\rangle=1\}$ certifies that $\mathbf{q}$ is visible from $\mathbf{z}$ according to Lemma 2.3.
(2)

Let $\mathbf{q}\notin\mathcal{C}_{i}\subset\mathrm{Q}$ for every $i\in I$ . For any supporting hyperplane of $\mathrm{Q}$ at $\mathbf{q}$ we have an equation $\langle\mathbf{q},\mathbf{x}\rangle=1$ with $\mathbf{x}\notin\bigcup_{I}\mathcal{C}_{i}$ . For each of them we have $\langle\mathbf{p},\mathbf{x}\rangle\leq 1$ for all $\mathbf{p}\in\mathrm{Q}$ and $\langle\mathbf{z},\mathbf{x}\rangle<1$ , so by Lemma 2.3 then $\mathbf{q}$ is not visible from $\mathbf{z}$ .

In conclusion we have that $\operatorname{V}_{\mathbf{z}}(\mathrm{Q})=\bigcup_{I}\mathcal{C}_{i}$ . Equation 3.1 is an open condition of $\mathbf{z}$ , hence the set of witnesses has non empty interior. Finally, since elements of $\mathcal{T}(\mathbf{K})$ are tangent to all $\mathrm{K}_{i}$ , the dual of these hyperplanes are points which lie in each $\mathcal{C}_{i}$ , the definition of $\textrm{Rainbow}(\mathrm{Q})$ . ∎

Remark 3.4.

The case of polytopes is simpler. Given a strongly separated family $\mathbf{P}$ of $m$ full dimensional polytopes in $\mathbb{R}^{d}$ , let $\mathrm{P}=\operatorname{conv}\{\mathbf{P}\}$ be their convex hull. We think of vertices of the polytope $\mathrm{P}_{j}$ as being of color $j$ , so that the vertices of $\mathrm{P}$ are colored with the set $[m]$ and we are interested in the faces that contain a vertex of every color. Let $\mathrm{Q}=\mathrm{P}^{\circ}$ be the polar of $\mathrm{P}$ . We color each facet with the color of the corresponding vertex. In this case we always have that the witness points for a visibility region has nonempty interior.

We have not defined a proper $1-$ coloring, since the whole boundary of $\mathrm{Q}$ is neither visible nor covisible. The case $m=1$ in Theorem A is trivial, as any $\mathbf{u}\in\mathbb{S}^{d-1}$ defines a tangent hyperplane. When $m>1$ Proposition 3.3 reduces Theorem A to the following statement.

Theorem 3.5.

Let $\mathrm{Q}\in\mathcal{K}^{d}$ with a proper $m-$ coloring. Then its rainbow set is homeomorphic to $\mathbb{S}^{d-m}$ .

We will prove Theorem 3.5 by induction on $m$ . We use Proposition 2.7 to lower the dimension, so we first verify that the conditions apply to our set up. To ease notation se write $\operatorname{Wit}_{\mathrm{Q}}(A)$ for $\operatorname{Wit}_{\mathrm{Q}}(\bigcup_{a\in A}\mathcal{C}_{a})$ whenever $A\subset[m]$ .

Lemma 3.6.

Let $\mathrm{Q}\in\mathcal{K}^{d}$ be a convex body with a proper $m-$ coloring. Let $\mathbf{a}\operatorname{Wit}_{\mathrm{Q}}(\{m\})$ , and $\mathrm{H}$ a separating hyperplane. For any nonempty $J\subsetneq[m-1]$ , let $I=J\cup\{m\}$ . The set $\operatorname{Wit}_{\mathrm{Q}}(I)$ contains an open ball $\mathrm{B}$ such that $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathrm{B})$ is disjoint from $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathcal{C}_{m})$ .

Before the proof we note that it is not true that the whole $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\operatorname{Wit}_{\mathrm{Q}}(I))$ is disjoint from $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathcal{C}_{m})$ .

Proof.

Without loss of generality assume that $1\notin J$ and after a projective transformation we can assume that $\mathcal{C}_{1}$ is covisible, so that its complement is visible, in particular we can assume that $\bigcup_{I}\mathcal{C}_{i}$ is visible.

We use the description of $\operatorname{Wit}_{\mathrm{Q}}(I)$ in Lemma 2.5. There exists a hyperplane $\mathrm{H}$ that is tangent to a $\mathbf{q}\in\operatorname{int}(\mathcal{C}_{m})$ and also to $\operatorname{Wit}_{\mathrm{Q}}(I)$ (otherwise $\operatorname{Wit}_{\mathrm{Q}}(I)=\operatorname{Wit}_{\mathrm{Q}}(J)$ ). Consider a sufficiently small open ball $\mathrm{B}$ in $\operatorname{Wit}_{\mathrm{Q}}(I)$ such that $d(\mathrm{B},\mathrm{H})<d(\mathbf{a},\mathrm{H})$ . We claim that the line $\mathrm{L}$ spanned by $\mathbf{a}$ and any $\mathbf{b}\in\mathrm{B}$ do not intersect $\mathrm{K}$ which would conclude the proof.

Let $\mathrm{H}^{\prime}$ be a hyperplane tangent to a point $\mathbf{p}\in\operatorname{int}(\bigcup_{J}\mathcal{C}_{j})$ that is also tangent to $\operatorname{Wit}_{\mathrm{Q}}(I)$ . The segment $[\mathbf{a},\mathbf{b}]$ intersects $\mathrm{H}^{\prime}$ in a point $\mathbf{c}$ . So we analyze the line $\mathrm{L}$ in two sections:

(1)

In the ray from $\mathbf{c}$ containing $\mathbf{b}$ its does not intersect $\mathrm{K}$ because it stays on the opposite side of $\mathrm{K}$ with respect to $\mathrm{H}$ .
(2)

In the ray from $\mathbf{c}$ containing $\mathbf{a}$ it does not intersect $\mathrm{K}$ for because it stays on the opposite side of $\mathrm{K}$ with respect to $\mathrm{H}^{\prime}$ .

∎

The following Proposition is the inductive step we need.

Proposition 3.7.

Let $\mathrm{Q}\in\mathcal{K}^{d}$ with a proper $m-$ coloring. There exists a convex body $\mathrm{Q}^{\prime}\subset\mathbb{R}^{d-1}$ with a proper $(m-1)-$ coloring such that $\textrm{Rainbow}(\mathrm{Q})$ is homeomorphic $\textrm{Rainbow}(\mathrm{Q}^{\prime})$ .

Proof.

The set $\operatorname{Wit}_{\mathrm{Q}}(\{m\})$ contains an open set, so we can pick a witness point $\mathbf{a}$ and hyperplane $\mathrm{H}$ separating $\mathbf{a}$ from $\mathrm{Q}$ that are sufficiently generic to apply Proposition 2.7.

The projection $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}$ maps $\mathcal{C}_{m}$ into a convex body $\mathrm{Q}^{\prime}$ . We claim that $\mathrm{Q}^{\prime}$ has a proper $(m-1)-$ coloring. For $i\in\{1,\dots,m-1\}$ let $\mathcal{C}^{\prime}_{i}$ be the image of $\mathcal{C}_{m}\cap\mathcal{C}_{i}\subset\partial\mathcal{C}_{m}$ under the projection $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}$ .

(1)

The interiors of $\mathcal{C}^{\prime}_{i}$ and $\mathcal{C}^{\prime}_{j}$ are disjoint because the interiors of $\mathcal{C}_{m}\cap\mathcal{C}_{i}$ and $\mathcal{C}_{m}\cap\mathcal{C}_{j}$ are disjoint. These intersections are equal to $\partial\mathcal{C}_{m}\cap\partial\mathcal{C}_{i}$ and $\partial\mathcal{C}_{m}\cap\partial\mathcal{C}_{j}.$ If $\mathbf{p}$ is a point in the intersection, then every open ball $\mathrm{B}$ centered in $\mathbf{p}$ intersects the interiors of $\mathcal{C}_{m},\mathcal{C}_{j},$ and $\mathcal{C}_{i}$ . This implies that $\mathbf{p}$ lies on the boundary of $\mathcal{C}_{m}\cup\mathcal{C}_{j}$ and thus on the boundary of $\mathcal{C}_{m}\cap\mathcal{C}_{j}$ , and the same for $i$ .

(2)

Let $J\subsetneq[m-1]$ and $I=J\cup\{m\}$ . By the same arguments as in the proof of Lemma 3.6 we can assume that both sets are visible. By Lemma 3.6 there exists an open ball of witness points $\mathbf{b}$ of the set $J$ , satisfying the hypotheses of Proposition 2.7. We have

\bigcup_{J}(\mathcal{C}_{i}\cap\mathcal{C}_{m})=\left(\bigcup_{J}\mathcal{C}_{i}\right)\cap\mathcal{C}_{m}=\partial\left(\bigcup_{J}\mathcal{C}_{i}\right)\cap\partial\mathcal{C}_{m},

since the interiors are disjoint. Also note that

\bigcup_{J}\mathcal{C}_{i}=\operatorname{cl}\left(\operatorname{V}_{\mathbf{b}}(\mathrm{Q})\backslash\operatorname{V}_{\mathbf{a}}(\mathrm{Q})\right),\quad\mathcal{C}_{m}=\operatorname{V}_{\mathbf{a}}(\mathrm{Q})

so by the second part of Proposition 2.7, we have

\mathbf{q}\in\bigcup_{J}(\mathcal{C}_{i}\cap\mathcal{C}_{m})\Longrightarrow\mathbf{q}^{\prime}\in\operatorname{V}_{\mathbf{b}^{\prime}}(\mathrm{M}),

where $\mathbf{q}^{\prime}$ and $\mathbf{b}^{\prime}$ are the projections of $\mathbf{q}$ and $\mathbf{b}$ respectively under $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}$ . It follows that $\mathbf{b}^{\prime}$ is a witness for the visibility(or covisibility) of $\bigcup_{J}\mathcal{C}^{\prime}_{j}$ . Furthermore, by assumption the set of such $\mathbf{b}$ had a non empty interior, so the image also have a nonempty interior.

Finally, by the first part of Proposition 2.7 the map $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}$ is an homeomorphism on the boundary. This homeomorphism restritcs to an homeomorphism between each set of colors and thus between the rainbow sets. ∎

The second condition in Definition 3.1 is used to ensure that $\mathbf{a}$ can be chosen to be generic which is an important hypothesis of the Theorem 2.6 that we use in Proposition 2.7.

Remark 3.8.

In the case where each convex body is a polytope we can find a projection center $\mathbf{a}$ as follows: Continuing with Remark 3.4, the polar $\mathrm{Q}$ is a polytope. Each facet of $\mathrm{Q}$ has an assigned color in $[m]$ and it is the intersection of an affine linear hyperplane $\{\mathbf{x}\in\mathbb{R}^{d}~{}:~{}\langle\mathbf{u},\mathbf{x}\rangle=b\}$ with $\mathrm{P}$ . We can assume that $\langle\mathbf{u},\mathbf{x}\rangle\leq b$ for all points in $\mathrm{P}$ . A point $\mathbf{a}$ outside of $\mathrm{Q}$ that sees only the facets of color $m$ is characterized by the following finite linear strict inequalities:

•

$\langle\mathbf{u},\mathbf{a}\rangle<b$ if the corresponding facet is not of color $m$ .
•

$\langle\mathbf{u},\mathbf{a}\rangle>b$ if the corresponding facet is of color $m$ .

To find such $\mathbf{a}$ we need to find a solution of a finite system of linear inequalities. This problem is equivalent to solving a linear program [17, Theorem 10.4], so it can be solved efficiently using the simplex method or any other linear programming algorithm.

We are now in position to prove our dual statement.

Proof of Theorem 3.5.

By using Proposition 3.3 and Lemma 3.7 we can reduce to the case where $\mathrm{Q}$ is a convex body in $\mathbb{R}^{d-m+2}$ with a proper 2-coloring. In this case by the visibility of one of the colors we have a generic point $\mathbf{a}$ such that the boundary of $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathrm{Q})$ is homeormophic to its rainbow set. But $\operatorname{Pr}_{\mathbf{a},\mathrm{H}}(\mathrm{Q})$ is a convex body in $\mathbb{R}^{d-m+1}$ so its boundary is homeomorphic to $\mathbb{S}^{d-m}$ . ∎

Remark 3.9.

The case $m=d$ of Theorem 3.5 is similar to the Knaster–Kuratowski–Mazurkiewicz Lemma [12]. For related results see an extension by Shapley [18] with an alternative proof by Komiya [13] and a recent generalization by Frick and Zerbib [8].

Example 3.10.

Strong separation is crucial to the statement of Theorem A since otherwise we can have an arbitrary number of tangents.

Consider an $N$ -agon $\mathrm{Q}$ in $\mathbb{R}^{2}$ with vertices in the unit circle. Embed $\mathbb{R}^{2}$ in $\mathbb{R}^{3}$ by setting the last coordinate equal to zero. We define the following family of convex bodies. Let

(1)

$\mathrm{P}$ be the pyramid over $\mathrm{Q}$ with apex $(0,0,1)$ .
(2)

$\mathrm{B}_{1}$ be the unit ball centered at $(0,0,10)$ .
(3)

$\mathrm{B}_{2}$ be the unit ball centered at $(0,0,-10)$ .

The family $\mathbf{K}=\{\mathrm{P},\mathrm{B}_{1},\mathrm{B}_{2}\}$ has three disjoint convex bodies (but it is not strongly separated) with $N$ common tangents. This highlights a difference with the algebraic approach in [20], where the number of common tangents to $d$ quadrics in $\mathbb{R}^{d}$ is either at most $2^{d}$ or infinite.

We briefly consider the situation where each individual body can be separated from the rest. The following example demonstrates that the result fails to hold.

Example 3.11.

Let $\mathbf{A}=\{\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3},\mathbf{p}_{4}\}\subseteq\mathbb{R}^{2}$ be a set the four vertices of a square oriented cyclically, so that the diagonals are $[\mathbf{p}_{1},\mathbf{p}_{3}]$ and $[\mathbf{p}_{2},\mathbf{p}_{4}]$ .

Consider the family of polytopes $\mathbf{P}=\{\mathrm{P}_{1},\mathrm{P}_{2},\mathrm{P}_{3},\mathrm{P}_{4}\}\subseteq\mathcal{K}^{4}$ where $\mathrm{P}_{1}=\mathbf{p}_{1}\times[-1,1]^{2},\mathrm{P}_{2}=\mathbf{p}_{2}\times[-2,2]^{2},\mathrm{P}_{3}=\mathbf{p}_{3}\times[-1,1]^{2},$ and $\mathrm{P}_{4}=\mathbf{p}_{4}\times[-2,2]^{2}$ . Every color can be separated from the rest by a hyperplane, but not all subsets can be separated. No facet of $\operatorname{conv}\{\mathbf{P}\}$ contains points from each polytope in the family.

Corollary 3.12.

Let $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{d}\}\subset\mathcal{K}^{d}$ be a family of strongly separated convex bodies in $\mathbb{R}^{d}$ . There exists exactly two hyperplanes tangent to each convex body and with all the bodies in the same side.

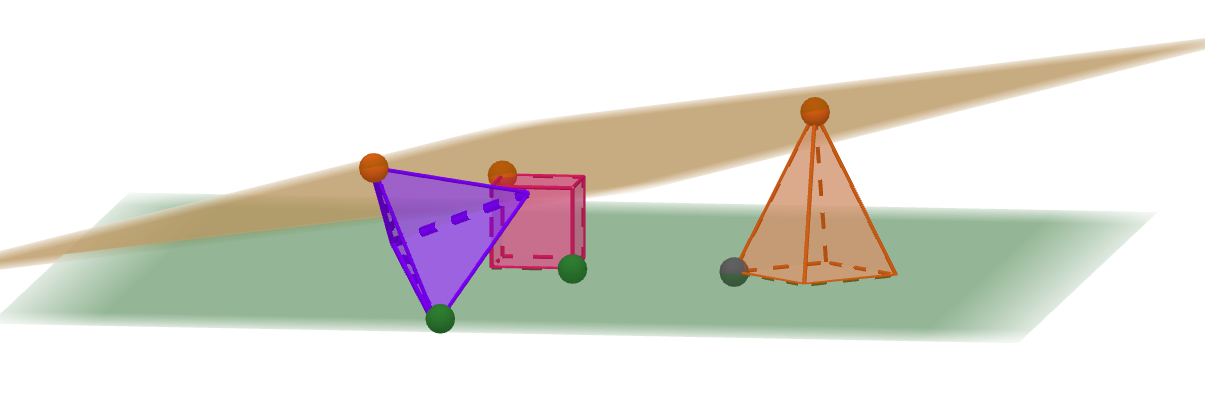
Refer to caption — Figure 4. Example of Corollary 3.12 with three polytopes in $\mathbb{R}^{3}$

Theorem 3.13.

Let $\mathbf{P}=\{\mathrm{P}_{1},\dots,\mathrm{P}_{m}\}\subset\mathcal{K}^{d}$ be a family of strongly separated full dimensional polytopes in $\mathbb{R}^{d}$ where $m\leq d$ . The set $\mathcal{T}(\mathbf{P})$ is a polytopal complex combinatorially equivalent to the boundary of a $d-m+1$ dimensional polytope.

Proof.

As mentioned in Remark 3.4, the polar $\mathrm{Q}$ is also polytopal and in the inductive step, Lemma 3.7, we reduce the number of colors by a projection. Since projections of polytopes are again polytopes we obtain the desired conclusion. ∎

4. Applications

4.1. Common tangents to $d$ convex bodies in $\mathbb{R}^{d}$

We now expand on the $m=d$ case of Theorem A with the goal of presenting an alternative Proof of Bisztriczky’s Theorem.

Theorem 4.1.

Let $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{d}\}\in\mathcal{K}^{d}$ be a family of strongly separated convex bodies in $\mathbb{R}^{d}$ . For each unordered set partition $A\sqcup B=[d]$ there exists exactly two affine hyperplanes $\mathrm{H}$ such that under an appropriate orientation of $\mathrm{H}$ :

•

$\mathrm{H}$ is tangent to each element of $\mathbf{K}$ .
•

$\bigcup_{a\in A}\mathrm{K}_{a}\subseteq\mathrm{H}^{\geq}$ .
•

$\bigcup_{b\in B}\mathrm{K}_{b}\subseteq\mathrm{H}^{\leq}$ .

Furthermore these affine hyperplanes are all different and thus there are $2^{d}$ tangent affine hyperplanes to the family $\mathbf{K}$ .

To prove the proposition, we first move into the linear setting, where the negation of a set changes its position with respect to some hyperplane. After we find a desired hyperplane in the linear setting, we return to the affine setting to finish the proof.

Proof.

We linearize the $\mathrm{K}_{i}$ to get a collection of cones $\mathrm{C}_{i}$ which is linearly spanning and acyclic. Furthermore, the $\mathrm{C}_{i}$ form a strongly separated family of cones¹¹1We call a family of cones strongly separated if their relative interiors are..

Let $\overline{\mathbf{C}}$ be the collection of cones which replaces $\mathrm{C}_{i}$ with $-\mathrm{C}_{i}$ for each $i\in B$ . Since the $\mathrm{C}_{i}$ are a strongly separated family, there is a hyperplane $\mathrm{H}_{\mathbf{a}}$ which separates $A$ and $B$ . The linearization of $\mathrm{H}_{\mathbf{a}}$ proves the acyclicity of $\overline{\mathbf{C}}$ . Every element of $B$ has been negated, so every cone lies on the same side of the linearized hyperplane. For some generic partition $D\sqcup E=[d]$ , by the strong separation of the $\mathrm{K}_{i}$ , there is a hyperplane $\mathrm{H}_{D}$ separating $D\Delta B$ from $E\Delta B$ , where $\Delta$ represents the symmetric difference. The linearization of $\mathrm{H}_{D}$ separates $D$ and $E$ in $\overline{\mathbf{C}}$ , since each element of $B$ swapped parts within the partition. This shows that $\overline{\mathbf{C}}$ is strongly separated as well.

We apply the Corollary 3.12 to the affinization of $\overline{\mathbf{C}}$ to get two affine hyperplanes that are tangent to each color with all points of this affinization on one side of the hyperplanes. By linearization, we obtain linear hyperplanes which are again tangent to each colored cone, and all cones $\{\mathrm{C}_{i}~{}:~{}i\in A\}\cup\{-\mathrm{C}_{i}~{}:~{}i\in B\}$ are on the positive side. Finally, undoing the negation of the cones in $B$ , and returning to the original affine setting, we have obtained two affine hyperplanes tangent to every $\mathrm{K}_{i}$ and such that it separates sets $A$ and $B$ .

From the $2^{d-1}$ partitions of $[d]$ we obtain $2^{d}$ common tangent hyperplanes. We simply need to conclude that all these hyperplanes are unique. Given two hyperplanes obtained from different partitions, there is a pair of bodies whose interiors are on a common side of one hyperplane, but separated by the other hyperplane, so no hyperplanes from different partitions can be the same. Since we already proved there are two distinct hyperplanes for each partition, there can be no repeated hyperplanes among the $2^{d}$ of them. ∎

Example 4.2.

In Figure 5 we illustrate an example of Theorem 4.1.

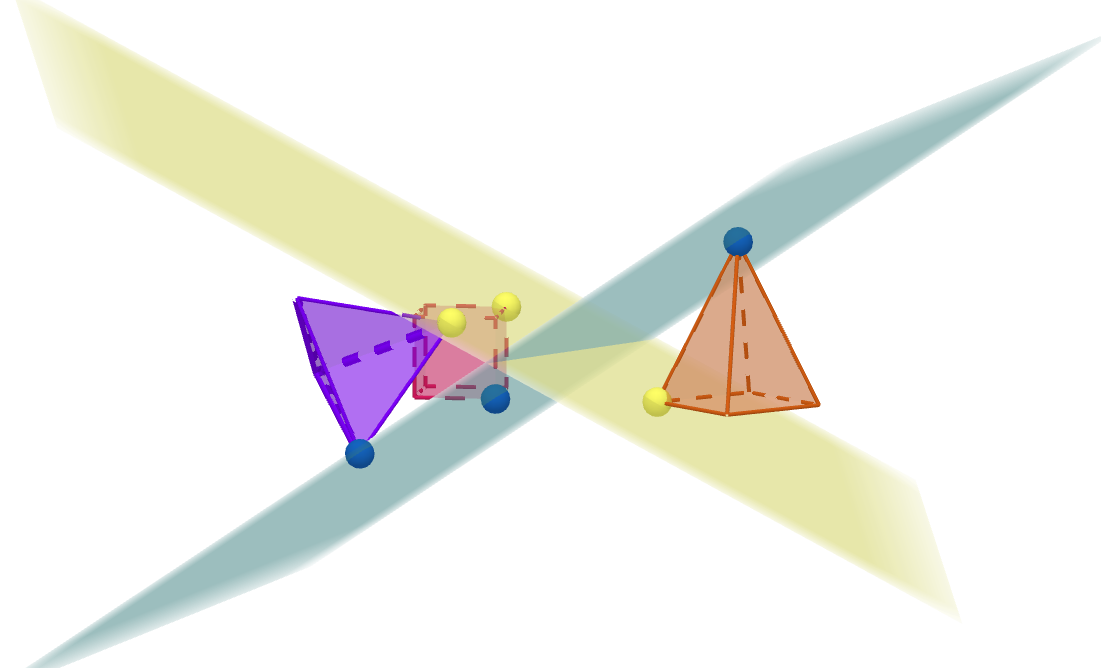
We finish this section with an open question.

Question 4.3.

Given two disjoint collections of partitions of $[n]$ , when is there a family of $n$ convex bodies in $\mathbb{R}^{n}$ , so that the first collection of partitions are all separated and none of the second collection of partitions are?

4.2. Collection of $d+1$ convex bodies

We first relax the conditions of Theorem 4.1 a little bit. We say a family $\mathrm{S}=\{\mathrm{S}_{1},\cdots,\mathrm{S}_{d}\}$ of compact convex sets in $\mathbb{R}^{d}$ is affinely spanning if $\operatorname{conv}(\mathrm{S})$ is full dimensional.

Proposition 4.4.

Let $\mathbf{S}=\{\mathrm{S}_{1},\cdots,\mathrm{S}_{d}\}$ be a strongly separated and affinely spanning family of compact convex sets in $\mathbb{R}^{d}$ . For each set partition $A\sqcup B=[d]$ there exists exactly two affine hyperplanes $\mathrm{H}$ such that:

•

$\mathrm{H}$ is tangent to each element of $\mathbf{K}$ .
•

$\bigcup_{a\in A}\mathrm{K}_{a}\subseteq\mathrm{H}^{\geq}$ .
•

$\bigcup_{b\in B}\mathrm{K}_{b}\subseteq\mathrm{H}^{\leq}$ .

Proof.

At the start of the proof of Proposition 3.3 we used the fact that the convex hull of a family of convex bodies is a convex body, that is it has a nonempty interior. This was needed to assume that $\mathbf{0}$ is in the interior which allowed us to take the polar body. With the extra assumption that $\operatorname{conv}(\mathbf{S})$ is full dimensional Theorem A still holds: by using Proposition 3.3 we can reduce it to Theorem 3.5. Then the proof of Theorem 4.1 applies in the present context without change, except that we cannot guarantee the hyperplanes are all different. ∎

Example 4.5.

As an example of the difference between Proposition 4.4 and Theorem 4.1 consider a triangle $\Delta\in\mathbb{R}^{2}$ and a disjoint point $\mathbf{p}$ . There exists two (as opposed to four) lines tangent to both of them

We cannot have a strongly separated family with $d+2$ or more convex sets in $\mathbb{R}^{d}$ since strong separation implies that their centroids are affinely independent. So we focus on the case with $d+1$ elements.

Proposition 4.6.

Let $\mathbf{S}=\{\mathrm{S}_{1},\dots,\mathrm{S}_{d+1}\}$ be a family of strongly separated convex bodies of $\mathbb{R}^{d}$ and let $A\sqcup B=[d+1]$ a set partition, together with a special element $a\in A$ . There exists a unique hyperplane $\mathrm{H}$ such that

(1)

$\mathrm{H}$ is tangent to $\mathbf{S}\setminus\mathrm{S}_{a}$ .
(2)

$\bigcup_{i\in A}\mathrm{S}_{i}\subseteq\mathrm{H}^{\geq}$ .
(3)

$\bigcup_{i\in B}\mathrm{S}_{i}\subseteq\mathrm{H}^{\leq}$ .
(4)

$\mathrm{S}_{a}\subseteq H^{+}$ .

Proof.

Without loss of generality we assume $a=d+1$ . Embed the family $\mathbf{S}=\{\mathrm{S}_{1},\dots,\mathrm{S}_{d+1}\}$ in $\mathbb{R}^{d+1}$ by using zero in the last coordinate, and additionally make a thickening of $\mathrm{S}_{d+1}$ : replace it by its Minkowski sum with the ball $\mathrm{B}(\epsilon)$ . If $\epsilon$ is small enough the strong separation still holds. The thickening ensures that the resulting family is affinely spanning in $\mathbb{R}^{d+1}$ .

Now we apply Proposition 4.4 with the sets $A,B$ . We obtain two distinct hyperplanes $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$ that are tangent to every set, including $\mathrm{S}_{d+1}+\mathrm{B}(\epsilon)$ . We go down to $\mathbb{R}^{d}$ by intersecting with the hyperplane $\mathrm{L}=\{x\in\mathbb{R}^{d+1}~{}:~{}x_{d+1}=0\}$ , to obtain two hyperplanes $\mathrm{H}_{1}=\mathrm{L}\cap\mathrm{L}_{1},\mathrm{H}_{2}=\mathrm{L}\cap\mathrm{L}_{2}$ in $\mathbb{R}^{d}$ satisfying the conditions (1)–(4).

To conclude the proof we must prove that actually $\mathrm{H}_{1}=\mathrm{H}_{2}$ . We argue by contradiction and assume they are different. Running the same argument with $\mathrm{S}_{d+1}$ on the $B$ -side strictly we get at least one hyperplane $\mathrm{H}_{3}$ in $\mathbb{R}^{d}$ satisfying (1)–(3) and (4) reversed. This hyperplane $\mathrm{H}_{3}$ is necessarily different from $\mathrm{H}_{1}$ and $\mathrm{H}_{2}$ since the set $\mathrm{S}_{d+1}$ lies on different sides with respect to the sets in $B$ . But then the three hyperplanes $\mathrm{H}_{1},\mathrm{H}_{2},$ and $\mathrm{H}_{3}$ are different and satisfy (2)–(3) with respect to $\{\mathrm{S}_{1},\dots,\mathrm{S}_{d}\}$ contradicting Proposition 4.4. This shows that $\mathrm{H}_{1}=\mathrm{H}_{2}$ concluding the uniqueness of $\mathrm{H}$ .

∎

4.3. A different separation condition

The motivation for this paper was certain conditions that arose in [6], which used a different definition of separation. We say a family $\mathbf{K}=\{\mathrm{K}_{1},\dots,\mathrm{K}_{d+1}\}$ of convex sets in $\mathbb{R}^{d}$ is simplicially separated if

$(\star)$

The intersection of all simplices having a vertex on each set of the family is full dimensional.

Theorem [6, Theorem 5.9] states that if a family satisfy the condition, then intersection of all rainbow simplices is itself a simplex. The proof uses a version of Proposition 4.6 when $A$ is a singleton, but in that case the existence of the hyperplane is almost given by assumption and one need to check only uniqueness.

Proposition 4.7.

Simplicial separation implies strong separation but the reverse is not true.

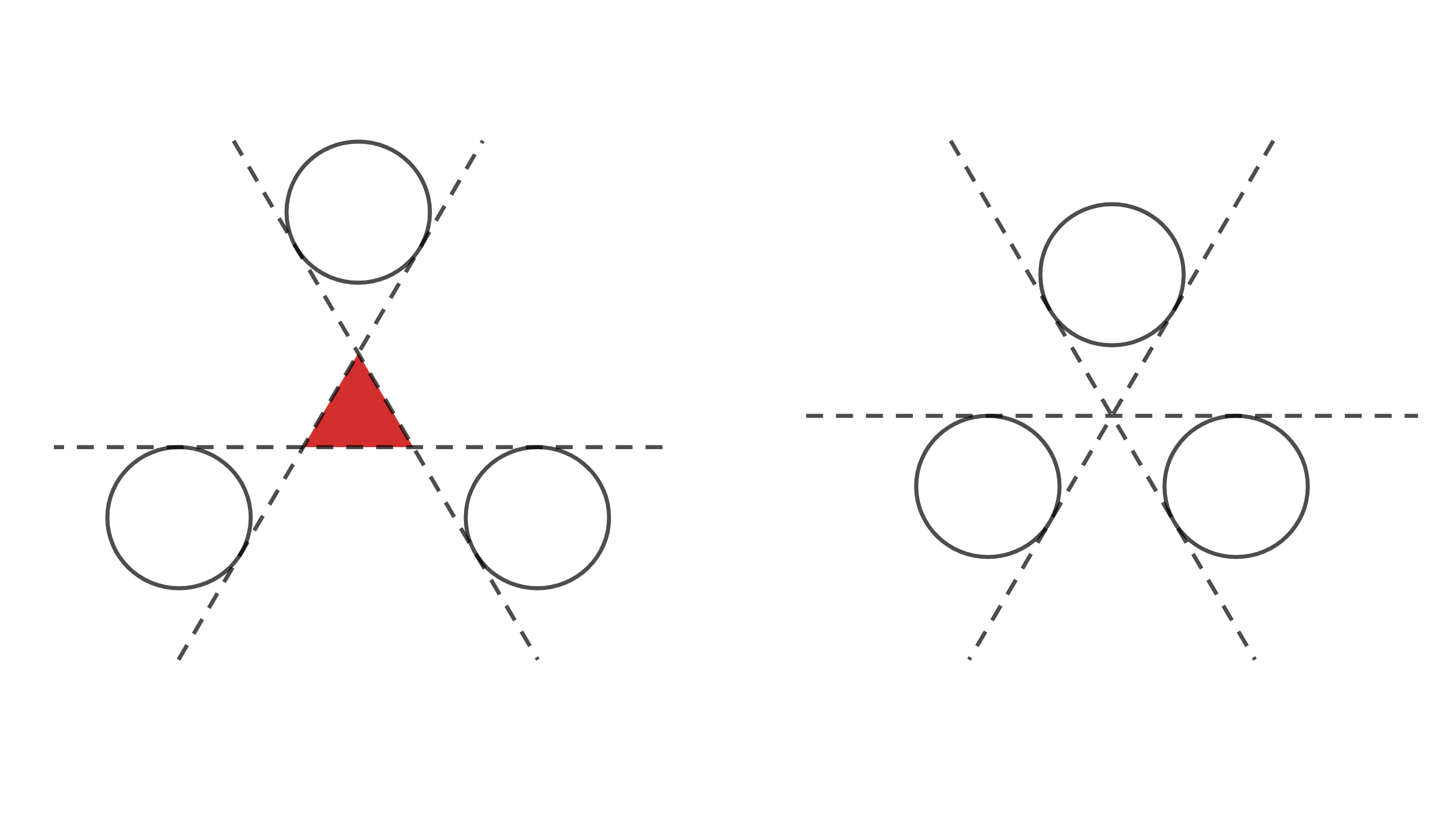
Proof.

Simplicial separation implies that the intersection of all rainbow simplices is a simplex $\mathrm{S}$ . The simplex $\mathrm{S}$ is described in [6] as follows. For each color $i$ there exists an affine hyperplane $\mathrm{H}_{i}$ such that $\mathrm{H}_{i}$ is tangent to $\mathrm{K}_{j}$ for $j\neq i$ , $\bigcup_{j\neq i}\mathrm{K}_{j}\subseteq\mathrm{H}^{\leq}$ whereas $\mathrm{K}_{i}\subseteq\mathrm{H}^{+}$ . The $d+1$ hyperplanes $\mathrm{H}_{i}$ define the facets of $\mathrm{S}$ . We denote $\mathbf{v}_{i}$ the vertex of $\mathrm{S}$ not contained in $\mathrm{H}_{i}$ .

Consider the affine hyperplane arrangement $\mathcal{H}=\{\mathrm{H}_{1},\dots,\mathrm{H}_{d+1}\}$ in $\mathbb{R}^{d}$ . There is a unique bounded region, the simplex $\mathrm{S}$ , and $d+1$ pointed cones, one opposite to each vertex of $\mathrm{S}$ . Each convex body $\mathrm{K}_{i}$ is contained in the pointed cone opposite (with respect to $\mathrm{S}$ ) to $\mathbf{v}_{i}$ .

Now consider any partition $A\sqcup B=[d+1]$ . We have $\dim\text{aff. span}\{\mathbf{v}_{a}:a\in A\}+\dim\text{aff. span}\{\mathbf{v}_{b}:b\in B\}=d-1$ , so their sum is an affine hyperplane $\mathrm{H}$ . If we translate $\mathrm{H}$ so that it contains the barycenter $\mathbf{b}$ of $\mathrm{S}$ , then we obtain an affine hyperplane that does not instersect any of the pointy regions. This hyperplane is a strict separator for $A,B$ .

On the other hand strong separation does not imply Property $(\star)$ , see for example Figure 6

∎

References

[1] Imre Bárány, Alfredo Hubard, and Jesús Jerónimo. Slicing convex sets and measures by a hyperplane. Discrete & Computational Geometry, 39(1-3):67–75, 2008.
[2] Tibor Bisztriczky. On separated families of convex bodies. Archiv der Mathematik, 54(2):193–199, 1990.
[3] Ciprian Borcea, Xavier Goaoc, Sylvain Lazard, and Sylvain Petitjean. Common tangents to spheres in $\mathbb{R}^{3}$ . Discrete & Computational Geometry, 35(2):287–300, 2006.
[4] Heinz Bruggesser and Peter Mani. Shellable decompositions of cells and spheres. Math. Scand., 29:197–205 (1972), 1971.
[5] Sylvain E Cappell, Jacob E Goodman, János Pach, Richard Pollack, Micha Sharir, and Rephael Wenger. Common tangents and common transversals. Advances in Mathematics, 106(2):198–215, 1994.
[6] Federico Castillo, Joseph Doolittle, Bennet Goeckner, Michael S. Ross, and Li Ying. Minkowski summands of cubes, 2020.
[7] G Ewald, DG Larman, and CA Rogers. The directions of the line segments and of the r-dimensional balls on the boundary of a convex body in euclidean space. Mathematika, 17(1):1–20, 1970.
[8] Florian Frick and Shira Zerbib. Colorful coverings of polytopes and piercing numbers of colorful $d$ -intervals. Combinatorica, 39(3):627–637, 2019.
[9] Roman N Karasev. Theorems of borsuk-ulam type for flats and common transversals of families of convex compact sets. Sbornik: Mathematics, 200(10):1453, 2009.
[10] J Kincses. The topological type of the $\alpha$ -sections of convex sets. Advances in Mathematics, 217(5):2159–2169, 2008.
[11] Victor Klee, Ted Lewis, and Balder Von Hohenbalken. Appollonius revisited: supporting spheres for sundered systems. Discrete & Computational Geometry, 18(4):385–395, 1997.
[12] Bronisław Knaster, Casimir Kuratowski, and Stefan Mazurkiewicz. Ein beweis des fixpunktsatzes für n-dimensionale simplexe. Fundamenta Mathematicae, 14(1):132–137, 1929.
[13] Hidetoshi Komiya. A simple proof of kkms theorem. Economic Theory, pages 463–466, 1994.
[14] Khazhgali Kozhasov and Antonio Lerario. On the number of flats tangent to convex hypersurfaces in random position. Discrete & Computational Geometry, 63(1):229–254, 2020.
[15] Ted Lewis, Balder von Hohenbalken, and Victor Klee. Common supports as fixed points. Geometriae Dedicata, 60(3):277–281, 1996.
[16] Rolf Schneider. Convex bodies: the Brunn-Minkowski theory, volume 151 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, expanded edition, 2014.
[17] Alexander Schrijver. Theory of linear and integer programming. John Wiley & Sons, 1998.
[18] Lloyd S Shapley. On balanced games without side payments. In Mathematical programming, pages 261–290. Elsevier, 1973.
[19] Frank Sottile and Thorsten Theobald. Lines tangent to 2n-2 spheres in $\mathbb{R}^{n}$ . Transactions of the American Mathematical Society, 354(12):4815–4829, 2002.
[20] Frank Sottile and Thorsten Theobald. Real k-flats tangent to quadrics in $\mathbb{R}^{n}$ . Proceedings of the American Mathematical Society, 133(10):2835–2844, 2005.
[21] Viktor Abramovich Zalgaller. On k-directions which are singular for a convex body f in r^n. Zapiski Nauchnykh Seminarov POMI, 27:67–72, 1972.
[22] Günter M. Ziegler. Lectures on polytopes, volume 152 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1995.

Common tangents to convex bodies

Abstract.

1. Introduction

Theorem A.

Acknowledgements

2. Preliminaries and notation

2.1. Polarity

2.2. Visibility

Definition 2.1.

Remark 2.2.

Lemma 2.3.

Proof.

Remark 2.4.

Lemma 2.5.

Proof.

Theorem 2.6 (Ewald, Larman, Rogers ).

Proposition 2.7.

Proof.

3. Proof of Theorem A

Definition 3.1.

Remark 3.2.

Proposition 3.3.

Proof.

Remark 3.4.

Theorem 3.5.

Lemma 3.6.

Proof.

Proposition 3.7.

Proof.

Remark 3.8.

Proof of Theorem 3.5.

Remark 3.9.

Example 3.10.

Example 3.11.

Corollary 3.12.

Theorem 3.13.

Proof.

4. Applications

4.1. Common tangents to dd convex bodies in ℝd\mathbb{R}^{d}

Theorem 4.1.

Proof.

Example 4.2.

Question 4.3.

4.2. Collection of d+1d+1 convex bodies

Proposition 4.4.

Proof.

Example 4.5.

Proposition 4.6.

Proof.

4.3. A different separation condition

Proposition 4.7.

Proof.

References

4.1. Common tangents to $d$ convex bodies in $\mathbb{R}^{d}$

4.2. Collection of $d+1$ convex bodies