Commuting graph of a group on a transversal
Abstract
Given a finite group and a subset of , the commuting graph of on , denoted by , is the graph that has as its vertex set with joined by an edge whenever and . Let be a transversal of the center of . When is a finite non-abelian group and , we denote the graph by . In this paper, we show that is a connected strongly regular graph if and only if is isoclinic to an extraspecial -group of order at least . We also characterize the finite non-abelian groups for which the graph is disconnected strongly regular.
Keywords: Commuting graph, isoclinism, extraspecial -group, strongly regular graph.
Mathematics Subject Classification 2010: 20D15, 05C25, 05E30
1 Introduction
Let be a subset of a finite group . The commuting graph of on the set , denoted by , is the graph that has as its vertex set with joined by an edge whenever and . Commuting graphs were first studied by Brauer and Fowler in [4] with . Many papers have investigated for different choices of . For example, the works [2, 7, 16] investigated the graph when consists of involutions and the papers [1, 8, 9, 14, 17] considered , where denotes the center of . Let us denote the graph by and refer to it simply as commuting graph of . We observe that highlights the relations of commutativity between non-central elements of the group . However, given , it is clear that any two elements of the coset commute with each other. Furthermore, as observed in [17], vertices and are adjacent in if and only if and are adjacent for all and . In this way, we may investigate the relations of commutativity in by observing only the relations of commutativity that occur between non-central elements of a transversal of in . Thus, in this work we consider the graph when is a finite non-abelian group and , where is a transversal of in . Note that it is a subgraph of . It is easy to see that if is another transversal of in , then the graphs and are isomorphic. Hence, we will denote the graph simply by without mentioning the choice of the transversal. It is worth mentioning that this type of graph has already been considered in [8, 9, 17]. Vahidi and Talebi [17] showed that the graphs and have the same independence number and diameter. Moreover, if denotes the clique number of the graph , then . In [8, 9] the authors examined the graph in their study of the diameter of a commuting graph.
We prove that presents the following relevant property: if and are isoclinic groups, then the graphs and are isomorphic (Proposition 2.3). This helps us to classify groups such that has certain particular properties.
We recall a graph is regular if each vertex has the same number of neighbors and it is -regular if each vertex has exactly neighbours. A strongly regular graph with parameters , where , is a graph -regular on vertices such that each pair of adjacent vertices has precisely common neighbours and any two non-adjacent vertices have exactly common neighbours.
Akbari and Moghaddamfar [1, Corollary 2] showed that if is strongly regular, then it is a disjoint union of at least two complete graphs and, therefore, it is disconnected. In this work, we prove that there exist groups for which the associated graph is connected strongly regular. Moreover, we present a description of these groups; more precisely, we get:
Theorem A.
Let be a finite non-abelian group. Then is a connected strongly regular graph if and only if admits a decomposition , where is an abelian subgroup of and is a Sylow -subgroup of isoclinic to an extraspecial -group of order , for some integer . In this case, the parameters of are .
We also characterize the finite non-abelian groups for which the graph is disconnected strongly regular (see Corollary 3.10).
In this text, we use the following notations and conventions: is the cyclic group of order and (with ) is the dihedral group of order . Let be a group. For , the commutator of and is given by and the derived subgroup of is denoted by . We write for the centralizer of in . The symbol represents the set formed by the sizes of the conjugation classes of the elements of . For , we say that is of conjugate type if . Thus, given a positive integer , the group is of conjugate type if , for any .
Given a graph its vertex set is represented by and its edge set by . The neighborhood of a vertex of is denoted by with degree deg. When the graphs and are isomorphic, we write and the disjoint union of the graphs and is denoted by . As usual, the complete graph on vertices is denoted by and the disjoint union of complete graphs is indicated by . The graph on vertices and without edges is represented by . Other concepts and basic results on graphs can be seen in [6].
2 Preliminary results
In this section we present some concepts and results which will be needed to the proof of Theorem A.
First, we observe the commuting graph of can be obtained from in the following manner: for each vertex of , put . We can see that is the graph that has as vertex set and such that a subset of is an edge of if and only if one of the following conditions is satisfied: (1) , for some vertex of ; or (2) and , where e are adjacent vertices in .
Example 2.1.
Consider the group , which is an extraspecial -group of order . Since , there are eight non-trivial cosets of in and is a transversal of in . The commuting graph of is isomorphic to and it can be seen in Figure 1. Each connected component of contains exactly two distinct cosets of . In the figure below, in each connected component of , vertices that are in the same coset of are represented with the same color. In Figure 2, we see that .
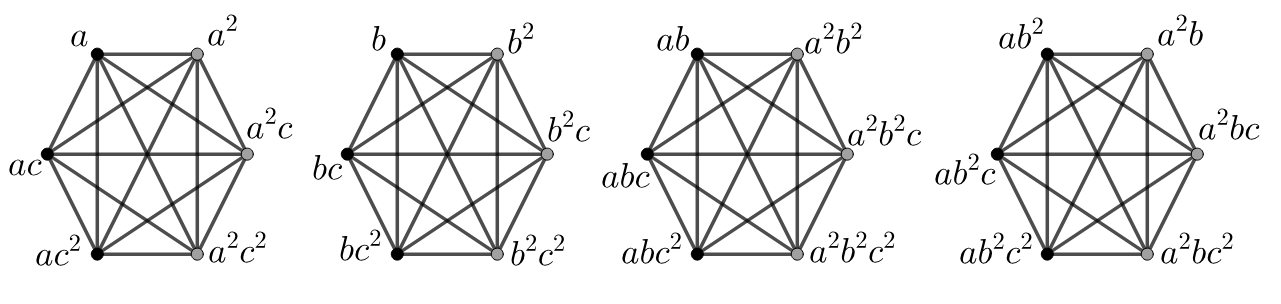
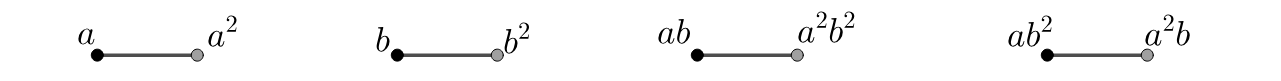
The concept below was introduced by Hall [11]. We observe that for all group , the commutator map given by is well defined.
Definition 2.2.
Let and be two groups. A pair is an isoclinism from to if the following conditions are satisfied:
- (i)
-
is an isomorphism from to ;
- (ii)
-
is an isomorphism from to ;
- (iii)
-
, for all .
When there is an isoclinism from to , we say that the groups and are isoclinic.
The relation of isoclinism is a equivalence relation on groups and the equivalence class of a group is called of isoclinism family of .
In general, isoclinic groups do not have isomophic commuting graphs, however for the graphs we have the following:
Proposition 2.3.
Let and be finite non-abelian groups. If and are isoclinic, then the graphs and are isomorphic.
Proof.
By hypothesis, there are isomorphisms and such that , for all . Let be a transversal of in , and, for each , let be a representative of the coset . Therefore is a transversal of in . If we put as the vertex set of and as the vertex set of , the mapping defines a bijection between and . In addition, if e are adjacent in , then , that is, and are adjacent in . On the other hand, if , we have . Since is an isomorphism, we obtain . Therefore and are isomorphic. ∎
The next example shows that the converse of Proposition 2.3 does not hold in general.
Example 2.4.
Consider the following groups :
.
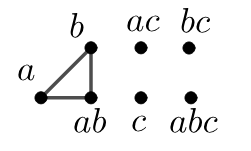
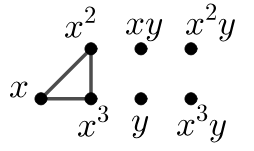
The next result gives the size of the common neighborhood of two vertices of .
Proposition 2.5.
Given a finite non-abelian group , let and be distinct vertices of . The following statements are true:
- (i)
-
deg;
- (ii)
-
if and are adjacent, then ;
- (iii)
-
if and are not adjacent, then .
Proof.
Let be a vertex of . If is the neighborhood of in and if , it is easy to verify that , so that deg. This proves (i).
Let and be distinct vertices of and put and . We note that . If and are adjacent in , then and, in this case, we obtain . It follows that , which proves (ii). If and are not adjacent in , then and and it is easy to see that . Therefore and part (iii) is proved. ∎
From Proposition 2.5 it follows that is regular if and only if , for all , that is, . Ito [13] gave a description of the finite groups of conjugate type .
Theorem 2.6.
([13, Theorem 1]) If is a finite group of conjugate type , then is a power of a prime and admits a decomposition , where is an abelian subgroup of and is a Sylow -subgroup of the same conjugate type as .
Let be a prime. Recall that a finite non-abelian -group is extraspecial if and , where denotes the Frattini subgroup of . It is well known that any non-abelian group of order is extraspecial. Further, an extraspecial -group has order , for some positive integer .
In this paper we will use the following Ishikawa’s classification:
Theorem 2.7.
([12, Proposition 3.1]) Let be a finite -group, prime. Then is of conjugate type if and only if is isoclinic to an extraspecial -group.
3 Main results
In this section we will present the proof of Theorem A, which will be done in steps. First let us show that the graph associated to an extraspecial -group of order , , is connected strongly regular. For it, we will need the following two lemmas:
Lemma 3.1.
Let be an extraspecial -group. If and , then .
Proof.
If or is the quaternion group of order , the result is clearly true. Consider an extraspecial -group of order and suppose that the result is true for all extraspecial -group of order less than . By [15, 5.3.8], contains subgroups and such that and are extraspecial -groups of order less than and is a central product. Hence, the elements of commute with the elements of and . By induction hypothesis, the following two conditions are satisfied:
(i) , for all such that .
(ii) , for all such that .
Let and be non-central elements of such that , where and . Thus, in virtue of (i) and (ii), we must have or . In the first situation, there is (or there is ) and it follows that (or ), which gives us . Analogously, implies , as required. ∎
The following result is taken from [10].
Lemma 3.2.
([10, Lemma 10.1.1] )If is a strongly regular graph with parameters , then the following statements are equivalent:
- (i)
-
is disconnected;
- (ii)
-
;
- (iii)
-
;
- (iv)
-
is isomorphic to for some integer .
Proposition 3.3.
If is an extraspecial -group of order , with , then is a connected strongly regular graph with parameters .
Proof.
Let be such that . By Lemma 3.1, we have and, by Theorem 2.7, is of conjugate type . This shows that . Write . Given , we have , and so , that is, . Hence . Applying Proposition 2.5 to calculate the degree of each vertex of and the size of the common neighborhood of two vertices, we conclude that is strongly regular with parameters . Since , Lemma 3.2 give us is connected. ∎
The next result establishes a necessary condition for a graph to be connected strongly regular.
Lemma 3.4.
Let be a finite non-abelian group such that is connected strongly regular. Then, for all such that , we have .
Proof.
Suppose there is a non-abelian group such that is a connected strongly regular graph with parameters and that there are such that and . For all and we have and . Hence, we may assume that are vertices of . From Proposition 2.5, it follows that if and , then , and . By Lemma 3.2 the graph is disconnected, a contradiction. ∎
Our intention is to characterize the groups for which is connected strongly regular . As we deal with a case where the graph is regular (and so is of conjugate type ), in virtue of Theorem 2.6, we can restrict our study to -groups.
Lemma 3.5.
Given an odd prime let be a finite non-abelian -group. If is strongly regular, then is disconnected.
Proof.
Suppose that is strongly regular. Given , we have ; further, as and deg=deg we get . Hence, by Lemma 3.4, the graph is disconnected, as desired. ∎
Lemma 3.5 say us that if is a -group such that is a connected strongly regular graph, then .
For the proof of the next two results we will need the following relation, that holds for any strongly regular graph with parameters (see [5, Proposition 2.6]):
| (1) |
Lemma 3.6.
Let be a finite non-abelian -group such that is a connected strongly regular graph with parameters . Suppose that , for any vertices of , with and . Then is isoclinic to an extraspecial -group of order at least .
Proof.
From the hypotheses it follows that there exist non-negative integers such that , and , for any distinct vertices and of . Thus, Proposition 2.5 provides us
Because , we must have . From (1) we obtain and, consequently, Because we get and from the last equality above we conclude . Thus and so , which implies . Hence, , for any , that is, is of conjugate type . Now, from Theorem 2.7 it follows that is isoclinic to an extraspecial -group . As and we obtain and so has order at least . ∎
Theorem 3.7.
If is a finite non-abelian -group such that is connected strongly regular, then is isoclinic to an extraspecial -group of order at least .
Proof.
By Lemma 3.6, it is sufficient to show that , for any vertices of , where and . Let us assume the contrary, that is, there are vertices of such that
| (2) |
Taking into account Proposition 2.5 and the fact that is strongly regular, we have two cases to analyze:
Case 1: and . Due to Proposition 2.5 and (2), we can write
where are non-negative integers, with . From we obtain
which is equivalent to
Since , this forces and
that is, . For such equality to occur, we must have , which give us , a contradiction.
Case 2: and . Considering (2), we may write
where are non-negative integers, with . Note that because and . From the identity we get and so , which implies . However, by Lemma 3.2, ; thus and, consequently,
It follows from the last equality that .
If , we obtain , that is, , a contradiction.
Suppose now . Since , we conclude that the number is odd and this implies . From the penultimate equality we get , which gives us , that is, . Hence, in this case, the parameters of are:
| (3) |
Putting , it follows from ([5], Theorem 2.16) that the numbers and given below are non-negative integers:
Note that and this number is nonzero for .
From the parameters obtained in (3), we obtain and, thus, . Since and are non-negative integers, there is such that . Then must be an odd integer, say , and we get , a contradiction.
Now, the result follows from Lemma 3.6. ∎
We are now ready to show Theorem A.
Proof of Theorem A.
Let be a finite non-abelian group such that is connected strongly regular. Theorem 2.6 tells us that admits a decomposition , where is an abelian subgroup of and is a Sylow -subgroup of of conjugate type for some positive integer . Now [3, page 286] ensures us that and are isoclinic and so . Lemma 3.5 forces and Theorem 3.7 yields us that is isoclinic to an extraspecial -group of order at least , that is, , for some . Now, the result follows from Propositions 3.3 and 2.3, taking into account that and are isoclinic groups. ∎
As an immediate consequence of the proof of Theorem A, we obtain
Corollary 3.8.
Let be a finite non-abelian group. The graph is connected strongly regular if and only if is isoclinic to an extraspecial -group of order at least .
We also characterize the finite non-abelian groups for which the graph is a disjoint union of complete graphs of the same size.
Proposition 3.9.
Let be a finite non-abelian group and let be positive integers. The graph is a disjoint union of copies of if and only if and for any we have is abelian and .
Proof.
Suppose that is a disjoint union of copies of . It is clear that . Let be the transversal of in such that . Given , there is such that . If is the neighborhood of in , then deg. Since deg (by Proposition 2.5), we have . Moreover, and is abelian, because the subgraph generated by is complete. Since , we conclude that and is abelian.
Conversely, assume that and for any , is abelian and . Let be a vertex of . If is the neighborhood of in , then the subgraph generated by is isomorphic to , because and is abelian. In addiction, as the non-central elements of have centralizers of equal size, is a disjoint union of graphs isomorphic to . ∎
It is worth mentioning that when is a non-abelian -group, the case in Proposition 3.9 is also a consequence of [1, Corollary 1]. Further, if is a group such that , the result above produces .
We have already seen ([10, Lemma 10.1.1]) that if a graph is disconnected strongly regular, then it is isomorphic to for some integers . Of course, the reciprocal also holds. Thus, as an immediate consequence from Proposition 3.9, we obtain
Corollary 3.10.
Let be a finite non-abelian group. The graph is disconnected strongly regular if and only if the centralizers of the non-central elements of are all abelian and there exists an integer such that , for all .
Akbari and Moghaddamfar [1, Corollary 2(a)] proved that a commuting graph is strongly regular if and only if it is a disjoint union of complete graphs on vertices. However, Example 2.1 shows that the connected components of a strongly regular graph do not necessarily have size equal to . In fact, we have the following result, which corrects the error in [1, Corollary 2(a)]:
Proposition 3.11.
Let be a finite non-abelian group. The graph is strongly regular if and only if , where and , for all .
Proof.
Suppose that is a strongly regular graph with parameters . As is regular, from Theorem 2.6 it follows . For all and , with , it is clear that and . Thus, we must have . As the graph is not complete, from the relation , we obtain . Hence, Lemma 3.2 ensures us , for some integers . Clearly, and by calculating the degree of each vertex we get , for all . ∎
Let be a finite non-abelian group. Since for we have if and only if , for all , , as a consequence of Proposition 3.11 we conclude that if is a strongly regular graph, then each connected component of this graph is an union of non-trivial cosets of , where .
Let be a prime and let be an extraspecial -group. If is odd and , Theorem 2.7 and Lemma 3.5 ensure us that is regular but not strongly regular. The next result tells us that if is a group isoclinic to an extraspecial -group of order , then is disconnected strongly regular.
Proposition 3.12.
Let be a finite non-abelian group and let be a prime number. We have if and only if is isoclinic to an extraspecial -group of order .
Proof.
Let be a group such that . Hence and as the graph is regular, by Lemma 2.6 and Proposition 2.3, we may assume that is a -group. Now Proposition 3.9 provides us , for all . Thus we conclude , for all and, consequently, is of conjugate type . From Theorem 2.7 it follows that is isoclinic to an extraspecial -group, say . Since and , we must have . The converse follows from Proposition 3.9 and Proposition 2.3. ∎
References
- [1] M. Akbari, A. R. Moghaddamfar, The Existence or Nonexistence of Non-Commuting Graphs with Particular Properties. J. Algebra Appl. 13 (2014) 1350064, 11 pp.
- [2] C. Bates, D. Bundy, S. Hart and P. Rowley, Commuting involution graphs for sporadic simple groups, J. Algebra 316 (2007), 849-868.
- [3] Y. Berkovich, Groups of Prime Power Order, Walter de Gruyter, vol. 1, Berlin/New York (2008).
- [4] R. Brauer and K. A. Fowler, On groups of even order. Ann. of Math. (2) 62 (1955), 567-583.
- [5] P. J. Cameron and J. H. van Lint, Designs, Graphs, Codes and Their Links. Cambridge University Press, 1991.
- [6] G. Chartrand and P. Zhang, A First Course in Graph Theory, Dover Publications (2012).
- [7] B. Fischer, Finite groups generated by 3-transpositions, J. Invent. Math. 13 (1971), 232-246.
- [8] M. Giudici and C. Parker, There is no upper bound for the diameter of the commuting graph of a finite group, J. Combin. Theory Ser. A 120 (2013), 1600-1603.
- [9] M. Giudici and A. Pope, On bounding the diameter of the commuting graph of a group, J. Group Theory 17 (2014), 131-149.
- [10] C. Godsil, G. Royle, Algebraic Graph Theory, Graduate Texts in Math. 207 Springer-Verlag (2001).
- [11] P. Hall, The classification of prime-power groups. J. Reine Angew. Math. 182 (1940), 130-141.
- [12] K. Ishikawa, Finite p-groups up to isoclinism, which have only two conjugacy lengths. J. Algebra 220 (1999), 333-345.
- [13] N. It , On finite groups with given conjugate types I. Nagoya Math. 6 (1953), 17-28.
- [14] G. L. Morgan and C. W. Parker, The diameter of the commuting graph of a finite group with trivial center, J. Algebra 393(1) (2013), 41-59.
- [15] D. J. S. Robinson, A course in the theory of groups, 2nd edition, Springer-Verlag, New York, 1996.
- [16] S. Perkins, Commuting involution graphs for n, Arch. Math. 86 (2006), 16-25.
- [17] J. Vahidi and A. A. Talebi, The commuting graphs on groups and , J. Math. Comput. Sci. 1 (2010), 123-127.