Compact Spin-Polarized Positron Acceleration in Multi-Layer Microhole Array Films

Zhen-Ke Dou Ministry of Education Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Shaanxi Province Key Laboratory of Quantum Information and Quantum Optoelectronic Devices, School of Physics, Xi’an Jiaotong University, Xi’an 710049, China Chong Lv Department of Nuclear Physics, China Institute of Atomic Energy, P. O. Box 275(7), Beijing 102413, China Yousef I. Salamin Department of Physics, American University of Sharjah, Sharjah, POB 26666 Sharjah, United Arab Emirates Nan Zhang Ministry of Education Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Shaanxi Province Key Laboratory of Quantum Information and Quantum Optoelectronic Devices, School of Physics, Xi’an Jiaotong University, Xi’an 710049, China Guangdong Provincial Key Laboratory of Semiconductor Optoelectronic Materials and Intelligent Photonic Systems, Shenzhen 518055, China Feng Wan wanfeng@xjtu.edu.cn Ministry of Education Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Shaanxi Province Key Laboratory of Quantum Information and Quantum Optoelectronic Devices, School of Physics, Xi’an Jiaotong University, Xi’an 710049, China Zhong-Feng Xu Ministry of Education Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Shaanxi Province Key Laboratory of Quantum Information and Quantum Optoelectronic Devices, School of Physics, Xi’an Jiaotong University, Xi’an 710049, China Jian-Xing Li jianxing@xjtu.edu.cn Ministry of Education Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Shaanxi Province Key Laboratory of Quantum Information and Quantum Optoelectronic Devices, School of Physics, Xi’an Jiaotong University, Xi’an 710049, China Department of Nuclear Physics, China Institute of Atomic Energy, P. O. Box 275(7), Beijing 102413, China

Abstract

Compact spin-polarized positron accelerators play a major role in promoting significant positron application research, which typically require high acceleration gradients and polarization degree, both of which, however, are still great challenging. Here, we put forward a novel spin-polarized positron acceleration method which employs an ultrarelativistic high-density electron beam passing through any hole of multi-layer microhole array films to excite strong electrostatic and transition radiation fields. Positrons in the polarized electron-positron pair plasma, filled in the front of the multi-layer films, can be captured, accelerated, and focused by the electrostatic and transition radiation fields, while maintaining high polarization of above $90\%$ and high acceleration gradient of about ${\rm TeV/m}$ . Multi-layer design allows for capturing more positrons and achieving cascade acceleration. Our method offers a promising solution for accelerator miniaturization, positron injection, and polarization maintaining, and also can be used to accelerate other charged particles.

Spin-polarized positron beams are widely used in medical diagnosis [1], materials physics [2, 3, 4], laboratory astrophysics [5], and high-energy physics [6, 7, 8, 9, 10], etc. Such as studying $\gamma$ -ray bursts [11, 12], measuring the proton elastic form factor ratio [13, 14] and nucleon electromagnetic structure [15], testing the Standard Model [16], and searching for new physics beyond the Standard Model [7]. In these applications, there is high demand for positron beam density (exceeding $10^{16}\>\rm{cm^{-3}}$ ), energy (hundreds of ${\rm MeV}$ to ${\rm TeV}$ ), and polarization degree ( $>30\>\%$ ) [5, 7, 17, 18]. Currently, their generation mainly relies on large-scale conventional accelerators with acceleration gradients below ${\rm 100\>MeV/m}$ [19]. A compact spin-polarized positron accelerator would play a major role in promoting research into the above, and possibly other, applications [20, 21].

Alternative mechanisms currently being explored towards reaching that goal include dielectric laser acceleration [22, 23, 24, 25] and solid-state wakefield acceleration using crystals[26, 27, 28] or carbon nanotube arrays [29, 30, 31], which can achieve gradients of tens of ${\rm GeV/m}$ and even ${\rm TeV/m}$ . However, energy gain in the former is limited due to the short laser-particle interaction length [25] and the latter requires ultra-high power x-ray lasers to excite crystals [30]. Meanwhile, significant progress has been made over the past decade in plasma wakefield acceleration (PWFA), which can achieve gradients of hundreds of ${\rm GeV/m}$ [32, 33, 34, 35]. PWFA is well-suited for trapping [36] and accelerating electrons [37], with gradients sustained over meters [38], high energy transfer efficiency [33], and low energy spread in the bubble regime [39, 40]. Effective trapping and acceleration of positrons, however, is limited by defocusing due to the transverse field in the bubble.

To ameliorate these limitations, various methods have been proposed [41], such as using a long positron beam to achieve energy transfer from head-to-tail in the self-loaded plasma wakefields [42, 43]. Hollow electron beams [44], Laguerre-Gaussian laser pulses [45], finite radius plasma columns [46, 47], plasma channel [48], and two-column plasma structures [49] are used to control wakefield structures for simultaneous accelerating and focusing positrons in the plasma bubble. Another attractive method involves using a hollow plasma channel, for which the longitudinal field is uniform in the transverse plane, and the transverse focusing fields vanish inside the channel, ensuring beam emittance preservation during acceleration [50, 51, 52, 53, 54]. The beam-breakup instability can be avoided by utilizing an asymmetric electron beam in hollow plasma channel [55]. Nevertheless, all of these methods require precise injection of the high-energy positrons, with their beam polarization properties often overlooked. Meanwhile, density of the accelerated positron beam seems very limited (less than $10^{18}\>\rm{cm^{-3}}$ ). A single-stage mechanism for polarized positron production, injection, and acceleration, has also been proposed through the interaction of a seed electron beam with a strong laser [56, 57, 58]. In this case, polarized positrons can be generated via nonlinear Compton scattering and nonlinear Breit-Wheeler process [59, 60, 61, 62, 63, 64, 65]. However, acceleration in a single stage requires precise spatiotemporal synchronization, which presents experimental difficulties, and faces large depolarization challenges due to spin precession in the fields with complicate structures [56].

Another positron acceleration scheme relies on mid-infrared [66] and terahertz [67, 68] radiation, both of which still require precise injection and overlook the polarization properties. Moreover, circularly polarized $\gamma-$ photons [69, 70] or polarized electron beams [71] hitting high-Z targets can generate polarized positrons via the Bethe-Heitler process [72]. The positrons can be accelerated by coherent transition radiation [73] or sheath fields [74]. However, the acceleration gradients are only ${\rm GeV/m}$ , and the positron beam density is less than $10^{15}\>{\rm cm^{-3}}$ . Thus, realization of a compact high-density polarized positron accelerator is still a great challenge.

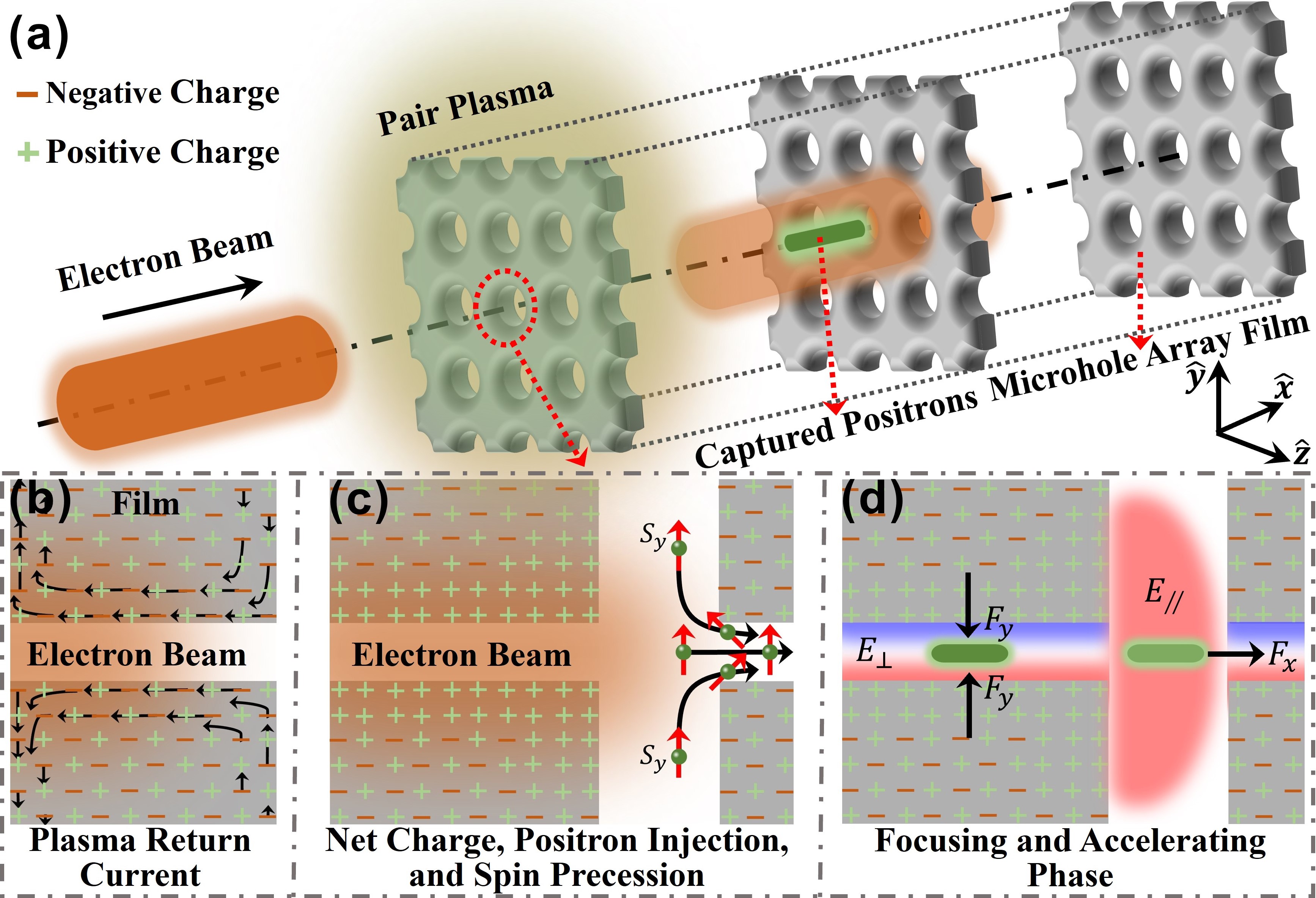
Refer to caption — FIG 1: (a) Electron beam passing through any hole of the multi-layer microhole array films, with front (one layer shown) filled with spin-polarized electron-positron pair plasma. Positrons in the pair plasma can be effectively captured, accelerated, and focused, while maintaining high polarization. (b) Plasma return current. Black arrows represent the direction of film’s electron motion. (c) Net charge, positron injection, and spin precession. Green balls represent the captured positrons. Black-solid lines with arrow and red arrows depict positron trajectory and spin component $S_{y}$ , respectively. (d) Focusing and accelerating phase: $E_{\perp}$ and $E_{\varparallel}$ (blue-red gradients) within and behind the hole focus and accelerate the positron beam. Forces $F_{y}$ and $F_{x}$ acting on a positron are represented by black arrows.

In this Letter, we put forward a novel polarized positron acceleration method, which uses an ultrarelativistic high-density electron beam passing through any hole of multi-layer microhole array films; see Fig. 1(a). The electron beam ionizes the film around the hole creating plasma and inducing plasma return current in the film [75]; see Fig. 1(b). This current causes net charge accumulation on the film surface; see Fig. 1(c). The net charge excites the transverse and longitudinal electrostatic fields ( $E_{y,{\rm sta.}}$ and $E_{x,{\rm sta.}}$ ) within and behind the hole, which generates focusing field $E_{\perp}\varpropto E_{y,{\rm sta.}}$ and acceleration field $E_{\varparallel}\varpropto E_{x,{\rm sta.}}$ for positrons; see Fig. 1(d). When the electron beam crosses the plasma-vacuum boundary (film’s rear surface), it excites the transition radiation field $E_{\rm rad.}$ behind the hole [76]. The longitudinal component $E_{x,{\rm rad.}}$ can significantly enhance the acceleration field via $E_{\varparallel}=E_{x,{\rm sta.}}+E_{x,{\rm rad.}}$ . The electron-positron pair plasma (which can be generated by radiation sources [77], nuclear reactions [78, 79, 80, 81], particle accelerators [82, 83], Bethe-Heitler processes [5, 11, 84], and Breit–Wheeler processes [85, 86, 87, 88, 89, 90, 91]) fills the front of the multi-layer films; see Fig. 1(a). Positrons within the pair plasma are attracted (electrons are repelled) towards the central axis ( $y=z=0$ ) by the electron beam and then accelerated in the $+\hat{x}$ direction by $E_{\varparallel}$ ; see Fig. 1(c). Subsequently, they enter the focusing and accelerating phase, forming a high-density polarized positron beam, which can be focused and accelerated to high energies; see Fig. 1(d). In our method, the acceleration gradient for the positron beam can reach about the order of ${\rm TeV/m}$ , which holds significant potential for accelerator miniaturization and cost-effectiveness. Depolarization caused by spin precession [see Fig. 1(c)] is small because most positrons near the central axis experience weak magnetic fields. Compared to slits and polygonal holes, circular holes have a better quality factor for focusing positron beams [92, 93]. Due to the strong self-generated field (ionized film) of the electron beam, the material of the film can be metal, plastic, etc. Our method is robust with respect to the multi-layer films, electron beam, and pair plasma parameters; see Fig. S1 in [94]. These advantages can lower the level of difficulty in running the experiment. Moreover, our method has the potential to accelerate electrons using positively charged particle beams; see Figs. S2 and S3 in [94].

We perform spin-resolved quantum electrodynamics particle-in-cell simulations, by using the spin-resolved SLIPs code [95, 85] to illustrate the dynamics of positrons; see simulation details in [94]. We also use cylindrical coordinate system ( $r,\phi,x$ ), with $r=\sqrt{y^{2}+z^{2}}$ , $\phi=\arctan(z/y)$ , and $x$ being the radial, azimuth, and vertical directions, respectively. The plasma critical density $n_{c}=\omega^{2}m_{e}\epsilon_{0}/e^{2}$ , period $T_{0}=\lambda/c$ , $E_{0}=m_{e}c\omega/e$ , and $B_{0}=m_{e}\omega/e$ are used for the normalization, where $\epsilon_{0}$ is the vacuum permittivity constant, $m_{e}$ is electron mass, $e$ is elementary charge, $\lambda=1\>{\rm\mu m}$ is reference wavelength, and $\omega=2\pi c/\lambda$ is reference frequency, respectively.

The typical positron acceleration results are shown in Fig. 2, with the following simulation parameters. A moving window along $+x$ -direction is used, with a simulation box covering $0\leq x\leq 6\>{\rm\mu m}$ , $-3\>{\rm\mu m}\leq y\leq 3\>{\rm\mu m}$ , and $-3\>{\rm\mu m}\leq z\leq 3\>{\rm\mu m}$ and divided into $600\times 600\times 600$ cells. Electron beam number density profile is $n_{b}=n_{b0}\exp(-r^{2}/2\sigma_{r}^{2})\exp(-(x-x_{0}-v_{b}t)^{2}/2\sigma_{x}^{2})$ , and truncated at $n_{b}=0.02\>n_{c}$ . Here, $\sigma_{x}=\sigma_{r}=0.85\>{\rm\mu m}$ are the longitudinal and transverse rms-length (the radius of the electron beam is $R_{b}=2\>{\rm\mu m}$ ), $v_{b}=c\sqrt{1-1/\gamma_{b}^{2}}$ is the beam velocity, $\gamma_{b}=20000$ is the beam relativistic factor, $x_{0}=4\>{\rm\mu m}$ is the beam center position at $t=0$ (when the electron beam contact with the front surface of first layer film at $x=0$ ), and $n_{b0}=0.4\>n_{c}$ is the peak number density, respectively. The electron beam parameters are feasible in e.g., PWFA [96, 97], the FACET-II facilities [98], and plasma lens [99]. We consider a partially ionized multi-layer polystyrene films composed of $e^{-}$ , $H^{+}$ , and $C^{6+}$ ions, with number densities $n_{e}(e^{-})=30\>n_{c}$ and $n_{p}(H^{+})=n_{C}(C^{6+})=n_{e}(e^{-})/7$ ; see Fig. S4 in [94]. The film thickness is $L=1\>{\rm\mu m}$ , the layer spacing is $D=1.5\>{\rm\mu m}$ , and the duty ratio is $D_{r}=L/(L+D)=40\>\%$ in $x$ -direction, respectively. The hole radius is $R_{h}=0.5\>{\rm\mu m}$ ( $R_{h}<R_{b}$ ) and the distance between the centers of adjacent holes in $y$ and $z$ directions is $R_{c}\geq R_{b}+R_{h}$ (to achieve the maximum acceleration field under these parameter conditions). Polarized pair plasma, generated by ultraintense laser pulses [100, 101, 102, 103, 104, 105, 106] irradiating a solid target [85, 86], has a uniform number density distributions with $0.01\>n_{c}$ in the region of $1\>{\rm\mu m}\leq x\leq 20\>{\rm\mu m}$ , $-3\>{\rm\mu m}\leq y\leq 3\>{\rm\mu m}$ , and $-3\>{\rm\mu m}\leq z\leq 3\>{\rm\mu m}$ . Each cell includes $10$ macroelectrons (electron beam), $10$ macroelectrons, $5$ macroprotons, and $5$ macrocarbon ions (film), and $10$ macropositrons and $10$ macroelectrons (pair plasma).

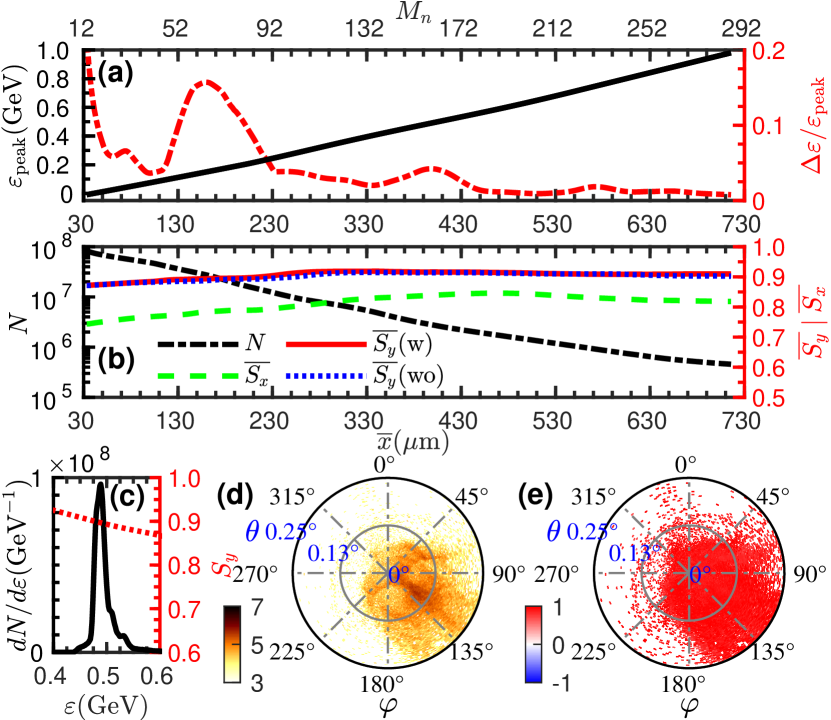
The multi-layer design allows for cascade acceleration of the positron beam, increasing its peak energy by $\varepsilon_{g}\sim 3.6\>{\rm MeV}$ per layer, and determining the final peak energy as $\varepsilon_{\rm peak}=\varepsilon_{g}M_{n}$ ; see Fig. 2(a). As the positrons accelerate, $\Delta\varepsilon/\varepsilon_{\rm peak}$ decreases oscillatingly to below $2.5\>\%$ in the later stages of acceleration; see Fig. 2(a). The main cause of oscillation is the weak defocusing field in the acceleration phase, which leads to the escape of some positrons. This, in turn, alters the shape of the positron beam energy spectrum. The escape of positrons lead to a gradual decrease in $N$ , approaching $4.6\times 10^{5}$ (density $>10^{20}\>{\rm cm^{-3}}$ ) at $\overline{x}=715\>{\rm\mu m}$ ; see Figs. 2(b). Due to the weak magnetic fields experienced by most positrons, the depolarization caused by precession is minimal; see Fig. 4. Moreover, the effect of radiation and spin flipping can be negligible; see Figs. 2(b) and S5 in [94]. Therefore, the positron beam has transverse (longitudinal) spin polarization if the pair plasma initially has transverse (longitudinal) polarization, with average spin polarization degree $\overline{S_{y}}=|\sum_{i}^{N}S_{y}/N|$ ( $\overline{S_{x}}=|\sum_{i}^{N}S_{x}/N|$ ) exceeding $90\%$ ( $80\%$ ), and it remains virtually unchanged during the acceleration process; see Fig. 2(b). In the case of longitudinal spin, due to positron’s spin direction being perpendicular to the circular magnetic field everywhere, spin precession has a greater impact, resulting in a lower $\overline{S_{x}}$ compared to $\overline{S_{y}}$ ; see Fig. 2(b). For the electron beam, due to radiation, it has the potential to be realized beam-self polarization; see Fig. S6 in [94]. The energy spectrum shows a single peak and $S_{y}$ decreases gradually with the increase in energy, surpassing $0.85$ within the full width at half maximum; see Fig. 2(c). The positron beam is well-collimated, majority of positrons are located within $\theta<0.25\degree$ , and exhibit a uniform $S_{y}$ distribution with $\theta$ and $\phi$ ; see Figs. 2(d) and 2(e). This result holds great potential for studies of $\gamma$ -ray bursts [11, 12], pulsar magnetospheres [107], and detection of dark matter particles [108]. Moreover, the externally injected positron and proton beams can still be accelerated well; see Figs. S7 and S8 in [94]. The maximum energy conversion efficiency can reach up to $25.5\%$ , and the emittance stabilizes in the later stages of acceleration; see Fig. S9 in [94]. The annihilation of electron-positron can be negligible; see Fig. S10 in [94].

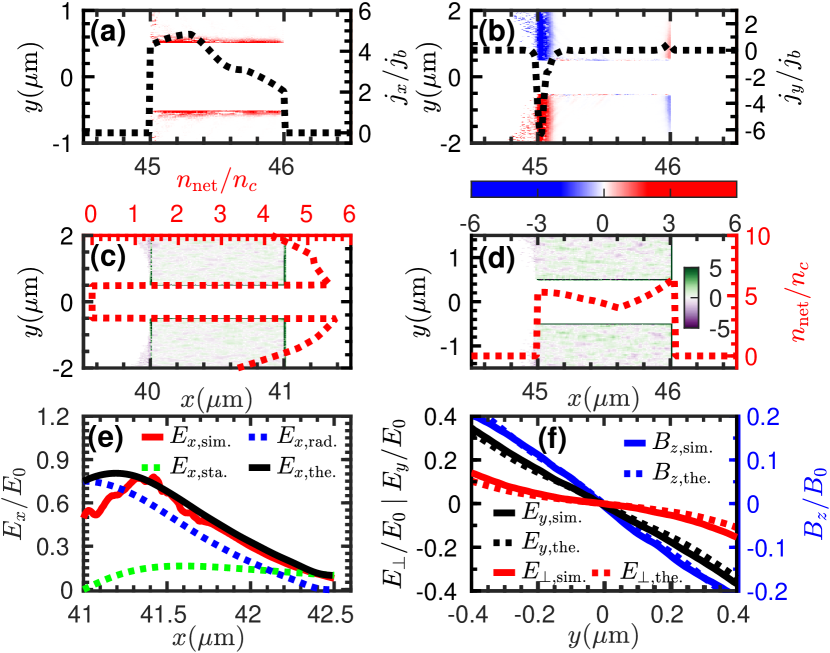
The generation mechanism of acceleration and focusing field in $x$ - $y$ plane are shown in Fig. $\>3$ . The return current has a high-density $j_{\rm ret.}\sim\left|j_{b}\right|L/2l_{s}{\exp}(1)\approx 6|j_{b}|$ [75, 109]; see Figs.3(a) and 3(b), where $l_{s}=c/\omega_{\rm p}=0.029\>{\rm\mu m}$ , $\omega_{\rm p}=\sqrt{n_{e}e^{2}/m_{e}\epsilon_{0}}$ , and $j_{b}=-ev_{b}n_{b}\approx-2.14\times 10^{16}\>{\rm A/m^{2}}$ are the skin length, plasma frequency, and electron beam current density, respectively. This return current accumulates net charge on the surface of the film; see Figs. 3(c) and 3(d), whose magnitude is proportional to the integral of $j_{\rm ret.}$ over duration of the electron beam’s action on the film, namely $n_{\rm net}\sim(j_{\rm ret.}\times D_{n}/v_{b})/e\approx 4.5\>n_{c}$ , where $D_{n}$ is the distance from the front of the electron beam to the rear surface of the $n$ th layer film. Behind the hole ( $41\>{\rm\mu m}\leq x\leq 42.5\>{\rm\mu m}$ ), the longitudinal acceleration field is composed of an electrostatic part, excited by the net charge, and a transition radiation part, excited by the electron beam. Distribution of the net charge can be approximately modeled by that of a uniformly charged disk of thickness $l_{s}$ , inner radius $R_{1}\approx R_{h}$ , and outer radius $R_{2}\approx 1.5\>{\rm\mu m}$ ; see Fig. 3(c). The electrostatic field strength at any point on the central axis can be approximated by $E_{x,{\rm sta.}}=\frac{(en_{\rm net}l_{s})(x-x_{n})}{2\epsilon_{0}}[\frac{1}{(R_{1}^{2}+(x-x_{n})^{2})^{1/2}}-\frac{1}{(R_{2}^{2}+(x-x_{n})^{2})^{1/2}}]$ of an ideal disk of charge; see Fig. 3(e), where $x_{n}$ is rear surface position of the $n$ th layer film. The transition radiation field can be found from $E_{x,{\rm rad.}}=\sum_{1}^{N_{e}^{n}}\frac{1}{4\pi\epsilon_{0}}\frac{e}{c\pi R}\frac{{\rm sin}\omega_{\rm p}(t-R/c)}{t-R/c}\frac{v_{e}/c{\rm sin}^{2}\theta}{1-(v_{e}/c)^{2}{\rm cos}^{2}\theta}$ [76]; see Fig. 3(e), where $N_{e}^{n}\approx 1.5\times 10^{9}$ is the total number of electrons in the electron beam, extending from $x_{n}$ to $x_{n}+D$ , $v_{e}\approx v_{b}$ is the electron velocity, and $R=\sqrt{(x-x_{n})^{2}+y^{2}+z^{2}}$ is distance between the observation point and rear surface position of the $n$ th layer film, respectively. The total longitudinal acceleration field is $E_{x,{\rm the.}}=E_{x,{\rm sta.}}+E_{x,{\rm rad.}}$ , in agreement with the simulation result $E_{x,{\rm sim.}}$ ; see Fig. 3(e).

Within the hole ( $45\>{\rm\mu m}\leq x\leq 46\>{\rm\mu m}$ ), the transverse field is composed of the transverse electrostatic field, the self-generated field of the electron and positron beams, and the magnetic field generated by the return current. Distribution of the net charge can be approximately modeled by that of a uniformly charged column shell of length $L$ , inner radius $R_{3}\approx R_{h}$ , and outer radius $R_{4}\approx R_{h}+1.5l_{s}$ ; see Fig. 3(d). The transverse electrostatic field excited by this column shell can be approximated by $E_{r,\rm{sta.}}=\frac{2en_{\rm net}}{\pi\epsilon_{0}}\int_{0}^{\infty}[R_{3}K_{1}(kR_{3})-R_{4}K_{1}(kR_{4})][-I_{1}(kr){\rm cos}(kx)]{\rm sin}(k\frac{L}{2})\frac{dk}{k},(k=1,2,3\cdots$ ), where $K_{1}$ and $I_{1}$ are modified Bessel functions. Moreover, initial self-generated field of the electron beam has the components: $E_{r}^{b}=\frac{1}{4\pi\epsilon_{0}}\frac{-2eN_{e}}{\sqrt{2\pi}\sigma_{x}}\frac{1}{r}(1-{\exp}(\frac{-r^{2}}{2\sigma_{r}^{2}})){\exp}(-(x-x_{0}-v_{b}t)^{2}/2\sigma_{x}^{2})$ , $E_{x}^{b}=0$ , and $B_{\phi}^{b}=\sqrt{\mu_{0}\epsilon_{0}}\frac{v_{b}}{c}E_{r}^{b}$ [110, 111], where $N_{e}\approx 3.8\times 10^{9}$ is the total number of electrons in the electron beam. Similarly, the field generated by the positron beam is given by $E_{r}^{b^{\prime}}=\frac{1}{4\pi\epsilon_{0}}\frac{2eN_{p}}{\sqrt{2\pi}\sigma^{\prime}_{x}}\frac{1}{r}(1-{\exp}(\frac{-r^{4}}{{\sigma^{\prime}_{r}}^{4}})){\exp}(-(x-vt)^{4}/{\sigma^{\prime}_{x}}^{4})$ , $E_{x}^{b^{\prime}}=0$ , and $B_{\phi}^{b^{\prime}}=\sqrt{\mu_{0}\epsilon_{0}}\frac{v}{c}E_{r}^{b^{\prime}}$ , where $N_{p}\approx 6.8\times 10^{7}$ is the total number of positrons in the positron beam, $\sigma^{\prime}_{x}\approx 0.3\>{\rm\mu m}$ , and $\sigma^{\prime}_{r}\approx 0.2\>{\rm\mu m}$ , respectively. In the $x$ - $y$ plane, the transverse electric field components are: $E_{y,{\rm sta.}}=E_{r,{\rm sta.}}{\rm cos}\phi$ , $E_{y}^{b}=E_{r}^{b}{\rm cos}\phi$ , and $E_{y}^{b^{\prime}}=E_{r}^{b^{\prime}}{\rm cos}\phi$ . The total transverse electric field is $E_{y,{\rm the.}}=E_{y,{\rm sta.}}+E_{y}^{b}+E_{y}^{b^{\prime}}$ , consistent with $E_{y,\rm{sim.}}$ ; see Fig. 3(f). Furthermore, the plasma return current can be approximated as a finite-length current-carrying cylindrical surface with a radius $R_{5}\approx R_{h}$ ; see Fig. 3(a). The magnetic field is, therefore, given by $B_{r,{\rm ret.}}\approx\frac{\mu_{0}\overline{j_{\rm ret.}}}{4\pi r}(1+\frac{r^{2}-R_{5}^{2}}{\sqrt{(R_{5}^{2}-r^{2})^{2}}})$ . Inside the cylindrical surface ( $r<R_{h}$ ), $B_{r,{\rm ret.}}=0$ . In the $x$ - $y$ plane, the transverse magnetic field is $B_{z}^{b}=B_{\phi}^{b}{\rm cos}\phi$ and $B_{z}^{b^{\prime}}=B_{\phi}^{b^{\prime}}{\rm cos}\phi$ . The total transverse magnetic field is $B_{z,{\rm the.}}=B_{z}^{b}+B_{z}^{b^{\prime}}$ , in agreement with $B_{z,\rm{sim.}}$ ; see Fig. 3(f). Hence, the total transverse focusing field is $E_{\perp,{\rm{\rm the.}}}=E_{y,{\rm{\rm the.}}}-cB_{z,{\rm the.}}$ , in good agreement with $E_{\perp,\rm{sim.}}$ ; see Fig. 3(f). Because $E_{y}^{b}-cB_{z}^{b}=0$ and $E_{y}^{b^{\prime}}-cB_{z}^{b^{\prime}}=0$ , the focusing force is only provided by $E_{y,\rm{sta.}}$ . Moreover, the beam loading effect makes $E_{\varparallel}$ more gentle, which can improve the quality of the positron beam [53], while having little effect on $E_{\perp}$ ; see Figs. S11, S12, and S13.

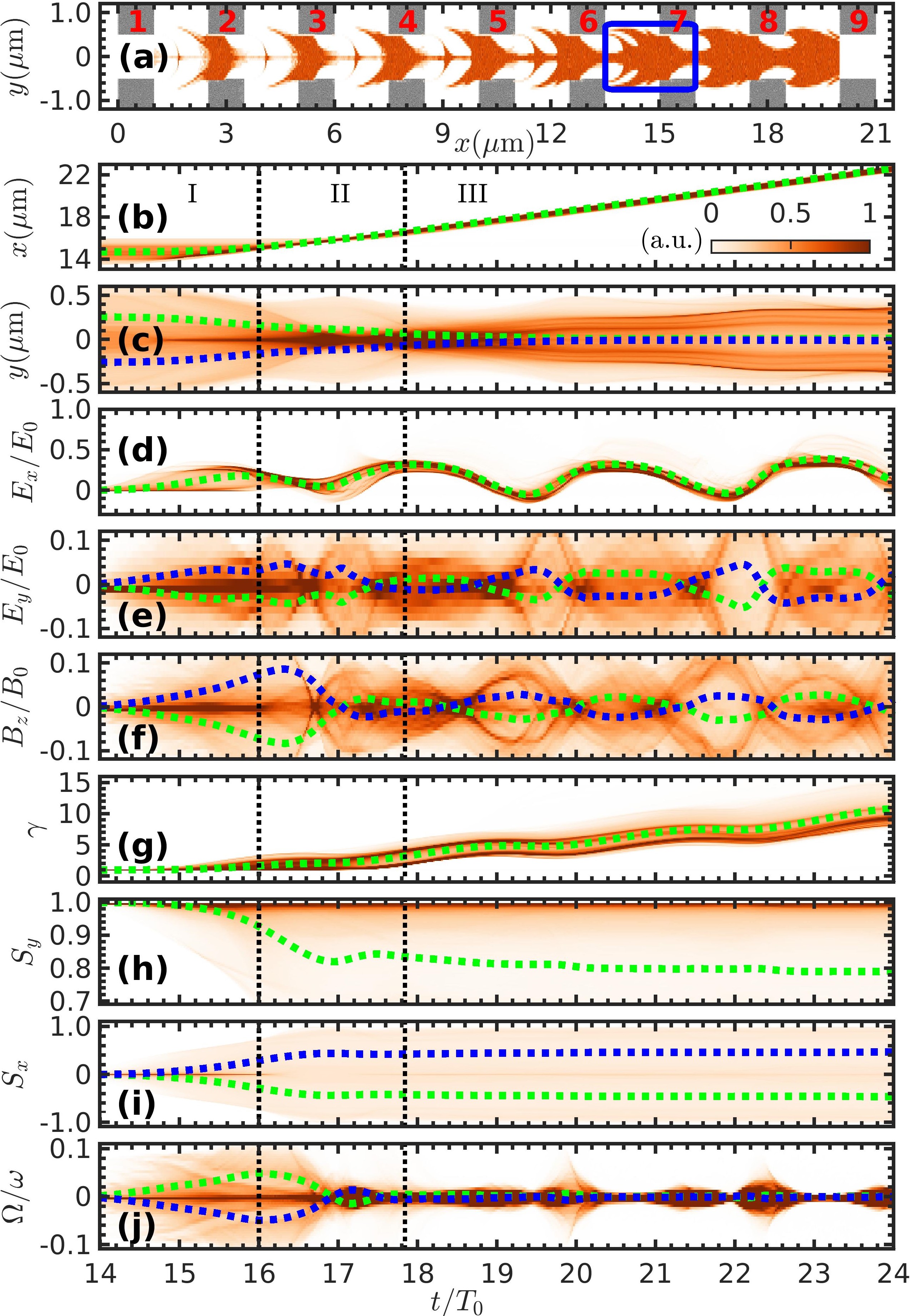
Due to the cylindrical symmetry of our method, for simplicity, we use two-dimensional particle tracking simulation in Fig. $\>4$ to illustrate the capture and spin evolution of the positrons. Other parameters are the same as those in Fig. 2. As the electron beam traverses the multi-layer films, some positrons between adjacent layers and within the hole get captured, exhibiting a periodic structure; see Fig. 4(a). Relative stability of density distribution of the electron beam, throughout the entire capture process; see Fig. S14 in [94], results in small changes to the self-generated, electrostatic, and transition radiation fields. Therefore, capture and spin evolution of the positrons in each period are similar. Here, we only analyze the detailed capture and spin evolution process of the positrons within the period marked by the blue rectangle in Fig. 4(a). This process can be divided into three stages. Stage I ( $14\>T_{\rm 0}\leq t<16\>T_{\rm 0}$ ), positrons move towards the central axis under the action of $E_{y}^{b}$ ; see Figs. 4(c) and 4(e). Meanwhile, $E_{x}$ begins to form and intensify as the electron beam passes through the sixth layer; see Fig. 4(d). The combined action of $E_{x}$ and $B_{z}^{b}$ causes positrons to move in the $+x$ -direction; see Figs. 4(b), 4(d), and 4(f). Under the influence of $B_{z}^{b}$ , spins of the positrons begin to process: $\overline{S_{y}}$ changes from $1$ to $0.93$ , and $\overline{S_{x}}$ changes from $0$ to $\pm\>0.3$ ; see Figs. 4(h) and 4(i). Moreover, due to the relativistic factor $\gamma$ approaches $1$ in this stage; see Fig. 4(g), $\bm{\Omega}_{\rm T}\gg\bm{\Omega}_{\rm a}$ , hence the positron spin precession frequency $\bm{\Omega}\approx\bm{\Omega}_{\rm T}\varpropto-B_{z}\varpropto-B_{z}^{b}$ ; see Figs. 4(f) and 4(j). In Stage II ( $16\>T_{\rm 0}\leq t<17.84\>T_{\rm 0}$ ), most positions are located in the hole of the seventh layer at $16\>T_{\rm 0}$ , and finally pass through the hole driven by $E_{x}$ , moving from $x=15\sim 16\>{\rm\mu m}$ to $16\sim 17\>{\rm\mu m}$ ; see Fig. 4(b). The relativistic factor $\gamma$ increases from $1$ to about $2$ ; see Fig. 4(g). Meanwhile, as the electron beam continues to pass through the seventh layer, $E_{\perp}$ forms in the hole at $t>17\>T_{\rm 0}$ ; see Figs. 4(e) and 4(f), when the net charge begins to form. Under the action of $E_{\perp}$ , positrons continue to move towards the central axis; see Fig. 4(c). The positron spin procession frequency $\bm{\Omega}\approx\bm{\Omega}_{\rm T}\varpropto-B_{z}\varpropto-B_{z,{\rm the.}}$ ; see Figs. 4(f) and 4(j). Consequently, $\overline{S_{y}}$ decreases from $0.93$ to $0.83$ , and $\overline{S_{x}}$ changes from $\pm$ 0.3 to $\pm$ 0.43; see Figs. 4(h) and 4(i). In Stage III ( $t\geq 17.84\>T_{\rm 0}$ ), the positrons undergo cascade acceleration in the middle of the adjacent layer and focusing within the hole; see Figs. 4(d), 4(e), and 4(f). As the positron energy increases, the spin precession frequency $\bm{\Omega}$ approaches zero; see Fig. 4(j), so $\overline{S_{y}}$ and $\overline{S_{x}}$ undergo no significant changes; see Figs. 4(h) and 4(i). We underline that the multi-layer design allows for capturing more positrons, and depolarization by spin precession is small due to the weak magnetic field experienced by most positrons; see Figs. 4(a), and 4(h).

In conclusion, our novel polarized positron acceleration method combines transition radiation and electrostatic fields to achieve high acceleration gradients, providing a promising solution for accelerator miniaturization and cost-effectiveness. It also addresses challenges commonly encountered in PWFA, such as injection and large depolarization. The high-energy, spin-polarized, and dense positron beam generated through our method has great potential for fundamental physics research and practical applications.

Acknowledgments: This work is supported by the National Natural Science Foundation of China (Grants No. U2267204, No. 12275209, No. 12005305, No. U2267204, and No. U2241281), the Foundation of Science and Technology on Plasma Physics Laboratory (No. JCKYS2021212008), the Shaanxi Fundamental Science Research Project for Mathematics and Physics (Grant No. 22JSY014), the Fundamental Research Funds for Central Universities (No. xzy012023046), the Science and Technology Development Fund, Macao SAR (File No. FDCT-0060-2023-RIA1), the Foundation under (Grants No. FY222506000201 and No. FC232412000201), and the Foundation of China Institute of Atomic Energy under (Grant No. YZ222402000401). YIS is supported by an American University of Sharjah Faculty Research Grant (FRG24-E-S29) and acknowledges hospitality at the School of Physics, Xi’an Jiaotong University.

References

Raichle [1985] M. E. Raichle, Positron emission tomography: Progress in brain imaging, Nature 317, 574 (1985).
Gidley et al. [1982] D. W. Gidley, A. R. Köymen, and T. W. Capehart, Polarized low-energy positrons: A new probe of surface magnetism, Phys. Rev. Lett. 49, 1779 (1982).
Hugenschmidt [2016] C. Hugenschmidt, Positrons in surface physics, Surf. Sci. Rep. 71, 547 (2016).
Selim [2021] F. Selim, Positron annihilation spectroscopy of defects in nuclear and irradiated materials- a review, Mater. Charact. 174, 110952 (2021).
Chen and Fiuza [2023] H. Chen and F. Fiuza, Perspectives on relativistic electron–positron pair plasma experiments of astrophysical relevance using high-power lasers, Phys. Plasmas 30, 020601 (2023).
Musumeci et al. [2022] P. Musumeci, C. Boffo, S. S. Bulanov, I. Chaikovska, A. F. Golfe, S. Gessner, J. Grames, R. Hessami, Y. Ivanyushenkov, A. Lankford, G. Loisch, G. Moortgat-Pick, S. Nagaitsev, S. Riemann, P. Sievers, C. Tenholt, and K. Yokoya, Positron sources for future high energy physics colliders (2022), arXiv:2204.13245 .
Moortgat-Pick et al. [2008] G. Moortgat-Pick, T. Abe, G. Alexander, B. Ananthanarayan, A. Babich, V. Bharadwaj, D. Barber, A. Bartl, A. Brachmann, S. Chen, J. Clarke, J. Clendenin, J. Dainton, K. Desch, M. Diehl, B. Dobos, T. Dorland, H. Dreiner, H. Eberl, J. Ellis, K. Flöttmann, H. Fraas, F. Franco-Sollova, F. Franke, A. Freitas, J. Goodson, J. Gray, A. Han, S. Heinemeyer, S. Hesselbach, T. Hirose, K. Hohenwarter-Sodek, A. Juste, J. Kalinowski, T. Kernreiter, O. Kittel, S. Kraml, U. Langenfeld, W. Majerotto, A. Martinez, H.-U. Martyn, A. Mikhailichenko, C. Milstene, W. Menges, N. Meyners, K. Mönig, K. Moffeit, S. Moretti, O. Nachtmann, F. Nagel, T. Nakanishi, U. Nauenberg, H. Nowak, T. Omori, P. Osland, A. Pankov, N. Paver, R. Pitthan, R. Pöschl, W. Porod, J. Proulx, P. Richardson, S. Riemann, S. Rindani, T. Rizzo, A. Schälicke, P. Schüler, C. Schwanenberger, D. Scott, J. Sheppard, R. Singh, A. Sopczak, H. Spiesberger, A. Stahl, H. Steiner, A. Wagner, A. Weber, G. Weiglein, G. Wilson, M. Woods, P. Zerwas, J. Zhang, and F. Zomer, Polarized positrons and electrons at the linear collider, Phys. Rep. 460, 131 (2008).
Arı et al. [2016] V. Arı, A. Billur, S. İnan, and M. Köksal, Anomalous ww $\gamma$ couplings with beam polarization at the compact linear collider, Nucl. Phys. B 906, 211 (2016).
Duan et al. [2019] Z. Duan, J. Gao, X. P. Li, D. Wang, Y. W. Wang, W. Xia, Q. Xu, C. H. Yu, and Y. Zhang, Concepts of longitudinally polarized electron and positron colliding beams in the circular electron positron collider (2019).
Chaikovska et al. [2022] I. Chaikovska, R. Chehab, V. Kubytskyi, S. Ogur, A. Ushakov, A. Variola, P. Sievers, P. Musumeci, L. Bandiera, Y. Enomoto, M. Hogan, and P. Martyshkin, Positron sources: from conventional to advanced accelerator concepts-based colliders, J. Instrum. 17, P05015 (2022).
Sarri et al. [2015] G. Sarri, K. Poder, J. M. Cole, W. Schumaker, A. Di Piazza, B. Reville, T. Dzelzainis, D. Doria, L. A. Gizzi, G. Grittani, S. Kar, C. H. Keitel, K. Krushelnick, S. Kuschel, S. P. D. Mangles, Z. Najmudin, N. Shukla, L. O. Silva, D. Symes, A. G. R. Thomas, M. Vargas, J. Vieira, and M. Zepf, Generation of neutral and high-density electron–positron pair plasmas in the laboratory, Nat. Commun. 6, 6747 (2015).
Warwick et al. [2017] J. Warwick, T. Dzelzainis, M. E. Dieckmann, W. Schumaker, D. Doria, L. Romagnani, K. Poder, J. M. Cole, A. Alejo, M. Yeung, K. Krushelnick, S. P. D. Mangles, Z. Najmudin, B. Reville, G. M. Samarin, D. D. Symes, A. G. R. Thomas, M. Borghesi, and G. Sarri, Experimental observation of a current-driven instability in a neutral electron-positron beam, Phys. Rev. Lett. 119, 185002 (2017).
Bernauer [2018] J. C. Bernauer, Positron beams and two-photon exchange: The key to precision form factors, AIP Conf. Proc. 1970, 020009 (2018).
Boyko et al. [2023] I. Boyko, V. Bytev, and A. Zhemchugov, Two-photon physics at future electron-positron colliders*, Chinese Phys. C 47, 013001 (2023).
Afanasev et al. [2019] A. Afanasev, I. Albayrak, S. Ali, M. Amaryan, A. D’Angelo, J. Annand, J. Arrington, A. Asaturyan, H. Avakian, T. Averett, L. Barion, M. Battaglieri, V. Bellini, V. Berdnikov, J. Bernauer, A. Biselli, M. Boer, M. Bondì, K. T. Brinkmann, B. Briscoe, V. Burkert, A. Camsonne, T. Cao, L. Cardman, M. Carmignotto, L. Causse, A. Celentano, P. Chatagnon, G. Ciullo, M. Contalbrigo, D. Day, M. Defurne, S. Diehl, B. Dongwi, R. Dupré, D. Dutta, M. Ehrhart, L. Elouadrhiri, R. Ent, I. Fernando, A. Filippi, Y. Furletova, H. Gao, A. Gasparian, D. Gaskell, F. Georges, F. X. Girod, J. Grames, C. Gu, M. Guidal, D. Hamilton, D. Hasell, D. Higinbotham, M. Hoballah, T. Horn, C. Hyde, A. Italiano, N. Kalantarians, G. Kalicy, D. Keller, C. Keppel, M. Kerver, P. King, E. Kinney, H. S. Ko, M. Kohl, V. Kubarovsky, L. Lanza, P. Lenisa, N. Liyanage, S. Liuti, J. Mamei, D. Marchand, P. Markowitz, L. Marsicano, M. Mazouz, M. McCaughan, B. McKinnon, M. Mihovilovič, R. Milner, A. Mkrtchyan, H. Mkrtchyan, A. Movsisyan, C. M. Camacho, P. Nadel-Turońs, M. D. Napoli, J. Nazeer, S. Niccolai, G. Niculescu, R. Novotny, L. Pappalardo, R. Paremuzyan, E. Pasyuk, T. Patel, I. Pegg, D. Perera, A. Puckett, N. Randazzo, M. Rashad, M. Rathnayake, A. Rizzo, J. Roche, O. Rondon, A. Schmidt, M. Shabestari, Y. Sharabian, S. Širca, D. Sokhan, A. Somov, N. Sparveris, S. Stepanyan, I. Strakovsky, V. Tadevosyan, M. Tiefenback, R. Trotta, R. D. Vita, H. Voskanyan, E. Voutier, R. Wang, B. Wojtsekhowski, S. Wood, H. G. Zaunick, S. Zhamkochyan, J. Zhang, S. Zhao, X. Zheng, and C. Zorn, Physics with positron beams at jefferson lab 12 GeV (2019), arXiv:1906.09419 .
Androic et al. [2013] D. Androic, D. S. Armstrong, A. Asaturyan, T. Averett, J. Balewski, J. Beaufait, R. S. Beminiwattha, J. Benesch, F. Benmokhtar, J. Birchall, R. D. Carlini, G. D. Cates, J. C. Cornejo, S. Covrig, M. M. Dalton, C. A. Davis, W. Deconinck, J. Diefenbach, J. F. Dowd, J. A. Dunne, D. Dutta, W. S. Duvall, M. Elaasar, W. R. Falk, J. M. Finn, T. Forest, D. Gaskell, M. T. W. Gericke, J. Grames, V. M. Gray, K. Grimm, F. Guo, J. R. Hoskins, K. Johnston, D. Jones, M. Jones, R. Jones, M. Kargiantoulakis, P. M. King, E. Korkmaz, S. Kowalski, J. Leacock, J. Leckey, A. R. Lee, J. H. Lee, L. Lee, S. MacEwan, D. Mack, J. A. Magee, R. Mahurin, J. Mammei, J. W. Martin, M. J. McHugh, D. Meekins, J. Mei, R. Michaels, A. Micherdzinska, A. Mkrtchyan, H. Mkrtchyan, N. Morgan, K. E. Myers, A. Narayan, L. Z. Ndukum, V. Nelyubin, Nuruzzaman, W. T. H. van Oers, A. K. Opper, S. A. Page, J. Pan, K. D. Paschke, S. K. Phillips, M. L. Pitt, M. Poelker, J. F. Rajotte, W. D. Ramsay, J. Roche, B. Sawatzky, T. Seva, M. H. Shabestari, R. Silwal, N. Simicevic, G. R. Smith, P. Solvignon, D. T. Spayde, A. Subedi, R. Subedi, R. Suleiman, V. Tadevosyan, W. A. Tobias, V. Tvaskis, B. Waidyawansa, P. Wang, S. P. Wells, S. A. Wood, S. Yang, R. D. Young, and S. Zhamkochyan, First determination of the weak charge of the proton, Phys. Rev. Lett. 111, 141803 (2013).
Scott et al. [2011] D. J. Scott, J. A. Clarke, D. E. Baynham, V. Bayliss, T. Bradshaw, G. Burton, A. Brummitt, S. Carr, A. Lintern, J. Rochford, O. Taylor, and Y. Ivanyushenkov, Demonstration of a high-field short-period superconducting helical undulator suitable for future tev-scale linear collider positron sources, Phys. Rev. Lett. 107, 174803 (2011).
Vauth and List [2016] A. Vauth and J. List, Beam polarization at the ILC: Physics case and realization, Int. J. Mod. Phys. Conf. Ser. 40, 1660003 (2016).
Gschwendtner and Muggli [2019] E. Gschwendtner and P. Muggli, Plasma wakefield accelerators, Nat. Rev. Phys. 1, 246 (2019).
Ruffini et al. [2010] R. Ruffini, G. Vereshchagin, and S.-S. Xue, Electron–positron pairs in physics and astrophysics: From heavy nuclei to black holes, Phys. Rep. 487, 1 (2010).
Harding and Lai [2006] A. K. Harding and D. Lai, Physics of strongly magnetized neutron stars, Rep. Prog. Phys. 69, 2631 (2006).
Breuer and Hommelhoff [2013] J. Breuer and P. Hommelhoff, Laser-based acceleration of nonrelativistic electrons at a dielectric structure, Phys. Rev. Lett. 111, 134803 (2013).
Peralta et al. [2013] E. A. Peralta, K. Soong, R. J. England, E. R. Colby, Z. Wu, B. Montazeri, C. McGuinness, J. McNeur, K. J. Leedle, D. Walz, E. B. Sozer, B. Cowan, B. Schwartz, G. Travish, and R. L. Byer, Demonstration of electron acceleration in a laser-driven dielectric microstructure, Nature 503, 91 (2013).
England et al. [2014] R. J. England, R. J. Noble, K. Bane, D. H. Dowell, C.-K. Ng, J. E. Spencer, S. Tantawi, Z. Wu, R. L. Byer, E. Peralta, K. Soong, C.-M. Chang, B. Montazeri, S. J. Wolf, B. Cowan, J. Dawson, W. Gai, P. Hommelhoff, Y.-C. Huang, C. Jing, C. McGuinness, R. B. Palmer, B. Naranjo, J. Rosenzweig, G. Travish, A. Mizrahi, L. Schachter, C. Sears, G. R. Werner, and R. B. Yoder, Dielectric laser accelerators, Rev. Mod. Phys. 86, 1337 (2014).
Wei et al. [2017] Y. Wei, M. Ibison, G. Xia, J. D. A. Smith, and C. P. Welsch, Dual-grating dielectric accelerators driven by a pulse-front-tilted laser, Appl. Opt. 56, 8201 (2017).
Tajima and Cavenago [1987] T. Tajima and M. Cavenago, Crystal x-ray accelerator, Phys. Rev. Lett. 59, 1440 (1987).
Chen and Noble [1997] P. Chen and R. J. Noble, Crystal channel collider: Ultra-high energy and luminosity in the next century, AIP Conf. Proc. 398, 273 (1997).
Sahai et al. [2019] A. A. Sahai, T. Tajima, P. Taborek, and V. D. Shiltsev, Solid-state tube wakefield accelerator using surface waves in crystals, Int. J. Mod. Phys. A 34, 1943009 (2019).
Gilljohann et al. [2023] M. F. Gilljohann, Y. Mankovska, P. San Miguel Claveria, A. Sytov, L. Bandiera, R. Ariniello, X. Davoine, H. Ekerfelt, F. Fiuza, L. Gremillet, A. Knetsch, B. Martinez, A. Matheron, H. Piekarz, D. Storey, P. Taborek, T. Tajima, V. Shiltsev, and S. Corde, Channeling acceleration in crystals and nanostructures and studies of solid plasmas: new opportunities, J. Instrum. 18, P11008 (2023).
Bonatto et al. [2023] A. Bonatto, G. Xia, O. Apsimon, C. Bontoiu, E. Kukstas, V. Rodin, M. Yadav, C. P. Welsch, and J. Resta-López, Exploring ultra-high-intensity wakefields in carbon nanotube arrays: An effective plasma-density approach, Phys. Plasmas 30, 033105 (2023).
Martín-Luna et al. [2023] P. Martín-Luna, A. Bonatto, C. Bontoiu, G. Xia, and J. Resta-López, Excitation of wakefields in carbon nanotubes: a hydrodynamic model approach, New J. Phys. 25, 123029 (2023).
Chen et al. [1985] P. Chen, J. M. Dawson, R. W. Huff, and T. Katsouleas, Acceleration of electrons by the interaction of a bunched electron beam with a plasma, Phys. Rev. Lett. 54, 693 (1985).
Litos et al. [2014] M. Litos, E. Adli, W. An, C. I. Clarke, C. E. Clayton, S. Corde, J. P. Delahaye, R. J. England, A. S. Fisher, J. Frederico, S. Gessner, S. Z. Green, M. J. Hogan, C. Joshi, W. Lu, K. A. Marsh, W. B. Mori, P. Muggli, N. Vafaei-Najafabadi, D. Walz, G. White, Z. Wu, V. Yakimenko, and G. Yocky, High-efficiency acceleration of an electron beam in a plasma wakefield accelerator, Nature 515, 92 (2014).
Tajima and Dawson [1979] T. Tajima and J. M. Dawson, Laser electron accelerator, Phys. Rev. Lett. 43, 267 (1979).
Esarey et al. [2009] E. Esarey, C. B. Schroeder, and W. P. Leemans, Physics of laser-driven plasma-based electron accelerators, Rev. Mod. Phys. 81, 1229 (2009).
Kalmykov et al. [2009] S. Kalmykov, S. A. Yi, V. Khudik, and G. Shvets, Electron self-injection and trapping into an evolving plasma bubble, Phys. Rev. Lett. 103, 135004 (2009).
Lu et al. [2007] W. Lu, M. Tzoufras, C. Joshi, F. S. Tsung, W. B. Mori, J. Vieira, R. A. Fonseca, and L. O. Silva, Generating multi-gev electron bunches using single stage laser wakefield acceleration in a 3d nonlinear regime, Phys. Rev. Accel. Beams 10, 061301 (2007).
Blumenfeld et al. [2007] I. Blumenfeld, C. E. Clayton, F.-J. Decker, M. J. Hogan, C. Huang, R. Ischebeck, R. Iverson, C. Joshi, T. Katsouleas, N. Kirby, W. Lu, K. A. Marsh, W. B. Mori, P. Muggli, E. Oz, R. H. Siemann, D. Walz, and M. Zhou, Energy doubling of 42 GeV electrons in a metre-scale plasma wakefield accelerator, Nature 445, 741 (2007).
Wu et al. [2019] Y. P. Wu, J. F. Hua, Z. Zhou, J. Zhang, S. Liu, B. Peng, Y. Fang, Z. Nie, X. N. Ning, C.-H. Pai, Y. C. Du, W. Lu, C. J. Zhang, W. B. Mori, and C. Joshi, Phase space dynamics of a plasma wakefield dechirper for energy spread reduction, Phys. Rev. Lett. 122, 204804 (2019).
Pompili et al. [2021] R. Pompili, D. Alesini, M. P. Anania, M. Behtouei, M. Bellaveglia, A. Biagioni, F. G. Bisesto, M. Cesarini, E. Chiadroni, A. Cianchi, G. Costa, M. Croia, A. Del Dotto, D. Di Giovenale, M. Diomede, F. Dipace, M. Ferrario, A. Giribono, V. Lollo, L. Magnisi, M. Marongiu, A. Mostacci, L. Piersanti, G. Di Pirro, S. Romeo, A. R. Rossi, J. Scifo, V. Shpakov, C. Vaccarezza, F. Villa, and A. Zigler, Energy spread minimization in a beam-driven plasma wakefield accelerator, Nat. Phys. 17, 499 (2021).
Cao et al. [2024] G. J. Cao, C. A. Lindstrøm, E. Adli, S. Corde, and S. Gessner, Positron acceleration in plasma wakefields, Phys. Rev. Accel. Beams 27, 034801 (2024).
Blue et al. [2003] B. E. Blue, C. E. Clayton, C. L. O’Connell, F.-J. Decker, M. J. Hogan, C. Huang, R. Iverson, C. Joshi, T. C. Katsouleas, W. Lu, K. A. Marsh, W. B. Mori, P. Muggli, R. Siemann, and D. Walz, Plasma-wakefield acceleration of an intense positron beam, Phys. Rev. Lett. 90, 214801 (2003).
Corde et al. [2015] S. Corde, E. Adli, J. M. Allen, W. An, C. I. Clarke, C. E. Clayton, J. P. Delahaye, J. Frederico, S. Gessner, S. Z. Green, M. J. Hogan, C. Joshi, N. Lipkowitz, M. Litos, W. Lu, K. A. Marsh, W. B. Mori, M. Schmeltz, N. Vafaei-Najafabadi, D. Walz, V. Yakimenko, and G. Yocky, Multi-gigaelectronvolt acceleration of positrons in a self-loaded plasma wakefield, Nature 524, 442 (2015).
Jain et al. [2015] N. Jain, T. M. Antonsen, and J. P. Palastro, Positron acceleration by plasma wakefields driven by a hollow electron beam, Phys. Rev. Lett. 115, 195001 (2015).
Vieira and Mendonça [2014] J. Vieira and J. T. Mendonça, Nonlinear laser driven donut wakefields for positron and electron acceleration, Phys. Rev. Lett. 112, 215001 (2014).
Diederichs et al. [2019] S. Diederichs, T. J. Mehrling, C. Benedetti, C. B. Schroeder, A. Knetsch, E. Esarey, and J. Osterhoff, Positron transport and acceleration in beam-driven plasma wakefield accelerators using plasma columns, Phys. Rev. Accel. Beams 22, 081301 (2019).
Diederichs et al. [2020] S. Diederichs, C. Benedetti, E. Esarey, J. Osterhoff, and C. B. Schroeder, High-quality positron acceleration in beam-driven plasma accelerators, Phys. Rev. Accel. Beams 23, 121301 (2020).
Liu et al. [2023] W.-Y. Liu, X.-L. Zhu, M. Chen, S.-M. Weng, F. He, Z.-M. Sheng, and J. Zhang, Tail-wave-assisted positron acceleration in nonlinear laser plasma wakefields, Phys. Rev. Appl. 19, 044048 (2023).
Reichwein et al. [2022] L. Reichwein, A. Pukhov, A. Golovanov, and I. Y. Kostyukov, Positron acceleration via laser-augmented blowouts in two-column plasma structures, Phys. Rev. E 105, 055207 (2022).
Yi et al. [2014] L. Yi, B. Shen, L. Ji, K. Lotov, A. Sosedkin, XiaomeiZhang, W. Wang, J. Xu, Y. Shi, L. Zhang, and Z. Xu, Positron acceleration in a hollow plasma channel up to tev regime, Sci. Rep. 4, 4171 (2014).
Gessner et al. [2016] S. Gessner, E. Adli, J. M. Allen, W. An, C. I. Clarke, C. E. Clayton, S. Corde, J. P. Delahaye, J. Frederico, S. Z. Green, C. Hast, M. J. Hogan, C. Joshi, C. A. Lindstrøm, N. Lipkowitz, M. Litos, W. Lu, K. A. Marsh, W. B. Mori, B. O’Shea, N. Vafaei-Najafabadi, D. Walz, V. Yakimenko, and G. Yocky, Demonstration of a positron beam-driven hollow channel plasma wakefield accelerator, Nat. Commun. 7, 11785 (2016).
Li et al. [2019] Y. Li, G. Xia, K. V. Lotov, A. P. Sosedkin, and Y. Zhao, High-quality positrons from a multi-proton bunch driven hollow plasma wakefield accelerator, Plasma Phys. Controlled Fusion 61, 025012 (2019).
Silva et al. [2021] T. Silva, L. D. Amorim, M. C. Downer, M. J. Hogan, V. Yakimenko, R. Zgadzaj, and J. Vieira, Stable positron acceleration in thin, warm, hollow plasma channels, Phys. Rev. Lett. 127, 104801 (2021).
Zhou et al. [2022] S. Zhou, J. Hua, W. Lu, W. An, Q. Su, W. B. Mori, and C. Joshi, High efficiency uniform positron beam loading in a hollow channel plasma wakefield accelerator, Phys. Rev. Accel. Beams 25, 091303 (2022).
Zhou et al. [2021] S. Zhou, J. Hua, W. An, W. B. Mori, C. Joshi, J. Gao, and W. Lu, High efficiency uniform wakefield acceleration of a positron beam using stable asymmetric mode in a hollow channel plasma, Phys. Rev. Lett. 127, 174801 (2021).
Liu et al. [2022] W.-Y. Liu, K. Xue, F. Wan, M. Chen, J.-X. Li, F. Liu, S.-M. Weng, Z.-M. Sheng, and J. Zhang, Trapping and acceleration of spin-polarized positrons from $\gamma$ photon splitting in wakefields, Phys. Rev. Res. 4, L022028 (2022).
Martinez et al. [2023] B. Martinez, B. Barbosa, and M. Vranic, Creation and direct laser acceleration of positrons in a single stage, Phys. Rev. Accel. Beams 26, 011301 (2023).
Vranic et al. [2018] M. Vranic, O. Klimo, G. Korn, and S. Weber, Multi-gev electron-positron beam generation from laser-electron scattering, Sci. Rep. 8, 4702 (2018).
Fedotov et al. [2023] A. Fedotov, A. Ilderton, F. Karbstein, B. King, D. Seipt, H. Taya, and G. Torgrimsson, Advances in QED with intense background fields, Phys. Rep. 1010, 1 (2023).
Di Piazza et al. [2012] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, and C. H. Keitel, Extremely high-intensity laser interactions with fundamental quantum systems, Rev. Mod. Phys. 84, 1177 (2012).
Gonoskov et al. [2022] A. Gonoskov, T. G. Blackburn, M. Marklund, and S. S. Bulanov, Charged particle motion and radiation in strong electromagnetic fields, Rev. Mod. Phys. 94, 045001 (2022).
Li et al. [2020] Y.-F. Li, R. Shaisultanov, Y.-Y. Chen, F. Wan, K. Z. Hatsagortsyan, C. H. Keitel, and J.-X. Li, Polarized ultrashort brilliant multi-gev $\gamma$ rays via single-shot laser-electron interaction, Phys. Rev. Lett. 124, 014801 (2020).
Xue et al. [2020] K. Xue, Z.-K. Dou, F. Wan, T.-P. Yu, W.-M. Wang, J.-R. Ren, Q. Zhao, Y.-T. Zhao, Z.-F. Xu, and J.-X. Li, Generation of highly-polarized high-energy brilliant $\gamma$ -rays via laser-plasma interaction, Matter Radiat. at Extremes 5, 054402 (2020).
Wan et al. [2020] F. Wan, R. Shaisultanov, Y.-F. Li, K. Z. Hatsagortsyan, C. H. Keitel, and J.-X. Li, Ultrarelativistic polarized positron jets via collision of electron and ultraintense laser beams, Phys. Lett. B 800, 135120 (2020).
Chen et al. [2019] Y.-Y. Chen, P.-L. He, R. Shaisultanov, K. Z. Hatsagortsyan, and C. H. Keitel, Polarized positron beams via intense two-color laser pulses, Phys. Rev. Lett. 123, 174801 (2019).
Si et al. [2023] M. Si, Y. Huang, B. Shen, Z. Xu, M. Ruan, T. Yu, X. Wang, and Y. Chen, Novel positron acceleration by continuous coherent mid-infrared radiation in a micro-tube (2023), arXiv:2302.12418 .
Zhao et al. [2023] J. Zhao, Y.-T. Hu, H. Zhang, Y. Lu, L.-X. Hu, F.-Q. Shao, and T.-P. Yu, Multistage positron acceleration by an electron beam-driven strong terahertz radiation, Photonics 10, 364 (2023).
Xu et al. [2023] Z. Xu, B. Shen, M. Si, and Y. Huang, Positron acceleration by terahertz wave and electron beam in plasma channel, New J. Phys. 25, 063013 (2023).
Alexander et al. [2008] G. Alexander, J. Barley, Y. Batygin, S. Berridge, V. Bharadwaj, G. Bower, W. Bugg, F.-J. Decker, R. Dollan, Y. Efremenko, V. Gharibyan, C. Hast, R. Iverson, H. Kolanoski, J. Kovermann, K. Laihem, T. Lohse, K. T. McDonald, A. A. Mikhailichenko, G. A. Moortgat-Pick, P. Pahl, R. Pitthan, R. Pöschl, E. Reinherz-Aronis, S. Riemann, A. Schälicke, K. P. Schüler, T. Schweizer, D. Scott, J. C. Sheppard, A. Stahl, Z. M. Szalata, D. Walz, and A. W. Weidemann, Observation of polarized positrons from an undulator-based source, Phys. Rev. Lett. 100, 210801 (2008).
Omori et al. [2006] T. Omori, M. Fukuda, T. Hirose, Y. Kurihara, R. Kuroda, M. Nomura, A. Ohashi, T. Okugi, K. Sakaue, T. Saito, J. Urakawa, M. Washio, and I. Yamazaki, Efficient propagation of polarization from laser photons to positrons through compton scattering and electron-positron pair creation, Phys. Rev. Lett. 96, 114801 (2006).
Abbott et al. [2016] D. Abbott, P. Adderley, A. Adeyemi, P. Aguilera, M. Ali, H. Areti, M. Baylac, J. Benesch, G. Bosson, B. Cade, A. Camsonne, L. S. Cardman, J. Clark, P. Cole, S. Covert, C. Cuevas, O. Dadoun, D. Dale, H. Dong, J. Dumas, E. Fanchini, T. Forest, E. Forman, A. Freyberger, E. Froidefond, S. Golge, J. Grames, P. Guèye, J. Hansknecht, P. Harrell, J. Hoskins, C. Hyde, B. Josey, R. Kazimi, Y. Kim, D. Machie, K. Mahoney, R. Mammei, M. Marton, J. McCarter, M. McCaughan, M. McHugh, D. McNulty, K. E. Mesick, T. Michaelides, R. Michaels, B. Moffit, D. Moser, C. Muñoz Camacho, J.-F. Muraz, A. Opper, M. Poelker, J.-S. Réal, L. Richardson, S. Setiniyaz, M. Stutzman, R. Suleiman, C. Tennant, C. Tsai, D. Turner, M. Ungaro, A. Variola, E. Voutier, Y. Wang, and Y. Zhang (PEPPo Collaboration), Production of highly polarized positrons using polarized electrons at MeV energies, Phys. Rev. Lett. 116, 214801 (2016).
Myatt et al. [2009] J. Myatt, J. A. Delettrez, A. V. Maximov, D. D. Meyerhofer, R. W. Short, C. Stoeckl, and M. Storm, Optimizing electron-positron pair production on kilojoule-class high-intensity lasers for the purpose of pair-plasma creation, Phys. Rev. E 79, 066409 (2009).
Xu et al. [2020] Z. Xu, L. Yi, B. Shen, J. Xu, L. Ji, T. Xu, L. Zhang, S. Li, and Z. Xu, Driving positron beam acceleration with coherent transition radiation, Commun. Phys. 3, 191 (2020).
Yan et al. [2017] Y. Yan, Y. Wu, J. Chen, M. Yu, K. Dong, and Y. Gu, Positron acceleration by sheath field in ultra-intense laser–solid interactions, Plasma Phys. Controlled Fusion 59, 045015 (2017).
Miller [2012] R. Miller, An introduction to the physics of intense charged particle beams (Springer Science & Business Media, 2012).
Bolotovskii and Serov [2009] B. M. Bolotovskii and A. V. Serov, Features of the transition radiation field, Phys.Usp. 52, 487 (2009).
Greaves and Surko [1995] R. G. Greaves and C. M. Surko, An electron-positron beam-plasma experiment, Phys. Rev. Lett. 75, 3846 (1995).
Pedersen et al. [2012] T. S. Pedersen, J. R. Danielson, C. Hugenschmidt, G. Marx, X. Sarasola, F. Schauer, L. Schweikhard, C. M. Surko, and E. Winkler, Plans for the creation and studies of electron–positron plasmas in a stellarator, New J. Phys. 14, 035010 (2012).
Hugenschmidt et al. [2012] C. Hugenschmidt, C. Piochacz, M. Reiner, and K. Schreckenbach, The NEPOMUC upgrade and advanced positron beam experiments, New J. Phys. 14, 055027 (2012).
Stenson et al. [2018] E. V. Stenson, S. Nißl, U. Hergenhahn, J. Horn-Stanja, M. Singer, H. Saitoh, T. S. Pedersen, J. R. Danielson, M. R. Stoneking, M. Dickmann, and C. Hugenschmidt, Lossless positron injection into a magnetic dipole trap, Phys. Rev. Lett. 121, 235005 (2018).
Stoneking et al. [2020] M. R. Stoneking, T. S. Pedersen, P. Helander, H. Chen, U. Hergenhahn, E. V. Stenson, G. Fiksel, J. von der Linden, H. Saitoh, C. M. Surko, J. R. Danielson, C. Hugenschmidt, J. Horn-Stanja, A. Mishchenko, D. Kennedy, A. Deller, A. Card, S. Nißl, M. Singer, M. Singer, S. König, L. Willingale, J. Peebles, M. R. Edwards, and K. Chin, A new frontier in laboratory physics: magnetized electron–positron plasmas, J. Plasma Phys. 86, 155860601 (2020).
Arrowsmith et al. [2021] C. D. Arrowsmith, N. Shukla, N. Charitonidis, R. Boni, H. Chen, T. Davenne, A. Dyson, D. H. Froula, J. T. Gudmundsson, B. T. Huffman, Y. Kadi, B. Reville, S. Richardson, S. Sarkar, J. L. Shaw, L. O. Silva, P. Simon, R. M. G. M. Trines, R. Bingham, and G. Gregori, Generating ultradense pair beams using 400 $\mathrm{GeV}/c$ protons, Phys. Rev. Res. 3, 023103 (2021).
Dumas et al. [2009] J. Dumas, J. Grames, and E. Voutier, Polarized Positrons at Jefferson Lab, AIP Conf. Proc. 1149, 1184 (2009).
il Kim et al. [2024] H. il Kim, Y. Noh, J. Song, S. Lee, J. Won, C. Song, L. Bae, C.-M. Ryu, C. H. Nam, and W. Bang, Electron-positron generation by irradiating various metallic materials with laser-accelerated electrons, Results Phys. 57, 107310 (2024).
Xue et al. [2023] K. Xue, T. Sun, K.-J. Wei, Z.-P. Li, Q. Zhao, F. Wan, C. Lv, Y.-T. Zhao, Z.-F. Xu, and J.-X. Li, Generation of high-density high-polarization positrons via single-shot strong laser-foil interaction, Phys. Rev. Lett. 131, 175101 (2023).
Song et al. [2022] H.-H. Song, W.-M. Wang, and Y.-T. Li, Dense polarized positrons from laser-irradiated foil targets in the qed regime, Phys. Rev. Lett. 129, 035001 (2022).
Zhu et al. [2016] X.-L. Zhu, T.-P. Yu, Z.-M. Sheng, Y. Yin, I. C. E. Turcu, and A. Pukhov, Dense gev electron–positron pairs generated by lasers in near-critical-density plasmas, Nat. Commun. 7, 13686 (2016).
Luo et al. [2018] W. Luo, S.-D. Wu, W.-Y. Liu, Y.-Y. Ma, F.-Y. Li, T. Yuan, J.-Y. Yu, M. Chen, and Z.-M. Sheng, Enhanced electron-positron pair production by two obliquely incident lasers interacting with a solid target, Plasma Phys. Controlled Fusion 60, 095006 (2018).
He et al. [2021] Y. He, T. G. Blackburn, T. Toncian, and A. V. Arefiev, Dominance of $\gamma$ - $\gamma$ electron-positron pair creation in a plasma driven by high-intensity lasers, Commun. Phys. 4, 139 (2021).
Gu et al. [2019] Y.-J. Gu, M. Jirka, O. Klimo, and S. Weber, Gamma photons and electron-positron pairs from ultra-intense laser-matter interaction: A comparative study of proposed configurations, Matter Radiat. at Extremes 4, 064403 (2019).
Gu et al. [2018] Y.-J. Gu, O. Klimo, S. V. Bulanov, and S. Weber, Brilliant gamma-ray beam and electron–positron pair production by enhanced attosecond pulses, Commun. Phys. 1, 93 (2018).
Lukin et al. [2023] D. M. Lukin, M. A. Guidry, J. Yang, M. Ghezellou, S. Deb Mishra, H. Abe, T. Ohshima, J. Ul-Hassan, and J. Vučković, Two-emitter multimode cavity quantum electrodynamics in thin-film silicon carbide photonics, Phys. Rev. X 13, 011005 (2023).
Reiserer and Rempe [2015] A. Reiserer and G. Rempe, Cavity-based quantum networks with single atoms and optical photons, Rev. Mod. Phys. 87, 1379 (2015).
[94] See Supplemental Materials for detailed simulation methods, experimental feasibility, other acceleration cases, energy transfer efficiency and emittance, film ionization, influence of spin flip, electron-positron annihilation, beam loading effect, and electron beam self-polarization and progation.
Wan et al. [2023] F. Wan, C. Lv, K. Xue, Z.-K. Dou, Q. Zhao, M. Ababekri, W.-Q. Wei, Z.-P. Li, Y.-T. Zhao, and J.-X. Li, Simulations of spin/polarization-resolved laser–plasma interactions in the nonlinear QED regime, Matter Radiat. at Extremes 8, 064002 (2023).
Gonsalves et al. [2019] A. J. Gonsalves, K. Nakamura, J. Daniels, C. Benedetti, C. Pieronek, T. C. H. de Raadt, S. Steinke, J. H. Bin, S. S. Bulanov, J. van Tilborg, C. G. R. Geddes, C. B. Schroeder, C. Tóth, E. Esarey, K. Swanson, L. Fan-Chiang, G. Bagdasarov, N. Bobrova, V. Gasilov, G. Korn, P. Sasorov, and W. P. Leemans, Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide, Phys. Rev. Lett. 122, 084801 (2019).
Zhu et al. [2020] X.-L. Zhu, M. Chen, S.-M. Weng, T.-P. Yu, W.-M. Wang, F. He, Z.-M. Sheng, P. McKenna, D. A. Jaroszynski, and J. Zhang, Extremely brilliant GeV $\gamma$ -rays from a two-stage laser-plasma accelerator, Sci. Adv. 6, eaaz7240 (2020).
Yakimenko et al. [2019] V. Yakimenko, L. Alsberg, E. Bong, G. Bouchard, C. Clarke, C. Emma, S. Green, C. Hast, M. J. Hogan, J. Seabury, N. Lipkowitz, B. O’Shea, D. Storey, G. White, and G. Yocky, FACET-II facility for advanced accelerator experimental tests, Phys. Rev. Accel. Beams 22, 101301 (2019).
Doss et al. [2019] C. E. Doss, E. Adli, R. Ariniello, J. Cary, S. Corde, B. Hidding, M. J. Hogan, K. Hunt-Stone, C. Joshi, K. A. Marsh, J. B. Rosenzweig, N. Vafaei-Najafabadi, V. Yakimenko, and M. Litos, Laser-ionized, beam-driven, underdense, passive thin plasma lens, Phys. Rev. Accel. Beams 22, 111001 (2019).
Yoon et al. [2019] J. W. Yoon, C. Jeon, J. Shin, S. K. Lee, H. W. Lee, I. W. Choi, H. T. Kim, J. H. Sung, and C. H. Nam, Achieving the laser intensity of $5.5\times 10^{22}{\rm W/cm^{2}}$ with a wavefront-corrected multi-PW laser, Opt. Express 27, 20412 (2019).
Yoon et al. [2021] J. W. Yoon, Y. G. Kim, I. W. Choi, J. H. Sung, H. W. Lee, S. K. Lee, and C. H. Nam, Realization of laser intensity over $10^{23}{\rm W/cm^{2}}$ , Optica 8, 630 (2021).
Danson et al. [2019] C. N. Danson, C. Haefner, J. Bromage, T. Butcher, J.-C. F. Chanteloup, E. A. Chowdhury, A. Galvanauskas, L. A. Gizzi, J. Hein, D. I. Hillier, N. W. Hopps, Y. Kato, E. A. Khazanov, R. Kodama, G. Korn, R. Li, Y. Li, J. Limpert, J. Ma, C. H. Nam, D. Neely, D. Papadopoulos, R. R. Penman, L. Qian, J. J. Rocca, A. A. Shaykin, C. W. Siders, C. Spindloe, S. Szatmári, R. M. G. M. Trines, J. Zhu, P. Zhu, and J. D. Zuegel, Petawatt and exawatt class lasers worldwide, High Power Laser Sci. Eng. 7, e54 (2019).
[103] Extreme Light Infrastructure - ELI Beamlines, http://www.eli-beams.eu.
Extreme Light Infrastructure - Nuclear Physics () [ELI-NP] Extreme Light Infrastructure - Nuclear Physics (ELI-NP), http://www.eli-np.ro.
Gan et al. [2021] Z. Gan, L. Yu, C. Wang, Y. Liu, Y. Xu, W. Li, S. Li, L. Yu, X. Wang, X. Liu, J. Chen, Y. Peng, L. Xu, B. Yao, X. Zhang, L. Chen, Y. Tang, X. Wang, D. Yin, X. Liang, Y. Leng, R. Li, and Z. Xu, The shanghai superintense ultrafast laser facility (SULF) project, in Progress in Ultrafast Intense Laser Science XVI, edited by K. Yamanouchi, K. Midorikawa, and L. Roso (Springer International Publishing, Cham, 2021) pp. 199–217.
Exawatt Center for Extreme Light Studies () [XCELS] Exawatt Center for Extreme Light Studies (XCELS), https://xcels.iapras.ru/.
Brambilla et al. [2018] G. Brambilla, C. Kalapotharakos, A. N. Timokhin, A. K. Harding, and D. Kazanas, Electron–positron pair flow and current composition in the pulsar magnetosphere, Astrophys. J. 858, 81 (2018).
Boehm et al. [2004] C. Boehm, D. Hooper, J. Silk, M. Casse, and J. Paul, Mev dark matter: Has it been detected?, Phys. Rev. Lett. 92, 101301 (2004).
Jiang et al. [2023] K. Jiang, T. W. Huang, R. Li, M. Y. Yu, H. B. Zhuo, S. Z. Wu, C. T. Zhou, and S. C. Ruan, Branching of high-current relativistic electron beam in porous materials, Phys. Rev. Lett. 130, 185001 (2023).
Sampath [2020] A. Sampath, Strong-field QED and collisional effects in electron beam-plasma interaction, Ph.D. thesis (2020).
Sampath et al. [2021] A. Sampath, X. Davoine, S. Corde, L. Gremillet, M. Gilljohann, M. Sangal, C. H. Keitel, R. Ariniello, J. Cary, H. Ekerfelt, C. Emma, F. Fiuza, H. Fujii, M. Hogan, C. Joshi, A. Knetsch, O. Kononenko, V. Lee, M. Litos, K. Marsh, Z. Nie, B. O’Shea, J. R. Peterson, P. S. M. Claveria, D. Storey, Y. Wu, X. Xu, C. Zhang, and M. Tamburini, Extremely dense gamma-ray pulses in electron beam-multifoil collisions, Phys. Rev. Lett. 126, 064801 (2021).