Compact Stein surfaces as branched covers with same branch sets
Abstract.
Loi and Piergallini showed that a smooth compact, connected -manifold with boundary admits a Stein structure if and only if is a simple branched cover of a -disk branched along a positive braided surface in a bidisk . For each integer , we construct a braided surface in and simple branched covers of branched along such that the covers have the same degrees, and they are mutually diffeomorphic, but the Stein structures associated to the covers are mutually not homotopic. Furthermore, by reinterpreting this result in terms of contact topology, for each integer , we also construct a transverse link in the standard contact -sphere and simple branched covers of branched along such that the covers have the same degrees, and they are mutually diffeomorphic, but the contact structures associated to the covers are mutually not isotopic.
2010 Mathematics Subject Classification:
Primary 57M12; Secondary 32Q28, 57R17, 57R651. Introduction.
Compact Stein surfaces are sublevel sets of exhausting strictly plurisubharmonic functions on Stein manifolds. They have been studied by using complex and symplectic geometry. For example, Eliashberg [5] characterized handle decompositions of compact Stein surfaces, and Gompf [11] gave how to draw Kirby diagrams of them. Since early 2000s, compact Stein surfaces also have been examined by using combinatorial techniques, and research on them has been dramatically altered. This development was caused by results of Loi and Piergallini [19] and Akbulut and Ozbagci [1]. They showed that a smooth, oriented, connected, compact -manifold with boundary admits a Stein structure if and only if admits a positive allowable Lefschetz fibration (see Section 2.3). It is known that Lefschetz fibrations are studied through mapping class groups, so group theoretical approaches of them help us to treat compact Stein surfaces. For example, by using such techniques, uniqueness results for Stein fillings of contact -manifolds were proven in [24, 15, 16, 21]. For more various results, we refer the reader to [23] as a survey on this subject.
Loi and Piergallini also showed that a smooth, oriented, connected, compact -manifold with boundary admits a Stein structure if and only if is a simple branched cover of a -disk branched along a positive braided surface in a bidisk (see Definition 2.1 and 2.2), where, by rounding the corner of , it is identified with . Unfortunately, although the fact is well-known, little is known about how Stein structures behave towards positive braided surfaces. We can describe braided surfaces by using combinatorial tools such as chart descriptions, quandles, and braid monodromies (cf. [14]). In order to use them effectively for research on compact Stein surfaces, we need to better understand interactions between Stein structures and braided surfaces.
In this paper, we consider whether or not, for a given positive braided surface , there exist more than one compact Stein surfaces as covers of branched along such that the covers have the same degrees, and they are mutually diffeomorphic but admit mutually distinct Stein structures. The following theorem is a positive answer to this problem.
Theorem 1.1.
For a given integer , there exist a positive braided surface and simple branched covers of branched along such that
-
(1)
the degrees of these covers are same,
-
(2)
are mutually diffeomorphic, and
-
(3)
Stein structures on respectively, which are associated to the covers, are mutually not homotopic.
In the above theorem, we consider as a Stein structure on the branched cover one given by a Lefschetz fibration associated to the branched covering (see Remark 2.5).
This theorem become more interesting, compared with the case of branched covers of and cuspidal curves in . Here, a cuspidal curve is a projective plane curve whose singular points are ordinary nodes and ordinary cusps. Chisini’s conjecture (see [4]) claims that if is a cuspidal curve, a generic branched covering of whose branch set is and degree is at least is unique up to covering isomorphism. Kulikov [17, 18] showed that this conjecture is true under certain conditions. The degree of each simple branched covering we will constructed in the proof of Theorem 1.1 is for each . In addition, according to Rudolph [25], a positive braided surface is isotopic to the intersection of a complex analytic curve with , and the converse is also true. Hence, an analogue of Chisini’s conjecture does not hold for simple branched coverings of whose branch sets are the intersections of complex analytic curves with .
We can reinterpret Theorem 1.1 in terms of contact -manifolds and transverse links. Let be an oriented, connected, closed -manifold. A -plane field on is called a contact structure on if there exists a -form on such that and with respect to the orientation of , and the pair is called a contact manifold. An oriented link in is called a transverse link if is transverse to the contact plane at any point in . Write for a supporting open book decomposition of the standard contact -sphere (cf. [7] for instance). Bennequin [3] showed that any transverse link in can be braided about the binding of .
Corollary 1.2.
For a given integer , there exist a transverse link in and simple branched covers of branched along such that
-
(1)
the degrees of these covers are same,
-
(2)
are mutually diffeomorphic, and
-
(3)
contact structures on respectively, which are associated to the covers, are mutually not isotopic.
Here, a contact structure on a branched cover means one supported by an open book associated to the branched covering.
This article is organized as follows: In Section , we review some definitions and properties of mapping class groups, braided surfaces, positive Lefschetz fibrations and supporting open book decompositions. In Section , first, we observe braids satisfying a certain condition, called liftable braids, and, by using this notion, prove a lemma to construct branched covers of in the proof of Theorem 1.1. Next, we review how to evaluate , where is the first Chern class of a compact Stein surface . Finally, we prove Theorem 1.1 by using contact structures, PALFs and Kirby diagrams coupled with the above lemma.
Throughout this article we will work in the smooth category. We assume that the reader is familiar with basics of Kirby diagrams (see [12, Chapter , ]).
Aknowledgments.
The author would like to express his gratitude to Professor Hisaaki Endo for his encouragement and helpful comments for the draft of this article. He would also like to thank Burak Ozbagci for his helpful comments and fruitful discussions. The author was partially supported by JSPS KAKENHI Grant Number 15J05214.
2. Preliminaries.
2.1. Mapping class groups
Let be an oriented, connected genus surface with marked points and boundary components. We denote the mapping class group of by . More precisely, is the group of isotopy classes of orientation preserving self-diffeomorphisms of which fix the marked points setwise and the boundary pointwise. We also use the notations if , and for . For a simple closed curve in , denotes the right-handed Dehn twist along . Furthermore, for a simple arc connecting two distinct marked points in , write for the right-handed half-twist along . We will use the opposite notation to the usual functional one for the products in , i.e. means that we apply first and then . Moreover, for a subset and , the notation means the image of under .
It is well known that the braid group on strands can be identified with the mapping class group as follows (cf. [9, Section 3.2]): Consider an -marked disk as the unit closed disk with marked points which lie on the real axis. Set as the marked points, where . Define an arc on the real axis to be one with end points in and . Then, the -th standard generator of can be identified with the right-handed half-twist . In this article, under this identification, a simple arc with end points in the set of marked points represents the corresponding element of to the half-twist along the arc.
2.2. Braided surfaces.
Let and be oriented -disks.
Definition 2.1.
A properly embedded surface in is called a (simply) braided surface of degree if the first projection restricts to a simple branched covering of degree .
We will review briefly braid monodromies of braided surfaces (see, for more details, [2, Section 3], [14, Chapter 16, 17], [26, §1, 2]). Before that, we recall a special basis for the fundamental group of a punctured disk. Let be a set of points in the interior of an oriented -disk with the standard orientation and let be a point in . Since the fundamental group is a free group of rank , we give a basis for this group as follows: Take a collection of oriented paths starting from to each , respectively. Assume that and , if , are disjoint except , and the arcs are indexed so that they appear in order as we move counterclockwise about . By using the path , connect to a small oriented disk around each with the same orientation of . Then, we obtain an oriented loop based at , and freely generate . The ordered -tuple is called a Hurwitz system for (see Figure 1).
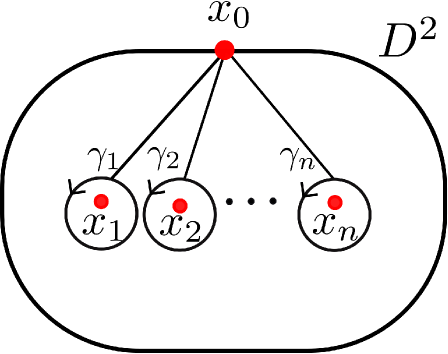
We now turn to the case of braided surfaces. Let be the set of branch points of the branched covering . Fix a point in and Hurwitz system for . For each , the restriction of to induces a trivial disk bundle over . Since for any point , consists of points, each fiber of the disk bundle contains points, which are the intersection points of and . Hence, we associate an element to as a motion of the set over . By this correspondence, we can define a homomorphism by for each . This homomorphism is called a braid monodromy of . The ordered -tuple is also called a braid monodromy of . Since is a simple branched covering, each is a conjugate of for some and . It is known that, for a finite set and representation as above, we can construct a braided surface of degree whose branch set is and braid monodromy is . Obviously, since is a branched covering, we consider a covering monodromy of , i.e. a representation , where is the symmetric permutation group of degree . Note that each is a transposition because is simple. Furthermore, we also remark that is a lift of to .
At the end of this subsection, we define a crucial notion to examine compact Stein surfaces by braided surfaces.
Definition 2.2.
A braided surface is called positive if each is positive, that is, for a braid monodromy of , each is .
2.3. Lefschetz fibrations and simple branched coverings.
We will briefly review positive Lefschetz fibrations and their monodromies (see [12, Chapter 8]).
Let be an oriented, connected, compact -manifold.
Definition 2.3.
A smooth map is called a positive Lefschetz fibration if there exists the set of points of the interior of such that
-
(1)
is a smooth fiber bundle over with fiber diffeomorphic to an oriented compact surface with boundary,
-
(2)
are the critical values of , and each singular fiber has a unique critical point , and
-
(3)
for each and , there are local complex coordinate charts with respect to the orientations of and such that locally f can be written as .
A positive Lefschetz fibration can be described by the mapping class group of the fiber of . Let be a fixed base point. Take a Hurwitz system for . We can consider a homomorphism as follows: The positive Lefschetz fibration restricts to a fiber bundle for each . The monodromy of this fiber bundle is the right-handed Dehn twist along a simple closed curve in . The simple closed curve is called a vanishing cycle of the singular fiber . Define by for each and call a monodromy of . We also call the ordered -tuple a monodromy of . We say a positive Lefschetz fibration to be allowable if all of the vanishing cycles are homologically non-trivial in the fiber. After this, we call a positive allowable Lefschetz fibration a PALF shortly.
The following theorem tells us that PALFs and positive braided surfaces are so important to study compact Stein surfaces.
Theorem 2.4 (Loi and Piergallini [19, Theorem 3] (cf. Akbulut and Ozbagci [1, Theorem 5])).
Let be an oriented, connected, compact -manifold with boundary. Then the following conditions are equivalent:
-
(1)
is a compact Stein surface, that is, admits a Stein structure ;
-
(2)
admits a PALF ;
-
(3)
is a simple branched cover of branched along a positive braided surface in .
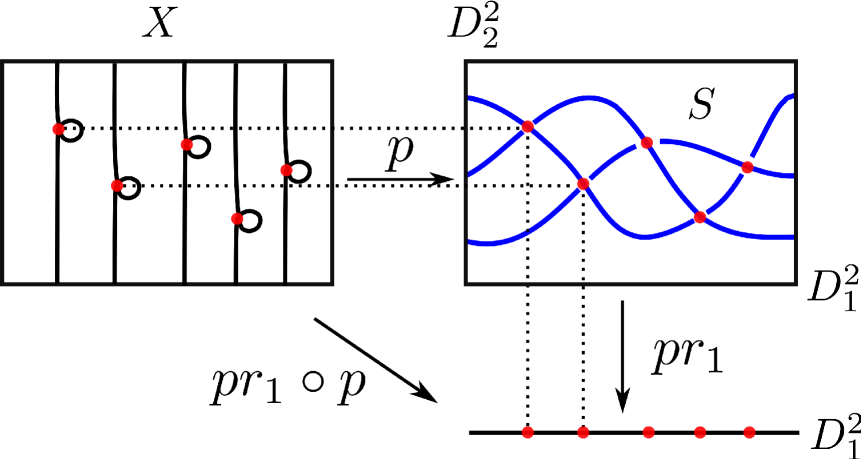
Note that according to [19, Proposition 1, 2] and the proof of Theorem 2.4, for a given PALF , we can construct a simple branched covering whose branch set is a positive braided surface so that and . Conversely, for a given simple branched covering whose branch set is a positive braided surface , is a PALF, and (cf. Figure 2). Suppose is a regular point of the above PALF . The point is also a regular point of . Since is a simple branched covering branched along , restricts to a simple branched covering whose branch set is . It is easy to check that is the regular fiber of .
Remark 2.5.
It is known that the total space of a PALF admits a Stein structure by using the handle decomposition given by the PALF (see. [1, Theorem 5]). As mentioned above, a simple branched covering branched along a positive braided surface gives a PALF . Thus, we equip the cover with the Stein structure coming from the PALF .
2.4. Supporting open book decompositions of tight lens spaces
In order to show Theorem 1.1, we will discuss contact structures on the lens space via open books. Hence, we review contact structures on and their supporting open book decompositions (see [7], [24, Section 2] for more details).
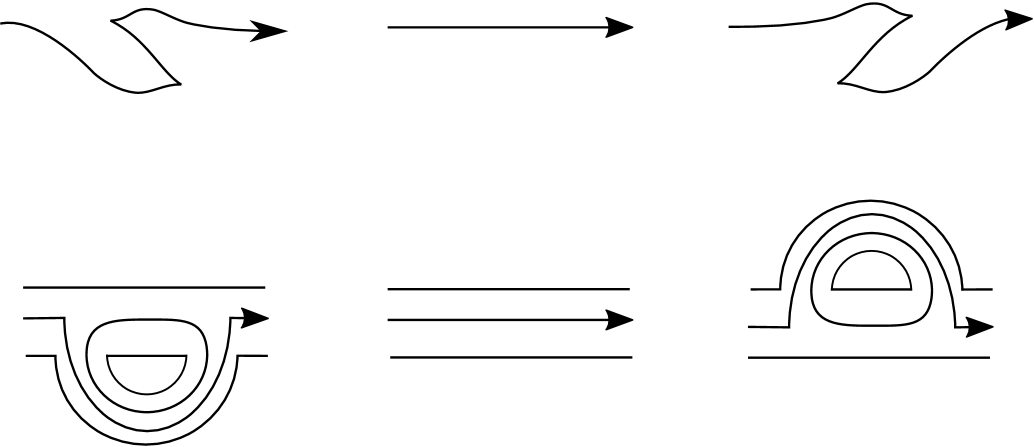
To begin with, we recall a stabilization of a Legendrian knot. Let be a Legendrian knot in . A positive (resp. negative) stabilization on is a Legendrian knot (resp. ) obtained from adding a zig-zag to as depicted in the left (resp. right) of Figure 3. If lies on a page of a supporting open book decomposition of , we stabilize the open book and modify as shown in the bottom of Figure 3.
Let be a tight contact manifold obtained from the Legendrian surgery on the Legendrian knot shown in Figure 4. Since is a Legendrian knot with and , are mutually not Legendrian isotopic by [6, THEOREM 1.1]. Thus, according to Honda’s classification of tight contact structures on (see [13, Theorem 2.1]), are mutually not isotopic tight contact structures. To obtain a supporting open book decomposition of , we explain how is obtained from the Legendrian unknot with . Repeat times positively and negatively stabilizing alternately and, after that, perform times negatively stabilizing the resulting Legendrian knot. Hence, the corresponding open book decomposition of is given as in Figure 5. We write for this open book, where the monodromy is given by

3. Main Results.
Let be an oriented, connected, compact surface with boundary. Suppose is a simple branched covering of degree . This covering determines a covering monodromy . Identifying with as in Section 2.1, we associate with a given the mapping class . We call or liftable with respect to the branched covering with branch points if there exists an orientation preserving diffeomorphism of such that for some representative of . Note that, in this definition, we identify with the base disk with branch points and consider as the mapping class group of . In [20, Lemma ], it is shown that, if is liftable with respect to , then we have
| (3.1) |
for the induced isomorphism .
The following lemma is useful to construct simple branched covers of .
Lemma 3.1.
Let be a positive braided surface of degree with braid monodromy and let be a fixed base point in . Suppose is a simple branched covering of degree with branch set and covering monodromy . If each is liftable with respect to , then there exist an oriented, connected, compact -manifold and a simple branched covering branched along such that .
Proof.
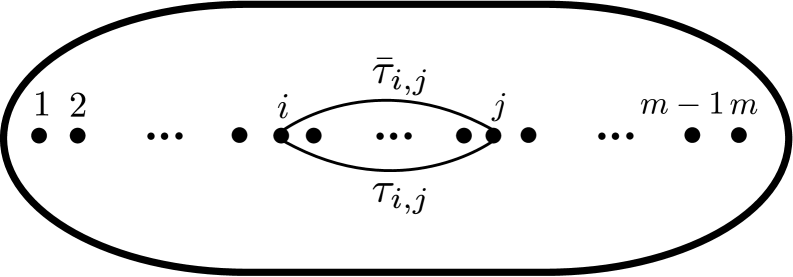
Fix a point . Let be the standard Hurwitz system for as in Figure 1. It is known that
where each is the Artin automorphism of the free group defined by
More precisely we refer the reader to [10, p.133] and [26, PROPOSITION ] about this fundamental group. If we show for each , we conclude that induces a homomorphism , and this determines a simple branched covering of degree whose branch set is .
For each , we have
Since each is liftable and the equation (3.1) holds for any liftable braid,
According to the above construction of , we can easily check .
∎
In the proof of Theorem 1.1, we use the first Chern class of a compact Stein surface. In order to compute them, we make use of the following facts in [8, Section 3] and [11, Proposition 2.3]. Let denote a PALF with fiber and let be the its vanishing cycles. Note that admits a Stein structure by Theorem 2.4. Once choosing a trivialization of the regular fiber of , the rotation number of a simple closed curve is defined with respect to this trivialization. Give an orientation to a vanishing cycle and regard this as a generator of the chain group (cf. [12, Section 4.2]). Then, we have for the first Chern class of ,
Proof of Theorem 1.1.
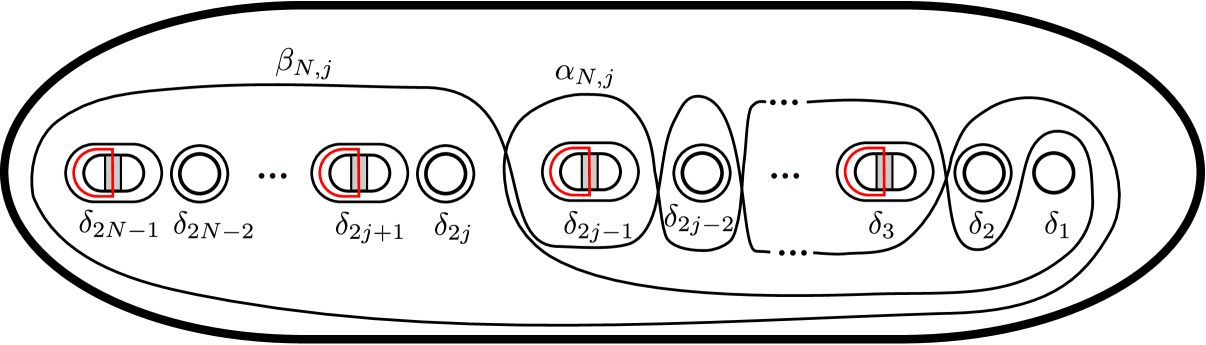
Fix in and in . At first, in order to construct a braided surface, we give elements of for as depicted in Figure 6. After this proof, we give explicit braid words of these braids. Now we define a braided surface of degree to be one with braid monodromy
| (3.2) |
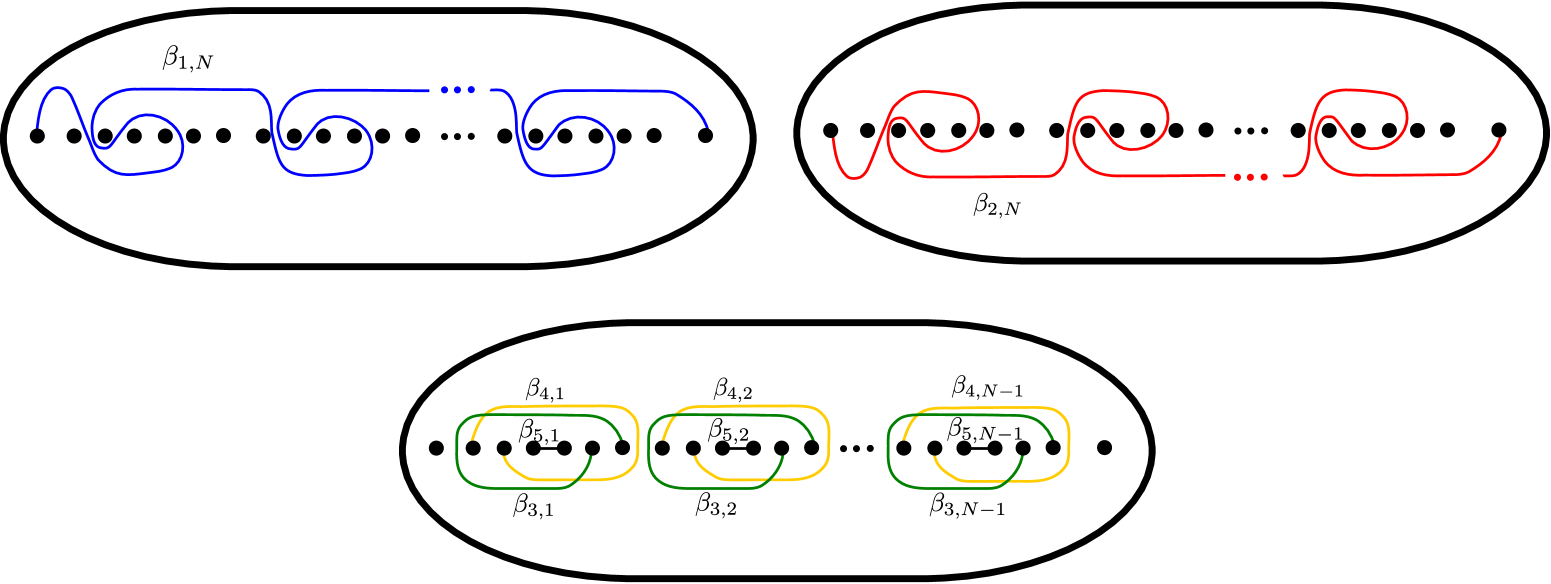
In order to use Lemma 3.1, we need to construct appropriate simple branched covers of . Define a simple branched covering of degree for each as shown in Figure 7. After this proof, by using a covering monodromy, we will describe this covering more explicitly. According to [20, Lemma 3.2.3] for example, we can check that each braid of the tuple (3.2) is liftable with respect to each covering (see Figure 7). It follows from Lemma 3.1 that for each covering , there exists a simple branched covering branched along such that .
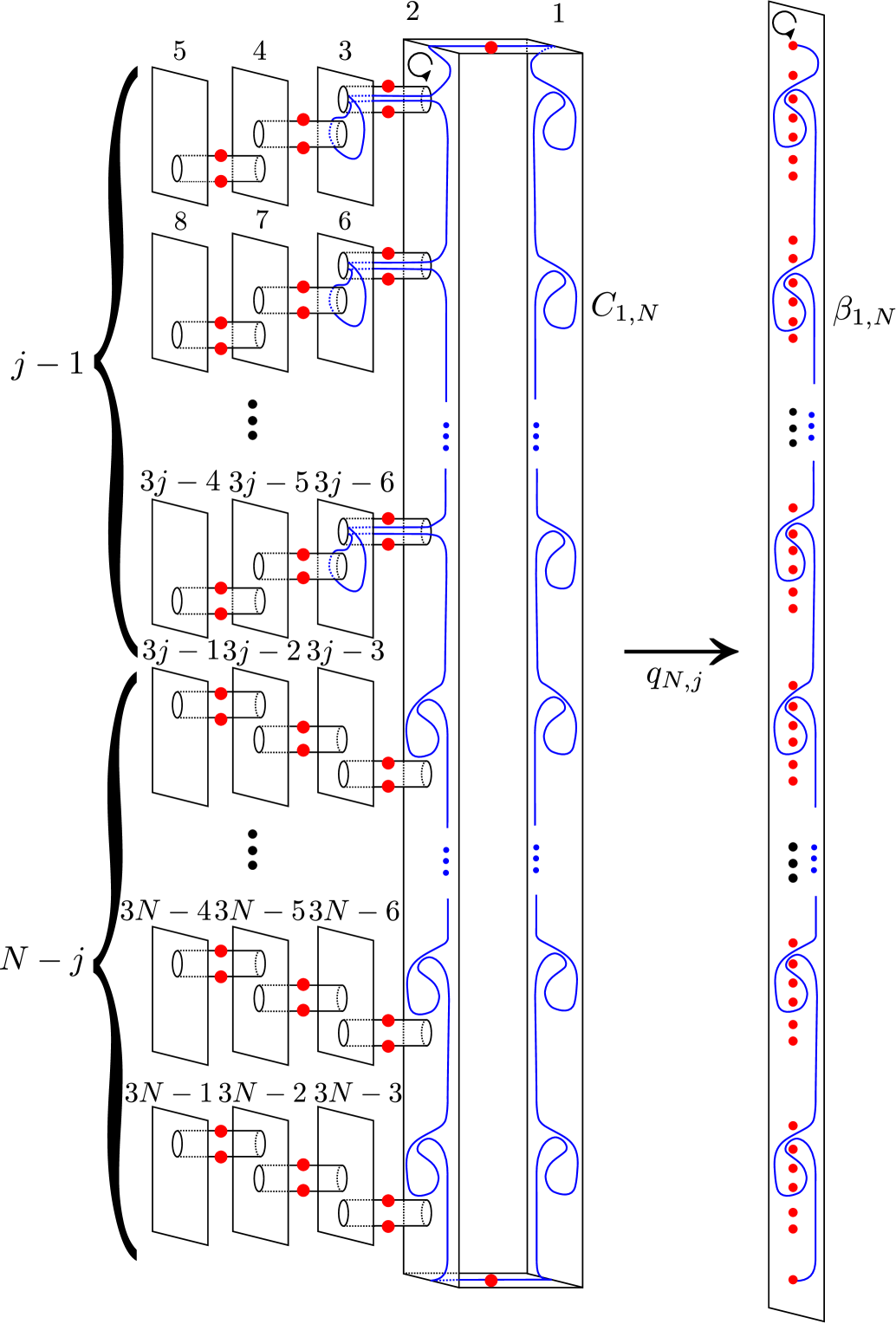
We show that are mutually diffeomorphic. To do this, we will make use of stabilizations of open books and the classification of Stein fillings of a contact manifold. The map is a PALF, and a monodromy of this PALF is the lift of the braid monodromy (3.2) of by . Write
for this monodromy of , where each is the simple closed curve generating the right-handed Dehn twist as the lift of by (see Figure 8). We obtain from this PALF an open book decomposition of with page and monodromy
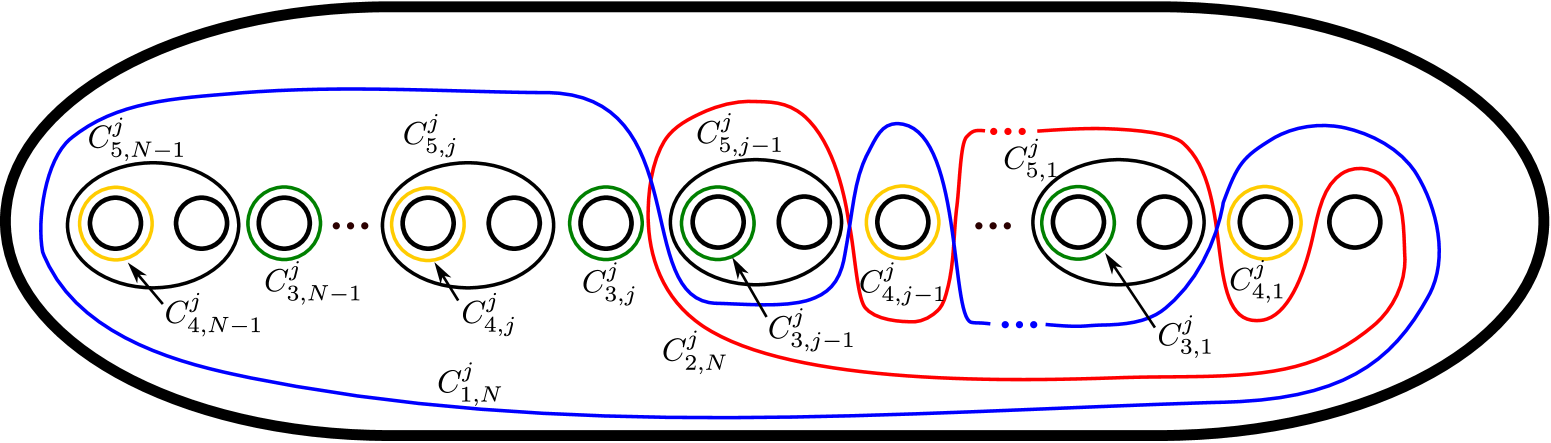
Stabilize the open book times as shown in Figure 10. We can easily check that the resulting stabilization is .
Hence, each is diffeomorphic to . Furthermore, since a positive stabilization of an open book supports the same contact structure supported by the previous one, supports the contact structure . Consider as a Stein filling of and apply to the classification of Stein fillings of . By [24, Corollary 1.3], is diffeomorphic to the disk bundle over with Euler number if ; otherwise either or the rational ball with Euler characteristic . In our case, since admits the PALF with fiber and critical points, the Euler characteristic of is . Thus, every is diffeomorphic to .
To finish the proof, we compute the first Chern class of each , where is the Stein structure associated to . To begin with, we draw a Kirby diagram of from the PALF structure to examine a generator of . Since the regular fiber of is , a Kirby diagram of has dotted -handles . We give orientations to the dotted circles of these -handles, and the attaching circles of these -handles as in Figure 9. These and freely generate the chain group and respectively (cf. [12, Section 4.2] and [22, Section 2.3]). We claim that, for each ,
is a generator of . Let denote the boundary operator on the two chain groups and defined by on the generators and extended linearly. Here, is the linking number of and . We have
and
Therefore,
and is an element of . Since is abelian and the coefficient of each term in is either or , it is a generator of . Now, we can compute . Strictly speaking, can evaluate on the generator of as follows:
Therefore, if , and the Stein structures are mutually not homotopic. ∎
In the following, we give explicit descriptions of the braids and covering in the above proof. These are not essential in this article, hence the reader can skip them if he or she likes.
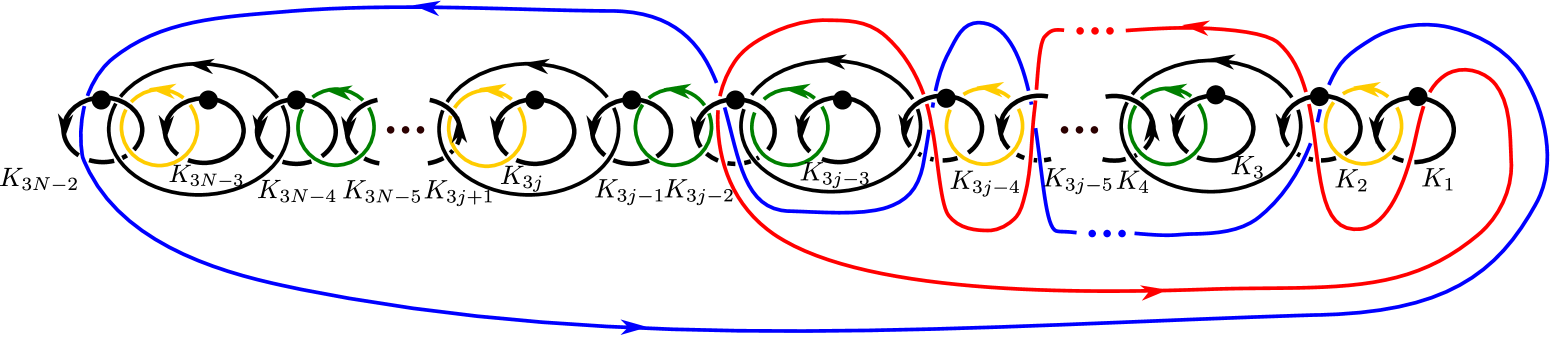
We give first explicit braid words of the above braids. For convenience, set
for , and
where (see Figure 11). Obviously, if , both and are .
Define
Then, we have
Next, we describe the covering by using a covering monodromy. Let be the standard Hurwitz system for . By observing Figure 7, we can check that a covering monodromy of the covering is a homomorphism defined by
Remark 3.2.
In the above proof, the case of is crucial, so we explain how the author found the braided surface . First, he fixed two different branched coverings and and considered liftable braids with respect to both coverings. He observed how corresponding lifts change if we change into , and he chose some braids among them to obtain the braided surface . Finally, drawing Kirby diagrams of the two corresponding covers branched along , he checked whether these covers satisfied the conditions of our theorem. Hence, his construction is very ad hoc. As far as he knows, there is no systematic construction of such a braided surface.
Proof of Corollary 1.2.
Note that the boundary of a given braided surface is contained in , and it is the closure of a braid. Letting be the core of , we obtain from the product structure on , an open book decomposition of whose page is a disk and binding is . This open book supports the standard contact structure on . Thus, we can regard as a transverse link in .
Let be the boundary of in the proof of Theorem 1.1. By the previous argument, can be seen as a transverse link in . Set . are mutually diffeomorphic to . Here, restricts on the boundary to the simple branched cover of branched along . By the proof of Theorem 1.1, the associated open book to the covering is adapted to . By the classification of tight contact structures on in [13, Theorem 2.1], are mutually not isotopic. ∎
References
- [1] S. Akbulut and B. Ozbagci, Lefschetz fibrations on compact Stein surfaces, Geom. Topol. 5 (2001), 939–945.
- [2] N. Apostolakis, R. Piergallini, and D. Zuddas, Lefschetz fibrations over the disc, Proc. Lond. Math. Soc. (3) 107 (2013), no. 2, 340–390.
- [3] D. Bennequin, Entrelacements et équations de Pfaff, Astérisque 107–108 (1983), 87–161.
- [4] O. Chisini, Sulla identita birazionale delle funzioni algebriche di due variabili dotate di una medesima curva di diramazione, Ist. Lombardo Sci. Lett. Cl. Sci. Mat. Nat. Rend. (3) 8(77) (1944). 339–356.
- [5] Y. Eliashberg, Topological characterization of Stein manifolds of dimension 2, Internat. J. Math. 1 (1990), no. 1, 29–46.
- [6] Y. Eliashberg and M. Fraser, Classification of topologically trivial Legendrian knots, Geometry, topology, and dynamics (Montreal, PQ, 1995), 17–51, CRM Proc. Lecture Notes, 15, Amer. Math. Soc., Providence, RI, 1998.
- [7] J. Etnyre, Lectures on open book decompositions and contact structures, Floer Homology, Gauge Theory, and Low Dimensional Topology, Clay Math. Proc. 5, Amer. Math. Soc., Providence, RI, 2006.
- [8] J. Etnyre and B. Ozbagci, Invariants of contact structures from open books, Trans. Amer. Math. Soc. 360 (6) (2008), 3133–3151.
- [9] J. Etnyre and J. Van Horn-Morris, Monoids in the mapping class groups, to appear in Geom. and Topl. Monogr: arXiv:1504.02106.
- [10] R. H. Fox, A quick trip through knot theory, Topology of 3-manifolds and related topics (Prentice-Hall, Englewood Cliffs, N.J., 1962), pp. 120–167.
- [11] R. Gompf, Handlebody construction of Stein surfaces, Ann. of Math. (2) 148 (1998), no. 2, 619–693.
- [12] R. Gompf and A. Stipsicz, 4-Manifolds and Kirby Calculus, Grad. Stud. Math. 20, Amer. Math. Soc., Providence, RI, 1999.
- [13] K. Honda, On the classification of tight contact structures, I.,Geom. Topol. 4 (2000), 309–368.
- [14] S. Kamada, Braid and knot theory in dimension four, Mathematical Surveys and Monographs, 95. American Mathematical Society, Providence, RI, 2002.
- [15] A. Kaloti, Stein fillings of planar open books, arXiv:1311.0208.
- [16] A. Kaloti and Y. Li, Stein fillings of contact -manifolds obtained as Legendrian surgeries, arXiv:1307.4726.
- [17] Vik. S. Kulikov, On Chisini’s conjecture, Izv. Ross. Akad. Nauk Ser. Mat. 63 (1999), no. 6, 83–116; translation in Izv. Math. 63 (1999), no. 6, 1139–1170.
- [18] Vik. S. Kulikov, On Chisini’s conjecture. II, Izv. Ross. Akad. Nauk Ser. Mat. 72 (2008), no. 5, 63–76; translation in Izv. Math. 72 (2008), no. 5, 901–913.
- [19] A. Loi and R. Piergallini, Compact Stein surfaces with boundary as branched covers of , Invent. Math. 143 (2001), no. 2, 325–348.
- [20] J. M. Montesinos-Amilibia and H. R. Morton, Fibred links from closed braids, Proc. London Math. Soc. (3) 62 (1991), no. 1, 167–201.
- [21] T. Oba, Stein fillings of homology -spheres and mapping class groups, arXiv:1407.5257.
- [22] B. Ozbagci and A. Stipsicz, Surgery on contact 3-manifolds and Stein surfaces, Bolyai Soc. Math. Stud. 13, Springer-Verlag, 2004.
- [23] B. Ozbagci, On the topology of fillings of contact 3-manifolds, to appear in Geom. Topol. Monogr. Vol (2015).
- [24] O. Plamenevskaya and J. Van Horn-Morris, Planar open books, monodromy factorizations and symplectic fillings, Geom. Topol. 14 (2010), 2077–2101.
- [25] L. Rudolph Algebraic functions and closed braids, Topology 22 (1983), no. 2, 191–202.
- [26] L. Rudolph, Braided surfaces and Seifert ribbons for closed braids, Comment. Math. Helv. 58 (1983), no. 1, 1–37.