Comparison-based Conversational Recommender System with Relative Bandit Feedback
Abstract.
With the recent advances of conversational recommendations, the recommender system is able to actively and dynamically elicit user preference via conversational interactions. To achieve this, the system periodically queries users’ preference on attributes and collects their feedback. However, most existing conversational recommender systems only enable the user to provide absolute feedback to the attributes. In practice, the absolute feedback is usually limited, as the users tend to provide biased feedback when expressing the preference. Instead, the user is often more inclined to express comparative preferences, since user preferences are inherently relative. To enable users to provide comparative preferences during conversational interactions, we propose a novel comparison-based conversational recommender system. The relative feedback, though more practical, is not easy to be incorporated since its feedback scale is always mismatched with users’ absolute preferences. With effectively collecting and understanding the relative feedback from an interactive manner, we further propose a new bandit algorithm, which we call RelativeConUCB. The experiments on both synthetic and real-world datasets validate the advantage of our proposed method, compared to the existing bandit algorithms in the conversational recommender systems.
1. Introduction
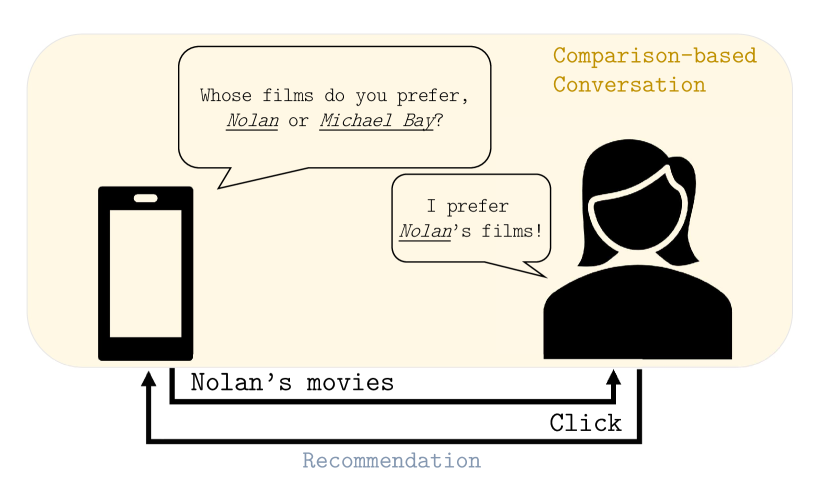
[An illustration for the proposed framework]An illustration for the proposed comparison-based conversational recommender system.
Recommender systems have received enormous attention in this age of big data. In many scenarios, for a recommender system to interact adaptively and optimally with users, it must learn effectively from user feedback. However, for cold-start users with little historical data, it is very challenging to recommend optimally in an online manner. Moreover, the data collected from users during recommendation can be extremely skewed, as users only express their preference on the recommended item. To better elicit users’ preference, the idea of conversational recommender system (CRS) was proposed (Christakopoulou et al., 2016). In addition to collecting responses (e.g., click behaviors) on recommended items, the system also periodically conducts conversations with the user to better elicit preference. This allows the system to provide personalized recommendations based on the responses.
Despite the success of CRSs in recent years, we argue that current conversation mechanism is still limited. Most existing CRSs only allow the user to provide absolute feedback, from which it can be hard to collect useful and accurate information in practice (Joachims et al., 2017; Radlinski et al., 2008; Chapelle et al., 2012; Yue and Joachims, 2009). For example, in a movie recommendation scenario, the agent may query about the user’s preference on a particular category: “Do you like Nolan’s movies?”. As a big fan of Nolan, the user would answer positively. But for a similar question “What about Michael Bay’s movies?”, it could be difficult to answer as the user holds a very mixed attitude towards the director’s works. The love felt for the series of Transformers would eventually induce another positive answer. The contradictory feedback misleads the agent to believe that the user admires both directors equally. To address this issue, we consider asking relative questions to elicit the user’s preference. We argue that relative feedback can be more accurate, since user preferences are inherently relative.
Motivated by the above considerations, we propose to build a comparison-based conversational recommender system. To the best of our knowledge, few works have reached this topic. The system follows the conventional CRS scenario, recommending items sequentially to the user based on contextual information. Compared to existing CRSs, the proposed framework differs on how to conduct conversations. The comparison-based conversational recommender asks relative questions over key-terms, and then receives relative feedback inferring the user’s comparative preference. Similar to that in (Zhang et al., 2020), a key-term is a category-like concept, representing a specific group of items. Movies directed by Nolan is an example of a key-term in the mentioned scenario.
In spite of the mentioned superiority of relative feedback, it could be difficult to incorporate relative feedback due to the mismatch between comparative signals and the underlying user preferences. With effectively collecting and understanding the relative feedback from an interactive manner, we further propose a new bandit algorithm, which we call RelativeConUCB. RelativeConUCB formulates conversation and recommendation as a two-stage learning process. When conducting conversations, RelativeConUCB selects the pair of key-terms which maximizes error reduction, and queries the user’s comparative preference over it. To incorporate relative feedback, we develop three different mechanisms. The experiments show that our algorithm performs competitively well compared to existing bandit algorithms in the conversational recommender systems.
In summary, we make three major contributions:
-
•
We present a novel comparison-based CRS, which allows users to provide relative feedback to the comparisons of key-terms. This extends the framework of existing CRSs.
-
•
We propose a new bandit algorithm RelativeConUCB to build a comparison-based CRS.
-
•
Experiments on both synthetic and real-world datasets clearly show the advantages of our method.
The rest of the paper is organized as follows. We specify the considered comparison-based conversational recommender system in Section 2. In Section 3 we introduce the RelativeConUCB algorithm in details. The experimental setup and results for evaluation are presented in Section 4. Finally, we discuss some related works in Section 5 and then conclude our work in Section 6.
2. System Overview
In this section we will formulate how our comparison-based conversational recommender system works. We start by introducing the conventional contextual bandit scenario, and then extend the system, equipping it with the power to conduct comparison-based conversations.
2.1. Contextual Bandit
Contextual bandits’ objective is to optimize the expected cumulative rewards in a long run. To achieve this, they need to acquire enough information about arms while simultaneously utilizing the available knowledge to choose the best arm.
Suppose there is a finite set of arms (e.g., movies in the domain of movie recommendation) denoted by an index set in the system. The agent will interact with a user with unknown feature consecutively for rounds. At each round , the agent only has access to a subset of arms , from which the agent needs to choose an arm based on its observed contextual vector and recommend it to the user. The agent will then receive a binary reward representing the click behavior:
| (1) |
The target of the agent is to maximize the cumulative reward or, equivalently, to minimize the cumulative regret in rounds of interaction:
| (2) |
where regret accumulates as sub-optimal arms are selected.
2.2. Comparison-based CRS
A recent work (Zhang et al., 2020) extends the contextual bandit scenario for conversational recommendation. It allows the agent to occasionally conduct conversations with users, asking the user’s preference over key-terms. Specifically, a key-term can be a category or a common attribute (e.g., the category of comedy movies in movie recommendation). Key-terms in the system are denoted by an index set . The relationship between arms and key-terms are defined by a weighted bipartite graph , where key-term is associated to arm with weight . To normalize, we assume , . The contextual vector for key-term is then formulated as .
2.2.1. Relative Feedback
In the above conversational recommender system, the agent is only allowed to ask the user absolute questions like “Are you interested in Nolan’s films?” We argue that it is usually unpractical, as the user may have very biased attitudes towards the key-terms, in which case the agent can only collect limited information. Comparative preferences in the meanwhile are potentially more informative and cheaper to collect. Therefore, we design the comparison-based conversation scenario. To conduct conversations, the agent queries relative questions over pairs of key-terms. For example, as illustrated in Figure 1, the agent may ask “Whose films do you prefer, Nolan or Michael Bay?”. It then receives the feedback inferring the user’s comparative preference. To simplify, we assume no abstention, making the feedback binary. Furthermore, we assume the feedback may be corrupted by Gaussian noise. Suppose the user has an internal valuation towards key-term :
where denotes the random noise. The relative feedback for key-term and is:
| (3) |
2.2.2. Conversation Frequency
Similarly to (Zhang et al., 2020), we model the conversation frequency by a function . Specifically, if , the agent will conduct
| (4) |
conversations with user at the -th round of interaction. In such a manner, the agent will conduct conversations with the user up to round .
2.2.3. Long-run Interaction
To simulate the long-run process of interaction with multiple users, we consider a sequence of iterations described in Algorithm 1. Assume there is an arbitrary distribution over users indicating the user frequency. At each iteration111It needs to clarify that ‘iteration’ considers interaction with multiple users, while ‘round’ refers to interaction with a specific user., an arbitrary user drawn randomly from will arrive. The agent, unknowing the user’s real feature, will then interact with the user as described in Line 1-1 of Algorithm 1. This framework extends the original contextual bandit scenario by considering one particular user may not arrive consecutively.
The overall objective for an agent in the comparison-based CRS is to minimize the cumulative regret induced by all interacted users in a long run:
| (5) |
where index set denotes the users that have interacted with the agent for at least one round and denotes the cumulative regret induced by the historical interaction with user defined in Equation 2.
3. Algorithm
To build a comparison-based conversational recommender system, we propose the RelativeConUCB algorithm.
2) candidate arms , candidate key-terms , weight , and conversation budget ;
3) hyper-parameters , , , , and .
Algorithm 2 describes the proposed RelativeConUCB which implements Line 1-1 of Algorithm 1. Following the work (Zhang et al., 2020), we model the arms and key-terms separately. Specifically, for user the agent has two sets of estimated features and . models the user’s preference on arms, whereas models the user’s preference on key-terms.
At each iteration , user with unknown feature will interact with the agent. The agent then decides whether to conduct conversation based on the user’s historical interactions and the system’s preset conversational frequency function. When conducting conversations, RelativeConUCB selects the pair of key-terms which maximizes error reduction, and queries the user’s comparative preference over them. The received feedback will then be utilized to update , which helps the agent to quickly capture users’ preference and, as the result, to recommend the user’s desired item. To efficiently incorporate feedback, three update mechanisms are proposed. We will discuss them thoroughly in Section 3.1. Finally, RelativeConUCB recommends an item to the user, and receives a reward. The recommendation process relies on a upper-confidence-based strategy. The detailed methods for item recommendation can be found in Section 3.2.
3.1. Comparison-Based Conversation
In this section we will discuss how to conduct comparison-based conversations (Line 2-2 of Algorithm 2). In each conversation, the agent needs to ask a relative question. Once the user expresses comparative preference over the question, our estimation of the user’s parameters can then be updated. To be specific, two key problems will be discussed in details and conquered: 1) how to select key-terms to conduct comparison-based conversations (Line 2 of Algorithm 2); and 2) how to update the model effectively with relative feedback (Line 2 of Algorithm 2).
In this work, we propose three variants of the RelativeConUCB algorithm: Pos, Pos&Neg, and Difference.
3.1.1. Pos and Pos&Neg
On the first attempt, we adopt an absolute model for relative questions inspired by (Christakopoulou et al., 2016). The insight behind the model is that relative feedback inferring the user’s comparative preference can be interpreted as two individual observations of key-term. For example, if the user shows more inclination to comedy movies than sci-fi ones, the agent will translate it into absolute information: 1) the user likes comedy movies; and 2) the user dislikes sci-fi movies. In this manner, we estimate the key-term level preference of user by:
| (6) |
where stands for an absolute observation of key-term with and , and denotes the collected observation dataset of user . Equation 6 has a closed-form solution , where
Based on the above model, we formulate two variants of the proposed algorithm Pos and Pos&Neg. They use the same mechanism to select relative questions. Suppose at -th round of interaction with user , the agent has access a subset of arms and a subset of key-term . The contextual vectors for arms are denoted by , whose rows are composed of . To collect the most informative observations, we expect to select key-terms that minimize the estimation error . To select the optimal key-term to observe, we can approximately choose:
| (7) |
according to Theorem 2 in (Zhang et al., 2020). The essence behind Equation 7 is to greedily choose an key-term that could reduce the most uncertainty in the upcoming round of recommendation.
In this manner, we apply the following mechanism to choose the pair of key-terms: 1) we select a key-term with feature according to Equation 7; 2) then, we conduct a pseudo update by updating the model with according to Algorithm 3; 3) finally, we select another key-term according to Equation 7 with the updated model.
The only difference between two variants is how to interpret relative feedback to update the model or, equivalently, how to construct observation samples.
Suppose during the conversation at round , user expresses that is preferred rather than . The agent will therefore receive relative feedback . Then the agent will update the model for user according to Algorithm 3. For Pos, it incorporates only positive information . For Pos&Neg, the relative feedback is interpreted as two observations of absolute feedback: a positive observation for the preferred key-term and a negative observation for the less preferred key-term.
3.1.2. Difference
The above updating methods deal with relative feedback the same as with absolute feedback, which may not fully utilize the advantages of relative feedback. To improve, we consider training a linear classifier directly on paired data, and develop the updating method Difference.
We still apply the estimation of according to Equation 6. But for Difference, we incorporate the relative feedback as a single observation . This is essentially training a linear classifier of feature difference using ridge regression. Note that the unknown parameters can not be fully identified by relative feedback, as and induce the same comparison results for any pair in expectation. Rather, what the linear classifier actually estimates is the normalized feature vector . On the other hand, in the arm-level recommendation, the agent learns the norm of the feature . In this manner, RelativeConUCB learns users’ preferences effectively in the sense of both absolute correctness and relative relationship.
To design relative questions, we follow the maximum error reduction strategy which leads us to choose the pair based on the feature difference :
| (8) |
The key-term selection strategy described above induces the standard Difference variant. However, since the number of key-terms can be extremely large, the strategy may not be practical as it has a quadratic time complexity. To eschew the problem, we further propose an optimized variant called Difference (fast). When selecting key-terms, it first selects a key-term by Equation 7. Then, with the first key-term fixed, it chooses another key-term based on Equation 8. In Section 4, we will compare these two variants, showing that Difference (fast) only suffers little decrease of performance.
3.2. Item Recommendation
The arm-level recommendation (Line 2-2 of Algorithm 2) is essentially similar to that of LinUCB (Li et al., 2010). The difference is that, to accelerate the process of arm preference learning, the agent utilizes as a guidance of by penalizing the difference between and :
The hyper-parameter balances arm-level and key-term level learning. The closed-form solution for is , where
To balance exploration and exploitation, RelativeConUCB selects an arm to recommend in a upper-confidence based strategy:
| (9) |
where are hyper-parameters, and .
The strategy exploits the current estimation on the reward of arm (the first term of Equation 9). A higher value of the first term indicates that in the previous interaction user has expressed more inclination to arm . On the other hand, in order to eschew being misled by wrong perception, the strategy needs to choose some sub-optimal arms for exploration. This is achieved by including uncertainty estimation (the second and third term of Equation 9). The second term estimates the uncertainty in the arm-level, while the third term estimates the uncertainty from key-term level parameters. Please refer to (Zhang et al., 2020) for more insights.
3.3. Feedback Sharing
In the former sections, we have made no assumption on users’ features. However, in practice, groups of users usually share some similar preferences. A rich body of methods has been proposed to model and exploit users’ similar behaviors such as collaborative filtering (Das et al., 2007). We take a step further and claim that, compared to absolute preferences, comparative preferences could be more consistent among users. The reason is that user biases can be eliminated from the feedback when making comparisons. Therefore, no matter how biased each user is, we can still consider users with similar comparative preferences are of the same type.
Based on the hypothesis, we propose to utilize the similarity by feedback sharing. Suppose the agent interacts with user at iteration . Once we receive relative feedback from , we can update parameters of the similar users all at once:
In this manner, conversation and recommendation actually form a two-stage learning process. When conducting conversations, the agent learns common preferences of a group of users. In the meantime, the received rewards from item recommendation imply users’ individual bias. In section 4, we will compare the performance of sharing absolute feedback and relative feedback. We leave more comprehensive study of sharing mechanism as future work.
4. Experiments
To validate our proposed RelativeConUCB algorithm empirically, we evaluate and compare the performances of several state-of-the-art algorithms on both synthetic and real-world datasets222The source code is available at https://github.com/fffffarmer/RelativeConUCB..
4.1. Experimental Setup
In this section we describe our experimental setup. We start with the baselines to compare. Then we describe how the simulation environment is constructed and the evaluation metrics. Finally, we list several research questions that we seek to answer.
4.1.1. Baselines
The following algorithms are selected as the representative baselines to be compared with:
-
•
LinUCB (Li et al., 2010): A state-of-the-art non-conversational contextual bandit approach.
-
•
ConUCB (Zhang et al., 2020): A recently proposed conversational contextual bandit approach. When conducting conversations with user , it chooses the key-term which maximizes error reduction, queries the user’s preference on it, and receives absolute feedback .
For LinUCB, we set hyper-parameters . For both ConUCB and RelativeConUCB, we set hyper-parameters , , , , according to the default configuration in ConUCB’s public source code.
4.1.2. Simulation
For all experiments, we sequentially simulate iterations. At each iteration , the incoming user with rounds of historical interaction is chosen randomly from the user set . For item recommendation, the agent can select one out of 50 arms in the candidate set , which is randomly drawn from without replacement. The key-term candidate set contains those key-terms that are related to any arm in . Furthermore, we set the conversation frequency function which induces more conversations at the early stage to quickly capture preferences (Zhang et al., 2020). The reward for arms and relative feedback for key-terms are generated by Equation 1 and Equation 3 where . The distribution over users is set uniform, suggesting that each user will averagely interact with the agent for 400 rounds. The final results are reported by conducting 10 repeated runs.
4.1.3. Metrics
We mainly use cumulative regret in Equation 5 to measure the performance of algorithms. As a widely used metric in the multi-armed bandit scenario, it captures the degree of satisfaction the user feels towards recommendation in a long run. Besides, in Section 4.2, we report averaged reward over iterations to help clearly show the gap between different algorithms.
4.1.4. Research Questions
The designed experiments aim to answer the following evaluation questions:
-
RQ1.
Can relative feedback be incorporated well to help preference learning, and which variant of our algorithm is more effective?
-
RQ2.
Can we observe the benefit brought from feedback sharing?
-
RQ3.
Under which circumstances will relative feedback be more superior to absolute feedback?
| Synthetic | Last.FM | Movielens | |
|---|---|---|---|
| # of key-terms | 500 | 2,726 | 5,585 |
| avg. # of related key-terms | 0.521 | 16.55 | 11.37 |
| avg. # of related items | 5.214 | 12.14 | 4.071 |
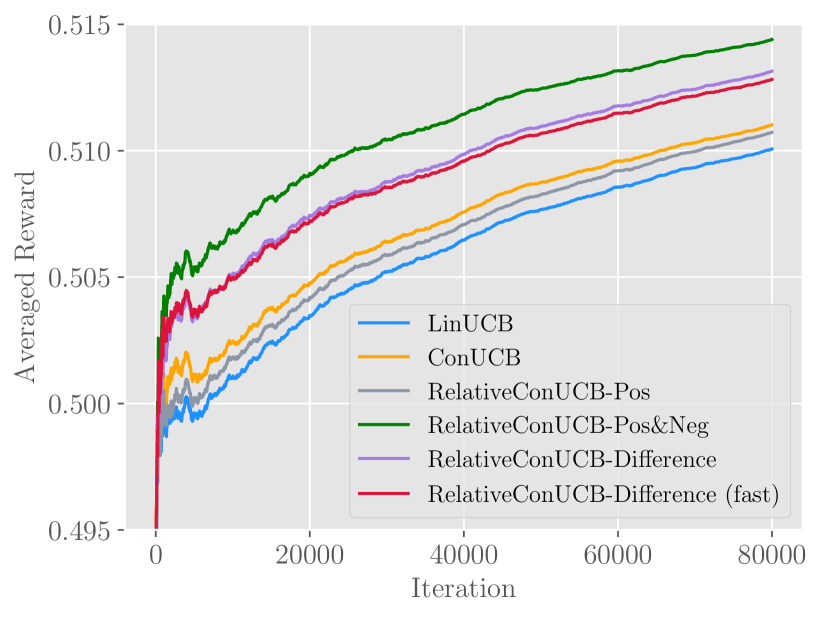
A figure demonstrating the proposed algorithm can outperform the baselines on synthetic data.
4.2. Synthetic Data
To answer RQ1, we first evaluate the algorithms on the synthetic data.
4.2.1. Data Generation
We consider a setting of a user set with , an arm set with and a key-term set with . The relation matrix between arms and key-terms is constructed by the following procedures: 1) for each key-term , we uniformly sample a subset of related arms without replacement, where is an integer drawn uniformly from ; 2) we assign , assuming arm is related to a subset of key-terms .
To generate the arms’ feature vector, we follow similar procedures in (Zhang et al., 2020): 1) we first sample a pseudo feature in dimension for each , where and ; 2) for each arm , its feature vector is drawn from ; 3) finally, feature vectors are normalized and added one more dimension with constant : .
For the ground-truth feature of each user , we first randomly sample a feature vector from . Then we introduce two parameters: and They are drawn uniformly from and respectively, controlling the variance and mean of expected reward. The final feature vector of user is . Note that the normalization step on both item features and user features aims to bound the expected reward , .
4.2.2. Results
The results are given in Figure 2, which plots the averaged reward over 80,000 iterations. We can first notice that all other algorithms outperform LinUCB, indicating the advantage of conducting conversations. The improvements are mainly reflected in the early stage, when the agent frequently converses with users.
Answer to RQ1.
We can clearly observe that variant Pos&Neg and Difference have significant improvements over ConUCB. Pos, on the other hand, performs similarly to LinUCB.
Besides, the performances of Difference (fast) and Difference are very close. This validates that Difference (fast), as an approximation of Difference, can significantly reduce time complexity with little performance decrease.
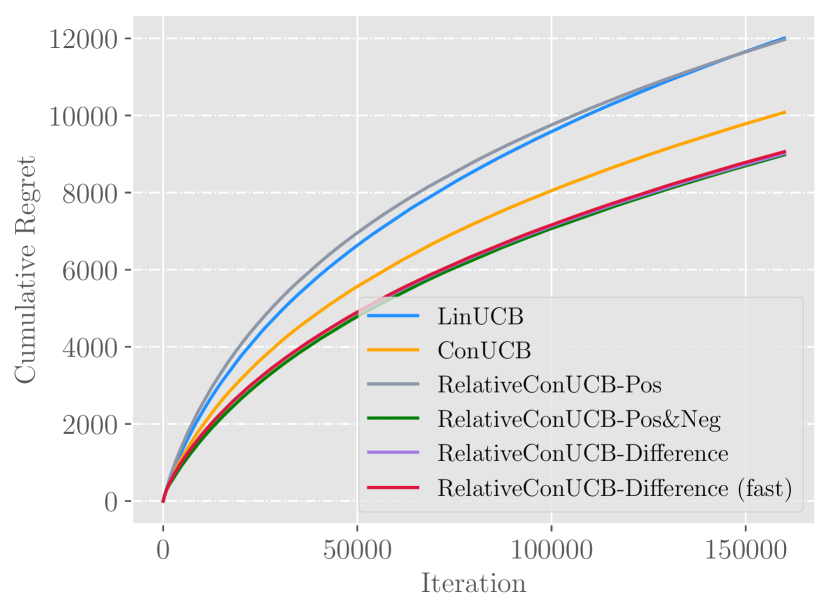
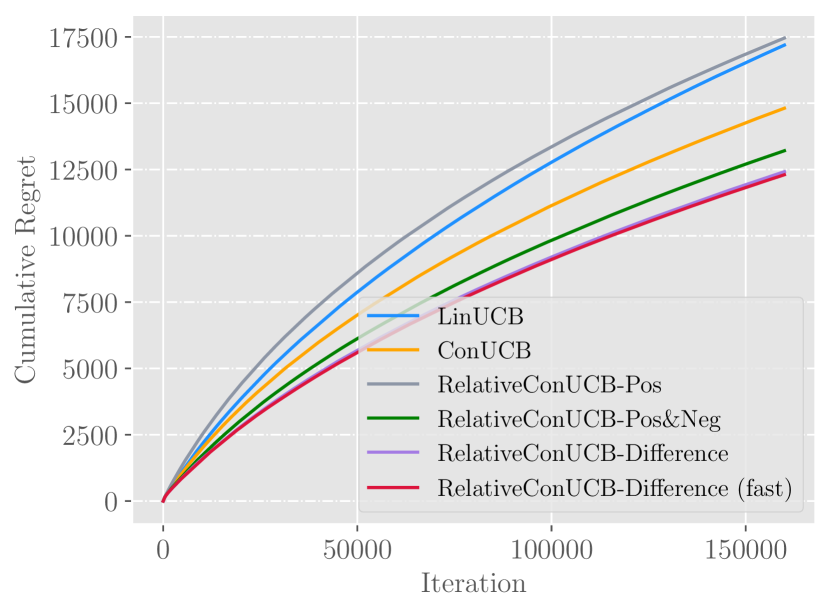
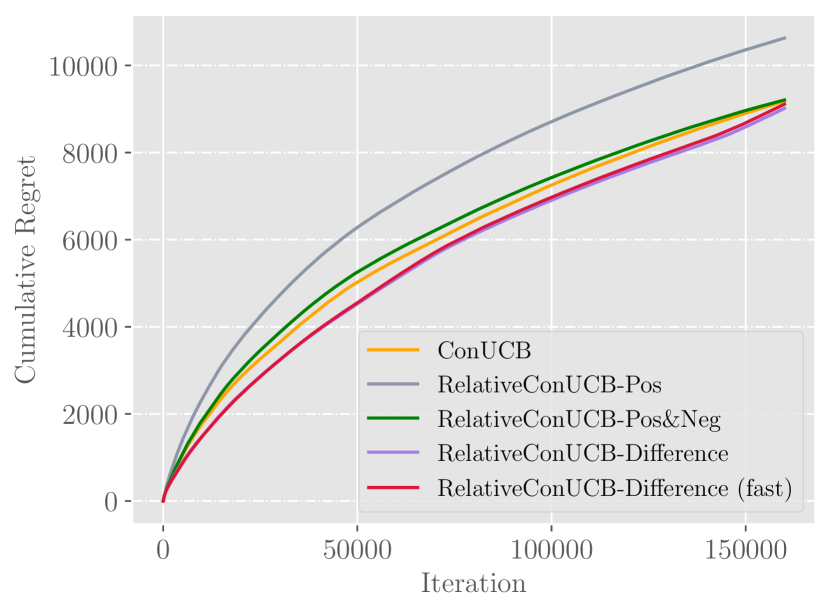
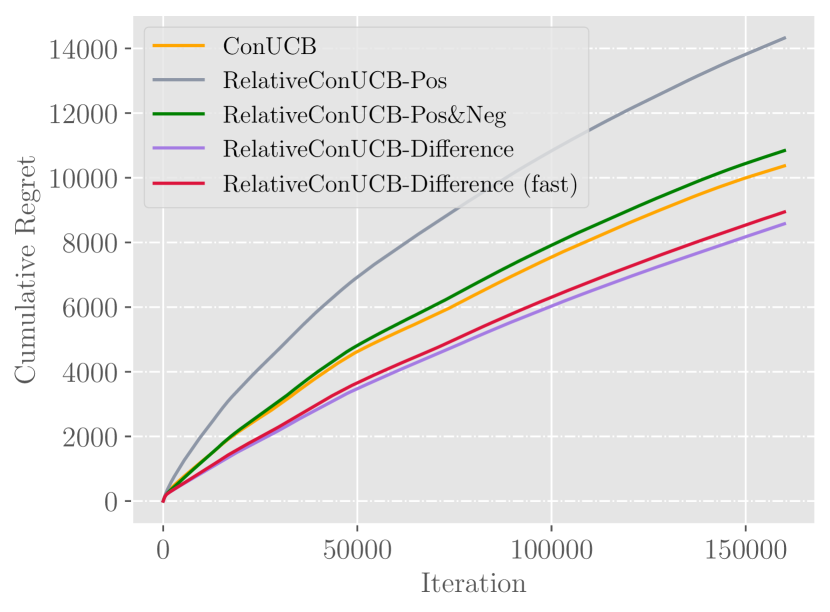
Figures of experimental results on real datasets. They verify the conclusion of synthetic experiment, and show that feedback sharing can not directly bring significant improvements.
4.3. Real-world Datasets
We next evaluate RelativeConUCB on two real-world datasets from different domains, which are released in (Cantador et al., 2011): Last.FM333http://www.lastfm.com for music artist recommendation and Movielens444http://www.grouplens.org for movie recommendation. Last.FM dataset contains 186,479 interaction records between 1,892 users and 17,632 artists. Movielens dataset, which extends the original MovieLens10M dataset to include tagging information in IMDb555http://www.imdb.com and Rotten Tomatoes666http://www.rottentomatoes.com, contains 47,957 interaction records between 2,113 users and 10,197 movies. Artists and movies are treated as items in our setting. We then infer users’ real feedback on items based on the interaction records: if the user has assigned attributes to the item, the feedback is 1, otherwise the feedback is missing. For each dataset, we extract 2,000 items with most assigned attributes and 500 users who have assigned most attributes. For each item, we only leave at most 20 attributes that are associated with most items, and consider them as the related key-terms of the item. The statistics of processed data is shown in Table 1, where the average number of related key-terms for items and the average number of related items for key-terms are also reported.
4.3.1. Data Generation
Before we start, we randomly choose 100 users and formulate a binary matrix which stands for the interaction history. We derive feature vectors in () dimension for items by applying one-class matrix factorization (Chin et al., 2016) on , and then normalize them by , . The constructed features will be used to conduct experiments on the records of the remaining 400 users.
For missing feedback of the remaining users, we again apply the matrix factorization technique to reconstruct the feedback matrix . Next, in order to derive the ground truth user features, we use a simple autoencoder (Rumelhart et al., 1985) with four hidden layers and ReLU activation function. The autoencoder takes the user’s feedback (i.e., the corresponding row of ) as its input, encodes it into a latent representation , and normalizes it by . Finally, we reconstruct the feedback by .
When training, we use MSE loss as the criterion and Adam with learning rate as the optimizer. The training runs 200 epochs.
4.3.2. Results
In this experiment, we compare the performance of algorithms both in the original setting and the feedback sharing setting. For ConUCB, it shares conversational absolute feedback to all users. For RelativeConUCB, relative feedback is shared instead. The experimental results on real-world dataset are shown in Figure 3.
Answer to RQ1.
We first evaluate the results with feedback sharing disabled. In Figure 3(a) and 3(b), we again observe the advantage of using relative feedback, comparing all algorithms in terms of cumulative regret. On Last.FM dataset, Difference (fast) and Pos&Neg outperforms ConUCB by and respectively. On Movielens dataset, Difference (fast) and Pos&Neg outperforms ConUCB by and respectively.
Answer to RQ2.
As illustrated in Figure 3(c) and 3(d), directly sharing relative feedback among all users may not result in good performance. Compared to ConUCB, Difference and Pos&Neg do not show any advantage, which suggests that feedback sharing needs to be conducted more carefully by only considering similar users.
4.4. Drifted Real-world Datasets
As previously shown, sharing feedback among various kinds of users can not generally improve the performance of RelativeConUCB. But what if we only share feedback among similar users? Can user biases be effectively eliminated by using relative feedback instead of absolute one?
To take a step further, we design a drifted environment based on the real-world datasets. It models the users to be in some sense similar, sharing common comparative preferences. But individuals have their own bias, viewing items with different criteria. Specifically, for any two items, they may agree on which one is preferred. But the absolute attitude (like or dislike) towards each of them can be quite different among the users, depending on how critical each user is.
4.4.1. Data Generation
In the drifted environment, we assume the users’ comparative preferences are inherently the same. To be specific, we model the feature vectors of user to be different only in the bias term. Following similar procedures in Section 4.3.1, we apply a four-layer autoencoder with two trainable embeddings and to construct drifted user features. aims to extract the common preferences of users and controls the variance of expected reward. Taking the user’s feedback as the input, the autoencoder outputs a real number . The user feature is then constructed by , where . In this manner, the autoencoder constructs a drifted user group where preferences only differ in .
When training on the autoencoder, we use MSE loss as the criterion and Adam with learning rate as the optimizer. The training runs 1,000 epochs.
4.4.2. Results
The results are shown in Figure 4.
Answer to RQ1.
As illustrated in the figures, Difference outperforms other algorithms by a substantial degree. Based on the result, we argue that Difference can better capture the intrinsic common preferences of users.
Answer to RQ2.
As we can observe, among a group of similar users, sharing relative feedback can bring significant improvements. Compared to ConUCB, Difference (fast) outperforms by and on Last.FM and Movielens dataset respectively. The result demonstrates that relative feedback can conquer the problem of user bias, which makes it more effective to utilize user feedback.
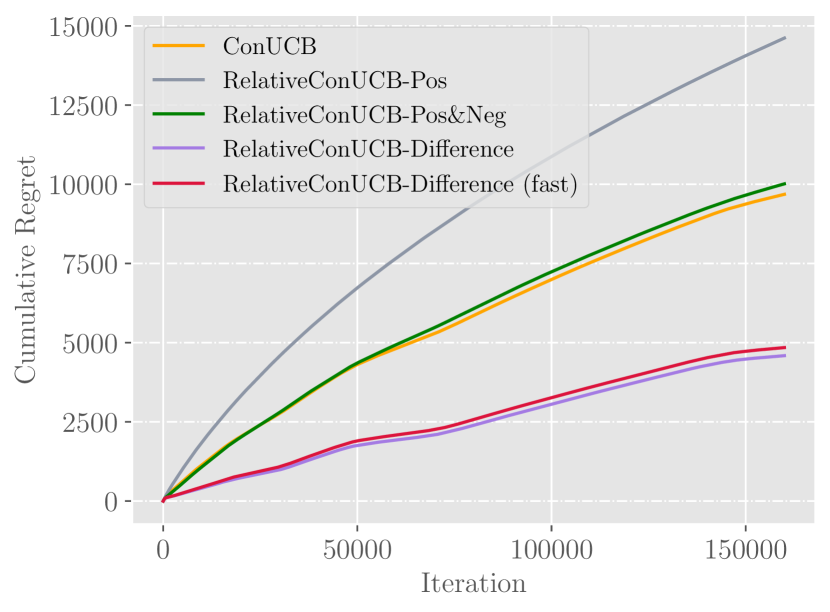
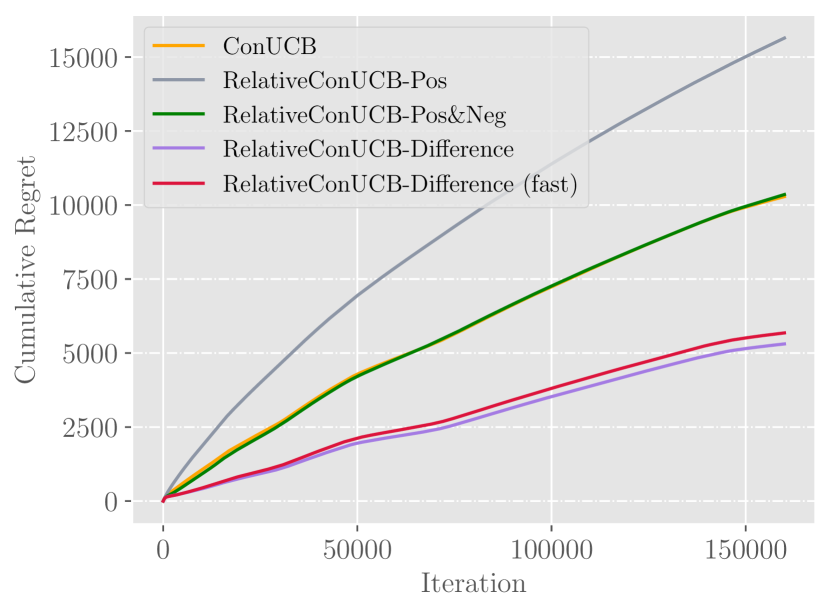
Figures presenting results on drifted datasets. In an idealized environment, we can observe significant improvements brought from feedback sharing.
4.5. Different User Groups
In Section 4.4, we have observed that when users have similar but biased preferences, relative feedback can be greatly utilized by sharing among users to better help recommendation. To explore the superiority in a fine-grained prospective, we setup another set of experiments to answer RQ3.
4.5.1. Data Generation
We modify the procedures of user feature generation based on the synthetic experiment. For each user , we consider the ground-truth feature is composed of three parts: users’ common feature , the user’s individual feature 777It is a slight abuse of notion, as usually stands for the estimated user feature., and the user’s bias . and are both in dimension, and are drawn randomly from . We introduce two parameters and to control the reward variance and user similarity. The final feature vector of user is , where is drawn uniformly from . In this experiment we set .
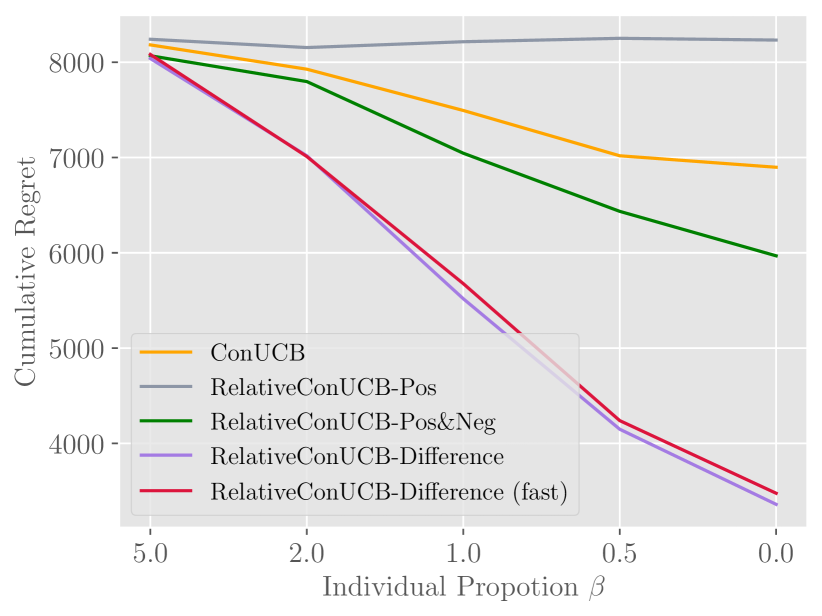
A figure demonstrating the trend of performance as users become similar. This helps validate the advantage of relative feedback.
4.5.2. Results
Figure 5 shows the outcome of the experiment, a comparison of the performances of algorithms under different user individual partitions (i.e., ). As the value of gets smaller, users share more similarity in preferences. Meanwhile, the scale of user bias over the user group remains the same.
Answer to RQ3.
From Figure 5 we can clearly observe a trend of increasing performance over all algorithms when we decrease the proportion of users’ individual feature. However, for ConUCB, the benefit brought from smaller is limited. The main reason is that absolute feedback is contaminated by user biases, which makes it difficult to share. On the contrary, the improvement of Difference over other algorithms gets larger as gets smaller. The trend validates our intuition that, compared to absolute feedback, relative feedback can better capture the intrinsic similarity by eliminating user biases. This allows the comparison-based algorithms to further utilize feedback information.
5. Related Work
There are mainly two lines of research that are related to and motivate our work: conversational recommender system and preference-based learning.
5.1. Conversational Recommender System
The most related works are a series of studies on conversational recommender systems. Although traditional recommender systems have shown significant success in practice (Pazzani and Billsus, 2007; Das et al., 2007; Salakhutdinov and Mnih, 2007), there are still several shortages. One of the shortages is that the user’s preference estimated from the historical interaction data by the traditional recommender system is static and thus the dynamic changes of user preference can not be well captured in this manner. As an emerging topic in the community of recommender system, the conversational recommender system (CRS) is an appealing solution which aims to tackle the cold-start problem as well as the dynamic changes of user preferences (Gao et al., 2021; Lei et al., 2020a).
Due to the significant developments of deep learning, many CRS equipped with natural language processing techniques have been emerging in recent years (Fu et al., 2020). Li et al. (2018) propose a hierarchical recurrent encoder-decoder to address the cold-start problem in conjunction with classification of sentiment of dialogues. Yu et al. (2019) devise a visual dialog augmented model utilizing the user feedback presented in natural language. Zhou et al. (2020b) adopt knowledge graphs to eliminate the semantic gap between natural language expression and item-level user preferences for more accurate recommendations. Lei et al. (2020b) make conversations on graphs to enhance the model’s explainability. Other works (Chen et al., 2019; Zhang et al., 2018) utilize natural language understanding and generation to improve the accuracy of recommendations.
Some other works adopt reinforcement learning (RL) methods to address when and what to ask as the agent interacts with the users. Sun and Zhang (2018) incorporate a deep policy network into the CRS to decide whether to conduct conversations or to recommend. Zhang et al. (2019) design a constraint-augmented reinforcement learning framework to avoid recommendations violating user historical preferences. Zhou et al. (2020a) integrate the CRS, knowledge graph and bandit-based algorithm in order to face the fast-changing preferences and rich user expressions in music recommendation. Christakopoulou et al. (2016) first introduce the multi-armed bandits into CRS. And one of our main baselines, ConUCB (Zhang et al., 2020) gives a clear and theoretically supported integration of linear contextual bandits and CRS. A follow-up (Li et al., 2020) proposes another bandit-based method for CRS using Thompson Sampling.
5.2. Preference-Based Learning
Another line that is closely related to our work is preference-based learning (Wirth et al., 2017). In many RL scenarios such as games (Christiano et al., 2017) and robotics (Tucker et al., 2020), the success of applications is highly dependent on a well-designed reward function. However, users usually have difficulties in providing their absolute feedback explicitly, which makes it hard to define such a reward function. In the meanwhile, the comparative preferences could better capture the user’s intentions. Therefore, a rich body of methods has been proposed to directly learn from users’ preference.
Christiano et al. (2017) use comparison feedback provided by humans rather than absolute numerical scores to train an agent without a well-defined reward function in a complex environment. In the area of robotics, Tucker et al. (2020) and Sadigh et al. (2017) also use users’ pairwise preferences for trajectories rather than numerical feedback to instruct the learning of robots. In the field of information retrieval, Joachims et al. (2017) and Radlinski et al. (2008) find that user’s clicks are sometimes biased and conclude that paired comparisons can be more accurate than absolute numerical scores to evaluate retrieval quality. To address the exploration-exploitation dilemma with constrained relative feedback, dueling bandits (Sui et al., 2018) have been proposed and well-studied. Saha and Gopalan (2019) further explore the topic of combinatorial bandits with relative feedback provided instead of absolute bandit feedback.
6. Conclusion
In this paper, we introduce a comparison-based conversation framework for item recommendation, utilizing relative feedback to better understand user preferences. Within the framework, we develop the RelativeConUCB algorithm to effectively collect and incorporate relative bandit feedback. To further explore the advantages of relative feedback, we propose to share relative feedback among similar users. Extensive experiments on both synthetic and real-world datasets demonstrate the competitiveness of RelativeConUCB. With relative feedback, our recommender system can efficiently elicit user preferences, especially among similar users, and provide satisfactory recommendations.
In the future, we plan to explore the following directions: 1) to improve the applicability of our framework, one may consider a more flexible system that can seamlessly query relative questions and absolute questions; or 2) one may focus on the feedback sharing mechanism to make it more robust and adaptive by incorporating techniques such as online clustering.
References
- (1)
- Cantador et al. (2011) Iván Cantador, Peter Brusilovsky, and Tsvi Kuflik. 2011. Second workshop on information heterogeneity and fusion in recommender systems (HetRec2011). In Proceedings of the 2011 ACM Conference on Recommender Systems, RecSys 2011, Chicago, IL, USA, October 23-27, 2011, Bamshad Mobasher, Robin D. Burke, Dietmar Jannach, and Gediminas Adomavicius (Eds.). ACM, 387–388. https://doi.org/10.1145/2043932.2044016
- Chapelle et al. (2012) Olivier Chapelle, Thorsten Joachims, Filip Radlinski, and Yisong Yue. 2012. Large-scale validation and analysis of interleaved search evaluation. ACM Transactions on Information Systems (TOIS) 30, 1 (2012), 1–41.
- Chen et al. (2019) Qibin Chen, Junyang Lin, Yichang Zhang, Ming Ding, Yukuo Cen, Hongxia Yang, and Jie Tang. 2019. Towards Knowledge-Based Recommender Dialog System. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP). Association for Computational Linguistics, Hong Kong, China, 1803–1813. https://doi.org/10.18653/v1/D19-1189
- Chin et al. (2016) Wei-Sheng Chin, Bo-Wen Yuan, Meng-Yuan Yang, Yong Zhuang, Yu-Chin Juan, and Chih-Jen Lin. 2016. LIBMF: A Library for Parallel Matrix Factorization in Shared-memory Systems. Journal of Machine Learning Research 17, 86 (2016), 1–5. http://jmlr.org/papers/v17/15-471.html
- Christakopoulou et al. (2016) Konstantina Christakopoulou, Filip Radlinski, and Katja Hofmann. 2016. Towards Conversational Recommender Systems. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13-17, 2016, Balaji Krishnapuram, Mohak Shah, Alexander J. Smola, Charu C. Aggarwal, Dou Shen, and Rajeev Rastogi (Eds.). ACM, 815–824. https://doi.org/10.1145/2939672.2939746
- Christiano et al. (2017) Paul F. Christiano, Jan Leike, Tom B. Brown, Miljan Martic, Shane Legg, and Dario Amodei. 2017. Deep Reinforcement Learning from Human Preferences. In Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, Isabelle Guyon, Ulrike von Luxburg, Samy Bengio, Hanna M. Wallach, Rob Fergus, S. V. N. Vishwanathan, and Roman Garnett (Eds.). 4299–4307. https://proceedings.neurips.cc/paper/2017/hash/d5e2c0adad503c91f91df240d0cd4e49-Abstract.html
- Das et al. (2007) Abhinandan Das, Mayur Datar, Ashutosh Garg, and Shyamsundar Rajaram. 2007. Google news personalization: scalable online collaborative filtering. In Proceedings of the 16th International Conference on World Wide Web, WWW 2007, Banff, Alberta, Canada, May 8-12, 2007, Carey L. Williamson, Mary Ellen Zurko, Peter F. Patel-Schneider, and Prashant J. Shenoy (Eds.). ACM, 271–280. https://doi.org/10.1145/1242572.1242610
- Fu et al. (2020) Zuohui Fu, Yikun Xian, Yongfeng Zhang, and Yi Zhang. 2020. Tutorial on Conversational Recommendation Systems. In RecSys 2020: Fourteenth ACM Conference on Recommender Systems, Virtual Event, Brazil, September 22-26, 2020, Rodrygo L. T. Santos, Leandro Balby Marinho, Elizabeth M. Daly, Li Chen, Kim Falk, Noam Koenigstein, and Edleno Silva de Moura (Eds.). ACM, 751–753. https://doi.org/10.1145/3383313.3411548
- Gao et al. (2021) Chongming Gao, Wenqiang Lei, Xiangnan He, Maarten de Rijke, and Tat-Seng Chua. 2021. Advances and Challenges in Conversational Recommender Systems: A Survey. CoRR abs/2101.09459 (2021). arXiv:2101.09459 https://arxiv.org/abs/2101.09459
- Joachims et al. (2017) Thorsten Joachims, Laura Granka, Bing Pan, Helene Hembrooke, and Geri Gay. 2017. Accurately interpreting clickthrough data as implicit feedback. In ACM SIGIR Forum, Vol. 51. Acm New York, NY, USA, 4–11.
- Lei et al. (2020a) Wenqiang Lei, Xiangnan He, Maarten de Rijke, and Tat-Seng Chua. 2020a. Conversational Recommendation: Formulation, Methods, and Evaluation. In Proceedings of the 43rd International ACM SIGIR conference on research and development in Information Retrieval, SIGIR 2020, Virtual Event, China, July 25-30, 2020, Jimmy Huang, Yi Chang, Xueqi Cheng, Jaap Kamps, Vanessa Murdock, Ji-Rong Wen, and Yiqun Liu (Eds.). ACM, 2425–2428. https://doi.org/10.1145/3397271.3401419
- Lei et al. (2020b) Wenqiang Lei, Gangyi Zhang, Xiangnan He, Yisong Miao, Xiang Wang, Liang Chen, and Tat-Seng Chua. 2020b. Interactive Path Reasoning on Graph for Conversational Recommendation. In KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, August 23-27, 2020, Rajesh Gupta, Yan Liu, Jiliang Tang, and B. Aditya Prakash (Eds.). ACM, 2073–2083. https://dl.acm.org/doi/10.1145/3394486.3403258
- Li et al. (2010) Lihong Li, Wei Chu, John Langford, and Robert E. Schapire. 2010. A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th International Conference on World Wide Web, WWW 2010, Raleigh, North Carolina, USA, April 26-30, 2010, Michael Rappa, Paul Jones, Juliana Freire, and Soumen Chakrabarti (Eds.). ACM, 661–670. https://doi.org/10.1145/1772690.1772758
- Li et al. (2018) Raymond Li, Samira Ebrahimi Kahou, Hannes Schulz, Vincent Michalski, Laurent Charlin, and Chris Pal. 2018. Towards Deep Conversational Recommendations. In Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, December 3-8, 2018, Montréal, Canada, Samy Bengio, Hanna M. Wallach, Hugo Larochelle, Kristen Grauman, Nicolò Cesa-Bianchi, and Roman Garnett (Eds.). 9748–9758. https://proceedings.neurips.cc/paper/2018/hash/800de15c79c8d840f4e78d3af937d4d4-Abstract.html
- Li et al. (2020) Shijun Li, Wenqiang Lei, Qingyun Wu, Xiangnan He, Peng Jiang, and Tat-Seng Chua. 2020. Seamlessly Unifying Attributes and Items: Conversational Recommendation for Cold-Start Users. CoRR abs/2005.12979 (2020). arXiv:2005.12979 https://arxiv.org/abs/2005.12979
- Pazzani and Billsus (2007) Michael J Pazzani and Daniel Billsus. 2007. Content-based recommendation systems. In The adaptive web. Springer, 325–341.
- Radlinski et al. (2008) Filip Radlinski, Madhu Kurup, and Thorsten Joachims. 2008. How does clickthrough data reflect retrieval quality?. In Proceedings of the 17th ACM conference on Information and knowledge management. 43–52.
- Rumelhart et al. (1985) David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. 1985. Learning internal representations by error propagation. Technical Report. California Univ San Diego La Jolla Inst for Cognitive Science.
- Sadigh et al. (2017) Dorsa Sadigh, Anca D Dragan, Shankar Sastry, and Sanjit A Seshia. 2017. Active Preference-Based Learning of Reward Functions.. In Robotics: Science and Systems.
- Saha and Gopalan (2019) Aadirupa Saha and Aditya Gopalan. 2019. Combinatorial Bandits with Relative Feedback. In Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, Hanna M. Wallach, Hugo Larochelle, Alina Beygelzimer, Florence d’Alché-Buc, Emily B. Fox, and Roman Garnett (Eds.). 983–993. https://proceedings.neurips.cc/paper/2019/hash/5e388103a391daabe3de1d76a6739ccd-Abstract.html
- Salakhutdinov and Mnih (2007) Ruslan Salakhutdinov and Andriy Mnih. 2007. Probabilistic Matrix Factorization. In Advances in Neural Information Processing Systems 20, Proceedings of the Twenty-First Annual Conference on Neural Information Processing Systems, Vancouver, British Columbia, Canada, December 3-6, 2007, John C. Platt, Daphne Koller, Yoram Singer, and Sam T. Roweis (Eds.). Curran Associates, Inc., 1257–1264. https://proceedings.neurips.cc/paper/2007/hash/d7322ed717dedf1eb4e6e52a37ea7bcd-Abstract.html
- Sui et al. (2018) Yanan Sui, Masrour Zoghi, Katja Hofmann, and Yisong Yue. 2018. Advancements in Dueling Bandits. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI 2018, July 13-19, 2018, Stockholm, Sweden, Jérôme Lang (Ed.). ijcai.org, 5502–5510. https://doi.org/10.24963/ijcai.2018/776
- Sun and Zhang (2018) Yueming Sun and Yi Zhang. 2018. Conversational Recommender System. In The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, SIGIR 2018, Ann Arbor, MI, USA, July 08-12, 2018, Kevyn Collins-Thompson, Qiaozhu Mei, Brian D. Davison, Yiqun Liu, and Emine Yilmaz (Eds.). ACM, 235–244. https://doi.org/10.1145/3209978.3210002
- Tucker et al. (2020) Maegan Tucker, Ellen Novoseller, Claudia Kann, Yanan Sui, Yisong Yue, Joel W Burdick, and Aaron D Ames. 2020. Preference-based learning for exoskeleton gait optimization. In 2020 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2351–2357.
- Wirth et al. (2017) Christian Wirth, Riad Akrour, Gerhard Neumann, Johannes Fürnkranz, et al. 2017. A survey of preference-based reinforcement learning methods. Journal of Machine Learning Research 18, 136 (2017), 1–46.
- Yu et al. (2019) Tong Yu, Yilin Shen, and Hongxia Jin. 2019. A Visual Dialog Augmented Interactive Recommender System. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2019, Anchorage, AK, USA, August 4-8, 2019, Ankur Teredesai, Vipin Kumar, Ying Li, Rómer Rosales, Evimaria Terzi, and George Karypis (Eds.). ACM, 157–165. https://doi.org/10.1145/3292500.3330991
- Yue and Joachims (2009) Yisong Yue and Thorsten Joachims. 2009. Interactively optimizing information retrieval systems as a dueling bandits problem. In Proceedings of the 26th Annual International Conference on Machine Learning, ICML 2009, Montreal, Quebec, Canada, June 14-18, 2009 (ACM International Conference Proceeding Series, Vol. 382), Andrea Pohoreckyj Danyluk, Léon Bottou, and Michael L. Littman (Eds.). ACM, 1201–1208. https://doi.org/10.1145/1553374.1553527
- Zhang et al. (2019) Ruiyi Zhang, Tong Yu, Yilin Shen, Hongxia Jin, Changyou Chen, and Lawrence Carin. 2019. Text-Based Interactive Recommendation with Constraint-Augmented Reinforcement Learning. (2019).
- Zhang et al. (2020) Xiaoying Zhang, Hong Xie, Hang Li, and John C. S. Lui. 2020. Conversational Contextual Bandit: Algorithm and Application. In WWW ’20: The Web Conference 2020, Taipei, Taiwan, April 20-24, 2020, Yennun Huang, Irwin King, Tie-Yan Liu, and Maarten van Steen (Eds.). ACM / IW3C2, 662–672. https://doi.org/10.1145/3366423.3380148
- Zhang et al. (2018) Yongfeng Zhang, Xu Chen, Qingyao Ai, Liu Yang, and W. Bruce Croft. 2018. Towards Conversational Search and Recommendation: System Ask, User Respond. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, CIKM 2018, Torino, Italy, October 22-26, 2018, Alfredo Cuzzocrea, James Allan, Norman W. Paton, Divesh Srivastava, Rakesh Agrawal, Andrei Z. Broder, Mohammed J. Zaki, K. Selçuk Candan, Alexandros Labrinidis, Assaf Schuster, and Haixun Wang (Eds.). ACM, 177–186. https://doi.org/10.1145/3269206.3271776
- Zhou et al. (2020a) Chunyi Zhou, Yuanyuan Jin, Xiaoling Wang, and Yingjie Zhang. 2020a. Conversational Music Recommendation based on Bandits. In 2020 IEEE International Conference on Knowledge Graph (ICKG). IEEE, 41–48.
- Zhou et al. (2020b) Kun Zhou, Wayne Xin Zhao, Shuqing Bian, Yuanhang Zhou, Ji-Rong Wen, and Jingsong Yu. 2020b. Improving Conversational Recommender Systems via Knowledge Graph based Semantic Fusion. In KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, August 23-27, 2020, Rajesh Gupta, Yan Liu, Jiliang Tang, and B. Aditya Prakash (Eds.). ACM, 1006–1014. https://dl.acm.org/doi/10.1145/3394486.3403143