Competition and interplay between topology and quasi-periodic disorder in Thouless pumping of ultracold atoms
Abstract
Robustness against perturbations lies at the heart of topological phenomena. If, however, a perturbation such as disorder becomes dominant, it may cause a topological phase transition between topologically non-trivial and trivial phases. Here we experimentally reveal the competition and interplay between topology and quasi-periodic disorder in a Thouless pump realized with ultracold atoms in an optical lattice, by creating a quasi-periodic potential from weak to strong regimes in a controllable manner. We demonstrate a disorder-induced pumping in which the presence of quasi-periodic disorder can induce a non-trivial pump for a specific pumping sequence, while no pump is observed in the clean limit. Our highly controllable system, which can also straightforwardly incorporate interatomic interaction, could be a unique platform for studying various disorder-related novel effects in a wide range of topological quantum phenomena.
While arbitrarily weak random disorder drives non-interacting particles in one or two dimensions into a localized state, known as the Anderson localization 50AL , topological quantum phenomena are robust against weak disorder Niu84 ; Niu85 , i.e., topological phenomena avoid to be Anderson-localized. Robustness to disorder is an important property defining the topological states, the examples of which are the classification of three-dimensional topological insulators into strong and weak Kobayashi ; Bryan ; Yamakage . More recent investigations focus not only on the robustness but also on the novel interplay between disorder and topology, exhibiting complex but interesting phenomena Li2009 ; McGinley . A striking example is the topological Anderson insulator (TAI) Li2009 ; Shen . Here, the introduction of a disorder potential into a two-dimensional system is essential to create a topologically non-trivial phase: Counter-intuitively, while the system is topologically trivial in the clean limit, disorder acts as a protection, instead of suppression, of the topological invariant, such as the Chern number. Two recent experiments Meier ; Stutzer2018 studied a non-interacting bosonic or photonic waveguide system of TAI using a Bragg-coupled one-dimensional array of Bose-Einstein condensates in a momentum-space lattice Meier or a two-dimensional array of evanescently coupled helical waveguides described by the paraxial wave equation Stutzer2018 , revealing the disorder-induced chiral displacement or edge states, respectively. Moreover, several topological properties of edge-state propagation in a photonic TAI have been recently demonstrated in a two-dimensional disordered gyromagnetic photonic crystal in the microwave regime Liu2020 . Further theoretical works on TAI envision rich varieties of disorder-induced topological phenomena like an anomalous Floquet Anderson insulator Titum , a Majorana topological phase McGinley , a Dirac-semi-metal Sriluckshmy , and topological insulators Kobayashi ; Mondragon-Shem ; Yamakage .
Historically, the robustness of the topological invariant of Chern number against perturbations was first discussed by Niu and Thouless Niu84 ; Niu85 who investigated the effects of spatial potential disorder and inter-particle interaction on a topological Thouless pump Thouless . This Thouless pump is quantum transport of a fermionic gas in a one-dimensional periodic potential driven in an adiabatic cycle. The charge pumped per cycle is equal to the Chern number defined over a two-dimensional Brillouin zone with one spatial and one temporal dimension, and thus it can be regarded as a (1+1)-dimensional counterpart of the quantum Hall effect. They derived an effective Chern number even under perturbations by introducing the twisted boundary conditions. As a result, they revealed that the amount of pumping corresponding to the Chern number does not change unless the gap between the associated energy bands is closed. The experimental realization of Thouless pump in a clean system using ultracold atoms in optical lattices Nakajima ; Lohse ; Schweizer2016 ; Lohse2018 and photonic waveguides Kraus ; Zilberberg2018 triggers various interesting theoretical investigations on the effect of the perturbation like on-site static Qin2016 ; Wauters ; Imura_2018 ; Kuno and dynamic Titum potentials as well as interatomic interaction Nakagawa ; Hayward ; Stenzel ; Mei_2019 .
Here, employing a Thouless pump realized with ultracold fermions in a dynamical optical lattice, we experimentally reveal the competition and interplay between topology and quasi-periodic disorder by generating a controllable quasi-periodic potential from weak to strong regimes. As the highlight, by choosing pump parameters appropriately, we successfully demonstrate a disorder-induced pumping, i.e., a trivial phase with no pump in the clean limit is driven to a nontrivial phase with finite pump, due to the presence of quasi-periodic disorder, and is driven back to a trivial phase at larger disorder strengths. This phenomenon is the (1+1) dimensional analogue of TAI originally discussed in a two-dimensional system Li2009 . Moreover, our experimental observations not only demonstrate the realization of disorder-induced pump, but also quantitatively reveals the degree of robustness and breakdown of the Thouless pump against quasi-periodic disorder. On the one hand, the pumped charge does not change even at disorder strengths comparable to the Anderson-localization transition point and to the minimum band gap in the clean limit, while on the other hand, the pumped charge drastically decreases when the disorder strength exceeds the threshold value determined by the pump parameters. In addition, our further measurement suggests that the gap closes at the threshold of the disorder strength, indicating that the quasi-periodic disorder induces a topological phase transition from topologically non-trivial to trivial phases.
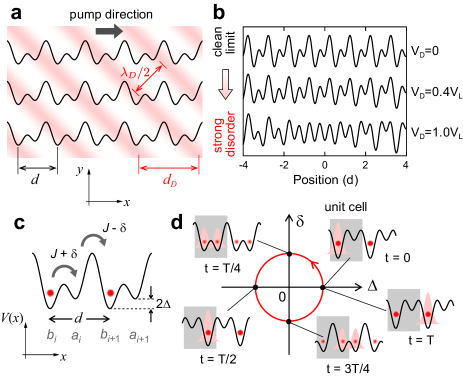
Experimental setup of Thouless pumping with quasi-periodic disorder
We experimentally implement Thouless pumping in the presence of quasi-periodic disorder with precisely controllable strength, using an ultracold non-interacting Fermi gas of ytterbium (171Yb) atoms in a two-dimensional (2D) array of continuous Rice-Mele (cRM) lattices (see Methods) Nakajima . Each lattice is a dynamically controlled optical superlattice which consists of a dynamical interferometric lattice with the lattice constant nm (“long lattice”) and a stationary lattice with the constant (“short lattice”). We superimpose another optical lattice at wavelength on it, which is tilted by with respect to the pumping direction as depicted in Fig. 1a. Hereafter we refer to this lattice as the “disorder lattice”. Due to strong confinement along the and axes provided by other optical lattices, the following time-dependent one-dimensional (1D) superlattice is created:
| (1) | |||||
where , , and correspond to the depth of the short, long, and disorder lattices, respectively. is the lattice constant of the disorder lattice along the pumping direction. When , i.e. nm, the quasi-periodic disorder is produced, and its strength can be controlled by adjusting the depth as shown in Fig. 1b. is the phase difference between the short and long lattices and is the phase difference between the short and disorder lattices. Note that this phase takes a different value for different 1D superlattice due to our configuration in Fig. 1a (see Methods). Hereafter, we use the lattice constant as the unit of length and the recoil energy as the unit of energy, where denotes Planck’s constant and is the atomic mass of 174Yb. We load the ytterbium atoms into the 2D array of 1D cRM lattices in the staggered phase (), first by ramping-up the long lattice followed by the simultaneous ramping-up of short and disorder lattices adiabatically, ensuring that they occupy the lowest energy band, and slowly sweep over time. The lattice potential returns to its initial configuration whenever changes by , thus completing a pumping cycle. The typical length of a 1D superlattice is about 12 unit cells around the center of the atomic cloud.
Our Thouless pump under quasi-periodic disorder can be approximately described by the tight-binding Rice-Mele (tRM) model RM ; Atala with on-site quasi-periodic disorder:
| (2) | |||||
where () and () are fermionic creation (annihilation) operators in the two sublattices of the -th unit cell, is the tunneling amplitude within and between unit cells, denotes a staggered on-site energy offset (), and is the on-site quasi-periodic disorder of sublattices () of the -th unit cell (, see Supplementary Information S1 for details). Figure 1c represents this system in the corresponding cRM model in the clean limit (or ). By sweeping the long lattice phase , dynamical parameters and change adiabatically and draw a closed trajectory in a space (Fig. 1d). The parameters are determined by matching the band structures of the tRM and cRM models corresponding to the points () of the actual pumping sequences. For example, when and for , we get , whereas for , we get . We then swipe along the circular path in Fig. 1d. Such mapping does preserve the topological properties of the system. Note that the actual experiment is only approximately described by the tRM model, so that we use the circular trajectory only as a pictorial description of the pumping sequences Nakajima .
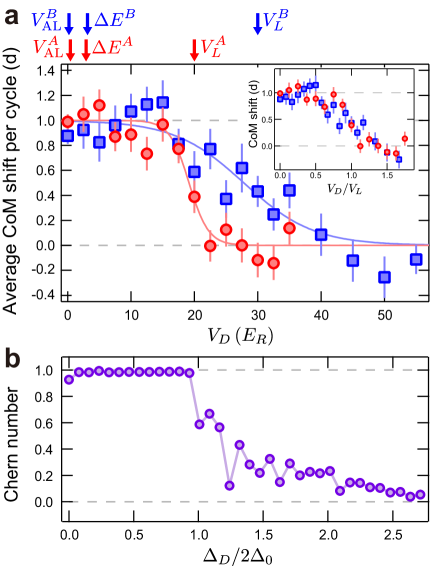
Effect of quasi-periodic disorder on Thouless pump
We begin by considering the effects of quasi-periodic disorder added to our cRM version of the Thouless pump. While Niu and Thouless showed that the pump is robust against disorder as long as the band gap remains open, it is yet unclear how much quasi-periodic disorder is needed in order to close the gap. While infinitely small random disorder induces localization in 1D systems, a finite quasi-periodic disorder is needed in order to induce localization. In our system, there are three energy scales which might be relevant for gap-closing: 1) the Anderson-localization (AL) transition point , 2) the minimum band gap ( maximum ) in the pumping cycle of the bare cRM lattice in the clean limit, and 3) the maximum on-site offset of the staggered potential. By performing the experiments we can answer which energy scale is truly relevant. Figure 2a shows the results of cRM pump under the quasi-periodic disorder potential with nm for two sets of superlattice parameters, (set A, red circles) and (set B, blue squares) as a function of the disorder strength . The pumped charge per cycle was obtained by evaluating the shift of the center of mass (CoM) of the atomic cloud, which corresponds to the Chern number Nakajima . The vertical red (blue) arrows in Fig. 2a indicate the above-mentioned three energy scales for the superlattice parameters of the set A (B). Here, the arrows at with and those at with correspond to the AL transition points (see Supplementary Information S2) and the minimum gap for the superlattice parameter A (B), respectively. The arrows with and at and represent the lattice-depth of for the parameter set A and B, respectively. The measured results demonstrate that the Thouless pump is robust against disorder strengths around the AL transition point and minimum gap , and it breaks only when the disorder strength becomes comparable with . In our cRM lattice, the value of is comparable to the maximum on-site offset in the tRM model. By normalizing the horizontal axes of Fig. 2a with the values of for each lattice setting, we can evaluate the pumping behavior in terms of the adimensional disorder strength , as shown in inset of Fig. 2a. Indeed, the pumping is suppressed at the disorder strength of . Although non-adiabatic processes shift the suppression point toward weaker disorder, they result in only a small underestimation of the suppression point and do not play the dominant role Hayward2020 . Our experiment shows that the topological transition occurs well in the regime where all states are Anderson-localized and is not regarded as a delocalization-localization transition of instantaneous Hamiltonian eigenstates Hayward2020 . Instead, the observed breakdown of quantized pumping is regarded as manifestation of a delocalization-localization transition of Floquet eigenstates Wauters .
To explain the experimental results in Fig. 2a, we numerically calculate the Chern number of the tRM model with on-site quasi-periodic disorder. In general, the Chern number corresponds to the total pumped charge per pumping cycle if the band gap is kept open during the pumping cycle Asboth . Here, due to the presence of quasi-periodic disorder, the tRM model does not have translational invariance: Hence, the conventional definition of Chern number in momentum space cannot be applied. Instead, we applied the dimensional extension for the tRM model and introduced twisted phase boundary condition, and by employing the coupling matrix method YFZhang ; Sriluckshmy ; Kuno we calculate a modified Chern number, i.e., extracted a quantity related to the total pumped charge from the real space disorded Hamiltonian (see Supplementary Information S3).
Figure 2b shows the results of numerical calculations of the Chern number for a superlattice with 20 unit cells. In our numerical result, the Chern number takes non-integer values around the transition point (moderate disorder regime). This has two reasons. The first reason is that the evaluated Chern number corresponds to the average over the quasi-periodic disorder phase . Because the phase varies among 1D superlattices, the transition strength at which the Chern number changes from one to zero is different for a different lattice. In the actual experiment, all the 1D lattices are measured simultaneously, so that the phase dependency is averaged out. The second reason is that the gap fluctuates by varying the twisted phases at the boundary in the strong disorder regime YFZhang ; Kuno . The numerical calculations and measured results are in reasonable agreement, and also consistent with the numerical results in Refs. Wauters and Hayward2020 . In general, we expect deviations between numerical calculations and experiments due to various factors: (I) effects of residual non-adiabaticity in the experiment, (II) absence of disorder in the hopping terms of the tRM model, (III) effects of the trapping potential not considered in tRM model. These factors are also relevant for the experimental results and numerical calculations presented in Fig. 5.
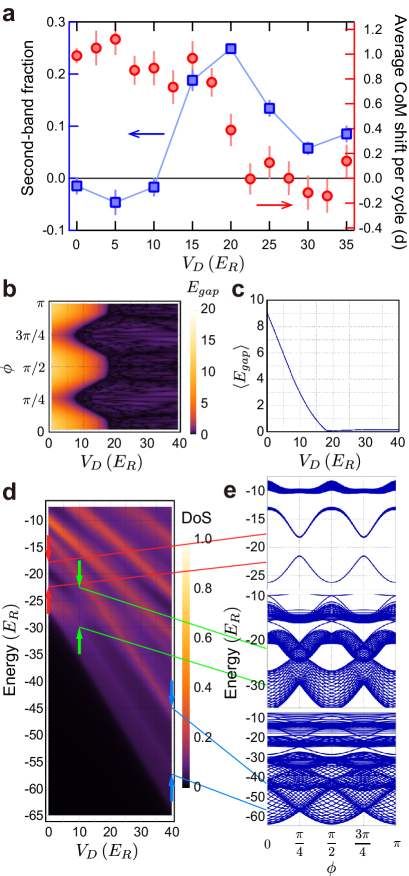
It is important to clarify whether the observed suppression of the charge pumping is the manifestation of a topological phase transition or not. A fundamental property which is useful to identify a topological phase transition is the behavior of the excited band population. This has been the key to reveal the topological phase transition of the Haldane model Jotzu14 , in which the population of the second band increases at the topological transition point, where the gap closes, due to the Landau-Zener transition during the Bloch oscillation. Here, we investigate the gap closing between the first and the second bands by the presence of the quasi-periodic disorder with a band mapping technique (see Supplementary Information S5). Figure 3a shows the fraction of atoms excited to the second band, with respect to the total number of atoms, after three cycles of cRM pumping with the parameter set A . We evaluate the population of the second Brillouin zone of the basic cRM lattice. To this end, we remove the disorder lattice by adiabatically ramping down its strength before the band-mapping measurements, so that the fraction of atoms in the second-band under quasi-periodic disorder is adiabatically transferred to the corresponding one in the clean limit. The experimental result shows that the excitation to the second band initially increases as disorder increases and reaches the maximum at and then decreases as the disorder further increases. Such increase of the excitation to the second band around suggests that the gap initially opened in a clean limit is closed around and becomes open again. The band gap changes dynamically during the pump cycle, and a Landau-Zener-like non-adiabatic transition could occur at the gap closing point. Note that, for strong disorder, the gap may close during the removal of the disorder lattice, which is performed at (see Fig. 3b). However, if the gap remains closed even in the region of , it is not expected to observe a decrease in the second-band fraction in the strong disorder region, as it is instead observed in the experiment.
We check this gap closing and opening around numerically. Figure 3b shows a numerical calculation of the energy gap for the set A as functions of and based on a continuous modelDas2019 ; Marra2020 in the presence of a quasi-periodic superlattice with half filling and a total length of 198 (see Supplementary Information S4 for details). The energy gap averaged over becomes zero around (see Fig. 3c). It qualitatively supports our experimental observations that the pumping is suppressed at the disorder strength of . The disappearance of the bulk energy gap also can be seen in the density of states (DoS) calculation and the band calculation (Fig. 3d and e). Here, as increasing , some in-gap states are formed and the bulk band gap observed in the clean limit gradually disappears. On the other hand, the numerical calculations do not show such re-opening of the gap. However, the energy difference between the ground vibrational level (the local first band) and the first excited vibrational level (the local second band) within one lattice site would become large in the strong (deep) disorder lattice regime. This large local (on-site) energy gap in large suppresses again the excitation to the second band during pumping sequence as is observed in our experiment. Our consideration of the sliding and disorder lattices (see Supplementary Information S6 and later in the main text) indicates that the gap should be open locally on each site for . We also numerically confirmed that the gap closing and reopening can be seen more clearly in the case of shallower lattice parameter sets (see Supplementary Information S4 for details). Consequently, the observed pumping suppression due to the quasi-periodic disorder should indicate a topological phase transition in which the non-trivial Chern number changes into a trivial one via gap closing as the disorder strength increases.
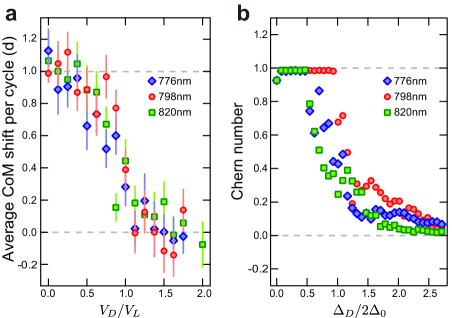
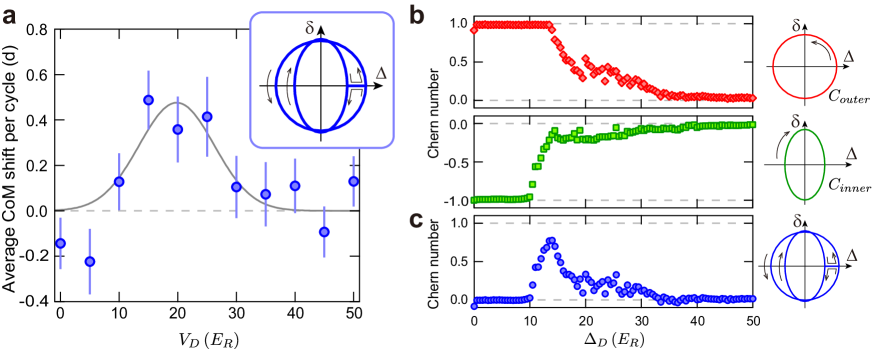
We also examined the dependence of the pumping suppression on the wavelength of the disorder lattice . Figure 4a shows the pumping amounts measured at the quasi-periodic disorder wavelengths nm (red diamond), 798 nm (blue circle), and 820 nm (green square). The data at 798 nm are the same as those with the set A in Fig. 2. There is no clear difference among the results for those different wavelengths. Our numerical calculation with a tRM model supports the tendency of the measured results (see Fig. 4b). As one can see, the charge pumping starts to decrease from one at a certain critical disorder strength, which depends on the wavelength. However, the pumping is largely suppressed at almost the same value for all three wavelengths.
Although it is difficult to fully describe the pump in the strong disorder regime with such a tRM model, intuitively we can understand why the pump is suppressed at regardless of the wavelength of the disorder lattice. Our cRM pump is topologically equivalent to a simple sliding lattice, namely, the second term of Eq.(1) describing the long lattice only Nakajima . Thus we can capture the essence of the results by considering a sliding lattice superimposed with a disorder lattice. A simple calculation shows that, in the case of , the sliding long lattice is dominant, so that the total combined lattice slides similarly. On the other hand, when , the minima of the total lattice do not slide (see Supplementary Information S6). From this point of view, the former corresponds to a quantized pumping, whereas the latter gives no pump.
Disorder-induced pumping
The introduction of strong quasi-periodic disorder suppresses the topological charge pumping as described above. However, the interplay between topology and quasi-periodic disorder could lead to more counter-intuitive phenomena like TAI Li2009 ; Shen . Here, we demonstrate the novel phenomenon of disorder-induced pumping, realized with a newly configured pumping sequence. We designed a pumping sequence in which the charge pumping is implemented in three stages: using the lattice parameters in the first stage, then using different parameters with pumping in the reverse direction in the second stage, and finally using the lattice parameters of the first stage to obtain a closed pumping cycle. This sequence is depicted in a pictorial way in Fig. 5a, in the tRM model. In a clean system, the gap closes only at and is open in the other region, so that the outer loop yields the Chern number of and the inner loop . Thus the overall pumping amount in this sequence can be given by . Theoretically, if the two loops are far apart, a quantized pump is expected under moderate disorder (See Supplementary Information S3). We added the disorder lattice to this basic sequence and measured the pumping amount per one cycle shown in Fig. 5b. The pumping amount was obtained by evaluating the CoM shift after three cycles for each disorder strength. At zero disorder strength, the pumping amount is zero as discussed above. However, as the disorder strength increases, the pumping amount takes a finite value. Subsequently, the pumping amount reaches its maximum value and then reduces to zero. This clearly demonstrates the observation of disorder-induced pumping in the Thouless pump system.
Our finding can be explained intuitively in the following manner. As discussed in Figs. 2a and b, the pumping is suppressed at disorder strengths of the order of . Namely, in Fig. 5a, the pumping is expected to be suppressed around and in the outer and the inner trajectories, respectively. This indicates that in the intermediate region the pumping during the inner and outer trajectories do not cancel each other, resulting in a non-zero total pumping.
We qualitatively reproduced this behaviour by numerical calculations as shown in Fig. 5b. For each circular trajectory, we calculated the Chern number by using the quasi-periodic disordered Harper-Hofstadter-Hatsugai model (see Supplementary Information S3 for details). For all data sets, we averaged over 60 samples corresponding to different values of . The numerical results for each trajectory are shown in Fig. 5b. The data display -dependence (not scale) of the Chern number. Furthermore, Fig. 5c shows the sum of the Chern number between and trajectories. The result clearly captures the presence of a non-trivial pump between , quantified by the imperfect cancellation between the Chern numbers for and trajectories. Note that the experimental trajectory surely yields the disorder-induced pumping; however, this does not necessarily mean that this pump is topological. It could be topological if we adjust appropriately the lattice parameters including the phase connecting the outer and inner trajectories.
Discussion
Our unique experimental platform provides us with interesting opportunities for studying a wide range of topological quantum phenomena with disorder. By introducing a disorder lattice with nm, it is possible to add a quasi-periodic disorder where approximates the golden ratio, which is often studied in the Aubry-André model AAmodel , or to add a genuinely random (non quasi-periodic) disorder by using a speckle pattern. Moreover, in this study we connect two non-trivial pump trajectories to create a trivial trajectory in the clean limit and then add disorder to observe disorder-induced pumping. This method presented here allows the realization of disorder-induced pumping, and will give a suggestion or guideline for the future study of a wide range of disorder-induced topological phases. Our highly controllable optical lattice system loaded with ultracold fermions can straightforwardly incorporate interatomic on-site interaction with reasonably large strengths compared with tunneling energy. Consequently, we can study the effect of the disorder on Thouless pump in a strongly correlated regime Nakagawa ; Stenzel , especially in the regime of many-body localization Huse ; Nandkishore which may protect topological phenomena up to higher excited states. The pumping can be extended to higher dimensions Lohse2018 ; Zilberberg2018 ; Price2015 . For example, the two-dimensional extension of our experiment is directly related to disordered quantum Hall system Ippoliti2020 . The introduced disorder can also be dynamically controlled, enabling us to study an anomalous Floquet Anderson topological phase Titum only possible for a Floquet system, revealed by nonadiabatic pumping. Our experimental setup can also allow us to study the effect of nonadiabaticity Citro2018 . Moreover, the effect of disorder on the higher-order topological phenomena Benalcazar61 ; Xie ; SQShen is an interesting new research direction Araki .
I Methods
I.1 Preparation of a degenerate Fermi gas of 171Yb
Since 171Yb atoms have a very small -wave scattering length of -0.15 nm Kitagawa08 , they can be regarded to be non-interacting. Therefore, we use sympathetic evaporative cooling with 173Yb atoms to obtain the degenerate Fermi gas of 171Yb Taie10 .
The number of atoms for each spin is typically 3500. A typical atom temperature before lattice loading is for the measurements in Figs. 2-4 and for Fig. 5 at the end of the evaporation with the trap frequencies of the far-off resonant optical trap of Hz, where the - and -axes are tilted from the lattice axes ( and ) by . The estimated sizes of our atomic clouds (full width at half maximum, FWHM) are about , , and for the , , and directions, respectively. The system size along the pumping direction () is about , corresponding to about 12 unit cells around the center of the atomic clouds. The whole atomic system consists of about 1D lattices along the - and -axes, and totally about 360 lattices.
I.2 Setup for the cRM superlattice and quasi-periodic disorder lattice
An incommensurate optical lattice potential created by a retro-reflected laser beam (wavelength at ) and tilted by 45 degrees to the pumping direction is superimposed on a 2D array of one-dimensional cRM superlattice. This superimposed optical lattice (disorder lattice) creates a periodic potential whose lattice constant in the pumping direction of the cRM, acting as a quasi-periodic disorder. In our setup, the wavelength can range from 776 nm to 820 nm realized by a Ti:Sapphire laser, and the relative incommensurate lattice constant ranges from 1.03 to 1.09, respectively. Because the ratio of this wavelength is relatively close to 1, this quasi-periodic disorder does not take the same structure in the trap region. Also, because this lattice is tilted by 45 degrees, the phase of the quasi-periodic disorder shifts by 3.05, 2.96, and 2.88 rad for 776, 798, and 820 nm, respectively, in the adjacent array (Fig. 1a).
I.3 Pumping speed and adiabadicity
An essential requirement of the topological Thouless pump is adiabaticity. This is necessary to avoid non-adiabatic Landau-Zener transitions to the higher band during the pumping process, at least in the clean limit. The pumping times per cycle take 130 ms on average for the normal charge pumping in Figs. 2-4 and 460 ms for the disorder-induced pumping in Fig. 5, in particular 100 ms for outer and inner trajectories and 130 ms for the connecting region (two times), respectively. These pumping times are sufficiently longer than the Landau-Zener-transition time scales, which are estimated to be 1 ms based on the maximum and minimum bandgaps during the pumping cycles Nakajima .
Additional information
Correspondence and requests for materials should be addressed to S. Nakajima.
Acknowledgements
We thank H. Aoki, Y. Hatsugai, and K. Imura for valuable discussions and A. Sawada for experimental assistance. This work was supported by the Grant-in-Aid for Scientific Research of JSPS (Nos. JP25220711, JP26247064, JP16H00990, JP16H01053, JP17H06138, JP18H05405, JP18H05228, and JP18K13480), the Impulsing Paradigm Change through Disruptive Technologies (ImPACT) program, JST CREST (No. JPMJCR1673), and MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant No. JPMXS0118069021. Y. K. acknowledges the support of the Grant-in-Aid for JSPS Fellows (No.17J00486). P. M. is supported by the Japan Science and Technology Agency (JST) of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), JST CREST Grant. No. JPMJCR19T2 and by the (MEXT)-Supported Program for the Strategic Research Foundation at Private Universities “Topological Science” (Grant No. S1511006) and by JSPS Grant-in-Aid for Early-Career Scientists (Grant No. 20K14375).
Author contributions
S. N. and N. T. contributed equally to this work. S. N., N. T. and K. S. carried out experiments and the data analysis. Y. K. and P. M. carried out the theoretical calculation. Y. T. conducted the whole experiment. All the authors contributed to the writing of the manuscript.
Competing interests
The authors declare no competing interests.
References
References
- (1) Lagendijk, A., Tiggelen, B. v. & Wiersma, D. S. Fifty years of Anderson localization. Physics Today 62, 24–29 (2009).
- (2) Niu, Q. & Thouless, D. J. Quantised adiabatic charge transport in the presence of substrate disorder and many-body interaction. J. Phys. A: Math. Gen. 17, 2453–2462 (1984).
- (3) Niu, Q., Thouless, D. J. & Wu, Y.-S. Quantized Hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377 (1985).
- (4) Kobayashi, K., Ohtsuki, T. & Imura, K.-I. Disordered weak and strong topological insulators. Phys. Rev. Lett. 110, 236803 (2013).
- (5) Leung, B. & Prodan, E. Effect of strong disorder in a three-dimensional topological insulator: Phase diagram and maps of the invariant. Phys. Rev. B 85, 205136 (2012).
- (6) Yamakage, A., Nomura, K., Imura, K.-I. & Kuramoto, Y. Disorder-induced multiple transition involving topological insulator. J. Phys. Soc. Jpn. 80, 053703 (2011).
- (7) Li, J., Chu, R.-L., Jain, J. K. & Shen, S.-Q. Topological Anderson insulator. Phys. Rev. Lett. 102, 136806 (2009).
- (8) McGinley, M., Knolle, J. & Nunnenkamp, A. Robustness of Majorana edge modes and topological order: Exact results for the symmetric interacting Kitaev chain with disorder. Phys. Rev. B 96, 241113 (2017).
- (9) Shen, S.-Q. Topological Insulators: Dirac Equation in Condensed Matters (Springer, 2013).
- (10) Meier, E. J. et al. Observation of the topological Anderson insulator in disordered atomic wires. Science 362, 929–933 (2018).
- (11) Stützer, S. et al. Photonic topological Anderson insulators. Nature 560, 461–465 (2018).
- (12) Li, G.-G. et al. Topological Anderson insulator in Disordered Photonic Crystals. Phys. Rev. Lett. 125, 133603 (2020).
- (13) Titum, P., Berg, E., Rudner, M. S., Refael, G. & Lindner, N. H. Anomalous Floquet-Anderson insulator as a nonadiabatic quantized charge pump. Phys. Rev. X 6, 021013 (2016).
- (14) Sriluckshmy, P. V., Saha, K. & Moessner, R. Interplay between topology and disorder in a two-dimensional semi-Dirac material. Phys. Rev. B 97, 024204 (2018).
- (15) Mondragon-Shem, I. & Hughes, T. L. Signatures of metal-insulator and topological phase transitions in the entanglement of one-dimensional disordered fermions. Phys. Rev. B 90, 104204 (2014).
- (16) Thouless, D. J. Quantization of particle transport. Phys. Rev. B 27, 6083–6087 (1983).
- (17) Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296–300 (2016).
- (18) Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 12, 350–354 (2016).
- (19) Schweizer, C., Lohse, M., Citro, R. & Bloch, I. Spin pumping and measurement of spin currents in optical superlattices. Phys. Rev. Lett. 117, 170405 (2016).
- (20) Lohse, M., Schweizer, C., Price, H. M., Zilberberg, O. & Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 553, 55–58 (2018).
- (21) Kraus, Y. E., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).
- (22) Zilberberg, O. et al. Photonic topological boundary pumping as a probe of 4D quantum Hall physics. Nature 553, 59–62 (2018).
- (23) Qin, J. & Guo, H. Quantum pumping induced by disorder in one dimension. Phys. Lett. A 380, 2317–2321 (2016).
- (24) Wauters, M. M., Russomanno, A., Citro, R., Santoro, G. E. & Privitera, L. Localization, topology, and quantized transport in disordered Floquet systems. Phys. Rev. Lett. 123, 266601 (2019).
- (25) Imura, K.-I., Yoshimura, Y., Fukui, T. & Hatsugai, Y. Bulk-edge correspondence in topological transport and pumping. J. Phys. Conf. Ser. 969, 012133 (2018).
- (26) Kuno, Y. Disorder-induced Chern insulator in the Harper-Hofstadter-Hatsugai model. Phys. Rev. B 100, 054108 (2019).
- (27) Nakagawa, M., Yoshida, T., Peters, R. & Kawakami, N. Breakdown of topological Thouless pumping in the strongly interacting regime. Phys. Rev. B 98, 115147 (2018).
- (28) Hayward, A., Schweizer, C., Lohse, M., Aidelsburger, M. & Heidrich-Meisner, F. Topological charge pumping in the interacting bosonic Rice-Mele model. Phys. Rev. B 98, 245148 (2018).
- (29) Stenzel, L., Hayward, A. L. C., Hubig, C., Schollwöck, U. & Heidrich-Meisner, F. Quantum phases and topological properties of interacting fermions in one-dimensional superlattices. Phys. Rev. A 99, 053614 (2019).
- (30) Mei, F., Chen, G., Goldman, N., Xiao, L. & Jia, S. Topological magnon insulator and quantized pumps from strongly-interacting bosons in optical superlattices. New J. Phys. 21, 095002 (2019).
- (31) Rice, M. J. & Mele, E. J. Elementary excitations of a linearly conjugated diatomic polymer. Phys. Rev. Lett. 49, 1455–1459 (1982).
- (32) Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 9, 795–800 (2013).
- (33) Hayward, A. L. C., Bertok, E., Schneider, U. & Heidrich-Meisner, F. Effect of disorder on topological charge pumping in the Rice-Mele model. Phys. Rev. A 103, 043310 (2021).
- (34) Asbóth, J. K., Oroszlány, L. & Pályi, A. A short course on topological insulators. Lecture notes in physics 919 (2016).
- (35) Zhang, Y.-F. et al. Coupling-matrix approach to the Chern number calculation in disordered systems. Chin. Phys. B 22, 117312 (2013).
- (36) Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).
- (37) Das, K. K. & Christ, J. Realizing the Harper model with ultracold atoms in a ring lattice. Phys. Rev. A 99, 013604 (2019).
- (38) Marra, P. & Nitta, M. Topologically quantized current in quasiperiodic Thouless pumps. Phys. Rev. Research 2, 042035 (2020).
- (39) Aubry, S. & André, G. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Israel Phys. Soc. 3, 133–164 (1980).
- (40) Huse, D. A., Nandkishore, R., Oganesyan, V., Pal, A. & Sondhi, S. L. Localization-protected quantum order. Phys. Rev. B 88, 014206 (2013).
- (41) Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).
- (42) Price, H. M., Zilberberg, O., Ozawa, T., Carusotto, I. & Goldman, N. Four-dimensional quantum Hall effect with ultracold atoms. Phys. Rev. Lett. 115, 195303 (2015).
- (43) Ippoliti, M. & Bhatt, R. N. Dimensional crossover of the integer quantum Hall plateau transition and disordered topological pumping. Phys. Rev. Lett. 124, 086602 (2020).
- (44) Privitera, L., Russomanno, A., Citro, R. & Santoro, G. E. Nonadiabatic Breaking of Topological Pumping. Phys. Rev. Lett. 120, 106601 (2018).
- (45) Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
- (46) Xie, B.-Y. et al. Second-order photonic topological insulator with corner states. Phys. Rev. B 98, 205147 (2018).
- (47) Li, C.-A., Fu, B., Hu, Z.-A., Li, J. & Shen, S.-Q. Topological Phase Transitions in Disordered Electric Quadrupole Insulators. Phys. Rev. Lett. 125, 166801 (2020).
- (48) Araki, H., Mizoguchi, T. & Hatsugai, Y. Phase diagram of a disordered higher-order topological insulator: A machine learning study. Phys. Rev. B 99, 085406 (2019).
- (49) Kitagawa, M. et al. Two-color photoassociation spectroscopy of ytterbium atoms and the precise determinations of s-wave scattering lengths. Phys. Rev. A 77, 012719 (2008).
- (50) Taie, S. et al. Realization of a SU(2) SU(6) system of fermions in a cold atomic gas. Phys. Rev. Lett. 105, 190401 (2010).
Supplementary Information for:
Competition and interplay between topology and quasi-periodic disorder in Thouless pumping of ultracold atoms
Shuta Nakajima1,2, Nobuyuki Takei1, Keita Sakuma1, Yoshihito Kuno1,3, Pasquale Marra4,5, and Yoshiro Takahashi1
1 Department of Physics, Graduate School of Science, Kyoto University, Kyoto 606-8502, Japan
2 The Hakubi Center for Advanced Research, Kyoto University, Kyoto 606-8502, Japan
3 Department of Physics, University of Tsukuba, Tsukuba, Ibaraki 305-8571, Japan
4 Graduate School of Mathematical Sciences, The University of Tokyo, Komaba, Tokyo, 153-8914, Japan
5 Department of Physics, and Research and Education Center for Natural Sciences, Keio University, Hiyoshi, Kanagawa, 223-8521, Japan
S1 Approximated tight-binding model
In order to estimate the qualitative properties of our experimental system modeled by the cRM model, we consider an approximated tight-binding picture. Our experimental system is based on the following dynamical superlattice potential in a clean limit:
Hereafter, since in our experiments only the first band is almost occupied, and the band gap between the second and third bands are fairly large, we can focus on only the first and second bands created by our experimental superlattice potential. Then, we can describe the system with an effective tight-binding model, namely, the tRM model in a clean limit, which reads
| (S2) | |||||
In the topological charge pumping (TCP), and are adiabatic dynamical parameters, which can be approximately determined by the band structure induced by the superlattice potential . Here, we approximate these dynamical sequence for and as a circular trajectory, , , where . Although the actual dynamical sequence for and in our experimental system is subtly different from the circular one, this approximation facilitates the ideal theoretical treatment of the TCP phenomena, especially for calculating the Chern number, and can gives insight for qualitative properties of the TCP described by the cRM in our experiment. The physical values of , and can be directly determined by the band structure of the superlattice potential . The values of and are determined by the band width in the double-well lattice case (, ), while the value of by the band gap in the staggered lattice case (, ) as discussed in the previous study Nakajima . For the band structure determined by our experimental setup, the tRM parameters are approximately determined. The tRM model is expected to capture the qualitative behavior for our experimental system, since in the clean limit, the circular parameter sequence for and is topologically connected to our actual experimental sequence without gap closing. Regarding the basic topological aspect of the tRM model, for (at inversion symmetric point, , ), the model reduces to the celebrated Su-Schrieffer-Heeger (SSH) model, classified in the Altland-Zirnbauer class BDI of the periodic classification of topological statesSchnyder ; Kitaev . The SSH model exhibits a topological phase and zero energy topological edge modes Asboth . However, a finite breaks the chiral symmetry without gap closing, i.e., where is the bulk momentum Hamiltonian of Eq. (S2). Accordingly, the tRM model is not necessarily in the BDI class.
In our experiment, a quasi-periodic disorder lattice created by an additional laser with wavelength (= 798 nm) applied by tilting 45∘ for the one-dimensional superlattice axis, is given by
| (S3) |
(see Fig. 1a of the main text). This quasi-periodic disorder potential can be effectively implemented in the tRM model as an on-site potential given by
| (S4) | |||||
where . The potential amplitude in does not strictly correspond to the value of the continuous system potential , but gives a good approximation. The quasi-periodic disorder potential is diagonal and breaks the chiral symmetry even for or SSH case. In general, this type of the disorder strongly affects the topological system and leads to the breakdown of the topological phase, compared to a chiral symmetric disorder employed in a recent experiment Meier . On the other hand, in this tight-binding picture we ignore modulated effects of to the tRM parameters, , and . Thus, we consider as an approximated tight-binding model for our experimental system.
For the sake of simplicity, we consider the effect of quasi-periodic disorder only on the on-site potential and ignore the effects of the trapping potential. However, the resulting model is nevertheless able to capture the essence of the physical behavior of the cRM model and of the experimental system. In particular, for small , the tRM model reasonably approximates the cRM model. However, for large , deviations between the tRM model and cRM models become noticeable. Since is diagonal, the total tight-binding model has no chiral symmetry even for inversion symmetric point, therefore is expected to have strong influence to the TCP.
S2 Localization transition in a quasi-periodic disordered SSH model
To estimate the Anderson localization point in our experimental system, we calculate effects of quasi-periodic disorder created in a disordered SSH model, corresponding to the case in the tRM model of Eq. (S2) including the of Eq. (S4) as an effect of the disordered lattice potential. Here, we consider a quasi-periodic disorder lattice with a wavelength of nm. In general, since we consider quasi-periodic disorder, we expect an Anderson localization transition at a finite disorder strength even in the one dimensional system. In conventional Anderson localization, single atoms are localized at each single lattice site. To estimate the localization transition in our considering system, we employ the inverse participation ratio (IPR). The IPR for each eigenstate is defined as
| (S5) |
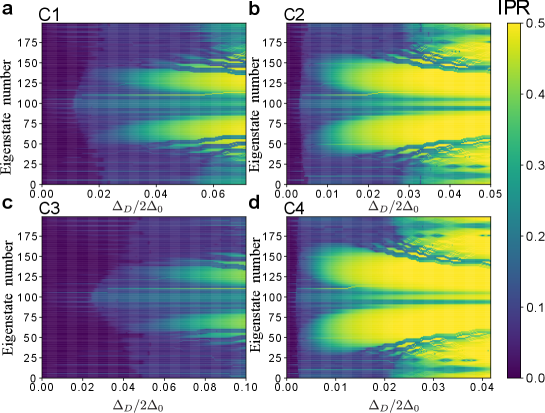
where is a -site localized single particle state and is -th eigenstate in the SSH model with quasi-periodic disorder potential. Large value of the IPR is a signature of the localized tendency of the single particle wave function. We perform the IPR calculation for four different parameter sets of (,) corresponding to those in the four different pump trajectories in our experiments. The results are shown in Fig. S1, where we plot the IPR as a function of and of the eigenstate number in lattice site system with periodic boundary conditions. The sets and correspond to the parameter sets A and B in Fig. 2a in the main text, and the set and correspond to the trajectories and in Fig. 5b, respectively. The order of the eigenstate numbers corresponds to the eigenenergy in ascending order. Due to the quasi-periodic disorder, all cases in Fig. S1 exhibit mobility edges, i.e., different eigenstates localize for different disorder strengths. Here we take the condition as a localization criterion, while the transition point is determined by the case where all eigenstates fulfill this condition. For all the cases in Fig. S1, all the eigenstates already tend to be localized for . We define the Anderson localization transition point in the main text, using eigenstates with lower eigenenergies. These states are localized at and for the pump trajectories and (or the set A and B in the main text), respectively. These values correspond to and . Even though from the numerical calculation our experimental system (cRM model) is also expected to be localized around the SSH parameters points, this fact does not mean gap closing directly. Even when the system exhibits localization and fulfills our criteria, the pumping does not necessarily break down, as shown numerically in Ref. Wauters .
S3 Chern number calculation from a dimensional extended tight-binding model
The tRM model can be mapped into the Harper–Hofstadter–Hatsugai (HHH) model Hatsugai through a dimensional extension Kraus ; Lohse . By regarding the pumping parameter in of Eq. (S2) as -direction momentum and applying the Fourier transformation for , we can obtain the HHH model from the tRM model:
| (S6) | |||||
Here is the annihilation (creation) operator at a two dimensional lattice site , where and , i.e., lattice system. The HHH model is known to have two topological bands with a non-zero Chern number Hatsugai ; Kraus . This is a peculiar property compared to a conventional quantum Hall system on lattice described by the Hofstadter model Hofstadter , since the Hofstadter model does not exhibit two separated bands with non-trivial topology. The two topological bands with a non-zero Chern number in the HHH model is the origin of the TCP in the tRM model. The value of the Chern number corresponds to the total pumped current per one pumping cycle in the tRM model Asboth . For the HHH model, we can further implement the effect of the quasi-periodic disorder of the tRM model as . Here, it should be noted that depends only on the -component site and is uniform along -direction.
In our experimental system, atoms almost occupy the lowest band and the occupation of atom in higher bands is fairly suppressed. We assume that the lower band of the tRM model is fully-occupied approximately. Accordingly, in the numerical calculation of the HHH model the half-filling case is considered. Then, to make comparison with the experimental results shown in the main text, we set the HHH model parameters (, , ) to four experimental parameter sets: (I) (,, (,,, (II) (,, (,,, (III) (,, (,,, and (IV) (,, (,,. These approximated circular pumping trajectories determined by the above four parameter sets are denoted by , , and . These parameter sets (, , ) are determined by comparing to the energy spectra of the cRM model as in the previous paper Nakajima . The and trajectories are the approximated version of the set A and B in the experimental pumping sequences in Fig. 2a in the main text, respectively. The and trajectories correspond to the experimental pumping sequences and in Fig. 5b, respectively. In what follows, We numerically calculated the Chern number for , and trajectories and use (20 unit cells). This -direction system size is close to our experimental system.
We calculate the Chern number for the model of in the following manner. Since discrete translational invariance is broken due to the term , we employ a calculation method to obtain the Chern number from the real space Hamiltonian, namely, the so-called coupling matrix method YFZhang ; Castro ; Sriluckshmy ; Kuno . In this method, we impose twisted periodic boundary conditions with two twisted phase and for each spatial direction. Their twisted phases play a role of the momentum and (corresponding to ) in the TKNN formula Niu85 . Since this twisted phase boundary conditions can be employed even for a system without translational invariant such as a disordered system, we can calculate the Chern number for the model of .
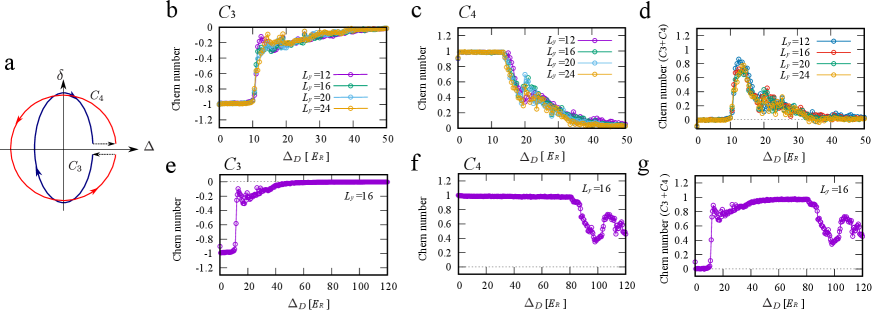
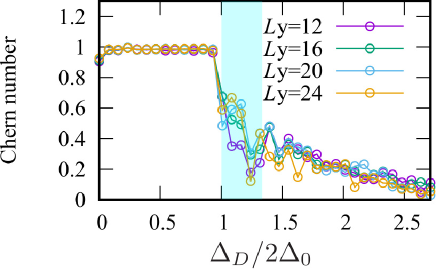
Figure S2 displays the calculated Chern number in the presence of quasi-periodic disorder and its dependence of the artificial -spatial system size with fixed (20 unit cells system from the view point of the tRM model). The result indicates that the system-size dependence is fairly small, and the topological phase transition point does not depend much on the value of . Therefore, the system size used in the numerical calculation is large enough to capture the behavior of our experimental system. data in Fig. S2 is displayed in Fig. 2b in the main text.
Next, we employ this numerical method to study the disorder-induced charge pump (DICP). The schematic pumping trajectory plotted in the plane is shown in Fig. S3a. This trajectory is a combination of circular and trajectories. Our experiment is conducted with a trajectory similar to this schematic trajectory. In particular, the experimental trajectory can be connected by continuous deformation, and it is therefore topologically equivalent, to the trajectory shown in Fig. S3a. The DICP trajectory does not wrap the origin corresponding to the gap closing point in the tRM model in the clean limit. In this sense, in the clean limit, the tight-binding RM model of Eq. (S2) exhibits no TCP, i.e., total pumped current is zero. However, once the quasi-periodic disorder is switched on, the disordered model has possibility to exhibit a non-trivial pumped current that could not occur at the clean limit. This corresponds to the fact that the disordered HHH model also has possibility to exhibit a topological non-trivial phase with a non-vanishing Chern number, .
To study the DICP, we split the DICP trajectory into two circles, and . For each circular trajectory, we calculate the Chern number by using the disordered HHH model. Here, various system sizes for are calculated to check the finite size effects. Moreover, for all data we average over different samples corresponding to different values of (60 samples). The numerical results for each trajectory are shown in Fig. S3b and c. The data display -dependence (not scale) of the Chern number. Furthermore, Fig. S3d shows the sum of the Chern number between and trajectories. The result clearly captures the presence of a non-trivial pump between , quantified by the imperfect cancellation between the Chern numbers for and trajectories. All results in Fig. S3b-d indicate that the finite system size () dependence is fairly small. data in Fig. S3 are used in Fig. 5b and c in the main text.
In addition, we show that this type of pump protocol in Fig. S3a theoretically exhibits a topological DICP. Here, we consider that the inner and outer trajectories are farther apart compared with the experimental ones, i.e., we set the inner circle (C3) with and the outer circle (C4) with . The numerical results are shown in Fig. S3e-g. As seen in Fig.S3g, there exists a quantized plateau within the errors or fluctuations due to numerical instability inevitable for disordered systems for moderate disorder strength.
S4 Continuous model
To obtain the band structure in the continuous system, we use a continuous model with a lattice potential given by
| (S7) | |||||
and we solve the time-independent Schrödinger equation
| (S8) |
using space discretization. Using the recoil energy as the energy unit and the lattice constant of the long lattice as the length unit one has .
Since is an irrational number, the quasi-periodic disorder lattice is incommensurate with respect to the short and the long lattice. As a consequence, the translational symmetry of the lattice is broken, and thus the unit cell of superlattice is not well-defined. Hence, one cannot meaningfully define the periodic boundary conditions for the system. Therefore, we will approach the irrational value by taking a succession of rational approximations of the irrational number, obtained in terms of continued fraction representation continued_fractions_hardy . Every irrational number can be written uniquely as an infinite continued fraction as
| (S9) |
with integers. The successive approximations are obtained by truncating the continued fraction representation . Since are rational numbers one can write as
| (S10) |
where are coprimes. These represent successive rational approximations of the irrational number .
In our specific case one has
For the unit cell of the superlattice has length . For and being a rational number with coprimes, the total unit cell of the superlattice has length as one can see by direct substituting Eq. (S7). The energy levels are then obtained by solving the Schrödinger equation with periodic boundary conditions over a system of length where is the total number of unit cells. We take and a total length of .
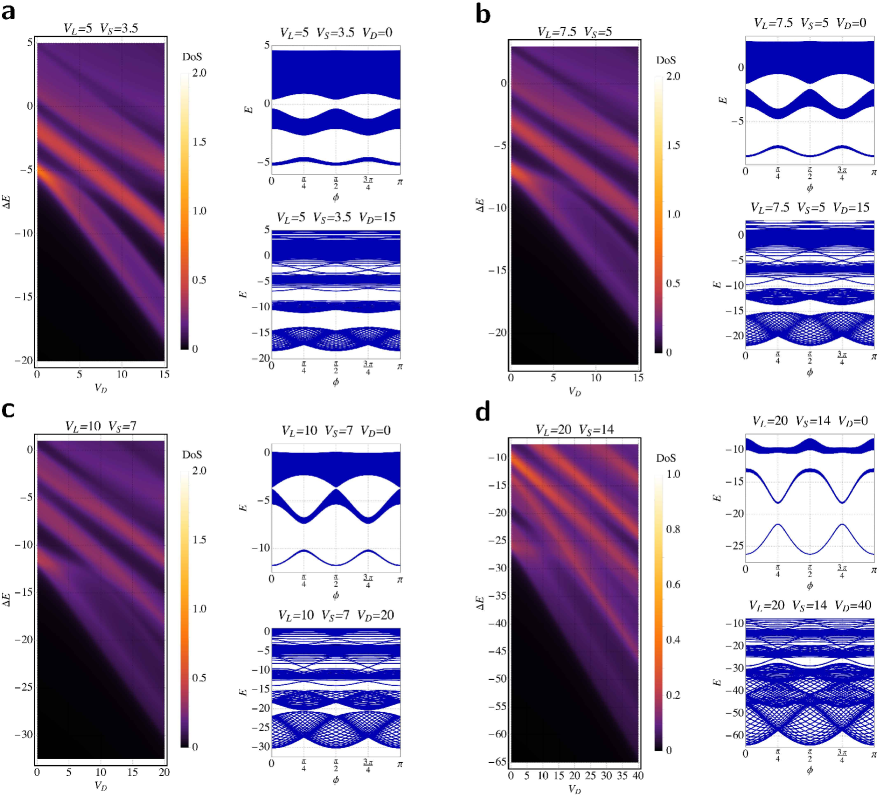
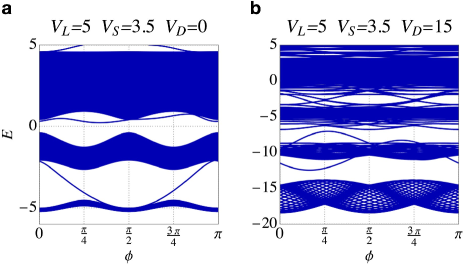
Figure S4 shows the bulk density of states (DoS) as a function of and the band structure in the clean and in the strong disorder regimes, for different values of the lattice depths and . The DoS and the band structure are calculated using closed (periodic) boundary conditions. In the shallower lattice cases (a and b) we can clearly see from the DoS that the global gap closes and reopens at . For the case (c) , a very small gap closes and reopens at . In the case (d) , which is the same as Fig. 3d of the main text, the numerical calculations show the gap closing at but do not show such re-opening of the gap.
Figure S5 shows the band structure calculated in the case of open boundary conditions in the clean and strong disorder regimes, for the parameter set (as in Fig. S4a). In the clean limit, one can clearly see an edge state which connects the lowest energy band with the first excited band. Therefore the lowest energy gap is topologically non-trivial. In the strong disorder case there is an intraband state in the lowest energy gap. This intraband state do not connect the two bands and it is therefore topologically trivial. Non-trivial edge states are also present in the lowest energy gap in the clean limit for , , and . However, for these choices of the lattice depths, the energy bands dispersion becomes so broad that the lowest energy gaps become very narrow, and the presence and identification of intraband edge states cannot be resolved unambiguously.
S5 Evaluation of excitation fraction
In Fig. 3a of the main text, we investigate the gap closing between the first and second bands by measuring the fraction of atoms excited to the second band after three cycles of cRM pumping under quasi-periodic disorder with the lattice parameter . The band structure is defined for the long lattice, spanned by the quasi-momentum , since we adiabatically turn off the quasi-periodic disorder lattice from the whole lattice setup in 130 ms. We then utilize a band-mapping technique, where an adiabatic turn-off of the remaining optical lattices maps quasi-momentum of -th band to free-particle momentum of -th Brillouin zone Greiner2001 ; Kohl2005 . By taking absorption images after time-of-flight of 10 ms, we evaluate atom fractions in the first and second band from the momentum distribution.
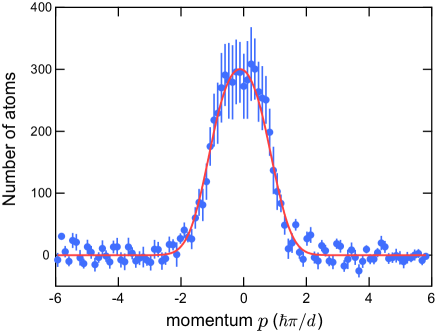
In the case of a clean limit with fixed at 0, it is expected that only the first band is occupied. Figure S6 shows the measured momentum distribution corresponding to this case. An almost homogeneous distribution is obtained within the first Brillouin zone. However, the homogenous distribution was smoothed around owing to experimental imperfection such as non-adiabaticity in the band mapping. We approximate this smoothing by the following function :
| (S12) |
here and are fitting parameters and the fitted value denotes the smoothness. We assume that this fitted function represents the momentum distribution when the first band is homogeneously occupied.
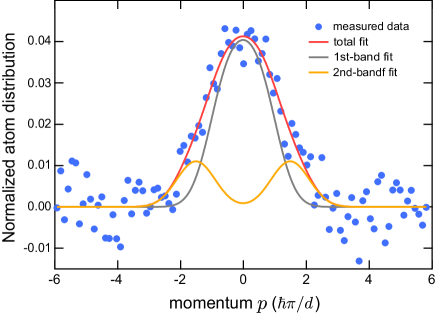
During the pumping under the quasi-periodic disorder, atoms can be excited to the second band. Suppose that the atom distribution in the second band is also homogeneous, and the smoothness of the value obtained above is common for both the first and second bands. Then we fit the measured data for the pumping under the quasi-periodic disorder using the following function :
| (S13) |
here
and is a fitting parameter. The fitted functions and show the momentum distributions in the first and second bands, respectively. Figure S7 shows one of the fitted results at the disorder in Fig. 3a in the main text. After normalizing the integral of the fitted , we evaluated the second-band fraction by calculating . The mean and error bar representing the standard deviation in Fig. 3a of the main text are obtained for ten independent measurements at each disorder strength.
S6 Intuitive understanding of pump suppression
We can understand intuitively why the pump is suppressed at in the following way. As long as the lowest band is occupied, Thouless pumping with a cRM lattice is topologically equivalent to that only with a sliding long lattice Nakajima . Therefore we can capture the essence of the results of the pump suppression by considering a sliding lattice superimposed with a quasi-periodic disorder lattice, namely the second and third terms of Eq (1) in the main text.
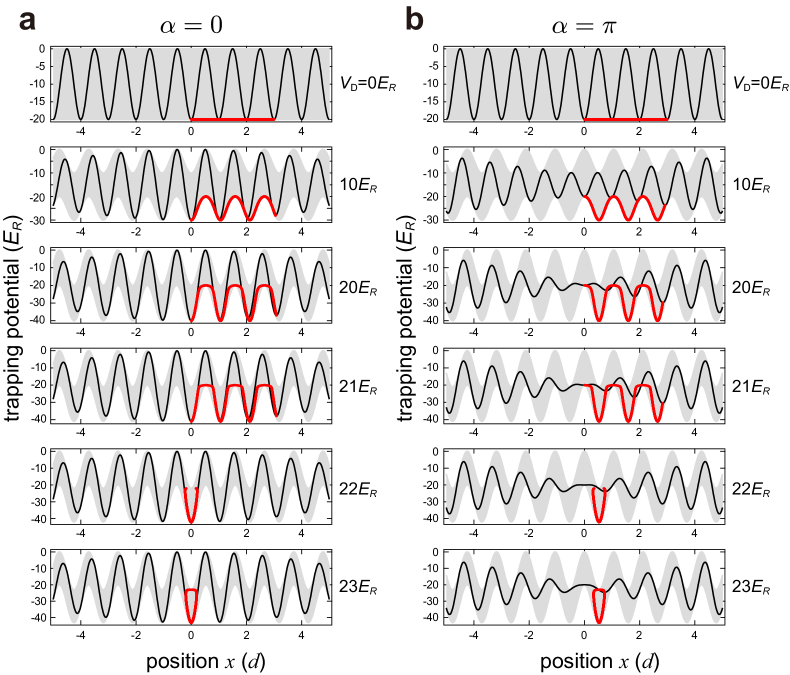
Figure S8 shows the trapping potential produced by these two lattices as a function of position . In addition, the position change of the local minimum point of the trap during three pump cycles is depicted by the red line. The trap depth of the long lattice is fixed to , whereas the disorder strength is varied from to (from top to bottom). When , the local minimum point moves across several lattice sites during the pump cycle in accordance with the sliding lattice. This means that the whole lattice is sliding with the phase swept. For , however, the minimum point stops moving and wanders around the particular trap minimum. Accordingly the whole lattice does not slide. This transition happens around . Therefore it is expected that the pump is suppressed at . Because this discussion does not depend largely on the wavelength of the quasi-periodic disorder lattices, it is reasonable that we observe no clear difference among three measurements in Fig. 4 in the main text.
Since the dominant lattice is that of the static quasi-periodic disorder lattice in the case of , the above-mentioned situation also indicates that the trivial band gap should be open. Although the re-opening of the gap is not clearly visible in the numerical calculations in Fig. 3 in the main text, this does not necessarily mean that the state is metallic. In fact, the energy difference between the ground and first-excited vibrational levels within individual lattice sites becomes large in the strong disorder as shown in Fig. S9. This large local energy gap should suppress the excitations to higher levels as observed in Fig. 3a in the main text.

References
- (1) Nakajima, S. et al. Topological thouless pumping of ultracold fermions. Nature Physics 12, 296 (2016).
- (2) Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
- (3) Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conference Proceedings 1134, 22–30 (2009).
- (4) Asbóth, J. K., Oroszlány, L. & Pályi, A. A short course on topological insulators. Lecture notes in physics 919 (2016).
- (5) Meier, E. J. et al. Observation of the topological anderson insulator in disordered atomic wires. Science 362, 929–933 (2018).
- (6) Wauters, M. M., Russomanno, A., Citro, R., Santoro, G. E. & Privitera, L. Localization, topology, and quantized transport in disordered Floquet systems. Phys. Rev. Lett. 123, 266601 (2019).
- (7) Hatsugai, Y. & Kohmoto, M. Energy spectrum and the quantum hall effect on the square lattice with next-nearest-neighbor hopping. Phys. Rev. B 42, 8282–8294 (1990).
- (8) Kraus, Y. E., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).
- (9) Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nature Physics 12, 350 (2016).
- (10) Hofstadter, D. R. Energy levels and wave functions of bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
- (11) Zhang, Y.-F. et al. Coupling-matrix approach to the chern number calculation in disordered systems. Chinese Physics B 22, 117312 (2013).
- (12) Castro, E. V., López-Sancho, M. P. & Vozmediano, M. A. H. Anderson localization and topological transition in chern insulators. Phys. Rev. B 92, 085410 (2015).
- (13) Sriluckshmy, P. V., Saha, K. & Moessner, R. Interplay between topology and disorder in a two-dimensional semi-dirac material. Phys. Rev. B 97, 024204 (2018).
- (14) Kuno, Y. Disorder-induced chern insulator in the harper-hofstadter-hatsugai model. Phys. Rev. B 100, 054108 (2019).
- (15) Niu, Q., Thouless, D. J. & Wu, Y.-S. Quantized hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377 (1985).
- (16) Hardy, G. H. & Wright, E. M. An Introduction to the Theory of Numbers (Oxford University Press, Oxford, 2008), 6 edn. See chapters 10 and 11.
- (17) Greiner, M., Bloch, I., Mandel, O., Hänsch, T. W. & Esslinger, T. Exploring phase coherence in a 2d lattice of bose-einstein condensates. Phys. Rev. Lett. 87, 160405 (2001).
- (18) Köhl, M., Moritz, H., Stöferle, T., Günter, K. & Esslinger, T. Fermionic atoms in a three dimensional optical lattice: Observing fermi surfaces, dynamics, and interactions. Phys. Rev. Lett. 94, 080403 (2005).