11email: {coe11b012,coe14d002,sadagopan}@iiitdm.ac.in
Complexity of Steiner Tree in Split Graphs - Dichotomy Results
Abstract
Given a connected graph and a terminal set , Steiner tree asks for a tree that includes all of with at most edges for some integer . It is known from [ND12,Garey et. al [1]] that Steiner tree is NP-complete in general graphs. Split graph is a graph which can be partitioned into a clique and an independent set. K. White et. al [2] has established that Steiner tree in split graphs is NP-complete. In this paper, we present an interesting dichotomy: we show that Steiner tree on -free split graphs is polynomial-time solvable, whereas, Steiner tree on -free split graphs is NP-complete. We investigate -free and -free (also known as claw-free) split graphs from a structural perspective. Further, using our structural study, we present polynomial-time algorithms for Steiner tree in -free and -free split graphs. Although, polynomial-time solvability of -free split graphs is implied from -free split graphs, we wish to highlight our structural observations on -free split graphs which may be used in other combinatorial problems.
1 Introduction
Steiner tree is a classical combinatorial optimization problem which continues to attract researchers from both mathematics and computing. Interestingly, this problem finds applications in Network Design, Circuit Layout Design, etc., [3]. Given a connected graph and a subset of vertices (terminal set) , Steiner tree asks for a tree spanning the terminal set. The objective is to minimize either the number of edges in the Steiner tree or the number of additional vertices (, also known as Steiner vertices). It is apparent from the definition that Steiner tree generalizes well-known Minimum Spanning Tree (MST) and Shortest Path problems in general graphs [4].
On the complexity front, Steiner tree in general graphs is NP-complete as there is a polynomial-time reduction from Exact 3 Cover [5]. Under the assumption, NP-complete problems are unlikely to have polynomial-time algorithms, it is natural to identify the gap between polynomial-time solvability and NP-completeness by restricting the input instances. Towards this end, many special graph classes such as chordal, bipartite, planar, split, etc., were discovered in the literature [6]. Classical problems such as Vertex cover, Clique, Odd-cycle transversal have polynomial-time algorithms when the input is restricted to chordal graphs which are otherwise NP-complete for arbitrary graphs [5]. However, other famous problems such as Hamiltonian Path (Cycle), Steiner tree, etc., remain NP-complete even on chordal graphs [2, 7]. In fact, Steiner tree is NP-complete on Split graphs which are a strict subclass of chordal graphs [6]. Steiner tree is considered to be a difficult combinatorial problem compared to other problems as it is NP-complete on almost all special graph classes. For example, it is NP-complete on planar [8], chordal [2], bipartite [5], chordal bipartite [9] graphs. Due to its inherent difficulty, this problem has been an active research problem in the literature for the past three decades.
When a combinatorial problem is NP-complete on special graph classes such as chordal and split, it is natural to restrict the input further by means of forbidden subgraphs. For example, Hamiltonian cycle problem is NP-complete in chordal graphs, whereas it is polynomial-time solvable on interval graphs which are chordal and asteroidal-triple free [10, 11, 12, 13]. In this paper, we revisit Steiner tree restricted to split graphs. It is known from [2], that Steiner tree on split graphs is NP-complete. We investigate the complexity of Steiner tree on subclasses of split graphs and present an interesting dichotomy. Towards this end, we study -free (claw free) and -free split graphs from both structural and algorithmic perspectives. In particular, we establish the following results;
-
Steiner tree on -free split graphs is NP-complete.
-
Steiner tree on -free split graphs is polynomial-time solvable.
Towards this end, we present a tight lower bound on the size of the Steiner set and our algorithm correctly produces such a Steiner set. The above results rightly identify the gap between NP-completeness and polynomial-time solvable input instances of Steiner tree problem restricted to split graphs. Since our contribution evolved from -free split graphs, we highlight structural results of both -free and -free split graphs. Although, the complexity of Steiner tree in -free split graphs is inferred from -free split graphs, out of combinatorial curiosity, we investigate both graphs from structural perspective and present polynomial-time algorithms for Steiner tree.
To the best of our knowledge, this line of investigation has not been reported in the literature. The polynomial-time results known in the literature for Steiner tree are for trees and 2-trees [14].
As far as parameterized-complexity results are concerned, in [15] it is shown that Steiner tree in general is Fixed-parameter Tractable(FPT) if the parameter is the size of the terminal set and it is -hard if the parameter is the size of the Steiner set [16]. From the domain of approximation algorithms, Steiner tree has a polynomial-time approximation algorithm with ratio [17]. Variants of Steiner tree include Euclidean Steiner tree [18], Rectilinear Steiner tree [8], and Directed Steiner tree [19, 20].
Roadmap: We present the structural characteristics of -free split graphs in Section 2. Using the structural observations made, we also present a polynomial-time algorithm to output a Steiner tree in -free split graphs. Structural characteristics of -free split graph and a polynomial-time algorithm to output a Steiner tree in -free split graphs is presented in Section 3. Hardness result is addressed in Section 4.
Graph-theoretic Preliminaries:
In this paper, we work with connected, simple, unweighted graphs. Notations are as per [6, 21]. For a graph the vertex set is and the edge set is and is adjacent to in and . The neighborhood of vertex is . The degree of a vertex is . min . For a graph and , represents the subgraph of induced on the vertex set . The subgraph relation is represented as .
A Split graph is such that can be partitioned into an Independent Set and a Clique , . A clique is maximal if there does not exist a clique such that . For all split graphs mentioned in this paper we consider to be a maximal clique unless otherwise stated. is a split graph on vertices such that and , . is also termed as claw. Centre vertex of a is the vertex of degree . A graph is -free if forbids as an induced subgraph. For a vertex , and . For , , and . For a split graph , maximum and .
Two edges and are non adjacent if they do not share an end vertex in common. A set of edges forms a matching of if every pair of edges in are non adjacent. Maximum matching is a matching of maximum cardinality in . denotes the size of the maximum matching in .
2 -free Split Graphs: Structural Results
In this section, we analyze the structure of -free split graphs and we present some interesting structural results. Further, we show that for a claw-free split graph , if , then . This acts as a good handle in yeilding a linear-time algorithm for Steiner tree problem which we see in the later half of this section.
Theorem 2.1
Let be a connected split graph. is claw free if and only if one of the following conditions hold.
1.
2. and for every such that ,
Proof
Necessity: Suppose , and let has at least 3 neighbours, say . Then the set forms a claw in with as its centre vertex. It follows that if is claw-free, then . Now suppose . Let such that there exist vertices . We assume on the contrary that there exist such that . Since is a clique, . It follows that vertices forms a claw in with as its centre, a contradiction. This proves Condition 2, and completes the proof of the forward direction.
Sufficiency: On the contrary assume that is not claw free. No claw in can have its centre vertex in the set , since for any in , the set and hence induces a clique in . So every claw in has its centre vertex in the set .
Consider a claw with the vertex set , with the centre being in . No two of the other three vertices of the claw can be in , because then there would be an edge between them. So at most one of is in , and the rest (of which there are at least two) are in . It follows that if contains a claw, then . Equivalently, if then is claw-free.
Finally, consider the case where . Suppose the vertex set induces a claw in , with its centre vertex being . Then is in , and at least two of are in , as we argued above. Since we get that exactly two of , say and , are in . Then is in , and . It follows that which is a contradiction to Condition 2. Therefore, our assumption that there exist a claw in is wrong, and this completes the sufficiency. Therefore, the theorem follows.
Lemma 1
For a claw-free split graph , if , then .
Proof
Since , let there exist a vertex such that . On the contrary, assume that , that is, such that . Let and as shown in Figure 1. If there exist a vertex such that , and , then vertices induces a claw. Therefore, . If , then induces a larger clique, which is a contradiction to the assumption on the maximality of clique . Therefore, and similarly, . It follows that, and . For every vertex , and otherwise, induces .
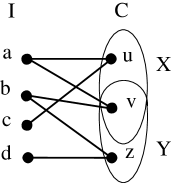
Case 1 Case 2
Therefore, the vertices can have adjacency in two disjoint sets or .
Case 1: and . Edge where and where . Observe that otherwise induces . Similarly, otherwise induces . From the discussion, it follows that the vertices induces a claw, which is a contradiction. Similar argument holds for and .
Case 2: and . Let such that . Note that there exist at least one vertex . If , then the vertices induces a claw. If , then the vertices induces a claw as, . The argument is symmetric for and .
Cases 1 and 2 give a contradiction to the fact that is claw free. Therefore, our assumption that is wrong, and hence, the lemma follows. ∎
2.1 Application: Steiner tree in -free Split Graphs
Using the structural results presented in Section 2, in this section, we present a polynomial-time algorithm to find minimum Steiner tree in -free split graphs. Optimum version of Steiner tree problem is defined as follows;
OPT Steiner tree(G,R) Instance: Graph , Terminal Set Question: Find a minimum cardinality set such that is connected?
We here consider the Steiner tree problem on split graph . Due to pruning, we iteratively construct split graphs , from the input graph . We simplify the input by pruning the vertices which are not part of any optimum solution. The pruned graph is the graph induced on the vertex set . Clearly, and let . We prune three sets of vertices one after the other and are defined as follows.
.
and .
Let . .
Consider the Steiner tree optimization problems , and defined as follows.
: OPT Steiner tree()
: OPT Steiner tree()
Lemma 2
An optimum solution to is also an optimum solution to .
Proof
Note that the first two sets pruned from are not part of any optimum solution. induces a connected subgraph of which is also pruned to obtain . If , then Steiner set of is empty. i.e., induces a connected subgraph of . On the other hand if , then there exist at least one vertex in the Steiner set of . connects all terminal vertices . If , then there exist at least one vertex such that and . and therefore, induces a connected subgraph of and is a minimum Steiner set for . Hence, the lemma follows. ∎
2.1.1 A polynomial-time algorithm to find a minimum Steiner tree
Given a -free split graph with terminal vertex set , we present a polynomial-time algorithm to find a minimum Steiner tree. As part of preprocessing step, we prune the sets and , which are not part of any optimum solution. Further, we delete terminals which are in , and their neighbours in , namely the set . Now we have an instance of Steiner Tree in claw-free split graphs where all the terminals are in the independent set. An optimum solution to the pruned graph is also an optimum solution to the original graph by the previous lemma. We now present a sketch of algorithm and the detailed one is presented in Algorithm 1. If , then the instance is trivial. If , then Steiner set should contain one neighbor vertex in of each terminal in . In the remaining case, and therefore, by Lemma 1 . The only non-trivial case is when . From the constraints of the instance, we know that it is necessary and sufficient to pick exactly two Steiner vertices from in this case.
2.1.2 Proof of Correctness of Algorithm 1
By Lemma 2, a minimum Steiner set of pruned graph is an optimum Steiner set for . Therefore, pruning in Step is a solution preserving operation. We present a case analysis to show that our algorithm outputs a minimum Steiner tree of a claw-free split graph.
Case 1: . Note that for every vertex , Step includes exactly one vertex in , which is a minimum Steiner set.
Case 2: .
Observe by Lemma 1. for , respectively, which is done by Steps . Therefore, is a minimum Steiner set for , and by Lemma 2, is also a minimum Steiner set for . Step outputs a Steiner tree by running standard Breadth First Search algorithm on .
2.1.3 Run Time Analysis
We represent the input claw-free split graph using an adjacency list, as we can easily find a neighbor of a given vertex. Vertices in adjacency list are arranged such that follow . Intuition behind this ordering is that, first neighbor of a vertex encountered in the list is always a vertex , if it exists. If , then can be determined in constant time. Therefore, Algorithm 1 takes linear time to output a minimum Steiner set.
3 -free Split Graphs: Structural Results
In this section, we first analyze the structure of -free split graphs. Subsequently we investigate Steiner tree problem restricted to -free split graphs. Towards this end, we give a nice bound on the cardinality of any minimum Steiner set. Further, we present a structural characterization of -free split graph meeting the bound. Interestingly, the characterization yields a polynomial-time algorithm to output a minimum Steiner tree, which we shall present in Section 3.1.
Before we present the structural results, we introduce some additional terminologies.
A split graph is a -split graph if . Note that a -free split graph is a -split graph for some , and the converse does not always hold. In a split graph , closed neighborhood of a vertex is .
For a -split graph , we construct a labeled graph such that and and and label the edge as . Note that in denotes a vertex . Also, we pick exactly one to label the edge . For any edge set , we define the corresponding vertex set as follows.
Corresponding to each edge , include exactly one vertex in . It follows that, and . Clearly, as we are including not more than one vertex in corresponding to each edge in . Suppose , then there exist at least two edges labelled in such that and . Since edges can share atmost one vertex in common, it follows that, , which is a contradiction as is -split, and is the labelled graph of . Therefore, . We also define the Corresponding clique set of a vertex set as follows. Corresponding to each vertex , include exactly one vertex in such that . Clearly, and . For a -split graph, .
We now present some structural observations on -free split graphs.
Lemma 3
Let be a -split graph. is free if and only if for every and for every , .
Proof
Necessity: On the contrary, let us assume there exist such that . Since , vertices induces a , which is a contradiction and the necessary condition follows.
Sufficiency: On the contrary, assume that is not free and there exists a induced on with as the centre vertex. No in can have its centre vertex in the set , since for any in , the set is a subset of the set and hence induces a clique in . So every in has its centre vertex in the set particularly, . Since is a -split graph, .
This implies that there exist at least one vertex of , say , and . It follows that , which is a contradiction and the sufficiency follows. This completes the proof of the lemma. ∎
Corollary 1
Let be a -free -split graph. For any , the graph induced on the vertex set is a -split graph for some .
On the contrary, suppose there exists a vertex such that . i.e., . It follows that . By previous lemma, induces a , which is a contradiction. ∎
Corollary 2
Let be a -free split graph and . If , then .
Proof
By Lemma 3, for every , . This implies that for every , . It follows that . ∎
Now onwards, we investigate the Steiner tree problem on -free split graphs. For our discussions on Steiner tree problem, we fix the terminal set to be . Observe that -split graphs for are -free split graphs. If is a -split graph, then there does not exist a vertex such that . Therefore, the corresponding clique set of forms the minimum Steiner set of where . We shall now consider -split graphs for discussions. For a -split graph , recall that the labelled graph is such that , and there exist such that . The following lemma gives the cardinality of a minimum Steiner set of any -split graphs.
Lemma 4
Let be a -split graph, and be the labeled graph of with . Then any minimum Steiner set of is such that .
Proof
If is a connected graph, then the minimum Steiner set in corresponds to the minimum edge cover in . For any graph with maximum matching , the cardinality of minimum edge cover is . Therefore, a minimum Steiner set is such that . If is not connected, let be the components such that are non-trivial components with at least one edge and are trivial ones. For components , we find the maximum matching where and be the corresponding vertex set of the matching . Clearly, . Let be the corresponding clique set of . From the definition of the corresponding clique set, . Note that, there does not exist two vertices such that , otherwise it contradicts the maximality of . Since there does not exist the possibility to have two such vertices , it follows that and the graph induced on is a -split graph. Therefore, , and . It follows that the set forms a Steiner set of and . ∎
Lemma 5
For any -split graph , OPT Steiner tree problem is polynomial-time solvable.
Proof
Finding the labeled graph of , incurs effort where . Maximum matching of can be found in time. Note that the corresponding vertex set of can be found in linear time. Similarly, the corresponding clique set also can be obtained in linear time. Therefore, the overall running time for finding the Steiner set is and OPT Steiner tree in any -split graph is polynomial-time solvable. ∎
The following lemma characterizes a special -split graph constructed from a -split graph. Particularly, Lemma 6 gives an upper bound on the matching size of the labelled graph of a -split graph.
Lemma 6
Let be a -free -split graph. For any , let be the graph induced on , and be the labelled graph of . Then size of any maximum matching
Proof
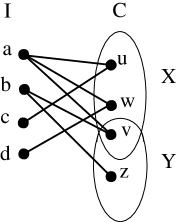
Recall from Corollary 1 that, is a -split graph for some . On the contrary, let . Let vertices be those vertices participating in the matching of size at least such that and , , as shown in Figure 2. Clearly, from Lemma 3, . Similarly, and . We consider the following scenario.
Suppose and . Since , without loss of generality, . Observe that induces a . Therefore, . Similar argument holds true for and . Since the clique is maximal, is not adjacent to all vertices of , and therefore there exist such that . Clearly, , and . Observe that in , and is not a -split graph, . This is a contradiction to Corollary 1. It follows that our assumption is wrong and therefore, . This completes the proof of the lemma. ∎
We now present some structural observations pertaining to -split graphs.
Lemma 7
For a -free -split graph , any Steiner set of is such that .
Proof
Observe that as is -split. For any , is the graph induced on . By Corollary 1, is a -split graph, . Let be the minimum Steiner set of such that and . If is the labeled graph of , then by Lemma 6, . Let be the matching edges of a maximum matching in . Observe that there exist two vertices such that , . Notice that for each vertex , there exist a vertex in such that . The graph induced on is a -split graph, and it follows that . It can be concluded that as . This completes the proof of the lemma. ∎
We below characterize -free -split graphs based on the cardinality of a minimum Steiner set. In particular, in Theorem 3.2, we characterize -free split graphs whose minimum Steiner set is , and in Theorem 3.3, we characterize -free split graphs whose minimum Steiner set is . To present Theorem 3.1 to Theorem 3.4, we fix the following notation. Let be a -free -split graph. For any , let be the graph induced on , and be the labelled graph of . In Theorem 3.1, we present a stronger result of Lemma 7.
Theorem 3.1
For a -free -split graph , any minimum Steiner set of is such that .
Proof
On the contrary assume that there exist a minimum Steiner set such that .
Suppose that . Note that , say and for every vertex , as per Lemma 3. i.e., for every , there exist an edge , where . The graph induced on is a -split graph, by Corollary 1. Consider the Steiner set of such that . Note that as is a -split graph, and for each vertex , . Notice that and implies that . This shows that is not possible.
Next we shall consider the scenario . Consider the -split graph, induced on where . Let the labeled graph of be . For and note that . Clearly, and . We now claim that there exist at least vertices say such that , and , . Suppose if there exist at most two vertices such that and , then observe that . It follows that , which is a contradiction as is . Therefore, there exist at least vertices such that , and , . Consider the labeled graph of . There exist such that , , . It follows that , , forms a matching of size in which is a contradiction to Lemma 6. Therefore our assumption is wrong and . This completes the proof. ∎
Theorem 3.2
For any minimum Steiner set of , if and only if .
Proof
Necessity: If , then for every vertex , . i.e., for every , there exist an edge , where . Similar to the proof of Theorem 3.1, it follows that . Therefore, . Let and the graph induced on vertex set is a -split graph, by Corollary 1. Let . Clearly in . Note that and . This implies that there exist a matching of size at least in . From Lemma 6, . Therefore, .
Sufficiency: Let be the edges that form the matching of size such that label( and label(. Clearly, and , where . Let be the corresponding clique set of . Observe that forms a Steiner set of , and . This completes the proof. ∎
Apart from the labelled graph , we make use of one more labelled graph in Theorem 3.3, which is defined as follows. is the -split graph, induced on the vertex set , and is the labeled graph of . Note that the two labeled graphs and , are constructed differently. is constructed on the vertex set whereas is the labeled graph on . We fix to be a minimum Steiner set of . The following theorem characterizes -free -split graphs with .
Theorem 3.3
if and only if one of the following is true.
1. and .
2. and .
Proof
Necessity: If then we come across the following two cases.
Case 1: .
Let and . Observe that, in , the -split graph, induced on the vertex set , . i.e., and . This implies that there exist a matching of size at least in . By Lemma 6, . Suppose , then by Theorem 3.2, . However, we know that and therefore . We can therefore conclude that . If , then since is connected and -free, . In this case, . Therefore, it follows that .
Case 2: .
Since , is a minimum Steiner set in and since is the induced on the vertex set , is also a minimum Steiner set in . Observe that if , then the size of the minimum Steiner set in is by Lemma 4. Since we can conclude that .
Sufficiency:
Case 1: and
Let and be the edge that forms the matching of size , such that label()=. Clearly, , where . Let be the corresponding clique set of .
Observe that forms a Steiner set of , and .
Case 2: and
Let be the edges that form the matching of size , such that label()=, label()=, label()=. Clearly, , where . Let be the corresponding clique set of . Observe that forms a Steiner set of , and . This completes the proof. ∎
Theorem 3.4
.
Proof
The lower bound is true by Theorem 3.1. Theorem 3.2, and Theorem 3.3 characterizes the -split graphs such that , and , respectively. We shall now look into the upper bound. Since is -split, there exist . Let be the corresponding clique set of . Observe that and . Since , it follows that . Therefore the theorem. ∎
3.1 Polynomial-time algorithm to find a minimum Steiner tree
Using the structural results presented in Section , in this section, we shall present a polynomial-time algorithm to find a minimum Steiner tree in -free split graphs. Algorithm 3 finds a minimum Steiner set of a given -free split graph with being terminal vertices. Further, the minimum Steiner tree is obtained using standard Breadth First Search on .
We shall now present a sketch of the algorithm and a detailed one is presented in Algorithm 3. As part of preprocessing, we prune the sets and as defined in Section 2.1. Since is a -free split graph, is -split, . We come across four cases as follows. If is a -split graph, then is connected and the minimum Steiner set . If is a -split graph, then the corresponding clique set of is a minimum Steiner set. If is a -split graph, then we find the labelled graph of and the maximum matching of . Subsequently, we find the corresponding vertex set of the matching and the corresponding clique set of . The minimum Steiner set is ( from Lemma 4 ). Given a -split graph, we perform a transformation to obtain a -split graph. We identify the size of a minimum Steiner set and the Steiner set with the help of the labelled graph associated with the transformed -split graph. Interestingly, based on the matching size, we get to identify the size of minimum Steiner set and the corresponding clique set helps us to identify the Steiner set. It is important to highlight the fact that if matching size is , we look at two different labelled graphs to identify the minimum Steiner set. The detailed algorithm is presented in Algorithm 3.
3.1.1 Proof of correctness of Algorithm 3
Step 2 of Algorithm 3 prunes the input graph to obtain and by Lemma 2, an optimal Steiner set of is also an optimal Steiner set of . If is a -split graph, then and our algorithm correctly computes such a Steiner set in step 5. If is a -split or -split graph, then Algorithm 3 calls Algorithm 4, or Algorithm 5, respectively. Now we shall look into Algorithm 4 in detail. The algorithm finds the labeled graph in Step . Note that Algorithm 4 in Step 4 finds a maximum matching in , and finds the corresponding vertex set of such that . Step 5 finds such that . The Steiner set is returned in Step where , which is correct due to Lemma 4 and hence Algorithm 4 returns an optimum Steiner set.
In Algorithm 5, for every , we find and its labeled graph in Step . A maximum matching on is obtained in Step . Step and 8 updates maximum matching and its corresponding vertex set found so far. Note that by Theorem 3.4, Steiner set of is bounded as . We can see the following cases.
Case (i) . By Theorem 3.2, and it follows that and . Step finds such that . Step returns where .
Case (ii) . By Theorem 3.3, either or . If , then and . Step finds such that . Note that . If , then and . Step finds such that . Observe .
Case (iii) . It follows that . Since we initialized with a vertex , and . Observe that and . This completes the case analysis and Algorithm 5 correctly computes a Steiner set of . Therefore, Algorithm 3 correctly computes the minimum Steiner tree in Step .
3.1.2 Run-time analysis of Algorithm 3
Let represents the size of vertex set, and the edge set, respectively of the input graph . We shall first analyze the run-time of Algorithm 4 and Algorithm 5 as Algorithm 3 invokes Algorithm 4 or Algorithm 5 at Steps , , respectively. For Algorithm 4, observe that creation of the labeled graph in Step needs effort as . Step finds a maximum matching of which can be done in time using general graph maximum matching algorithm [22]. Corresponding clique set in Step can be found in time. Therefore, the run-time of Algorithm 4 is . Consider Algorithm 5, Steps to are iterated at most times. Step needs effort. Finding a matching of in step 5 needs time. Steps incurs constant effort. Therefore, the iteration of Steps to involves effort. Note that Steps , need , , respectively and Step 15 incurs a effort. Finding in step 18 can be done in time. Overall, the run-time of Algorithm 5 is .
Now we shall discuss run time of Algorithm 3. Pruning of verices in step 2 of Algorithm 3 takes effort where denotes maximum degree of the input graph . Step 5 takes time. Steps , takes time, time, respectively. Step incurs time. Therefore the run time of Algorithm 3 is . Thus, Steiner tree in -free split graph is polynomial-time solvable.
4 Steiner tree in -free Split Graphs is NP-complete
In the earlier section, we have presented a polynomial-time algorithm for Steiner tree in -free split graphs. In this section, we present the other half of the dichotomy, which is to show that Steiner tree in -free split graph is NP-complete. Interestingly, the reduction presented in [2] generates instances of -free split graphs. For the sake of completeness, we present our observations along with proofs. Towards this attempt, we recall the classical problem Exact 3 cover [23] which is a candidate NP-complete problem for our investigation.
Exact-3-cover(Z,T) Instance: A Collection of element subsets of a set . Question: Is there a sub collection such that for every , belongs to exactly one member of ?
We recall the decision version of Steiner tree problem, restricted to -free split graphs.
Steiner tree(G,R,k) Instance: -free Split Graph , Terminal Set , Integer Question: Is there a set such that and is connected?
Theorem 4.1
Steiner tree problem in -free split graph is NP-complete.
Proof
Steiner tree is in NP Given a certificate , we show that there exist a deterministic polynomial-time algorithm for verifying the validity of the certificate . Note that the standard Breadth First Search algorithm can be employed to check whether is connected. can be verified in linear time and therefore, overall certificate verification need time, where . Therefore, we can conclude that Steiner tree is in NP.
Steiner tree is NP-Hard
An instance of Exact cover(Z,T) is reduced to an instance of Steiner tree (G,R,k) problem as follows: , , and . Informally, for every element , create a vertex such that . For every member , create a vertex such that . , , and . and . In this reduction, and . The above construction is therefore polynomial to the size of input. We now show that instances created by this reduction are -free split graphs. On the contrary, assume that there exist a induced on vertices . Note that at most two vertices (say ) from clique can be included in the . Clearly, and without loss of generality, . This implies that there exist a element subset corresponding to the clique vertex , which is a contradiction as all subsets are of size in collection . Therefore it follows that the reduced graph is -free split graph. We now show that there exist an Exact-3-cover(Z,T) if and only if there exist a Steiner tree(G,R,k) in the reduced graph on at most Steiner vertices. For Necessity: If there exist , which covers all the elements of , then the set of vertices where is the corresponding vertex of forms a Steiner set in as . Also note that . For Sufficiency: If there exist a Steiner set in the reduced graph on at most Steiner vertices, then observe that for all vertex , , and . It follows that there does not exist such that . Therefore, where is the corresponding vertex of forms an exact 3 cover of . This completes the proof of the claim.
We can conclude that Steiner tree problem is NP-complete in -free split graphs. ∎
5 Conclusions and Future Work
We have presented an interesting dichotomy result that Steiner tree problem is polynomial-time solvable in -free split graphs and NP-complete in -free split graphs. This result is tight and it identifies the right gap between NP-completeness and polynomial-time solvability of Steiner tree in split graphs. Using the structural results presented here, an interesting direction for further research would be to explore the complexity of other classical problems which are NP-complete restricted to split graphs.
References
- [1] M. R. Garey, R. L. Graham, D. S. Johnson: The complexity of computing steiner minimal trees. SIAM Journal on Applied Mathematics 32(4) 835–859 (1977)
- [2] Kevin White, Martin Farber, William Pulleyblank: Steiner trees, connected domination and strongly chordal graphs. Networks 15(1) 109–124 (1985)
- [3] Stefan Vo: Steiner tree problems in telecommunications. In: Handbook of Optimization in Telecommunications, Springer US 459–492 2006
- [4] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms (3. ed.). MIT Press (2009)
- [5] Michael R. Garey, David S. Johnson: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman and Company, New York (1979)
- [6] M.C.Golumbic: Algorithmic Graph Theory and Perfect Graphs. Academic Press, New York (1980)
- [7] A.A.Bertossi, M.A.Bonuccelli: Hamiltonian circuits in interval graph generalizations. Information Processing Letters 195–200 (1986)
- [8] Michael R. Garey, David S. Johnson: The rectilinear Steiner tree problem is NP-complete. SIAM Journal on Applied Mathematics 32(4) 826–834 (1977)
- [9] Haiko Muller, Andreas Brandstadt: The NP-completeness of steiner tree and dominating set for chordal bipartite graphs. Theoretical Computer Science 53(2) 257 – 265 (1987)
- [10] J.M.Keil: Finding hamiltonian circuits in interval graphs. Information Processing Letters 201–206 (1985)
- [11] R.W.Hung, M.S.Chang: Linear-time certifying algorithms for the path cover and hamiltonian cycle problems on interval graphs. Applied Mathematics Letters 648–652 (2011)
- [12] B.S.Panda, S.K.Das: A linear time recognition algorithm for proper interval graphs. Information Processing Letters 153–161 (2003)
- [13] L.Ibarra: A simple algorithm to find hamiltonian cycles in proper interval graphs. Information Processing Letters 1105 – 1108 (2009)
- [14] Joseph A. Wald, Charles J. Colbourn: Steiner trees, partial 2-trees, and minimum IFI networks. Networks 13(2) 159–167 (1983)
- [15] S.E. Dreyfus, R.A. Wagner: The steiner problem in graphs. Networks 1 195–207 (1972)
- [16] Michael Dom, Daniel Lokshtanov, Saket Saurabh: Incompressibility through colors and IDs. In: Automata, Languages and Programming. Volume 5555. 378–389 2009
- [17] Naveen Garg: Saving an epsilon: A 2-approximation for the k-mst problem in graphs. In: Proceedings of the Thirty-seventh Annual ACM Symposium on Theory of Computing. 396–402 2005
- [18] Marcus Brazil, Ronald L. Graham, Doreen A. Thomas, Martin Zachariasen: On the history of the euclidean steiner tree problem. Archive for History of Exact Sciences 68(3) 327–354 (2014)
- [19] M. Jones, D. Lokshtanov, M.S. Ramanujan, S. Saurabh, O. Suchy: Parameterized complexity of directed steiner tree on sparse graphs. In: Algorithms - ESA 2013. Volume 8125. 671–682 2013
- [20] Leonid Zosin, Samir Khuller: On directed steiner trees. In: Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms. 59–63 2002
- [21] D.B.West: Introduction to graph theory 2nd Edition. (2003)
- [22] S. Micali, V. V. Vazirani: An algorithm for finding maximum matching in general graphs. In: IEEE Annual Symposium on Foundations of Computer Science. 1980
- [23] R.M.Karp: Reducibility among combinatorial problems. In: Proc. of a Symposium on the Complexity of Computer Computations. 85–103 1972