Compound Poisson particle approximation for McKean-Vlasov SDEs
Abstract.
We present a comprehensive discretization scheme for linear and nonlinear stochastic differential equations (SDEs) driven by either Brownian motions or -stable processes. Our approach utilizes compound Poisson particle approximations, allowing for simultaneous discretization of both the time and space variables in McKean-Vlasov SDEs. Notably, the approximation processes can be represented as a Markov chain with values on a lattice. Importantly, we demonstrate the propagation of chaos under relatively mild assumptions on the coefficients, including those with polynomial growth. This result establishes the convergence of the particle approximations towards the true solutions of the McKean-Vlasov SDEs. By only imposing moment conditions on the intensity measure of compound Poisson processes, our approximation exhibits universality. In the case of ordinary differential equations (ODEs), we investigate scenarios where the drift term satisfies the one-sided Lipschitz assumption. We prove the optimal convergence rate for Filippov solutions in this setting. Additionally, we establish a functional central limit theorem (CLT) for the approximation of ODEs and show the convergence of invariant measures for linear SDEs. As a practical application, we construct a compound Poisson approximation for 2D-Navier Stokes equations on the torus and demonstrate the optimal convergence rate.
Keywords: Compound Poisson approximation, McKean-Vlasov stochastic differential equation, Invariance measure, Navier-Stokes equation, Central Limit Theorem.
AMS 2010 Mathematics Subject Classification: 65C35, 60H10, 35Q30
1. Introduction
Let and be two Borel measurable functions. Throughout this paper, for a probability measure over , we write
Fix and consider the following McKean-Vlasov SDE or distribution-dependent SDE (abbreviated as DDSDE):
| (1.1) |
where denotes the probability distribution of , stands for a -dimensional standard Brownian motion, and for , is a symmetric and rotationally invariant -stable process with infinitesimal generator (the usual fractional Laplacian operator).
In the literature, DDSDE (1.1) is also considered as a nonlinear SDE due to the dependence of its coefficients on the distribution of the solution. By applying Itô’s formula, solves the following nonlinear Fokker-Planck equation in the distributional sense:
where is the adjoint operator of the generator (local/nonlocal ) of SDE (1.1): for ,
and for ,
where stands for the transpose of matrix and p.v. stands for the Cauchy principle value.
In the seminal work by McKean [31], the study of nonlinear SDE (1.1) driven by Brownian motions was initiated. His paper established a natural connection between nonlinear Markov processes and nonlinear parabolic equations. Since then, the McKean-Vlasov SDE has evolved into a fundamental mathematical framework, offering a powerful tool for analyzing complex systems comprising a large number of interacting particles. The McKean-Vlasov SDE discribes the dynamics of a single particle, influenced by the collective behavior of the entire system. Its applications have expanded across various fields, including statistical physics, stochastic analysis, economics, and biology. Through the study of the McKean-Vlasov SDE, researchers have gained significant understanding of diverse phenomena, ranging from the behavior of particles in statistical mechanics to intricate dynamics in economic and biological systems. Its utility extends beyond theoretical investigations, playing a vital role in the development of numerical methods, data analysis techniques, and decision-making models. For a more comprehensive overview and references, the survey paper by [6] provides valuable insights into the McKean-Vlasov SDE and its wide-ranging applications.
When and satisfy the following Lipschitz assumption
| (1.2) |
it is well-known that for any initial value , there is a unique strong solution to DDSDE (1.1) (see [40], [6]). From the perspective of Monte-Carlo simulations and practical applications, the McKean-Vlasov SDEs (1.1) are often approximated using an interaction particle system. In the case of Brownian motions (), the approximation takes the following form: For fixed , let solve the following SDE in :
| (1.3) |
where is a sequence of i.i.d. Brownian motions, and for a point , the empirical measure of is defined by
where is the usual Dirac measure concentrated at point . Under Lipschitz assumption (1.2), it is well-known that for any , there is a constant such that for any ,
where solves SDE (1.1) driven by Brownian motion . Since are independent, the above estimate indicates that the particle system becomes statistically independent as . This property is commonly referred to as the propagation of chaos (see [40], [6]). Furthermore, the fluctuation
weakly converges to an Ornstein-Uhlenbeck process (cf. [13]). However, for numerical simulation purposes, it is still necessary to discretize the particle system (1.3) along the time direction by employing methods such as the explicit or implicit Euler’s scheme (see [25]).
The objective of this paper is to present a comprehensive discretization scheme for DDSDE (1.1). Our approximation SDE is driven by compound Poisson processes and possesses the advantage of being easily simulated on a computer. Moreover, our proposed scheme not only allows for efficient numerical simulation of the DDSDE but also provides lattice approximations for the equation.
1.1. Poisson processes approximation for ODEs
Numerical methods for ordinary differential equations (ODEs) encompass well-established techniques such as Euler’s method, the Runge-Kutta methods, and more advanced methods like the Adams-Bashforth methods and the backward differentiation formulas. These methods enable us to approximate the solution of an ODE over a given interval by evaluating the function at discrete points. In this work, we aim to develop a stochastic approximation method tailored for rough ODEs, which exhibit irregular behavior or involve coefficients that are not smooth.
Let us consider the classical ordinary differential equation (ODE)
| (1.4) |
Suppose that the time-dependent vector field satisfies the one-sided Lipschitz condition
| (1.5) |
and linear growth assumption:
| (1.6) |
Note that under (1.5), need not even be continuous. By smooth approximation, it is easy to see that in the sense of distributions, (1.5) is equivalent to (see [5, Lemma 2.2])
| (1.7) |
where stands for the identity matrix. In particular, if is a semiconvex function, that is, the Hessian matrix has a lower bound in the distributional sense, then for , (1.7) and (1.5) hold.
When is Lipshcitz continuous in , it is well-known that the flow associated to ODE (1.4) is closely related to the linear transport equation
| (1.8) |
and the dual continuity equation
| (1.9) |
In [11], DiPerna and Lions established a well-posedness theory for ODE (1.4) for Lebesgue almost all starting point by studying the renormalization solution to linear transport equation (1.8) with being -regularity and having bounded divergence, where is the usual first order Sobolev space and . Subsequently, Ambrosio [1] extended the DiPerna-Lions theory to the case that and by studying the continuity equation (1.9) and using deep results from geometric measure theory. It is noticed that these aforementioned results do not apply to vector field that satisfies the one-sided Lipschitz condition (1.5).
On the other hand, under the conditions (1.5) and (1.6), the ODE (1.4) can be uniquely solved in the sense of Filippov [14], resulting in a solution family that forms a Lipschitz flow in (see Theorem 2.8 below). In a recent study, Lions and Seeger [28] investigated the relationship between the solvability of (1.8) and (1.9) and ODE (1.4) when satisfies (1.5) and (1.6). Condition (1.5) naturally arise in fluid dynamics (cf. [5] and [28]), optimal control theory and viability theory (cf. [2]). From a practical application standpoint, it is desirable to construct an easily implementable numerical scheme. However, the direct Euler scheme is not suitable for solving the ODE (1.4) when satisfies condition (1.5) or -regularity conditions. Our objective in the following discussion is to develop a direct discretization scheme that is well-suited for addressing the aforementioned cases.
For given , let be a Poisson process with intensity (see (2.1) below for a precise definition). We consider the following simple SDE driven only by Poisson process :
| (1.10) |
where stands for the left-hand limit. Since the Poisson process only jumps at exponentially distributed waiting times, the above SDE is always solvable as long as the coefficient takes finite values. Under (1.5) and (1.6), we show the following convergence: for any ,
where is the unique Filippov solution of ODE (1.4) and (see Theorem 2.11). Furthermore, in the sense of DiPerna and Lions (cf. [11] and [9]), we establish the convergence of in probability to the exact solution under certain assumptions on (see Corollary 2.14). This convergence result is particularly significant as it allows for the construction of Monte-Carlo approximations for the first-order partial differential equations (PDEs) (1.8) or (1.9). In fact, in subsection 2.4, we delve into the study of particle approximations for distribution-dependent ODEs, which are closely related to nonlinear PDEs.
One important aspect to highlight is that unlike the classical Euler scheme, our proposed scheme does not rely on any continuity assumptions in the time variable . In fact, for any and , we have
We complement the theoretical analysis with numerical experiments to showcase the scheme’s performance, as illustrated in Remark 2.3.
1.2. Compound Poisson approximation for SDEs
Now we consider the classical stochastic differential equation driven by -stable processes: for ,
| (1.11) |
The traditional Euler scheme, also known as the Euler-Maruyama scheme, for SDE (1.11) and its variants have been extensively studied in the literature from both theoretical and numerical perspectives. When the coefficients and are globally Lipschitz continuous, it is well-known that the explicit Euler-Maruyama algorithm for SDEs driven by Brownian motions exhibits strong convergence rate of and weak convergence rate of (see [4], [19]).
In the case where the drift satisfies certain monotonicity conditions and the diffusion coefficient satisfies locally Lipschitz assumptions, Gyöngy [15] proved almost sure convergence and convergence in probability of the Euler-Maruyama scheme (see Krylov’s earlier work [26]). However, Hutzenthaler, Jentzen, and Kloeden [21] provided examples illustrating the divergence of the absolute moments of Euler’s approximations at a finite time. In other words, it is not possible to establish strong convergence of the Euler scheme in the -sense for SDEs with drift terms exhibiting super-linear growth. To overcome this issue, Hutzenthaler, Jentzen, and Kloeden [22] introduced a tamed Euler scheme, where the drift term is modified to be bounded. This modification allows them to demonstrate strong convergence in the -sense with a rate of to the exact solution of the SDE, assuming the drift coefficient is globally one-sided Lipschitz continuous. Subsequently, Sabanis [35] improved upon the tamed scheme of [22] to cover more general cases and provided simpler proofs for the strong convergence.
On the other hand, there is also a considerable body of literature addressing the Euler approximations for SDEs with irregular coefficients, such as Hölder and even singular drifts (see [3], [33], [39], and references therein). However, to the best of our knowledge, there are relatively few results concerning the Euler scheme for SDEs driven by -stable processes and under non-Lipschitz conditions (with the exception of [32], [27] which focus on the additive noise case).
Our goal is to develop a unified compound Poisson approximation scheme for the SDE (1.11), which is driven by either purely jumping -stable processes or Brownian motions. To achieve this, let be a sequence of independent and identically distributed random variables taking values in , such that for any integer lattice value ,
| (1.12) |
where is a normalized constant. Let . We define a -valued compound Poisson process by
| (1.13) |
where is a Poisson process with intensity . Let be the associated Poisson random measure, i.e., for and ,
Consider the following SDE driven by compound Poisson process :
| (1.14) |
where the integral is a finite sum since the compound Poisson process only jumps at exponentially distributed waiting times. Let be the -th jump time of . It is easy to see that (see Lemma 3.4)
Indeed, it is possible to choose different independent Poisson processes for the drift and diffusion coefficients in the compound Poisson approximation scheme. However, it is worth noting that doing so would increase the computational time required for simulations. By using the same compound Poisson process for both coefficients, the computational efficiency can be improved as the generation of random numbers for the Poisson process is shared between the drift and diffusion terms.
We note that the problem of approximating continuous diffusions by jump processes has been studied in [23, p.558, Theorem 4.21] under rather abstract conditions. However, from a numerical approximation or algorithmic standpoint, the explicit procedure (1.14) does not seem to have been thoroughly investigated. In this paper, we establish the weak convergence of to in the space of all càdlàg functions under weak assumptions. Notably, these assumptions allow for coefficients with polynomial growth. Furthermore, under nondegenerate and additive noise assumptions, as well as Hölder continuity assumptions on the drift, we establish the following weak convergence rate: for some , for any and ,
It is worth mentioning that when and is the identity matrix, the convergence of to corresponds to the classical Donsker invariant principle. Additionally, when the drift satisfies certain dissipativity assumptions, we show the weak convergence of the invariant measure of SDE (1.14) to the invariant measure of SDE (1.11), provided that the latter is unique.
As an application, we consider the discretized probabilistic approximation in the time direction for the 2D-Navier-Stokes equations (NSEs) on the torus. Specifically, for a fixed , we focus on the vorticity form of the backward 2D-Navier-Stokes equations on the torus, given by:
where is a smooth divergence-free vector field on the torus, and represents the Biot-Savart law (as described in (4.8) below). The stochastic Lagrangian particle method for NSEs has been previously studied in [8] and [43]. In this paper, we propose a discretized version of the NSEs, defined as follows: for , let solve the following stochastic system
| (1.15) |
where is defined in (1.13). We establish that there exists a constant such that for all and ,
The scheme (1.15) provides a novel approach for simulating 2D-NSEs using Monte Carlo methods, offering a promising method for computational simulations of these equations.
1.3. Compound Poisson particle approximation for DDSDEs
Motivated by the aforementioned scheme, we can develop a compound Poisson particle approximation for the nonlinear SDE (1.1). Fix . Let be a sequence of i.i.d. Poisson processes with intensity and i.i.d -valued random variables with common distribution (1.12). Define for ,
Then is a sequence of i.i.d. compound Poisson processes. Let be the associated Poisson random measure, that is,
Let be a sequence of symmetric random variables and solve the following interaction particle system driven by :
| (1.16) |
Under suitable assumptions on , , and , we will show that for any ,
| (1.17) |
where represents the law of the solution of the DDSDE (1.1) in the space of càdlàg functions, and denotes the -fold product measure induced by . Here, we have chosen in (1.14). In contrast to the traditional particle approximation (1.3), the stochastic particle system (1.16) is fully discretized and can be easily simulated on a computer. The convergence result (1.17) can be interpreted as the propagation of chaos in the sense of Kac [24]. Furthermore, in the case of additive noise, we also establish the quantitative convergence rate with respect to the Wasserstein metric under Lipschitz conditions.
1.4. Organization of the paper and notations
This paper is structured as follows:
In Section 2, we introduce the Poisson process approximation for ordinary differential equations (ODEs). We investigate the case where the vector field is bounded Lipschitz continuous and establish the optimal convergence rate in both the strong and weak senses. Additionally, we present a functional central limit theorem in this setting. Furthermore, we consider the case where satisfies the one-sided Lipschitz condition (not necessarily continuous), allowing for linear growth. We demonstrate the -strong convergence of to the unique Filippov solution. When the vector field belongs to the first-order Sobolev space and has bounded divergence, we also show the convergence in probability of to . Moreover, we explore particle approximation methods for nonlinear ODEs.
In Section 3, we focus on the compound Poisson approximation for stochastic differential equations (SDEs), which provides a more general framework than the one described in (1.14) above. Under relatively weak assumptions, we establish the weak convergence of , the convergence of invariant measures, as well as the weak convergence rate.
In Section 4, we concentrate on the 2D Navier-Stokes/Euler equations on the torus and propose a novel compound Poisson approximation scheme for these equations.
In Section 5, we specifically examine the compound Poisson particle approximation for DDSDEs driven by either -stable processes or Brownian motions. Notably, we consider the case where the interaction kernel exhibits linear growth in the Brownian diffusion case. In the additive noise case, we establish the convergence rate in terms of the metric.
In the Appendix, we provide a summary of the relevant notions and facts about martingale solutions that are utilized throughout the paper.
Throughout this paper, we use with or without subscripts to denote constants, whose values may change from line to line. We also use to indicate a definition and set
By or simply , we mean that for some constant , . For the readers’ convenience, we collect some frequently used notations below.
-
•
: The space of all probability measures over a Polish space .
-
•
: The Borel -algebra of a Polish space .
-
•
: Weak convergence of probability measures or random variables.
-
•
: The space of all càdlàg functions from to .
-
•
: The jump of at time .
-
•
: The set of all bounded stopping times.
-
•
: The usual Hölder spaces of -order.
-
•
: The ball in with radius and center .
2. Poisson process approximation for ODEs
In this section, we focus on the simple Poisson approximation for ODEs. A distinguishing feature of our approach is that we do not make any regularity assumptions on the time variable. Moreover, we allow the coefficient to satisfy only the one-sided Lipschitz condition (1.5). The convergence analysis relies on straightforward stochastic calculus involving Poisson processes.
Let be a sequence of i.i.d. random variables on some probability space with common exponential distribution of parameter , i.e.,
Let , and for , define
and for ,
Then is a standard Poisson process with intensity . In particular, is the jump time of .
Note that
For given , we introduce
| (2.1) |
Then is a Poisson process with intensity . In this paper, we choose a sub- field , which is independent of and therefore independent of . We assume that is sufficiently rich so that for any , there exists an -measurable random variable such that . In particular, if we introduce the filtration
then one can verify that is an -martingale.
In the following, we will utilize an SDE driven by Poisson process to construct a discrete approximation for ODEs. We will demonstrate the convergence of this approximation under various assumptions and establish certain functional central limit theorems.
2.1. Classical solutions for ODEs with Lipschitz coefficients
In this section, we begin by considering the case where the vector fields are bounded and Lipschitz. We demonstrate the optimal rates of strong and weak convergence for the Poisson process approximation as introduced in the introduction. Additionally, we establish a central limit theorem for this approximation scheme.
Let be a measurable vector field. Suppose that
| (2.2) |
where is the usual -norm in . For any -measurable initial value , by the Cauchy-Lipschitz theorem, there is a unique global solution to the following ODE:
| (2.3) |
Let be the unique solution starting from . Then
Now we consider the following SDE driven by Poisson process :
| (2.4) |
Since is a step function (see Figure 1), it is easy to see that
where and . In particular,
| (2.5) |
and
| (2.6) |
where we have used that except countable many points . It is worth noting that the solvability of the SDE (2.5) does not need any regularity assumptions on , and the second integral term is a martingale. In a sense, we can view (2.5) as an Euler scheme with random step sizes. Furthermore, let be the unique solution of (2.4) starting from . Then
Hence, if has a density, then for each , also possesses a density.
First of all we show the following simple approximation result.
Theorem 2.1.
Proof.
Noting that by (2.6) and (2.3),
we have
Hence, by Gronwall’s inequality and Doob’s maximal inequality,
(ii) Fix and . Let solve the backward transport equation:
| (2.7) |
In fact, the unique solution of the above transport equation is given by
where solves the following ODE:
Since , , by the chain rule, it is easy to derive that
and for the solution of (2.3),
| (2.8) |
Moreover, by Itô’s formula we have
The proof is complete. ∎
Remark 2.2.
It is noted that the rate of weak convergence is better than the rate of strong convergence in the Poisson process approximation. The order of convergence, both in terms of strong and weak convergence, is the same as the classical Euler approximation of SDEs (see [25]).
Remark 2.3.
Consider a measurable function . For , let us define
By applying Doob’s maximal inequality, we obtain
It is worth noting that the calculation of can be easily implemented on a computer, where the step size is randomly chosen according to the exponential distribution. As a result, we can utilize the Monte Carlo method to theoretically compute the integral . To illustrate the effectiveness of our scheme, we provide an example involving a highly oscillatory function:
where stands for the integer part of and or depends on being odd or even. Note that oscillates between and . We simulate the graph using both Euler’s scheme and the Poisson approximation scheme, as depicted in Figure 2. From the graph, we can observe that Euler’s scheme exhibits instability due to the regular choice of partition points. Conversely, Poisson’s scheme demonstrates stability, with partition points being chosen randomly.
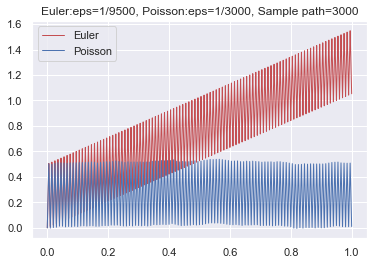
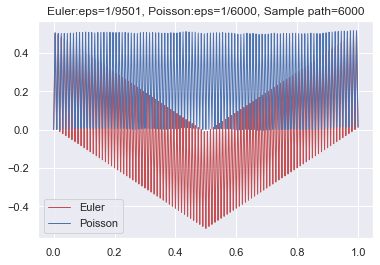
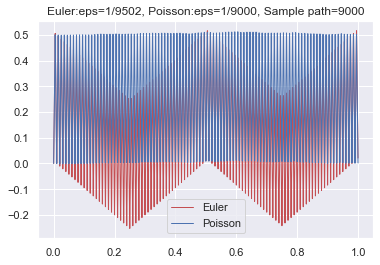
Next, we investigate the asymptotic distribution of the following deviation as ,
By (2.4) and (2.6), it is easy to see that
| (2.9) | ||||
where
Note that as ,
This implies that weakly converges to a one-dimensional standard Brownian motion . Therefore, we formally have , where solves the following linear SDE:
| (2.10) |
Clearly, is an OU process and it’s infinitesimal generator is given by
| (2.11) |
Proposition 2.4.
Proof.
Since the diffusion coefficient does not depend on and the drift is linear in , it is easy to see that for any , there is a unique martingale solution . Moreover, by Proposition 6.3 in appendix, concentrates on the space of continuous functions. ∎
Now we show the following functional CLT about the above .
Theorem 2.5.
Suppose that is bounded and Lipschitz continuous. Let be the unique martingale solution associated with starting from at time . Let be the law of in the space of càdlàg functions, where is the unique solution of SDE (2.4) with the same fixed initial value as . Then we have
Proof.
First of all, for any , by (2.9) and Itô’s formula, we have
where is a martingale and
Therefore, the infinitesimal generator of is given by
From the very definition, it is easy to see that for any ,
| (2.12) |
In fact, noting that by Taylor’s expansion,
one sees that for each ,
Moreover, by the definition of , we clearly have
Thus we have (2.12). On the other hand, by (2.9) and Gronwall’s lemma, it is easy to see that for some ,
and for any stopping time and ,
Thus, by Aldous’ criterion (see [23, p356, Theorem 4.5]), is tight. Let be any accumulation point. By (2.12) and Theorem 6.4 in appendix, . By the uniqueness (see Proposition 2.4), one has . The proof is complete. ∎
Remark 2.6.
We emphasize that in the above theorem, the initial value is a nonrandom fixed point. We shall consider the general random initial value in Theorem 2.19 below.
2.2. Filippov solutions for ODEs with one-sided Lipschitz coefficients
In this section, our focus is on the Poisson process approximation for the ODE (2.3) with one-sided Lipschitz coefficients. We will explore the convergence properties and effectiveness of this approximation scheme in this setting.
-
(Hb)
We assume that for some and all ,
Due to the lack of continuity of , assumption (Hb) does not guarantee the existence of a solution to the ODE (2.3) in the classical sense. In such cases, Filippov [14] introduced a concept of solution in the sense of differential inclusions, providing a unique solution to the ODE (2.3). This notion is closely connected to the study of differential inclusions as discussed in [2].
To define Filippov solutions, we introduce the supporting function of , defined by
where the essential supremum is taken with respect to the Lebesgue measure. The essential convex hull of is then given by
Note that is a closed convex subset and is precisely the support function of .
Definition 2.7.
We call an absolutely continuous curve in a Filippov solution of ODE (2.3) starting from if and for Lebesgue almost all ,
Theorem 2.8.
Under (Hb), for any starting point , there is a unique Filippov solution to ODE (2.3). Moreover, for any and ,
| (2.13) |
Let be the mollifier approximation of , where and is a smooth density function with compact support. Let be the unique solution of ODE (2.3) corresponding to and starting from . Then for any , we have
| (2.14) |
The existence of a Filippov solution can be established through a compactness argument, while the uniqueness follows from the one-sided Lipschitz condition. It is remarkable that we can show that the Filippov solution of the ODE (2.3) coincides with the -limit of under assumption (Hb). This result is particularly significant as it provides an explicit time discretization scheme for Filippov solutions. To prove this result, we begin by demonstrating a simple convergence estimate in the case where is continuous in .
Lemma 2.9.
Let . Suppose that (Hb) and for each , is continuous. Then for any and , there is a constant such that
| (2.15) |
and for all ,
| (2.16) |
where is the unique solution of ODE (2.3) starting from .
Proof.
For , by Itô’s formula and , we have
Hence, by the linear growth of in ,
which implies the first estimate by Gronwall’s inequality.
Next, we look at (2.16). Since is continuous in for each , it is well-known that there is a unique classical solution to ODE (2.3) under (Hb). Note that
By Itô’s formula and (Hb), we have
Hence, by Gronwall’s inequality, (2.15) and BDG’s inequality, we get for ,
which in turn implies the desired estimate (2.16). ∎
Next we show the continuous dependence of with respect to and the initial values.
Lemma 2.10.
(i) Let and be the solution of ODE (2.4) corresponding to , where is the smooth approximation of as in Theorem 2.8. Suppose (Hb) and has a density with respect to the Lebesgue measure. Then for any and , there is a constant such that for all ,
| (2.17) |
(ii) Let and , be the solutions of ODE (2.4) corresponding to initial values and , respectively. Under (Hb), for any and , there is a constant such that for all ,
| (2.18) |
Proof.
We will only prove (i) since (ii) follows in the same manner. Note that
where
By Itô’s formula and (Hb), we have
Hence, for , by BDG’s inequality and (2.15), we have
where in the last step we have used the linear growth of and estimate (2.15), and the implicit constant only depends on . By Gronwall’s inequality, we get
Since for fixed and , the law of is absolutely continuous with respect to the Lebesgue measure, by the dominated convergence theorem, we have
where is the density of . Thus we obtain the limit (2.17). ∎
Now we can show the following main result of this section.
Theorem 2.11.
Let and be the unique Filippov solution of ODE (2.3) with . Then for any and , there is a constant such that for all ,
| (2.19) |
Proof.
We dive the proof into two steps.
(Step 1). In this step we assume that has a density. Let be the unique solution of ODE (2.4) corresponding to and starting from . By (2.16), for any and , there is a constant such that for any ,
2.3. DiPerna-Lions solutions for ODEs with -coefficients
In this section, we focus on the ODE in the sense of DiPerna-Lions. In this case, the coefficient is permitted to belong to the Sobolev space , but the initial value is assumed to possess a density. Specifically, we make the following assumption:
-
(H)
is bounded measurable, and for some and each , there is a Borel measurable function such that for Lebesgue almost all ,
(2.20)
We first show the following result.
Theorem 2.13.
Let with . Suppose that (H) holds, and ODE (2.3) admits a solution with initial value and has a density , where . Then for any , there is a constant such that for all and ,
Proof.
We follow the proof in [34]. By (2.6) we have
Fix . By applying Itô’s formula to function , we have
For , define a stopping time
For , by the assumption we have
For , by Doob’s maximal inequality, we have
Note that
| (2.21) |
and for and ,
| (2.22) |
In particular, we further have for ,
Similarly, for , by (2.21) and (2.22), we have for ,
Combining the above calculations, we obtain that for ,
Now for any and , by Chebyschev’s inequality we have
| (2.23) |
On the other hand, it is standard to show that
which together with (2.23) yields the desired estimate. ∎
As a consequence, we have
Corollary 2.14.
Assume that for some and . Let and . For any with density , there is a unique solution to ODE (2.3) so that admits a density . Moreover, there is a constant such that for all ,
Proof.
Let . By Morrey’s inequality (see [12, p143, Theorem 3]), there is a constant such that for Lebesgue almost all ,
where
Hence, (2.20) holds with and by the -boundedness of the maximal function (cf. [36]),
By the DiPerna-Lions theory (see [11, Corollary II.1] and [1, 9]), for any with a density , there is a unique solution to ODE (2.3) with density . Now by Theorem 2.13 with , we obtain the desired estimate. ∎
Remark 2.15.
Corollary 2.14 provides a discretization approximation for ODEs with -coefficients. Let us consider the case where and the vector field is defined as
where and . It can be easily seen that and for any . Additionally, it should be noted that is Hölder continuous at the point .
2.4. Particle approximation for DDODEs
In this section, we turn our attention to the study of nonlinear or distribution-dependent ODEs (DDODEs) and the corresponding interaction particle system. We establish the strong convergence of the particle approximation scheme, as well as a central limit theorem, similar to what was discussed earlier. It is important to note that our scheme is fully discretized, with the time scale chosen as . This choice allows for efficient numerical implementation and analysis of the particle system.
Let and be Borel measurable functions. For a (sub)-probability measure over , we define
where
Now we consider the following DDODE:
| (2.24) |
where is any random variable and stands for the distribution of . Suppose that
| (2.25) |
and
| (2.26) |
Under the above conditions, it is well-known that DDODE (2.24) has a unique solution. In particular, solves the following nonlinear first order PDE in the distributional sense:
Remark 2.16.
If is a fixed point, then is a Dirac measure and
In this case, there is no interaction. Now, suppose that has a density , and let . Then, also has a density , and in the distributional sense, we have
In particular, if we consider the case where , we obtain
which is the classical Burgers equation.
Now we construct the interaction particle approximation for DDODE (2.24). Let be a family of i.i.d. standard Poisson processes. Fix . For , define
Let be a sequence of i.i.d. -measurable random variables with common distribution . We consider the following interaction particle system driven by Poisson processes: for
where we have chosen in Poisson approximation (2.4), and
In order to show the convergence rate, we need the following simple lemma (see [40]).
Lemma 2.17.
Let be a sequence of i.i.d. -valued random variables with common distribution . Let be the empirical measure of . Then there is a universal constant such that for any nonnegative measurable function and , and ,
| (2.27) | ||||
In particular,
| (2.28) |
Proof.
By definition we have
Since for , are independent and have the same distribution , we have
Thus,
From this, we derive the desired estimate. ∎
Let solve the following DDODE:
| (2.29) |
Clearly, are i.i.d. random processes. We present a simple result regarding the propagation of chaos, which is consistent with [40]. This result highlights the independence of the particle system as the number of particles increases, and provides support for the validity and effectiveness of the approximation scheme.
Theorem 2.18.
Proof.
Let Note that
Below for a nonnegative function , we write
For , by Doob’s maximal inequality we have
For , by the Lipschitz assumptions (2.25), we have
For , by (2.28) we have
Combining the above calculations, we obtain that for each ,
By Gronwall’s inequality, we get
where the implicit constant does not depend on . The desired estimate now follows by Gronwall’s inequality again. ∎
Next we consider the asymptotic distribution of the following fluctuation:
Note that
Since is bounded, one sees that the martingale part converges to zero in . Indeed,
Therefore, it is not expected that converges to some non-degenerate Gaussian distribution. Moreover, let
By (2.25), (2.28) and Theorem 2.18, it is easy to see that for all ,
where does not depend on . We aim to show the following result about the fluctuation.
Theorem 2.19.
Proof.
By definition it is easy to see that
| (2.31) |
where
For any stopping time and , by Doob’s maximal inequality we have
To prove the result, we consider an auxiliary process , which satisfies (2.30) with starting point independent of . Clearly, we also have
Thus by Aldous’ criterion (see [23, p356, Theorem 4.5]), the law of in is tight. Without loss of generality, we assume that weakly converges to . We show that is a martingale solution of the following second order operator starting from at time
For , we need to show that for ,
is a -martingale. On one hand, let
Since is dense in , it suffices to consider , where . On the other hand, since solves ODE (2.29), we have
Therefore, we only need to consider . By (2.31) and Itô’s formula, we have
where is a martingale, and
and
Below, for simplicity of notations, we write
By Theorem 6.4, it suffices to show
Observe that by Taylor’s expansion,
Let
Then
By Theorem 2.18, it is easy to see that
Moreover, since , by (2.28), we also have
Hence,
Thus, by Theorem 6.4 in appendix, we get and conclude the proof. ∎
Remark 2.20.
By the above theorem, one sees that weakly converges to a Gaussian martingale with covariance matrix .
3. Compound Poisson approximation for SDEs
The main objective of this section is to introduce a unified compound Poisson approximation for SDEs driven by either Brownian motions or -stable processes. This is accomplished by selecting different scaling parameters. We establish the convergence of the approximation SDEs under relatively mild assumptions, as demonstrated in Theorem 3.16. Furthermore, under more restrictive assumptions, we derive the convergence rate in Theorem 3.19. Additionally, we obtain the convergence of the invariant measures under dissipativity assumptions, as presented in Theorem 3.17. The convergence of the generators plays a pivotal role in our proofs. In essence, our results can be interpreted as a form of nonlinear central limit theorem. In the subsequent section, we will apply this framework to address nonlinear partial differential equations (PDEs), with a specific focus on the 2D-Navier-Stokes equations on the torus.
Let be a sequence of i.i.d. -valued symmetric random variables with common distribution . Let . For , we define a compound Poisson process by
| (3.1) |
where is the Poisson process with intensity (see (2.1)). Let be the associated Poisson random measure, i.e., for and ,
| (3.2) |
where . More precisely, for a function ,
| (3.3) |
where is the -th jump time of . Note that the compensated measure of is given by . We also write
which is called the compensated Poisson random measure of .
Fix . We make the following assumptions for the probability measure above:
-
(H)
is symmetric, i.e., . If , we suppose that
If , we suppose that
(3.4) and there is a Lévy measure and constants , such that for any measurable function satisfying
(3.5) it holds that
(3.6) where
(3.7)
Remark 3.1.
In the following we provide several examples for to illustrate the above assumptions.
Example 1. Let with , where is a cone with vertex and is a normalized constant so that . It is easy to see that (H) holds with and , . In this case . In particular, if , then up to a constant, is just the Lévy measure of a rotationally invariant and symmetric -stable process.
Example 2. Let with , where is a constant so that and denotes the remaining variables except . It is easy to see that (H) holds with and , . In this case, is a cylindrical Lévy measure.
Example 3. Let with , where is a constant so that . First of all it is easy to see that (3.4) holds. We now verify that (3.6) holds for and and . Note that
where , and denotes the integer part of a real number . Here we have used the convention . Thus,
For , by (3.5) we clearly have
Since , we have for ,
and
Hence,
For , noting that by (3.5),
we have
Combining the above calculations, we obtain (3.6) for any and .
Remark 3.2.
For the above examples, one sees that for ,
The following lemma is useful.
Lemma 3.3.
Under (H), for and , we have
| (3.8) |
where
Proof.
First of all, by (H) we have
The desired estimate follows by the change of variables. ∎
Now, we introduce a general approximating scheme for SDEs driven by either Brownian motions or -stable processes. Let and , where , be two families of Borel measurable functions. Suppose that
Note that the above assumption implies that
Consider the following SDE driven by compound Poisson process :
| (3.9) | ||||
Note that and jump simultaneously, that is, if and only if . In particular,
Moreover, by the symmetry of and ,
| (3.10) |
we thus can write SDE (3.9) as the following form:
| (3.11) |
where the last term is the stochastic integral with respect to the compensated Poisson random measure , which is a local càdlàg martingale.
Without any conditions on and , SDE (3.9) is always solvable since there are only finite terms in the summation of (3.9) and it can be solved recursively. In fact, we have the following explicit construction for the solution of SDE (3.9).
Lemma 3.4.
Let . For , we define recursively by
where . Then is a Markov chain, and for any ,
Based on the above lemma, we have the following algorithm.
-
(1)
Fix a step and iteration number .
-
(2)
Initialize and . Let satisfy (H).
-
(3)
Generate -i.i.d. random variables and .
-
(4)
For to
; . -
(5)
For given , let and output .
The following simple lemma provides a tail probability estimate for , which informs us on how to choose the value of in practice.
Lemma 3.5.
For any , we have
Proof.
By Chebyschev’s inequality we have
∎
Remark 3.6.
The sequence forms a Markov chain with a state space of . These lemmas provide us with a practical method for simulating using a computer. It is important to note that approximating a diffusion process with a Markov chain is a well-established topic, as discussed in [38, Chapter 11.2]. Therein, the focus is on the time-homogeneous case, and piecewise linear interpolation is used for approximation. In our approach, we embed the Markov chain into a continuous process using a Poisson process. It is crucial to highlight that is not independent of due to the time-inhomogeneous nature of and . Our computations heavily rely on the calculus of stochastic integrals with jumps.
Note that for a bounded measurable function ,
| (3.12) |
where is a martingale defined by
This is just the Itô formula of jump processes. In particular,
where the infinitesimal generator of Markov process is given by
with
and
| (3.13) |
By convention we have used that
| (3.14) |
Note that by the symmetry of and ,
| (3.15) |
The concrete choices of (depending on ) and will be given in the following subsection.
3.1. Weak convergence of approximating SDEs
In this section, our aim is to construct appropriate functions and such that the law of the approximating SDE converges to the law of the classical SDE driven by -stable processes or Brownian motions. The key aspect of our construction lies in demonstrating the convergence of the generators. It is important to note that the drift term is assumed to satisfy dissipativity conditions and can exhibit polynomial growth.
Let
be two Borel measurable functions. We make the following assumptions on and :
-
(H)
and are locally bounded and continuous in , and for some ,
(3.16) and for the same as in (3.5),
(3.17) and for some , and ,
(3.18)
We introduce the coefficients of the approximating SDE (3.9) by
| (3.19) |
Remark 3.7.
The purpose of introducing the function is to ensure the dissipativity of the approximating SDEs, as demonstrated in Lemma 3.11 below. On the other hand, the introduction of with different scaling parameters for different values of is aimed at ensuring the convergence of the generators, as shown in Lemma 3.9 below. It is worth noting that the drift term can exhibit polynomial growth, and in the case of linear growth (i.e., ), one can simply choose . Furthermore, by the definition of , it is evident that
| (3.20) |
In the next lemma we shall show that as , converges to with
| (3.21) |
where
This observation suggests that is expected to weakly converge to a solution of the following SDE:
| (3.22) |
where is a -dimensional standard Brownian motion, and
and when , for a -dimensional symmetric Lévy process with Lévy measure ,
and
| (3.23) |
Remark 3.8.
Let and , where satisfies , and represents the remaining variables except for . Let , where is Borel measurable. In this case, we can take
Let be the canonical basis of . Suppose that , and
Then is the standard discrete Laplacian.
The following lemma is crucial for taking limits.
Lemma 3.9.
Under (H) and (H), for any , there is a constant such that for any , and for all , and ,
where is from (H). Moreover, if is bounded measurable and in (H), then the constant can be independent of .
Proof.
Below we drop the time variable for simplicity. Recalling , by Taylor’s expansion and the definition (3.19), we have
| (3.24) |
Next, by (3.14) and Taylor’s expansion again, we have
| (3.25) |
When , recalling , by (3.15) and (3.25) we have
Hence, recalling , by (3.16), we have for ,
| (3.26) |
and for ,
| (3.27) |
When , recalling and by (3.15) and the change of variables, we have
| (3.28) |
where
Hence, for , we have
For , set
Then by (3.25), we have
and
Thus by (3.17) and (3.6), we have
For , noting that by (3.25),
and by (3.20),
we have
Combining the above calculations and by (H) and Lemma 3.3, we obtain
| (3.29) |
which together with (3.24), (3.26) and (3.27) yields the desired estimate. If is bounded and , that is, , from the above proof, one sees that is independent of . ∎
For , we define
We need the following elementary Hölder estimate about .
Lemma 3.10.
For any , there is a constant such that for all ,
Proof.
For , noting that
where , and by , we immediately have
For , by Taylor’s expansion we have
In view of , it suffices to show
furthermore, for each ,
where stands for the remaining variables except . The above estimate can be derived as a consequence of the following two estimates: for any ,
and
Set
For , it is easy to see that
Hence, for ,
and for ,
and
The proof is complete. ∎
We need the following technical lemma.
Lemma 3.11.
Proof.
Now we show the following Lyapunov’s type estimate.
Lemma 3.12.
Under (H) and (H), for any and satisfying (3.30), there are constants , , and such that for all , and ,
| (3.32) |
Proof.
It suffices to prove the above estimate for being large. We divide the proofs into three steps. For the sake of simplicity, we drop the time variable.
(Step 1). Note that
and
| (3.33) |
We have the following estimate: there is an such that for any and ,
| (3.34) |
In fact, noting that by (3.20) and (3.18),
| (3.35) |
for with small enough, we have
and for ,
and for ,
Hence, we have (3.34). Thus, for ,
which implies by Young’s inequality that for some ,
| (3.36) |
(Step 2). In the remaining steps we treat . First of all, we consider the case of and . By (3.15), (3.25) and , we have
Since , by (3.33) and (3.35), we have for ,
By (3.16) and (H), we further have
(Step 3). Next we consider the case of . Let be the same as in (3.16) and write . By (3.15) we have
where
and
For , by (3.25) and (3.33), we have
where we have used that for ,
For small enough, and for , and ,
Thus for , by (H),
For , since , by Lemma 3.10, (H) and Lemma 3.3, we directly have
Hence, for ,
| (3.37) |
The proof is complete. ∎
Remark 3.13.
As an easy corollary, we have
Corollary 3.14.
Under (H) and (H), for any and , it holds that for some depending on ,
| (3.38) |
and for some independent of and ,
| (3.39) |
where (see Lemma 3.12).
Proof.
By Itô’s formula and Lemma 3.12, we have
| (3.40) |
where is a local martingale given by
By applying stochastic Gronwall’s lemma (see [41, Lemma 3.7]) and utilizing the fact that can be chosen arbitrarily in the interval , we obtain equation (3.38). Moreover, for , define
By the optimal stopping theorem and taking expectations for (3.40), we also have
Letting and by Fatou’s lemma, we obtain (3.39). ∎
For given , let be the set of all stopping times bounded by .
Lemma 3.15.
For any , it holds that
Proof.
Let with . For any , define
We prove the limit for . For , it is easier. By (3.9), we can write
For , by (3.20) and (3.18), we have
For , by (3.10) and the isometry of stochastic integrals, we have
Fix . For , by we have
Hence, by Chebyshev’s inequality and (3.38),
which converges to zero by firstly letting and then . ∎
Let be the law of in . Now we can show the following main result of this section.
Theorem 3.16.
Let be the law of . Suppose that (H) and (H) hold, and weakly converges to as , and there is a unique martingale solution associated with starting from at time . Then weakly converges to as . Moreover, if , then concentrates on the space of all continuous functions.
Proof.
By Lemma 3.15 and Aldous’ criterion (see [23, p356, Theorem 4.5]), is tight in . Let be any accumulation point. By Lemma 3.9 and Theorem 6.4 in appendix, one has . By the uniqueness, we have and weakly converges to as . If , then by Proposition 6.3, concentrates on the space of all continuous functions. ∎
3.2. Convergence of invariant measures
In this section we show the following convergence of invariant measures under dissipativity assumptions.
Theorem 3.17.
Suppose that and do not depend on the time variable. Under (H) and (H), if for some ,
where the above constants appear in Lemma 3.12, then for each , there is an invariant probability measure associated with the semigroup , where is the unique solution of SDE (3.9) starting from . Moreover, is tight and any accumulation point is a stationary distribution of SDE (3.22).
Proof.
Let . If , then by (3.39), it is easy to see that
| (3.41) |
For and , we define a probability measure over by
By (3.41), one sees that is tight. Let be any accumulation point of . By the classical Krylov-Bogoliubov argument (cf. [10, Section 3.1]), one can verify that is an invariant probability measure associated with the semigroup , and by (3.41),
From this, by Prohorov’s theorem we derive that is tight. Let be any accumulation point of and for subsequence , weakly converges to as . Let have the distribution and be the unique solution of SDE (3.9). Since is an invariant probability measure of SDE (3.9), we have for each and ,
By Theorem 3.16 and taking weak limits, we obtain
where is a martingale solution of SDE (3.22) with initial distribution . In other words, is a stationary distribution of . ∎
Remark 3.18.
If SDE (3.22) has a unique stationary distribution (or invariant probability measure), then as .
Example. Let and consider the following SDE
| (3.42) |
where for , is a standard rotationally invariant and symmetric -stable process, and for , is a -dimensional standard Brownian motion, and are two locally Lipschitz continuous functions. Suppose that for some ,
and for some and and (with in the case of ),
It is well-known that SDE (3.42) has a unique invariant probability measure (see [42]). If we consider the approximating SDE (3.9) with and being defined by (3.19), then SDE (3.9) admits an invariant probability measure , and by Theorem 3.17,
3.3. Rate of weak convergence
Now we aim to show the rate of weak convergence as done for ODE (see Theorem 2.1). However, in this case, we will utilize the regularity estimate for the associated parabolic equation. To achieve this, we will require the following stronger assumptions:
-
(H′)
Suppose that for some and all ,
and for any and , the following parabolic equation admits a solution ,
with regularity estimate that for some and ,
(3.43)
We can show
Theorem 3.19.
Under (H) and (H′), for any and , there is a constant such that for all and ,
| (3.44) |
where is from (H) and is from (H′).
Proof.
Fix . Under (H′), by Itô’s formula, we have
and
Hence, by Lemma 3.15,
which yields the desired estimate by . ∎
Remark 3.20.
Estimate (3.43) is the classical Schauder estimate, which is well-studied in the literature of partial differential equations (PDEs), particularly for the case of continuous diffusion with . In the case of , the estimate can be found in [17]. Here, we provide a brief proof specifically for the additive noise case. We consider the following forward PDE:
Let be the semigroup associated with , that is,
By Duhamel’s formula, we have
It is well-known that by the gradient estimate of heat kernels, for (see [7] [17]),
Hence, for and ,
By Gronwall’s inequality of Volterra’s type, we obtain that for any ,
In this case we have the weak convergence rate (3.44) for Hölder drift .
4. Compound Poisson approximation for 2D-NSEs
In this section, we develop a discrete compound Poisson approximation for the 2D Navier-Stokes or Euler equations on the torus. We shall show the optimal rate of convergence for this approximation. Our scheme heavily relies on the stochastic Lagrangian particle representation of the NSEs, which has been previously studied in works such as [30], [8], and [43].
4.1. Diffeomorphism flow of SDEs driven by compound Poisson processes
In this subsection we show the diffeomorphism flow property of SDEs driven by compound Poisson processes and the connection with difference equations. More precisely, fix and let solve the following SDE:
where is a bounded continuous function, and is defined as in (3.2). By the definition, we can rephrase the above SDE as follows:
| (4.1) |
where is defined by (2.1) and is defined by (3.1). For given , bounded continuous functions and , define
Since is stochastically continuous and is bi-continuous, by (4.1) and the dominated convergence theorem, it is easy to see that
| is bi-continuous on . | (4.2) |
The following lemma states that solves the backward Kolmogorov equation. Although the proof is standard, we provide a detailed proof for the convenience of the readers.
Lemma 4.1.
For each , the function is continuous differentiable, and
| (4.3) |
where
Proof.
Fix with . Note that by the flow property of ,
This follows directly from the unique solvability of SDE (4.1). Since and are independent, by definition we have
Applying Itô’s formula to , we have
Hence,
By the dominated convergence theorem and (4.2), it is easy to see that
where (resp. ) stands for the right (resp. left) hand derivative. Similarly, we can show
Since is continuous, we complete the proof. ∎
Remark 4.2.
The continuity of and in time variable can be dropped by smooth approximation. In this case, (4.3) holds only for Lebesgue almost all .
Next, we investigate the -diffeomorphism property of the mapping . To ensure the homeomorphism property of this mapping, we need to impose a condition on the gradient of . More specifically, we assume that the gradient of is not too large.
Theorem 4.3.
Suppose that is continuous and for some ,
| (4.4) |
Then there is an such that for all , forms a -diffeomorphism flow and for some constant ,
Proof.
Without loss of generality, we assume and write . Let . By (4.1) we clearly have
and by Itô’s formula,
| (4.5) |
Note that for a matrix with (see [45, Lemma 2.1]),
By (4.4) we have
and there is an small enough so that for all ,
Thus by (4.5), we have
Hence,
and also
By Gronwall’s inequality, we obtain the desired estimates. ∎
4.2. Compound Poisson approximation for 2D-NSEs
Fix . In this subsection we consider the following backward 2D-NSE on the torus :
| (4.6) |
where stands for the viscosity constant and is the pressure, is a divergence free smooth velocity field. Let be the curl of . Then solves the following vorticity equation
| (4.7) |
If we assume
then the velocity field can be uniquely recovered from vorticity by the Biot-Savart law:
where is the Biot-Savart kernel on the torus and takes the following form (see [30, (2.19)] and [37, p256, Theorem 2.17]):
| (4.8) |
Since , we clearly have
| (4.9) |
Let solve the following nonlinear SDE on the torus :
| (4.10) |
It is well-known that there is a one-to-one correspondence between (4.6) and (4.7) (see [30] [8] [43]). Motivated by the approximation in Section 3, we may construct the compound Poisson approximation for system (4.10) as follows: for ,
| (4.11) |
where is a compound Poisson process defined in (1.13). By Lemma 4.1, solves the following nonlinear discrete difference equation:
where
The following Beale-Kato-Majda’s estimate for the Biot-Savart law on the torus is crucial for solving stochastic system (4.11).
Lemma 4.4.
For any , there is a constant such that for any ,
where .
Proof.
Let . By (4.8), it suffices to make an estimate for . For , by definition and the cancellation property , we have
where
For , since , we have
For , we have
Combining the above two estimates and choosing , we obtain
The proof is complete. ∎
Remark 4.5.
In the whole space, the above estimates need to be modified as follows (see [30]):
The presence of and the Jacobian determinant in Theorem 4.3, which depend on the bound of , pose challenges when solving the approximating equation (4.11) for NSEs on the entire space. This is why we consider NSEs on the torus instead.
Now we can establish the solvability for stochastic system (4.11).
Theorem 4.6.
For any , there is a unique solution to stochastic system (4.11) so that and there is a constant such that for all and ,
| (4.12) |
Proof.
We use Picard’s iteration method. Let . For , let solve
| (4.13) |
and define recursively,
| (4.14) |
Clearly, we have and
By Gronwall’s inequality we get
Moreover, by (4.9) and Lemma 4.4 with , we have
and by definition (4.14),
| (4.15) |
Hence,
By Gronwall’s inequality again, we obtain
| (4.16) |
On the other hand, by (4.13) we have
which together with (4.16) implies by Gronwall’s inequality that
Thus, by (4.9) we get
By Gronwall’s inequality again, we have
and also,
By taking limits for (4.13) and (4.14), we obtain the desired result. Moreover, estimate (4.12) follows by (4.15) and (4.16). ∎
Now we can show the following main result of this section.
Theorem 4.7.
Suppose that is divergence free and satisfies . Let be the unique solution of NSE (4.6). Then there is a constant such that for all ,
Proof.
For , let solve the following SDE on torus ,
| (4.17) |
where is a compound Poisson process defined in (1.13). Since is a function on and for any , one sees that
Let and ,
By (4.7) and Itô’s formula, we have
where is the generator of SDE (4.17) and given by
Hence,
| (4.18) |
Noting that for ,
and
we have
Substituting this into (4.18), we obtain that for all ,
| (4.19) |
On the other hand, by (4.17) and (4.11), we have
which implies by Gronwall’s inequality that
and
Combining this with (4.19) and (4.9) yields that
By Gronwall’s inequality and (4.9), we obtain the desired estimate. ∎
Remark 4.8.
In addition to the 2D-Navier-Stokes equations on the torus, we can also consider the construction of a compound Poisson approximation for 3D-Navier-Stokes equations on the torus. This will be the focus of our future work. We anticipate that similar convergence results for short time will be obtained in this case as well, following the methodology described in [43].
5. Propagation of chaos for the particle approximation of DDSDEs
In this section, we investigate the propagation of chaos in the context of the interaction particle approximation for McKean-Vlasov SDEs driven by either Brownian motions or -stable processes. The notion of propagation of chaos refers to the convergence of the particle system to the solution of the McKean-Vlasov SDE as the number of particles tends to infinity. This provides a direct full discretization scheme for nonlinear SDEs, allowing for efficient numerical simulations.
Fix an and a symmetric probability measure . Let be a sequence of i.i.d. Poisson process with intensity and i.i.d -valued random variables with common distribution . Define for ,
Then is a sequence of i.i.d. compound Poisson processes with intensity . Let be the associated Poisson random measure, that is,
and the compensated Poisson random measure, that is,
For a point , the empirical measure of is defined by
where is the usual Dirac measure concentrated at point . Let
be two Borel measurable functions. Suppose that
For a probability measure , we write
Let solve the following interaction particle system driven by :
| (5.1) | ||||
where is a symmetric -measurable random variables. For a function , by Itô’s formula (see (3.12)), we have
| (5.2) |
where for a probability measure ,
| (5.3) |
and
| (5.4) |
As in Section 2, we write
where
and
Note that by the symmetry of and ,
We shall give precise choices of and below in different cases.
5.1. Fractional diffusion with bounded interaction kernel
In this section we fix and let
be two Borel measurable functions. We make the following assumptions:
-
In addition to (H) with , we suppose that and are continuous in , and
and for the same as in (3.5),
where . Moreover, for some and ,
(5.5) and for some and ,
(5.6)
In the above assumptions, we have assumed boundedness of the coefficients with respect to the variable , which imposes a restriction on the interaction kernel. However, in the next subsection, we relax this assumption and consider the case of unbounded kernels. Now, we introduce the approximation coefficients and as defined in (3.19).
| (5.7) |
and also define for and ,
| (5.8) |
where
and is the Lévy measure from (H). We consider the following McKean-Vlasov SDE:
| (5.9) |
where is defined as (3.23) and is the law of . By Itô’s formula, the nonlinear time-inhomogeneous infinitesimal generator of is given by .
The following lemma is the same as Lemma 3.9.
Lemma 5.1.
Under , where , for any , there is a constant such that for any and ,
where is from (H). Moreover, if is bounded measurable and , then can be independent of .
Proof.
The following lemma is similar to Lemma 3.12.
Lemma 5.2.
Under , where , for any , there are constants , , and such that for all , and , ,
where and is given in (3.30).
Proof.
For simplicity we drop the time variable. For , by Taylor’s expansion we have
| (5.10) |
By (5.5) and (5.6), for any , there are large enough so that for all ,
| (5.11) |
and as in Lemma 3.11, for the given in (3.30),
Thus, for all and ,
and
Hence, as in (3.36), we have
For , as in (3.37) we also have
Combining the above two estimates, we obtain the desired estimate. ∎
By the above Lyapunov estimate and Itô’s formula, the following corollary is the same as Corollary 3.14. We omit the details.
Corollary 5.3.
Under , for any and , there is a constant such that
| (5.12) |
where . Moreover, there is a constant such that for all ,
| (5.13) |
where (see Lemma 5.2).
The following lemma is similar to Lemma 3.15.
Lemma 5.4.
Under , for any , it holds that
| (5.14) |
Proof.
Let with . For fixed , define
By (5.1), we can write
For , by (5.5) and , we have
For , by (3.10) and the isometry of stochastic integrals, we have
Let By the change of variables, we further have
For , let . By , we have
Hence, by Chebyshev’s inequality and (5.12),
which converges to zero by firstly letting and then . ∎
Now we can show the following main result of this subsection about the propagation of chaos.
Theorem 5.5.
Proof.
We use the classical martingale method (see [18]). Consider the following random measure with values in ,
By Lemma 5.4, Aldous’ criterion (see [23]) and [40, (ii) of Proposition 2.2], the law of in is tight. Without loss of generality, we assume that the law of weakly converges to some . Our aim below is to show that is a Dirac measure, i.e.,
where is the unique martingale solution of DDSDE (5.9). If we can show the above assertion, then by [40, (i) of Proposition 2.2], we conclude (5.16).
Let . For given , we define a functional on by
where is defined by (5.8) with . Fix and . For given and , we also introduce a functional over by
By definition we have
and
| (5.17) |
By definition (5.8) and , it is easy to see that
| is bounded continuous on . |
Hence, by the weak convergence of to ,
| (5.18) |
On the other hand, let
| (5.19) |
where is defined by (5.3). By Itô’s formula (5.2), we have
where is defined by (5.4). By the isometry of stochastic integrals,
Let . Noting that by (5.4), (5.11) and ,
by Lemma 3.3 and (5.12), we have
| (5.20) |
where the implicit constant does not depend on .
Claim: The following limit holds:
| (5.21) |
Indeed, by definition (5.17), (5.19) and Lemma 5.1, for any , we have
Combining (5.18), (5.20) and (5.21) we obtain that for each and , ,
Since and are separable, one can find a common -null set such that for all and for all , and , , ,
Moreover, by (5.15), we also have
Thus by the definition of (see Definition 6.2 in appendix), for -almost all ,
Since only contains one point by uniqueness, all the points are the same. Hence, weakly converges to the one-point measure . The proof is complete. ∎
Remark 5.6.
For each , let be the unique solution of SDE (5.1) with starting point . Suppose that (see (5.13)). Then for each , the semigroup admits an invariant probability measure , which is symmetric in the sense
Indeed, by (5.13), for any , we have
| (5.22) |
Now we define a probability measure over by
By (5.22), the family of probability measures is tight. By the classical Krylov-Bogoliubov argument (cf. [10, Section 3.1]), any accumulation point of is an invariant probability measure of , that is, for any nonnegative measurable function on ,
The symmetry of follows from the symmetry of . Moreover, by (5.22) one sees that
where is the -marginal distribution of .
Note that the existence of invariant probability measures for DDSDE (5.9) has been investigated in [16] under dissipativity assumptions. However, an open question remains regarding the conditions under which any accumulation point of becomes an invariant probability measure of DDSDE (5.9). This question is closely connected to the problem of propagation of chaos in uniform time, as discussed in [29]. In future research, we plan to address this question and explore the assumptions on the coefficients that lead to convergence of empirical measures and the emergence of invariant probability measures for DDSDE (5.9). Such investigations will contribute to a deeper understanding of the dynamics and statistical properties of DDSDEs and their particle approximations.
5.2. Brownian diffusion with unbounded interaction kernel
In the previous section, we focused on interaction terms that are bounded in the second variable , which excluded unbounded interaction kernels such as , where exhibits linear growth. In this section, we address the case of unbounded interaction kernels in the context of Brownian diffusion. Our results provide insights into the behavior of DDSDEs with unbounded interaction kernels and broaden the applicability of compound Poisson approximations in modeling and numerical simulations.
Fix . We make the following assumptions about and :
-
We suppose that (H) holds, and and are continuous in , and for some ,
(5.23) Suppose that
where for some and ,
(5.24) and for some and ,
(5.25) and for some ,
(5.26)
As in (3.19), we introduce the approximation coefficients of and as:
and
| (5.27) |
For and , we also define
| (5.28) |
where
Consider the following McKean-Vlasov SDE:
| (5.29) |
where is a -dimensional standard Brownian motion, and
By Itô’s formula, the nonlinear time-inhomogeneous generator of DDSDE (5.29) is given by .
Lemma 5.7.
Under , where , for any , there is a constant such that for any , and for all and with ,
Moreover, if is bounded measurable and , then can be independent of .
The following lemma is similar to Lemma 5.2.
Lemma 5.8.
Under , where , for any , there are constants such that for all ,
| (5.30) |
Moreover, if , then for any , there are constants , and such that for all , and , ,
| (5.31) |
Proof.
We only prove (5.31). For simplicity we drop the time variable. By (5.24)-(5.26), we have
Since and , for any , by (5.24), there are large enough and such that for all ,
Thus, for any , there is an large enough such that for all ,
| (5.32) |
For , substituting (5.32) into (5.10), we get
On the other hand, for any , by , we have
Moreover, for any , by (5.24) and (5.26), there is an large enough so that for all ,
| (5.33) |
Thus for any , one can choose large enough so that for all and ,
Hence, for any , there is an large enough so that for all ,
| (5.34) |
For , as in the Step 2 of Lemma 3.12 and by (5.33), we have
which together with (5.34) and the arbitrariness of yields the desired estimate. ∎
Remark 5.9.
When , the similar estimate of (5.31) still hold, but parameter dependence becomes cumbersome.
We have the following corollary.
Corollary 5.10.
Under , where , for any and , it holds that
| (5.35) |
Moreover, if , then for any , there is a constant such that for all ,
| (5.36) |
and for any ,
| (5.37) |
Proof.
For fixed , by Itô’s formula (5.2) and (5.30), we have
| (5.38) | ||||
where
is a local martingale. Noting that
| (5.39) |
we have
For any and , by stochastic Gronwall’s inequality (see [41, Lemma 3.7]), we have
and
In particular, is a martingale. If , then by (5.38) and (5.31), for any ,
and
Solving these two differential inequalities, we obtain the desired estimates. ∎
Remark 5.11.
The following lemma is similar to Lemma 5.4.
Lemma 5.12.
For any , it holds that
| (5.40) |
Proof.
The following propagation of chaos result can be proven using the same methodology as presented in Theorem 5.5. Due to the similarity of the arguments, we omit the detailed proof here.
5.3. -convergence rate under Lipschitz assumptions
In this section, we establish the quantitative convergence rate of the propagation of chaos phenomenon for the additive noise particle system given by:
| (5.41) |
where , and are the same as in the beginning of this section, and satisfies that for some and for all ,
| (5.42) |
The associated limiting McKean-Vlasov SDE is given by
| (5.43) |
Under (5.42), it is well-known that (5.43) has a unique solution for any . We aim to show the following result.
Theorem 5.14.
Suppose that are i.i.d. -measurable random variables with common distribution . Under (H) and (5.42), where , for any , there is a constant such that for all ,
where is from (H) , and for two probability measures , denotes the Wasserstein 1-distance defined by
| (5.44) |
Proof.
Let and solve the following particle system:
| (5.45) |
Clearly, are i.i.d. By (5.41) and (5.45), we have
For , by (5.42) we have
For , since are i.i.d., by (2.27), (5.42) and definition (5.44), we have
On the other hand, by Theorem 3.19 and Remark 3.20, we have
| (5.46) |
Combining the above calculations, we get
which implies by Gronwall’s inequality that for all ,
and
These together with (5.46) yield the desired estimate. ∎
Remark 5.15.
Based on the aforementioned convergence result, an interesting direction for future work is to investigate the convergence of the fluctuation of the empirical measure given by:
This corresponds to studying the central limit theorem for the particle system, which characterizes the asymptotic behavior of the fluctuations around the mean behavior.
6. Appendix: Martingale solutions
In this section, we provide a brief overview of some key notions and results related to the martingale solutions associated with the operators . These concepts and results are well-known and can be found in Jacob-Shiryaev’s textbook [23]. We include them here for the convenience of the readers.
Let be the space of all càdlàg functions from to , which is endowed with the Skorokhod topology (see [23, p325] for precise definition). The canonical process in is defined by
Let be the natural filtration and . For , we introduce
and
| (6.1) |
and
| (6.2) |
It is well-known that is an -stopping time, that is, for all , . Moreover, the function is nondecreasing and left continuous, and , and are at most countable (see [23, p340, Lemma 2.10]). The following proposition can be found in [23, p341, Propositions 2.11 and 2.12] and [23, p349, Lemma 3.12].
Proposition 6.1.
For each , the mappings and are continuous with respect to the Skorokhod topology at each point such that . Moreover, for any , the set is at most countable.
Let be a family of linear operators from to . We introduce the following notion of martingale solutions (see [38]).
Definition 6.2.
Let and . We call a probability measure a martingale solution associated with and with initial distribution at time if , and for all , the process
is a local -martingale after time under the probability measure . All the martingale solutions starting from at time is denoted by . If for some , we shall simply write . If the operator also depends on the probability measure itself, then we shall call the probability measure a solution of nonlinear martingale problems.
First of all we present the following purely technical result.
Proposition 6.3.
Suppose that for each , there is a unique martingale solution so that for each measurable , is Borel measurable. Then is a family of strong Markov probability measures. If in addition, is a second order differential operator with the form:
where is a symmetric matrix-valued locally bounded measurable function and is a vector-valued locally bounded measurable function, then for each , concentrates on the space of continuous functions.
Proof.
The statement that the uniqueness of martingale solutions implies the strong Markov property is a well-known result (see [38, Theorem 6.2.2]). We omit the details here. Now, let us prove the second conclusion. Without loss of generality we assume . To show that concentrates on the space of continuous functions, by Kolmogorov’s continuity criterion, it suffices to show that for any and ,
| (6.3) |
Let . Since for , we have
Since , by the Markov property one sees that
| (6.4) |
Fix and . Define . Note that
In particular, for any and ,
Now for , by the definition of martingale solutions, we have
By Gronwall’s inequality, we get
In particular, if one takes , then for any ,
Furthermore, taking , we get
Substituting this into (6), we obtain (6.3). The proof is complete. ∎
Next we show a result that provides a way to construct a martingale solution for the operator . Let be a family of -valued càdlàg adapted processes on some stochastic basis . Let be the law of in . Let be a family of random linear operators from to . Suppose that
-
(H)
weakly converges to in as , and for any ,
(6.5) is a local -martingale with localized stopping time sequence , where for each ,
Moreover, for each ,
(6.6)
We have the following result about the martingale solutions.
Theorem 6.4.
Under (H), it holds that , where .
Proof.
For given , define
| (6.7) |
Recall the definitions and in (6.1) and (6.2). Since is at most countable and , to show , it suffices to show that for each and ,
or equivalently, for any , and ,
| (6.8) |
where Note that by the assumption,
| (6.9) |
where is defined by (6.5) and . We want to take weak limits. Since by Proposition 6.1,
is bounded and -a.s. continuous, we have
Thus, by definitions (6.5) and (6.7), to prove (6.8), it remains to show
| (6.10) |
Since for each , is a continuous function, by Proposition 6.1, one sees that
is bounded and -a.s. continuous. Thus,
which together with (6.6) yields (6.10). The proof is complete. ∎
Acknowledgement: The author would like to express their gratitude to Zimo Hao, Rongchan Zhu, and Xiangchan Zhu for their valuable discussions and helpful suggestions. The numerical experiments presented in Remark 2.3 were conducted by Ming-Yang Lai.
References
- [1] Ambrosio L. (2004). Transport equation and Cauchy problem for BV vector fields. Invent. Math. 158, 2 (2004), 227-260.
- [2] Aubin J.P. and Cellina A. (1984). Differential inclusions: set-valued maps and viability theory. Springer-Verlag, 1984.
- [3] Bao J., Huang X. and Yuan C. (2019). Convergence rate of Euler-Maruyama scheme for SDEs with Hölder-Dini continuous drifts. J. Theoret. Probab., 32(2):848-871, 2019.
- [4] Bally V. and Talay D. (1996). The law of the Euler scheme for stochastic differential equations. I. Convergence rate of the distribution function. Probab. Theory Related Fields 104 43-60.
- [5] Bouchut F., James F., and Mancini S. (2005). Uniqueness and weak stability for multi-dimensional transport equations with one-sided Lipschitz coefficient. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 4, 1 (2005), 1-25.
- [6] Chaintron L.P. and Diez A. (2021). Propagation of chaos: a review of models, methods and applications. Available in arXiv:2106.14812.
- [7] Chen Z.Q. and Zhang X. (2023). Heat kernels for time-dependent non-symmetric mixed Lévy-type operators. Journal of Functional Analysis 285 (2023) 109947.
- [8] Constantin P., Iyer G.(2008). A stochsatic Lagrangian representation of the three-dimensional incompressible Navier-Stokes equations. Comm. Pure Appl. Math. LXI, 330–345 (2008).
- [9] Crippa G. and De Lellis C.(2008). Estimates and regularity results for the DiPerna– Lions flow. J. Reine Angew. Math. 616 (2008), 15-46.
- [10] Da Prato G., Zabczyk J. (1996). Ergodicity for Infinite-Dimensional Systems. London Mathematical Society Lecture Note Series, vol. 229. Cambridge University Press, Cambridge (1996).
- [11] DiPerna R.J., Lions P.L. (1989). Ordinary differential equations, transport theory and Sobolev spaces, Invent. Math. 98(1989) 511-547.
- [12] Evans L.C., Gariepy R.F. (1992). Measure Theory and Fine Properties of Functions, Studies in Advanced Mathematics, CRC Press, London, 1992.
- [13] Fernandez B. and Méléard S.: A Hilbertian approach for fluctuations on the McKean-Vlasov model. Stochastic Processes and their Applications, 71 (1997) 33-53.
- [14] Filippov A.F.: Differential equations with discontinuous right-hand side, Amer.Math.Soc.Transl. Ser. 2 42 (1960), 199-231.
- [15] Gyöngy I. (1998). A note on Euler’s approximations. Potential Anal. 8, (1998), 205–216.
- [16] Hammersley W.R.P., ika D. and Szpruch L. (2021). McKean–Vlasov SDEs under measure dependent Lyapunov conditions. Annales de l’Institut Henri Poincaré - Probabilités et Statistiques 2021, Vol. 57, No. 2, 1032-1057.
- [17] Hao Z., Wu M. and Zhang X. (2020). Schauder estimates for nonlocal kinetic equations and applications. J. Math. Pures Appl., 140 (2020) 139-184.
- [18] Hao Z., Röckner M. and Zhang X. (2022). Strong convergence of propagation of chaos for McKean-Vlasov SDEs with singular interactions. Available in arXiv:2204.07952.
- [19] Higham D. J., Mao X. and Stuart A. M. (2002). Strong convergence of Euler type methods for nonlinear stochastic differential equations. SIAM J. Numer. Anal. 40, (2002), 1041–1063.
- [20] Hörmander L.: Lectures on Nonlinear Hyperbolic Differential Equations. Springer-Verlag, Berlin Heidelberg, 1997.
- [21] Hutzenthaler M., Jentzen A. and Kloeden P.E. (2011). Strong and weak divergence in finite time of Euler’s method for stochastic differential equations with non-globally Lipschitz continuous coefficients. Proc. R. Soc. A 467, (2011), 1563-1576.
- [22] Hutzenthaler M., Jentzen A. and Kloeden P.E. (2012). Strong convergence of an explicit numerical method for SDEs with non-globally Lipschitz continuous coefficients. Ann. Appl. Probab. 22, (2012), 1611–1641.
- [23] Jacod J. and Shiryaev N. (2002). Limit Theorems for Stochastic Processes. Wissenschaften, vol. 288, Springer, Heidelberg.
- [24] Kac,M., Probability and Related Topics in the Physical Sciences (NewYork: Interscience, 1958).
- [25] Kloeden P. E. and Platen E. (1992). Numerical solution of stochastic differential equations, vol. 23 of Applications of Mathematics (New York). Springer-Verlag, Berlin, 1992.
- [26] Krylov N. V. (1990). A simple proof of the existence of a solution to the Ito equation with monotone coefficients. Theory Probab. Appl. 35, (1990), 583–587.
- [27] Li Y. and Zhao G. (2023). Euler-Maruyama scheme for SDE driven by Lévy processes with Hölder drift. https://arxiv.org/abs/2304.13952v1.
- [28] Lions P.L. Seeger B. (2023). Transport equations and flows with one-sided Lipschitz velocity fields. arXiv:2306.13288v1.
- [29] Liu W., Wu L. and Zhang C. (2021). Long-Time Behaviors of Mean-Field Interacting Particle Systems Related to McKean–Vlasov Equations. Commun. Math. Phys. 387, 179-214 (2021).
- [30] Majda A.J., Bertozzi A.L.(2002). Vorticity and incompressible flow. Cambridge Texts in Applied Mathematics. Cambridge: Cambridge University Press, 2002.
- [31] McKean H. P. (1967). Propagation of chaos for a class of non-linear parabolic equations. In Stochastic Differential Equations (Lecture Series in Differential Equations, Session 7, Catholic Univ., 1967), pages 41-57. Air Force Office Sci. Res., Arlington, Va.
- [32] Mikulevicius M. and Xu F. (2018). On the rate of convergence of strong Euler approximation for SDEs driven by Lévy processes. Stochastics, 90(4):569-604, 2018.
- [33] Ngo H.L. and Taguchi D. (2016). Strong rate of convergence for the Euler-Maruyama approximation of stochastic differential equations with irregular coefficients. Mathematics of Computation, Vol. 85, Number 300, July 2016, Pages 1793-1819.
- [34] Röckner M. and Zhang X. (2010). Weak uniqueness of Fokker–Planck equations with degenerate and bounded coefficients. C. R. Acad. Sci. Paris, Ser. I 348 (2010) 435-438.
- [35] Sabanis S. (2013). A note on tamed Euler approximations. Electron. Commun. Probab. 18 (2013), no. 47, 1-10.
- [36] Stein E.M. (1970). Singular Integrals and Differentiability Properties of Functions. Princeton University Press, 1970.
- [37] Stein E.M. and Weiss G. (1971). Introduction to Fourier analysis on Euclidean spaces. Princeton University Press, 1971.
- [38] Stroock D.W. and Varadhan S.R.S. (2006). Multidimensional Diffusion Processes. Springer-Verlag Berlin Heidelberg, 2006.
- [39] Suo Y., Yuan C. and Zhang S.Q. (2022). Weak convergence of Euler scheme for SDEs with low regular drift. Numer. Algorithms, 90(2):731-747, 2022.
- [40] Sznitman A.-S. (1991). Topics in propagation of chaos. In École d’Été de Probabilités de Saint-Flour XIX—1989, volume 1464 of Lecture Notes in Math., pages 165-251. Springer, Berlin.
- [41] Xie L. and Zhang X. (2020). Ergodicity of stochastic differential equations with jumps and singular coefficients. Ann. Inst. Henri Poincaré Probab. Stat. 56 (2020), no. 1, 175-229.
- [42] Zhang X. and Zhang X.(2023). Ergodicity of supercritical SDEs driven by -stable processes and heavy-tailed sampling. Bernoulli 29(3), 2023, 1933-1958.
- [43] Zhang X. (2010). A stochastic representation for backward incompressible Navier-Stokes equations. Prob.Theory and Rel. Fields 148(1-2), 305-332 (2010).
- [44] Zhang X. (2012): Stochastic functional differential equations driven by Lévy processes and quasi-linear partial integro-differential equations. Ann. of Appl. Aprob., Vol. 22, No. 6, 2505-2538(2012).
- [45] Zhang X. (2013). Degenerate irregular SDEs with jumps and application to integro-differential equations of Fokker-Planck type. Electron. J. Probab. 18 (2013), no. 55, 1-25.