Comprehensive investigation of the phase diagram of quasi-one-dimensional molecular solids
Abstract
An ab initio investigation of the family of molecular compounds TM2X is conducted, where TM is either TMTSF or TMTTF and X takes centrosymmetric monovalent anions. By deriving the extended Hubbard-type Hamiltonians from first-principles band calculations and evaluating not only the intermolecular transfer integrals but also the Coulomb parameters, we discuss their material dependence in the unified phase diagram. Furthermore, we apply the many-variable variational Monte Carlo method to accurately determine the symmetry-breaking phase transitions, and show the development of the charge and spin orderings. We show that the material-dependent parameter can be taken as the correlation effect, represented by the value of the screened on-site Coulomb interaction relative to the intrachain transfer integrals, for the comprehensive understanding of the spin and charge ordering in this system.
Introduction—. Molecular solids serve as textbook materials to study many-body physics in condensed matter, despite their complex crystal structures with many atoms in the unit cell, owing to the success in modeling the low-energy electronic properties based on the frontier molecular orbitals [1, 2]. A general challenge is to understand multiple symmetry-broken phases observed in different systems in a systematic way, where the charge, spin, and lattice degrees of freedom are coupled to each other, based on the effective Hamiltonians and identifying the factors governing them [3].
The family of compounds constituted by TMTSF (= tetramethyltetraselenafulvalene) or TMTTF (= tetramethyltetrathiafulvalene) molecules, which we call together TM here, forming 2:1 salts with monovalent anions X-1, TM2X, has been studied for decades as a typical example showing such a rich variety of phases [4, 3, 2, 5]. TMTSF2X historically outstands as the first organic system undergoing superconductivity [6]. Unconventional superconductivity with an anisotropic gap function is realized, whose ‘glue’ for the Cooper pair formation is the strong spin fluctuation, supported by the pressure-temperature phase diagram with the superconducting phase neighboring an antiferromagnetic (AFM) phase driven by the nesting of the Fermi surface [7, 8, 9, 10, 11].
Later, the isostructural TMTTF counterparts became realized as strongly-correlated electron systems, owing to the atomic substitution resulting in smaller bandwidths than in the TMTSF compounds [12, 5, 13]. In particular, at high temperatures of the order of 100 K, TMTTF2X hosts a competition between a Mott insulating state, the so-called dimer-Mott (DM) insulator, and a charge ordering (CO) state with electron-rich and poor molecules spontaneously arranging to avoid the Coulomb repulsion: a common framework for the understanding of correlated quarter-filled systems [14, 15, 16]. In the low-temperature region (K), on the other hand, where the magnetic interactions start to develop between the localized spins in the strongly correlated regime, the AFM state competes with the spin-Peierls instability accompanying lattice distortion owing to the quasi-one-dimensionality [17, 18, 19].
The variation among the symmetry-breaking states, in which both the charge and spin degrees of freedom are involved, depending on the applied pressure to the compounds and on the choice of the combination of TM and X (chemical pressure), has been extensively discussed [20, 21, 22, 23, 24]. Nevertheless, there is room toward a comprehensive understanding of them. There are different views on how the choice of X and the amount of applied pressure affect the microscopic parameters, and the impact of the difference between TMTSF and TMTTF is still obscure. Conventionally, the two systems are drawn in a unified pressure-temperature phase diagram [4, 5, 22, 23], as shown in Fig. 1(a). Although there are different versions in the literature, here we simply draw the ‘ambient pressure’ positions of the representative compounds in an equally spaced manner, together with the reported transition temperatures [27, 28, 29, 30, 13].
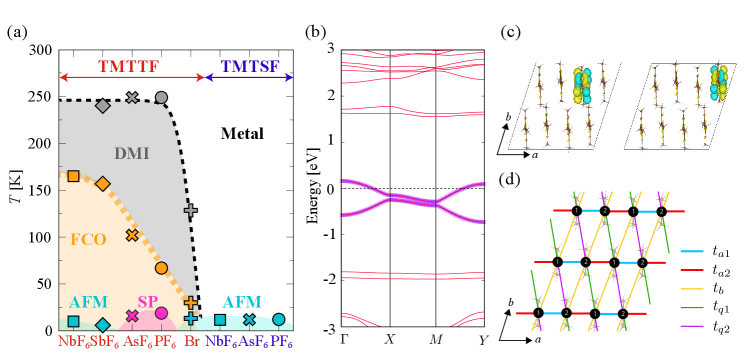
From the early days, in the TMTSF salts, it is discussed that the applied pressure increases the dimensionality [6]. On the other hand, the degree of dimerization along the one-dimensional chain direction was also pointed out to be an important factor, especially for the TMTTF salts [31]. And more recently, to understand the complicated interplay between the phases toward the left-hand end of the phase diagram, it was proposed that the CO instability can be the controlling factor [22]; this suggests the essential role of electron correlation. Whether we can choose a parameter that varies monotonically as we go along the compounds listed in the horizontal axis is the question we ask here.
In this work, to investigate these issues, we apply first-principles density functional theory (DFT) calculations [32, 33] to a number of members of the TM2X family with centrosymmetric ; we numerically derive not only the transfer integrals between the molecules but also the correlation parameters. We then use these parameters as inputs to a highly-accurate numerical solver, i.e., the many-variable variational Monte Carlo (mVMC) method [34, 35, 36], for the effective extended Hubbard-type Hamiltonian and seek possible long-range ordering in the charge and spin degree of freedoms. As a result, we can directly compare with the experimentally observed phases and comprehensively extract the determining factor at a quantitative level.
Ab initio derivation of microscopic parameters—. The DFT calculations are performed using Quantum Espresso (version 6.6) [37] for the experimental crystal structures [13]. We employ norm-conserving pseudopotentials based on the Vanderbilt formalism with plane-wave basis sets [38, 39]. The exchange-correlation functional used in this study is the generalized gradient approximation by Perdew, Burke, and Ernzerhof [40], which is commonly used for accurately describing electronic states of molecular compounds [41]. The cutoff energies for plane waves and charge densities are and Ry, respectively. A uniform -point mesh was used with a Gaussian smearing method during self-consistent loops.
For deriving the interaction parameters, we use the constrained random phase approximation (cRPA) method [42, 43]. In fact, previous studies applying the cRPA method to molecular solids show good agreement between the results for the derived effective Hamiltonians and the experiments [44, 45, 46, 47, 48, 49]. On the basis of the obtained DFT electronic states, we construct maximally localized Wannier function(MLWF)s and derive the parameters using RESPACK [50]. In the calculations, the energy cutoff for the dielectric function was set to be Ry.
Figures 1(b) and (c) show the band structure and the MLWFs, respectively, of TMTTF2PF6 as an example. The two bands crossing the Fermi energy are constituted from the bonding and anti-bonding combination of the highest occupied molecular orbitals situated on the two TMTTF molecules in the unit cell shown in Fig. 1(b). Using these MLWFs, we evaluated the transfer integrals and the density-density interactions, i.e. the on-site and off-site Coulomb interactions (the exchange interactions are negligibly small so we omit them in the following). The obtained microscopic parameters are listed in Table II in the supplemental materials [25]. We adopt the indices of bonds from refs. [22, 51], as shown in Fig. 1(d).
Then the following ab initio extended Hubbard-type Hamiltonian is obtained:
| (1) |
where and are the creation and annihilation operators of an electron with spin at the -th site, respectively. The number operators are defined as and ., , and represent the transfer integrals, on-site and off-site Coulomb interactions, respectively. We note that, although TM2X show quasi-one-dimensional electronic band structures, the Coulomb parameters show large values also for the interchain bonds.
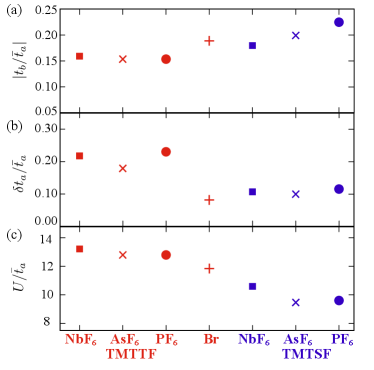
First, let us discuss the material dependence of intermolecular transfer energies based on our evaluation. Since it is known that the temperature variation of structural parameters is large [52], here we show the results for TMTTF2X with X= NbF6, AsF6, Br, and PF6 at fixed K, and for TMTSF2X with X= NbF6, AsF6, and PF6 at room temperature [25]. In Fig. 2, we show the variation of three different values along the horizontal axis of the phase diagram Fig. 1(a). The first two, the degree of interchain couplings and the degree of dimerization plotted in Figs. 2(a) and 2(b), respectively, have been discussed in the literature as mentioned above. We renormalize them by the mean transfer integral along the -axis, , which is larger than those along the other directions.
The largest interchain transfer integral, which is , is plotted in Fig. 2(a); the interlayer transfer integrals along the -axis are negligible. Our results show larger for the TMTSF salts than the TMTTF salts as a general trend; TMTSF has a broader extent of the wave function in the transverse direction than TMTTF, owing to the difference between the Se and S atoms at the sides of the molecules. As for the degree of dimerization, [Fig. 2(b)], the overall tendency is that it decreases from the left to the right side, while some deviates from the monotonic variation; for example, TMTTF2Br shows a similar value to the TMTSF salts.
Finally, Fig. 2 (c) shows the on-site Coulomb interaction, , which is a measure of the strength of electron correlation. The intermolecular parameters, , also show similar tendencies. We can see that monotonically decrease from the left to the right side, except for the two salts at the right end: TMTSF2PF6 () is slightly larger than TMTSF2AsF6 (). Since the electron correlation is responsible for all the phases, from the strongly correlated DM insulating and CO phases, to the nesting-driven AFM and the spin-fluctuation mediated superconducting phases, this behavior is consistent with the temperature scale for their occurrence, decreasing from left to right of the phase diagram in Fig. 1(a).
This tendency in can be understood by the effect of chemical pressure. More concretely, first, by the unit cell volume decreasing from left to right, the transfer integrals reflecting the overlap between MLWFs increase. Next, since the screening effect becomes stronger with increasing the band width, the screened is smaller with increasing the pressure. As a combination of them, together with the difference in the bare onsite Coulomb parameter between the molecules, monotonically decreases from left to right in Fig. 2 (c). For more detailed information about the parameters and their numerical accuracy, see ref. [25].
mVMC analysis—. To directly detect the symmetry-breaking phase transitions, we solve the effective Hamiltonian by using the mVMC method [34, 35, 36]. The form of the variational wave function used in this study is given by
| (2) |
where () represents the Gutzwiller factor [53] (Jastrow factor [54]) and is the total spin projection. We use the spin singlet total spin projection () for the ground states. The pair-product wave function is defined as
| (3) |
where represents the variational parameters, and and are the number of sites and electrons, respectively. In the mVMC calculations, we map the lattice structure shown in Fig. 1(d) onto the square lattice without loss of generality. The total number of sites is given by . We impose a sublattice structure and the periodic boundary conditions, and optimize all the variational parameters simultaneously using the stochastic reconfiguration method [55, 34] to obtain the ground state.
We consider all the bonds that are listed in Table II in the supplemental materials [25]; they contain all the bonds shown in Fig. 1(d) as well as that is the next-nearest-neighbor Coulomb interaction along the chain direction. We note that the effective Coulomb interactions are reduced by a constant shift eV [25], adopting the results of the previous study [56, 57], to take into account dimensional screening effects. We calculate the spin/charge structure factors defined as
| (4) | ||||
| (5) |
where () represents the number (spin) operator at site . The Fourier transformation is performed for the mapped square lattice.
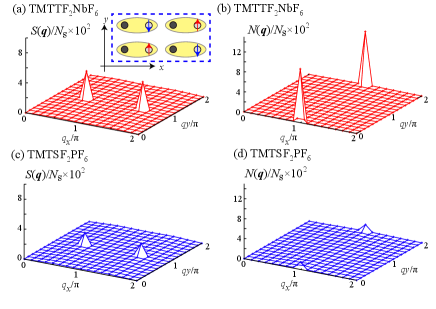
Let us present and for the two end members of the phase diagram, TMTTF2NbF6 and TMTSF2PF6. As shown in Figs. 3(a) and 3(b), for TMTTF2NbF6, which has the strongest electronic correlation, the spin (charge) structure factors has a sharp peak at []. The corresponding ordering pattern in the real space is shown in the inset of Fig. 3(a). Since these peak values remain finite after size extrapolation, the CO state with spin ordering is the ground state, consistent with previous studies [14, 22]. Note that, in the previous studies the long range Coulomb interactions are introduced by hand to stabilize the CO state with the ferroelectric pattern which is observed experimentally. We emphasize that, here the condition favoring the ferroelectric CO state is satisfied from the way, displayed in Fig. S1 (d) in the supplemental materials [25]. In contrast, we find that the peak values of the structure factors for parameters of TMTSF2PF6 become significantly small as shown in Figs. 3(c) and 3(d). This result is consistent with our results above that TMTSF2PF6 has much weaker electronic correlation.
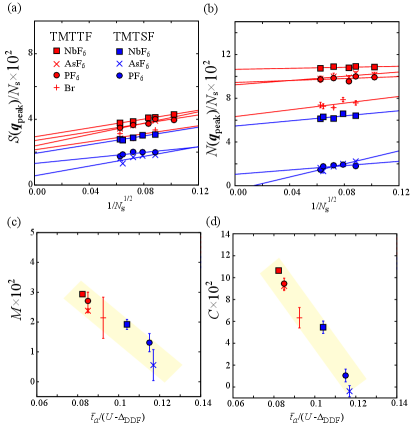
To clarify the material dependence, we perform the mVMC calculations for all the members and conduct the size extrapolation for the obtained peak values, in the spin and charge structure factors, as shown in Figs. 4(a) and (b), respectively. The thermodynamic limits are defined as , . Both the spin and charge structure factors show nearly linear dependencies as a function of the linear dimension of the number of sites, i.e., .
The material dependence of and is shown in Figs. 4 (c) and (d), respectively, as a function of the inverse of the normalized Coulomb interaction, . We find that the amplitude of the charge and spin orders decrease monotonically with respect to the amplitude of the Coulomb interactions. This tendency is consistent with the experimental results where the transition temperature of CO decreases by varying the material from left to right. At the border, TMTSF2AsF6 and TMTSF2PF6 show a small but finite value of of the order of 10-2, and almost vanishes.
These results, combined with the ab initio results in Fig. 2(c), both clearly show that the charge and spin orderings are governed by the relative amplitude of the Coulomb interactions. This is the first evidence that the correlation effects play key roles in stabilizing the spin/charge ordering in TM and serve as the good index for the horizontal axis of the unified phase diagram. The success here also indicates that our low-energy effective model is reliable at a quantitative level, considering the high precision of the mVMC method. This is owing to the fact that the band structure near the Fermi energy is simple, as shown in Fig. 1 (b), which guarantees the accuracy of the cRPA method, since it incorporates the effect of bands other than the target bands. In fact, in many of the molecular solids, bands near the Fermi energy are isolated, thus it is expected that our approach can be applicable to a wide range of functional molecular materials.
Perspectives—. We have shown that the material dependence in the unified phase diagram for TM is governed by the correlation effect, represented by the on-site Coulomb interaction , which gives a comprehensive understanding of the spin and charge orderings in this system. One point that disagrees with the experiments is that in our results, spin patterns with long periodicity such as incommensurate AFM (spin-density-wave) states suggested experimentally are difficult to reproduce in our finite-size systems. Finally, superconductivity is not found in our study, which is consistent with experiments showing it under pressure for the compounds we studied; its ab initio investigation is left for future studies.
Acknowledgements.
We thank R. Kato, S. Kitou, and T. Nakamura for fruitful discussions. This work was supported by MEXT/JSPJ KAKENHI under grant numbers 19K03723, 19K21860, 20H04463, 21H01041, 22K03526, 23H03818, and 23H04047. KY and TM were supported by Building of Consortia for the Development of Human Resources in Science and Technology, MEXT, Japan. The computation in this work was performed using the facilities of the Supercomputer Center, Institute for Solid State Physics, University of Tokyo.References
- Ishiguro et al. [1998] T. Ishiguro, K. Yamaji, and G. Saito, Organic superconductors, 2nd ed., Springer series in solid-state sciences, 88 (Springer, Berlin; New York, 1998).
- [2] A. Lebed, The Physics of organic superconductors and conductors, Springer Series in Materials Science (Springer, Berlin, Heidelberg, 2008) .
- Seo et al. [2004] H. Seo, C. Hotta, and H. Fukuyama, Toward systematic understanding of diversity of electronic properties in low-dimensional molecular solids, Chem. Rev. 104, 5005 (2004).
- Jérome [2004] D. Jérome, Organic Conductors: From Charge Density Wave TTF-TCNQ to Superconducting (TMTSF)2PF6, Chem. Rev. 104, 5565 (2004).
- Brown et al. [2008] S. E. Brown, P. M. Chaikin, and M. J. Naughton, La tour des sels de bechgaard, in The Physics of Organic Superconductors and Conductors, edited by A. Lebed (Springer, Berlin, Heidelberg, 2008) pp. 49–87.
- Jérome et al. [1980] D. Jérome, A. Mazaud, M. Ribault, and K. Bechgaard, Superconductivity in a synthetic organic conductor (TMTSF)2PF6, J. Physique Lett. 41, 95 (1980).
- Béal-Monod et al. [1986] M. T. Béal-Monod, C. Bourbonnais, and V. J. Emery, Possible superconductivity in nearly antiferromagnetic itinerant fermion systems, Phys. Rev. B 34, 7716 (1986).
- Hasegawa and Fukuyama [1987] Y. Hasegawa and H. Fukuyama, NMR Relaxation Time of the Anisotropic Superconducting State in Quasi-One-Dimensional Systems, J. Phys. Soc. Jpn. 56, 877 (1987).
- Takigawa et al. [1987] M. Takigawa, H. Yasuoka, and G. Saito, Proton spin relaxation in the superconducting state of (tmtsf)2clo4, J. Phys. Soc. Jpn 56, 873 (1987).
- Shimahara [1989] H. Shimahara, Long-Range Spin-Fluctuations and Superconductivity in Quasi-One-Dimensional Organic Compounds, J. Phys. Soc. Jpn. 58, 1735 (1989).
- Brown [2015] S. E. Brown, Organic superconductors: The Bechgaard salts and relatives, Physica C 514, 279 (2015).
- Chow et al. [2000] D. S. Chow, F. Zamborszky, B. Alavi, D. J. Tantillo, A. Baur, C. A. Merlic, and S. E. Brown, Charge Ordering in the TMTTF Family of Molecular Conductors, Phys. Rev. Lett. 85, 1698 (2000).
- Kitou et al. [2021] S. Kitou, L. Zhang, T. Nakamura, and H. Sawa, Complex changes in structural parameters hidden in the universal phase diagram of the quasi-one-dimensional organic conductors (, and Br), Phys. Rev. B 103, 184112 (2021).
- Seo and Fukuyama [1997] H. Seo and H. Fukuyama, Antiferromagnetic Phases of One-Dimensional Quarter-Filled Organic Conductors, J. Phys. Soc. Jpn. 66, 1249 (1997).
- Seo [2000] H. Seo, Charge Ordering in Organic ET Compounds, J. Phys. Soc. Jpn. 69, 805 (2000).
- Powell and McKenzie [2006] B. J. Powell and R. H. McKenzie, Strong electronic correlations in superconducting organic charge transfer salts, J. Phys.: Cond. Matter. 18, R827 (2006).
- Zamborszky et al. [2002] F. Zamborszky, W. Yu, W. Raas, S. E. Brown, B. Alavi, C. A. Merlic, and A. Baur, Competition and coexistence of bond and charge orders in , Phys. Rev. B 66, 081103 (2002).
- Iwase et al. [2011] F. Iwase, K. Sugiura, K. Furukawa, and T. Nakamura, 13C NMR study of the magnetic properties of the quasi-one-dimensional conductor (TMTTF)2SbF6, Phys. Rev. B 84, 115140 (2011).
- Dressel et al. [2012] M. Dressel, M. Dumm, T. Knoblauch, and M. Masino, Comprehensive Optical Investigations of Charge Order in Organic Chain Compounds (TMTTF)2X, Crystals 2, 528 (2012).
- Kuwabara et al. [2003] M. Kuwabara, H. Seo, and M. Ogata, Coexistence of Charge Order and Spin–Peierls Lattice Distortion in One-Dimensional Organic Conductors, J. Phys. Soc. Jpn. 72, 225 (2003).
- Sugiura et al. [2005] M. Sugiura, M. Tsuchiizu, and Y. Suzumura, Spin-Peierls Transition Temperature in Quarter-Filled Organic Conductors, J. Phys. Soc. Jpn. 74, 983 (2005).
- Yoshimi et al. [2012a] K. Yoshimi, H. Seo, S. Ishibashi, and S. E. Brown, Tuning the Magnetic Dimensionality by Charge Ordering in the Molecular TMTTF Salts, Phys. Rev. Lett. 108, 096402 (2012a).
- Clay and Mazumdar [2019] R. T. Clay and S. Mazumdar, From charge- and spin-ordering to superconductivity in the organic charge-transfer solids, Physics Reports 788, 1 (2019).
- Yoshioka et al. [2012] H. Yoshioka, Y. Otsuka, and H. Seo, Theoretical Studies on Phase Transitions in Quasi-One-Dimensional Molecular Conductors, Crystals 2, 996 (2012).
- [25] See Supplemental Material URL_will_be_inserted_by_publisher for details of experimental data and microscopic parameters in Hamiltonians, and the explanation of the screened Coulomb interaction trends and their effects on the electronic state, which includes Refs. [58, 59, 60, 61].
- Momma and Izumi [2011] K. Momma and F. Izumi, Vesta 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr. 44, 1272 (2011).
- Dumm et al. [2000] M. Dumm, A. Loidl, B. W. Fravel, K. P. Starkey, L. K. Montgomery, and M. Dressel, Electron spin resonance studies on the organic linear-chain compounds , Phys. Rev. B 61, 511 (2000).
- Sakata et al. [2006a] M. Sakata, Y. Yoshida, M. Maesato, G. Saito, K. Matsumoto, and R. Hagiwara, Preparation of superconducting (TMTSF)2NbF6 by electrooxidation of TMTSF using ionic liquid as electrolyte, Mol. Cryst. Liq. Cryst. 452, 103 (2006a).
- Rohwer et al. [2020] A. Rohwer, M. Dressel, and T. Nakamura, Deuteration Effects on the Transport Properties of (TMTTF)2X Salts, Crystals 10, 1085 (2020).
- Köhler et al. [2011] B. Köhler, E. Rose, M. Dumm, G. Untereiner, and M. Dressel, Comprehensive transport study of anisotropy and ordering phenomena in quasi-one-dimensional (TMTTF)2 salts (= PF6, AsF6, SbF6, BF4, ClO4, ReO4), Phys. Rev. B 84, 035124 (2011).
- Y. Nogami et al. [2005] Y. Nogami, T. Ito, K. Yamamoto, N. Irie, S. Horita, T. Kambe, N. Nagao, K. Oshima, N. Ikeda, and T. Nakamura, X-ray structural study of charge and anion orderings of TMTTF salts, J. Phys. IV France 131, 39 (2005).
- Hohenberg and Kohn [1964] P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev. 136, B864 (1964).
- Kohn and Sham [1965] W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev. 140, A1133 (1965).
- Tahara and Imada [2008] D. Tahara and M. Imada, Variational Monte Carlo Method Combined with Quantum-Number Projection and Multi-Variable Optimization, J. Phys. Soc. Jpn. 77, 114701 (2008).
- Misawa et al. [2019] T. Misawa, S. Morita, K. Yoshimi, M. Kawamura, Y. Motoyama, K. Ido, T. Ohgoe, M. Imada, and T. Kato, mVMC—Open-source software for many-variable variational Monte Carlo method, Comput. Phys. Commun. 235, 447 (2019).
- [36] https://www.pasums.issp.u-tokyo.ac.jp/mvmc/en/.
- Giannozzi et al. [2017] P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. of Phys.: Cond. Matt. 29, 465901 (2017).
- Hamann [2013] D. R. Hamann, Optimized norm-conserving Vanderbilt pseudopotentials, Phys. Rev. B 88, 085117 (2013).
- Schlipf and Gygi [2015] M. Schlipf and F. Gygi, Optimization algorithm for the generation of ONCV pseudopotentials, Comput. Phys. Commun. 196, 36 (2015).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Ishibashi [2009] S. Ishibashi, First-principles electronic-band calculations on organic conductors, Science and Technology of Advanced Materials 10, 024311 (2009), https://doi.org/10.1088/1468-6996/10/2/024311 .
- Aryasetiawan et al. [2004] F. Aryasetiawan, M. Imada, A. Georges, G. Kotliar, S. Biermann, and A. I. Lichtenstein, Frequency-dependent local interactions and low-energy effective models from electronic structure calculations, Phys. Rev. B 70, 195104 (2004).
- Imada and Miyake [2010] M. Imada and T. Miyake, Electronic structure calculation by first principles for strongly correlated electron systems, J. Phys. Soc. Jpn. 79, 112001 (2010).
- Shinaoka et al. [2012] H. Shinaoka, T. Misawa, K. Nakamura, and M. Imada, Mott Transition and Phase Diagram of -(BEDT-TTF)2Cu(NCS)2 Studied by Two-Dimensional Model Derived from Ab initio Method, J. Phys. Soc. Jpn 81, 034701 (2012).
- Misawa et al. [2020] T. Misawa, K. Yoshimi, and T. Tsumuraya, Electronic correlation and geometrical frustration in molecular solids: A systematic ab initio study of , Phys. Rev. Research 2, 032072 (2020).
- Yoshimi et al. [2021] K. Yoshimi, T. Tsumuraya, and T. Misawa, Ab initio derivation and exact diagonalization analysis of low-energy effective hamiltonians for -, Phys. Rev. Research 3, 043224 (2021).
- Ido et al. [2022] K. Ido, K. Yoshimi, T. Misawa, and M. Imada, Unconventional dual 1d–2d quantum spin liquid revealed by ab initio studies on organic solids family, npj Quantum Mater. 7, 48 (2022).
- Ohki et al. [2022] D. Ohki, K. Yoshimi, and A. Kobayashi, Interaction-induced quantum spin Hall insulator in the organic Dirac electron system , Phys. Rev. B 105, 205123 (2022).
- Ohki et al. [2020] D. Ohki, K. Yoshimi, and A. Kobayashi, Transport properties of the organic Dirac electron system , Phys. Rev. B 102, 235116 (2020).
- Nakamura et al. [2021] K. Nakamura, Y. Yoshimoto, Y. Nomura, T. Tadano, M. Kawamura, T. Kosugi, K. Yoshimi, T. Misawa, and Y. Motoyama, RESPACK: An ab initio tool for derivation of effective low-energy model of material, Comp. Phys. Comm. 261, 107781 (2021).
- Yoshimi et al. [2012b] K. Yoshimi, H. Seo, S. Ishibashi, and S. E. Brown, Spin frustration, charge ordering, and enhanced antiferromagnetism in TMTTF2SbF6, Physica B: Condensed Matter 407, 1783 (2012b).
- Jacko et al. [2013] A. C. Jacko, H. Feldner, E. Rose, F. Lissner, M. Dressel, R. Valentí, and H. O. Jeschke, Electronic properties of fabre charge-transfer salts under various temperature and pressure conditions, Phys. Rev. B 87, 155139 (2013).
- Gutzwiller [1963] M. C. Gutzwiller, Effect of Correlation on the Ferromagnetism of Transition Metals, Phys. Rev. Lett. 10, 159 (1963).
- Jastrow [1955] R. Jastrow, Many-Body Problem with Strong Forces, Phys. Rev. 98, 1479 (1955).
- Sorella [2001] S. Sorella, Generalized Lanczos algorithm for variational quantum Monte Carlo, Phys. Rev. B 64, 024512 (2001).
- Nakamura et al. [2010] K. Nakamura, Y. Yoshimoto, Y. Nohara, and M. Imada, Ab initio low-dimensional physics opened up by dimensional downfolding: application to LaFeAsO, J. Phys. Soc. Jpn 79, 123708 (2010).
- Nakamura et al. [2012] K. Nakamura, Y. Yoshimoto, and M. Imada, Ab initio two-dimensional multiband low-energy models of [(dmit)2]2 and -(BEDT-TTF)2Cu(NCS)2 with comparisons to single-band models, Phys. Rev. B 86, 205117 (2012).
- Thorup et al. [1981] N. Thorup, G. Rindorf, H. Soling, and K. Bechgaard, The structure of di(2,3,6,7-tetramethyl-1,4,5,8-tetraselenafulvalenium) hexafluorophosphate, (TMTSF)2PF6, the first superconducting organic solid, Acta Crystallographica Section B 37, 1236 (1981).
- Wudl [1981] F. Wudl, Three-dimensional structure of the superconductor (TMTSF)2AsF6 and the spin-charge separation hypothesis, Journal of the American Chemical Society 103, 7064 (1981), https://doi.org/10.1021/ja00414a007 .
- Sakata et al. [2006b] M. Sakata, Y. Yoshida, M. Maesato, G. Saito, K. Matsumoto, and R. Hagiwara, Preparation of superconducting (TMTSF)2NbF6 by electrooxidation of tmtsf using ionic liquid as electrolyte, Molecular Crystals and Liquid Crystals 452, 103 (2006b), https://doi.org/10.1080/15421400500377511 .
- [61] https://isspns-gitlab.issp.u-tokyo.ac.jp/k-yoshimi/tm-salts.
Supplemental Materials for “Comprehensive investigation of the phase diagram of quasi-one-dimensional molecular solids”
I 1. Transition temperatures
In Table 1, we list the experimental transition temperatures reported in the literature, which we plot in Fig. 1(a) to construct the unified phase diagram of the TM2X family. is the temperature where the electrical resistivity takes the minimum (sometimes written as ), below which the dimer-Mott insulating state is stabilized; there is no symmetry breaking there, since it is a crossover temperature. Others exhibit symmetry breaking and show continuous phase transitions.
| TMTSF2PF6[27] | – | – | 12 | – |
| TMTSF2AsF6[27] | – | – | 12 | – |
| TMTSF2NbF6[28] | – | – | 12 | – |
| TMTTF2Br[29] | 130 | 30 | 13 | – |
| TMTTF2PF6[30] | 250 | 67 | – | 19 |
| TMTTF2AsF6[30] | 250 | 102 | – | 19 |
| TMTTF2SbF6[30] | 240 | 157 | 6 | – |
| TMTTF2NbF6[13] | – 111Although the presence of DMI phase has been reported in Ref. [13], the value of is not reported. | 165 | 10 | – |
II 2. Model parameters
Since molecular solids have strong temperature dependencies on structure parameters due to their softness, the model parameters derived for structures at different temperatures can be different. In fact, it is shown that in a Pd(dmit)2 based system, as the temperature decreases, the amplitude of electron correlation effectively decreases [46]. Therefore, in this work, we performed a systematic analysis based on the structures at a fixed temperature of K for TMTTF2X (X=Br, PF6, AsF6, and NbF6) provided by Kitou et al [13]. The analysis was based on room temperature structures for TMTSF2X (X=PF6[58], AsF6[59], and NbF6[60]). The conclusion that the electron correlation effect is weaker for the TMTSF salts than for the TMTTF salts holds, despite the difference in the temperature used between the two systems, since the amplitude of the correlations in TMTSF becomes weaker at lower temperatures.
| TMTSF2PF6 | RT | 714.3 | -0.209 | -0.235 | 0.050 | 0.027 | 0.006 | 5.27 | 2.13 | 0.998 | 1.016 | 0.645 | 0.731 | 0.635 | 0.588 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TMTSF2AsF6 | RT | 719.9 | -0.210 | -0.232 | 0.044 | 0.019 | 0.004 | 5.19 | 2.09 | 0.996 | 1.009 | 0.636 | 0.724 | 0.624 | 0.589 |
| TMTSF2NbF6 | RT | 735.3 | -0.195 | -0.217 | 0.037 | 0.019 | - | 5.21 | 2.18 | 1.05 | 1.07 | 0.662 | 0.751 | 0.650 | 0.619 |
| TMTTF2Br | 200K | 611.7 | -0.188 | -0.204 | 0.037 | 0.029 | 0.019 | 5.54 | 2.32 | 1.06 | 1.07 | 0.635 | 0.709 | 0.647 | 0.603 |
| TMTTF2PF6 | 200K | 661.4 | -0.173 | -0.218 | 0.03 | 0.012 | 0.005 | 5.64 | 2.50 | 1.14 | 1.18 | 0.70 | 0.788 | 0.684 | 0.666 |
| TMTTF2AsF6 | 200K | 672.6 | -0.178 | -0.213 | 0.03 | 0.011 | - | 5.64 | 2.50 | 1.14 | 1.18 | 0.70 | 0.783 | 0.677 | 0.664 |
| TMTTF2NbF6 | 200K | 683.0 | -0.168 | -0.209 | 0.03 | 0.011 | - | 5.64 | 2.49 | 1.14 | 1.17 | 0.688 | 0.767 | 0.667 | 0.66 |
In Table 2, we show the calculated values of the transfer integrals, the bare on-site Coulomb interaction , and the screened Coulomb interactions using DFT and MLWFs. The unitcell volumes obtained by the crystallographic information file are also listed. Due to the numerical errors, values of crystallographically equivalent bonds were slightly different. We averaged over the transfer integrals and Coulomb interactions for corresponding bonds. We also confirmed that in the actual analysis of the low-energy effective models, meV order differences in the parameter do not change the results. We uploaded the output files containing the transition integrals and Coulomb interactions obtained by RESPACK to the data repository[61].
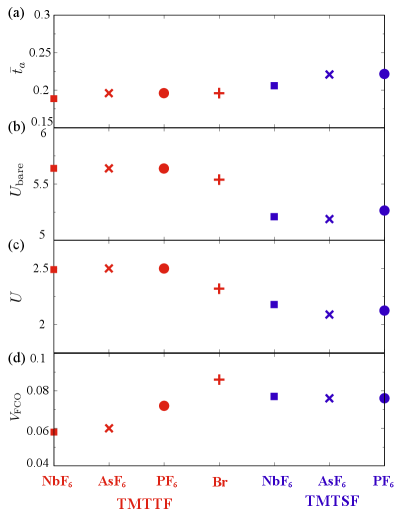
Figure 5 (a) shows mean transfer integral between TM molecules along -axis (). The obtained results can be understood by the effect of chemical pressure, namely the change in the unit cell volume. When the radius of the anion is small, the unit cell volume becomes small and then the transfer integrals increase. Figure 5 (b) shows the bare on-site Coulomb interaction . Since is determined by the charge distribution on the TM molecule, the magnitude of depends mostly on the type of TM molecule (for TMTSF molecules, is smaller than for TMTTF molecules because the electron density in the molecule expands, by the difference between Sulfur in TMTTF molecule and Selenium in TMTSF molecule). As the transfer integrals increase, in the cRPA method, the screening effect increases and thus the screened on-site Coulomb interaction decreases as shown in Fig. 5 (c). As a result, the material dependence of becomes pronounced and systematically varied among the investigated members.
The intersite Coulomb interactions are crucial in stabilizing the CO state. Since the Coulomb interactions and are notably large compared to other Coulomb interactions, the “rich-poor” charge pattern along the axis is favored. Thus, in order to stabilize the ferroelectric state, the classical condition is that sum of the long-range Coulomb interactions connected by and bonds are larger than twice of that connected by the bond: . As seen from Fig. 5 (d), the intersite Coulomb interactions derived in an way here indeed satisfy this condition for all of the compounds.