P[1]¿\arraybackslashp#1
Computational Design of Wiring Layout on Tight Suits with Minimal Motion Resistance
Abstract.
An increasing number of electronics are directly embedded on the clothing to monitor human status (e.g., skeletal motion) or provide haptic feedback. A specific challenge to prototype and fabricate such a clothing is to design the wiring layout, while minimizing the intervention to human motion. We address this challenge by formulating the topological optimization problem on the clothing surface as a deformation-weighted Steiner tree problem on a 3D clothing mesh. Our method proposed an energy function for minimizing strain energy in the wiring area under different motions, regularized by its total length. We built the physical prototype to verify the effectiveness of our method and conducted user study with participants of both design experts and smart cloth users. On three types of commercial products of smart clothing, the optimized layout design reduced wire strain energy by an average of 77% among 248 actions compared to baseline design, and 18% over the expert design.
1. Introduction
Smart clothes augment traditional garments, by installing a variety of electronic units, including but not limited to IMUs (Wang et al., 2015), flexible sensors (Pointner et al., 2020), pressure sensors (Lee et al., 2015), haptic actuators (Ramachandran et al., 2021; Lopes and Baudisch, 2017), etc. Notably, most smart clothes (for example, the commercial products Tesla Suit, Athos) are tight-fitting to guarantee the close conformability with human skin, to avoid sensor displacement and to accurately monitor human status. Electronic components are connected using either wired or wireless (Bluetooth, WiFi, etc.) approaches (Stanley et al., 2022). Wireless connection enjoys its advantage in being cable-free. Compared to wireless connection, the necessity of wired connection for smart clothes stems from its lower susceptibility to environmental interference and easy time synchronization among multiple electronic devices. Currently, the popular adoption of wired connections is evidenced by both previous literature (Ancans et al., 2021) and in various commercial products like Tesla Suit (Teslasuit, 2022). Typically, Bluetooth (as one of the most popular wireless solutions) only supports a maximum number of 7 connected devices, which falls short of the demand for smart garment design. Therefore, exploring the layout of wiring design offers the benefit for future development of smart clothes. However, wiring inevitably impacts human motion while motion-driven deformation may also damage wiring connection when being stretched. Therefore, wire layout greatly affects the mechanical durability, activity performance and user experience when the user is wearing smart clothing (Ruckdashel et al., 2022; Agcayazi et al., 2018). Therefore, it is crucial to optimize on-garment wiring to minimize intervention with user’s physical activity, thereby improving user comfort (Yokus et al., 2016). Previous works sidestepped this issue by adding redundancies (e.g., “waviness”, “interdigitation”) to circuit design. For example, Vervust et al. [2012] developed a novel electronic circuit technology that adds “waviness” to the circuits to make them stretchable. However, these strategies did not directly solve the problem and are suboptimal due to the redundancies they introduce, which require additional manufacturing processes and costs. In addition, they contradict a common strategy in the fabrication of existing products that encloses wires and straps inside the fabric by hot pressing, whose benefits are three-fold: i) guaranteed structural firmness of the enclosed wire; ii) insulation from skin conductance; iii) waterproof, including the prevention of sweating. Hence, a direct and automated wiring solution that can improve user comfort without introducing redundancies is desired, but its existence remains an open question.
In general, there are two primary obstacles that hinder the development of a feasible automated solution. Firstly, the mathematical model required for the solution has not yet been constructed. Secondly, there is a lack of a reliable method for quantifying the impact caused by motion. For the first obstacle, a minimum spanning tree constructed on a graph with on-body electronics as vertices and pair-wise shortest paths (i.e., wires) as edges is a sub-optimal solution as it does not allow for wire branching, which provides a larger search space and better solutions. It is also worth noting that a recent work (Vechev et al., 2022) proposed a method to optimize garment design for kinesthetic feedback obtained from electrostatic (ES) clutches. While their approach is effective, it is not suitable for our specific task as we solve the problem of wiring layout with a fixed strap width and least motion resistance, rather than determining arbitrarily shaped regions, leading to a completely different solution. Therefore, effective wiring on garments with respect to a set of on-body electronic components remains an open problem.
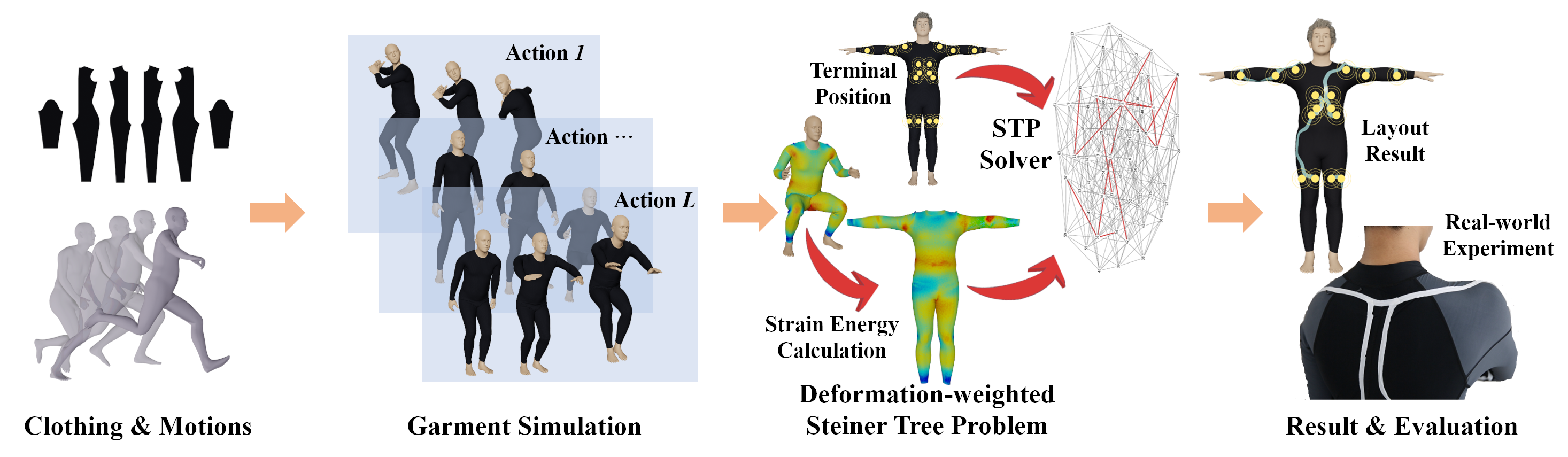
In this work, we propose a novel automated wiring method for smart clothing that effectively tackles the aforementioned challenges, including i) a novel formulation of on-garment wiring as a deformation-weighted Steiner tree problem (STP), providing a fresh perspective on the problem; ii) a novel edge weighting scheme that accurately captures the wire deformation resulting from a range of input motions. We chose STP over other related combinatorial optimization methods like the traveling salesman problem (TSP) and minimum spanning tree (MST) as: STP distinguishes terminal vertices from other vertices on the mesh and only connects them, while TSP and MST treat all vertices equally and traverse them all. Thus, TSP and MST cannot be applied directly, but require a preparatory step to create another topology on top of the mesh, e.g., a graph connecting all pairs of terminal vertices with the shortest paths. However, this is a sub-optimal solution compared to STP because it does not allow branching (a popular example is that it is shorter to connect the three endpoints of an equilateral triangle from its center than to use its two sides). In our approach, users can specify the positions of electronic components, and the algorithm generates a wire layout to connect the electronic components automatically. Our main contributions can be summarized as the following:
-
•
We directly address one of the key challenges in smart clothing design, i.e., the automatic wiring problem, by transforming it into the construction of a deformation-weighted Steiner tree (a topology optimization problem) to minimize motion resistance and improve system robustness.
-
•
We propose a novel deformation-inspired edge weighting scheme that models the effects of human motion on wire stretching by its area strain and regularizes it with wire length.
-
•
In addition to positive subjective feedback, real-world experimental results show that our approach produces wiring layouts that outperform expert designs, reducing wire strain energy by an average of 77% among 248 actions, which demonstrates the effectiveness of our method.
2. Related Work
Design and Application of Smart Clothing
Smart clothing, as an emerging domain, integrates electronics with textiles to create functional solutions for physiological state monitor (Angelucci et al., 2021), skeletal motion capture (Chen et al., 2022) and body shape reconstruction (Zhang et al., 2020; Chen et al., 2021). Its applications have been demonstrated in fields including rehabilitation (Ramachandran et al., 2021), assistive walking (Kim et al., 2019; Lee et al., 2018) and interactive entertainment (Al Maimani and Roudaut, 2017). Its associated physical prototypes include full-body suit (Chen et al., 2022), upper-body shirt (Chen et al., 2021; Rognon et al., 2018), jacket (Delazio et al., 2018; Günther et al., 2019), pants (Gholami et al., 2019), sock (Zhang et al., 2020), elbow pad (Liu et al., 2019; Chen et al., 2023), gloves (Glauser et al., 2019; Cai et al., 2019), etc.
Recent years have seen a booming in commercial products for smart clothing, including Athos, Tesla Suit, Bhaptics, Nadi X, Sensoria Fitness Socks, Siren Diabetic Socks, Ambiotex, AIO smart sleeve, Hexoskin (please refer to the supplementary materials for detailed information). These products encompass a wide range of monitoring capabilities, covering diverse aspects such as environmental factors, human activity metrics and key biometrics. It can be envisioned that a growing number of innovative technology, and most likely electronic gadgets, will be integrated to enhance the functionality of smart clothing.
Despite the increasing demand for smart clothing, methods to aid the design of smart clothing are relatively under-explored. Existing software solutions in the clothing industry often overlook the complex integration of textile and electronics. Our work focuses on addressing one of these challenges, namely the automatic wiring problem, aiming to minimize interference with human motion.
Deformation Analysis for Garment Design
Garment deformation caused by human motion is critical for both virtual fitting (Pan et al., 2022; Hu et al., 2022; Shi et al., 2021; Wu et al., 2022) and real-world clothing design (Sati et al., 2021; Wolff et al., 2022; Kwok et al., 2015). Therefore, existing studies have incorporated the impact of body movement on fabric simulation into clothing design to simulate the potential impact in real-world situations (Sati et al., 2021; Deng et al., 2016; Li and Lu, 2011). Wolff et al. propose an interactive design tool for creating custom clothing based on 3D body scanning of the intended wearer, by optimizing the shape of the clothing through interpolation and movement of different input postures (Wolff et al., 2022). Liu et al. consider comfort during physical activity and optimize knitted clothing through careful control of the distribution of elasticity to reduce uncomfortable pressure and unnecessary slippage caused by physical activity (Liu et al., 2021). Pietroni et al. propose an optimization-driven method for automating, based on physics, pattern design for tight clothing (Pietroni et al., 2022). These recent works offer in-depth investigation on the intertwined relationship between human posture and garment design, particularly tight suits. Another recent work extends to the design of smart clothing, and optimizes the connection structure of electrostatic (ES) clutches for clothing design that provides haptic feedback (Vechev et al., 2022). Montes et al. [2020] proposed an optimization-driven approach for automated, physics-based pattern design for tight-fitting clothing. However, they focused on the stretching of the clothing rather than the wires. Our work addresses the distinct problem from existing works, i.e., wire layout on tight suits.
We systematically analyzed the garment deformation, in the focused case of tight suit, under more than 248 motion sequences, and aimed to minimize the motion resistance on the deformation surface.
Steiner Tree Problem (STP)
The definition of STP extends the shortest path problem and minimum spanning tree problem, and has been widely applied in fields such as path planning and circuit design. We formulate our problem as an STP variant, i.e., the electronic components as terminals and the wiring layout as paths. Unfortunately, there is still no polynomial-time algorithm for the general case of the Steiner tree problem (Ljubić, 2021), so the solution algorithms for the problem mainly consist of precise algorithms (Dreyfus and Wagner, 1971; Nederlof, 2009) and approximation algorithms (Gröpl et al., 2001; Robins and Zelikovsky, 2005). The precise algorithms mainly rely on dynamic programming (DP) to list and compare all possible solutions. Their time complexity is mainly determined by the number of terminals , the number of vertices , and the number of edges , and the result can be obtained in exponential time. The Dreyfus-Wagner algorithm (Dreyfus and Wagner, 1971; Levin, 1971) is a classical precise algorithm based on dynamic programming, with a running time of . Subsequently, Fuchs et al. [2007] and Nederlof [2009] provide improvements on this algorithm. The latter two methods calculate the worst-case time algorithm complexity for the special case where all edge weights come from the set , and they obtain an upper bound of for the running time. Another DP method produces the running time bounds for a wide range of values (Vygen, 2011). Therefore, in cases where the number of terminals is limited and relatively small, precise algorithms can achieve extremely high accuracy. In addition, DP algorithms for tree decomposition problems also use a polynomial time algorithm for and an exponential polynomial time algorithm for the tree width, resulting in a polynomial time algorithm for graphs with limited tree width (Bodlaender et al., 2015; Chimani et al., 2012; Hougardy et al., 2017). We adopt a precise STP solver (Iwata and Shigemura, 2019), which made dedicated efforts for the case of few terminal nodes, achieving extremely high computational efficiency.
Our work solves the topology optimization problem on the garment deformation surface, by formulating it as a Steiner tree problem. We discretize it into the clothing mesh and propose a novel energy to comprehensively consider both wire elongation and area strain.
3. Unobtrusive Wiring on Garments
Our goal is to create a novel solution for unobtrusive wiring layout on tight suits, which houses multiple electronics. The primary aim of our solution is to minimize motion resistance during physical activities, ensuring an unobtrusive user experience.
3.1. Problem Definition
Definition 3.0 (Unobtrusive Wiring on Smooth Surfaces).
Given a smooth surface with terminals , unobtrusive wiring is achieved by constructing a Steiner Tree whose strain energy (edge weights) is minimized according to a set of motions with length :
| (1) |
Strain energy is the elastic potential energy gained by a wire during elongation with a tensile (stretching).
Given the intricate nature of the surface and motion set in real-world scenarios, although Definition 1 is precise, it must be discretized for effective numerical analysis. To avoid confusion, we use similar notations for the corresponding concepts in both definitions as follows.
Definition 3.0 (Unobtrusive Wiring on Discrete Surfaces).
Given a polygon mesh where and are the sets of vertices and edges of respectively, terminals , unobtrusive wiring is achieved by constructing a Steiner tree with whose strain energy (edge weights) is minimized according to a set of motions with length :
| (2) |
It is worth noting that in Definition 2, rather than solely focusing on the surface, we simultaneously discretize the underlying surface into polygon meshes and the wiring Steiner tree into its graph-based version. This approach stems from the fact that, to the best of our knowledge, there are currently no efficient algorithms available to solve this particular problem, namely the Steiner Tree Problem on arbitrary polygon surfaces (Caffarelli et al., 2014). Thus, we believe that our definition represents the most suitable approach at this juncture. Nevertheless, we maintain an optimistic outlook for future breakthroughs that may inspire new variations of Definition 2.
Remark. Definition 2 is also applicable to cases where is placed within the faces of . In such cases, we can subdivide the corresponding face, add as a new vertex in , and include the newly generated edges in .
3.2. Problem Input
The input includes:
-
(1)
A set of motion sequences: , where a motion sequence is a set of continuous frames of human posture: .
-
(2)
A tight suit model: it includes a 3D mesh model as and a 2D pattern model. In our current work we use three different sizes of the suit: M, L, XL.
-
(3)
A resting state: we use the 2D pattern model as the resting state to measure the deformation, since the 2D pattern mesh is flat and does not involve any deformation.
-
(4)
A set of terminals , indicating the electronics to be connected.
3.3. Deformation-weighted Steiner Tree Problem
Cloth-based Deformation Simulation
To obtain the surface deformation when performing various movements, we conduct cloth simulation on a tight suit mesh , which is worn by a virtual character when performing the motion in the motion set . We import the motion sequence generated by the standard human body SMPL (Pavlakos et al., 2019) into Marvelous Designer (Designer, 2022) for cloth simulation. Three SMPL models are generated by matching the body girths on SMPL models (Chen et al., 2021) according to the expected values of standard garment size. For utmost realism, we used the cloth simulation engine from the mainstream cloth design software of Marvelous Designer, which captures friction/displacement between a tight suit and human skin. Detailed simulation parameters can be found in Supplementary Sec. 7. To validate the effectiveness of our simulation, we use the strain sensing system to measure strain deformation on real cloth, which reveals consistency with the simulation.
3.3.1. Deformation-inspired Edge Weights
As specified in Definition 2, the key challenge to maintaining an unobtrusive user experience during physical activities is to minimize the strain energy exerted by motions onto the on-garment wires . Since is essentially a Steiner Tree in mesh , can be decomposed into the individual contribution of each edge . Hence, we focus on calculating the strain energy for each edge of mesh , which will serve as the edge weights during the construction of Steiner Trees:
| (3) |
where denotes the faces of mesh , is a regularization term of wire length to avoid excessive redundancy of the wire. A smaller value of selects straighter/shorter wires. denotes the area of the selected mesh, i.e., the area of the cloth straps accommodating wires that are fixed to smart clothes, which should be avoided from stretching. This is important as wires are secured to the cloth straps, thus stretching the cloth straps both along and perpendicular to the direction of the wires will affect its performance. denotes a local neighborhood of (e.g., of a rectangular shape with as the midline) which simulates the width of the wire strip in real-world scenarios. We compute the intersection using the Shapely library (Gillies et al., 2007). is the strain energy of with respect to motions :
| (4) |
where is the number of frames in motion sequence and we follow the St. Venant-Kirchhoff model introduced in (Liu, 2018) to calculate :
| (5) | ||||
where we set the Young’s modulus of the clothing to 5.4 MPa and the Poisson’s ratio to 0.33 (Montes et al., 2020), and calculate the Green strain tensor as:
| (6) |
where the deformation matrix is obtained from the difference between and , where is the shape of in a reference state and is the shape of in motion . is the identify matrix. In Eq. 3, represents the energy sum in the area, and represents the energy density, which needs to be multiplied by the area in order to get the energy of the wire-attached area (with fixed width).
3.3.2. Steiner Tree Solver
With edge weights defined, we can effectively address unobtrusive wiring on garments using state-of-the-art Steiner Tree algorithms. In this paper, we employ a highly efficient method (Iwata and Shigemura, 2019), which leverages dynamic programming and pruning techniques.
3.4. Curve Smoothing & Generation
The computed Steiner Tree is a set of connected edges on the mesh . However, its polyline nature often leads to non-smooth and sharp bending points at endpoints, hindering the wiring in real-world scenarios. Addressing this issue, we propose to iteratively smooth the computed Steiner tree with spline curves (e.g., circular arcs) on the 2D pattern model until its curvature satisfies: , where is the width of the wire strip on the garment. This ensures that the wires do not self-overlap locally. In our experiments, we observed that this requirement can be easily satisfied in a few iterations. Please see the supplementary materials for details of our iterative smoothing strategy.
4. Garment Fabrication
The fabric of the tight suit is made from 82% nylon and 18% polyester. The fabrication is assisted by a tailor with experiences of over 20 years. The strip is hot stamped onto the fabric, at the temperature of 160 Celsius with the heat-fusion press machine of Maike MK-TH40*60. The strip width is 1.5 cm.
5. Experimental Results
5.1. Implementation Details
Hardware & Software
We conducted experiments on a standard Windows PC with an Intel(R) Core(TM) i7-12700H (2.30 GHz) CPU. We implemented our algorithm using Python and developed a visualization interface with Unity3D. We will release all source code and datasets to the public upon acceptance.
Motion Dataset
We employed a standard human SMPL model to represent the human body mesh. To facilitate character rigging and animation, we utilized the automatic rigging function provided by the Mixamo website. Our dataset encompassed a total of 248 human action files, encompassing a diverse range of sports and dances (such as boxing, baseball, jazz dance, etc.). The combined duration of these action files amounted to 40,108 frames, equivalent to 1,336.9 seconds. These action files consist of either periodic actions with multiple cycles of actions or discrete actions with complete performances. Please see the supplementary materials for more details on the type and duration of motions.
Time Costs.
The time costs associated with our solution can be divided into three parts: i) Calculation of deformation energy. Given a set of motion sequences , we compute the deformation energy for each face of the human body mesh in every frame. This computation process requires approximately 2.62 seconds per frame. Please note that the time cost mentioned is solely dependent on the input motion and is independent of the wiring. As a result, it can be reused for multiple wiring designs. ii) Calculation of edge weights. As aforementioned, we calculate our deformation-inspired edge weights using Eq. 3. This part takes approximately 24 minutes for a mesh with 23,514 vertexes (46,912 faces and 70,430 edges). This preprocessing step only needs to be computed once per mesh per motion set and can be reused for different wiring layouts (i.e., low amortized cost). Same as above, this part is solely dependent on the input motion and can be reused for multiple wiring designs. iii) Construction of Steiner tree. Given the calculated edge weights and user-defined terminals, the Steiner Tree can be constructed in a short time, taking 1.80s for 36 terminals on a mesh with 23,514 vertexes.
5.2. Evaluation Baseline & Metrics
Baseline.
To demonstrate the effectiveness of our wiring solution, we compare it with a naive baseline, namely minimum length, which adheres to standard manufacturing requirements and aims to minimize the total wire length without taking motion resistance into consideration. Specifically, our baseline used a non-deformation-weighted version of the proposed solution (i.e., the original STP solution producing wiring layouts with minimum total lengths) to justify the effectiveness of our deformation weighting scheme (Sec. 3.3). That is, instead of using edge weights (Eq. 3), the baseline uses for all to compute a minimum-length solution.
Metrics.
Given that our work encompasses both simulation and real-world experiments, we utilize a set of three evaluation metrics. Two of these metrics are employed to assess the simulation results, while the third metric is utilized to evaluate real-world performance:
-
•
Maximum Wire Elongation Rate (for simulation). Given a set of motion sequences, this metric quantifies the maximal amount of elongation experienced by the wire relative to its original length. Please note that we focus solely on the elongation of the wire and disregard any shortening that may occur, as in the context of smart clothing, the wire does not shrink but rather rolls up or deforms along with the clothing.
-
•
Deformation Energy (for simulation). This metric can be viewed as an extension of the edge weights (as defined in Eq. 3) applied to the smoothed curves. In short, we extend the rectangles used in Eq. 3 to trapezoidals inscribed within the osculating circles of the spline curves (circular arcs). Please see the Supplementary Sec. 5 for more details.
-
•
Capacitance Value of Strain Sensor (for real-world scenarios). To verify the effectiveness of our method in real-world scenarios, we fabricated a strain sensing system, as a prototype of a one-piece tight suit along with 24 capacitive strain sensors (purchased from Elastech). The suit size fits a male of 175cm/75kg. These sensors were affixed to the tights with the hook-and-loop velcro structure, to capture the clothing deformation during motion. The change in capacitance values of the strain sensors exhibits a highly linear relationship (99.9%) and high resolution (0.05%) with respect to strain deformation (Liu et al., 2022). This makes it a reliable indicator of wire elongation in real-world scenarios. The sensor reading is wirelessly transmitted to a PC at a frequency of 50Hz, with a digitized value range [0, 1023].
5.3. Body-specific Wiring
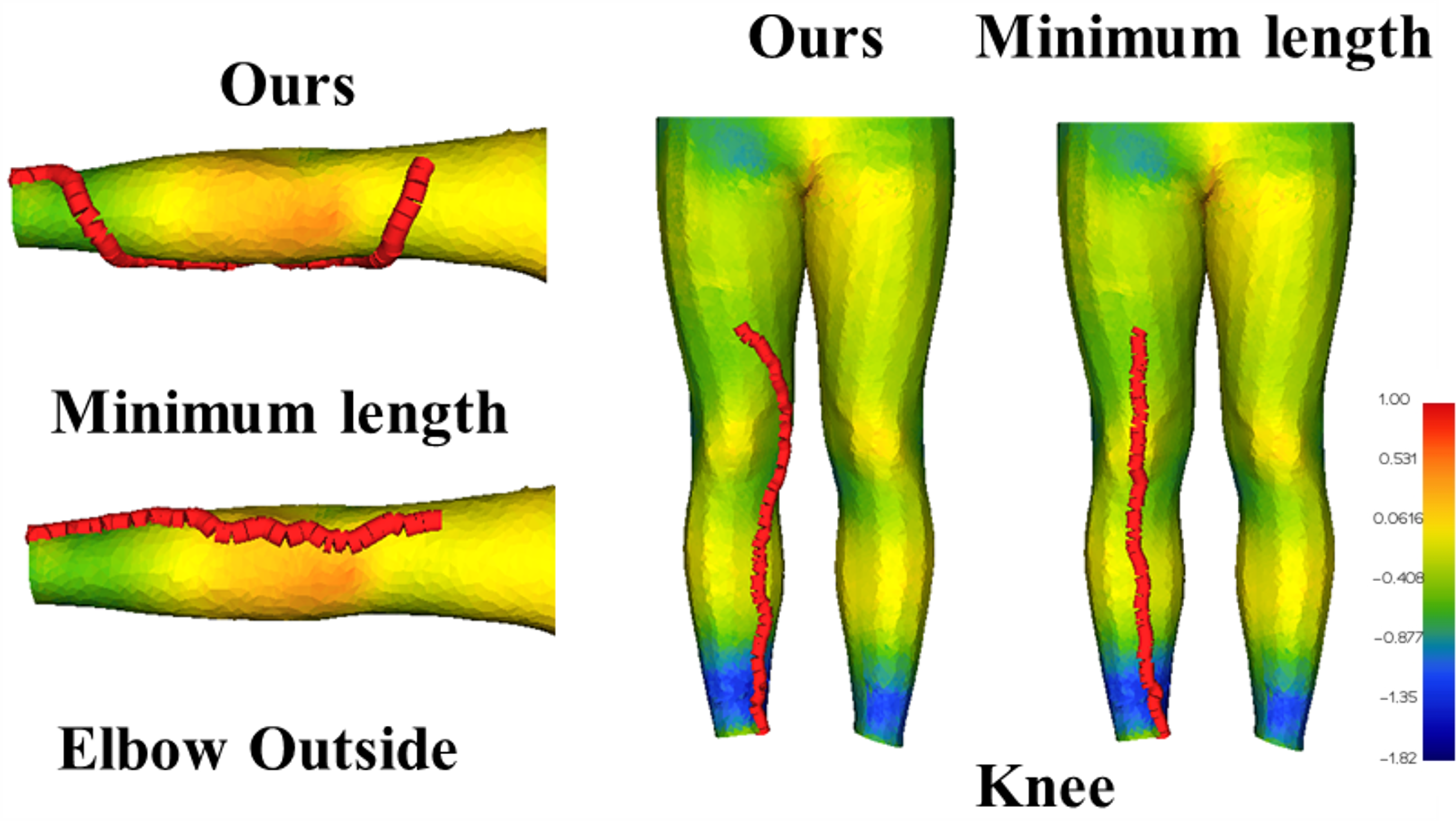
To validate the effectiveness of our method, we examine two scenarios involving a single joint (elbow and knee). We generate two layouts for each scenario: our method and the baseline (minimum length) specified in Sec. 5.2.
Simulation Experiment
As Fig. 3(a) shows, our solution adeptly avoids regions characterized by high deformation energy, which aligns perfectly with our prior knowledge that the elbow and knee joints exhibit the most significant stretching. Quantitatively, we compare the maximum wire elongation rates between our method and the minimum length baseline across a variety of elbow-driven (e.g., push up) and knee-driven (e.g., back squat) motion sequences, respectively. As Fig. 3(b) shows, our method consistently outperforms the baseline in all scenarios, showcasing significant improvements.
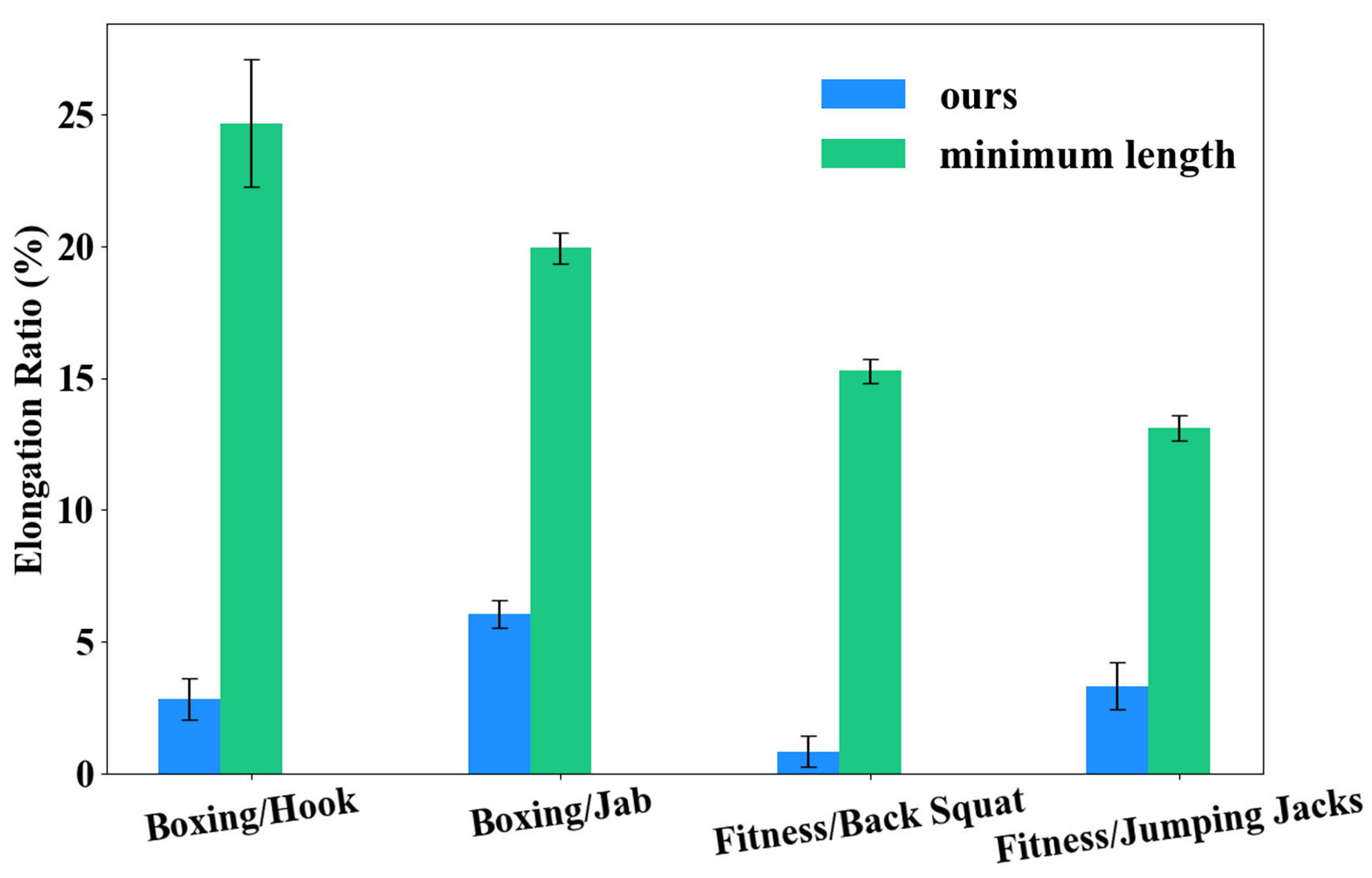
Real-world Experiment
A participant with the suitable body size tried on the strain sensing system (Fig. 4(a)), and conducted the aforementioned four motion sequences: hook, push-up, back squat and jumping jacks. Sensors were placed at the corresponding elbow and knee joints. As Fig. 4(b) shows, compared to the minimum length baseline, our method achieves a significantly lower change in the capacitance values of the strain sensors affixed to the fabricated tights. This observation further substantiates the effectiveness of our wiring solution in minimizing motion resistance.

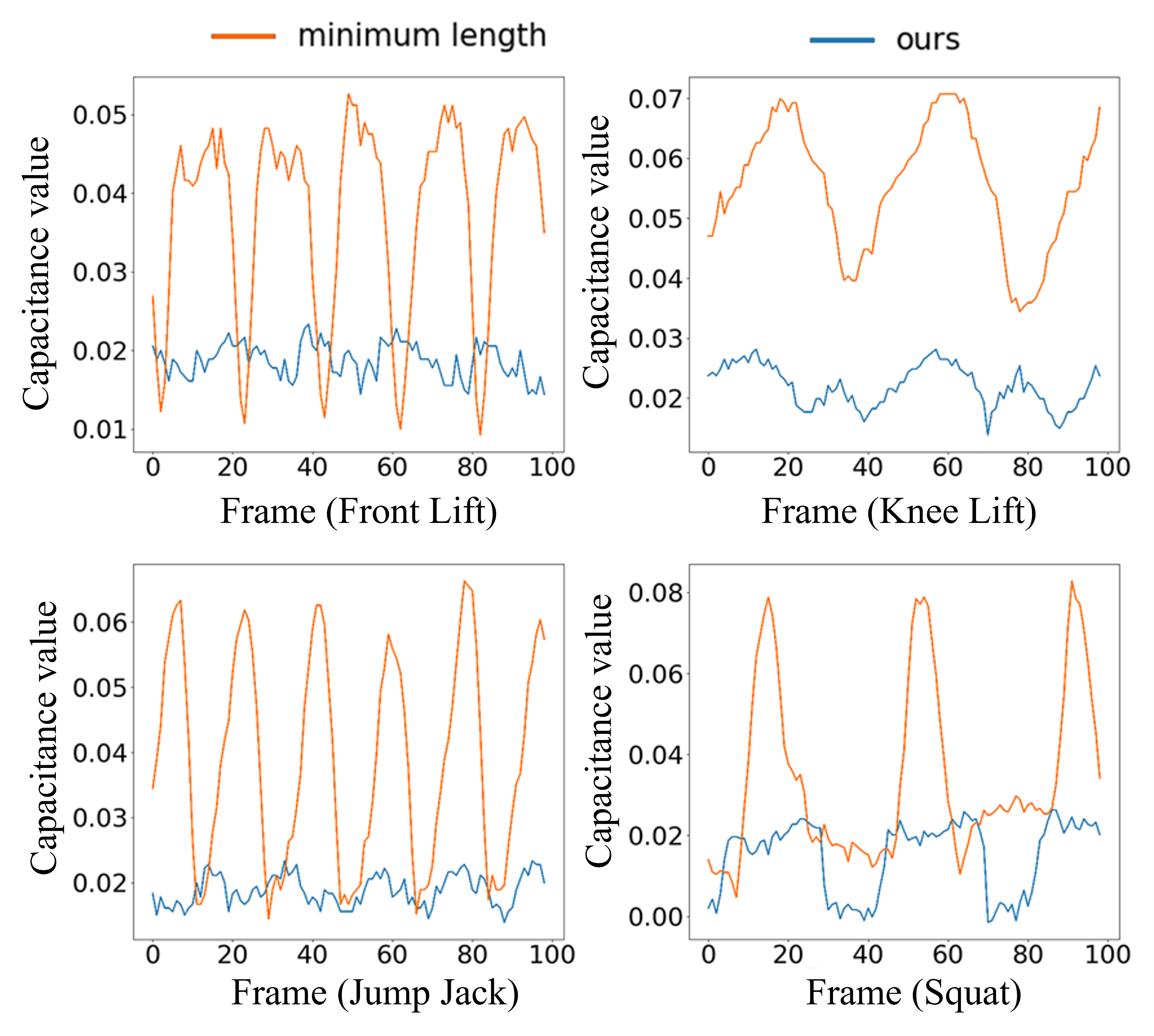
5.4. Motion-specific Wiring
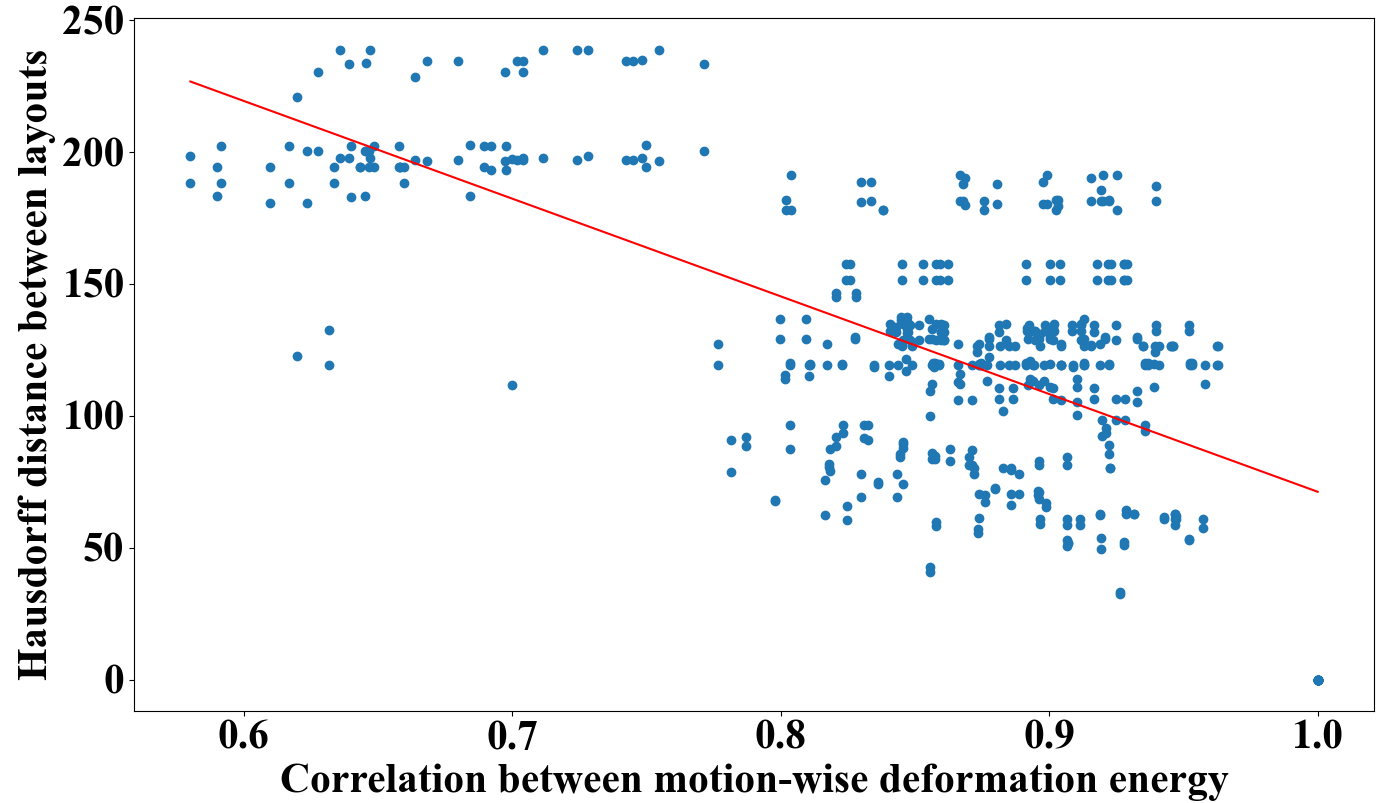
Specifically, we explore the correlation between similar motions and the resulting wiring layouts. We first calculated the deformation energy for each motion sequence, then the Pearson-correlation between motion-wise deformation energy. After obtaining the motion-wise layout, we calculated the Hausdorff distance on mesh between wire layouts. A linear regression between and (Fig. 5) reveals the correlation coefficient r = -0.66, indicating a negative correlation between the two, i.e., a similar energy distribution leads to a consistent layout. Fig. 7 visualizes a notable correlation between the similarity of the layouts and the similarity of the weight distribution. The aforementioned observations collectively unveil the correlation between motion and wiring layout, showcasing the robustness of our wiring solution.
5.5. Wiring and Electronics Configurations
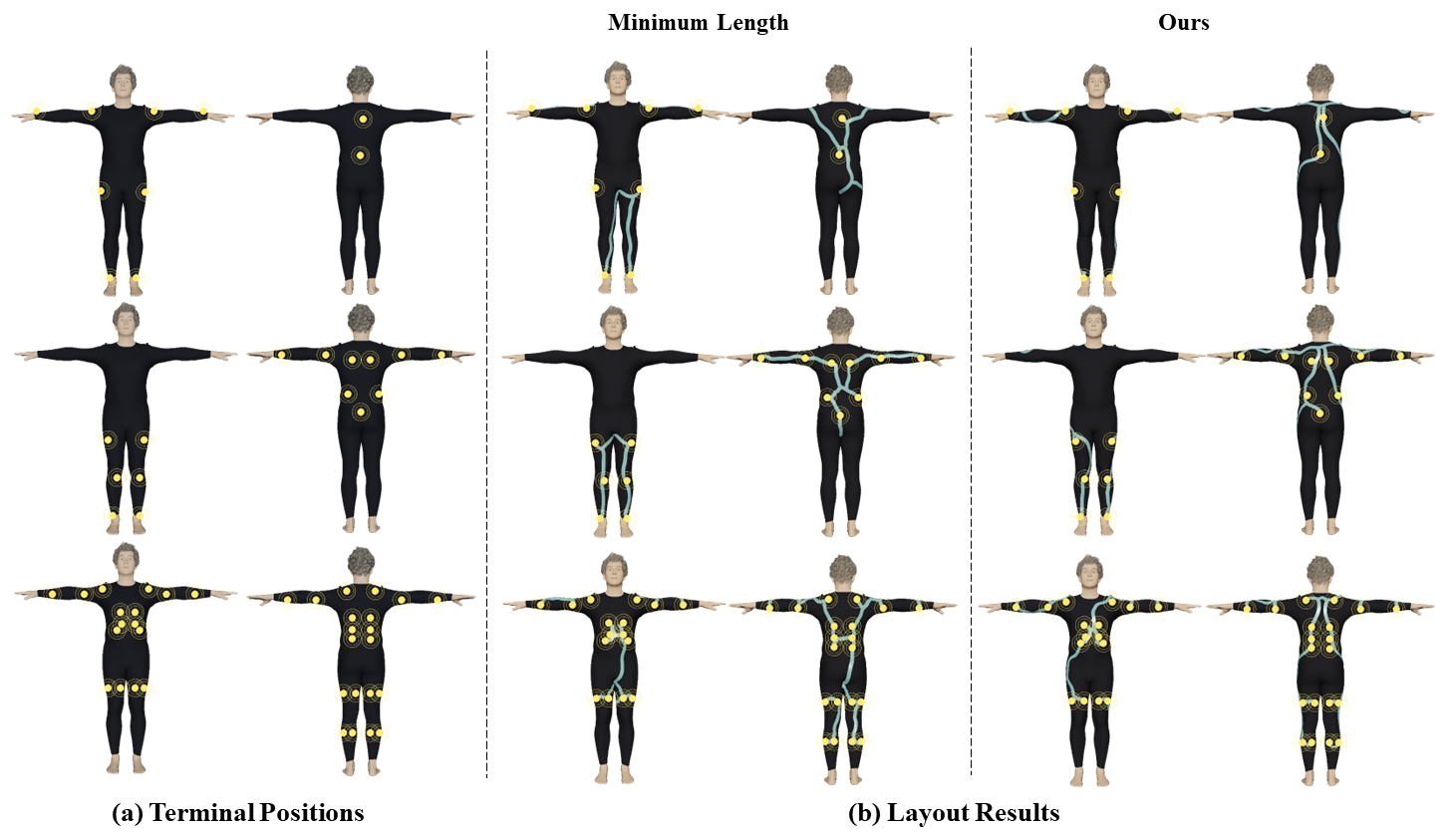
This section evaluates the performance of our wiring solution under three electronics configurations, considering the complete motion collection of 248 sequences. The placement of electronics was inspired by the corresponding commercial products: Xsens, Tesla Suit Motion Capture and Haptic Feedback (Fig. 8).
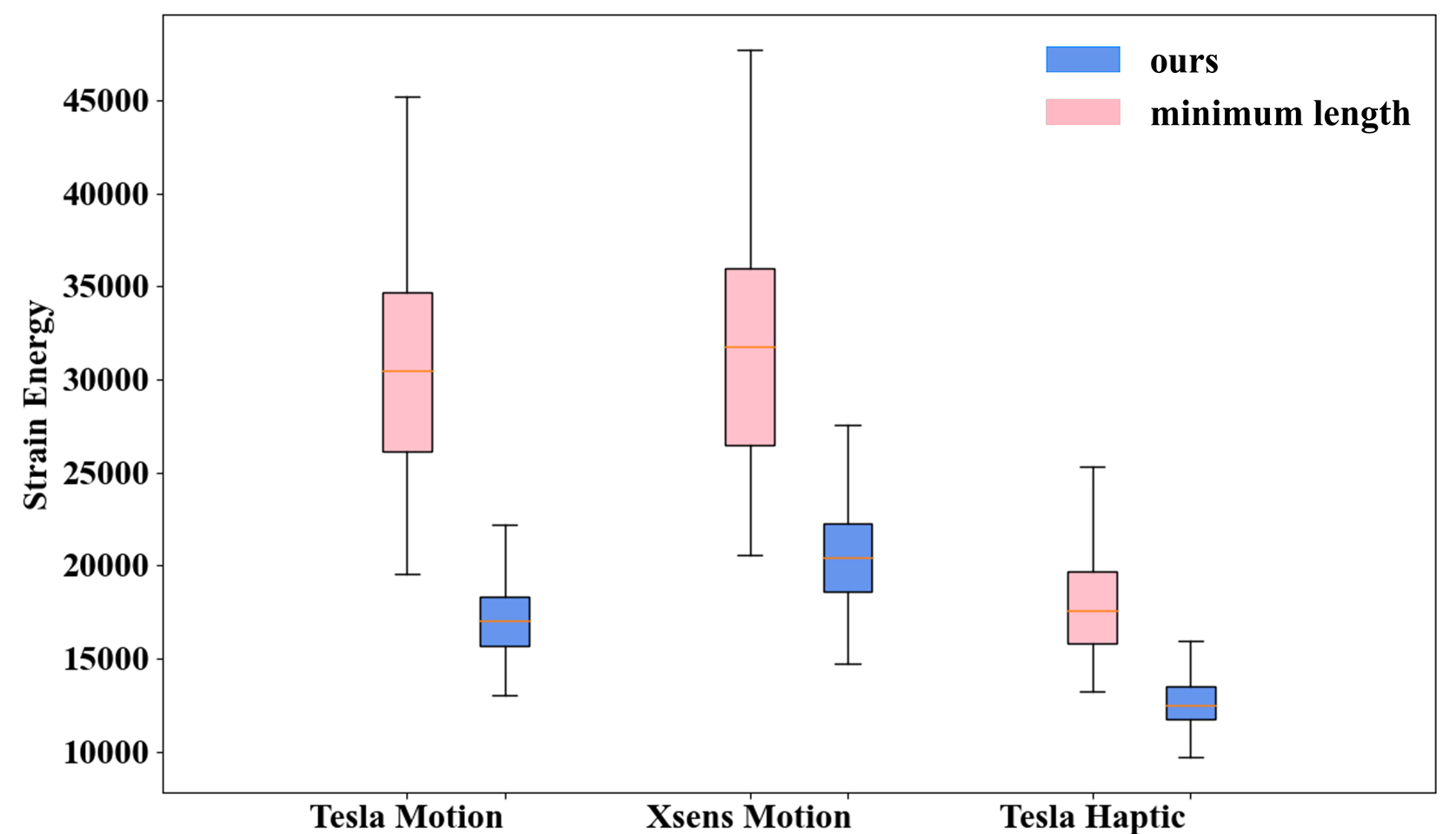
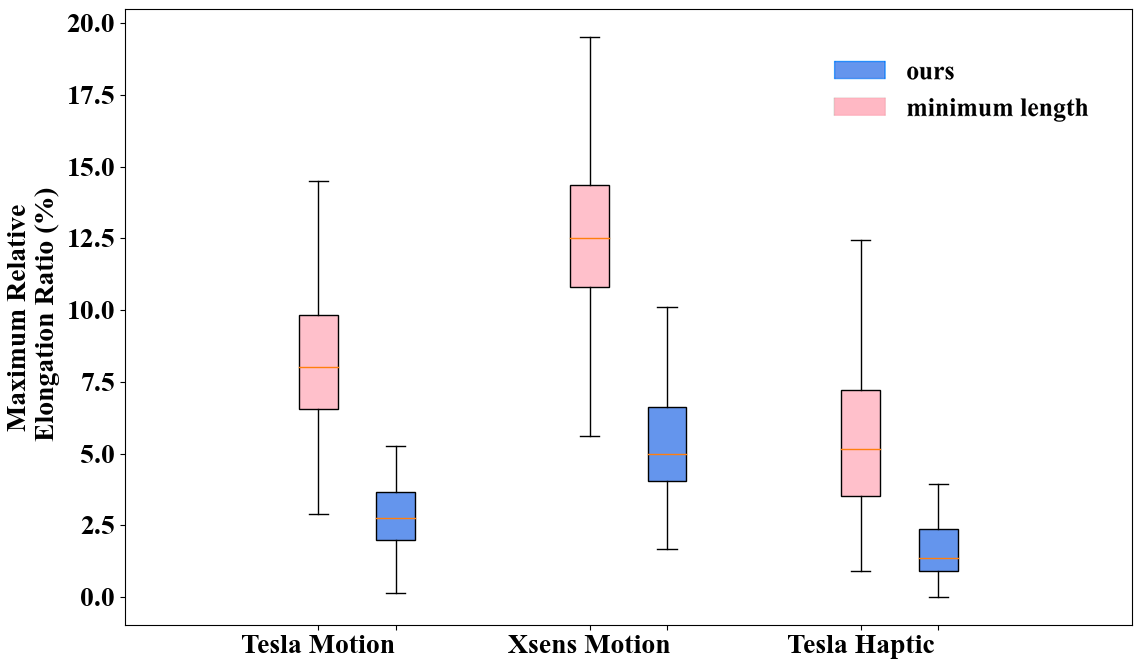
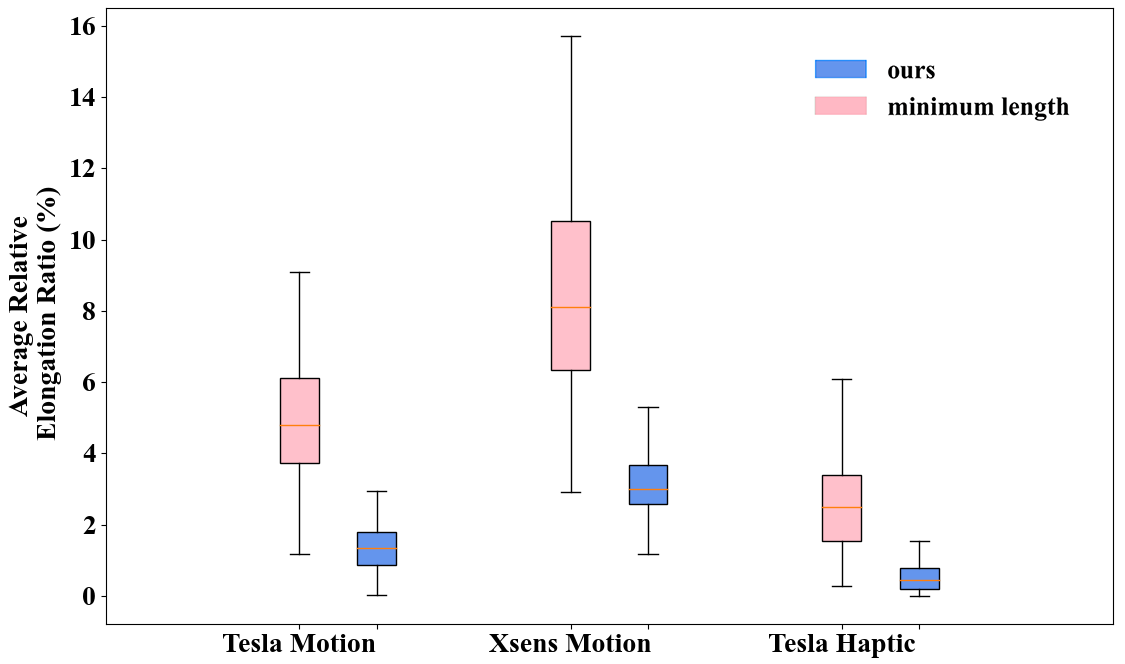
As shown in Fig. 9, i) our method proves effective in reducing wire strain on a Tesla suit, which features ten sensor locations covering every joint in the body. On average, our layout achieves a remarkable 43% reduction in energy sum, coupled with reductions of over 65% in both maximum and average stretch ratios (ave. 66.2% and 70.6%). ii) For the Xsens motion capture suit, our layout achieves an average 35% reduction in energy sum and over 55% reductions in maximum and average stretch ratios (ave. 55.7% and 61.9%). iii) As a more challenging case, the Tesla Haptic Feedback configuration deliberately avoids stretching areas to some extent by carefully positioning the sensors. Despite this configuration, our layout outperforms the minimum length baseline, resulting in a smaller stretch. Both the maximum and average stretching are reduced by over 65% (ave. 66.7% and 77.5%).
5.6. User Experiment, Evaluation & Feedback
We conducted two user experiments to evaluate both the design process and results: one with expert designers (simulation) and another with clothing wearers (real-world experiment using capacitive sensors). The experiment received ethical approval from the authors’ institution’s ethics committee. All participants were provided with information about the experiment’s purpose and procedure, and they signed an agreement prior to participation.
5.6.1. Design Experiment of Experts
Participants
Two experts in the field of smart clothing were invited to design the wiring layout. One expert is an industry designer with 23 years of experience, while the other expert is an associate professor and dean in the department of clothing and fashion design at a university. Both experts have more than 5 years of experience working with smart clothing, in commercial products and research prototypes respectively.
Procedure
We used the two commercial sensor configurations (Xsens, Tesla Suit Motion Capture) mentioned in the previous section as a reference. The experts were tasked with designing a wiring layout that aimed to minimize stretching and redundancy for the types of actions in our motion dataset, including dancing, boxing, golfing, football, and other sports (see Supplementary Sec. 4). Each design for the two reference configurations took approximately 3 days. We evaluated the performance of both the expert layout and our layout, and compared the differences in the layout through feedback obtained from user experiments. Following the experiment, the experts participated in a semi-structured interview to gather their subjective feedback.
Results & Findings
As Table 1 shows, in the simulation, our layout continues to outperform the expert layout in terms of reducing deformation energy and the maximum wire elongation rate. Moreover, our wiring algorithm is significantly faster than expert designs.
| Deformation Energy | Max Elongation Ratio (%) | Average Elongation Ratio (%) | |
|---|---|---|---|
| Expert | 25,404.92 | 6.39 | 3.92 |
| Ours | 20,753.09 | 5.63 | 3.22 |
| Min-Len | 31,986.91 | 12.72 | 8.45 |
During the interview, experts acknowledge that our layout effectively avoids significant areas of stretching and aligns with their design expertise. It is also worth noting that based on our pattern diagram, manufacturers can swiftly capture the necessary production information within the clothing pattern.
5.6.2. Try-on Experiment of Participants
Participants
We recruited a total of 10 participants for this experiment, comprising undergraduate and graduate students from our institution. The participants’ ages ranged from 21 to 35 years. Their height varied from 168 cm to 178 cm, and their weight ranged from 61 kg to 72 kg. All participants exhibited normal motor capability and reported no motor injuries within the past six months.
Procedure
We evaluated three layouts: minimum length (baseline), ours, and the expert layouts. Tight suits with these layouts were fabricated in the standard size (175cm, 75kg). The participants were unaware of the layout type during the evaluation. The order of try-ons was counterbalanced. We conducted tests involving routine movements and free play movements. Participants rated the resistance and comfort for each layout using a 5-point Likert scale questionnaire. After the experiment, participants were interviewed to gather their subjective feedback.
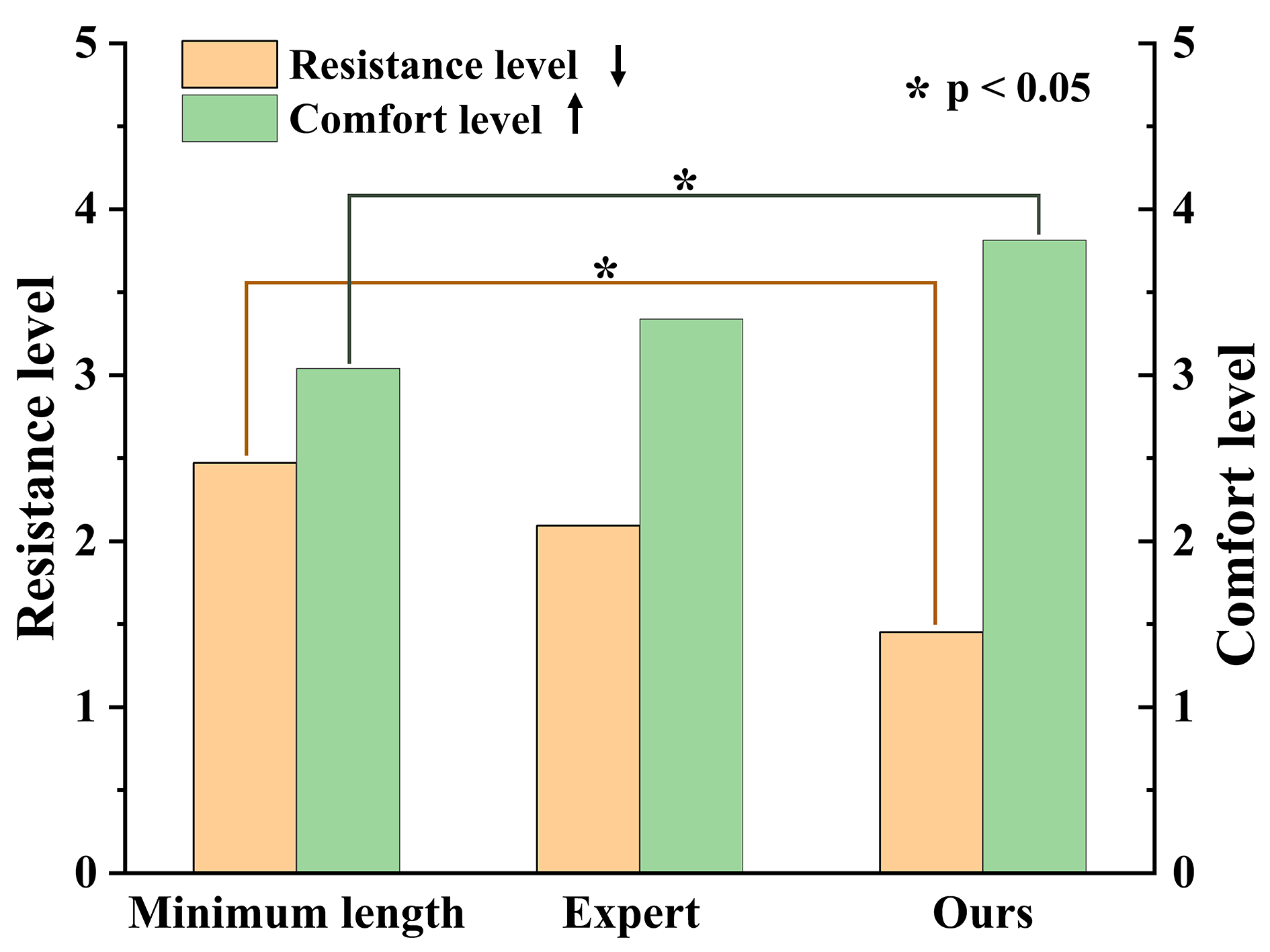
Results & Findings
The experimental results indicate that our layout performed slightly better than the expert layout and significantly better than the minimum length baseline in terms of user scoring (Fig. 6). One-way ANOVA analysis revealed a significant difference between our method and the minimum length baseline in terms of both resistance (p-value: 0.047, F-score: 4.559) and comfort (p-value: 0.026, F-score: 5.860) levels. Interestingly, there was no significant difference between our layout and the expert layout, although our layout exhibited a moderate numerical advantage over the expert layout.
5.7. Discussions
Impact of Body Shape
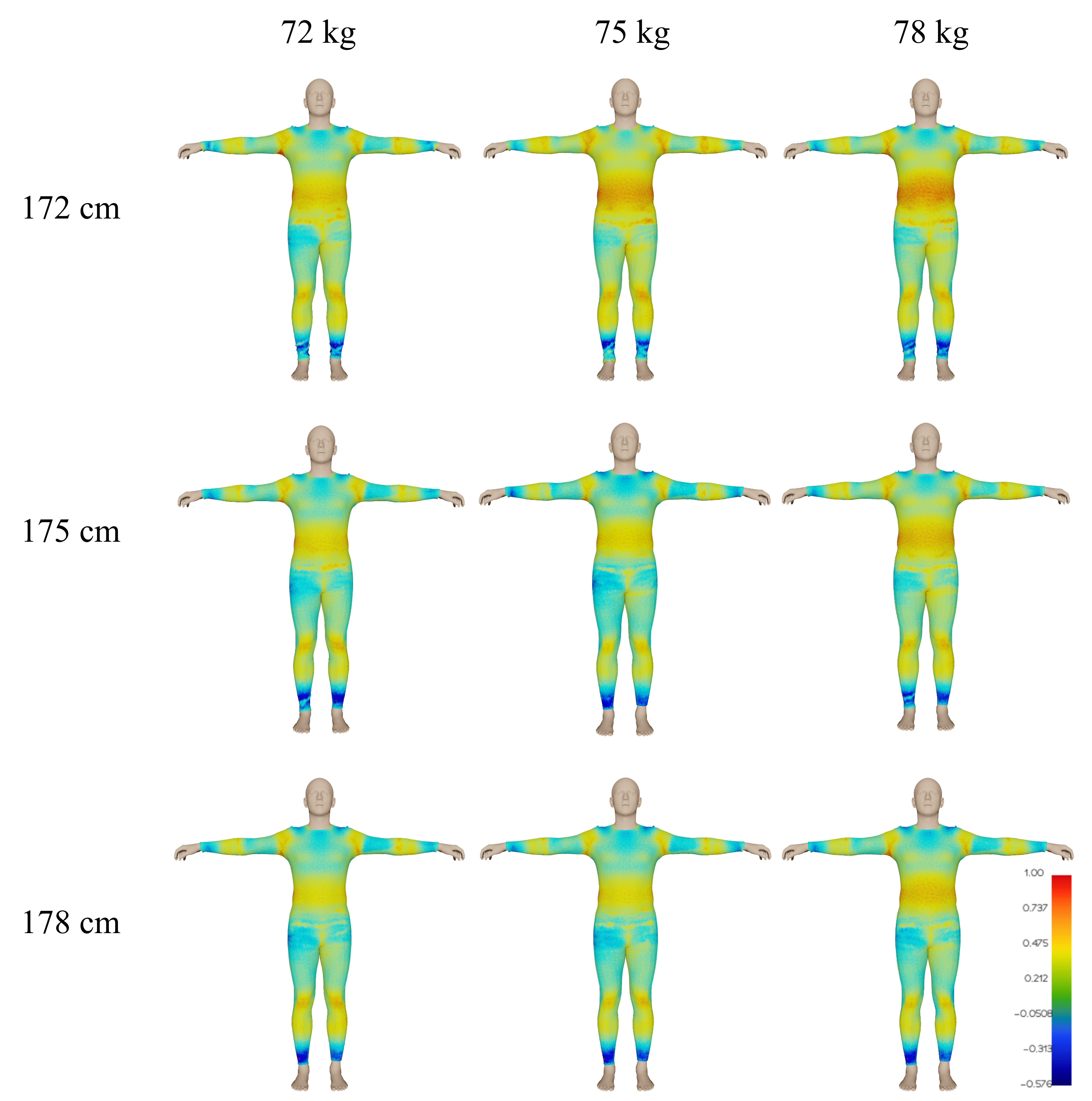
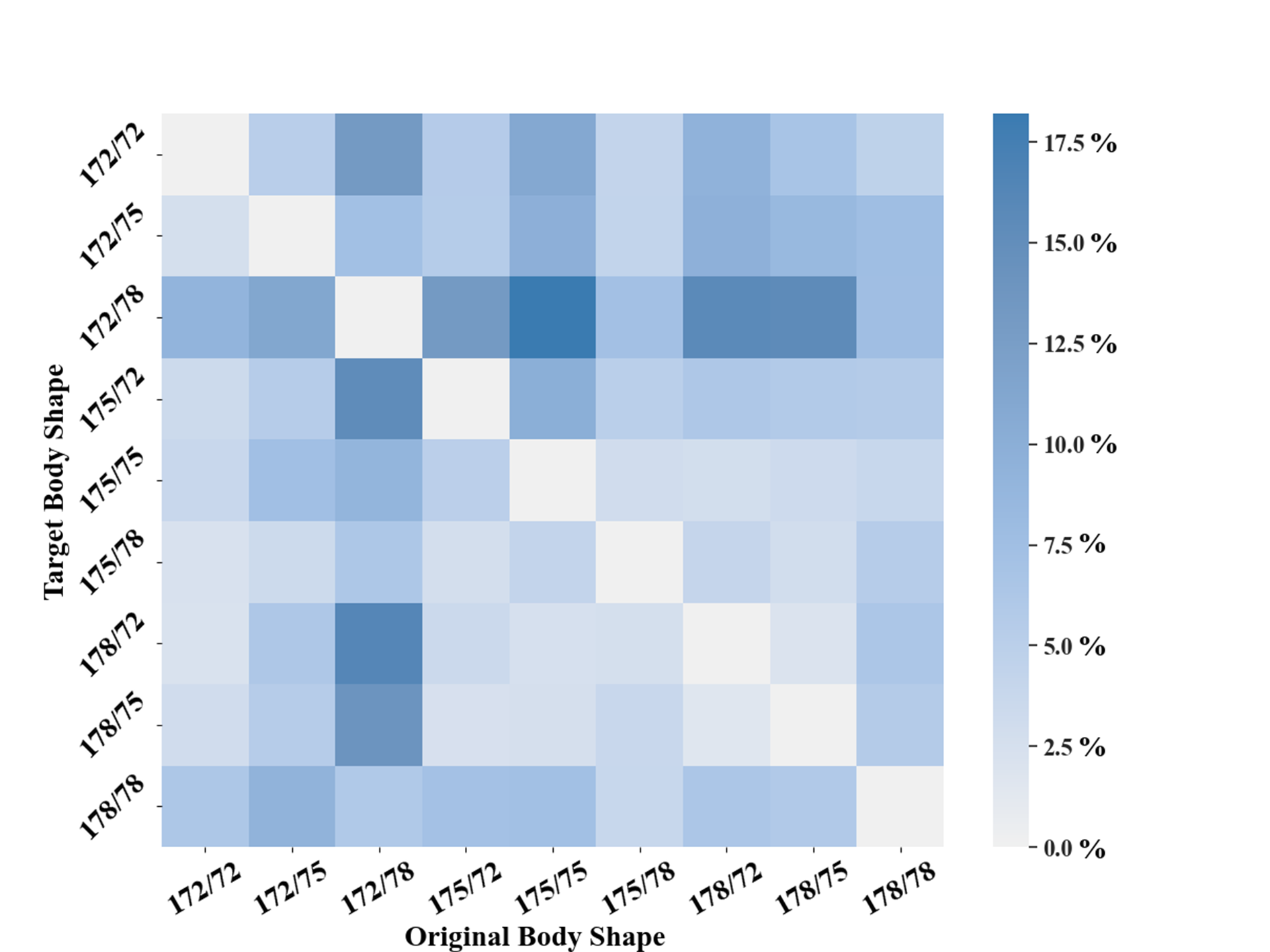
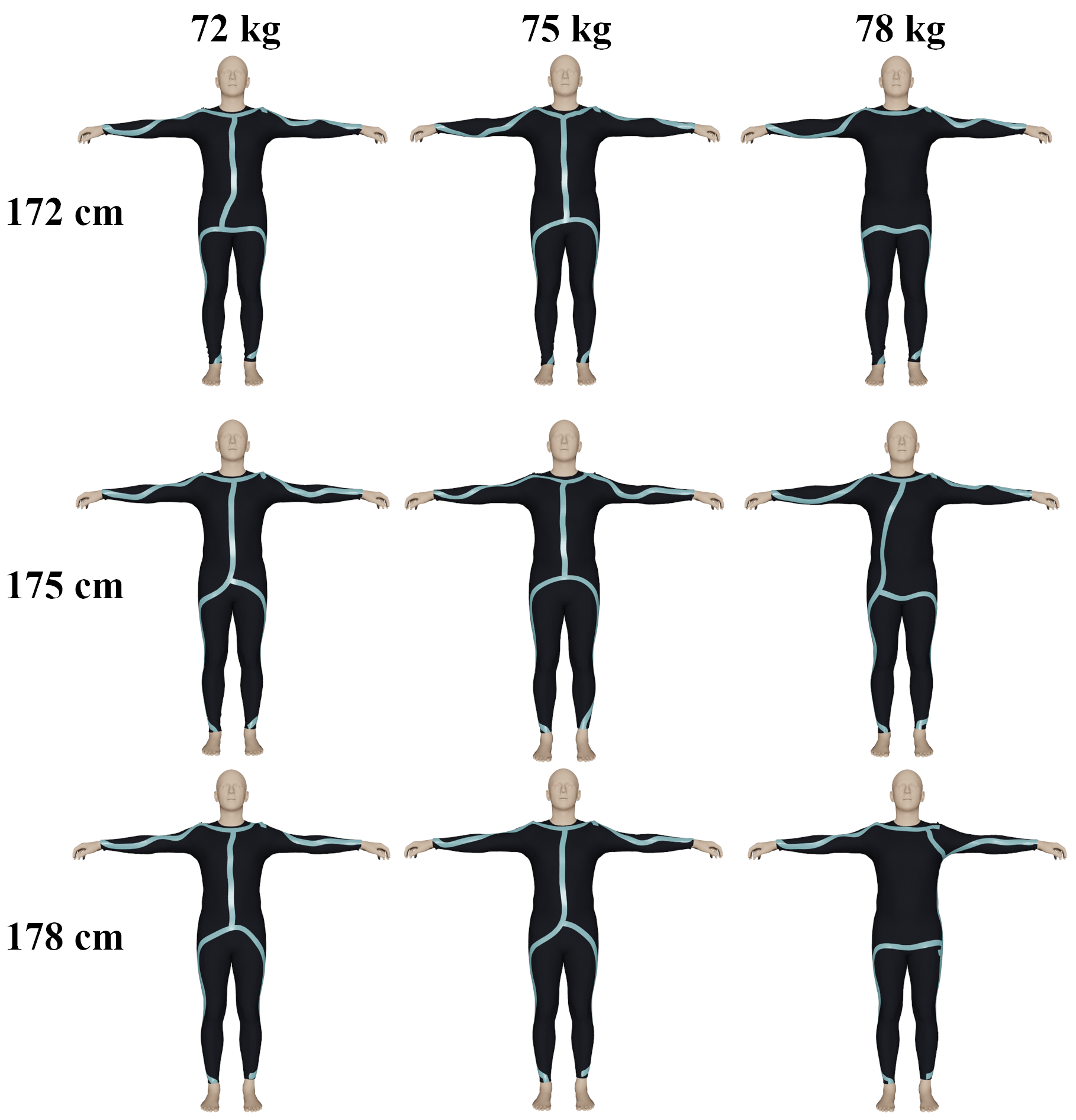
We conducted an analysis of the optimal layouts for similar but different body shapes performing the same action. Using the standard SMPL model, we generated eight body types (1753 cm, 753 kg) that closely resemble the standard body type (175 cm, 75 kg) (Fig. 10). The strain energy distribution exhibited similarities across these body types, with minor variations in magnitude. After generating the optimal layout for each body shape, we cross-validated the layouts on all body types and calculated the deformation energy values. The results depicted in Fig. 11 show that the differences between the calculated layouts for different body types were below 20% in terms of their deformation energy. Furthermore, the experimental results indicated that the optimal layouts for body weights below 75 kg exhibited significant similarity, while the layout for 78 kg body weight showed slight differences compared to other layouts (Fig. 12).
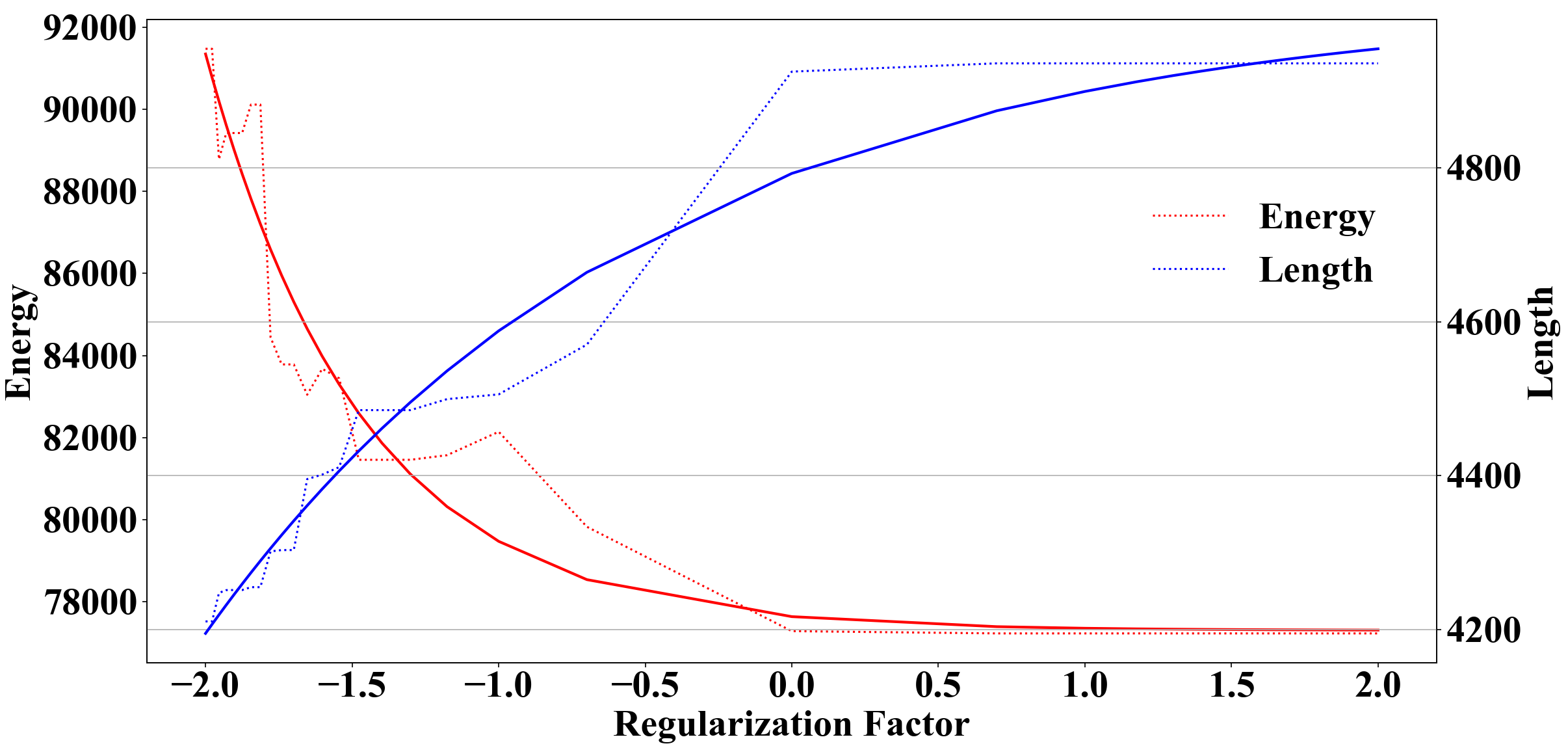
Impact of Regularization Factor
Impact of Mesh Resolution & Terminal Numbers
The precision and time cost of our wiring solution are influenced by two key factors: the number of terminals and the mesh resolution. As discussed in Sec. 3, the discretization of the surface can result in a slight loss of precision and affect the time required to solve the STP. In this experiment, we use the centers of the triangles to subdivide the mesh at different levels. While the mesh resolution has a minimal impact on the precision () when solving the STP problem with the same number of terminals (), it significantly affects the time performance, with differences of an order of magnitude (Table 2). With the current mesh resolution (e.g., =23,515 in our case), the time performance remains at an interactive rate, regardless of the variation in the number of terminals .
| Time (Weight) | ||||
|---|---|---|---|---|
| 10 | 15 | 36 | ||
| 23,515 | 0.43 (4,360.48 ) | 0.47 (4,067.24 ) | 1.80 (5,435.95 ) | |
| 164,251 | 4.152 (4,360.46 ) | 5.20 (4,067.23 ) | 20.34 (5,435.92 ) | |
| 727,195 | 23.43 (4,360.41 ) | 25.46 (4,067.18 ) | 109.05 (5,435.86 ) | |
Limitations & Future Work
Computer-aided clothing design is an emerging topic (Muthukumarana et al., 2021; Albaugh et al., 2019; Kaspar et al., 2019; McCann et al., 2016; Narayanan et al., 2018, 2019; Zhang et al., 2019; Wu et al., 2019), and our work extends to a more focused category: smart clothing. One potential area to improve our method is the discretization in our current solution, which involves solving the STP on a mesh as an approximation to that on a surface. As a result, the wiring layout is represented by a set of mesh edges rather than a smooth curve. A post-processing step can be applied to slightly refine the results. In our experiments, the difference in deformation energy before and after post-processing is 4.782.36%. Future work could aim to develop an integrated solution that combines wire layout optimization with curve generation, potentially achieving more accurate and refined results. Also, our algorithm decouples strain computation from wiring layout optimization. Although decoupling these steps provides computational advantages, it fails to account for how wiring layouts influence strain energy in the fabric. Future work could investigate coupling strain computations with wiring optimization to better capture wiring effects on strain and user comfort. Finally, our work focused on wire stretching, while other factors that affect wearing comfort or damage the wire (e.g., wire bending) will also be interesting for future work.
6. Conclusion
Our work addresses the challenge of automatic wiring on tight suits to minimize motion resistance for users. We formulate the wiring as a Steiner Tree Problem on the clothing mesh and propose an energy function to evaluate wire stretching. We fabricate the clothing based on the generated designs and conduct real-world experiments, collecting qualitative subject feedback and quantitative sensor measurements. The results demonstrate that our designs are effective in reducing wire strain energy by an average of 77% across 248 different actions.
Acknowledgement
This work is supported by National Natural Science Foundation of China (62072383), the Fundamental Research Funds for the Central Universities (20720210044). This work is partially supported by Royal Society (IEC\NSFC\211022). Xiaohu Guo was partially supported by National Science Foundation (OAC-2007661).
References
- (1)
- Agcayazi et al. (2018) Talha Agcayazi, Kony Chatterjee, Alper Bozkurt, and Tushar K Ghosh. 2018. Flexible interconnects for electronic textiles. Advanced Materials Technologies 3, 10 (2018), 1700277.
- Al Maimani and Roudaut (2017) Ahmed Al Maimani and Anne Roudaut. 2017. Frozen suit: designing a changeable stiffness suit and its application to haptic games. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems. 2440–2448.
- Albaugh et al. (2019) Lea Albaugh, Scott Hudson, and Lining Yao. 2019. Digital fabrication of soft actuated objects by machine knitting. In Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems. 1–13.
- Ancans et al. (2021) Armands Ancans, Modris Greitans, Ricards Cacurs, Beate Banga, and Artis Rozentals. 2021. Wearable sensor clothing for body movement measurement during physical activities in healthcare. Sensors 21, 6 (2021), 2068.
- Angelucci et al. (2021) Alessandra Angelucci, Matteo Cavicchioli, Ilaria A Cintorrino, Giuseppe Lauricella, Chiara Rossi, Sara Strati, and Andrea Aliverti. 2021. Smart textiles and sensorized garments for physiological monitoring: A review of available solutions and techniques. Sensors 21, 3 (2021), 814.
- Bodlaender et al. (2015) Hans L Bodlaender, Marek Cygan, Stefan Kratsch, and Jesper Nederlof. 2015. Deterministic single exponential time algorithms for connectivity problems parameterized by treewidth. Information and Computation 243 (2015), 86–111.
- Caffarelli et al. (2014) Elena A Caffarelli, Denise M Halverson, and Ryan J Jensen. 2014. The Steiner problem on surfaces of revolution. Graphs and Combinatorics 30 (2014), 315–342.
- Cai et al. (2019) Shaoyu Cai, Pingchuan Ke, Shanshan Jiang, Takuji Narumi, and Kening Zhu. 2019. Demonstration of thermairglove: A pneumatic glove for material perception in virtual reality through thermal and force feedback. In SIGGRAPH Asia 2019 Emerging Technologies. 11–12.
- Chen et al. (2023) Xiaowei Chen, Xiao Jiang, Jiawei Fang, Shihui Guo, Juncong Lin, Minghong Liao, Guoliang Luo, and Hongbo Fu. 2023. DisPad: Flexible On-Body Displacement of Fabric Sensors for Robust Joint-Motion Tracking. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 7, 1, Article 5 (2023), 27 pages.
- Chen et al. (2022) Xiaowei Chen, Xiao Jiang, Lishuang Zhan, Shihui Guo, Qunsheng Ruan, Guoliang Luo, Minghong Liao, and Yipeng Qin. 2022. Full-body human motion reconstruction with sparse joint tracking using flexible sensors. ACM Transactions on Multimedia Computing, Communications, and Applications (2022).
- Chen et al. (2021) Zhiyong Chen, Ronghui Wu, Shihui Guo, Xiangyang Liu, Hongbo Fu, Xiaogang Jin, and Minghong Liao. 2021. 3D upper body reconstruction with sparse soft sensors. Soft Robotics 8, 2 (2021), 226–239.
- Chimani et al. (2012) Markus Chimani, Petra Mutzel, and Bernd Zey. 2012. Improved Steiner tree algorithms for bounded treewidth. Journal of Discrete Algorithms 16 (2012), 67–78.
- Delazio et al. (2018) Alexandra Delazio, Ken Nakagaki, Roberta L Klatzky, Scott E Hudson, Jill Fain Lehman, and Alanson P Sample. 2018. Force jacket: Pneumatically-actuated jacket for embodied haptic experiences. In Proceedings of the 2018 CHI conference on human factors in computing systems. 1–12.
- Deng et al. (2016) Yiwen Deng, Tianlu Mao, Min Shi, and Zhaoqi Wang. 2016. Cloth deformation prediction based on human motion. In 2016 International Conference on Virtual Reality and Visualization (ICVRV). IEEE, 258–263.
- Designer (2022) Mavelous Designer. 2022. Homepage. https://marvelousdesigner.com/ [accessed: 01.05.2023].
- Dreyfus and Wagner (1971) Stuart E Dreyfus and Robert A Wagner. 1971. The Steiner problem in graphs. Networks 1, 3 (1971), 195–207.
- Fuchs et al. (2007) Bernhard Fuchs, Walter Kern, D Molle, Stefan Richter, Peter Rossmanith, and Xinhui Wang. 2007. Dynamic programming for minimum Steiner trees. Theory of Computing Systems 41 (2007), 493–500.
- Gholami et al. (2019) Mohsen Gholami, Ahmad Rezaei, Tyler J Cuthbert, Christopher Napier, and Carlo Menon. 2019. Lower body kinematics monitoring in running using fabric-based wearable sensors and deep convolutional neural networks. Sensors 19, 23 (2019), 5325.
- Gillies et al. (2007) Sean Gillies et al. 2007. Shapely: manipulation and analysis of geometric objects. https://github.com/Toblerity/Shapely
- Glauser et al. (2019) Oliver Glauser, Shihao Wu, Daniele Panozzo, Otmar Hilliges, and Olga Sorkine-Hornung. 2019. Interactive hand pose estimation using a stretch-sensing soft glove. ACM Transactions on Graphics (ToG) 38, 4 (2019), 1–15.
- Gröpl et al. (2001) Clemens Gröpl, Stefan Hougardy, Till Nierhoff, and Hans Jürgen Prömel. 2001. Approximation algorithms for the Steiner tree problem in graphs. Steiner trees in industry (2001), 235–279.
- Günther et al. (2019) Sebastian Günther, Mohit Makhija, Florian Müller, Dominik Schön, Max Mühlhäuser, and Markus Funk. 2019. PneumAct: Pneumatic kinesthetic actuation of body joints in virtual reality environments. In Proceedings of the 2019 on Designing Interactive Systems Conference. 227–240.
- Hougardy et al. (2017) Stefan Hougardy, Jannik Silvanus, and Jens Vygen. 2017. Dijkstra meets Steiner: a fast exact goal-oriented Steiner tree algorithm. Mathematical Programming Computation 9 (2017), 135–202.
- Hu et al. (2022) Xinrong Hu, Ziyi Zhang, Ruiqi Luo, Junjie Huang, Jinxing Liang, Jin Huang, Tao Peng, and Hao Cai. 2022. MMTrans: MultiModal Transformer for realistic video virtual try-on. In The 18th ACM SIGGRAPH International Conference on Virtual-Reality Continuum and its Applications in Industry. 1–8.
- Iwata and Shigemura (2019) Yoichi Iwata and Takuto Shigemura. 2019. Separator-based pruned dynamic programming for steiner tree. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33. 1520–1527.
- Kaspar et al. (2019) Alexandre Kaspar, Liane Makatura, and Wojciech Matusik. 2019. Knitting skeletons: A computer-aided design tool for shaping and patterning of knitted garments. In proceedings of the 32nd annual ACM symposium on user interface software and technology. 53–65.
- Kim et al. (2019) Jinsoo Kim, Giuk Lee, Roman Heimgartner, Dheepak Arumukhom Revi, Nikos Karavas, Danielle Nathanson, Ignacio Galiana, Asa Eckert-Erdheim, Patrick Murphy, David Perry, et al. 2019. Reducing the metabolic rate of walking and running with a versatile, portable exosuit. Science 365, 6454 (2019), 668–672.
- Kwok et al. (2015) Tsz-Ho Kwok, Yan-Qiu Zhang, Charlie CL Wang, Yong-Jin Liu, and Kai Tang. 2015. Styling evolution for tight-fitting garments. IEEE transactions on visualization and computer graphics 22, 5 (2015), 1580–1591.
- Lee et al. (2015) Jaehong Lee, Hyukho Kwon, Jungmok Seo, Sera Shin, Ja Hoon Koo, Changhyun Pang, Seungbae Son, Jae Hyung Kim, Yong Hoon Jang, Dae Eun Kim, et al. 2015. Conductive fiber-based ultrasensitive textile pressure sensor for wearable electronics. Advanced materials 27, 15 (2015), 2433–2439.
- Lee et al. (2018) Sangjun Lee, Nikos Karavas, Brenna T Quinlivan, Danielle LouiseRyan, David Perry, Asa Eckert-Erdheim, Patrick Murphy, Taylor Greenberg Goldy, Nicolas Menard, Maria Athanassiu, et al. 2018. Autonomous multi-joint soft exosuit for assistance with walking overground. In 2018 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2812–2819.
- Levin (1971) Anatoly Yur’evich Levin. 1971. Algorithm for the shortest connection of a group of graph vertices. In Doklady Akademii Nauk, Vol. 200. Russian Academy of Sciences, 773–776.
- Li and Lu (2011) Jituo Li and Guodong Lu. 2011. Customizing 3D garments based on volumetric deformation. Computers in Industry 62, 7 (2011), 693–707.
- Liu et al. (2019) Ruibo Liu, Qijia Shao, Siqi Wang, Christina Ru, Devin Balkcom, and Xia Zhou. 2019. Reconstructing human joint motion with computational fabrics. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies 3, 1 (2019), 1–26.
- Liu (2018) Tiantian Liu. 2018. Towards real-time simulation of hyperelastic materials. PhD dissertation. University of Pennsylvania.
- Liu et al. (2022) Yiwei Liu, Jincai Li, and Kepeng Wu. 2022. The invention relates to a capacitive elastic strain sensor with high safety and high detection range and a preparation method, Patented on 2022-09-20, CN113670187A, Invention Patent (China).
- Liu et al. (2021) Zishun Liu, Xingjian Han, Yuchen Zhang, Xiangjia Chen, Yu-Kun Lai, Eugeni L Doubrovski, Emily Whiting, and Charlie CL Wang. 2021. Knitting 4D garments with elasticity controlled for body motion. ACM Transactions on Graphics (TOG) 40, 4 (2021), 1–16.
- Ljubić (2021) Ivana Ljubić. 2021. Solving Steiner trees: Recent advances, challenges, and perspectives. Networks 77, 2 (2021), 177–204.
- Lopes and Baudisch (2017) Pedro Lopes and Patrick Baudisch. 2017. Interactive systems based on electrical muscle stimulation. In ACM SIGGRAPH 2017 Studio. 1–2.
- McCann et al. (2016) James McCann, Lea Albaugh, Vidya Narayanan, April Grow, Wojciech Matusik, Jennifer Mankoff, and Jessica Hodgins. 2016. A compiler for 3D machine knitting. ACM Transactions on Graphics (TOG) 35, 4 (2016), 1–11.
- Montes et al. (2020) Juan Montes, Bernhard Thomaszewski, Sudhir Mudur, and Tiberiu Popa. 2020. Computational design of skintight clothing. ACM Transactions on Graphics (TOG) 39, 4 (2020), 105–1.
- Muthukumarana et al. (2021) Sachith Muthukumarana, Moritz Alexander Messerschmidt, Denys JC Matthies, Jürgen Steimle, Philipp M Scholl, and Suranga Nanayakkara. 2021. Clothtiles: A prototyping platform to fabricate customized actuators on clothing using 3d printing and shape-memory alloys. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems. 1–12.
- Narayanan et al. (2018) Vidya Narayanan, Lea Albaugh, Jessica Hodgins, Stelian Coros, and James Mccann. 2018. Automatic machine knitting of 3D meshes. ACM Transactions on Graphics (TOG) 37, 3 (2018), 1–15.
- Narayanan et al. (2019) Vidya Narayanan, Kui Wu, Cem Yuksel, and James McCann. 2019. Visual knitting machine programming. ACM Transactions on Graphics (TOG) 38, 4 (2019), 1–13.
- Nederlof (2009) Jesper Nederlof. 2009. Fast polynomial-space algorithms using möbius inversion: Improving on steiner tree and related problems. In Automata, Languages and Programming: 36th International Colloquium, ICALP 2009, Rhodes, Greece, July 5-12, 2009, Proceedings, Part I 36. Springer, 713–725.
- Pan et al. (2022) Xiaoyu Pan, Jiaming Mai, Xinwei Jiang, Dongxue Tang, Jingxiang Li, Tianjia Shao, Kun Zhou, Xiaogang Jin, and Dinesh Manocha. 2022. Predicting loose-fitting garment deformations using bone-driven motion networks. In ACM SIGGRAPH 2022 Conference Proceedings. 1–10.
- Pavlakos et al. (2019) Georgios Pavlakos, Vasileios Choutas, Nima Ghorbani, Timo Bolkart, Ahmed AA Osman, Dimitrios Tzionas, and Michael J Black. 2019. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 10975–10985.
- Pietroni et al. (2022) Nico Pietroni, Corentin Dumery, Raphael Falque, Mark Liu, Teresa Vidal-Calleja, and Olga Sorkine-Hornung. 2022. Computational pattern making from 3D garment models. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1–14.
- Pointner et al. (2020) Andreas Pointner, Thomas Preindl, Sara Mlakar, Roland Aigner, and Michael Haller. 2020. Knitted resi: A highly flexible, force-sensitive knitted textile based on resistive yarns. In ACM SIGGRAPH 2020 Emerging Technologies. 1–2.
- Ramachandran et al. (2021) Vivek Ramachandran, Fabian Schilling, Amy R Wu, and Dario Floreano. 2021. Smart Textiles that Teach: Fabric-Based Haptic Device Improves the Rate of Motor Learning. Advanced Intelligent Systems 3, 11 (2021), 2100043.
- Robins and Zelikovsky (2005) Gabriel Robins and Alexander Zelikovsky. 2005. Tighter bounds for graph Steiner tree approximation. SIAM Journal on Discrete Mathematics 19, 1 (2005), 122–134.
- Rognon et al. (2018) Carine Rognon, Stefano Mintchev, Fabio Dell’Agnola, Alexandre Cherpillod, David Atienza, and Dario Floreano. 2018. Flyjacket: An upper body soft exoskeleton for immersive drone control. IEEE Robotics and Automation Letters 3, 3 (2018), 2362–2369.
- Ruckdashel et al. (2022) Rebecca R Ruckdashel, Ninad Khadse, and Jay Hoon Park. 2022. Smart E-Textiles: Overview of Components and Outlook. Sensors 22, 16 (2022), 6055.
- Sati et al. (2021) Abhinit Sati, Ioannis Karamouzas, and Victor Zordan. 2021. DIGISEW: Anisotropic Stitching for Variable Stretch in Textiles. In Proceedings of the 6th Annual ACM Symposium on Computational Fabrication. 1–10.
- Shi et al. (2021) Guangyuan Shi, Chengying Gao, Dong Wang, and Zhuo Su. 2021. Automatic 3D virtual fitting system based on skeleton driving. The Visual Computer 37 (2021), 1075–1088.
- Stanley et al. (2022) Jessica Stanley, John A Hunt, Phil Kunovski, and Yang Wei. 2022. A review of connectors and joining technologies for electronic textiles. Engineering Reports 4, 6 (2022), e12491.
- Teslasuit (2022) VR Electronics Ltd Teslasuit. 2022. Tesla Suit 4. https://teslasuit.io/products/teslasuit-4/ [accessed: 01.05.2023].
- Vechev et al. (2022) Velko Vechev, Ronan Hinchet, Stelian Coros, Bernhard Thomaszewski, and Otmar Hilliges. 2022. Computational Design of Active Kinesthetic Garments. In Proceedings of the 35th Annual ACM Symposium on User Interface Software and Technology. 1–11.
- Vervust et al. (2012) Thomas Vervust, Guy Buyle, Frederick Bossuyt, and Jan Vanfleteren. 2012. Integration of stretchable and washable electronic modules for smart textile applications. Journal of The Textile Institute 103, 10 (2012), 1127–1138.
- Vygen (2011) Jens Vygen. 2011. Faster algorithm for optimum Steiner trees. Inform. Process. Lett. 111, 21-22 (2011), 1075–1079.
- Wang et al. (2015) Q. Wang, W. Chen, A.A.A. Timmermans, C. Karachristos, J.B. Martens, and P. Markopoulos. 2015. Smart Rehabilitation Garment for posture monitoring. In 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 5736–5739.
- Wolff et al. (2022) Katja Wolff, Philipp Herholz, Verena Ziegler, Frauke Link, Nico Brügel, and Olga Sorkine-Hornung. 2022. Designing Personalized Garments with Body Movement. In Computer Graphics Forum. Wiley Online Library.
- Wu et al. (2022) Botao Wu, Zhendong Wang, and Huamin Wang. 2022. A GPU-based multilevel additive schwarz preconditioner for cloth and deformable body simulation. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1–14.
- Wu et al. (2019) Kui Wu, Hannah Swan, and Cem Yuksel. 2019. Knittable stitch meshes. ACM Transactions on Graphics (TOG) 38, 1 (2019), 1–13.
- Yokus et al. (2016) Murat A Yokus, Rachel Foote, and Jesse S Jur. 2016. Printed stretchable interconnects for smart garments: design, fabrication, and characterization. IEEE Sensors Journal 16, 22 (2016), 7967–7976.
- Zhang et al. (2020) Hechuan Zhang, Zhiyong Chen, Shihui Guo, Juncong Lin, Yating Shi, Xiangyang Liu, and Yong Ma. 2020. Sensock: 3D foot reconstruction with flexible sensors. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems. 1–13.
- Zhang et al. (2019) Xiaoting Zhang, Guoxin Fang, Mélina Skouras, Gwenda Gieseler, Charlie CL Wang, and Emily Whiting. 2019. Computational design of fabric formwork. ACM Transactions on Graphics 38, 4 (2019), 1–13.