Computational universality of fungal sandpile automata
Abstract
Hyphae within the mycelia of the ascomycetous fungi are compartmentalised by septa. Each septum has a pore that allows for inter-compartmental and inter-hyphal streaming of cytosol and even organelles. The compartments, however, have special organelles, Woronin bodies, that can plug the pores. When the pores are blocked, no flow of cytoplasm takes place. Inspired by the controllable compartmentalisation within the mycelium of the ascomycetous fungi we designed two-dimensional fungal automata. A fungal automaton is a cellular automaton where communication between neighbouring cells can be blocked on demand. We demonstrate computational universality of the fungal automata by implementing sandpile cellular automata circuits there. We reduce the Monotone Circuit Value Problem to the Fungal Automaton Prediction Problem. We construct families of wires, cross-overs and gates to prove that the fungal automata are P-complete.
keywords:
fungi, sandpile automata, computational universality1 Introduction
Fungi are ubiquitous organisms that are present in all ecological niches. They can grow as single cells but can also form mycelium networks covering up to 10 km2 of forest soil [43, 14]. Fungi can sense what humans sense and more, including tactile stimulation [26, 29], pH [50], metals [15], chemicals [24], light [40] and gravity [36]. Fungi exhibit a rich spectrum of electrical activity patterns [42, 39, 1], which can be tuned by external stimulation. On studying electrical responses of fungi to stimulation [1] we proposed design and experimental implementation of fungal computers [2]. Further numerical experiments demonstrated that it is possible to compute Boolean functions with spikes of electrical activity propagating on mycelium networks [4]. At this early stage of developing a fungal computer architecture we need to establish a strong formal background reflecting several alternative ways of computing with fungi.
In [3] we introduced one-dimensional fungal automata, based on a composition of two elementary cellular automaton functions. We studied the automata space-time complexity and discovered a range of local events essential for a future computing device on a single hypha. In present paper we aim to demonstrate a computational universality of fungal automata. To do this we modify state transition rules of sand pile, or chip firing, automata [11, 18, 10, 5, 17] to allow a control for moving of sand grains, or chips, between neighbouring cells. The local control of the interactions between cells is inspired by a control of cytosol flow control in fungal hyphae [37, 30, 7, 6, 46]. Then we used developed tools of sand pile automata universality [19, 21, 9, 34, 16, 33] to show that functionally complete sets of Boolean gates can be realised in in the fungal automata.
The paper is structured as follows. We define two dimensional fungal automata in Sect. 2. We represent the fungal automata as sand pile, or chip firing, automata in Sect. 3. Section 4 places fungal automata in the context of computational complexity. The P-completeness of the fungal automata is demonstrated via implementation of Boolean circuits in Sect. 5. Alternative versions of the Woronin body states updates are presented in Sect. 6. Future developments and feasibility of practical implementation are discussed in Sect. 7.
2 Two dimensional Fungal Automata
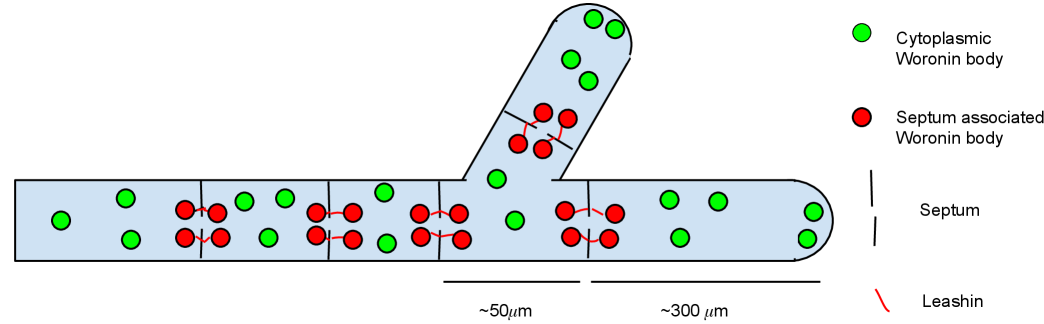




Filamentous fungi of the phylum Ascomycota have porous septa that allow for cytoplasmic streaming throughout hyphae and the mycelium [37, 30]. The pores of damaged hyphae will be plugged by a peroxisome-derived organelle to prevent bleeding of cytoplasm into the environment [48, 41, 49, 28]. These Woronin bodies can also plug septa of intact hyphae [7, 45]. The septal pore occlusion in these hyphae can be triggered by septal ageing and stress conditions [7, 8, 46].
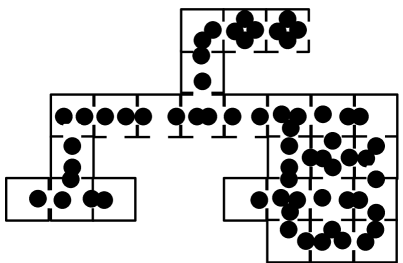
A scheme of the mycelium with Woronin bodies is shown in Fig. 1. An apical compartment has one neighbouring sub-apical compartment, while a sub-apical compartment has a neighbouring compartment at both ends. Because compartments can also branch, they can have one or more additional neighbouring compartments. Thus, the compartment with pores and Woronin bodies is a elementary unit of fungal automata (Fig. 1bcd). From these compartments one can assemble quasi-one-dimensional (Fig. 1e) and two-dimensional (Fig. 1f) structures.
In this context, let us consider a cellular automaton in the two dimensional grid with the von Neumann neighbourhood, with set of states and a global function . Each cell of the grid has four sides that could be open or closed. An open side means that the information (the state) of both cells is shared. If not, when the side is closed, both sites mutually ignore each other. When every side is open we have the usual cellular automata model [51]. On the other hand, if sides are open or closed in some random or periodical way we get for the same local functions different dynamic behaviours. In this paper we will consider only “uniform” ways to open-close the sides. Actually at a given step to open every vertical side (every column of the grid) or every horizontal side, rows of the array. So the fungal automata model becomes a tuple , where is the von Neumann neighbourhood, is a finite word on the alphabet (horizontal, vertical). Each iteration of automaton evolution is associated with one letter of .
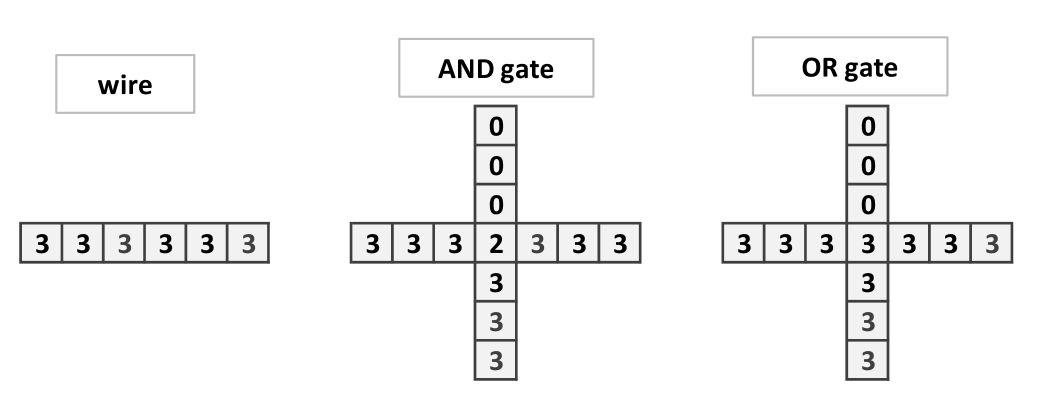
In this work we focus on “particles” rules. That is to say at each site there are a finite amount of particles or chips, that, according to a specific rule are disseminated in the vicinity of a site. Every step is going synchronously, so each site lose and receive chips simultaneously. In this context the set of states is , the number of particles.
3 The chip firing automata
The chip firing automaton, also know as the sandpile model [20, 22, 35], is a particular case of the above described particle automata , with the following local function. If a site has chips then:
| (1) |
where is the von Neumann neihborhood of the site .
By adding the condition of open or close sides of the site proposed here; the rule changes as follows:
| (2) |
where is the number of gates that are open.
When the rule is applied in parallel on every site, the new state at a site is:
where is the number of chips which the site receives from its open and firing neighbours.
If every side (columns and rows) is always open, then we have the usual chip firing automaton. When a word of open or close sides is considered, for instance , at each step we open (or close) the rows or columns of the grid periodically
| (3) |
4 Computational Complexity notions
In order to study the complexity of an automaton we can analyse a power of the automaton to simulate Boolean functions, i.e., by selecting specific initial conditions and sites as inputs and outputs to determine the different Boolean functions the automaton may compute by its dynamics [23]. More Boolean functions are founded, more complex is the automaton. A similar notion, related to some prediction problems, appears in the framework of the theory of computational complexity. Essentially this is similar to trying to determine the computational time related to the size of a problem, that a Turing Machine take to solve it. In our context, let us consider the following decision or prediction problem.
PRE: Consider the chip firing fungal automaton , an initial assignment of chips to every site , , an integer number of steps of the automaton and a site
, such that . Question: Will be for some ?
Of course one may give an answer by running the automaton at most steps, which can be done in a serial computer in polynomial time. But the question is a little more tricky: could we answer faster than the serial algorithm, ideally, exponentially faster in polylogarithmic time in a parallel computer with a polynomial number of processor?
To answer the questions we consider two classes of decision problems, those belonging to , the class of problems solved by a polynomial algorithm, and the class , being the problems solved in a parallel computer in steps (polylogarithmic time). This is straightforward that because any parallel algorithm solved in polylogarithmic time can be simulated efficiently in a serial computer. But the strict inclusion is a very hard open problem (like the well know ).
An other notion from computational complexity related with the possibility that the two classes melt is P-completeness. A problem is P-complete if it is in the class , (that is to say, there exist a polynomial algorithm to solve it) and every other problem in can be reduced, by a polynomial transformation, to it. Clearly, if one of those P-complete problems is in , both classes collapsed in one. So, to prove that a problem is gives us an idea of its complexity.
One well known P-complete problem is the Circuit Value Problem, i.e., the evaluation of a Boolean Circuit (Boolean function). Roughly because any polynomial problem solved in a serial computer (a Turing machine) can be represented as a Boolean circuit. On the other hand, Boolean circuits intuitively are essentially serial because in order to compute a layer of functions it is necessary to compute previous layers so in principle it is not clear how to determine the output of the circuit in parallel. Further, when the circuit is monotonous, i.e., it admits only or and and gates (no negations) it is also a P-complete problem. This is because negation can be put in the input (the two bits of the variable 0 and 1) and for the gates which are a negation, to use the De Morgan laws.
The complexity of the chip firing automata was first studied in [20, 22], where it was proved that in arbitrary graphs (in particular, non-planar ones) the chip firing automata are Turing Universal. To prove this a universal set of Boolean circuits is built by using specific automata configurations, so, also PRE is P-complete. In a similar way, but in a d-dimensional grid, , it was proved in [35] that for the problem is P-complete and the complexity, until today, remains open for a two-dimensional grid. In [16] it was proved that in a two-dimensional grid and the von Neumann and Moore neighbourhood it is not possible to cross signals by constructing wires over quiescent configurations. That can be done only for bigger neighbourhood, so, in fact, over non planar graphs.
5 Computational Complexity of the Fungal Automata
We will study the computational complexity of the Fungal Sand Pile Automaton, by proving that for the word , the Prediction Problem, PRE, is P-complete. That is to say one can not determine an exponentially faster algorithm to answer unless .
Proposition 1.
For the word the fungal chip firing automaton is P-complete.
Proof.
Clearly the problem is in . It suffices to run the automaton at most steps and see if the site changes, which is done in : in fact we have to compute the “cone” between site , its neighbourhood at step , , and so on, until the initial values in the site in an square . So the number of sites is to consider is which is bounded by a cubic polynomial, so one may compute the state of site in .
To establish the completeness, we will reduce the Monotone Circuit Value Problem to the Fungal Automaton Prediction Problem, PRE. That is to say, to establish specific automaton configurations which simulates a wire, the and and the or gates, as well as a cross-over. This last gadget is important to compute non-planar circuits in the two dimensional grid.
In the constructions below every cell which is not in the diagram is understood initially empty, without chips ().
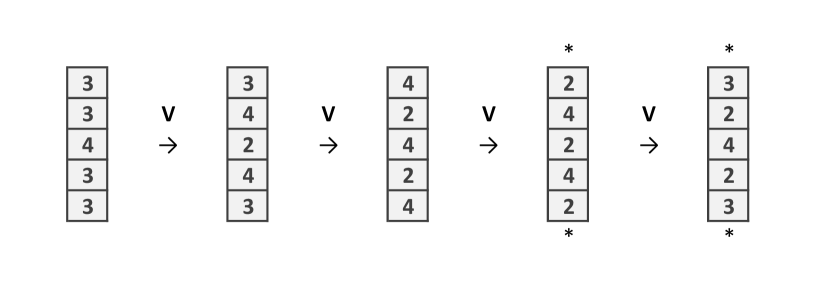
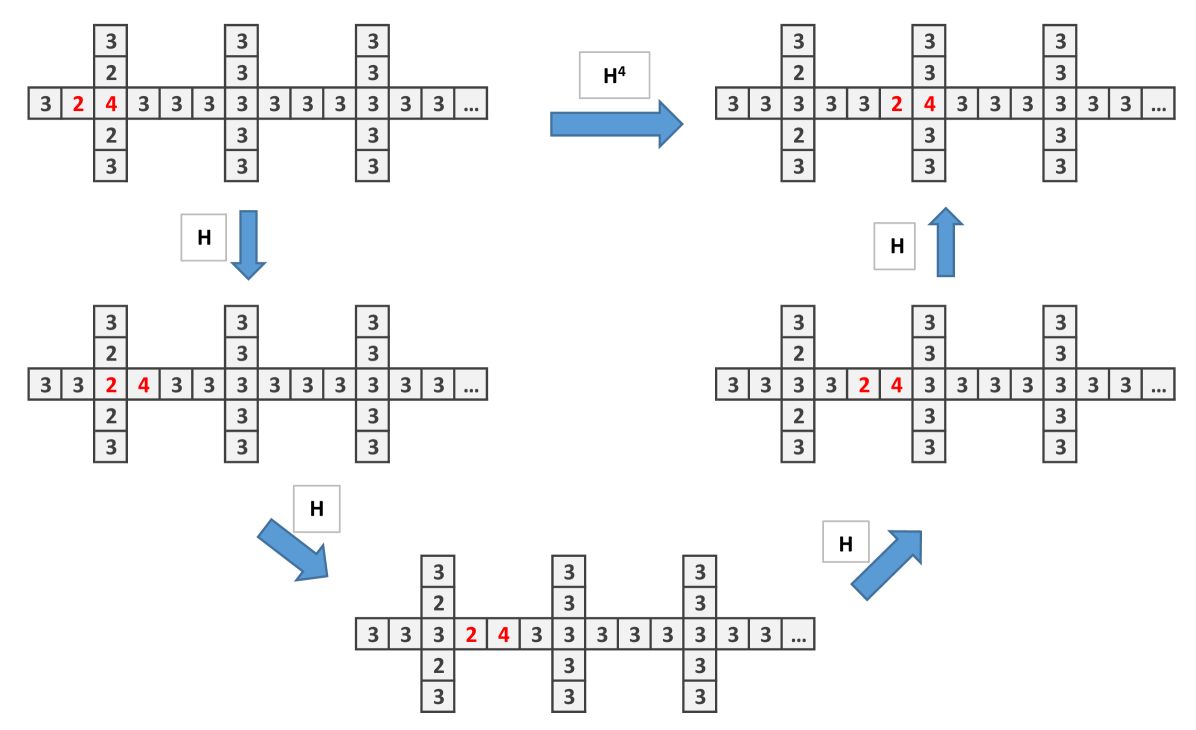
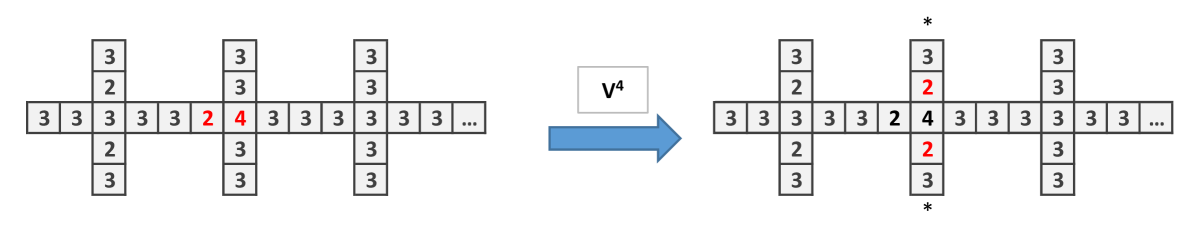
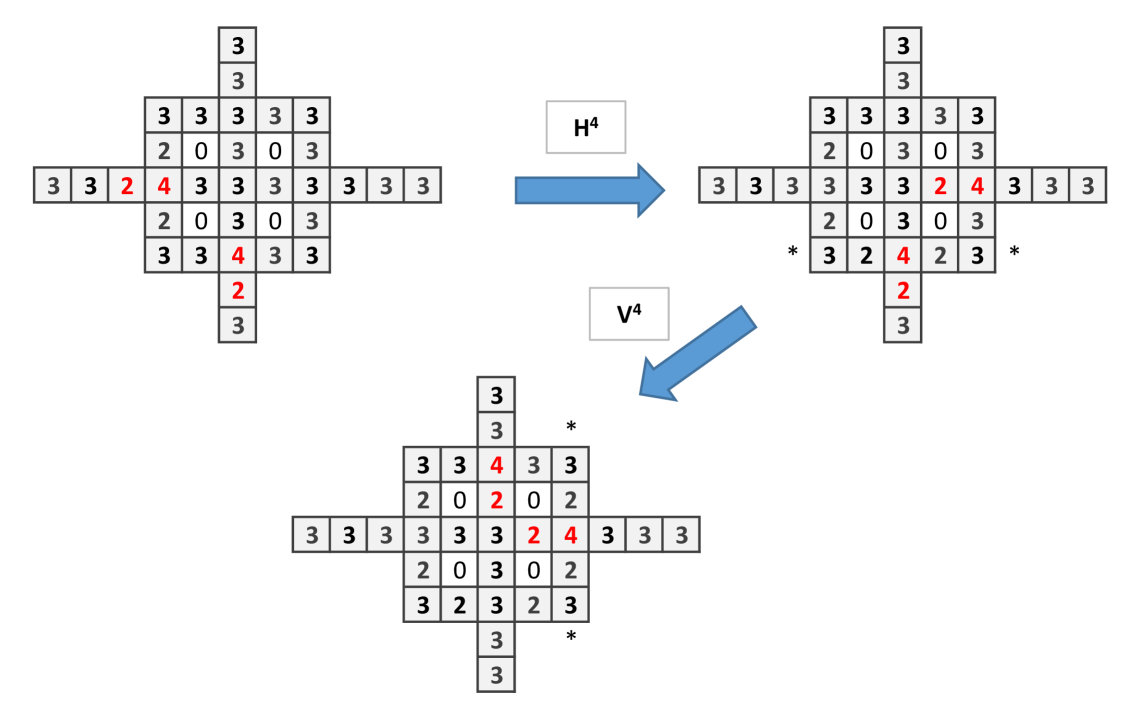
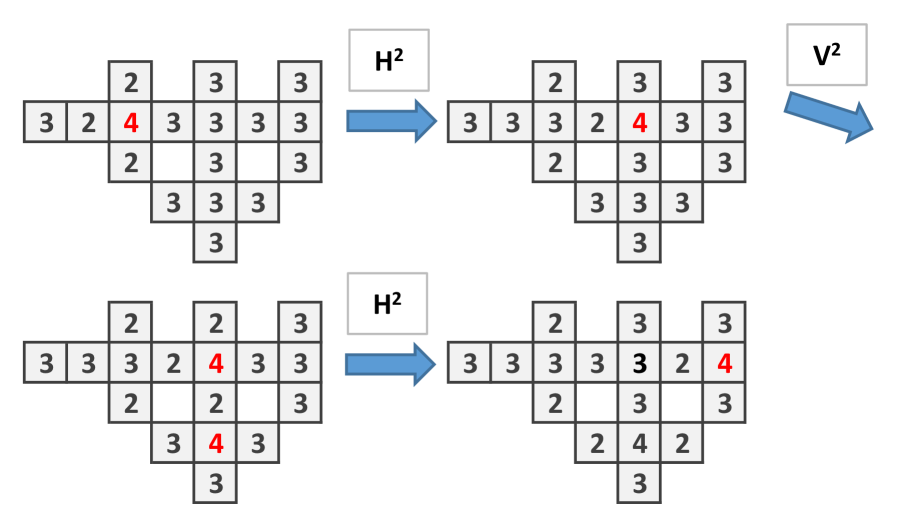
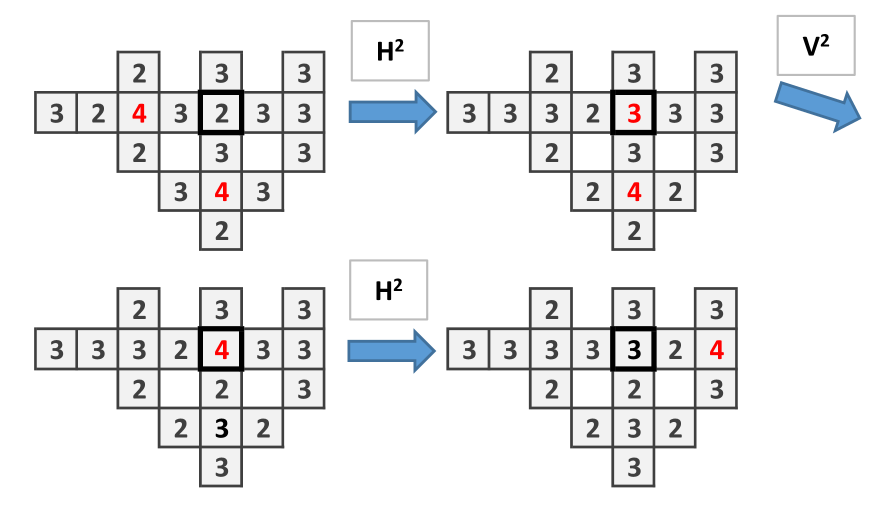
To construct the wire let us first see what happen when is applied in the particular structure showed in (Fig. 2a). The important issue is that the initial site with 4 chips, after the application of , remains with 4 chips. Only the adjacent sites and down change their number of chips.Then one applies to obtain Fig. 2b which is similar to the initial configuration, shifted to the right (Fig. 2c).
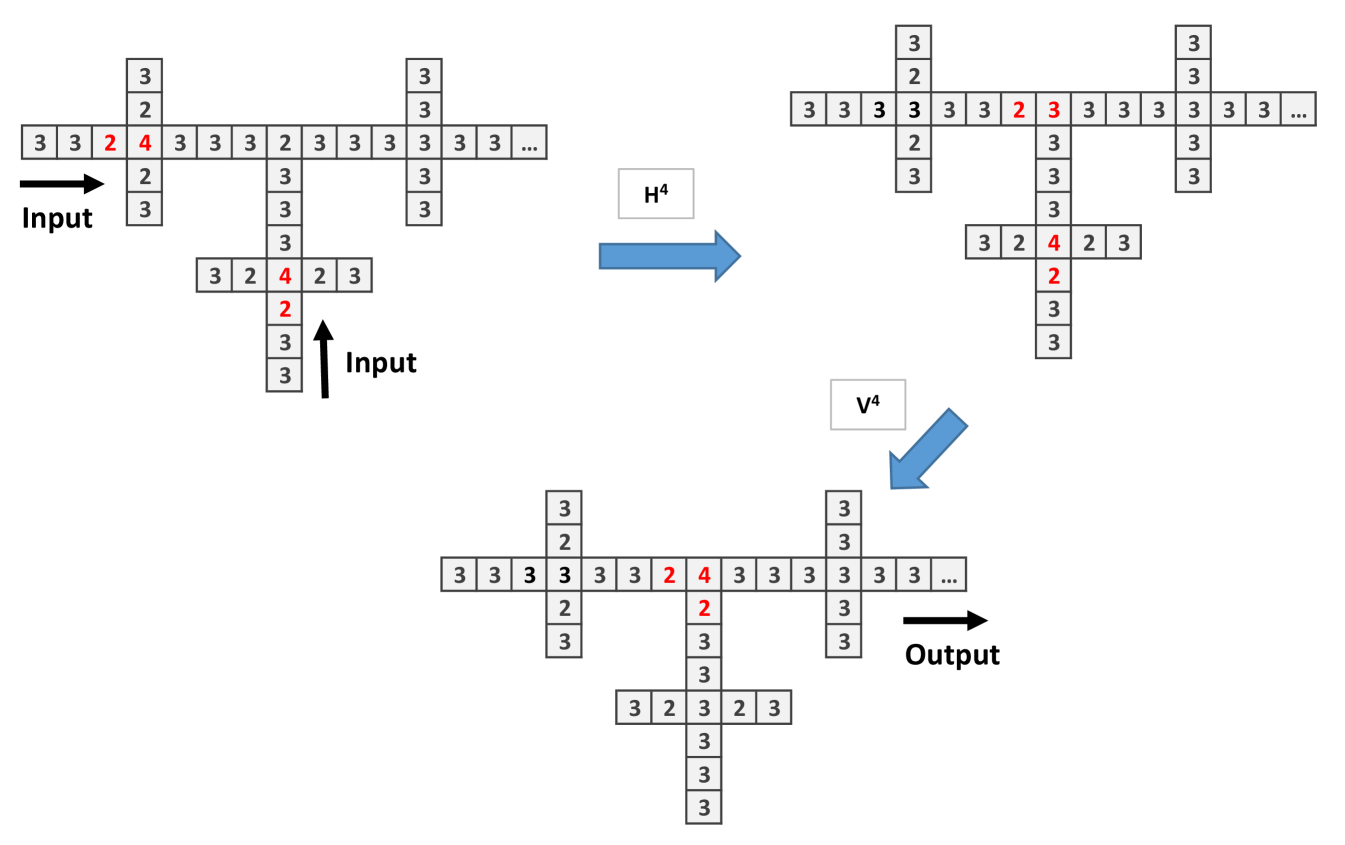
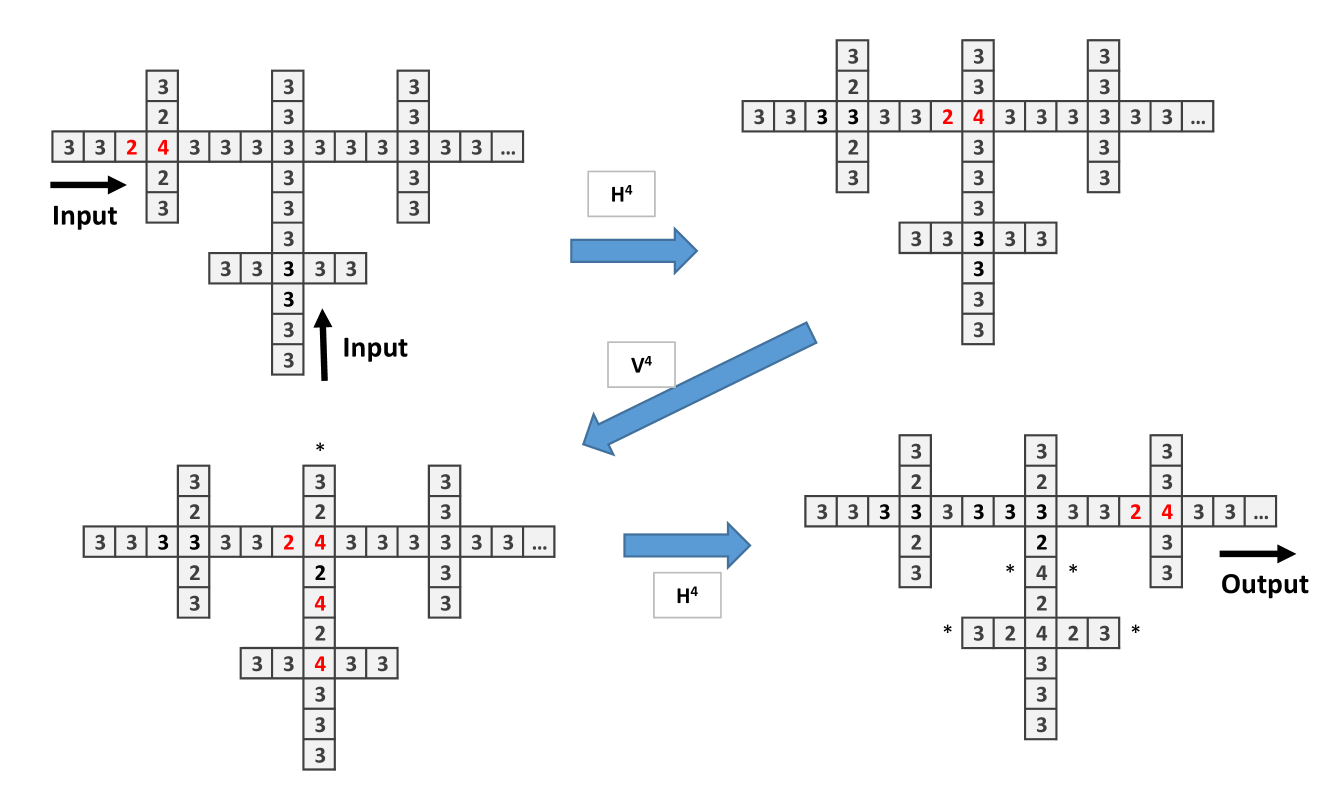
To implement and gate (Fig. 3) and or gate (Fig. 4) we have to connect two wires (this corresponds to a branching of mycelium). In the and gate two single chips arrive to a central site with 2 chips, so to trigger firing, threshold 3, the signal has to arrive. With the signal continues to the right, thus the output is 1. The or gate functions similarly to and gate but the central site has 3 chips. There is an unwanted signal coming back signal but the computation is made to the right.
6 Other words of automaton updates
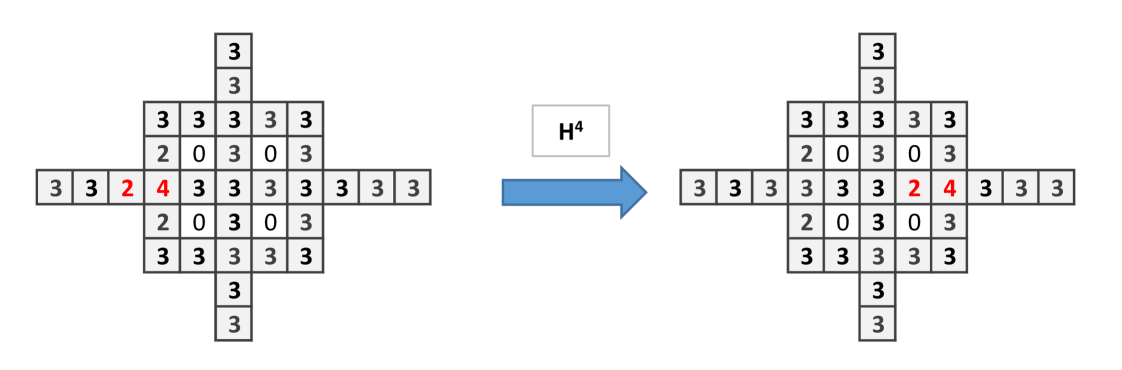
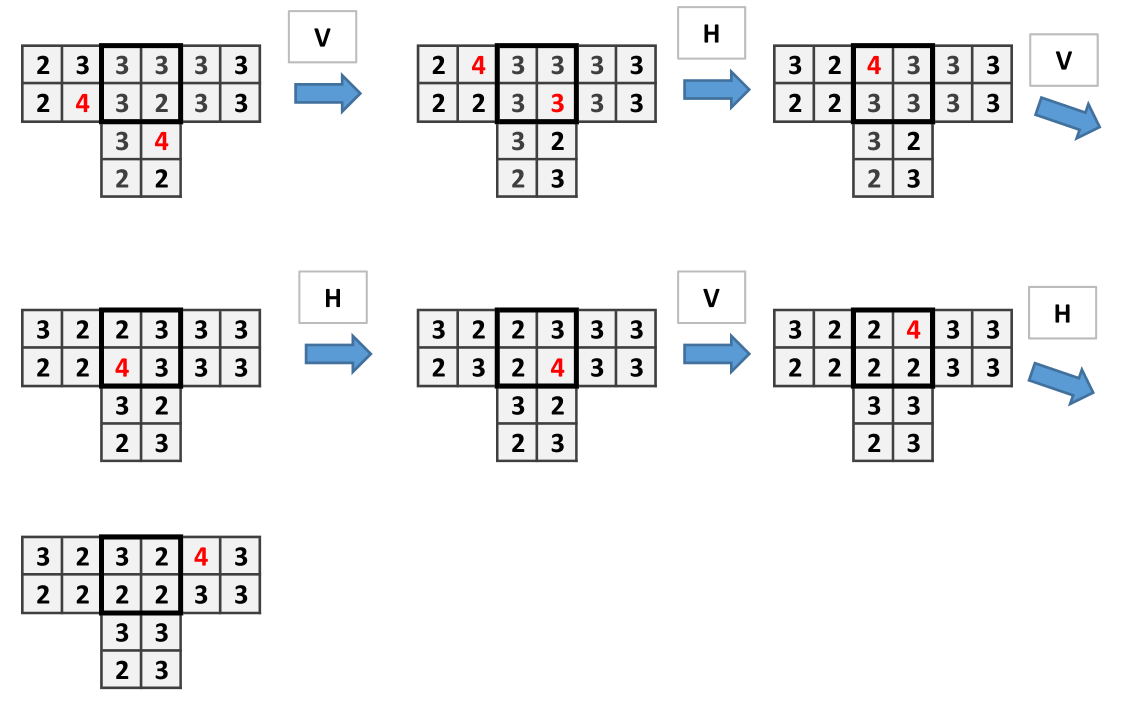
For other shorter words, like the usual chip firing (with sides always open) and the words in the set we are able to construct wires, the or and the and gates, but we are unable to built a cross-over. In such cases we can only implement planar circuits with non-crossing wires.
Below we exhibit the different constructions for those words. It is important to point out that the strategy we used to built the constructions has been by taking as initial framework a quiescent configuration, i.e. a fixed point of the automaton. In [16] it has been proved that with this strategy, for a two dimensional grid with the von Neumann or Moore neighbourhoods it is impossible to cross information, i.e. to built a cross-over. It seems that is also the case for the words in the set . In this sense one may say that our result is the best possible: no shortest word allows to cross information, at least following the quiescent strategy.

7 Discussion
Using sandpile, or chip firing, automata we proved that Fungal Automata are computationally universal, i.e., by arranging positions of branching in mycelium it is possible to calculate any Boolean function.

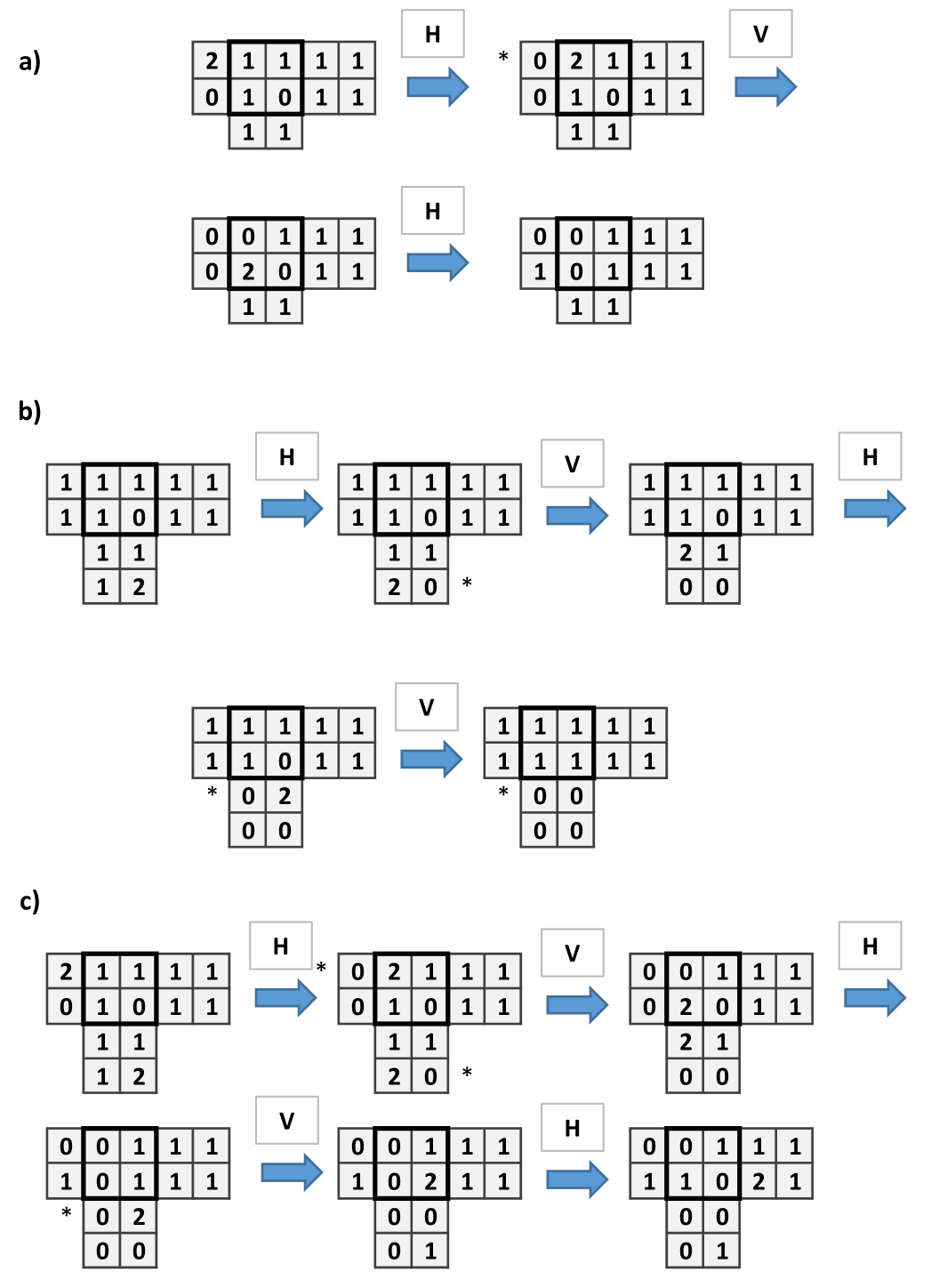
The structure of Fungal Automata presented can be relaxed by consider the site firing chips only when it has as many chips as open side. In present model, since at each step there are only two sides can be open, the firing threshold is 2. In this situation, the wire and and the or gates can be built as in previous cases but not the cross-over. Dynamics of the wire is shown in Fig. 9, the and gate in Fig. 10.
Consider the grid . Another possibility to open-close sides could be the following: at even steps , open the even rows and columns and at odd steps, open the odd rows and columns.
If we do that we simulate exactly the Margolous partitions ( blocks) [31]. This give us another way to determine the universality and, in this case, reversibility of this specific Fungal Automaton, because with this strategy one may simulate the Margolous billiard [32]. Not only that, given any other block partition automaton, say by blocks there exist a way to open-close the sides which simulates it [38, 13, 25, 12].
A significance of the results presented for future implementations of fungal automata with living fungal colonies in experimental laboratory conditions is the following: in our previous research, see details in [4], we used FitzHugh-Nagumo model to imitate propagation of excitation on the mycelium network of a single colony of Aspergillus niger. Boolean values are encoded by spikes of extracellular potential. We represented binary inputs by electrical impulses on a pair of selected electrodes and we record responses of the colony from sixteen electrodes. We derived sets of two-inputs-on-output logical gates implementable the fungal colony and analyse distributions of the gates [4]. Indeed, there were combination of functionally complete sets of gates, thus computing with travelling spikes is universal. However, in [4], we made a range of assumptions about origins, mechanisms of propagation and interactions of impulses of electrical activity. If the spikes of electrical potential do not actually propagate along the mycelium the model might be incorrect. The sandpile model designed in present paper is more relaxed because does not any auto-catalytic processes: avalanches can be physically simulated by applying constant currents, chemical stimulation to mycelium network. This is because the avalanches can be seen as movement of cytoplasm of products of fungal metabolism.
Whilst thinking about potential experimental implementation initiating avalanches is just one part of the problem. Selective control of the Woronin bodies might bring substantial challenges. As previous studies indicate the Woronin bodies can block the pores due to cytoplasmic flow [45] or mechanical stimulation of the cell wall, high temperatures, carbon and nitrogen starvation, high osmolarity and low pH [47, 44, 27]. We are unaware of experimental studies on controlling Woronin bodies with light but we believe this is not impossible.
Acknowledgement
AA, MT, HABW have received funding from the European Union’s Horizon 2020 research and innovation programme FET OPEN “Challenging current thinking” under grant agreement No 858132. EG residency in UWE has been supported by funding from the Leverhulme Trust under the Visiting Research Professorship grant VP2-2018-001 and from the project the project 1200006, FONDECYT-Chile.
References
- [1] Andrew Adamatzky. On spiking behaviour of oyster fungi Pleurotus djamor. Scientific reports, 7873, 2018.
- [2] Andrew Adamatzky. Towards fungal computer. Interface focus, 8(6):20180029, 2018.
- [3] Andrew Adamatzky, Eric Goles, Genaro Martinez, Michail-Antisthenis Tsompanas, Martin Tegelaar, and Han A. B. Wosten. Fungal automata. arXiv preprint arXiv:2003.08168, 2020.
- [4] Andrew Adamatzky, Martin Tegelaar, Han AB Wosten, Anna L Powell, Alexander E Beasley, and Richard Mayne. On boolean gates in fungal colony. arXiv preprint arXiv:2002.09680, 2020.
- [5] Javier Bitar and Eric Goles. Parallel chip firing games on graphs. Theoretical Computer Science, 92(2):291–300, 1992.
- [6] Robert-Jan Bleichrodt, Marc Hulsman, Han AB Wösten, and Marcel JT Reinders. Switching from a unicellular to multicellular organization in an aspergillus niger hypha. MBio, 6(2):e00111–15, 2015.
- [7] Robert-Jan Bleichrodt, G Jerre van Veluw, Brand Recter, Jun-ichi Maruyama, Katsuhiko Kitamoto, and Han AB Wösten. Hyphal heterogeneity in a spergillus oryzae is the result of dynamic closure of septa by w oronin bodies. Molecular microbiology, 86(6):1334–1344, 2012.
- [8] Robert-Jan Bleichrodt, Arman Vinck, Nick D Read, and Han AB Wösten. Selective transport between heterogeneous hyphal compartments via the plasma membrane lining septal walls of Aspergillus niger. Fungal Genetics and Biology, 82:193–200, 2015.
- [9] Alessandro Chessa, H Eugene Stanley, Alessandro Vespignani, and Stefano Zapperi. Universality in sandpiles. Physical Review E, 59(1):R12, 1999.
- [10] Kim Christensen, Hans C Fogedby, and Henrik Jeldtoft Jensen. Dynamical and spatial aspects of sandpile cellular automata. Journal of statistical physics, 63(3-4):653–684, 1991.
- [11] Deepak Dhar. Self-organized critical state of sandpile automaton models. Physical Review Letters, 64(14):1613, 1990.
- [12] Jérôme Durand-Lose. Representing reversible cellular automata with reversible block cellular automata. Discrete Mathematics and Theoretical Computer Science, 145:154, 2001.
- [13] Jérôme O Durand-Lose. Reversible space–time simulation of cellular automata. Theoretical Computer Science, 246(1-2):117–129, 2000.
- [14] BA Ferguson, TA Dreisbach, CG Parks, GM Filip, and CL Schmitt. Coarse-scale population structure of pathogenic Armillaria species in a mixed-conifer forest in the blue mountains of northeast oregon. Canadian Journal of Forest Research, 33(4):612–623, 2003.
- [15] Marina Fomina, Karl Ritz, and Geoffrey M Gadd. Negative fungal chemotropism to toxic metals. FEMS Microbiology Letters, 193(2):207–211, 2000.
- [16] Anahí Gajardo and E Goles. Crossing information in two-dimensional sandpiles. Theoretical Computer Science, 369(1-3):463–469, 2006.
- [17] Eric Goles. Sand piles, combinatorial games and cellular automata. In Instabilities and Nonequilibrium Structures III, pages 101–121. Springer, 1991.
- [18] Eric Goles. Sand pile automata. In Annales de l’IHP Physique théorique, volume 56, pages 75–90, 1992.
- [19] Eric Goles and Maurice Margenstern. Sand pile as a universal computer. International Journal of Modern Physics C, 7(02):113–122, 1996.
- [20] Eric Goles and Maurice Margenstern. Sand pile as a universal computer. International Journal of Modern Physics C, 7(02):113–122, 1996.
- [21] Eric Goles and Maurice Margenstern. Universality of the chip-firing game. Theoretical Computer Science, 172(1-2):121–134, 1997.
- [22] Eric Goles and Maurice Margenstern. Universality of the chip-firing game. Theoretical Computer Science, 172(1-2):121–134, 1997.
- [23] Raymond Greenlaw, H James Hoover, Walter L Ruzzo, et al. Limits to parallel computation: P-completeness theory. Oxford University Press on Demand, 1995.
- [24] Konrad T Howitz and David A Sinclair. Xenohormesis: sensing the chemical cues of other species. Cell, 133(3):387–391, 2008.
- [25] Katsunobu Imai and Kenichi Morita. A computation-universal two-dimensional 8-state triangular reversible cellular automaton. Theoretical Computer Science, 231(2):181–191, 2000.
- [26] Mordecai J Jaffe, A Carl Leopold, and Richard C Staples. Thigmo responses in plants and fungi. American Journal of Botany, 89(3):375–382, 2002.
- [27] Gregory Jedd. Fungal evo–devo: organelles and multicellular complexity. Trends in cell biology, 21(1):12–19, 2011.
- [28] Gregory Jedd and Nam-Hai Chua. A new self-assembled peroxisomal vesicle required for efficient resealing of the plasma membrane. Nature cell biology, 2(4):226–231, 2000.
- [29] Ching Kung. A possible unifying principle for mechanosensation. Nature, 436(7051):647, 2005.
- [30] Roger R Lew. Mass flow and pressure-driven hyphal extension in neurospora crassa. Microbiology, 151(8):2685–2692, 2005.
- [31] Norman Margolus. Physics-like models of computation. Physica D: Nonlinear Phenomena, 10(1-2):81–95, 1984.
- [32] Norman Margolus. Universal cellular automata based on the collisions of soft spheres. In Collision-based computing, pages 107–134. Springer, 2002.
- [33] Bruno Martin. On goles’ universal machines: A computational point of view. Theoretical Computer Science, 504:83–88, 2013.
- [34] Cristopher Moore and Martin Nilsson. The computational complexity of sandpiles. Journal of statistical physics, 96(1-2):205–224, 1999.
- [35] Cristopher Moore and Martin Nilsson. The computational complexity of sandpiles. Journal of statistical physics, 96(1-2):205–224, 1999.
- [36] David Moore. Perception and response to gravity in higher fungi–a critical appraisal. New Phytologist, 117(1):3–23, 1991.
- [37] Royall T Moore and James H McAlear. Fine structure of mycota. 7. observations on septa of ascomycetes and basidiomycetes. American Journal of Botany, 49(1):86–94, 1962.
- [38] Kenichi Morita and Masateru Harao. Computation universality of one-dimensional reversible (injective) cellular automata. IEICE TRANSACTIONS (1976-1990), 72(6):758–762, 1989.
- [39] S Olsson and BS Hansson. Action potential-like activity found in fungal mycelia is sensitive to stimulation. Naturwissenschaften, 82(1):30–31, 1995.
- [40] Janina Purschwitz, Sylvia Müller, Christian Kastner, and Reinhard Fischer. Seeing the rainbow: light sensing in fungi. Current opinion in microbiology, 9(6):566–571, 2006.
- [41] RE Reichle and JV Alexander. Multiperforate septations, woronin bodies, and septal plugs in fusarium. The Journal of cell biology, 24(3):489, 1965.
- [42] Clifford L Slayman, W Scott Long, and Dietrich Gradmann. “Action potentials” in Neurospora crassa, a mycelial fungus. Biochimica et Biophysica Acta (BBA)-Biomembranes, 426(4):732–744, 1976.
- [43] Myron L Smith, Johann N Bruhn, and James B Anderson. The fungus Armillaria bulbosa is among the largest and oldest living organisms. Nature, 356(6368):428, 1992.
- [44] Shanthi Soundararajan, Gregory Jedd, Xiaolei Li, Marilou Ramos-Pamploña, Nam H Chua, and Naweed I Naqvi. Woronin body function in magnaporthe grisea is essential for efficient pathogenesis and for survival during nitrogen starvation stress. The Plant Cell, 16(6):1564–1574, 2004.
- [45] Gero Steinberg, Nicholas J Harmer, Martin Schuster, and Sreedhar Kilaru. Woronin body-based sealing of septal pores. Fungal Genetics and Biology, 109:53–55, 2017.
- [46] Martin Tegelaar, Robert-Jan Bleichrodt, Benjamin Nitsche, Arthur FJ Ram, and Han AB Wösten. Subpopulations of hyphae secrete proteins or resist heat stress in aspergillus oryzae colonies. Environmental microbiology, 22(1):447–455, 2020.
- [47] Martin Tegelaar and Han AB Wösten. Functional distinction of hyphal compartments. Scientific reports, 7(1):1–6, 2017.
- [48] Karen Tenney, Ian Hunt, James Sweigard, June I Pounder, Chadonna McClain, Emma Jean Bowman, and Barry J Bowman. Hex-1, a gene unique to filamentous fungi, encodes the major protein of the woronin body and functions as a plug for septal pores. Fungal Genetics and Biology, 31(3):205–217, 2000.
- [49] Wei Kiat Tey, Alison J North, Jose L Reyes, Yan Fen Lu, and Gregory Jedd. Polarized gene expression determines woronin body formation at the leading edge of the fungal colony. Molecular biology of the cell, 16(6):2651–2659, 2005.
- [50] Ingrid M Van Aarle, Pål Axel Olsson, and Bengt Söderström. Arbuscular mycorrhizal fungi respond to the substrate ph of their extraradical mycelium by altered growth and root colonization. New Phytologist, 155(1):173–182, 2002.
- [51] Stephen Wolfram. Cellular automata and complexity: collected papers. Addison-Wesley Pub. Co., 1994.