Conditional Balance Tests: Increasing Sensitivity and Specificity With Prognostic Covariates
Abstract
Researchers often use covariate balance tests to assess whether a treatment variable is assigned “as-if” at random. However, standard tests may shed no light on a key condition for causal inference: the independence of treatment assignment and potential outcomes. We focus on a key factor that affects the sensitivity and specificity of balance tests: the extent to which covariates are prognostic, that is, predictive of potential outcomes. We propose a “conditional balance test” based on the weighted sum of covariate differences of means, where the weights are coefficients from a standardized regression of observed outcomes on covariates. Our theory and simulations show that this approach increases power relative to other global tests when potential outcomes are imbalanced, while limiting spurious rejections due to imbalance on irrelevant covariates.
Keywords: Balance tests, natural experiments, prognostic covariates, ignorability, weights
Acknowledgments: We are grateful to Lily Medina for valuable assistance.
1 Introduction
Methodologists often urge researchers to test observable implications of assumptions needed for causal inference. In natural experiments, regression-discontinuity designs, and related methods, a common approach is to test for statistical balance on pre-treatment covariates across the treatment and control groups. The logic appears straightforward: if a coin flip determined treatment assignment, as assumed or as stipulated by design in such studies, we would expect equal distributions of all covariates in the two groups—since covariate values are determined prior to treatment assignment.444Covariates could also be defined to include “placebo outcomes,” i.e., post-treatment variables known or assumed to be unaffected by treatment assignment (EggersTunonDafoe2021, CaugheyDafoeSeawright2017). Thus, up to chance error, we should find proportionately as many men as women, or as many young as old people, assigned to treatment and control conditions. A statistically insignificant association between treatment assignment and gender, age, or other covariates is consistent with “as-if” random assignment of a treatment—while the presence of such an association may suggest a flaw in the design.555See e.g. Freedman1999; Rosenbaum2002; Rosenbaum2010; HansenBowers2008; Sekhon2009; imai_keele_yamamoto_2010; Dunning2012; CaugheyDafoeSeawright2017; or EggersTunonDafoe2021.
Unfortunately, such tests may shed no light on a key condition for causal inference: the independence of treatment assignment and potential outcomes, that is, the outcomes that would be realized under counterfactual assignment to different treatments.666Neyman1923, Holland_1986, Rubin1974. Self-selection processes that lead to failures of as-if random may imply imbalances on some covariates but not on others. In an observational study of the efficacy of a new drug, for example, sicker patients may select into the treatment group—but men may be as likely to do so as women. This leads to expected balance on gender across the treatment and control groups but substantial imbalance on prior health. These covariates differ, however, in their informativeness about potential outcomes: health status after an intervention is likely tightly related to prior health status while gender may be unrelated to potential outcomes. If we only have data on gender, we may fail to reject random assignment; and yet the potential outcomes—the potential health outcomes under assignment to treatment or control—are very likely imbalanced. Even if we do have data on both gender and prior health, the asymmetry in the informativeness of these covariates is not well captured by standard procedures, such as covariate-by-covariate or (unweighted) multivariate balance tests. Such tests may reject spuriously, due to imbalances on irrelevant covariates unrelated to potential outcomes; or they may fail to reject when potential outcomes are in fact imbalanced, because they do not take sufficient account of the extent to which covariates are prognostic, that is, predictive of potential outcomes.
We show in this paper how to diagnose and increase the power of balance tests to detect the dependence of treatment assignment on potential outcomes. When covariates are sufficient for potential outcomes, in a sense we define, finding imbalance on covariates implies imbalance of potential outcomes. However, tests using irrelevant covariates—those unrelated to potential outcomes—can lead researchers to over-reject as-if random when it is true or under-reject it when it is false. Projecting potential outcomes onto covariates before conducting balance tests helps to avoid this problem. A key insight is that post-treatment data on outcomes are often available at the time researchers conduct balance tests. This implies that the extent to which covariates are predictive of potential outcomes can be assessed empirically, for example, by using control- or treatment-group samples to estimate a finite-population relation between covariates and potential outcomes. Our principal test statistic is based on the difference between the fitted value of the average , the covariate-adjusted average potential outcome under control, in the treatment and control group samples. This yields a “conditional balance test,” with which we assess the independence of treatment assignment and . The statistic is equivalent to a weighted sum of the differences of means for each individual covariate, where the weights are the fitted coefficients from the standardized regression of potential outcomes on covariates in the control group sample. This omnibus test—“omnibus” because unlike covariate-by-covariate tests, it is based on the joint distribution of covariate differences—thus takes account of the “importance” of each covariate, or the extent to which different covariates are linearly prognostic. The test upweights covariates that we would expect to be imbalanced if treatment assignment were in fact dependent on potential outcomes, while downweighting irrelevant, non-prognostic covariates.
Our theoretical and simulation results suggest several key findings and advantages of our approach. First and most importantly, the test is both more sensitive and more specific than existing approaches in the following sense: it tends to fail to reject as-if random assignment due to imbalances on irrelevant covariates more often than existing approaches (and is thus more specific); but it will boost rejection probabilities relative to standard tests when prognostic covariates are imbalanced (and thus it is sensitive). Methodologists have rightly pointed out that balance tests are often poorly powered to reject false null hypotheses stipulating as-if random assignment (CattaneoEtAl2015). Moreover, failing to reject a null hypothesis of as-if random assignment is not the same as accepting it, leading some methodologists to recommend alternatives to standard balance tests (HartmanHidalgo2018; hartman_2021).777See also ImaiEtAl2008, who develop critiques of balance tests that differ from the issues we raise in this article. Our results suggest a subtle relationship between the prognostic value of covariates and the power of tests, however. Unweighted omnibus tests may overreject null hypotheses when treatment assignment is independent of potential outcomes, because they give too much weight to irrelevant covariates unrelated to potential outcomes. Our weighted procedure can reduce false positives or Type I error in this case. However, when treatment assignment does depend on potential outcomes and we have prognostic covariates availables, our regression-weighted approach rejects as-if random more often than unweighted approaches, thus limiting false negatives or Type II error and increasing power. In other words, the test limits both false negatives and false positives.
Second, unlike covariate-by-covariate tests, our approach provides a clear rejection rule based on a combination of covariate differences. Researchers often appear to rely on an informal rule of thumb in assessing the results of covariate-by-covariate tests. For example, if a treatment is randomly assigned, we would expect significant covariate imbalances at the 0.05 level in only 1 out of 20 or 5% of independent tests. However, when making multiple statistical comparisons across different covariates and when tests are dependent—which occurs whenever covariates are correlated with each other, that is to say, almost always in practice—such a rule-of-thumb is not reliable. It can therefore be a matter of opinion whether the totality of the evidence from a set of covariate balance tests undercuts a claim of as-if random. We thus add to recent work that proposes the use of omnibus statistics or combinations of -values, including those that allow for dependence among covariates.888See e.g. HansenBowers2008; CaugheyDafoeSeawright2017; or Gagnon-Bartsch_Shem-Tov2019.
Finally, our approach provides a basis for assessing the evidentiary value of balance tests. Pre-treatment (lagged) measures of outcome variables tend to be highly prognostic, leading methodologists to counsel their use in falsification tests.999imbens_rubin_2015: 483-4. Yet such predictive covariates may or may not be available. It is also an empirical question whether a lagged outcome or any other covariate is in fact prognostic in any study, as our motivating example in the next section suggests. In some settings all available covariates may be only weakly related to potential outcomes. Our approach suggests diagnostics that can help researchers assess the strength of the test of as-if random. When none of the pre-treatment covariates to which researchers have access are prognostic, balance tests may have especially weak power over an alternative hypothesis that potential outcomes are imbalanced. Their results should then not be taken as strong evidence in favor of the key identifying assumption for causal inference.
We take inspiration from a large literature on multiple testing in statistics and epidemiology, which recommends upweighting tests for “important” hypotheses—or those that are most plausibly false—in -value combinations.101010Examples include Holm1979; BenjaminiHochberg1997; and GenoveseEtAl2006. See also Fisher1935; KostMcDermott2002; or Westfall2005. However, our approach gives specific content to which hypotheses are most likely to be false in balance tests, by upweighting covariates that are related to potential outcomes. We also recommend constructing an omnibus -value by evaluating the weighted sum of differences of covariate means directly, rather than by combining -values from separate covariate-by-covariate tests; this differs from e.g. CaugheyDafoeSeawright2017, who develop a non-parametric combination approach to generating omnibus -values for placebo tests, including balance tests, using a combination metric owing to Fisher1935. However, the choice of combination metric can introduce discretion; and this choice is not required for balance tests, in which mean differences for different covariates can be readily combined. Our approach is related to papers by HansenBowers2008, who develop a procedure for conducting balance tests based on combining covariate differences of means in block- (and cluster-) randomized experiments, and Gagnon-Bartsch_Shem-Tov2019, who provide a classification permutation test. None of these important papers, however, considers variation in the prognostic power of different covariates. While many works on causal inference mention the usefulness of conducting tests for balance on prognostic covariates, the rationale is not always explicit, nor are the potential gains of doing so in terms of increased statistical power against a clear null hypothesis. Hansen_2008 proposes a “prognostic score” that is akin to our measure of prognosis, but he develops this approach for purposes of covariate adjustment in an outcome model. Our major innovation is therefore our focus on the association between covariates and potential outcomes as the basis for balance testing.
In the next Section 2, we discuss examples and give intuition for why pre-treatment covariates are created unequal. Section 3 then develops statistical theory behind our approach. In Section 4, we present simulation evidence on the power of our approach under different assumptions about data-generating processes. We conclude by discussing several possible extensions, including conditional balance tests based on more flexible, non-linear regression fits.
2 Motivation: the varying prognostic power of covariates
In an important study, caughey_sekhon_2011 appraise the use of regression-discontinuity designs to study the effect of incumbency, taking data from close U.S. House elections (1942-2008). A priori, in a very close election, which party winds up with a slightly greater vote share at time seems quite plausibly as-if random. If so, assignment of the treatment—party incumbency—is independent of potential outcomes, as well as pre-treatment covariates. For this reason, the close-election design has become extremely widespread. Concerningly, however, Caughey and Sekhon’s plot of -values from balance tests (their Figure 2) suggests statistically significant imbalances in past incumbency, as well as the winning party’s past vote share, campaign spending, and measures of candidate quality, suggesting a possible failure of as-if random in very close elections.111111caughey_sekhon_2011 also present evidence of “sorting” at the 0% vote margin: the incumbent party wins the closest elections more than twice as often as it loses (see their Figure 1). Still, districts barely won by Democrats at time do not differ from those barely won by Republicans on several other political and demographic variables, e.g. whether the state has a Democratic governor or secretary of state, the margin of victory in the presidential race, voter turnout, whether the seat is open (i.e., the incumbent candidate is not running), or the percentage of urban, Black, or foreign-born residents. Thus, we see imbalances on some covariates but lack of imbalance on several others.
How should one interpret the totality of the evidence in a balance plot such as Caughey and Sekhon’s? These researchers (rightly, in our view) attribute particular importance to the imbalance on the winning party’s past incumbency and vote share at time , since these variables are presumably highly correlated with future incumbency and vote share. However, there is no formal procedure that takes into account the extent to which covariates are prognostic; and the covariates included in the balance tests are correlated, so simply comparing the number of rejections to the number of tests (e.g. to see if the ratio is greater than 1 out of 20) is not informative. In a subsequent study, eggers_et_al_2015 confirm that lagged incumbency seems to be the major driver of imbalances in Caughey and Sekhon’s data: in a procedure conceptually related to one we propose in Section 3, they show that Democratic near-winners and near-losers are not significantly different on pre-treatment covariates other than lagged incumbency, once the latter is controlled in a regression. They then extend the Caughey and Sekhon study to a broad range of majoritarian elections around the world, comparing close election winners and losers only on a measure of lagged incumbency. They find balance on this covariate in every other setting they examine, leading them to argue that the observed imbalance in U.S. House elections in the latter part of the twentieth century is unusual and may reflect special features of that context or may simply be due to chance.
The extent to which lagged incumbency is prognostic thus appears critical to adjudicating this debate about whether close elections are as-if random. The same is true of pre-treatment covariates in many other natural experiments or discontinuity designs. However, these studies and many others do not take prognosis into account formally or empirically. eggers_et_al_2015 are right to assess covariate balance across a wide range of elections. Yet they effectively assert that lagged incumbency is the only important covariate on which to test for balance across these contexts.121212Eggers et al. (2015: 262-3) argue that (a) the variety of characteristics on which winners and losers of close elections may vary can all be viewed as proxies for (are highly correlated with) incumbency; (b) testing for other covariates introduces multiple testing concerns; and (c) incumbency “confers electoral benefits in a variety of electoral settings around the world.” In fact, the prognostic value of lagged incumbency varies across countries and types of elections. As we show in Appendix Tables 1-2, in their data, the correlation between the vote share of the incumbent party at time and time is across all countries and election types but varies from a low of in Brazilian mayoral elections to a high of in the German Bundestag (full data set); in close elections (defined by a bandwidth of 0.5, i.e., the margin between the winning and runner-up party is less than 1 percentage point), it varies from a high of in New Zealand’s post-war parliament to a low of is the Canadian House of Commons (1867-1911).131313This comports also with findings on the varied causal effects of incumbency across contexts; see e.g. Schiumerini2015. Perhaps most importantly, the average correlation is just across all close elections studied by Eggers et al., while it is substantially higher in the post-war U.S. House elections studied by Caughey and Sekhon (0.83 in the full data and 0.24 in close elections).141414Restricting the analysis to close elections attenuates the correlations by truncating the range of variation on incumbent vote share at time ; yet this is arguably the relevant subset of the data in which to assess prognosis, since this is the set in which balance tests are typically conducted.
The prognosis of covariates is rarely considered systematically in balance testing, however. We coded a random sample of 150 articles using randomized experiments, natural experiments, and regression-discontinuity designs in three top journals in political science (the American Political Science Review, the American Journal of Political Science, and the Journal of Politics), stratifying by journal, over the time period 2000-2019.151515For code used in the sampling, see https://github.com/lilymedina/JSTOR_query. Overall, 52 percent of the sampled articles presented covariate balance tests in the body or appendix of the paper. The majority (56 percent) of those use only covariate-by-covariate tests, rather than some omnibus test statistic (such as the -value for the -statistic from the regression of a treatment indicator on all covariates). Only 18 percent of tests used a lagged dependent variable as a covariate. And we found no examples of systematic efforts to account for the prognostic importance of covariates in balance tests, for instance, using a weighted procedure like that we propose in this paper. The situation does not appear dissimilar in economics or other social science disciplines; in particular, procedures that take account of covariates’ degree of prognosis appear absent in the applied literature.
In practice, the covariates used in balance tests vary substantially in the extent to which they predict potential outcomes. We took a small further random sample from the 150 studies we coded, excluding the randomized experiments, stratifying by natural experiment versus discontinuity and on the presence of a lagged dependent variable or explicit discussion of prognosis in the paper. We then used replication data, where available, to calculate two measures for each study: the multiple from the regression of observed potential outcomes in the control group on all available covariates (“Prognosis”) and the multiple from the regression of a treatment assignment indicator on all available covariates (“Imbalance”). We note that we do not intend these measures as providing formal tests of prognosis or imbalance; we elaborate approaches to testing in the next section.
Figure 1, which plots these measures for our smaller sample of studies, suggests several insights. While a great deal of attention in balance testing focuses on the extent of imbalance, there is in fact considerable variation across studies in prognosis. Close to the vertical axis, covariates are non-prognostic and thus bear little apparent relationship to potential outcomes. For reasons we develop in the next section, such studies therefore provide less powerful tests of as-if random. Moreover, studies located in the upper-left quadrant may be prone to spurious rejection with standard procedures—because covariates unrelated to potential outcomes are imbalanced. In the lower left quadrant, the important concern may be that none of the measured covariates are prognostic of potential outcomes but we find balance on treatment assignment—leading to a form of Type I error in which we fail to reject, yet potential outcomes themselves may be imbalanced.
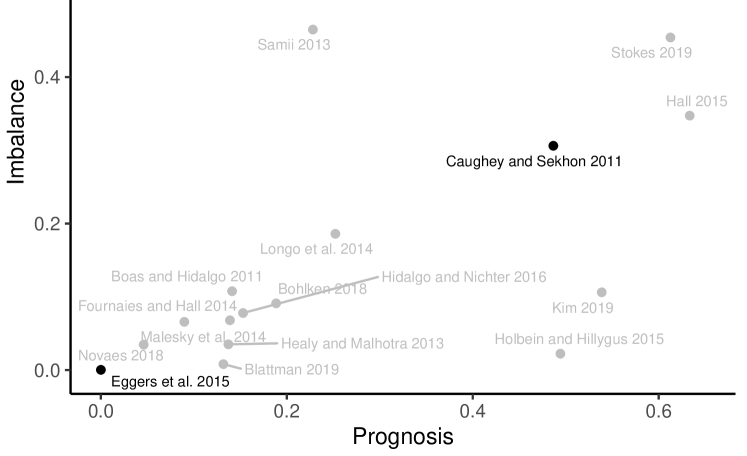
The figure plots a random sample of natural experiments and regression-discontinuity (RD) designs drawn from all those published in the American Political Science Review, American Journal of Political Science, and Journal of Politics, 2000-2019; Caughey and Sekhon (2011) is added. Prognosis is the from a regression of potential outcomes under control on all available covariates (control group only). Imbalance is the from a regression of treatment assignment on all available covariates.