Confidence bands for a log-concave density

Guenther Walther Research supported by NSF grants DMS-1501767 and DMS-1916074 Department of Statistics, Stanford University Alnur Ali Research supported by the Intelligence Community Postdoctoral Research Fellowship Program Department of Statistics, Stanford University Department of Electrical Engineering, Stanford University Xinyue Shen Research supported by the National Key R&D Program of China with grant No. 2018YFB1800800, the Key Area R&D Program of Guangdong Province with grant No. 2018B030338001, the Shenzhen Outstanding Talents Training Fund, and the Guangdong Research Project No. 2017ZT07X152 Department of Electrical Engineering, Stanford University Shenzhen Research Institute of Big Data and Future Network of Intelligence Institute, Chinese University of Hong Kong
{gwalther,alnurali,xinyues,boyd}@stanford.edu Stephen Boyd Department of Electrical Engineering, Stanford University

(revised May 2022)

Abstract

We present a new approach for inference about a univariate log-concave distribution: Instead of using the method of maximum likelihood, we propose to incorporate the log-concavity constraint in an appropriate nonparametric confidence set for the cdf $F$ . This approach has the advantage that it automatically provides a measure of statistical uncertainty and it thus overcomes a marked limitation of the maximum likelihood estimate. In particular, we show how to construct confidence bands for the density that have a finite sample guaranteed confidence level. The nonparametric confidence set for $F$ which we introduce here has attractive computational and statistical properties: It allows to bring modern tools from optimization to bear on this problem via difference of convex programming, and it results in optimal statistical inference. We show that the width of the resulting confidence bands converges at nearly the parametric $n^{-\frac{1}{2}}$ rate when the log density is $k$ -affine.

1 Introduction

Statistical inference under shape constraints has been the subject of continued considerable research activity. Imposing shape constraints on the inference about a function $f$ , that is, assuming that the function satisfies certain qualitative properties, such as monotonicity or convexity on certain subsets of its domain, has two main motivations: First, such shape constraints may directly arise from the problem under investigation and it is then desirable that the result of the inference reflects this fact. The second reason is that alternative nonparametric estimators typically involve the choice of a tuning parameter, such as the bandwidth in the case of a kernel estimator. A good choice for such a tuning parameter is usually far from trivial. More importantly, selecting a tuning parameter injects a certain amount of subjectivity into the estimator, and the resulting choice may prove quite consequential for relevant aspects of the inference. In contrast, imposing shape constraints often allows to derive an estimator that does not depend on a tuning parameter while at the same time exhibiting a good statistical performance, such as achieving optimal minimax rates of convergence to the underlying function $f$ .

This paper is concerned with inference about a univariate log-concave density, i.e. a density of the form

f(x)=\exp\phi(x),

where $\phi:{\bf R}\rightarrow[–\infty,\infty)$ is a concave function. It was argued in Walther (2002) that log-concave densities represent an attractive and useful nonparametric surrogate for the class of Gaussian distributions for a range of problems in inference and modeling. The appealing properties of this class are that it contains most commonly encountered parametric families of unimodal densities with exponentially decaying tails and that the class is closed under convolution, affine transformations, convergence in distribution and marginalization. In a similar vein as a normal distribution can be seen as a prototypical model for a homogenous population, one can use the class of log-concave densities as a more flexible nonparametric model for this task, from which heterogenous models can then be built e.g. via location mixtures. Historically such homogenous distributions have been modeled with unimodal densities, but it is known that the maximum likelihood estimate (MLE) of a unimodal density does not exist, see e.g. Birgé (1997). In contrast, it was shown in Walther (2002) that the MLE of a log-concave density exists and can be computed with readily available algorithms. Therefore, the class of log-concave densities is a sufficiently rich nonparametric model while at the same time it is small enough to allow nonparametric inference without a tuning parameter.

Due to these attractive properties there has been a considerable research activity in the last 15 years about the statistical properties of the MLE, computational aspects, applications in modeling and inference, and the multivariate setting. Many of the key properties of the MLE are now well understood: Existence of the MLE was shown in Walther (2002), consistency was proved by Pal, Woodroofe and Meyer (2007), and rates of convergence in certain uniform metrics was established by Dümbgen and Rufibach (2009). Balabdaoui, Rufibach and Wellner (2009) provided pointwise limit distributribution theory, while Doss and Wellner (2016) and Kim and Samworth (2016) gave rates of convergence in the Hellinger metric, and Kim, Guntuboyina and Samworth (2018) proved adaptation properties. Accompanying results for the multivariate case are given in e.g. Cule, Samworth and Stewart (2010), Schuhmacher and Dümbgen (2010), Seregin and Wellner (2010), Kim and Samworth (2016), and Feng, Guntuboyina, Kim and Samworth (2020).

Computation of the univariate MLE was initially approached with the Iterative Convex Minorant Algorithm, see Walther (2002), Pal, Woodroofe and Meyer (2007) and Rufibach (2007), but it appears that the fastest algorithms currently available are the active set algorithm given in Dümbgen, Hüsler and Rufibach (2007) and the constrained Newton method proposed by Liu and Wang (2018).

Overviews of some of these results and other work involving modeling and inference with log-concave distributions are given in the review papers of Walther (2009), Saumard and Wellner (2014) and Samworth (2018).

Notably, the existing methodology for estimating a log-concave density appears to be exclusively focused on the method of maximum likelihood. Here we will employ a different methodology: We will derive a confidence band by intersecting the log-concavity constraint with a goodness-of-fit test. One important advantage of this approach is that such a confidence band satisfies a key principle of statistical inference: an estimate needs to be accompanied by some measure of standard error in order to be useful for inference. There appears to be no known method for obtaining such a confidence band via the maximum likelihood approach. Balabdaoui et al. (2009) construct pointwise confidence intervals for a log-concave density based on asymptotic limit theory, which requires to estimate the second derivative of $\log f(x)$ . Azadbakhsh et al. (2014) compare several methods for estimating this nuisance parameter and they report that this task is quite difficult. An alternative approach is given by Deng et al. (2020). In Section 5 we compare the confidence bands introduced here with pointwise confidence intervals obtained via the asymptotic limit theory as well as with the bootstrap. Of course, pointwise confidence intervals have a different goal than confidence bands. The pointwise intervals will be be shorter but the the confidence level will not hold simultaneously across multiple locations. In contrast, the method we introduce here comes with strong guarantees in terms of finite sample valid coverage levels across locations.

2 Constructing a confidence band for a log-concave density

Given data $X_{1},\ldots,X_{n}$ from a log-concave density $f$ we want to find functions $\hat{\ell}(x)=\hat{\ell}(x,X_{1},\ldots,X_{n})$ and $\hat{\mu}(x)=\hat{\mu}(x,X_{1},\ldots,X_{n})$ such that

{\rm I\!P}_{f}\left\{\hat{\ell}(x)\leq f(x)\leq\hat{\mu}(x)\ \mbox{ for all }x\in{\bf R}\right\}\geq 1-\alpha

for a given confidence level $1-\alpha\in(0,1)$ . It is well known that in the case of a general density $f$ no non-trivial confidence interval $(\hat{\ell}(x),\hat{\mu}(x))$ exists, see e.g. Donoho (1988). However, assuming a shape-constraint for $f$ such as log-concavity allows to construct pointwise and uniform confidence statements as follows:

Let ${\cal C}_{n}(\alpha)$ be a $1-\alpha$ confidence set for the distribution function $F$ of $f$ , i.e.

{\rm I\!P}_{F}\left\{F\in{\cal C}_{n}(\alpha)\right\}\geq 1-\alpha.

(1)

Such a nonparametric confidence set always exists, e.g. the Kolmogorov-Smirnov bands give a confidence set for $F$ (albeit a non-optimal one). Define

\hat{\ell}(x):=\ \inf_{f\mbox{ is log-concave and }F\in{\cal C}_{n}(\alpha)}f(x)

(2)

and define $\hat{\mu}(x)$ analogously with sup in place of inf. If $f$ is log-concave then (1) and (2) imply

{\rm I\!P}_{f}\left\{\hat{\ell}(x)\leq f(x)\leq\hat{\mu}(x)\right\}\geq 1-\alpha,

so we obtain a $1-\alpha$ confidence interval for $f(x)$ by solving the optimization problem (2). Moreover, if we solve (2) at multiple locations $x_{1},\ldots,x_{m}$ , then we obtain

{\rm I\!P}_{f}\left\{\hat{\ell}(x_{i})\leq f(x_{i})\leq\hat{\mu}(x_{i})\ \mbox{ for all }i=1,\ldots,m\right\}\geq 1-\alpha.

(3)

So the coverage probability is automatically simultaneous across multiple locations and comes with a finite sample guarantee, since it is inherited from the confidence set ${\cal C}_{n}$ in (1). Likewise, the quality of the confidence band, as measured e.g. by the width $\hat{\mu}(x)-\hat{\ell}(x)$ , will also derive from ${\cal C}_{n}$ , which therefore plays a central role in this approach. Finally, the log-concavity constraint allows to extend the confidence set (3) to a confidence band on the real line, as we will show in Section 2.4.

Hengartner and Stark (1995), Dümbgen (1998), Dümbgen (2003) and Davies and Kovac (2004) employ the above approach for inference about a unimodal or a $k$ -modal density. Here we introduce a new confidence set ${\cal C}_{n}(\alpha)$ for $F$ . This confidence set is adapted from methodology developed in the abstract Gaussian White Noise model by Walther and Perry (2019) for optimal inference in settings related to the one considered here. Therefore this confidence set should also prove useful for the works about inference in the unimodal and $k$ -modal setting cited above.

The key conceptual problem for solving the optimization problem (2) is that $f$ is infinite dimensional. We will overcome this by using the log-concavity of $f$ to relax ${\cal C}_{n}(\alpha)$ to a finite dimensional superset, which makes it possible to compute (2) with fast optimization algorithms. We will address these tasks in turn in the following subsections.

2.1 A confidence set for $F$

Given $X_{1},\ldots,X_{n}$ i.i.d. from the continuous cdf $F$ we set $s_{n}:=\lceil\log_{2}\log n\rceil$ and

x_{i}:=X_{\left(1+(i-1)2^{s_{n}}\right)},\ \ i=1,\ldots,m:=\left\lfloor\frac{n-1}{2^{s_{n}}}\right\rfloor+1,

(4)

where $X_{(j)}$ denotes the $j$ th order statistic. Our analysis will use only the subset $\{x_{i}\}$ of the data, i.e. the set containing every $\log n\,$ th order statistic; see Remark 3 for why this is sufficient.

Translating the methodology of the ‘Bonferroni scan’ developed in Walther and Perry (2019) from the Gaussian White Noise model to the density setting suggests employing a confidence set of the form

{\cal C}_{n}(\alpha)\ :=\ \left\{F:\ c_{jkB}\leq F(x_{k})-F(x_{j})\leq d_{jkB}\mbox{ for all }(j,k)\in{\cal I}=\bigcup_{B}{\cal I}_{B}\right\}.

with $c_{jkB},d_{jkB},{\cal I}$ given below. The idea is to choose an index set ${\cal I}$ that is rich enough to detect relevant deviations from the empirical distribution, but which is also sparse enough so that the $|{\cal I}|$ constraints can be combined with a simple weighted Bonferroni adjustment and still result in optimal inference. The second key ingredient of this construction is to let the weights of the Bonferroni adjustment depend on $j-i$ in a certain way. See Walther and Perry (2019) for a comparison of the finite sample and asymptotic performance of this approach with other relevant calibrations, such as the ones used in the works cited above.

Note that the confidence set ${\cal C}_{n}(\alpha)$ checks the probability content of random intervals $(x_{j},x_{k})$ , which automatically adapt to the empirical distribution. This makes it possible to detect relevant deviations from the empirical distribution with a relatively small number of such intervals, which is key for making the Bonferroni adjustment powerful as well as for efficient computation. Moreover, using such random intervals makes the bounds $c_{jkB},d_{jkB}$ distribution-free since $F(x_{k})-F(x_{j})\sim\textrm{ Beta}((k-j)2^{s_{n}},n+1-(k-j)2^{s_{n}})$ , see Ch. 3.1 in Shorack and Wellner (1986).

The precise specifications of $c_{jkB},d_{jkB},{\cal I}$ are as follows:

	$\displaystyle{\cal I}$	$\displaystyle:=\bigcup_{B=0}^{B_{max}}{\cal I}_{B},\ \mbox{ where $B_{max}:=\lfloor\log_{2}\frac{n}{8}\rfloor-s_{n}$}$
	$\displaystyle{\cal I}_{B}$	$\displaystyle:=\Bigl{\{}(j,k):\ j=1+(i-1)2^{B},\ k=1+i2^{B}\ \mbox{ for }i=1,\ldots,n_{B}:=\Big{\lfloor}\frac{n-1}{2^{B+s_{n}}}\Big{\rfloor}\Bigr{\}}$
	$\displaystyle c_{jkB}$	$\displaystyle:=c_{B}:=q\textrm{Beta }\Bigl{(}\frac{\alpha}{2(B+2)n_{B}t_{n}},2^{B+s_{n}},n+1-2^{B+s_{n}}\Bigr{)}$
	$\displaystyle d_{jkB}$	$\displaystyle:=d_{B}:=q\textrm{Beta }\Bigl{(}1-\frac{\alpha}{2(B+2)n_{B}t_{n}},2^{B+s_{n}},n+1-2^{B+s_{n}}\Bigr{)}$

where $t_{n}:=\sum_{B=0}^{B_{max}}\frac{1}{B+2}$ and $q\textrm{Beta }(\alpha,r,s)$ denotes the $\alpha$ -quantile of the beta distribution with parameters $r$ and $s$ . The term $\frac{1}{B+2}$ is a weighting factor in the Bonferroni adjustment which results in an advantageous statistical performance, see Walther and Perry (2019). It follows from the union bound that ${\rm I\!P}_{F}(F\in{\cal C}_{n}(\alpha))\geq 1-\alpha$ whenever $F$ is continuous.

Remarks: 1. An alternative way to control the distribution of $F(x_{k})-F(x_{j})$ is via a log-likelihood ratio type transformation and Hoeffding’s inequality, see Rivera and Walther (2013) and Li, Munk, Sieling and Walther (2020). This results in a loss of power due to the slack in Hoeffding’s inequality and the slack from inverting the log-likelihood ratio transformation with an inequality. Simulations show that the above approach using an exact beta distribution is less conservative despite the use of Bonferroni’s inequality to combine the statistics across ${\cal I}$ .

2. The inference is based on the statistic $F((x_{j},x_{k}))$ , i.e. the unknown $F$ evaluated on the random interval $(x_{j},x_{k})$ , rather than on the more commonly used statistic $F_{n}(I)$ , which evaluates the empirical measure on deterministic intervals $I$ . The latter statistic follows a binomial distribution whose discreteness makes it difficult to combine these statistics across ${\cal I}$ using Bonferroni’s inequality without incurring substantial conservatism and hence loss of power. This is another important reason for using random intervals $(x_{j},x_{k})$ besides the adaptivity property mentioned above. Moreover, a deterministic system of intervals would have to be anchored around the range of the data and this dependence on the data is difficult to account for and is therefore typically glossed over in the inference.

3. The definition of $x_{i}$ in (4) means that we do not consider intervals $(X_{(j)},X_{(k)})$ with $k-j<\log n$ . Thus, as opposed to the regression setting in Walther and Perry (2019) we omit the first block¹¹1We also shift the index $B$ to let it start at 0 rather than at 2. This results in a simpler notation but does not change the methodology. of intervals. This derives from the folklore knowledge in density estimation that at least $\log n$ observations are required in order to obtain consistent inference simultaneously across such intervals. Indeed, this choice is sufficient to yield the asymptotic optimality result in Theorem 1.

We further simplify the construction in Walther and Perry (2019) by restricting ourselves to a dyadic spacing of the indices $k-j$ since we already obtain quite satisfactory results with this set of intervals.

2.2 Bounds for $\int_{a}^{b}f$ when $f$ is log-concave

The confidence set ${\cal C}_{n}(\alpha)$ describes a set of plausible distributions in terms of $\int_{x_{j}}^{x_{k}}f(t)\,dt$ for infinite dimensional $f$ . In the special case when $f$ is log-concave it is possible to construct a finite dimensional superset of ${\cal C}_{n}(\alpha)$ by deriving bounds for this integral in terms of functions of a finite number of variables:

Lemma 1

Let $f$ be a univariate log-concave function. For given $x_{1}<\ldots<x_{m}$ write $\ell_{i}:=\log f(x_{i})$ , $i=1,\ldots,m$ . Then there exist real numbers $g_{2},\ldots,g_{m-1}$ such that

\ell_{j}\leq\ell_{i}+g_{i}\,(x_{j}-x_{i})\ \ \mbox{ for all }i\in\{2,\ldots,m-1\},\ j\in\{i-1,i+1\}

and

(x_{i+1}-x_{i})\exp(\ell_{i})\,E(\ell_{i+1}-\ell_{i})\ \leq\ \int_{x_{i}}^{x_{i+1}}f(t)\,dt\ \leq\ \begin{cases}\exp(\ell_{i})(x_{i+1}-x_{i})\,E\bigl{(}g_{i}(x_{i+1}-x_{i})\bigr{)},&i\in\{2,\ldots,m-1\}\\ \exp(\ell_{i+1})(x_{i+1}-x_{i})\,E\bigl{(}g_{i+1}(x_{i}-x_{i+1})\bigr{)},&i\in\{1,\ldots,m-2\}\end{cases}

where

E(s)\ :=\ \int_{0}^{1}\exp(st)\,dt\ =\begin{cases}\frac{\exp(s)-1}{s}&\mbox{ if }s\neq 0\\ 1&\mbox{ if }s=0\end{cases}

is a strictly convex and infinitely often differentiable function.

Importantly, the bounds given in the lemma are convex and smooth functions of the $g_{i}$ and $\ell_{i}$ , despite the fact that these variables appear in the denominator in the formula for $E$ . This makes it possible to bring fast optimization routines to bear on the problem (2).

2.3 Computing pointwise confidence intervals

We are now in position to define a superset of ${\cal C}_{n}(\alpha)$ by relaxing the inequalities $c_{B}\leq\int_{x_{j}}^{x_{k}}f(t)\,dt\leq d_{B}$ in the definition of ${\cal C}_{n}(\alpha)$ . To this end define for $i=1,\ldots,m-1$ the functions

	$\displaystyle L_{i}({\boldsymbol{x}},{\boldsymbol{\ell}})$	$\displaystyle:=(x_{i+1}-x_{i})\exp(\ell_{i})\,E(\ell_{i+1}-\ell_{i})$
	$\displaystyle U_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}})$	$\displaystyle:=\begin{cases}\exp(\ell_{i})(x_{i+1}-x_{i})\,E\bigl{(}g_{i}(x_{i+1}-x_{i})\bigr{)},&i=m-1\\ \exp(\ell_{i+1})(x_{i+1}-x_{i})\,E\bigl{(}g_{i+1}(x_{i}-x_{i+1})\bigr{)},&i\in\{1,\ldots,m-2\}\end{cases}$
	$\displaystyle V_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}})$	$\displaystyle:=\begin{cases}\exp(\ell_{i})(x_{i+1}-x_{i})\,E\bigl{(}g_{i}(x_{i+1}-x_{i})\bigr{)},&i\in\{2,\ldots,m-1\}\\ \exp(\ell_{i+1})(x_{i+1}-x_{i})\,E\bigl{(}g_{i+1}(x_{i}-x_{i+1})\bigr{)},&i=1\end{cases}$

where ${\boldsymbol{x}}=(x_{1},\ldots,x_{m})$ , ${\boldsymbol{\ell}}=(\ell_{1},\ldots,\ell_{m})$ , ${\boldsymbol{g}}=(g_{1},\ldots,g_{m-1})$ and $E(\cdot)$ is defined in Lemma 1.

Given the subset $x_{1}<\ldots<x_{m}$ of the order statistics defined in (4), we define $\tilde{{\cal C}}_{n}(\alpha)$ to be the set of densities $f$ for which there exist real $g_{1},\ldots,g_{m-1}$ such that $\ell_{i}:=\log f(x_{i})$ , $i=1,\ldots,m$ , satisfy (5)-(8):

$\displaystyle\ell_{j}$	$\displaystyle\leq\ell_{i}+g_{i}(x_{j}-x_{i})\ \ \mbox{ for all }i\in\{2,\ldots,m-1\},\ j\in\{i-1,i+1\}$	(5)
$\displaystyle\mbox{For }B=0,\ldots,B_{max}$	$\displaystyle:$
$\displaystyle c_{B}\$	$\displaystyle\leq\ \sum_{i=j}^{k-1}U_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}})\ \ \mbox{ for all }(j,k)\in{\cal I}_{B}$	(6)
$\displaystyle c_{B}\$	$\displaystyle\leq\ \sum_{i=j}^{k-1}V_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}})\ \ \mbox{ for all }(j,k)\in{\cal I}_{B}$	(7)
$\displaystyle\sum_{i=j}^{k-1}L_{i}({\boldsymbol{x}},{\boldsymbol{\ell}})\$	$\displaystyle\leq\ d_{B}\ \ \mbox{ for all }(j,k)\in{\cal I}_{B}.$	(8)

Now we can implement a computable version of the confidence bound (2) by optimizing over $\tilde{{\cal C}}_{n}(\alpha)$ rather than over ${\cal C}_{n}(\alpha)$ . Note that if $f$ is log-concave then it follows from Lemma 1 that $f\in{\cal C}_{n}(\alpha)$ implies $f\in\tilde{{\cal C}}_{n}(\alpha)$ . This proves the following key result:

Proposition 1

If $f$ is log-concave then ${\rm I\!P}_{f}\{f\in\tilde{{\cal C}}_{n}(\alpha)\}\geq 1-\alpha$ . Consequently, if we define pointwise lower and upper confidence bounds at the $x_{i}$ , $i=1,\ldots,m$ , via the optimization problems

$\displaystyle\hat{\ell}(x_{i}):=\$	$\displaystyle\min\ \ell(x_{i})$	(9)
	$\displaystyle\mbox{subject to }f\in\tilde{{\cal C}}_{n}(\alpha),\mbox{ i.e. subject to (\ref{CONC})-(\ref{UP})}$
$\displaystyle\hat{\mu}(x_{i}):=\$	$\displaystyle\max\ \ell(x_{i})$
	$\displaystyle\mbox{subject to }f\in\tilde{{\cal C}}_{n}(\alpha),\mbox{ i.e. subject to (\ref{CONC})-(\ref{UP})},$

then the following simultaneous confidence statement holds whenever $f$ is log-concave:

{\rm I\!P}_{f}\left\{\exp(\hat{\ell}(x_{i}))\leq f(x_{i})\leq\exp(\hat{\mu}(x_{i}))\ \mbox{ for all }i=1,\ldots,m\right\}\geq 1-\alpha.

It is an important feature of these confidence bounds that they come with a finite sample guaranteed confidence level $1-\alpha$ . On the other hand, it is desirable that the construction is not overly conservative (i.e. has coverage not much larger than $1-\alpha$ ) as otherwise it would result in unnecessarily wide confidence bands. This is the motivation for deriving a statistically optimal confidence set in Section 2.1 and for deriving bounds in Lemma 1 that are sufficiently tight. Indeed, it will be shown in Section 4 that the above construction results in statistically optimal confidence bands.

2.4 Constructing confidence bands

The simultaneous pointwise confidence bounds $\left(\hat{\ell}(x_{i}),\hat{\mu}(x_{i})\right),i=1,\ldots,m$ , from the optimization problem (9) imply a confidence band on the real line due to the concavity of $\log f$ . In more detail, we can extend the definition of $\hat{\ell}$ to the real line simply by interpolating between the $\hat{\ell}(x_{i})$ :

\hat{\ell}(x):=\begin{cases}\hat{\ell}(x_{i})+(x-x_{i})\frac{\hat{\ell}(x_{i+1})-\hat{\ell}(x_{i})}{x_{i+1}-x_{i}}&\mbox{if }x\in[x_{i},x_{i+1}),\ i\in\{1,\ldots,m-1\}\\ -\infty&\mbox{otherwise.}\end{cases}

(10)

Then $\log f(x_{i})\geq\hat{\ell}(x_{i})$ for $i=1,\ldots,m$ implies $\log f(x)\geq\hat{\ell}(x)$ for $x\in{\bf R}$ since $\log f$ is concave and $\hat{\ell}$ is piecewise linear. (In fact, it follows from (9) that $\hat{\ell}$ is also concave.)

In order to construct an upper confidence bound note that concavity of $\log f$ together with $\hat{\ell}(x_{i})\leq\log f(x_{i})\leq\hat{\mu}(x_{i})$ for all $i\in\{1,\ldots,m\}$ implies for $x>x_{k}$ with $k\in\{2,\ldots,m\}$ :

	$\displaystyle\frac{\log f(x)-\hat{\mu}(x_{k})}{x-x_{k}}$	$\displaystyle\leq\frac{\log f(x)-\log f(x_{k})}{x-x_{k}}\leq\min_{j\in\{1,\ldots,k-1\}}\frac{\log f(x_{k})-\log f(x_{j})}{x_{k}-x_{j}}$
		$\displaystyle\leq\min_{j\in\{1,\ldots,k-1\}}\frac{\hat{\mu}(x_{k})-\hat{\ell}(x_{j})}{x_{k}-x_{j}}\ =:L_{k}$

and likewise for $x<x_{k}$ with $k\in\{1,\ldots,m-1\}$ :

\frac{\hat{\mu}(x_{k})-\log f(x)}{x_{k}-x}\,\geq\,\max_{j\in\{k+1,\ldots,m\}}\frac{\hat{\ell}(x_{j})-\hat{\mu}(x_{k})}{x_{j}-x_{k}}\ =:R_{k}

Hence $\log f$ is bounded above by

\hat{\mu}(x):=\begin{cases}\hat{\mu}(x_{i+1})+R_{i+1}(x-x_{i+1})&\mbox{if }x\in(x_{i},x_{i+1}),\ i\in\{0,1\},\ \mbox{ where }x_{0}:=-\infty\\ M_{i}(x)&\mbox{if }x\in[x_{i},x_{i+1}),\ i\in\{2,\dots,m-2\}\\ \hat{\mu}(x_{i})+L_{i}(x-x_{i})&\mbox{if }x\in[x_{i},x_{i+1}),\ i\in\{m-1,m\},\ \mbox{ where }x_{m+1}:=\infty\end{cases}

with

	$\displaystyle M_{i}(x)$	$\displaystyle:=\min\Bigl{(}\hat{\mu}(x_{i})+L_{i}(x-x_{i}),\,\hat{\mu}(x_{i+1})+R_{i+1}(x-x_{i+1})\Bigr{)}$
		$\displaystyle=\Bigl{(}\hat{\mu}(x_{i})+L_{i}(x-x_{i})\Bigr{)}1(x\in[x_{i},\bar{x}_{i}))\,+\,\Bigl{(}\hat{\mu}(x_{i+1})+R_{i+1}(x-x_{i+1})\Bigr{)}1(x\in[\bar{x}_{i},x_{i+1}))$

where $\bar{x}_{i}:=\frac{\hat{\mu}(x_{i+1})-\hat{\mu}(x_{i})+L_{i}x_{i}-R_{i+1}x_{i+1}}{L_{i}-R_{i+1}}$ .

Thus we proved:

Proposition 2

If $f$ is log-concave then

{\rm I\!P}_{f}\left\{\exp(\hat{\ell}(x))\leq f(x)\leq\exp(\hat{\mu}(x))\ \mbox{ for all }x\in{\bf R}\right\}\geq 1-\alpha.

The upper bound $\hat{\mu}(x)$ need not be concave but it is minimal in the sense that it can be shown that for every real $x$ there exist a concave function $g$ with $\hat{\ell}(x_{i})\leq g(x_{i})\leq\hat{\mu}(x_{i})$ for all $i\in\{1,\ldots,m\}$ and $g(x)=\hat{\mu}(x)$ .

As an alternative to $\exp(\hat{\mu}(x))$ we tried a simple interpolation between the points $(x_{i},\exp(\hat{\mu}(x_{i})))$ . This interpolation will result in a smoother bound than $\exp(\hat{\mu}(x))$ , but the coverage guarantee of Proposition 2 does not apply any longer. However, the difference between $\exp(\hat{\mu}(x))$ and the interpolation will vanish as the sample size increases (or by increasing the number $m$ of design points $x_{i}$ in (4) for a given sample size $n$ ), and the simulations in Section 5 show that the empirical coverage exceeds the nominal level in all cases considered. Therefore we also recommend this interpolation as a simple and smoother alternative to $\exp(\hat{\mu}(x))$ .

Finally, we point out that the computational effort can be lightened simply by solving the optimization problem (9) for a subset of $\{x_{i},\,1\leq i\leq m\}$ and then constructing $\hat{\ell}$ and $\hat{\mu}$ as described above based on that smaller subset of $x_{i}$ . Such a confidence band will still satisfy Proposition 2, but it will be somewhat wider at locations between those design points $x_{i}$ as it is based on fewer pointwise confidence bounds. Hence there is a trade-off between the width of the band and the computational effort required. While a larger subset of the $x_{i}$ will result in a somewhat reduced width of the band between the $x_{i}$ , there are diminishing returns as the width at the $x_{i}$ will not change. It follows from Theorem 1 below that solving the optimization problem (9) for $\{x_{i},\,1\leq i\leq m\}$ with $m$ given in (4) is sufficient to produce statistically optimal confidence bands in a representative setting.

3 Solving the optimization problem

Next we describe a method for computing the pointwise confidence intervals $(\hat{\ell}(x_{i}),\hat{\mu}(x_{i})),\;i=1,\ldots,m$ , from observations $X_{i},\;i=1,\ldots,n$ , by efficiently solving the optimization problems (9). Constructing the confidence band is then straightforward with the post-processing steps given in Section 2.4.

Inspecting the optimization problems (9), we see that these problems possess some interesting structure: The criterion functions are linear, and the constraints (5) and (8) are convex. However, the constraints (6) and (7) are non-convex. Finding the global minimizer of a non-convex optimization problem (even a well-structured one) can be challenging; instead, we focus on a method for finding critical points of the problems (9). Taking a closer look at the non-convex constraints (6) and (7), we make the simple observation that they may be expressed as the difference of two convex functions (namely, a constant function minus a convex function). This property puts the problems (9) into the special class of non-convex problems commonly referred to as difference of convex programs (Hartman, 1959; Tao, 1986; Horst and Thoai, 1999; Horst et al., 2000), for which a critical point can be efficiently found. The class of difference of convex programs is quite broad, encompassing many problems encountered in practice, with a good amount of research into this area continuing on today. Important references include Hartman (1959), Tao (1986), Horst and Thoai (1999), Horst et al. (2000), Yuille and Rangarajan (2003), Smola et al. (2005), and Lipp and Boyd (2016).

Algorithm 1 Penalty convex-concave procedure for computing pointwise confidence intervals for a log-concave density

Input: Subset of observations

x_{t},\;t=1,\ldots,m

; collection of interval endpoints

{\cal I}=\bigcup_{B}{\cal I}_{B}

; initial points

{\boldsymbol{\ell}}^{(0)}

{\boldsymbol{g}}^{(0)}

; initial penalty strength

\tau_{0}>0

; penalty growth factor

\kappa>1

; maximum penalty strength

\tau_{\max}>\tau_{0}

; maximum number of iterations

K_{\max}

For

t=1,\ldots,m

K=0,\ldots,K_{\max}

Convexify the constraints (6) and (7), by forming the linearizations, for

i=1,\ldots,m-1

	$\displaystyle\hat{U}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})$	$\displaystyle=U_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})+\big{\langle}\nabla U_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)}),\,({\boldsymbol{\ell}},{\boldsymbol{g}})-({\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\big{\rangle}$
	$\displaystyle\hat{V}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})$	$\displaystyle=V_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})+\big{\langle}\nabla V_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)}),\,({\boldsymbol{\ell}},{\boldsymbol{g}})-({\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\big{\rangle}.$

Solve the pair of convexified problems

$\displaystyle\ell_{t}^{(K+1)}=$	$\displaystyle\min\ \ell_{t}+\tau_{K}\cdot\sum_{B=0}^{B_{max}}\sum_{(j,k)\in{\cal I}_{B}}s_{B,j,k}$	(11)
	$\displaystyle\mbox{subject to \eqref{CONC}, \eqref{UP}},\textrm{ and}$
	$\displaystyle\hskip 46.97505pt\mbox{For }B=0,\ldots,B_{max}:$
	$\displaystyle\hskip 126.47249ptc_{B}-\sum_{i=j}^{k-1}\hat{U}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\leq s_{B,j,k}\;\mbox{ for all }(j,k)\in{\cal I}_{B}$
	$\displaystyle\hskip 126.47249ptc_{B}-\sum_{i=j}^{k-1}\hat{V}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\leq s_{B,j,k}\;\mbox{ for all }(j,k)\in{\cal I}_{B}$
	$\displaystyle\hskip 126.47249pts_{B,j,k}\geq 0\;\mbox{ for all }(j,k)\in{\cal I}_{B}$

$\displaystyle\mu_{t}^{(K+1)}=$	$\displaystyle\max\ \ell_{t}-\tau_{K}\cdot\sum_{B=0}^{B_{max}}\sum_{(j,k)\in{\cal I}_{B}}s_{B,j,k}$	(12)
	$\displaystyle\mbox{subject to \eqref{CONC}, \eqref{UP}},\textrm{ and}$
	$\displaystyle\hskip 46.97505pt\mbox{For }B=0,\ldots,B_{max}:$
	$\displaystyle\hskip 126.47249ptc_{B}-\sum_{i=j}^{k-1}\hat{U}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\leq s_{B,j,k}\;\mbox{ for all }(j,k)\in{\cal I}_{B}$
	$\displaystyle\hskip 126.47249ptc_{B}-\sum_{i=j}^{k-1}\hat{V}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\leq s_{B,j,k}\;\mbox{ for all }(j,k)\in{\cal I}_{B}$
	$\displaystyle\hskip 126.47249pts_{B,j,k}\geq 0\;\mbox{ for all }(j,k)\in{\cal I}_{B}.$

Update the penalty strength, by setting

\tau_{K+1}=\min\{\kappa\cdot\tau_{K},\,\tau_{\max}\}

Output: Pointwise confidence intervals

(\ell_{t}^{(K)}\mu_{t}^{(K)}),\;t=1,\ldots,m.

A natural approach to finding a critical point of a difference of convex program is to linearize the non-convex constraints, then solve the convexified problem using any suitable off-the-shelf solver, and repeating these steps as necessary. This strategy underlies the well-known convex-concave procedure in Yuille and Rangarajan (2003), a popular heuristic for difference of convex programs. In more detail, the convex-concave iteration as applied to the problems (9) works as follows: Given feasible initial points, we first replace the (non-convex) constraints (6) and (7) by their first-order Taylor approximations centered around the inital points. Formally, letting ${\boldsymbol{\ell}}^{(K)}$ and ${\boldsymbol{g}}^{(K)}$ denote the log-densities and subgradients on iteration $K$ , respectively, we form

	$\displaystyle\hat{U}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})$	$\displaystyle:=U_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})+\big{\langle}\nabla U_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)}),\,({\boldsymbol{\ell}},{\boldsymbol{g}})-({\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\big{\rangle}$		(13)
	$\displaystyle\hat{V}_{i}({\boldsymbol{x}},{\boldsymbol{\ell}},{\boldsymbol{g}};{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})$	$\displaystyle:=V_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})+\big{\langle}\nabla V_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)}),\,({\boldsymbol{\ell}},{\boldsymbol{g}})-({\boldsymbol{\ell}}^{(K)},{\boldsymbol{g}}^{(K)})\big{\rangle},$		(14)

for $i=1,\ldots,m-1$ . We then solve the convexified problems (using the constraints (13), (14) instead of (6), (7)) with any off-the-shelf solver. Then we re-compute the approximations using the obtained solutions to the convexified problems and repeat these steps until an appropriate stopping criterion has been satisfied (e.g., some pre-determined maximum number of iterations has been reached, the change in criterion values are smaller than some specified tolerance, the sum of the slack variables is less than some tolerance, and/or we have that $\tau_{K}\geq\tau_{\max}$ ). From this description, it may be apparent to the reader that the convex-concave procedure is actually a generalization of the majorization-minimization class of algorithms (which includes the well-known expectation-maximization algorithm as a special case).

We give a complete description of the convex-concave procedure as applied to the optimization problems (9) in Algorithm 1 appearing above, along with one important modification that we explain now. In practice it is not easy to obtain feasible initial points for the problems (9). Therefore, the penalty convex-concave procedure, a modification to the basic convex-concave procedure that was introduced by Le Thi and Dinh (2014), Dinh and Le Thi (2014), and Lipp and Boyd (2016), works around this issue by allowing for an (arbitrary) infeasible initial point and then gradually driving the iterates into feasibility by adding a penalty for constraint violations into the criterion that grows with the number of iterations (explaining the word “penalty” in the name of the procedure), through the use of slack variables.

Standard convergence theory for the (penalty) convex-concave procedure (see, e.g., Section 3.1 in Lipp and Boyd (2016) as well as Theorem 10 in Sriperumbudur and Lanckriet (2009) and Proposition 1 in Khamaru and Wainwright (2018) tells us that the criterion values (11) and (12) generated by Algorithm 1 converge. Moreover, under regularity conditions (see Section 3.1 in Lipp and Boyd (2016)), the iterates generated by Algorithm 1 converge to critical points of the problems (9). At convergence, the pointwise confidence intervals generated by Algorithm 1 can be turned in confidence bands as described in Section 2.4.

Finally, we mention that although not necessary, additionally linearizing the (convex) constraints (8) around the previous iterate, i.e., forming

L_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)})+\big{\langle}\nabla L_{i}({\boldsymbol{x}},{\boldsymbol{\ell}}^{(K)}),\,{\boldsymbol{\ell}}-{\boldsymbol{\ell}}^{(K)}\big{\rangle},\;i=j,\ldots,k-1,\;(j,k)\in{\cal I}_{B},\;B=0,\ldots,B_{max},

on iteration $K$ , can help circumvent numerical issues. Furthermore, as all the constraints in the problems (11) and (12) are now evidently affine functions, this relaxation has the added benefit of turning the problems (11) and (12) into linear programs, for which there (of course) exist heavily optimized solvers.

4 Large sample statistical performance

The large sample performance of the log-concave MLE has been studied intensively, see e.g. Dümbgen and Rufibach (2009), Kim and Samworth (2016) and Doss and Wellner (2016). The main message is that the MLE attains the optimal minimax rate of convergence of $O\left(n^{-2/5}\right)$ with respect to various global loss functions. Recently, Kim, Guntuboyina and Samworth (2018) have shown that the MLE can achieve a faster rate of convergence when the log density is $k$ -affine, i.e. when $\log f$ consists of $k$ linear pieces . They show that the MLE is able to adapt to this simpler model, where it will converge with nearly the parametric rate, namely with $O\left(n^{-1/2}\log^{5/8}n\right)$ . Here we show that the construction of our confidence band via the particular confidence set ${\cal C}_{n}(\alpha)$ will also result in a nearly parametric rate of convergence for the width of the confidence band in that case. To this end, we first consider the case where some part of $f$ is log-linear:

Theorem 1

Let $f$ be a log-concave density and suppose $\log f$ is linear on some interval $J$ . (So $J$ may be a proper subset of the support of $f$ ). Then on every closed interal $I\subset int\,J$ :

{\rm I\!P}_{f}\left\{\sup_{x\in I}\Bigl{|}\hat{u}(x)-f(x)\Bigr{|}\ \leq\ C\sqrt{\frac{\log\log n}{n}}\right\}\rightarrow 1

for some constant $C$ , and the same statement holds for $\hat{\ell}$ in place of $\hat{u}$ . In particular, the width of the confidence band satisfies $\max_{x\in I}\bigl{(}\hat{u}(x)-\hat{\ell}(x)\bigr{)}\leq 2C\sqrt{\frac{\log\log n}{n}}$ with probability converging to 1.

If there are $k$ such intervals, then the theorem holds for the maximum width over the $k$ intervals. This includes $k$ -affine log densities as a special case.

We conjecture that the width of the confidence band will likewise achieve the optimal minimax rate if $\log f$ is smooth rather than linear.

5 Some examples

Finally, we present some numerical examples of our methodology, highlighting the empirical coverage and widths of our confidence bands as well as the computational cost of computing the bands, for a number of different distributions.

To calculate coverage, we first simulated $n\in\{100,1000\}$ observations from a (i) standard normal distribution, (ii) uniform distribution on $[-10,10]$ , (iii) chi-squared distribution with three degrees of freedom, and (iv) exponential distribution with parameter 1. Then, we computed our confidence bands from the data by running the penalty convex-concave procedure described in Algorithm 1 and then computing $\exp(\hat{\ell}(x))$ and $\exp(\hat{\mu}(x))$ as discussed in Section 2.4, where $\exp(\hat{\mu}(x))$ was computed by linearly interpolating between the $(x_{i},\exp(\hat{\mu}(x_{i})))$ . We repeated these two steps (simulating data and computing bands) 1000 times. We calculated the empirical coverage for each density $f$ by evaluating the band at 10000 points $\{t_{j}\}$ , evenly spaced across the range of the data, to check whether $\exp(\hat{\ell}(t_{j}))\leq f(t_{j})\leq\exp(\hat{\mu}(t_{j}))$ for all $j$ , and then computed the empirical frequency of this event across the 1000 repetitions. In order to calculate the widths of the bands, we averaged the widths at the sample quartiles over all of the repetitions. We calculated the computational effort by averaging the runtimes, obtained by running Algorithm 1 on a workstation with four Intel E5-4620 2.20GHz processors and 15 GB of RAM, over all the repetitions. To speed up the computation for $n\geq 1000$ , we ran Algorithm 1 on a subset of 30% of the points $x_{i},\;i=1,\ldots,m$ , as discussed at the end of Section 2.4; the coverages and widths were virtually indistinguishable from those obtained using the full set of points $x_{i},\;i=1,\ldots,m$ .

Algorithm 1 requires a few tuning parameters, which are important for assuring quick convergence. In general, we found that the initial penalty strength $\tau_{0}$ , the maximum penalty strength $\tau_{\max}$ , and the penalty growth factor $\kappa$ had the greatest impact on convergence. In our experience, setting $\tau_{0}$ to a small value and $\tau_{\max}$ to a large value worked well; we used $\tau_{0}\in\{10^{-5},10^{-4},10^{-3}\}$ and $\tau_{\max}\in\{10^{3},10^{4},10^{5}\}$ , with the most suitable values depending on the characteristics of the problem. We experimented with various penalty growth factors $\kappa\in\{1,2,\ldots,10\}$ , finding that the best value of $\kappa$ again varied with the problem setup. We always set the maximum number of iterations $K_{\max}=50$ as our method usually converged after around 20-30 iterations across all problem settings. We initialized the points ${\boldsymbol{\ell}}^{(0)},{\boldsymbol{g}}^{(0)}$ randomly. Finally, we set the miscoverage level $\alpha=0.1$ but we also report results for $\alpha=0.05$ .

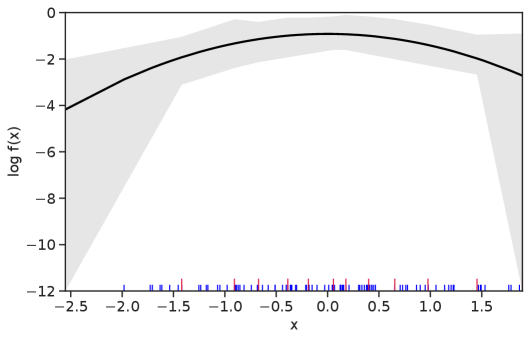
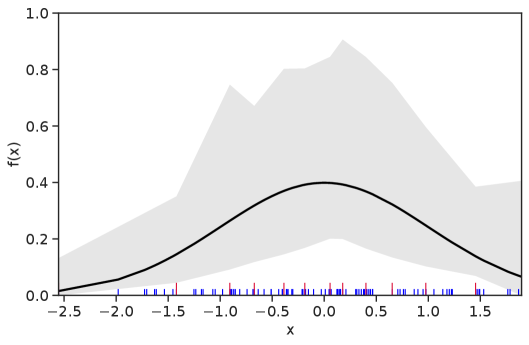
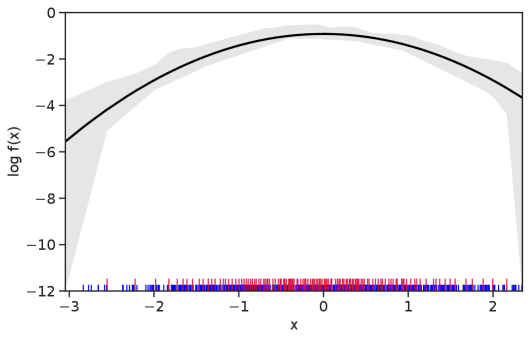
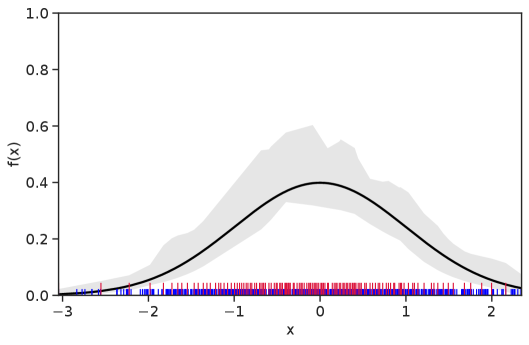
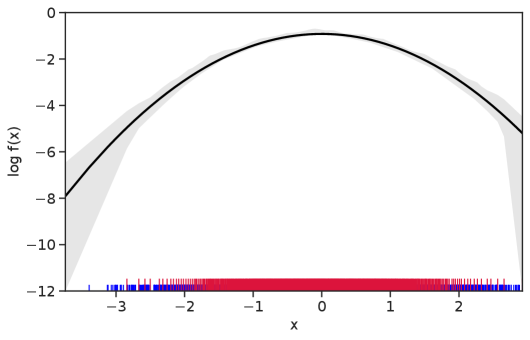
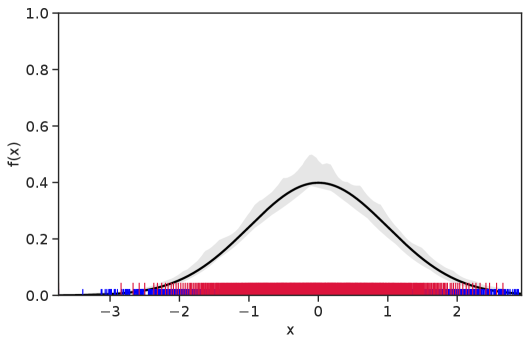
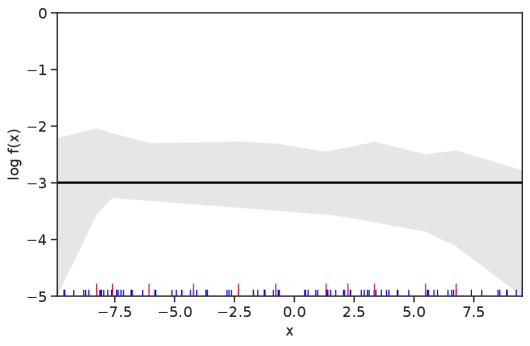
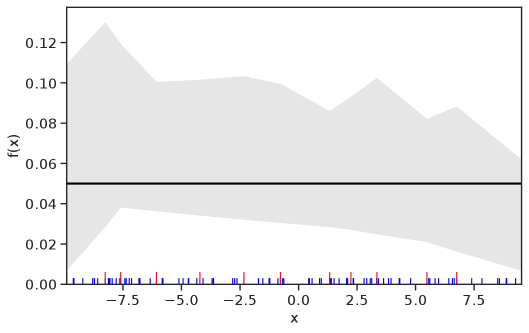
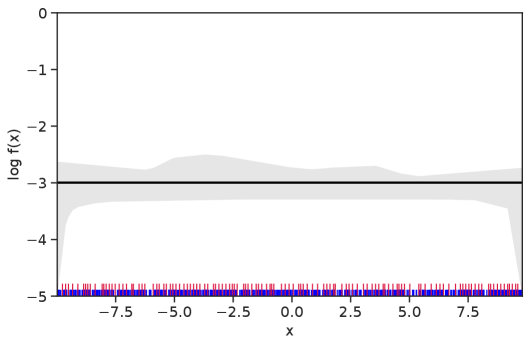
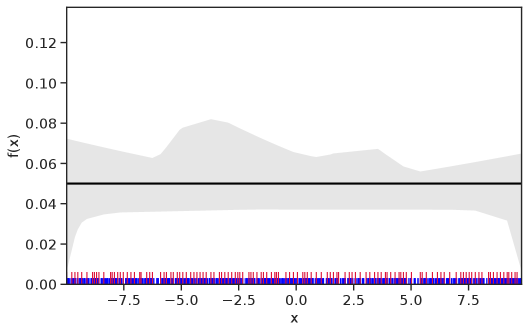
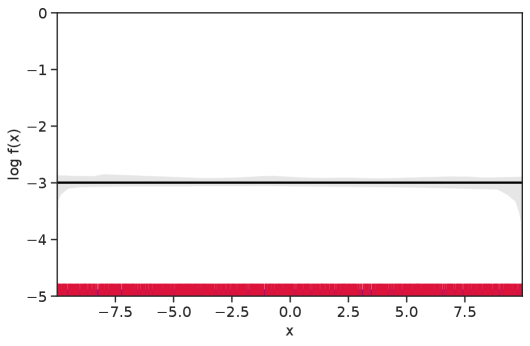
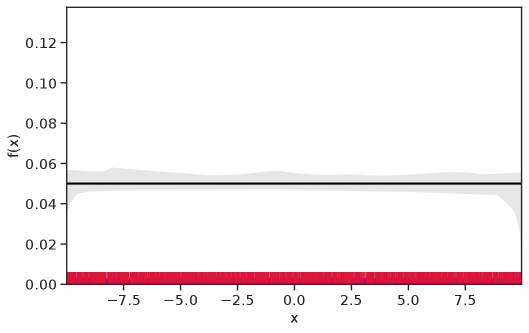
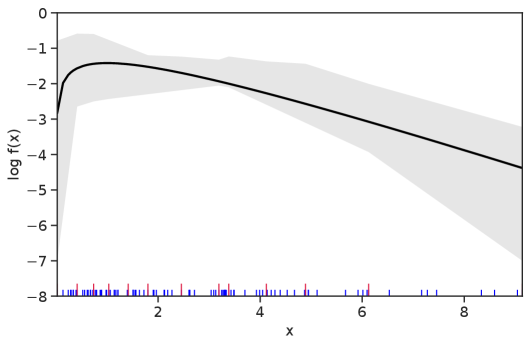
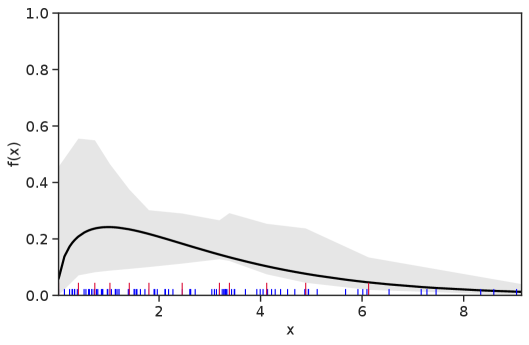
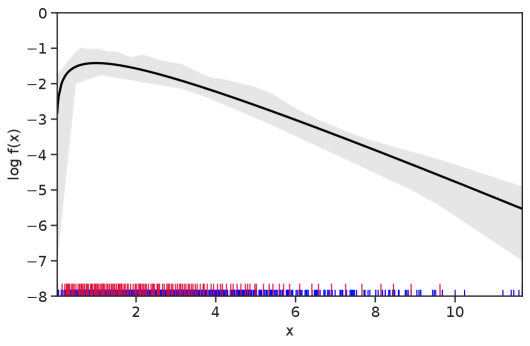
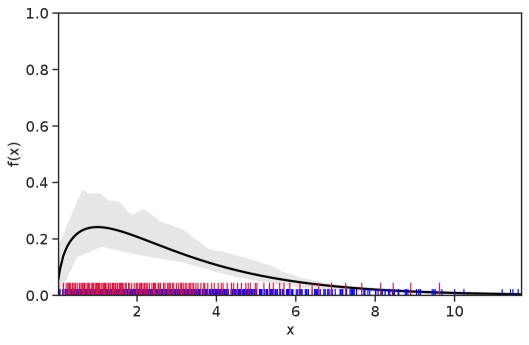
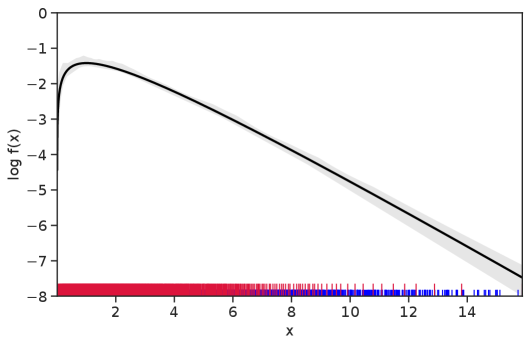
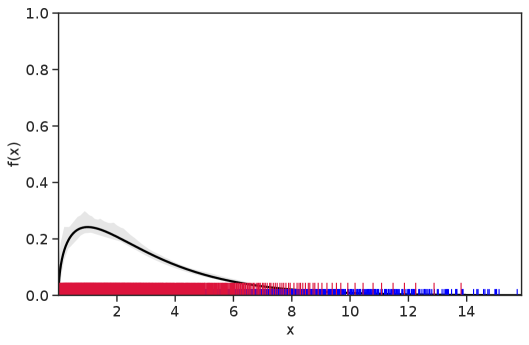
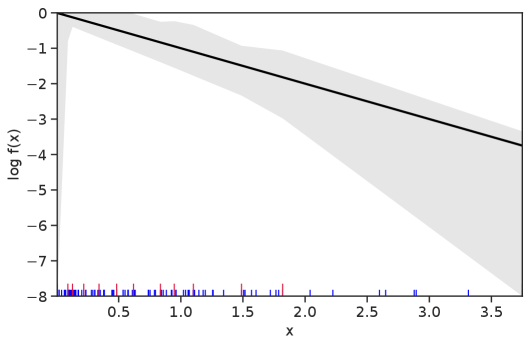
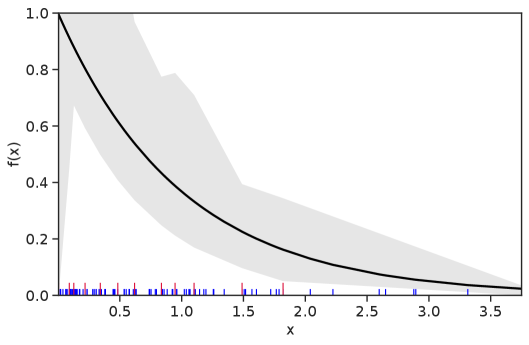
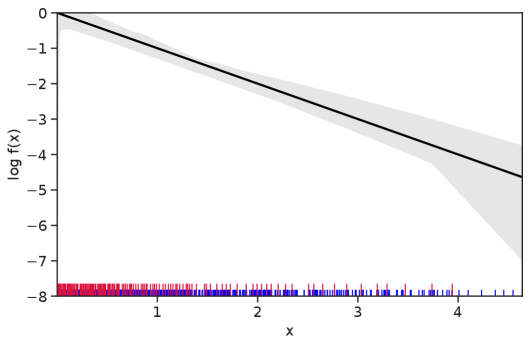
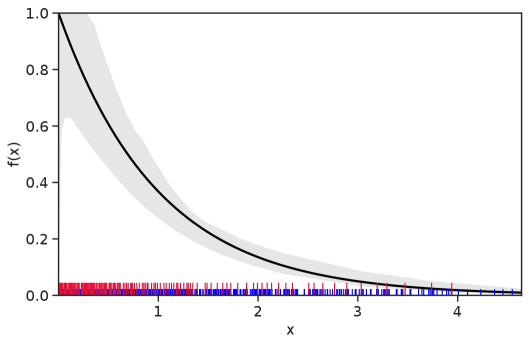
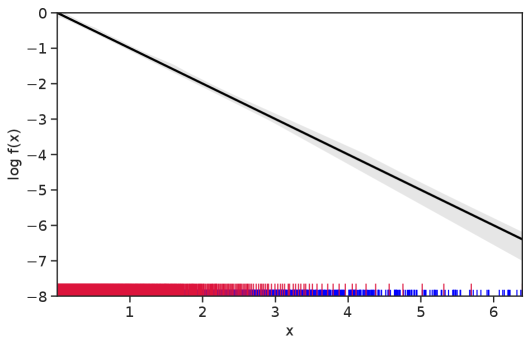
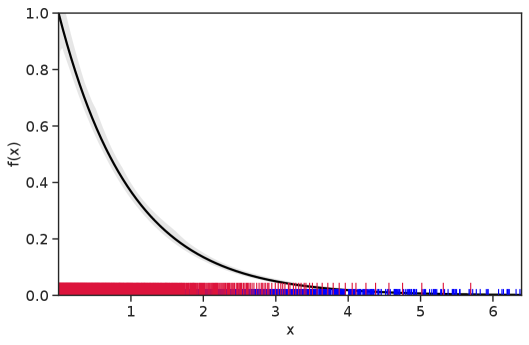
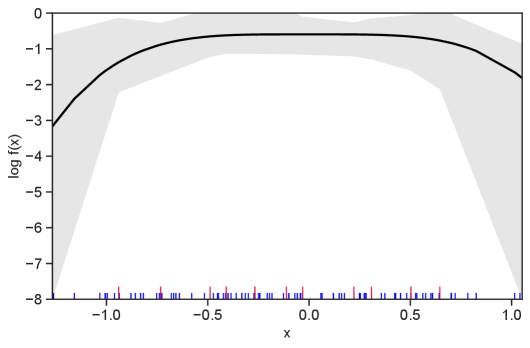
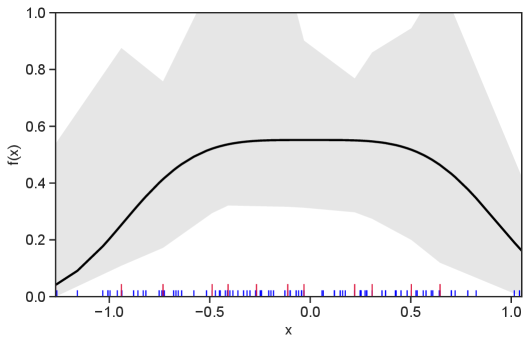
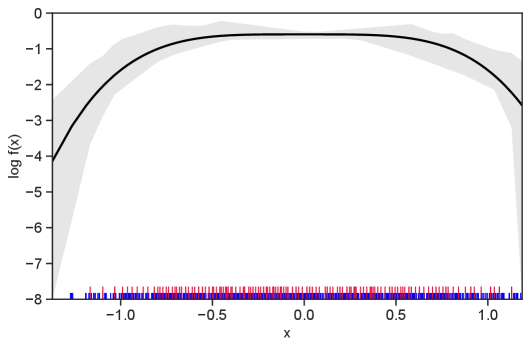
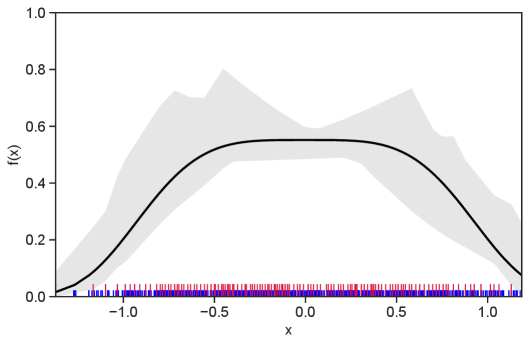
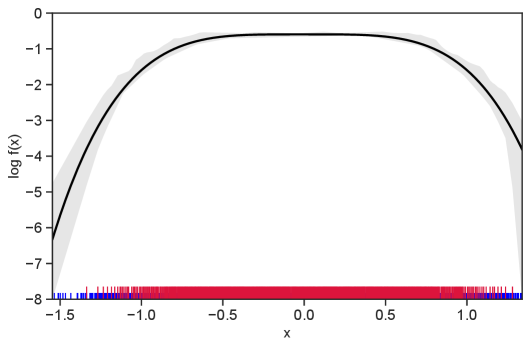
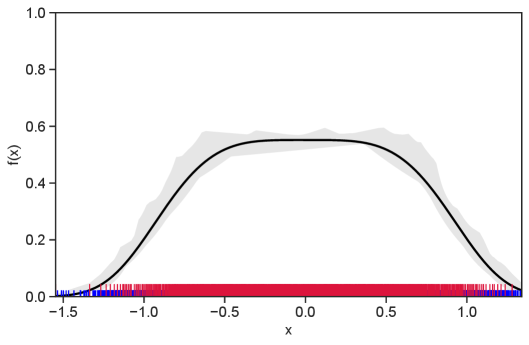
Table 1 summarizes the results. The table (reassuringly) shows us that the bands achieve coverage at or above the nominal level. In Figures 1–5 we present a visualization of the bands, from a single repetition chosen at random, for each of the four underlying densities as well as for a density that is proportional to $\exp(-x^{4})$ . In addition, we depict the bands for the case of a larger sample with $n=10000$ . The figures and Table 1 show that while the bands are naturally wider when the sample size is small ( $n=100$ ), they quickly tighten as the sample size grows ( $n\in\{1000,10000\}$ ).

As for the computational cost, we found that around 20-30 iterations of Algorithm 1 were enough to reach convergence, for each point $x_{i},\;i=1,\ldots,m$ . Table 1 shows that this translates into just a few seconds to compute the entire band when $n=100$ , and a couple of minutes when $n=1000$ . We found that Algorithm 1 converged to the exact same solutions even when started from a number of different initial points, suggesting that it is in fact finding the global minimizers of the problems (9). Therefore, these runtimes appear to be reasonable, as it is worth bearing in mind that Algorithm 1 is effectively solving a potentially large number of non-convex optimization problems (precisely: 13, 39, and 188 such problems, corresponding to $n\in\{100,1000,10000\}$ , respectively). Moreover, we point out that the computation in Algorithm 1 can easily be parallelized, e.g. across the points $x_{i},\;i=1,\ldots,m$ .

In order to compare the confidence band with pointwise confidence intervals, we performed these experiments also with two methods that compute pointwise confidence intervals for log-concave densities. Azadbakhsh et al. (2014) compare several such methods and report that no one approach appears to uniformly dominate the others and that each method works well only in a certain range of the data. The first group of methods examined by Azadbakhsh et al. (2014) is based on the pointwise asymptotic theory developed in Balabdaoui et al. (2009) and requires estimating a nuisance parameter, for which Azadbakhsh et al. (2014) investigate several options. We picked the option that they report works best, namely their method (iv) in their Section 4. This method is called ‘Asymptotic theory with approximation’ in Table 2. The second group of methods analyzed by Azadbakhsh et al. (2014) concerns various bootstrapping schemes, and we chose the one that they report to have the best performance, namely the ECDF-bootstrap, listed as (v) in their Section 4, which we use with 250 bootstrap repetitions. This method computes the MLE for each bootstrap sample and then computes the bootstrap percentile interval at a point $x_{0}$ based on the 250 bootstrap replicates of the MLE at $x_{0}$ . We used the R function logConCI produced by Azadbakhsh et al. (2014) for implementing both methods. With each of the two methods we compute the pointwise 90% confidence interval for each point $x_{0}$ in the grid of points that we use to evaluate empirical coverage. Since these are pointwise 90% confidence intervals, we expect that the coverage for the band (i.e. the simultaneous coverage across all $x_{0}$ in the grid) is smaller than 90%, but that the intervals are narrower than those for a simultaneous confidence band. This is confirmed by the results in Table 2, which show that both methods seriously undercover. The bootstrap is also seen to be significantly more computationally intensive than the method based on asymptotic theory as well as Algorithm 1.

		Nominal coverage 90%				Nominal coverage 95%
Distribution	$n$	Coverage	Width			Coverage	Width			Time
Distribution	$n$	Coverage	$Q_{1}$	$Q_{2}$	$Q_{3}$	Coverage	$Q_{1}$	$Q_{2}$	$Q_{3}$	(secs.)
Gaussian	100	0.96	0.58	0.65	0.61	0.98	0.66	0.74	0.70	5.6
Gaussian	1000	0.95	0.24	0.28	0.24	0.97	0.27	0.31	0.27	151.2
Uniform	100	0.93	0.08	0.07	0.08	0.96	0.09	0.08	0.09	5.1
Uniform	1000	0.91	0.03	0.03	0.03	0.97	0.03	0.03	0.03	128.8
Chi-squared	100	0.94	0.36	0.28	0.19	0.98	0.41	0.33	0.23	5.4
Chi-squared	1000	0.94	0.16	0.12	0.07	0.97	0.18	0.13	0.08	132.5
Exponential	100	0.93	0.94	0.69	0.44	0.96	1.06	0.77	0.51	5.7
Exponential	1000	0.91	0.38	0.25	0.15	0.97	0.43	0.29	0.17	140.4

Table 1: Empirical coverages, average widths at the sample quartiles (denoted

Q_{1}

Q_{2}

, and

Q_{3}

), and average runtimes in seconds, for the confidence bands generated by Algorithm 1 with linear interpolation and nominal coverage levels 90% and 95%, when applied to

n\in\{100,1000\}

observations drawn from four different underlying densities (Gaussian, uniform, chi-squared, and exponential). All results are based on 1000 simulations. The runtimes for the nominal coverage of 90% are similar to the case of 95% and are not displayed.

		Asymptotic theory with approximation					Bootstrap
Distribution	$n$	Coverage	Width			Time	Coverage	Width			Time
Distribution	$n$	Coverage	$Q_{1}$	$Q_{2}$	$Q_{3}$	(secs.)	Coverage	$Q_{1}$	$Q_{2}$	$Q_{3}$	(secs.)
Gaussian	100	0.22	0.13	0.20	0.13	1.4	0.37	0.16	0.16	0.12	98.2
Gaussian	1000	0.08	0.04	0.08	0.04	6.4	0.15	0.04	0.07	0.03	194.8
Uniform	100	0.32	0.03	0.03	0.03	1.4	0.01	0.02	0.01	0.02	97.4
Uniform	1000	0.15	0.01	0.01	0.01	6.5	0.11	0.01	0.01	0.01	184.5
Chi-squared	100	0.06	0.08	0.04	0.02	1.4	0.52	0.04	0.03	0.02	97.2
Chi-squared	1000	0.00	0.02	0.01	0.00	6.6	0.31	0.02	0.01	0.01	191.0
Exponential	100	0.37	0.04	0.02	0.01	1.4	0.05	0.07	0.05	0.03	95.7
Exponential	1000	0.15	0.01	0.01	0.01	6.5	0.04	0.02	0.01	0.01	180.0

Table 2: Empirical coverages, average widths at the sample quartiles (denoted

Q_{1}

Q_{2}

, and

Q_{3}

), and average runtimes in seconds, for the confidence bands obtained from pointwise asymptotic theory and approximation (iv) in Azadbakhsh et al. (2014) and by the bootstrap, with nominal level 90% in the same settings as in Table 1.

Refer to caption — Figure 1: Confidence bands (shaded in gray) generated by Algorithm 1 and linear interpolation as described in Section 2.4, for a Gaussian density. The left column shows the bands for the log density, while the right column shows the bands for the density. The solid black line marks the underlying (log)density. Top, middle and bottom rows show results for sample sizes $n=100$ , $1000$ , and $10000$ , respectively. At the bottom of each plot, the observations $X_{i}$ are indicated in blue (short lines), while the points $x_{i},\;i=1,\ldots,m$ are marked in red (long lines).

6 Discussion

The paper shows how to construct confidence bands for a log-concave density by intersecting the log-concavity constraint with an appropriate nonparametric confidence set. This approach has three strong points: First, it produces confidence bands with a finite sample guaranteed confidence level. Our simulations have shown that this guaranteed confidence level is not overly conservative. Second, the approach allows to bring modern tools from optimization to bear on this problem. This aspect is particularly important in a multivariate setting where it is known that computing the MLE is very time consuming. We expect that the key ideas of the univariate construction introduced here can be carried over to the multivariate setting and we are working on implementing this program in the multivariate setting. Third, it was shown that this approach results in attractive statistical properties, namely that the confidence bands converge at nearly the parametric $n^{-\frac{1}{2}}$ rate when the log density is $k$ -affine. We conjecture that the width of these confidence bands will likewise achieve the optimal minimax rate if $\log f$ is smooth rather than piecewise linear, and we leave the proof of such a result as an open problem.

7 Proofs

7.1 Proof of Lemma 1

It is well known that if $\log f(x)$ is a concave function then there exist real numbers $g_{1},\ldots,g_{m}$ such that

\log f(x)\leq\ell_{i}+g_{i}\,(x-x_{i})\ \ \mbox{ for }i=1,\ldots,m,

see e.g. Boyd and Vandenberghe (2004). We found it computationally advantageous to employ these inequalities only for $i=2,\ldots,m-1$ . Those inequalities immediately yield

\ell_{j}\leq\ell_{i}+g_{i}\,(x_{j}-x_{i})\ \ \mbox{ for all }i\in\{2,\ldots,m-1\},\ j\in\{i-1,i+1\},

(15)

as well as for $i=2,\ldots,m-1$ :

\int_{x_{i}}^{x_{i+1}}f(x)\,dx\leq\exp(\ell_{i})\int_{x_{i}}^{x_{i+1}}\exp\bigl{(}g_{i}(x-x_{i})\bigr{)}\,dx=\exp(\ell_{i})(x_{i+1}-x_{i})\,E\bigl{(}g_{i}(x_{i+1}-x_{i})\bigr{)}

and for $i=1,\ldots,m-2$ :

\int_{x_{i}}^{x_{i+1}}f(x)\,dx\leq\exp(\ell_{i+1})\int_{x_{i}}^{x_{i+1}}\exp\bigl{(}g_{i+1}(x-x_{i+1})\bigr{)}\,dx=\exp(\ell_{i+1})(x_{i+1}-x_{i})\,E\bigl{(}g_{i+1}(x_{i}-x_{i+1})\bigr{)}.

On the other hand, since $\log f$ is concave on $(x_{i},x_{i+1})$ it cannot be smaller than the chord from $x_{i}$ to $x_{i+1}$ . Hence for $i=1,\ldots,m-1$ :

\int_{x_{i}}^{x_{i+1}}f(x)\,dx\geq\int_{x_{i}}^{x_{i+1}}\exp\Bigl{(}\ell_{i}+(x-x_{i})\frac{\ell_{i+1}-\ell_{i}}{x_{i+1}-x_{i}}\Bigr{)}\,dx=\ (x_{i+1}-x_{i})\exp(\ell_{i})\,E\bigl{(}\ell_{i+1}-\ell_{i}\bigr{)},

proving the lemma. For later use we note the following fact:

If (15) holds, then (15) holds for all

j\in\{1,\ldots,m\}

, and the

g_{i}

are non-increasing in

i

(16)

This is because (15) implies both $\ell_{i+1}\leq\ell_{i}+g_{i}(x_{i+1}-x_{i})$ and $\ell_{i}\leq\ell_{i+1}+g_{i+1}(x_{i}-x_{i+1})$ , hence $g_{i}\geq\frac{\ell_{i+1}-\ell_{i}}{x_{i+1}-x_{i}}\geq g_{i+1}$ . This monotonicity property and (15) yield for $j>i$ :

\ell_{j}\leq\sum_{k=i}^{j-1}g_{k}(x_{k+1}-x_{k})+\ell_{i}\leq g_{i}\sum_{k=i}^{j-1}(x_{k+1}-x_{k})+\ell_{i}=\ell_{i}+g_{i}(x_{j}-x_{i})

and analogously for $j<i$ . $\Box$

7.2 Proof of Theorem 1

Let $d>0$ be an integer that will be determined later as a function of $f,I,J$ , and set $B:=B_{max}-d$ . So $d$ does not change with $n$ but $B$ does as $B_{max}$ increases with $n$ . Define the event

{\cal A}_{n}(d):=\ \left\{\left|\int_{x_{j}}^{x_{k}}f(t)\,dt-p_{jk}\right|\ \leq\ \sqrt{\frac{p_{jk}(1-p_{jk})}{n}}\sqrt{\log\log n}\ \mbox{ for all $(j,k)\in{\cal I}_{B}$}\right\}

where $p_{jk}:=\frac{k-j}{n+1}2^{s_{n}}$ . We will prove the theorem with a sequence of lemmata. The first lemma bounds the width of the confidence band on the discrete set $\{x_{j},j\in{\cal K}\}$ , where ${\cal K}:=\{j:\,j=1+i2^{B}$ with $3\leq i\leq n_{B}-3$ and $(x_{j-3\cdot 2^{B}},x_{j+3\cdot 2^{B}})\subset J\}$ :

Lemma 2

If $\{\ell_{1},\ldots,\ell_{m}\,g_{2},\ldots,g_{m-1}\}$ is a feasible point for the optimization problem (9), then on ${\cal A}_{n}(d)$

\max_{j\in{\cal K}}\left|\ell_{j}-\log f(x_{j})\right|\ \leq\ 17\sqrt{2^{d}\frac{\log\log n}{n}}.

In order to extend the bound over the discrete set $\{x_{j},\ j\in{\cal K}\}$ to a uniform bound over the interval $I$ we will use the following fact, which is readily proved using elementary calculations:

If the linear function $L(t)$ and the concave function $g(t)$ satisfy $|L(t_{i})-g(t_{i})|\leq D$ for $t_{1}<t_{2}<t_{3}<t_{4}$ , then $\sup_{t\in(t_{2},t_{3})}|L(t)-g(t)|\leq D\left(1+2\min\left(\frac{t_{3}-t_{2}}{t_{2}-t_{1}},\frac{t_{3}-t_{2}}{t_{4}-t_{3}}\right)\right)$ .

Lemma 3

On the event ${\cal A}_{n}(d)$

\min\left(\max_{j\in{\cal K}}\frac{x_{j+2^{B}}-x_{j}}{x_{j}-x_{j-2^{B}}},\max_{j\in{\cal K}}\frac{x_{j+2^{B}}-x_{j}}{x_{j+2\cdot 2^{B}}-x_{j+2^{B}}}\right)\leq\frac{9}{8}.

Therefore any concave function $g$ for which $\{g(x_{j}),j\in{\cal K}\}$ is feasible for (9) must satisfy

\sup_{x\in[x_{\underline{j}+2^{B}},x_{\overline{j}-2^{B}}]}\Bigl{|}g(x)-\log f(x)\Bigr{|}\ \leq\ \frac{13}{4}17\sqrt{2^{d}\frac{\log\log n}{n}}

on ${\cal A}_{n}(d)$ , where $\underline{j}:=\min{\cal K}$ and $\overline{j}:=\max{\cal K}$ . Hence this bound applies to the lower and upper confidence limits $\hat{\ell}$ and $\hat{\mu}$ since $\hat{\ell}$ is a concave function and $\{\hat{\ell}(x_{i})$ , $i=1,\ldots,m\}$ is feasible for (9), and for every real $x$ there exist a concave function $g$ such that $g(x)=\hat{\mu}(x)$ and $\{g(x_{i})$ , $i=1,\ldots,m\}$ is feasible for (9).

In order to conclude the proof of the theorem we will show

Lemma 4

{\rm I\!P}\left\{{\cal A}_{n}(d)\right\}\ \rightarrow\ 1\ \mbox{ as $n\rightarrow\infty$}

and

Lemma 5

{\rm I\!P}\left\{I\subset(x_{\underline{j}-2^{B}},x_{\overline{j}+2^{B}})\right\}\ \rightarrow\ 1\ \mbox{ as $n\rightarrow\infty$}

for a certain $d=d(f,I,J)$ .

Then the claim of the theorem follows since the bound on the log densities carries over to the densities as $\sup_{x\in I}|g(x)-\log f(x)|\leq 1$ implies

\sup_{x\in I}\Bigl{|}\exp(g(x))-f(x)\Bigr{|}\ \leq\ 2\Bigl{(}\sup_{x\in I}f(x)\Bigr{)}\ \sup_{x\in I}\Bigl{|}g(x)-\log f(x)\Bigr{|}.

It remains to prove the Lemmata 2–5. We will use the following two facts:

Fact 1

If $L(x)$ is a linear function, then $\int_{\alpha}^{\beta}\exp(L(x))\,dx=(\beta-\alpha)\exp(L(\alpha))\,E\bigl{(}L(\beta)-L(\alpha)\bigr{)}$ , where $E(\cdot)$ is given in Lemma 1. One readily checks that the function ${\bf R}^{2}\ni(s,t)\mapsto\exp(t)\,E(s-t)$ is increasing in both $s$ and $t$ . Furthermore, since $\frac{sinh(x)}{x}$ is increasing for $x>0$ we have for $s<t$ and $C>0$ :

	$\displaystyle\exp(t+C)\,E\bigl{(}s-(t+C)\bigr{)}$	$\displaystyle=\frac{\exp(s)-\exp(t+C)}{s-(t+C)}$
		$\displaystyle=\exp\left(\frac{s+t+C}{2}\right)\frac{\sinh\left(\frac{t+C-s}{2}\right)}{\frac{t+C-s}{2}}$
		$\displaystyle\geq\exp\left(\frac{C}{2}\right)\,\exp\left(\frac{s+t}{2}\right)\,\frac{\sinh\left(\frac{t-s}{2}\right)}{\frac{t-s}{2}}$
		$\displaystyle\geq\left(1+\frac{C}{2}\right)\frac{\exp(s)-\exp(t)}{s-t}$
		$\displaystyle=\left(1+\frac{C}{2}\right)\exp(t)\,E(s-t)$

and this inequality also holds for $s=t$ since $E$ is continuous.

Fact 2

Let $k\in(0,n+1)$ and $p:=\frac{k}{n+1}$ . Then for $\alpha\in(0,1)$

\left.\begin{aligned} q\textrm{Beta }(1-\alpha,k,n+1-k)-p\\ -\Bigl{(}q\textrm{Beta }(\alpha,k,n+1-k)-p\Bigr{)}\end{aligned}\right\}\leq\sqrt{\frac{p(1-p)}{n+1}}\sqrt{2\log\frac{1}{\alpha}}+\frac{\log\frac{1}{\alpha}}{n+1}

where $q\textrm{Beta }(\alpha,r,s)$ denotes the $\alpha$ -quantile of the beta distribution with parameters $r$ and $s$ . This fact follows from Propostion 2.1 in Dümbgen (1998).

Proof of Lemma 2: Since $\log f$ is linear on $J$ we will assume that it is non-increasing on $J$ . The non-decreasing case is proved analogously. Let $j\in{\cal K}$ and set $k:=j+2^{B}$ , so $(j,k)\in{\cal I}_{B}$ . The concavity constraint (5) implies that the function $h_{jk}(t):=\sum_{i=j}^{k-1}1(x_{i}\leq t<x_{i+1})\left(\ell_{i}+(t-x_{i})\frac{\ell_{i+1}-\ell_{i}}{x_{i+1}-x_{i}}\right)$ is concave on $(x_{j},x_{k})$ and hence not smaller than its secant $g_{jk}(t):=\ell_{j}+(t-x_{j})\frac{\ell_{k}-\ell_{j}}{x_{k}-x_{j}}$ . Hence

$\displaystyle\sum_{i=j}^{k-1}(x_{i+1}-x_{i})\exp(\ell_{i})\,E(\ell_{i+1}-\ell_{i})$	$\displaystyle=\sum_{i=j}^{k-1}\int_{x_{i}}^{x_{i+1}}\exp\left(\ell_{i}+(t-x_{i})\frac{\ell_{i+1}-\ell_{i}}{x_{i+1}-x_{i}}\right)\,dt$
	$\displaystyle=\int_{x_{j}}^{x_{k}}\exp\left(h_{jk}(t)\right)\,dt$
	$\displaystyle\geq\int_{x_{j}}^{x_{k}}\exp\left(g_{jk}(t)\right)\,dt$
	$\displaystyle=(x_{k}-x_{j})\exp(\ell_{j})\,E(\ell_{k}-\ell_{j})$	(17)

Suppose $\ell_{j}>\log f(x_{j})+C$ where $C:=17\cdot 2^{\frac{d}{2}}\sqrt{\frac{\log\log n}{n}}$ . If $\ell_{k}\geq\log f(x_{k})$ then Fact 1 shows (note that $\log f(x_{j})\geq\log f(x_{k})$ as $f$ is non-increasing) that (17) is not smaller than

	$\displaystyle(x_{k}-x_{j})\exp\bigl{(}\log f(x_{j})+C\bigr{)}\,E\Bigl{(}\log f(x_{k})-\left(\log f(x_{j})+C\right)\Bigr{)}$
	$\displaystyle\geq(x_{k}-x_{j})\left(1+\frac{C}{2}\right)\exp\left(\log f(x_{j})\right)\,E\Bigl{(}\log f(x_{k})-\log f(x_{j})\Bigr{)}$
	$\displaystyle=\left(1+\frac{C}{2}\right)\int_{x_{j}}^{x_{k}}f(t)\,dt$		(18)

since $\log f(t)$ is linear on $(x_{j},x_{k})$ . Now $p_{jk}\geq 2^{-d-4}$ since $B=B_{max}-d$ , and hence $C\geq\frac{17}{4}\sqrt{\frac{\log\log n}{p_{jk}n}}$ . So on the event ${\cal A}_{n}(d)$ , (18) is not smaller than

	$\displaystyle\left(1+\frac{17}{8}\sqrt{\frac{\log\log n}{p_{jk}\,n}}\right)\left(p_{jk}-\sqrt{\frac{p_{jk}(1-p_{jk})}{n}}\sqrt{\log\log n}\right)$
	$\displaystyle>p_{jk}+\frac{9}{8}\sqrt{\frac{p_{jk}(1-p_{jk})}{n}}\sqrt{\log\log n}$
	$\displaystyle>q\textrm{Beta }\left(1-\frac{\alpha}{2(B+2)n_{B}t_{n}},(k-j)2^{s_{n}},n+1-(k-j)2^{s_{n}}\right)\,=d_{B}$

by Fact 2, since $B=B_{max}-d$ implies $n_{B}\leq\frac{n}{2^{B_{max}+s_{n}-d}}\leq 16\cdot 2^{d}$ , while $t_{n}\leq\log(B_{max}+2)\leq\log\log_{2}n$ , and therefore $2(B+2)n_{B}t_{n}\leq\alpha(\log n)^{2}$ for $n$ large enough. Thus we arrive at a violation of the constraint (8).

On the other hand, suppose $\ell_{j}>\log f(x_{j})+C$ and $\ell_{k}<\log f(x_{k})$ . Set $k=j+2^{B}$ , $r:=j+2\cdot 2^{B}$ and $s:=j+3\cdot 2^{B}$ . Then $x_{r}-x_{k}\geq\frac{8}{9}(x_{k}-x_{j})$ by (21). By (5) and (16)

g_{i}\ \leq\ g_{k}\ \leq\ \frac{\ell_{k}-\ell_{j}}{x_{k}-x_{j}}\ \leq\ \frac{\log f(x_{k})-\log f(x_{j})-C}{x_{k}-x_{j}}\ \ \ \mbox{ for $i=k,\ldots,s-1$}.

Hence for $k\leq i<m\leq s-1$ :

g_{i}(x_{m}-x_{i})\ \leq\ \log f(x_{m})-\log f(x_{i})-\frac{x_{m}-x_{i}}{x_{k}-x_{j}}C

(19)

since $\log f$ is linear on $(x_{k},x_{s})$ . This yields

	$\displaystyle\ell_{r}$	$\displaystyle\leq\ell_{k}+g_{k}(x_{r}-x_{k})$
		$\displaystyle\leq\log f(x_{k})+\log f(x_{r})-\log f(x_{k})-\frac{x_{r}-x_{k}}{x_{k}-x_{j}}C$
		$\displaystyle\leq\log f(x_{r})-\frac{8}{9}C$

and likewise for $m=r+1,\ldots,s-1$ :

	$\displaystyle\ell_{m}$	$\displaystyle\leq\ell_{r}+g_{r}(x_{m}-x_{r})$
		$\displaystyle\leq\log f(x_{r})-\frac{8}{9}C+\log f(x_{m})-\log f(x_{r})-\frac{x_{m}-x_{r}}{x_{k}-x_{j}}C$
		$\displaystyle\leq\log f(x_{m})-\frac{8}{9}C$

Since the function $E(s)$ is positive and increasing for $s\in{\bf R}$ we obtain with (19):

	$\displaystyle\sum_{i=r}^{s-1}\exp(\ell_{i})(x_{i+1}-x_{i})\,E\left(g_{i}(x_{i+1}-x_{i})\right)$
	$\displaystyle\leq\sum_{i=r}^{s-1}\exp\left(\log f(x_{i})-\frac{8}{9}C\right)(x_{i+1}-x_{i})\,E\Bigl{(}\log f(x_{i+1})-\log f(x_{i})\Bigr{)}$
	$\displaystyle=\exp\left(-\frac{8}{9}C\right)\sum_{i=r}^{s-1}\int_{x_{i}}^{x_{i+1}}\exp\Bigl{(}\log f(t)\Bigr{)}\,dt$
	$\displaystyle<\left(1-\frac{7}{9}C\right)\int_{x_{r}}^{x_{s}}f(t)\,dt\ \ \ \ \ \mbox{ since $C\in\left[\frac{17}{4}\sqrt{\frac{\log\log n}{p_{rs}n}},\frac{1}{4}\right]$}$
	$\displaystyle\leq\left(1-\frac{7\cdot 17}{9\cdot 4}\sqrt{\frac{\log\log n}{p_{rs}n}}\right)\left(p_{rs}+\sqrt{\frac{p_{rs}(1-p_{rs})}{n}}\sqrt{\log\log n}\right)\ \mbox{ on ${\cal A}_{n}(d)$}$
	$\displaystyle<p_{rs}-2\sqrt{\frac{p_{rs}(1-p_{rs})}{n}}\sqrt{\log\log n}$
	$\displaystyle<q\textrm{Beta }\left(\frac{\alpha}{2(B+2)n_{B}t_{n}},(s-r)2^{s_{n}},n+1-(s-r)2^{s_{n}}\right)\,=c_{B}$

by Fact 2, yielding a violation of (7). Therefore we conclude $\ell_{j}\leq\log f(x_{j})+C$ as claimed. The lower bound for $\ell_{j}$ follows analogously. $\Box$

Proof of Lemma 3: $f$ is monotone on $J$ since it is log-linear. Consider first the case where $f$ is non-increasing on $J$ . On ${\cal A}_{n}(d)$ we have for $j\in{\cal K}$ and $k:=j+2^{B}$ , $r:=j+2\cdot 2^{B}$ :

\frac{\int_{x_{k}}^{x_{r}}f(t)\,dt}{\int_{x_{j}}^{x_{k}}f(t)\,dt}\geq\frac{p_{kr}-\sqrt{\frac{p_{kr}(1-p_{kr})}{n}}\sqrt{\log\log n}}{p_{jk}+\sqrt{\frac{p_{jk}(1-p_{jk})}{n}}\sqrt{\log\log n}}\geq\frac{8}{9}

(20)

for $n$ large enough, since $p_{kr}=p_{jk}\geq 2^{-d-4}$ . Since $f$ is non-increasing on $J$ , (20) implies

x_{k}-x_{j}\leq\int_{x_{j}}^{x_{k}}\frac{f(t)}{f(x_{k})}\,dt\leq\frac{9}{8}\int_{x_{k}}^{x_{r}}\frac{f(t)}{f(x_{k})}\,dt\leq\frac{9}{8}(x_{r}-x_{k})

(21)

and the claim of the Lemma follows. If $f$ is non-decreasing on $J$ then we obtain analogously $x_{j+2^{B}}-x_{j}\leq\frac{9}{8}(x_{j}-x_{j-2^{B}})$ for all $j\in{\cal K}$ and the claim of the Lemma follows also. $\Box$

Proof of Lemma 4: Set $\alpha_{n}:=(\log n)^{-\frac{1}{3}}$ . Then for $(j,k)\in{\cal I}_{B}$

\sqrt{\frac{p_{jk}(1-p_{jk})}{n+1}}\sqrt{2\log\frac{1}{\alpha_{n}}}+\frac{\log\frac{1}{\alpha_{n}}}{n+1}\ \leq\ \sqrt{\frac{p_{jk}(1-p_{jk})}{n}}\sqrt{\log\log n}

for $n$ large enough as $p_{jk}=\frac{k-j}{n+1}2^{s_{n}}=\frac{2^{B+s_{n}}}{n+1}\sim\frac{2^{-d}}{8}$ . There are $n_{B}\leq\frac{n}{2^{B_{max}+s_{n}-d}}\leq 16\cdot 2^{d}$ tuples $(j,k)$ in ${\cal I}_{B}$ and

\int_{x_{j}}^{x_{k}}f(t)\,dt\ \sim\ \textrm{ Beta }(2^{B+s_{n}},n+1-2^{B+s_{n}}).

Hence, setting $j:=1$ , $k:=1+2^{B}$ and using Fact 2:

	$\displaystyle{\rm I\!P}$	$\displaystyle\Bigl{\{}{\cal A}_{n}(d)^{c}\Bigr{\}}\ \leq\ n_{B}\,{\rm I\!P}\left\{\left\|\int_{x_{j}}^{x_{k}}f(t)\,dt-p_{jk}\right\|>\sqrt{\frac{p_{jk}(1-p_{jk})}{n}}\sqrt{\log\log n}\right\}$
		$\displaystyle\leq 16\cdot 2^{d}\,{\rm I\!P}\left\{\int_{x_{j}}^{x_{k}}f(t)\,dt\not\in\Bigl{(}q\textrm{Beta }(\alpha_{n},2^{B+s_{n}},n+1-2^{B+s_{n}}),q\textrm{Beta }(1-\alpha_{n},2^{B+s_{n}},n+1-2^{B+s_{n}})\Bigr{)}\right\}$
		$\displaystyle=16\cdot 2^{d}(2\alpha_{n})\ \rightarrow\ 0$

$\hfill\Box$

Proof of Lemma 5: Note that $J\setminus I=D_{1}\cup D_{2}$ , where $D_{1}$ is the interval between the left endpoints of $I$ and $J$ , and $D_{2}$ is the interval between the right endpoints. Recall that $\underline{j}$ is the smallest index $j=1+i2^{B}$ such that $x_{\underline{j}-3\cdot 2^{B}}\in J$ . Hence $x_{\underline{j}-3\cdot 2^{B}}$ and $x_{\underline{j}-2^{B}}$ must both fall into $D_{1}$ if at least $4\cdot 2^{B}$ points $x_{i}$ fall into $D_{1}$ , i.e. if at least $4\cdot 2^{B+s_{n}}$ observations $X_{i}$ fall into $D_{1}$ . Therefore

{\rm I\!P}\left\{I\subset\left(x_{\underline{j}-2^{B}},x_{\underline{j}+2^{B}}\right)\right\}\ \geq\ {\rm I\!P}\left\{F_{n}(D_{i})\geq\frac{4\cdot 2^{B+s_{n}}}{n},\ i=1,2\right\}

where $F_{n}$ denotes the empirical distribution. Since $f$ is log-linear on $J$ :

q:=q(f,I,J):=\min\left(\int_{D_{1}}f(t)\,dt,\ \int_{D_{2}}f(t)\,dt\right)\ >\ 0.

Therefore

4\frac{2^{B+s_{n}}}{n}-F(D_{1})\ \leq\ 4\frac{2^{\log_{2}\frac{n}{8}-d}}{n}-q\ =\ 2^{-1-d}-q\ <0

for $d>\log_{2}\frac{1}{2q}$ , in which case Chebychev’s inequality gives

{\rm I\!P}\left\{F_{n}(D_{1})<4\frac{2^{B+s_{n}}}{n}\right\}\ \leq\ \frac{1}{4n(2^{-1-d}-q)^{2}}\ \rightarrow 0

and the same result holds for $F_{n}(D_{2})$ . $\Box$

References

: Azadbakhsh, M., Jankowski, H. and Gao, X. (2014). Computing confidence intervals for log-concave densities. Comput. Statist. Data Anal. 75, 248–264.
: Balabdaoui, F., Rufibach, K. and Wellner, J. A. (2009). Limit distribution theory for maximum likelihood estimation of a log-concave density. Ann. Statist. 37, 1299–1331.
: Birgé, L. (1997). Estimation of unimodal densities without smoothness assumptions. Ann. Statist. 25, 970–981.
: Boyd, S. and Vandenberghe, L. (2004). Convex Optimization. Cambridge University Press, New York.
: Chan, H.P. and Walther, G. (2013). Detection with the scan and the average likelihood ratio. Statist. Sinica 23, 409–428.
: Cule, M., Samworth, R. and Stewart, M. (2010). Maximum likelihood estimation of a multi-dimensional log-concave density. J. R. Stat. Soc. Ser. B Stat. Methodol. 72, 545–607.
: Davies, P.L. and Kovac, A. (2004). Densities, spectral densities and modality. Ann. Statist. 32, 1093-1136.
: Deng, H., Han, Q. and Sen, B. (2020). Inference for local parameters in convexity constrained models. arXiv preprint arXiv:2006.10264.
: Dinh, T. P. and Le Thi, H. A. (2014). Recent advances in DC programming and DCA. In Transactions on computational intelligence XIII, 1-37. Springer, Berlin, Heidelberg.
: Donoho, D.L. (1988). One-sided inference for functionals of a density. Ann. Statist. 16, 1390-1420.
: Doss, C. R. and Wellner, J. A. (2016). Global rates of convergence of the MLEs of log-concave and s-concave densities. Ann. Statist. 44, 954–981.
: Dümbgen, L. (1998). New goodness-of-fit tests and their application to nonparametric confidence sets. Ann. Statist. 26, 288–314.
: Dümbgen, L. (2003). Optimal confidence bands for shape-restricted curves. Bernoulli 9, 423–449.
: Dümbgen, L., Hüsler, A. and Rufibach, K. (2007). Active set and EM algorithms for log-concave densities based on complete and censored data. arXiv preprint arXiv:0707.4643v4.
: Dümbgen, L. and Rufibach, K. (2009). Maximum likelihood estimation of a log-concave density and its distribution function: basic properties and uniform consistency. Bernoulli 15, 40–68.
: Feng, O., Guntuboyina, A., Kim, A. K. H. and Samworth, R. J. (2020+). Adaptation in multivariate log-concave density estimation. Ann. Statist., to appear.
: Hartman, P. (1959). On functions representable as a difference of convex functions. Pacific Journal of Mathematics 9(3), 707-713.
: Hengartner, N.W. and Stark, P.B. (1995). Finite-sample confidence envelopes for shaperestricted densities. Ann. Statist. 23, 525–550.
: Horst, R., Pardalos, P. M. and Van Thoai, N. (2000). Introduction to global optimization. Springer Science and Business Media.
: Horst, R. and Thoai, N. V. (1999). DC programming: overview. Journal of Optimization Theory and Applications 103(1), 1-43.
: Khamaru, K. and Wainwright, M. J. (2018). Convergence guarantees for a class of non-convex and non-smooth optimization problems. arXiv preprint arXiv:1804.09629.
: Kim, A. K. H. and Samworth, R. J. (2016). Global rates of convergence in log-concave density estimation. Ann. Statist. 44, 2756–2779.
: Kim, A. K. H., Guntuboyina, A. and Samworth, R. J. (2018). Adaptation in log-concave density estimation. Ann. Statist. 46, 2279–2306.
: Le Thi, H. A. and Dinh, T. P. (2014). DC programming and DCA for general DC programs. In Advanced Computational Methods for Knowledge Engineering, 15-35. Springer, Cham.
: Li, H., Munk, A., Sieling, H. and Walther, G. (2020). The essential histogram. Biometrika 107, 347–364.
: Lipp, T. and Boyd, S. (2016). Variations and extension of the convex–concave procedure. Optimization and Engineering 17(2), 263-287.
: Liu, Y. and Wang, Y. (2018). A fast algorithm for univariate log-concave densityi estimation. Aust. N. Z. J. Stat. 60(2), 258–275.
: Pal, J. K., Woodroofe, M. and Meyer, M. (2007). Estimating a Polya frequency function. In Complex datasets and inverse problems. IMS Lecture Notes Monogr. Ser. 54, 239–249. Inst. Math. Statist., Beachwood, OH.
: Rivera, C. and Walther, G. (2013). Optimal detection of a jump in the intensity of a Poisson process or in a density with likelihood ratio statistics. Scand. J. Stat. 40, 752–769.
: Samworth, R.J. (2018). Recent progress in log-concave density estimation. Statist. Sci. 33, 493-509.
: Saumard, A. and Wellner, J.A. (2014). Log-concavity and strong log-concavity: a review. Statistics Surveys 8, 45-114.
: Schuhmacher, D. and Dümbgen, L. (2010). Consistency of multivariate log-concave density estimators. Statist. Probab. Lett. 80, 376–380.
: Seregin, A. and Wellner, J. A. (2010). Nonparametric estimation of multivariate convex-transformed densities. Ann. Statist. 38, 3751–3781.
: Shorack, G.R. and Wellner, J.A. (1986). Empirical Processes with Applications to Statistics. Wiley, New York.
: Smola, A. J., Vishwanathan, S. V. N. and Hofmann, T. (2005). Kernel Methods for Missing Variables. In AISTATS.
: Sriperumbudur, B. K. and Lanckriet, G. R. (2009, December). On the convergence of the concave-convex procedure. In Proceedings of the 22nd International Conference on Neural Information Processing Systems, 1759-1767. Curran Associates Inc.
: Tao, P. D. (1986). Algorithms for solving a class of nonconvex optimization problems. Methods of subgradients. In North-Holland Mathematics Studies 129, 249-271. North-Holland.
: Walther, G. (2002). Detecting the presence of mixing with multiscale maximum likelihood. J. Amer. Statist. Assoc. 97, 508–513.
: Walther, G. (2009). Inference and modeling with log-concave distributions. Statist. Sci. 24, 319–327.
: Walther, G. (2010). Optimal and fast detection of spatial clusters with scan statistics. Ann. Statist. 38, 1010–1033.
: Walther, G. and Perry, A. (2019). Calibrating the scan statistic: finite sample performance vs. asymptotics. arXiv preprint arXiv:2008.06136.
: Yuille, A. L. and Rangarajan, A. (2003). The concave-convex procedure. Neural computation 15(4), 915-936.