Conflict-Free Coloring of Intersection Graphs111This work was partially supported by the DFG Research Unit ”Controlling Concurrent Change”, funding number FOR 1800, project FE407/17-2, ”Conflict Resolution and Optimization”.
Abstract
A conflict-free -coloring of a graph assigns one of different colors to some of the vertices such that, for every vertex , there is a color that is assigned to exactly one vertex among and ’s neighbors. Such colorings have applications in wireless networking, robotics, and geometry, and are well studied in graph theory. Here we study the conflict-free coloring of geometric intersection graphs. We demonstrate that the intersection graph of geometric objects without fatness properties and size restrictions may have conflict-free chromatic number in and in for disks or squares of different sizes; it is known for general graphs that the worst case is in . For unit-disk intersection graphs, we prove that it is NP-complete to decide the existence of a conflict-free coloring with one color; we also show that six colors always suffice, using an algorithm that colors unit disk graphs of restricted height with two colors. We conjecture that four colors are sufficient, which we prove for unit squares instead of unit disks. For interval graphs, we establish a tight worst-case bound of two.
1 Introduction
Coloring the vertices of a graph is one of the fundamental problems in graph theory, both scientifically and historically. The notion of proper graph coloring can be generalized to hypergraphs in several ways. One natural generalization is conflict-free coloring, which asks to color the vertices of a hypergraph such that every hyperedge has at least one uniquely colored vertex. This problem has applications in wireless communication, where “colors” correspond to different frequencies.
The notion of conflict-free coloring can be brought back to simple graphs, e.g., by considering as hyperedges the neighborhoods of the vertices of . The resulting problem arises in certain variants of frequency assignment problems if one is not interested in achieving signal coverage for all points in a region, but only at certain points of interest. For an illustration, consider a scenario in which one has a given set of nodes in the plane and wants to establish a communication network between them. Moreover, assume that constructing nodes at new locations is either very expensive or forbidden, and one can only “upgrade” any existing node to a wireless base station.
Conflict-free coloring also plays a role in robot navigation, where different beacons are used for providing direction. To this end, it is vital that in any given location, a robot is adjacent to a beacon with a frequency that is unique among the ones that can be received.
Both in the frequency assignment setting and in the robot navigation setting, one typically wants to avoid placing unnecessary base stations or beacons. Abstractly speaking, this corresponds to leaving some vertices uncolored, yielding the following formalization of conflict-free coloring of graphs. For any vertex of a simple graph , the neighborhood consists of all vertices adjacent to and itself. A conflict-free -coloring of assigns one of colors to a (possibly proper) subset of vertices such that every vertex has a uniquely colored neighbor. The conflict-free chromatic number of is the smallest for which a conflict-free coloring exists. Depending on the situation it may also be more natural to consider open neighborhood conflict-free coloring, where each vertex must have a uniquely colored neighbor in its open neighborhood not including .
Conflict-free coloring has received an increasing amount of attention. Because of the motivation arising from frequency assignment, it is natural to investigate the conflict-free coloring of intersection graphs, in particular, of simple shapes such as disks or squares. In addition, previous work has considered either general graphs and hypergraphs (e.g., see [27]) or other geometric scenarios in the presence of obstacles (e.g., see [20]); we give a more detailed overview further down. This adds to the relevance of conflict-free coloring of intersection graphs, which lie in the intersection of general graphs and geometry.
There is a spectrum of different scientific challenges when studying conflict-free coloring. What are worst-case bounds on the necessary number of colors? When is it NP-hard to determine the existence of a conflict-free -coloring? We address these questions for the case of intersection graphs.
Our contribution. We present the following results.
-
•
We demonstrate that geometric objects without fatness properties and size restrictions may induce intersection graphs with conflict-free chromatic number in .
-
•
We prove that non-unit square and disk graphs may require colors. Deciding conflict-free -colorability is NP-hard for any for these graph classes.
-
•
It is NP-complete for unit-disk intersection graphs to decide the existence of a conflict-free coloring with one color. The same holds for intersection graphs of unit squares and other shapes.
-
•
Six colors are always sufficient for conflict-free coloring of unit disks. This uses an algorithm that colors unit disk graphs contained in a strip of restricted height with two colors.
-
•
Using a similar argument, we prove that four colors are always sufficient for conflict-free coloring of unit squares.
-
•
As a corollary, we get a tight worst-case bound of two on the conflict-free chromatic number of interval graphs.
Related work. In the geometric context, motivated by frequency assignment problems, the study of conflict-free coloring of hypergraphs was initiated by Even et al. [15] and Smorodinsky [28]. For disk intersection hypergraphs, Even et al. [15] prove that colors suffice. For disk intersection hypergraphs with degree at most , Alon and Smorodinsky [4] show that colors are sufficient. Cheilaris et al. [10] prove that colors suffice for the case of hypergraphs induced by planar Jordan regions with linear union complexity. If every edge of a disk intersection hypergraph must have distinct unique colors, Horev et al. [21] prove that suffice. Moreover, for unit disks, Lev-Tov and Peleg [24] present an -approximation algorithm for the conflict-free chromatic number. Abam et al. [1] consider the problem of making a conflict-free coloring robust against removal of a certain number of vertices, and prove worst-case bounds for the number of colors required. The online version of the problem has been studied as well; see, e.g., the work of Chen et al. [12] that presents, among other results, a randomized online algorithm using colors to maintain a conflict-free coloring of a set of intervals, or the work of Bar-Nov et al. [6] that presents an online algorithm using colors for some classes of -degenerate hypergraphs.
The dual problem in which one has to color a given set of points such that each region contains a uniquely colored point has also received some attention. Har-Peled and Smorodinsky [19] prove that for families of pseudo-disks, every set of points can be colored using colors. For rectangles, Ajwani et al. [3] show that colors suffice, whereas Elbassioni and Mustafa [14] show that it is possible to add a sublinear number of points such that sublinearly many colors suffice. For coloring points on a line with respect to intervals, Cheilaris et al. [9] present a 2-approximation algorithm, and a -approximation algorithm when every interval must contain uniquely colored points.
In general hypergraphs, i.e., hypergraphs not necessarily arising from a geometric context, Ashok et al. [5] prove that maximizing the number of conflict-freely colored hyperedges is FPT with respect to the number of conflict-freely colored hyperedges in the solution.
Conflict-free coloring also arises in the context of the conflict-free variant of the chromatic Art Gallery Problem, which asks to guard a polygon using colored guards such that each point sees a uniquely colored guard. Fekete et al. [16] prove that computing the chromatic number is NP-hard in this context. On the positive side, Hoffman et al. [20] prove colors are sometimes necessary and always sufficient for the conflict-free chromatic art gallery problem under rectangular visibility in orthogonal polygons. For straight-line visibility, Bärtschi et al. [8] prove that colors suffice for orthogonal and monotone polygons and colors suffice for simple polygons. This is generalized by Bärtschi et al. [7], who prove that colors suffice for simple polygons.
There also has been work regarding the scenario where the hypergraph is induced by the neighborhoods of vertices of a simple graph. Except for the need to color all vertices, this corresponds to the scenario considered in this work. This does not change the asymptotic number of colors required, since it suffices to insert one additional color to color all vertices that would otherwise remain uncolored. In this situation, Pach and Tardos [27] prove that the conflict-free chromatic number of an -vertex graph is in . Glebov et al. [18] extend this result by proving that almost all -graphs have conflict-free chromatic number . Moreover, they show that the upper bound of Pach and Tardos [27] is tight by giving a randomized construction for graphs having conflict-free chromatic number . In more recent work, Gargano and Rescigno [17] show that finding the conflict-free chromatic number for general graphs is NP-complete, and prove that the problem is FPT w.r.t. vertex cover or neighborhood diversity number. In our work with Abel et al. [2], we consider conflict-free coloring of general and planar graphs and proved a conflict-free variant of Hadwiger’s conjecture, which implies that planar graphs have conflict-free chromatic number at most three. Most recently, Keller and Smorodinsky [23] consider conflict-free coloring on intersection graphs of geometric objects, in a scenario very similar to ours. Among other results, they prove that colors suffices to color a family of pseudodisks in a conflict-free manner. With respect to open neighborhoods (also known as pointed neighborhoods), they prove that this is tight; for closed neighborhoods as studied in this paper, the tightness of this bound is not proven and remains open. They also consider the list coloring variant of the problem.
Conflict-free coloring has also been studied for other graph-based hypergraphs. For instance, Cheilaris and Tóth [11] consider the case of hypergraphs induced by the paths of a graph. If the input is the graph, they prove that it is coNP-complete to decide whether a given coloring is conflict-free.
Conflict-free coloring is not the only type of coloring for which unit disk graphs have been found to require a bounded number of colors. In their recent work, McDiarmid et al. [25] consider clique coloring of unit disk graphs, in particular with regard to the asymptotic behavior of the clique chromatic number of random unit disk graphs. They also prove that every unit disk graph in the plane can be colored with nine colors, while three colors are sometimes necessary. Similar to the present paper, they prove this by cutting the plane into strips of height ; for each of these strips it is then proven that three colors suffice.
2 Preliminaries
In the following, denotes a graph on vertices. For a vertex , denotes its open neighborhood and denotes its closed neighborhood. A conflict-free -coloring of a graph is a coloring of a subset of the vertices of , such that each vertex has at least one conflict-free neighbor , i.e., a neighbor whose color occurs only once in . The conflict-free chromatic number is the minimum number of colors required for a conflict-free coloring of .
A graph is a disk graph iff is the intersection graph of disks in the plane. is a unit disk graph iff is the intersection graph of disks with fixed radius in the plane, and a unit square graph iff is the intersection graph of axis-aligned squares with side length 1 in the plane. A unit disk (square) graph is of height iff can be modeled by the intersection of unit disks (squares) with center points in . In the following, when dealing with intersection graphs, we assume that we are given a geometric model. In the case of unit disk and unit square graphs, we identify the vertices of the graph with the center points of the corresponding geometric objects in this model.
3 General Objects
Intersection graphs of geometric objects can generally contain cliques of arbitrary size, so their chromatic number may be unbounded. However, cliques do not require a large number of colors in a conflict-free coloring, so it is not immediately clear whether the intersection graphs for a family of geometric objects have bounded conflict-free chromatic number.
If the intersecting objects can be scaled down arbitrarily, i.e., if every representable graph can be represented using arbitrarily small area, we can make use of the following lemma to prove lower bounds on the number of colors required.
Lemma 1.
Let be a graph with , and let be a graph containing two disjoint copies and of . Let be vertices of , not contained in or , and let each vertex be adjacent to every vertex of and . Moreover, let these vertices be the only neighbors of and . Then in every conflict-free -coloring of , one of the vertices has a color that appears only once in .
Proof.
Assume there was a conflict-free -coloring of such that none of the vertices has a unique color. Therefore, each vertex in has a conflict-free neighbor in , and restricting to yields a conflict-free -coloring of . As , each color is used on at least once. The same holds for . Therefore, each vertex has at least two occurrences of each color in its neighborhood; this contradicts the fact that is a conflict-free coloring of . ∎
For general objects like freely scalable ellipses or rectangles, it is possible to model a complete graph of arbitrary size , such that the following conditions hold: (1) For every object , there is some non-empty area of not intersecting any other objects. (2) For every pair of objects , there is a non-empty area common to these objects not intersecting any other objects. This can be seen by choosing intersecting lines such that no three lines intersect in a common point. These lines can then be approximated using sufficiently thin objects to achieve the desired configuration.
In this case, the conflict-free chromatic number is unbounded, because we can inductively build a family of intersection graphs with as follows. Starting with and (a four-vertex cycle), we construct by starting with a modeled according to conditions (1) and (2). For every object , we place two scaled-down non-intersecting copies of into an area covered only by ; Figure 1 depicts the construction of for ellipses. According to Lemma 1, these gadgets enforce that every vertex of the underlying is colored. For every pair of objects , we place two scaled-down non-intersecting copies of into an area covered only by and . Using an argument similar to that used in the proof of Lemma 1, these gadgets enforce that and have to receive different colors. Thus the resulting graph requires colors.
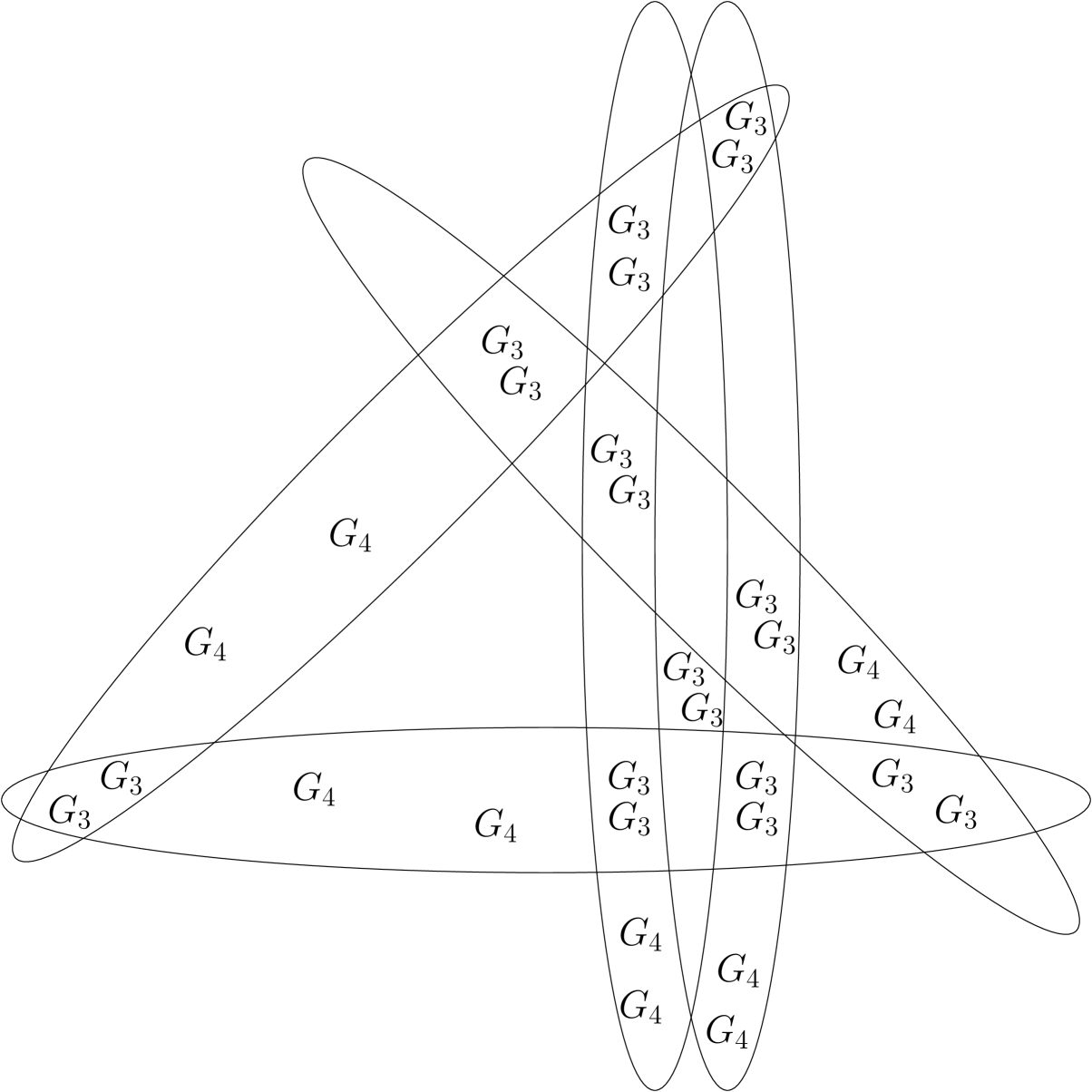
The number of vertices used by this construction satisfies the recurrence
To estimate the growth of , let for and ; clearly, for all . The recurrence has the closed-form solution
implying that the number of colors required in geometric intersection graphs on vertices may be
We summarize.
Theorem 2.
The intersection graph of convex objects in the plane may have conflict-free chromatic number in .
The best upper bound on the number of colors required in this scenario that we are aware of is , which holds for general graphs and is due to Pach and Tardos [27].
4 Different-Sized Squares and Disks
Due to their fatness, squares and disks do not allow us to construct an arbitrarily big clique such that condition (2) of Section 3 holds. However, we can still prove that there is no constant bound on their conflict-free chromatic number. The proof is based on Lemma 1, which enables us to reduce the conflict-free coloring problem on intersection hypergraphs to our problem.
Theorem 3.
The conflict-free chromatic number of disk intersection graphs and square intersection graphs can be .
Proof.
We begin our proof by inductively constructing, for any number of colors , a disk intersection graph with conflict-free chromatic number and vertices. The first level of the construction is , consisting of an isolated vertex. The remainder of the construction is based on a lower-bound example due to Even et al. [15], requiring colors when each point in the union of all disks must lie in a uniquely colored disk. This lower-bound example consists of chain disks on a horizontal line segment, placed such that all disks overlap in the center. For each interval , , there is one region with non-zero area in which exactly the disks from this interval overlap. This situation is depicted in Figure 2.
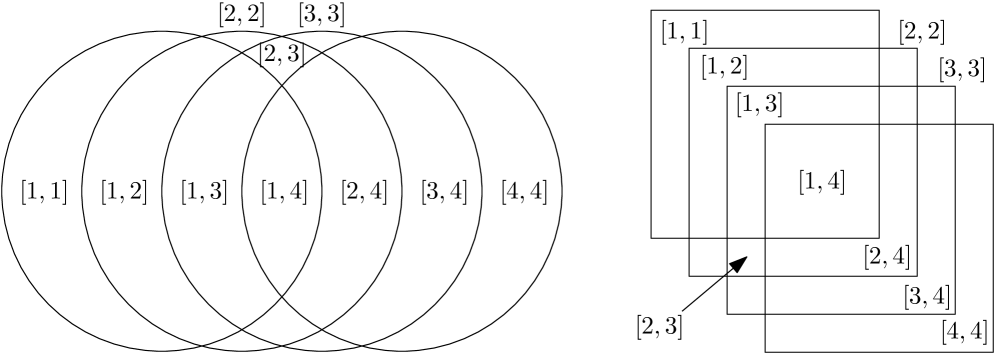
To construct , for each such interval , we choose one such region and place two scaled-down disjoint copies of in it. We prove that requires colors by induction on . That requires one color is clear. Given that requires colors for some , we can prove that requires colors as follows. Assume there was a conflict-free -coloring of . Due to Lemma 1, we know that, for every interval , , at least one of the chain disks in has a unique color. We now prove using induction that any color assignment with this property has at least colors. For a chain of length , one color is required for the interval . For a chain of length , we require one unique color for the interval . Let be the chain disk colored using this color. At least one of the intervals has length at least . By induction, this interval requires colors. These colors must all be distinct from the color used for , therefore forcing us to use colors in total. This contradicts the fact that uses only colors; therefore, . The number of vertices used by satisfies the recurrence
which is in . All our arguments can also be applied to squares instead of disks. ∎
Theorem 4.
For any fixed number of colors , deciding whether a disk (or square) intersection graph is conflict-free -colorable is NP-complete.
Proof.
Conflict-free coloring of disk intersection graphs is clearly in NP. We prove NP-hardness inductively by reducing conflict-free -colorability to conflict-free -colorability. For , NP-hardness follows from Theorem 5. In order to reduce -colorability to -colorability, consider a graph for which conflict-free -colorability is to be decided. We construct a graph that is conflict-free -colorable iff is conflict-free -colorable. For the sake of simplicity, we will refer to the disk representation of and in the description of our construction; however, the construction does not require this representation unless a disk representation of is desired. We start construction of with a chain of length . For every interval , the hypergraph contains a corresponding hyperedge. By the argument used in the proof of Theorem 3, in a conflict-free hypergraph coloring of , colors are required. For each , we choose a region corresponding to the interval and place two disjoint copies of inside. For all other intervals , we choose a region corresponding to the interval and place one copy of inside; see Figure 3.
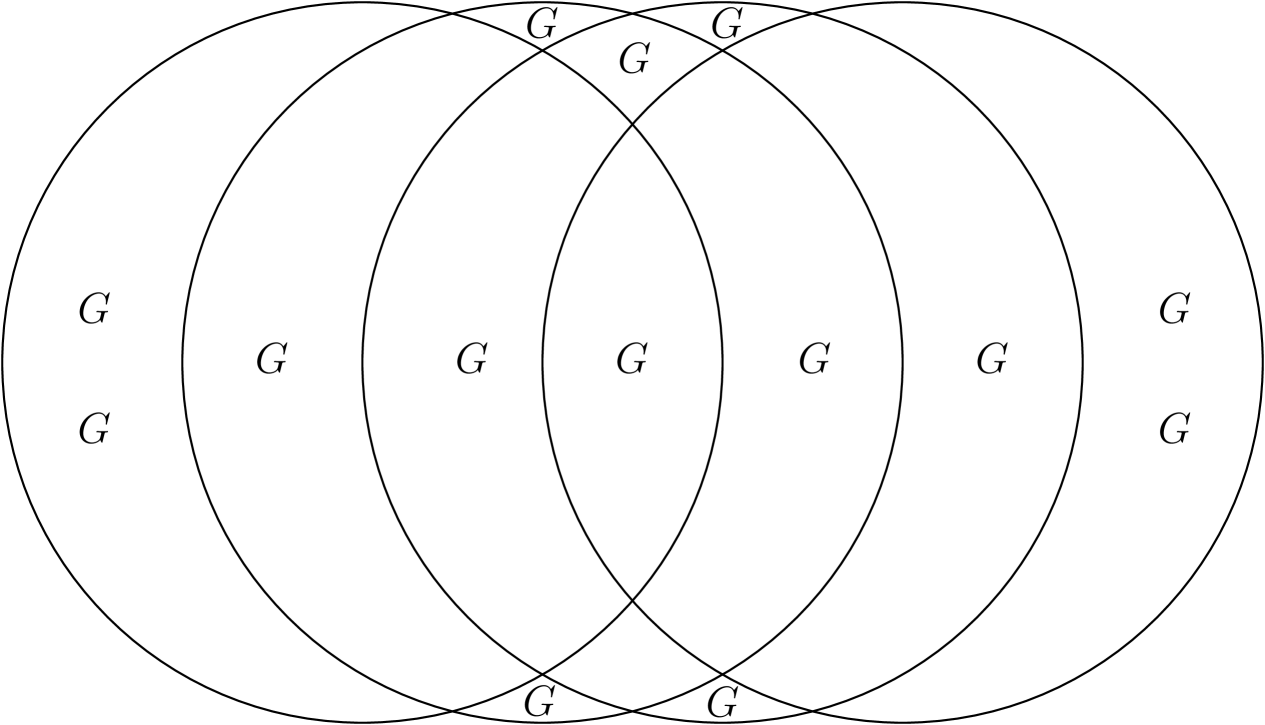
If is conflict-free -colorable, is conflict-free -colorable as follows. Each copy of can be colored using colors in a conflict-free manner. In order to give each chain vertex a conflict-free neighbor, in one of the two copies of in interval , we can color an arbitrary vertex of with color .
If is not conflict-free -colorable, by Lemma 1 we have to color all chain vertices. Given such a coloring of the chain vertices, there are two possibilities for each interval . (1) The chain vertices corresponding to the interval are colored such that there is a uniquely colored vertex. (2) Every color occurring on the corresponding chain vertices occurs more than once.
As does not have a conflict-free hypergraph -coloring, case (2) must occur for at least one interval . Let be the copy of placed in . Vertices in cannot use the chain vertices as conflict-free neighbors. Moreover, at least one color already appears twice in the neighborhood of every vertex of and thus cannot be the color of a conflict-free neighbor of any vertex in . Therefore a conflict-free -coloring of would yield a conflict-free -coloring of , which is a contradiction.
For fixed , this construction works in polynomial time. Therefore, conflict-free -coloring of disk intersection graphs is NP-complete for any fixed . All our arguments can also be applied to squares instead of disks. ∎
In [15], Even et al. prove that colors are always sufficient and sometimes necessary to color a disk intersection hypergraph in a conflict-free manner. This implies that colors are sufficient in our case, leaving a gap of .
5 Unit-Disk Graphs
The construction used in the previous section hinges on high aspect ratios of the intersecting shapes. In the setting of frequency assignment for radio transmitters, it is natural to only consider fat objects with bounded aspect ratio, such as unit disks and unit squares. As it turns out, their intersection graphs have conflict-free chromatic number bounded by a small constant; on the other hand, even deciding the existence of a conflict-free coloring with a single color is NP-complete.
5.1 Complexity: One Color
While it is trivial to decide whether a graph has a regular chromatic number of 1 and straightforward to check a chromatic number of 2, it is already NP-complete to decide whether a conflict-free coloring with a single color exists, even for unit-disk intersection graphs. This is a refinement of Theorem 4.1 in Abel et al. [2], which shows the same results for general planar graphs.
Theorem 5.
It is NP-complete to decide whether a unit-disk intersection graph has a conflict-free coloring with one color.
Proof.
Membership in NP is straightforward. We prove NP-hardness by reduction from Positive Planar 1-in-3-SAT, see Mulzer and Rote [26]. Given a Boolean formula in 3-CNF with only positive literals and planar clause-variable incidence graph, we construct a unit disk intersection graph that has a conflict-free -coloring iff is 1-in-3-satisfiable. Let consist of variables and clauses . In , variables are represented by a cycle of length and clauses are represented by a clause gadget; see Figure 4.
The clause gadgets have distinguished clause vertices. Every third vertex of a variable gadget is a true vertex; these are the vertices that are colored if the corresponding variable is set to true. We connect the clause vertex of each clause to a true vertex of each variable occurring in the clause using paths of length divisible by 3. There are sufficiently many true vertices in each variable gadget to avoid having to use a true vertex for more than one clause.
A clause vertex cannot be colored and cannot have a conflict-free neighbor in the clause gadget. Its neighbors along the paths connecting to variables require conflict-free neighbors themselves. Therefore either must be colored itself or its predecessor on the path must be colored. Along the path to the variable, every third vertex must be colored, starting with either or . Thus it is only possible to color if the true vertices of the corresponding variable are colored; can only be colored if the true vertices of the corresponding variable are not colored, see Figure 5.
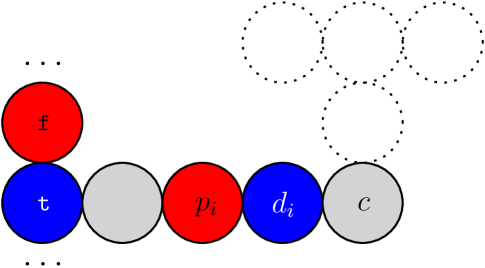
In a conflict-free -coloring of , each clause vertex has a conflict-free neighbor. This implies that for each clause , exactly one of the vertices is colored, which in turn implies that exactly one variable gadget connected to has all its true vertices colored. Therefore setting the variables that have all their true vertices colored to true yields a 1-in-3-satisfying assignment for . Analogously, a 1-in-3-satisfying assignment for induces a conflict-free -coloring of .
We still have to argue that is a unit disk graph that can be constructed in polynomial time. We consider a straight-line embedding of ’s clause-variable incidence graph with vertices placed on an integer grid; such an embedding can be obtained in polynomial time based on the graph-drawing techniques of Fraysseix, Pach and Pollack [13]. We enlarge this embedding by an appropriate polynomial factor to ensure that clauses and variables are far enough from each other and edges do not come too close to gadgets they are not incident to. We use the embedding of the variables and clauses to place the center of variables gadgets (marked by a cross in Figure 4) and clause vertices accordingly. The edges between variables and clauses can then be replaced by paths; we can ensure that their length is divisible by 3 by simple local modifications (shifting a constant number of disks closer to each other and inserting a constant number of new disks). When deciding which true vertex to use for a clause and where to place the disk adjacent to the clause vertex, we preserve the order of edges around the clause and variables vertices of the embedding. If multiple possible true vertices exist, we use a closest one. This excludes intersections between different paths close to variables and unintended intersections between paths and variable gadgets. We may have to bend the paths around the clause gadgets; however, for every clauses this involves only a constant number of disks. ∎
5.2 A Worst-Case Upper Bound: Six Colors
On the positive side, we show that the conflict-free chromatic number of unit disk graphs is bounded by six. We do not believe this result to be tight. In particular, we conjecture that the number is bounded by four; in fact, we do not even know an example for which two colors are insufficient. One of the major obstacles towards obtaining tighter bounds is the fact that a simple graph-theoretic characterization of unit disk graphs is not available, as recognizing unit disk graphs is complete for the existential theory of the reals [22]. This makes it hard to find unit disk graphs with high conflict-free chromatic number, especially considering the size that such a graph would require: The smallest graph with conflict-free chromatic number three we know has 30 vertices, and by enumerating all graphs on 12 vertices one can show that at least 13 vertices are necessary, even without the restriction to unit disk graphs.
One approach to conflict-free coloring of unit disk graphs is by subdividing the plane into strips, coloring each strip independently. We conjecture the following.
Conjecture 6.
Unit disk graphs of height are conflict-free -colorable.
If this conjecture holds, every unit disk graph is conflict-free 4-colorable. In this case, one can subdivide the plane into strips of height 2, and then color the subgraphs in all even strips using colors and the subgraphs in odd strips using colors . Instead of Conjecture 6, we prove the following weaker result.
Theorem 7.
Unit disk graphs of height are conflict-free 2-colorable.
Proof.
Given a realization of consisting of unit disks with center points with -coordinate in , we compute a conflict-free 2-coloring of using the following simple greedy approach. In an order corresponding to the lexicographic order of the points in (denoted by ), we build a set of colored vertices to which we alternatingly assign colors 1 and 2. In each step, we add a new point to until all points are covered, i.e., they are either colored or have a colored neighbor. In order to select the next colored point, we find the lexicographically maximal point such that every point is already colored or has a colored neighbor in . We observe that this point may already have a colored neighbor, but then there must be an uncovered point between and previously colored point.
In this procedure, every point is assigned a colored neighbor . It remains to exclude the following three cases. (1) A colored point is adjacent to another point of the same color, (2) an uncolored point is adjacent to two or more points of one color and none of the other color, (3) an uncolored point is adjacent to two or more points of both colors.
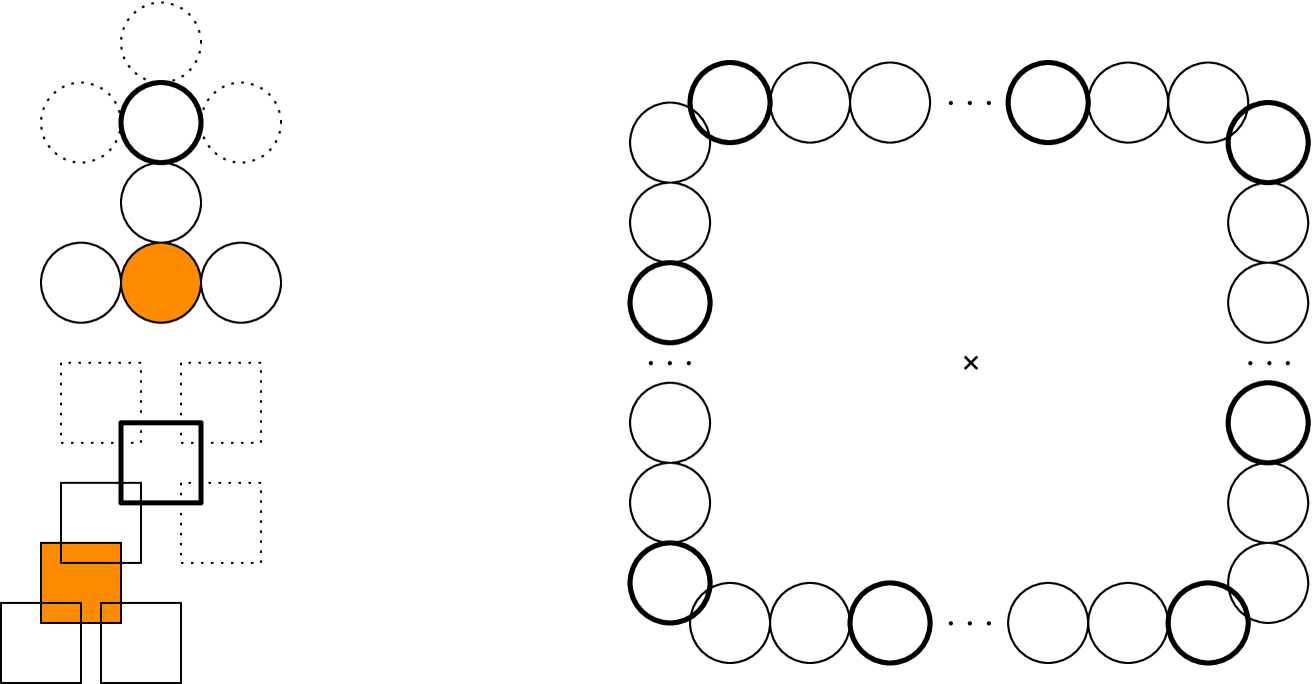
To this end, we use the following observation. Each colored point induces a closed vertical strip of width 2 centered around . As shown in Figure 6, every point in this strip is adjacent to .
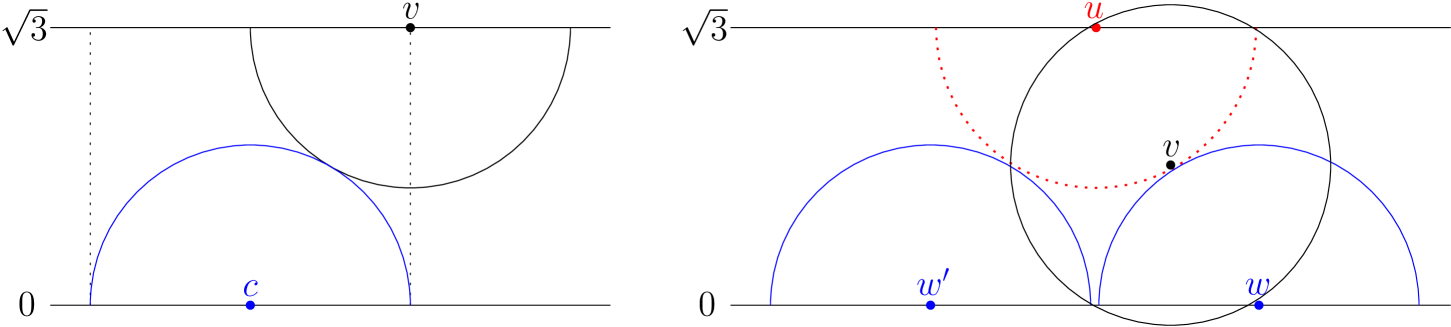
Thus, the horizontal distance between two colored points must be greater than 1. For case (1), assume there was a point of color 1 adjacent to a point of color 1. This cannot occur, because between and , there must be a point of color 2; therefore, the horizontal distance between and must be greater than 2, a contradiction.
Regarding case (2), assume there was an uncolored point adjacent to two points of color 1; see Figure 6. Between points and , there must be a point of color 2, and must not be adjacent to . There are two possible orderings: and . W.l.o.g., let ; the other case is symmetric. In this situation, the -coordinates of the points have to satisfy , , and thus in contradiction to the assumption that and are adjacent.
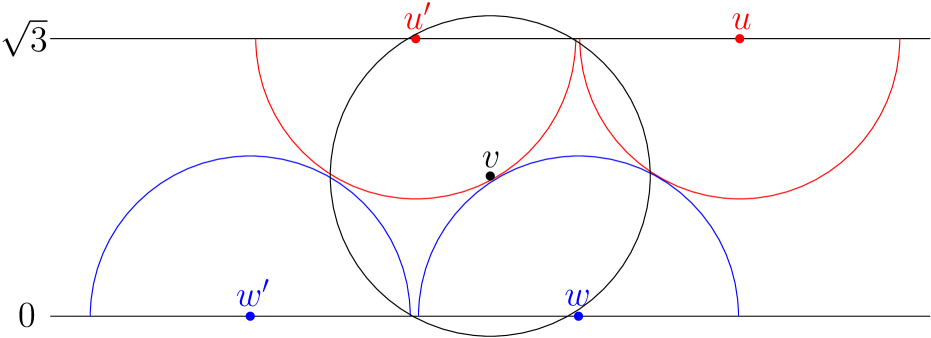
Regarding case (3), assume there was an uncolored point adjacent to two points of color 1 and two points of color 2. W.l.o.g., assume as depicted in Figure 7; the case is symmetric. Because and are adjacent, the vertical strip induced by intersects the strip induced by . Thus, there cannot be a point with not adjacent to or . This is a contradiction to the choice of : The algorithm would have chosen , or a larger point, instead of . ∎
The following corollary follows by subdividing the plane into strips of height .
Corollary 8.
Unit disk graphs are conflict-free -colorable.
5.3 Unit-Disk Graphs of Bounded Area
Proving Conjecture 6 is non-trivial, even when all center points lie in a -square. In this setting, a circle packing argument can be used to establish the sufficiency of three colors. If a unit disk graph with conflict-free chromatic number 3 can be embedded into a -square, the following are necessary. (1) Every minimum dominating set has size 3, and every pair of dominating vertices must have a common neighbor not shared with the third dominating vertex. Thus, every minimum dominating set lies on a 6-cycle without chords connecting a vertex with the opposite vertex. (2) has diameter 2; otherwise, one could assign the same color to two vertices at distance 3.
Using the domination number, one can further restrict the position of the points in the -square: There is an area in the center of the square, depicted in Figure 8, that cannot contain the center of any disk because this would yield a dominating set of size 2.
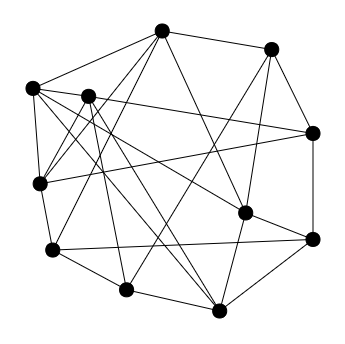
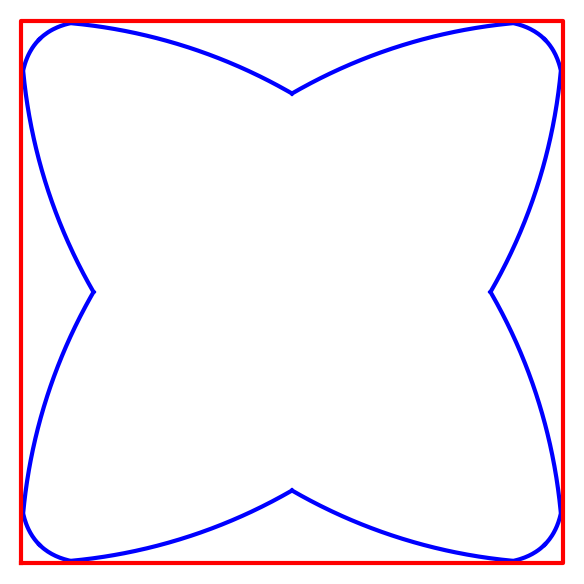
The smallest graph satisfying constraints (1) and (2) has 11 vertices and is depicted in Figure 8. It is not a unit disk graph and it is still conflict-free 2-colorable, but every coloring requires at least four colored vertices, proving that coloring a minimum dominating set can be insufficient. This implies that a simple algorithm like the one used in the proof of Theorem 7 will most likely be insufficient for strips of greater height. We are not aware of any unit disk graph satisfying these constraints.
6 Unit-Square and Interval Graphs
The constructions of the previous section can also be applied to the case of squares; for interval graphs, we get a tight worst-case bound.
6.1 Complexity: One Color
It is straightforward to see that the construction of Theorem 5 can be applied for unit square instead of unit disks.
Corollary 9.
It is NP-complete to decide whether a unit square graph has a conflict-free coloring with one color.
6.2 A Worst-Case Upper Bound: Four Colors
The proof of Theorem 7 can be applied to unit square graphs of height 2 instead of unit disk graphs of height ; see Figure 9.
Corollary 10.
Unit square graphs of height are conflict-free -colorable. Unit square graphs are conflict-free -colorable.
6.3 Interval Graphs: Two Colors
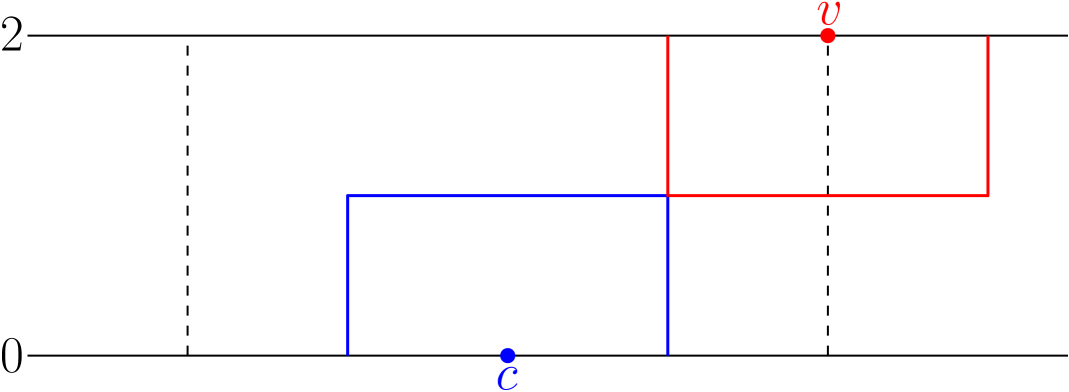
Unit interval graphs correspond to unit disk or unit square graphs with all centers lying on a line. Even then, two colors in a conflict-free coloring may be required; the Bull Graph is such an example, see Figure 10.

In this case, the bound of 2 is tight: By Theorem 7, unit interval graphs are conflict-free -colorable. By adapting the algorithm used in the proof to always choose the interval extending as far as possible to the right without leaving a previous interval uncovered, this can be extended to interval graphs with non-unit intervals. For an example of this procedure, refer to Figure 10.
7 Conclusion
There are various directions for future work. In addition to closing the worst-case gap for unit disks (and proving Conjecture 6), the worst-case conflict-free chromatic number for unit square graphs also remains open. Other questions include a tight bound for disk (or square) intersection graphs, and a necessary criterion for a family of geometric objects to have intersection graphs with unbounded conflict-free chromatic number.
References
- [1] Mohammad Ali Abam, Mark de Berg, and Sheung-Hung Poon. Fault-tolerant conflict-free colorings. In Proc. 20th Canadian Conference on Computational Geometry (CCCG), pages 13–16, 2008.
- [2] Zachary Abel, Victor Alvarez, Erik D. Demaine, Sándor P. Fekete, Aman Gour, Adam Hesterberg, Phillip Keldenich, and Christian Scheffer. Three colors suffice: Conflict-free coloring of planar graphs. In Proc. 28th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 1951–1963, 2017.
- [3] Deepak Ajwani, Khaled Elbassioni, Sathish Govindarajan, and Saurabh Ray. Conflict-free coloring for rectangle ranges using colors. In Proc. 19th ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), pages 181–187, 2007.
- [4] Noga Alon and Shakhar Smorodinsky. Conflict-free colorings of shallow discs. In Proc. 22nd Symposium on Computational Geometry (SoCG), pages 41–43, 2006.
- [5] Pradeesha Ashok, Aditi Dudeja, and Sudeshna Kolay. Exact and FPT algorithms for max-conflict free coloring in hypergraphs. In Proc. 26th International Symposium on Algorithms and Computation, pages 271–282, 2015.
- [6] Amotz Bar-Noy, Panagiotis Cheilaris, Svetlana Olonetsky, and Shakhar Smorodinsky. Online conflict-free colouring for hypergraphs. Combinatorics, Probability and Computing, 19(04):493–516, 2010.
- [7] Andreas Bärtschi, Subir Kumar Ghosh, Matúš Mihalák, Thomas Tschager, and Peter Widmayer. Improved bounds for the conflict-free chromatic art gallery problem. In Proc. 30th Symposium on Computational Geometry (SoCG), pages 144–153, 2014.
- [8] Andreas Bärtschi and Subhash Suri. Conflict-free chromatic art gallery coverage. Algorithmica, 68(1):265–283, 2014.
- [9] Panagiotis Cheilaris, Luisa Gargano, Adele A. Rescigno, and Shakhar Smorodinsky. Strong conflict-free coloring for intervals. Algorithmica, 70(4):732–749, 2014.
- [10] Panagiotis Cheilaris, Shakhar Smorodinsky, and Marek Sulovsky. The potential to improve the choice: list conflict-free coloring for geometric hypergraphs. In Proc. 27th Annual Symposium on Computational Geometry, pages 424–432. ACM, 2011.
- [11] Panagiotis Cheilaris and Géza Tóth. Graph unique-maximum and conflict-free colorings. Journal of Discrete Algorithms, 9(3):241–251, 2011.
- [12] Ke Chen, Amos Fiat, Haim Kaplan, Meital Levy, Jiří Matoušek, Elchanan Mossel, János Pach, Micha Sharir, Shakhar Smorodinsky, Uli Wagner, and Emo Welzl. Online conflict-free coloring for intervals. SIAM Journal on Computing, 36(5):1342–1359, 2006.
- [13] Hubert de Fraysseix, János Pach, and Richard Pollack. How to draw a planar graph on a grid. Combinatorica, 10(1):41–51, 1990.
- [14] Khaled Elbassioni and Nabil H. Mustafa. Conflict-free colorings of rectangles ranges. In 23rd Proc. Symposium on Theoretical Aspects of Computer Science (STACS), pages 254–263, 2006.
- [15] Guy Even, Zvi Lotker, Dana Ron, and Shakhar Smorodinsky. Conflict-free colorings of simple geometric regions with applications to frequency assignment in cellular networks. SIAM Journal on Computing, 33(1):94–136, 2003.
- [16] Sándor P. Fekete, Stephan Friedrichs, Michael Hemmer, Joseph B. M. Mitchell, and Christiane Schmidt. On the chromatic art gallery problem. In Proc. 26th Canadian Conference on Computational Geometry (CCCG), pages 1–6, paper 11, 2014.
- [17] Luisa Gargano and Adele A. Rescigno. Complexity of conflict-free colorings of graphs. Theoretical Computer Science, 566:39–49, 2015.
- [18] Roman Glebov, Tibor Szabó, and Gábor Tardos. Conflict-free coloring of graphs. Combinatorics, Probability and Computing, 23:434–448, 2014.
- [19] Sariel Har-Peled and Shakhar Smorodinsky. Conflict-free coloring of points and simple regions in the plane. Discrete & Computational Geometry, 34(1):47–70, 2005.
- [20] Frank Hoffmann, Klaus Kriegel, Subhash Suri, Kevin Verbeek, and Max Willert. Tight bounds for conflict-free chromatic guarding of orthogonal art galleries. In Proc. 31st Symposium on Computational Geometry (SoCG), pages 421–435, 2015.
- [21] Elad Horev, Roi Krakovski, and Shakhar Smorodinsky. Conflict-free coloring made stronger. In Proc. 12th Scandinavian Symposium and Workshops on Algorithm Theory (SWAT), pages 105–117, 2010.
- [22] Ross J. Kang and Tobias Müller. Sphere and dot product representations of graphs. Discrete & Computational Geometry, 47(3):548–568, 2012.
- [23] Chaya Keller and Shakhar Smorodinsky. Conflict-free coloring of intersection graphs of geometric objects. arXiv preprint arXiv:1704.02018, 2017.
- [24] Nissan Lev-Tov and David Peleg. Conflict-free coloring of unit disks. Discrete Applied Mathematics, 157(7):1521–1532, 2009.
- [25] Colin McDiarmid, Dieter Mitsche, and Pawel Pralat. Clique colourings of geometric graphs. arXiv preprint arXiv:1701.02693, 2017.
- [26] Wolfgang Mulzer and Günter Rote. Minimum-weight triangulation is NP-hard. Journal of the ACM, 55(2):11, 2008.
- [27] János Pach and Gábor Tardos. Conflict-free colourings of graphs and hypergraphs. Combinatorics, Probability and Computing, 18(05):819–834, September 2009.
- [28] Shakhar Smorodinsky. Combinatorial Problems in Computational Geometry. PhD thesis, School of Computer Science, Tel-Aviv University, 2003.