II.1 Solution
The theory we consider consists of the Einstein gravity, conformally coupled scalar field, and conformal electrodynamics, whose bulk action reads
|
|
|
(1) |
where
|
|
|
(2) |
|
|
|
(3) |
|
|
|
(4) |
with
|
|
|
(5) |
|
|
|
(6) |
, is the Ricci scalar, is the conformally coupled scalar field, the electromagnetic field strength is given by , with the vector potential. and are gauge-invariant Lorentz electromagnetic field invariants, which in the Minkowski spacetime are both zero. is a dimensionless parameter characterizing the NLE. When , reduces to the Maxwell theory, when increases, we can deem that the extent of the NLE’s deviation from the Maxwell theory also increases. The value of is chosen to be with the spacetime dimensions, such that together with the equation of motion for the scalar field is invariant under the conformal transformations
|
|
|
(7) |
with a transformation function, and this is the reason of the scalar being conformally coupled, though the full action is not necessarily conformal invariant [17, 23].
possesses both duality-rotation (or electromagnetic duality) invariance and conformal invariance and it is a generalization of the Maxwell theory. To see this, we can see the Euler–Lagrange equation and the Bianchi identity
|
|
|
(8) |
|
|
|
(9) |
where the strength tensor is defined by
|
|
|
(10) |
with
|
|
|
(11) |
|
|
|
(12) |
Under the electromagnetic duality rotation, we have
|
|
|
(13) |
|
|
|
(14) |
which mean that is invariant under rotation. On the other hand, under the conformal transformation (7), the field equations (8) and (9) are also invariant, as and .
Varying the action (1) individually with respect to the metric , the scalar field , we obtain
|
|
|
(15) |
|
|
|
(16) |
where we denoted , the energy-momentum tensor of the scalar field is
|
|
|
|
(17) |
|
|
|
|
and the traceless stress-energy tensor of the conformal electromagnetic field is
|
|
|
|
(18) |
|
|
|
|
where the criterion for conformal invariance
|
|
|
(19) |
was used in the second step [24].
We assume the metric as
|
|
|
(20) |
with the blackening factor, the NUT parameter, the metric on the unit sphere, and the electromagnetic potential
|
|
|
(21) |
where . We will seek for solutions of and in the theory described by the action (1), which gives the equations of motion (8) and (9) for the conformal electromagnetic field, as well as the ones for the spacetime and the scalar field in (15) and (16).
For the electromagnetic field under the spacetime ansatz, we can obtain the following quantities
|
|
|
(22) |
|
|
|
|
(23) |
|
|
|
|
|
|
|
(24) |
|
|
|
(25) |
|
|
|
|
(26) |
|
|
|
|
|
|
|
|
(27) |
|
|
|
|
where the ′ denotes derivative with respect to . Then the field equation gives
|
|
|
(28) |
from which we have the specific expressions of ,
|
|
|
(29) |
where and are integral constants restricted by the asymptotic conditions
|
|
|
(30) |
|
|
|
(31) |
meaning that the asymptotic electric charge and magnetic charge are and , respectively. As a result, we get the values of the constants and , dependent on the asymptotic charges, as
|
|
|
|
(32) |
|
|
|
|
(33) |
Thus, the electromagnetic gauge potential is
|
|
|
|
(34) |
|
|
|
|
From the Eq. (16), we have
|
|
|
(35) |
for which either or
|
|
|
(36) |
solves it. As the former solution is trivial, we just consider the latter one. The specific values of and can be restricted by the Eq. (15), which just yields
|
|
|
(37) |
|
|
|
(38) |
where is the conformal scalar parameter, rendering the scalar field being constant. This scalar hair does not vanish even when the electric charge is absent. Notice that in this paper we will only consider the real scalar field, so that or . It is obvious that in the former parameter range, the black hole tends to be Reissner-Nordström-like, while for the latter one, the black hole tends to be Schwarzschild-like, and in the and limit, this solution reduces to the one in the Maxwell case obtained in [18].
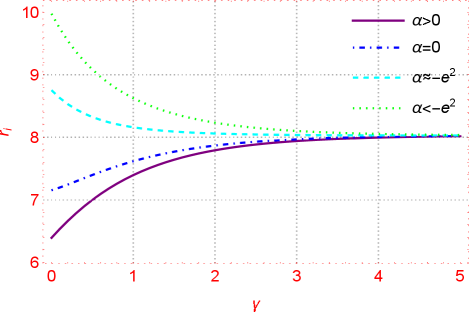
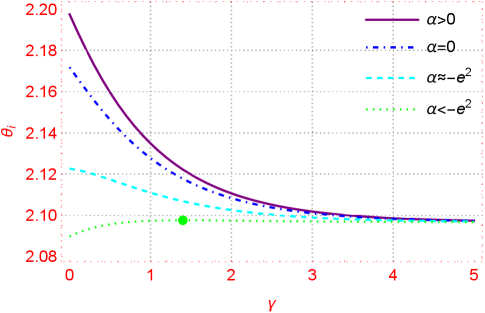
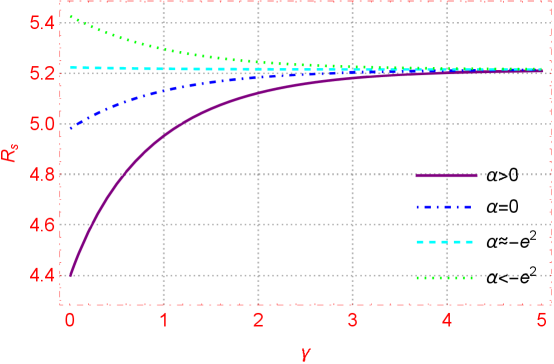
II.2 Cohomogeneity Thermodynamics
Thermodynamics of the black hole with NUT charge have been studied recently in [25, 26, 27, 28, 29, 30, 31], especially in [7] for the Taub-NUT solution in Einstein case with conformal electrodynamics, which are main references for our study here. The event horizon of the NUTty dyon black hole generated by the Killing vector is
|
|
|
(39) |
The temperature, entropy, and mass of the black hole can be obtained as
|
|
|
|
(40) |
|
|
|
|
|
|
|
(41) |
|
|
|
(42) |
where is a normal bivector which satisfies , is the determinant of the induced line element from at the hypersurface and , the mass can be obtained by the Euclidean method [17, 32], as we will show in what follows.
As mentioned above in Eqs. (30) and (31), the asymptotic electric and magnetic charges of the black hole are
|
|
|
(43) |
and they are related by the electromagnetic duality
|
|
|
(44) |
At the event horizon, the charges become
|
|
|
(45) |
|
|
|
(46) |
The gauge electric potential can be calculated by extracting the Killing vector with the vector potential as
|
|
|
|
(47) |
|
|
|
|
|
|
|
|
|
|
|
|
The magnetic potential
|
|
|
|
(48) |
|
|
|
|
can be yielded directly based on the electric potential by using the electromagnetic duality (44).
The Gibbs free energy can be obtained by the Euclidean action [33, 34, 35, 36, 25]
|
|
|
|
(49) |
|
|
|
|
|
|
|
|
|
|
|
|
where is the extrinsic curvature of the background flat spacetime. Notice that the Wick rotations (or ) should be conducted to calculate the action and finally the reverse procedure should also be done (For the term, one can first directly calculate , then do Wick rotation to conduct the integral, and finally rotate back). Then we have the specific expression for the Gibbs energy,
|
|
|
|
(50) |
|
|
|
|
|
|
|
|
|
|
|
|
where is the inverse of the temperature. The Gibbs function satisfies
|
|
|
(51) |
where is the Misner charge conjugated to the Misner potential . The conformal scalar, though being a primary hair, here will not enter the first law of the black hole, which reads
|
|
|
(52) |
After taking the Misner potential as
|
|
|
(53) |
where are surface gravity corresponding to the Killing vectors
|
|
|
(54) |
the integration Smarr relation for the black hole then can be written as
|
|
|
(55) |
Note that can also be attributed physical treatment of angular velocity of the string, as discussed in [37, 38]. Then the quantity conjugate to the angular velocity is interpreted as string angular momentum. By conducting the method of Komar integration raised in [38], alternative Smarr relation can be dervied, with “reduced string angular momentum”. But one can prove that it can be reduced to Eq. (55), only by identifying the string angular velocity as the Misner potential and the string angular momentum as the Misner charge [29, 38, 30].
In above, it is obvious that we have not set . Correspondingly, the electromagnetic potential , and neither does the magnetic charge. If, in the other way, the regularity condition is imposed on, like the Einstein case, we will have the electric first law
|
|
|
(56) |
together with the supplementary Smarr relation
|
|
|
(57) |
In such situation the magnetic parameter is encoded into the electric parameter by the relation
|
|
|
(58) |