Consensus of Hybrid Multi-agent Systems
Abstract
In this paper, we consider the consensus problem of hybrid multi-agent system. First, the hybrid multi-agent system is proposed which is composed of continuous-time and discrete-time dynamic agents. Then, three kinds of consensus protocols are presented for hybrid multi-agent system. The analysis tool developed in this paper is based on the matrix theory and graph theory. With different restrictions of the sampling period, some necessary and sufficient conditions are established for solving the consensus of hybrid multi-agent system. The consensus states are also obtained under different protocols. Finally, simulation examples are provided to demonstrate the effectiveness of our theoretical results.
Index Terms:
Consensus, hybrid multi-agent system, discrete-time, continuous-time.I Introduction
The investigation of multi-agent coordination has regularly attracted contributions from mathematicians, physicists and engineers over the two decades. Classic multi-agent coordination of interest includes consensus [1], flocking [2], containment control [3], formation control [4], coverage control [5], and distributed estimation [6]. Much interest is focusing on dynamic models of agents. Examples include the study of distributed coordination of first-order, second-order, continuous-time and discrete-time dynamic agents. By using the matrix theory, the graph theory, the frequency-domain analysis method and the Lyapunov method etc., lots of results about multi-agent coordination have been obtained [7, 8, 9, 10].
As a fundamental problem of distributed coordination, consensus means that a group of agents reach an agreement on the consistent quantity of interest by designing appropriate control input based on local information. Vicsek et al. [11] proposed a discrete-time model of agents all moving in the plane with the same speed and demonstrated by simulation that all agents move to one direction. By virtue of graph theory, Jadbabaie et al. [12] explained the consensus behaviour of Vicsek model theoretically and shown that consensus can be achieved if the union of interaction graphs are connected frequently enough. By utilizing the pre-leader-follower decomposition, Wang and Xiao [13] studied the state consensus of discrete-time multi-agent systems with bounded time-delays. Second-order consensus of discrete-time multi-agent systems was considered in [14] with nonuniform time-delays. Gossip algorithms [15] and broadcast gossip algorithms [16] were also used to analyze the consensus problem, respectively. For continuous-time dynamic agents, Olfati-Saber and Murray [17] considered the consensus problem of multi-agent systems with switching topologies and time-delays and obtained some necessary and/or sufficient conditions for solving the average consensus. Ren and Beard [18] extended the results given in [17] and presented some more relaxable conditions for solving the consensus. Xie and Wang [19] studied the second-order consensus of multi-agent systems with fixed and switching topologies. Ren [20] investigated the second-order consensus of multi-agent systems in four cases.
Hybrid systems are dynamical systems that involve the interaction of continuous and discrete dynamics. As a class of classic hybrid systems, switched systems have received a major research [21]. For multi-agent systems, lots of references were concerned with consensus problem under switching topologies [17, 22]. However, Zheng and Wang [23] considered the consensus of switched multi-agent system that consists of continuous-time and discrete-time subsystems. They proved that the consensus of switched multi-agent system is solvable under arbitrary switching. Zhu et al. [24] studied the containment control of such switched multi-agent system. In the practical systems, the dynamics of the agents coupled with each others are different, i.e., the dynamics of agents are hybrid. In general, hybrid means heterogeneous in nature or composition. Different from the previous study, Zheng et al. [25] considered the consensus of heterogeneous multi-agent system which is composed of first-order and second-order dynamic agents. The consensus criteria were obtained under different topologies [26, 27]. Finite-time consensus and containment control of the heterogeneous multi-agent system were also studied in [28, 29], respectively.
To the best of our knowledge, however, the existing results of consensus analysis are on the homogeneous and heterogeneous multi-agent systems, i.e., all the agents are continuous-time or discrete-time dynamic behavior at the same time. In the real world, natural and artificial individuals can show collective decision-making. For example, autonomous robots were used to control self-organized behavioral patterns in group-living cockroaches [30]. When the continuous-time and discrete-time dynamic agents coexist and interact with each other, it is important to study the consensus problem of such hybrid multi-agent system. Owing to the coexistence of continuous-time and discrete-time dynamic agents, it is difficult to design the consensus protocol and analyze the consensus problem for hybrid multi-agent system. Up to now, it is not found any approach to analyze the consensus of multi-agent systems with different time-scale. The main objective of this paper is to design the consensus protocols and obtain the consensus criteria of hybrid multi-agent system in different topologies. The main contribution of this paper is threefold. First, we propose the hybrid multi-agent system and give the definition of consensus. Second, three kinds of consensus protocols are presented for hybrid multi-agent system. Finally, by utilizing of the graph theory, some necessary and sufficient conditions are obtained for solving the consensus of hybrid multi-agent system.
The rest of this paper is organized as follows. In Section II, we present some notions in graph theory and propose the hybrid multi-agent system. In Section III, three kinds of consensus protocols are provided for solving the consensus of hybrid multi-agent system. In Section IV, numerical simulations are given to illustrate the effectiveness of theoretical results. Finally, some conclusions are drawn in Section V.
Notation: Throughout this paper, the following notations will be used: denotes the set of real number, denotes the dimensional real vector space. , . For a given vector or matrix denotes its transpose, denotes the Euclidean norm of a vector , denotes its mathematical expectation. A vector is nonnegative if all its elements are nonnegative. Denote by (or ) the column vector with all entries equal to one (or all zeros). is an dimensional identity matrix. defines a diagonal matrix with diagonal elements being . Let denote the canonical vector with a in the -th entry and 0’s elsewhere.
II Preliminaries
II-A Graph theory
A weighted directed graph of order consists of a vertex set , an edge set and a nonnegative matrix . The neighbor set of the agent is . A directed path between two distinct vertices and is a finite ordered sequence of distinct edges of with the form . A directed tree is a directed graph, where there exists a vertex called the root such that there exists a unique directed path from this vertex to every other vertex. A directed spanning tree is a directed tree, which consists of all the nodes and some edges in . If a directed graph has the property that , the directed graph is called undirected. An undirected graph is said to be connected if there exists a path between any two distinct vertices of the graph. The degree matrix is a diagonal matrix with and the Laplacian matrix of the graph is defined as It is easy to see that .
A nonnegative matrix is said to be a (row) stochastic matrix if all its row sums are . A stochastic matrix is called indecomposable and aperiodic (SIA) if , where is some column vector. is said the graph associated with when if and only if . The following results propose the relationship between a stochastic matrix and its associated graph.
Lemma 1
([18]) A stochastic matrix has algebraic multiplicity equal to one for its eigenvalue if and only if the graph associated with the matrix has a spanning tree. Furthermore, a stochastic matrix with positive diagonal elements has the property that for every eigenvalue not equal to one.
Lemma 2
([18]) Let be a stochastic matrix. If A has an eigenvalue with algebraic multiplicity equal to one, and all the other eigenvalues satisfy , then is SIA, that is, , where satisfies and . Furthermore, each element of is nonnegative.
Lemma 3
Let and , . Then, is SIA, i.e., , if and only if graph has a spanning tree. Furthermore, , and each element of is nonnegative.
Proof. (Sufficiency) Let . From the definition of , we have where . It follows from that is a positive diagonal matrix. Consequently, it is easy to obtain that is a stochastic matrix with positive diagonal entries. Obviously, for all , the -th entry of is positive if and only if . Then, is the graph associated with . Combining Lemma 1 and Lemma 2, we have when graph has a spanning tree, where is a nonnegative vector. Moreover, satisfies and .
(Necessary) From Lemma 1, if does not have a spanning tree, the algebraic multiplicity of eigenvalue of is . Then, it is easy to prove that the rank of is greater than 1, which implies that .
II-B Hybrid multi-agent system
Suppose that the hybrid multi-agent system consists of continuous-time and discrete-time dynamic agents. The number of agents is , labelled through , where the number of continuous-time dynamic agents is . Without loss of generality, we assume that agent through agent are continuous-time dynamic agents. Then, each agent has the dynamics as follows:
| (1) |
where is the sampling period, and are the position-like and control input of agent , respectively. The initial conditions are . Let .
Each agent is regraded as a vertex in a graph. Each edge corresponds to an available information link from agent to agent . Moreover, each agent updates its current state based on the information received from its neighbors. In this paper, we suppose that there exists communication behavior in hybrid multi-agent system (1), i.e., there are agent and agent which make .
Definition 1
Hybrid multi-agent system (1) is said to reach consensus if for any initial conditions, we have
| (2) |
and
| (3) |
III Main results
In this section, the consensus problem of hybrid multi-agent system (1) will be considered under three kinds of control inputs (consensus protocols) respectively.
III-A Case 1
In this subsection, we assume that all agents communicate with their neighbours and update their control inputs in the sampling time . Then, the consensus protocol for hybrid multi-agent system (1) is presented as follows.
| (4) |
where is the weighted adjacency matrix associated with the graph , is the sampling period.
Theorem 1
Proof. (Sufficiency) Firstly, we will prove that equation (2) holds. From (4), we know that
| (5) |
Therefore, it follows that
| (6) |
Let . Then, equation (6) can be written in matrix form as
| (7) |
According to Lemma 3, since has a directed spanning tree and , we have , where . Thus, it is easy to obtain
and . As a consequence, equation (2) holds. Moreover,
Secondly, we have
From (5), it is easy to know that
when , we have . Thus,
Moreover,
which implies that equation (3) holds.
III-B Case 2
In this subsection, we still assume that the interaction among agents happens in sampling time . However, different from Case 1, we assume that each continuous-time dynamic agent can observe its own state in real time. Thus, the consensus protocol for hybrid multi-agent system (1) is presented as follows.
| (8) |
where is the weighted adjacency matrix associated with the graph , is the sampling period.
Theorem 2
Proof. (Sufficiency) Firstly, we will prove that equation (2) holds. Solving hybrid multi-agent system (1) with protocol (8), we have
| (9) |
Accordingly, at time , the states of agents are
| (10) |
Hence, (10) can be rewritten in compact form as
| (11) |
where , .
It is easy to know that , . Owing to , we have for . From Lemma 3, because has a directed spanning tree, is an SIA matrix, i.e., , where . Hence,
which means that
Obviously, equation (2) holds. Moreover, it follows from that .
Therefore, from Definition 1, hybrid multi-agent system (1) with protocol (8) reaches consensus. Moreover, the consensus state is .
III-C Case 3
In this subsection, we assume that all agents interact with each other in a gossip-like manner. Some assumptions are given as follows.
(A1) The communication network of hybrid multi-agent system (1) is undirected, i.e., for all .
(A2) At time , two agents and () satisfying are chosen with probability , where and .
When agents and are chosen, their interplay follows the below situations, where is the sampling period.
-
•
If and are continuous-time dynamic agents, i.e., , they will communicate during . The control inputs of two agents are
(12) -
•
If is continuous-time dynamic agent and is discrete-time dynamic agent, i.e., , the control inputs of two agents are
(13) -
•
If and are discrete-time dynamic agents, i.e., , the control inputs of two agents are
(14)
For each , it keeps static, i.e.,
| (15) |
Theorem 3
Proof. (Sufficiency) It suffices to prove that
| (16) |
and
| (17) |
hold for any initial states.
Firstly, we will show that equation (16) holds. From (12)–(15), if agents and are selected to interplay at time , the states of all agents at time are three cases:
| (18a) | ||||
| (18b) | ||||
| (18c) | ||||
Note that (18) can be rewritten in the following compact form as
where
| (19) |
According to (A2), it is not hard to know that is a stochastic linear system
Therefore, it follows that
| (20) |
Due to , we have , and . Thus, is a stochastic matrix with positive diagonal entries. Moreover, the -th and -th entries of are positive, while all other non-diagonal entries are zeros. Hence, noticing that
we know that is a stochastic matrix satisfying
-
•
all diagonal entries are positive;
-
•
the -th and -th entries are positive if and only if .
Consequently, is the graph associated with . Since is connected, combining Lemma 1 and Lemma 2, we have
From (20), we have
which implies that equation (16) holds.
Secondly, at time , the state of each follows the below three scenarios:
-
•
if is selected to communicate with its continuous-time dynamical neighbour ,
-
•
if is selected to communicate with its discrete-time dynamical neighbour ,
-
•
if is not selected,
Thus, we have
| (21) | ||||
where
Since when , it is easy to obtain from (21) that
holds for all , which means equation (17) holds.
Therefore, hybrid multi-agent system (1) with control inputs (12)–(15) can solve consensus problem in mean sense.
(Necessity) When is not connected, similar to the proof of necessity in Theorem 1, we know that hybrid multi-agent system (1) can not reach consensus.
Remark 2
Note that hybrid multi-agent system (1) presents a unified framework for both the discrete-time multi-agent system and the continuous-time multi-agent system. In other words, if , hybrid multi-agent system (1) becomes a discrete-time multi-agent system. And if , hybrid multi-agent system (1) becomes a continuous-time multi-agent system.
IV Simulations
In this section, we provided some simulations to demonstrate the effectiveness of the theoretical results in this paper.
Suppose that there are 6 agents. The continuous-time dynamic agents and the discrete-time dynamic agents are denoted by 1–3 and 4–6, respectively. In the following, all networks with 0-1 weights will be needed. Let and .
Example 1
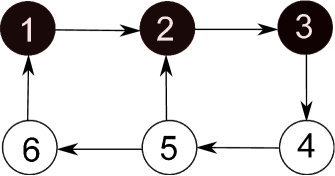
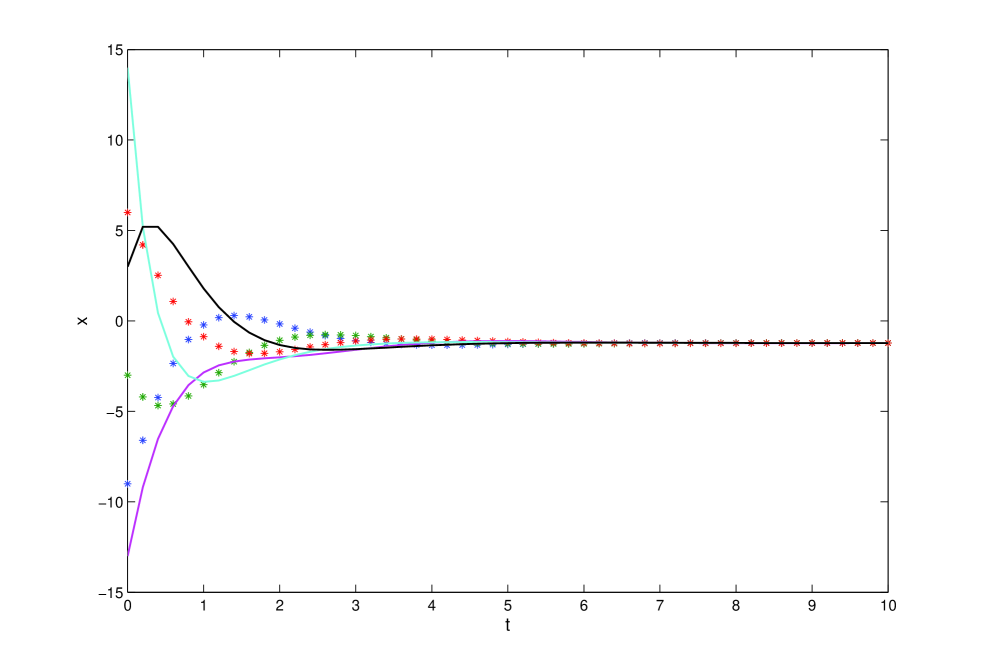
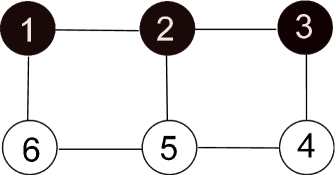
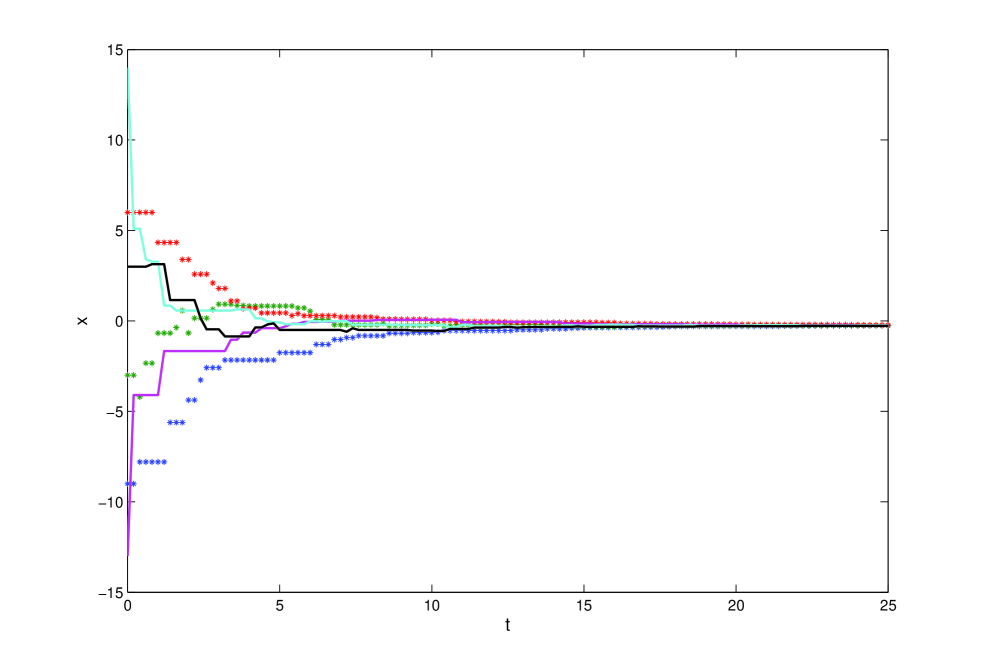
The communication network is shown in Fig. 1. It can be noted that has a directed spanning tree. It is easy to calculate that the sampling period . By using consensus protocol (4), the state trajectories of all the agents are shown in Fig. 2, which is consistent with the sufficiency of Theorem 1.
Example 2
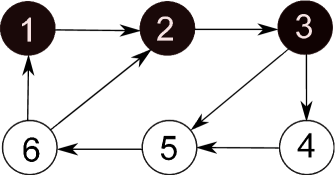
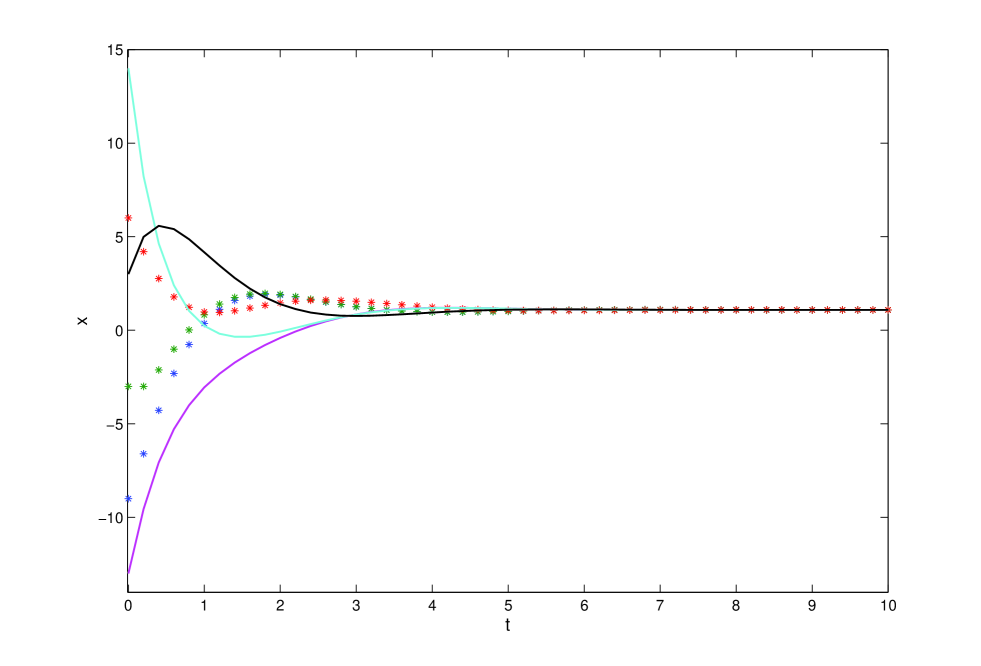
Assume that the communication network is shown in Fig. 3. It is easy to know that has a directed spanning tree. By calculation, the sampling period . By using consensus protocol (8), the state trajectories of all the agents are shown in Fig. 4, which is consistent with the results in Theorem 2.
Example 3
Suppose that hybrid multi-agent system (1) runs with control inputs (12)–(15). The communication network is depicted in Fig. 5. It is shown that the sampling period . At time , each edge is chosen with probability . The state trajectories of all the agents are drawn in Fig 6. Obviously, the simulation results is consistent with the sufficiency of Theorem 3.
V Conclusions
In this paper, the consensus problem of hybrid multi-agent system which is composed of continuous-time and discrete-time dynamic agents was considered. First, we assumed that all agents communicate with their neighbours and update their strategies in the sampling time. When the sampling period , we proved that the hybrid multi-agent system can achieve the consensus if and only if the communication network has a directed spanning tree. Then, we further assumed that each continuous-time agent can observe its own state in real time. The consensus of hybrid multi-agent system can be solved with . Finally, a gossip-like consensus protocol was proposed. The necessary and sufficient condition was also given for solving the consensus problem if . The future work will focus on the second-order consensus of hybrid multi-agent system, consensus of hybrid multi-agent system with time-delays etc.
References
- [1] R. Olfati-Saber, J.A. Fax and R.M. Murray, “Consensus and cooperation in networked multi-agent systems,” Proceedings of the IEEE, vol. 95, no. 1, pp. 215-233, 2007.
- [2] R. Olfati-Saber, “Flocking for multi-agent dynamics systems: algorithms and theory,” IEEE Transactions on Automatic Control, vol. 51, no.3, pp. 401-420, 2006.
- [3] Y. Cao, D. Stuart, W. Ren and Z. Meng, “Distributed containment control for multiple autonomous vehihcles with double-integrator dynamics: algorithms and experiments,” IEEE Transactions on Control Systems Technology, vol. 19, no. 4, pp. 929-938, 2011.
- [4] F. Xiao, J. Chen and L. Wang, “Finite-time formation control for multi-agent systems,” Automatica, vol. 45, no. 11, pp. 2605-2611, 2009.
- [5] J. Corts, S. Martnez, T. Karatas and F. Bullo, “Coverage control for mobile sensing networks,” IEEE Transactions on Robotics and Automation, vol. 20, no. 2, pp. 243-255, 2002.
- [6] P. Yang, R. Freeman and K. M. Lynch, “Multi-agent coordination by decentralized estimation and control,” IEEE Transactions on Automatic Control, vol. 53, no. 11, pp. 2480-2496, 2008.
- [7] W. Ren and R. W. Beard, Distributed consensus in multi-vehicle cooperative control, Springer-Verlag, London, 2008.
- [8] F. Xiao and L. Wang, “Asynchronous consensus in continuous-time multi-agent systems with switching topology and time-varying delays,” IEEE Transactions on Automatic Control, vol. 53, no.8, pp. 1804-1816, 2008.
- [9] Z. Ji, Z. Wang, H. Lin and Z. Wang, “Interconnection topologies for multi-agent coordination under leader-follower framework,” Automatica, vol. 45, no. 12, pp. 2857-2863, 2009.
- [10] H. Su, M. Chen, J. Lam and Z. Lin, “Semi-global leader-following consensus of linear multi-agent systems with input saturation via low gain feedback,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 60, no. 7, pp. 1881-1889, 2013.
- [11] T. Vicsek, A. Czirok, E. B. Jacob, I. Cohen and O. Schochet, “Novel type of phase transition in a system of self-driven particles,” Physical Review Letters, vol. 75, no. 6, pp. 1226-1229, 1995.
- [12] A. Jadbabaie, J. Lin and A. S. Morse, “Coordination of groups of mobile autonomous agents using neaest neighbor rules,” IEEE Transactions on Automatic Control, vol. 48, no. 6, pp. 988-1001, 2003.
- [13] L. Wang and F. Xiao, “A new approach to consensus problem in discrete-time multiagent systems with time-delays,” Science in China Series F: Information Sciences, vol. 50, no. 4, pp. 625-635, 2007.
- [14] P. Lin and Y. Jia, “Consensus of second-order discrete-time multi-agent systems with nonuniform time-delays and dynamically changing topologies,” Automatica, vol. 45, no. 9, pp. 2154-2158, 2009.
- [15] S. Boyd, A. Ghosh, B. Prabhakar and D. Shah, “Randomized gossip algorithms,” IEEE Transactions on Information Theory, vol. 52, no. 6, pp. 2508-2530, 2006.
- [16] T. C. Aysal, M. E. Yildiz, A. D. Sarwate and A. Scaglione, “Broadcast gossip algorithms for consensus,” IEEE Transactions on Signal Processing, vol. 57, no. 7, pp. 2748-2761, 2009.
- [17] R. Olfati-Saber and R.M. Murray, “Consensus problems in networks of agents with switching topology and time-delays,” IEEE Transactions on Automatic Control, vol. 49, no. 9, pp. 1520-1533, 2004.
- [18] W. Ren and R. W. Beard, ”Consensus seeking in multiagent systems under dynamically changing interaction topologies,” IEEE Trans Autom. Control, vol. 50, no. 5, pp. 655-661, 2005.
- [19] G. Xie and L. Wang, “Consensus control for a class of networks of dynamic agents,” International Journal of Robust and Nonlinear Control, vol. 17, no. 10-11, pp. 941-959, 2007.
- [20] W. Ren, “On consensus algorithms for double-integrator dynamics,” IEEE Transactions on Automatic Control, vol. 53, no. 6, pp. 1503-1509, 2008.
- [21] P. J. Antsaklis, “A brief introduction to the theory and applications of hybrid systems,” Proceedings of the IEEE, Special Issue on Hybrid Systems: Theory and Applications, vol. 88, no. 7, pp. 879-887, 2000.
- [22] Y. Sun, L. Wang and G. Xie, “Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays,” Systems and Control Letters, vol. 57, no. 2, pp. 175-183, 2008.
- [23] Y. Zheng and L. Wang, “Consensus of switched multi-agent systems,” IEEE Transactions on Circuits and Systems II, DOI: 10.1109/TCSII.2015.2482138, 2015.
- [24] Y. Zhu, Y. Zheng and L. Wang, “Containment control of switched multi-agent systems,” International Journal of Control, vol. 88, no. 12, pp. 2570-2577, 2015.
- [25] Y. Zheng, Y. Zhu and L. Wang, “Consensus of heterogeneous multi-agent systems,” IET Control Theory and Applications, vol. 5, no. 16, pp. 1881-1888, 2011.
- [26] Y. Zheng and L. Wang, “Distributed consensus of heterogeneous multi-agent systems with fixed and switching topologies,” International Journal of Control, vol. 85, no. 12, pp. 1967-1976, 2012.
- [27] Y. Zheng and L. Wang, “Consensus of heterogeneous multi-agent systems without velocity measrements,” International Journal of Control, vol. 85, no. 7, pp. 906-914, 2012.
- [28] Y. Zheng and L. Wang, “Finite-time consensus of heterogeneous multi-agent systems with and without velocity measurements,” Systems and Control Letters, vol. 61, no. 8, pp. 871-878, 2012.
- [29] Y. Zheng and L. Wang, “Containment control of heterogeneous multi-agent systems,” International Journal of Control, vol. 87, no. 1, pp. 1-8, 2014.
- [30] J. Halloy, G. Sempo, G. Caprari, et al., “Social integration of robots into groups of cockroaches to control self-organized choices,” Science, vol. 318, no. 5853, pp. 1155-1158, 2007.