Constant Approximation Algorithms for Guarding Simple Polygons using Vertex Guards
Abstract
The art gallery problem enquires about the least number of guards sufficient to ensure that an art gallery, represented by a simple polygon , is fully guarded. Most standard versions of this problem are known to be NP-hard. In 1987, Ghosh provided a deterministic -approximation algorithm for the case of vertex guards and edge guards in simple polygons. In the same paper, Ghosh also conjectured the existence of constant ratio approximation algorithms for these problems. We present here three polynomial-time algorithms with a constant approximation ratio for guarding an -sided simple polygon using vertex guards. (i) The first algorithm, that has an approximation ratio of 18, guards all vertices of in time. (ii) The second algorithm, that has the same approximation ratio of 18, guards the entire boundary of in time. (iii) The third algorithm, that has an approximation ratio of 27, guards all interior and boundary points of in time. Further, these algorithms can be modified to obtain similar approximation ratios while using edge guards. The significance of our results lies in the fact that these results settle the conjecture by Ghosh regarding the existence of constant-factor approximation algorithms for this problem, which has been open since 1987 despite several attempts by researchers. Our approximation algorithms exploit several deep visibility structures of simple polygons which are interesting in their own right.
1 Introduction
1.1 The art gallery problem and its variants
The art gallery problem enquires about the least number of guards sufficient to ensure that an art gallery
(represented by a polygon ) is fully guarded, assuming that a guard’s field of view covers 360° as well
as unbounded distance. This problem was first posed by Victor Klee in a conference in 1973, and has become a well investigated problem in computational geometry.
A polygon is defined to be a closed region in the plane bounded by
a finite set of line segments, called edges of , such that between any two points of ,
there exists a path which does not intersect any edge of .
If the boundary of a polygon consists of two or more cycles, then is called a polygon with holes
(see Figure 2).
Otherwise, is called a simple polygon or a polygon without holes (see Figure 2).
An art gallery can be viewed as an -sided polygon (with or without holes) and guards as points inside . Any point is said to be visible from a guard if the line segment does not intersect the exterior of . In general, guards may be placed anywhere inside . If the guards are allowed to be placed only on vertices of , they are called vertex guards. If there is no such restriction, then they are called point guards. The point guards that are constrained to lie on the boundary of , but not necessarily at the vertices, are referred to as perimeter guards. Point, vertex and perimeter guards together are also referred to as stationary guards. If guards are allowed to patrol along a line segment inside , they are called mobile guards. If they are allowed to patrol only along the edges of , they are called edge guards [13, 26].
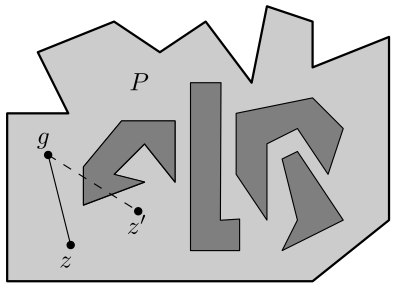
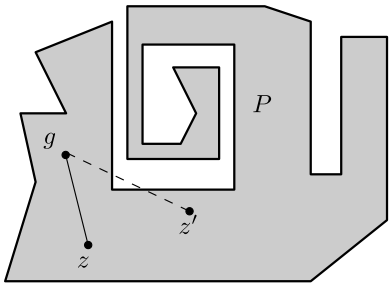
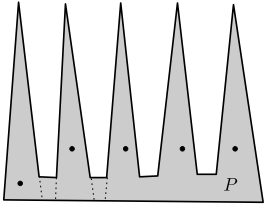
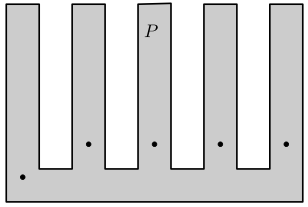
In 1975, Chvátal [6] showed that stationary guards are sufficient and sometimes necessary (see Figure 4) for guarding a simple polygon. In 1978, Fisk [11] presented a simpler and more elegant proof of this result. For a simple orthogonal polygon, whose edges are either horizontal or vertical, Kahn et al. [18] and also O’Rourke [25] showed that stationary guards are sufficient and sometimes necessary (see Figure 4).
1.2 Related hardness and approximation results
The decision version of the art gallery problem is to determine, given a polygon and a number as input, whether
the polygon can be guarded with or fewer point guards.
This problem was first shown to be NP-hard for polygons with holes by O’Rourke and Supowit [27].
This problem was also shown to be NP-hard for simple polygons for guarding using only vertex guards by Lee and Lin [24]. Their proof was generalized to work for point guards by Aggarwal [2].
The problem was shown to be NP-hard even for simple orthogonal polygons by Katz and Roisman [20] and Schuchardt and Hecker [28].
Abrahamsen, Adamaszek and Miltzow [1] have recently shown that the art gallery problem for point guards is ETR-complete.
In 1987, Ghosh [12, 14] provided a deterministic -approximation algorithm for the case of vertex and edge guards by discretizing the input polygon and treating it as an instance of the Set Cover problem.
As pointed out by King and Kirkpatrick [21], newer methods for improving the approximation ratio of the Set Cover problem itself have been developed in the time after Ghosh’s algorithm was published.
By applying these methods, the approximation ratio of Ghosh’s algorithm becomes for guarding simple polygons
and for guarding a polygon with holes, where denotes the size of the smallest guard
set for . Deshpande et al. [7] obtained an approximation factor of for point guards or
perimeter guards by developing a sophisticated discretization method that runs in pseudo-polynomial time. Efrat and Har-Peled [8] provided a randomized algorithm with the same approximation ratio that runs in fully polynomial expected time.
Bonnet and Miltzow [5] obtained an approximation factor of for the point guard problem assuming integer coordinates and a specific general position.
For guarding simple polygons using perimeter guards, King and Kirkpatrick [21] designed a deterministic -approximation
algorithm in 2011. The analysis of this result was simplified by Kirkpatrick [22].
In 1998, Eidenbenz, Stamm and Widmayer [9, 10] proved that the problem is APX-complete, implying that an approximation
ratio better than a fixed constant cannot be achieved unless NP = P.
They also proved that if the input polygon is allowed to
contain holes, then there cannot exist a polynomial time algorithm for the problem with an approximation ratio better than
for any , unless NP TIME(). Extending their method,
Bhattacharya, Ghosh and Roy [3] proved that, even for the special subclass of polygons with holes that are
weakly visible from an edge, there cannot exist a polynomial time algorithm for the problem with an approximation ratio better
than for any , unless NP = P. These inapproximability results establish that the approximation
ratio of obtained by Ghosh in 1987 is in fact the best possible for the case of polygons with holes. However, for simple
polygons, the existence of a constant factor approximation algorithm for vertex and edge guards was conjectured
by Ghosh [12, 15] in 1987.
Ghosh’s conjecture has been shown to be true for vertex guarding in two special sub-classes of simple polygons, viz. monotone polygons and polygons weakly visible from an edge. In 2012, Krohn and Nilsson [23] presented an approximation algorithm that computes in polynomial time a guard set for a monotone polygon , such that the size of the guard set is at most . Bhattacharya, Ghosh and Roy [3, 4] presented a 6-approximation algorithm that runs in time for vertex guarding simple polygons that are weakly visible from an edge. For vertex guarding this subclass of simple polygons that are weakly visible from an edge, a PTAS has recently been proposed by Katz [19].
1.3 Our contributions
In this paper, we present three polynomial-time algorithms with a constant approximation ratio for guarding an -sided simple polygon using vertex guards. The first algorithm, that has an approximation ratio of 18, guards all vertices of in time.
The second algorithm, that has the same approximation ratio of 18,
guards the entire boundary of in time.
The third algorithm, that has an approximation ratio of 27, guards all interior and boundary points of
in time.
As an extension we show, using similar techniques, constant-factor approximation can also be achieved for guarding
we also present identical algorithms, maintaining both the approximation bounds as well as the running times,
can be obtained using edge guards.
In particular, we show that the same approximation ratios of 18, 18 and 27 hold
for guarding all vertices, the entire boundary, and the interior of ,
with time complexities ,
and respectively.
The significance of our results lies in the fact that these results settle the long-standing conjecture by Ghosh [12] regarding the existence of constant-factor approximation algorithms for these problem, which has been open since 1987 despite several attempts by researchers.
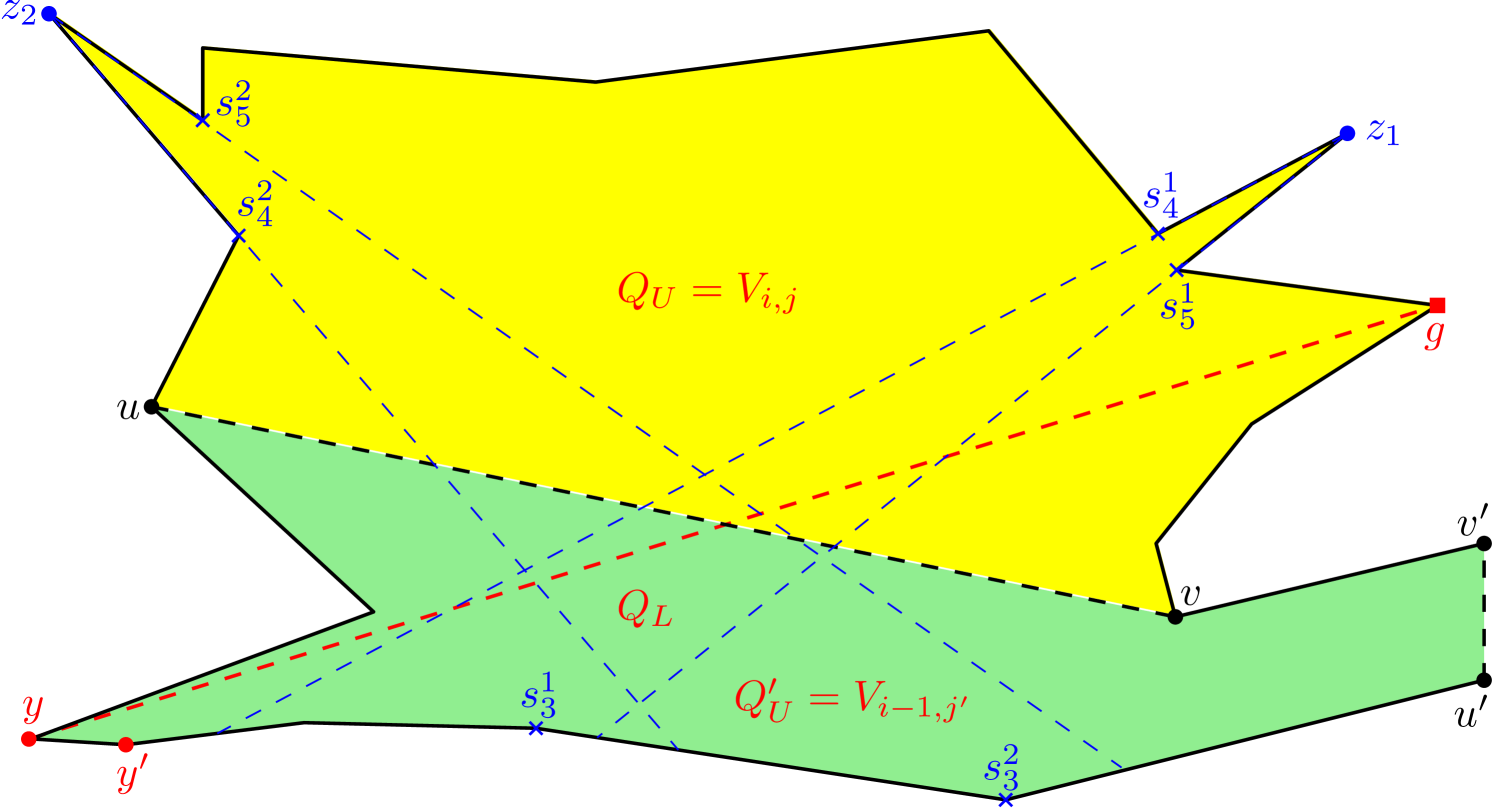
In each of our algorithms, is first partitioned into a hierarchy of weak visibility polygons according to the link distance from a starting vertex (see Figure 6). This partitioning is very similar to the window
partitioning given by Suri [29, 30] in the context of computing minimum link paths. Then, starting with the farthest level in the hierarchy (i.e. the set of weak visibility polygons that are at the maximum link distance from the starting vertex), the entire hierarchy is traversed backward level by level, and at each level,
vertex guards (of two types, viz. inside and outside)
are placed for guarding every weak visibility polygon at that level of .
At every level, a novel procedure is used that has been developed for placing guards in (i) a simple polygon that is weakly visible from an internal chord,
or (ii) a union of overlapping polygons that are weakly visible from multiple disjoint internal chords.
Note that these chords are actually the constructed edges introduced during the hierarchical partitioning of .
Due to partitioning according to link distances, guards can only see points within the adjacent weak visibility polygons in the hierarchical partitioning of . This property locally restricts the visibility of the chosen guards, and thereby ensures that the approximation bound on the number of vertex guards placed by our algorithms at any level leads directly to overall approximation bounds for guarding . Thus, a constant factor approximation bound on the overall number of guards placed by our algorithms is a direct consequence of choosing vertex guards in a judicious manner for guarding each collection of overlapping weak visibility polygons obtained from the hierarchical partitioning of . Our algorithms exploit several deep visibility structures of simple polygons which are interesting in their own right.
1.4 Organization of the paper
In Section 2, we introduce some preliminary definitions and notations that are used throughout the rest of the paper. In Section 3, we present the hierarchical partitioning of a simple polygon into weak visibility polygons. Next, in Section 4, we describe how the algorithm traverses the hierarchy of visibility polygons, starting from the farthest level, and uses the procedures from Section 5 at each level as a sub-routine for guarding . In Section 5, we present a novel procedure for placing vertex guards necessary for guarding a simple polygon that is weakly visible from a single internal chord or from multiple disjoint chords. In Section 6, we establish the overall approximation ratios for the three approximation algorithms. In Section 7, we show how these algorithms can be modified to obtain similar approximation bounds while using edge guards. Finally, in Section 8, we conclude the paper with a few remarks.
2 Preliminary definitions and notations
Let be a simple polygon. Assume that the vertices of are labelled in clockwise order.
Let denote the set of all vertices.
Let (or ) denote the clockwise (respectively, counterclockwise) boundary of from a vertex
to another vertex . Note that by definition, . Also, we denote the entire boundary of by
. So, for any chosen vertex belonging to .
The visibility polygon of from a point , denoted as , is defined to be the set of all points of
that are visible from . In other words, .
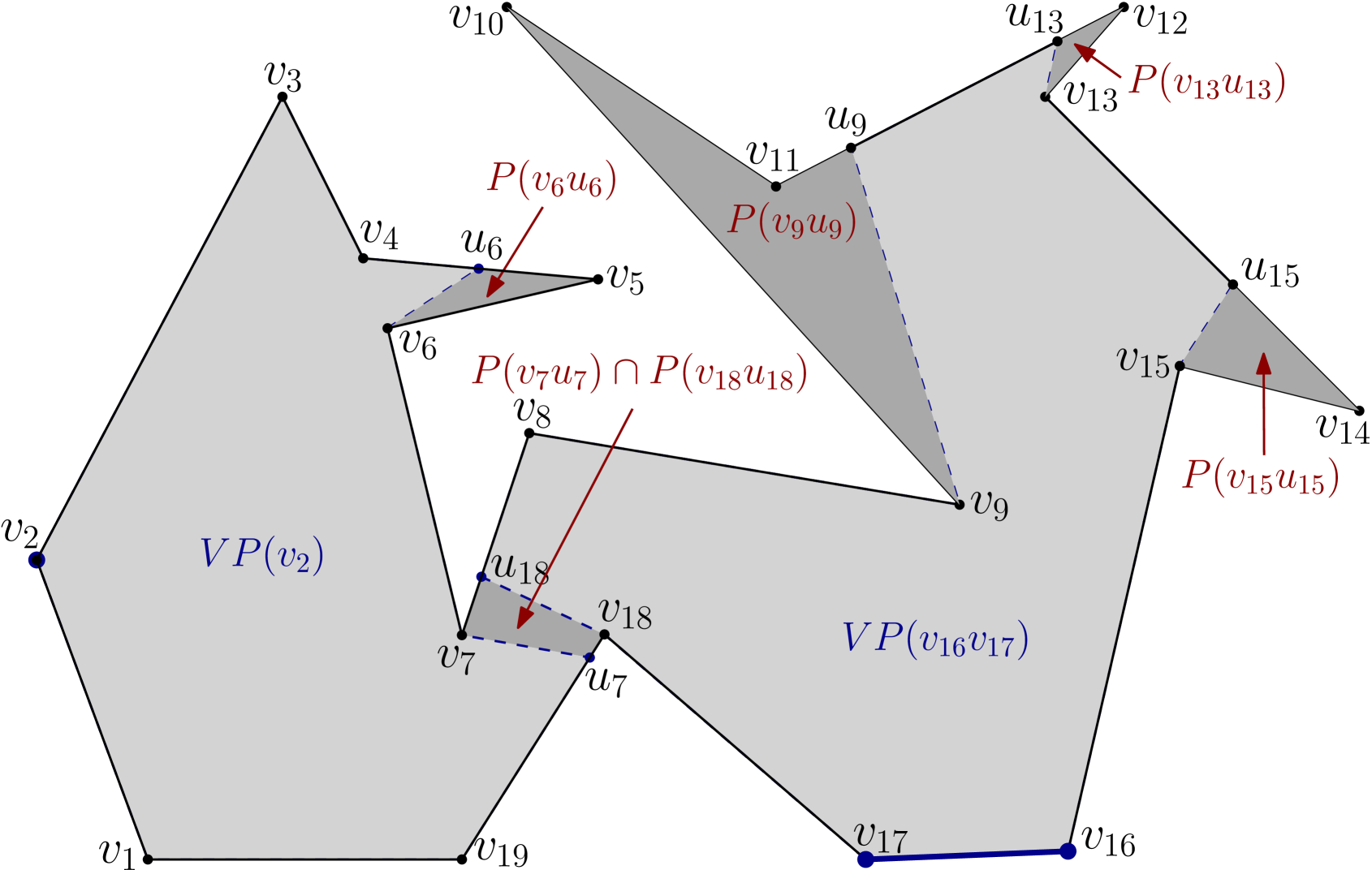
Observe that the boundary of consists of polygonal edges and non-polygonal edges. We refer to the non-polygonal edges as constructed edges. Note that one point of a constructed edge is a vertex
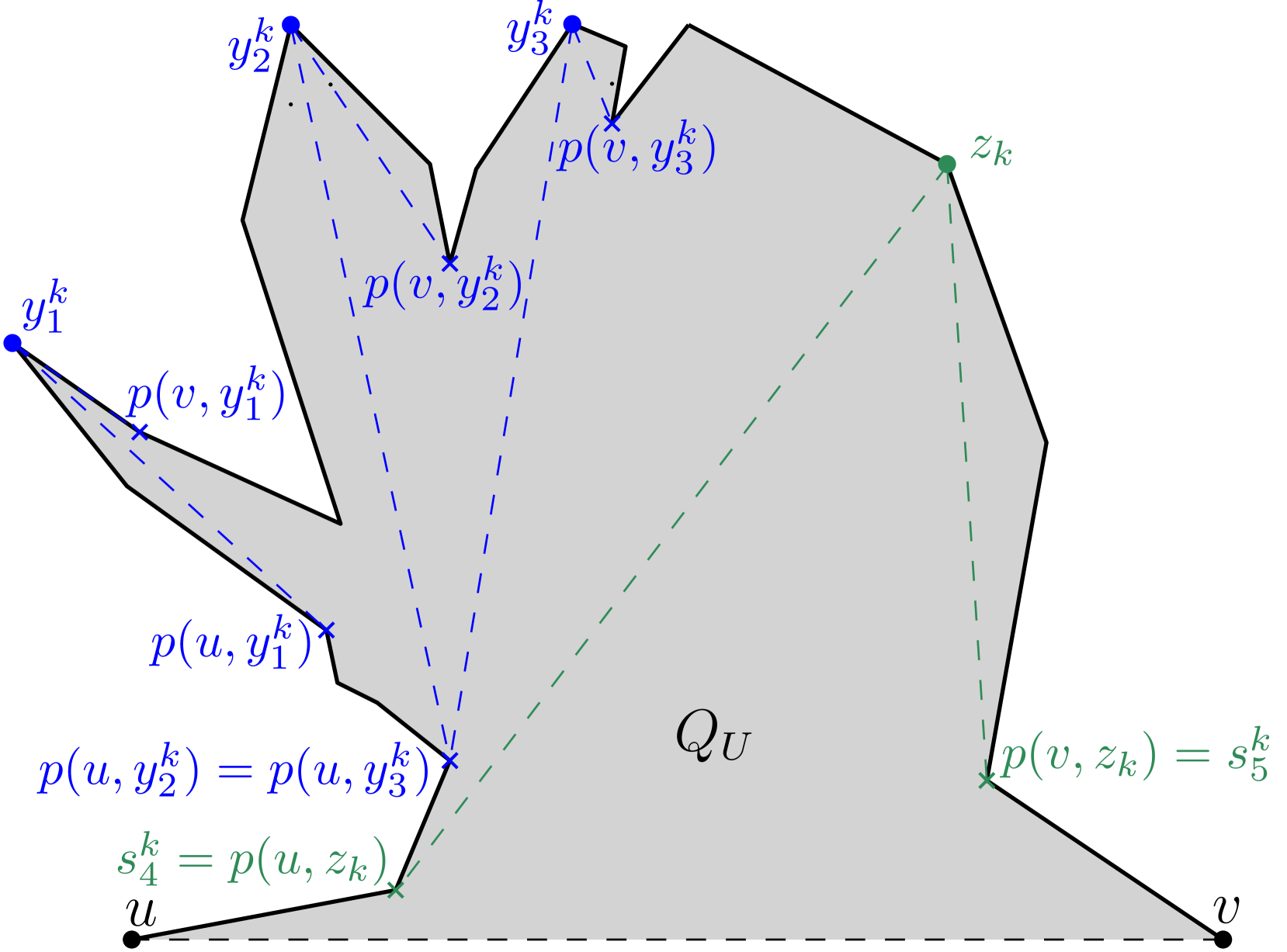
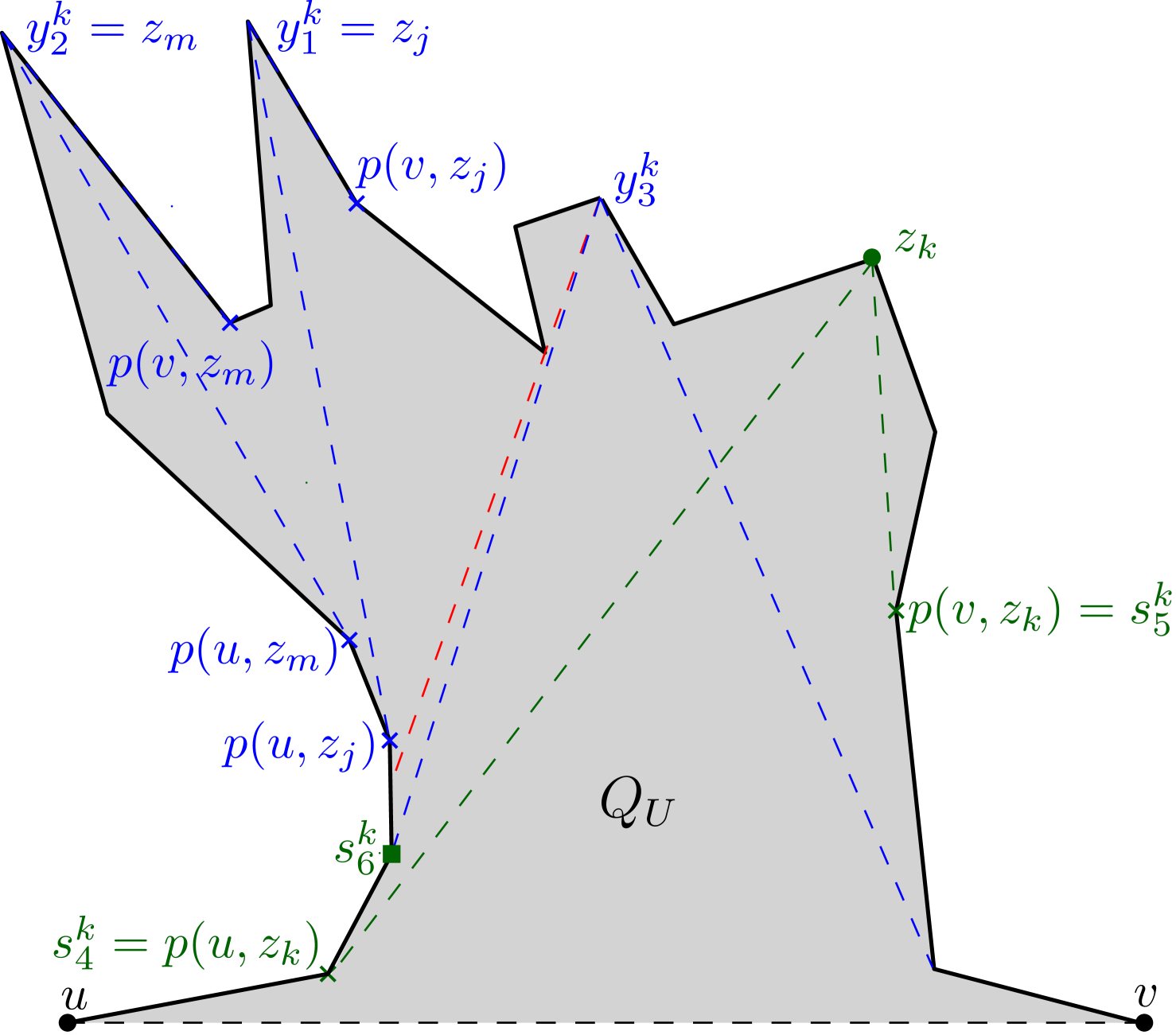
(say, ) of , while the other point (say, ) lies on . Moreover, the points , and are collinear (see Figure 6).
Let be an internal chord or an edge of . A point of is said to be weakly visible from if there exists a point such that is visible from . The set of all such points of is said to be the weak visibility polygon of from , and denoted as . If , then is said to be weakly visible from . Like , the boundary of also consists of polygonal edges and constructed edges (see Figure 6). If (or ) does not belong to , then is called a left constructed edge of (respectively, ). Otherwise, is called a right constructed edge. For any constructed edge of (or ), observe that divides into two subpolygons. One of the subpolygons is bounded by and , whereas the other one is bounded by and . Out of these two, the subpolygon that does not contain (respectively, ) is referred to as the pocket of , and is denoted by (see Figure 6). If is a left (or right) constructed edge, then is called a left pocket (or right pocket).
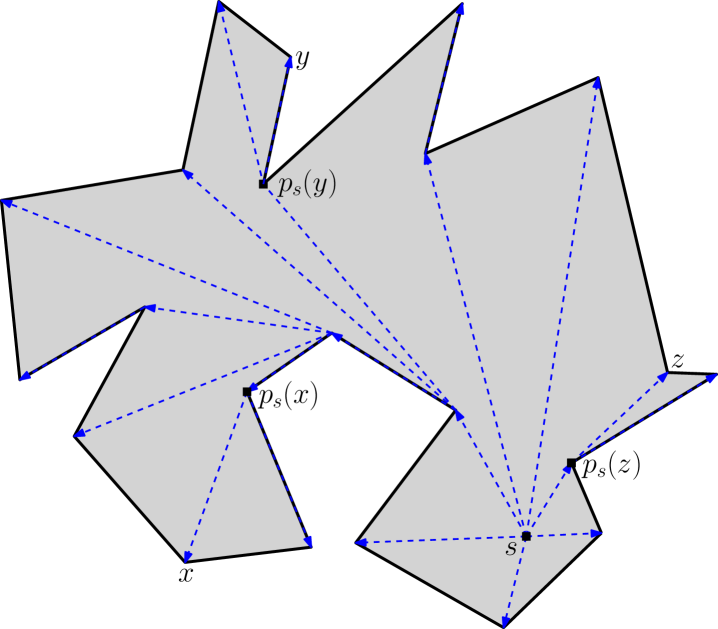
Let define the Euclidean shortest path from a point to another point within . The shortest path tree of rooted at any point of , denoted by , is the union of Euclidean shortest paths from to all vertices of (see Figure 7). This union of paths is a planar tree, rooted at , which has nodes, namely the vertices of . For every vertex of , let denote the parent of in .
A link path between two points and in is a path inside that connects and by a chain of line segments called links. A minimum link path between and is a link path connecting and that has the minimum number of links. Observe that there may be several different minimum link paths between and . The link distance between any two points of is defined to be the number of links in a minimum link path between them.
3 Partitioning a simple polygon into weak visibility polygons
The partitioning algorithm partitions into regions according to their link distance from .
The algorithm starts by computing ,
which is the set of all points of whose link distance from is 1.
Let us denote as .
Then the algorithm computes the weak visibility polygons from every constructed edge of . Let denote the constructed edges of along in clockwise order from ,
where is the number of constructed edges in . Then the algorithm removes from . It can be seen that the remaining polygon consists of disjoint polygons .
For each , the weak visibility polygon is computed inside the pocket ,
and it is denoted as , i.e. .
Let and . Observe that is the set
of all the disjoint regions of , such that every point of each disjoint region in is at link distance two from .
Repeating the same process, the algorithm computes , where denotes the maximum link distance of any point of from . Note that it is not possible for any visibility polygon belonging to to have any constructed edge. Therefore, no further visibility polygon is computed. Hence, . Thus, the algorithm returns the set , which is a partition of . We present the pseudocode for the entire partitioning algorithm below as Algorithm 1.
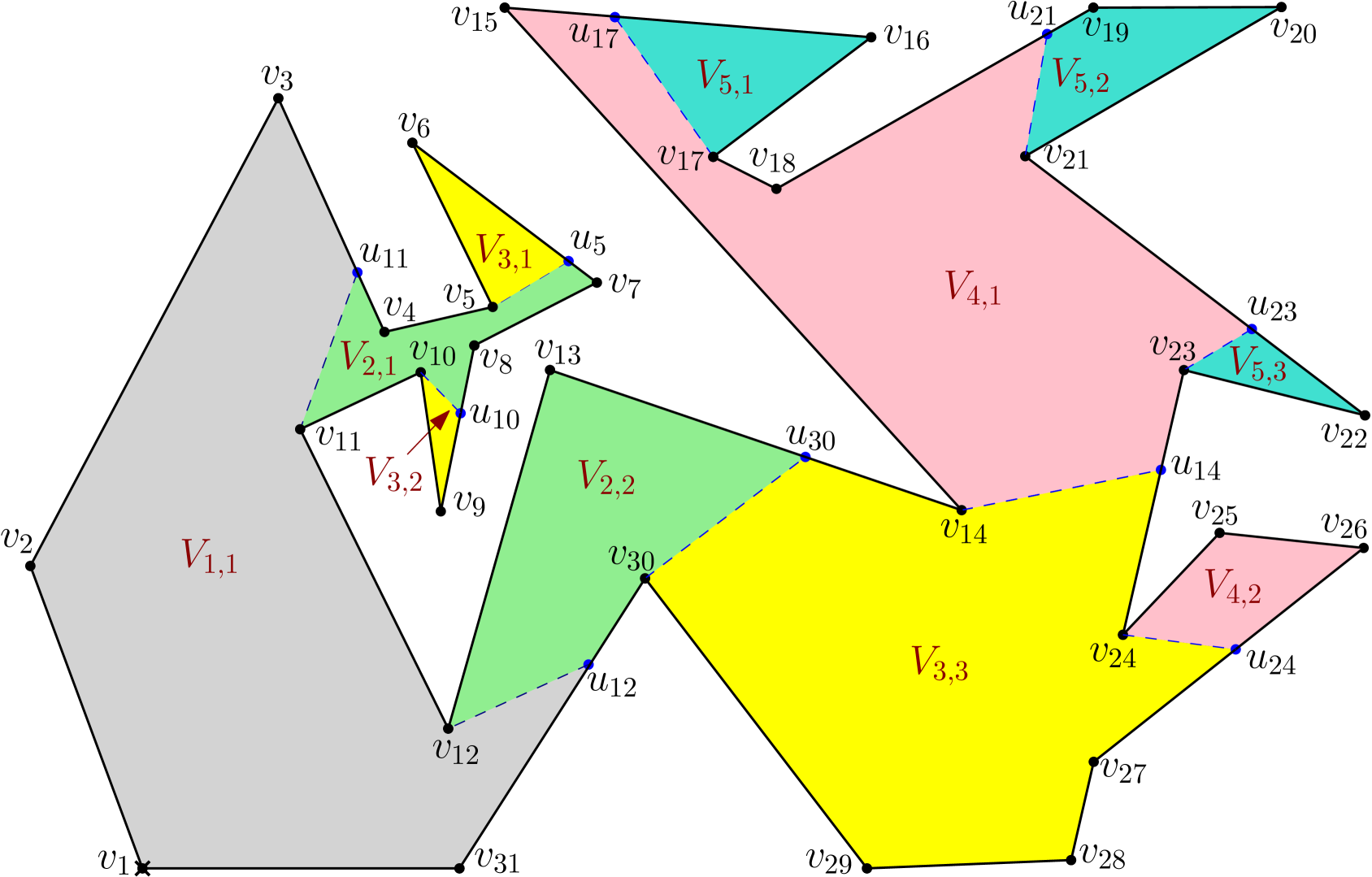
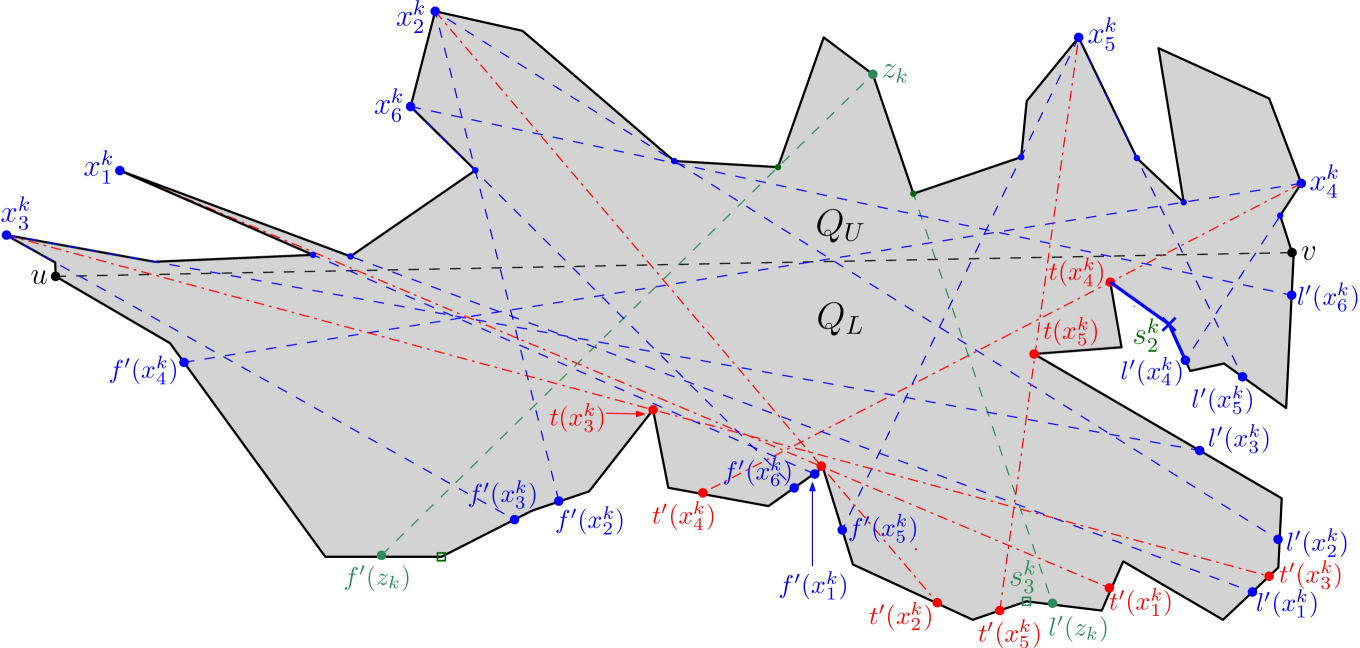
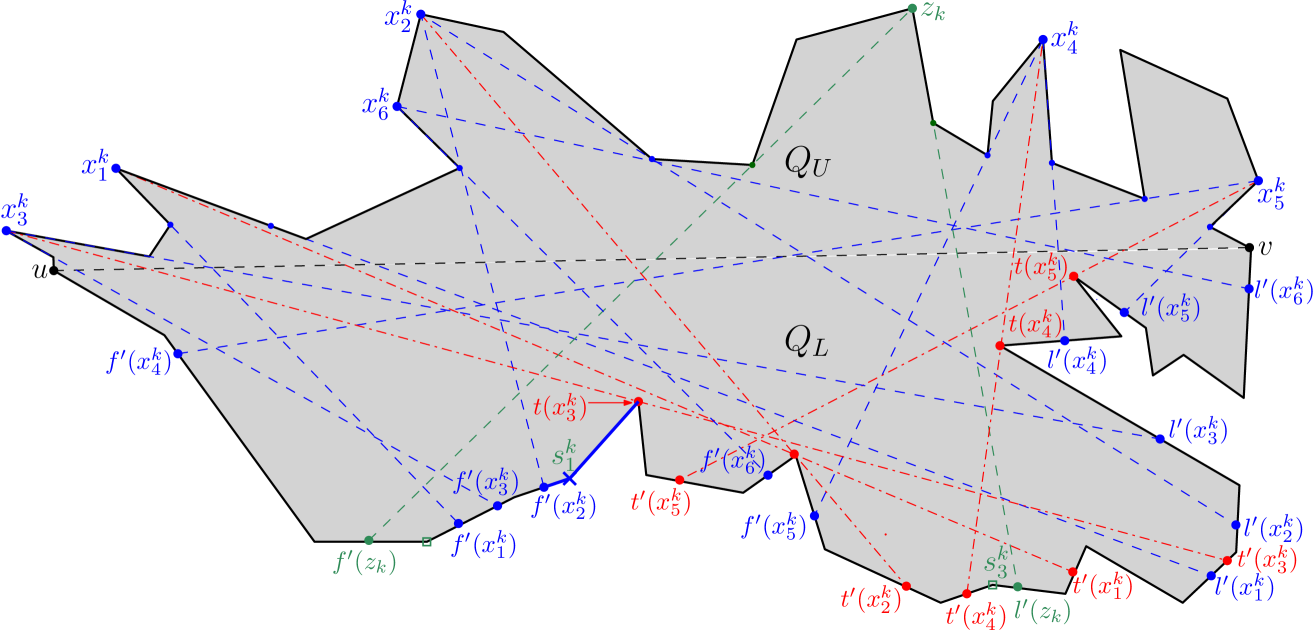
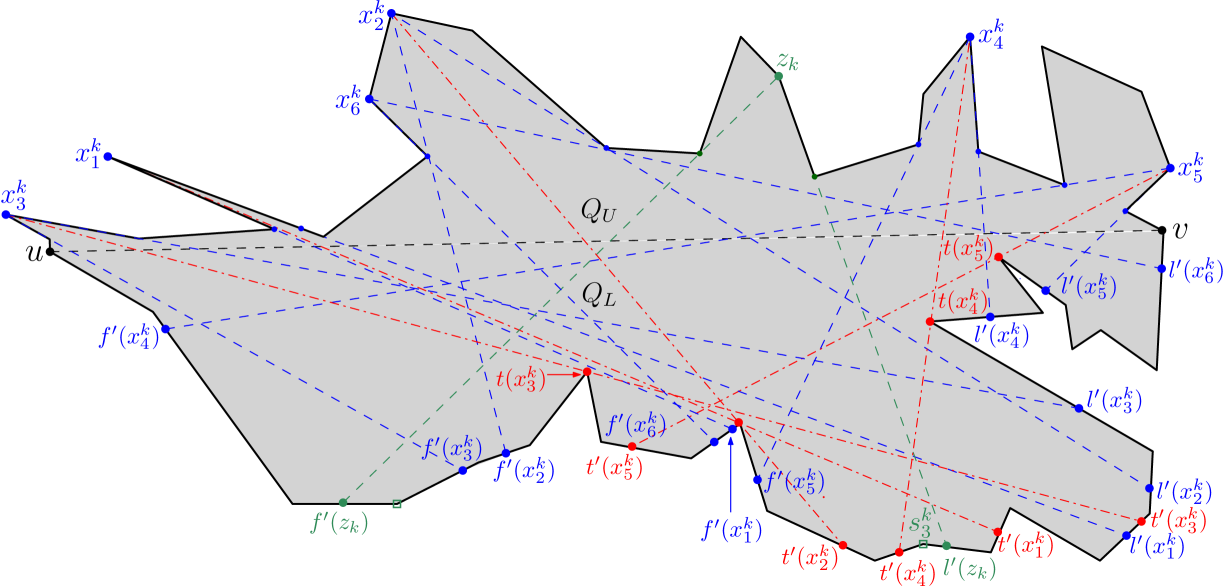
Figure 6 shows the outcome of running Algorithm 1 on a simple polygon having 31 vertices,
where the maximum link distance of any point of from is 5.
The algorithm returns the partition .
It can be seen that Algorithm 1, as stated above, requires time, since the visibility polygons are computed separately. However, the running time can be improved to by using the partitioning method given by Suri [29, 30] in the context of computing minimum link paths. Using the algorithm of Hershberger [17] for computing visibility graphs of , Suri’s algorithm computes weak visibility polygons from selected constructed edges. The same method can be used to compute weak visibility polygons from all constructed edges of visibility polygons in in time. The visibility graph of is a graph which has a node corresponding to every vertex of and there is an edge between a pair of nodes if and only if the corresponding pair of vertices are visible from each other in . We summarize the result in the following theorem.
Theorem 1.
A simple polygon can be partitioned into visibility polygons according to their link distance from any vertex in time.
4 Traversing the hierarchy of visibility polygons
Our algorithm for placement of vertex guards uses the hierarchy of visibility polygons , as computed in Section 3. Let be the set of vertex guards chosen for guarding vertices of visibility polygons in respectively. Since and , we have . So the algorithm essentially has to decide guards in . We have the following observation.
Lemma 2.
For every , every vertex guard in belongs to some visibility polygon in , and every vertex guard in belongs to some visibility polygon in .
Proof.
Consider any vertex guard , where . Now can guard only vertices in , and every vertex in must be at a link distance of 1 from . Let denote the set of vertices in that also belong to any . The inclusion of in guarantees that is not empty, since there exists at least one vertex that is guarded by . Now, if we consider any such , then the link distance between and must be 1, and also the link distance of from must be . Therefore, the link distance of from can only be , , or , and hence must belong to some visibility polygon in . Using the same argument, for any vertex guard , must belong to some visibility polygon in (rather than ), since the level does not exist in the hierarchy . ∎
As can be seen from the proof of Lemma 2, the placement of guards is locally restricted to visibility polygons belonging to adjacent
levels in the partition hierarchy . We formalize this intuition by introducing the notion of the partition tree of , which is a
dual graph denoted by .
Each visibility polygon is represented as a vertex of (also denoted by ), and two vertices of are connected
by an edge in if and only if the corresponding visibility polygons share a constructed edge.
Treating as the root of , the standard parent-child-sibling relationships can be imposed between the visibility polygons in .
Our algorithm starts off by guarding all vertices belonging to the visibility polygons in ,
which are effectively the nodes of furthest from the root .
The algorithm scans ,,…separately for identifying the respective guards in . We know from Lemma 2 that every vertex guard in belongs to some visibility polygon in .
Consider a particular , and let be the parent of in .
Consider the constructed edge between and .
For guarding the vertices of , it is enough to focus on
the subpolygon consisting of itself and the portion of that is weakly visible from .
So, the subproblem of guarding (or any other visibility polygon belonging to ) essentially reduces to placing
vertex guards in a polygon containing a weak visibility chord (corresponding to in the original subproblem)
in order to guard only the vertices lying on one side of ; however, vertex guards can be chosen freely from either side of the chord . We discuss the placement of guards in this reduced problem in Section 5.
Instead of guarding each weak visibility polygon separately, common vertex guards can be placed by traversing the boundary of overlapping weak visibility polygons.
Let us explain by considering any .
Let us denote the constructed edges that are shared between and the children of as
respectively.
Using all these constructed edges,
let us construct the weak visibility polygons , , , .
Observe that each such weak visibility polygon is divided into two portions by the corresponding constructed edge;
one of the portions forms a child of belonging to , whereas the other portion is a subregion of itself.
Moreover, for several of the weak visibility polygons among , the second portions may have overlapping subregions in .
Thus, there may exist vertex guards in these overlapping subregions that can see portions of several of the children of .
Therefore, for guarding vertices of polygons from ,
let us extend the definition of to be the union of all the overlapping weak visibility polygons defined by the constructed edges corresponding to the children of each .
For instance, consider the constructed edges , and on the boundary of in Figure 6; for guarding the corresponding children , and respectively, we define as and traverse .
After having successively computed for guarding vertices belonging to visibility polygons in , the algorithm next computes for guarding vertices belonging to visibility polygons in . Since all vertices belonging to visibility polygons in are already marked by guards chosen belonging to , all remaining unmarked vertices of can have link distance at most from . So, any weak visibility polygon can now be treated as a weak visibility polygon that is the farthest link distance from . Therefore, the guards of are chosen in a similar way as those of . It can be seen that this same method can be used for computing for every . Thus, in successive phases, our algorithm computes the guard sets for guarding vertices belonging to visibility polygons in respectively, until it finally terminates after placing a single guard at for guarding vertices of . The final guard set returned by the algorithm guards all vertices of . The pseudocode for the entire algorithmic framework is provided below.
5 Placement of Vertex Guards in a Weak Visibility Polygon
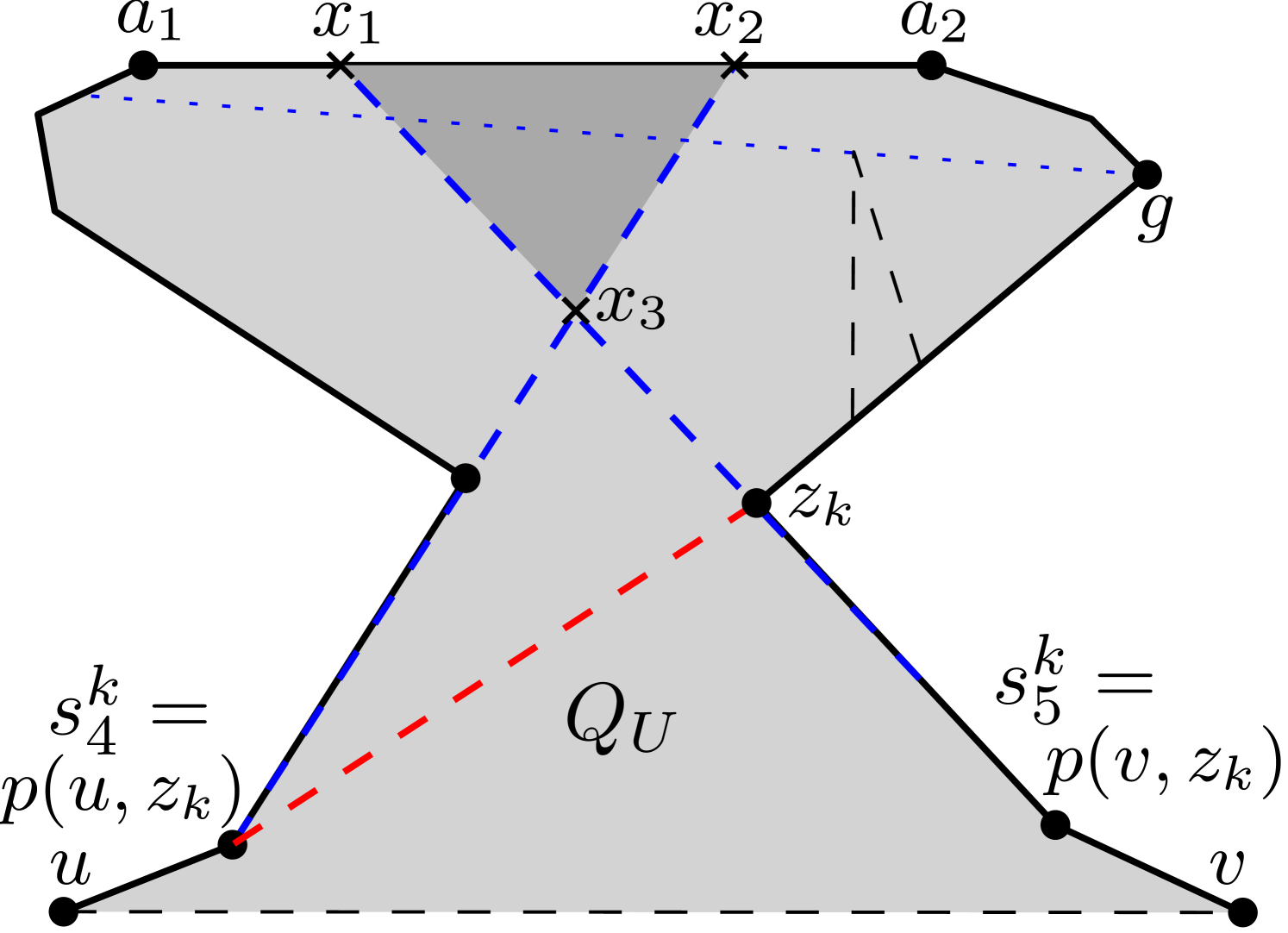
Let be a simple polygon that is weakly visible from an internal chord , i.e. we have .
Observe that the chord splits into two sub-polygons and as follows.
The sub-polygon bounded by and , is denoted as ,
and the sub-polygon bounded by and , is denoted as .
As a first step, our algorithm (see Algorithm 2) places a set of vertex guards,
denoted by , for guarding only the vertices belonging to ,
though is allowed to contain guards from both and .
Let be a set of optimal vertex guards for guarding all points of , including interior points. Let and be the subsets of guards in that belong to (i.e. lie on ) and (i.e. lie on ) respectively. Since and form a partition of , .
5.1 Concept of Inside and Outside Guards
Suppose we wish to guard an arbitrary vertex of .
Then, a guard must be placed at a vertex of belonging to .
Henceforth, let denote the set of all polygonal vertices of .
Further, let us define the inward visible vertices and the outward visible vertices of , denoted by and respectively, as follows.
We shall henceforth refer to the vertex guards belonging to and as inside guards
and outside guards for respectively.
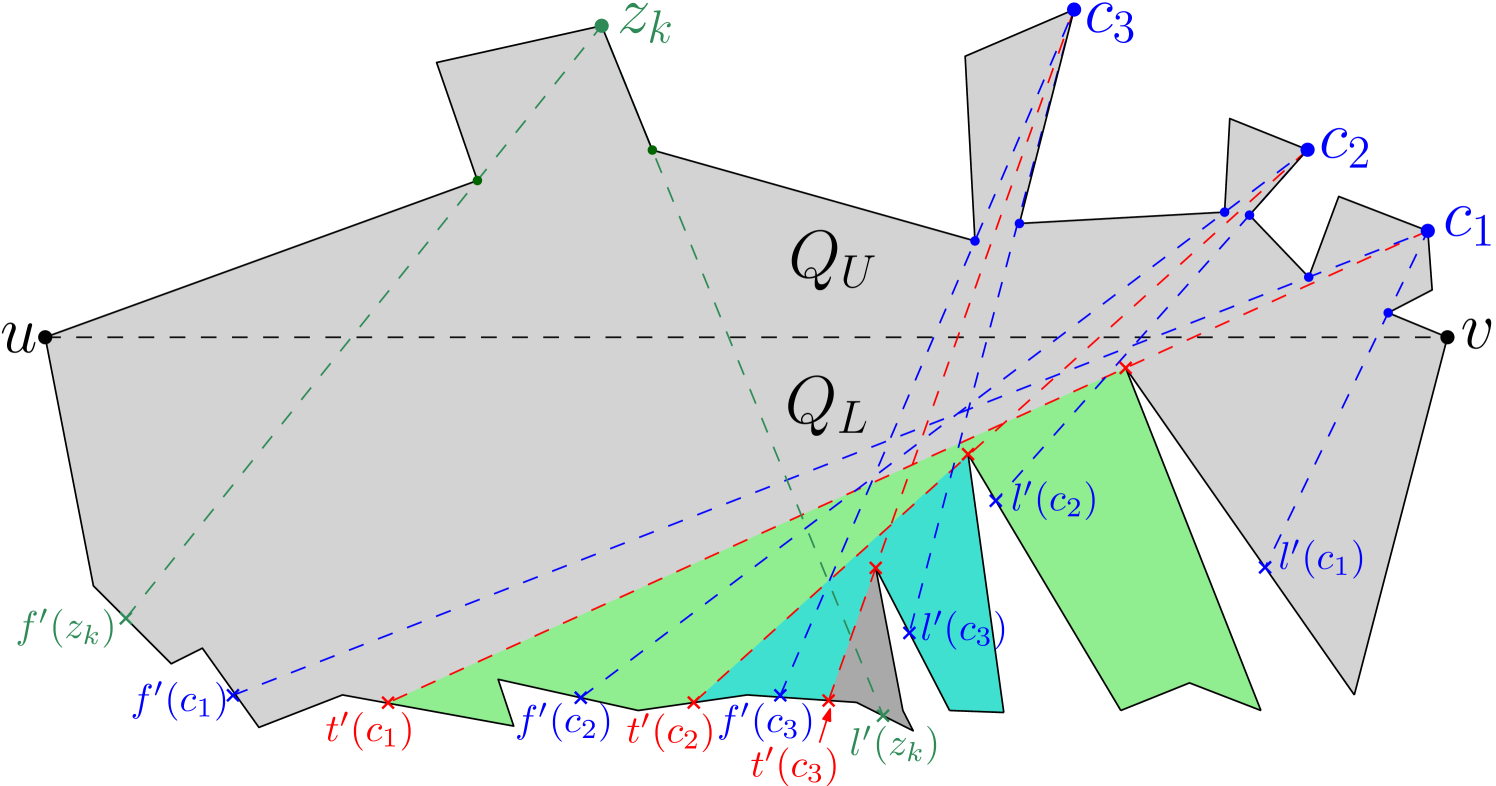
Consider the weakly visible polygon in Figure 9, where the three vertices , and of are such that their respective sets of outward visible vertices are pairwise disjoint, i.e. , , and . If an algorithm chooses only outside guards, then three separate guards are required for guarding , and . However, an optimal solution may place a single guard on any one of the five vertices of for guarding , and .
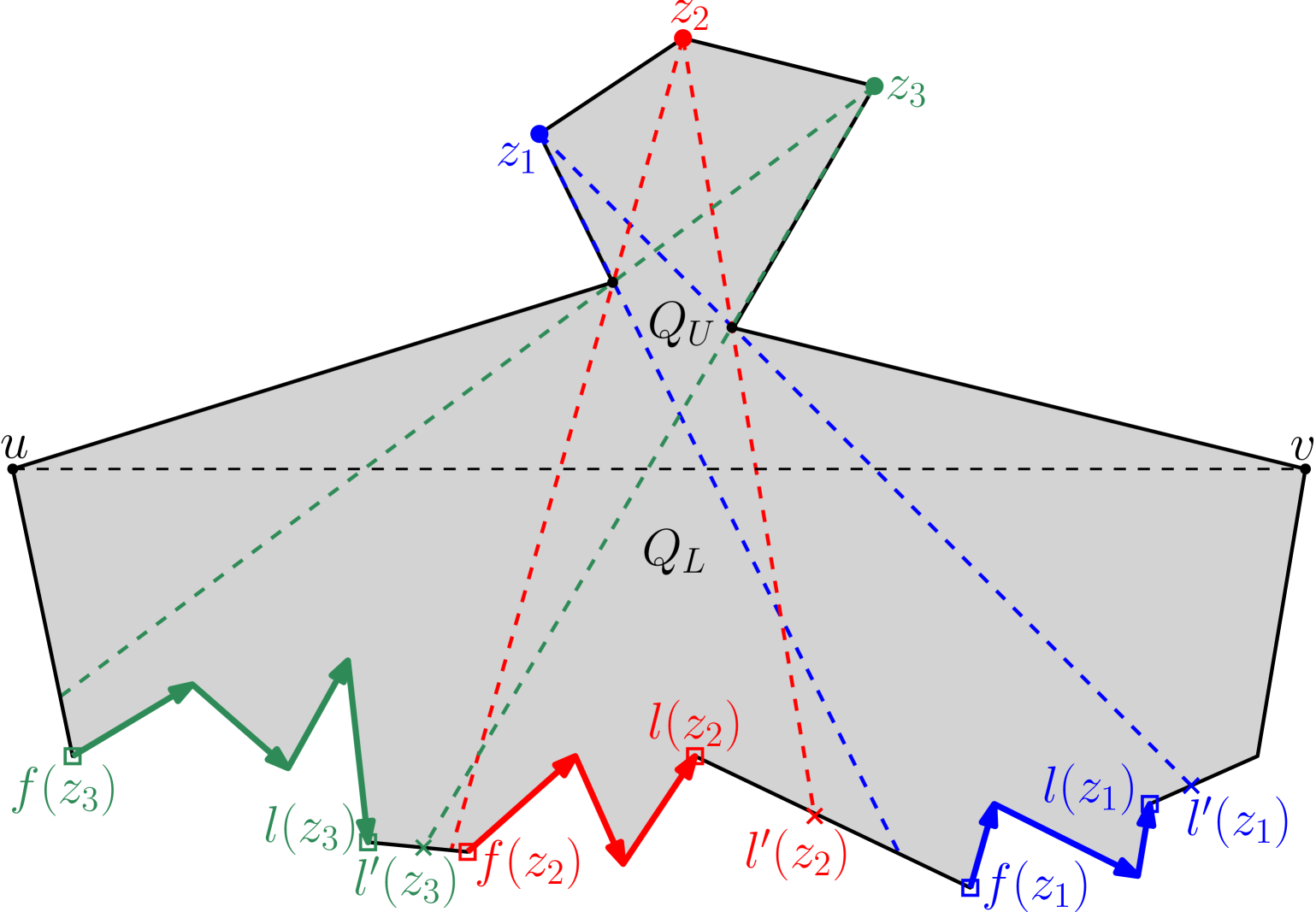
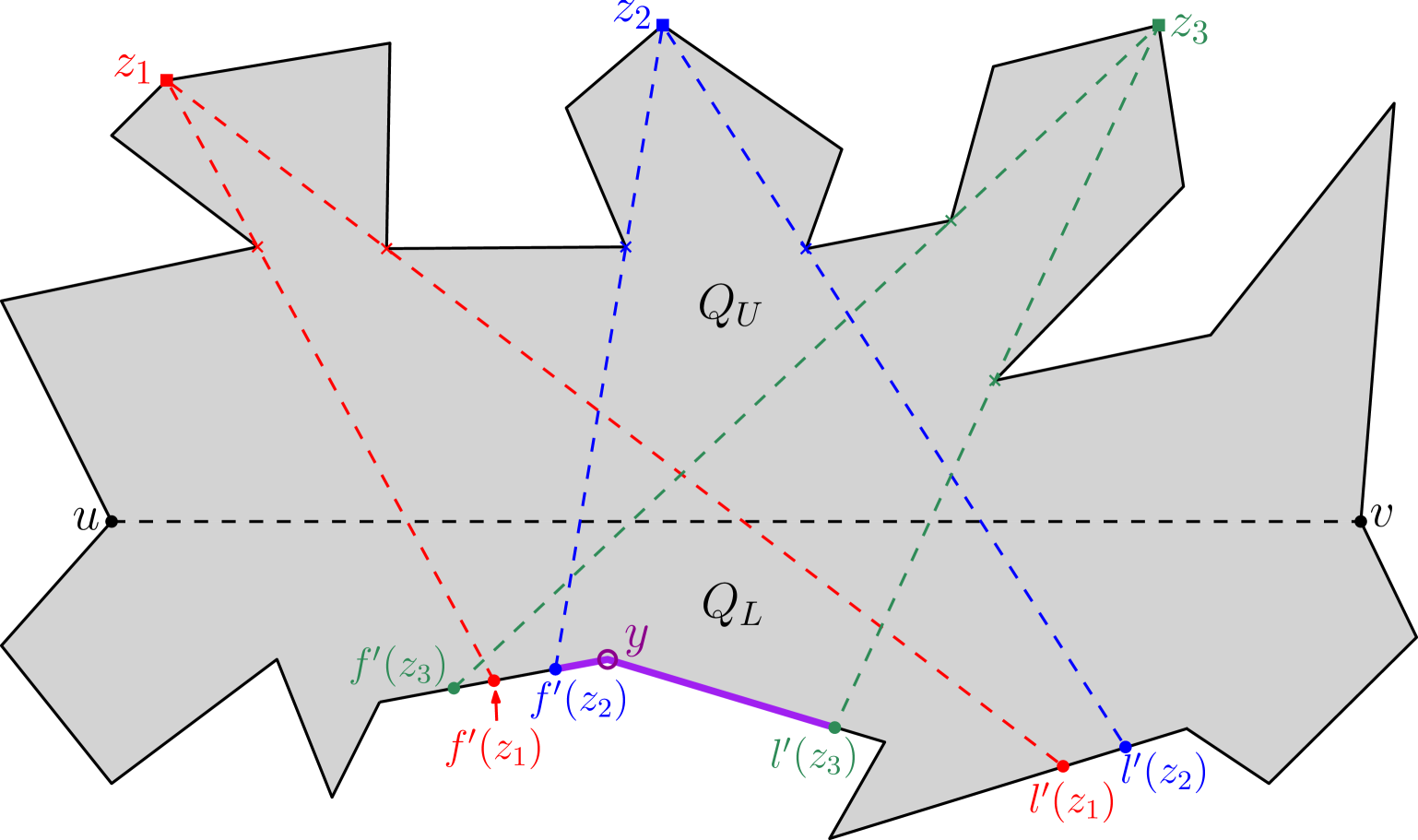
On the other hand, in Figure 9, the three vertices , and of are such that their respective sets of inward visible vertices are pairwise disjoint, i.e. , , and .
If an algorithm chooses only inside guards, then three separate guards are required for guarding , and .
However, the outward visible vertices of , and overlap; and moreover there exists a vertex of such that . Thus, an optimal solution may choose as an outside guard for guarding , and together.
The above discussion suggests that it is better to choose guards from both and for guarding the same vertex of , in order to prevent computing a guard that is arbitrarily large compared to . Therefore, our algorithm selects a subset of vertices of , and places a fixed number of both inside and outside guards corresponding to each of them, so that these guards together see the entire . Moreover, the vertices in (and also the guards corresponding to them) are selected in such a way that they correspond to the guards in , though the correspondence is not necessarily one-to-one, and this enables us to provide an approximation bound on our chosen set of guards. We henceforth refer to this subset of selected vertices as primary vertices. Further, let be such that each primary vertex in is visible from at least one guard in . Similarly, let be such that each primary vertex in is visible from at least one guard in . Since any must be visible from at least one guard of or , we have , and so we have:
| (1) |
The general strategy for placement of guards by our algorithm for guarding only the vertices of aims to establish a constant-factor approximation bound on by separately proving the following three bounds.
| (2) |
| (3) |
| (4) |
The above inequalities (1), (2), (3) and (4) together imply the following conclusion.
| (5) |
5.2 Selection of Primary Vertices
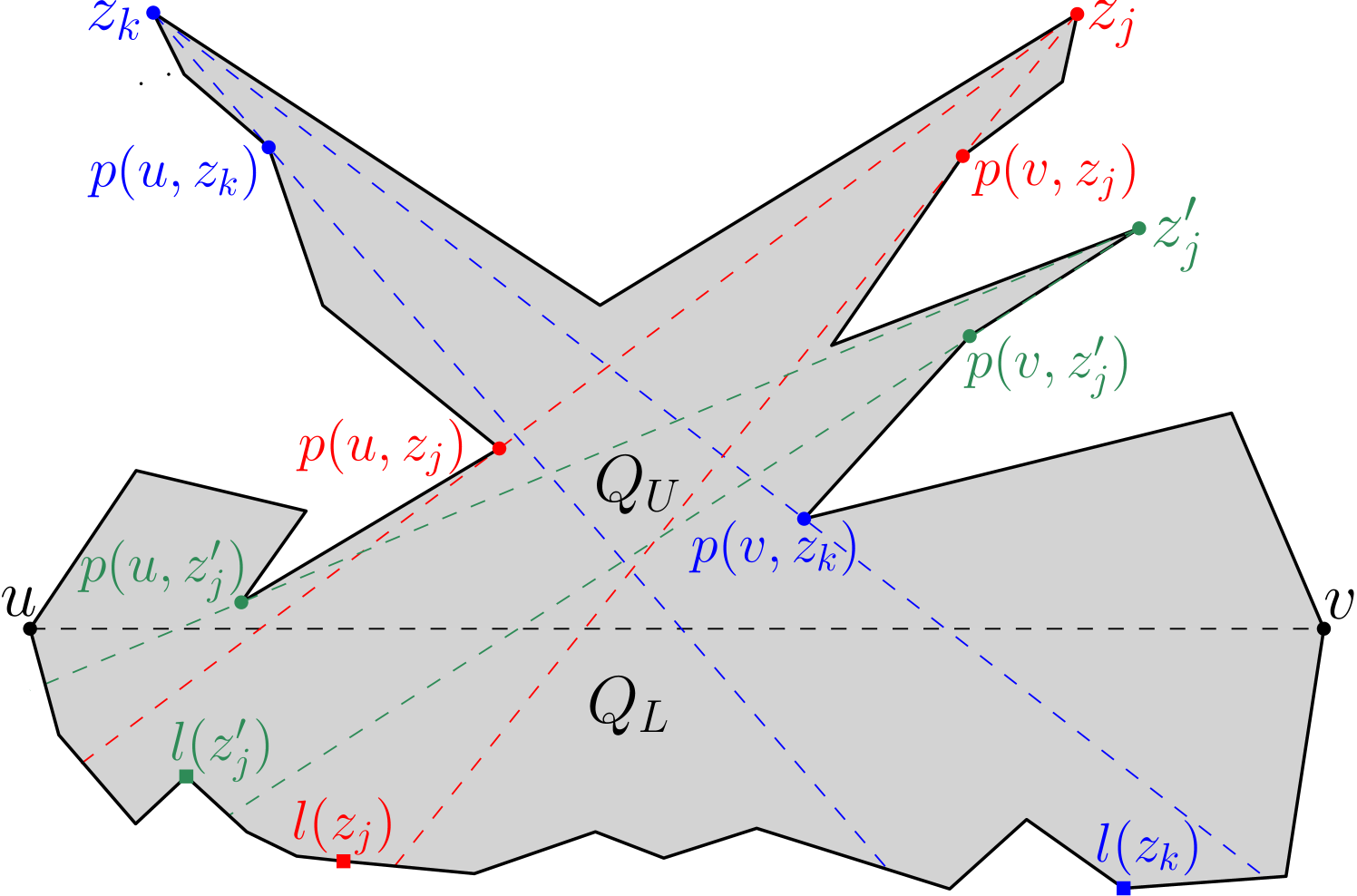
Observe that, for any vertex , both and may be considered to be ordered sets by taking into account the natural ordering of the visible vertices of in clockwise order along and in counter-clockwise order along respectively.
Let us denote the first visible vertex and the last visible vertex belonging to the ordered set by and respectively (see Figure 9).
Also, we denote by (similarly, ) the last visible point (similarly, first visible point)
of ,
which is obtained by extending the ray (respectively, ) till it touches , where (similarly, ) is the parent of in (respectively, ).
Observe that is the only
portion of the boundary that has vertices visible from .
Note that all vertices of may not be visible from ,
since some of them may lie inside left or right pockets of .
Similarly, observe that is the only portion of the
boundary that has vertices visible from .
Note that all vertices of may not be visible from , since some of them may lie inside left or right pockets of .
Let us discuss how primary vertices are selected by our algorithm.
Initially, since all vertices of are unguarded, they are considered to be unmarked.
As vertex guards are placed over successive iterations, vertices of are marked as soon as they become visible from some guard placed so far.
In the -th iteration, the next primary vertex chosen by our algorithm is an unmarked vertex such that precedes (henceforth denoted notationally as ) for any other unmarked vertex of . An immediate consequence of such choice of the primary vertex is that all vertices on must already be marked.
Lemma 3.
If is chosen as the next primary vertex by Algorithm 1, then no unmarked vertices exist on .
Proof.
Let us assume, on the contrary, that there exists a vertex on that is yet to be marked. Observe that the ray must intersect the ray at a point between and , which implies that on (see Figure 11). So, in the current iteration, rather than is chosen as the next primary vertex, which is a contradiction. ∎
In Section 5.3, we consider guarding vertices of in a special scenario where uses vertex guards only from . In Section 5.4, we consider guarding vertices of in the general scenario where the guards of are not restricted to . In Section 5.5, we enhance the procedure for guarding vertices to ensure that all interior points of are guarded as well.
5.3 Placement of guards in a special scenario
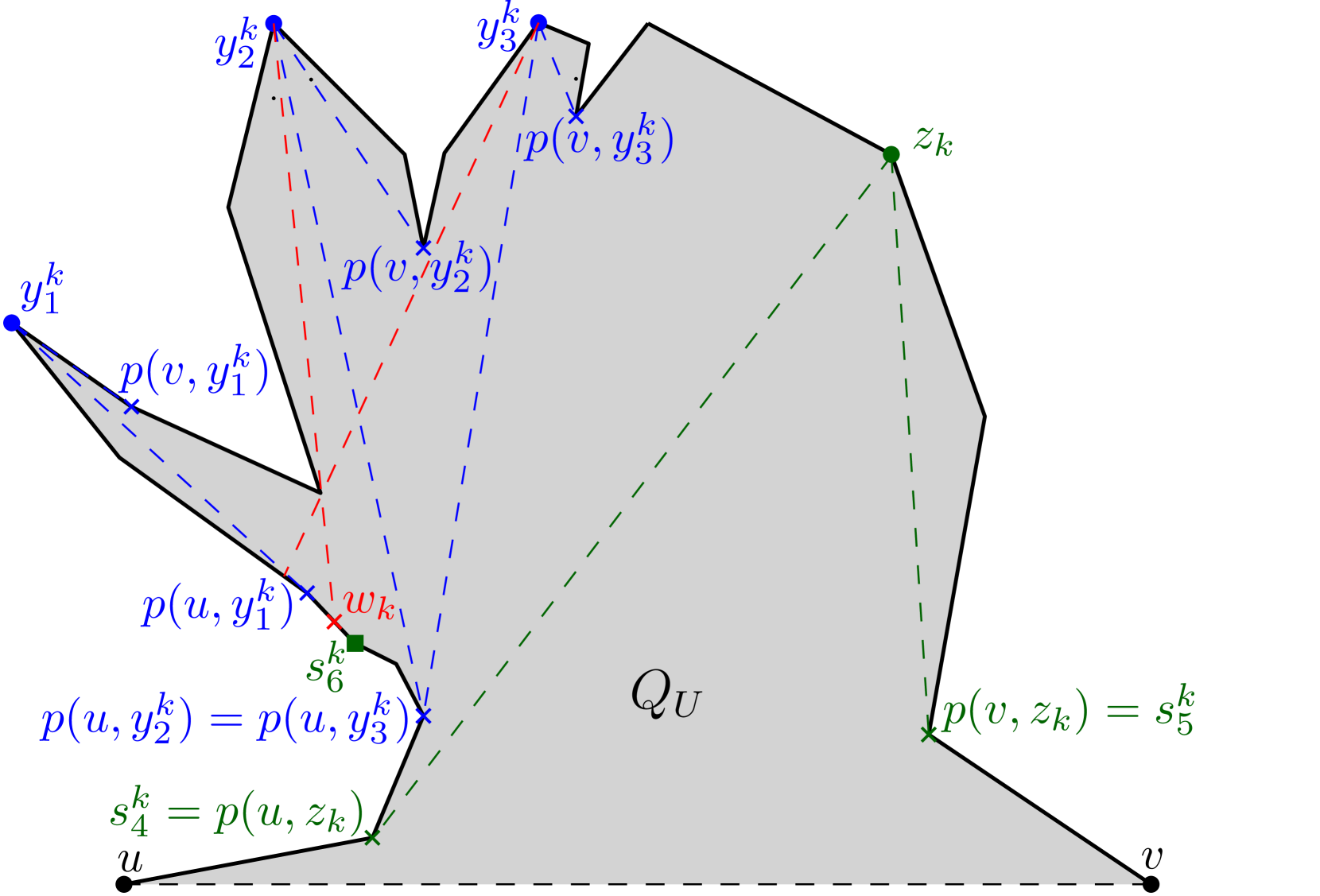
Let us consider a special scenario where and , i.e. uses only vertex guards from . In such a scenario, for every vertex , must contain a guard from . So, a natural idea is to place outside guards in a greedy manner so that they lie in the common intersection of outward visible vertices of as many vertices of as possible. For any primary vertex , let us denote by the set of unmarked vertices of whose outward visible vertices overlap with those of . In other words,
So, each vertex of belonging to is visible from at least one vertex of .
Further, can be considered to be an ordered set, where for any pair of elements ,
we define if and only if precedes in counter-clockwise order on .
For the current primary vertex , let us assume without loss of generality that such that in counter-clockwise order on .
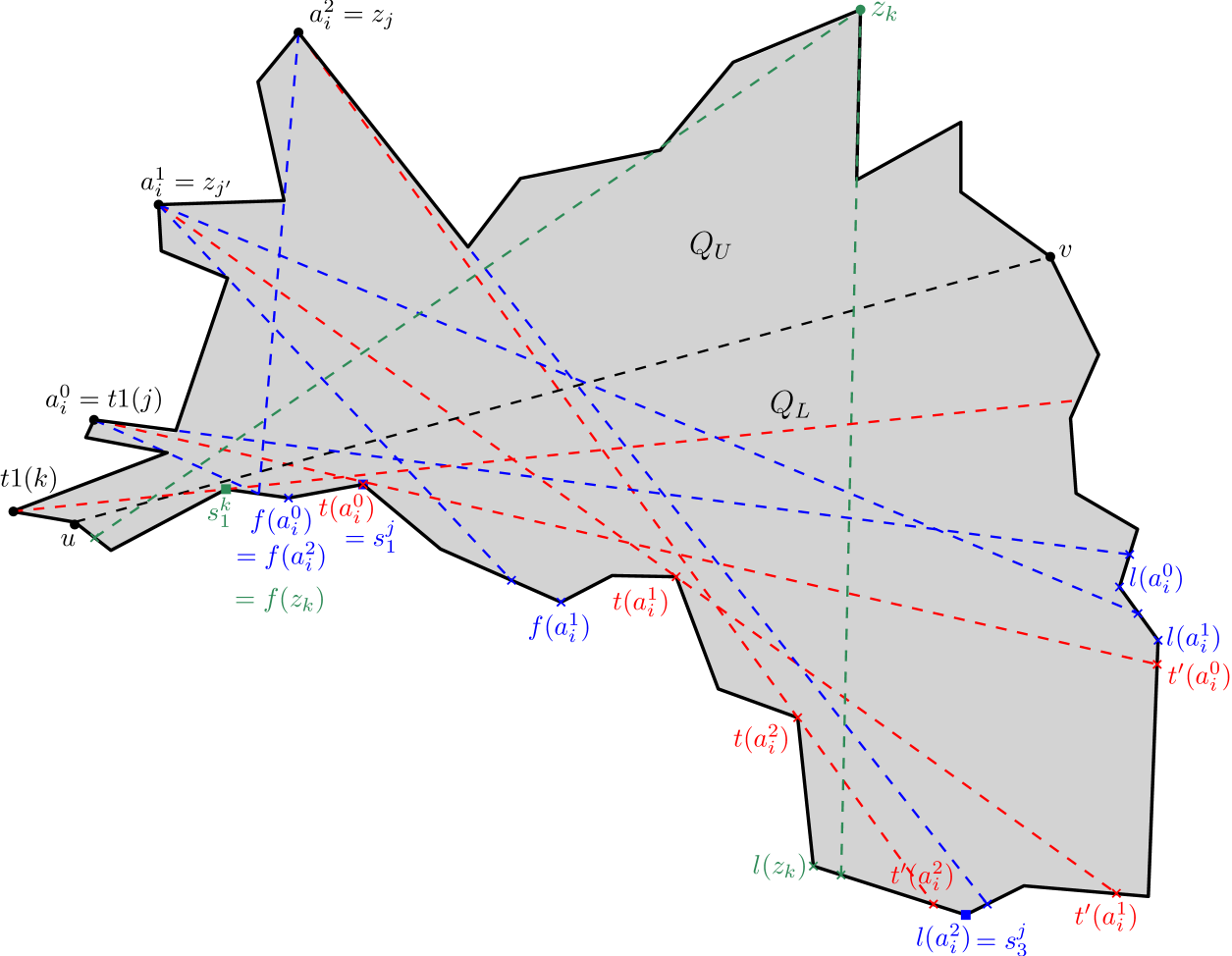
Let us partition the vertices belonging to into 3 sets, viz. , and in the following manner. Every vertex of visible from is included in . Observe that, by definition . Obviously, for each vertex , is not visible from due to the presence of some constructed edge. The vertices of are categorized into and based on whether this constructed edge creates a right pocket or a left pocket. Suppose is a vertex such that creates a constructed edge , where is a polygonal vertex and is the point where first intersects . If lies on and lies on , i.e. if and , then is included in . For instance, in Figure 11, due to the constructed edge . On the other hand, if lies on and lies on , i.e. if and , then is included in . For instance, in Figure 11, due to the constructed edge . Observe that, all vertices of must lie on , whereas all vertices of must lie on .
Lemma 4.
The vertex sees all vertices belonging to .
Proof.
We know that, due to the choice of the primary vertex , for every vertex . Therefore, if is not visible from , then there must exist a constructed edge of such that (i) either , in which case must belong to , or (ii) lies on , in which case must belong to . So, if , must be visible from . In other words, sees all vertices belonging to . ∎
Corollary 5.
The shortest paths from to any vertex of makes only left turns, whereas the shortest paths from to any vertex of makes only right turns.
Corollary 6.
If is convex, then and , which implies that all vertices of are visible from .
For any , we define , which implies that, for each vertex , all the vertices belonging to are visible from , and hence can be guarded by placing a vertex guard at . By definition, for any , the vertices belonging to lie on .
Lemma 7.
For every , .
Proof.
It follows directly from Lemma 4 that for every . Thus, , i.e. . ∎
Depending on the vertices in , and , we have the following exhaustive cases because by Lemma 4.
Consider Case 1, where (see Figure 11, and line 16 of Algorithm 1). Here, the algorithm places a vertex guard at any vertex belonging to (in line 19). So, every vertex in is visible from and are hence marked after the placement of the guard at .
Lemma 8.
If , then all vertices belonging to are visible from the vertex guard placed at . Therefore, no vertex can be a primary vertex for any .
Now consider Case 2a, where , , and (see Figure 12). Here, Algorithm 1 places three vertex guards, viz. , , and (in lines 21, 33 and 19 respectively). So, the three vertex guards placed by the algorithm together see all the vertices of , and of course itself. It is important to note that or may not belong to , but must belong to .
Lemma 9.
If , , and , then all vertices belonging to are visible from at least one of the three vertex guards placed at , , and . Therefore, no vertex can be a primary vertex for any .
Consider Case 2b, where , , and (see Figure 13). Observe that a vertex of may not lie within , but rather lie on . The algorithm places two vertex guards, one at a vertex , and another one at a vertex . Note that or may see some of the vertices of , which may get marked as a consequence. However, assuming that none of the vertices of are marked due to the placement of and (in lines 33 and 19 respectively of Algorithm 1), a third vertex guard is also chosen to guard at least a subset of , since . In order to choose the vertex guard for guarding a subset of , is traversed counter-clockwise starting from , till a vertex is encountered such that there exists a vertex which is visible from but not from any subsequent vertex of . So, this vertex is chosen (in line 27 for Algorithm 1) as the vertex guard . It can be seen that once such a guard is placed at , some of the vertices in are visible from , and are therefore marked. Let us denote the remaining vertices of that are still unmarked as . We have the following lemma.
Lemma 10.
If , , and , then all vertices belonging to are visible from one of the vertex guards placed at , , and . Therefore, no vertex can be a primary vertex for any unless .
Consider Case 2c, where , , and (see Figure 14). Observe that a vertex of may not lie within , but rather lie on . The algorithm places two vertex guards, one at a vertex , and another one at a vertex (in lines 33 and 21 respectively of Algorithm 1). Note that or may see some of the vertices of , which may get marked as a consequence. However, as a worst case, we assume that none of the vertices of are marked due to the placement of and . In such a scenario, a third vertex guard is chosen to guard a subset of , since . In order to choose , is traversed counter-clockwise, starting from , till a vertex is encountered such that there exists a vertex which is visible from but not from any subsequent vertex of . So, this vertex , which is effectively the vertex of immediately preceding , and hence denoted by , is chosen (in line 39 of Algorithm 1) as the vertex guard . It can be seen that once a guard is placed at , a subset of the vertices in are visible from , and hence marked. Let us denote the remaining vertices of that are still unmarked as . The following lemma summarizes Case 2c.
Lemma 11.
If , , and , then all vertices belonging to are visible from one of the vertex guards placed at , , and . Therefore, a vertex cannot be a primary vertex for any unless .
Consider Case 2d, where , , and (see Figure 15). The algorithm first places a guard at a vertex . Note that may see some of the vertices of and , which may get marked as a consequence. However, assuming that none of the vertices of or are marked due to the placement of , another vertex guard is chosen from , following a procedure similar to that in Case 2c. Similarly, another vertex guard is chosen from following a procedure similar to that in Case 2b. It can be seen that once guards are placed at and , some subsets of and are visible from them, and hence marked. So, let us denote the yet unmarked vertices of and as and , respectively.
Lemma 12.
If , , and , then all vertices belonging to ) are visible from one of the three vertex guards placed at , , and . Therefore, no vertex can be a primary vertex for any unless .
Lemma 13.
Let and be any two primary vertices, where . If , then () must require two distinct vertex guards for guarding both and .
Proof.
For the sake of contradiction, assume there exists a single guard that can see both and . This is only possible if , which in turn means that . Therefore, by the definition of , a contradiction. ∎
Lemma 14.
Let and be any two primary vertices, where . Assume that and . If , then (=) must require two distinct vertex guards for guarding both and .
Proof.
After the placement of guards for , the only vertices of that are still unmarked belong to or . Since is unmarked when it is chosen as a primary vertex, implies that . So, it follows directly from Lemma 13 that (=) must require two distinct vertex guards for guarding both and . ∎
Lemma 15.
For every , assume that for any , . Then, .
Proof.
We know from Lemma 14, that for any arbitrary pair and , where and , (=) requires two distinct vertex guards for guarding both and . Thus, applying Lemma 14 repeatedly over all such possible pairs shows that requires as many guards as the number of primary vertices, i.e. . Since at most three vertex guards , , and are placed corresponding to each primary vertex , . So, combining the above two inequalities, we obtain . ∎
So far we have assumed the special case where, for every , there is no such that a
primary vertex belongs to .
Therefore, we now focus on the general case where, for some ,
we have the primary vertex .
Let where .
Observe that, if we consider any two arbitrary vertices , then these vertices
may be overlapping, i.e. ,
or disjoint, i.e. .
So, it is possible to create a partition of , such that each set in the partition
consists of a particular vertex , called the leading vertex, and all the other vertices of that are overlapping with .
Obviously, two leading vertices belonging to different sets of such a partition are always disjoint.
Therefore, if a subset of is formed by choosing the leading vertex from each set of the partition,
then we obtain a maximal disjoint subset of , i.e. a maximal subset of whose elements are all pairwise disjoint.
In the following, we first formally define maximum disjoint subsets of and , and establish various properties of these subsets in Lemmas 16 to 28, Using these properties, we establish a lower bound on , which finally leads towards obtaining a constant approximation ratio.
Lemma 16.
Consider any two arbitrary vertices , where . If and are disjoint, i.e. if , then is geometrically nested inside , i.e. .
Proof.
Since , we must have and also . Therefore, the only possibility is to have . Moreover, if or , then , which contradicts that and are disjoint. Hence, we must have . So, is geometrically nested inside . ∎
Lemma 17.
Consider any two arbitrary vertices , where . If and are disjoint, i.e. if , then is geometrically nested inside , i.e. .
Proof.
Since , we must have and also . Therefore, the only possibility is to have . Moreover, if or , then , which contradicts that and are disjoint. Hence, we must have . So, is geometrically nested inside . ∎
Observe that the size of any maximal disjoint subset of depends on the choice of the leading element for each set of the partition.
We are interested in choosing the leading elements in such a way so as to construct a
canonical partitioning of corresponding to a particular maximum disjoint subset , defined as follows.
First include in and construct the set consisting of all other vertices
such that .
Note that .
Also note that, if , then
(i.e. , so this corresponds to cases 2a and 2c in Algorithm 1).
Otherwise, for each , pick the vertex where is the least index such that ,
and include in . Construct the set .
The process is repeated till . Thus, a canonical partition is constructed.
Analogously, a similar canonical partitioning of corresponding to a maximum disjoint subset is defined as follows.
Let
where .
First include in and construct the set consisting of all other vertices
such that .
Note that .
Also note that, if , then
(i.e. , so this corresponds to cases 2a and 2b in Algorithm 1).
Otherwise, for each , pick the vertex where is the least index such that ,
and include in . Construct the set .
The process is repeated till .
Thus, a canonical partition is constructed.
We now study the properties of and as constructed above. Firstly, it is easy to see that, by their very construction, is a maximal disjoint subset of , and is a maximal disjoint subset of . We show that is also a maximum disjoint subset of , using an interesting pairwise intersection property established in the following lemma.
Lemma 18.
For every and for any two vertices , we have .
Proof.
Without loss of generality let us assume that . For the sake of contradiction, suppose . This means and , i.e. is geometrically nested within . On the other hand, we know that both and are overlapping with the leading vertex of . By the construction of , we have . Therefore, implies , and implies . However, if both and are true, then , contradicting the initial assumption that . ∎
Lemma 19.
is a maximum disjoint subset of .
Proof.
On the contrary, assume that there exists a larger maximal disjoint subset of , say . Then, by the pigeonhole principle there exists at least two vertices such that both belong to the same set . Thus, by Lemma 18, we have , which contradicts the fact that is a disjoint subset of . Hence, is a maximum disjoint subset of . ∎
In the following lemmas, we show in an analogous manner that is also a maximum disjoint subset of .
Lemma 20.
For every and for any two vertices , we have .
Proof.
Without loss of generality let us assume that . For the sake of contradiction, suppose . This means and , i.e. is geometrically nested within . On the other hand, we know that both and are overlapping with the leading vertex of . By the construction of , we have . Therefore, implies , and implies . However, if both and are true, then , contradicting the initial assumption that . ∎
Lemma 21.
is a maximum disjoint subset of .
Proof.
On the contrary, assume that there exists a larger maximal disjoint subset of , say . Then, by the pigeonhole principle there exists at least two vertices such that both belong to the same set . Thus, by Lemma 20, we have , which contradicts the fact that is a disjoint subset of . Hence, is a maximum disjoint subset of . ∎
Lemma 22.
For any , any outward vertex guard placed on can see at most one vertex of .
Lemma 23.
For any , any outward guard set requires at least distinct vertex guards to guard all vertices of .
Lemma 24.
For any , any outward vertex guard placed on can see at most one vertex of .
Lemma 25.
For any , any outward guard set requires at least distinct vertex guards to guard all vertices of .
Lemma 26.
For any , any outward optimal guards placed on can see at most one vertex of and at most one vertex of .
For every set belonging to the partition of , let us define the corresponding two sets and as follows. We define to be a minimal subset of the optimal set of guards required to guard all the vertices belonging to . Similarly, we define to be the subset of primary vertices chosen by our algorithm from amongst the vertices of . Now we are in a position to show that the cardinality of is lower bounded by , which never exceeds two.
Lemma 27.
For every set belonging to the partition of , or , i.e. .
Proof.
First, let us consider the case where .
This implies that at least one of the conditions below holds:
(i) for every , or
(ii) for every .
Observe that, for any vertex , if is chosen by our algorithm as a later primary vertex ,
where , then we have and .
If condition (i) is true, then the vertex guard sees all vertices belonging to .
If condition (ii) is true, then the vertex guard sees all vertices belonging to .
Thus, in either case, no further primary vertices will be chosen by our algorithm from .
So, when , we also have .
Let us now consider the other case where . It is possible that all the vertices belonging to are marked by vertex guards corresponding to primary vertices chosen from , in which case we have . Otherwise, let be the first primary vertex chosen from (see Figure 18). Then, as before, we have and . Observe that, for any vertex , if , then the vertex guard sees , and if , then the vertex guard sees . Therefore, if any vertex is left unmarked even after the placement of vertex guards corresponding to , then . Since , by the definition of we have . So, the condition would force the condition for any vertex that is left unmarked even after the placement of vertex guards corresponding to . Now, if be another primary vertex chosen from among the yet unmarked vertices of , then for any other unmarked vertex , and hence sees all the remaining unmarked vertices of . So, when , we have . Therefore, in general, we have and . ∎
Analogously, for every set belonging to the partition of , let us define the corresponding two sets and as follows. We define to be a minimal subset of the optimal set of guards required to guard all the vertices belonging to . Similarly, we define to be the subset of primary vertices chosen by our algorithm from amongst the vertices of . Now we are in a position to show that the cardinality of is lower bounded by , which never exceeds two.
Lemma 28.
For every set belonging to the partition of , we have or , i.e. .
Proof.
First, let us consider the case where .
This implies that at least one of the conditions below holds:
(i) for every , or
(ii) for every .
Observe that, for any vertex , if is chosen by our algorithm as a later primary vertex ,
where , then we have and .
If condition (i) is true, then the vertex guard sees all vertices belonging to .
If condition (ii) is true, then the vertex guard sees all vertices belonging to .
Thus, in either case, no further primary vertices will be chosen by our algorithm from .
So, when , we also have .
Let us now consider the other case where . It is possible that all the vertices belonging to are marked by vertex guards corresponding to primary vertices chosen from , in which case we have . Otherwise, let be the first primary vertex chosen from . Then, as before, we have and . Observe that, for any vertex , if , then the vertex guard sees , and if , then the vertex guard sees . Therefore, if any vertex is left unmarked even after the placement of vertex guards corresponding to , then . Since , by the definition of we have . So, the condition would force the condition for any vertex that is left unmarked even after the placement of vertex guards corresponding to . Now, if be another primary vertex chosen from among the yet unmarked vertices of , then for any other unmarked vertex , and hence sees all the remaining unmarked vertices of . So, when , we have . Therefore, in general, we have and . ∎
Two special subsets of vertices of are constructed, where each subset consists of primary vertices having certain properties
as well as some special vertices belonging to and .
Then, lower bounds are established on the number of optimal guards required to guard just the vertices belonging to these subsets
(see Lemmas 32 and 33), which ultimately leads us to a lower bound on ,
which is equal to in the current scenario.
Let denote the subset of primary vertices such that is non-empty for each .
Also, let denote the subset of primary vertices where each belongs to
for some previously chosen primary vertex , where .
In other words, we have , and
.
Finally, for every , if the corresponding guard is placed at ,
then is denoted by and included in the set ,
i.e .
Observe that, for every vertex , is marked by placed due to the corresponding , where . Also, may be partitioned into the two sets and .
Similarly, let denote the subset of primary vertices such that is non-empty for each .
Also, let denote the subset of primary vertices where each belongs to
for some previously chosen primary vertex , where .
In other words, we have , and
.
Finally, for every , if the corresponding guard is placed at ,
then is denoted by and included in the set ,
i.e. .
Observe that, for every vertex , is marked by the vertex guard placed due to the corresponding , where .
Also, may be partitioned into the two sets and .
Let , and let denote the minimal subset of required to see all vertices of .
Lemma 29.
.
Proof.
Observe that, for each vertex , and , i.e. . Moreover, does not belong to for any other where . Therefore, for any other , and by Lemma 13, we know that a single distinct optimal guard is required for guarding each . Hence, . ∎
Let us define the minimal subsets and of optimal guards required for guarding all vertices belonging to and respectively. In the lemmas below, lower bounds are established on the sizes of the sets and respectively.
Lemma 30.
.
Proof.
Assume that
for every pair .
Then clearly a distinct optimal guard is required in for guarding each primary vertex in ,
and therefore .
However, as per Lemma 18, there may exist some pair
for which does not hold,
and a single optimal guard in is sufficient to see both and .
Then, both and belong to the same set in the partition of
corresponding to some (see Figure 18).
We prove below that, in such a situation, an additional guard for is required
in to compensate for the single optimal that sees two primary vertices in .
Recall that two primary vertices in can be overlapping
only if they both belong to the same set in .
Moreover, since we know from Lemma 27 that at most only two primary vertices can be chosen from any ,
such compensation can be applied to every for which , and hence, still holds.
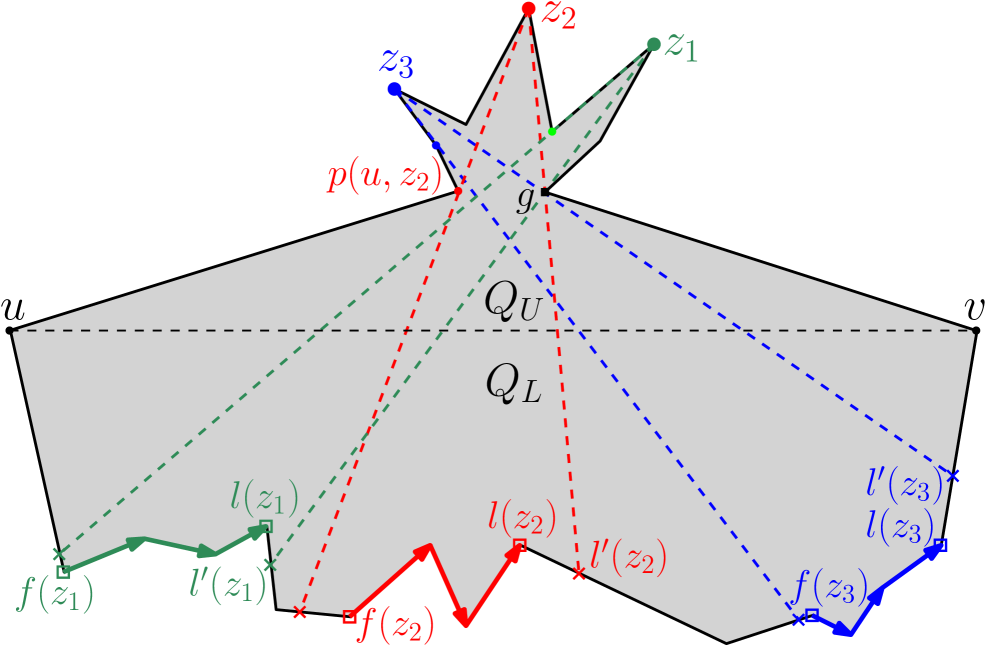
Let be the leading vertex belonging to . Let us assume without loss of generality that , i.e. was chosen as a primary vertex earlier than by Algorithm 1. Then, observe that , and so . As is unmarked even after placement of and , we have and , and they can both be possible only if . Thus, the common optimal guard that sees both and must lie on . But in that case, , which means that does not see , and so a separate optimal guard is required in for guarding . Thus, two distinct optimal guards are required to guard the three vertices and , whenever both and belong to the same set . ∎
Lemma 31.
.
Proof.
Assume that
for every pair .
Then clearly a distinct optimal guard is required in for guarding each primary vertex in ,
and therefore .
However, as per Lemma 20, there may exist some pair
for which does not hold,
and a single optimal guard in is sufficient to see both and .
Then, both and belong to the same set in the partition of
corresponding to some . We prove below that, in such a situation, an additional guard for is required
in to compensate for the single optimal that sees two primary vertices in .
Recall that two primary vertices in can be overlapping
only if they both belong to the same set in .
Moreover, since we know from Lemma 28 that at most only two primary vertices can be chosen from any ,
such compensation can be applied to every for which , and hence, still holds.
Let be the leading vertex belonging to . Let us assume without loss of generality that , i.e. was chosen as a primary vertex earlier than by Algorithm 1. Then, observe that , and so . As is unmarked even after placement of and , we have and , and they can both be possible only if . Thus, the common optimal guard that sees both and must lie on . But in that case, , which means that does not see , and so a separate optimal guard is required in for guarding . Thus, two distinct optimal guards are required to guard the three vertices and , whenever both and belong to the same set . ∎
Consider the two sets and respectively. Let us denote by the minimal subset of that see all vertices of , and similarly, let us denote by the minimal subset of that see all vertices of . In order to obtain a lower bound on the number of optimal guards, we establish the following two lemmas.
Lemma 32.
.
Proof.
Observe that , since is also required to guard the vertices belonging
to in addition to those guarded by .
We claim that, for every ,
there exists an optimal guard in for guarding or
which is distinct from all the optimal guards already counted in .
This is enough to prove the lemma, as it implies in conjunction with Lemma 30 that
.
The above claim is proven below.
Let be an optimal guard that sees .
If does not coincide with any of the optimal guards already counted in ,
then clearly our claim holds.
Otherwise, let us consider the situation where coincides with that guards
a primary vertex or some vertex , or may be both.
Let us first consider the subcase where sees some primary vertex .
If , then clearly does not see .
Thus, a separate optimal guard is required in for guarding , and our claim still holds.
So, let us consider the other case where and also sees .
Observe that, as sees , we have either or .
However, since and coincide, we must have ,
which rules out the latter possibility. So, we must have ,
which in turn implies that .
Note that, if is not visible from due to a right pocket,
then either it means that belongs to rather than ,
or it contradicts the fact that is the leading vertex of .
On the other hand, if is not visible from due to a left pocket,
then again it means that belongs to or rather than .
So, must be visible from , and is thus marked by the placement of ,
which contradicts the assumption that .
Let us now consider the other subcase where sees only a vertex , but sees no primary vertex . Once again, if , then clearly does not see . So, let us consider the other case where and also sees . Observe that, as sees , we have either or . However, since and coincide, we must have , which rules out the latter possibility. So, we must have , which in turn implies that . Note that, if is not visible from due to a right pocket, then either it means that belongs to rather than , or it contradicts the fact that is the leading vertex of . On the other hand, if is not visible from due to a left pocket, then again it means that belongs to or rather than . So, must be visible from , and is thus marked by the placement of , which contradicts the assumption that . Hence, it is established that for every , there exists an optimal guard in for guarding or , which is distinct from all the optimal guards already counted in , and this completes our proof. ∎
Lemma 33.
.
Proof.
Observe that , since is also required to guard the vertices belonging
to in addition to those guarded by .
We claim that, for every ,
there exists an optimal guard in for guarding or
which is distinct from all the optimal guards already counted in .
This is enough to prove the lemma, as it implies in conjunction with Lemma 31 that
.
The above claim is proven below.
Let be an optimal guard that sees .
If does not coincide with any of the optimal guards already counted in ,
then clearly our claim holds.
Otherwise, let us consider the situation where coincides with that guards
a primary vertex or some vertex , or may be both.
Let us first consider the subcase where sees some primary vertex .
If , then clearly does not see .
Thus, a separate optimal guard is required in for guarding ,
and our claim still holds.
So, let us consider the other case where and also sees .
Observe that, as sees , we have either or .
However, since and coincide, we must have ,
which rules out the latter possibility. So, we must have ,
which in turn implies that .
Note that, if is not visible from due to a right pocket,
then either it means that belongs to rather than ,
or it contradicts the fact that is the leading vertex of .
On the other hand, if is not visible from due to a left pocket,
then again it means that belongs to or rather than .
So, must be visible from , and is thus marked by the placement
of , which contradicts the assumption that .
Let us now consider the other subcase where sees only a vertex , but sees no primary vertex . Once again, if , then clearly does not see . So, let us consider the other case where and also sees . Observe that, as sees , we have either or . However, since and coincide, we must have , which rules out the latter possibility. So, we must have , which in turn implies that . Note that, if is not visible from due to a right pocket, then either it means that belongs to rather than , or it contradicts the fact that is the leading vertex of . On the other hand, if is not visible from due to a left pocket, then again it means that belongs to or rather than . So, must be visible from , and is thus marked by the placement of , which contradicts the assumption that . Hence, it is established that for every , there exists an optimal guard in for guarding or , which is distinct from all the optimal guards already counted in , and this completes our proof. ∎
Lemma 34.
.
Proof.
Theorem 35.
Proof.
Theorem 36.
Algorithm 1 has a worst-case time complexity of .
5.4 Placement of guards in the general scenario
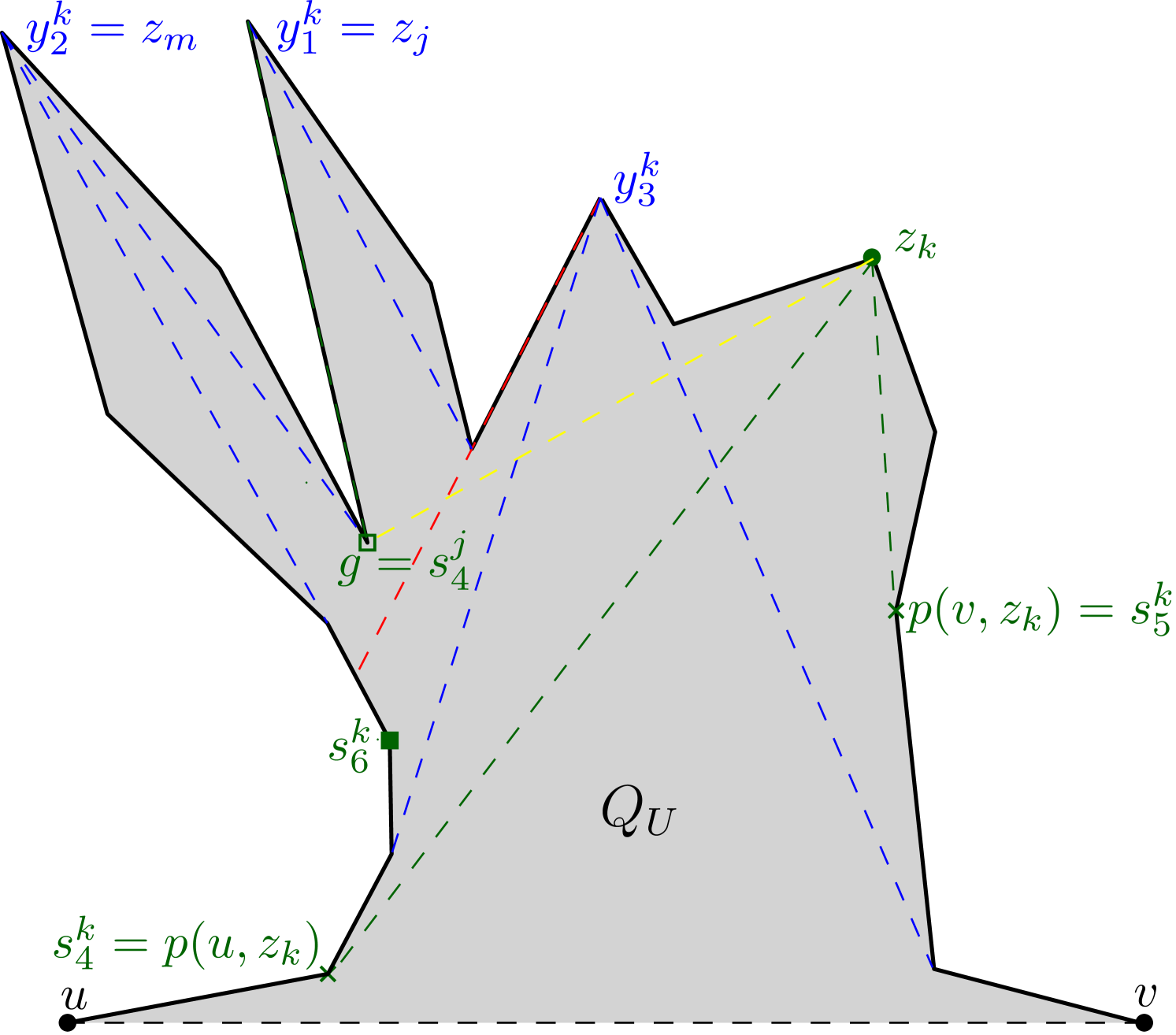
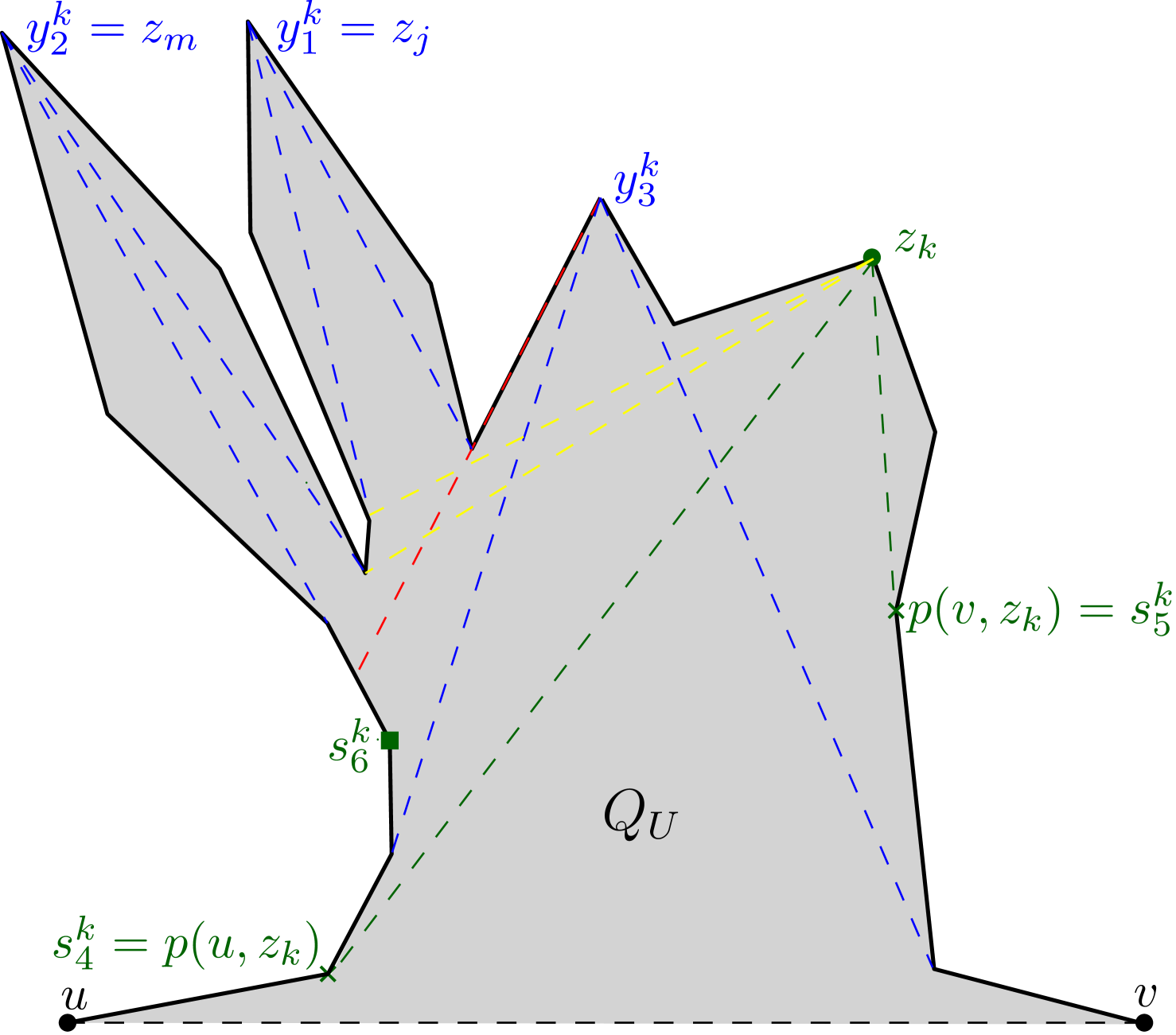
Let us consider the general scenario where and . If Algorithm 1 is executed in this scenario, there may exist a subset of primary vertices that are visible from an optimal guard belonging to (see Figure 19).
Therefore, it is necessary to choose both inside and outside vertex guards corresponding to each primary vertex ,
so that it is ensured that distinct optimal guards are required for guarding every two primary vertices.
So, keeping this in mind, let us modify Algorithm 1 so that,
in addition to the three outside guards , and it also places at most three inside guards , and for every .
For any primary vertex , let us denote by the set of unmarked vertices of whose inward visible vertices overlap with those of . In other words,
Note that all vertices of may not belong to . Further, every vertex of is at a link distance of 1 from some vertex of and at a link distance of 2 from . In the modified algorithm, two inside guards and are placed at and respectively, for every primary vertex . For the placement of an additional inside guard , consider the following cases.
- Case 1:
-
All vertices of are visible from or . So, placement of is not required.
- Case 2:
-
If all vertices of are not visible from or , and there exists one common vertex that sees all vertices of , then is placed on that common vertex.
- Case 3:
-
If all vertices of are not visible from or , and there does not exist any common vertex that sees all vertices of (see Figure 21), then is placed as follows. The vertex guard is placed at the farthest vertex of in clockwise order, starting from , so that it can see all vertices of that are visible from any vertex of lying on (see Figure 23).
Let us discuss these cases in the presence of guards of . Assume that the current primary vertex is visible from an optimal guard . So, and . Thus, if Case 1 true for , then all visible vertices of from are also visible from and . Similarly, if Case 2 holds for , then all visible vertices of from are also visible from , or . However, if Case 3 holds for , then there exists a non-empty subset of vertices that are visible from but not visible from , or . If does not become a primary vertex later, then is guarded by guards placed due to some other primary vertex. Moreover, if this happens for every , then no additional inside guard on is required.
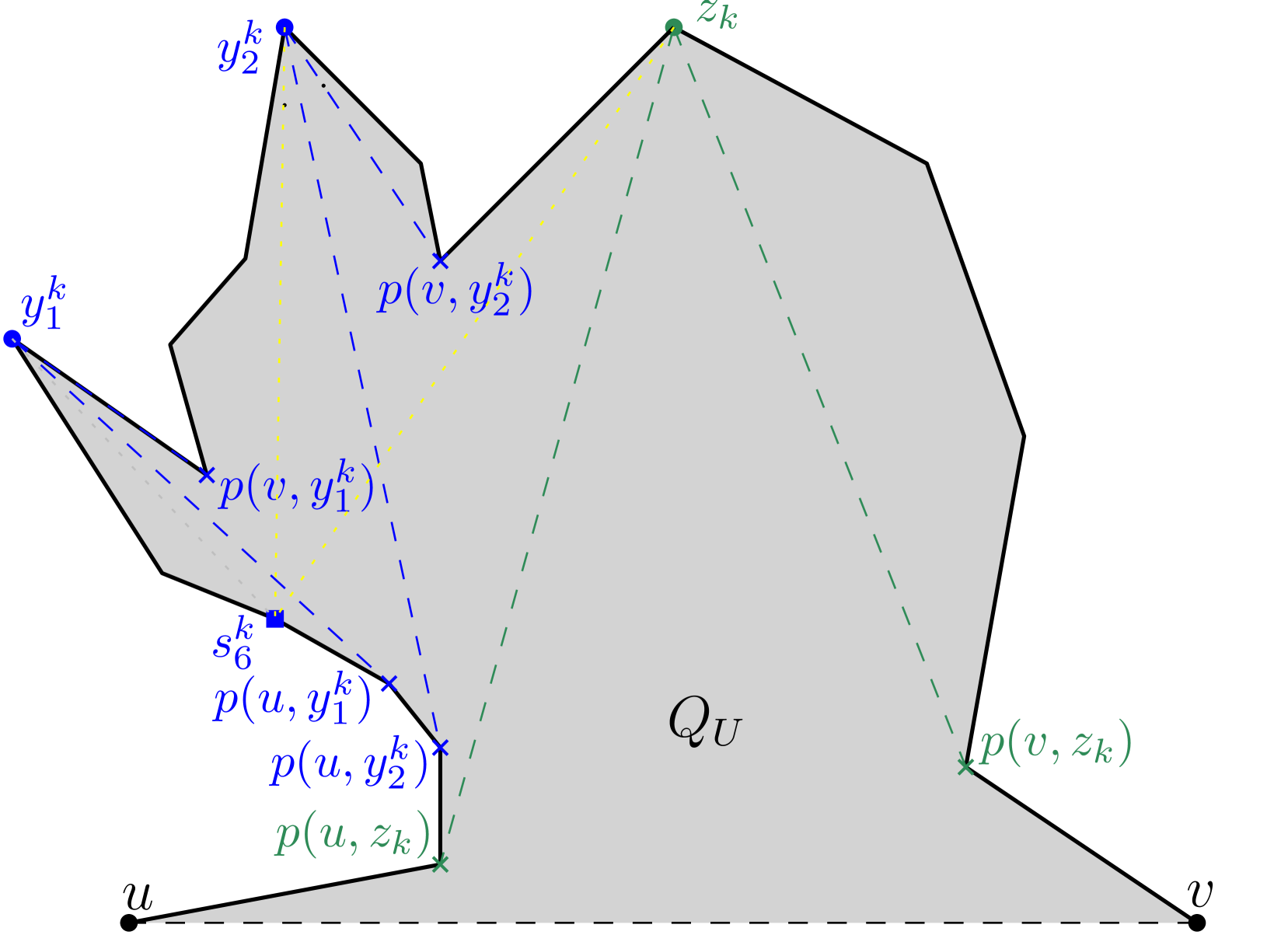
Consider the other case where there exists two primary vertices and , where , such that . Consider the other primary vertex , where , such that . Since and are later primary vertices, we know that neither nor is visible from , or . If is visible from , then and . Similarly, if is visible from , then and . Now, if and are disjoint parts of (see Figure 25), then cannot simultaneously belong to and , and therefore needs another optimal lying on in order to guard both. Consider the special case where , and so and are not totally disjoint (see Figure 23). In this case, if has to simultaneously belong to and , then the only possibility for is to lie on . But in this case, cannot be a primary vertex later, since it becomes visible from , and hence marked. Finally, consider the case where is a part of (see Figure 25). Even in this case, there exists no vertex on which can see both and . Therefore, cannot simultaneously see both and . We summarize these observations in the following lemma.
Lemma 37.
If three primary vertices , and , where , are such that and are both part of , then an optimal guard that sees cannot also see both and .
Corollary 38.
Any optimal guard can see at most two primary vertices.
The above corollary leads to the following theorem.
Theorem 39.
For Algorithm 2, .
Theorem 40.
For Algorithm 2, .
Proof.
Theorem 41.
The running time for Algorithm 2 is .
Proof.
While executing Algorithm 2 as stated, we need to precompute and respectively.
Also, for every vertex belonging to , we need to precompute , ,
which we can do by constructing the visibility graph of in using the algorithm by Ghosh and Mount [16].
Note that vertices are chosen in total.
Therefore, in order to get the overall running time for Algorithm 2, let us consider the running times for all the operations performed by Algorithm 2 in the outer while-loop corresponding to each primary vertex .
Since and are precomputed, it takes only time to choose the guards and .
For choosing the guard , it is required to compute and then .
The former operation takes time, since is precomputed.
For the latter operation, it is required to compute intersections, and since each intersection takes time, the total time required for the operation is .
If is non-empty, then the choice of requires only additional time.
Otherwise, the choice of requires a linear scan along , which takes time. Since is precomputed, it takes only time to choose the guard .
However, for choosing the guards and , it is required to compute , which takes time, and then partition into the sets , and , which takes a further amount of time.
Finally, the the choice of (and similarly ) requires a linear scan along , which takes time.
5.5 Guarding all interior points of a polygon
In the previous subsection, we have presented an algorithm (see Algorithm 2) that returns a guard set such that all vertices of are visible from guards in .
Recall that the art gallery problem demands that must see all interior points of as well.
However, it may not always be true that the guards in see all interior points of .
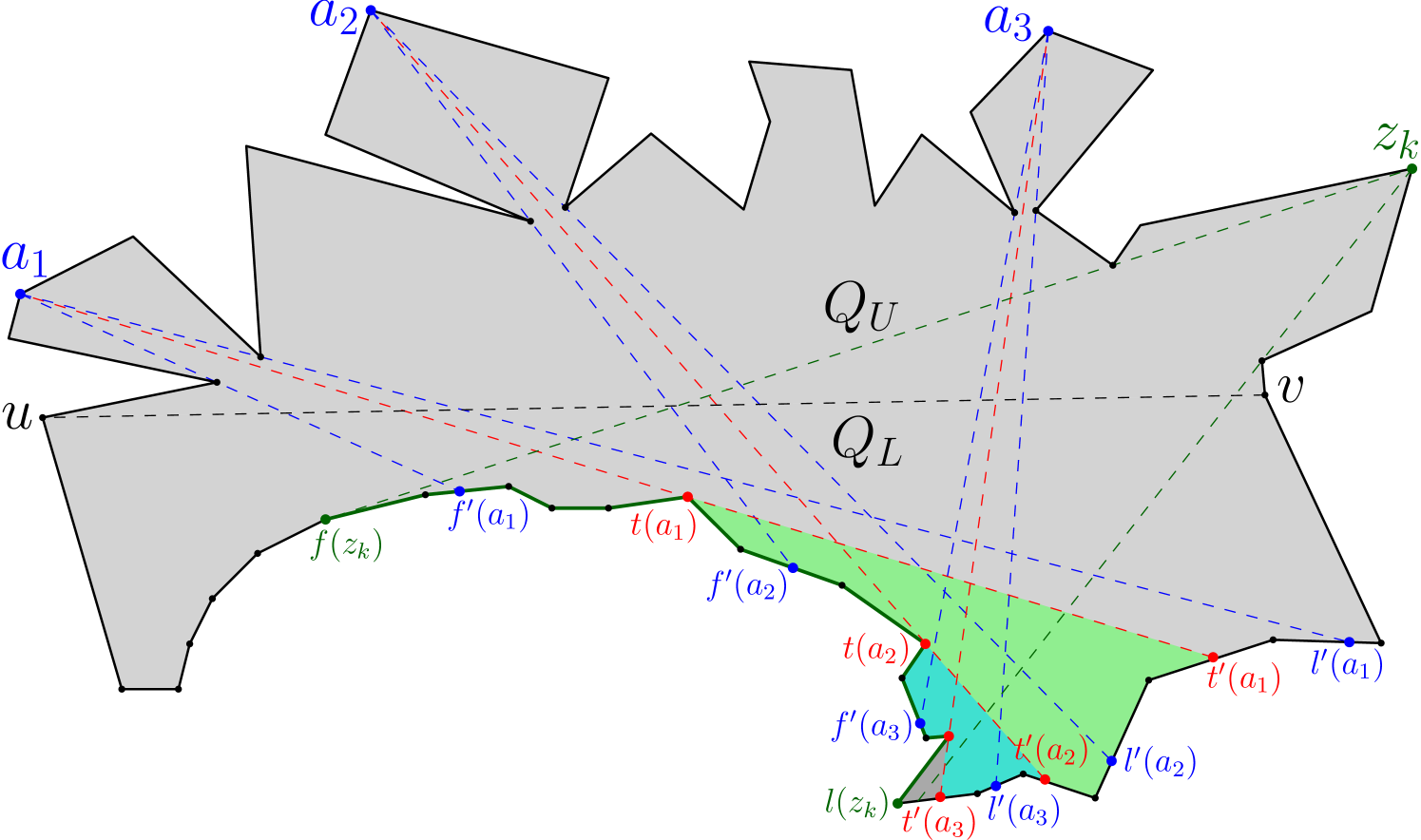
Consider the polygon shown in Figure 27.
Assume that Algorithm 2 places guards at and , and all vertices of become visible from or .
However, the triangular region , bounded by the segments , and , is not visible from or . Also, one of the sides of the triangle is a part of the polygonal edge .
Suppose there exists another guard lying on (see Figure 27) that sees the part of the triangle containing the side ,
but does not see the other part containing .
In that case, such a vertex cannot be weakly visible from , which is a contradiction.
Hence, for any such region invisible from guards corresponding to some , henceforth referred to as an invisible cell, one of the sides must always be a part of a polygonal edge.
The polygonal edge which contributes as a side to the invisible cell is referred to as its corresponding partially invisible edge.
Observe that and can in fact create several invisible cells,
as shown in Figure 27.
Each invisible cell must be wholly contained within the intersection region (which is a triangle) of a left pocket and a right pocket. For example, in Figure 27, the invisible cell is actually the entire intersection region of the left pocket of
and the right pocket of .
In general, where has several left pockets and has several right pockets which intersect pairwise to create multiple invisible cells (as shown in Figure 27),
every such cell can be seen by placing guards on the common vertices between adjacent pairs of cells.
Further, if is also constrained to guard these invisible cells using only inward guards from , then the number of such additional guards required can be at most twice of ,
as shown by Bhattacharya et al. [4].
However, in the absence of any constraint on placing guards, may place an outside guard in that sees several such invisible cells.
So, it is natural to explore the possibility of being able to guard all such invisible cells by using additional guards from , in combination with guards from .
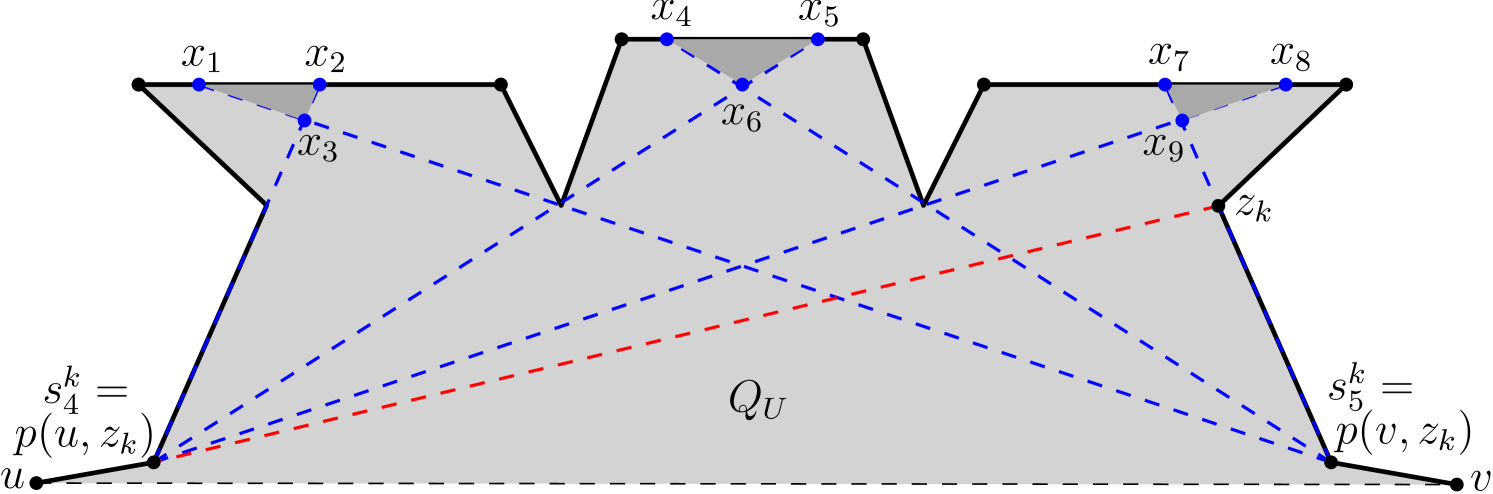
We present a modified algorithm that ensures that all partially invisible edges are guarded completely, and therefore the entire is guarded. For every pair of visible vertices in , extend the visible segment connecting them till they intersect the boundary of . These intersection points partition the boundary of into distinct intervals called minimal visible intervals. We have the following lemmas.
Lemma 42.
Every minimal visible interval on the boundary of is either entirely visible from a vertex or totally not visible from that vertex.
Proof.
Let be a minimal visible interval. If is partially visible from a vertex , then there must exist another vertex such that the extension of the segment intersects at some point, which contradicts the fact that is a minimal visible interval. ∎
Corollary 43.
If a minimal visible interval is entirely visible from a vertex of , then the entire triangle lies totally inside .
The modified Algorithm 3 first computes all minimal visible intervals and chooses one internal representative point from each minimal visible interval on the boundary of . These representative points are referred to as pseudo-vertices. Alongside the original polygonal vertices of , all pseudo-vertices are introduced on the boundary of , and the modified polygon is denoted by . Note that the endpoints of minimal visible intervals are not introduced in . In Algorithm 3, the pseudo-vertices of are treated in almost the same manner as the original vertices. We compute and for all vertices of , irrespective of whether it is a pseudo-vertex, and some of the psuedo-vertices may even be chosen as primary vertices. However, while computing for any vertex of , no pseudo-vertices are included in , since they cannot be vertex guards in any case.
Suppose an invisible cell is created by the guards placed on the parents of some primary vertex. This implies that there exists a pseudo-vertex on the partially invisible edge contained in the invisible cell which has been left unmarked.
So, either this pseudo-vertex is marked due to the guards chosen for some later primary vertex, or else it is eventually chosen as a primary vertex itself.
If a pseudo-vertex on a partially invisible edge is chosen as a primary vertex by Algorithm 3, then the entire invisible cell containing the partially invisible edge must be visible from and . Moreover, if the adjacent invisible cell to the left or right shares a parent, then or also sees both invisible cells. Therefore, if all invisible cells are guarded by guards in , then the number of pseudo-vertices that are chosen as primary vertices is at most twice of the number of guards in [4].
Observe that several invisible cells may be seen by a few outside guards belonging to , unlike which can see only two such cells at the most. Assume that a pseudo-vertex is chosen as a primary vertex . Every vertex and pseudo-vertex belonging to is marked due to the placement of the guard at , and therefore no additional guards are introduced for guarding the vertices or pseudo-vertices in . Consider the outside guards introduced due to . Assume that has pseudo-vertices. If does not have pseudo-vertices, then the pseudo-vertices do not create new disjoint right pockets, and therefore guards placed to guard vertices of are enough to guard pseudo-vertices in . If contains a pseudo-vertex, then a new disjoint right pocket is created, and therefore guards placed for other disjoint right pockets cannot see this pseudo-vertex. So, an additional outside guard is required, as well as an additional optimal guard in . The same argument holds for and . Thus Lemmas 16 to 34, Lemma 37 and Corollary 38, and Theorems 35 and 39 hold even after the introduction of pseudo-vertices, and so the overall bound remains , as in Theorem 40. We state this result in Theorem 44.
Theorem 44.
For the guard set computed by Algorithm 3, .
Theorem 45.
The running time of Algorithm 3 is .
Proof.
While executing Algorithm 3 as stated, the precomputation of and
requires time as the number of pseudo-vertices is .
Also, for every vertex (or pseudo-vertex) belonging to , the precomputation of and can be done by constructing the visibility graph using the output-sensitive algorithm of Ghosh and Mount [16].
Since the total number of vertices (including pseudo-vertices) in is , and the visibility edges are not computed between pseudo-vertices, the size of the visibility graph for is , and thus time is required to precompute and .
Note that, while each of the original vertices of may be chosen as primary vertices, only at most one of the pseudo-vertices belonging to a single edge may be chosen as a primary vertex, which means that there can be at most primary vertices chosen by Algorithm 3.
Therefore, in order to get the overall running time for Algorithm 2, let us consider the running times for all the operations performed by Algorithm 2 in the outer while-loop (see lines …) corresponding to each primary vertex .
Since and are precomputed, it takes only time to choose the guards and .
For choosing the guard , it is necessary to compute and then .
The former operation takes time, since is precomputed.
For the latter operation, intersections are computed; since each intersection takes time, the total time required for the operation is .
If is non-empty, then the choice of requires only additional time.
Otherwise, the choice of requires a linear scan along , which takes time. Since is precomputed, it takes only time to choose the guard .
However, for choosing the guards and , it is required to compute , which takes time, and then the partition of into the sets , and requires a further amount of time.
Finally, the the choice of (and similarly ) requires a linear scan along , which takes time.
Algorithm 3 chooses a guard set that ensures no partially invisible edge in . However, there is no guarantee that sees the entire interior of , as there may remain residual invisible cells in the interior of (see Figure 29). Consider a residual invisible cell that is a part of an invisible cell , where is contained in a partially invisible edge. For such a residual invisible cell, there exists a pseudo-vertex on whose parents can see the entire cell , as discussed earlier in the context of placing inside guards for guarding entire visibility cell. So, placing a guard at an appropriate parent, such as in Figure 29, guarantees that the residual invisible cell is totally visible. Since such an additional inside guard on corresponds to an unique outward guard in , the additional number of inside guards can be at most the number of outside guards. This amounts to placing at most (3+3)=6 inside guards and 3 outside guards corresponding to each primary vertex, while the number of primary vertices chosen remains at most . We summarize the result in the following theorem.
Theorem 46.
Let be a polygon of vertices that is weakly visible from an internal chord . Then, a vertex guard set can be computed in time, and , where is a an optimal vertex guard cover for the entire boundary of .
6 Final Results
In Section 5, we have presented an approximation algorithm
for guarding a polygon weakly visible from a chord .
This algorithm chooses primary vertices according to the ordering of their last visible point .
So the algorithm does not depend on a chord of the weak visibility polygon.
Therefore, if this algorithm is executed on the union of overlapping weak visibility polygons , then it chooses primary vertices in the same way irrespective of chords in , producing a guard set that sees the entire union .
So, if this algorithm is used for every overlapping weak visibility polygon in , then the entire polygon can be guarded by the union of the guard sets produced for guarding these overlapping weak visibility polygons.
Note that there is no increase in running time for this overall algorithm, since each vertex can appear in at most 2 weak visibility polygons from the hierarchy .
Let be an optimal guard in . It can be seen that is either a guard in in the weak visibility polygon whose chord is the constructed edge between and its parent (say ), or a guard in for the overlapping weak visibility polygon whose chords are constructed edges that separate from its children. Let . So is a guard in in or a guard in in . Consider the case where belongs to in . Observe that all vertices of that are visible from any such in are guarded by , , for all primary vertices . Therefore, the approximation bound for Algorithm 3 run on does not change in this case.
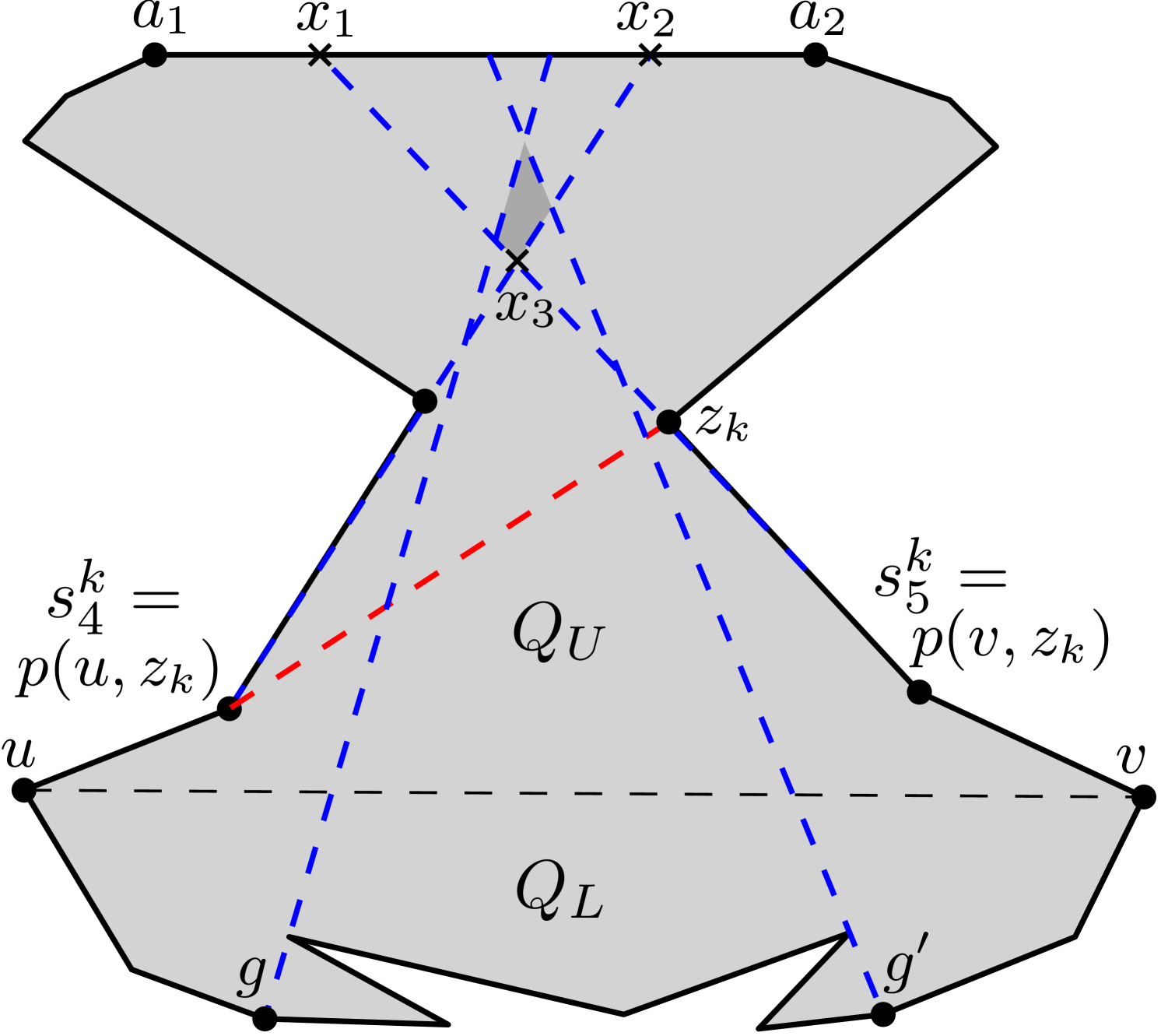
Consider the other case where in .
Observe that all vertices of that are visible from any such in
are guarded by , , for all primary vertices .
However, all vertices of that are visible from any such in may not necessarily be guarded by , , ,, , for all primary vertices (see Figure 29), since the guards chosen by Algorithm 3 are not meant for guarding vertices in .
Let be a vertex that is visible from on , but not visible from any of the guards placed in by Algorithm 3. Since remains unmarked, can be chosen as a primary vertex during the execution of 3 on . Then, the guards placed on the parents see not only , but also see all other such vertices visible from (see Figure 29) due to cross-visibility across two adjacent weak visibility polygons in the partition hierarchy . So, this amounts to choosing an extra primary vertex in , and thus the number of primary vertices visible from also increases by at most 1. Since there could be at most one extra primary corresponding to every , for counting purposes, we can attribute these to as an extra primary vertex. So, is replaced by in our bound for all such . We have the following results.
Theorem 47.
Let be a simple polygon of vertices. Then, a vertex guard set for guarding all vertices of can be computed in time, and , where is a an optimal vertex guard cover for all vertices of .
Theorem 48.
Let be a simple polygon of vertices. Then, a vertex guard set for guarding the entire boundary of can be computed in time, and , where is a an optimal vertex guard cover for the entire boundary of .
Theorem 49.
Let be a simple polygon of vertices. Then, a vertex guard set for guarding interior and boundary points of can be computed in time, and , where is a an optimal vertex guard cover for the entire interior and boundary of .
7 Algorithms for Polygon Guarding using Edge Guards
Let us consider a slightly different version of the art gallery problem,
where edge guards rather than vertex guards are used for guarding a simple -sided polygon .
The hierarchical partitioning method used is almost exactly the same as
Algorithm 1 (presented in Section 3),
where we guard the polygon using vertex guards.
While using edge guards instead, the only modification to Algorithm 1 is that now we initially choose an arbitrary edge
instead of a vertex, and compute
(compare with Lines 1-2 of Algorithm 1).
As before, each weak visibility polygon in the hierarchy is used to generate
one weak visibility polygon in the next level corresponding to each of its constructed edges.
As discussed in Section 5, let denote a simple polygon that is weakly visible from an internal chord , i.e. we have , and observe that the chord similarly splits into two sub-polygons and . Suppose we wish to guard an arbitrary vertex of using an edge guard. Then, a guard must be placed at an edge of that belongs fully or even partially to . Henceforth, let denote the set of all polygonal edges that contain at least one point belonging to . Further, let us define the inward visible edges and the outward visible edges of , denoted by and respectively, as follows.
: for any point , the segment does not intersect }
: for any point , the segment intersects }
We shall henceforth refer to the vertex guards belonging to and as inside guards and outside guards for respectively.
Observe that, for any vertex , both and may be considered to be ordered sets by taking into account the natural ordering of the visible edges of in clockwise order along and in counter-clockwise order along respectively.
Let us denote the first visible edge and the last visible edge belonging to the ordered set by and respectively (see Figure 9).
Also, we denote by the last visible point from , which is obtained by extending the ray till it touches .
As in Section 5,
our algorithm selects a subset of vertices of , and places a fixed number of both inside and outside edge guards corresponding to each of them,
so that these edge guards together see the entire . As before, we refer to this subset of special vertices as primary vertices, and denote it by .
Moreover, the choice of primary vertices is also made in a manner identical to that discussed in Section 5.
Once again, a natural idea is to place outside edge guards in a greedy manner so that they lie in the common intersection of outward visible edges of as many vertices of as possible. For any primary vertex , let us denote by the set of unmarked vertices of whose outward visible edges overlap with those of . In other words,
So, each vertex of belonging to is visible from at least one edge of .
Further, can be considered to be an ordered set, where for any pair of elements , we define if and only if precedes in counter-clockwise order on .
For the current primary vertex , let us assume without loss of generality that such that in counter-clockwise order on .
Just as we partitioned while guarding the polygon using vertex guards, let us partition the vertices belonging to into 3 sets, viz. , and , in the following manner. Consider any vertex , such that creates a constructed edge , where is a polygonal vertex and is the point where first intersects . Every vertex of visible from is included in . Observe that, by definition . Obviously, for each vertex , is not visible from due to the presence of some constructed edge. The vertices of are categorized into and based on whether this constructed edge creates a right pocket or a left pocket. Suppose is a vertex such that creates a constructed edge , where is a polygonal vertex and is the point where first intersects . If lies on and lies on , i.e. if and , then is included in . For instance, in Figure 11, due to the constructed edge . On the other hand, if lies on and lies on , i.e. if and , then is included in . For instance, in Figure 11, due to the constructed edge . Observe that, all vertices of must lie on , whereas all vertices of must lie on . We have the following lemma, whose proof is similar to the proof of Lemma 4.
Lemma 50.
The edge sees all vertices belonging to .
Depending on the vertices in , and , we have the following cases, just as in Section 5.3.
In each of the above cases, we also proceed to choose the three outside edge guards , and in a similar manner as was done in Section 5.3, with the only difference being that here we use the new definitions of and instead of and respectively.
To elaborate further, we choose the edge guard ; if the guards and are chosen from a common intersection region, then we use rather than ; if the guards and are chosen greedily, then we use the last edge along the traversal after which some vertex belonging to and respectively is no longer visible.
We can establish lemmas similar to Lemmas 8 to 35 (in Section 5.3) from these choices of edge guards.
As far as the choice of inside edge guards is concerned, we again choose them following the same case analysis (see Figures 23, 25 and 25) as described in Section 5.4. To elaborate further, we choose the edge guards and to be the edges adjacent to and respectively that lie on , whereas for the greedily chosen guard (if required at all) we use the last edge along the traversal after which some vertex belonging to is no longer visible. Again, we can establish lemmas similar to Lemmas 37 to 40 (in Section 5.4) from these choices of edge guards. As a consequence, we obtain the following theorems.
Theorem 51.
Let be the set of primary vertices chosen by our modified algorithm, and let be the set of all edge guards placed by it. Then, .
Theorem 52.
It is possible to compute in time a set of inside and outside edge guards for guarding all vertices of a weak visibility polygon such that the number of edge guards chosen is at most , where is an optimal edge guard cover for all vertices of .
In Theorem 52, we established the existence of an approximation algorithm for guarding a polygon weakly visible from a chord . If this same algorithm is executed on the union of overlapping weak visibility polygons , then it chooses primary vertices in the same way irrespective of chords in , thereby producing a set of edge guards that sees the entire union . So, if this algorithm is used for every overlapping weak visibility polygon in , then the entire polygon can be guarded by the union of the guard sets produced for guarding these overlapping weak visibility polygons. Note that there is no increase in running time for this overall algorithm. Moreover, since each vertex can appear in at most two weak visibility polygons from the hierarchy , we obtain the following theorem.
Theorem 53.
Let be a simple polygon having vertices. Then, an edge guard set for guarding all vertices of can be computed in time, such that , where is an optimal edge guard cover for all vertices of .
However, it may not always be true that the guards in see all interior points of .
Consider the polygon shown in Figure 31.
Assume that our previous algorithms places guards at and , and all vertices of become visible from or .
However, the triangular region , bounded by the segments , and ,
is not visible from or . Also, one of the sides of the triangle is a part of the polygonal edge . In fact, for any such region invisible from edge guards corresponding to some ,
henceforth referred to as an invisible cell, one of the sides must always be a part of a polygonal edge.
The polygonal edge which contributes as a side to the invisible cell is referred to as its corresponding partially invisible edge.
Observe that and can in fact create several invisible cells,
in a manner very similar to that shown in Figure 27.
Each invisible cell must be wholly contained within the intersection region (which is a triangle) of a left pocket and a right pocket.
For example, in Figure 31,
the invisible cell is actually the entire intersection region of the left pocket of and the right pocket of .
In general, where has several left pockets and has several right pockets which intersect pairwise to create multiple invisible cells (as shown in Figure 27),
every such cell can be seen by placing guards on the common vertices between adjacent pairs of cells.
Further, if is also constrained to guard these invisible cells using only inward guards from , then the number of such additional guards required can be at most twice of ,
as shown by Bhattacharya et al. [4].
However, in the absence of any constraint on placing guards, may place an outside guard in that sees several such invisible cells.
So, it is natural to explore the possibility of being able to guard all such invisible cells by using additional edge guards from ,
in combination with guards from .
Just as in Section 5.5, we present a modified algorithm that ensures that all partially invisible edges are guarded completely, and therefore the entire is guarded. Let us compute the weak visibility polygons corresponding to every edge of . Then, the non-vertex endpoints of all the constructed edges belonging to these weak visibility polygons partition the boundary of into distinct intervals called minimal visible intervals. We have the following lemmas.
Lemma 54.
Every minimal visible interval on the boundary of is either entirely visible from an edge or totally not visible from that edge.
The modified algorithm first computes all minimal visible intervals and chooses one internal representative point from each minimal visible interval on the boundary of . These representative points are referred to as pseudo-vertices. Alongside the original polygonal vertices of , all pseudo-vertices are introduced on the boundary of , and the modified polygon is denoted by . Note that the endpoints of minimal visible intervals are not introduced in . In the modified algorithm, the pseudo-vertices of are treated in the same manner as the original vertices. We compute and for all vertices of , irrespective of whether it is a pseudo-vertex, and some of the psuedo-vertices may even be chosen as primary vertices.
Theorem 55.
For the edge guard set computed by our modified algorithm with pseudo-vertices, , where is an optimal edge guard cover for the entire boundary of .
Theorem 56.
Let be a simple polygon having vertices. Then, an edge guard set for guarding the entire boundary of can be computed in time, such that , where is an optimal edge guard cover for the entire boundary of .
Proof.
This result follows directly from Theorem 55. The running time bound of can be established through arguments very similar to those in the proof of Theorem 45. The only difference lies in the computation of and , in place of and respectively, for every primary vertex , but the time complexity of these computations are also same. ∎
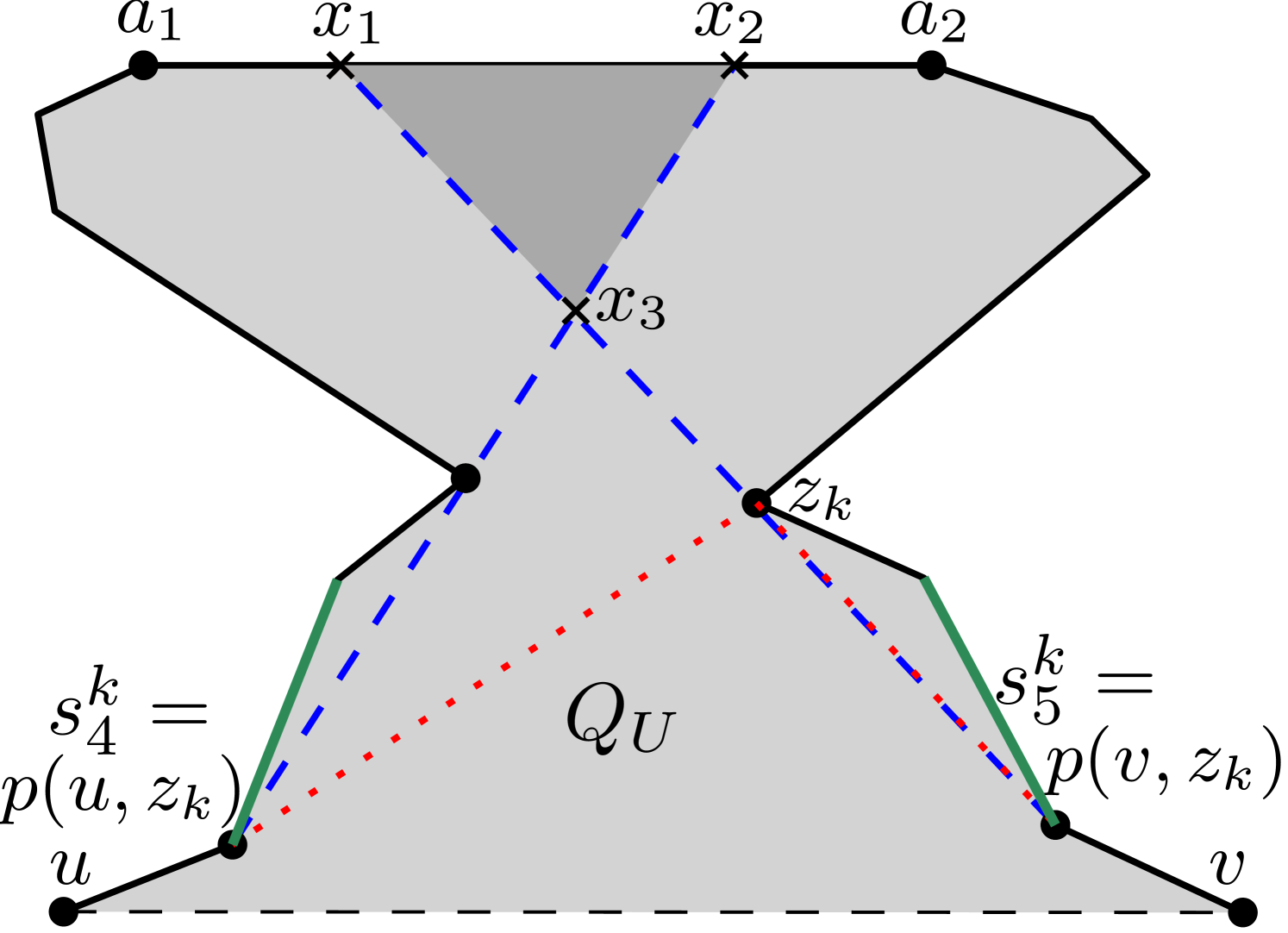
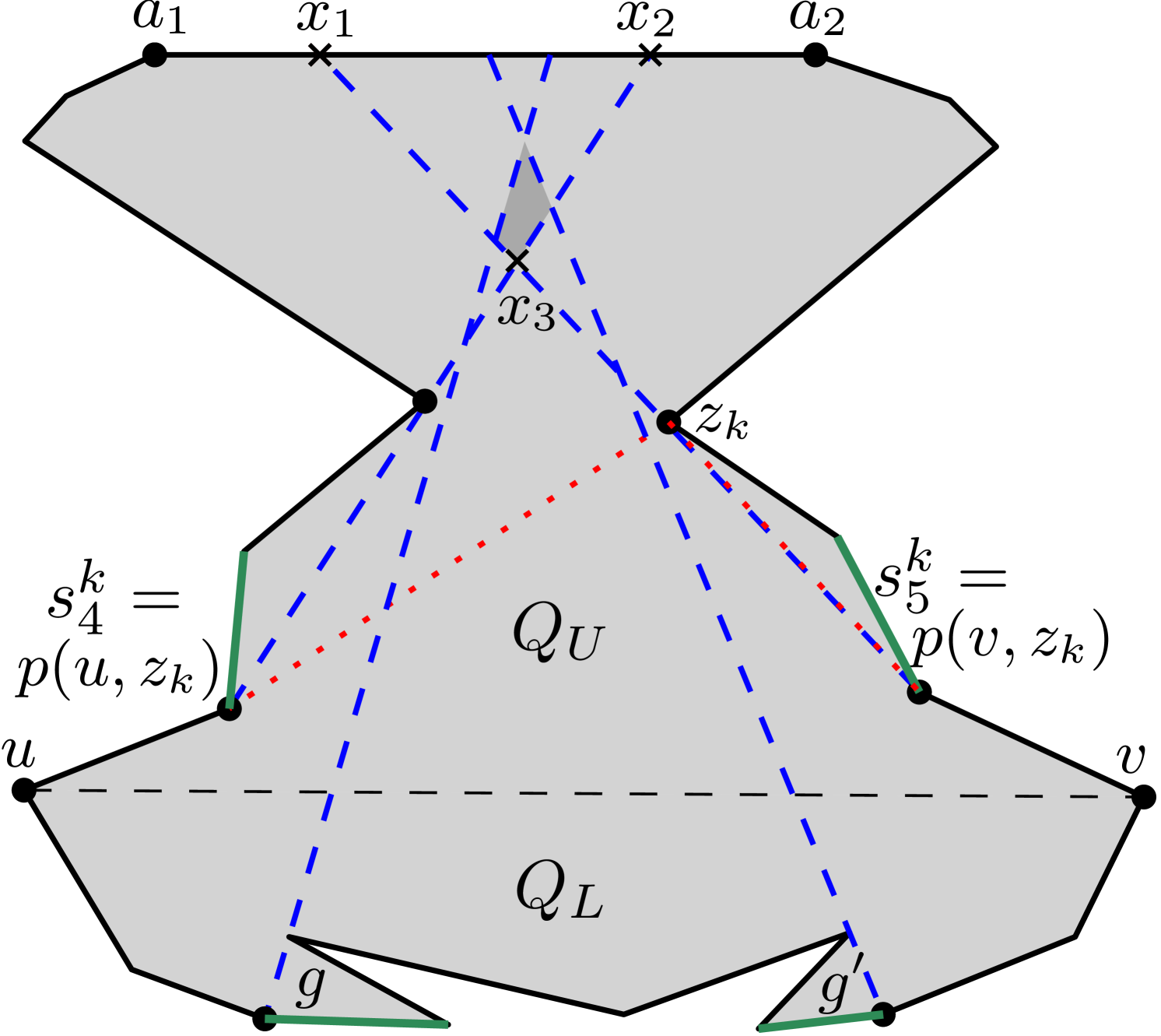
However, there is no guarantee that sees the entire interior of , as there may remain residual invisible cells in the interior of (see Figure 29). Consider a residual invisible cell that is a part of an invisible cell , where is contained in a partially invisible edge. For such a residual invisible cell, there exists a pseudo-vertex on whose parents can see the entire cell , as discussed earlier in the context of placing inside guards for guarding entire visibility cell. So, placing a guard at an appropriate parent, such as the parent for the pseudo-vertex that will be placed on the minimal visible interval in Figure 29, guarantees that the residual invisible cell is totally visible. Since such an additional inside guard on corresponds to an unique outward guard in , the additional number of inside guards can be at most the number of outside guards. This amounts to placing at most (3+3)=6 inside guards and 3 outside guards corresponding to each primary vertex, while the number of primary vertices chosen remains at most . We summarize the result in the following theorem.
Theorem 57.
Let be a simple polygon having vertices. Then, an edge guard set for guarding the entire interior and boundary points of can be computed in time, such that , where is a an optimal edge guard cover for the entire interior and boundary of .
8 Concluding Remarks
We have presented three approximation algorithms for guarding simple polygons using vertex guards. We have also shown how these algorithms can be modified to obtain similar approximation bounds while using edge guards. Though the approximation ratios for our algorithms are slightly on the higher side, they do successfully settle the long-standing conjecture by Ghosh by providing constant-factor approximation algorithms for this problem. We feel that, in practice, our algorithms will provide guard sets that are much closer in size to an optimal solution. This can be further ensured by introducing a redundancy check after the placement of each new guard, which removes each (inside or outside) guard placed previously by the algorithm that does not see at least one vertex of not seen by any other guard placed so far. By incorporating such a redundancy check, we conjecture that our analysis of the approximation bound can be tightened further, and the existence of smaller approximation ratios can be proven for these three variations of the polygon guarding problem. Our algorithms exploit several deep visibility structures of simple polygons which are interesting in their own right.
References
- [1] Mikkel Abrahamsen, Anna Adamaszek, and Tillmann Miltzow. The art gallery problem is R-complete. CoRR, abs/1704.06969, 2017.
- [2] Alok Aggarwal. The art gallery theorem: its variations, applications and algorithmic aspects. PhD thesis, The Johns Hopkins University, Baltimore, Maryland, 1984.
- [3] Pritam Bhattacharya, Subir Kumar Ghosh, and Bodhayan Roy. Vertex Guarding in Weak Visibility Polygons. In Proceedings of the 1st International Conference on Algorithms and Discrete Applied Mathematics (CALDAM 2015), volume 8959 of Lecture Notes in Computer Science (LNCS), pages 45–57. Springer, 2015.
- [4] Pritam Bhattacharya, Subir Kumar Ghosh, and Bodhayan Roy. Approximability of guarding weak visibility polygons. Discrete Applied Mathematics, 228:109 – 129, 2017.
- [5] Édouard Bonnet and Tillmann Miltzow. An Approximation Algorithm for the Art Gallery Problem. In Boris Aronov and Matthew J. Katz, editors, 33rd International Symposium on Computational Geometry (SoCG 2017), volume 77 of Leibniz International Proceedings in Informatics (LIPIcs), pages 20:1–20:15, Dagstuhl, Germany, 2017. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik.
- [6] Václav Chvátal. A combinatorial theorem in plane geometry. Journal of Combinatorial Theory, Series B, 18(1):39–41, 1975.
- [7] Ajay Deshpande, Taejung Kim, Erik D. Demaine, and Sanjay E. Sarma. A pseudopolynomial time o(log n)-approximation algorithm for art gallery problems. In WADS, pages 163–174, 2007.
- [8] Alon Efrat and Sariel Har-Peled. Guarding galleries and terrains. Information Processing Letters, 100(6):238–245, 2006.
- [9] Stephan Eidenbenz, Christoph Stamm, and Peter Widmayer. Inapproximability of some art gallery problems. Canadian Conference on Computational Geometry, pages 1–11, 1998.
- [10] Stephan Eidenbenz, Christoph Stamm, and Peter Widmayer. Inapproximability results for guarding polygons and terrains. Algorithmica, 31(1):79–113, 2001.
- [11] Steve Fisk. A short proof of Chvátal’s watchman theorem. Journal of Combinatorial Theory, Series B, 24(3):374, 1978.
- [12] Subir Kumar Ghosh. Approximation algorithms for art gallery problems. In Proceedings of Canadian Information Processing Society Congress, page 429–434. Canadian Information Processing Society, 1987.
- [13] Subir Kumar Ghosh. Visibility Algorithms in the Plane. Cambridge University Press, 2007.
- [14] Subir Kumar Ghosh. Approximation algorithms for art gallery problems in polygons. Discrete Applied Mathematics, 158(6):718–722, 2010.
- [15] Subir Kumar Ghosh. Approximation algorithms for art gallery problems in polygons and terrains. WALCOM: Algorithms and Computation, pages 21–34, 2010.
- [16] Subir Kumar Ghosh and David M. Mount. An output-sensitive algorithm for computing visibility graphs. SIAM Journal of Computing, 20(5):888–910, 1991.
- [17] John Hershberger. An optimal visibility graph algorithm for triangulated simple polygons. Algorithmica, 4(1):141–155, 1989.
- [18] J. Kahn, M. Klawe, and D. Kleitman. Traditional galleries require fewer watchmen. SIAM Journal of Algebraic and Discrete Methods, 4(2):194–206, 1983.
- [19] Matthew J Katz. A PTAS for vertex guarding weakly-visible polygons. arXiv preprint arXiv:1803.02160, 2018.
- [20] Matthew J. Katz and Gabriel S. Roisman. On guarding the vertices of rectilinear domains. Computational Geometry, 39(3):219–228, 2008.
- [21] James King and David G. Kirkpatrick. Improved approximation for guarding simple galleries from the perimeter. Discrete & Computational Geometry, 46(2):252–269, 2011.
- [22] David G. Kirkpatrick. An o(lg lg opt)-approximation algorithm for multi-guarding galleries. Discrete & Computational Geometry, 53(2):327–343, 2015.
- [23] Erik A Krohn and Bengt J Nilsson. Approximate Guarding of Monotone and Rectilinear Polygons. Algorithmica, 66:564–594, 2013.
- [24] D.T. Lee and A. Lin. Computational complexity of art gallery problems. IEEE Transactions on Information Theory, 32(2):276–282, 1986.
- [25] Joseph O’Rourke. An alternative proof of the rectilinear art gallery theorem. Journal of Geometry, 211:118–130, 1983.
- [26] Joseph O’Rourke. Art gallery theorems and algorithms. Oxford University Press, London, 1987.
- [27] Joseph O’Rourke and Kenneth J. Supowit. Some NP-hard polygon decomposition problems. IEEE Transactions on Information Theory, 29(2):181–189, 1983.
- [28] Dietmar Schuchardt and Hans-Dietrich Hecker. Two NP-Hard Art-Gallery Problems for Ortho-Polygons. Mathematical Logic Quarterly, 41:261–267, 1995.
- [29] Subhash Suri. A linear time algorithm with minimum link paths inside a simple polygon. Comput. Vision Graph. Image Process., 35(1):99–110, July 1986.
- [30] Subhash Suri. Minimum link paths in polygons and related problems. PhD thesis, The Johns Hopkins University, Baltimore, Maryland, 1987.