Constraint on the magnetic field for the stable strange quark matter

It is well known that the interaction of quarks and gluons is described by quantum chromodynamics (QCD). Due to the conversion of u-, d-quarks into s-quarks by the weak reactions, strange quark matter (SQM) could be more stable than hadronic matter. SQM is suggested to occur in extreme hot and high density condition at relativistic heavy ion collision experiment or in neutron stars. With growing evidence, strongly interacting Quark Gluon Plasma is realized near $T_{c}$ in relativistic heavy-ion collisions [1, 2]. A first order transition is expected to happen from the cold nuclear matter to quark matter. However, the location of the phase transition to deconfined quark matter remain poorly known to this day. In fact, the transition can be accounted for by the stability of the quark matter with respect to nuclear matter at zero temperature and the structure of condense stars [3, 4]. Furthermore, this is related to the possibility of the entire stars being made up of self-bound quark matter [5, 6, 7].

The cold dense quark matter is investigated in MIT bag model dating back 50 years [8]. The interaction between quarks is represented by a phenomenological bag constant and produces a bag pressure to the non-interacting system [10, 9]. 40 years ago, Bodmer-Witten hypothesis suggested that clusters of SQM can be more stable than the most stable atomic nucleus. The possibility that dark matter could be composed of macroscopic clusters of SQM would rely on the stability of SQM with a suitable confinement. The first order transition seemed to not be a crucial requirement in order to produce large clusters of quarks [11]. In the bag model, the quark mass is infinitely large outside while it is constant within the bag. As is well known in nuclear physics, particle masses vary with environment. Taking advantage of the medium effect, the strong interactions between the elementary degrees of freedom are incorporated through the medium-dependent quasiparticle mass [12, 13]. The quark confinement can be described by the density dependence of quark masses [14, 15]. The quasiparticle model with a chemical potential and/or temperature dependent quark mass is considered to be superior to the plain bag model. Peshier proposed that the thermal mass depends on the perburbative expression for plasma frequencies [17, 16]. Bannur et.al. improved the model by the density dependent expression and the full HTL dispersion relation instead of the approximate dispersion relation [18]. In Leonidov’s approach, the entropy and baryon number conservation is maintained with effective bag pressure in the deconfinement phase transition [19, 20]. Under the density and/or temperature dependent mass scale, the vacuum energy is described by effective bag function, which is crucial to the thermodynamical consistence [21]. At zero temperature, the quark mass depends merely on chemical potentials [22, 23]. It will be more convenient to investigate the self-consistent thermodynamics and pave the way for further work with such models. The aim of this paper is to demonstrate the magnetic field effect on the equation of state at finite chemical potentials.

This paper is organized as follows. In Section 2, we present the self-consistent thermodynamics of the quasiparticle model in a strong magnetic field. The effective bag constant is derived to reflect confinement scheme. In Section 3, the numerical results are shown at the finite density in a strong magnetic field. The detailed discussions are focused on the stability of SQM. The last section is a short summary.

The quark-gluon plasma phase is a new state of matter consisting of three flavor quarks. The whole understanding of the QCD phase should be based on the properties of quark matter surrounded by the medium at finite temperatures and densities. The important feature of the medium dependence is quark effective masses influenced by QCD nonperturbative properties. In a simple case, the medium is characterized by a whole se of collective quasiparticles in the vacuum. For the medium dependence of the quark quasiparticle model, the effective quark mass $m_{i}^{*}$ is derived at the zero momentum limit of the dispersion relation following from the effective quark propagator by resuming one-loop self energy diagrams in the hard dense loop (HDL) approximation [22]. The in-medium effective mass of quarks can thus be expressed as [22, 24, 16, 25, 23]

$$m_{i}^{*}(\mu_{i})=\frac{m_{i}}{2}+\sqrt{\frac{m_{i}^{2}}{4}+\frac{g^{2}\mu_{i}^{2}}{6\pi^{2}}},\ \ (i=u,d,s),$$

(1)

where $m_{i}$ is the current mass of corresponding quarks and the constant $g$ is related to the strong interaction constant $\alpha_{s}$ by the equation $g=\sqrt{4\pi\alpha_{s}}$. The quasi-particle idea can be recalled backward to the work by Fowler et.al.[14] that the particle mass may change with the environment parameters. The effective quark mass $m_{i}^{*}$ increases with $g$ at the fixed quark chemical potential $\mu_{i}$. The unknown coupling $g$ is to be determined as a decreasing function of the temperature and density reflecting the asymptotic freedom of QCD.

The quasiparticle contribution to the thermodynamic potential density is given as .

$\displaystyle\Omega_{i}$

$\displaystyle=$

$\displaystyle\frac{d_{i}|q_{i}B_{m}|}{2\pi^{2}}\sum_{\nu=0}^{\nu_{i}^{\mathrm{max}}}(2-\delta_{\nu 0})\int_{0}^{p_{F}}\left(E_{i}-\mu_{i}\right)\mbox{d}p_{z}\,,$

(2)

where the degeneracy factor $d_{i}=3$ for the color freedom of $i$-flavor quarks. The single particle energy eigenvalue $E_{i}=\sqrt{{m_{i}^{*}}^{2}+p_{z}^{2}+2\nu_{i}|q_{i}B_{m}|}$ sensitively depends on the magnetic fields, the thermal mass $m^{*}_{i}$ and $z$-component momentum $p_{z}$. At zero temperature, the upper limit $\nu_{i}^{\mathrm{max}}$ of the summation index $\nu_{i}$ can be understood from the positive value requirement on Fermi momentum and is defined by $\nu_{i}^{\mathrm{max}}=(\mu_{i}^{2}-{m_{i}^{*}}^{2})/(2|q_{i}B_{m}|)$. In order to include the vacuum contribution, the total pressure should be a sum of a matter pressure and a bag constant $P(\mu_{i})=-\Omega_{i}-B(\mu_{i})$. The $B(\mu_{i})$ represents the model of confinement used in our studies of SQM.

The pressure function would include the contribution of the matter pressure and density-dependent bag pressure, namely, $P=-\Omega-B$. If the thermodynamic potential depends on the state variable implicitly via phenomenological parameters $m_{i}^{*}$, the corresponding stationarity condition should be required as [26]

$\displaystyle\left.\frac{\partial P}{\partial m_{i}^{*}}\right|_{T,\mu_{i}}=0.$

(3)

which has been widely employed in the quasiparticel model at finite temperature and density [16, 27, 28, 29]. The condition respects the chiral symmetry restoration in the plasma [30]. At zero temperature, we get the bag function through the integral

$\displaystyle B_{i}^{*}(\mu_{i})$

$\displaystyle=$

$\displaystyle-\frac{d_{i}|q_{i}B_{m}|}{2\pi^{2}}\sum_{\nu=0}^{\nu_{i}^{\mathrm{max}}}(2-\delta_{\nu 0})\int^{\mu_{i}}_{0}\int_{0}^{p_{F}}\frac{m_{i}^{*}}{E_{i}}\frac{\mathrm{d}m^{*}_{i}}{\mathrm{d}\mu_{i}}\mathrm{d}p_{z}\mathrm{d}\mu_{i},$

(4)

where the allowed chemical potential in the outer integral should start from zero. Specially, the equality $\mu_{i}=m_{i}^{*}$ would lead to the vanishing Fermi momentum and the zero bag function. The upper limit of the inner integral is the Fermi momentum dependent on $\mu_{i}$. So the total bag pressure is a sum of the flavor and vacuum contributions as $B=\sum_{i}B^{*}_{i}(\mu_{i})+B_{0}$. For a stable SQM, the proposed value of the Bag constant should be within the following range $(55\sim 75)$ MeV/fm³ [10]. Compared with the standard Statistical Mechanics (SM), one can recover the thermodynamics consistency of system $T$-$\mu$-$B_{m}$- dependent Hamiltonian with the extra term $B(T,\mu,B_{m})$. The meaning of $B$ plays an important role in the physical conclusion. The interpretation of $B$ was first given by Gorenstein and Yang in Ref.[31]. In quasiparticle model, $B$ is the system energy in the absence of quasi-particle excitations, which cannot be discarded from the energy spectrum [32]. In this sense, $B$ plays as bag energy or bag pressure through application in bag-like model. One can interpret the confinement mechanism considering $B$ as the difference of perturbative vacuum and physical vacuum [33]. The bag constant is taken as a critical parameter in the determination of whether the ground state of baryon matter in QCD is the ordinary nucleus or a quark matter state [35] In literature, many work have been devoted to the description of the bag constant.

The number density will not feel the influence of the bag constant, because of the followings [23],

$\displaystyle n_{i}=\frac{\partial P}{\partial\mu}+\frac{\partial P}{\partial m^{*}_{i}}\frac{\partial m^{*}_{i}}{\partial\mu_{i}}=\frac{\partial P}{\partial\mu},$

(5)

where the second partial derivative vanishes due to the condition (3). The essential thermodynamic relation will not change with the inclusion of the quark mass scale and the density-dependent bag constant. We can give the number density by the sum of landau levels,

$\displaystyle n_{i}=\frac{d_{i}|q_{i}B_{m}|}{2\pi^{2}}\sum_{\nu=0}^{\nu_{i}^{\mathrm{max}}}(2-\delta_{\nu 0})\sqrt{\mu_{i}^{2}-{m_{i}^{*}}^{2}-2\nu|q_{i}B_{m}|}.$

(6)

It is well known to us that the asymptotic freedom is an essential feature of QCD. In literature, it can be included in effective chiral quark models by the running coupling constant. The approximate expression for the running quantity $g(\mu)$ was proposed as a decreasing function of chemical potential in Ref. [33]. Based on the fact of the magnetic catalysis of chiral symmetry breaking that incorporates the effects of the field in the running coupling, we take the following expression,

$\displaystyle g^{2}(\mu,B_{m})=\frac{48\pi^{2}}{(33-2N_{f})\ln(0.8\frac{\mu^{2}}{\Lambda_{1}^{2}})[1+\alpha\ln(1+\beta\frac{eB_{m}}{\Lambda_{2}^{2}})]}$

(7)

where the scale-fixing parameters are $\Lambda_{1}=120$ MeV, and $\Lambda_{2}=200$ MeV in our work. The free parameters are adopted as $\alpha=2$ and $\beta=0.000327$ [34]. Accordingly, the derivative of the mass with respect to the chemical potential $dm^{*}_{i}/d\mu_{i}$ in Eq. (4) is modified as,

$\displaystyle\frac{dm^{*}_{i}}{d\mu_{i}}=\frac{\partial m^{*}_{i}}{\partial\mu_{i}}+\frac{\partial m^{*}_{i}}{\partial g}\frac{dg}{d\mu_{i}}.$

(8)

The running coupling constant changes the slope of the mass $m^{*}$ with respect to the quark chemical potential.

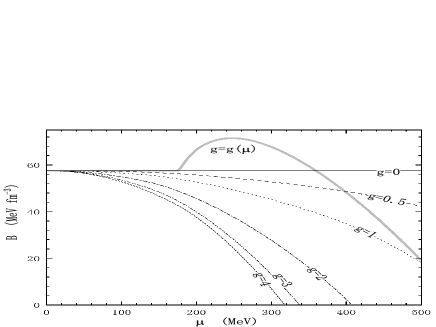
It is known to us that the low limit of the bag constant is required for the assumption of the stable quark matter. A lower value $B^{1/4}=76.8$ MeV is estimated from GMOR [35]. On the other hand, the equation of state with a larger value $B^{1/4}=174.2$ MeV is possible to mimic the mass-radius behavior of nucleonic stars [36]. To form stars with a larger mass, it was proposed to set the bag constant to a low value. The most probable range of values $B^{1/4}\cong 150\sim 200$MeV is proposed to be consistent with the estimate from hadron spectroscopy [37]. In Figure 1, the density dependent bag constant is shown as a decreasing function the chemical potential at the fixed coupling constant. At larger coupling constant, the bag constant would more rapidly drop down with a larger slope. At $g=0$, the medium effect is vanished and we get the conventional bag model with a fixed bag constant $B_{0}^{1/4}=145$ MeV. As the coupling constant increases in the figure, the bag constant seems to have lower value. Under the running coupling $g(\mu)$, the effective bag constant is evaluated by submitting Eq.(8) into Eq. (4). At lower chemical potential, the vacuum bag constant is hold due to the larger mass resulted by the larger value $g(\mu)$. A sudden increase occurs only for the chemical potential larger than the quark mass. The non-monotonous behavior is produced by the parameterization of the running coupling. In the region of high chemical potential, the bag constant for different couplings will have common trend. A natural question to ask is: how strong coupling constant is permitted for the stable state? We will give the answer by the following analysis.

In Fig. 2, the bag constant is shown as a non-monotonic function of the coupling constant at fixed chemical potential. The bag constant would return to the vacuum constant $B_{0}$ at larger coupling for a given chemical potential. At the coupling constant larger than $\sqrt{6}\pi$, the particle with larger mass would have zero number density $n=0$ in vacuum state, which is consistent with the density-density parameterization of bag constant $B(n)=B_{\infty}+(B_{0}-B_{\infty})\exp(-\gamma(n/n_{0})^{2})$ in the work of Burgio [38]. In the context of compact stars we are not interested, the chemical potential is large and the temperature practically zero. At larger chemical potential $\mu=500$ MeV, the medium effect becomes so evident that the bag constant is suppressed at an intermediate coupling constant.

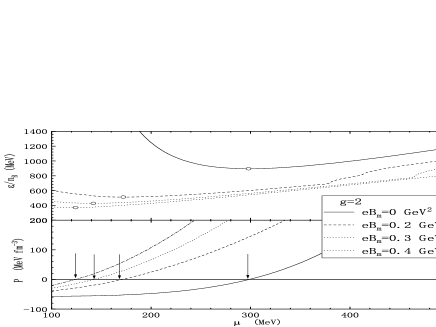
The free energy density is defined as $\epsilon=\Omega+B+\mu\sum_{i}n_{i}$, which will include the bag constant as in the pressure. The free energy per baryon has a minimum value $3\mu$ at the zero pressure. In Fig. 3, the free energy per baryon and the pressure function are shown with and without the strong magnetic field at the coupling constant $g=2$. For stable quark matter, the matter pressure must balance the bag pressure $-B$ at the quark chemical potential smaller than the critical value $\mu_{c}=\mu_{B}/3=310$ MeV. It is shown that the minimum free energy per baryon marked by the empty circle occurs exactly at the zero pressure indicated by the arrows. Furthermore, the zero pressure position moves far smaller than the $\mu_{c}$ with the increase in the magnetic field. It can be concluded that the stability of the SQM is absolutely enhanced by the strong magnetic field.

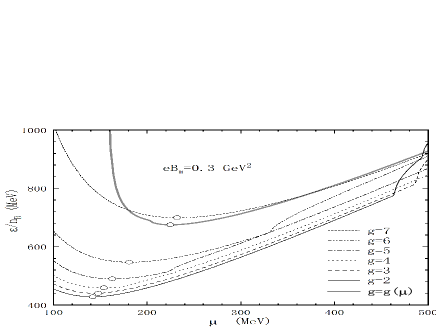
In Fig. 4, the free energy per baryon is shown at the fixed magnetic field $eB_{m}=0.3$ GeV². The minimum free energy per baryon is marked by the empty circle, which is zero pressure point. As the coupling constant increases, the $\epsilon/n_{B}$ is becoming large, and therefore the stability would be reduced. By comparison with the magnetic field in Fig. 3, the coupling interaction has an opposite effect on the stability of SQM. It should be mentioned that the vacuum bag is adopted as $B_{0}^{1/4}=145$ MeV. As long as the chemical potential position $``\circ"$ is located on the left of $\mu_{c}=310$ MeV, the SQM is absolutely stable with respect to ordinary nuclear matter. The $\epsilon/n_{B}$ for the running coupling $g(\mu)$ marked by the grey line is higher than other cases of $g<6$ due to its larger value of the bag constant. Moreover, the slope of $\epsilon/n_{B}$ on the left branch of $\mu<\mu_{\circ}$ is more steep for the running coupling $g(\mu)$ becomes much larger than the fixed coupling constant.

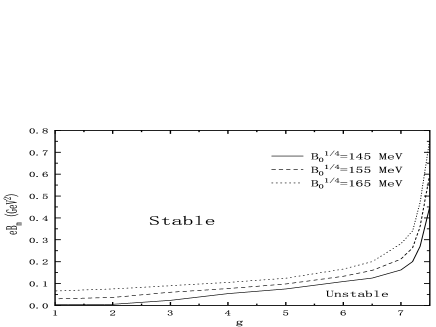
Since the coupling constant and the magnetic field have opposite effect on the stability of SQM, the minimum magnetic field would be changed by the increase in the coupling constant. The stability of the SQM can be described by the free energy per baryon smaller than the iron nuclei $930$ MeV. In Fig. 5, the stability window is shown in the $eB_{m}$-$g$ plane for different vacuum bag constants $B_{0}$. The line $\epsilon/n_{B}=930$ MeV marks the estimated lower limit of the range of the strong magnetic field. The stable region would shrink as the vacuum bag constant $B_{0}$ increases, and the boundary of the region would move to the stronger magnetic field and smaller coupling constant. In other words, the weak coupling constant is favored at a fixed magnetic field. For much larger vacuum bag constant $B_{0}$, the stronger magnetic field is required for the existence of the stable SQM.

In this paper the quasiparticle model has been employed to investigate the stability of SQM in a strong magnetic field. We have derived the effective bag constant self-consistently instead of the ansatz to describe the density dependent bag for the confinement scheme. The effective bag constant has been shown as a decreasing function of the chemical potential. However, as the increase in the coupling constant, the bag constant displays a non-monotonous behavior, which approaches the vacuum bag constant $B_{0}$ at both the zero coupling and the much larger coupling constant. The stability of SQM has been reflected by the free energy per baryon. The thermodynamically self-consistence is fulfilled that minimum free energy per baryon occurs at the zero pressure. Finally, we have found that the increase in magnetic field would enhance the stability of quark matter, even though the larger coupling constant and the vacuum bag would reduce its stability. The lower limit of the magnetic field would rise as the coupling constant becomes larger. A realistic calculation of the magnetic field profile inside strongly magnetized neutron stars is reported in Ref. [40]. They suggested that the magnetic fields increase relativistic slowly with increasing baryon chemical potential of magnetized matter. So there is a strong possibility that the SQM exists in the core of neutron stars. We hope our work could provide a simple method to the constraint on the magnetic field strength in the SQM, which could be the consistent of the massive compact object [41].

Acknowledgements

The authors would like to thank the National Natural Science Foundation of China for support through Grants No.11875181 and No.12047571. This work was also sponsored by the Fund for Shanxi “1331 Project” Key Subjects Construction.