^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: also at National Research Nuclear University “MEPhI” and Moscow Institute of Physics and Technology, Moscow, Russia^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at the Graduate University of Science and Technology, Vietnam Academy of Science and Technology^†^†thanks: deceased^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at JINR, Dubna, Russia^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: also at Nambu Yoichiro Institute of Theoretical and Experimental Physics (NITEP)^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: also at J-PARC, Tokai, Japan^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan^†^†thanks: deceased^†^†thanks: also at Nambu Yoichiro Institute of Theoretical and Experimental Physics (NITEP)^†^†thanks: also at BMCC/CUNY, Science Department, New York, New York, U.S.A.^†^†thanks: affiliated member at Kavli IPMU (WPI), the University of Tokyo, Japan

The T2K Collaboration

Constraint on the Matter-Antimatter Symmetry-Violating Phase in Neutrino Oscillations

K. Abe University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan R. Akutsu University of Tokyo, Institute for Cosmic Ray Research, Research Center for Cosmic Neutrinos, Kashiwa, Japan A. Ali Kyoto University, Department of Physics, Kyoto, Japan C. Alt ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland C. Andreopoulos STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom University of Liverpool, Department of Physics, Liverpool, United Kingdom L. Anthony University of Liverpool, Department of Physics, Liverpool, United Kingdom M. Antonova IFIC (CSIC & University of Valencia), Valencia, Spain S. Aoki Kobe University, Kobe, Japan A. Ariga University of Bern, Albert Einstein Center for Fundamental Physics, Laboratory for High Energy Physics (LHEP), Bern, Switzerland Y. Asada Yokohama National University, Faculty of Engineering, Yokohama, Japan Y. Ashida Kyoto University, Department of Physics, Kyoto, Japan E.T. Atkin Imperial College London, Department of Physics, London, United Kingdom Y. Awataguchi Tokyo Metropolitan University, Department of Physics, Tokyo, Japan S. Ban Kyoto University, Department of Physics, Kyoto, Japan M. Barbi University of Regina, Department of Physics, Regina, Saskatchewan, Canada G.J. Barker University of Warwick, Department of Physics, Coventry, United Kingdom G. Barr Oxford University, Department of Physics, Oxford, United Kingdom C. Barry University of Liverpool, Department of Physics, Liverpool, United Kingdom M. Batkiewicz-Kwasniak H. Niewodniczanski Institute of Nuclear Physics PAN, Cracow, Poland A. Beloshapkin Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia F. Bench University of Liverpool, Department of Physics, Liverpool, United Kingdom V. Berardi INFN Sezione di Bari and Università e Politecnico di Bari, Dipartimento Interuniversitario di Fisica, Bari, Italy S. Berkman University of British Columbia, Department of Physics and Astronomy, Vancouver, British Columbia, Canada TRIUMF, Vancouver, British Columbia, Canada L. Berns Tokyo Institute of Technology, Department of Physics, Tokyo, Japan S. Bhadra York University, Department of Physics and Astronomy, Toronto, Ontario, Canada S. Bienstock Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France A. Blondel Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France University of Geneva, Section de Physique, DPNC, Geneva, Switzerland S. Bolognesi IRFU, CEA Saclay, Gif-sur-Yvette, France B. Bourguille Institut de Fisica d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Campus UAB, Bellaterra (Barcelona) Spain S.B. Boyd University of Warwick, Department of Physics, Coventry, United Kingdom D. Brailsford Lancaster University, Physics Department, Lancaster, United Kingdom A. Bravar University of Geneva, Section de Physique, DPNC, Geneva, Switzerland D. Bravo Berguño University Autonoma Madrid, Department of Theoretical Physics, 28049 Madrid, Spain C. Bronner University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan A. Bubak University of Silesia, Institute of Physics, Katowice, Poland M. Buizza Avanzini Ecole Polytechnique, IN2P3-CNRS, Laboratoire Leprince-Ringuet, Palaiseau, France J. Calcutt Michigan State University, Department of Physics and Astronomy, East Lansing, Michigan, U.S.A. T. Campbell University of Colorado at Boulder, Department of Physics, Boulder, Colorado, U.S.A. S. Cao High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan S.L. Cartwright University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom M.G. Catanesi INFN Sezione di Bari and Università e Politecnico di Bari, Dipartimento Interuniversitario di Fisica, Bari, Italy A. Cervera IFIC (CSIC & University of Valencia), Valencia, Spain A. Chappell University of Warwick, Department of Physics, Coventry, United Kingdom C. Checchia INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy D. Cherdack University of Houston, Department of Physics, Houston, Texas, U.S.A. N. Chikuma University of Tokyo, Department of Physics, Tokyo, Japan G. Christodoulou CERN European Organization for Nuclear Research, CH-1211 Genève 23, Switzerland J. Coleman University of Liverpool, Department of Physics, Liverpool, United Kingdom G. Collazuol INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy L. Cook Oxford University, Department of Physics, Oxford, United Kingdom Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan D. Coplowe Oxford University, Department of Physics, Oxford, United Kingdom A. Cudd Michigan State University, Department of Physics and Astronomy, East Lansing, Michigan, U.S.A. A. Dabrowska H. Niewodniczanski Institute of Nuclear Physics PAN, Cracow, Poland G. De Rosa INFN Sezione di Napoli and Università di Napoli, Dipartimento di Fisica, Napoli, Italy T. Dealtry Lancaster University, Physics Department, Lancaster, United Kingdom P.F. Denner University of Warwick, Department of Physics, Coventry, United Kingdom S.R. Dennis University of Liverpool, Department of Physics, Liverpool, United Kingdom C. Densham STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom F. Di Lodovico King’s College London, Department of Physics, Strand, London WC2R 2LS, United Kingdom N. Dokania State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. S. Dolan CERN European Organization for Nuclear Research, CH-1211 Genève 23, Switzerland T.A. Doyle Lancaster University, Physics Department, Lancaster, United Kingdom O. Drapier Ecole Polytechnique, IN2P3-CNRS, Laboratoire Leprince-Ringuet, Palaiseau, France J. Dumarchez Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France P. Dunne Imperial College London, Department of Physics, London, United Kingdom L. Eklund University of Glasgow, School of Physics and Astronomy, Glasgow, United Kingdom S. Emery-Schrenk IRFU, CEA Saclay, Gif-sur-Yvette, France A. Ereditato University of Bern, Albert Einstein Center for Fundamental Physics, Laboratory for High Energy Physics (LHEP), Bern, Switzerland P. Fernandez IFIC (CSIC & University of Valencia), Valencia, Spain T. Feusels University of British Columbia, Department of Physics and Astronomy, Vancouver, British Columbia, Canada TRIUMF, Vancouver, British Columbia, Canada A.J. Finch Lancaster University, Physics Department, Lancaster, United Kingdom G.A. Fiorentini York University, Department of Physics and Astronomy, Toronto, Ontario, Canada G. Fiorillo INFN Sezione di Napoli and Università di Napoli, Dipartimento di Fisica, Napoli, Italy C. Francois University of Bern, Albert Einstein Center for Fundamental Physics, Laboratory for High Energy Physics (LHEP), Bern, Switzerland M. Friend High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan Y. Fujii High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan R. Fujita University of Tokyo, Department of Physics, Tokyo, Japan D. Fukuda Okayama University, Department of Physics, Okayama, Japan R. Fukuda Tokyo University of Science, Faculty of Science and Technology, Department of Physics, Noda, Chiba, Japan Y. Fukuda Miyagi University of Education, Department of Physics, Sendai, Japan K. Fusshoeller ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland K. Gameil University of British Columbia, Department of Physics and Astronomy, Vancouver, British Columbia, Canada TRIUMF, Vancouver, British Columbia, Canada C. Giganti Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France T. Golan Wroclaw University, Faculty of Physics and Astronomy, Wroclaw, Poland M. Gonin Ecole Polytechnique, IN2P3-CNRS, Laboratoire Leprince-Ringuet, Palaiseau, France A. Gorin Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia M. Guigue Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France D.R. Hadley University of Warwick, Department of Physics, Coventry, United Kingdom J.T. Haigh University of Warwick, Department of Physics, Coventry, United Kingdom P. Hamacher-Baumann RWTH Aachen University, III. Physikalisches Institut, Aachen, Germany M. Hartz TRIUMF, Vancouver, British Columbia, Canada Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan T. Hasegawa High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan S. Hassani IRFU, CEA Saclay, Gif-sur-Yvette, France N.C. Hastings High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan T. Hayashino Kyoto University, Department of Physics, Kyoto, Japan Y. Hayato University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan A. Hiramoto Kyoto University, Department of Physics, Kyoto, Japan M. Hogan Colorado State University, Department of Physics, Fort Collins, Colorado, U.S.A. J. Holeczek University of Silesia, Institute of Physics, Katowice, Poland N.T. Hong Van Institute For Interdisciplinary Research in Science and Education (IFIRSE), ICISE, Quy Nhon, Vietnam International Centre of Physics, Institute of Physics (IOP), Vietnam Academy of Science and Technology (VAST), 10 Dao Tan, Ba Dinh, Hanoi, Vietnam F. Iacob INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy A.K. Ichikawa Kyoto University, Department of Physics, Kyoto, Japan M. Ikeda University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan T. Ishida High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan T. Ishii High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan M. Ishitsuka Tokyo University of Science, Faculty of Science and Technology, Department of Physics, Noda, Chiba, Japan K. Iwamoto University of Tokyo, Department of Physics, Tokyo, Japan A. Izmaylov IFIC (CSIC & University of Valencia), Valencia, Spain Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia M. Jakkapu High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan B. Jamieson University of Winnipeg, Department of Physics, Winnipeg, Manitoba, Canada S.J. Jenkins University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom C. Jesús-Valls Institut de Fisica d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Campus UAB, Bellaterra (Barcelona) Spain M. Jiang Kyoto University, Department of Physics, Kyoto, Japan S. Johnson University of Colorado at Boulder, Department of Physics, Boulder, Colorado, U.S.A. P. Jonsson Imperial College London, Department of Physics, London, United Kingdom C.K. Jung State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. M. Kabirnezhad Oxford University, Department of Physics, Oxford, United Kingdom A.C. Kaboth Royal Holloway University of London, Department of Physics, Egham, Surrey, United Kingdom STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom T. Kajita University of Tokyo, Institute for Cosmic Ray Research, Research Center for Cosmic Neutrinos, Kashiwa, Japan H. Kakuno Tokyo Metropolitan University, Department of Physics, Tokyo, Japan J. Kameda University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan D. Karlen University of Victoria, Department of Physics and Astronomy, Victoria, British Columbia, Canada TRIUMF, Vancouver, British Columbia, Canada K. Kasetti Louisiana State University, Department of Physics and Astronomy, Baton Rouge, Louisiana, U.S.A. Y. Kataoka University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan T. Katori King’s College London, Department of Physics, Strand, London WC2R 2LS, United Kingdom Y. Kato University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan E. Kearns Boston University, Department of Physics, Boston, Massachusetts, U.S.A. Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan M. Khabibullin Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia A. Khotjantsev Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia T. Kikawa Kyoto University, Department of Physics, Kyoto, Japan H. Kim Osaka City University, Department of Physics, Osaka, Japan J. Kim University of British Columbia, Department of Physics and Astronomy, Vancouver, British Columbia, Canada TRIUMF, Vancouver, British Columbia, Canada S. King King’s College London, Department of Physics, Strand, London WC2R 2LS, United Kingdom J. Kisiel University of Silesia, Institute of Physics, Katowice, Poland A. Knight University of Warwick, Department of Physics, Coventry, United Kingdom A. Knox Lancaster University, Physics Department, Lancaster, United Kingdom T. Kobayashi High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan L. Koch Oxford University, Department of Physics, Oxford, United Kingdom T. Koga University of Tokyo, Department of Physics, Tokyo, Japan A. Konaka TRIUMF, Vancouver, British Columbia, Canada L.L. Kormos Lancaster University, Physics Department, Lancaster, United Kingdom Y. Koshio Okayama University, Department of Physics, Okayama, Japan A. Kostin Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia K. Kowalik National Centre for Nuclear Research, Warsaw, Poland H. Kubo Kyoto University, Department of Physics, Kyoto, Japan Y. Kudenko Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia N. Kukita Osaka City University, Department of Physics, Osaka, Japan S. Kuribayashi Kyoto University, Department of Physics, Kyoto, Japan R. Kurjata Warsaw University of Technology, Institute of Radioelectronics and Multimedia Technology, Warsaw, Poland T. Kutter Louisiana State University, Department of Physics and Astronomy, Baton Rouge, Louisiana, U.S.A. M. Kuze Tokyo Institute of Technology, Department of Physics, Tokyo, Japan L. Labarga University Autonoma Madrid, Department of Theoretical Physics, 28049 Madrid, Spain J. Lagoda National Centre for Nuclear Research, Warsaw, Poland M. Lamoureux INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy M. Laveder INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy M. Lawe Lancaster University, Physics Department, Lancaster, United Kingdom M. Licciardi Ecole Polytechnique, IN2P3-CNRS, Laboratoire Leprince-Ringuet, Palaiseau, France T. Lindner TRIUMF, Vancouver, British Columbia, Canada R.P. Litchfield University of Glasgow, School of Physics and Astronomy, Glasgow, United Kingdom S.L. Liu State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. X. Li State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. A. Longhin INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy L. Ludovici INFN Sezione di Roma and Università di Roma “La Sapienza”, Roma, Italy X. Lu Oxford University, Department of Physics, Oxford, United Kingdom T. Lux Institut de Fisica d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Campus UAB, Bellaterra (Barcelona) Spain L.N. Machado INFN Sezione di Napoli and Università di Napoli, Dipartimento di Fisica, Napoli, Italy L. Magaletti INFN Sezione di Bari and Università e Politecnico di Bari, Dipartimento Interuniversitario di Fisica, Bari, Italy K. Mahn Michigan State University, Department of Physics and Astronomy, East Lansing, Michigan, U.S.A. M. Malek University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom S. Manly University of Rochester, Department of Physics and Astronomy, Rochester, New York, U.S.A. L. Maret University of Geneva, Section de Physique, DPNC, Geneva, Switzerland A.D. Marino University of Colorado at Boulder, Department of Physics, Boulder, Colorado, U.S.A. L. Marti-Magro University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan J.F. Martin University of Toronto, Department of Physics, Toronto, Ontario, Canada T. Maruyama High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan T. Matsubara High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan K. Matsushita University of Tokyo, Department of Physics, Tokyo, Japan V. Matveev Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia K. Mavrokoridis University of Liverpool, Department of Physics, Liverpool, United Kingdom E. Mazzucato IRFU, CEA Saclay, Gif-sur-Yvette, France M. McCarthy York University, Department of Physics and Astronomy, Toronto, Ontario, Canada N. McCauley University of Liverpool, Department of Physics, Liverpool, United Kingdom J. McElwee University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom K.S. McFarland University of Rochester, Department of Physics and Astronomy, Rochester, New York, U.S.A. C. McGrew State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. A. Mefodiev Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia C. Metelko University of Liverpool, Department of Physics, Liverpool, United Kingdom M. Mezzetto INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy A. Minamino Yokohama National University, Faculty of Engineering, Yokohama, Japan O. Mineev Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia S. Mine University of California, Irvine, Department of Physics and Astronomy, Irvine, California, U.S.A. M. Miura University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan L. Molina Bueno ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland S. Moriyama University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan J. Morrison Michigan State University, Department of Physics and Astronomy, East Lansing, Michigan, U.S.A. Th.A. Mueller Ecole Polytechnique, IN2P3-CNRS, Laboratoire Leprince-Ringuet, Palaiseau, France L. Munteanu IRFU, CEA Saclay, Gif-sur-Yvette, France S. Murphy ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland Y. Nagai University of Colorado at Boulder, Department of Physics, Boulder, Colorado, U.S.A. T. Nakadaira High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan M. Nakahata University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan Y. Nakajima University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan A. Nakamura Okayama University, Department of Physics, Okayama, Japan K.G. Nakamura Kyoto University, Department of Physics, Kyoto, Japan K. Nakamura Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan S. Nakayama University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan T. Nakaya Kyoto University, Department of Physics, Kyoto, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan K. Nakayoshi High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan C. Nantais University of Toronto, Department of Physics, Toronto, Ontario, Canada T.V. Ngoc Institute For Interdisciplinary Research in Science and Education (IFIRSE), ICISE, Quy Nhon, Vietnam K. Niewczas Wroclaw University, Faculty of Physics and Astronomy, Wroclaw, Poland K. Nishikawa High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan Y. Nishimura Keio University, Department of Physics, Kanagawa, Japan E. Noah University of Geneva, Section de Physique, DPNC, Geneva, Switzerland T.S. Nonnenmacher Imperial College London, Department of Physics, London, United Kingdom F. Nova STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom P. Novella IFIC (CSIC & University of Valencia), Valencia, Spain J. Nowak Lancaster University, Physics Department, Lancaster, United Kingdom J.C. Nugent University of Glasgow, School of Physics and Astronomy, Glasgow, United Kingdom H.M. O’Keeffe Lancaster University, Physics Department, Lancaster, United Kingdom L. O’Sullivan University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom T. Odagawa Kyoto University, Department of Physics, Kyoto, Japan K. Okumura University of Tokyo, Institute for Cosmic Ray Research, Research Center for Cosmic Neutrinos, Kashiwa, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan T. Okusawa Osaka City University, Department of Physics, Osaka, Japan S.M. Oser University of British Columbia, Department of Physics and Astronomy, Vancouver, British Columbia, Canada TRIUMF, Vancouver, British Columbia, Canada R.A. Owen Queen Mary University of London, School of Physics and Astronomy, London, United Kingdom Y. Oyama High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan V. Palladino INFN Sezione di Napoli and Università di Napoli, Dipartimento di Fisica, Napoli, Italy J.L. Palomino State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. V. Paolone University of Pittsburgh, Department of Physics and Astronomy, Pittsburgh, Pennsylvania, U.S.A. M. Pari INFN Sezione di Padova and Università di Padova, Dipartimento di Fisica, Padova, Italy W.C. Parker Royal Holloway University of London, Department of Physics, Egham, Surrey, United Kingdom J. Pasternak Imperial College London, Department of Physics, London, United Kingdom P. Paudyal University of Liverpool, Department of Physics, Liverpool, United Kingdom M. Pavin TRIUMF, Vancouver, British Columbia, Canada D. Payne University of Liverpool, Department of Physics, Liverpool, United Kingdom G.C. Penn University of Liverpool, Department of Physics, Liverpool, United Kingdom L. Pickering Michigan State University, Department of Physics and Astronomy, East Lansing, Michigan, U.S.A. C. Pidcott University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom G. Pintaudi Yokohama National University, Faculty of Engineering, Yokohama, Japan E.S. Pinzon Guerra York University, Department of Physics and Astronomy, Toronto, Ontario, Canada C. Pistillo University of Bern, Albert Einstein Center for Fundamental Physics, Laboratory for High Energy Physics (LHEP), Bern, Switzerland B. Popov Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France K. Porwit University of Silesia, Institute of Physics, Katowice, Poland M. Posiadala-Zezula University of Warsaw, Faculty of Physics, Warsaw, Poland A. Pritchard University of Liverpool, Department of Physics, Liverpool, United Kingdom B. Quilain Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan T. Radermacher RWTH Aachen University, III. Physikalisches Institut, Aachen, Germany E. Radicioni INFN Sezione di Bari and Università e Politecnico di Bari, Dipartimento Interuniversitario di Fisica, Bari, Italy B. Radics ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland P.N. Ratoff Lancaster University, Physics Department, Lancaster, United Kingdom E. Reinherz-Aronis Colorado State University, Department of Physics, Fort Collins, Colorado, U.S.A. C. Riccio INFN Sezione di Napoli and Università di Napoli, Dipartimento di Fisica, Napoli, Italy E. Rondio National Centre for Nuclear Research, Warsaw, Poland S. Roth RWTH Aachen University, III. Physikalisches Institut, Aachen, Germany A. Rubbia ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland A.C. Ruggeri INFN Sezione di Napoli and Università di Napoli, Dipartimento di Fisica, Napoli, Italy C.A. Ruggles University of Glasgow, School of Physics and Astronomy, Glasgow, United Kingdom A. Rychter Warsaw University of Technology, Institute of Radioelectronics and Multimedia Technology, Warsaw, Poland K. Sakashita High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan F. Sánchez University of Geneva, Section de Physique, DPNC, Geneva, Switzerland C.M. Schloesser ETH Zurich, Institute for Particle Physics and Astrophysics, Zurich, Switzerland K. Scholberg Duke University, Department of Physics, Durham, North Carolina, U.S.A. J. Schwehr Colorado State University, Department of Physics, Fort Collins, Colorado, U.S.A. M. Scott Imperial College London, Department of Physics, London, United Kingdom Y. Seiya Osaka City University, Department of Physics, Osaka, Japan T. Sekiguchi High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan H. Sekiya University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan D. Sgalaberna CERN European Organization for Nuclear Research, CH-1211 Genève 23, Switzerland R. Shah STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom Oxford University, Department of Physics, Oxford, United Kingdom A. Shaikhiev Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia F. Shaker University of Winnipeg, Department of Physics, Winnipeg, Manitoba, Canada A. Shaykina Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia M. Shiozawa University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan W. Shorrock Imperial College London, Department of Physics, London, United Kingdom A. Shvartsman Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia A. Smirnov Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia M. Smy University of California, Irvine, Department of Physics and Astronomy, Irvine, California, U.S.A. J.T. Sobczyk Wroclaw University, Faculty of Physics and Astronomy, Wroclaw, Poland H. Sobel University of California, Irvine, Department of Physics and Astronomy, Irvine, California, U.S.A. Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan F.J.P. Soler University of Glasgow, School of Physics and Astronomy, Glasgow, United Kingdom Y. Sonoda University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan J. Steinmann RWTH Aachen University, III. Physikalisches Institut, Aachen, Germany S. Suvorov Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia IRFU, CEA Saclay, Gif-sur-Yvette, France A. Suzuki Kobe University, Kobe, Japan S.Y. Suzuki High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan Y. Suzuki Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan A.A. Sztuc Imperial College London, Department of Physics, London, United Kingdom M. Tada High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan M. Tajima Kyoto University, Department of Physics, Kyoto, Japan A. Takeda University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan Y. Takeuchi Kobe University, Kobe, Japan Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan H.K. Tanaka University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan H.A. Tanaka SLAC National Accelerator Laboratory, Stanford University, Menlo Park, California, USA University of Toronto, Department of Physics, Toronto, Ontario, Canada S. Tanaka Osaka City University, Department of Physics, Osaka, Japan L.F. Thompson University of Sheffield, Department of Physics and Astronomy, Sheffield, United Kingdom W. Toki Colorado State University, Department of Physics, Fort Collins, Colorado, U.S.A. C. Touramanis University of Liverpool, Department of Physics, Liverpool, United Kingdom T. Towstego University of Toronto, Department of Physics, Toronto, Ontario, Canada K.M. Tsui University of Liverpool, Department of Physics, Liverpool, United Kingdom T. Tsukamoto High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan M. Tzanov Louisiana State University, Department of Physics and Astronomy, Baton Rouge, Louisiana, U.S.A. Y. Uchida Imperial College London, Department of Physics, London, United Kingdom W. Uno Kyoto University, Department of Physics, Kyoto, Japan M. Vagins Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan University of California, Irvine, Department of Physics and Astronomy, Irvine, California, U.S.A. S. Valder University of Warwick, Department of Physics, Coventry, United Kingdom Z. Vallari State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. D. Vargas Institut de Fisica d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Campus UAB, Bellaterra (Barcelona) Spain G. Vasseur IRFU, CEA Saclay, Gif-sur-Yvette, France C. Vilela State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. W.G.S. Vinning University of Warwick, Department of Physics, Coventry, United Kingdom T. Vladisavljevic Oxford University, Department of Physics, Oxford, United Kingdom Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo Institutes for Advanced Study, University of Tokyo, Kashiwa, Chiba, Japan V.V. Volkov Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia T. Wachala H. Niewodniczanski Institute of Nuclear Physics PAN, Cracow, Poland J. Walker University of Winnipeg, Department of Physics, Winnipeg, Manitoba, Canada J.G. Walsh Lancaster University, Physics Department, Lancaster, United Kingdom Y. Wang State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. D. Wark STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom Oxford University, Department of Physics, Oxford, United Kingdom M.O. Wascko Imperial College London, Department of Physics, London, United Kingdom A. Weber STFC, Rutherford Appleton Laboratory, Harwell Oxford, and Daresbury Laboratory, Warrington, United Kingdom Oxford University, Department of Physics, Oxford, United Kingdom R. Wendell Kyoto University, Department of Physics, Kyoto, Japan M.J. Wilking State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. C. Wilkinson University of Bern, Albert Einstein Center for Fundamental Physics, Laboratory for High Energy Physics (LHEP), Bern, Switzerland J.R. Wilson King’s College London, Department of Physics, Strand, London WC2R 2LS, United Kingdom R.J. Wilson Colorado State University, Department of Physics, Fort Collins, Colorado, U.S.A. K. Wood State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. C. Wret University of Rochester, Department of Physics and Astronomy, Rochester, New York, U.S.A. Y. Yamada High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki, Japan K. Yamamoto Osaka City University, Department of Physics, Osaka, Japan C. Yanagisawa State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. G. Yang State University of New York at Stony Brook, Department of Physics and Astronomy, Stony Brook, New York, U.S.A. T. Yano University of Tokyo, Institute for Cosmic Ray Research, Kamioka Observatory, Kamioka, Japan K. Yasutome Kyoto University, Department of Physics, Kyoto, Japan S. Yen TRIUMF, Vancouver, British Columbia, Canada N. Yershov Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia M. Yokoyama University of Tokyo, Department of Physics, Tokyo, Japan T. Yoshida Tokyo Institute of Technology, Department of Physics, Tokyo, Japan M. Yu York University, Department of Physics and Astronomy, Toronto, Ontario, Canada A. Zalewska H. Niewodniczanski Institute of Nuclear Physics PAN, Cracow, Poland J. Zalipska National Centre for Nuclear Research, Warsaw, Poland K. Zaremba Warsaw University of Technology, Institute of Radioelectronics and Multimedia Technology, Warsaw, Poland G. Zarnecki National Centre for Nuclear Research, Warsaw, Poland M. Ziembicki Warsaw University of Technology, Institute of Radioelectronics and Multimedia Technology, Warsaw, Poland E.D. Zimmerman University of Colorado at Boulder, Department of Physics, Boulder, Colorado, U.S.A. M. Zito Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), Paris, France S. Zsoldos King’s College London, Department of Physics, Strand, London WC2R 2LS, United Kingdom A. Zykova Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia

(July 30, 2025)

I Introduction

The symmetry between matter and antimatter, charge-conjugation parity-reversal ( $CP$ ) symmetry, was believed to be a perfect symmetry of nature. In 1964, asymmetric behavior of particles and anti-particles, $CP$ violation, was observed Christenson:1964fg , and $CP$ violation in the weak interactions of quarks was soon established Tanabashi:2018oca . Sakharov proposed Sakharov:1967dj that $CP$ violation is one of the necessary conditions for an explanation of the observed imbalance of matter and antimatter abundance in the universe. However, the $CP$ violation in quarks is too small to provide this explanation. To date, we have not found $CP$ violation in any non-quark elementary particle systems. It has been shown that $CP$ violation in the lepton sector could generate the matter-antimatter disparity through the process called leptogenesis Fukugita:1986hr . Leptonic mixing, which appears in the Standard Model charged current interactions Fukuda:1998mi ; Ahmad:2002jz , provides a potential source of $CP$ violation through a complex phase $\delta_{CP}$ , which may have consequences for theoretical models of leptogenesis Pascoli:2006ie ; Hagedorn:2017wjy ; RevModPhys.84.515 . This $CP$ violation can be measured in muon neutrino to electron neutrino oscillations and the corresponding antineutrino oscillations, which are experimentally accessible with accelerator-produced beams as established by the Tokai-to-Kamioka (T2K) and NOvA experiments Abe:2013hdq ; Acero:2019ksn . Until now, the value of $\delta_{CP}$ has not been significantly constrained by neutrino oscillation experiments. Here the T2K collaboration reports a measurement that favors large enhancement of the neutrino oscillation probability, excluding values of $\delta_{CP}$ which result in a large enhancement of the observed antineutrino oscillation probability at three standard deviations ( $3\sigma$ ). The $3\sigma$ confidence level interval for $\delta_{CP}$ , which is cyclic and repeats every $2\pi$ , is [ $-3.41$ , $-0.03$ ] for the so-called normal mass ordering, and [ $-2.54$ , $-0.32$ ] for the inverted mass ordering. Our results show an indication of $CP$ violation in the lepton sector. Herein we establish methods for sensitive searches for a matter-antimatter asymmetry in neutrino oscillations using accelerator-produced neutrino beams. Future measurements with larger data samples will test whether leptonic $CP$ violation is larger than the $CP$ violation in the quark sector.

II Main

Previous observations of neutrino oscillations have established that the three known neutrino flavour states, $\nu_{e}$ , $\nu_{\mu}$ and $\nu_{\tau}$ are mixtures of three mass states, $\nu_{1}$ , $\nu_{2}$ and $\nu_{3}$ Abe:2018wpn ; Abe:2008aa ; Adey:2018zwh ; Aharmim:2011vm . This mixing is described by a unitary matrix called the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix Maki:1962mu ; Pontecorvo:1967fh , which can be parameterized by three mixing angles $\theta_{12}$ , $\theta_{13}$ and $\theta_{23}$ , and complex phases. Of these phases, neutrino oscillations are sensitive to $\delta_{CP}$ . The probabilities for the neutrinos to oscillate from one flavour state to another as they travel depend on these mixing parameters and the mass squared differences ( $\Delta m^{2}_{ij}=m^{2}_{i}-m^{2}_{j}$ ) between the neutrino mass states. The PMNS parameters and the mass squared differences are referred to as “oscillation parameters”. It is known that $\nu_{1}$ and $\nu_{2}$ lie close to each other in mass, with $\Delta m^{2}_{21}=(7.53\pm 0.18)\times 10^{-5}$ $\text{eV}^{2}/c^{4}$ , while $\lvert\Delta m^{2}_{32}\lvert$ is approximately 30 times larger. However, it is not known whether $m_{3}$ has a larger or smaller mass than $m_{1}$ and $m_{2}$ Tanabashi:2018oca . The case where the mass of $m_{3}$ is larger (smaller) is called the normal (inverted) ordering. The $CP$ symmetry violating effect in neutrino and antineutrino oscillations has a magnitude that depends on the Jarlskog invariant Krastev:1988yu ; Jarlskog:1985cw :

J_{CP,l}=\frac{1}{8}\cos\theta_{13}\sin(2\theta_{12})\sin(2\theta_{23})\sin(2\theta_{13})\sin(\delta_{CP})

(1)

. According to current measurements, this is approximately $0.033\sin(\delta_{CP})$ Tanabashi:2018oca . This value has the potential to be three orders of magnitude larger than the measured quark sector $CP$ violation ( $J_{CP,q}=3\times 10^{-5}$ ) Tanabashi:2018oca . Prior to this work, no experiment has excluded any values of $\delta_{CP}$ (taking into account both mass orderings) at the 99.73% ( $3\sigma$ ) confidence level, considered as evidence in the particle physics community.

T2K is a long-baseline neutrino experiment that uses beams of muon neutrinos and antineutrinos, with energy spectra peaked at 0.6 GeV. We observe interactions of the neutrinos at a near detector facility 280 m from the beam production point which characterizes the beam and the interactions of the neutrinos before oscillations. The beam then propagates 295 km through the Earth to the T2K far detector, Super-Kamiokande (SK). SK measures the oscillated beam, which gives sensitivity to the oscillation parameters.

For this beam energy and propagation distance, the probability for muon neutrinos(antineutrinos) to oscillate to electron neutrinos(antineutrinos) is given at leading order in $\delta_{CP}$ , including the $CP$ -violating term but neglecting effects from propagation through matter, by:

\begin{split}\text{P}\left(\nu_{\mu}\rightarrow\nu_{e}\right)\approx\sin^{2}(2\theta_{13})\sin^{2}(\theta_{23})\sin^{2}\left(\frac{1.27\Delta m^{2}_{32}L}{E}\right)\\ \mp\frac{1.27\Delta m^{2}_{21}L}{E}8J_{CP}\sin^{2}\left(\frac{1.27\Delta m^{2}_{32}L}{E}\right).\end{split}

(2)

Here, $E$ is the energy of the neutrino in GeV, the mass squared differences are given in $\text{eV}^{2}/c^{4}$ and $L$ is the propagation baseline in km. The second term in Eq. 2 has a negative sign for neutrinos and a positive sign for antineutrinos. The baseline and beam energy are optimised so that at our baseline, the probability to oscillate to electron neutrinos reaches a maximum at energies around the beam energy. While the probability of oscillation to electron neutrinos is small, muon neutrinos also oscillate to tau neutrinos, which are not identifiable at SK as T2K’s beam energy is too low for a charged tau lepton to be produced. Overall, the probability for muon neutrinos and antineutrinos to maintain their initial flavour is:

\begin{split}\text{P}(\nu_{\mu}&\rightarrow\nu_{\mu})\approx 1-4\cos^{2}(\theta_{13})\sin^{2}(\theta_{23})\\ &\times\left[1-\cos^{2}(\theta_{13})\sin^{2}(\theta_{23})\right]\sin^{2}\left(\frac{1.27\Delta m^{2}_{32}L}{E}\right).\end{split}

(3)

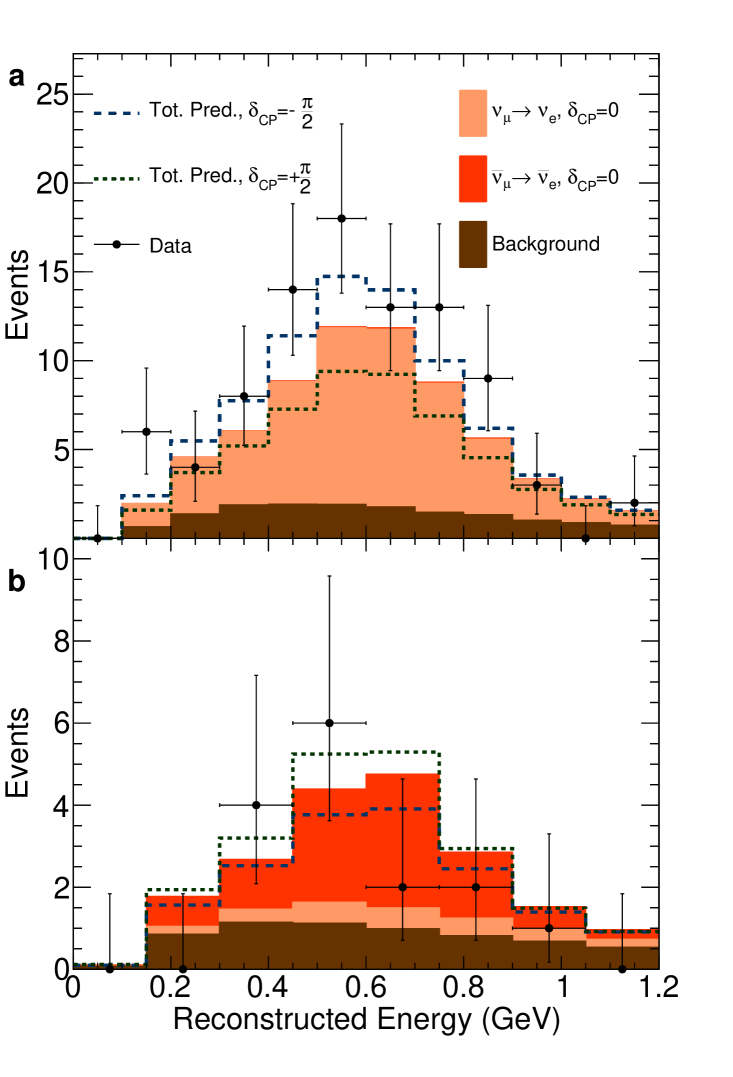
As the probability for oscillation to tau neutrinos is large at our modal beam energy and baseline, there is a minimum in the muon neutrino energy spectrum. The position of this minimum gives the experiment sensitivity to the magnitude of $\Delta m^{2}_{32}$ and the depth gives sensitivity to $\sin^{2}(2\theta_{23})$ . The height of the peak in the electron neutrino energy spectrum at the oscillation maximum is, at leading order, determined by $\sin^{2}(\theta_{23})$ and $\sin^{2}(2\theta_{13})$ (see Eq. 2). However, it also has a sub-leading dependence on $\delta_{CP}$ and the neutrino mass ordering, giving sensitivity to these parameters. Due to this interdependence, determining the other PMNS mixing parameters is important in measuring $\delta_{CP}$ . As can be seen from Figure 1, changing $\delta_{CP}$ from $+\frac{\pi}{2}$ to $-\frac{\pi}{2}$ can lead to $\mathcal{O}$ (40%) changes in the number of electron neutrinos expected at SK. In our analysis we model the observed kinematic distributions of the final state particles using the full oscillation probability including the effect of the neutrinos propagating through matter, which is an O(10%) perturbation to the probability discussed in Equations 2 & 3 PhysRevD.22.2718 .

The T2K neutrino beam is generated at the Japan Proton Accelerator Research Complex (J-PARC) by impinging a 30 GeV beam of protons onto a graphite target Abe:2011ks . This interaction creates a large number of secondary hadrons, which are focused using magnetic horns. A neutrino(antineutrino)-enhanced beam is selected by focusing positively(negatively)-charged particles –dominantly pions–, by choosing the polarity of the magnetic field produced by the horns, thereby enabling us to study the differences between neutrino and antineutrino oscillations. The beam axis is directed 2.5^∘ away from the SK detector, taking advantage of the kinematics of the two-body pion decay to produce a narrow neutrino spectrum peaked at the expected energy of maximum oscillation probability osti_52878 . The results reported here are based on SK data collected between 2009 and 2018 in neutrino(antineutrino) mode and include a beam exposure of $1.49\times 10^{21}$ ( $1.64\times 10^{21}$ ) protons hitting the T2K neutrino production target.

Neutrinos are detected by observing the particles they produce when they interact. At neutrino energies of 0.6 GeV the dominant interaction process is Charged-Current Quasi-Elastic (CCQE) scattering via the exchange of a W boson with a single neutron or proton bound in the target nucleus. In this process the neutrino (antineutrino) turns into a charged lepton (antilepton) of the same flavour. We are thereby able to identify the incoming neutrino’s flavour.

Refer to caption — Figure 1: Observed $\nu_{e}$ and $\bar{\nu}_{e}$ candidate events at SK. Subfigure a (b) shows the reconstructed neutrino energy spectra for the SK samples containing electron-like events in neutrino(antineutrino)-mode beam running. The uncertainty shown around the data points accounts for statistical uncertainty. The uncertainty range is chosen to include all points for which the measured number of data events is inside the 68% confidence interval of a Poisson distribution centred at that point. The solid stacked chart shows the predicted number of events for the $CP$ -conserving point $\delta_{CP}=0$ separated according to whether the event was from an oscillated neutrino or antineutrino or from a background process. The dashed lines show the total predicted number of events for the two most extreme $CP$ -violating cases. Subfigure c shows the predicted number of events for $\delta_{CP}=-\frac{\pi}{2}$ and the measured number of events in the three electron-like samples at SK. The predicted number of events is broken down into the same categories as subfigures a and b and the systematic uncertainty shown is after the near-detector fit. In both a and b for all predictions, normal ordering is assumed, and $\sin^{2}\theta_{23}$ and $\Delta m^{2}_{32}$ are at their best-fit values. $\sin^{2}\theta_{13}$ , $\sin^{2}\theta_{12}$ and $\Delta m^{2}_{21}$ take the values indicated by external world average measurements Tanabashi:2018oca . The parameters accounting for systematic uncertainties take their best-fit values after the near-detector fit.

c	1 $e$ 0de $\nu$ -mode	1 $e$ 0de $\bar{\nu}$ -mode	1 $e$ 1de $\nu$ -mode
$\nu_{\mu}\rightarrow\nu_{e}$	59.0	3.0	5.4
$\bar{\nu}_{\mu}\rightarrow\bar{\nu}_{e}$	0.4	7.5	0.0
Background	13.8	6.4	1.5
Total Pred.	73.2	16.9	6.9
Syst. Unc.	8.8%	7.1%	18.4%
Data	75	15	15

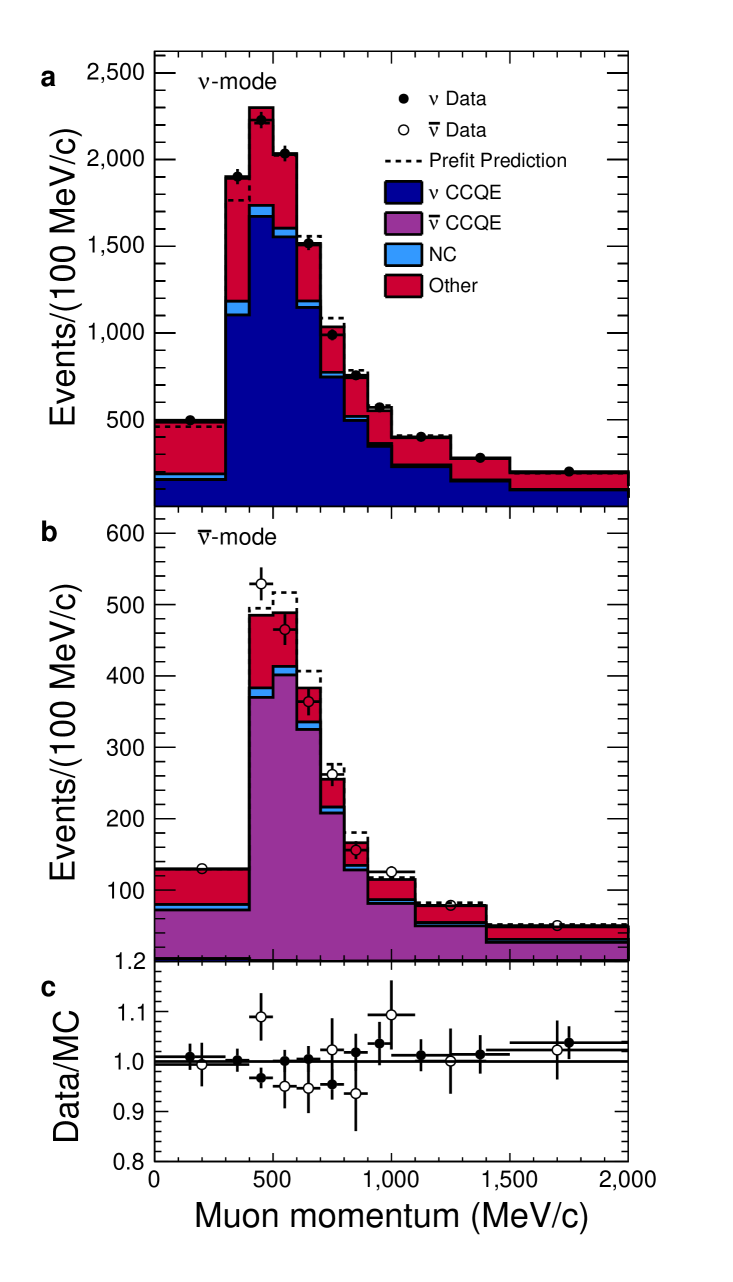
Our near detector facility consists of two detectors both located 280 m downstream of the beam production target Abe:2011ks . The INGRID detector Otani:2010zza , located on the beam axis, monitors the direction and stability of the neutrino beam. The ND280 detector Amaudruz:2012agx ; Assylbekov:2011sh ; Abgrall:2010hi ; Allan:2013ofa ; Aoki:2012mf is located at the same angle away from the beam axis as SK, and characterizes the rate of neutrino interactions from the beam before oscillations have occurred, thereby reducing systematic errors. ND280 is magnetized so that charged leptons and antileptons bend in opposite directions as they traverse the detector. This effect is used to measure the fraction of events in each beam mode that are from neutrino and antineutrino interactions. In this analysis, we select samples enriched in CCQE events and also several control samples enriched in interactions from other processes, allowing their rates to be measured separately. Here we use ND280 data that include a neutrino beam exposure of $5.8\times 10^{20}$ ( $3.9\times 10^{20}$ ) protons hitting the T2K neutrino production target in neutrino(antineutrino)-mode. The explanation for the smaller data set in ND280 and its impact on the analysis method is described in the Methods Section.

SK is a 50 kt water detector instrumented with photo-multiplier tube light sensors Fukuda:2002uc . In SK, Cherenkov light is produced as charged particles above a momentum threshold travel through the water. This light is emitted in ring patterns which are detected by the light sensors. Due to their lower mass, electrons scatter significantly more frequently (both elastically and inelastically) than muons so their Cherenkov rings are blurred. We use this blurring to identify the charged lepton’s flavour, as illustrated in Figure 2. More information on the event reconstruction technique for SK data and the systematic uncertainty on SK modeling can be found in the Methods Section. SK is not magnetized, so therefore relies on ND280’s measurement of the neutrino and antineutrino composition of the beam in each mode.

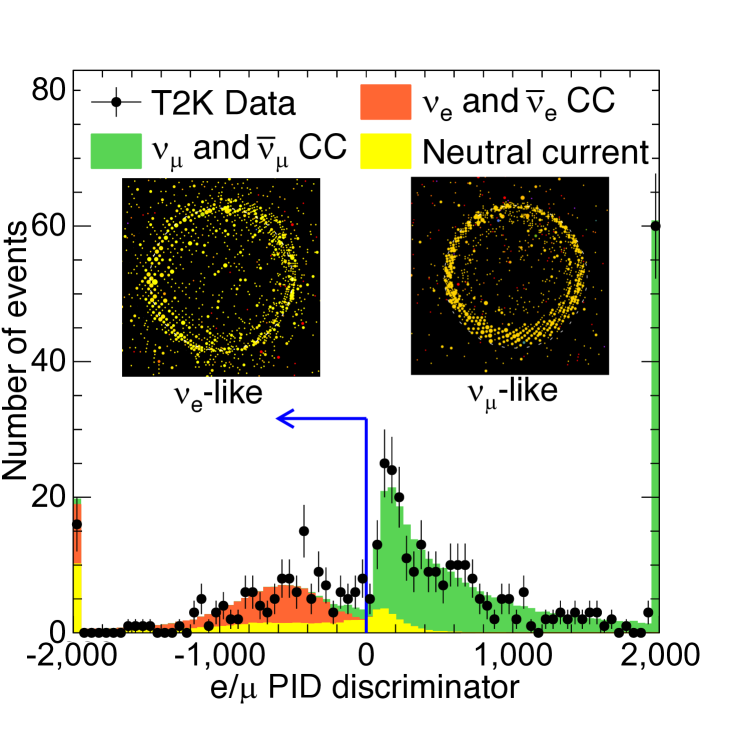
We form five independent samples of SK events. For both neutrino- and antineutrino-beam mode there is a sample of events that contain a single muon-like ring (denoted 1 $\mu$ ), and a sample of events that contain only a single electron-like ring (denoted 1 $e$ 0de). These single-lepton samples are dominated by CCQE interactions. In neutrino-mode there is a sample containing an electron-like ring as well as the signature of an additional delayed electron from the decay of a charged pion and subsequent muon (denoted 1 $e$ 1de). We do not use this sample in antineutrino-mode because charged pions from antineutrino interactions are mostly absorbed by a nucleus before they decay. Identifying both muon and electron neutrino interactions in both the neutrino- and antineutrino-mode beams allows us to measure the probabilities for four oscillation channels: $\nu_{\mu}\rightarrow\nu_{\mu}$ and $\bar{\nu}_{\mu}\rightarrow\bar{\nu}_{\mu}$ , $\nu_{\mu}\rightarrow\nu_{e}$ and $\bar{\nu}_{\mu}\rightarrow\bar{\nu}_{e}$ .

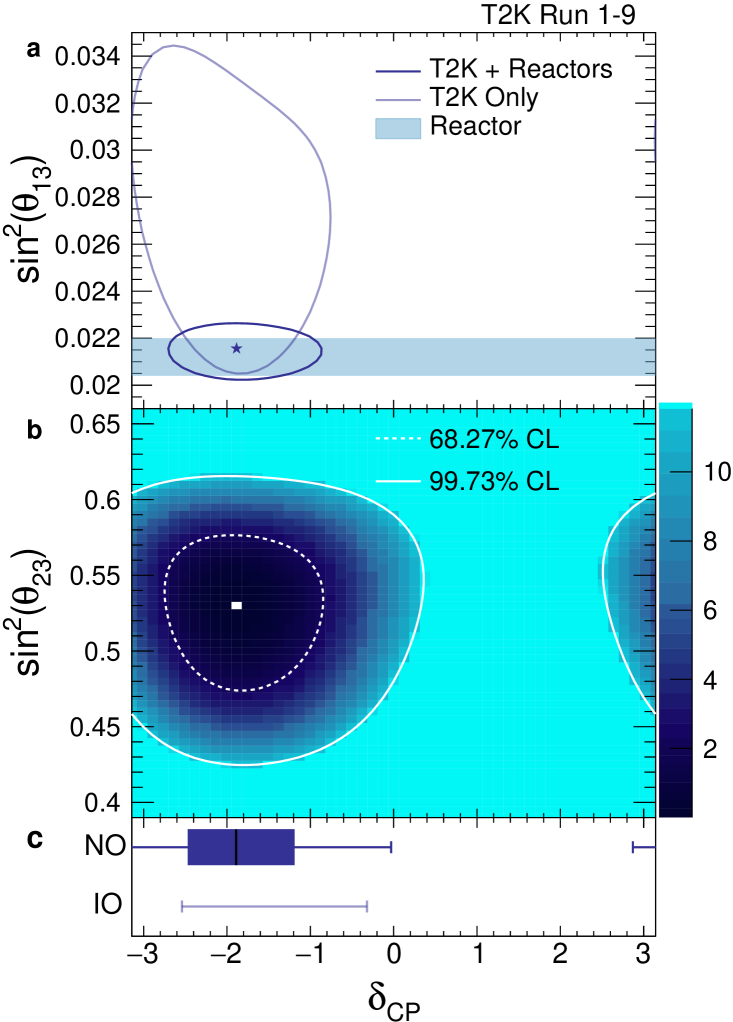
We define a model of the expected number of neutrino events as a function of kinematic variables measured in our detectors with degrees of freedom for each of the oscillation parameters and for each source of systematic uncertainty. Systematic uncertainties arise in the modeling of neutrino-nucleus interactions in the detector, the modeling of the neutrino production, and the modeling of the detector’s response to neutrino interaction products. Where possible, we constrain the model using external data. For example, the solar oscillation parameters, $\Delta m^{2}_{21}$ and $\sin^{2}(\theta_{12})$ , whose values T2K is not sensitive to, are constrained using world average data Tanabashi:2018oca . Whilst we are sensitive to $\sin^{2}\theta_{13}$ , we use the combination of measurements from the Daya Bay, RENO and Double Chooz reactor experiments to constrain this parameter Tanabashi:2018oca , as they make a much more precise measurement than using T2K data alone (see Figure 4a). We measure the oscillation parameters by doing a marginal likelihood fit of this model to our near and far detector data. We perform several analyses using both Bayesian and frequentist statistical paradigms. Exclusive measurements of neutrino or antineutrino candidates in the near detector, one of which is shown in Figure 3, strongly constrain the neutrino production and interaction models, reducing the uncertainty on the predicted number of events in the four single-lepton SK samples from 13-17% to 4-9%, depending on the sample. The 1 $e$ 1de sample’s uncertainty is reduced from 22% to 19%.

A neutrino’s oscillation probability depends on its energy, as shown in Eqs. 2 and 3. While the energy distribution of our neutrino beam is well understood, we cannot directly measure the energy of each incoming neutrino. Instead the neutrino’s energy must be inferred from the momentum and direction of the charged lepton that results from the interaction. This inference relies on the correct modeling of the nuclear physics of neutrino-nucleus interactions. Modeling the strong nuclear force in multi-body problems at these energies is not computationally tractable, so approximate theories are used Nieves:2005rq ; Martini:2009uj ; Benhar:2005dj ; Salcedo:1987md . The potential biases introduced by approximations in these theories constitute the largest sources of systematic uncertainties in this measurement. For scale, the largest individual source contributes 7.1% of the overall 8.8% systematic uncertainty on the single electron-like ring $\nu$ -mode sample. Furthermore, as well as CCQE interactions, there are non-negligible contributions from interactions where additional particles were present in the final state but were not detected by our detectors. To check for bias from incorrect modeling of neutrino-nucleus interactions, we performed fits to simulated data sets generated assuming a range of different models of neutrino interactions Martini:2009uj ; Benhar:2005dj . We compared the measurements of the oscillation parameters obtained from these fits with the measurement from a fit to simulated data generated assuming our default model. We observed no significant biases in the obtained $\delta_{CP}$ best-fit values or changes in the interval sizes from any model tested. Biases are seen on $\Delta m^{2}_{32}$ , and these have been incorporated in the analysis through an additional error of $3.9\times 10^{-5}$ $\text{eV}^{2}/c^{4}$ on the $\Delta m^{2}_{32}$ interval. More details of the systematic uncertainties on neutrino interaction modeling can be found in the Methods Section.

The observed number of events at SK can be seen in Figure 1. The probability to observe an excess over prediction in one of our five samples at least as large as that seen in the electron-like charged pion sample is 6.9% assuming the best-fit value of the oscillation parameters. We find the data shows a preference for the normal mass ordering with a posterior probability of 89%, giving a Bayes factor of 8. We find $\sin^{2}(\theta_{23})=0.53^{+0.03}_{-0.04}$ for both mass orderings. Assuming the normal (inverted) mass ordering we find $\Delta m^{2}_{32}=(2.45\pm 0.07)\times 10^{-3}$ $(\Delta m^{2}_{13}=(2.43\pm 0.07)\times 10^{-3})$ $\text{eV}^{2}/c^{4}$ . For $\delta_{CP}$ our best-fit value and 68% ( $1\sigma$ ) uncertainties assuming the normal (inverted) mass ordering are $-1.89^{+0.70}_{-0.58}(-1.38^{+0.48}_{-0.54})$ , with statistical uncertainty dominating. Our data show a preference for values of $\delta_{CP}$ which are near maximal $CP$ violation (see Figure 4), while both $CP$ conserving points, $\delta_{CP}=0$ and $\delta_{CP}=\pi$ , are ruled out at the 95% confidence level. Here, we also produce 99.73% ( $3\sigma$ ) confidence and credible intervals on $\delta_{CP}$ . In the favoured normal ordering the confidence interval contains [ $-3.41$ , $-0.03$ ] (excluding 46% of the parameter space). We have investigated the effect of the excess seen in the 1 $e$ 1de sample on this interval and find that had the observed number of events in this sample been as expected for the best-fit parameter values the interval would have contained [ $-3.71$ , $0.17$ ] ( excluding 38% of parameter space). In the inverted ordering the confidence interval contains [ $-2.54$ , $-0.32$ ] (excluding 65% of the parameter space). The 99.73% credible interval marginalized across both mass orderings contains [ $-3.48$ , $0.13$ ] (excluding 42% of the parameter space). The $CP$ -conserving points are not both excluded at the 99.73% level. However, this is the first time an experiment has reported closed 99.73% ( $3\sigma$ ) intervals on the $CP$ -violating phase $\delta_{CP}$ (taking into account both mass orderings) and a large range of values around $+\pi/2$ are excluded.

Acknowledgements.

We thank the J-PARC staff for superb accelerator performance. We thank the CERN NA61/SHINE Collaboration for providing valuable particle production data. We acknowledge the support of MEXT, Japan; NSERC (Grant No. SAPPJ-2014-00031), NRC and CFI, Canada; CEA and CNRS/IN2P3, France; DFG, Germany; INFN, Italy; National Science Centre (NCN) and Ministry of Science and Higher Education, Poland; RSF (Grant #19-12-00325) and Ministry of Science and Higher Education, Russia; MINECO and ERDF funds, Spain; SNSF and SERI, Switzerland; STFC, UK; and DOE, USA. We also thank CERN for the UA1/NOMAD magnet, DESY for the HERA-B magnet mover system, NII for SINET4, the WestGrid and SciNet consortia in Compute Canada, and GridPP in the United Kingdom. In addition, participation of individual researchers and institutions has been further supported by funds from ERC (FP7), ”la Caixa” Foundation (ID 100010434, fellowship code LCF/BQ/IN17/11620050), the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreements no. 713673 and no. 754496, and H2020 Grants No. RISE-RISE-GA822070-JENNIFER2 2020 and RISE-GA872549-SK2HK; JSPS, Japan; Royal Society, UK; French ANR Grant No. ANR-19-CE31-0001; and the DOE Early Career program, USA.

III Methods

The measurement presented in this paper relies on the modeling of experimental apparatus to infer the parameters governing the oscillations of neutrinos. This modeling can be broken into three main categories: the modeling of the neutrino production in the beam line, the modeling of neutrino-nucleus interactions in the detectors, and the modeling of the detectors’ responses to final state particles and the inference of particle properties from the detector response. The main sources of systematic uncertainty in the data analysis arise in these three areas, and here we provide a description of the models and associated systematic uncertainties.

The inference of neutrino oscillation parameters from the data also relies on the statistical methods applied. In this section, we also provide a detailed description of the statistical methods used to infer the favored values and allowed regions for neutrino oscillation parameters.

III.1 Neutrino Production Modeling

The predicted neutrino and antineutrino fluxes, including the energies and flavours of neutrinos(antineutrinos), are estimated using a detailed simulation of the T2K beam line. Measurement of the proton beam orbit, transverse width and divergence, and intensity are used as the initial conditions before simulating the interactions of protons in the T2K target to produce the secondary particles that decay to neutrinos. Particle interactions and production inside the target are simulated with FLUKA2011 BOHLEN2014211 ; Ferrari:2005zk , while particle propagation outside of the target is simulated with GEANT3 Brun:1994aa . Interaction rates and hadron production in the simulation are tuned with hadron interaction data from external experiments, primarily the NA61/SHINE experiment which has collected data for T2K at the J-PARC proton beam energy of 30 GeV with the T2K target material of graphite Abgrall:2015hmv . Measurements of the magnetic horns’ currents during beam operation and of the horns’ magnetic fields before installation ensure accurate modeling of the charged particle focusing in the flux simulation. The simulated fluxes are used as inputs to simulations of neutrino interactions and particle detection in the ND280 and SK detectors. The spectrum of muon neutrinos (antineutrinos) produced from the decays of focused charged pions peaks at an energy of 0.6 GeV for an off-axis angle of 2.5^∘. Near the peak energy, 97.2% (96.2%) of the neutrino(antineutrino)-mode beam is initially $\nu_{\mu}$ $(\bar{\nu}_{\mu})$ . The remaining components are mostly $\bar{\nu}_{\mu}$ ( $\nu_{\mu}$ ); contaminations of $\nu_{e}+\bar{\nu}_{e}$ are only 0.47% (0.49%).

Since the neutrino flux prediction depends on the measured beam and beam line properties, which may vary with time, different flux predictions are made for each run period, and they are combined with weights proportional to the number of protons-on-target (POT) accumulated during periods of nominal detector operation. The collected ND280 data corresponds to $5.8\times 10^{20}$ POT in neutrino mode and $3.9\times 10^{20}$ POT in antineutrino mode. This amount is less than the amount of data collected at SK due to lower efficiency of nominal data taking at ND280, and longer data processing times for ND280 data, limiting the available data set. This POT difference between ND280 and SK is accounted for by combining the POT weighted flux predictions for each run period based on the beam exposures for the data collected at each detector.

The uncertainty on the flux calculation is evaluated by propagating uncertainties on the proton beam measurements, hadronic interactions, material modeling and alignment of beam line elements, and horn current and field measurements. In each case, variations of the source of uncertainty are considered and the effect on the flux simulation is evaluated. The INGRID on-axis neutrino detector is not used to tune the beam direction during operation. Hence, it provides an independent measurement of the beam direction Abe:2011xv , which is used to validate the flux simulation. The uncertainty on the INGRID beam direction measurement is propagated in the flux model. The variations are used to calculate covariances for the flux prediction in bins of energy, flavour, neutrino/antineutrino mode and detector (ND280 and SK). These covariances are used to propagate uncertainties on the flux prediction in the oscillation analysis. The dominant source of systematic uncertainty is from the hadron interaction data and models. The uncertainty on the flux normalization in this analysis near the peak energy of 0.6 GeV is 9%. In future analyses we aim to improve this to approximately 5% by using NA61/SHINE particle production data measured from a replica of the T2K target Abgrall:2016jif ; Berns:2018tap . Uncertainties on the proton beam orbit and alignment of beam line elements correspond to an uncertainty on the off-axis angle at the ND280 and SK detectors, corresponding to uncertainties on the peak energy of the neutrino spectrum at those detectors.

III.2 Neutrino Interaction Modeling

The T2K detectors measure products of neutrinos and antineutrinos interacting on nuclei and free protons with energies ranging from $\sim$ 0.1 GeV to 30 GeV. These interactions are modeled with the NEUT NEUT neutrino interaction generator, using version 5.3.2. NEUT uses a range of models to describe the physics of the initial nuclear state, the neutrino-nucleon(s) interaction, and the interactions of final state particles in the nuclear medium.

The primary signal processes in SK are defined by the presence of a single charged lepton candidate with no other visible particles. The dominant process at the peak energy of 0.6 GeV is Charged-Current Quasi-Elastic (CCQE) scattering. This process corresponds to the neutrino or antineutrino scattering on a single nucleon bound in the target nucleus. The neutrino-nucleon scattering in NEUT is implemented in the formalism of Llewellyn-Smith LlewellynSmith:1971uhs . For the initial nuclear state, NEUT implements a relativistic Fermi gas (RFG) model of the target nucleus, including long-range correlations evaluated using the random phase approximation (RPA) nieves_rpa ; *nieves_rpa_erratum. NEUT includes an alternative initial state model based on spectral functions describing the initial momentum and removal energy for bound nucleons Benhar-SF .

Additional processes that can produce a signal-like final state are modeled in NEUT. The 2p-2h model of Nieves et al. nieves ; nievesExtension predicts production of multinucleon excitations, where more than one nucleon and no pions are ejected in the final state. The ejected nucleons are typically below detection threshold in a water Cherenkov detector, making this process indistinguishable from the CCQE process.

The signal candidate sample with one prompt electron-like ring and the presence of an electron from muon decay consists primarily of interactions where a pion is produced. These single-pion interactions can also populate the samples without an additional electron from muon decay if the pion is absorbed in the target nucleus or on a nucleus in the detector, or if it is not detected. Processes producing a single pion and one nucleon are described by the Rein-Sehgal model ReinSehgal . Processes with multiple pions are simulated with a custom model below 2 GeV of hadronic invariant mass and by PYTHIA Sjostrand:1993yb otherwise. These processes may be selected as events with single Cherenkov rings if the pion is absorbed in the target nucleus or surrounding nuclei, or if it is not detected. The final state interactions of pions and protons in the target nucleus are modeled with the NEUT intranuclear cascade model where the density dependence of the mean free path for pions in the target nucleus is calculated based on the $\Delta$ -hole model of Oset et. al. Oset:1986sy at low momenta and from p- $\pi$ scattering data from the SAID database at high momenta. The microscopic interaction rates for exclusive pion scattering modes are then tuned to macroscopic $\pi$ -nucleus scattering data.

We consider two types of systematic uncertainties on neutrino interaction modeling in the oscillation measurement. In the first, parameters in the nominal interaction model are allowed to vary and are constrained by ND280 data. These parameters are then marginalized over when measuring oscillation parameters. They include uncertainties on nucleon form factors, the corrections for long-range correlations, the rates of different neutrino interaction processes, the final state kinematics of the CCQE, 2p-2h and single pion production processes, and the rates of pion final state interactions. Most of these are parameters in the models with physical interpretations, and they modify the overall rate of interactions, the final state topology, and the kinematics of final state particles. After the constraint from ND280 data, these parameters are correlated with the systematic parameters in the neutrino production model, and their combined impact on the predicted event distributions in Super-K is evaluated. The constrained interaction model and neutrino production model parameters contribute a 2.7% uncertainty on the prediction of the relative number of electron neutrino and electron antineutrino candidates, the third largest source of systematic uncertainty, as shown in Supplementary Table I.

We also include an uncertainty on the $\nu_{e}$ and $\bar{\nu}_{e}$ cross sections relative to the $\nu_{\mu}$ and $\bar{\nu}_{\mu}$ cross sections. This introduces a direct uncertainty on the relative prediction of $\nu_{e}$ and $\bar{\nu}_{e}$ candidates, and is motivated by uncertainties in the neutrino-nucleon scattering cross section arising from the charged lepton masses McFarland-Day . As shown in Supplementary Table I, this introduces a relative uncertainty of 3.0%, the second largest single source of systematic uncertainty in the $CP$ asymmetry measurement.

The second type of systematic uncertainty is evaluated by introducing simulated data generated with an alternative model into the analysis and evaluating the impact on measured oscillation parameters. This approach is used to evaluate the effect of changing the nuclear initial state model including the use of the spectral functions and changes to the removal energy for initial state nucleons. This approach is also applied to evaluate the impact of changes to the 2p-2h interaction cross section as a function of energy, using an alternative single pion production model Rein:1987cb ; Kabirnezhad:2017jmf , and applying alternative multi-pion production tuning Yang:2009zx . The largest biases observed in this approach are on the measurement of $\Delta m^{2}_{32}$ , while the impact on other parameters is typically small compared to the total systematic uncertainty. In the case of $\Delta m^{2}_{32}$ , an additional uncertainty of $3.9\times 10^{-5}$ eV²/c⁴ is included by taking a convolution of a Gaussian of width $3.9\times 10^{-5}$ eV²/c⁴ with the likelihood. For the measurement of the other oscillations parameters, it was found that the biases introduced by varying the removal energy by up to 18 MeV for initial state nucleons were not negligible. An additional uncertainty equal to the bias in the predicted event distributions when varying the removal energy by 18 MeV was added to the analysis. As shown in Supplementary Table I, this introduces a 3.7% uncertainty on the relative prediction of electron neutrino and electron antineutrino candidates, the largest single source of systematic uncertainty in the analysis.

III.3 Super-Kamiokande Event Reconstruction

Photosensors installed on the SK inner detector register Cherenkov light produced as charged particles produced by neutrino interactions travel through the water volume Fukuda:2002uc . Photosensor activity clustered in time, on the order of a micro-second, is called an event. Events coincident with the T2K-beam timing are selected as candidate beam neutrino interactions.

Neutrino interaction events in SK often have multiple periods of photosensor activity separated in time within an event. The most frequent example is a muon decaying into an electron. A decay electron can be used to tag a muon even when the muon energy is below the Cherenkov threshold, e.g. the case that the muon is produced by a charged pion decaying at rest. Such sub-events are searched for with a peak finding algorithm and reconstructed separately in later processes.

The kinematics of the charged particles are reconstructed from the timing and the number of detected photons of each photosensor signal by using a maximum likelihood algorithm 10.1093/ptep/ptz015 . The likelihood consists of the probability of each photosensor to detect photons or not and the charge and timing probability density functions of the hit photosensors. This new reconstruction algorithm makes use of the timing and charge information obtained by all the photosensors simultaneously, which leads to better kinematic resolutions and particle classifying performances compared to the previously used reconstruction algorithm.

The five signal samples are formed by using the reconstructed event kinematics. All the selected events are required to have little photosensor activity in an outer veto detector, and the reconstructed neutrino interaction position is required to be inside the inner detector fiducial volume. The reconstruction improvement enabled us to extend the fiducial volumes used in the analysis. We performed a dedicated study to optimize the fiducial volume to maximize T2K sensitivities to oscillation parameters taking into account both the statistical and systematical uncertainties. The position dependent SK detector systematics are estimated by using SK atmospheric neutrino interaction events. The fiducial volume expansion contributes to the increase of selected electron-like (muon-like) events by 25% (14%) Abe:2018wpn .

Systematic uncertainties regarding SK detector modeling were addressed by various control samples. Uncertainties on the position reconstruction bias and on the decay electron tagging are estimated by using cosmic-ray muons stopping inside the inner detector. Simulated atmospheric neutrino events are compared to data to evaluate systematic uncertainties on the modeling of signal selection efficiencies and the background contamination of the five analysis samples. Parameters describing possible mis-modeling of Cherenkov ring counting and particle identifications are introduced and constrained by a fit to the control samples. These parameters are varied according to the posterior distribution from the fit to the control samples, and the uncertainties on the T2K samples of interest are evaluated. The uncertainty on the modeling of the efficiency to select events with neutral pions, which is one of the dominant backgrounds in the electron neutrino CCQE-like event sample, is estimated by constructing a set of hybrid events that combine one data and one simulated electron-like Cherenkov ring to imitate the decay of a neutral pion. The uncertainties on the numbers of selected total events in SK are 2–4% depending on the signal categories. As shown in Supplementary Table I, the relative uncertainty on the predicted number of electron neutrino and electron antineutrino candidates for samples with no decay electrons is 1.5%.

III.4 Statistical Methods

We use a binned likelihood-ratio method comparing the observed and predicted numbers of muon- and electron-neutrino candidate events in our five samples. In neutrino beam mode these are electron-like, muon-like and electron-like charged pion samples, while in antineutrino beam mode these are electron-like and muon-like samples. The samples are binned in reconstructed energy and, for the electron-neutrino-like samples, the angle between the lepton and the beam direction. In particular, best-fits are determined by minimising the sum of the following likelihood function (marginalized over nuisance parameters) over all of our samples

\begin{split}-2\ln\lambda(\overline{\delta_{CP}};\mathbf{a})=2\sum_{i=1}^{N}\left[n_{i}^{obs}\ln\left(\frac{n_{i}^{obs}}{n_{i}^{exp}}\right)+n_{i}^{exp}-n_{i}^{obs}\right]\\ +(\mathbf{a}-\mathbf{a_{0}})^{T}\mathbf{C^{-1}}(\mathbf{a}-\mathbf{a_{0}})\end{split}

(4)

where $\overline{\delta_{CP}}$ is the estimated value of $\delta_{CP}$ , $\mathbf{a}$ is the vector of systematic parameter values (including the remaining oscillation parameters), $\mathbf{a_{0}}$ is the vector of default values of the systematic parameters, $\mathbf{C}$ is the systematic parameter covariance matrix, $N$ is the number of reconstructed energy and lepton angle bins, $n_{i}^{obs}$ is the number of events observed in bin $i$ and $n_{i}^{exp}=n_{i}^{exp}(\overline{\delta_{CP}};\mathbf{a})$ is the corresponding expected number of events. Systematic parameters are marginalized according to their prior constraints from the fit to ND280 data.

We perform both frequentist and Bayesian analyses of our data. The measurement of $\delta_{CP}$ from each of the analyses is in agreement, with the presented confidence intervals coming from a frequentist analysis and the Bayes factors and credible intervals coming from a Bayesian analysis. In the frequentist analysis a fit is first performed to the near detector samples binned in the momentum and cosine of the angle between the lepton and the beam direction, with penalty terms for flux, cross-section and detector systematic parameters at the near detector. Systematic parameter constraints are then propagated from the near to the far detector via the covariance matrix, $\mathbf{C}$ , in Eq. 4 and their fitted values. The matrix is the combination of the posterior covariance from the near detector fit with the priors for the oscillation parameters, with some parameters affecting both detectors directly, while others that affect only the far detector are constrained through their correlation with near detector affecting parameters. Gaussian priors for $\sin^{2}(\theta_{13})$ , $\sin^{2}(\theta_{12})$ , and $\Delta{}m^{2}_{21}$ are taken from the Particle Data Group’s (PDG) world combinations Tanabashi:2018oca , while $\sin^{2}(\theta_{23})$ and $\Delta{}m^{2}_{32}$ ( $\Delta{}m^{2}_{13}$ ) have uniform priors in normal (inverted) mass ordering. For the Bayesian analyses the prior for $\delta_{CP}$ is uniform, with an additional check applying a uniform prior in $\sin(\delta_{CP})$ producing the same conclusions. Furthermore, rather than fitting the near detector and propagating to the far detector as a two step process, the Bayesian analysis directly includes the near detector samples in its expression for the likelihood and therefore performs a simultaneous fit of the near and far detector data.

The neutrino oscillation probability depends non-linearly on the oscillation parameters, with different possible values of $\delta_{CP}$ corresponding to a bounded enhancement or suppression of the electron (anti)neutrino appearance probability. If statistical fluctuations in the data exceed these bounds they are not accommodated by the model, and as a result the critical $\Delta\chi^{2}$ value for a given confidence level is often different from the asymptotic rule of Wilks Wilks1938 . To address this problem the frequentist analysis constructs Neyman confidence intervals using the approach described by Feldman and Cousins FC and thus critical values of $\Delta\chi^{2}$ vary as a function of $\delta_{CP}$ and the mass ordering. The critical values at a given confidence level are determined by fitting at least 20,000 simulated datasets for each given true value of $\delta_{CP}$ and the mass ordering. The remaining oscillation parameters are varied according to their priors. In particular, for $\sin^{2}(\theta_{13})$ , $\sin^{2}(\theta_{12})$ , and $\Delta{}m^{2}_{21}$ these priors are taken from the PDG Tanabashi:2018oca , with $\sin^{2}(\theta_{13})$ determined by the reactor experiments noted in the main text. For $\sin^{2}(\theta_{23})$ , and $\Delta{}m^{2}_{32}$ ( $\Delta{}m^{2}_{13}$ ) the priors take the form of likelihood surfaces produced from fits of simulated datasets. The simulated datasets are generated using oscillation parameter best-fits in normal and inverted mass orderings. The remaining systematic parameters are varied according to their prior constraints from the fit to ND280 data.

The Bayesian analysis uses Markov Chain Monte Carlo (MCMC) to take random samples from the likelihood. The particular MCMC algorithm used is Metropolis-Hastings Hastings1970 . For a sufficiently large number of samples the Markov chain achieves an equilibrium probability distribution. The number of steps in the chain with a particular value of a parameter is proportional to the posterior probability for the parameter to have that value marginalized over all the other parameters. Credible intervals are then formed on the basis of highest posterior density, with bins of equal width in the parameter under study. Given the arbitrary initial state of the Markov chain, a finite number of samples must be obtained to allow the chain to converge to a state in which it is correctly sampling from the distribution. These preliminary ‘burn-in’ samples are discarded.

IV Author Contributions

The operation, Monte Carlo simulation, and data analysis of the T2K Experiment are carried out by the T2K Collaboration with contributions from all collaborators listed as authors on this manuscript. The scientific results presented here have been presented to and discussed by the full collaboration, and all authors have approved the final version of the manuscript.

V Data Availability

The likelihood surface data that support these findings will be made available for public access on http://t2k-experiment.org.

VI Code Availability

The T2K collaboration develops and maintains the code used for the simulation of the experimental apparatus and statistical analysis of the raw data used in this result. This code is shared among the collaboration, but not publicly distributed. Inquiries regarding the algorithms and methods used in this result may be directed to the corresponding author.

References

(1) J. H. Christenson, J. W. Cronin, V. L. Fitch, and R. Turlay, “Evidence for the $2\pi$ Decay of the $K_{2}^{0}$ Meson,” Phys. Rev. Lett., vol. 13, pp. 138–140, 1964.
(2) M. Tanabashi et al., “Review of Particle Physics,” Phys. Rev., vol. D98, no. 3, p. 030001, 2018.
(3) A. D. Sakharov, “Violation of CP Invariance, C asymmetry, and baryon asymmetry of the universe,” Pis’ma Zh. Eksp. Teor. Fiz., vol. 5, pp. 32–35, 1967. [Sov. Phys. Usp. 34,no.5,392-393(1991)].
(4) M. Fukugita and T. Yanagida, “Baryogenesis Without Grand Unification,” Phys. Lett., vol. B174, pp. 45–47, 1986.
(5) Y. Fukuda et al., “Evidence for oscillation of atmospheric neutrinos,” Phys. Rev. Lett., vol. 81, pp. 1562–1567, 1998.
(6) Q. R. Ahmad et al., “Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory,” Phys. Rev. Lett., vol. 89, p. 011301, 2002.
(7) S. Pascoli, S. T. Petcov, and A. Riotto, “Connecting low energy leptonic CP-violation to leptogenesis,” Phys. Rev., vol. D75, p. 083511, 2007.
(8) C. Hagedorn, R. N. Mohapatra, E. Molinaro, C. C. Nishi, and S. T. Petcov, “CP Violation in the Lepton Sector and Implications for Leptogenesis,” Int. J. Mod. Phys., vol. A33, no. 05n06, p. 1842006, 2018.
(9) G. C. Branco, R. González Felipe, and F. R. Joaquim, “Leptonic $cp$ violation,” Rev. Mod. Phys., vol. 84, pp. 515–565, 2012.
(10) K. Abe et al., “Observation of Electron Neutrino Appearance in a Muon Neutrino Beam,” Phys. Rev. Lett., vol. 112, p. 061802, 2014.
(11) M. A. Acero et al., “First Measurement of Neutrino Oscillation Parameters using Neutrinos and Antineutrinos by NOvA,” Phys. Rev. Lett., vol. 123, no. 15, p. 151803, 2019.
(12) K. Abe et al., “Search for CP Violation in Neutrino and Antineutrino Oscillations by the T2K Experiment with $2.2\times 10^{21}$ Protons on Target,” Phys. Rev. Lett., vol. 121, no. 17, p. 171802, 2018.
(13) S. Abe et al., “Precision Measurement of Neutrino Oscillation Parameters with KamLAND,” Phys. Rev. Lett., vol. 100, p. 221803, 2008.
(14) D. Adey et al., “Measurement of the Electron Antineutrino Oscillation with 1958 Days of Operation at Daya Bay,” Phys. Rev. Lett., vol. 121, no. 24, p. 241805, 2018.
(15) B. Aharmim et al., “Combined Analysis of all Three Phases of Solar Neutrino Data from the Sudbury Neutrino Observatory,” Phys. Rev., vol. C88, p. 025501, 2013.
(16) Z. Maki, M. Nakagawa, and S. Sakata, “Remarks on the unified model of elementary particles,” Prog. Theor. Phys., vol. 28, pp. 870–880, 1962.
(17) B. Pontecorvo, “Neutrino Experiments and the Problem of Conservation of Leptonic Charge,” Sov. Phys. JETP, vol. 26, pp. 984–988, 1968. [Zh. Eksp. Teor. Fiz.53,1717(1967)].
(18) P. I. Krastev and S. T. Petcov, “Resonance Amplification and t Violation Effects in Three Neutrino Oscillations in the Earth,” Phys. Lett., vol. B205, pp. 84–92, 1988.
(19) C. Jarlskog, “A Basis Independent Formulation of the Connection Between Quark Mass Matrices, CP Violation and Experiment,” Z. Phys., vol. C29, pp. 491–497, 1985.
(20) V. Barger, K. Whisnant, S. Pakvasa, and R. J. N. Phillips, “Matter effects on three-neutrino oscillations,” Phys. Rev. D, vol. 22, pp. 2718–2726, Dec 1980.
(21) K. Abe et al., “The T2K Experiment,” Nucl. Instrum. Meth., vol. A659, pp. 106–135, 2011.
(22) D. Beavis, A. Carroll, I. Chiang, and E889 Collaboration, “Long baseline neutrino oscillation experiment at the ags. physics design report,” doi:10.2172/52878, 1995.
(23) M. Otani et al., “Design and construction of INGRID neutrino beam monitor for T2K neutrino experiment,” Nucl. Instrum. Meth., vol. A623, pp. 368–370, 2010.
(24) P. A. Amaudruz et al., “The T2K Fine-Grained Detectors,” Nucl. Instrum. Meth., vol. A696, pp. 1–31, 2012.
(25) S. Assylbekov et al., “The T2K ND280 Off-Axis Pi-Zero Detector,” Nucl. Instrum. Meth., vol. A686, pp. 48–63, 2012.
(26) N. Abgrall et al., “Time Projection Chambers for the T2K Near Detectors,” Nucl. Instrum. Meth., vol. A637, pp. 25–46, 2011.
(27) D. Allan et al., “The Electromagnetic Calorimeter for the T2K Near Detector ND280,” JINST, vol. 8, p. P10019, 2013.
(28) S. Aoki et al., “The T2K Side Muon Range Detector (SMRD),” Nucl. Instrum. Meth., vol. A698, pp. 135–146, 2013.
(29) Y. Fukuda et al., “The Super-Kamiokande detector,” Nucl. Instrum. Meth., vol. A501, pp. 418–462, 2003.
(30) J. Nieves, M. Valverde, and M. J. Vicente Vacas, “Inclusive nucleon emission induced by quasi-elastic neutrino-nucleus interactions,” Phys. Rev., vol. C73, p. 025504, 2006.
(31) M. Martini, M. Ericson, G. Chanfray, and J. Marteau, “A Unified approach for nucleon knock-out, coherent and incoherent pion production in neutrino interactions with nuclei,” Phys. Rev., vol. C80, p. 065501, 2009.
(32) O. Benhar, N. Farina, H. Nakamura, M. Sakuda, and R. Seki, “Electron- and neutrino-nucleus scattering in the impulse approximation regime,” Phys. Rev., vol. D72, p. 053005, 2005.
(33) L. L. Salcedo, E. Oset, M. J. Vicente-Vacas, and C. Garcia-Recio, “Computer Simulation of Inclusive Pion Nuclear Reactions,” Nucl. Phys., vol. A484, pp. 557–592, 1988.
(34) T. Böhlen, F. Cerutti, M. Chin, A. Fassò, A. Ferrari, P. Ortega, A. Mairani, P. Sala, G. Smirnov, and V. Vlachoudis, “The fluka code: Developments and challenges for high energy and medical applications,” Nuclear Data Sheets, vol. 120, pp. 211 – 214, 2014.
(35) A. Ferrari, P. R. Sala, A. Fasso, and J. Ranft, “FLUKA: A multi-particle transport code (Program version 2005),” CERN-2005-010, SLAC-R-773, INFN-TC-05-11, 2005.
(36) R. Brun, F. Bruyant, F. Carminati, S. Giani, M. Maire, A. McPherson, G. Patrick, and L. Urban, “GEANT Detector Description and Simulation Tool,” CERN-W5013, 1994.
(37) N. Abgrall et al., “Measurements of $\pi^{\pm}$ , $K^{\pm}$ , $K^{0}_{S}$ , $\varLambda$ and proton production in protoncarbon interactions at 31 GeV/c with the NA61/SHINE spectrometer at the CERN SPS,” Eur. Phys. J., vol. C76, no. 2, p. 84, 2016.
(38) K. Abe et al., “Measurements of the T2K neutrino beam properties using the INGRID on-axis near detector,” Nucl. Instrum. Meth., vol. A694, pp. 211–223, 2012.
(39) N. Abgrall et al., “Measurements of $\pi^{\pm}$ differential yields from the surface of the T2K replica target for incoming 31 GeV/c protons with the NA61/SHINE spectrometer at the CERN SPS,” Eur. Phys. J., vol. C76, no. 11, p. 617, 2016.
(40) N. Abgrall et al., “Measurements of $\pi^{\pm}$ , $K^{\pm}$ and proton double differential yields from the surface of the T2K replica target for incoming 31 GeV/c protons with the NA61/SHINE spectrometer at the CERN SPS,” Eur. Phys. J., vol. C79, no. 2, p. 100, 2019.
(41) Y. Hayato, “A Neutrino Interaction Simulation Program Library NEUT,” Acta Physica Polonica B, vol. 40, p. 2477, Sep 2009.
(42) C. H. Llewellyn Smith, “Neutrino Reactions at Accelerator Energies,” Phys. Rept., vol. 3, pp. 261–379, 1972.
(43) J. Nieves, J. E. Amaro, and M. Valverde, “Inclusive quasielastic charged-current neutrino-nucleus reactions,” Phys. Rev. C, vol. 70, p. 055503, Nov 2004.
(44) J. Nieves, J. E. Amaro, and M. Valverde, “Erratum: Inclusive quasielastic charged-current neutrino-nucleus reactions [phys. rev. c 70, 055503 (2004)],” Phys. Rev. C, vol. 72, p. 019902, Jul 2005.
(45) O. Benhar and A. Fabrocini, “Two nucleon spectral function in infinite nuclear matter,” Phys. Rev., vol. C62, p. 034304, 2000.
(46) J. Nieves, I. R. Simo, and M. J. V. Vacas, “Inclusive charged-current neutrino-nucleus reactions,” Phys. Rev. C, vol. 83, p. 045501, Apr 2011.
(47) R. Gran, J. Nieves, F. Sanchez, and M. J. Vicente Vacas, “Neutrino-nucleus quasi-elastic and 2p2h interactions up to 10 GeV,” Phys. Rev., vol. D88, no. 11, p. 113007, 2013.
(48) D. Rein and L. M. Sehgal, “Neutrino-excitation of baryon resonances and single pion production,” Annals of Physics, vol. 133, no. 1, pp. 79–153, 1981.
(49) T. Sjostrand, “High-energy physics event generation with PYTHIA 5.7 and JETSET 7.4,” Comput. Phys. Commun., vol. 82, pp. 74–90, 1994.
(50) E. Oset, L. L. Salcedo, and D. Strottman, “A Theoretical Approach to Pion Nuclear Reactions in the Resonance Region,” Phys. Lett., vol. 165B, pp. 13–18, 1985.
(51) M. Day and K. S. McFarland, “Differences in quasi-elastic cross sections of muon and electron neutrinos,” Phys. Rev., vol. D86, p. 053003, 2012.
(52) D. Rein, “Angular Distribution in Neutrino Induced Single Pion Production Processes,” Z. Phys., vol. C35, pp. 43–64, 1987.
(53) M. Kabirnezhad, “Single Pion Production in Neutrino-Nucleon Interactions,” Phys. Rev., vol. D97, no. 1, p. 013002, 2018.
(54) T. Yang, C. Andreopoulos, H. Gallagher, K. Hoffmann, and P. Kehayias, “A Hadronization Model for Few-GeV Neutrino Interactions,” Eur. Phys. J., vol. C63, pp. 1–10, 2009.
(55) M. Jiang et al,, “Atmospheric neutrino oscillation analysis with improved event reconstruction in Super-Kamiokande IV,” Progress of Theoretical and Experimental Physics, vol. 2019, 05 2019.
(56) S. S. Wilks, “The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses,” The Annals of Mathematical Statistics, vol. 9, pp. 60–62, 1938.
(57) G. J. Feldman and R. D. Cousins, “A Unified approach to the classical statistical analysis of small signals,” Phys. Rev., vol. D57, pp. 3873–3889, 1998.
(58) W. K. Hastings, “Monte Carlo sampling methods using Markov chains and their applications,” Biometrika, vol. 57, pp. 97–109, apr 1970.

Supplementary Table 1: The systematic uncertainty on the predicted relative number of electron neutrino and electron antineutrino candidates in the Super-K samples with no decay electrons. Type of Uncertainty $\nu_{e}/\bar{\nu}_{e}$ Candidate Relative Uncertainty (%) Super-K Detector Model 1.5 Pion Final State Interaction and Rescattering Model 1.6 Neutrino Production and Interaction Model Constrained by ND280 Data 2.7 Electron Neutrino and Antineutrino Interaction Model 3.0 Nucleon Removal Energy in Interaction Model 3.7 Modeling of Neutral Current Interactions with Single $\gamma$ Production 1.5 Modeling of Other Neutral Current Interactions 0.2 Total Systematic Uncertainty 6.0