Constructing Families Of Cospectral Regular Graphs
Abstract
A set of graphs are called cospectral if their adjacency matrices have the same characteristic polynomial. In this paper we introduce a simple method for constructing infinite families of cospectral regular graphs. The construction is valid for special cases of a property introduced by Schwenk. For the case of cubic (3-regular) graphs, computational results are given which show that the construction generates a large proportion of the cubic graphs, which are cospectral with another cubic graph.
1 Introduction
The characteristic polynomial of a matrix is the polynomial in , . A set of simple graphs are called cospectral if their adjacency matrices have identical characteristic polynomials. A graph is not uniquely determined by its spectrum if there is at least one non-isomorphic graph with which it is cospectral. The investigation of the prevalence and properties of such graphs is one of the classical open problems in spectral graph theory, and hence, methods for constructing cospectral graphs are of interest. To date, such construction methods have mainly fallen into two categories. The first involves performing various operations on the edges or vertices of graphs to produce new graphs which are cospectral with the initial graphs. Perhaps the most well-known example of this is the switching method of Godsil and McKay which was introduced in [9] and then later generalised in [1]. The second category involves ‘pasting’ graphs together in intelligent ways to achieve the cospectrality. Recently, there has been some interest in the construction of cospectral graphs which provide control over certain graph properties. In particular, cospectral graphs which are regular, among other properties, are investigated in [3], [7] and [4]. A common feature of the existing constructions which ensure regularity is the use of operations which are similar to a product of graphs. However, the nature of these operations means that both the degree of regularity and the order of the resulting graphs can become very large, which may be undesirable. In the present work, we introduce a construction for regular cospectral graphs which avoids these problems; indeed, arbitrarily large cospectral regular graphs of any desired degree can be constructed. The construction is valid for special cases of the notion of removal cospectral vertices which was introduced by Schwenk [11] and studied further in [10]. We paraphrase Schwenk’s definition as follows:
Definition 1.1
For two graphs and , the subsets of vertices and are called removal cospectral if there exists a bijection such that for every subset , the graphs and are cospectral.
Note that, since , it is implicit in Definition 1.1 that and are cospectral. It was subsequently shown by Godsil [8] that the requirement that and be cospectral for every subset can be replaced with the same requirement for only those subsets which have cardinality at most two, and the converse is also true. That is, and are removal cospectral if and only if, for all choices of , the graphs and are cospectral.
Our present construction takes a set of cospectral (possibly isomorphic), -regular graphs and uses them to construct a new set of cospectral graphs, in which the resulting graphs are still -regular. This involves selecting any choice of a -regular graph to be combined with each graph in the former set. The order of the newly constructed graphs depends on this selection, and the growth in order can be made very small if desired. We then demonstrate that, for some small choices of order , a large proportion of the cubic graphs which are not uniquely determined by their spectrum can be produced by this construction. Interestingly, this proportion appears to be increasing with .
2 Preliminaries
Throughout this manuscript we use standard graph theory notation such as can be found in [6]. All graphs used here are simple, connected and undirected. The neighborhood of a vertex is the set of vertices adjacent to and is denoted by . The adjacency matrix of a graph is denoted by . A subgraph of arising by deleting a set of vertices and all edges incident to those vertices is denoted by . Edge deletions are denoted by where . We denote the characteristic polynomial of a graph by . The walk generating matrix of a graph is whose -th entry, denoted by , is the generating function for the set of all walks in from vertex to vertex . A walk starting at vertex and ending at vertex is an walk.
We next define a special case of Definition 1.1 and call vertices which satisfy this special case replaceable.
Definition 2.1
For two graphs and , the vertices and are called replaceable if their respective neighborhoods and are removal cospectral. If the bijection defining the removal cospectral set is , then we denote the replaceable vertices by the tuple .
Lemma 2.2
Let and be graphs with replaceable vertices , where and and . Then the set is removal cospectral with , with the new removal cospectral bijection being equal to on and .
Proof 2.1.
Godsil proved in [8] that and are removal cospectral if and only if for all , the following equation holds for some bijection .
| (1) |
In particular, if we set and , then we have . Then, (1) holds if and only if, for every , there is a bijection between walks of length in and walks of length in . To complete the proof, we show that this correspondence implies that there are analagous bijections when .
For each , let be any walk. Then can be uniquely extended to a walk from to by appending the edge . Also, can be uniquely extended to a walk by appending the edges and . These observations, along with the already existing correspondence between walks and walks, provide one bijection between walks and walks for each , and another bijection between walks and walks. Hence, there is a bijection between walks in starting and ending in , and walks in starting and ending in .
In Definition 3 we describe a type of graph composition which we call the vertex composition.
Definition 3.
Let and be graphs with the vertices and and their neighborhoods , . Define any bijection , then the graph is the graph with the vertex set and the additional edges ; . Note that . This vertex composition will be denoted by the tuple .
Note that if and are both -regular, then the graph will be as well. An example of such a composition is displayed in Figure 1.
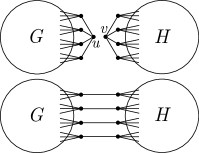
We will be applying the vertex composition in Definition 3 upon sets of graphs, to produce new sets of graphs. The new edges formed in each composition must be done so in a consistent manner. To this end, consider a set of graphs with replaceable vertices such that . Let be the bijections defining the removal cospectral neighborhoods, hence we denote the replaceable vertices as the tuples . Consider a fixed graph with a fixed vertex , and an arbirtrary bijection which is to determine the new edges formed in the first composition . Then the new edges formed in the rest of the compositions are determined by for .
Theorem 4.
Let and be graphs with replaceable vertices where , and . For a third graph with a fixed vertex , the compositions and are cospectral.
Proof 2.2.
The method of proof follows from results of Godsil in [8] which are outlined below. Consider two induced subgraphs within the graph , the first being the subgraph induced by the remaining vertices of , and the second being the subgraph induced by . Then plainly . The submatrix of the walk generating matrix corresponding to the row and column indicies from is denoted as . Then Theorem of Godsil in [8] asserts that
Taking the determinant of both sides, and then employing Theorem 3.1 from [8] on the left hand side, we see that
As is described in [8], the above shows that is determined by the polynomials , and . The terms inside the determinant expression are determined by and where ranges over all subsets of of cardinality at most two.
By considering the same representation for the composition , it is easily seen that the polynomials which determine are, by the cospectrality of and and by Lemma 2.2, the same as the polynomials which determine . Hence, the result follows.
Next, similarly to the definitions above, another special case of Definition 1.1 is in regards to replaceable edges.
Definition 5.
For two graphs and , the edges and are called replaceable if their sets of incident vertices are removal cospectral. If the bijection defining the removal cospectral set is , then we denote the replaceable edges by the tuple .
Lemma 6.
Let and be graphs with replaceable edges where and . Then the vertices incident to remain removal cospectral to the vertices incident to in the graphs and .
Proof 2.3.
Without loss of generality, let , and , . Note that deleting any one or two of the vertices and in gives the same graph as the deletion in the original . So the only case which needs to be considered is when none of the vertices are deleted. A well known representation of , e.g. see [8], is
The analogous representation of is
Comparing these two equations and considering cospectrality of the various vertex deleted graphs, reveals that , and hence the result follows.
In Definition 7, we describe another type of graph composition which we call the edge composition.
Definition 7.
Let and be graphs with the edges and and their respective incident vertices and . Define any bijection , then the graph is the graph with the vertex set , and edge set plus the additional edges . This edge composition will be denoted by the tuple . Figure 2 is an illustration of .
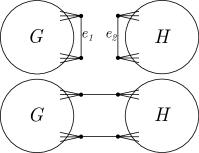
Theorem 8.
Let and be graphs with replaceable edges where , , and . For a third graph containing an edge , where , and an arbitrary bijection , the compositions and are cospectral.
Remark 9.
In the proceeding section we will discuss what happens when these constructions are applied to regular graphs. In the special case when all graphs involved are 3-regular, the vertex composition and edge composition mimic, respectively, the types 3 and 2 breeding operations discussed in [2]. From [2] we then know various properties of the resulting cospectral graphs. For example, is planar or bipartite if and only if and both are, similarly for . Also, and being Hamiltonian is a necessary condition for or to be Hamiltonian. The study of cospectral 3-regular graphs with differing Hamiltonicity is itself a topic of research, e.g. see [5, 7].
3 Constructing cospectral regular graphs
In the following, we only consider replaceable vertices, however an analogous method can be easily obtained for replaceable edges. We begin with a set of cospectral -regular graphs , each of order , with the vertices , such that are replaceable vertices for any choice of graphs and , and where We now illustrate how to use this set for the construction of new cospectral -regular graphs. Consider a second set of cospectral -regular graphs , of order , defined similarly to above with replaceable vertices , and let the bijections defining these removal cospectral sets be . Choose an arbitrary bijection for the first composition . Then, by applying Theorem 4 multiple times, all of the compositions for and are cospectral. This produces a set of cardinality cospectral -regular graphs on vertices. Note that choosing a different bijection could potentially produce an alternate set of cardinality cospectral graphs. The tedious notation here should be cleared up upon viewing the example below. Essentially we are just ensuring that the new edges are connected to the appropriate vertices.
Example 1
The cubic graphs in Figure 3 are cospectral with replaceable vertices and the cubic graphs in Figure 3 are also cospectral with replaceable vertices . The removal cospectral bijections are such that and for . First, consider the graph and an arbitrary bijection . For this example we chose for . Then the graph obtained from the composition is the first graph displayed in Figure 4. The second graph displayed in Figure 4 is obtained from the composition . By Theorem 4, these two graphs are cospectral. Next, we consider the graph and construct two more cospectral graphs with the compositions and , displayed as the final two graphs in Figure 4. Then, by Theorem 4, we can conclude that all four graphs displayed in Figure 4 are cospectral.
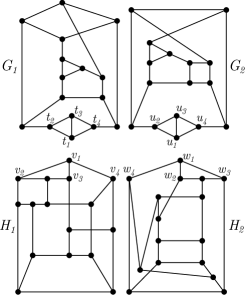
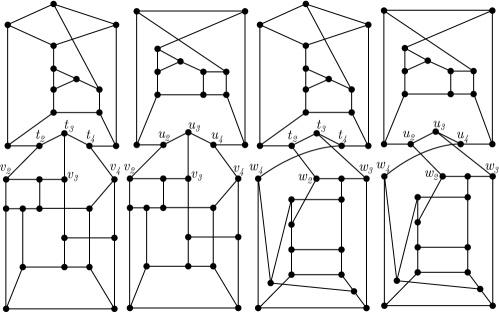
We now make a couple of remarks about this method. First, it should be noted that cospectral -regular graphs produced by this method have cyclic edge connectivity of at most . Hence, any cospectral graphs with larger cyclic edge connectivity can not be produced in this manner. Second, the set of graphs could be chosen to have cardinality one. In such a case, any vertex in the one graph may be chosen as its “replaceable” vertex.
4 Computational results
Cubic graphs provide a nice platform for conducting experiments because it is computationally tractable to perform exhaustive searches over the set of all cubic graphs of small order, say . We provide various computational results in relation to replaceable vertices/edges and cubic graphs. In Table 1 we display the number of cubic graphs that possess replaceable vertices or edges within themselves, such that those vertices or edges lie in different orbits.
Let NUS3 (non-unique spectrum) denote a cubic graph which is cospectral with at least one other cubic graph, then in Table 2 we demonstrate the commonness of replaceable vertices/edges among the cubic graphs which are NUS3.
| Order | Total graphs | Contain rep. edge | % | Contain rep. vertex | % |
|---|---|---|---|---|---|
| 12 | 85 | 3 | 3.6 | 2 | 2.4 |
| 14 | 509 | 16 | 3.1 | 8 | 1.6 |
| 16 | 4060 | 115 | 2.8 | 49 | 1.2 |
| 18 | 41301 | 670 | 1.6 | 354 | 0.9 |
| 20 | 510489 | 4516 | 0.9 | 1993 | 0.4 |
| Order | NUS3 graphs | Contain rep. edge | % | Contain rep. vertex | % |
|---|---|---|---|---|---|
| 14 | 6 | 6 | 100 | 4 | 66.7 |
| 16 | 83 | 77 | 92.8 | 65 | 78.3 |
| 18 | 956 | 868 | 90.8 | 800 | 83.7 |
| 20 | 9779 | 9529 | 97.4 | 9271 | 94.8 |
| 22 | 114635 | 114304 | 99.7 | 111325 | 97.1 |
One possible explanation for the dramatic increase in commonness from Table 1 to Table 2 is that replaceable edges and vertices are often, in some sense, “retained” when cospectral graphs are created. This implies that we should be able to construct an increasing proportion of such graphs as the order increases. This appears to be the case, as can be seen in Table 3 which displays the number of cubic graphs which are NUS3 and the number of those which can be obtained as a result of the construction in Section 3. Recall that NUS3 graphs obtained by the construction in Section 3 have cyclic edge connectivity no larger than three; since these are the only graphs that can be obtained by our method, we also include the number of these in Table 3, and use NUS3C to denote such graphs.
| Order | NUS3 graphs | NUS3C graphs | Number constructed | % (NUS3) | % (NUS3C) |
|---|---|---|---|---|---|
| 14 | 6 | 6 | 4 | 66.7 | 66.7 |
| 16 | 83 | 65 | 40 | 48.2 | 61.5 |
| 18 | 956 | 841 | 492 | 51.5 | 58.5 |
| 20 | 9779 | 7604 | 6163 | 63.0 | 81.0 |
| 22 | 114635 | 89858 | 78775 | 68.7 | 87.7 |
As a final remark, denote the set of all cubic graphs of order which are NUS3 as , and then the subset of which consists of graphs which are produced by one of the constructions, denote as . Then Table 3 suggests the following conjecture, which we leave untouched for future investigations.
Conjecture 1.
References
- [1] Abiad, A., Haemers, W. H. (2012) Cospectral graphs and regular orthogonal matrices of level 2. Electron. J. Combin. 19, 13–29.
- [2] Baniasadi, P., Ejov, V., Filar, J. A., Haythorpe, M. (2016) Genetic theory for cubic graphs, SpringerBriefs in Operations Research, Springer Publishing Company.
- [3] Bapat, R. B., Karimi, M. (2016) Construction of cospectral regular graphs, Mat. Vesnik 68, 66–76.
- [4] Blazsik, Z. L., Cummings, J., Haemers, W. H. (2015) Cospectral regular graphs with and without a perfect matching. Disc. Math. 338, 199–201.
- [5] Borkar, V. S., Ejov, V., Filar, J. A., Nguyen, G. T. (2012) Hamiltonian Cycle Problem and Markov Chains., Springer Science & Business Media, pp. 7.
- [6] Cvetkovic, D., Rowlinson, P., Simic, S. (1997) Eigenspaces of Graphs., Cambridge University Press.
- [7] Filar, J. A., Gupta, A., Lucas, S. K. (2005) Connected cospectral graphs are not necessarily both Hamiltonian. Aust. Math. Soc. Gaz. 32, 193.
- [8] Godsil, C. D. (1992) Walk Generating Functions, Christophell-Darboux Identities and the Adjacency Matrix of a Graph. Combin. Probab. Comput. 1, 13–25.
- [9] Godsil, C. D., Mckay, B. D. (1982) Construction of cospectral graphs. Aequationes Math. 25, 257–268.
- [10] Rowlinson, P. (1993) The Characteristic Polynomials of Modified Graphs. Disc. App. Math. 67, 209–219.
- [11] Schwenk, A. J. (1979) Removal-cospectral sets of vertices in a graph. Proc. 10th Southeastern International Conference on Combinatorics, Graph Theory & Computing, Utilitas Math., Winnipeg, Manitoba.