Contextual Bandits with Large Action Spaces: Made Practical

We provide the first efficient algorithms for contextual bandits with continuous, linearly structured action spaces and general function approximation. Following Chernozhukov et al. (2019); Xu and Zeevi (2020); Foster et al. (2020), we adopt a modeling approach, and assume rewards for each context-action pair $(x,a)$ are structured as

Here $\phi(x,a)\in\mathbb{R}^{d}$ is a known context-action embedding (or feature map) and $g^{\star}\in\mathcal{G}$ is a context embedding to be learned online, which belongs to an arbitrary, user-specified function class $\mathcal{G}$. Our algorithm, SpannerIGW, is computationally efficient (in particular, the runtime and memory are independent of the number of actions) whenever the user has access to (i) an online regression oracle for supervised learning over the reward function class, and (ii) an action optimization oracle capable of solving problems of the form

for any $\theta\in\mathbb{R}^{d}$. The former oracle follows prior approaches to finite-action contextual bandits (Foster and Rakhlin, 2020; Simchi-Levi and Xu, 2021; Foster and Krishnamurthy, 2021), while the latter generalizes efficient approaches to (non-contextual) linear bandits (McMahan and Blum, 2004; Dani et al., 2008; Bubeck et al., 2012; Hazan and Karnin, 2016). We provide a regret bound for SpannerIGW which scales as $\sqrt{\operatorname{poly}(d)\cdot T}$, and—like the computational complexity—is independent of the number of actions. Beyond these results, we provide a particularly practical variant of SpannerIGW (SpannerGreedy), which enjoys even faster runtime at the cost of slightly worse ($\operatorname{poly}(d)\cdot{}T^{2/3}$-type) regret.

On the technical side, we show how to efficiently combine the inverse gap weighting technique (Abe and Long, 1999; Foster and Rakhlin, 2020) previously used in the finite-action setting with optimal design-based approaches for exploration with linearly structured actions. This offers a computational improvement upon the results of Xu and Zeevi (2020); Foster et al. (2020), which provide algorithms with $\sqrt{\operatorname{poly}(d)\cdot{}T}$-regret for the setting we consider, but require enumeration over the action space. Conceptually, our results expand upon the class of problems for which minimax approaches to exploration (Foster et al., 2021b) can be made efficient.

As with previous approaches based on regression oracles, SpannerIGW is simple, practical, and well-suited to flexible, general-purpose function approximation. In extensive experiments ranging from thousands to millions of actions, we find that our methods typically enjoy superior performance compared to existing baselines. In addition, our experiments validate the statistical model in Eq. 1 which we find to be well-suited to learning with large-scale language models (Devlin et al., 2019).

Following a standard approach to developing efficient contextual bandit methods, we take a modeling approach, and work with a user-specified class of regression functions $\mathcal{F}\subseteq(\mathcal{X}\times\mathcal{A}\rightarrow[-1,1])$ that aims to model the underlying mean reward function. We make the following realizability assumption (Agarwal et al., 2012; Foster et al., 2018; Foster and Rakhlin, 2020; Simchi-Levi and Xu, 2021).

Without further assumptions, there exist function classes $\mathcal{F}$ for which the regret of any algorithm must grow proportionally to $\lvert\mathcal{A}\rvert$ (e.g., Agarwal et al. (2012)). In order to facilitate generalization across actions and achieve sample complexity and computational complexity independent of $\lvert\mathcal{A}\rvert$, we assume that each function $f\in\mathcal{F}$ is linear in a known (context-dependent) feature embedding of the action. Following Xu and Zeevi (2020); Foster et al. (2020), we assume that $\mathcal{F}$ takes the form

where $\phi(x,a)\in\mathbb{R}^{d}$ is a known, context-dependent action embedding and $\mathcal{G}$ is a user-specified class of context embedding functions.

This formulation assumes linearity in the action space (after featurization), but allows for nonlinear, learned dependence on the context $x$ through the function class $\mathcal{G}$, which can be taken to consist of neural networks, forests, or any other flexible function class a user chooses. For example, in news article recommendation, $\phi(x,a)=\phi(a)$ might correspond to an embedding of an article $a$ obtained using a large pre-trained language-model, while $g(x)$ might correspond to a task-dependent embedding of a user $x$, which our methods can learn online. Well-studied special cases include the linear contextual bandit setting (Chu et al., 2011; Abbasi-Yadkori et al., 2011), which corresponds to the special case where each $g\in\mathcal{G}$ has the form $g(x)=\theta$ for some fixed $\theta\in{\mathbb{R}}^{d}$, as well as the standard finite-action contextual bandit setting, where $d=\lvert\mathcal{A}\rvert$ and $\phi(x,a)=e_{a}$.

We let $g^{\star}\in\mathcal{G}$ denote the embedding for which $f^{\star}=f_{g^{\star}}$. We assume that $\sup_{x\in\mathcal{X},a\in\mathcal{A}}\|\phi(x,a)\|\leq 1$ and $\sup_{g\in\mathcal{G},x\in\mathcal{X}}\|g(x)\|\leq 1$. In addition, we assume that $\operatorname{span}(\{\phi(x,a)\})={\mathbb{R}}^{d}$ for all $x\in\mathcal{X}$.

For each regression function $f\in\mathcal{F}$, let $\pi_{f}(x_{t})\vcentcolon=\operatorname*{arg\,max}_{a\in\mathcal{A}}f(x_{t},a)$ denote the induced policy, and define $\pi^{\star}\vcentcolon=\pi_{f^{\star}}$ as the optimal policy. We measure the performance of the learner in terms of regret:

The computational efficiency of Algorithm 1 hinges on the ability to efficiently compute an approximate optimal design (or, by convex duality, the John ellipsoid (John, 1948)) for the set $\left\{\phi(x_{t},a)\right\}_{a\in\mathcal{A}}$. All off-the-shelf optimal design solvers that we are aware of require solving quadratic maximization subproblems, which in general cannot be reduced to a linear optimization oracle (Definition 1). While there are some special cases where efficient solvers exist (e.g., when $\mathcal{A}$ is a polytope (Cohen et al. (2019) and references therein)), computing an exact optimal design is NP-hard in general (Grötschel et al., 2012; Summa et al., 2014). To overcome this issue, we use the notion of a barycentric spanner, which acts as an approximate optimal design and can be computed efficiently using an action optimization oracle.

The following result shows that any barycentric spanner yields an approximate optimal design.

Using an algorithm introduced by Awerbuch and Kleinberg (2008), one can efficiently compute the $C$-approximate barycentric spanner for the set $\left\{\phi(x,a)\right\}_{a\in\mathcal{A}}$ using$O(d^{2}\log_{C}d)$ an action optimization oracle; their method is restated stated as Algorithm 5 in Appendix A.

While the regret bound for Algorithm 1 scales with $T^{2/3}$, which is not optimal, this result constitutes the first computationally efficient algorithm for contextual bandits with linearly structured actions and general function approximation. Additional features include:

• •

  Simplicity and practicality. Appealing to uniform exploration makes Algorithm 1 easy to implement and highly practical. In particular, in the case where the action embedding does not depend on the context (i.e., $\phi(x,a)=\phi(a)$) an approximate design can be precomputed and reused, reducing the per-round runtime to $\widetilde{O}(\mathcal{T}_{\mathsf{Sq}}+\mathcal{T}_{\mathsf{Opt}})$ and the maximum memory to $O(\mathcal{M}_{\mathsf{Sq}}+d)$.

• •

  Lifting optimal design to contextual bandits. Previous bandit algorithms based on optimal design are limited to the non-contextual setting, and to pure exploration. Our result highlights for the first time that optimal design can be efficiently combined with general function approximation.

To analyze Algorithm 1, we follow a recipe introduced by Foster and Rakhlin (2020); Foster et al. (2021b) based on the Decision-Estimation Coefficient (DEC),¹¹1The original definition of the Decision-Estimation Coefficient in Foster et al. (2021b) uses Hellinger distance rather than squared error. The squared error version we consider here leads to tighter guarantees for bandit problems where the mean rewards serve as a sufficient statistic. defined as $\mathsf{dec}_{\gamma}(\mathcal{F})\vcentcolon=\sup_{\widehat{f}\in\operatorname{{conv}}(\mathcal{F}),x\in\mathcal{X}}\mathsf{dec}_{\gamma}(\mathcal{F};\widehat{f},x)$, where

Foster et al. (2021b) consider a meta-algorithm which, at each round $t$, (i) computes $\widehat{f}_{t}$ by appealing to a regression oracle, (ii) computes a distribution $p_{t}\in\Delta(\mathcal{A})$ that solves the minimax problem in Eq. 3 with $x_{t}$ and $\widehat{f}_{t}$ plugged in, and (iii) chooses the action $a_{t}$ by sampling from this distribution. One can show (Lemma 7 in Appendix A) that for any $\gamma>0$, this strategy enjoys the following regret bound:

More generally, if one computes a distribution that does not solve Eq. 3 exactly, but instead certifies an upper bound on the DEC of the form $\mathsf{dec}_{\gamma}(\mathcal{F})\leq\macc@depth\char 1\relax\frozen@everymath{\macc@group}\macc@set@skewchar\macc@nested@a 111{}_{\gamma}(\mathcal{F})$, the same result holds with $\mathsf{dec}_{\gamma}(\mathcal{F})$ replaced by $\macc@depth\char 1\relax\frozen@everymath{\macc@group}\macc@set@skewchar\macc@nested@a 111{}_{\gamma}(\mathcal{F})$. Algorithm 1 is a special case of this meta-algorithm, so to bound the regret it suffices to show that the exploration strategy in the algorithm certifies a bound on the DEC.

Using Lemma 3, one can upper bound the first term in Eq. 4 by $O(T\sqrt{C_{\operatorname{{opt}}}d/\gamma})$. The regret bound in Theorem 1 follows by choosing $\gamma$ to balance the two terms.

We conduct experiments on three datasets, whose details are summarized in Table 1. oneshotwiki (Singh et al., 2012; Vasnetsov, 2018) is a named-entity recognition task where contexts are text phrases preceding and following the mention text, and where actions are text phrases corresponding to the concept names. amazon-3m (Bhatia et al., 2016) is an extreme multi-label dataset whose contexts are text phrases corresponding to the title and description of an item, and whose actions are integers corresponding to item tags. Actions are embedded into ${\mathbb{R}}^{d}$ with $d$ specified in Table 1. We construct binary rewards for each dataset, and report 90% bootstrap confidence intervals (CIs) of the rewards in the experiments. We defer other experimental details to Section D.1. Code to reproduce all results is available at https://github.com/pmineiro/linrepcb.

We compare SpannerGreedy and SpannerIGW with their finite-action counterparts $\varepsilon$-Greedy and SquareCB (Foster and Rakhlin, 2020) on the oneshotwiki-14031 dataset. We consider bilinear models in which regression functions take the form $f(x,a)=\langle\phi(a),Wx\rangle$ where $W$ is a matrix of learned parameters; the deep models of the form $f(x,a)=\langle\phi(a),W\macc@depth\char 1\relax\frozen@everymath{\macc@group}\macc@set@skewchar\macc@nested@a 111{g}(x)\rangle$, where $\macc@depth\char 1\relax\frozen@everymath{\macc@group}\macc@set@skewchar\macc@nested@a 111{g}$ is a learned two-layer neural network and $W$ contains learned parameters as before.²²2Also see Section D.1 for details. Table 2 presents our results. We find that SpannerIGW performs best, and that both spanner-based algorithms either tie or exceed their finite-action counterparts. In addition, we find that working with deep models uniformly improves performance for all methods. We refer to Table 4 in Section D.3 for timing information.

Finite-action contextual bandit algorithms can explore excessively in the presence of redundant actions. To evaluate performance in the face of redundancy, we augment oneshotwiki-311 by duplicating action the final action. Table 3 displays the performance of SpannerIGW and its finite-action counterpart, SquareCB, with a varying number of duplicates. We find that SpannerIGW is completely invariant to duplicates (in fact, the algorithm produces numerically identical output when the random seed is fixed), but SquareCB is negatively impacted and over-explores the duplicated action. SpannerGreedy and $\varepsilon$-Greedy behave analogously (not shown).

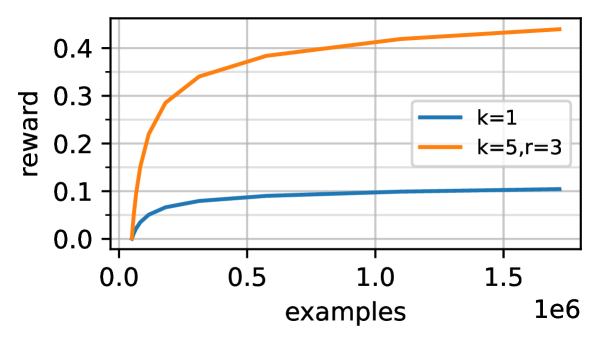
We conduct a large scale experiment using the amazon-3m dataset. Following Sen et al. (2021), we study the top-$k$ setting where $k$ actions are selected at each round. Out of the total number of actions sampled, we let $r$ denote the number of actions sampled for exploration. We apply SpannerGreedy for this dataset and consider regression functions similar to the deep models discussed before. The setting $(k=1)$ corresponds to running our algorithm unmodified, and $(k=5,r=3)$ corresponds to selecting 5 actions per round and using 3 exploration slots. Fig. 1 in Section D.4 displays the results. For $(k=1)$ the final CI is $[0.1041,0.1046]$, and for $(k=5,r=3)$ the final CI is $[0.438,0.440]$.

In the setup with $(k=5,r=3)$, our results are directly comparable to Sen et al. (2021), who evaluated a tree-based contextual bandit method on the same dataset. The best result from Sen et al. (2021) achieves roughly 0.19 reward with $(k=5,r=3)$, which we exceed by a factor of 2. This indicates that our use of embeddings provides favorable inductive bias for this problem, and underscores the broad utility of our techniques (which leverage embeddings). For $(k=5,r=3)$, our inference time on a commodity CPU with batch size 1 is 160ms per example, which is slower than the time of 7.85ms per example reported in Sen et al. (2021).

There is a long line of research on computationally efficient methods for contextual bandits with general function approximation, typically based on reduction to either cost-sensitive classification oracles (Langford and Zhang, 2007; Dudik et al., 2011; Agarwal et al., 2014) or regression oracles (Foster et al., 2018; Foster and Rakhlin, 2020; Simchi-Levi and Xu, 2021). Most of these works deal with a finite action spaces and have regret scaling with the number of actions, which is necessary without further structural assumptions (Agarwal et al., 2012). An exception is the works of Foster et al. (2020) and Xu and Zeevi (2020), both of which consider the same setting as the present paper. Both of the algorithms in these works require solving subproblems based on maximizing quadratic forms (which is NP-hard in general (Sahni, 1974)), and cannot directly take advantage of the linear optimization oracle we consider. Also related is the work of Zhang (2021), which proposes a posterior sampling-style algorithm for the setting we consider. This algorithm is not fully comparable computationally, as it requires sampling from specific posterior distribution; it is unclear whether this can be achieved in a provably efficient fashion.

The linear contextual bandit problem is a special case of our setting in which $g^{\star}(x)=\theta\in\mathbb{R}^{d}$ is constant (that is, the reward function only depends on the context through the feature map $\phi$). The most well-studied families of algorithms for this setting are UCB-style algorithms and posterior sampling. With a well-chosen prior and posterior distribution, posterior sampling can be implemented efficiently (Agrawal and Goyal, 2013), but it is unclear how to efficiently adapt this approach to accomodate general function approximation. Existing UCB-type algorithms require solving sub-problems based on maximizing quadratic forms, which is NP-hard in general (Sahni, 1974). One line of research aims to make UCB efficient by using hashing-based methods (MIPS) to approximate the maximum inner product (Yang et al., 2021; Jun et al., 2017). These methods have runtime sublinear (but still polynomial) in the number of actions.

For the problem of non-contextual linear bandits (with either stochastic or adversarial rewards), there is a long line of research on efficient algorithms that can take advantage of linear optimization oracles (Awerbuch and Kleinberg, 2008; McMahan and Blum, 2004; Dani and Hayes, 2006; Dani et al., 2008; Bubeck et al., 2012; Hazan and Karnin, 2016; Ito et al., 2019); see also work on the closely related problem of combinatorial pure exploration (Chen et al., 2017; Cao and Krishnamurthy, 2019; Katz-Samuels et al., 2020; Wagenmaker et al., 2021). In general, it is not clear how to lift these techniques to contextual bandits with linearly-structured actions and general function approximation. We also mention that optimal design has been applied in the context of linear bandits, but these algorithms are restricted to the non-contextual setting (Lattimore and Szepesvári, 2020; Lattimore et al., 2020), or to pure exploration (Soare et al., 2014; Fiez et al., 2019). The only exception we are aware of is Ruan et al. (2021), who extend these developments to linear contextual bandits (i.e., where $g^{\star}(x)=\theta$), but critically use that contexts are stochastic.

Another line of research provides efficient contextual bandit methods under specific modeling assumptions on the context space or action space that differ from the ones we consider here. Zhou et al. (2020); Xu et al. (2020); Zhang et al. (2021); Kassraie and Krause (2022) provide generalizations of the UCB algorithm and posterior sampling based on the Neural Tangent Kernel (NTK). These algorithms can be used to learn context embeddings (i.e., $g(x)$) with general function approximation, but only lead to theoretical guarantees under strong RKHS-based assumptions. For large action spaces, these algorithms typically require enumeration over actions. Majzoubi et al. (2020) consider a setting with nonparametric action spaces and design an efficient tree-based learner; their guarantees, however, scale exponentially in the dimensionality of action space. Sen et al. (2021) provide heuristically-motivated but empirically-effective tree-based algorithms for contextual bandits with large action spaces, with theoretical guarantees when the actions satisfy certain tree-structured properties. Lastly, another empirically-successful approach is the policy gradient method (e.g., Williams (1992); Bhatnagar et al. (2009); Pan et al. (2019)). On the theoretical side, policy gradient methods do not address the issue of systematic exploration, and—to our knowledge—do not lead to provable guarantees for the setting considered in our paper.