Continuous Decoding of Daily-Life Hand Movements from Forearm Muscle Activity for Enhanced Myoelectric Control of Hand Prostheses*
Abstract
State-of-the-art motorized hand prostheses are endowed with actuators able to provide independent and proportional control of as many as six degrees of freedom (DOFs). The control signals are derived from residual electromyographic (EMG) activity, recorded concurrently from relevant forearm muscles. Nevertheless, the functional mapping between forearm EMG activity and hand kinematics is only known with limited accuracy. Therefore, no robust method exists for the reliable computation of control signals for the independent and proportional actuation of more than two DOFs. A common approach to deal with this limitation is to pre-program the prostheses for the execution of a restricted number of behaviors (e.g., pinching, grasping, and wrist rotation) that are activated by the detection of specific EMG activation patterns. However, this approach severely limits the range of activities users can perform with the prostheses during their daily living. In this work, we introduce a novel method — based on a long short-term memory (LSTM) network — to continuously map forearm EMG activity onto hand kinematics. Critically, unlike previous work, which often focuses on simple and highly controlled motor tasks, we tested our method on a dataset of activities of daily living (ADLs): the KIN-MUS UJI dataset. To the best of our knowledge, ours is the first reported work on the prediction of hand kinematics that uses this challenging dataset. Remarkably, we show that our network is able to generalize to novel untrained ADLs. Our results suggest that the presented method is suitable for the generation of control signals for the independent and proportional actuation of the multiple DOFs of state-of-the-art hand prostheses.
I INTRODUCTION
The high costs and the often poor functional outcomes associated with hand transplantation [1] have spurred considerable research efforts into designing hand prostheses. Significant progress in mechatronics has allowed the development and commercialization of motorized hand prosthesesiiihttps://tinyurl.com/ottobockus-bebionic,iiiiiihttps://tinyurl.com/ossur-i-limb,iiiiiiiiihttps://www.taskaprosthetics.com/ endowed with as many as eighth degrees of freedom (DOF) actuated by up to six motors [2].
Despite these technological advances, major limitations in neural interfacing strongly affect the usability and functionality of these devices [3]. Such limitations are generally so severe that prosthetic hands often have functional capabilities not dissimilar to transplanted hands, tend to be considered as mere assisting tools by their users [4], and have an average abandonment rate as high as 23% [5].
Both invasive and non-invasive interfaces with either the central [6, 7] or the peripheral [8, 9] nervous system are theoretically suitable to extract adequate control signals for the prostheses.
However, in practice, non-invasive interfaces with the peripheral system — that record surface electromyographic signals (EMG) from remnant muscles [10] — are often preferred in clinical settings due to their better cost-effectiveness.
Despite being non-invasive, such methods still allow the extraction of information about the neural drive to the muscles, and thus about the motor task the user wants to perform [3]. Whenever possible, EMG signals are recorded from the forearm, where the 15 extrinsic muscles mediating wrist and finger movements are located [11]. However, despite the large body of research aimed at understanding the functional mapping between forearm EMG activity patterns and hand movements [12, 13, 14], this mapping is still currently known only with limited accuracy and is thus the subject of an active area of investigation [15]. Consequently, up to date, there is no established method to extract reliable control signals from the EMGs to actuate all the DOFs of state-of-the-art prostheses independently and proportionally.
| Training Set | Validation Set | Test Set | |||
|---|---|---|---|---|---|
| ID | Description | ID | Description | ID | Description |
| 1 | Coin: from table to change purse | 21 | Milk carton: pour content into jug | 24 | Toothpaste tube: squeeze content on toothbrush |
| 2 | Zip: open and close | 22 | Jug: pour content into glass | 25 | Spray bottle: spray content on table |
| 3 | Coin: from change purse to table | 23 | Glass: pour content into jug | 26 | Cloth: wipe table (5 sec) |
| 4 | Wooden cube: pick and place (twice) | ||||
| 5 | Iron: pick and place | ||||
| 6 | Screwdriver: grasp and screw 360∘ | ||||
| 7 | Nut: grasp and screw onto bolt | ||||
| 8 | Key: grasp, insert into lock, and turn 180∘ | ||||
| 9 | Door handle: turn 30∘ | ||||
| 10 | Shoelaces: tie | ||||
| 11 | Jar lid: grasp, unscrew, and place (twice) | ||||
| 12 | Button: pass through buttonholes (twice) | ||||
| 13 | Compression stockings: apply to left arm | ||||
| 14 | Knife: cut piece of clay | ||||
| 15 | Spoon: bring to mouth (five times) | ||||
| 16 | Pen: pick, write own name, and place | ||||
| 17 | Paper sheet: fold and insert into envelope | ||||
| 18 | Paper clip: put on envelope | ||||
| 19 | Keyboard: type | ||||
| 20 | Phone: grasp, bring to ear, and place | ||||
A traditional strategy to overcome this obstacle is to program the prostheses to only actuate a single DOF at a time. Such a strategy ensures that the extraction of two distinct activation patterns (one per direction) suffices to have robust control over the selected DOF. However, in this case, users have to use time-consuming heuristics (e.g., co-contractions) to switch between DOFs, until the desired one is selected [16]. Most modern hand prostheses adopt a similar principle: they can still only recognize two activation patterns, but these are directly mapped to distinct hand functions (e.g., grip types) rather than individual joint movements [2].
Recent research efforts have led to the development of techniques based on pattern recognition that can detect up to 12 activation patterns [17, 18, 19]. This strategy (implemented also in recent commercial devicesivivivhttps://coaptengineering.com/,vvvhttps://www.i-biomed.com/) eliminates the need to issue specific commands to switch between functions.
Despite the increase in efficiency, pattern recognition approaches still suffer from significant limitations. First, the users can only interact with the environment using the limited set of actions the prostheses can execute. Second, these actions can only be executed one at a time; this implies that, for example, the users cannot simultaneously perform a grasp and a wrist rotation (e.g., to rotate a doorknob) unless this combined action is explicitly programmed. Third, the users typically have little or no control over action speed and applied force.
Regression-based methods promise to address some of these issues by allowing independent, simultaneous and proportional control of multiple DOFs, and have been attracting the attention of several research groups [20, 21]. Such methods try to map EMG signals — concurrently recorded from multiple sites — onto the movement velocity of the available DOFs. A few recent studies conducted with amputees have demonstrated the robustness of linear regression methods and their superior functional performance compared to conventional control techniques in both laboratory settings [9] and daily life [22]. Nevertheless, the number of controlled DOFs in these studies was as small as two (namely, wrist rotation and hand aperture), which significantly limited participants’ dexterity. For instance, they could still not control their prosthetic fingers individually, which is one of the most desired features among amputees [23].
Numerous research groups have investigated the use of non-linear regression methods to extract richer control signals from the forearm EMGs for the independent and proportional control of multiple DOFs (e.g., [24, 25, 26, 27]). These studies achieved remarkable offline prediction of the kinematics of up to 22 hand joint angles by using simultaneously recorded multisite forearm EMG activation patterns. Nonetheless, the simple, repetitive, and highly controlled motor behaviors used in these studies cast doubt on the ability of the proposed methods to generalize to realistic motor behaviors and online settings. As a matter of fact, it is well documented that the EMG patterns recorded from movement-relevant muscles during the execution of specific movements involving few joints might change drastically depending on the configuration of other still joints. For example, [15] reported wrist-position-dependent amplitude modulations of finger flexor EMGs up to 70% during the execution of individual finger movements. This might partially explain the poor correlations observed between offline and online myoelectric control performance [21].
These reasons motivate the need to develop and validate prediction algorithms using EMGs and kinematics recorded during the execution of realistic motor behaviors. To this end, in this work, we introduce a long short-term memory (LSTM) network [28] to perform the online mapping of the forearm EMG activities, recorded during the execution of everyday activities, onto the corresponding hand kinematics. Specifically, we test our approach on a recently published dataset of activities of daily living (ADLs), the KIN-MUS UJI dataset [29]. Remarkably, we show that the trained network is able to generalize to novel ADLs that were not used during training. To the best of our knowledge, ours is the first reported work on the prediction of this dataset.
II METHODS
II-A Dataset
To validate our method, we tried to learn a stable functional mapping between the forearm EMG activities and hand kinematics recorded during the execution of activities of daily living (ADLs). To this end, we used the KIN-MUS UJI dataset [29]. This dataset contains recordings of muscle activities (7 channels) and hand kinematics (18 DOFs) of 22 participants during the execution of 26 representative activities of daily living. Each activity was performed by the participants only once and lasted several seconds. Further details about the performed activities are reported for convenience in Table I.
The muscle activities were recorded using surface bipolar electrodes, whose locations were chosen to maximize the extraction of information generated by the forearm muscles [30]. The hand kinematics were recorded using an instrumented glove (CyberGlove, CyberGlove Systems LLC), which tracked fingers’ and wrist’s joint angles. The recorded ADLs include the 20 actions of the Sollerman Hand Function Test (SHFT) [31], which are commonly used to assess hand function in clinical settings and involve the interaction with objects of different sizes and weights, such as coins, cutlery, and irons. All the analyses reported in this work are based on the data from participants 1 through 20. Data from participants 21 and 22 presented missing data and were thus discarded.
Importantly, most proposed methods for the online mapping of forearm EMGs onto hand kinematics and for the classification of hand movements are validated using the Ninapro database [32]. However, the datasets included in this database mainly consist of simple and highly controlled movements, such as fingers’ flexion with static wrist posture and different types of grips. This is in stark contrast with the dataset we used in this work, where every task involves a markedly different form of interaction with daily living objects, in addition to a reaching and a release phase. For this reason, mappings learned on this dataset promise a superior ability to generalize to online settings.
II-B Signal Preprocessing
The hand joint angles were acquired at a sampling rate of 100Hz. The EMG signals were acquired at a sampling rate of 1000Hz with a passband between 20Hz and 460Hz. The kinematic data were then zero-phase lowpass filtered with a Butterworth filter (cut-off frequency: 5Hz). To extract the EMG envelopes, the EMGs were rectified and zero-phase lowpass filtered with a Butterworth filter (half power frequency: 3Hz). The EMG signals were subsequently subsampled to 100Hz.
The reaching, manipulation, and release phases present in the original dataset were appropriately concatenated. Since previous studies have reported significant correlations between muscle activity and joint accelerations [33], we chose to adopt an acceleration-based kinematic representation. To this aim, we numerically differentiated the hand joint angles twice to compute joint accelerations. All the analyses present in this work were conducted in MATLAB (MATLAB 2020a, The MathWorks, Natick, MA).
II-C Feature Extraction
An influential study on feature selection for the classification of EMG signals [34] reported that features based on signal energy and those based on frequency content tend to provide superior classification performance. Inspired by this work, we built an EMG feature set composed of EMG envelopes and EMG spectrograms. The spectrograms were computed on 50ms Kaiser windows within the frequency range 20Hz-400Hz; the resulting signals were upsampled in time to 100Hz and binned in frequency (500 bins).
Subsequently, we applied principal component analysis (PCA) to reduce the dimensionality of the EMG feature set to 25; the extracted projections retained about 99% of the original data variance.
Since EMG signals might give rise to different movements depending on the starting kinematic properties, such as posture [15], we extended our feature set by also including information about the previous movements. Specifically, we included the hand joint accelerations observed 30ms in the past. The complete feature set thus includes EMG features and kinematic features. Finally, the resulting features were z-scored.
II-D Data Augmentation
To avoid over-reliance on the kinematic features, we augmented the training dataset by adding, for each action, 60 additional training examples. In these examples, the kinematic features were corrupted by noise, while the EMG features were left unchanged. Out of the 60 additional examples, 30 were corrupted by white Gaussian noise and 30 by colored noise with a maximum frequency of ; in both cases the maximum amplitude was . Overall, this procedure ensures that the networks learn robust features [35, 36].
II-E Network Architecture
To learn the mapping between the complete feature set and hand joint accelerations, we used LSTM-based networks [28]. This choice was motivated by previous work, which showed that the ability of gated recurrent neural networks to learn long-term relationships between signals is instrumental in allowing the prediction of whole-body human motion [37, 38]. Moreover, LSTM-based networks have recently been proved to be effective at predicting wrist position (3 DOFs) [39] and wrist flexion/extension (1 DOFs) [40] by tracking the EMG activity of 2-5 shoulder and arm muscles.
In brief, LSTM networks are recurrent networks of special units. Each unit is endowed with two memory cells (namely, an output memory and a hidden memory ) and three gates (namely, an input gate , a forget gate , and an output gate ). The hidden memory cell allows the network to store and use important input features indefinitely. The input gate modulates the extent to which incoming information is retained; the forget gate modulates the extent to which old information is erased; finally, the output gate extracts information from the hidden memory useful to generate an appropriate output for the current input .
The output, once computed, is stored in the output memory cell.
The gating mechanism is defined by the following equations:
| (1) | ||||||
| (2) | ||||||
| (3) |
where is the current time step and is the element-wise sigmoid function.
The hidden memory content is modified according to
| (4) | ||||
| (5) |
where denotes the element-wise product operator. Finally, the output is determined by
| (6) |
II-F Hyperparameter Optimization
In this work, we considered architectures composed of LSTM layers of units projecting onto a fully connected layer with 36 units, followed by a dropout layer ([41]) with probability , and a final fully connected layer of 18 units. The dynamics of each LSTM layer are defined by equations (1-6). We chose not to consider deeper LSTM architectures since evidence suggests that the benefit of adding more than two layers is generally limited [42].
We used Bayesian hyperparameter optimization (bayesopt() — [43]) to tune , initial learning rate, gradient threshold, and L2 regularization strength. The search ranges were , , and , respectively. The available LSTM units were equally distributed among the layers. The selected cost function was the fraction of unexplained variance on the validation set.
Hyperparameter optimization automatically stopped when the maximum number of 100 cost function evaluations was reached. To efficiently evaluate a candidate hyperparameter set, we trained the parameters of the corresponding network for only three epochs. To further speed up the training time, we based hyperparameter optimization only on the data recorded from participant 1. Following this procedure, we selected, for each depth , the three best networks in terms of validation error. Such networks were further trained for 25 epochs with subject-specific data only. Details about the parameter optimization are provided in the following section. Overall, this strategy allowed us to retrieve a good hyperpameter set reasonably fast: for example, for , hypeparameter optimization was completed in less than one hour (i.e., ).
II-G Parameter Training
The networks were implemented and trained in MATLAB, using the Neural Network Toolbox. Parameter optimization was performed using adaptive moment estimation (Adam, [44]) with a piecewise learning rate schedule with a drop period of 10 epochs and a drop factor of 10%. To speed up training, we performed all the optimizations on a shared GPU (NVIDIA GeForce RTX 2070) using mini batches of 40 sequences. This configuration allowed us to fully train a network in a limited amount of time: for example, for , the training speed was sec/epoch. Parameter optimization automatically stopped if the validation error did not decrease for three consecutive training epochs, or if the maximum number of 30 epochs was reached. For training, validation, and test we used the EMG signals and corresponding hand kinematics recorded during the execution of the tasks 1-20, 21-23, and 24-26, respectively. We refer to Table I for further details about the selected tasks.
II-H Assessment of Network Performance
To measure the reconstruction quality of the network’s predictions, we computed the Pearson’s correlation coefficients () between ground-truth and predicted angular accelerations, and the normalized reconstruction errors (). The normalized reconstruction error is defined as the fraction of unexplained variance (i.e., ).
To assess the potential benefit of the recurrence present in LSTM networks, we also considered standard non-linear feedforward (FF) networks as a baseline. Specifically, we considered FF networks of depth with hyperbolic tangent activation function. A dropout layer with probability was added between each couple of layers. For each depth, similarly to what was done for LSTM networks, we performed Bayesian hyper-parameter optimization. In this case, we set the maximum number of units to 3000. All the other parameter ranges are as above.
To measure the robustness of the trained networks, we also assessed their ability to make accurate predictions in the presence of random noise corrupting the angular acceleration measurements. Specifically, we considered noise levels of amplitudes . The amplitudes are defined as percentages of the maximum angular acceleration measured during a task, across all joints.
In the following sections, we report the test performance (measured on the independent activities of daily living 24, 25, and 26) of the resulting six networks: three LSTM and three FF networks.
III RESULTS
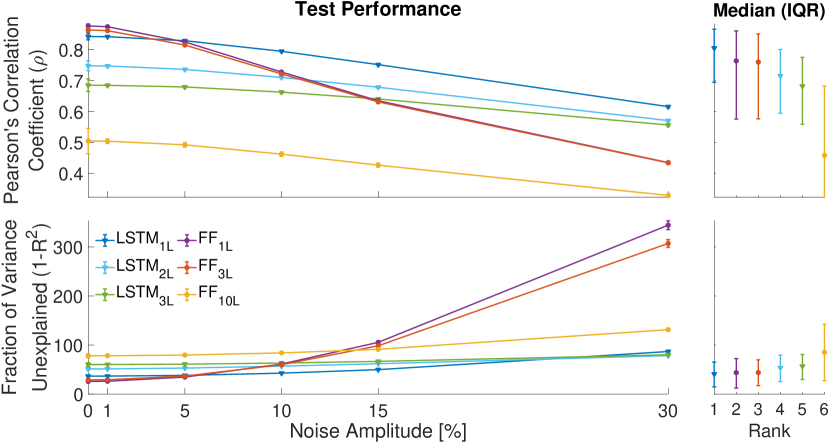
Figure 1 summarizes the performance of the networks trained after hyper-parameter optimization: for low levels noise () most networks are able to predict the joint angular velocities measured during the performance of the test tasks well (). This is not trivial since these test tasks were not used at any stage of the training. The only exception is represented by the 10-layer feedforward network, which shows poor performance also for low levels of noise. In this low noise regime, the 1-layer and 3-layer feedforward networks (FF1L, FF3L) and the 1-layer LSTM network (LSTM1L) display the best performance ().
However, as the noise increases ( — simulating a more realistic scenario of online usage of the prosthesis), the performance pattern changes drastically: whereas all feedforward networks become unable to make accurate predictions (), all LSTM-based networks are still able to track the ground-truth data with sufficient accuracy (). Overall, the network LSTM1L displayed the most accurate and robust performance across all tested noise levels (Fig. 1 — right), and will be the main focus of the following sections.
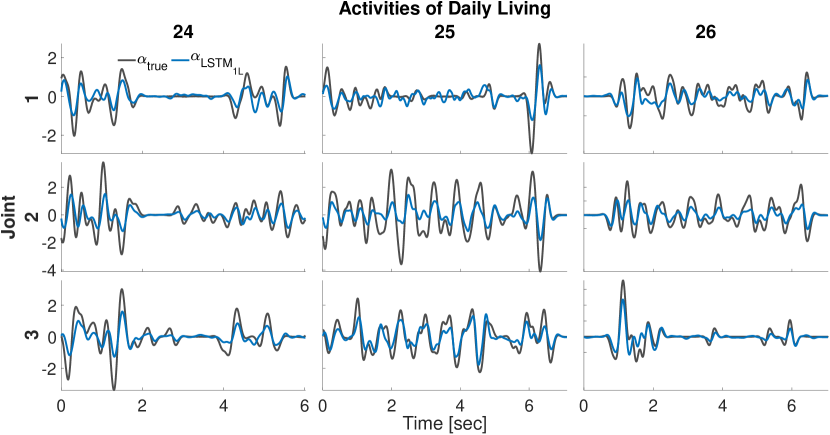
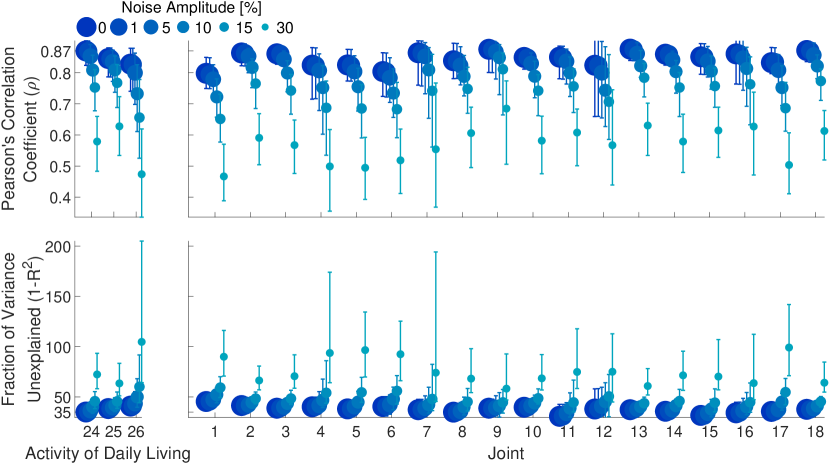
Figure 2 shows ground-truth and LSTM1L predictions of angular accelerations during test tasks for few representative joint angles. It is worth noting that the network makes good predictions even though the hand kinematics vary substantially across tasks. As a matter of fact, despite the heterogeneity of hand kinematics across joints and the variability across tasks, LSTM1L average performance does not drastically change across joints (Fig. 3 — right) or task (Fig. 3 — left). However, it is clear that the network’s prediction performance for some joints (e.g., joints 1, 4, and 17) degrades substantially when the noise amplitude is particularly high.
IV DISCUSSION
In this work, we trained LSTM and feedforward (FF) neural networks to predict hand kinematics during the execution of activities of daily living from forearm EMG muscles. In the presence of low noise levels, shallow FF networks and LTSM-based networks tend to perform similarly. In the presence of higher noise levels — which simulate a scenario that is more relevant for the online control of a hand prosthesis — LSTM-based networks tend to over-perform FF networks. This suggests that the mapping learned by the recurrent models is more robust and more suitable for online prosthesis control. Stacking multiple LSTM layers did not provide any apparent additional benefits, in agreement with previous reports [42]. In fact, we found that the best performing network was the one with only one hidden LSTM layer: LSTM1L
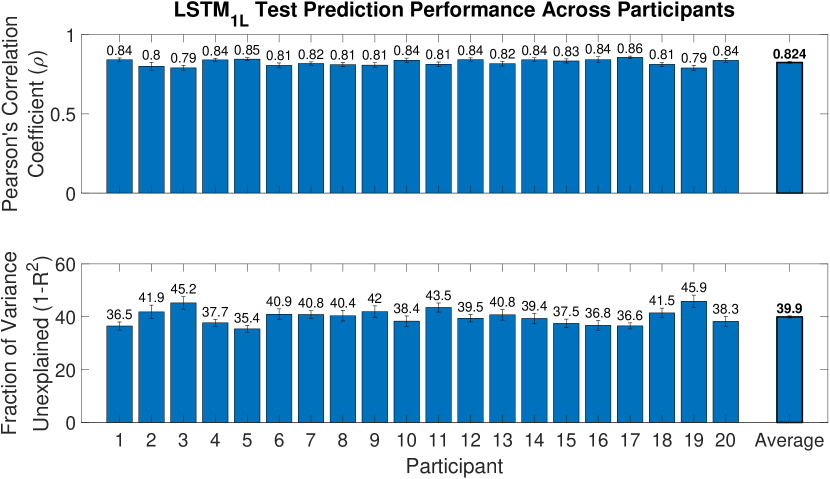
Remarkably, we showed that the mapping learned by LSTM1L is robust enough to generalize across activities of daily living it was never trained on. Furthermore, the overall performance is stable across tasks and hand joints. To the best of our knowledge, these are the first prediction results to ever be reported in the literature on this dataset.
Notable technological advances in mechatronics have led to the development of highly flexible human-like motorized hand prostheses. Nevertheless, the complex functional mapping between forearm muscle signals and hand kinematics, together with the tendency to validate control algorithms on datasets of highly simplified movements, have severely hampered the design of efficient algorithms capable of providing natural and dexterous control of these devices. In this work, we introduced a method based on LSTM networks to learn such a mapping. Critically, unlike previous works, we validated the method on a dataset of realistic arm and hand movements involving complex interactions with daily living objects. Our results show that the mapping is stable across postures and interaction types. This suggests that our method can be used to provide a natural interface between forearm muscle activity and state-of-the-art motorized hand prostheses. Future work will deal with developing a suitable interface layer between the network’s predictions and the actuators of the prosthesis.
References
- [1] Martin Aman et al. “Bionic hand as artificial organ: Current status and future perspectives” In Artificial Organs 43.2 Wiley Online Library, 2019, pp. 109–118
- [2] Alexandre Calado, Filomena Soares and Demétrio Matos “A review on commercially available anthropomorphic myoelectric prosthetic hands, pattern-recognition-based microcontrollers and sEMG sensors used for prosthetic control” In 2019 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), 2019, pp. 1–6 IEEE
- [3] Dario Farina et al. “The extraction of neural information from the surface EMG for the control of upper-limb prostheses: emerging avenues and challenges” In IEEE Transactions on Neural Systems and Rehabilitation Engineering 22.4 IEEE, 2014, pp. 797–809
- [4] Stefan Salminger et al. “Functional and psychosocial outcomes of hand transplantation compared with prosthetic fitting in below-elbow amputees: a multicenter cohort study” In PLoS One 11.9 Public Library of Science San Francisco, CA USA, 2016, pp. e0162507
- [5] Elaine A Biddiss and Tom T Chau “Upper limb prosthesis use and abandonment: a survey of the last 25 years” In Prosthetics and orthotics international 31.3 SAGE Publications Sage UK: London, England, 2007, pp. 236–257
- [6] Jennifer L Collinger et al. “High-performance neuroprosthetic control by an individual with tetraplegia” In The Lancet 381.9866 Elsevier, 2013, pp. 557–564
- [7] Jianjun Meng et al. “Noninvasive electroencephalogram based control of a robotic arm for reach and grasp tasks” In Scientific Reports 6 Nature Publishing Group, 2016, pp. 38565
- [8] Suzanne Wendelken et al. “Restoration of motor control and proprioceptive and cutaneous sensation in humans with prior upper-limb amputation via multiple Utah Slanted Electrode Arrays (USEAs) implanted in residual peripheral arm nerves” In Journal of neuroengineering and rehabilitation 14.1 Springer, 2017, pp. 121
- [9] Janne M Hahne, Meike A Schweisfurth, Mario Koppe and Dario Farina “Simultaneous control of multiple functions of bionic hand prostheses: Performance and robustness in end users” In Science Robotics 3.19 Science Robotics, 2018
- [10] Stefan Grushko, Tomáš Spurnỳ and Martin Černỳ “Control Methods for Transradial Prostheses Based on Remnant Muscle Activity and Its Relationship with Proprioceptive Feedback” In Sensors 20.17 Multidisciplinary Digital Publishing Institute, 2020, pp. 4883
- [11] Ebubechi Okwumabua, Margaret A. Sinkler and Bruno Bordoni “Anatomy, Shoulder and Upper Limb, Hand Muscles” In StatPearls [Internet] StatPearls Publishing, 2020
- [12] Charles Long and Mary Eleanor Brown “Electromyographic kinesiology of the hand: muscles moving the long finger” In JBJS 46.8 LWW, 1964, pp. 1683–1706
- [13] Marc H Schieber “Muscular production of individuated finger movements: the roles of extrinsic finger muscles” In Journal of Neuroscience 15.1 Soc Neuroscience, 1995, pp. 284–297
- [14] ZM Li, VM Zatsiorsky and ML Latash “Contribution of the extrinsic and intrinsic hand muscles to the moments in finger joints” In Clinical biomechanics 15.3 Elsevier, 2000, pp. 203–211
- [15] Carl R Beringer et al. “The effect of wrist posture on extrinsic finger muscle activity during single joint movements” In Scientific Reports 10.1 Nature Publishing Group, 2020, pp. 1–11
- [16] Anna Lisa Ciancio et al. “Control of prosthetic hands via the peripheral nervous system” In Frontiers in neuroscience 10 Frontiers, 2016, pp. 116
- [17] Ganesh R Naik, Ali H Al-Timemy and Hung T Nguyen “Transradial amputee gesture classification using an optimal number of sEMG sensors: an approach using ICA clustering” In IEEE Transactions on Neural Systems and Rehabilitation Engineering 24.8 IEEE, 2015, pp. 837–846
- [18] Marina M-C Vidovic et al. “Improving the robustness of myoelectric pattern recognition for upper limb prostheses by covariate shift adaptation” In IEEE Transactions on Neural Systems and Rehabilitation Engineering 24.9 IEEE, 2015, pp. 961–970
- [19] Youngmok Yun et al. “Maestro: an EMG-driven assistive hand exoskeleton for spinal cord injury patients” In 2017 IEEE International Conference on Robotics and Automation (ICRA), 2017, pp. 2904–2910 IEEE
- [20] Janne M Hahne et al. “Linear and nonlinear regression techniques for simultaneous and proportional myoelectric control” In IEEE Transactions on Neural Systems and Rehabilitation Engineering 22.2 IEEE, 2014, pp. 269–279
- [21] Han-Jeong Hwang, Janne Mathias Hahne and Klaus-Robert Müller “Real-time robustness evaluation of regression based myoelectric control against arm position change and donning/doffing” In PLoS One 12.11 Public Library of Science San Francisco, CA USA, 2017, pp. e0186318
- [22] Janne M Hahne et al. “Longitudinal Case Study of Regression-Based Hand Prosthesis Control in Daily Life” In Frontiers in neuroscience 14 Frontiers, 2020, pp. 600
- [23] Francesca Cordella et al. “Literature review on needs of upper limb prosthesis users” In Frontiers in neuroscience 10 Frontiers, 2016, pp. 209
- [24] Jimson G Ngeo, Tomoya Tamei and Tomohiro Shibata “Continuous and simultaneous estimation of finger kinematics using inputs from an EMG-to-muscle activation model” In Journal of neuroengineering and rehabilitation 11.1 BioMed Central, 2014, pp. 1–14
- [25] Parviz Ghaderi, Saeed Karimimehr, Mehran Emadi Andani and Hamid Reza Marateb “Hand kinematics estimation to control prosthetic devices: a nonlinear approach for simultaneous and proportional estimation of 15 dofs” In 2015 22nd Iranian Conference on Biomedical Engineering (ICBME), 2015, pp. 233–238 IEEE
- [26] Agamemnon Krasoulis, Sethu Vijayakumar and Kianoush Nazarpour “Evaluation of regression methods for the continuous decoding of finger movement from surface EMG and accelerometry” In 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), 2015, pp. 631–634 IEEE
- [27] Qin Zhang, Te Pi, Runfeng Liu and Caihua Xiong “Simultaneous and Proportional Estimation of Multijoint Kinematics From EMG Signals for Myocontrol of Robotic Hands” In IEEE/ASME Transactions on Mechatronics 25.4 IEEE, 2020, pp. 1953–1960
- [28] Sepp Hochreiter and Jürgen Schmidhuber “Long short-term memory” In Neural computation 9.8 MIT Press, 1997, pp. 1735–1780
- [29] Néstor J Jarque-Bou et al. “A calibrated database of kinematics and EMG of the forearm and hand during activities of daily living” In Scientific data 6.1 Nature Publishing Group, 2019, pp. 1–11
- [30] Néstor J Jarque-Bou et al. “Identification of forearm skin zones with similar muscle activation patterns during activities of daily living” In Journal of neuroengineering and rehabilitation 15.1 Springer, 2018, pp. 91
- [31] Christer Sollerman and Arvid Ejeskär “Sollerman hand function test: a standardised method and its use in tetraplegic patients” In Scandinavian Journal of Plastic and Reconstructive Surgery and Hand Surgery 29.2 Taylor & Francis, 1995, pp. 167–176
- [32] Manfredo Atzori et al. “Electromyography data for non-invasive naturally-controlled robotic hand prostheses” In Scientific data 1.1 Nature Publishing Group, 2014, pp. 1–13
- [33] Masataka Suzuki, Douglas M Shiller, Paul L Gribble and David J Ostry “Relationship between cocontraction, movement kinematics and phasic muscle activity in single-joint arm movement” In Experimental brain research 140.2 Springer, 2001, pp. 171–181
- [34] Angkoon Phinyomark, Pornchai Phukpattaranont and Chusak Limsakul “Feature reduction and selection for EMG signal classification” In Expert systems with applications 39.8 Elsevier, 2012, pp. 7420–7431
- [35] Stephan Zheng, Yang Song, Thomas Leung and Ian Goodfellow “Improving the robustness of deep neural networks via stability training” In Proceedings of the ieee conference on computer vision and pattern recognition, 2016, pp. 4480–4488
- [36] Andrew Ilyas et al. “Adversarial Examples Are Not Bugs, They Are Features” In NeurIPS, 2019
- [37] Julieta Martinez, Michael J Black and Javier Romero “On human motion prediction using recurrent neural networks” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 2891–2900
- [38] Hongsong Wang and Jiashi Feng “Vred: A position-velocity recurrent encoder-decoder for human motion prediction” In arXiv preprint arXiv:1906.06514, 2019
- [39] Peng Xia, Jie Hu and Yinghong Peng “EMG-based estimation of limb movement using deep learning with recurrent convolutional neural networks” In Artificial organs 42.5 Wiley Online Library, 2018, pp. E67–E77
- [40] Dongwon Kim et al. “Simultaneous Estimations of Joint Angle and Torque in Interactions with Environments using EMG” In 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020, pp. 3818–3824 IEEE
- [41] Nitish Srivastava et al. “Dropout: a simple way to prevent neural networks from overfitting” In The journal of machine learning research 15.1 JMLR. org, 2014, pp. 1929–1958
- [42] Andrej Karpathy, Justin Johnson and Li Fei-Fei “Visualizing and understanding recurrent networks” In arXiv preprint arXiv:1506.02078, 2015
- [43] Jasper Snoek, Hugo Larochelle and Ryan P Adams “Practical bayesian optimization of machine learning algorithms” In Advances in neural information processing systems 25, 2012, pp. 2951–2959
- [44] Diederik P Kingma and Jimmy Ba “Adam: A method for stochastic optimization” In arXiv preprint arXiv:1412.6980, 2014