2.5cm2cm2.5cm2.5 cm
Contribution of quadratic Casimir squared to rotational bands in the interacting boson model
Abstract
Rotational bands are commonly used in the analysis of the spectra of atomic nuclei. The early version of the interacting boson model of Arima and Iachello has been foundational to the description of rotations in nuclei. The model is based on a unitary spectrum generating algebra and an orthogonal (angular momentum) symmetry algebra . A solvable limit of the model contains in its dynamical symmetry chain. The corresponding Hamiltonian is written as a linear combination of linear and quadratic Casimir invariants of all the algebras in the chain. Prompted by these facts, a Hamiltonian containing the quadratic Casimir squared is proposed to evaluate its effects on rotational bands. The additional term yields three undetermined parameters into the theory, which need be obtained from experiment. The lack of data does not allow one to perform a detailed numerical analysis, but a rather restricted one in terms of a one-parameter fit. Nevertheless, these additional terms provide a good description of rotational bands of two nuclei of interest, and .
I Introduction
The atomic nucleus is a non-trivial many-body quantum system which has collective properties resulting in various deformed shapes. A strongly deformed nucleus rotates, exhibiting characteristic rotational band structures with noticeable regularity. A number of different methods have been used to study many-body quantum systems. One of the oldest methods is the shell model which assumes that a single nucleon behaves under the influence of a nuclear mean field. Formally, in this description nucleons populate shells that represent energy levels, going from lower to higher energies. When the number of nucleons equals 2, 8, 20, 28, 50, 82, and 126 the shells are completely filled. These so-called magic numbers represent nuclei with great stability.
A second method which has been widely used in the understanding of the collective behavior of nuclei is the interacting boson model (IBM) originally introduced by Arima and Iachello iach75 ; iach1 ; iach2 ; iach3 ; iach4 ; ibm . The earliest version of the model, applied to even-even nuclei, describes the collective properties in terms of pairs of valence nucleons, which conform a set of interacting and bosons with positive parity and with angular momenta and , respectively. The simplest version of the model, usually referred to as IBM-1, treats both types of nucleons the same so it assumes that there is only a single kind of boson, unlike IBM-2, which treats protons and neutrons separately.
From its very construction, the IBM possesses a symmetry-based formulation and in particular, dynamical symmetries are essential to it. Dynamical symmetries arise when the Hamiltonian of a system can be written in terms of the Casimir (or invariant) operators of a chain of groups (or algebras). A remarkable application of the group (or algebra) chains is in the construction of bases in which the Hamiltonian can be diagonalized, or equivalently, in the construction of bases that transform as representations of the appropriate groups, labeling those states with the corresponding quantum numbers iach75 .
In the IBM-1, with and bosons, the spectrum generating algebra is and it has as a subalgebra generating rotational spectrum iach75 ; iach2 . Rotational bands lie within irreducible representations (irreps) of , which are subspaces invariant under the generators of the group. The IBM-1 Hamiltonian in thus written as a linear combination of linear and quadratic Casimir invariants of all the algebras in a given chain iach75 . Those terms are usually refer to as - and -body terms, respectively. In most calculations only up to two-body terms are retained.
The aim of the present paper is to introduce a -body contribution to the IBM-1 Hamiltonian to study its effects on the rotational bands of nuclei. This contribution will thus be proportional to the quadratic Casimir squared.
This paper is organized as follows. In Sec. II some necessary material on the IBM is reviewed in order to introduce notation and conventions. This includes elementary definitions about dynamical symmetries. In Sec. III the Hamiltonian for 2-body structures is reviewed, to immediately discuss the -body Hamiltonian in Sec. IV. In Sec. V a fit to experimental data for rotational bands is presented, via a one-parameter fit. Results and conclusions are given in Sec. VI. The paper is complemented by two appendices, where some useful material can be found.
II A survey on the IBM
In this section, an elementary survey on the IBM is provided in order to introduce notation and conventions. For this purpose, the first concept to be reviewed is that of a dynamical symmetry. A comprehensive introduction on the subject can be found in Ref. leviatan , so only a few salient facts will be repeated here.
Dynamical symmetries arise when the Hamiltonian of a system can be written as a sum of commuting operators in the form
| (1) |
where are the Casimir operators of a chain of nested algebras111For ease of notation, no distinction between a group, for instance , and its algebra, , will be made, but denote both by a capital letter, .
| (2) |
If this is the case, the spectrum can be solved in an explicit analytic form: The eigenstates and eigenvalues are labeled by quantum numbers , which characterize irreps of the algebras in the chain. Note that the condition of the nesting of the algebras in (2) is indispensable for constructing a set of commuting operators and hence for obtaining an analytic solution. For definiteness, stands for the spectrum generating algebra of the system so operators corresponding to physical observables can be written in terms of its generators and is the symmetry algebra iach95 . Note also that the symmetry is broken and the only remaining symmetry is which is the true symmetry of the problem. A algebra can have several chains so analytic solutions can only be obtained whenever the Hamiltonian can be written in terms only of the Casimir operators of a given chain.
As for the IBM-1, it is based on a unitary spectrum generating algebra and an orthogonal (angular-momentum) symmetry algebra . The Hamiltonian is expanded in the elements of and consists of Hermitian, rotational-scalar interactions which conserve the total number of and bosons, leviatan . The IBM-1 admits three chain algebras, namely,
| (3) |
which are known as the vibrational iach1 , the rotational iach2 , and the -unstable limits iach4 . The labels attached to and in chains (3) will serve as a reminder that those algebras have two different realizations depending on the phase choices for the and bosons shi .
The present analysis is concerned with the study of rotational bands, so the chain algebra under consideration is
| (4) |
where the algebras and correspond to prolate and oblate shapes, respectively
A Hamiltonian exhibiting the chain algebra (4) can be constructed as
| (5) |
where and are the linear and quadratic Casimir operators of and and are the quadratic Casimir operators of and , respectively. Since a quadratic Casimir operator is obtained from the product of two creation and two annihilation operators, it is usually referred to as a -body operator. In general, -body operators are constructed from the product of creation and annihilation operators.
The eigenstates of the Hamiltonian (5) can be represented by
| (6) |
where , , , and label the relevant irreps of , , , and , respectively, and and are multiplicity labels leviatan . The quantum numbers for and are not identical but are obtained from each other under the interchange . Hereafter, only the labels are involved, so they will be loosely denoted by for simplicity. No confusion should arise because irreps with correspond to prolate shapes whereas irreps with correspond to oblate shapes bon .
Therefore, for a given , there are several irreps with defined as Pfeifer
| (7a) | |||||
| (7b) | |||||
and for a given irrep there are eigenstates with different expressed in terms of Elliott’s quantum number elliott1 ; elliott2
| (8a) | |||||
| (8d) | |||||
Since
| (9) |
where is the angular momentum operator for a fixed value of , then for a given irrep there is a rotational band with energy levels spaced according to the eigenvalues of , that is to say . In the -body Hamiltonian (5), the energy difference between these rotational bands is given by the quadratic Casimir . In general, the differences would be controlled by higher-order -body invariants in the IBM Hamiltonian. Therefore, in order to obtain a more accurate phenomenological description of the nuclear spectra and be able to understand the role that higher-order terms in the chain group (4) play, the aim of the present work is to propose a general -body Hamiltonian. For this task, the projection operators introduced in Ref. banda come in handy.
III IBM-1 in the rotational limit for -body operators
The building blocks of the IBM-1 are the creation and annihilation operators of the and bosons. Creation operators will be denoted as
so that the commutator of the creation and annihilation operators that are associated with the same boson state equals one, while all other commutators vanish.
In the IBM-1, a Hamiltonian that conserves the total number of bosons is constructed from -body operators, which represent the interactions between bosons. Up to -body operators, the most general Hamiltonian reads
| (12) |
where the Greek indices are a short-hand notation for the two indices in the creation and annihilation operators; for example, , and so on.
The eigenvalue problem for can be solved analytically for some particular cases. To illustrate this point, consider the algebra of the bilinear operators ibm
| (13) |
where , , and the right-hand side of Eq. (13) can be written as
| (14) |
where denote Clebsch-Gordan coefficients and , whose commutation relations are obtained as
| (15) |
The 36 operators defined in Eq. (13) satisfy the Lie algebra of the group. There are also linear combinations of these operators that satisfy the Lie algebras of the and groups ibm . This is referred to as the rotational limit of the IBM ibm ; iach2 . Those linear combinations are given by the following angular momentum and quadrupole operators,
| (16a) | |||||
| (16b) | |||||
Using the commutation relations (15), it is straightforward to show that
| (17a) | |||||
| (17b) | |||||
| (17c) | |||||
which correspond to the commutation relations for the spherical components of the angular momentum operator. Thus, defining the Cartesian components as
| (18a) | |||||
| (18b) | |||||
| (18c) | |||||
the Lie algebra of , namely, , with , is recovered. Henceforth, the sum over repeated indices will be implicit, so expressions as should be understood as .
Following similar steps, the commutation relations of the Lie algebra of can be obtained. Starting from the definitions
| (23) |
it is quite easy to verify that
| (24) |
Using the operators introduced in Eqs. (18c) and (29), the quadratic Casimir in the Hamiltonian (5) reads
| (30) |
whose eigenvalue for the irrep is greiner
| (31) |
The eigenvalues for the other Casimir operators in (5) can be found in Refs. ibm and Pfeifer and will not be given here.
In the -body Hamiltonian with the dynamical symmetry of the chain algebra (4), the energy difference between the rotational bands is given by the eigenvalue (31). In order to gain more control on this difference, a -body -invariant term will be added to Hamiltonian (5); this will be discussed in the following section.
IV Higher-order -invariant terms in the IBM-1 Hamiltonian
The operators listed in Eq. (29) are the generators of the Lie algebra of so they transform in the -dimensional adjoint representation. The tensor product of two adjoint representations can be separated into the symmetric product and the antisymmetric product as
| (32a) | |||
| (32b) | |||
where the different representations are denoted by their dimensions.
Prompted by the above decompositions, let
| (33) |
be an -body tensor operator constructed out of the product of two adjoints, where each term transforms according to the corresponding irrep indicated in the decomposition (32) and are unknown coefficients.
Using the method to construct projection operators which can decompose any of the reducible finite-dimensional representation spaces of contained in the tensor product of two adjoint spaces into irreducible components introduced in Ref. banda , the -body operators can straightforwardly written as
| (34a) | |||
| (34b) | |||
| (34c) | |||
| (34d) |
where should be understood. For definiteness, and are given by
| (35) |
where is a symmetric rank- tensor.
Now, using the tensor operator , Eq. (33), the -body term in the IBM-1 Hamiltonian can readily be constructed as
| (36) |
so a Hamiltonian with up to -body terms that respects the dynamical symmetry in (4) is given by
| (37) |
where the signs of the last two summands have been conveniently chosen to describe the experimental spectra of the nucleus. The eigenfunctions of Hamiltonian (37) have the same quantum numbers as the ones of Hamiltonian (5), namely, for the boson number, for a given irrep, for angular momentum, and for Elliott’s quantum number. Notice that the first three coefficients can be cast into a single one since they contribute only to binding energies and not to excitation energies ibm ; the remaining coefficients depend on the physical system under consideration.
Before evaluating the tensor contraction indicated in , an extra simplification can be exploited. Notice that
| (38) | |||||
where use of Eq. (49) has been made.
Therefore, reduces to
| (39) |
Now, the tensor identities listed in Appendix A of Ref. banda and the commutation relation can be recursively used to rewrite in the form
| (40) |
where
| (41a) | |||||
| (41b) | |||||
| (41c) | |||||
and has explicitly been set. Notice that not only pure -body terms are contained in Eq. (41), but also - and -body terms.
Equations (41), are they stand, can be algebraically worked out to readily obtain their eingenvalues by means of ordinary methods. Appendix B describes one of such methods. However, a further simplification of relations (41) is achieved by using the definition of the quadratic Casimir operator of the Lie algebra of , Eq. (30), along with Eqs. (50) and (56). These terms become
| (42a) | |||||
| (42b) | |||||
| (42c) | |||||
With the above expressions, the Hamiltonian (37) can now be written as
| (43) | |||||
V Fitting experimental data for rotational bands: The one-parameter fit
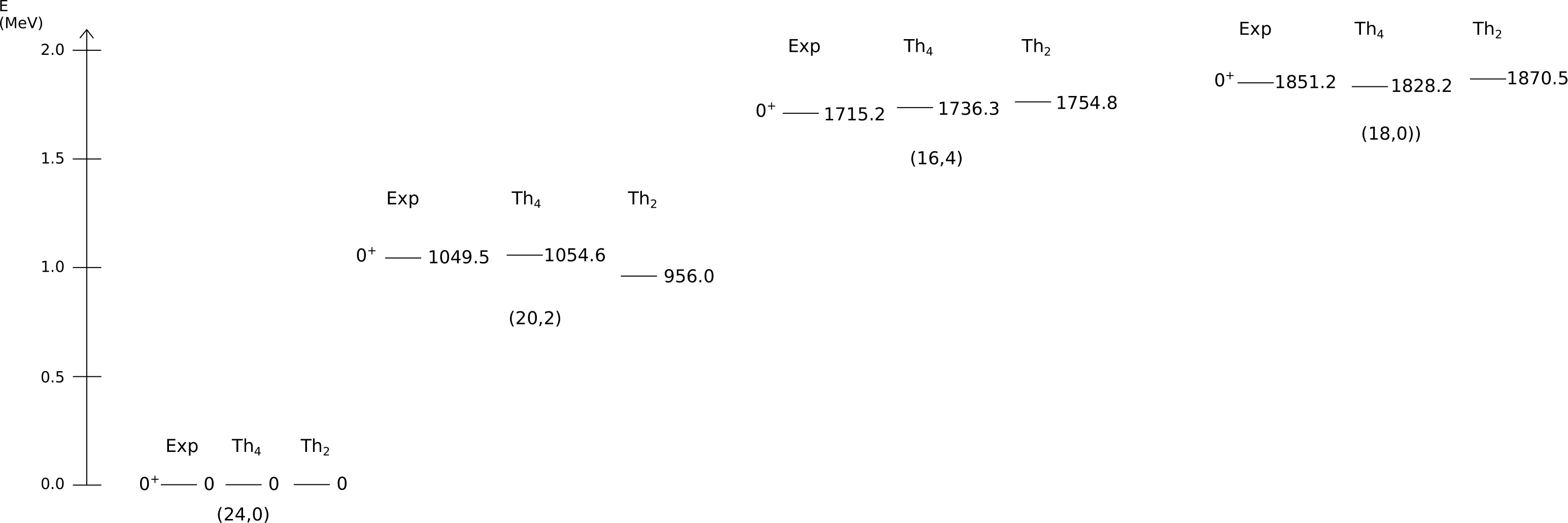
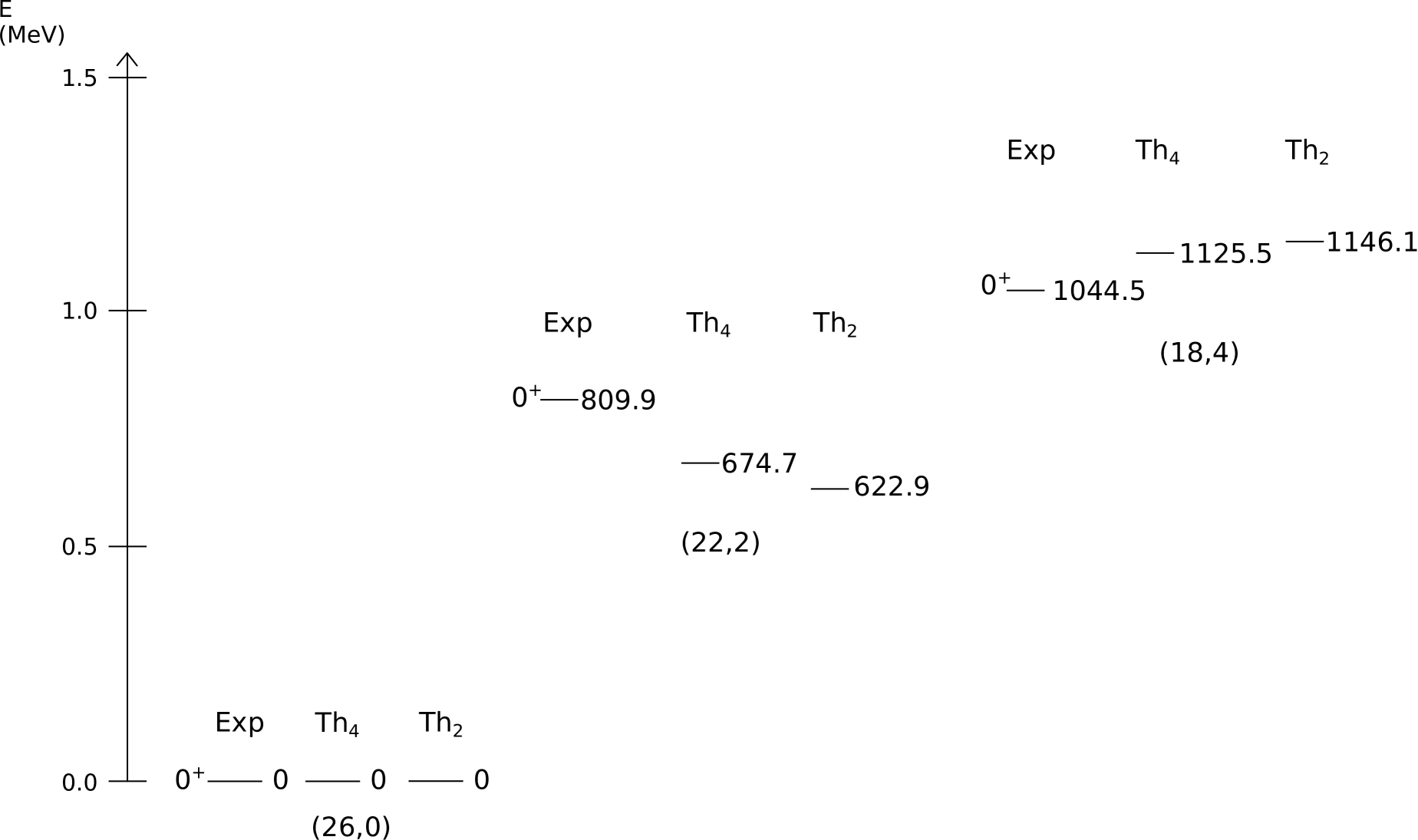
The energy gaps between rotational bands are described in Hamiltonian (43) by four parameters, namely, , , , and . Important information about energy gaps can be learned by determining these parameters via a fit to data. For this task, two effective parameters can be defined, namely, one accompanying the quadratic Casimir and another one accompanying the quadratic Casimir squared, so these four parameters need be recombined accordingly. Unfortunately, the lack of experimental data does not allow one to perform an exploratory fit using the effective parameters, much less using all four parameters. A pragmatic approach is thus required in order to overcome this obstacle. The simplest approach, although perhaps not the optimal one, is to consider a one-parameter fit, either , , , or .
The applicability of a one-parameter fit can be explored in two case examples: 156Gd and 234U. These nuclei are approximately described by the chain group (4), provided some of their rotational bands can be treated as degenerate iach2 . Thus, in this approximation, and taking the spacing between non-degenerate rotational bands as the energy difference of the states with zero angular momentum, the term in the Hamiltonian (43) that yields the best fitting with one parameter for these spacings are
| (46) |
In Figs. 1 and 2 the comparison between the experimental energies of some excited states with zero angular momenta for 156Gd and 234U ga ; u , and the theoretical prediction given by the parameters in (46) is made. In these figures, acccounts for effects of up to -body terms from Hamiltonian (5) whereas accounts for effects of up to -body terms from Hamiltonian (43), with the best-fit parameters indicated in (46). In the degenerate approximation these states correspond to the first excited states for each rotational band which are labelled by an irrep of the group.
VI Concluding remarks
In this work, the -invariant term with up to four-body operators, given in Eq. (36), is introduced in the standard Hamiltonian of the IBM-1, Eq. (5), for the chain symmetry . This term contributes to the energy spacing of the rotational bands that appear when nuclei are described by that specific symmetry.
The energy term originates from the most general -body operator , which is constructed out of tensor product of two generators as given in Eq. (39). The use of the projection operators introduced in Ref. banda applied to yields three main contributions to , each one transforming according to well defined irreps. These contributions are , and defined in Eqs. (41).
After some simplifications, it turns out that , and can be rewritten as linear combinations of the quadratic Casimir of the Lie algebra and its square as displayed in Eq. (42). Thus, the Hamiltonian proposed in (36), with up to fourth order -boson interactions and that respects the dynamical symetry of the rotational limit of the IBM-1, becomes the Hamiltonian given in Eq. (43). In that equation, the parameters , , and describe the energy gaps of the rotational bands that are labeled according to distinct irrep of . These four parameters can be recombined to obtain two effective parameters, one of them accompanying the quadratic Casimir , and the other one accompanying the quadratic Casimir squared. Thus, the fitting to the experimental data can be performed using these two effective parameters. However, because of the lack of experimental data, a one-parameter fitting, either with , , or , was done. That fitting analysis is exemplified for the nuclei 156Gd and 234U. For the former the best fitting arise from , choosing the specific values of the parameters as in (46). It means that, for this nuclei, instead of the standard -body IBM-1 Hamiltonian given in (5) which is used in the literature, a better description is achieved by updating this same Hamiltonian to a -body version using the Casimir squared instead. This situation where a higher-order interaction introduced into the IBM Hamiltonian improves the description of the experimental data is also reported in Refs. Stefanescu ; Heyde ; Casten . There it is shown how cubic terms in the IBM Hamiltonian can be used to describe features like triaxiality for some nuclei.
Similarly, for 234U the best fitting occurs from , with the parameters fixed as in (46). Again, as in the 156Gd case, the -body contribution represents a more accurate description of rotational bands than the standard -body Hamiltonian when fitting to experimental data.
A final closing remark about , , and is that, when they are used independently in the fitting analysis, the resulting energies are very close to each other, differing only in a few hundreds of eV. That subtlety comes from the different Casimir contribution in each term, as shown in (41). It means that the dominant part arises from the squared of .
Acknowledgements.
The authors are grateful to Consejo Nacional de Ciencia y Tecnología (Mexico) for partial support.Appendix A Some useful identities of generators
In this section, some useful identities involving generators are obtained to help simplify relations (41).
Let be the generators of the Lie algebra of the group, with commutation relations .
A simple algebraic manipulation yields
| (47) | |||||
In the same vein as the previous case, it can be shown that
| (50) |
which yields a simplified version of the second summand of Eq. (41c).
Now, reducing the terms containing four ’s is a little bit more involved. For this task, the projection operators and for introduced in Ref. banda , namely,
| (51) | |||||
and
| (52) | |||||
are useful. First, notice that
| (53) |
For , the case, the projector vanishes. Thus, from Eq. (53), it follows that
| (54) |
where the tensor is defined in the Lie algebra of the group.
Appendix B A general method to compute the eigenvalues of
The analyses of nuclei with a large number of valence nucleons involve irreps of high dimensionality. The numerical approach to obtain the corresponding eigenvalues becomes a rather difficult computational task. In this section a general procedure to find the eigenvalues of the operator defined in Eq. (40) is outlined. Recalling that each contribution to transforms according to a specific representation simplifies the analysis.
First, the eigenvalues of for an irrep are the simplest to obtain. Since is the quadratic Casimir of the Lie algebra of , from Eq. (31), simply reads
| (57) |
Now, the eigenvalues and of and given in Eqs. (41b) and (41c), respectively, can be obtained by computing the eigenvalues of the explicit matrix expressions for these operators in a given irrep . A few of those eigenvalues, mainly for the lowest irreps, have been computed with the help of the algorithm described in Ref. algorithm_su3 and are listed in Table 1. However, due to the huge computational effort required in the numerical evaluations, it is more convenient to have analytical expressions instead that can help complete Table 1. For this purpose, a linear regression analysis using the values formerly obtained through the algorithm of Ref. algorithm_su3 can be performed. The conventional technique of a linear regression (see for example Ref. bishop ) requires a linear combination of functions , with , to fit the data set , with . Here indicates the eigenvalue for the corresponding representation .
Let be the vector
| (58) |
in such a way that the function
| (59) |
minimizes the sum of squared errors given by
| (60) |
Since the entries of Table 1 are generated by an unknown function of , the right choice of the set of functions can perfectly fit these data without overfitting.
The choice of
| (63) |
for the regression analysis yields
| (64a) | |||||
| (64b) | |||||
The above expressions exactly reproduce the numerical values obtained with the help of the algorithm of Ref. algorithm_su3 and are also useful to complete Table 1. These entries also agree in full with the eigenvalues obtained from Eqs. (42b) and (42c), so the overall analysis is consistent.
References
- (1) A. Arima and F. Iachello, “Collective nuclear states as representations of a SU(6) group,” Phys. Rev. Lett. 35, 1069 (1975).
- (2) A. Arima and F. Iachello, “Interacting boson model of collective states. I. The vibrational limit,” Annals Phys. 99, 253 (1976).
- (3) A. Arima and F. Iachello, “Interacting boson model of collective nuclear states. II. The rotational limit,” Annals Phys. 111, 201 (1978).
- (4) O. Schollen, F. Iachello and A. Arima, “Interacting boson model of collective nuclear states III. The transition from SU(5) to SU(3),” Annals Phys. 115, 325 (1978).
- (5) A. Arima and F. Iachello, “Interacting boson model of collective nuclear states. IV. The O(6) limit,” Annals Phys. 123, 468 (1979).
- (6) F. Iachello and A. Arima, The Interacting Boson Model (Cambridge, Cambridge University Press, 1987).
- (7) A. Leviatan, “Dynamical symmetries and beyond: Lessons and advances,” AIP Conf. Proc. 2150, 020013 (2019).
- (8) F. Iachello, Lie Algebras and Applications (Springer-Verlag, Berlin, 1995).
- (9) A. M. Shirokov, N. A. Smirnova and Y. F. Smirnov, “Parameter symmetry of the interacting boson model,” Phys. Lett. B 434, 237 (1998).
- (10) D. Bonatsos, “Prolate over oblate dominance in deformed nuclei as a consequence of the SU(3) symmetry and the Pauli principle,” Eur. Phys. J. A 53, 148 (2017).
- (11) W. Pfeifer, An Introduction to the Interacting Boson Model of the Atomic Nucleus (vdf Hochschulverlag an der ETH Zurich, Switzerland, 1998).
- (12) J. P. Elliott, “Collective motion in the nuclear shell model. 1. Classification schemes for states of mixed configuration,” Proc. Roy. Soc. Lond. A 245, 128 (1958).
- (13) J. P. Elliott, “Collective motion in the nuclear shell model. 2. The Introduction of instrinsic wave functions,” Proc. Roy. Soc. Lond. A 245, 562 (1958).
- (14) V. M. Banda Guzmán, R. Flores-Mendieta, J. Hernández and F. d. Rosales-Aldape, “Spin and flavor projection operators in the spin-flavor group,” Phys. Rev. D 102, 036010 (2020).
- (15) W. Greiner and B. Müller, Quantum Mechanics. Symmetries (Springer-Verlag Berlin Heidelberg, 1994).
- (16) R. F. Dashen, E. E. Jenkins and A. V. Manohar, “Spin flavor structure of large baryons,” Phys. Rev. D 51, 3697 (1995).
- (17) C. W. Reich, Nucl. Data Sheets 113, 2537 (2012).
- (18) E. Browne, J. K. Tuli, Nucl. Data Sheets 108, 681 (2007).
- (19) R. Shurtleff, “Formulas for SU(3) matrices,” [arXiv:0908.3864 [math-ph]].
- (20) C. Bishop, Pattern Recognition and Machine Learning (Springer-Verlag New York, 2006).
- (21) I. Stefanescu et al. “IBM-1 description of the fission products Ru-108, Ru-110, Ru-112,” Nucl. Phys. A 789, 125 (2007).
- (22) K. Heyde, P. Van Isacker, M. Waroquier and J. Moreau, “Triaxial shapes in the interacting boson model,” Phys. Rev. C 29, 1420 (1984).
- (23) R. F. Casten, P. Von Brentano, K. Heyde, P. Van Isacker and J. Jolie, “The interplay of -softness and triaxiality in O(6)-like nuclei,” Nucl. Phys. A 439, 289 (1985).