Ssupp
Controlled Creation of a Singular Spinor Vortex
by Circumventing the Dirac Belt Trick
Abstract\\ \vskip21.33955pt
Persistent topological defects and textures are particularly dramatic consequences of superfluidity. Among the most fascinating examples are the singular vortices arising from the rotational symmetry group , with surprising topological properties illustrated by Dirac’s famous belt trick. Despite considerable interest, controlled preparation and detailed study of vortex lines with complex internal structure in fully three-dimensional spinor systems remains an outstanding experimental challenge. Here, we propose and implement a reproducible and controllable method for creating and detecting a singular line vortex from the decay of a non-singular spin texture in a ferromagnetic spin-1 Bose–Einstein condensate. Our experiment explicitly demonstrates the character and the unique spinor properties of the defect. Although the vortex is singular, its core fills with atoms in the topologically distinct polar magnetic phase. The resulting stable, coherent topological interface has analogues in systems ranging from condensed matter to cosmology and string theory.
Introduction
Quantized vortices are topological defects with universal properties that span seemingly disparate areas of science, such as high-energy physics, superconductivity, liquid crystals, and superfluidsVolovik (2003). Superfluids with internal degrees of freedom such as liquid 3He (Ref. (2)) and dilute-gas spinor Bose–Einstein condensatesKawaguchi and Ueda (2012); Stamper-Kurn and Ueda (2013) (BECs) may exist in diverse stable phases, characterised by different broken symmetries of the full interaction Hamiltonian. Distinct states within a given phase of matter transform into one another in several ways, such as through rotations of spin and condensate phase. As a result, a rich phenomenology emerges consisting of topological defects and textures that resemble those predicted to exist in quantum field theories and cosmologyVolovik (2003).
In ordinary scalar superfluids, such as superfluid liquid 4He and dilute Bose–Einstein condensates with frozen internal degrees of freedom, quantized vortices are characterised by the winding of the phase of the macroscopic wave function about any closed loop encircling the vortex lineDonnelly (1991); Fetter (2009). The whole spectrum of phase values converges to the singular vortex line, at which the superfluid density vanishes.
In contrast, spin-1 condensates are described by a three-component spinor, which admits both polar (P) and ferromagnetic (FM) ground-state magnetic phases. For atoms in the FM phase, the magnitude of the spin assumes its maximum value of oneKawaguchi and Ueda (2012); Stamper-Kurn and Ueda (2013), and all of the different physical states are related to each other by spatial rotations of the spinor. The distinguishable states of the system are fully represented by the orientation of a local, orthonormal vector triad defined by the orientation of the atomic spin and rotations about it, corresponding to the elements of the group of three-dimensional (3D) spatial rotations. Mathematical analysisMermin (1979) of this symmetry group indicates that vorticity must be carried either by coreless, non-singular spin textures, or by quantized, singular vortices.
Quantized singular vortices with even winding numbers have the unusual property that they are topologically equivalent to the defect-free state. When the local orientation of the vector triad describing the vortex undergoes an even number of rotations about an axis passing through the system, the triads can be locally and continuously reoriented, smoothly returning the system to a uniform configuration. Equivalently, joining two vortices with winding each can cancel their net vorticity, either when they circulate oppositely or — less obviously — when they wind in the same sense. This essential property has been attributed to Dirac as his eponymous belt trick, a demonstration in which two twists of a belt in the same direction may return it to its original configurationStaley (2010); but the concept also makes an appearance in diverse artistic contexts such as the Balinese candle dance. The significance of the belt trick to our work is that vortices with an odd number of rotations of the vector triad are all equivalent to one another but not to the defect-free state.
In light of their peculiar properties, which have no correspondence in scalar quantum fluids, singular vortices have attracted considerable attention in several different contexts. They have previously been described and indirectly detected in the superfluid liquid 3He- phase Simola et al. (1987); Parts et al. (1995); Vollhardt and Wölfle (1990), where their direct visualisation is challenging. In spin-1 BECs, they have been studied theoretically as the unique class of singular vortices in the FM phaseIsoshima and Machida (2002); Lovegrove et al. (2012); Kobayashi et al. (2012); Lovegrove et al. (2016). Of particular significance is the fact that, although the superfluid density in the FM phase must vanish along the line where the triad orientation is ill-defined, the singular vortex can lower its energy by developing a superfluid core consisting of atoms in the spinless P phase that are excited out of the FM ground-state manifoldRuostekoski and Anglin (2003); Lovegrove et al. (2012, 2016). This phenomenon has been observed experimentally in the spontaneous vorticity of randomly appearing singular defects in quasi-two-dimensional (2D) condensates during a rapid non-equilibrium phase transitionSadler et al. (2006), where the filled vortex cores were detected indirectly by their lack of longitudinal magnetisation. More recently, atomic condensates subjected to momentum-dependent artificial gauge potentials were shown to support filled-core vorticesChen et al. (2018) closely related to those studied in our work. Related but topologically different half-quantum vortices have also been observed in the P phase in a quasi-2D BECSeo et al. (2015). Despite these efforts, the controlled creation of singular vortices remains an experimental challenge.
Here, in a striking manifestation of the topological constraints of the order parameter, we transform a non-singular vortex that is topologically equivalent to one with a 4 winding of the FM order parameter into a pair of spatially-separated singular vortices with 2 winding each (Fig. 1). We thereby circumvent the smooth topological unwinding permitted by Dirac’s belt trick, dividing the equivalent of a rotation into two rotations that, once separated, cannot individually unwind. We find experimentally that the singular FM vortex cores are filled and expanded by atoms in the P phase. This establishes the existence of a coherent topological interfaceBorgh and Ruostekoski (2012); Lovegrove et al. (2016), where the order parameter continuously interpolates between the two magnetic phases within the vortex core. Such topological interfaces are universal across many areas of physics, including superfluid liquid 3He at the boundary between coexisting and phasesFinne et al. (2006); Bradley et al. (2008), early-universe cosmology and superstring theory as domain wallsKibble (1976) and branesSarangi and Tye (2002), and solid-state physics supporting exotic superconductivityBert et al. (2011). Finally, we explicitly demonstrate the character of the vortices by enacting a change of basis, which appears experimentally as a spatial separation of phase singularities in the three spinor components. Our work directly addresses the challenges of controlled creation and simple parameter tuning of a fully 3D, singular vortex, marking the path for a detailed study and direct imaging of the underlying topological phenomena.

Results
Theoretical background. The macroscopic wave function of a spin-1 BEC can be written in terms of the atomic density and the three-component spinor as . In the FM phase, we have Kawaguchi and Ueda (2012)
| (1) |
which can be obtained by applying a 3D spin rotation to the representative FM spinor . Any FM spinor is thus fully specified by the three Euler angles , , and , corresponding to the group of rotations in three dimensions, . As a consequence, any FM state can be represented by the orientation of a vector triad defined by the condensate spin vector () and an orthogonal vector (Methods).
The topological stability of a singular vortex is characterised by the way closed contours encircling the defect map into the order parameter spaceMermin (1979). If the order parameter space image of such a closed loop can be continuously contracted to a point, the defect is not topologically stable against transformations to the vortex-free state. The parameter space may be represented geometrically as a solid sphere of radius , where the direction of the radius vector of any point within the sphere gives an axis of rotation and its length gives the rotation angle (Fig. 2). However, rotations about axes and are equivalent, and thus diametrically opposite points on the surface must be identified. Therefore, only two topologically distinct classes of singular vortex lines exist: those that trace between identified, diametrically opposite points an even number of times, including zero; and those that trace between them an odd number of times. Mathematically, the vortex charges form the two-element group .
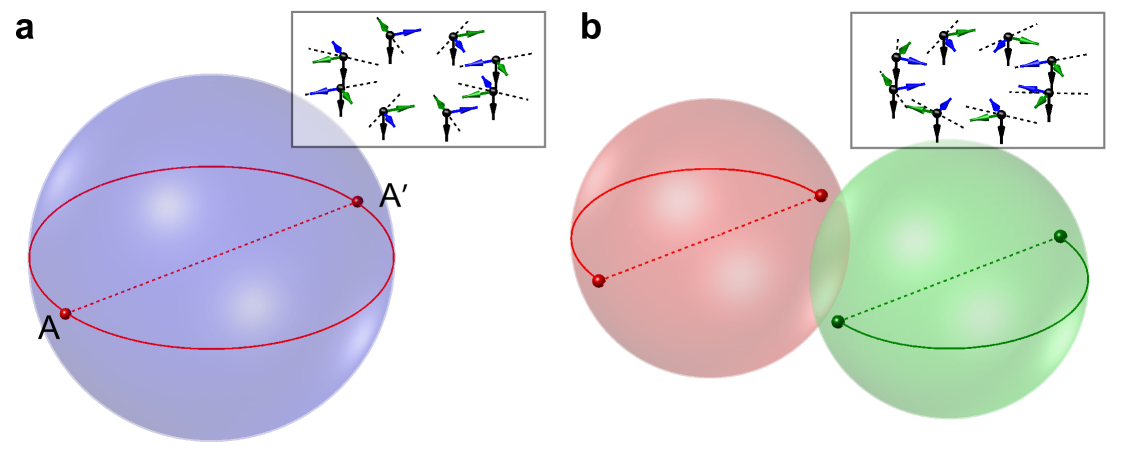
Since an even number of connections between identified points always corresponds to a loop contractible to a point, the vortices in the first (even) class can be continuously deformed into the defect-free state, and those in the second (odd) class can be continuously deformed to a singly quantized singular vortex. The essence of Dirac’s belt trick is that a 4 winding, with a path in parameter space that goes about the sphere once, is equivalent to the defect-free state.
SO(3) vortex creation. Our primary result is a controlled creation method of a pair of singular spinor vortices with non-trivial rotational topology from a non-singular texture. In the initial non-singular vortex — also known as a coreless vortex, baby skyrmion, or Anderson–Toulouse–Chechetkin/Mermin–HoVollhardt and Wölfle (1990) vortex in superfluid liquid helium — the circulation is not quantized and the spin forms a fountain-like profile that adjusts to the angular momentum of the superfluid. This characteristic fountain texture has been experimentally observed in BECsLeanhardt et al. (2003); Leslie et al. (2009); Choi et al. (2012a). If the non-singular spin texture is not constrained, e.g., energetically, it can continuously deform to a vortex-free state. We find, however, that a very sharp bending of the vortex spin profile, corresponding to a strong but incomplete longitudinal magnetisation, induces an instability wherein the non-singular spin texture decays by splitting into a pair of singly quantized vortices Lovegrove et al. (2016), as shown in Fig. 3a–d (see also Supplementary Note 1). Once separated, the resulting singly quantized vortices can no longer unwind on their own, thus circumventing the Dirac belt trick along the lines of Fig. 2. The decay paths of the non-singular vortex therefore include not only its unwinding by local spin rotations or departure from the condensate at its boundaryLeanhardt et al. (2003), but also its splitting into a pair of singly quantized vortices that will, in turn, also ultimately leave the condensate. Numerically, a bending with magnetisation that is explicitly conserved is sufficient to guarantee the splitting, as shown in Figs. 3 and 4.
The splitting process of the non-singular spin texture is fundamentally different from the previously observed decay of a multiply quantized singular vortex into multiple singly quantized vorticesLeanhardt et al. (2002); Shin et al. (2004); Huhtamäki et al. (2006); Isoshima et al. (2007), in which magnetic trapping fields froze the atomic spin degree of freedom to produce a scalar BEC. In contrast, our experiment relies upon an all-optical trap that allows the atoms to retain their spinor nature. Even so, imprinting a multiply quantized singular vortex fully spin-polarises the condensate and spinor dynamics do not occur due to conservation of the maximised longitudinal magnetisation. The critical feature of our experiment is that the decay dynamics begin with an imprinted non-singular spin texture. The incomplete magnetisation ensures active spin degrees of freedom, and a spinor description is required. The relevant algebra of the line-vortex charges in our splitting process in thus obeys the cyclic group with only the elements and . Both evenly quantized and non-singular vortices are represented by the trivial element and their splitting corresponds to the group operation , with no counterpart in a scalar BEC.
We use time-varying magnetic fields (Fig. 3e) to initiate the creation process experimentally with a condensate initially prepared in , where denotes the th spinor component. Such techniquesNakahara et al. (2000); Pietilä and Möttönen (2009) have been used to prepare, e.g., non-singularLeanhardt et al. (2003); Choi et al. (2012a, b) and multiply quantized vorticesShin et al. (2004), as well as monopolesRay et al. (2014), skyrmionsLee et al. (2018), and knotsHall et al. (2016).
Controlled creation of singular vortices in scalar BECsMatthews et al. (1999); Andersen et al. (2006) and continuous textures in spinor systemsLeslie et al. (2009) have also been achieved using phase imprinting methods. In our experiment the atoms experience an applied magnetic field described by
| (2) |
where is the strength of the quadrupole contribution and is a time-dependent bias field that shifts the location of the point at which the magnetic field vanishes (the field zero) to on the -axis. We initially choose such that the field zero is slightly above the condensate (see Methods) and the magnetic field is approximately uniform (Fig. 3e).
Reducing the bias field slowly induces adiabatic spin rotations as the magnetic field zero passes through the condensate from above, trailed by a 3D nodal lineRay et al. (2014) (Fig. 3e). At faster magnetic field ramp rates the otherwise identical experiment yields controllably incomplete adiabatic spin rotations, and results in a non-singular vortexLeanhardt et al. (2002); Choi et al. (2012b) with additional populations in and (Fig. 3a,b and Supplementary Note 1). The atoms are released from the trap after an evolution time , measured from the completion of the field ramp. Following a period of ballistic expansion they are imaged, whereupon we observe a pair of singly quantized vortices in with filled cores containing atoms in , as shown in Figs. 3c,d and 4. These results agree with a numerical simulation of the locally relaxed state (Supplementary Note 1). One of these singular spinor vortices typically departs the condensate before the other, thus lowering the condensate energyLovegrove et al. (2012, 2016) and leaving behind a single vortex (Fig. 5). The main dissipative sources, as in scalar BECsFetter (2009); Rosenbusch et al. (2002), are a non-vanishing thermal cloud and potential collisions with high-temperature atoms.

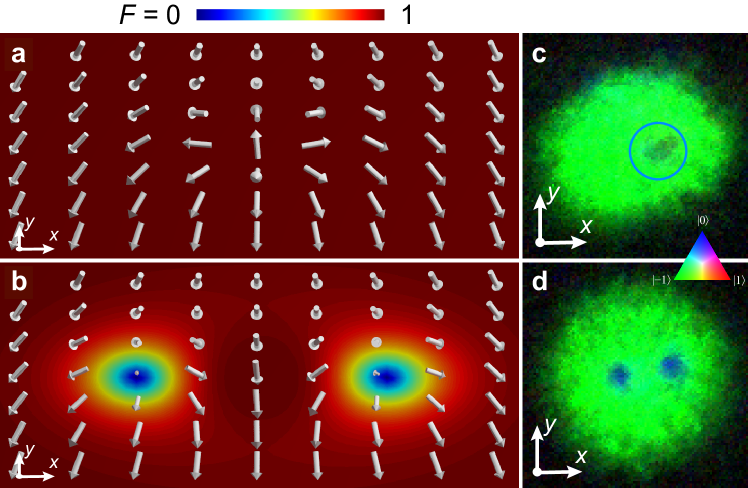
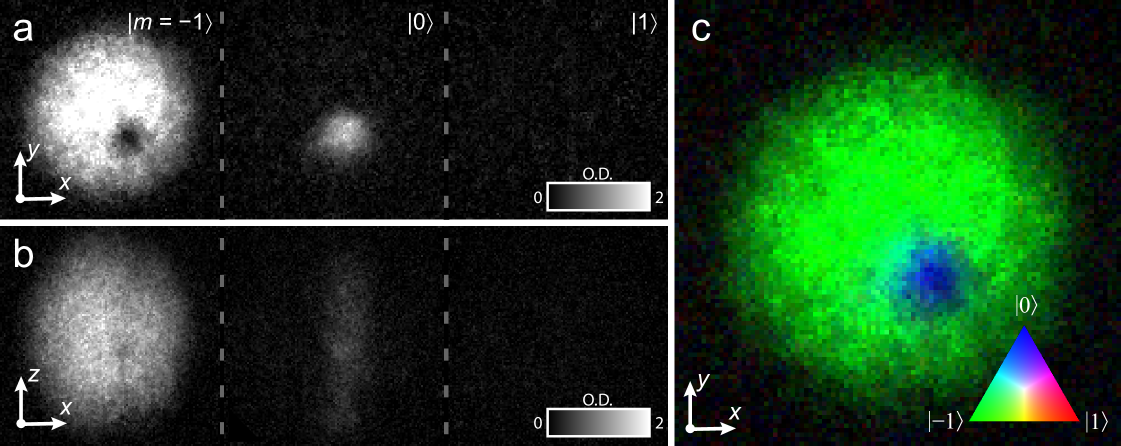
Vortex core filling and interface. For comparison, we also produce vortices with empty cores by reducing the ramp rate such that the spins rotate nearly adiabatically, leaving the system with unobservable populations in and . The size of the filled vortex core is typically much larger than that of an empty core, as shown in Fig. 6. We have numerically verified that for our experimental parameters the superfluid vortex core expands at a rate similar to that of the whole condensate after the release from the trap. In the experiment, the size of the filled vortex core is a further manifestation of the topology of the spinor where the spinor interactions break the spin condition of the FM phase. In the ground state, the size of a filled vortex core is determined by a spin healing lengthRuostekoski and Anglin (2003); Lovegrove et al. (2012) arising only from the spin–spin interactions, which is much larger than the density healing length that limits the size of an empty core. Thus, as the condensate evolves, dissipation causes the filled vortex cores to inflate as atoms accumulate there. We observe no corresponding growth of empty vortex cores, as also shown in Fig. 6.

Whereas the order parameter of the FM phase may be represented by the orientation of an orthonormal vector triad, the P order parameter is characterised by an unoriented nematic axis together with the condensate phase (Supplementary Note 2). The filling of the vortex core thus results in an interface between regions where the superfluid order parameter breaks different symmetries. In our system the interface appears in the internal structure of the defect itself and is observed directly in the experiment as a smooth transition between the FM vortex state in the surrounding superfluid and the P phase at the vortex core (Fig. 5). A numerical simulation of this transition allows us to portray the condensate spinor graphically in terms of a spherical-harmonic expansion, (see Fig. 1). The deformation of illustrates the continuous topological interface that connects the symmetric order parameter of the FM phase to the nematic order parameter of the P phase. Note that in the pure FM phase, the triad order parameter corresponds exactly to the orientation and argument of .
Analytically, the spinor describing the vortex and its superfluid core can be constructed as an interpolating filled-core vortex solution as in Ref. Lovegrove et al., 2016,
| (3) |
where represents the interpolation between the FM and P phases for varying from 1 to 0, respectively. The azimuthal angle around the vortex line is represented by , and is the polar angle. The spin vector is , and the unit vector orthogonal to it is , where is the radial unit vector relative to the vortex line. For , equation (3) reduces to the singular FM vortex, and for , the spinor represents the non-circulating P phase that occupies the vortex core.
Spinor analysis. Next, we explicitly demonstrate the nature of the vortex. The representation of the vortex wave function as a three-component spinor depends on the choice of the spinor basis, and the order parameter symmetry dictates how the representation transforms under a change of basis. Experimentally it is more convenient to change the orientation of the spin with respect to a fixed quantization axis by applying a radio-frequency (RF) pulse, which rotates the spin according to the unitary transformation where the arbitrary angle does not affect the outcome. The resulting density profiles are notably more complicated, as shown in Fig. 7. To understand these results theoretically, we assume cylindrical symmetry and neglect any small population in , leading to a qualitative model for the vortex
| (4) |
where approximates the vortex-core profile with size parameterised by . The FM part of the spinor (4) in the original basis transforms as , distributing the atoms across all three components. The P part transforms as , splitting the atoms evenly between the components. Thus, after the pulse, the original atomic density distribution of the FM phase is reproduced in the component as it only contains atoms that originated in the component. On the other hand, the other two components exhibit phase singularities that have shifted to different locations, leading to a split-core solution that appears to have broken the axial symmetry of the original state. This translation of the vortices after the basis transformation is a manifestation of the symmetry of the order parameter, and indicates the presence of a line singularity about which the spin vector rotates (disgyration). After the rotation, one can still identify the locations of the vortices by the density minima of the atoms in the component.
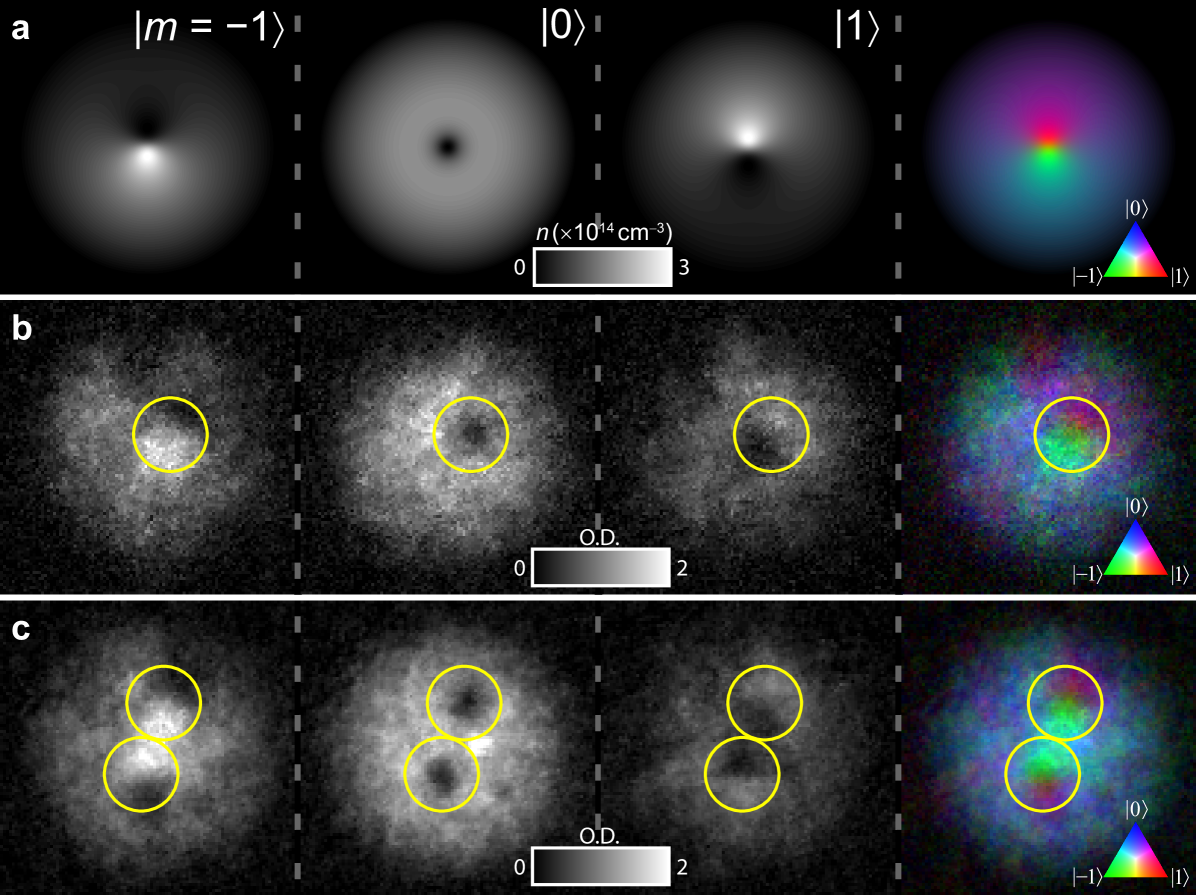
The matter wave in may also be interpreted as an interference between the overlapping spinor components before the spin-tip pulse. In all cases, the experimental density profiles of Fig. 7 agree well with the theoretical prediction obtained by applying a spin rotation to equation (4).
Discussion
Our results advance the experimental and theoretical investigations of defects containing topological interfaces. Similar techniques can be used to generate half-quantum vortices, as well as vortices with coherent interfaces involving the many diverse magnetic phases observed in spin-2 spinor condensatesSemenoff and Zhou (2007); Kobayashi et al. (2009); Mawson et al. (2015); Borgh and Ruostekoski (2016). The filled vortex cores themselves may be used as tracers to examine the longitudinal dynamics of the vortex linesFonda et al. (2014), which are otherwise difficult to discern. A further exciting extension would be to study the corresponding system in rotation where the nucleation and stability of vortices should dramatically depend on the precise value of the conserved magnetisationLovegrove et al. (2016) — determining whether non-singular or singular vortices will prevail.
Methods
Experiment. The experimental techniques resemble those described in Ref. (35), beginning with an optically trapped 87Rb condensate prepared in the FM phase . The optical trap frequencies are Hz and Hz in the radial and axial directions, respectively, and with an initial atom number of typically . The axial Thomas–Fermi radius of the condensate is 5 m and the corresponding radial extent is 7 m. The bias magnetic field is controlled by a single Helmholtz coil pair, and the quadrupole magnetic field strength by a second coaxial anti-Helmholtz pair. Two other pairs of coils for the and directions null those field components such that the field zero passes through the centre of the condensate.
The magnetic field zero is initially placed approximately 35 m above the condensate with an initial gradient strength and initial bias field mG. The bias field is then reduced to mG at the rate , and then to G over the following 10 ms. The atoms are then held in the trap for a time . An optional s, MHz RF spin-tip pulse is applied immediately afterwards. At the conclusion of the experiment the quadrupole field and the optical trap are extinguished. A brief exposure to a magnetic field gradient of during the 23 ms expansion separates the spinor components horizontally, after which they are imaged absorptively along the - and -axes in a 0.1 G field aligned with the -axis. Atom loss during the experiment, both during the ramp and during the subsequent evolution time, reduces the total number of atoms to approximately at the time of imaging.
Reducing the bias field at the rate results in a doubly-quantized vortex in and essentially no atoms in the other spinor components. The experiments with filled cores were conducted at higher ramp rates, between and . Ramp rates exceeding result in larger non-singular vortices that occupy all three spinor components. These are not observed to evolve into singular vortices.
Numerical model. We use experimental parameters for the Gross-Pitaevskii Hamiltonian density of the spin-1 BEC
| (5) |
where includes the harmonic trapping potential . Here is the reduced Planck constant and is the atomic mass. The spin is defined as the expectation value , where is a vector of dimensionless spin-1 Pauli matrices. The condensate spin vector corresponding to equation (1) is given by . The FM order parameter can be defined by the orientation of two orthogonal vectors and . The last two terms of equation (5) describe the linear and quadratic Zeeman shift of strengths and , respectively. The two interaction terms of strengths and arise from -wave scattering of the atoms.
In -wave scattering the only spin-flip processes are . The longitudinal magnetisation
| (6) |
where is the component of the condensate spin, is therefore approximately conserved on time scales for which -wave scattering dominates. This condition is broken when the Gross–Pitaevskii equations are made dissipative, e.g., by imaginary-time evolution. We employ an algorithm to strictly restore the conservation of magnetizationLovegrove et al. (2016) throughout energy relaxation in pure imaginary time evolution and in evolution dynamics following imprinting, in which case we set time to include a small imaginary component , where . All numerical simulations are carried out using a split-step algorithm on a minimum of -point grid.
Data Availability
All relevant datasets generated during and/or analysed during the current study are available from the corresponding author upon request. The source data underlying Figs. 1 and 3–7 are provided as a Source Data file in the Zenodo repository (doi:19.5281/zenodo.3404017) (Ref. Weiss et al., 2019).
References
References
- Volovik (2003) Grigory E. Volovik, The Universe in a Helium Droplet (Oxford University Press, 2003).
- Vollhardt and Wölfle (1990) Dieter Vollhardt and Peter Wölfle, The Superfluid Phases of Helium 3 (Taylor & Francis Ltd, London, UK, 1990).
- Kawaguchi and Ueda (2012) Yuki Kawaguchi and Masahito Ueda, “Spinor Bose–Einstein condensates,” Phys. Rep. 520, 253–382 (2012).
- Stamper-Kurn and Ueda (2013) Dan M. Stamper-Kurn and Masahito Ueda, “Spinor Bose gases: Symmetries, magnetism, and quantum dynamics,” Rev. Mod. Phys. 85, 1191–1244 (2013).
- Donnelly (1991) Russell J. Donnelly, Quantized Vortices in Helium II (Cambridge University Press, Cambridge, 1991).
- Fetter (2009) Alexander L. Fetter, “Rotating trapped Bose–Einstein condensates,” Rev. Mod. Phys. 81, 647–691 (2009).
- Mermin (1979) N. D. Mermin, “The topological theory of defects in ordered media,” Rev. Mod. Phys. 51, 591–648 (1979).
- Staley (2010) Mark Staley, “Understanding quaternions and the Dirac belt trick,” Eur. J. Phys. 31, 467–478 (2010).
- Simola et al. (1987) J. T. Simola, L. Skrbek, K. K. Nummila, and J. S. Korhonen, “Two different vortex states in rotating 3He–A observed by use of negative ions,” Phys. Rev. Lett. 58, 904–907 (1987).
- Parts et al. (1995) Ü. Parts, J. M. Karimäki, J. H. Koivuniemi, M. Krusius, V. M. H. Ruutu, E. V. Thuneberg, and G. E. Volovik, “Phase diagram of vortices in superfluid 3He–,” Phys. Rev. Lett. 75, 3320–3323 (1995).
- Isoshima and Machida (2002) Tomoya Isoshima and Kazushige Machida, “Axisymmetric vortices in spinor Bose–Einstein condensates under rotation,” Phys. Rev. A 66, 023602 (2002).
- Lovegrove et al. (2012) Justin Lovegrove, Magnus O. Borgh, and Janne Ruostekoski, “Energetically stable singular vortex cores in an atomic spin-1 Bose–Einstein condensate,” Phys. Rev. A 86, 013613 (2012).
- Kobayashi et al. (2012) Shingo Kobayashi, Yuki Kawaguchi, Muneto Nitta, and Masahito Ueda, “Topological classification of vortex-core structures of spin-1 Bose–Einstein condensates,” Phys. Rev. A 86, 023612 (2012).
- Lovegrove et al. (2016) Justin Lovegrove, Magnus O. Borgh, and Janne Ruostekoski, “Stability and internal structure of vortices in spin-1 Bose–Einstein condensates with conserved magnetization,” Phys. Rev. A 93, 033633 (2016).
- Ruostekoski and Anglin (2003) J. Ruostekoski and J. R. Anglin, “Monopole core instability and Alice rings in spinor Bose–Einstein condensates,” Phys. Rev. Lett. 91, 190402 (2003).
- Sadler et al. (2006) L. E. Sadler, J. M. Higbie, S. R. Leslie, M. Vengalattore, and D. M. Stamper-Kurn, “Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose–Einstein condensate,” Nature 443, 312–315 (2006).
- Chen et al. (2018) P.-K. Chen, L.-R. Liu, M.-J. Tsai, N.-C. Chiu, Y. Kawaguchi, S.-K. Yip, M.-S. Chang, and Y.-J. Lin, “Rotating atomic quantum gases with light-induced azimuthal gauge potentials and the observation of the Hess–Fairbank effect,” Phys. Rev. Lett. 121, 250401 (2018).
- Seo et al. (2015) Sang Won Seo, Seji Kang, Woo Jin Kwon, and Yong-il Shin, “Half-quantum vortices in an antiferromagnetic spinor Bose–Einstein condensate,” Phys. Rev. Lett. 115, 015301 (2015).
- Borgh and Ruostekoski (2012) Magnus O. Borgh and Janne Ruostekoski, “Topological interface engineering and defect crossing in ultracold atomic gases,” Phys. Rev. Lett. 109, 015302 (2012).
- Finne et al. (2006) A. P. Finne, V. B. Eltsov, R. Hänninen, N. B. Kopnin, J. Kopu, M. Krusius, M. Tsubota, and G. E. Volovik, “Dynamics of vortices and interfaces in superfluid 3He,” Rep. Prog. Phys. 69, 3157–3230 (2006).
- Bradley et al. (2008) D. I. Bradley, S. N. Fisher, A. M. Guenault, R. P. Haley, J. Kopu, H. Martin, G. R. Pickett, J. E. Roberts, and V. Tsepelin, “Relic topological defects from brane annihilation simulated in superfluid 3He,” Nat. Phys. 4, 46–49 (2008).
- Kibble (1976) T. W. B. Kibble, “Topology of cosmic domains and strings,” J. Phys. A Math. Gen. 9, 1387–1398 (1976).
- Sarangi and Tye (2002) Saswat Sarangi and S.-H. Henry Tye, “Cosmic string production towards the end of brane inflation,” Phys. Lett. B 536, 185–192 (2002).
- Bert et al. (2011) Julie A. Bert, Beena Kalisky, Christopher Bell, Minu Kim, Yasuyuki Hikita, Harold Y. Hwang, and Kathryn A. Moler, “Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface,” Nat. Phys. 7, 767–771 (2011).
- Leanhardt et al. (2003) A. E. Leanhardt, Y. Shin, D. Kielpinski, D. E. Pritchard, and W. Ketterle, “Coreless vortex formation in a spinor Bose–Einstein condensate,” Phys. Rev. Lett. 90, 140403 (2003).
- Leslie et al. (2009) L. S. Leslie, A. Hansen, K. C. Wright, B. M. Deutsch, and N. P. Bigelow, “Creation and detection of skyrmions in a Bose–Einstein condensate,” Phys. Rev. Lett. 103, 250401 (2009).
- Choi et al. (2012a) Jae-yoon Choi, Woo Jin Kwon, and Yong-il Shin, “Observation of topologically stable 2D skyrmions in an antiferromagnetic spinor Bose–Einstein condensate,” Phys. Rev. Lett. 108, 035301 (2012a).
- Leanhardt et al. (2002) A. E. Leanhardt, A. Görlitz, A. P. Chikkatur, D. Kielpinski, Y. Shin, D. E. Pritchard, and W. Ketterle, “Imprinting vortices in a Bose–Einstein condensate using topological phases,” Phys. Rev. Lett. 89, 190403 (2002).
- Shin et al. (2004) Y. Shin, M. Saba, M. Vengalattore, T. A. Pasquini, C. Sanner, A. E. Leanhardt, M. Prentiss, D. E. Pritchard, and W. Ketterle, “Dynamical instability of a doubly quantized vortex in a Bose–Einstein condensate,” Phys. Rev. Lett. 93, 160406 (2004).
- Huhtamäki et al. (2006) J. A. M. Huhtamäki, M. Möttönen, T. Isoshima, V. Pietilä, and S. M. M. Virtanen, “Splitting times of doubly quantized vortices in dilute Bose–Einstein condensates,” Phys. Rev. Lett. 97, 110406 (2006).
- Isoshima et al. (2007) T. Isoshima, M. Okano, H. Yasuda, K. Kasa, J. A. M. Huhtamäki, M. Kumakura, and Y. Takahashi, “Spontaneous splitting of a quadruply charged vortex,” Phys. Rev. Lett. 99, 200403 (2007).
- Nakahara et al. (2000) Mikio Nakahara, Tomoya Isoshima, Kazushige Machida, Shin-ichiro Ogawa, and Tetsuo Ohmi, “A simple method to create a vortex in Bose–Einstein condensate of alkali atoms,” Physica B 284–288, 17–18 (2000).
- Pietilä and Möttönen (2009) Ville Pietilä and Mikko Möttönen, “Creation of Dirac monopoles in spinor Bose–Einstein condensates,” Phys. Rev. Lett. 103, 030401 (2009).
- Choi et al. (2012b) Jae-yoon Choi, Woo Jin Kwon, Moonjoo Lee, Hyunseok Jeong, Kyungwon An, and Yong-il Shin, “Imprinting skyrmion spin textures in Bose–Einstein condensates,” New J. Phys. 14, 053013 (2012b).
- Ray et al. (2014) M. W. Ray, E. Ruokokoski, S. Kandel, M. Möttönen, and D. S. Hall, “Observation of Dirac monopoles in a synthetic magnetic field,” Nature 505, 657–660 (2014).
- Lee et al. (2018) W. Lee, A. H. Gheorghe, K. Tiurev, T. Ollikainen, M. Möttönen, and D. S. Hall, “Synthetic electromagnetic knot in a three-dimensional skyrmion,” Sci. Adv. 4, eaao3820 (2018).
- Hall et al. (2016) D. S. Hall, M. W. Ray, K. Tiurev, E. Ruokokoski, A. H. Gheorghe, and M. Möttönen, “Tying quantum knots,” Nat. Phys. 12, 478–483 (2016).
- Matthews et al. (1999) M. R. Matthews, B. P. Anderson, P. C. Haljan, D. S. Hall, C. E. Wieman, and E. A. Cornell, “Vortices in a Bose–Einstein condensate,” Phys. Rev. Lett. 83, 2498–2501 (1999).
- Andersen et al. (2006) M. F. Andersen, C. Ryu, Pierre Cladé, Vasant Natarajan, A. Vaziri, K. Helmerson, and W. D. Phillips, “Quantized rotation of atoms from photons with orbital angular momentum,” Phys. Rev. Lett. 97, 170406 (2006).
- Rosenbusch et al. (2002) P. Rosenbusch, V. Bretin, and J. Dalibard, “Dynamics of a single vortex line in a Bose–Einstein condensate,” Phys. Rev. Lett. 89, 200403 (2002).
- Semenoff and Zhou (2007) Gordon W. Semenoff and Fei Zhou, “Discrete symmetries and –quantum vortices in condensates of cold atoms,” Phys. Rev. Lett. 98, 100401 (2007).
- Kobayashi et al. (2009) Michikazu Kobayashi, Yuki Kawaguchi, Muneto Nitta, and Masahito Ueda, “Collision dynamics and rung formation of non-Abelian vortices,” Phys. Rev. Lett. 103, 115301 (2009).
- Mawson et al. (2015) Thomas Mawson, Gary Ruben, and Tapio Simula, “Route to non-Abelian quantum turbulence in spinor Bose–Einstein condensates,” Phys. Rev. A 91, 063630 (2015).
- Borgh and Ruostekoski (2016) Magnus O. Borgh and Janne Ruostekoski, “Core structure and non-Abelian reconnection of defects in a biaxial nematic spin-2 Bose–Einstein condensate,” Phys. Rev. Lett. 117, 275302 (2016).
- Fonda et al. (2014) Enrico Fonda, David P. Meichle, Nicholas T. Ouellette, Sahand Hormoz, and Daniel P. Lathrop, “Direct observation of Kelvin waves excited by quantized vortex reconnection,” Proc. Natl Acad. Sci. 111, 4707–4710 (2014).
- Weiss et al. (2019) L. S. Weiss, M. O. Borgh, A. Blinova, T. Ollikainen, M. Möttönen, J. Ruostekoski, and D.S. Hall, “Controlled creation of a singular spinor vortex by circumventing the Dirac belt trick,” Zenodo digital repository. doi:10.5281/zenodo.340417 (2019).
Acknowledgements
We acknowledge funding by the National Science Foundation (Grant Nos. PHY–1519174 and PHY–1806318), by the Emil Aaltonen Foundation, by the Kaupallisten ja teknillisten tieteiden tukisäätiö (KAUTE) foundation through its Researchers Abroad program, by the Academy of Finland through the Centre of Excellence Programme (grant no. 312300) and ERC Consolidator Grant QUESS (no. 681311), and by the EPSRC.
Author contributions
L.S.W., A.B., T.O., and D.S.H. developed and conducted the experiments and analysed the data. J.R. proposed the experiment. Numerical simulations were carried out by M.O.B., and the theoretical analysis was developed by M.O.B. and J.R. The manuscript was written by M.O.B., J.R. and D.S.H. All authors discussed the results and commented on the manuscript.
Additional information
Competing Interests: The Authors declare no competing interests.
Correspondence and requests for materials should be addressed to D.S.H.
(dshall@amherst.edu).
Controlled Creation of a Singular Spinor Vortex
by Circumventing the Dirac Belt Trick
Weiss et al.
Supplementary Notes
Supplementary Note 1 Theoretical details of the vortex creation process. A non-singular vortex with longitudinal magnetisation can be written as
| (1) |
where is the azimuthal angle around the vortex line. The condensate spin is and the profile function satisfies . The analytically constructed spinor wave function for the non-singular vortex used in Figs. 3a and 4a was obtained from supplementary equation (1) and embedded into the ground-state density profile of the condensate.
In these expressions is the second Euler angle appearing in equation (1), which in this case increases monotonically from zero on the vortex line to at the boundary to define a fountain-like spin texture. For strongly negative , corresponding to increasing rapidly, a large proportion of the condensate resides in the component. The two extremes of magnetisation correspond to constant : For , , to give the vortex-free state . For , on the other hand, we obtain the doubly-quantized vortex with its associated instability towards splitting. The two limits can be continuously connected through a family of functions , allowing the vortex to unwind\citeSho_prl_1998_s. Note, however, that conservation of longitudinal magnetisation suppresses the redistribution of the atom populations between the spinor components during the free evolution of the condensate.
Using numerical energy relaxation (Methods), we find that if the vortex is prepared such that the condensate spin vector bends rapidly towards with increasing radial distance from the vortex centre, the spin interactions can no longer maintain a non-singular profile while still preserving the spinor nature of the condensate. The threshold approximately corresponds to a strong longitudinal magnetisation that is explicitly conserved, and the vortex decays by splitting into a pair of singly quantized vortices as shown in Figs. 3 and 4. We show the state reached shortly after splitting of the initial vortex, exhibiting singular vortices with fully formed, filled cores. This state is locally stable: The singular vortices persist for a significant period of imaginary-time evolution, but do eventually leave the condensate over a significantly longer period of relaxation. The local stability is also reflected in the long lifetime of the vortices created in our experiment.
The observed splitting of the coreless vortex represents a particular case of the instability also found in supplementary Ref. lovegrove_pra_2016_s, . In imprinting of a non-singular vortex, its magnetisation is a controllable parameter determined by the rate of change of the imprinting magnetic field. Our idealised model thus indicates that singular vortices can be created by imprinting a non-singular vortex with sufficiently strong longitudinal magnetisation and allowing it to split.
Supplementary Note 2 Magnetic Phases. The spin-1 Bose-Einstein condensate exhibits both polar (P) and ferromagnetic (FM) phases\citeSkawaguchi_physrep_2012_s. In a 87Rb condensate, in equation (5), and hence the FM phase, which maximises , forms the ground state in a uniform system at zero magnetic field. The P phase, with , appears in the cores of the singular vortices and exhibits different symmetry properties. The P order parameter, and hence also the spinor in the P phase, are specified by a nematic axis together with a condensate scalar phase , with the property that . The P phase thus exhibits uniaxial nematic order, characterised by the continuous symmetry under spin rotations about the local, unoriented axis defined by . The order parameter space is therefore , where the factorisation by arises from the aforementioned nematic symmetry, which also allows the P phase to support half-quantum vortices\citeSseo_prl_2015_s.
Supplementary References
References
- (1) Ho, T.-L. Spinor Bose condensates in optical traps. Phys. Rev. Lett. 81, 742–745 (1998).
- (2) Lovegrove, J., Borgh, M. O. & Ruostekoski, J. Stability and internal structure of vortices in spin-1 Bose–Einstein condensates with conserved magnetization. Phys. Rev. A 93, 033633 (2016).
- (3) Kawaguchi, Y. & Ueda, M. Spinor Bose–Einstein condensates. Phys. Rep. 520, 253–382 (2012).
- (4) Seo, S. W., Kang, S., Kwon, W. J. & Shin, Y.-i. Half-quantum vortices in an antiferromagnetic spinor Bose–Einstein condensate. Phys. Rev. Lett. 115, 015301 (2015).