Convergence Rate of LQG Mean Field Games with Common Noise
Abstract
This paper focuses on exploring the convergence properties of a generic player’s trajectory and empirical measures in an -player Linear-Quadratic-Gaussian Nash game, where Brownian motion serves as the common noise. The study establishes three distinct convergence rates concerning the representative player and empirical measure. To investigate the convergence, the methodology relies on a specific decomposition of the equilibrium path in the -player game and utilizes the associated Mean Field Game framework.
1 Introduction
Mean Field Game (MFG) theory was introduced by Lasry and Lions in their seminal paper ([19]), and by Huang, Caines, and Malhame ([15, 13, 14, 12]). It aims to provide a framework for studying the asymptotic behavior of -player differential games being invariant under the reshuffling of the players’ indices. For a comprehensive overview of recent advancements and relevant applications of MFG theory, it is recommended to refer to the two-volume book by Carmona and Delarue ([4, 5]) published in 2018 and the references provided therein.
Mean Field Games (MFG) have become widely accepted as an approximation for -player games, particularly when the number of players, , is large enough. A fundamental question that arises in this context concerns the convergence rate of this approximation. Convergence can be analyzed from different perspectives, such as convergence in value, the trajectory followed by the representative player, or the behavior of the mean field term. Each of these perspectives offers valuable insights into the behavior and characteristics of the MFG approximation. Furthermore, they raise a variety of intriguing questions within this context.
To be more concrete, we examine the behavior of the triangular array as , where represents the equilibrium state of the -th player at time in the -player game, defined within the probability space . Additionally, we denote as the equilibrium path at time derived from the associated MFG, defined in the probability space .
Considering the identical but not independent distribution , the first question pertains to the convergence of , which represents the generic path. It can be framed as follows:
-
(Q1)
The -convergence rate of the representative equilibrium path,
Here, denotes the -Wasserstein metric.
The existing literature extensively explores the convergence rate in this context. For (Q1), Theorem 2.4.9 of the monograph [3] establishes a convergence rate of using the metric. More recently, [17] addresses (Q1) by introducing displacement monotonicity and controlled common noise, and Theorem 2.23 applies the maximum principle of forward-backward propagation of chaos to achieve the same convergence rate. Within the LQG framework, [18] also provides a convergence rate of for the representative player.
The second question pertains to the convergence of the mean-field term, which is equivalent to the convergence of the empirical measure of players. Given the Brownian motion, denoted as , to be the common noise, the problem lies in determining the rate of convergence of the empirical measures to the MFG equilibrium measure
Thus, the second question can be stated as follows:
-
(Q2)
The -convergence rate of empirical measures in sense,
As for (Q2), Theorem 3.1 of [8] provides an answer, stating that the empirical measures exhibit a convergence rate of in the distance for . In [8], they also explore a related question that is both similar and more intriguing, which concerns the uniform -convergence rate:
-
(Q3)
The -uniform -convergence rate of empirical measures in sense,
The answer provided by Theorem 3.1 in [8] reveals that the uniform convergence rate, as formulated in (Q3), is considerably slower compared to the convergence rate mentioned in (Q2). Specifically, the convergence rate for (Q3) is when , where represents the dimension of the state space.
In our paper, we specifically focus on a class of one-dimensional Linear-Quadratic-Gaussian (LQG) Mean Field Nash Games with Brownian motion as the common noise. It is important to note that the assumptions made in the aforementioned papers except [18] only account for linear growth in the state and control elements for the running cost, thus excluding the consideration of LQG. It is also noted that differences between [18] and the current paper lie in various aspects: (1) The problem setting in our paper considers Brownian motion as the common noise, whereas [18] employs a Markov chain. This discrepancy leads to significant differences in the subsequent analysis; (2) The work in [18] does not address the questions posed in (Q2) and (Q3).
Our main contribution is the establishment of the convergence rate of all three questions in the above in LQG framework. Firstly, the paper establishes that the convergence rate of the -Wasserstein metric for the distribution of the representative player is for . Secondly, it demonstrates that the convergence rate of the -Wasserstein metric for the empirical measure in the sense is for . Lastly, the paper shows that the convergence rate of the uniform -Wasserstein metric for the empirical measure in the sense is for , and for .
It is worth noting that the convergence rates obtained for (Q1) and (Q2) in the LQG framework align with the results found in existing literature, albeit under different conditions. Additionally, it is revealed that the uniform convergence rate of (Q3) may be slower than that of (Q2), which is consistent with the observations made by [8] from a similar perspective. Interestingly, when considering the specific case where and , the uniform convergence rate of (Q3) is established as according to [8], while it is determined to be within our framework that incorporates the LQG structure.
Regarding (Q2), if the states were independent, the convergence rate could be determined as based on Theorem 1 of [10] and Theorem 5.8 of [4], which provide convergence rates for empirical measures of independent and identically distributed sequences. However, in the mean-field game, the states are not independent of each other, despite having identical distributions. The correlation is introduced mainly by two factors: One is the system coupling arising from the mean-field term and the other is the common noise. Consequently, determining the convergence rate requires understanding the contributions of these two factors to the correlation among players.
In our proof, we rely on a specific decomposition (refer to Lemma 6 and the proof of the main theorem) of the underlying states. This decomposition reveals that the states can be expressed as a sum of a weakly correlated triangular array and a common noise. By analyzing the behavior of these components, we can address the correlation and establish the convergence rate.
Additionally, it is worth mentioning that a similar technique of dimension reduction in -player LQG games have been previously utilized in [16] and related papers to establish decentralized Nash equilibria and the convergence rate in terms of value functions.
The remainder of the paper is organized as follows: Section 2 outlines the problem setup and presents the main result. The proof of the main result, which relies on two propositions, is provided in Section 3. We establish the proof for these two propositions in Section 4 and Section 5. Some lemmas are given in the Appendix.
2 Problem setup and main results
2.1 The formulation of equilibrium in Mean Field Game
In this section, we present the formulation of the Mean Field Game in the sample space .
Let be a given time horizon. We assume that is a standard Brownian motion constructed on the probability space . Similarly, the process is a standard Brownian motion constructed on the probability space . We define the product structure as follows:
where is the completion of and is the complete and right continuous augmentation of .
Note that, and are two Brownian motions from separate sample spaces and , they are independent of each other in their product space . In our manuscript, is called individual or idiosyncratic noise, and is called common noise, see their different roles in the problem formulation later defined via fixed point condition (4). To proceed, we denote by the set of random variables on with finite -th moment with norm and by the space of all valued -progressively measurable random processes such that
Let denote the Wasserstein space of probability measures on satisfying endowed with -Wasserstein metric defined by
where is the collection of all probability measures on with its marginals agreeing with and .
Let be a random variable that is independent with and . For any control , consider the state of the generic player is governed by a stochastic differential equation (SDE)
| (1) |
with the initial value , where the underlying process . Given a random measure flow , the generic player wants to minimize the expected accumulated cost on :
| (2) |
with some given cost function .
The objective of the control problem for the generic player is to find its optimal control to minimize the total cost, i.e.,
| (3) |
Associated to the optimal control , we denote the optimal path by .
Next, to introduce the MFG Nash equilibrium, it is useful to emphasize the dependence of the optimal path and optimal control of the generic player, as well as its associated value, on the underlying measure flow . These quantities are denoted as , , , and , respectively.
We now present the definitions of the equilibrium measure, equilibrium path, and equilibrium control. Please also refer to page 127 of [5] for a general setup with a common noise.
Definition 1.
Given an initial distribution , a random measure flow is said to be an MFG equilibrium measure if it satisfies the fixed point condition
| (4) |
The path and the control associated with are called the MFG equilibrium path and equilibrium control, respectively.
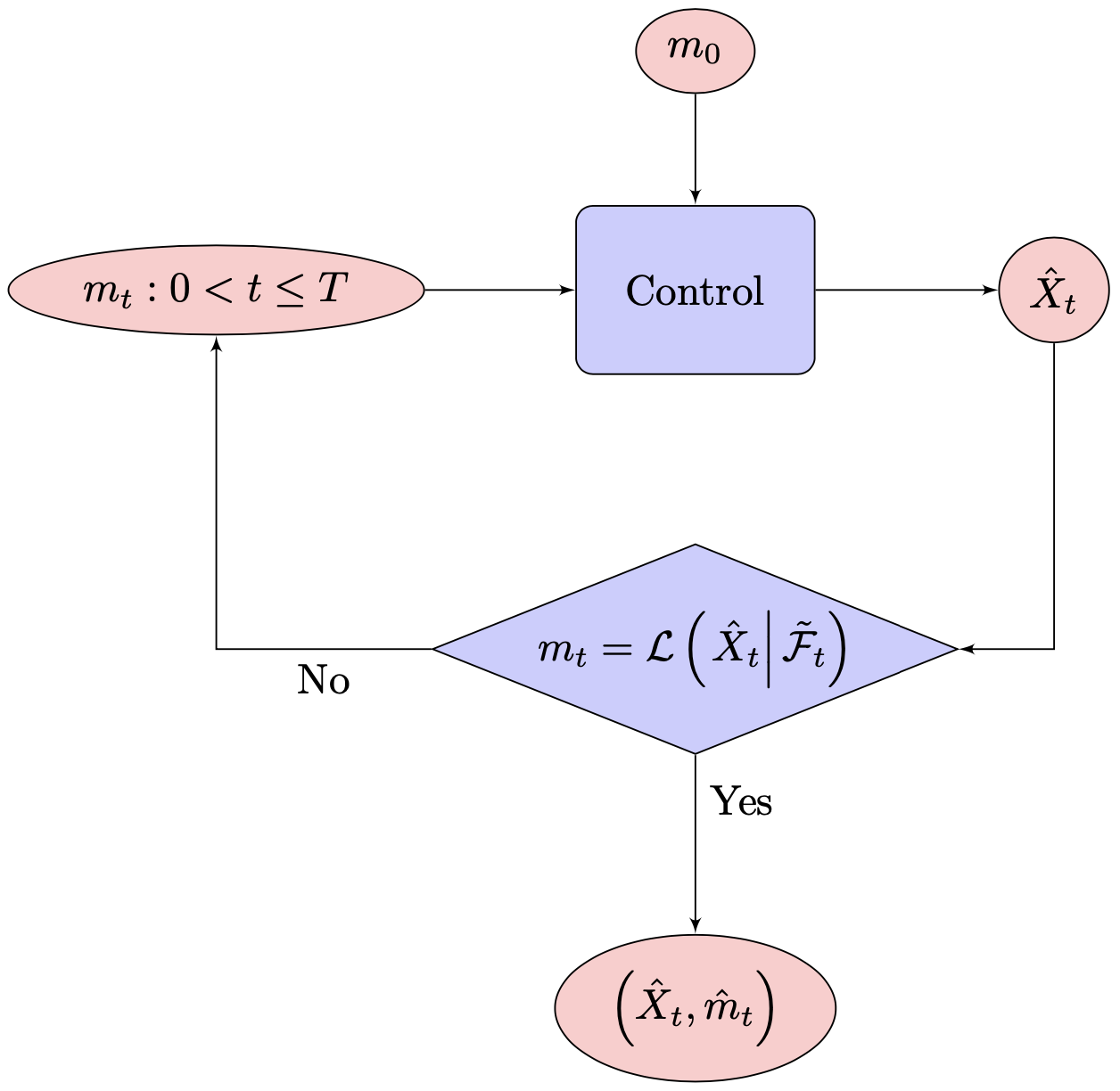
The flowchart of the MFG diagram is given in Figure 1. It is noted from the optimality condition (3) and the fixed point condition (4) that
holds for the equilibrium measure and its associated equilibrium control , while it is not
Otherwise, this problem turns into a McKean-Vlasov control problem, which is essentially different from the current Mean Field Games setup. Readers refer to [7, 6] to see the analysis of this different model as well as some discussion of the differences between these two problems.
2.2 The formulation of Nash equilibrium in -player game
In this subsection, we set up -player game and define the Nash equilibrium of -player game in the sample space . Firstly, let be an -dimensional standard Brownian motion constructed on the space and be the common noise in MFG defined in Section 2.1 on . The probability space for the -player game is , which is constructed via the product structure with
where is the completion of and is the complete and right continuous augmentation of .
Consider a stochastic dynamic game with players, where each player controls a state process in given by
| (5) |
with a control in an admissible set and random initial state .
Given the strategies from other players, the objective of player is to select a control to minimize her expected total cost given by
| (6) |
where is a -valued random vector in to denote the initial state for players, and
is the empirical measure of the vector with Dirac measure . We use the notation to denote the control from players as a whole. Next, we give the equilibrium value function and equilibrium path in the sense of the Nash game.
2.3 Main result
We consider three convergence questions on -player game defined in : The first one is the convergence of the representative path , the second one is the convergence of the empirical measure , while the last one is the -uniform convergence of the empirical measure . To be precise, we shall assume the following throughout the paper:
Assumption 1.
-
•
for some .
-
•
The initials of the -player game is i.i.d. random variables in with the same distribution as in the MFG.
Note that the equilibrium path is a vector-valued stochastic process. Due to the Assumption 1, the game is invariant to index reshuffling of players and the elements in have identical distributions, but they are not independent of each other.
So, the first question on the representative path is indeed about in and we are interested in how fast it converges to in in distribution:
-
(Q1)
The -convergence rate of the representative equilibrium path,
The second question is about the convergence of the empirical measure of the -player game defined by
We are interested in how fast this converges to the MFG equilibrium measure given by
-
(Q2’)
The -convergence rate of empirical measures,
Note that the left-hand side of the above equality is a random quantity and one shall be more precise about what the Big notation means in this context. Indeed, by the definition of the empirical measure, is a random distribution measurable by -algebra generated by the random vector . On the other hand, is a random distribution measurable by the -algebra . Therefore, from the construction of the product probability space in Section 2.2, both random distributions and are measurable with respect to . Consequently, is a random variable in the probability space and we will focus on a version of (Q2’) in the sense:
-
(Q2)
The -convergence rate of empirical measures in sense for each ,
In addition, we also study the following related question:
-
(Q3)
The -uniform -convergence rate of empirical measures in sense,
In this paper, we will study the above three questions (Q1), (Q2), and (Q3) in the framework of LQG structure with Brownian motion as a common noise with the following function in the cost functional (2).
Assumption 2.
Let the function be given in the form of
| (8) |
for some , where are the first and second moment of the measure .
The main result of this paper is presented below. Let us recall that denotes the parameter defined in Assumption 1.
Theorem 1.
We would like to provide some additional remarks on our main result. Firstly, the cost function defined in (6) applies to the running cost for the -th player in the -player game, and it takes the form:
| (9) |
Interestingly, if , although does satisfy the Lasry-Lions monotonicity ([2]) as demonstrated in Appendix 6.1 of [18], there is no global solution for MFG due to the concavity in . On the contrary, when , satisfies the displacement monotonicity proposed in [11] as shown by the following derivation:
3 Proof of the main result with two propositions
Our objective is to investigate the relations between and described in (Q1), (Q2), and (Q3). In this part, we will give the proof of Theorem 1 based on two propositions whose proof will be given later.
Proposition 1.
Proposition 2.
3.1 Preliminaries
We first recall the convergence rate of empirical measures of i.i.d. sequence provided in Theorem 1 of [10] and Theorem 5.8 of [4].
Lemma 1.
Let or . Suppose is a sequence of dimensional i.i.d. random variables with for some . Then, the empirical measure
satisfies
Next, we give the definition of some notations that will be used in the following part. Denote to be the collection of bounded and continuous functions on , and let be the space of functions on whose first order derivative is also bounded and continuous.
Lemma 2.
Suppose are two probability measures on and , where is the Borel set on . Then,
where is the pushforward measure for , and
Proof.
We define a function . Note that, for any , , i.e.,
Therefore, we have the following inequalities:
∎
Lemma 3.
Let be a sequence of dimensional random variables in . Let . We also denote by the sequence . Then
where
Proof.
For any sequence in , the empirical measure satisfies
since
This implies that
On the other hand, we also have
Therefore, the conclusion follows by applying Lemma 2. ∎
3.2 Empirical measures of a sequence with a common noise
We are going to apply lemmas from the previous subsection to study the convergence of empirical measures of a sequence with a common noise in the following sense.
Definition 3.
We say a sequence of random variables is a sequence with a common noise, if there exists a random variable such that
-
•
is a sequence of i.i.d. random variables,
-
•
is independent to .
By this definition, a sequence with a common noise is i.i.d. if and only if is a deterministic constant.
Example 1.
Let be a given constant and be a -dimensional sequence of random variables with a common noise term , where
In above, is a sequence of -dimensional i.i.d. random variables independent to , and is a given non-negative constant. Let be the empirical measure defined by
The first question is
-
(Qa)
In Example 1, where does converge to?
For any test function ,
Since is independent to , by Example 4.1.5 of [9] together with the Law of Large Numbers, we have
Therefore, we conclude that
Hence, the answer for the (Qa) is
-
•
, -a.s. More precisely, since all random variables are square-integrable, the weak convergence implies, for all ,
The next question is
-
(Qb)
In Example 1, what’s the convergence rate in the sense ?
Since is independent to , by Example 4.1.5 of [9], we have
or equivalently, if one takes ,
On the other hand, with ,
From the above two identities, with , we can write
| (15) |
Now we can conclude (Qb) in the next lemma.
Lemma 4.
Let be a given constant. For a sequence with a common noise as of Example 1, we have
Proof.
Next, we present the uniform convergence rate by combining Lemma 3.
Lemma 5.
In Example 1, we use to denote to emphasize its dependence on . Then,
3.3 Generalization of the convergence to triangular arrays
Unfortunately, of the -player’s game does not have a clean structure with a common noise term given in Example 1. Therefore, we need a generalization of the convergence result in Example 1 to a triangular array. To proceed, we provide the following lemma.
Lemma 6.
Let , , and
where
-
•
is a sequence of -dimensional i.i.d. random variables with distribution identical to with for some ,
-
•
is independent to the random variables ,
-
•
.
Let be the empirical measure given by
Then, we have the following three results: For ,
| (16) |
| (17) |
and
| (18) |
Proof.
We will omit the dependence of if there is no confusion, for instance, we use in lieu of . Since , the first result (16) directly follows from
Next, we set . By the definition of empirical measures, we have
| (19) |
From the third condition on , we obtain
By Lemma 4, we also have
In the end, (17) follows from the triangle inequality together with the fact that . Finally, for the proof of (18), we first use (19) to write
Applying Lemma 5 and the third condition on , we can conclude (18). ∎
3.4 Proof of Theorem 1
For simplicity, let us introduce the following notations:
for a deterministic function and a martingale . With these notations, one can write the solution to the Ornstein–Uhlenbeck process
for a determinant function in the form of
| (20) |
For MFG equilibrium, we define
According to (10) in Proposition 1, satisfies the following equation:
Next, we express the solution of the above SDE in the form of
Note that and are independent. Therefore, admits a decomposition of two independent processes as
Furthermore, we have
In the -player game, we define the following quantities:
and
It is worth noting that, by Proposition 2, we have
for all , then the mean-field term satisfies
and the -th player’s path deviated from the mean-field path can be rewritten by
where
Next, we introduce
Consequently, we obtain the following relationships:
and
To compare the process with the target process
| (21) | ||||
where
and
we write by
| (22) | ||||
where
and
| (23) | ||||
To apply Lemma 6 to the processes of (22) and (21), we only need to show the second moment on is for each . In the following analysis, we will utilize the explicit solution of the ODE:
-
•
Let be two constants. The solution of
is
(24)
We will employ this solution to derive the second-moment estimations of .
-
1.
From (24), we have an estimation of
(25) Therefore, we have
(26) and thus by Burkholder-Davis-Gundy (BDG) inequality
-
2.
Since is uniformly bounded by , is a martingale with its quadratic variance
So, we have
-
3.
From the estimation (26), we also have
-
4.
By the assumption of i.i.d. initial states, we have
As a result, we have the following expression:
| (27) |
By combining equations (21), (22), and (27), we can conclude Theorem 1 by applying Lemma 6.
4 Proposition 1: Derivation of the MFG path
This section is dedicated to proving Proposition 1, which provides insights into the MFG solution. To proceed, in Subsection 4.1, we begin by reformulating the MFG problem, assuming a Markovian structure for the equilibrium. Then, in Subsection 4.2, we solve the underlying control problem and derive the corresponding Riccati system. Finally, in Subsection 4.3, we examine the fixed-point condition of the MFG problem, leading to the conclusion.
4.1 Reformulation
To determine the equilibrium measure, as defined in Definition 2, one needs to explore the infinite-dimensional space of random measure flows until a measure flow satisfies the fixed-point condition for all , as illustrated in Figure 1.
The first observation is that the cost function in (8) is only dependent on the measure through the first two moments with the quadratic cost structure, which is given by
Consequently, the underlying stochastic control problem for MFG can be entirely determined by the input given by the valued random processes and , which implies that the fixed point condition can be effectively reduced to merely checking two conditions:
This observation effectively reduces our search from the space of random measure-valued processes to the space of -valued random processes .
It is important to note that if the underlying MFG does not involve common noise, the aforementioned observation is adequate to transform the original infinite-dimensional MFG into a finite-dimensional system. In this case, the moment processes become deterministic mappings . However, the following example demonstrates that this is not applicable to MFG with common noise, which presents a significant drawback in characterizing LQG-MFG using a finite-dimensional system.
Example 2.
To illustrate this point, let’s consider the following uncontrolled mean field dynamics: Let the mean field term , where the underlying dynamic is given by
Here are two key observations:
-
•
is path dependent on entire path of , i.e.,
This implies that the is a function on an infinite dimensional domain.
-
•
is Markovian, i.e.,
It is possible to express the via a SDE with finite-dimensional coefficient functions of .
To make the previous idea more concrete, we propose the assumption of a Markovian structure for the first and second moments of the MFG equilibrium. In other words, we restrict our search for equilibrium to a smaller space of measure flows that capture the Markovian structure of the first and second moments.
Definition 4.
The space is the collection of all -adapted measure flows , whose first moment and second moment satisfy a system of SDE
| (28) | ||||
for some smooth deterministic functions for all .
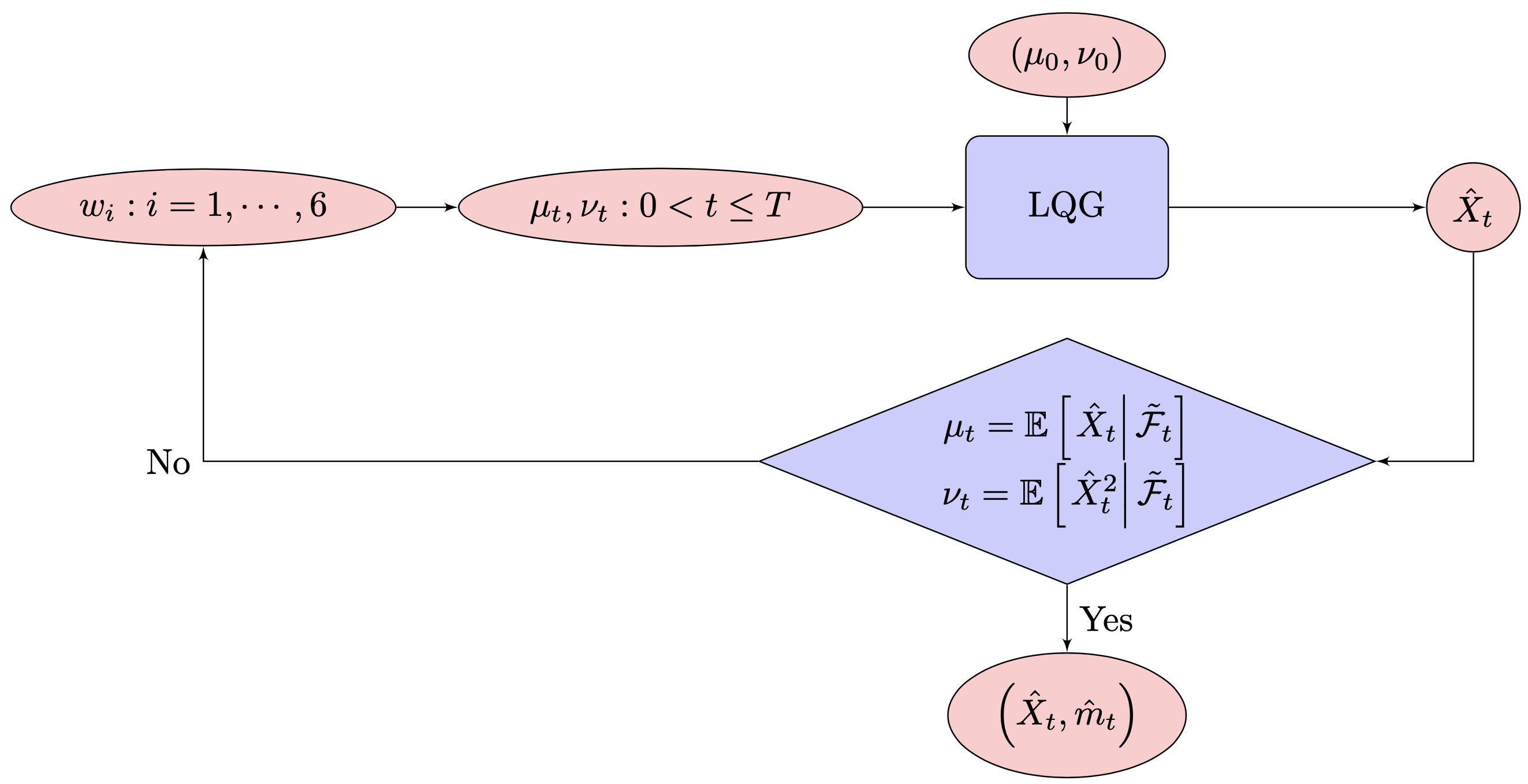
The MFG problem originally given by Definition 1 can be recast as the following combination of stochastic control problem and fixed point condition:
-
•
RLQG(Revised LQG):
-
•
RFP(Revised fixed point condition):
Determine satisfying the following fixed point condition:
(29) The equilibrium measure is then .
Remark 1.
It is important to highlight that the Markovian structure for the first and second moments of the MFG equilibrium in this manuscript differs significantly from that presented in [18]. In [18], the processes and are pairs of processes with finite variation, while in our case, they are quadratic variation processes.
4.2 The generic player’s control with a given population measure
This section is devoted to the control problem RLQG parameterized by .
4.2.1 HJB equation
To simplify the notation, let’s denote each function as for . Assuming sufficient regularity conditions, and according to the dynamic programming principle (refer to [20] for more details), the value function defined in the RLQG problem can be obtained as a solution of the following Hamilton-Jacobi-Bellman (HJB) equation
Therefore, the optimal control has to admit the feedback form of
| (30) |
and then the HJB equation can be reduced to
| (31) |
Next, we identify what conditions are needed for equating the control problem RLQG and the above HJB equation. Denote to be the set of such that satisfies
for all for some positive constant .
Lemma 7.
Consider the control problem RLQG with some given smooth functions .
- 1.
- 2.
Proof.
-
1.
First, we prove the verification theorem. Since , for any admissible , the process is well defined and one can apply Itô’s formula to obtain
where
Note that the HJB equation actually implies that
which again yields
Hence, we obtain that for all ,
In the above, if is replaced by given by the feedback form (30), then since is Lipschitz continuous in , there exists corresponding optimal path . Thus, is also in . One can repeat all the above steps by replacing and by and , and sign by sign to conclude that is indeed the optimal value.
-
2.
The opposite direction of the verification theorem follows by taking for the dynamic programming principle, for all stopping time
which is valid under our regularity assumptions on all the partial derivatives.
∎
4.2.2 LQG solution
It is worth noting that the costs of RLQG are quadratic functions in , while the drift function of the process of (28) is not linear in . Therefore, the stochastic control problem RLQG does not fit into the typical LQG control structure. Nevertheless, similarly to the LQG solution, we guess the value function to be a quadratic function in the form of
| (32) |
Under the above setup for the value function , for , the optimal control is given by
| (33) |
and the optimal path is
| (34) |
To proceed, we introduce the following Riccati system of ODEs for ,
| (35) |
with terminal conditions
| (36) |
Lemma 8.
Proof.
With the form of value function given in (32) and the conditional first and second moment of under the -algebra given in (28), we have
Plugging them back to the HJB equation in (31), we get a system of ODEs in (35) by equating , , -like terms in each equation with the terminal conditions given in (36).
Therefore, any solution of a system of ODEs (35) leads to the solution of HJB (31) in the form of the quadratic function given by (37). Since the are differentiable functions on the closed set , they are also bounded, and thus the regularity conditions needed for is valid. Finally, we invoke the verification theorem given by Lemma 7 to conclude the desired result. ∎
4.3 Fixed point condition and the proof of Proposition 1
Returning to the ODE system (35), there are equations, whereas we need to determine a total of deterministic functions of to characterize MFG. These are
In this below, we identify the missing equations by checking the fixed point condition of RFP. This leads to a complete characterization of the equilibrium for MFG in Definition 1.
Lemma 9.
Proof.
With the dynamic of the optimal path given by (34), we have
and since the functions are continuous on , then we can change of order of integration and expectation and it yields
Similarly, applying Itô’s formula, we obtain
and it follows that
Thus the desired result in (38) is obtained. Next, comparing the terms in (28) and (38), to satisfy the fixed point condition in MFG, we require another equations in (39) for the coefficient functions . ∎
Using further algebraic structures, one can reduce the ODE system of equations composed by (35) and (39) into a system of equations.
Proof of Proposition 1.
Let the smooth and bounded functions be given, the functions in (35) is a coupled linear system, and thus their existence, uniqueness and boundedness is shown by Theorem 12.1 in [1].
Let , and it easily to obtain
which implies that for all . This gives the result that and it yields . Then with , we have for all and thus one can obtain , which indicates that for all as . Therefore the ODE system (35) can be simplified to the following form about :
| (40) |
with the terminal conditions
| (41) |
The unique solvability of the Riccati system (40)-(41) is proven in Lemma 12 in the Appendix. Note that the solution of (11) is consistent with the solution of the Riccati system given by equations (40)-(41).
In this case, since and for all , it follows that for all from the fixed point result (38). Similarly,
Plugging and back to (33), we obtain the optimal control by
Moreover, since and for , the value function can be simplified from (32) to
This concludes Proposition 1.
∎
5 The -Player Game
This section focuses on proving Proposition 2 regarding the corresponding -player game. For simplicity, we can omit the superscript when referring to the processes in the sample space .
To begin, we address the -player game in Subsection 5.1, where we solve it and obtain a Riccati system containing equations. Subsequently, we reduce the relevant Riccati system to an ODE system in Subsection 5.2, which has a dimension independent of . This simplified system forms the fundamental component of the convergence result.
5.1 Characterization of the -player game by Riccati system
It is important to emphasize that based on the problem setting in Subsection 2.2 and the running cost for each player specified in (9), the -player game can be classified as an -coupled stochastic LQG problem. As a result, the value function and optimal control for each player can be determined by means of the following Riccati system:
For , consider
| (42) |
where is symmetric matrix, is -dimensional vector, is a real constant, and is the -th natural basis in for each .
Lemma 10.
Suppose is the solution of the Riccati system (42). Then, the value functions of -player game defined by (7) is
Moreover, the path and the control under the equilibrium are given by
| (43) |
and
for each , where denotes the -th column of matrix , denotes the -th entry of vector and .
Proof.
From the dynamic programming principle, it is standard that, under enough regularities, the players’ value function can be lifted to the solution of the following system of HJB equations, for ,
Note that with for each , the term in the infimum attains the optimal value and thus the HJB equation can be reduced to
| (44) |
Then, the value functions of -player game defined by (7) is for all . Moreover, the path and the control under the equilibrium are given by
and
for . The proof is the application of Itô’s formula and the details are omitted here. Due to its LQG structure, the value function leads to a quadratic function of the form
Plugging into (44), and matching the coefficient of variables, we get the Riccati system of ODEs in (42) and the desired results are obtained. ∎
5.2 Proof of Proposition 2: Reduced Riccati form for the equilibrium
At present, the MFG and the corresponding -player game can be characterized by Proposition 1 and Lemma 10, respectively. One of our primary objectives is to examine the convergence of the representative optimal path generated by the -player game defined in (42)-(43) to the optimal path of the MFG described in Proposition 1.
It should be noted that is solely dependent on the function , as indicated in the ODE (11). In contrast, depends on many functions derived from the solutions of a substantial Riccati system (42) involving matrices . Consequently, comparing these two processes meaningfully becomes an exceedingly challenging task without gaining further insight into the intricate structure of the Riccati system (42).
Proof of Proposition 2.
Inspired from the setup in [18] and [16], we may seek a pattern for the matrix in the following form:
| (45) |
The next result justifies the above pattern: the entries of the matrix can be embedded to a -dimensional vector space no matter how big is.
For the Riccati system (42), with the given of and suppose each function in is continuous on , it is obvious to see that for all and for all . Note that in this case, for , the optimal control is given by
where is the -th column of matrix .
Plugging the pattern (45) into the differential equation of , we obtain the following system of ODEs:
with the terminal conditions
It is worth noting that there are two ODEs for , and the two expressions should be equal, thus
which implies that or
After combining terms and substituting with , we get
which yields or . Note that, since and satisfies different differential equations, it follows that . Hence, we can conclude that . Next, from the equation , we have
In conclusion, for , has the following expressions:
where and satisfies the system of ODEs (46)
| (46) |
The existence and uniqueness of in (42) are equivalent to the existence and uniqueness of (46). Firstly, the existence, uniqueness, and boundness of in (46) is from the same argument for in (40), which is shown as the proof of Lemma 12 in Appendix. The explicit solution of is given by
for all . Next, with the given of , the existence, uniqueness, and boundness of in (46) is guaranteed by Theorem 12.1 in [1]. Therefore, we can express the equilibrium paths and associated controls as the following:
| (47) |
and
respectively for , where is the solution to the ODE for in (46). This concludes Proposition 2. ∎
6 Further remark
7 Appendix
Lemma 11.
Let be the -Wasserstein metric. If and are two real-valued random variables and is a constant, then
| (48) |
Moreover, if is a sequence of random variables, then
| (49) |
Proof.
By definition of the -Wasserstein metric, we have:
where is the set of all joint probability measures with marginals and . Similarly,
where is the set of all joint probability measures with marginals and .
Now, consider the mapping given by . For any , the pushforward measure of under belongs to , i.e., . Thus, we have
Moreover, is bijective and measure preserving, then
Therefore, we know that
by the definition of the -Wasserstein metric. If we apply the above inequality to , , and , the opposite inequality is provided. Thus, it completes the proof of (48).
Lemma 12.
Proof.
Firstly, with the given of , we can solve the ODE
explicitly by the method of separating variables. Note that with the differential form, we have
It follows that
for some constant by taking integration on both sides. Thus by calculation, we obtain
for some constant to be determined. Since , it yields that and thus
It is easily to verify that is in and is bounded. With the given of , the functions in the Riccati system (40)-(41) is a coupled linear system, and thus their existence, uniqueness, and boundedness are given by Theorem 12.1 in [1]. ∎
References
- [1] Panos J Antsaklis and Anthony N Michel. Linear systems. Springer Science & Business Media, 2006.
- [2] Pierre Cardaliaguet. Notes on mean field games. Technical report, Technical report, 2010.
- [3] Pierre Cardaliaguet, François Delarue, Jean-Michel Lasry, and Pierre-Louis Lions. The Master Equation and the Convergence Problem in Mean Field Games:(AMS-201), volume 201. Princeton University Press, 2019.
- [4] René Carmona and François Delarue. Probabilistic theory of mean field games with applications. I, volume 83 of Probability Theory and Stochastic Modelling. Springer, Cham, 2018. Mean field FBSDEs, control, and games.
- [5] René Carmona and François Delarue. Probabilistic theory of mean field games with applications. II, volume 84 of Probability Theory and Stochastic Modelling. Springer, Cham, 2018. Mean field games with common noise and master equations.
- [6] René Carmona and François Delarue. Forward–backward stochastic differential equations and controlled mckean–vlasov dynamics. The Annals of Probability, 43(5):2647–2700, 2015.
- [7] René Carmona, François Delarue, and Aimé Lachapelle. Control of mckean–vlasov dynamics versus mean field games. Mathematics and Financial Economics, 7(2):131–166, 2013.
- [8] François Delarue, Daniel Lacker, and Kavita Ramanan. From the master equation to mean field game limit theory: Large deviations and concentration of measure. Annals of Probability, 48(1):211–263, 2020.
- [9] Richard Durrett. Probability. The Wadsworth & Brooks/Cole Statistics/Probability Series. Wadsworth & Brooks/Cole Advanced Books & Software, Pacific Grove, CA, 3rd edition, 2005. Theory and examples.
- [10] Nicolas Fournier and Arnaud Guillin. On the rate of convergence in wasserstein distance of the empirical measure. Probability theory and related fields, 162(3-4):707–738, 2015.
- [11] Wilfrid Gangbo, Alpár R Mészáros, Chenchen Mou, and Jianfeng Zhang. Mean field games master equations with nonseparable hamiltonians and displacement monotonicity. The Annals of Probability, 50(6):2178–2217, 2022.
- [12] Minyi Huang, Peter E Caines, and Roland P Malhamé. An invariance principle in large population stochastic dynamic games. Journal of Systems Science and Complexity, 20(2):162–172, 2007.
- [13] Minyi Huang, Peter E Caines, and Roland P Malhamé. Large-population cost-coupled lqg problems with nonuniform agents: individual-mass behavior and decentralized -nash equilibria. IEEE transactions on automatic control, 52(9):1560–1571, 2007.
- [14] Minyi Huang, Peter E Caines, and Roland P Malhamé. The nash certainty equivalence principle and mckean-vlasov systems: an invariance principle and entry adaptation. In 2007 46th IEEE Conference on Decision and Control, pages 121–126. IEEE, 2007.
- [15] Minyi Huang, Roland P Malhamé, Peter E Caines, et al. Large population stochastic dynamic games: closed-loop mckean-vlasov systems and the nash certainty equivalence principle. Communications in Information & Systems, 6(3):221–252, 2006.
- [16] Minyi Huang and Xuwei Yang. Linear quadratic mean field games: Decentralized o (1/n)-nash equilibria. Journal of Systems Science and Complexity, 34(5):2003–2035, 2021.
- [17] Joe Jackson and Ludovic Tangpi. Quantitative convergence for displacement monotone mean field games with controlled volatility. arXiv preprint arXiv:2304.04543, 2023.
- [18] Jiamin Jian, Peiyao Lai, Qingshuo Song, and Jiaxuan Ye. The convergence rate of the equilibrium measure for the lqg mean field game with a common noise. arXiv preprint arXiv:2106.04762v3, 2022.
- [19] Jean-Michel Lasry and Pierre-Louis Lions. Mean field games. Japanese journal of mathematics, 2(1):229–260, 2007.
- [20] Huyên Pham. Continuous-time stochastic control and optimization with financial applications, volume 61. Springer Science & Business Media, 2009.