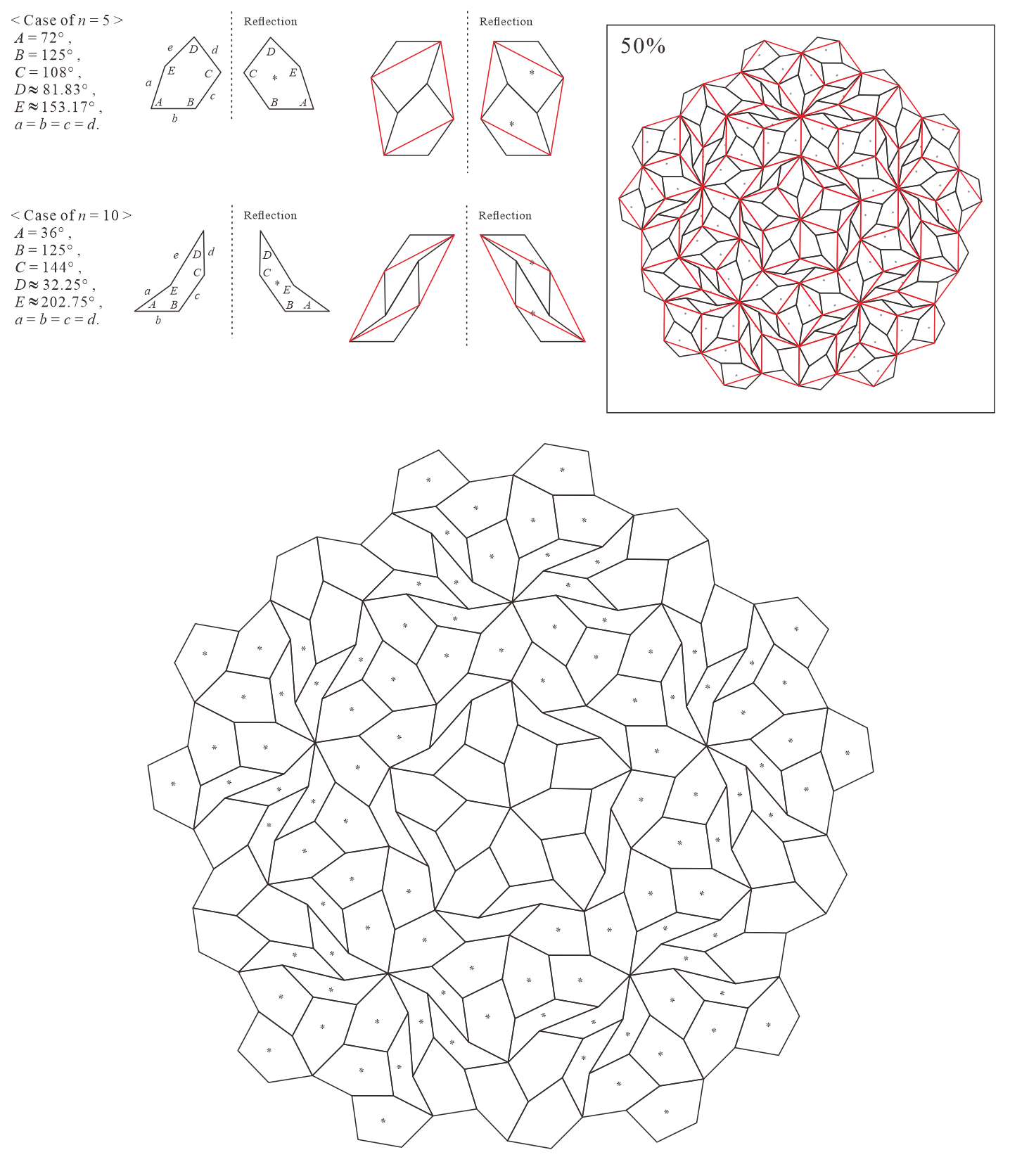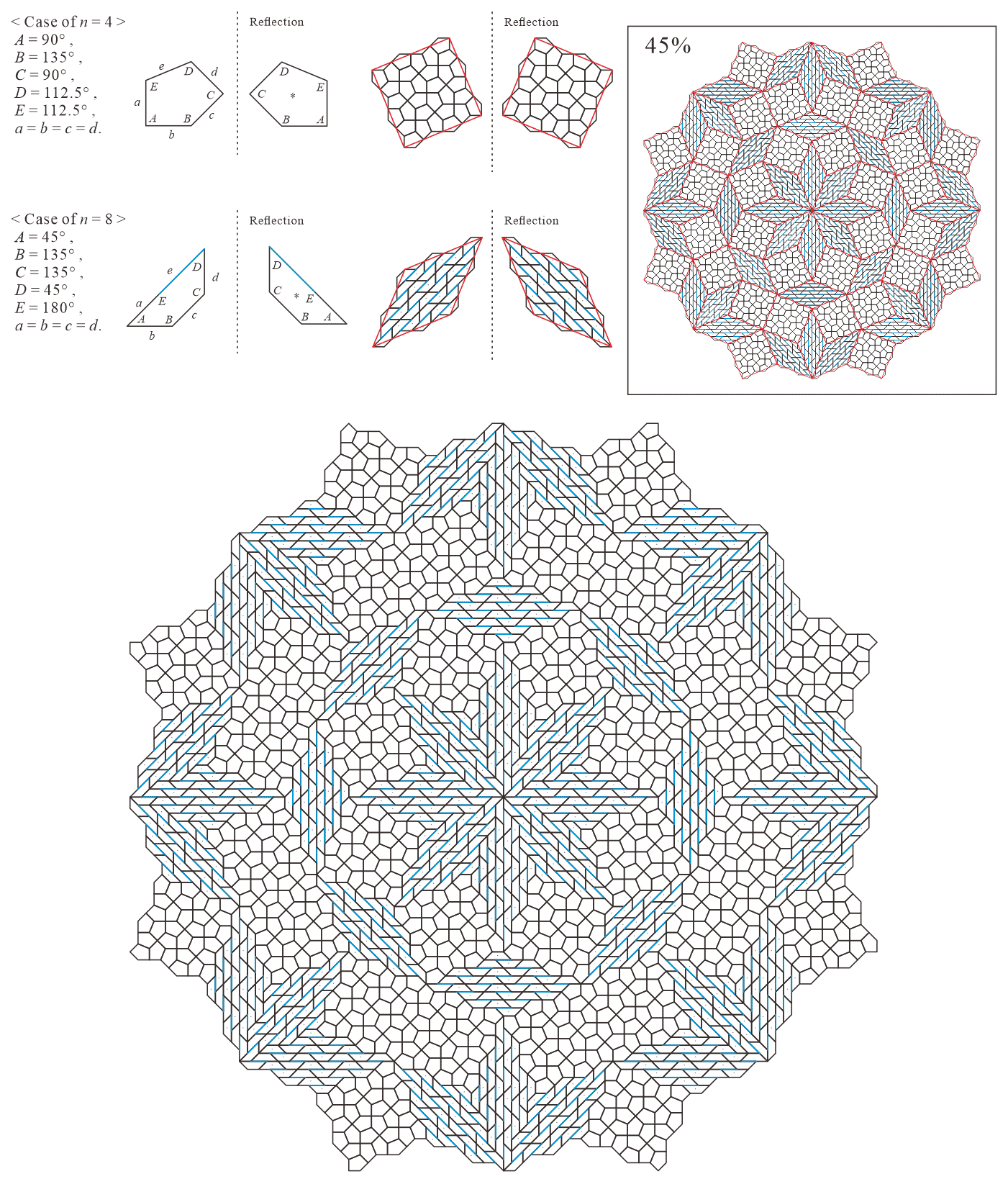Converting tilings with multiple types of rhombuses to pentagonal tilings
Abstract
The results involving rotationally symmetric tilings with multiple types of rhombuses, discovered by Penrose, Ammann, Beenker, or Socolar, are converted to tilings with multiple types of pentagons are presented. The pentagons can be convex or concave, and can be degenerated into a trapezoid or parallelogram. If the pentagons are convex, they belong to the Type 2 family.
1) The Interdisciplinary Institute of Science, Technology and Art
2) Japan Tessellation Design Association
E-mail: ismsugi@gmail.com
Keywords: pentagon, rhombus, tiling, rotational symmetry, Penrose
1 Introduction
Pentagonal tiles111 A tiling (or tessellation) of the plane is a collection of sets that are called tiles, which covers a plane without gaps and overlaps, except for the boundaries of the tiles. The term “tile” refers to a topological disk, whose boundary is a simple closed curve. If all the tiles in a tiling are of the same size and shape, then the tiling is monohedral [2, 9]. In this study, a polygon that admits a monohedral tiling is called a polygonal tile [5, 6]. Note that, in monohedral tiling, it admits the use of use reflected tiles. that can form rotationally symmetric tiling in [7] have been introduced, and regarding the tilings formed by this pentagonal tile, two adjacent pentagons in the tiling can be converted to a rhombus; hence, they are closely related to rhombic monohedral tiling.
The rhombus is a convex quadrilateral tile. Several types of tilings that use multiple types of rhombuses (i.e. tilings, that are not monohedral) are also known. As introduced in Section 6 of [7], tilings with multiple types of rhombuses can be converted into those with multiple types of pentagons, with the aid of pentagons that can be converted into rhombuses; however, not all the tilings allow this conversion. In this study, we present the results that indicate that a rotationally symmetric tiling with multiple types of rhombuses is converted to a pentagonal tiling (tiling formed by pentagons). Specifically, we present tilings with two types of pentagons based on five-fold or eight-fold rotationally symmetric tilings with the aid of two types of rhombuses, and tilings with three types of pentagons based on 12-fold rotationally symmetric tiling with the aid of three types of rhombuses.
2 Conditions of pentagon related to rhombic tiling
Note that the content of this section is almost the same as that in Section 2 of [7].
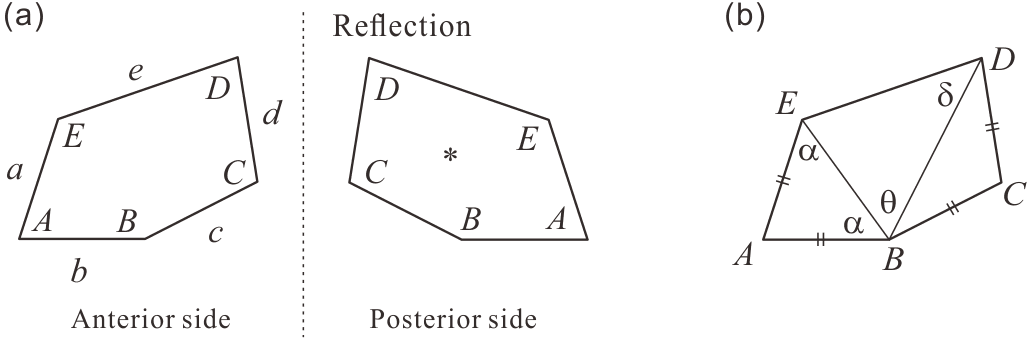
In this study, the vertices (interior angles) and edges of the pentagon will be referred to using the nomenclature shown in Figure 2.1(a). As introduced in [7], if a pentagon related to a rhombic tiling (tiling formed by rhombuses) is convex, it is a convex pentagonal tile belonging to the Type 2 family.222 To date, fifteen families of convex pentagonal tiles, each of them referred to as a “Type,” are known [2, 5, 6, 9]. For example, if the sum of three consecutive angles in a convex pentagonal tile is , the pentagonal tile belongs to the Type 1 family. Convex pentagonal tiles belonging to some families also exist. Known convex pentagonal tiles can form periodic tiling. In May 2017, Michaël Rao declared that the complete list of Types of convex pentagonal tiles had been obtained (i.e., they have only the known 15 families), but it does not seem to be fixed as of January 2022 [9]. In [8], we consider edge-to-edge333 A tiling by convex polygons is edge-to-edge if any two convex polygons in a tiling are either disjoint or share one vertex or an entire edge in common. Then other case is non-edge-to-edge [2, 5, 6]. tilings with a convex pentagon and named the convex pentagonal tile “C20-T2.” C20-T2 shown in [8] is a convex pentagon that satisfies the conditions
| (1) |
and can form the representative tiling (tiling of edge-to-edge version) of Type 2 that has the relations “.” Because this convex pentagon has four equal-length edges, it can be divided into an isosceles triangle BCD, an isosceles triangle ABE with a base angle , and a triangle BDE with and , as shown in Figure 2.1(b). Accordingly, using the relational expression for the interior angle of each vertex of C20-T2, the conditional expressions of (1) can be rewritten as follows:
| (2) |
where
and because and [8]. This pentagon has two degrees of freedom ( and parameters), besides its size. If the edge of this pentagon exists and the pentagon is convex, then . But depending on the value of , even if is selected in , the pentagon may not be convex or may be geometrically nonexistent. If , then the length of edge can be expressed as follows:
Let the interior angle of vertex be (i.e., ) so that pentagons satisfying (2) can form an -fold rotationally symmetric tiling. (Remark: Due to the properties of the pentagons, the interior angle of vertex , and not vertex , will be .) Note that is an integer greater than or equal to three, because . Therefore, the conditions of pentagonal tiles that can form -fold rotationally symmetric tilings are expressed in (3).
| (3) |
3 Relationships between pentagon and rhombus
Note that the content of this section is almost the same as that in Section 3 of [7].
The convex pentagon shown in Figure 2.1 satisfies (3), where and . Note that it is equivalent to the case where and , in (2). By using this convex pentagon of Figure 2.1, the method of forming tilings with pentagons satisfying the conditions of (2) or (3) is described below. In accordance with the relationship between the five interior angles of the pentagon, the vertex concentrations that can be always used in tilings are “.” According to (2) and (3), the edge of the pentagon is the sole edge of different length. Therefore, the edge of one convex pentagon is always connected in an edge-to-edge manner with the edge of another convex pentagon. A pentagonal pair with their respective vertices and concentrated forms the basic unit of the tiling. This basic unit can be made of two types: a (anterior side) pentagonal pair as shown in Figure 3.1(a) and a reflected (posterior side) pentagonal pair as shown in Figure 3.1(b). Four different types of units, as shown in Figures 3.1(c), 3.1(d), 3.1(e), and 3.1(f), are obtained by combining two pentagonal pairs shown in Figures 3.1(a) and 3.1(b), so that can be assembled.
As shown in Figures 3.1(a) and 3.1(b), a rhombus (red line), with an acute angle of , formed by connecting the vertices and of the pentagon, is applied to each basic unit of the pentagonal pair. (Remark: In this example, because the interior angle of the vertex is , the rhombus has an acute angle of . That is, the interior angles of the rhombus corresponding to the pair of pentagons in Figures 3.1(a) and 3.1(b) are the same as the interior angles of vertices and in (2) and (3).) Consequently, the parts of pentagons that protrude from the rhombus match exactly with the parts that are more dented than the rhombus (refer to Figures 3.1(c), 3.1(d), 3.1(e), and 3.1(f)). In fact, tilings in which “” using pentagons satisfying (2) and (3) are equivalent to rhombic tilings. (Though a rhombus is a single entity, considering its internal pentagonal pattern, it will be considered as two entities.)
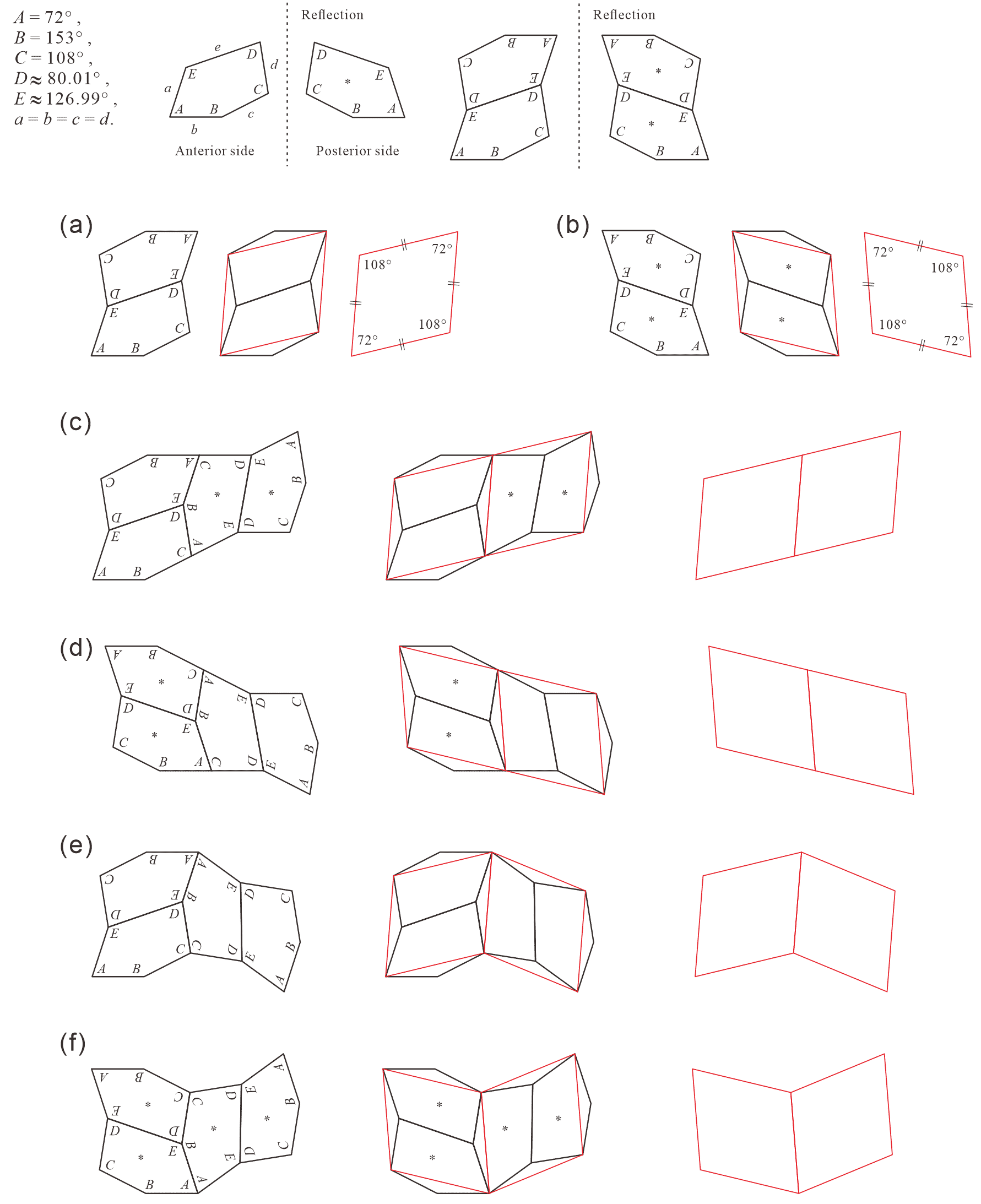
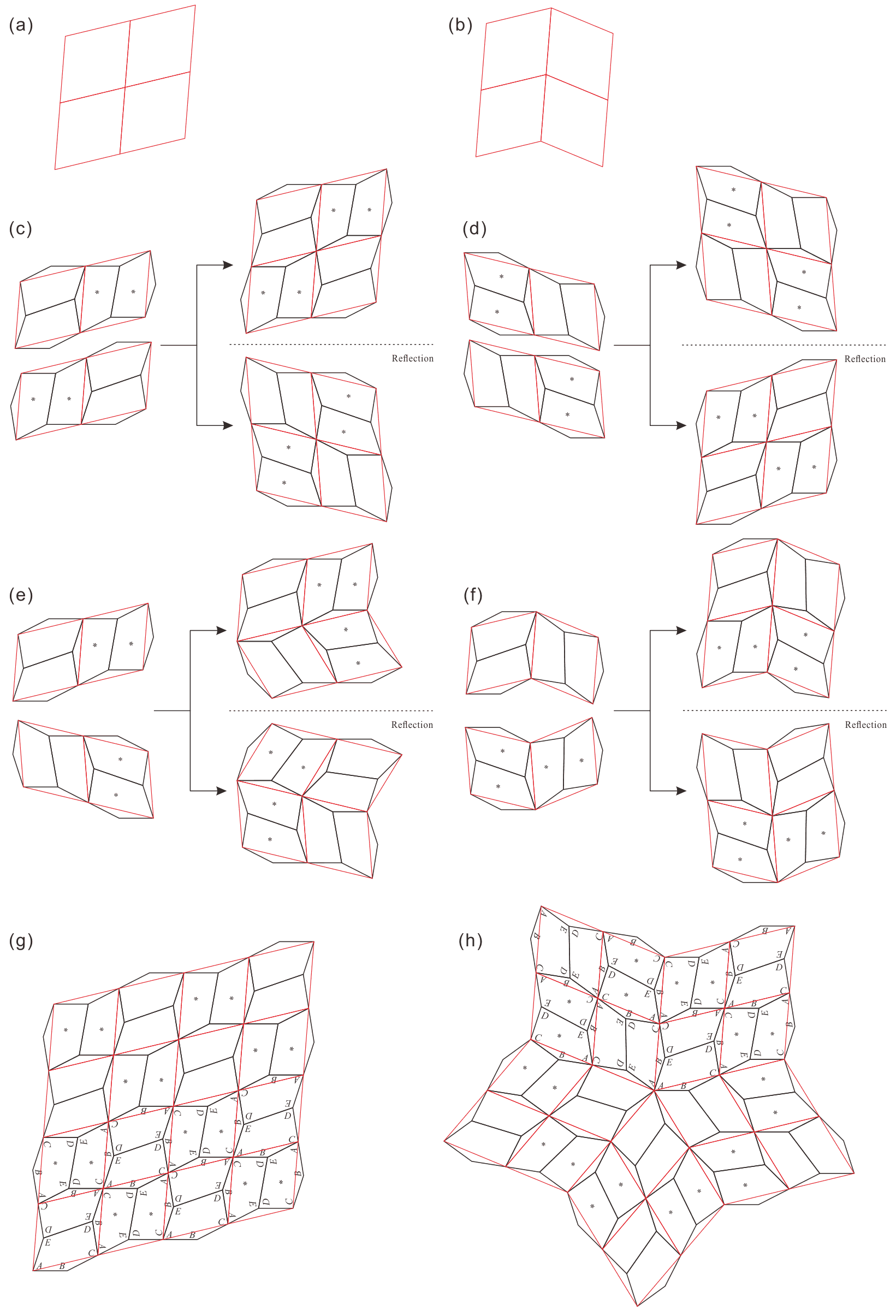
Rhombuses have two-fold rotational symmetry and two axes of reflection symmetry passing through the center of the rotational symmetry (hereafter, this property is described as symmetry444 “” is based on the Schoenflies notation for symmetry in a two-dimensional point group [10, 11]. “” represents an -fold rotation axis with reflection symmetry axes. The notation for symmetry is based on that presented in [3]. ). Therefore, the rhombus and the reflected rhombus have identical outlines. Thus, the two methods of concentrating the four rhombic vertices at a point without gaps or overlaps are: Case (i) an arrangement by parallel translation as shown in Figure 3.2(a); Case (ii) an arrangement by rotation (or reflection) as shown in Figure 3.2(b). This concentration corresponds to forming a “” at the center by four pentagons. In Case (i), because the pentagonal vertices circulate as “” at the central “,” one combination (refer to Figure 3.2(c)) is obtained by using two units of Figure 3.1(c) and another combination (refer to Figure 3.2(d)) is obtained by using two units of Figure 3.1(d). In Case (ii), because the pentagonal vertices circulate as “” at the central “,” one combination (refer to Figure 3.2(e)) is obtained by using units of Figures 3.1(c) and 3.1(d), and another combination (refer to Figure 3.2(f)) is obtained by using units of Figures 3.1(e) and 3.1(f).
Only when the unit comprising eight pentagons in Figures 3.2(c) or 3.2(d) are arranged in a parallel manner, a tiling, as shown in Figure 3.2(g), is formed that represents a tiling of Type 2, in which “.” Because rhombuses can form rhombic belts by translation in the same direction vertically, rhombic tilings can also be formed by the belts that are freely connected horizontally by the connecting method shown in Figures 3.2(a) and 3.2(b). Further, pentagonal tilings corresponding to those rhombic tilings can be formed.
When vertices, with interior angles of , of rhombuses are concentrated at a point, an -fold rotationally symmetric arrangement is formed, with adjacent rhombuses connected as shown in Figure 3.2(b). Therefore, an -fold rotationally symmetric tiling with rhombuses can be formed by dividing each rhombus, in that arrangement, into similar shapes. By converting the rhombuses of such rhombic tiling into pentagons satisfying (3), the rotationally symmetric tilings with convex pentagons can be obtained (refer to Figure 3.2(h)). Therefore, when forming -fold rotationally symmetric tilings from a pentagon satisfying (3), the pentagonal arrangement can be known from the corresponding -fold rotationally symmetric tilings with a rhombus.
4 Conversion method of tilings with multiple types of rhombuses
4.1 Preparation
Countless tilings with multiple types of rhombuses exist, and several rotationally symmetric tilings with multiple types of rhombuses are known as well. By using pentagons that satisfy (2) or (3), the values of in (2) and (3) are important when a tiling with multiple types of rhombuses is converted into one with multiple types of pentagons, which is simply referred to as “pentagonal tiling.” The reason is because each pentagon must have the same value of (vertex ) to be “” to hold within that pentagonal tiling.
As mentioned in [7], pentagons that satisfy (2) or (3) can be concave, convex, trapezoidal, or parallelogram depending on the parameters. Therefore, when a tiling with multiple types of rhombuses is converted into a pentagonal tiling, the pentagons in the tiling could be solely convex or concave, possess both a concave and convex shape simultaneously, etc. The pentagons that satisfy (2) with two parameters, and , are difficult to treat as an example because it leaves the value of without a clear guideline after determining the value of , which is an important factor in generating a pentagonal tiling. The pentagons that satisfy (3) have two parameters, and , where is an integer of three or more. Specifically, a pentagon that satisfies (3) is easy to treat as an example, because the shape of the pentagon can be determined only by the value of after the value of is determined. (Of course, the pentagon that satisfies (3) is also the pentagon that satisfies (2), but here it is distinguished for the sake of explanation.)
Therefore, in this study, we utilize rotationally symmetric tilings with pentagons that satisfy (3) a case example where a tiling with multiple types of rhombuses is converted into a pentagonal tiling. Specifically, we introduce pentagonal tilings based on five-fold or eight-fold rotationally symmetric tilings with two types of rhombuses (i.e., the tilings are formed by two types of pentagons that satisfy (3)), and pentagonal tilings based on a 12-fold rotationally symmetric tiling with three types of rhombuses (i.e., the tilings are formed by three types of pentagons that satisfy (3)).
The properties of the shape of pentagons that satisfy (3) depending on the values of and are arranged below. If the pentagons that satisfy (3) exist geometrically, then , because . It is because the edge of the pentagon that satisfies (3) exists and does not intersect the edge . As mentioned in Section 4 of [7], the pentagons that satisfy (3) with and correspond to rhombuses with an acute angle of , and these pentagons are opposite to each other. The shapes of the pentagons that satisfy (3) change depending on the values of and are as follows:
-
Case where the pentagons that satisfy (3) admit
-
•
: Convex pentagons
-
•
: Parallelograms ()
-
•
: Concave pentagons ()
-
•
-
Cases where the pentagons that satisfy (3) admit
-
•
: Concave pentagons ()
-
•
: Trapezoids ()
-
•
: Convex pentagons
-
•
: Parallelograms ()
-
•
: Concave pentagons ()
-
•
-
Cases where the pentagons that satisfy (3) become the polygons with
-
•
Case where and (Convex pentagon with )
-
•
Case where and (Convex pentagon with )
-
•
Case where and (Trapezoid of )
-
•
Case where and (Concave pentagon with )
-
•
If the pentagons that satisfy (3) have (i.e., ), then they are parallelograms (the case of is a rectangle). Such parallelograms correspond to half of the rhombus corresponding to the basic unit of Figures 3.1(a) or 3.1(b).
If the pentagons that satisfy (3) have , then “.” Thus, they are trapezoids with a line of symmetry and holds. It is when that the pentagons that satisfy (3) become trapezoids, because .
If the pentagons that satisfy (3) have , then where . In this case, for to exist.
4.2 Conversion method
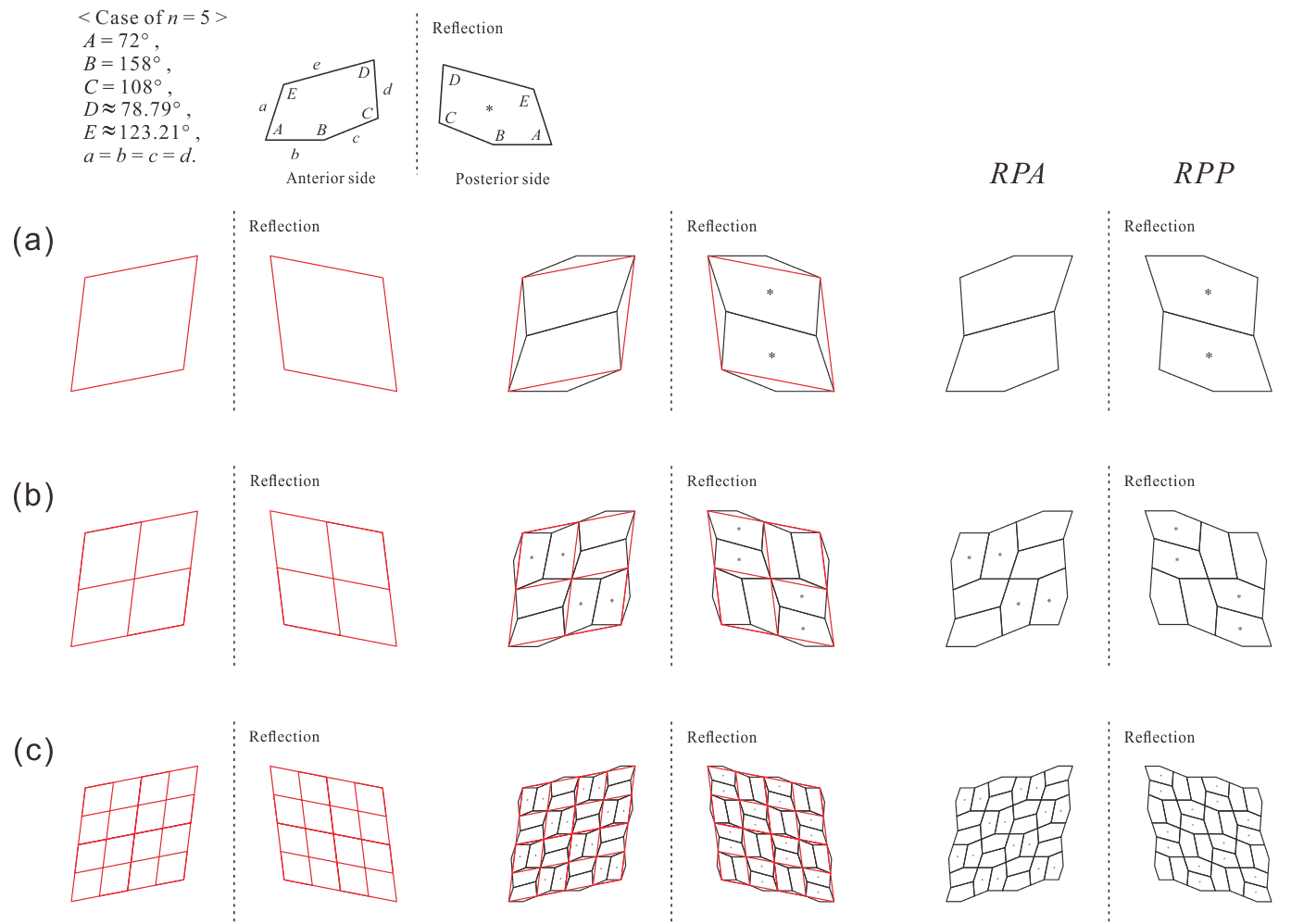
By using pentagons that satisfy (2) or (3), when a tiling with multiple types of rhombuses is converted into a pentagonal tiling, there are two possible methods. The first method is to convert each rhombus in the tiling into two pentagons, as illustrated in Figure 4.1(a). The second method is to divide each rhombus in the tiling by its own similar figures and convert each rhombus formed by division into two pentagons. If a tiling with rhombuses is monohedral, the pentagonal tiling generated by conversion of the above methods is the same, but if it is a tiling with multiple types of rhombuses, the pentagonal tiling generated by the conversion differs depending on how the rhombuses are divided.
In the tiling with multiple types of rhombuses, the method of dividing a rhombus into its own similar figures has two rules that must be followed to be able to convert it into a pentagonal tiling. First, it is necessary to divide the base rhombus so that it contains for of its own similar rhombuses. Accordingly, when converted to a pentagon, the base rhombus contains pentagons. To form a pentagonal tiling as illustrated in Figures 3.2(g), 3.2(h), etc., we combine basic units of the pentagonal pair with the anterior and posterior sides as illustrated in Figures 3.1(a) and 3.1(b). Specifically, when dividing the base rhombus into its own similar figures, the four divisions in Figure 4.1(b) are the standard units of division. Because the standard unit of division contains eight pentagons, with four pentagons each on the anterior and posterior sides, it is considered as “divide a rhombus into eight (congruent) pentagons” or “convert a rhombus into eight (congruent) pentagons.” Therefore, dividing a rhombus by its own similar figures, which can be converted into a pentagonal tiling, is allowed as follows: four divisions with one standard unit of division (refer to Figure 4.1(b)), 16 divisions with four standard units of division arranged in two rows and two columns (refer to Figure 4.1(c)), 36 divisions with nine standard units of division arranged in three rows and three columns, etc. The second rule is that each rhombus in the tiling must have the same number of divisions. For example, in the case where a tiling with two types of rhombuses, and , is converted into a pentagonal tiling, if is divided into 16 by its own similar figures, is also divided into 16 by its own similar figures (i.e., unifying all rhombuses and in the tiling into 16 divisions).
5 Conversion results
5.1 Five-fold rotationally symmetric tilings
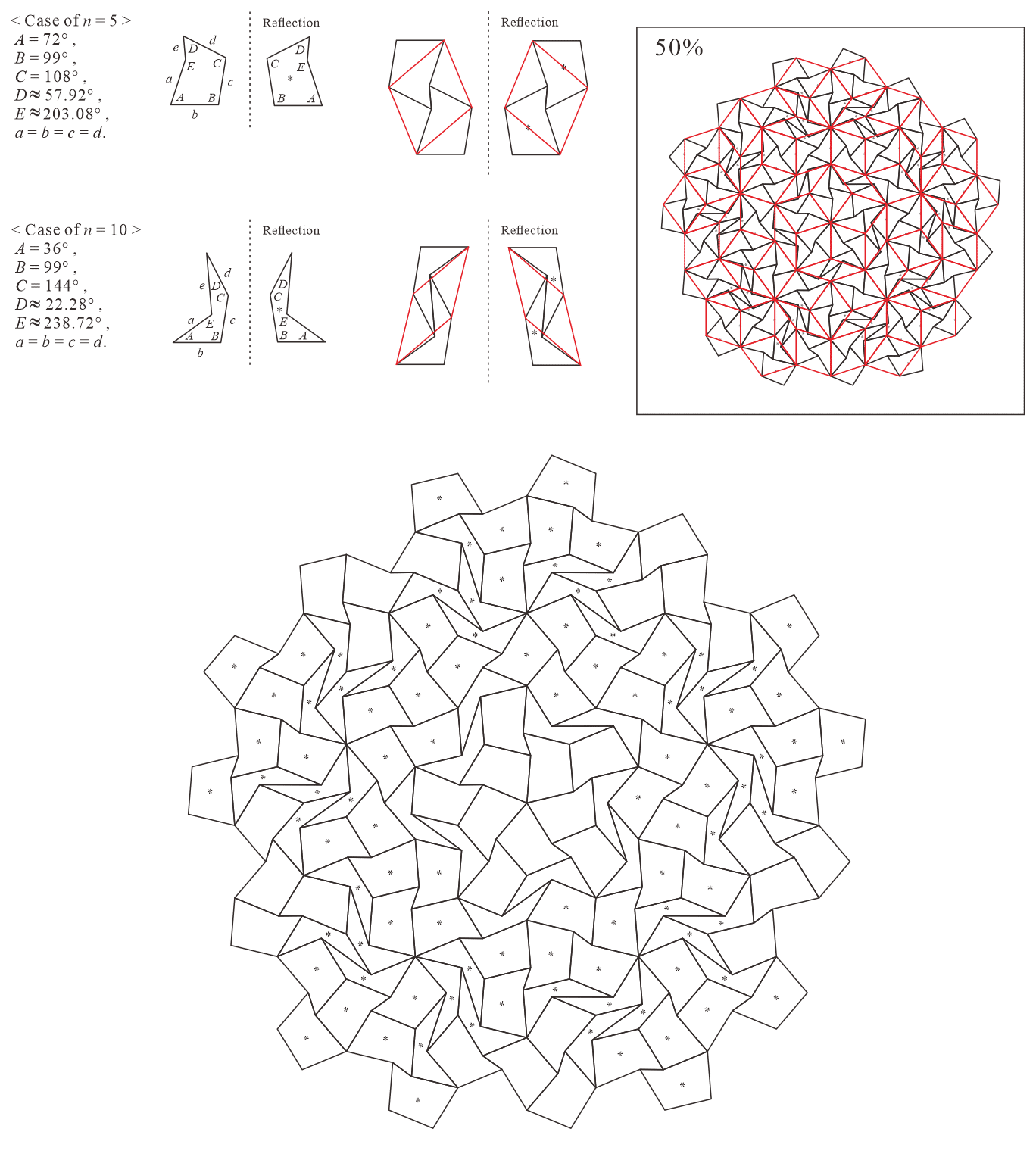
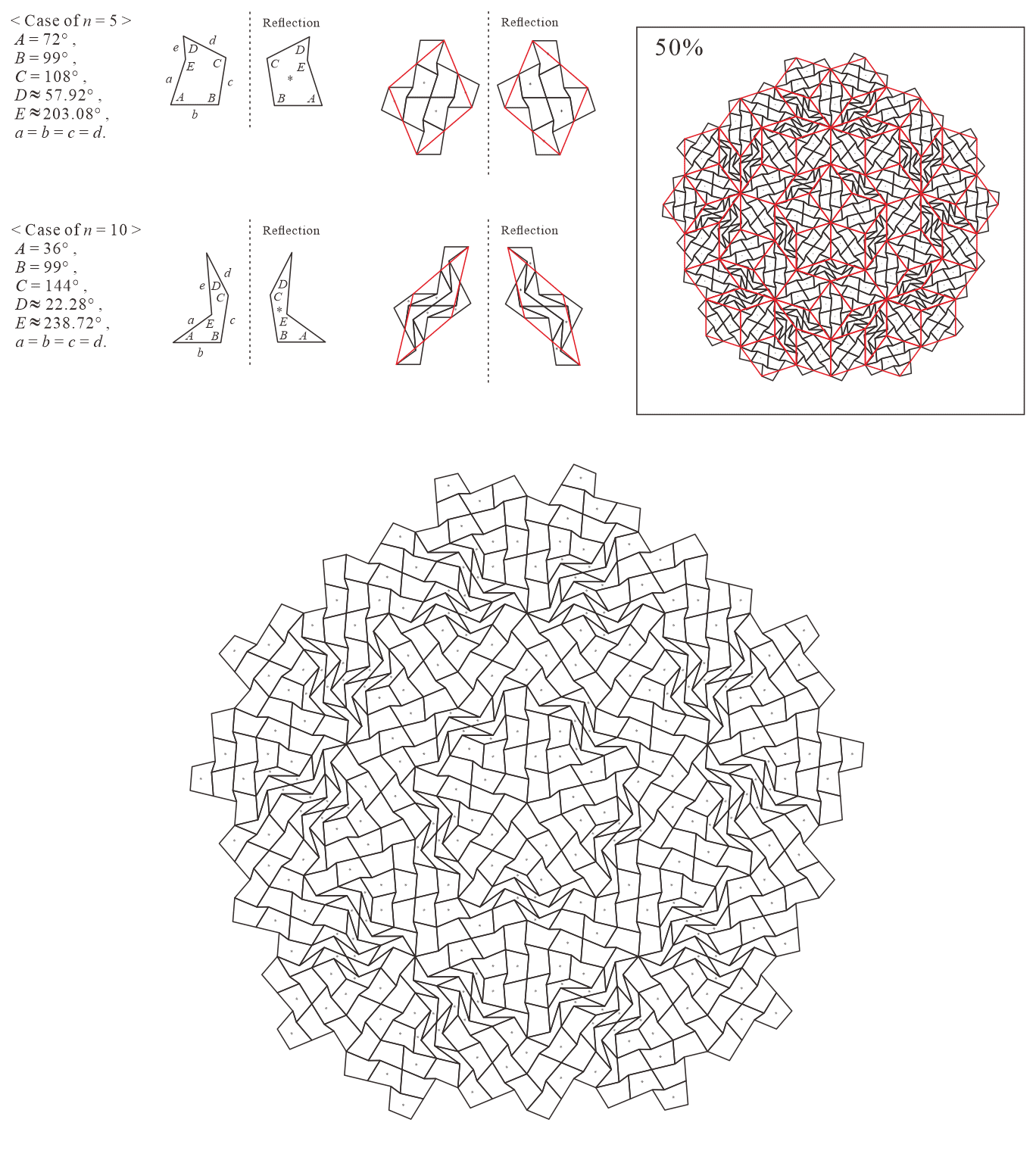
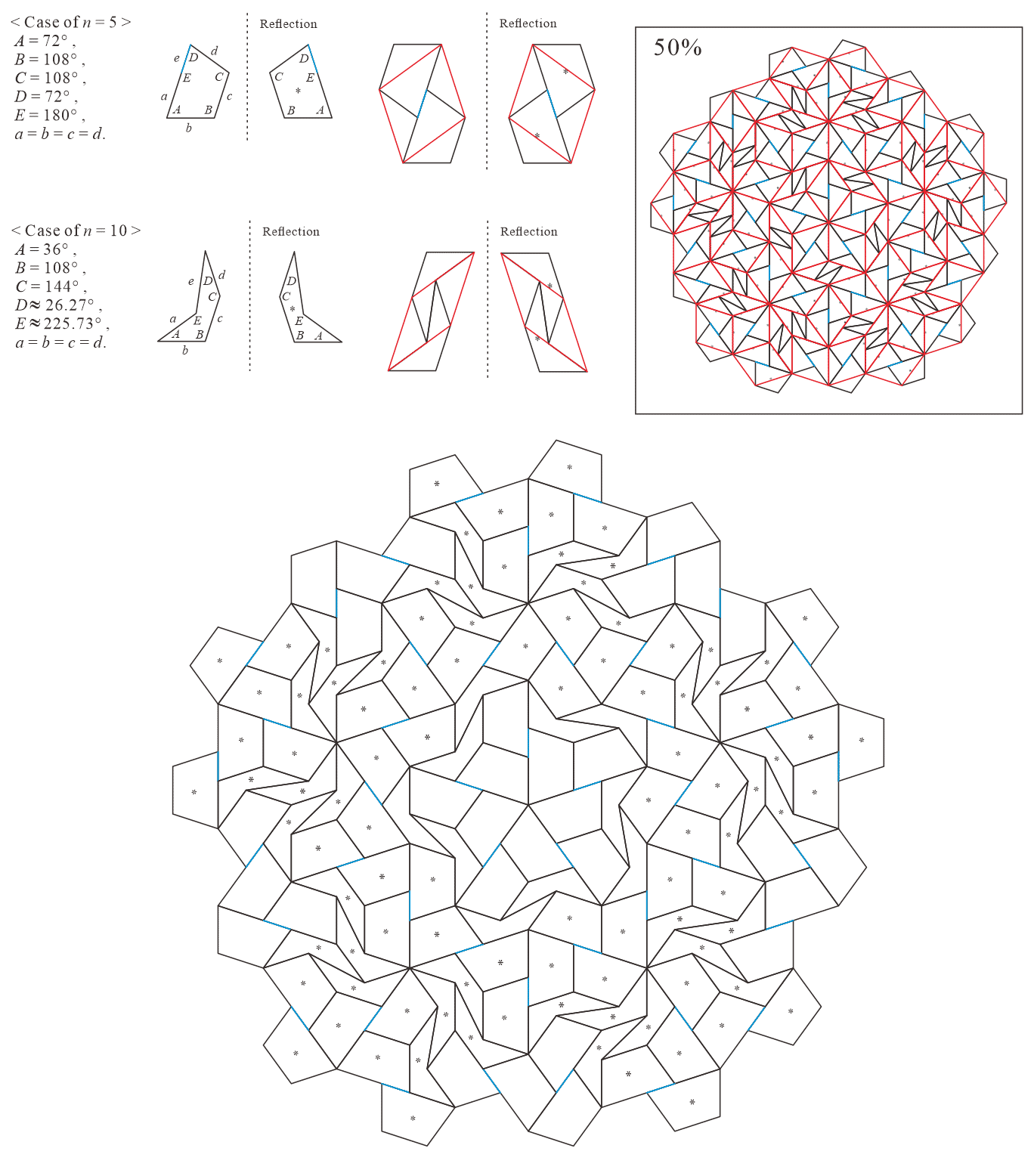
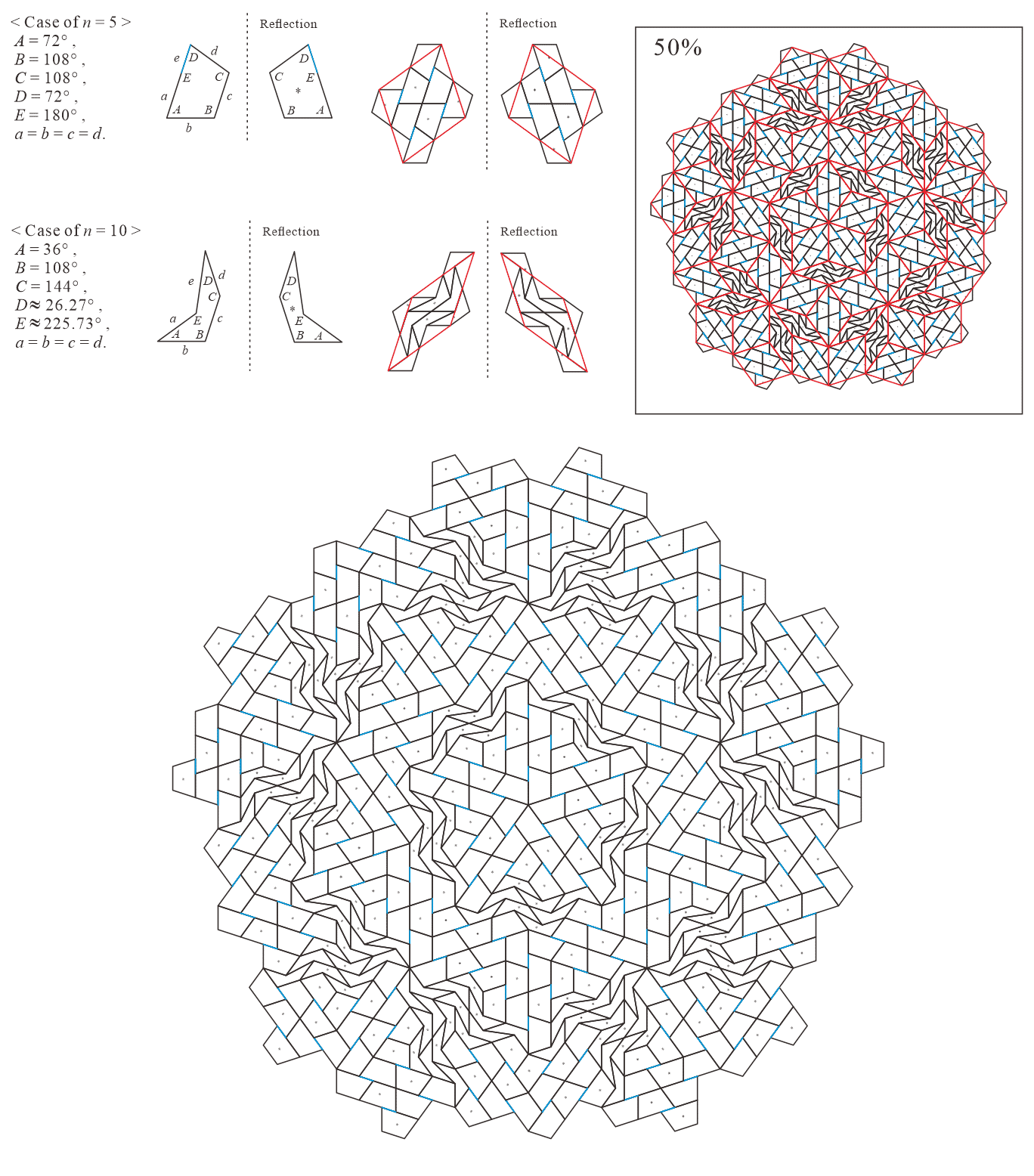
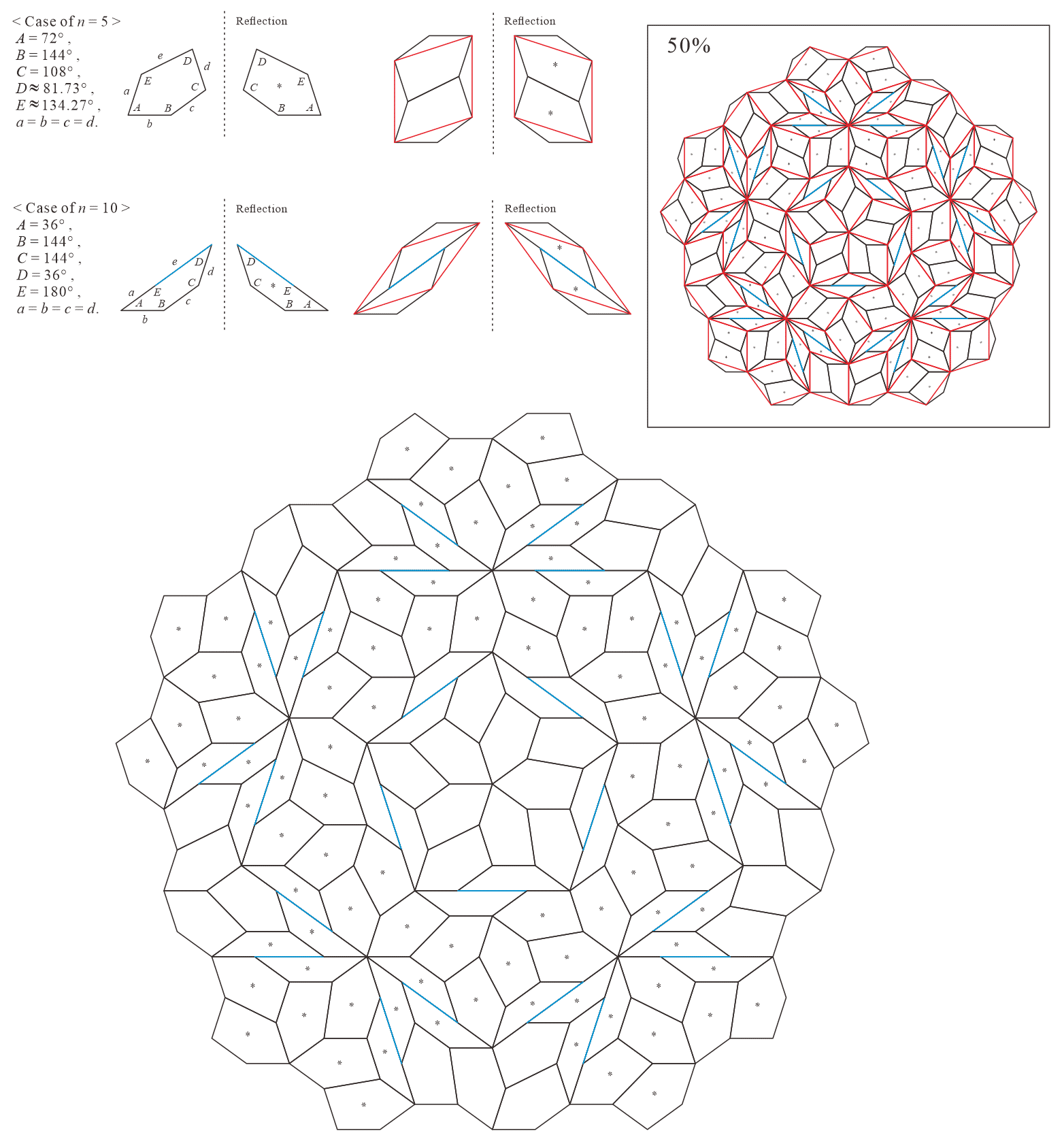
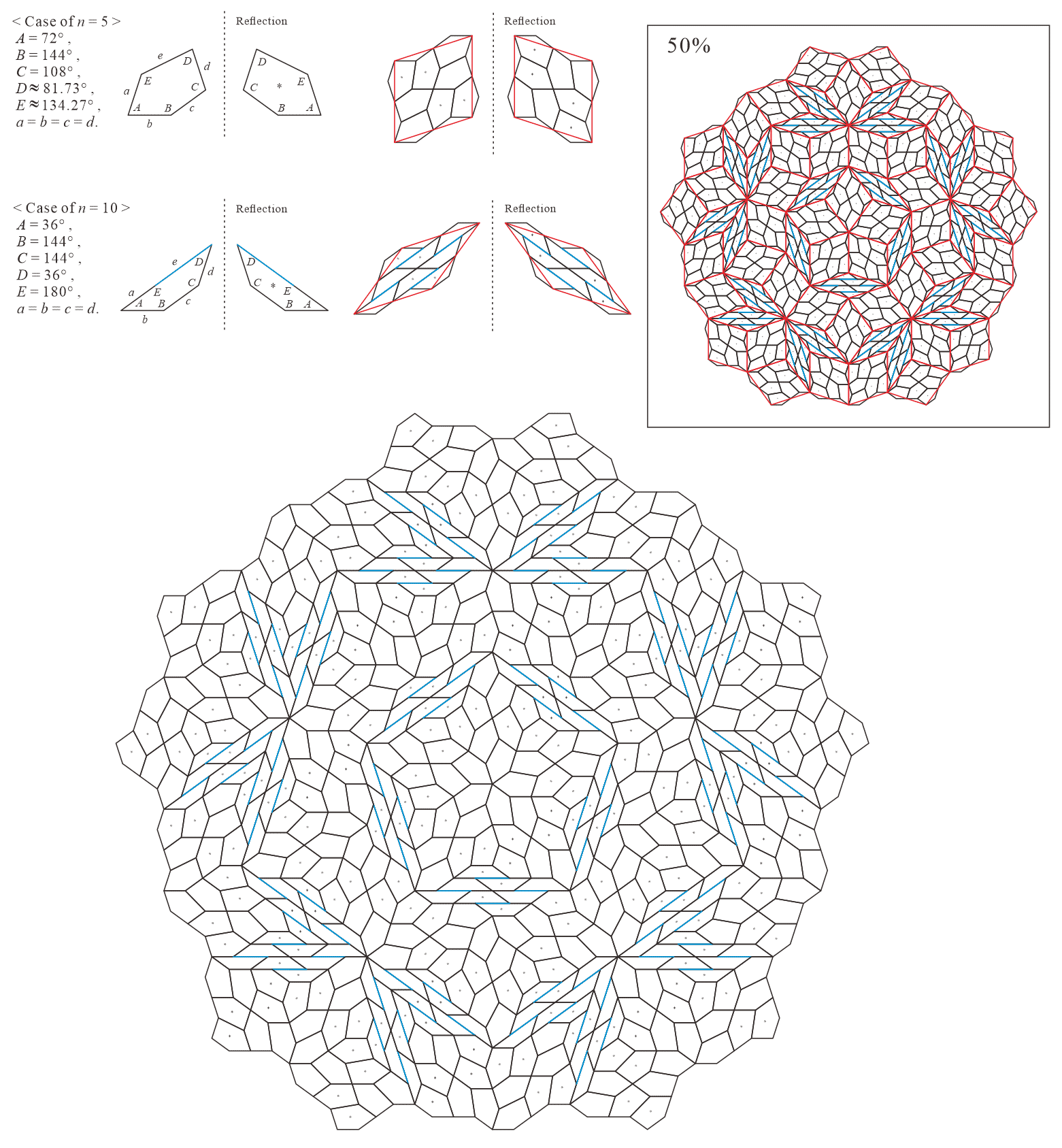
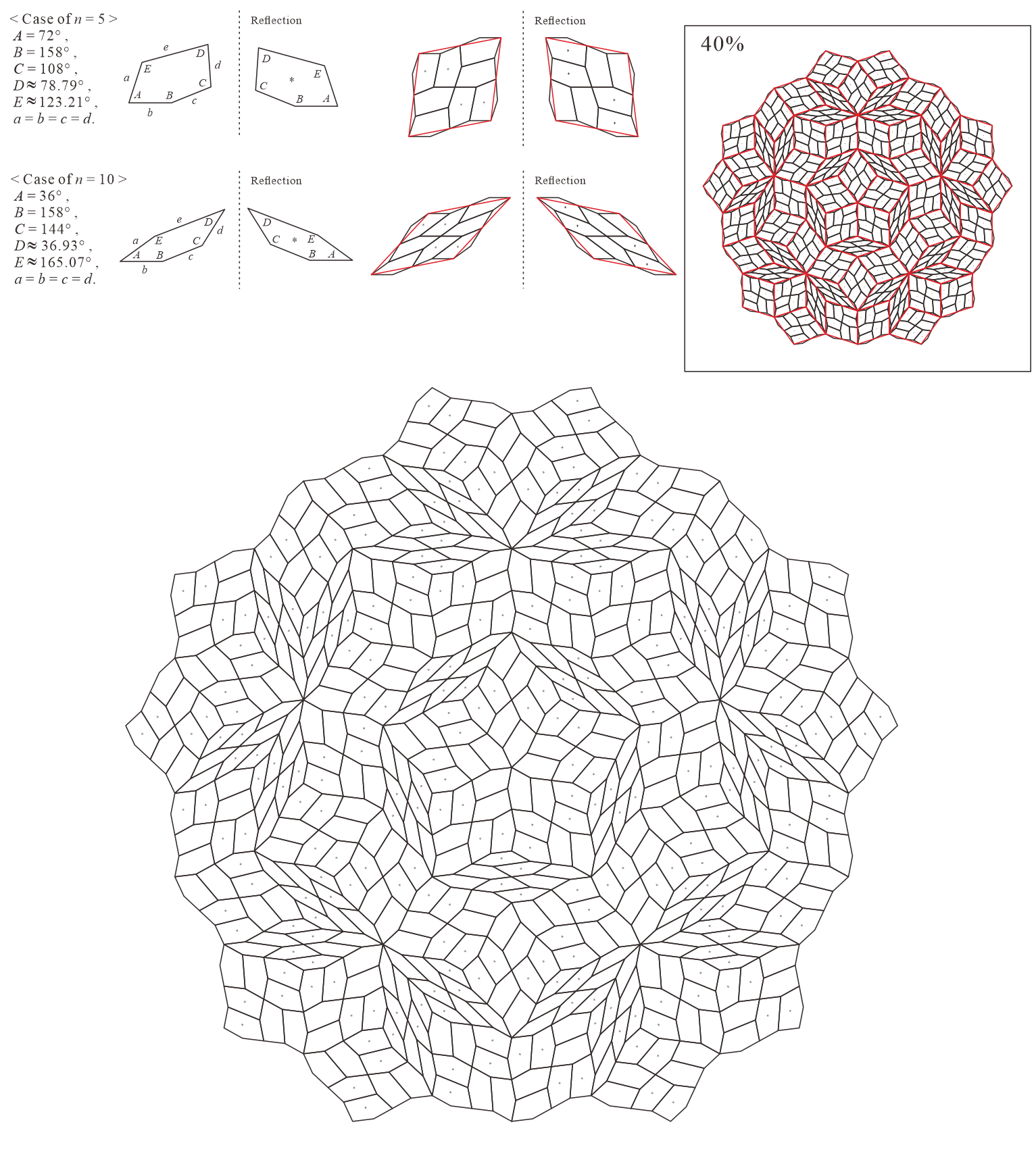
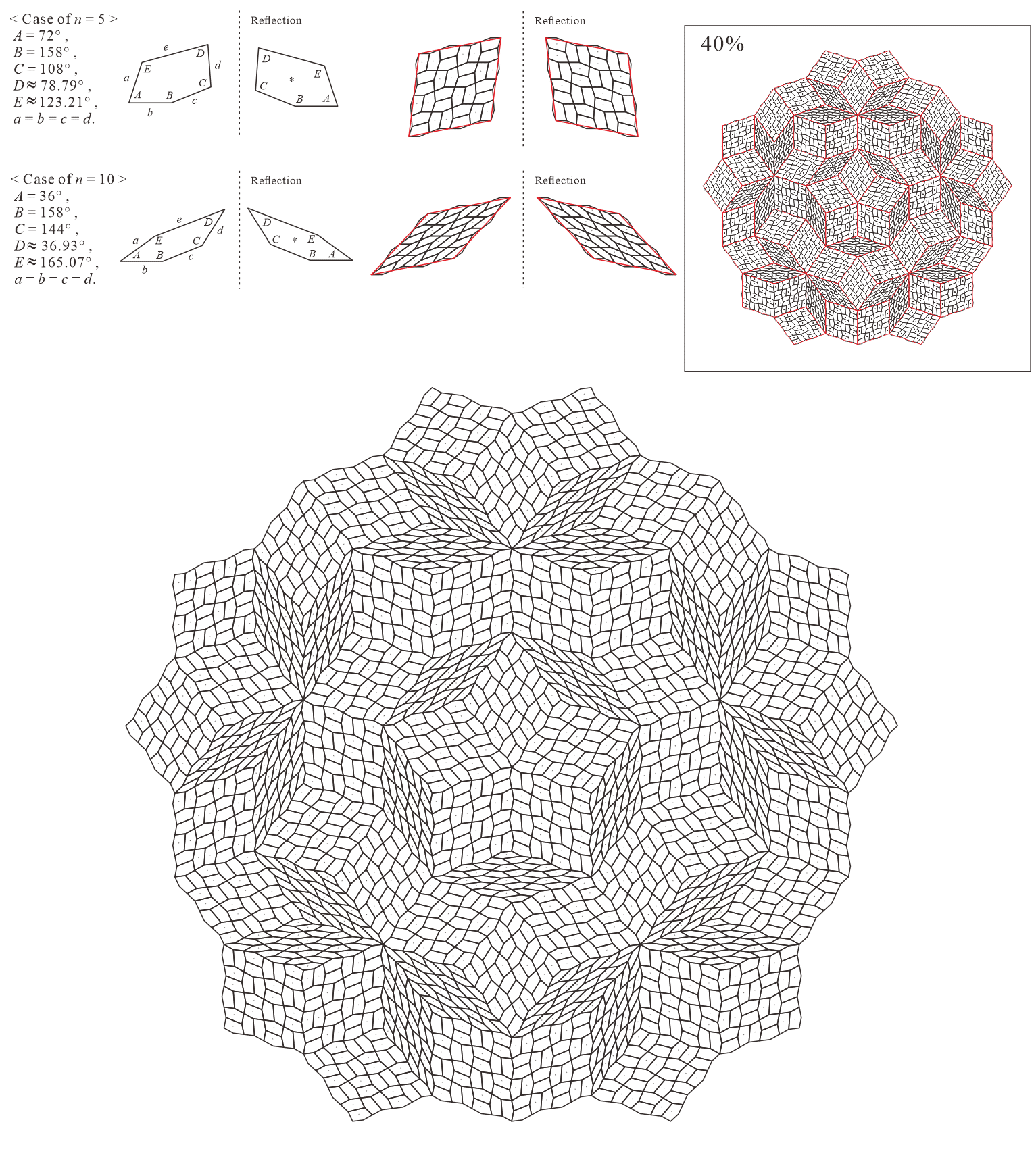
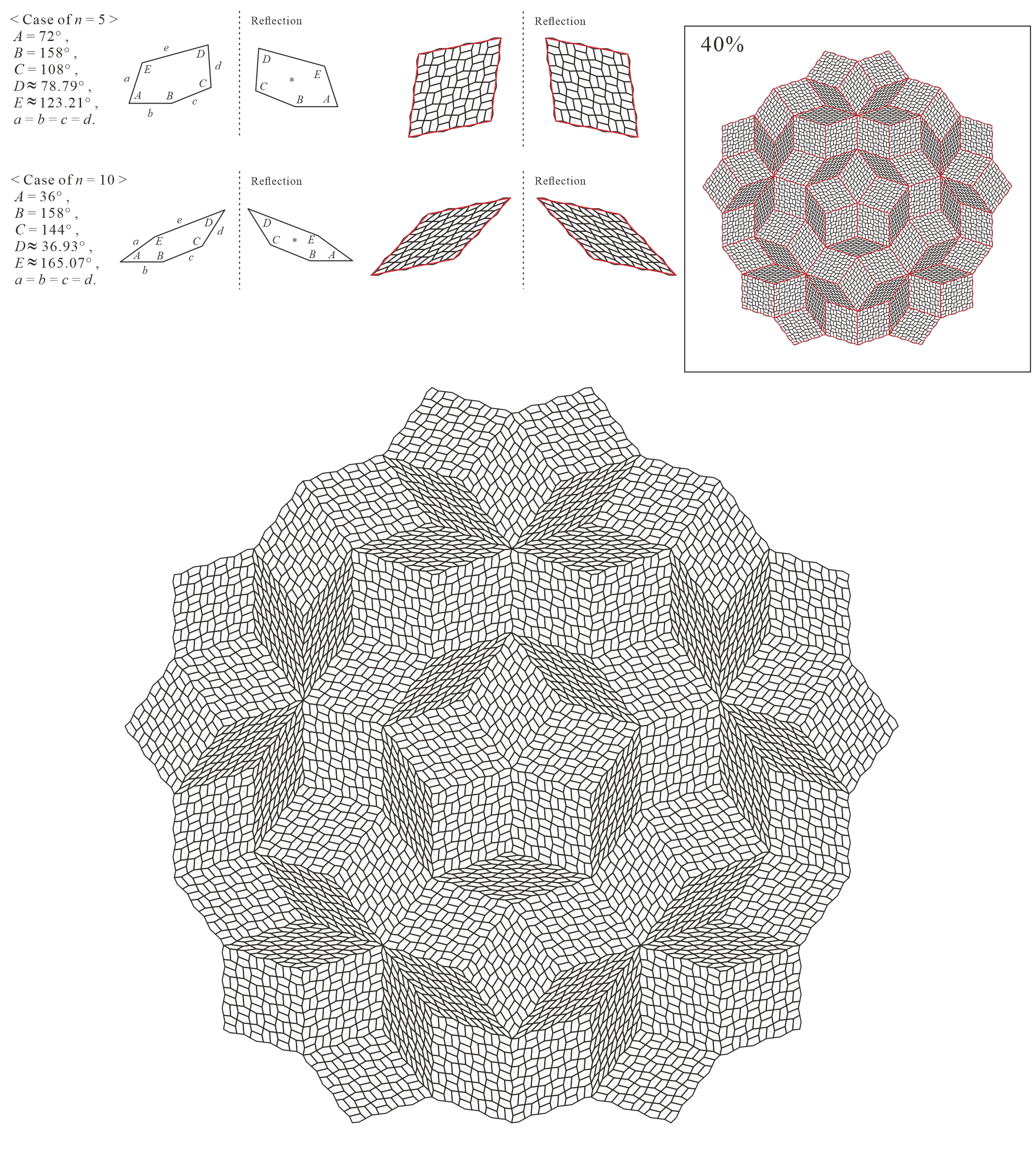
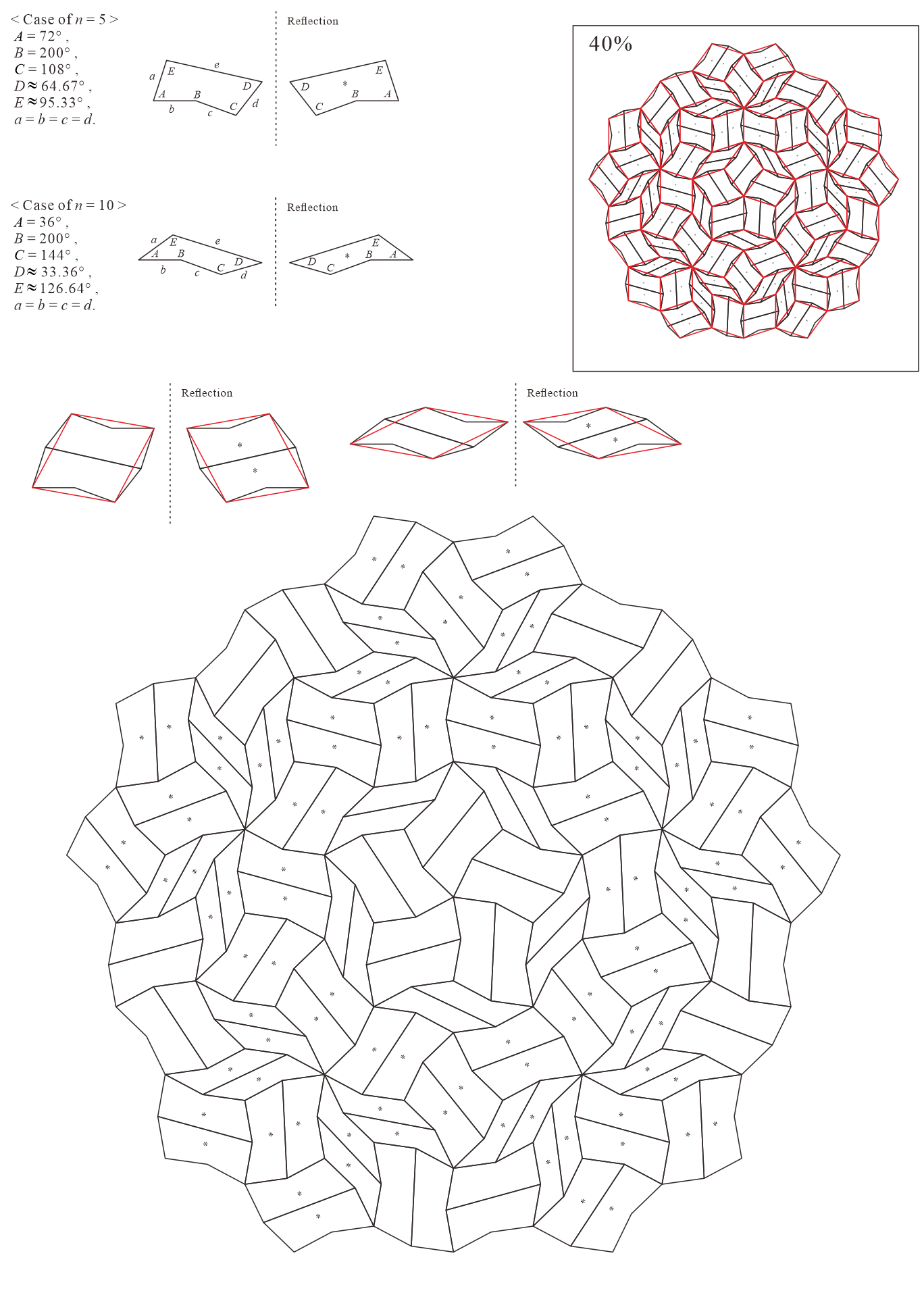
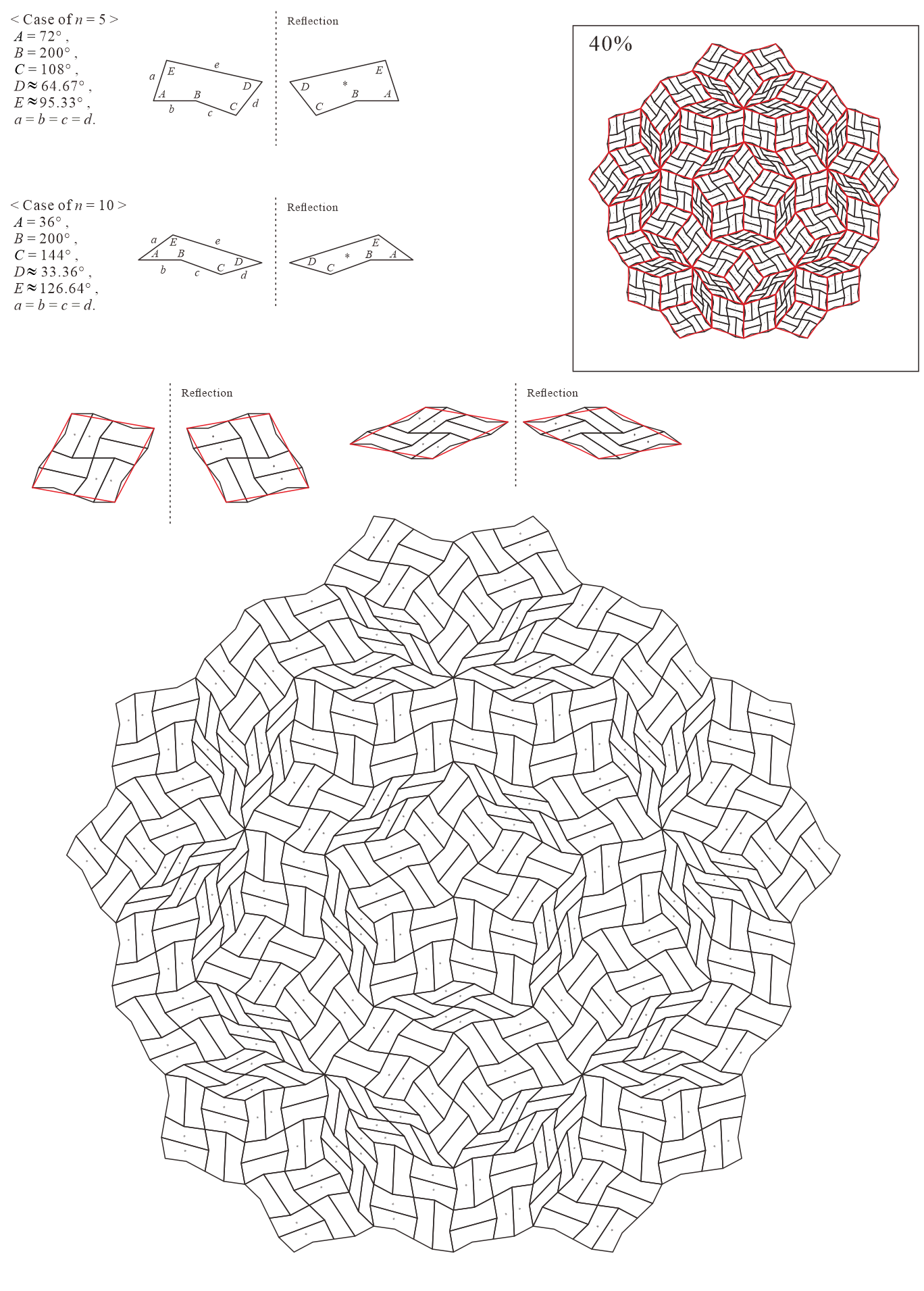
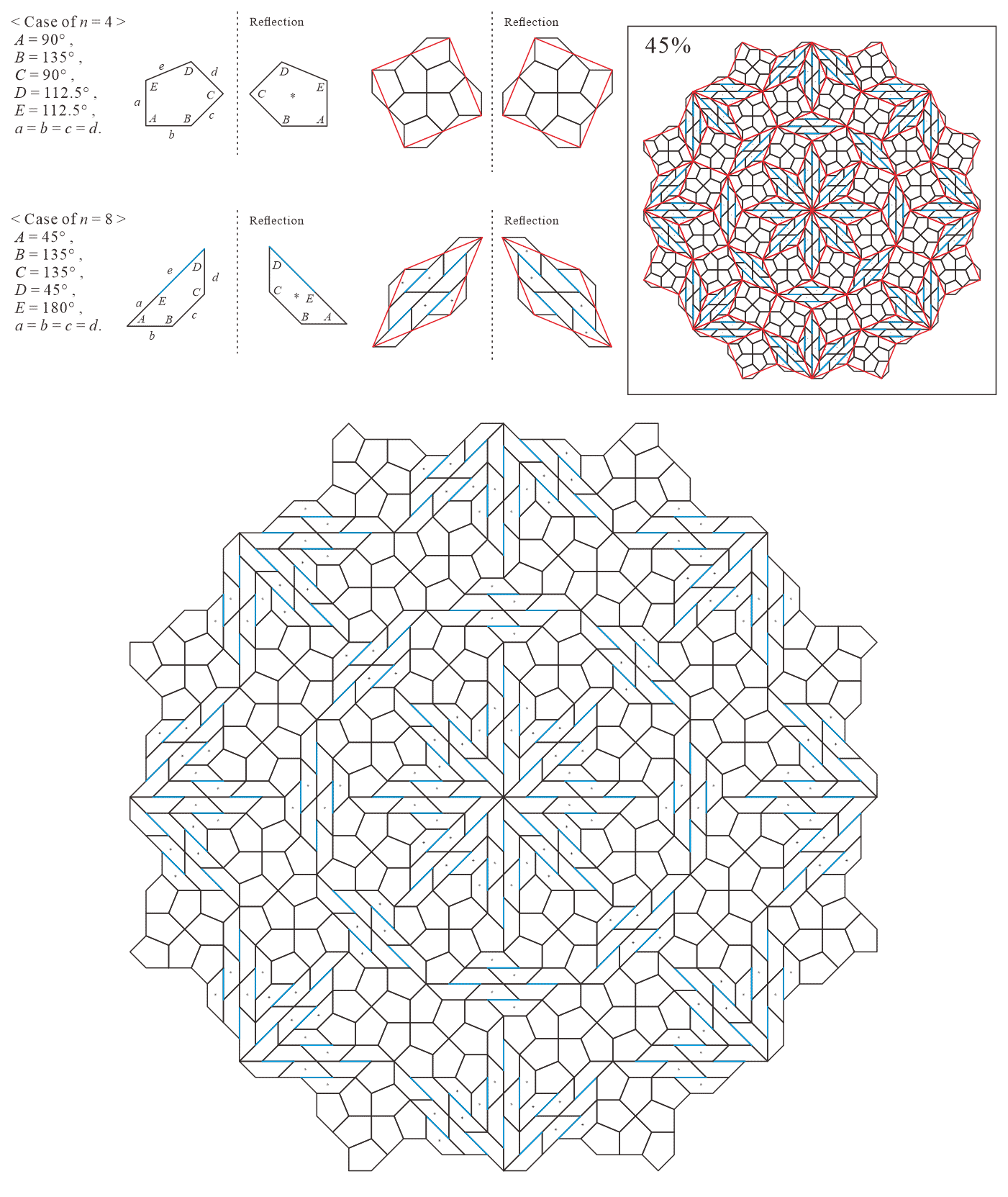
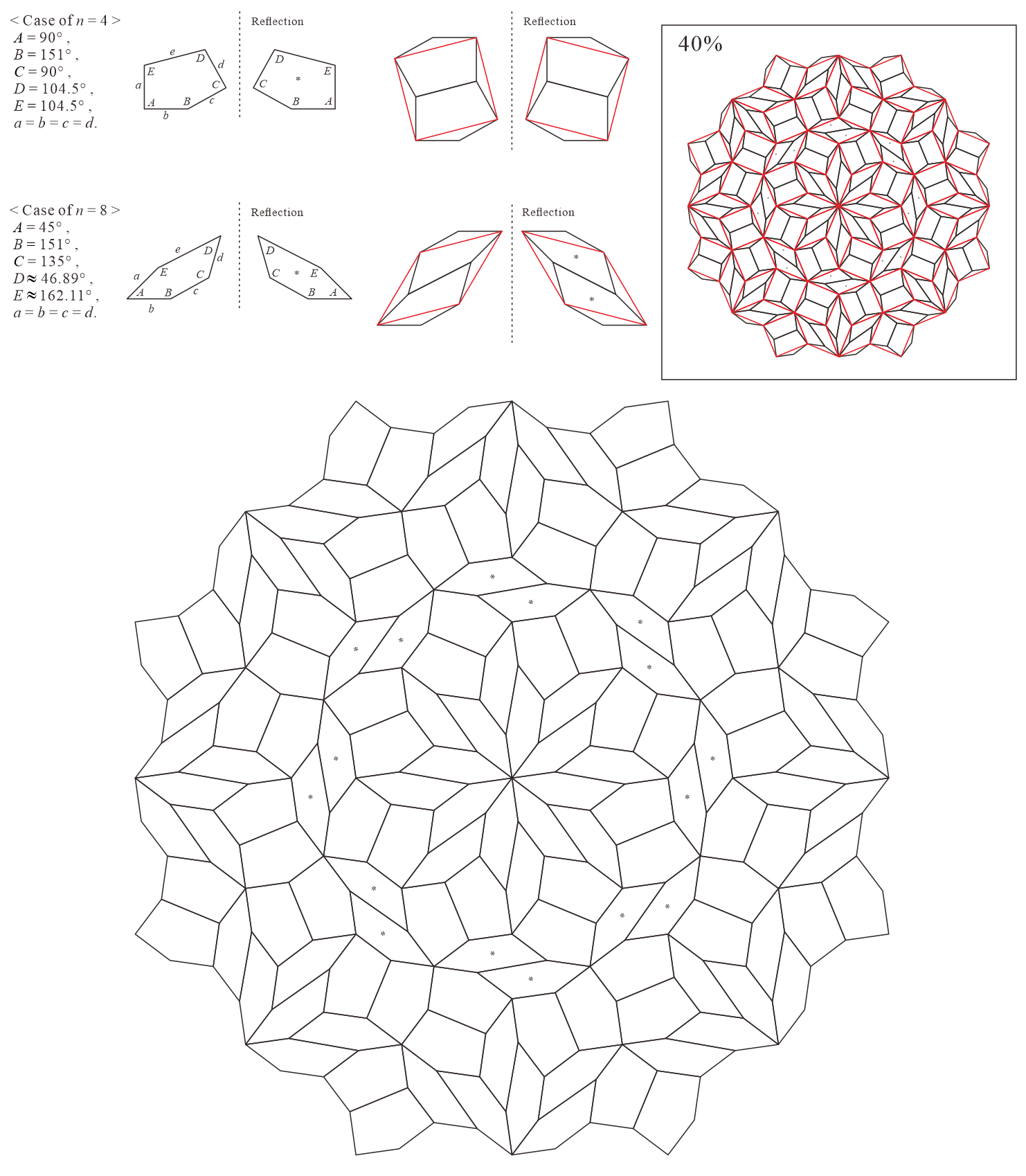
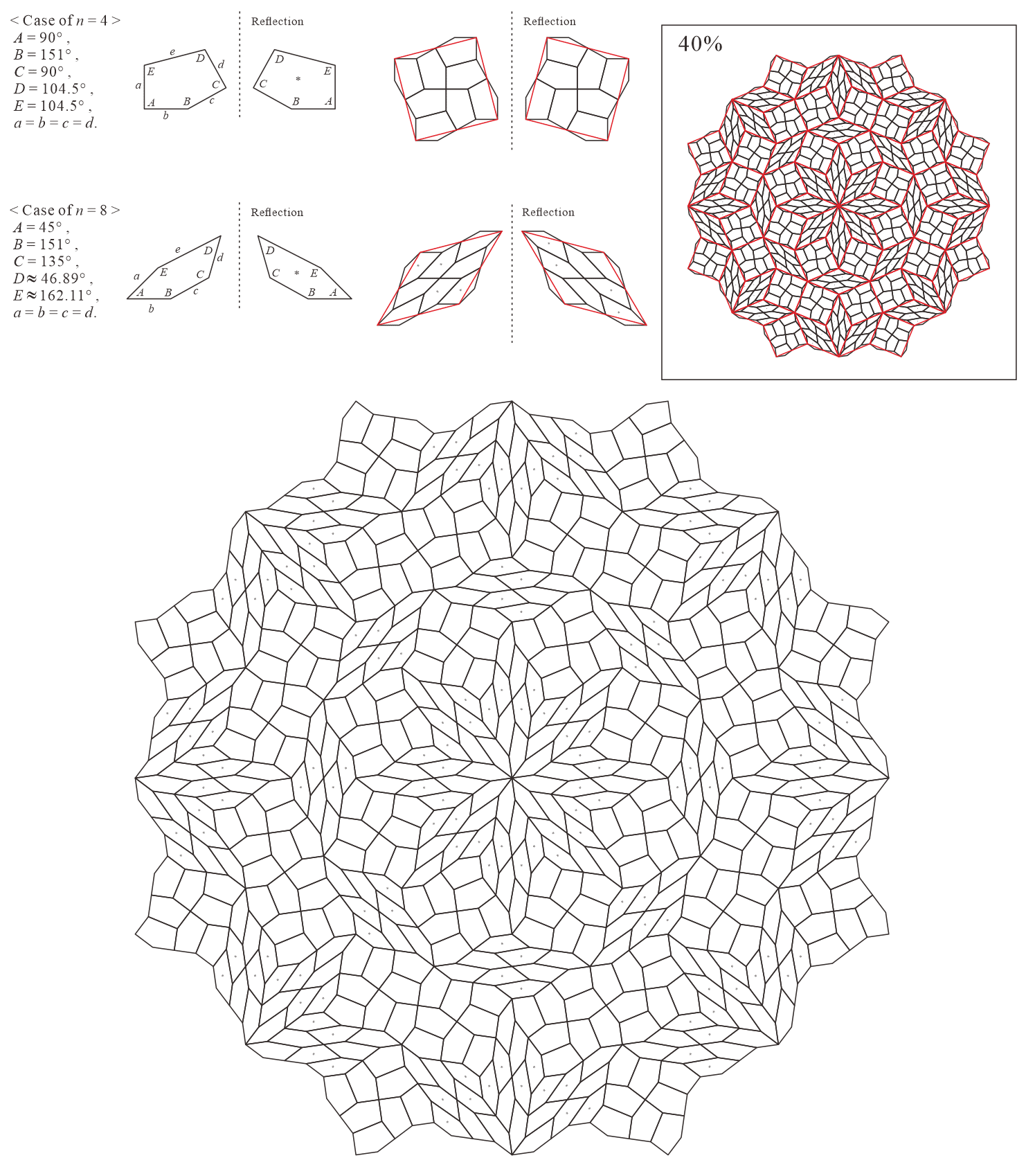
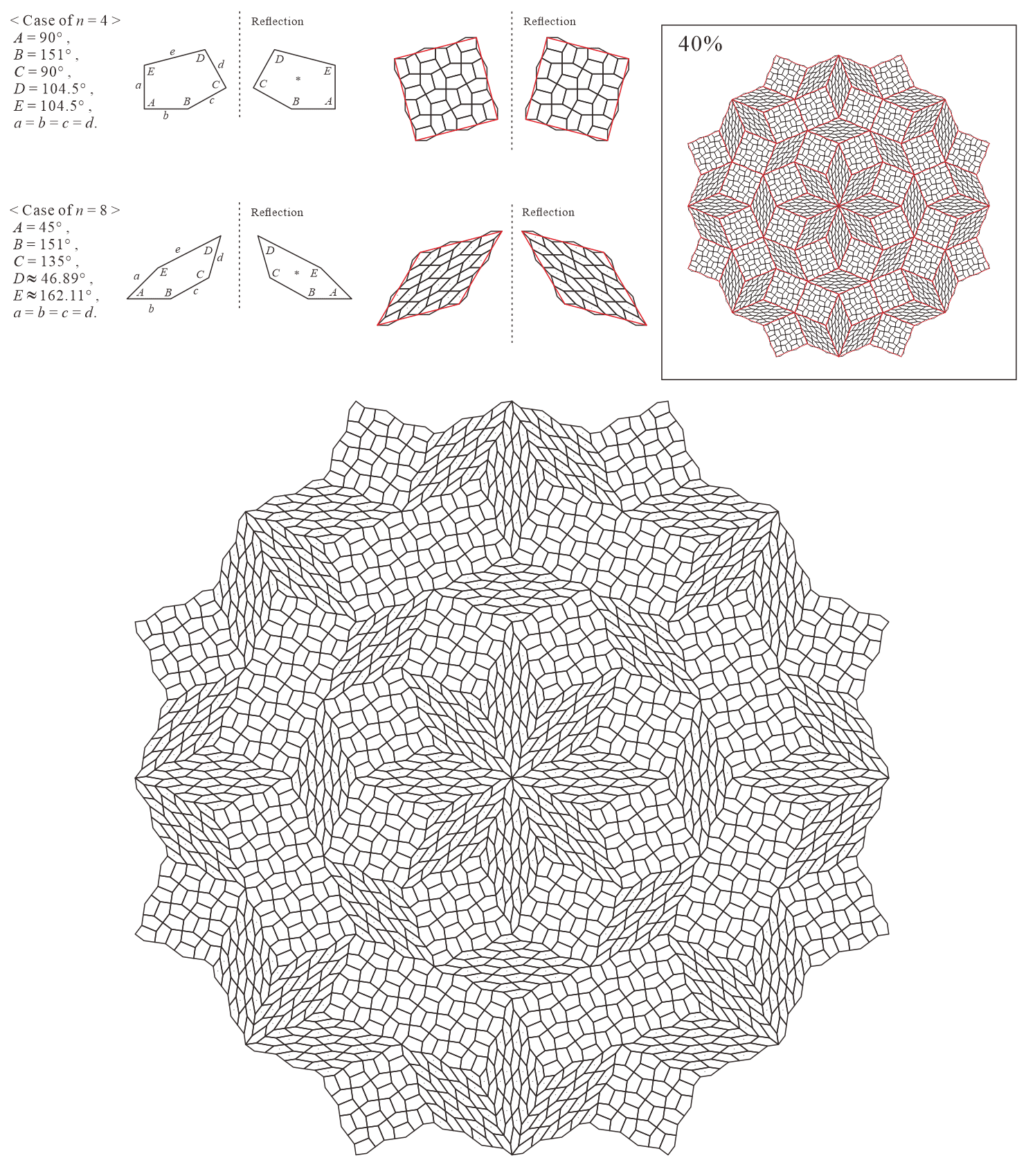
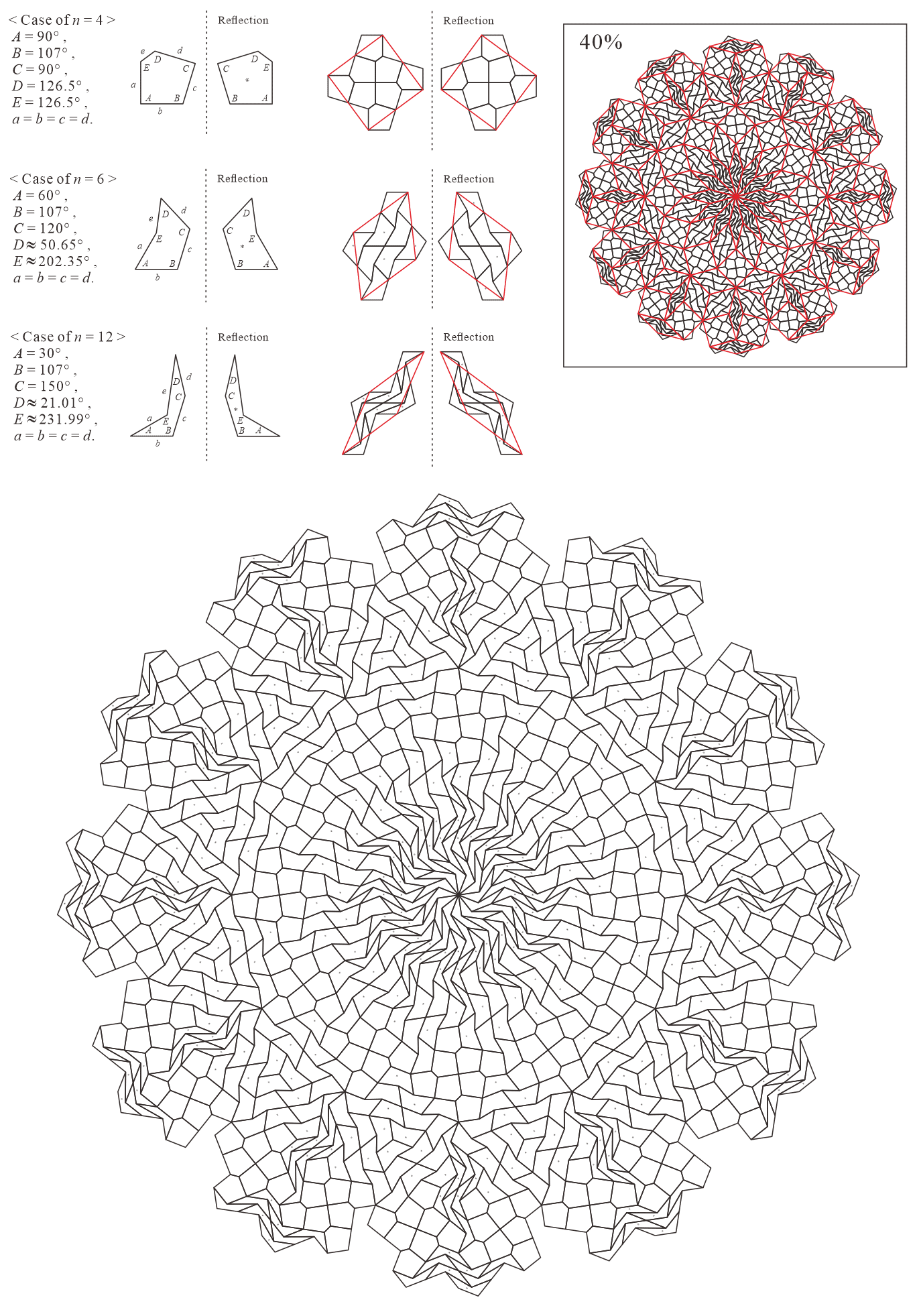
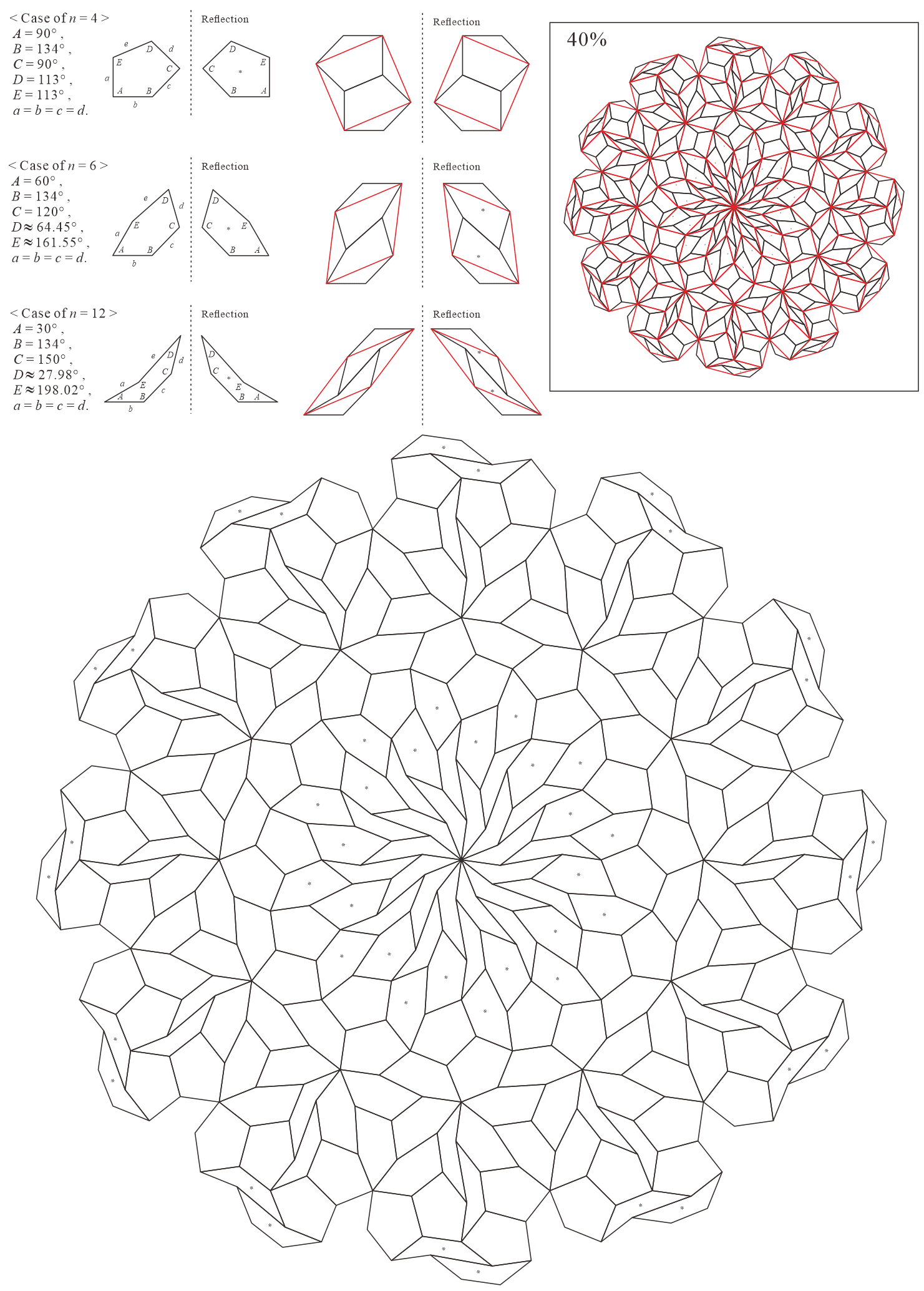
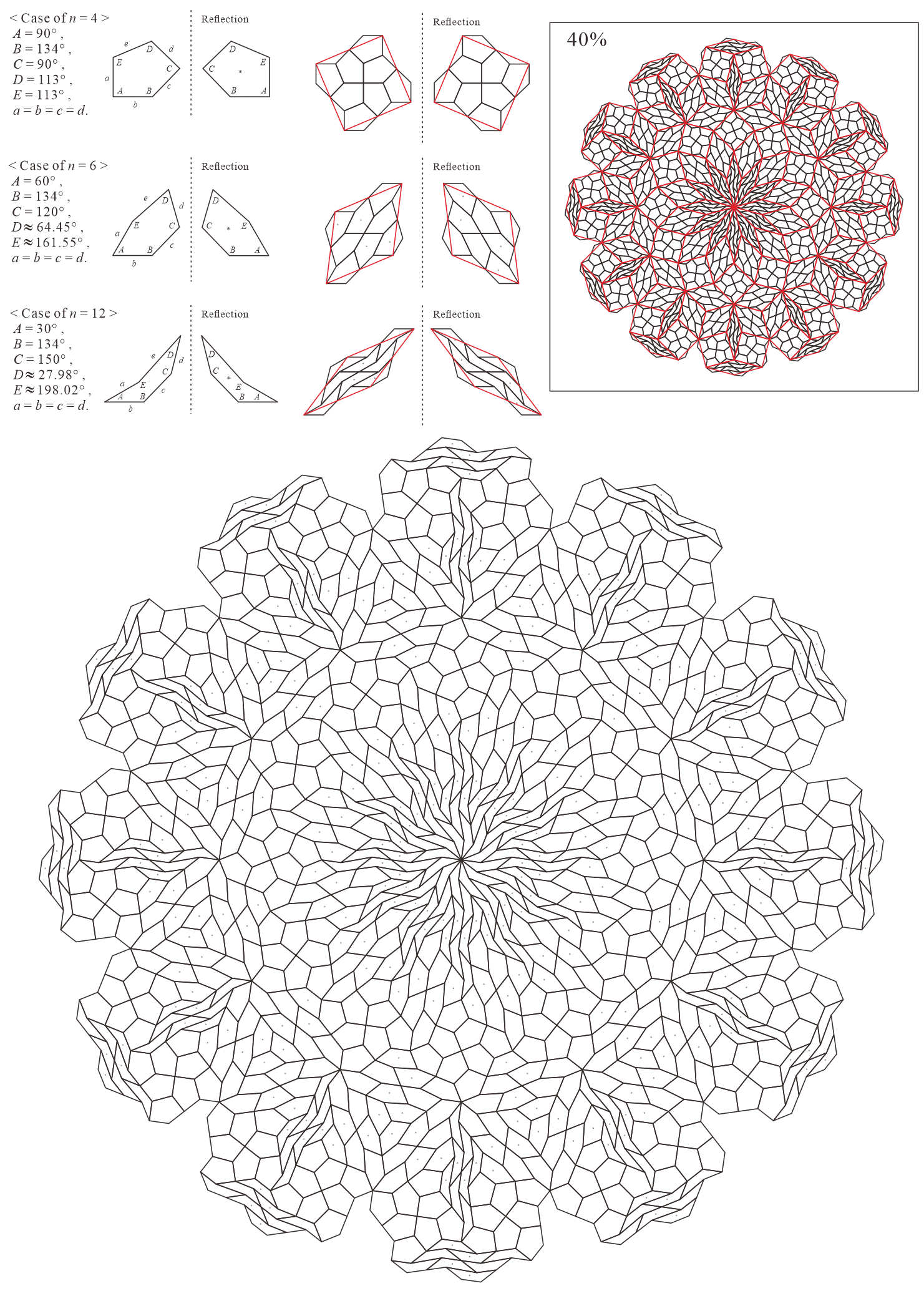
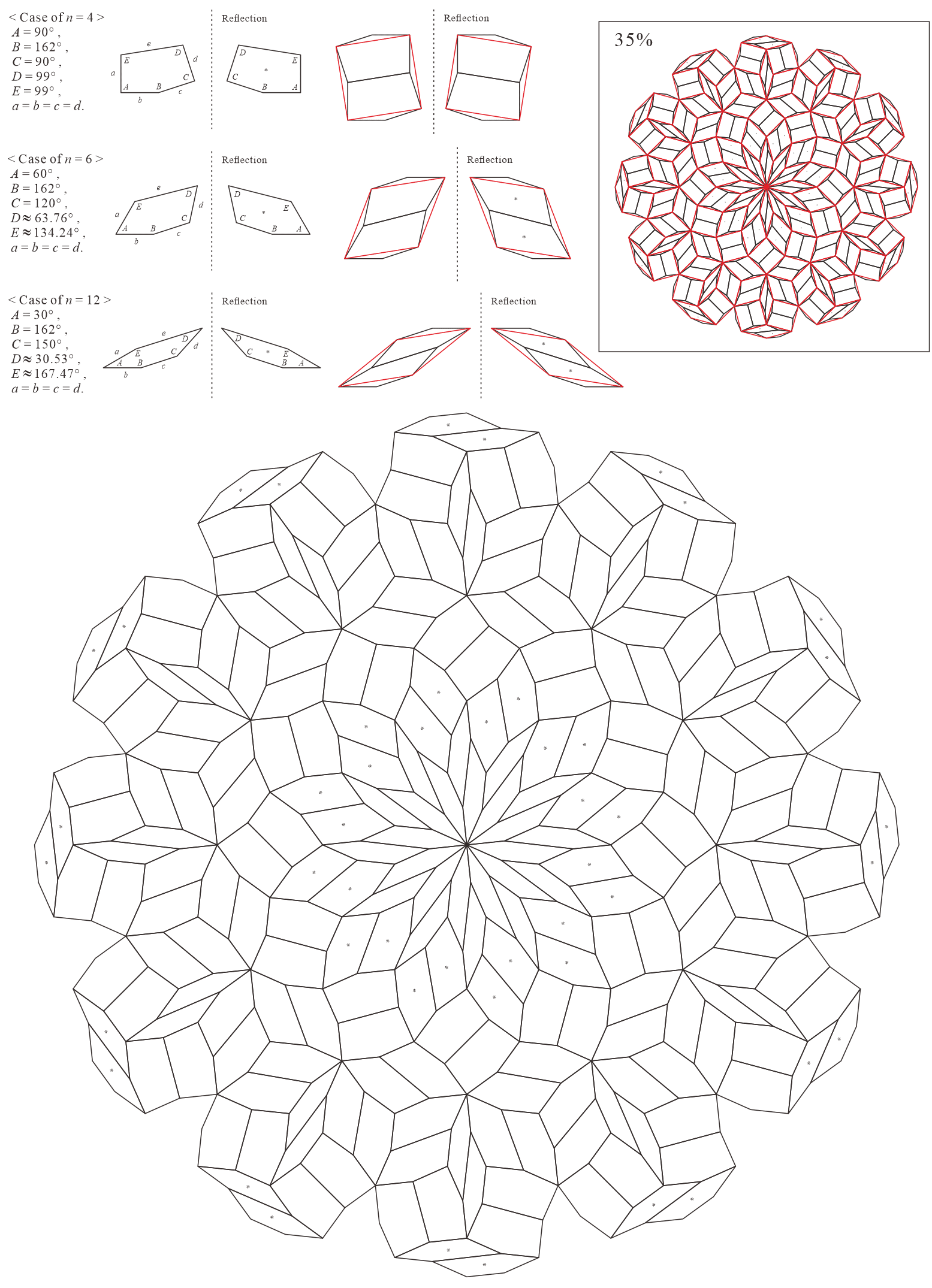
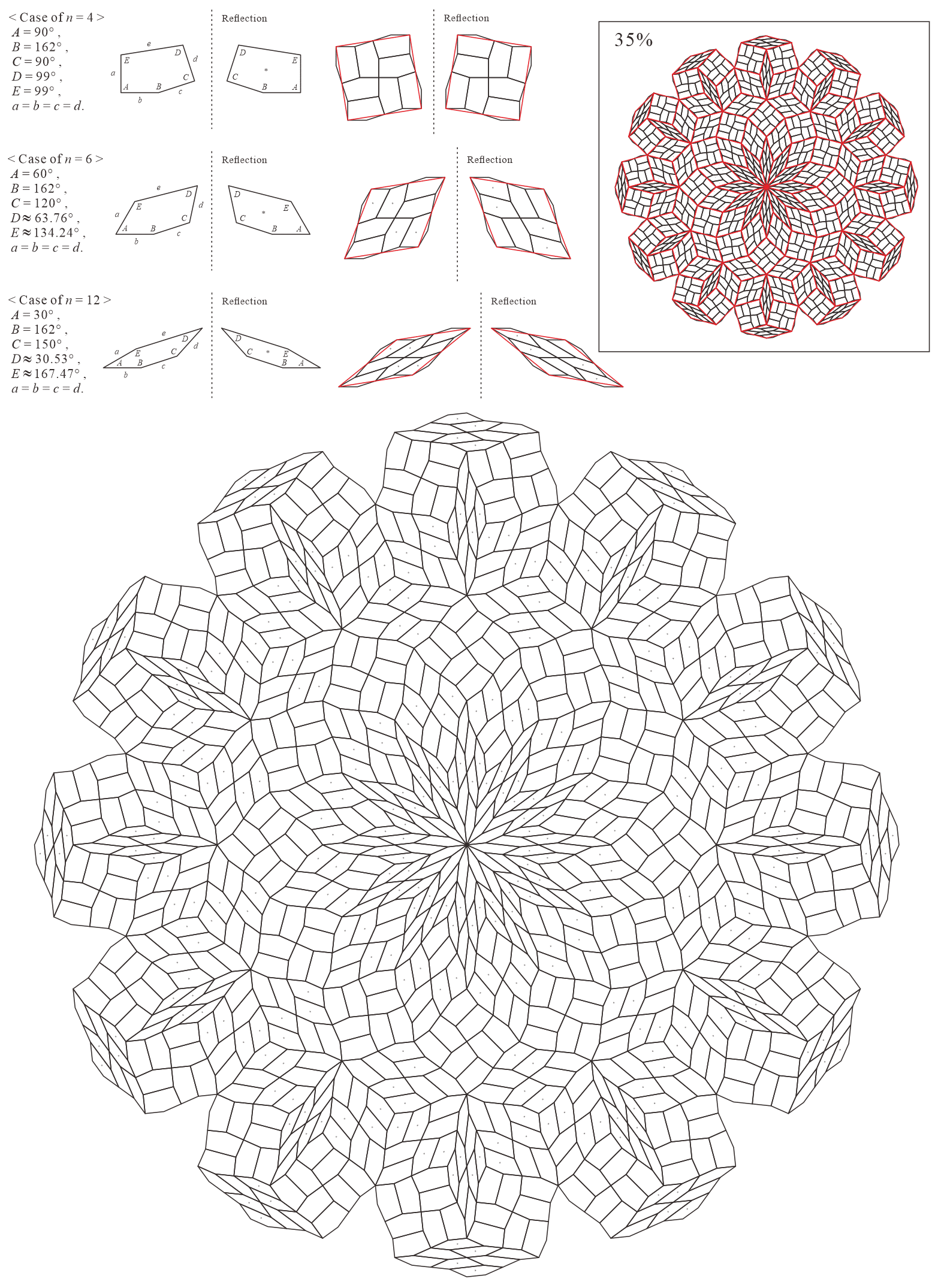
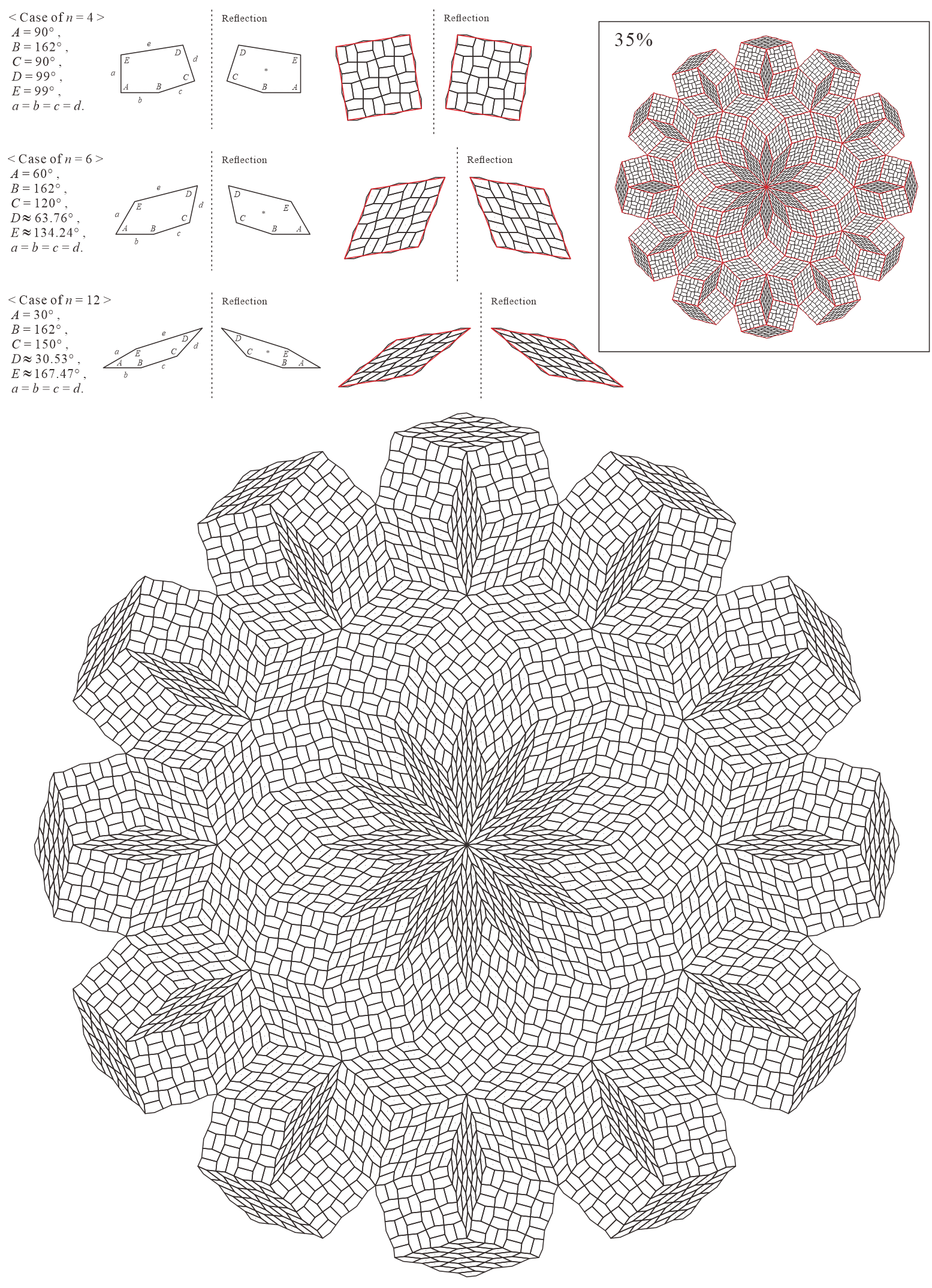
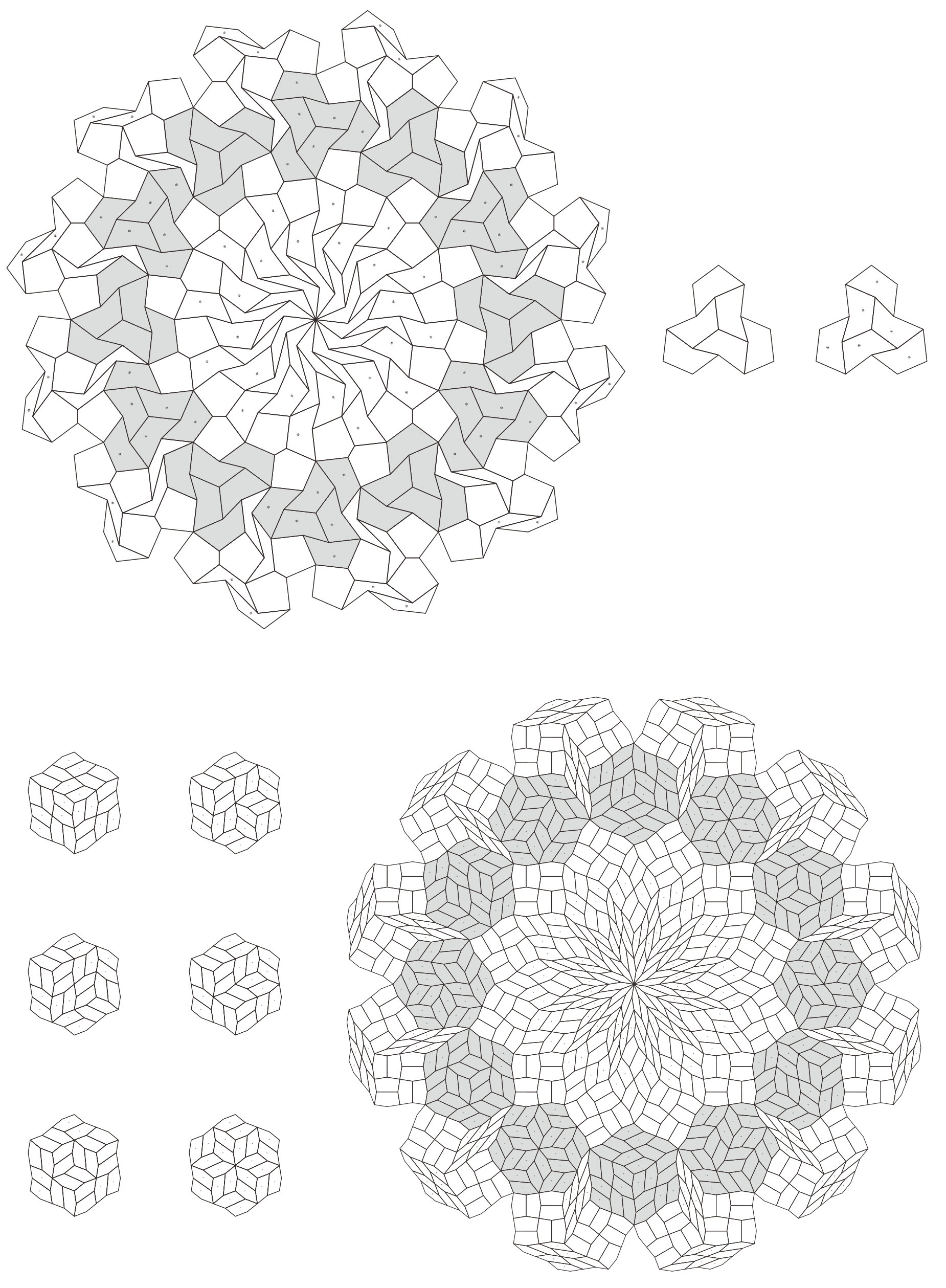
In this subsection, we present pentagonal tilings based on the five-fold rotationally symmetric tiling with rhombuses of acute angles and discovered by Penrose, as illustrated in Figure 5.1 [1]. For this conversion, two types of pentagons corresponding to in (3) are utilized. When the pentagons that satisfy (3) are degenerated into trapezoids, the trapezoids are axisymmetric; hence, they have no distinction between their anterior and posterior sides. A shape of two trapezoids based on rhombuses, as illustrated in Figures 3.1(a) and 3.1(b), has two-fold rotational symmetry but no axis of reflection symmetry (refer to Figure A-3, etc.). Specifically, the shape has a distinction between the anterior and posterior sides. Therefore, in the figures of tilings in this study, the trapezoids that correspond to the posterior side arrangement are given an asterisk mark “*,” indicating that they are for the posterior side.
When combining two types of pentagons corresponding to in (3), their shapes in a tiling change depending on the value of are as follows:
-
•
: are both concave pentagons with
-
•
: is a trapezoid () and is a concave pentagon with
-
•
: is a convex pentagon and is a concave pentagon with
-
•
: is a convex pentagon and is a trapezoid ()
-
•
: are both convex pentagons
-
•
: are both parallelograms ()
-
•
: are both concave pentagons with
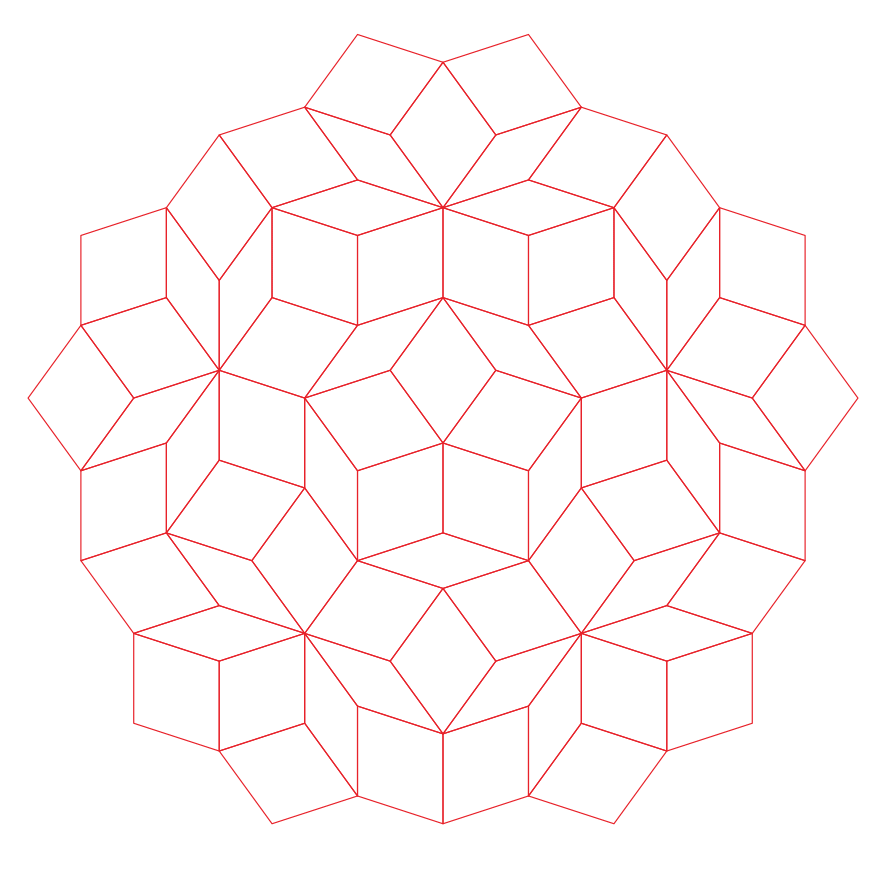
5.1.1 : are both concave pentagons with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.1.1.
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
Corresponding tiling figures:
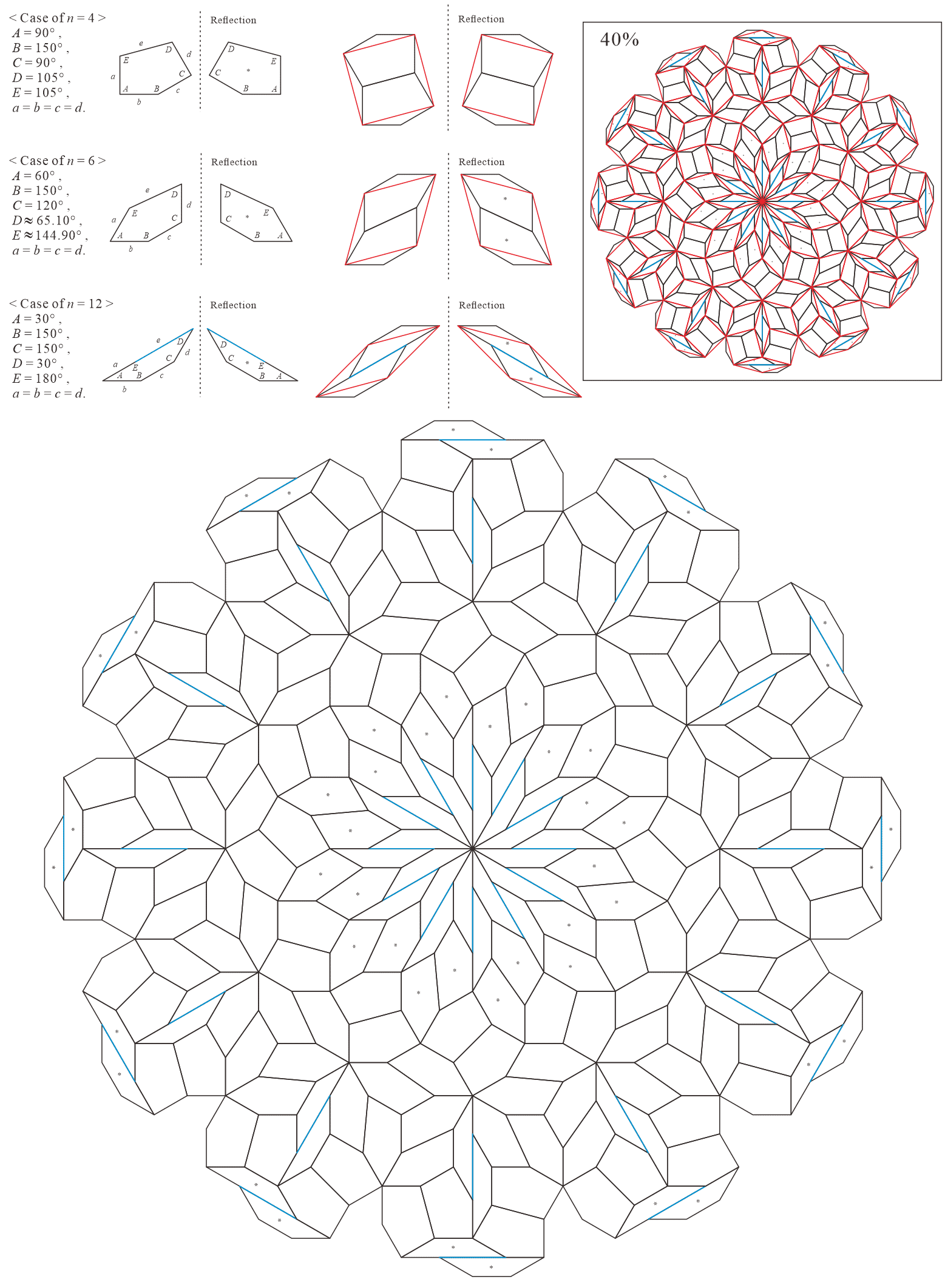
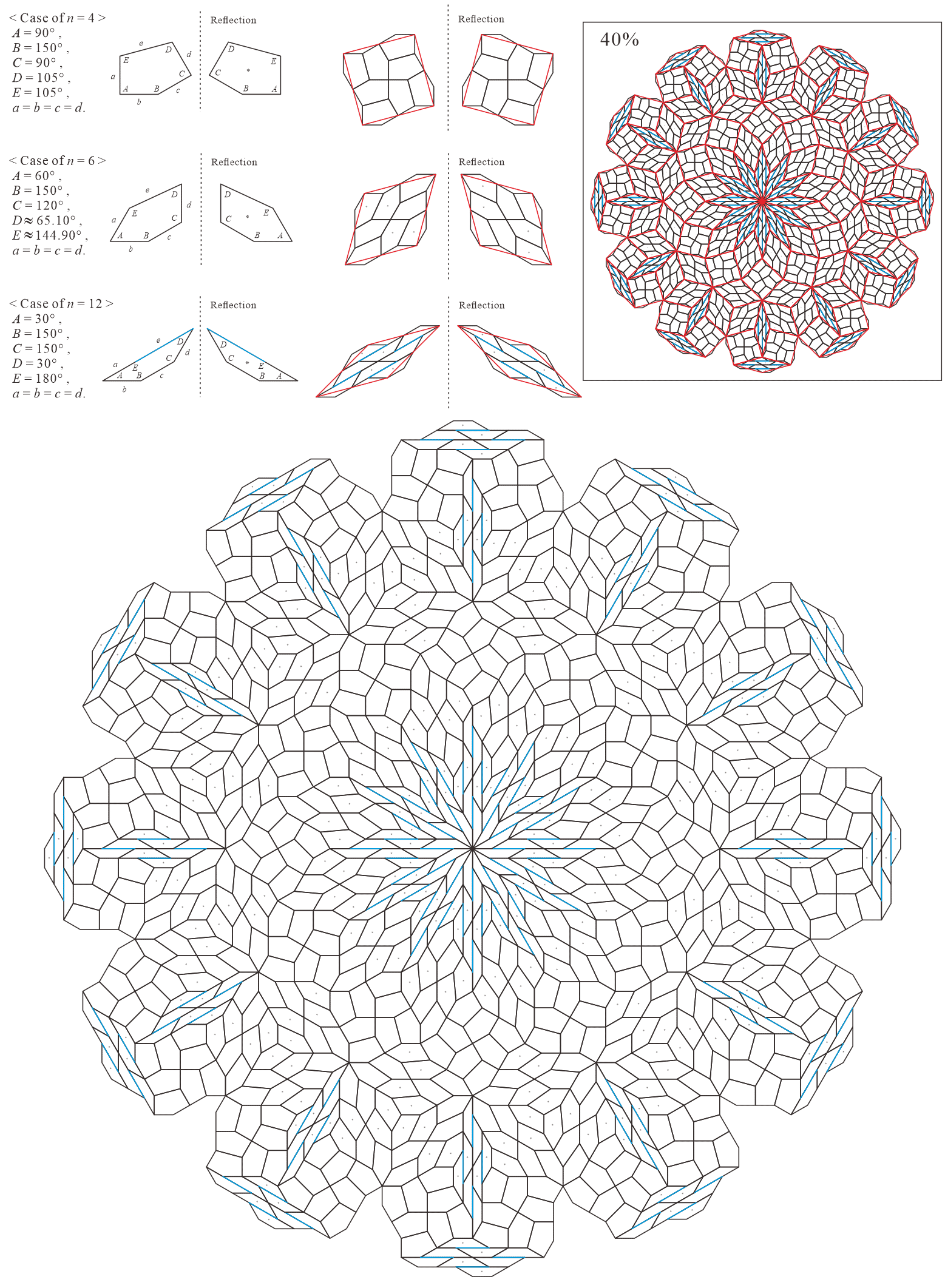
5.1.2 : is a trapezoid () and is a concave pentagon with
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
Corresponding tiling figures (Note that the line corresponding to edge of pentagons degenerated into trapezoids in the figures is shown as a blue line):
5.1.3 : is a convex pentagon and is a concave pentagon with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.1.3.
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
Corresponding tiling figures:
5.1.4 : is a convex pentagon and is a trapezoid ()
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
Corresponding tiling figures (Note that the line corresponding to edge of pentagons degenerated into trapezoids in the figures is shown as a blue line):
5.1.5 : are both convex pentagons
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.1.5.
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
Corresponding tiling figures:
-
Case converting a rhombus to two pentagons: Figure A-9
-
Case converting a rhombus divided into four by its own similar figures to eight pentagons: Figure A-10
-
Case converting a rhombus divided into 16 by its own similar figures to 32 pentagons: Figure A-11
-
Case converting a rhombus divided into 36 by its own similar figures to 72 pentagons: Figure A-12
5.1.6 : are both parallelograms ()
Both are parallelograms, and the original rhombuses are formed by connecting edge of the parallelograms. The interior angles of pentagons (parallelograms) satisfying (3) with and are the values in Table 5.1.6. The converted tiling is equal to one of the tilings in which the rhombus of the original rhombic tiling is bisected into a parallelogram. The figure is omitted.
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
5.1.7 : are both concave pentagons with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.1.7.
| 5 | |||||
|---|---|---|---|---|---|
| 10 |
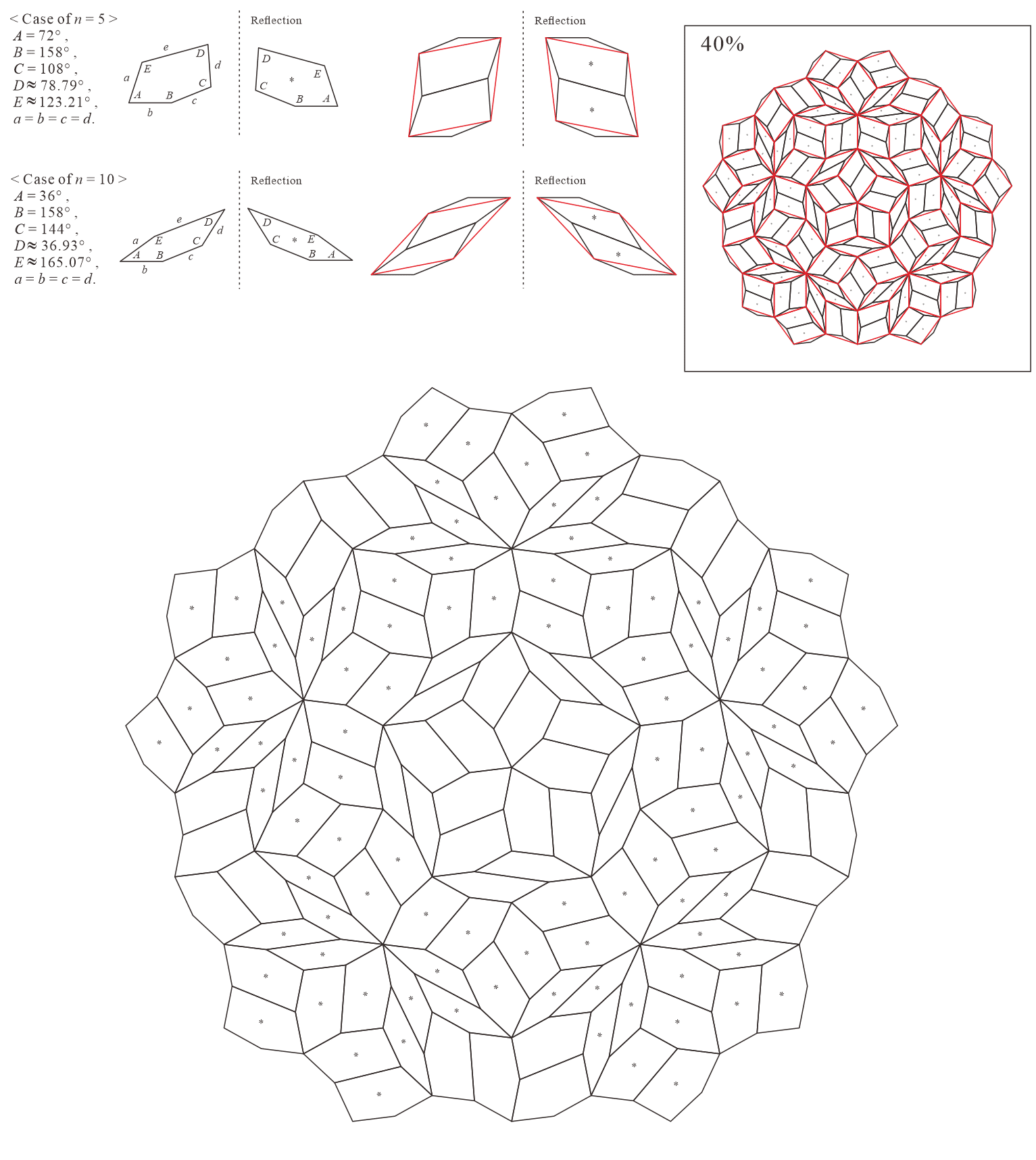
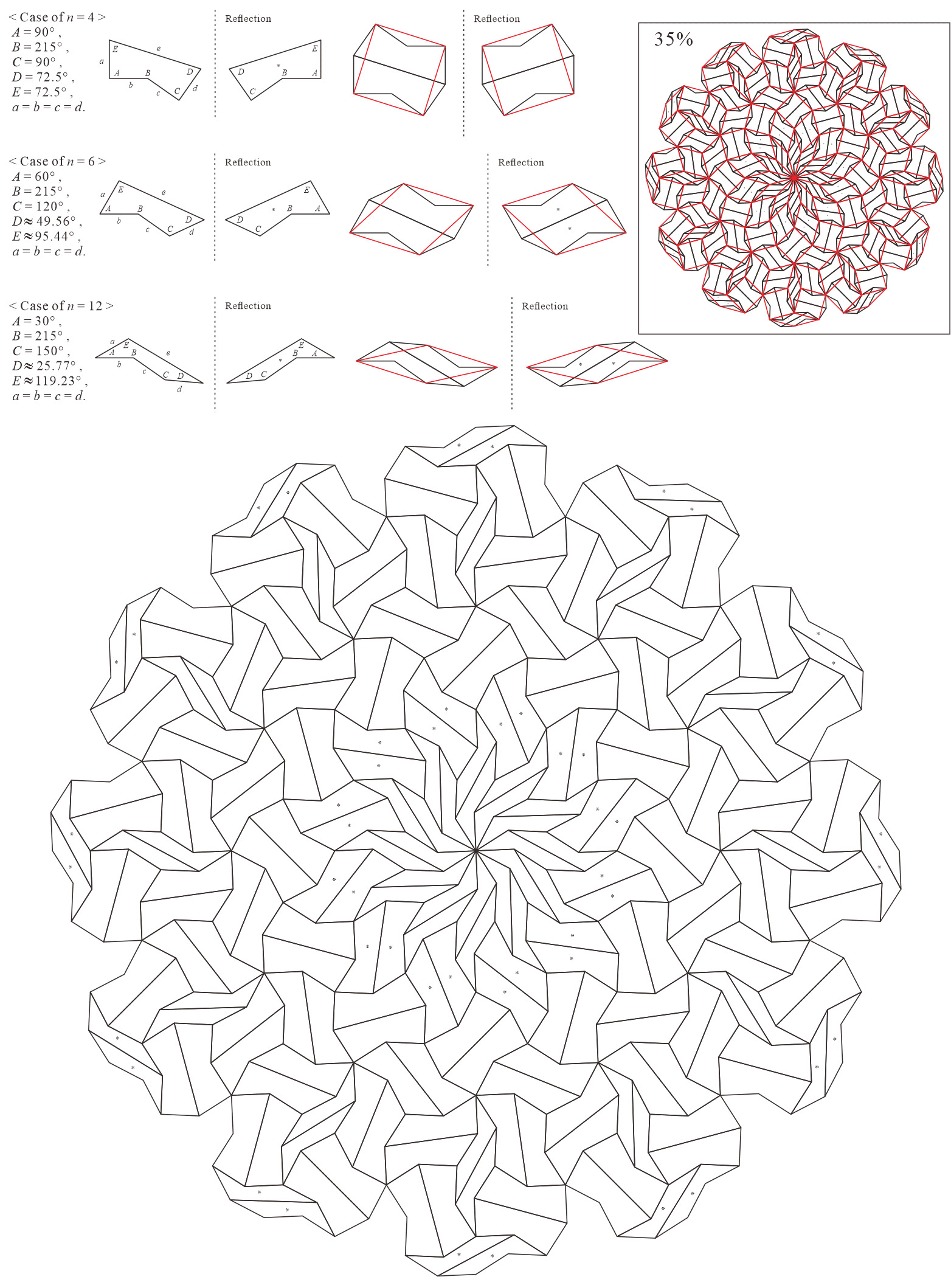
5.2 Eight-fold rotationally symmetric tilings
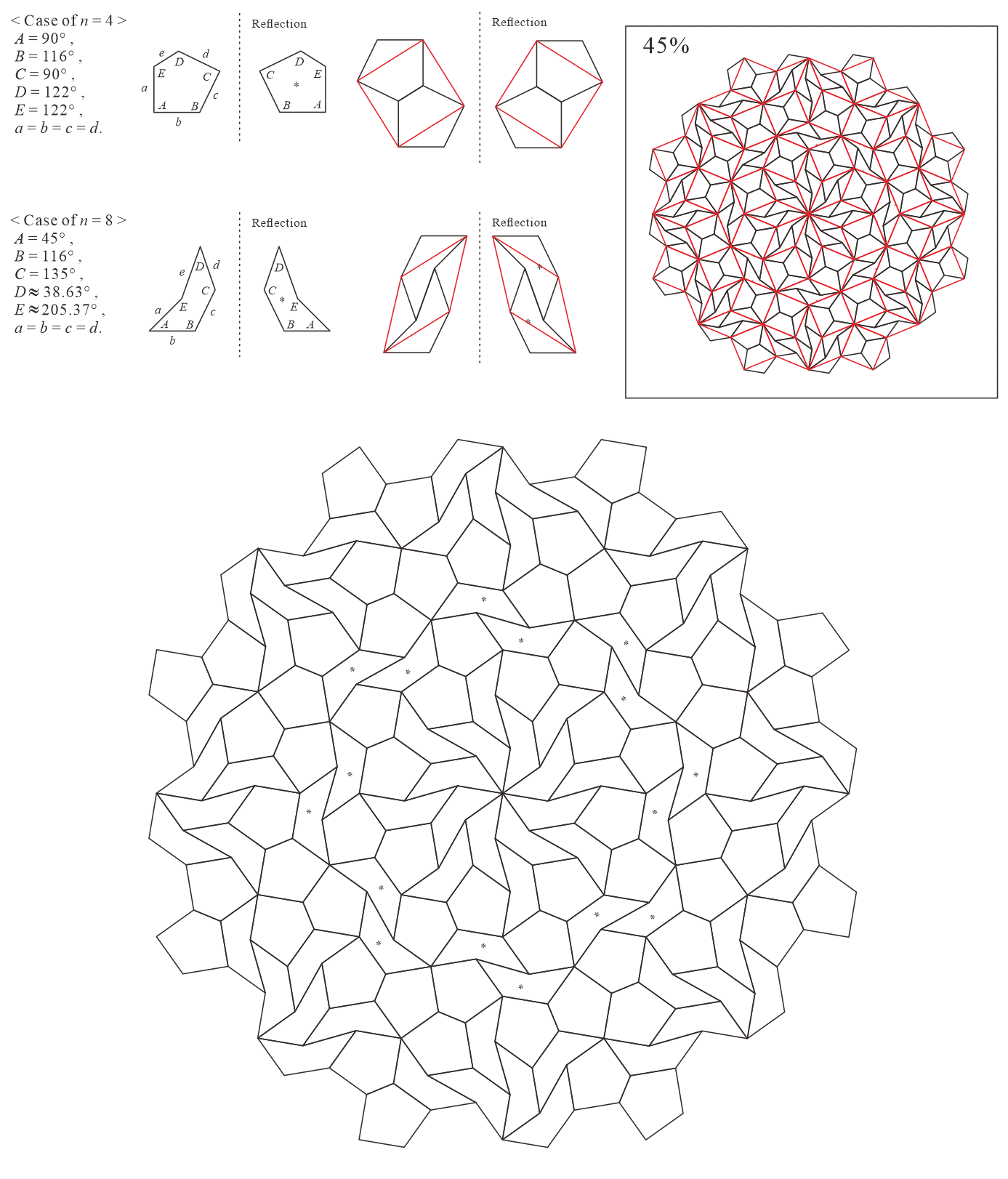
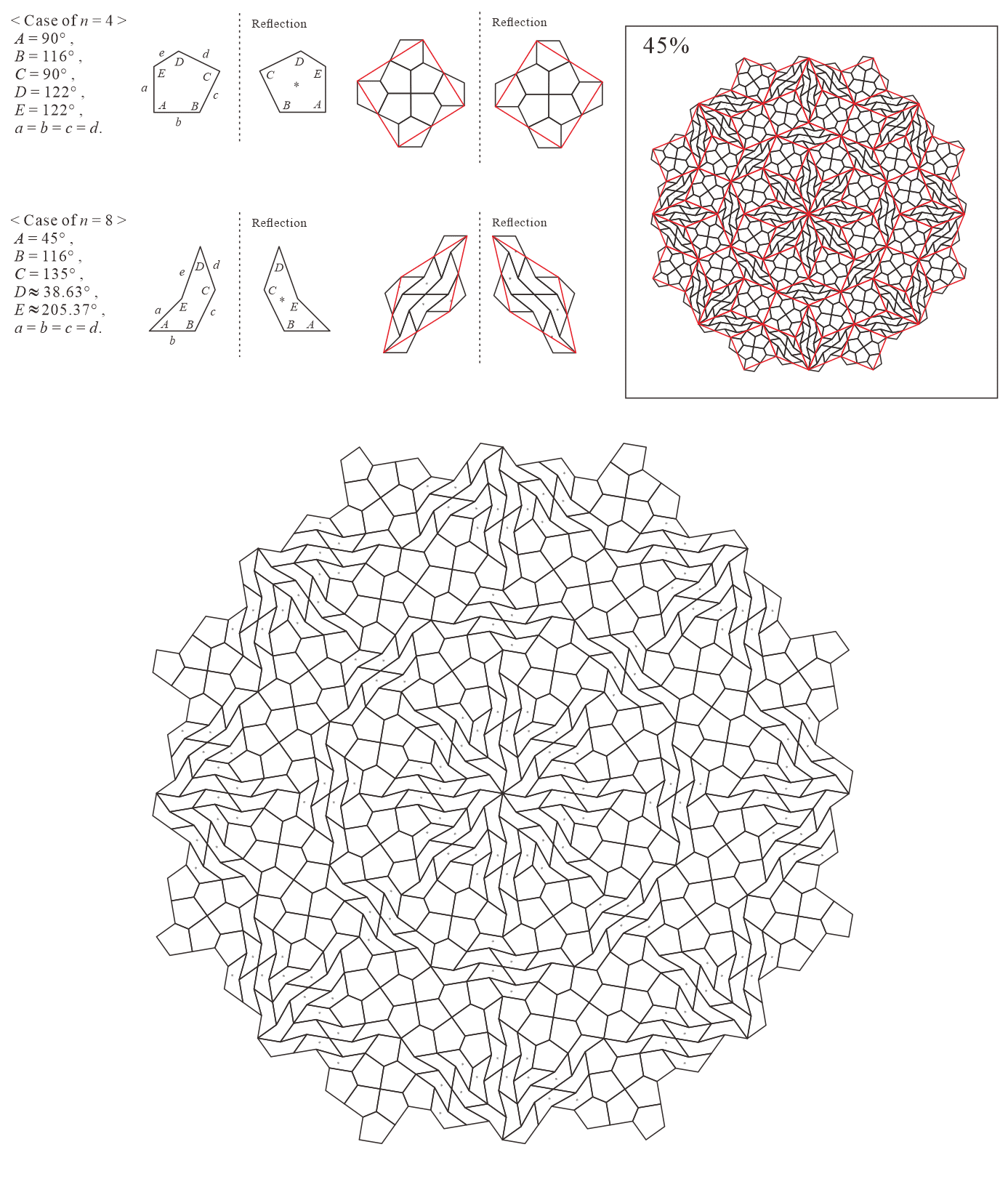
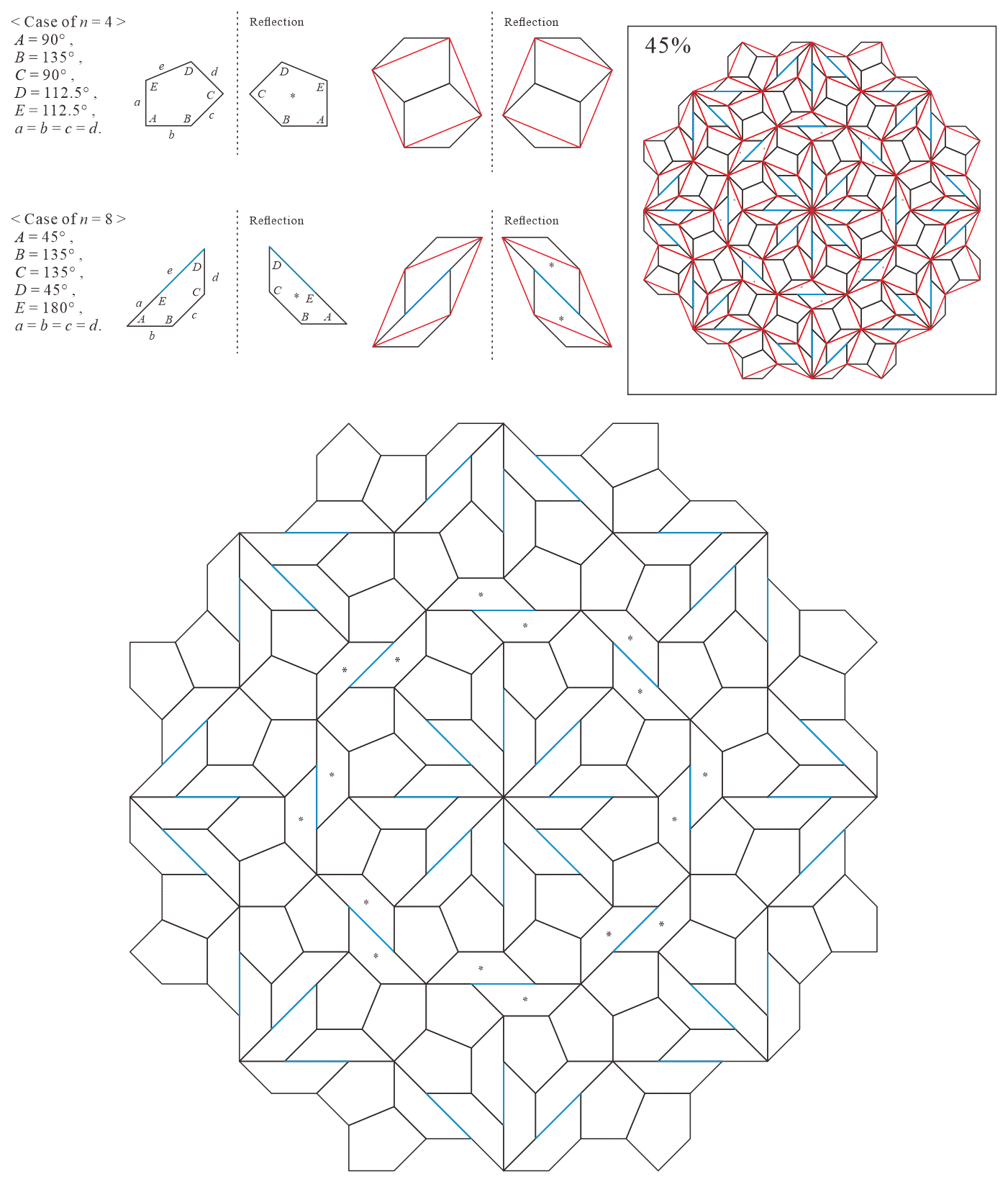
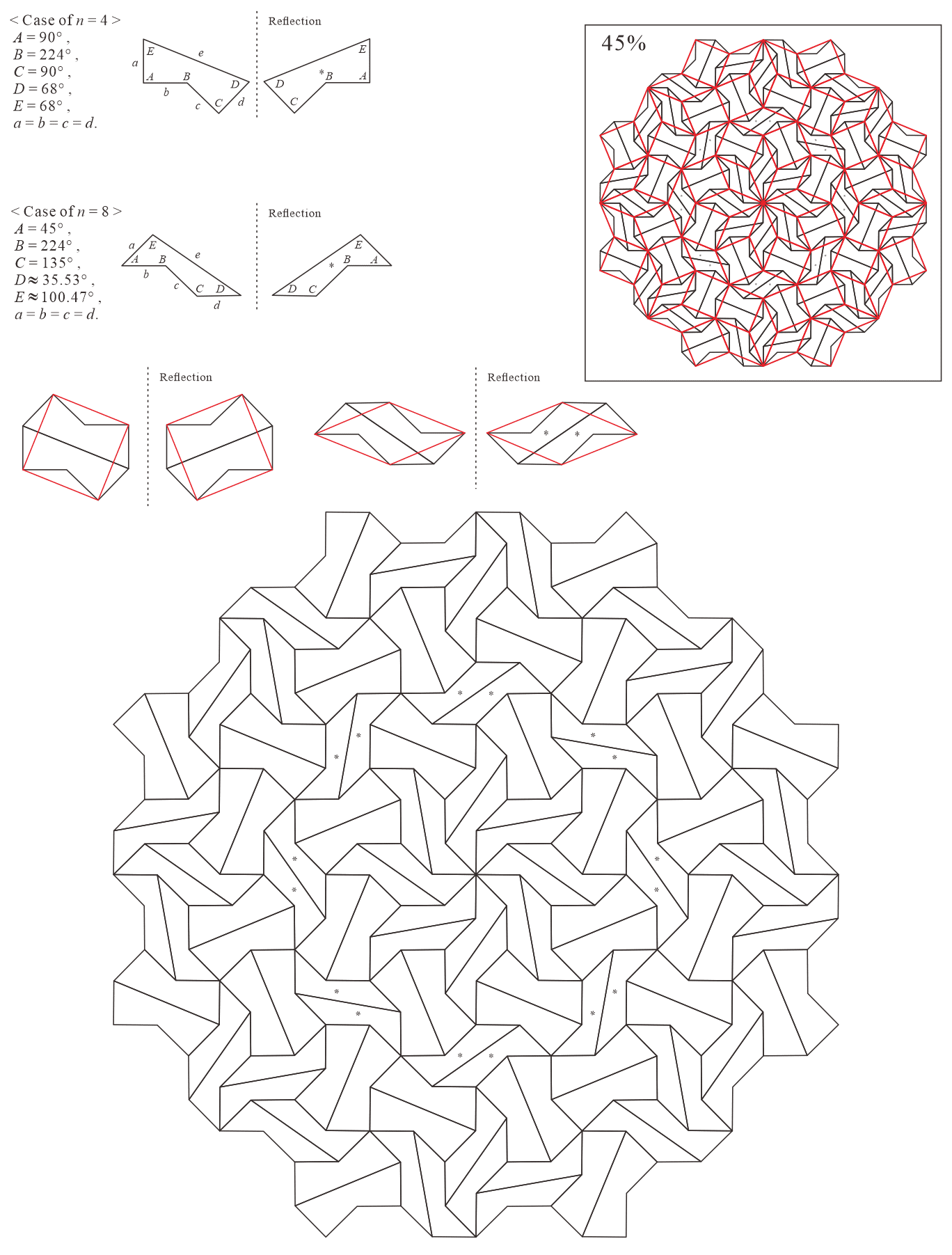
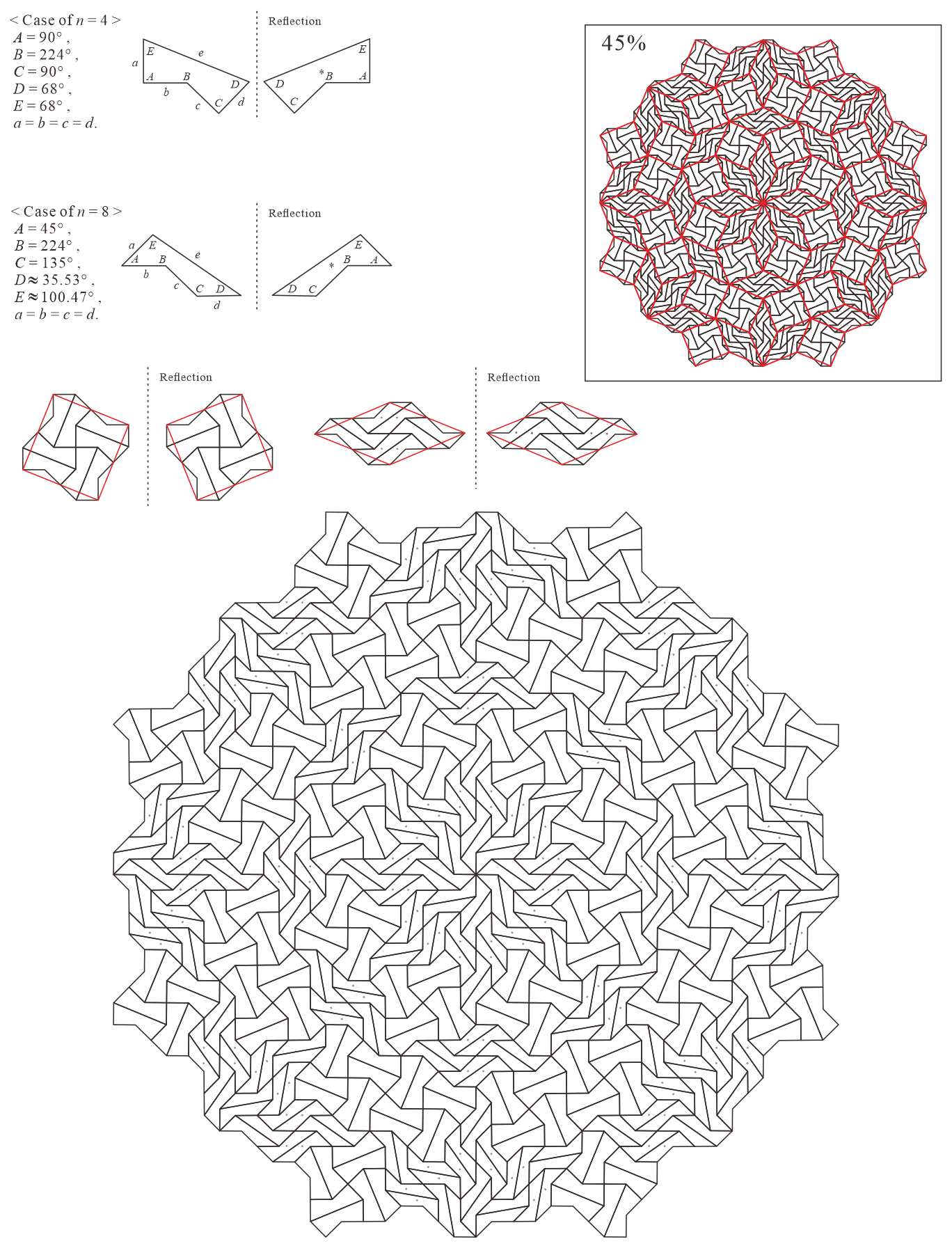
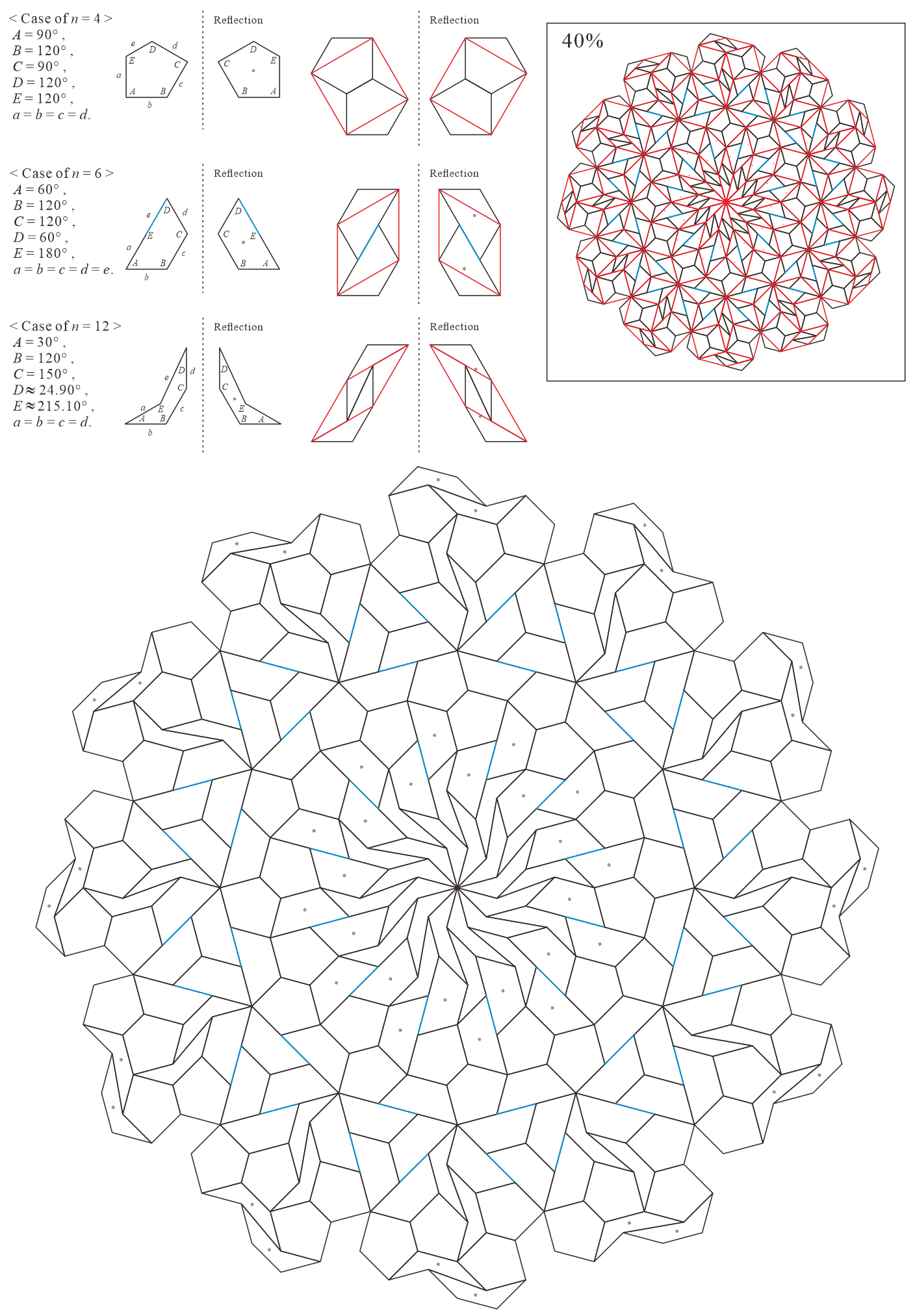
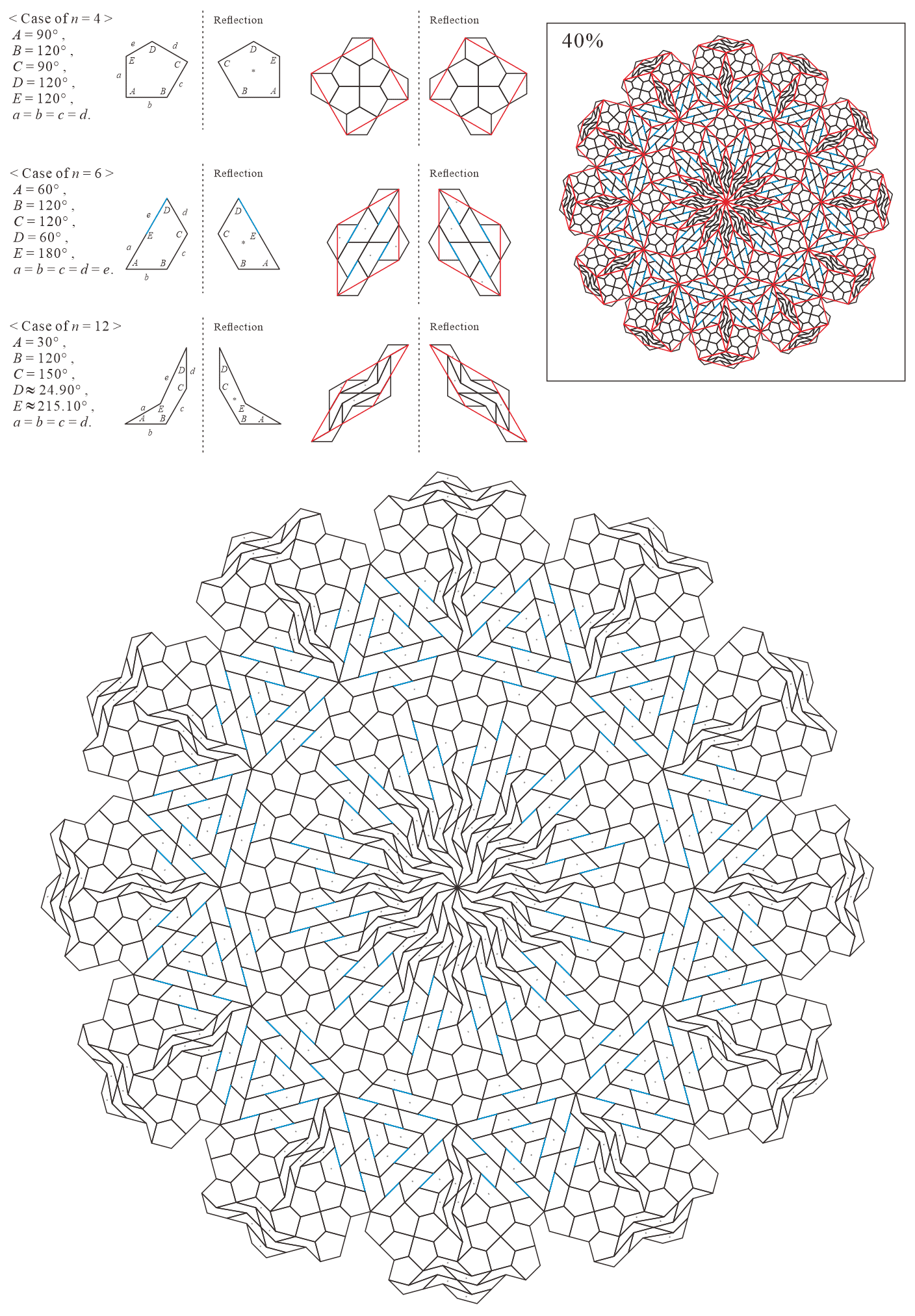
In this subsection, we present pentagonal tilings based on the eight-fold rotationally symmetric tiling with rhombuses of acute angles and discovered by Ammann and Beenker, as illustrated in Figure 5.2 [1]. Of course, a rhombus with angles is a square. For this conversion, two types of pentagons corresponding to in (3) are utilized. As described in Subsection 5.1, the trapezoids corresponding to the posterior side in the tiling are given an asterisk mark. The pentagons corresponding to in (3) have a line of symmetry connecting the vertex to the midpoint of the edge , i.e., there is no distinction between its anterior and posterior sides. A shape of square converted into two pentagons corresponding to in (3), as illustrated in Figures 3.1(a) and 3.1(b), has symmetry. In other words, because the shape has no distinction between its anterior and posterior sides (refer to Figure A-15, etc.), a unit comprising two anterior pentagons can be freely replaced with one comprising two posterior pentagons. Therefore, in the figures of tilings in this study, the pentagons with in (3) that correspond to the posterior side are not given an asterisk mark.
When combining two types of pentagons corresponding to in (3), their shapes in a tiling change depending on the values of are as follows:
-
•
: is a convex pentagon and is a concave pentagon with
-
•
: is a convex pentagon and is a trapezoid ()
-
•
: are both convex pentagons
-
•
: are both parallelograms ()
-
•
: are both concave pentagons with
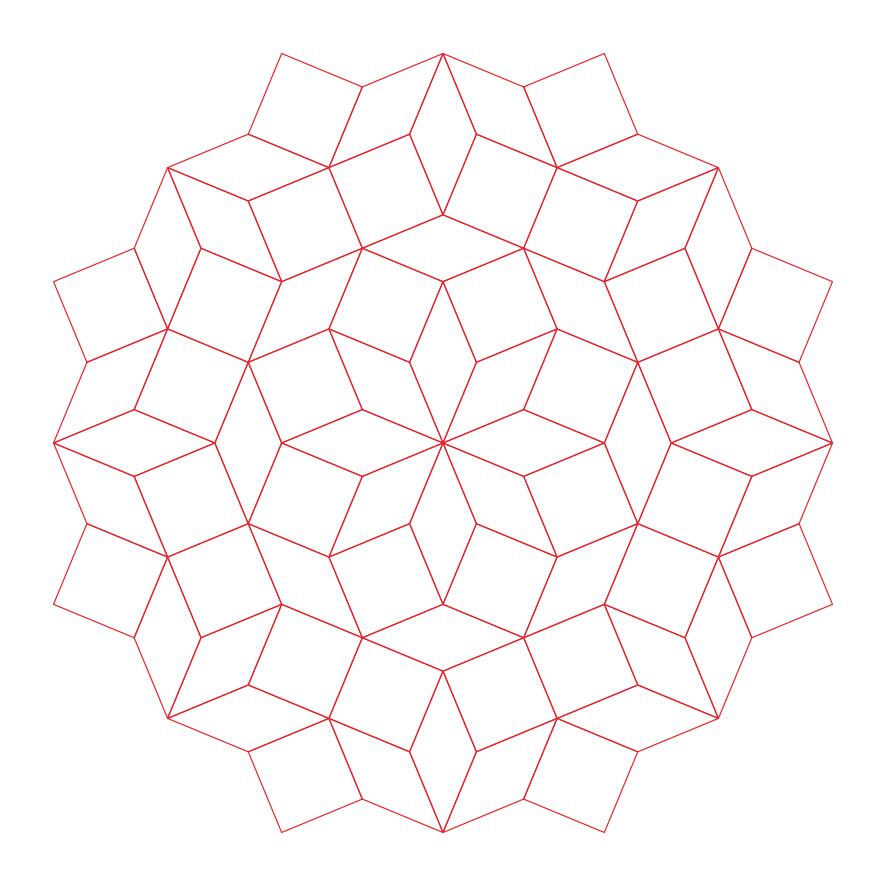
5.2.1 : is a convex pentagon and is a concave pentagon with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.2.1.
| 4 | |||||
|---|---|---|---|---|---|
| 8 |
5.2.2 : is a convex pentagon and is a trapezoid ()
The interior angles of pentagons satisfying (3) with and are the values in Table 5.2.2. In this case, because the shapes of the pentagon of and trapezoid of have no distinction between its anterior and posterior sides, it can be considered as a tiling that formed of only two complete pieces, the same as the original rhombic tiling. (Because the rhombuses have symmetry, the original rhombic tiling forms two complete pieces. However, if the pentagons of the anterior and posterior sides are not congruent when stacked on top of each other, we can treat them as separate pieces and consider the tiling to be formed of three or more different pieces.)
| 4 | |||||
|---|---|---|---|---|---|
| 8 |
Corresponding tiling figures (Note that the line corresponding to edge of pentagons degenerated into trapezoids in the figures is shown as a blue line):
5.2.3 : are both convex pentagons
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.2.3.
| 4 | |||||
|---|---|---|---|---|---|
| 8 |
5.2.4 : are both parallelograms ()
Both are parallelograms ( is a rectangle), and the original rhombuses are formed by connecting edge of the parallelograms. The interior angles of pentagons (parallelograms) satisfying (3) with and are the values in Table 5.2.4. The converted tiling is equal to one of the tilings in which the rhombus of the original rhombic tiling is bisected into a parallelogram. The figure is omitted.
| 4 | |||||
|---|---|---|---|---|---|
| 8 |
5.2.5 : are both concave pentagons with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.2.5.
| 4 | |||||
|---|---|---|---|---|---|
| 8 |
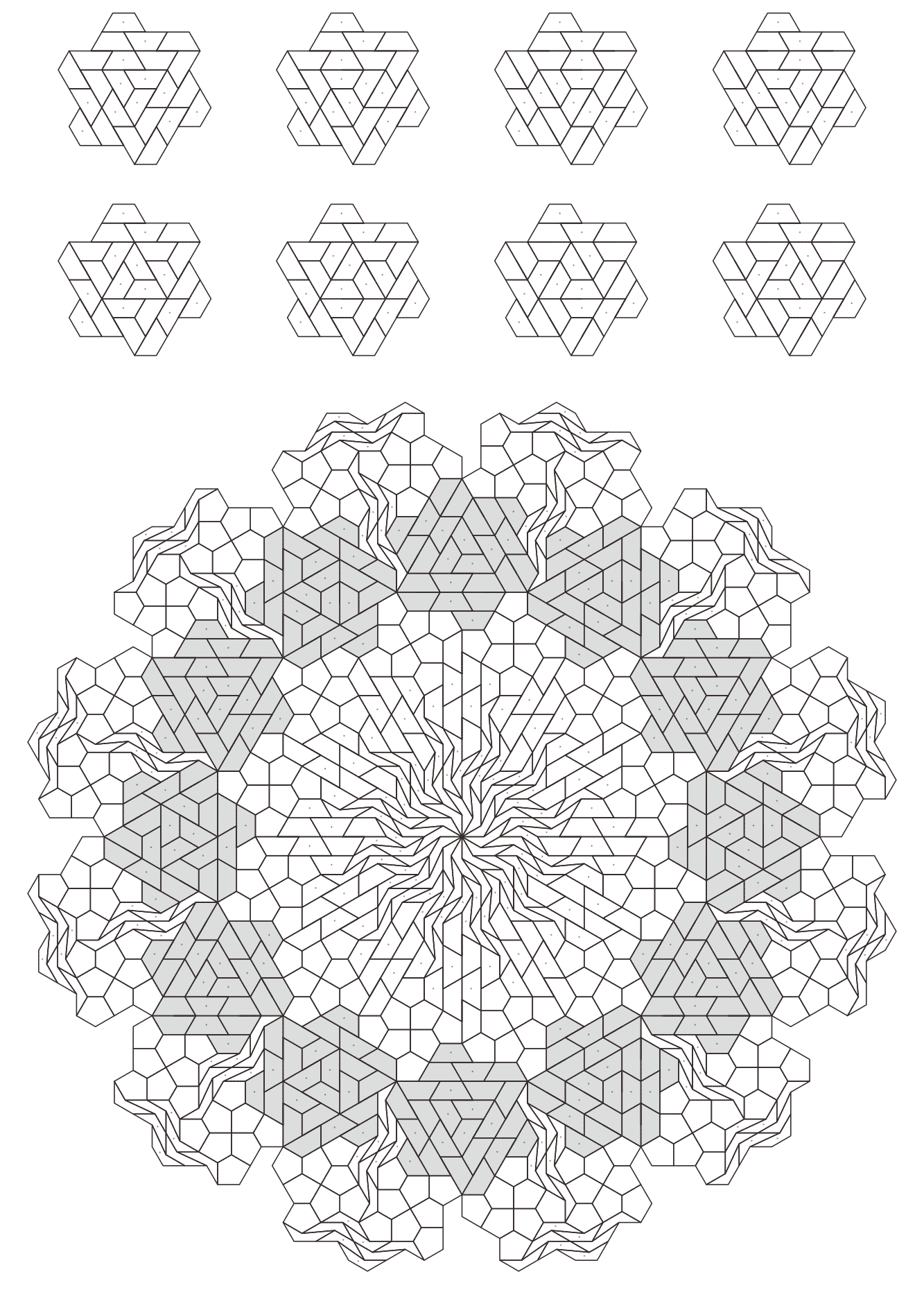
5.3 12-fold rotationally symmetric tilings
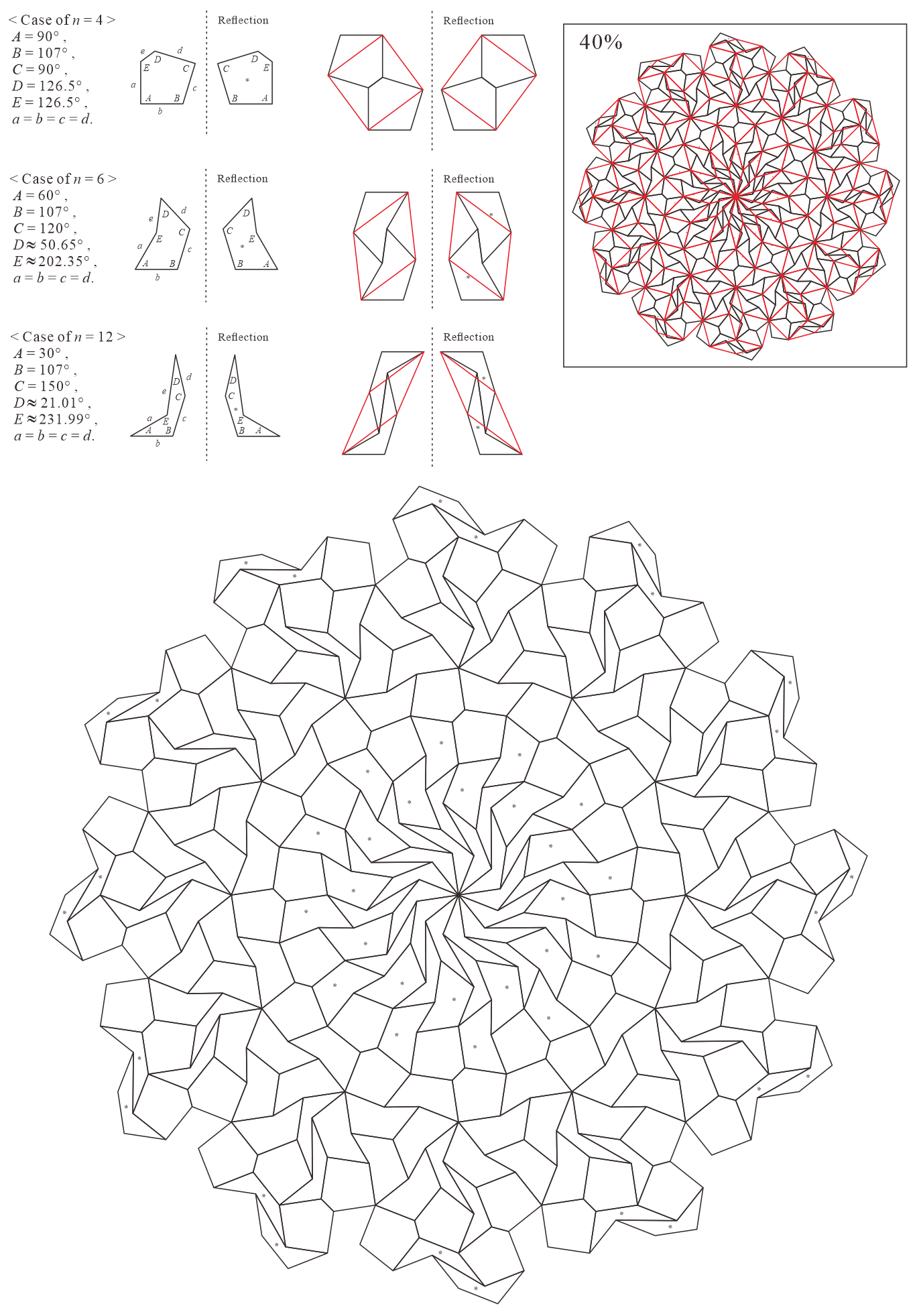
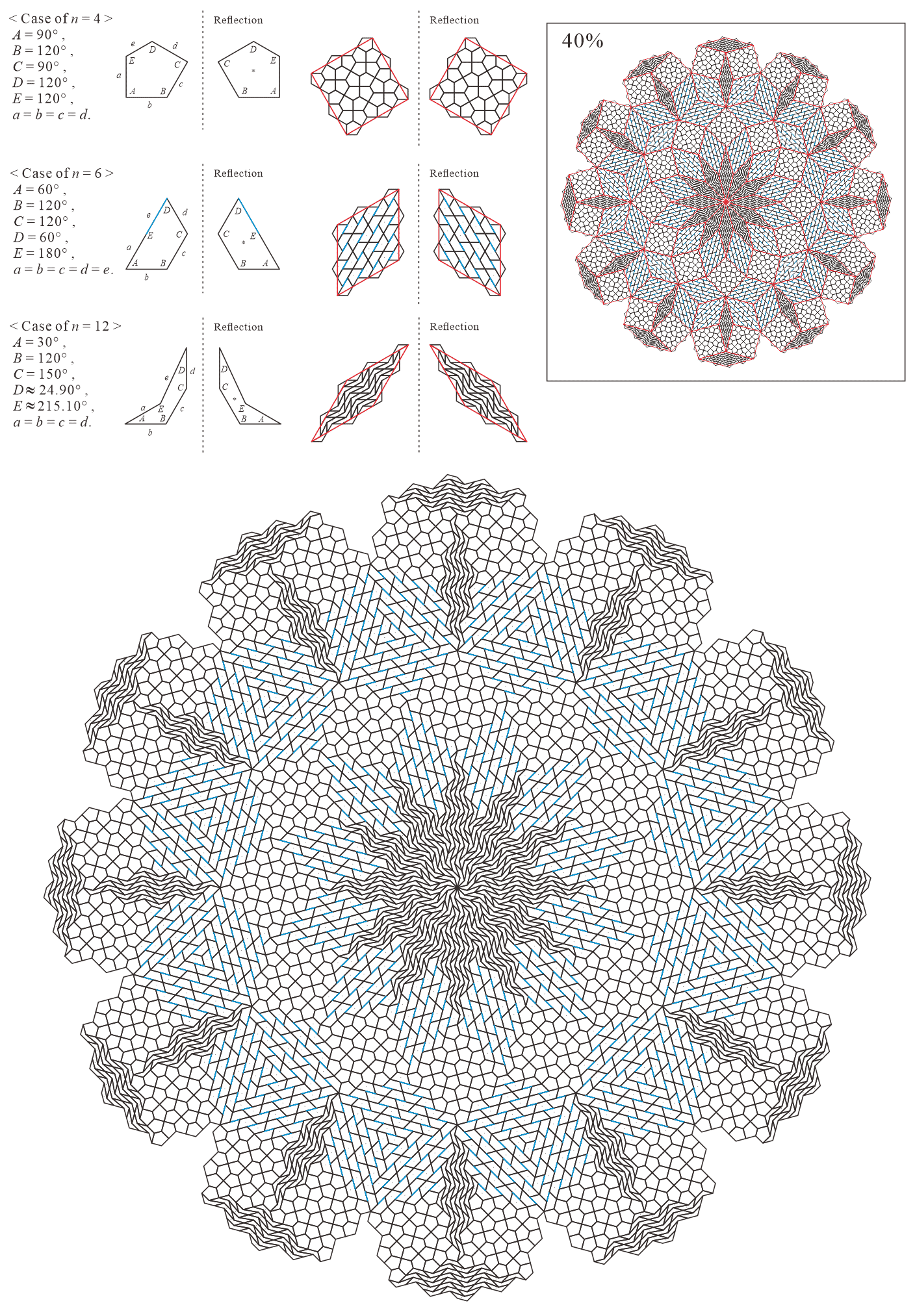
In this subsection, we present pentagonal tilings based on the 12-fold rotationally symmetric tiling with rhombuses with of acute angles , , and discovered by Socolar, as illustrated in Figure 5.3 [1, 4]. Of course, a rhombus with angles is a square. For this conversion, three types of pentagons corresponding to in (3) are utilized. As described in Subsections 5.1 and 5.2, in the figures of tilings in this study, the trapezoid corresponding to the posterior side is given an asterisk mark, and the pentagons with in (3) are not given an asterisk mark.
When combining three types of pentagons corresponding to in (3), their shapes in a tiling change depending on the values of are as follows:
-
•
: is a convex pentagon and are concave pentagons with
-
•
: is a convex pentagon, is a trapezoid (), and is a concave pentagon with
-
•
: are convex pentagons and is a concave pentagon with
-
•
: are convex pentagons and is a trapezoid ()
-
•
: are all convex pentagons
-
•
: are all parallelograms ()
-
•
: are all concave pentagons with
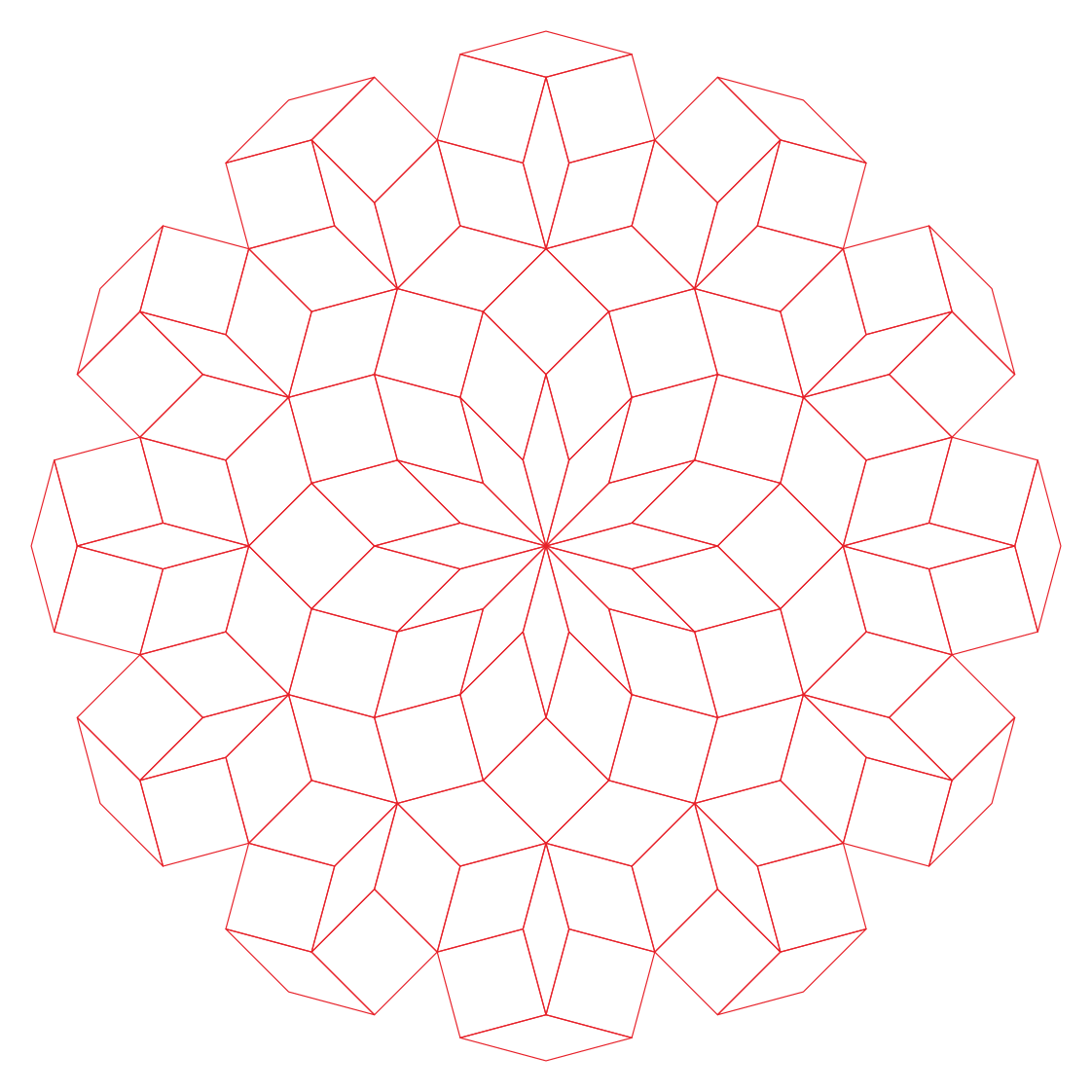
5.3.1 : is a convex pentagon and are concave pentagons with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.3.1.
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
5.3.2 : is a convex pentagon, is a trapezoid (), and is a concave pentagon with
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
Corresponding tiling figures (Note that the line corresponding to edge of pentagons degenerated into trapezoids in the figures is shown as a blue line):
5.3.3 : are convex pentagons and is a concave pentagon with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.3.3.
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
5.3.4 : are convex pentagons and is a trapezoid ()
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
Corresponding tiling figures (Note that the line corresponding to edge of pentagons degenerated into trapezoids in the figures is shown as a blue line):
5.3.5 : are all convex pentagons
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values Table 5.3.5.
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
5.3.6 : are all parallelograms ()
All cases are parallelograms, and the original rhombuses are formed by connecting edge of the parallelograms. The interior angles of pentagons (parallelograms) satisfying (3) with and are the values in Table 5.3.6. The converted tiling is equal to one of the tilings in which the rhombus of the original rhombic tiling is bisected into a parallelogram. The figure is omitted.
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
5.3.7 : are all concave pentagons with
In this study, as examples, the tilings in the case of are drawn. The interior angles of pentagons satisfying (3) with and are the values in Table 5.3.7.
| 4 | |||||
|---|---|---|---|---|---|
| 6 | |||||
| 12 |
5.3.8 Pattern generation using the properties of pentagons corresponding to rhombus with acute angle of
As introduced in [7], the pentagons satisfying (3) with , corresponding to the rhombus with an acute angle of have the property of being able to form a unit that has an outline shape with symmetry. By using that property, the interior of the tilings can be replaced with different patterns (refer to Figures 14, 16, 22, and 29 in [7]). For example, Figure A-39 illustrates such replacements to the tilings in Figures A-25 and A-35. In particular, the pentagon satisfying (3) with and becomes a trapezoid, and the trapezoid has the ability to form equilateral triangles. Therefore, the corresponding parts in the tilings can be replaced by more different patterns (Figure A-40 illustrates such a replacement in the tiling of Figure A-28).
6 Conclusions
In [7], we mainly dealt with rotationally symmetric tiling with pentagonal tiles, and discussed the relationship between the pentagon and rhombus. They were mainly discussions of monohedral tiling.
In this study, we focused on the conversion of tiling with multiple types of rhombuses into tiling with multiple types of pentagons, and presented the results of the conversion in detail using rotationally symmetric tilings, which are also the tiling model for quasicrystals.
When a rhombus is converted into pentagons, there are two types of rhombuses, rhombus with acute angles corresponding to pentagons of Anterior side (RPA) and rhombus with acute angles corresponding to pentagons of Posterior side (RPP), and they are reflection symmetry (refer to Figure 4.1). In the conversion that divides each rhombus of a rotationally symmetric tiling with multiple types of rhombuses as indicated in this study into two pentagons, the tiling must be done using RPA and RPP. However, if a rotationally symmetric tiling with multiple types of rhombuses is converted so that each rhombus is divided into eight or more pentagons, as indicated in this study, the tiling is formed from either RPA or RPP only. In this study, the converted pentagonal tilings were arranged in such a way that its center of rotational symmetry has an RPA; hence, the tilings generated by a conversion that divides a rhombus into eight or more pentagons were formed by a group of pentagons of rhombus that correspond to the RPA.
In the tiling with multiple types of rhombuses, the method of dividing a rhombus into its own similar figures has the rule that must be followed for its conversion into a pentagonal tiling. A tiling with multiple types of rhombuses generated by a division that does not follow the rule cannot be converted into a pentagonal tiling. Therefore, not all rhombic tilings can be converted into pentagonal tilings by the method introduced in this study. However, using the method described in this study, various pentagonal tilings will be generated from the knowledge of various patterns about rhombic tilings, and the patterns will be interesting.
References
- [1] D. Frettlöh, E. Harriss, F. Gähler, Tilings encyclopedia, https://tilings.math.uni-bielefeld.de/ (accessed on 5 December 2021).
- [2] B. Grünbaum, G.C. Shephard, Tilings and Patterns. W. H. Freeman and Company, New York, 1987, pp.15–35 (Chapter 1), pp.471–518 (Chapter 9).
- [3] B. Klaassen, Rotationally symmetric tilings with convex pentagons and hexagons, Elemente der Mathematik, 71 (2016) 137–144. doi:10.4171/em/310. Available online: https://arxiv.org/abs/1509.06297 (accessed on 23 February 2020).
- [4] K. Niizeki, Mathematics in quasiperiodic patterns (in Japanese), Journal of the Crystallographic Society of Japan, 31 (19899, 1–7. https://www.jstage.jst.go.jp/article/jcrsj1959/31/1/31_1_1/_pdf/-char/ja (accessed on 23 February 2020).
- [5] T. Sugimoto, Tiling problem: Convex pentagons for edge-to-edge tiling and convex polygons for aperiodic tiling (2015). https://arxiv.org/abs/1508.01864 (accessed on 23 February 2020).
- [6] —, Properties of strongly balanced tilings by convex polygons, Research and Communications in Mathematics and Mathematical Sciences, 8 (2017) 95–114. Available online: https://www.jyotiacademicpress.net/properties_of_strongly.pdf (accessed on 27 February 2022).
- [7] —, Pentagons and rhombuses that can form rotationally symmetric tilings (2020). https://arxiv.org/abs/2005.12709 (accessed on 4 March 2022).
- [8] T. Sugimoto, T. Ogawa, Systematic study of convex pentagonal tilings, II: Tilings by convex pentagons with four equal-length edges, Forma, 24 (2009) 93–109. Available online: https://forma.katachi-jp.com/abstract/2403/24030093.html (accessed on 4 March 2022).
- [9] Wikipedia contributors, Pentagonal tiling, Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Pentagonal_tiling (accessed on 20 February 2022).
- [10] —, Point group, Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Point_group (accessed on 23 February 2020).
- [11] —, Schoenflies notation, Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Schoenflies_notation (accessed on 23 February 2020).
- [12]
Appendix