Cosmic Accelerations Characterize the Instability of the Critical Friedmann Spacetime

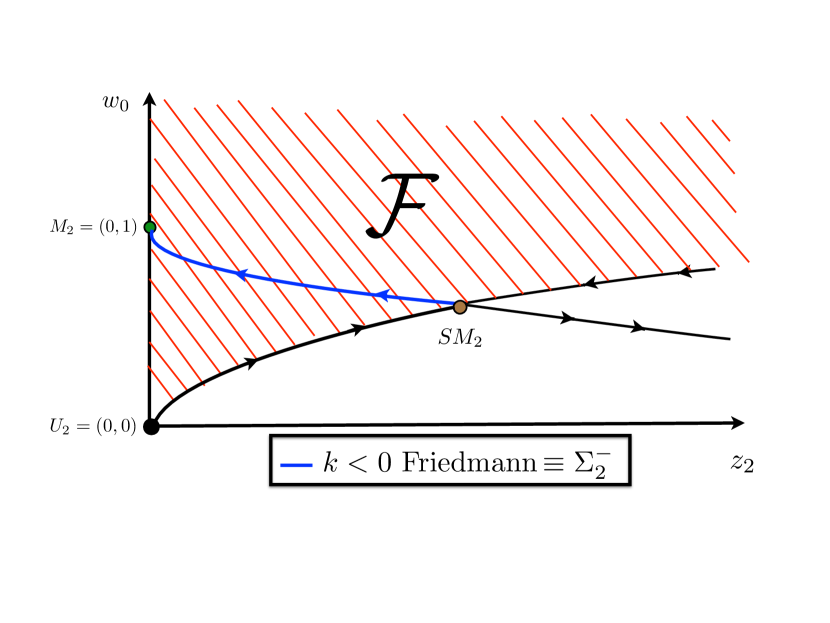
We argued in [29] that solutions of the $p=0$ STV-PDE which are smooth at the center of symmetry can be expanded in even powers of $\xi$ by Taylor’s theorem (see Section 3) and from the $n^{th}$ order term we obtain an approximation which solves the STV-ODE of order $n$. In the present paper we go on to prove that, for each such solution, there exists a solution dependent time translation $t\to t-t_{*}$ of the SSC time coordinate $t$, which we call time since the Big Bang, such that making the SSC gauge transformation to time since the Big Bang has the effect of eliminating the leading order negative eigenvalue at $SM$. Moreover, this gauge transforms every solution to either the rest point $SM$ or one of the two trajectories in the unstable manifold of $SM$ at $n=1$. As a result of this, every solution agrees exactly with a $k<0$, $k=0$ or $k>0$ Friedmann spacetime in the phase portrait of the STV-ODE at leading order $n=1$, see Figure 1. There is an important distinction to make here: The STV-ODE are autonomous in log-time $\tau=\ln t$, so translation in $\tau$ maps solutions to physically different solutions which traverse the same trajectory of the STV-ODE, but translation in $t$ is a gauge freedom of the SSC metric ansatz which maps trajectories of the STV-ODE to different trajectories which represent the same physical solution. Thus choosing time since the Big Bang eliminates a physical redundancy in the solution trajectories of the STV-ODE. When time since the Big Bang is imposed, there are only three remaining trajectories in the leading order $n=1$ phase portrait of the STV-ODE: The unstable rest point $SM$, the underdense (left) component of the unstable manifold and the overdense (right) component of the unstable manifold, see Figure 1. The underdense component of the unstable manifold of $SM$ at $n=1$ is the unique trajectory which takes $SM$ to $M$ and corresponds to $k<0$ Friedmann spacetimes, with the value of $k$ determined by translation in $\tau$ along this unique trajectory. The unique trajectory exiting $SM$ in the opposite overdense direction is the component of the unstable manifold of $SM$ corresponding to $k>0$ Friedmann spacetimes. The three (including the fixed point $SM$) trajectories of the $n=1$ phase portrait, after time since the Big Bang is imposed, is diagrammed in Figure 2.

In this paper we identify and study the entire subset of solutions $\mathcal{F}$ of the STV-PDE defined by the condition that, when time $t$ is taken to be time since the Big Bang, the resulting solution agrees with an underdense $k<0$ Friedmann solution in the leading order $n=1$ STV-ODE phase portrait. That is, the solution projects to the unique trajectory in the unstable manifold of $SM$ which takes $SM$ to $M$ at order $n=1$, parameterized by $\tau-\tau_{0}$ for some log-time translation constant $\tau_{0}=\ln t_{0}$ of the autonomous STV-ODE. We identify $\mathcal{F}$ as a new maximal asymptotically stable family of outwardly expanding solutions of the STV-PDE defined by the condition that solutions agree with a $k<0$ Friedmann spacetime in the leading order phase portrait of the expansion in even powers of $\xi$ when the SSC time is translated to time since the Big Bang associated with each solution. The main purpose of this paper is to demonstrate and characterize the instability of the $k=0$ Friedmann spacetime and the large time asymptotic stability and early time instability of the $k<0$ Friedmann spacetimes within the family of solutions $\mathcal{F}$.

We first characterize the forward time dynamics and asymptotic stability of solutions in $\mathcal{F}$ by proving that every solution which decays to the rest point $M$ as $t\to\infty$ in the phase portrait of the STV-ODE at order $n=1$, that is, every solution in $\mathcal{F}$, also decays as $t\to\infty$ to a corresponding unique stable rest point $M$ in the phase portrait of the STV-ODE at every order $n\geq 1$. This characterizes the forward time dynamics of solutions in $\mathcal{F}$ because it implies that every solution in $\mathcal{F}$ decays, as $t\to\infty$, to a $k<0$ Friedmann spacetime faster than it decays to Minkowski space as $t\to\infty$ at each fixed radii $r>0$ at every order $n\geq 1$. The asymptotic decay of solutions in $\mathcal{F}$ as $t\to\infty$ immediately implies uniform bounds on solutions of the STV-ODE for all time $t>t_{0}>0$ and $n\geq 1$ in terms of bounds on the initial data at $t=t_{0}>0$ alone. The STV-ODE are linear in the highest order variables when lower order solutions are interpreted as known inhomogeneous terms, so solutions of the STV-ODE exist for all time $0<t<\infty$ at every order. For the purposes of asymptotic analysis, we formally assume convergence of solutions of the STV-ODE up to order $n$, with errors at order $n$ estimated by bounds at order $n+1$ according to Taylor’s theorem, an assumption justified rigorously by simply restricting to an appropriate space of analytic solutions.⁶⁶6The convergence of solutions in $\mathcal{F}$ in the limit $n\to\infty$ for $|\xi|<1$, with estimates provided by Taylor’s theorem, follows directly from mild assumptions on the growth rate of the initial data, due to the fact that all solutions lie on bounded trajectories which tend to $M$ as $t\to\infty$ at every order $n\geq 1$.

The backward time dynamics $t\to 0$ ($\tau\to-\infty$) of solutions in $\mathcal{F}$ is determined at each order $n\geq 1$ by the instability of the $k=0$ Friedmann spacetime, that is, by the eigenvalues of the saddle rest point $SM$ as it is represented in the STV-ODE phase portrait at each order $n\geq 1$. By definition, each solution in $\mathcal{F}$ agrees at leading order ($n=1$) with a $k<0$ Friedmann spacetime represented as the unique trajectory in the unstable manifold of $SM$ which tends to $M$ as $t\to\infty$ and to $SM$ as $t\to 0$. To understand the backward time dynamics of solutions in $\mathcal{F}$ at higher orders $n\geq 2$, we demonstrate that $k<0$ Friedmann solutions correspond to a single trajectory in the unstable manifold of $SM$ in the phase portrait of the STV-ODE at every order $n\geq 1$, with the value of $k$ determined by log-time translation at order $n=1$. We then prove that two new eigenvalues of the rest point $SM$ appear at each new order $n\geq 2$ and all of them are positive except one negative eigenvalue which appears at order $n=2$. From this we conclude that the family $\mathcal{F}$ decomposes into two essential components: The underdense component of the unstable manifold of $SM$, consisting of trajectories which connect $SM$ to $M$ at every order $n\geq 1$, and solutions which tend to $M$ in forward time but do not tend to $SM$ in backwards time. Because of the presence of the order $n=2$ negative eigenvalue at $SM$, solutions in $\mathcal{F}$ will generically not tend to $SM$ in backward time, but rather will follow the one-dimensional stable manifold of $SM$, the unique trajectory which emerges from $SM$ in backward time as $t\to 0$ ($\tau\to-\infty$). Thus the Big Bang limit $t\to 0$ of a generic solution in $\mathcal{F}$ is not self-similar like $SM$ beyond the leading order, but rather, generically displays a non-self-similar character at the Big Bang for all orders $n=2$ and above. This provides an important example of the self-similarity hypothesis, that solutions which approach a singularity exhibit self-similarity to leading order [4]. However, in this case, such solutions are generically not self-similar beyond leading order.

To reiterate, each spacetime in $\mathcal{F}$ agrees with a unique $k<0$ Friedmann spacetime in the phase portrait of the STV-ODE at leading order $n=1$ (all the way into the Big Bang at $t=0$) and agrees with the same $k<0$ Friedmann spacetime in the limit $t\to\infty$ (for each fixed $r>0$), but generically accelerates away from this $k<0$ Friedmann spacetime at intermediate times in the phase portraits of the STV-ODE of order $n\geq 2$. Since each member of the family $\mathcal{F}$ by definition contains the component of the unstable manifold of $SM$ which contains the leading order behavior of $k<0$ Friedmann spacetimes imposed at $n=1$, $\mathcal{F}$ represents a maximal extension of the one parameter family of $k<0$ Friedmann spacetimes to a robust asymptotically stable family of spacetimes which exist within the family of smooth spherically symmetric spacetimes. Since the family $\mathcal{F}$ is the full space of solutions into which underdense perturbations of $SM$ evolve, $\mathcal{F}$ characterizes the instability of $SM$ to underdense perturbations. Because a negative eigenvalue of $SM$ does not exist above order $n=2$, it follows that a solution in $\mathcal{F}$ lies in the unstable manifold of $SM$ if and only if its projection onto the $n=2$ phase portrait of the STV-ODE lies in the unstable manifold of $SM$, so the unstable manifold of $SM$ at $n=2$ characterizes the unstable manifold of $SM$ at all orders. A main goal of this paper is to prove that, even though $\mathcal{F}$ is asymptotically stable, solutions in $\mathcal{F}$ generically accelerate away from $k<0$ Friedmann spacetimes at early times due to an instability at $t=0$.

To establish the instability of $k<0$ Friedmann spacetimes at $t=0$, it suffices to demonstrate that there are multiple solutions of the $STV-ODE$ which agree with $k<0$ Friedmann spacetimes at order $n=1$ and in the limit $t\to 0$ but which diverge from $k<0$ Friedmann spacetimes at $t>0$ for some $n\geq 2$. Imposing time since the Big Bang, every solution in $\mathcal{F}$ lies on the unique trajectory in the unstable manifold of $SM$ which takes $SM$ to $M$ and hence every solution agrees with a $k<0$ Friedmann solution at order $n=1$. Thus to establish the instability of $k<0$ Friedmann spacetimes at order $n=2$, it suffices to prove that: (1) Solution trajectories corresponding to $k<0$ Friedmann lie in the unstable manifold of $SM$ and (2) there exist other solutions in $\mathcal{F}$ in the unstable manifold of $SM$ which diverge from $k<0$ Friedmann at $t>0$. For this, we use known exact formulas to prove that the solution trajectory of $k<0$ Friedmann spacetimes lies in the unstable manifold of $SM$ at order $n=2$ with time translation differentiating $k$. Since a solution in $\mathcal{F}$ lies in the unstable manifold of $SM$ at every order if and only if it lies in the unstable manifold of $SM$ order $n=2$, we can conclude that $k<0$ Friedmann spacetimes lie on a single trajectory in the unstable manifold of $SM$ at every order $n\geq 2$ as well. Next we use exact formulas to prove that the trajectory corresponding to $k<0$ Friedmann spacetimes at order $n=2$ is an eigensolution of the eigenvalue $\lambda_{A1}$ which enters at order $n=1$ (this is also shown to order $n=3$ in Section 12). Thus to establish the instability of $k<0$ Friedmann spacetimes it suffices only to prove that a second positive eigenvalue $\lambda_{B2}\neq\lambda_{A1}$ emerges at $SM$ at order $n=2$. From this, the early time instability of the $k<0$ Friedmann spacetimes is established in the phase portrait of the STV-ODE of order $n=2$, diagrammed in Figure 3, even though the whole family $\mathcal{F}$ is asymptotically stable. We discuss the phase portrait at order $n=2$ in Section 1.6.

At this stage it is convenient to introduce a refined notation that distinguishes the family $\mathcal{F}$ of solutions of the STV-PDE from the solutions of the STV-ODE which approximate solutions in $\mathcal{F}$ up to arbitrary order. To this end, we define $\mathcal{F}_{n}$ as the set of solutions of the STV-ODE of order $n$ which satisfy the property that the trajectory reduces at order $n=1$ to the unique trajectory which connects $SM$ to $M$, but not necessarily at higher orders. We also define $\mathcal{F}_{n}^{\prime}\subset\mathcal{F}_{n}$ to be the subset of solutions which lie in the unstable manifold of the rest point $SM$ in STV-ODE of order $n$. Note that by definition $\mathcal{F}_{1}^{\prime}=\mathcal{F}_{1}$. Finally, let $\mathcal{F}^{\prime}\subset\mathcal{F}$ denote the set of solutions of the STV-PDE whose $n^{th}$ order approximation lies in the unstable manifold of rest point $SM$ in the phase portrait of the STV-ODE of order $n$ for every $n\geq 1$. We may sometimes refer to $\mathcal{F}_{n}$ as $\mathcal{F}$ at order $n$ and $\mathcal{F}_{n}^{\prime}$ as the stable manifold of $SM$ in $\mathcal{F}$ at order $n$.

Having set out the main elements, we now discuss them in detail.

In Section 7 we give a new derivation of the Einstein field equations $G=\kappa T$ in what we call SSCNG coordinates. These coordinates are standard Schwarzschild coordinates (SSC), that is, where the metric takes the form

$\displaystyle ds^{2}=-B(t,r)dt^{2}+\frac{dr^{2}}{A(t,r)}+r^{2}d\Omega^{2},$

(1.1)

in addition to possessing a normal gauge (NG) when expressed in the variables $(t,\xi)$. An arbitrary spherically symmetric spacetime can generically⁷⁷7That is, under the condition $\frac{\partial C(t,r)}{\partial r}\neq 0$, where $C(t,r)d\Omega^{2}$ is the angular part of the metric, see [29]. be transformed to SSC metric form by defining $r$ so $r^{2}d\Omega^{2}$ is the angular part of the metric and then constructing a time coordinate $t$, complementary to $r$, such that the metric is diagonal in $(t,r)$-coordinates [31, 34]. The SSC metric form is invariant under the gauge freedom of arbitrary time transformation $t\to\phi(t)$, so to set the gauge, we impose the condition that $B(t,0)=1$, that is, geodesic (proper) time at $r=0$ [29]. We refer to this as the normal gauge (NG).

The STV-PDE use density and velocity variables:

$\displaystyle z$

$\displaystyle=\frac{\kappa\rho r^{2}}{1-v^{2}},$

$\displaystyle w$

$\displaystyle=\frac{v}{\xi},$

coupled to the SSC metric components $A$ and $D=\sqrt{AB}$. Recall that the STV-PDE are not the Einstein field equations in $(t,\xi)$ coordinates but rather the Einstein field equations with an SSC metric form expressed in terms of $z$ and $w$ with independent variables $(t,\xi)$ [29]. We extend the derivation of the STV-PDE to equations of state of the form $p=\sigma\rho$, with $\sigma$ constant, in Theorem 32 below. However, our concern in this paper is with the case $p=\sigma=0$, applicable to late time Big Bang Cosmology.⁸⁸8In the Standard Model of Cosmology, the pressure drops precipitously to zero at about 10,000 years after the Big Bang, an order of magnitude before the uncoupling of matter and radiation [17].

Equations (1.2)–(1.5) are the STV-PDE. The NG is imposed by defining a time transformation $t\to\phi(t,r)$ which sets $B=1$ at $r=0$ [29]. From here on, when we refer to a solution of the STV-PDE we always assume the NG gauge is imposed. Note that there is one remaining freedom left in this gauge, this being the time translation freedom $t\to t-t_{0}$ for some constant $t_{0}$.

The STV-ODE are derived by expanding smooth solutions of the STV-PDE (1.2)–(1.5) in powers of $\xi$ with time dependent coefficients, collecting like powers of $\xi$ and assuming the NG gauge. The assumption of smoothness at the center implies that the non-zero coefficients in the expansion occur only for even powers $\xi^{2n}$ and this significantly reduces the solution space of the Einstein field equations by disentangling solutions smooth at the center from the larger generic solution space. Fortuitously, the resulting equations in the fluid variables $z$ and $w$ uncouple from the equations for the metric components $A$ and $D$, leading to the expansions:

	$\displaystyle z(t,\xi)$	$\displaystyle=z_{2}(t)\xi^{2}+z_{4}(t)\xi^{4}+\dotsc+z_{2n}(t)\xi^{2n}+\dots,$		(1.6)
	$\displaystyle w(t,\xi)$	$\displaystyle=w_{0}(t)+w_{2}(t)\xi^{2}+\dotsc+w_{2n-2}(t)\xi^{2n-2}+\dots,$		(1.7)

which close in $(z_{2k},w_{2k-2})$ for $1\leq k\leq n$ at every order $n\geq 1$ when $p=0$. We prove in Theorem (13) that the STV-ODE of order $n$ closes to form a $2n\times 2n$ autonomous system

$\displaystyle t\dot{\boldsymbol{U}}=\boldsymbol{F}_{n}(\boldsymbol{U})$

(1.8)

in unknowns

$\displaystyle\boldsymbol{U}:=(z_{2},w_{0},\dots,z_{2n},w_{2n-2})^{T},$

such that the leading order variables are determined by an inhomogeneous $2\times 2$ system of the form

$\displaystyle\frac{d}{d\tau}\boldsymbol{v}_{n}=\left(\begin{array}[]{cc}(2n+1)(1-w_{0})-1&-(2n+1)z_{2}\\ -\frac{1}{4n+2}&(2n+2)(1-w_{0})-1\end{array}\right)\boldsymbol{v}_{n}+\boldsymbol{q}_{n}$

where $\boldsymbol{v}_{n}=(z_{2n},w_{2n-2})^{T}$ and $\boldsymbol{q}_{n}$ involves only lower order terms which are determined by the STV-ODE of order $n-1$. We refer to the $2n\times 2n$ system of equations (1.8) as the STV-ODE of order $n$.

It follows that the STV-ODE are nested in the sense that each STV-ODE of order $n\geq 2$ contains as a sub-system the STV-ODE of order $k$ for all $1\leq k\leq n-1$. Thus the self-similar formulation decouples solutions at every order in the sense that one can solve for solutions up to order $n-1$ and use the STV-ODE at order $n$ to solve for $(z_{2n}(t),w_{2n-2}(t))$ from arbitrary initial conditions $(z_{2n}(0),w_{2n-2}(0))$. Assuming lower order solutions $k\leq n-1$ are fixed, the STV-ODE of order $n$ turn out to be linear in the highest order terms $(z_{2n},w_{2n-2})$. For approximations up to orders $n=2$ we can use the approximation $z=\kappa\rho r^{2}$ in place of $z=\frac{\kappa\rho r^{2}}{1-v^{2}}$ because this incurs errors of the order $O(\xi^{6})$ given that $v^{2}=O(\xi^{2})$. The derivation of the general STV-ODE of order $n$ is carried out carefully in following sections but to set up the picture and highlight the main results we first describe the phase portraits of the STV-ODE which emerge at orders $n=1$ and $n=2$ of this expansion.⁹⁹9The STV-ODE at order $n=1$ and $n=2$ were introduced in [29] without detailed derivation. Here we derive the STV-ODE up to order $n=3$ and derive the form of the STV-ODE at all orders $n\geq 4$ together with an explicit algorithm for computing them. Note that Figure 1 is take from [29] with the modification that in this paper, the coordinate system is centered on $(z_{2},w_{0})=0$, while coordinates were centered at $SM$ in [29]. We also record a correction to the $z_{4}$ equation incorrectly expressed in equation (3.33) of [29]. This error occurred at fourth order in $\xi$ and did not affect the results claimed in [29], see (1.20)–(1.23) below. Unanticipated by the authors ahead of time, it turns out that the global character of the phase portrait of the STV-ODE at any order $n\geq 3$ emerges from orders $n=1$ and $n=2$.

A calculation shows that the STV-ODE of order $n=1$ is the $2\times 2$ system:

	$\displaystyle t\dot{z}_{2}$	$\displaystyle=2z_{2}-3z_{2}w_{0},$		(1.9)
	$\displaystyle t\dot{w}_{0}$	$\displaystyle=-\frac{1}{6}z_{2}+w_{0}-w_{0}^{2}.$		(1.10)

Using $\frac{d}{d\tau}=t\frac{d}{dt}$, system (1.9)–(1.10) converts to an autonomous $2\times 2$ system of ODE in $\tau=\ln t$. It is easy to verify that the system admits three rest points: The source $U=(0,0)$, the unstable saddle rest point $SM=(\frac{4}{3},\frac{2}{3})$ and the degenerate stable rest point $M=(0,1)$. The rest point $U$ plays no role once time since the Big Bang is imposed, the rest point $M$ describes the asymptotics of solutions tending to Minkowski space as $t\to\infty$ and the coordinates of rest point $SM$ are precisely the first two terms in the self-similar expansion of the critical ($k=0$) Friedmann spacetime, viewed here as the Standard Model due to the central role it has played in the history of Cosmology. A calculation gives the eigenvalues and eigenvectors of rest points $M$ and $SM$ as:

	$\displaystyle\lambda_{M}$	$\displaystyle=-1,$	$\displaystyle\boldsymbol{R}_{M}$	$\displaystyle=\left(\begin{array}[]{cc}0\\ 1\end{array}\right),$
	$\displaystyle\lambda_{A1}$	$\displaystyle=\frac{2}{3},$	$\displaystyle\boldsymbol{R}_{A1}$	$\displaystyle=\left(\begin{array}[]{cc}-9\\ \frac{3}{2}\end{array}\right),$
	$\displaystyle\lambda_{B1}$	$\displaystyle=-1,$	$\displaystyle\boldsymbol{R}_{B1}$	$\displaystyle=\left(\begin{array}[]{cc}4\\ 1\end{array}\right),$

respectively. The phase portrait for system (1.9)–(1.10) is diagrammed in Figure 1. The two components of the unstable manifold of $SM$ correspond to the two trajectories associated with the positive eigenvalue $\lambda_{A1}=\frac{2}{3}$, the underdense component being the trajectory which connects $SM$ to $M$ and the overdense component leaving $SM$ in the opposite direction, see Figure 1. The trajectory connecting $U$ to $SM$ is the underdense trajectory in the stable manifold of $SM$ corresponding to the negative eigenvalue $\lambda_{B1}=-1$ and the overdense stable trajectory emerges opposite to this at $SM$. Using classical formulas for Friedmann spacetimes which set the time of the Big Bang to $t=0$, we verify that the underdense trajectory connecting $SM$ to $M$ corresponds to $k<0$ Friedmann spacetimes and the overdense trajectory in the unstable manifold of $SM$ corresponds to $k>0$ spacetimes. We obtain an exact formula for the trajectory connecting $SM$ to $M$ from an expansion of such formulas for Friedmann spacetimes in powers of $\xi$. The variable $\Delta_{0}$, which parameterizes the one-parameter family of Friedmann spacetimes under scalings that set $k=-1,0,1$, is given by $\Delta_{0}=\ln t_{0}$, so the entire one-parameter family of Friedmann spacetimes at order $n=1$ consists of $SM$ together with the two trajectories in its unstable manifold, parameterized by the time translation freedom $\tau-\tau_{0}$, which determines the value of $\Delta_{0}$ and thereby determines a unique solution in the Friedmann family [34].

Now the SSC metric ansatz with NG still leaves one gauge freedom yet to be set, namely, the freedom to impose time translation $t\to t-t_{0}$. The time translation freedom of the SSC system leaves open an unresolved redundancy in solutions of the the STV-ODE in the sense that time translation maps each trajectory of the STV-ODE of order $n=1$ to a different trajectory which represents the same physical solution. We show that for each trajectory of the system (1.9)–(1.10), there exists a unique time translation $t\to t-t_{0}$, which we call time since the Big Bang, which converts that trajectory either to $SM$ or to one of the two trajectories in the unstable manifold of $SM$. In particular, referring to the phase portrait depicted in Figure 1 and making the gauge transformation to time since the Big Bang, the trajectories in the stable manifold of $SM$, that is, the one taking $U$ to $SM$ and the trajectory opposite it at $SM$, go over to $SM$, whereas all the trajectories above these, that is, trajectories in the domain of attraction of $M$, go over to the underdense portion of the unstable manifold of $SM$ corresponding to $k<0$ Friedmann. Trajectories below the stable manifold of $SM$ go over to the overdense portion of the unstable manifold of $SM$, corresponding to $k>0$ Friedmann spacetimes. From this it follows that imposing the solution dependent time since the Big Bang has the effect of eliminating the negative eigenvalue $\lambda_{B1}=-1$ together with the rest point $U$, and we can, without loss of generality, restrict our analysis to the space of solutions which agree with $SM$ or a trajectory in its unstable manifold, in the phase portrait of the solution at $n=1$. Since these trajectories agree with the Friedmann spacetimes, we conclude that, under appropriate change of time gauge, all smooth solutions of the STV-PDE agree with a Friedmann spacetime at leading order in the STV-ODE. Our purpose here is to study the space $\mathcal{F}$ of solutions which lie on the trajectory which takes $SM$ to $M$ at leading order, and hence agree with a $k<0$ Friedmann spacetime at order $n=1$ of the STV-ODE. We do not consider the $k>0$ Friedmann spacetimes, but observe that these exit the first quadrant of our coordinate system at $w_{0}=0$, the time of maximal expansion.

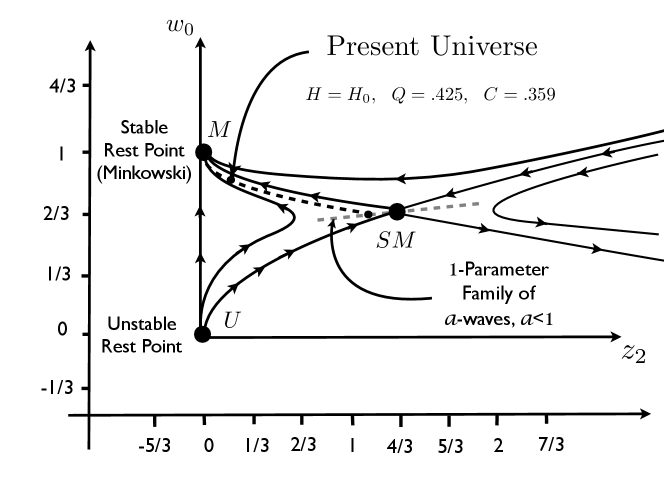
The rest point $M$ describes the time asymptotic decay of solutions in $\mathcal{F}$ to Minkowski space as $t\to\infty$. A calculation shows that $M$ is a degenerate stable rest point with repeated eigenvalue $\lambda_{M}=-1$ and single eigenvector $\boldsymbol{R}_{M}=(0,1)^{T}$. Thus solutions in $\mathcal{F}$ decay to $M$ time asymptotically along the $w_{0}$-axis as $t\to\infty$. Moreover, as is standard for degenerate stable rest points with the character of $M$, $z_{2}(t)$ and $w_{0}(t)$ decay to $M$ at leading order like $O(t^{-1})$ and $O(t^{-1}\ln t)$ respectively. Thus, assuming solutions in $\mathcal{F}$ agree with Friedmann at leading order, but diverge at higher orders with errors estimated by Taylor’s theorem, we can use the $n=1$ phase portrait of the STV-ODE alone to conclude that, to leading order as $t\to\infty$, every solution in $\mathcal{F}$ decays to $w=\frac{v}{\xi}=1$ and $z=0$ at the same rate for fixed $\xi$ and decays to Friedmann faster than to Minkowski for fixed $r$ (since $\xi\to 0$). Theorem 14 below establishes that $M$ is a degenerate stable rest point in the phase portrait of the STV-ODE at every order $n\geq 1$, exhibiting the same negative eigenvalue $\lambda_{M}=-1$ with a single eigenvector $\boldsymbol{R}_{M}$ at each order. The degenerate structure of rest point $M$ at all orders implies that the estimate for the discrepancy between a solution in $\mathcal{F}$ and the Friedmann spacetime it agrees with at leading order, is estimated by the discrepancy at second order as $t\to\infty$. We conclude that one would see perfect alignment between solutions in $\mathcal{F}$ and $k<0$ Friedmann at order $n=1$ and the error between them tends to zero by a factor $O(t^{-1})$ faster as $t\to\infty$ than what you would see without taking account of the decay of solutions to rest point $M$ at higher orders. The result, which uses standard rates of decay at degenerate stable rest points with the character of $M$, is recorded in the following theorem.

Note that in Theorem 2 the extra factor $t^{-1}$ in the density gives the faster rate of decay of $k<0$ Friedmann over the $O(t^{-2})$ decay rate known for the $k=0$ Friedmann spacetime. From this we conclude faster decay to Friedmann than to Minkowski and faster decay in the density than in the velocity.

The trajectory taking $SM$ to $M$ at order $n=1$ can be defined implicitly, which provides a canonical leading order evolution shared by all underdense solutions in $\mathcal{F}$, including $k<0$ Friedmann spacetimes. This spacetime is discussed in Subsection 9. The rest point $SM$ persists to every order because the the critical Friedmann spacetime is self-similar at every order of the STV-ODE. Somewhat surprisingly, the crucial behavior of solutions in $\mathcal{F}$ emerges at order $n=2$.

The nested property of the STV-ODE in (1.8) implies that lower order eigenvalues of $SM$ persist to higher orders. We prove that two distinct additional eigenvalues always emerge at $SM$ in going from the STV-ODE of order $n-1$ to the STV-ODE of order $n$ for all $n\geq 2$. These are given by the formulas:

$\displaystyle\lambda_{An}$

$\displaystyle=\frac{2n}{3},$

$\displaystyle\lambda_{Bn}$

$\displaystyle=\frac{1}{3}(2n-5).$

(1.19)

From (1.19) we conclude that both eigenvalues $\lambda_{An}$ and $\lambda_{Bn}$ are positive except at orders $n=1$ and $n=2$. We argued above that $\lambda_{B1}$ is eliminated by changing to time since the Big Bang, an assumption equivalent to assuming a solution agrees with Friedmann at leading order $n=1$. At order $n=2$, $\lambda_{A2}=\frac{4}{3}>0$ and $\lambda_{B2}=-\frac{1}{3}<0$. A calculation also shows that at second order, the $k<0$ Friedmann solutions continue to lie on the trajectory associated with the leading order eigenvalue $\lambda_{A1}=\frac{2}{3}$. Recall that assuming time since the Big Bang eliminates the leading order negative eigenvalue by transforming the solution space to solutions which agree at order $n=1$ with either $SM$ or a trajectory in the unstable manifold of $SM$. The existence of the negative eigenvalue $\lambda_{B2}$ implies that $SM$ is an unstable saddle rest point with a one-dimensional stable manifold and a codimension one unstable manifold at each order $n\geq 2$. Also recall that we let $\mathcal{F}_{n}^{\prime}\subset\mathcal{F}_{n}$ denote the subset of solutions with trajectories in the unstable manifold of $SM$ identified as an $n-1$ dimensional space of trajectories taking $SM$ to $M$ in the phase portrait of the STV-ODE of order $n\geq 2$. The appearance of one positive and one negative eigenvalue at order $n=2$, and only positive eigenvalues at higher orders, immediately implies the following theorem.

It follows from the theory of non-degenerate hyperbolic rest points that all solution trajectories in $\mathcal{F}_{n}^{\prime}$ emerge tangent to the eigendirection associated with the smallest positive eigenvalue at $SM$. Of course at order $n=1$ the leading order eigenvalue associated with the solution trajectory of the $k<0$ Friedmann spacetime is the smallest eigenvalue and this remains the smallest positive eigenvalue at $n=2$. However, an eigenvalue smaller than this emerges at order $n=3$ namely, $\lambda_{B3}=\frac{1}{3}$. Thus solutions in $\mathcal{F}_{n}^{\prime}$ generically emerge tangent to the leading order eigendirection of the $k<0$ Friedmann spacetimes only up to order $n=2$, but all solutions in $\mathcal{F}_{n}^{\prime}$ which have a component of $\lambda_{B3}$ will emerge from $SM$ tangent to its eigenvector $\boldsymbol{R}_{B3}$, which is not tangent to the Friedmann direction $\boldsymbol{R}_{A1}$, corresponding to the leading order eigenvalue $\lambda_{A1}=\frac{2}{3}$ at $SM$. From this we establish that although all the solutions in $\mathcal{F}_{n}$ tend to rest point $M$ as $t\to\infty$, solutions in $\mathcal{F}_{n}$ in the complement of $\mathcal{F}_{n}^{\prime}$, that is, those that miss $SM$ in backward time, follow the backward stable manifold of $SM$, consistent with the standard phase portrait picture of a non-degenerate saddle rest point. Since the only negative eigenvalue of $SM$ enters at order $n=2$, we can conclude that any solution that lies in the unstable manifold of $SM$ in the phase portrait of the STV-ODE at order $n=2$, also lies in the unstable manifold of $SM$ at all higher orders $n\geq 3$. In this sense, the unstable manifold of $SM$ is characterized at order $n=2$. Note that all solutions of the STV-ODE in $\mathcal{F}$ which lie in the unstable manifold of $SM$, take $SM$ to $M$ in the phase portrait of the STV-ODE at all orders, and hence are bounded for all time $0\leq t\leq\infty$. Trajectories not in the unstable manifold of $SM$ miss $SM$ in backwards time in every STV-ODE of order $n\geq 2$ and tend in backward time instead to the stable manifold associated with the unique negative eigenvalue, that is, a single trajectory. Thus $\mathcal{F}$, which consists of the domain of attraction of $M$ at every order, contains trajectories which do not emanate from $SM$, and hence correspond to a Big Bang at $t=0$ which is qualitatively different from the self-similar blow-up $t\to 0$ at $SM$, and hence qualitatively different from the Big Bang observed in Friedmann spacetimes. An immediate conclusion of this analysis is a rigorous characterization the self-similar nature of the Big Bang in general spherically symmetric smooth solutions to the Einstein field equations when $p=0$.

Since all eigenvalues which emerge at $SM$ at orders above $n=2$ are positive, the unstable manifold of $SM$, and the entire phase portrait of the STV-ODE at higher orders, is determined from the $STV-ODE$ phase portrait at order $n=2$. In particular, the unstable manifold of $SM$ is determined at order $n=2$ in the sense that a solution in $\mathcal{F}$ lies in the unstable manifold of $SM$ at all orders $n\geq 1$ if and only if it lies in the unstable manifold of $SM$ at order $n=2$. We now describe the phase portrait of the STV-ODE at order $n=2$ in detail.

The corrections to $k<0$ Friedmann accounted for by solutions in $\mathcal{F}$ at order $n=2$ are most important as this is the order in which a negative eigenvalue emerges at $SM$ and also the leading order in which divergence from Friedmann spacetimes is observed. The order $n=2$ is important because it determines $w_{2}(t)\xi^{2}$, which provides the third order correction to redshift vs luminosity, the correction at the order of the anomalous acceleration of the galaxies which are purportedly accounted for by dark energy in the standard $\Lambda$CDM model of Cosmology [29].

The STV-ODE of order $n=2$ is the $4\times 4$ system:¹⁰¹⁰10Note that this corrects an error in [29] in the terms involving $z_{4}$, a mistake at fourth order in $\xi$ which did not affect the conclusions.

	$\displaystyle t\dot{z}_{2}$	$\displaystyle=2z_{2}-3z_{2}w_{0},$		(1.20)
	$\displaystyle t\dot{w}_{0}$	$\displaystyle=-\frac{1}{6}z_{2}+w_{0}-w_{0}^{2},$		(1.21)
	$\displaystyle t\dot{z}_{4}$	$\displaystyle=\frac{5}{12}z_{2}^{2}w_{0}-5w_{0}z_{4}+4z_{4}-5z_{2}w_{2},$		(1.22)
	$\displaystyle t\dot{w}_{2}$	$\displaystyle=-\frac{1}{24}z_{2}^{2}+\frac{1}{4}z_{2}w_{0}^{2}-\frac{1}{10}z_{4}-4w_{0}w_{2}+3w_{2}.$		(1.23)

Note first that the STV-ODE of order $n=1$ appears as the subsystem (1.20)–(1.21). Viewed as a $4\times 4$ autonomous system, (1.20)–(1.23) admits the three rest points: $U=(0,0,0,0)$, $M=(0,1,0,0)$ and $SM=(\frac{4}{3},\frac{2}{3},\frac{40}{27},\frac{2}{9})$. Imposing time since the Big Bang restricts the solution space to solutions in the unstable manifold of $SM$ at order $n=1$ and this eliminates $U$ from the solution space. A calculation gives eigenvalues and eigenvectors of rest point $M$ and $SM$ in the STV-ODE of order $n=4$ as:

	$\displaystyle\lambda_{M}$	$\displaystyle=-1,$	$\displaystyle\boldsymbol{R}_{M}$	$\displaystyle=(0,1,0,1)^{T};$
	$\displaystyle\lambda_{A1}$	$\displaystyle=\frac{2}{3},$	$\displaystyle\boldsymbol{R}_{1}:=\boldsymbol{R}_{A1}$	$\displaystyle=\bigg{(}-9,\frac{3}{2},-\frac{10}{3},-1\bigg{)}^{T};$
	$\displaystyle\lambda_{B1}$	$\displaystyle=-1,$	$\displaystyle\boldsymbol{R}_{B1}$	$\displaystyle=\bigg{(}4,1,\frac{80}{9},1\bigg{)}^{T};$
	$\displaystyle\lambda_{A2}$	$\displaystyle=\frac{4}{3},$	$\displaystyle\boldsymbol{R}_{3}:=\boldsymbol{R}_{A2}$	$\displaystyle=(0,0,-10,1)^{T};$
	$\displaystyle\lambda_{B2}$	$\displaystyle=-\frac{1}{3},$	$\displaystyle\boldsymbol{R}_{B2}$	$\displaystyle=\bigg{(}0,0,\frac{20}{3},1\bigg{)}^{T},$

where $\lambda_{M}$ and $\boldsymbol{R}_{M}$ correspond to the eigenvalue and eigenvector of $M$ and the rest to $SM$. The phase portrait for solutions of (1.20)–(1.23) is depicted in Figure 3. Note that $SM$ and $M$ are referred to as $SM_{2}$ (and $SM_{4}$) and $M_{2}$ (and $M_{4}$) in Figure 3 respectively to indicate that the fixed points are those for the $2\times 2$ (and $4\times 4$) system.

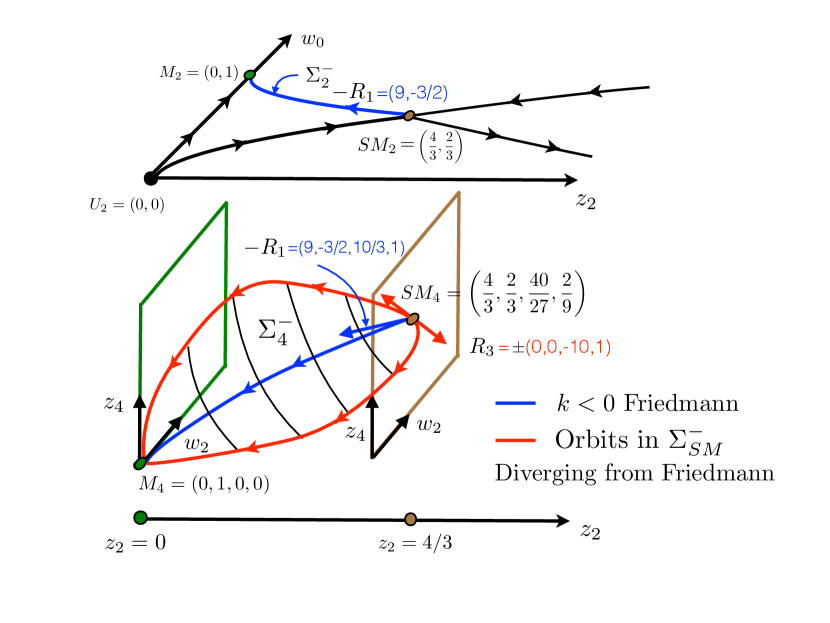
The time since the Big Bang gauge choice is assumed in Figure 3, so all elements of $\mathcal{F}$ agree with $k<0$ Friedmann at leading order, that is, they lie on the unstable trajectory taking $SM$ to $M$ in the leading order phase portrait associated with (1.20)–(1.21). This is denoted by $\Sigma_{SM}^{-}$ in Figure 3, with $\Sigma_{2}^{-}$ and $\Sigma_{4}^{-}$ specifying the unstable manifold for the $2\times 2$ and $4\times 4$ systems respectively. The phase portraits of Figures 1 and 3 are consistent because the first two components of $-\boldsymbol{R}_{1}$ give the direction of the trajectory which connects $SM_{2}$ to $M_{2}$ at level $n=1$ and the second two components represent the higher order corrections. The projections of the $k<0$ Friedmann solutions onto solutions of the STV-ODE of orders $n=1$ and $n=2$ are represented by the blue curves in Figure 3. Note that the presence of a second positive eigenvalue $\lambda_{A2}=\frac{4}{3}$ implies the unstable manifold of $SM$ intersects $\mathcal{F}$ in a two dimensional space of trajectories emanating from $SM$. We prove that only the eigensolution of $\lambda_{A1}$ corresponds to the Friedmann spacetime at order $n=2$. This immediately implies that there exist solutions in the unstable manifold of $SM$ which agree with a $k<0$ Friedmann spacetime at order $n=1$ but diverge from Friedmann at intermediate times. Since all solutions in $\mathcal{F}$ decay to $M$ as $t\to\infty$, this implies that solutions in the unstable manifold of $SM$ agree with $k<0$ Friedmann in the limits $t\to 0$, $t\to\infty$ and at leading order $n=1$, but which diverge, and hence introduce accelerations away from Friedmann, at intermediate times. By the Hartman–Grobman Theorem, nonlinear solutions correspond to linearized solutions in a neighborhood of a rest point, so solutions in the unstable manifold of $SM$ are determined by their limiting eigendirection $\boldsymbol{R}=a\boldsymbol{R}_{1}+b\boldsymbol{R}_{3}$ at $SM$, and hence we conclude that the magnitude of the acceleration away from Friedmann is measured by $\frac{b}{a}$, which can be arbitrarily large. We state this precisely in the following theorem.