Cosmic Core-Collapse Supernovae from Upcoming Sky Surveys
Abstract
Large synoptic (repeated scan) imaging sky surveys are poised to observe enormous numbers of core-collapse supernovae. We quantify the discovery potential of such surveys, and apply our results to upcoming projects, including DES, Pan-STARRS, and LSST. The latter two will harvest core-collapse supernovae in numbers orders of magnitude greater than have ever been observed to date. These surveys will map out the cosmic core-collapse supernova redshift distribution via direct counting, with very small statistical uncertainties out to a redshift depth which is a strong function of the survey limiting magnitude. This supernova redshift history encodes rich information about cosmology, star formation, and supernova astrophysics and phenomenology; the large statistics of the supernova sample will be crucial to disentangle possible degeneracies among these issues. For example, the cosmic supernova rate can be measured to high precision out to for all core-collapse types, and out to redshift for Type IIn events if their intrinsic properties remain the same as those measured locally. A precision knowledge of the cosmic supernova rate would remove the cosmological uncertainties in the study of the wealth of observable properties of the cosmic supernova populations and their evolution with environment and redshift. Because of the tight link between supernovae and star formation, synoptic sky surveys will also provide precision measurements of the normalization and history of cosmic star-formation rate in a manner independent of and complementary to than current data based on UV and other proxies for massive star formation. Furthermore, Type II supernovae can serve as distance indicators and would independently cross-check Type Ia distances measured in the same surveys. Arguably the largest and least-controlled uncertainty in all of these efforts comes from the poorly-understood evolution of dust obscuration of supernovae in their host galaxies; we outline a strategy to determine empirically the obscuration properties by leveraging the large supernova samples over a broad range of redshift. We conclude with recommendations on how best to use (and to tailor) these galaxy surveys to fully extract unique new probes on the physics, astrophysics, and cosmology of core-collapse explosions.
1 Introduction
A new generation of deep, large-area, synoptic (repeated-scan) galaxy surveys is coming online and is poised to revolutionize cosmology in particular and astrophysics in general. The scanning nature of these surveys will open the way for a systematic study of the celestial sphere in the time domain. In particular, ongoing and planned surveys are sensitive to the transient cosmos on timescales from hours to years, and to supernova flux limits down to and sometimes fainter. As we will see, these capabilities will reap a huge harvest in cosmic supernovae and will offer a new and direct probe of the cosmic supernova history out to high redshifts.
In the past decade, supernovae in nearby and distant galaxies have come to play crucial role for cosmology, via the use of Type Ia explosions as “standardizable” candles (e.g., Phillips, 1993; Riess et al., 1996). These powerful beacons are detectable out to very high redshift and thus reveal the cosmic expansion history for much of the lifetime of the universe; the stunning result has been the detection of the acceleration of the Universe and the inference that dark energy of some form dominates the mass-energy content of the cosmos today (e.g., Riess et al., 1998; Perlmutter et al., 1999; Astier et al., 2006; Wood-Vasey et al., 2007). The detection of large numbers of Type Ia supernovae over a large redshift range, and their use as cosmological probes, represents a major focus of future galaxy surveys (e.g., Wang et al., 2004).
While studies of supernova Type Ia (thermonuclear explosions) justly receive enormous attention due to their cosmological importance, there has been relatively little focus on the detection of the more numerous population of core-collapse supernovae. These explosions of massive stars show great diversity in their observed properties, e.g. including several varieties of Type II events, but also Types Ib and Ic events. Despite their heterogeneous nature, some core-collapse events may nonetheless provide standardized candles, via their early lightcurves whose nature is set by the physics of their expanding photospheres (Kirshner & Kwan, 1974; Baron et al., 2004; Dessart & Hillier, 2005, see below). Moreover, core-collapse events are of great intrinsic importance for cosmology, astrophysics, and particle physics. These events play a crucial role in cosmic energy feedback processes and thus in the formation and evolution of galaxies and of cosmological structure.
Synoptic surveys tuned for Type Ia events will also automatically detect core-collapse supernovae. Indeed, as survey coverage and depth increase, they will, for the first time, image a large fraction of all unobscured cosmic core-collapse supernovae out to moderate redshift. These photometric detections of supernovae and their light curves will shed new light on a wide variety of problems spanning cosmology, particle astrophysics, and supernova studies. Moreover, these data will “come for free” so long as surveys include core-collapse events in their analysis pipelines.
For example, Madau et al. (1998) already pointed out the link between the cosmic star formation history and the cosmic supernova history, and showed that when integrated over all redshifts, the all-sky supernova event rate is enormous, events/sec in their estimate. Upcoming synoptic surveys will probe most or all of the sky at great depth, and thus are positioned to observe a large fraction of these events. Consequently, these surveys will reveal the history of cosmic supernovae via directly counting their numbers as a function of redshift.
Already, recent and ongoing surveys have begun to detect core-collapse supernovae. However, to date, surveys have focused on Type Ia events, and thus core-collapse discovery and observation has been a serendipitous or even accidental byproduct of SNIa searches. As a result of these surveys, the supernova discovery rate is accelerating, and the current all-time, all-Type supernova count is since SN1006.111 Central Bureau for Astronomical Telegrams (2008); see also http://www.cfa.harvard.edu/iau/lists/Supernovae.html Thus core-collapse data is currently sparsely analyzed and reported in an uneven manner. This situation will drastically improve in the near future, when the supernova count increase by large factors, culminating in up to 100,000 core-collapse events seen by LSST annually. In this paper we therefore will anticipate this future, rather than make extensive comparison with the present data though we will make quantitative contact with current results.
Our work draws upon several key analyses. The thorough and elegant work of Dahlén & Fransson (1999) laid out the framework for rates and observability of cosmic supernovae of all types. Their work assembled a large body of supernova data and applied it to make rate and discovery predictions for the wide variety of star formation histories and normalizations viable at that time, with a particular focus on forecasts for very high redshift (out to ) observable by the infrared James Webb Space Telescope. Sullivan et al. (2000) estimated the rates for supernovae lensed by the matter distribution–particularly rich clusters–along the line of sight; these objects further extend the reach of infrared searches, and identified a possible supernova candidate from Hubble Space Telescope archival images of an intermediate-redshift cluster. Gal-Yam et al. (2002) made similar calculations of the infrared observability of supernovae, and identified additional events in archival data. Gal-Yam & Maoz (2004) and Oda & Totani (2005) presented forecasts for then-upcoming ground-based surveys. These studies considered all cosmic supernovae, but with a focus on Type Ia events, specifically with an eye towards revealing the Type Ia delay time as well as a parameterized characterization of the cosmic star formation history based on Type Ia counts. In addition, these first studies reasonably chose to emphasize near-term (i.e., now-completed or ongoing) relatively modest surveys, or on future space-based missions such as SNAP, with little to no study of the impact of large synoptic surveys. Moreover, while these works included dust extinction effects in host galaxies, but because of their focus on Type Ia events, they did not study the possibility of a redshift evolution in extinction (Mannucci et al., 2007).
We build on the important studies of Dahlén & Fransson (1999), Gal-Yam et al. (2002); Gal-Yam & Maoz (2004), and Oda & Totani (2005) in several respects: (1) we explore the promise of synoptic surveys and forecast the very large numbers of supernovae they will find; (2) we focus on less-studied core-collapse events; (3) we incorporate the (pessimistic) possibility of strong dust evolution of Mannucci et al. (2007) which is a dominant obstacle to observing massive star death at high redshifts; (4) we present a strategy for empirically calibrating the obscuration properties across a broad range of redshift by studying the evolution of the supernova luminosity function; and (5) we study the unique opportunities that become available with the large supernova harvest of synoptic surveys; in particular, we show how the cosmic supernova rate can be recovered based on core-collapse counts, without assumption as to its functional form.
Our goal in this paper is to explore the impact synopic surveys will make on core-collapse supernova astrophysics and cosmology. We summarize key upcoming surveys in §2. In §3 we review expectations for the CSNR, core-collapse supernova observables, and the effect of cosmic dust and its evolution. We combine these inputs in §4 where we forecast the core-collapse supernova discovery potential for upcoming surveys. We quantify in detail the strong dependence of the supernova harvest on the survey limiting magnitude, which we find to be the key figure of merit for supernova studies. We discuss some of the supernova science payoff in §6, and conclude in §7 with some recommendations for synoptic surveys.
2 Synoptic Surveys
Current and future sky surveys build on the pioneering approach of the Sloan Digital Sky Survey (SDSS; York et al., 2000). Following SDSS, these surveys will produce high-quality digital photometric maps of large regions of the celestial sphere. The powerful innovation the new surveys to extend the original SDSS approach into the time domain. Each program will scan part of their survey domain frequently, with revisit periods of days and in some cases even hours, and maintain this systematic effort throughout the survey’s multi-year operating lifespans. The result will be unprecedented catalogs of transient phenomena over timescales from hours to years. These surveys are thus ideal for supernova discovery and matched to supernova light curve evolution timescales; the result will be a revolution in our observational understanding of supernovae.
| Survey | Scan Area | SN Depth | Scan | Expected |
|---|---|---|---|---|
| Name | -band | Region | Operation | |
| SDSS-II | 300 | 21.5 | SDSS southern equatorial strip | 2005–2008 |
| DES | 40 | 24.2 | South Galactic Cap | 2011–2016 |
| Pan-STARRS | 30000 | 23 | of the Hawai’ian sky | 2010–2020 |
| LSST | 20000 | 23–25 | southern hemisphere | 2014–2024 |
The science harvest in the time domain depends on both the depth of the scans and their breadth across the celestial sphere. These scale with collecting area and sky coverage , respectively. Consequently, the figure of merit for scan power is the étendue . Forthcoming projects are designed to maximize this quantity.
The viability of supernova discovery, typing, and followup by large-scale synoptic surveys has now been tested by the SDSS-II supernova search (Frieman et al., 2008). This program extended SDSS (York et al., 2000) into the time domain, scanning at a day cadence, identifying and typing supernova candidates from photometric data in real time, and following up with spectroscopic confirmation. This survey will serve as a testbed for the larger future campaigns. It is thus very important and encouraging that SDSS-II has reported the discovery of 403 confirmed supernovae in the first two seasons of operation (Sako et al., 2008). The search algorithms and followup were focused on Type Ia events, for which light curves and spectra have been recovered over ; human input was used for supernova typing, but automated routines appear promising and will be essential for larger surveys. Follow-up spectroscopy (Zheng et al., 2008) yields accurate supernova and host-galaxy redshifts ( and ); host-galaxy contamination is found to be well-addressed by fitting and a principal component analysis.
Table 1 lists several major current and future synoptic surveys, and gives the values or current estimates of their performance characteristics. The values are derived from the survey detections for single visit exposures, which have been corrected shallower as noted above. SDSS-II (Frieman et al., 2008) is recently completed, as discussed above; we adopt an -band limiting magnitude of (J. Frieman, private communication). The Dark Energy Survey (DES; The Dark Energy Survey Collaboration, 2005) will push down to in -band; as we will see below, this will already enormously increase the supernova harvest. Finally, looking out farther into the next decade, Pan-STARRS (Jewitt, 2003; Tonry, 2003) and then LSST (The LSST Collaboration, 2007; Tyson, 2002) will introduce a huge leap in both sky coverage and in depth. These ambitious projects represent a culmination of the synoptic survey approach, and we will make a particular effort to examine their potential for supernova science.
For our analysis, we will characterize each survey with four parameters
-
1.
the survey supernova depth, i.e., single exposure limiting magnitude for supernova detection when used in scan mode; this is set by collecting area (and monitoring time)
-
2.
the total survey scanning sky coverage, i.e., solid angle
-
3.
the scan revisit time (“cadence”)
-
4.
the total monitoring time , which (for a single cadence) is proportional to the total number of visits
For a fixed survey design and lifetime, these parameters are not independent, since exposure time comes at the expense of sky coverage and number of visits.
There are numerous challenges and complexities in the process of extracting supernovae and their redshifts from surveys (and for sorting out their types; see, e.g., Dahlén & Goobar, 2002; Poznanski et al., 2007; Kim & Miquel, 2007; Kunz et al., 2006; Blondin & Tonry, 2007; Wang, 2007). Tonry et al. (2003) gives thorough discussion of these issues with emphasis on Type Ia events; see also Dahlén & Fransson (1999), Gal-Yam & Maoz (2004) and Oda & Totani (2005), and the SDSS-II papers (Frieman et al., 2008; Sako et al., 2008; Zheng et al., 2008).
Our simple survey parameterization cannot capture all of these subtleties, not do we intend it to; rather, we wish our treatment to provide a rough illustration of the surveys’ potential for core-collapse detection and science. Consequently, our parameter choices should be viewed as typical effective values, which may be different from (and weaker than) the raw survey specifications.
For example, supernova identification and typing requires knowledge of the light curve. Thus, one cannot only observe the supernova at peak brightness, but also follow it after (and ideally before). Tonry (2003) recommends following the supernova for least below peak brightness; we will adopt this value as well. Thus, the effective supernova detection depth is , where is the survey scan depth (i.e., depth for a single exposure).
Note also that some upcoming surveys (such as DES) will only repeatedly scan a fraction of the sky which they map; but only the scanned regions will host the discovery of supernovae and other transients. Also, some surveys (e.g., Pan-STARRS and LSST) envision multiple periodicities and associated limiting magnitudes; for simplicity we will here chose conservative depths for the values given in Table 1, to be consistent with the advertised scanning sky coverage. Thus one should bear in mind that in our analysis we have chosen the minimal parameterization one could use, which give only a simplified and idealized sketch of the real surveys. Given this, and the ongoing planning of future survey characteristics, our forecasts for the surveys’ supernova results should be understood as indicative of the order of magnitude expected, but not as high-precision predictions.
3 Core-Collapse Supernovae in a Cosmic Context
3.1 The Cosmic Core-Collapse Supernova Rate: Expectations
The total cosmic supernova rate (hereafter CSNR)
| (1) |
is the number of events per comoving volume per unit time in the emission frame (i.e., cosmic time dilation effects in the observer’s frame are not included). The total rate, and the various differential rates below, can of course be specialized to distinguish different groups of supernovae classified by intrinsic type and/or dependence on local environment.
The present data on high-redshift core-collapse supernovae are too poor to construct an accurate CSNR. But the CSNR is intimately related to cosmic star-formation rate (Madau et al., 1998). The connection is
| (2) |
where is the fraction, by mass, of stars which become supernovae, and is the average supernova progenitor mass (see Appendix A). A key point is that due to the short core-collapse progenitor lifetimes the two rates scale linearly, . The constant of proportionality depends on the initial mass function (IMF). If the IMF changes with time (or environment) this complicates the picture. In producing quantitative estimates we will follow most studies in assuming time-independent IMF. Thus the supernova/star-formation rate proportionality is a constant fixed for all time, namely (Appendix A).
Uncertainties in the cosmic rates for both supernovae and star-formation remain considerable. As illustrated in detail by (Strigari et al., 2005), the cosmic star-formation rate is known to rise sharply towards redshift . In this low-to-moderate redshift regime, the shape of the rate versus redshift is fairly well known, but as emphasized by Hopkins & Beacom (2006) the normalization remains uncertain to within a factor . At higher redshifts, the rate becomes even more uncertain, largely due to the paucity of data and also to uncertainties in our knowledge of the degree of dust obscuration. It is also worth noting that most studies to date directly or indirectly use massive stars as proxies for star formation. Consequently, the rate for cosmic massive star formation–and for cosmic supernovae–is less uncertain and IMF-dependent than the total rate.
To illustrate the effects of these uncertainties on the synoptic survey supernova harvest, we have adopted two possible CSNR forms. These appear in Figure 1, which shows the expected supernovae rate assuming a perfect environment (i.e. no dust extinction, etc). The solid curve in Figure 1(a) is the CSNR derived from the cosmic star-formation rate of Cole et al. (2001) with parameters fitted by Hopkins & Beacom (2006) (hereafter the “benchmark” CSNR). This rate sharply rises to a peak at , followed a strong but less rapid declines out to high redshift. To investigate the impact of the falloff from the peak, we also show in the broken curve an alternate CSNR due to current observational data fitted by Botticella et al. (2008) (hereafter the “alternative” CSNR). This rate also rise to redshift , though with a different slope; we somewhat arbitrarily set the alternative rate to a constant at where the data are unclear; in any case we will find that few events from this high-redshift regime will be accessible to the all-sky surveys which are our focus.
Synoptic surveys will measure several observables associated with cosmic supernovae: their numbers and location, and some portion of their light curves in different bands. Spectroscopic redshifts of host galaxies can also be determined (when visible; see §6.5). Using the number counts and redshift indicators, one can deduce an observed core-collapse rate, per unit redshift and per unit time and solid angle. This observed rate distribution directly encodes the CSNR via
| (3) |
where is the comoving volume and is the comoving distance out to redshift . The factor corrects for time dilation via .
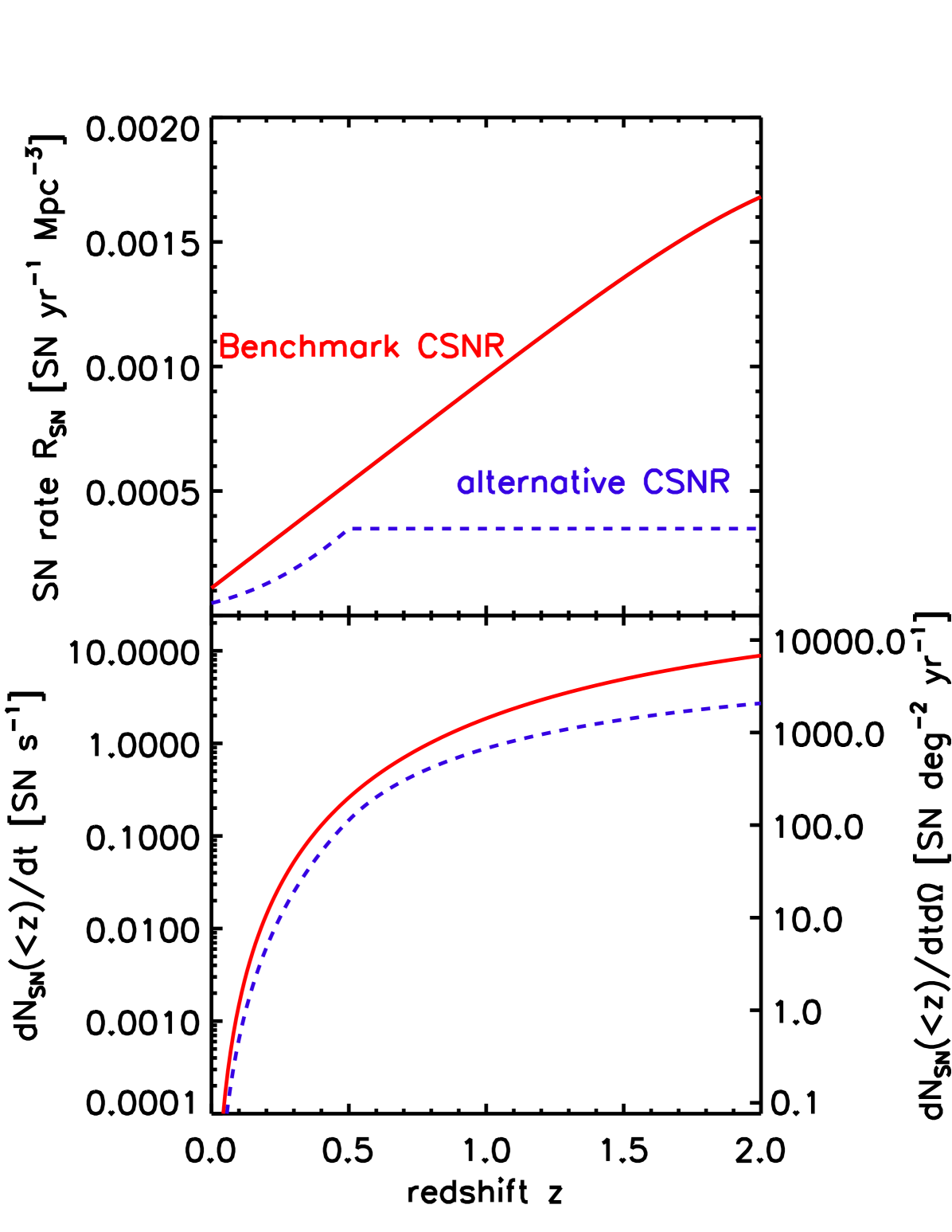
Figure 1(b) shows the all-sky cumulative frequency of cosmic supernovae for an observer at , i.e.,
| (4) |
These curves give the total rate of observed cosmic supernova explosions out to redshift for an idealized observer monitoring the entire sky out to unlimited depth and without any dust obscuration anywhere along the line of sight.
All of these idealizations will fail, some of them drastically, for real observational programs. Nevertheless, one cannot help but be tantalized by the enormous explosion frequencies indicated in Figure 1(b). With our benchmark CSNR, out to redshift , something like supernova explodes per second somewhere in the sky. Out to redshift , this rate increases to events/sec. Clearly, even with a small detection efficiency, synoptic surveys are poised to discover core-collapse supernovae in numbers far exceeding all supernovae in recorded history to date.
3.2 The Effect of Dust Obscuration
The enormous inventory of cosmic supernovae is not, unfortunately, fully observable even for arbitrarily deep surveys. In a realistic environment there are several factors which will hide the supernovae from us; dust extinction is one of the most important, and probably the most uncertain. Core-collapse supernovae mostly explode within regions of vigorous star formation which are thus likely to be dusty environments. Consequently, we expect that some core-collapse supernovae will be obscured to the point where they are not detected in synoptic surveys. The fraction of supernovae lost to dust obscuration, and particularly the possible redshift dependence of this extinction, represents a crucial systematic error which must be addressed before one can use survey data to infer information about supernova populations and their cosmic rates.
For the purposes of our present estimates of survey supernova yields, we follow the approach of Mannucci et al. (2007). These authors characterize losses due to dust extinction and/or reddening in the host galaxies via a fraction of undetected events at each redshift. This fraction could in principle differ for the various core-collapse types; for the present treatment we will assume it is the same for all such events. As core-collapse statistics become available from surveys, this issue can and should be revisited; more on this below. and in §5. The resulting fraction of detected supernovae is thus the complement , which measures the reduced supernova detection efficiency in the presence of dust. Expressed as an effective extinction for the supernova population at , we have .
Mannucci et al. (2007) estimate the fraction of missing supernovae by comparing the observed detections in the optical with those in radio and near-IR. They conclude that dust evolution is very strong; this becomes a dominant limitation to the discovery of core-collapse events at high redshift. In the local universe, Mannucci et al. (2007) find that the vast majority of the events occurring in massive starbursts (luminous infrared galaxies) are missed. Because these galaxies harbor only a small fraction of the local supernova population, the overall optically missing fraction at is estimated to be rather modest: . If, however, high-redshift star formation occurs in starburst environments (i.e., luminous and ultra-luminous galaxies, which are highly extincted; see e.g. Smail et al., 1997; Hughes et al., 1998; Pérez-González et al., 2003; Le Floc’h et al., 2005; Choi et al., 2006) then the fraction of missing events rises sharply with redshift. Multiwavelength observations of light from pre-supernova massive stars also supports the idea of increasing dust obscuration at high redshift. Adelberger & Steidel (2000) find that ultraviolet light from massive stars in galaxies is mostly reprocessed by dust into thermal submillimeter emission, so that the observable galaxy luminosities have .
Mannucci et al. (2007) estimate the portion of supernovae which will be “catastrophic losses” to severe extinction, and propose that the missing fraction can be described by a linear relation for the core-collapse supernovae for redshift z2. Thus, the fraction of the supernovae which remain optically detectable is for . At higher redshift, Chen et al. (2007) and Gnedin et al. (2008) argue that is small; they find limits consistent with for these redshifts.
We will smoothly match these two estimates, and adopt a fraction of the supernovae which can be detected after dust extinction of
| (5) |
For these values of , the effective extinction varies from at to at . In practice, we will find that cosmological dimming of supernovae beyond is itself so large that surveys up to and including LSST will see relatively few events, so that the details of the adopted dust model in this regime will not affect our conclusions.
The strong redshift evolution of dust obscuration in the empirical Mannucci et al. (2007) model deserves comment. From a physical point of view, the rise in dust losses towards high redshift implies that at earlier times, the birth environments of supernovae are significantly more enshrouded than those now. This interesting result itself deserves a deeper elucidation, one which will likely be easier to formulate and test in the presence of survey supernova data. From more practical point of view, our adoption of a model wherein dust losses grow rapidly with should yield conservative (or at least not optimistic) predictions for the supernova harvest at large redshifts. That is, if it turns out that host galaxy effects do not change rapidly with cosmic time so that the efficiency of supernova detection remains close to the high local value, then our rate predictions at would be boosted by a factor of .
Note also that as Mannucci et al. (2007) and we have defined it characterizes the observable portion of the ensemble of supernovae at a particular redshift. Implicitly, individual supernovae are treated as either detectable or not, i.e., dust effects are considered negligible or total; our calculation treats total, catastrophic losses of supernovae using this formalism. We separately include the effect of partial extinction due to dust, where the apparent magnitude of supernova is reduced but still visible, as discussed in the next section. Of course in reality, all supernovae will experience some level of extinction in their host galaxies, with the distribution of host-galaxy extinctions changing with redshift. A more detailed study of dust effects on supernovae (and uses of supernovae to quantify and calibrate these effects) would be of interest for further investigation; see discussion in §5.
3.3 Supernova Observability at Cosmic Distances
3.3.1 The Supernova Luminosity Function
Locally observations of core-collapse supernovae reveal diverse light curves, with a wide range in peak luminosity, and very different evolution after maximum brightness. The vast majority of supernovae discovered by synoptic surveys will lie at cosmological distances, and thus will be detectable mostly near their maximum luminosity. Thus we will focus on the observed distribution of peak brightness, and the timescales on which supernovae sustain it.
The distribution of peak absolute magnitude is given by the supernova luminosity function which may have a redshift dependence; we choose a normalization such that at any , , with this, we may write the cosmic supernova rate per absolute peak magnitude as
| (6) |
where here and throughout the possible redshift dependence of the luminosity function is understood.
Richardson et al. (2002) find the best-fit formulae for the supernova peak luminosity functions in -band for different types of supernovae based on their tabulation of 279 supernovae of all types, for which absolute magnitudes were available at peak brightness. Of these, there were 168 events of all core-collapse types: II-P,L,n and I-ab. For each type, Richardson et al. (2002) fit the observed -band absolute magnitude distributions with gaussian profiles, in some cases including two profiles where the data suggested “bright” and “dim” subclasses. Their results provide the basis for the luminosity functions used in this paper.
Note that we use the observed distributions rather than intrinsic, dust-corrected versions. Thus we automatically include the mean extinctions (ranging from for different types) found at low redshift. The redding effect due to dust (ranging from across different bands and redshifts) is also added, based on the information given by Kim & Lee (2007). As noted in the previous section, catastrophic losses of supernovae due to large extinction and its possible evolution at high redshift is treated separately via our parameter.
We adjust the Richardson et al. (2002) distributions in two ways. First, we converted from their Hubble constant of ot our adopted value . More importantly, we assume that each gaussian is a good representation of the data around the peak, but we do not allow the wings to extend arbitrarily far. Instead, we cut off the distributions at , where no data exist in the Richardson et al. (2002) sample. We introduce these cutoffs in order to avoid extrapolating to very rare, bright events which in a large survey could extend the redshift reach considerably. Below (§4.2) we discuss the effect of this cutoff and its effect on the predicted supernova redshift range.
3.4 Supernova Discovery in Magnitude-Limited Surveys
Surveys will discover supernovae monitor lightcurves in one or more passbands Here we will adopt the SDSS photometric system, which uses AB magnitudes (Fukugita et al., 1996).
The light curve of any supernova will suffer redshifting and time dilation effects. For passband we put
| (7) |
with the luminosity distance and is the usual distance modulus with pc. The dust extinction is included via the factor (eq. 5). The -correction accounts for redshifting of the supernova spectrum, and is discussed in Appendix C.
As noted above, at each redshift the effect of dust will be to obscure some fraction of supernovae. The remaining unobscured events will have apparent -filter magnitudes of . The expected distribution thus reflects the underlying distribution of absolute magnitudes . Since the Richardson et al. (2002) supernova luminosity function we use is in the -band, we need to find the corresponding -band magnitude in order to find the right corresponding number of supernovae; this transformation to is straightforward and is given by , where
| (8) |
is a color index which translates between the and magnitudes in the rest frame, and zeropoint correction is the correction for different zeropoint of the SDSS magnitude system and the Johnson magnitude system. For the spectral shapes we use the prescriptions of Dahlén & Fransson (1999) as described in Appendix C.
The absolute -band magnitude distribution of unobscured supernovae at redshift is , where is the luminosity function in -band as tabulated by Richardson et al. (2002). Therefore the distribution of a certain type of supernova apparent magnitudes in -filter is , Thus the fraction of all (unobscured) supernovae at which fall within the survey -band magnitude limit is a sum over the luminosity functions for all core-collapse types:
which is the cumulative fraction of supernovae whose absolute magnitude is brighter than
| (9) |
To develop some intuition, suppose the supernova peak brightnesses lie in a range , and ignore for now the effects of dust. Then for low redshifts such that the absolute magnitude limit from eq. (9) is fainter than , we can expect to see all supernovae, and . For these redshifts, we can study the entire supernova luminosity function and test whether it varies with redshift. On the opposite extreme, for high redshifts such that is dimmer than we can see no supernovae, so ; this then defines the survey redshift cutoff (for fixed ). Finally, for intermediate such that , we have ; over these redshifts the survey samples the bright end of the supernova luminosity function.
Both magnitude limit and dust extinction reduce the expected supernova detection, and do so independently of each other. Consequently, we can find the net supernova detection probability by simply taking the product of the individual factors:
| (10) |
Figure 2 shows the resulting detectable fraction of supernovae. The left panel shows the shape of for the and bands. At redshifts close to zero, which means that almost all supernovae are detected in the local universe. And it approaching to zero at high redshift, which reflects the fact that no supernovae can be detected at high redshift because of the survey deepness. Note that and bands are competitive for , but for higher , in -band drops a lot faster than those in -band especially around z 0.4, which is cause by the effect of -correction. The figure also shows that for higher , decays less rapidly. The right panel shows for different , using our adopted dust model (eq. 5). We see shows the same trend as except the detectable fraction is reduced due to dust and we can no longer observe all supernovae even in the local universe. It is also clear to see that going to fainter significantly boosts the detectable fraction at high redshift. For , is almost zero at redshift for both and bands. But going to , of the supernovae at redshift remain visible both the and bands.
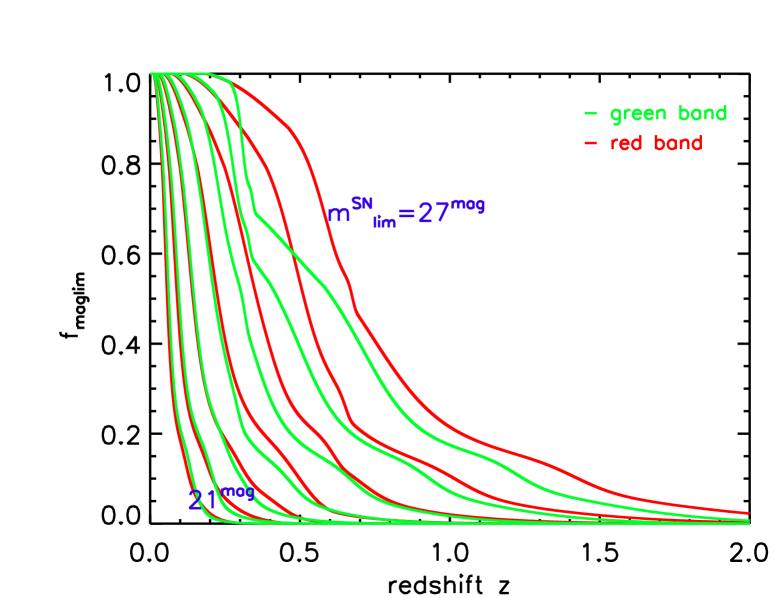
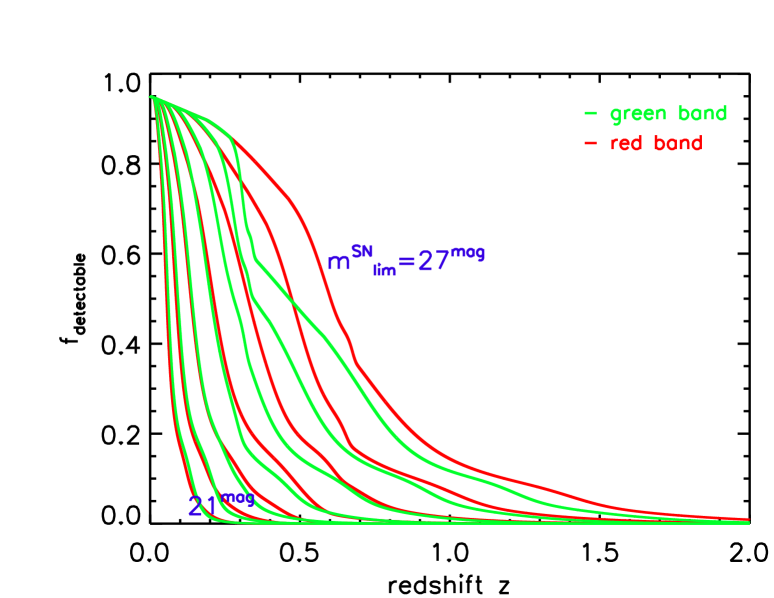
This means that deeper surveys (and/or scanning modes in which smaller areas are scanned more deeply) will probe supernovae out to much higher redshifts. Deep survey modes will also probe a much wider regime of the supernova luminosity function and light curves over a broad range of cosmic epochs, thus testing for redshift evolution in supernova properties. The clear lesson is that the scan is critical in determining the quality and reach of the supernova science. In particular, we urge that scans strategies include modes which push deeper than the all-sky depth.
3.4.1 Supernova Light Curves
The observed population of core-collapse supernovae shows a broad range of timescales and time histories in their decline from peak brightness (e.g., Doggett & Branch, 1985; Leibundgut & Suntzeff, 2003). The amplitude and time behavior of these curves encodes a wealth of information about the underlying physics of the supernovae as well as their interaction with the circumstellar and interstellar medium.
Empirically, light curves broadly fall into phenomenological categories, those whose magnitudes decline in a relatively steep, linear way (Type II-L) and those which linger near peak brightness with a relative plateau in magnitude (Type II-P). Patat et al. (1993) compiled 51 Type II light curves, and analysis in Patat et al. (1994) showed that plateau-type supernovae typically decline from peak brightness at rates which vary the range days, while linear-type events typically have days. Unfortunately, the lightcurves available at the time of these studies were poorly sampled near the peak itself, where the behavior is most critical for our purposes.
Fortunately, subsequent data, particularly using Swift, gives a clearer picture of the early light curves for a few events. For plateau event SN 2005cs, data in Pastorello et al. (2006) show that days after peak brightness, the supernova dimming was strongly depending on passband: , , , and . Another Type II-P event, SN 2006bp, after days declined by in , but within errors was essentially constant in and (Dessart et al., 2008). For Type Ib, the recent event SN 2008D was seen from shock breakout (Modjaz et al., 2008); after dropping from this brief initial outburst, the flux increased for days to a maximum. Afterwards, the brightness decline rates lengthen with wavelength, with a drop of after days in -band, but after about 15 and 20 days in and respectively.
These multicolor data show that brightness decline in and longer passbands comparable to if not slower than the typical range of found in Type Ia events (Phillips, 1993). This implies that surveys timed for Type Ia discovery will automatically be well-suited and possibly even better-sampled for core-collapse events. In particular, we will find below that the and also passbands are the most promising for survey supernova detections. Thus, if cosmic supernovae follow the behavior of these local events, we expect that the light curves will remain within, e.g., of peak brightness (a factor 1.5 in flux) for a timescale of at least a week. In some cases this timescale will be longer, and possibly also with detections in the rising phase.
For synoptic surveys to detect core-collapse supernovae near their peak brightness, the cadence needs to be shorter than the (observer-frame) brightness decline time. Thus weekly revisits are sufficient for marginal detections, and cadences of days will often see the event three or more times. In the cases of plateau events, the supernova should remain near peak brightness for many such revisit times. Furthermore, due to cosmological time dilation effects, the observed brightness decline timescale is increased by a factor of , which extends the detection window and offers a greater opportunity to recover a well-sampled lightcurve. Also, we see that color evolution is not strong in and bands. The UV and blue do fade more rapidly, and the supernova reddening depends on the type. For events where bluer rest-frame colors are available, this might be a useful means of photometrically determining supernova type.
4 The Cosmic Core-Collapse Supernova Rate: Forecasts for Synoptic Surveys
In this section we will work out general formalism for supernova observations by synoptic surveys. We then apply this formalism to specific current and proposed surveys
4.1 Connecting Cosmic Supernovae and Survey Observables
4.1.1 General Formalism
It is useful to define a differential supernova detection rate per unit redshift, solid angle, and apparent magnitude in -band:
| (11) |
This expression adds the effects of supernova luminosity (cf eq. 6) and of dust obscuration (eq. 5) to the ideal rate of eq. (3). Throughout, we will for simplicity refer to the entire core-collapse supernova population, but the formalism could equally well distinguish the various core-collapse types, and compute the rates of each. An example of such a treatment is the Scannapieco et al. (2005) study of the rate and detectability of pair-instability supernovae.
The differential rate in eq. (11) relates the observables in a synoptic survey to underlying properties of cosmic supernovae. As such, a wealth of information can be recovered by a good statistical sample of supernovae over a redshift range: one probe different terms and their underlying physics. For example, at fixed , the range of observed supernova magnitudes in -band probes the supernova peak luminosity function at magnitudes . Comparing these results at different redshifts with local determinations can reveal any redshift- and/or environment-dependence in the core-collapse supernova luminosity function.
Another aspect of cosmic supernovae probed by synoptic surveys, and central focus of this paper, is the cosmic supernova rate. Whereas the supernova luminosity function can be determined from the distribution of supernova magnitudes at the same redshift, the cosmic supernova rate comes from the distribution of supernova counts across different redshifts. The observed differential rate for supernovae of all magnitudes in the -band is
| (12) |
Note that this is the idealized rate of eq. (3) reduced by the detection in -band .
One can get a sense of the orders of magnitude in play via the definition of a dimensionful scale factor
| (13) | |||||
| (14) | |||||
| (15) |
We may then define a dimensionless distance , with the Hubble length, and write
| (16) |
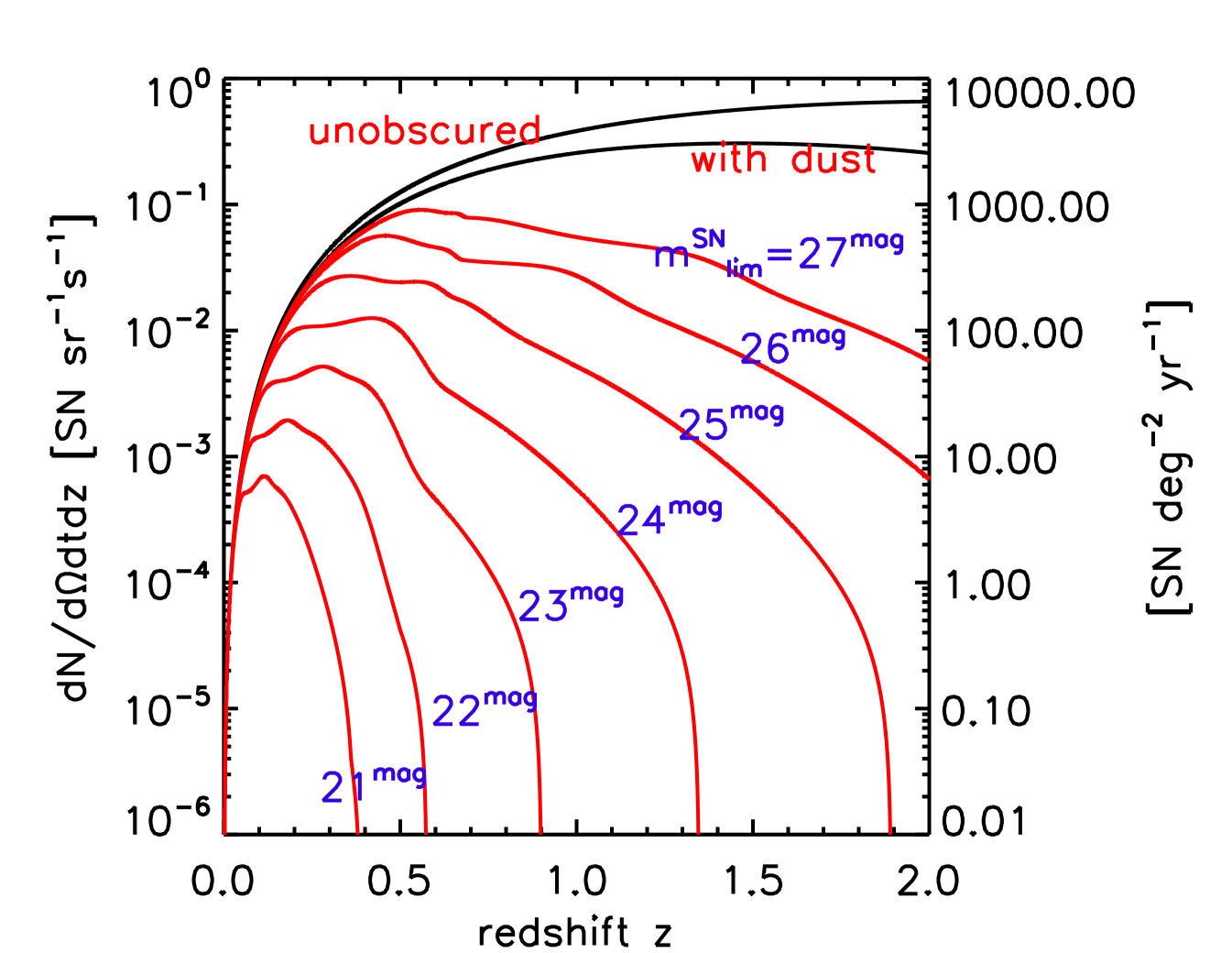
Figure 3 plots the observed supernova rate per solid angle in -band. For comparison, we show the idealized cases of and , as well as realistic cases in the presence of dust and with different . The amplitudes of the curves in Figure 3 confirm the large numbers of events expected from eq. (13).
The shapes of the curves can also be readily understood. At low redshifts, the surveys see most of the supernovae that occur–i.e., the entire luminosity function is sampled; cf Figure 2. Hence at small , the supernova sample is simply limited by the cosmic volume within : Thus the detection rate initially rises quadratically with ; this volume effect is essentially independent of survey magnitude limit, as we see by the overlap of the curves in this regime.
In the high redshift limit, several effects act to suppress supernova detectability. At , rapidly saturates at the comoving horizon scale, and nearly all observable cosmic volume is sampled; in this regime, the volume factor decreases as . In addition, time dilation effects become large and add another factor of . For these reasons, even the idealized (unobscured, ) rate drops. Moreover, in some models (such as that of Cole et al., 2001), the CSNR itself is intrinsically expected to drop after a peak, perhaps somewhere in the range . On top of this, the effects of dust obscuration become large at and removes further supernovae in this range. Finally, a finite survey magnitude limit truncates still more events at high .
The combination of the low-redshift rise and high-redshift drop acts to create a peak in supernova detectability. The position of the peak is sensitive to the CSNR itself, and the details of dust obscuration. But the peak position and amplitude are also both very sensitive to the survey magnitude limit; both rise sharply as survey depth increases. This illustrates a key conclusion which will be manifest in several other ways below: for discovery of core-collapse supernovae at high redshifts, the most important aspect of a synoptic survey is its limiting magnitude; investment in deep scan modes ( mag) will reap substantial rewards.
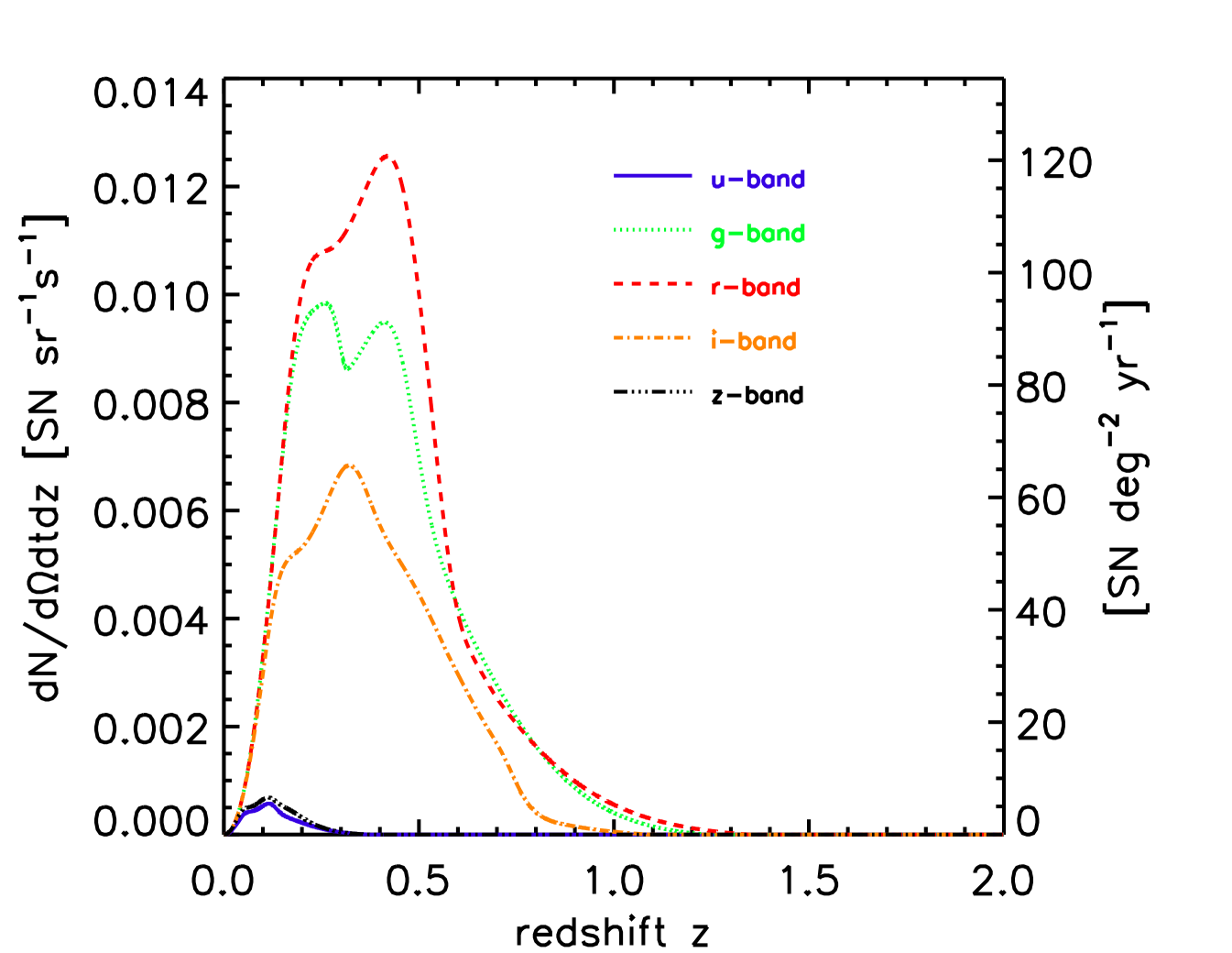
Figure 4 shows the same supernova rate redshift distribution as in Fig. 3, but for the five passbands with SDSS filters and efficiencies. For each band we fix . We see that the discovery rate is the highest in for essentially all redshifts, with -band counts very nearly the same except around the peak at . The relative smallness of the counts in other bands traces back predominantly to low detector efficiency in and , and redshifting effects for . The upshot is that for synoptic surveys, and bands are (in that order) clearly the most promising for supernova search.
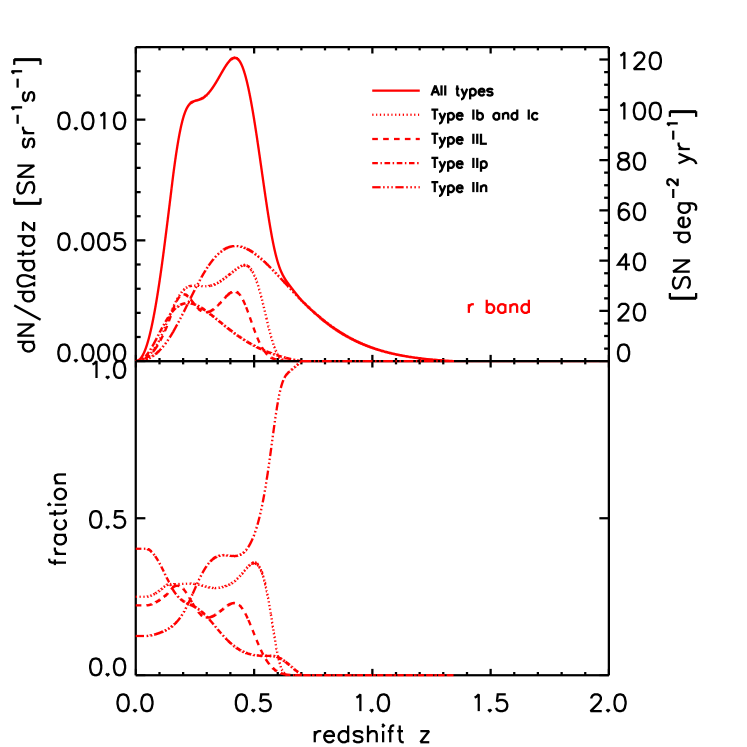
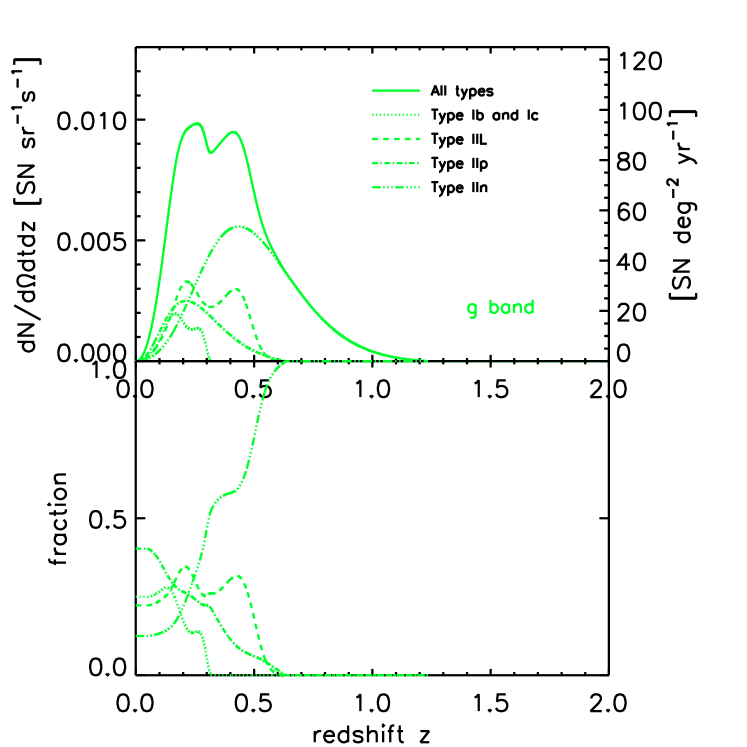
We have thus far shown the total supernova rate redshift distribution, summed over all core-collapse subtypes. Figure 5 illustrates how the different subtypes contribute to the aggregate. Here we fix and show results for the and bands. It is worth recalling that we have assumed the low-redshift Richardson et al. (2002) determination of luminosity functions and type distributions holds for all redshifts. In this scenario, we see that in both bands, Type IIn events give the largest contribution to the signal at , and totally dominate the counts at . This is expected, since it is the intrinsically brightest core-collapse subtype. Thus the redshift reach of supernova discovery (and associated results such as the CSNR) in synoptic surveys will depend sensitively on nature Type IIn events at . It will thus be crucial to determine whether these events show evolution in their luminosity function and/or relative fraction of core-collapse events with redshift (e.g., via metallicity effects). Also, it is worth noting that the Richardson et al. (2002) luminosity function we have used is relatively narrow. As noted recently by Cooke (2008), some Type IIn events have now been observed with luminosities far above the range of values we consider. If so, then the redshift range of synoptic surveys could thus extend significantly further than in our estimates.
Figure 5 further predicts that the other core-collapse types should have observably distinct redshift ranges in different bands, again assuming no evolution in luminosity function or type distribution. The upper panels of Fig. 5 show the individual subtype detection rates, as well as their sum. Type II-L events have simlilar behavior in both and bands, peaking at then rapidly dropping off. Although Type II-P events are the largest core-collapse subtype in the Richardson et al. (2002) sample, they are also by far the intrinsically dimmest, fainter than the other types. We thus find that Type II-P have a smaller redshift range than Type II-L and IIn events. The counts and redshift range of Type Ib and Ic events are notably different in the two passbands. This traces to the effects of UV lineblanketing which removes blue flux; thus at high redshift the -correction first shifts photons out of the band, with the -band signal surviving until higher redshift. Note also that the “bright” and “normal” Type Ib and Ic events lead to the double-peaked structure in their redshift distribution.
The lower panels of Fig. 5 shows our forecast for subtype fraction detected as a function of redshift, i.e., the ratio of each subtype rate to the total. At , the subtype fractions go to the observed local values we have adopted from Richardson et al. (2002), as required by our model design. For , we see that all subtypes make significant contributions tot the total, and thus for this redshift range, the sharp rise in the total detection rate (top panel) is due to contributions from all subtypes. The features around the maximum in the total rate () are due to the interplay between the rise of the Type IIn events and the successive dropout of the other types. Finally, we see that for , Type IIn events essentially completely set the total rate.
Because the highest-redshift detections will be dominated by Type IIn events, the nature of and evolution of this subtype will play a crucial role in setting the high-redshift impact of surveys for core-collapse events, as also pointed out by Cooke (2008). As we have noted, intrinsic evolution of the Type IIn fraction of core-collapse events would directly change–and be written into–the high-redshift signal. But at present, the uncertainties are very large even when evolution issues are set aside. Namely, published data are as yet very uncertain concerning the local, fraction of core-collapse events which explode as Type IIn. Our forecasts use the Richardson et al. (2002) sample which finds 9 Type IIn events out of 72 core-collapse events, for a fraction of 12.5%. However, this discovery fraction are very uncertain. For example, the prior work of Dahlén & Fransson (1999) compiled their own core-collapse discovery statistics, and adopted a Type IIn event fraction of , while noting that Cappellaro et al. (1997) recommend a Type IIn fraction of . Because the high-redshift core-collapse detections will be dominated by Type IIn events, if these values better reflect the intrinsic fraction, this would dramatically reduce our predicted detection rates for by factors of , and thus also reduce the maximum redshift at which core-collapse events can be seen in surveys. Clearly, the small numbers available when all of these compilations were made render the Type IIn fraction estimates uncertain; indeed, to a lesser extent the estimates for the more common core-collapse types suffer similar problems.
In light of the uncertainties in the Richardson et al. (2002) and prior compilations, it is worth noting that considerably more supernova data already exists. A detailed, systematic study of the luminosity function and intrinsic subtype fractions of local events would be of the utmost value for forecasts of the sort we have presented. Moreover, precise and accurate local measurements will play an essential role as a basis of comparison for the future medium- to high-redshift data, in order to empirically probe for evolution within and among the core-collapse subtypes.
4.1.2 Unveiling the Cosmic Core-Collapse Supernova Rates
As noted above, synoptic surveys will revolutionize our understanding of the CSNR because they will directly determine the rate through counting. We now are in a position to determine the supernova counts for realistic (magnitude-limited, dust-obscured) surveys. Using these, we can demonstrate how the CSNR can be extracted. We can further determine its statistical uncertainty and the impact of survey depth and sky coverage.
Consider a survey with scan area and limiting magnitude , the total number of supernovae seen in -band in time , in a small redshift bins of width centered around is
| (17) | |||||
| (18) |
Thus we see that the cosmic supernova rate is directly encoded in our binned data. This means we can use the binned data to extract the supernova rate:
| (19) |
this result is a major goal of this paper. Physically, we see that as we accumulate supernovae, i.e., as fills out the redshift range accessible to the survey, we obtain an ever better measure of the SN rate.
We can also compute the statistical uncertainty in the CSNR derived from counts in surveys. The statistical error arises from the counting statistics in the supernova number. Expressing this as a fractional error, we have
| (20) |
But from eq. (18), we see that scales linearly with the product of detected fraction and survey sky coverage, as well as monitoring time and redshift bin width. Thus we find the CSNR statistical error should scale as
| (21) | |||||
| (22) |
Consequently, for a fixed redshift bin size , the CSNR accuracy grows with the product , and implicitly with via the detection fraction. Thus survey sky coverage and magnitude limit (i.e., collecting area) enter together, and we see the payoff of a large survey étendue.
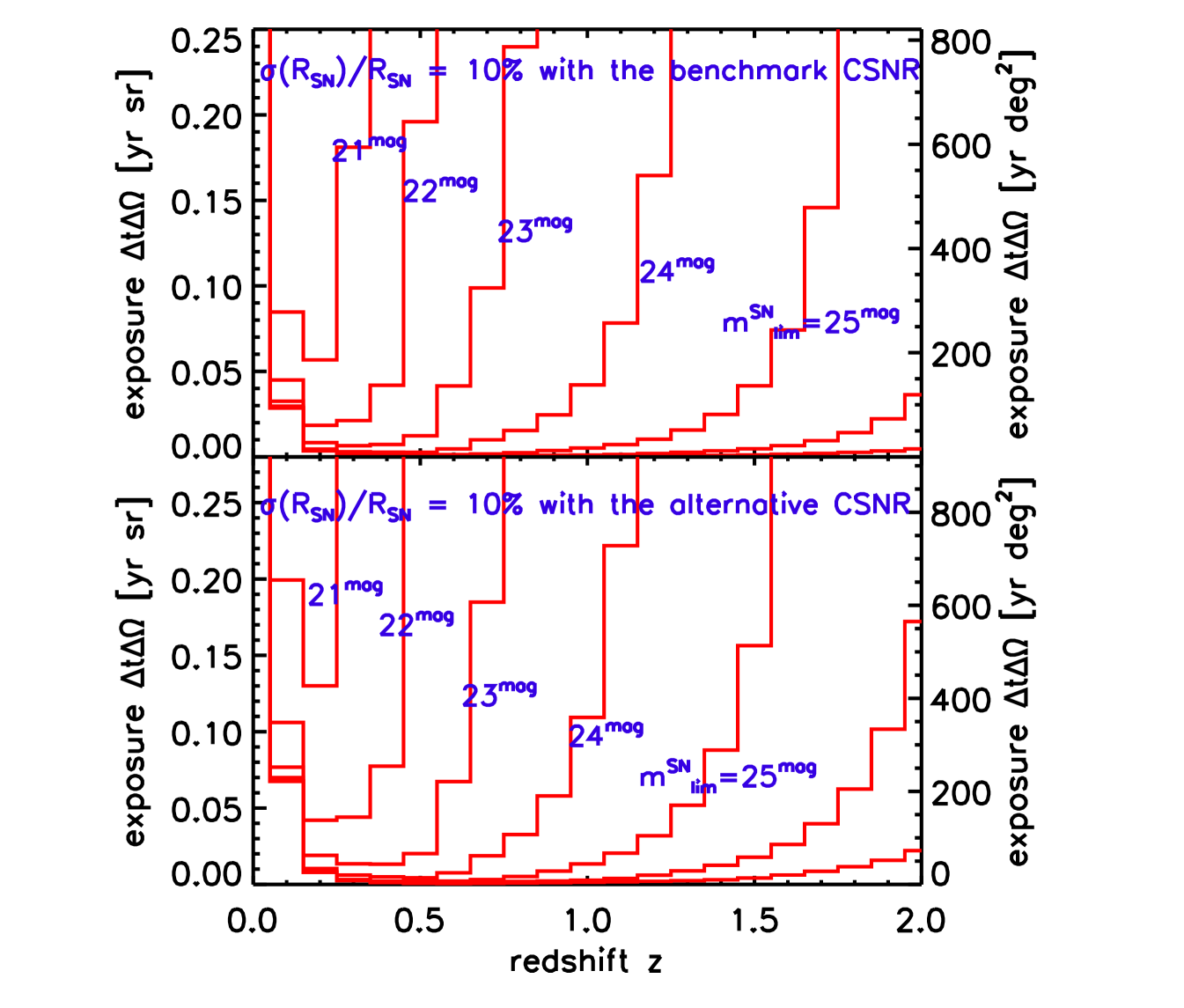
Thus, we can find the survey properties. needed to achieve any desired precision in the CSNR at some redshift . For a fixed and thus , monitoring time and sky coverage enter together as the product . Figure 6 shows the needed monitoring time to measure the CSNR to a statistical precisions of , and with different survey in -band. In both panels we choose for the redshift bin size. The two panels show our baseline and alternative CSFR. From these figures we can see that these two different adopted CSNR behaviors both yield very similar results for the survey CSNR detectability.
Again the shapes of the curves can be understood. As shown in eq. (21), that the precision at each bin scales inversely with the supernova differential redshift distribution as . Not surprisingly therefore, the least monitoring is needed to measure the CSNR for near the peak in the redshift distribution On the other hand, redshifts in the high- and low-redshift tails of require increasing monitoring, eventually to the point of unfeasibility.
Figure 6 makes clear that increasing brings a huge payoff reducing the needed monitoring . To achieve a precision at redshift , the monitoring becomes about 1000 times smaller in -band if we increase from to . Clearly, for any survey, increasing will drastically shorten the observing time needed for the high redshift supernovae. In practice, given fixed survey lifetimes, this means that sets the maximum redshift reach over which the survey may determine the CSNR (via eq. 9).
4.2 Forecasts for Synoptic Surveys
| Survey | Expected Total 1-year | SNII Redshift |
|---|---|---|
| Name | SNII Detections | Range |
| SDSS-II∗ | 0.03 0.37 | |
| DES | 0.06 1.20 | |
| Pan-STARRS | 0.01 0.89 | |
| LSST | 0.01 0.89 |
Note: ∗Reflects SDSS-II supernova scan season of 3 months per calendar year.
For a given survey with a fixed scanning sky coverage , we can determine the total number of supernovae expected in each redshift bin. We can also forecast the accuracy of the resulting survey determination of the CSNR. Namely, we can turn our sky coverage–monitoring time result (Figure 6) into a specific prediction for the needed time to determine the CSNR to a given precision. In practice, this amounts to a determination of the redshift range over which different surveys can measure the CSNR. Our detailed predictions appear in Appendix B; here we summarize the results.
Several main lessons emerge from considerations of specific surveys. When Pan-STARRS and LSST are online, these surveys will collect a core-collapse supernova harvest far larger than the current set of events ever reported. This alone will make synoptic surveys a transformational point in the study of supernovae.
Moreover, synoptic surveys will detect core-collapse events over a wide redshift ranges. Table 2 summarizes the supernova redshift ranges correspond to the most likely of the surveys. The total supernova harvest depends sensitively on the survey depth, and in Appendix B the sensitivity to is shown. To determine the redshift ranges shown in Table 2, we set an (arbitrary) lower limit on the number of total supernova counts at . We choose a lower redshift limit such the cumulative survey supernova count in one year is . Similarly, the upper limit is set by is the number of supernovae detected within redshift within a year.
As seen in Tables 2 and 3, the future surveys will find abundant supernovae over a wide redshift range. At low redshifts, the surveys will detect nearly all of the supernovae within the nearby cosmic volume accessible in their sky coverage. So surveys with a large , such as LSST and Pan-STARRS, have which does not depends on . For DES, is not as large, so that the number of supernovae brighter than does not accumulate to =10 until =0.081. But for depths fainter than , the survey does become volume-limited and the supernova counts accumulate to 10 at the same redshift. The upper limit of the redshift depends not only on sky coverage but also survey depth. For planned survey depths, DES will gather core-collapse supernovae to about ; LSST will extend to , and could go further in modes with smaller sky coverage but deeper exposure.
The large supernova counts and wide redshift ranges together mean that surveys will, by direct counting, map out the CSNR to high precision out to high redshifts. Future surveys should easily achieve 10 statistical precision for the CSNR for redshifts around which the survey’s counts peak. We see that, with , LSST will reach out to , presuming that the relative fraction of the brightest, farthest-reaching events (of Type IIn and Ic) do not evolve with redshift. If so, then by direct counting future survey should witness the sharp CSNR rise. With deeper exposures and corresponding increases in redshift reach, surveys could begin to test for the behavior of the CSNR above , a regime that is currently poorly understood.
Both the survey yields of supernova discoveries, as well as their redshift ranges, are strong functions of survey depth. As shown in Table 3 of Appendix B, each magnitude increase in survey depth yields a large enhancement (a factor ) in total supernova counts. This in turn leads to large enhancements in redshift range, and thus in the range over which the CSNR is measured. As shown in Appendix B, increased monitoring time needed to achieve higher will come at some cost, though this will be partially offset by the higher supernova yield in a deeper exposure. Finally, for the large population of low-redshift supernovae, deeper surveys will lead to better lightcurve determination, allow for a more accurate photometry over a larger brightness range and thus longer timescales.
As noted in §3.3.1, our fiducial results are for supernova peak magnitudes whose luminosity functions (each of which is one or two gaussians for each core-collapse type) are nonzero only within away from the mean. This arbitrary cutoff is meant as a compromise which shows the effect of nonzero width of the luminosity functions, without extrapolating too far into the tails in which there is as yet no data. To give a feel for the sensitivity of our results to the assumed luminosity function width we repeated our analysis for luminosity functions with larger and narrower ranges, (but with fixed observed intrinsic ). We find that the total supernova counts vary less than 0.88% when ranges from to ; this insensitivity reflects the fact that the bulk of supernova counts are from events near the means of the distribution. One the other hand, we found that the maximum observed supernova redshift (and thus the depth to which one can probe the CSNR) is very sensitive to the choice of . For example, the LSST maximum supernova redshift in 1 year is for our fiducial choice of , as seen in Table 2. On the other hand for and , we find and 1.06, respectively. Here rare, intrinsically bright events determine the redshift reach, and the deeper the luminosity function reaches into the bright-end tail, the larger the resulting . Thus we would expect the intrinsically brightest events, of Type Ibc and Type IIn, to give the greatest redshift reach. Indeed, Cooke (2008) has recently illustrated how Type IIn events can be mapped out to by ground-based 8 meter-class telescopes.
Of course, all of our forecasts assume that the luminosity functions of each supernova type, and the relative frequencies among the supernova types, all remain unchanged at earlier epochs. However, it is entirely plausible and even likely that these properties could evolve, e.g., with metallicity and/or environment. These effects are likely to be crucial in determining the true redshift reach of future sky surveys, and thus predictions such as ours will improve only as real supernova data becomes available with good statistics at ever-increasing redshifts, and one can directly constrain and/or measure evolutionary effects. Moreover, the relatively small sample sizes available to Richardson et al. (2002) could well lead to underestimates of the true range of luminosities of each type. For example, (Gezari et al., 2008) very recently report of an unusually bright Type II-L event, SN 2008es, with peak magnitude , far outside of the absolute magnitude range we have adopted for this subtype.
Indeed, the enormous statistics gathered by future surveys will allow for cross-checks and empirical determination of other evolutionary and systematic effects. A major such effect is dust obscuration, to which we now turn.
5 Dust Obscuration: Disentangling the Degeneracies and Probing High-Redshift Star-Forming Environments
The loss of some supernovae due to dust obscuration must be understood accurately and quantitatively in order to take full advantage of the large data samples of supernovae which are detected. As noted above in §3.2, currently we have very limited knowledge of supenova extinction and particularly its evolution, and most of what is reliably known is based on empirical studies of supernova counts. Precisely for this reason, future surveys offer an opportunity to address this problem in great detail by leveraging the enormous numbers of supernovae of all types, seen over a wide range of redshifts and in a wide range of environments. Here we sketch a procedure for recovering this information.
Future surveys will produce well-populated distributions of supernovae; these encode information about extinction and reddening due to dust. Specifically, in redshift bin around one can measure, often with very high statistical accuracy, the apparent magnitude distribution for each subtype of core-collapse events. These distributions can be made for all bands, but as we have shown, detections and/or light curve information will be most numerous in and bands; we will focus on these for the purposes of discussion. Within a redshift bin, the distance modulus is fixed, and the light curve and associated -correction should reflect intrinsic variations within the core-collapse subtype.
Thus, for a given core-collapse subtype and redshift , one can construct histograms of and peak magnitudes. From redshift and supernova type, one can compute the distance modulus and -correction, and use these to infer, for each event, the dust-obscured peak magnitude where is the intrinsic peak magnitude for the event, and is the extinction for this event in its host galaxy. By comparing two passbands we can also evaluate colors, for example , where is the reddening. In general, within a redshift bin we expect the and to vary on an event-by-event basis, reflecting the properties of dust along the particular line of sight through the particular host galaxy.
Invaluable insight into these issues comes from the Hatano et al. (1998) analysis of extinction in observation of local supernovae. These authors argue that the data are consistent with very strong dependence of extinction with the inclination of the host galaxy; this alone guarantees that must vary strongly from event to event even within subtypes. Hatano et al. (1998) also argue that the variation of dust column with galactic radius also suggests that extinction is responsible for the paucity of supernovae at small radii. (Shaw, 1979). Finally, Hatano et al. (1998) also point out that core-collapse events are more extincted than Type Ia events because the Ia’s have a higher scale height and thus are more likely to occur in less extincted regions.
On an event-by-event basis, intrinsic light curve and color evolution are degenerate with dust evolution. However, the large sample size may allow for a physically motivated empirical approach to lifting this degeneracy. If on theoretical grounds we can assume that at least one core-collapse subtype has negligible intrinsic evolution in its lightcurve, then for that subtype and are effectively known and moreover are constant across events in a particular redshift bin. In this case, the apparent magnitude and color distributions can be directly translated into distributions of extinction and reddening. By comparing these distributions (or e.g., their means and variances) across different redshifts, one directly probes dust evolution.
Moreover, if one can use one core-collapse subtype as an approximate “standard distribution” from which to extract dust properties, one might press further by assuming that other core-collapse events will be born in similar environments and thus encounter similar extinction and reddening. One can thus use the empirically determined dust evolution to statistically infer the degree of intrinsic lightcurve variation in the other core-collapse subtypes.
If subtype can be firmly established, comparison of magnitude distributions of different core-collapse subtypes allows for a purely empirical approach. namely, one can compare the evolution of the magnitudes distributions of different subtypes. One could first provisionally treat each supernova subtype as a “standard distribution” with no intrinsic evolution; then for each subtype one would infer dust extinction and reddening at each redshift. It is reasonable to expect that the different subtypes sample the same dust properties, as long as the host environments are not systematically different for the different subtypes (all of which arise in massive-star-forming environments). Indeed, Nugent et al. (2006) have performed such an analysis to use colors of Type II-P events to infer reddening for events out to .
A comparison of the dust extinction inferred the different subtypes amounts to a test for intrinsic variation. With information from multiple subtypes, it may be possible to isolate dust effects common to all, and intrinsic variation peculiar to each subtype. For example, if one subtype distribution evolves significantly more than another (e.g., one subtype variance grows more than another) then the difference in variance must be intrinsic, and that the lesser variance is an upper limit to the variance due to dust effects.
The ability to empirically measure extinction depends on the intrinsic width of the distribution, and on surveys’ ability to probe this distribution. At low redshift, Hatano et al. (1998) find a wide () range of extinctions, much of which they attribute to inclination which will remain an issue at higher redshift. On the other hand, as a given survey pushes to higher redshift, progressively less of the distribution is observable. For the case of LSST, we see in Fig. 10 that with the least obscured events are visible out to redshift , while those which have suffered of extinction would correspond to the curves, which reach to about . Thus over this shallower redshift range, extinction can be probed in detail, but with a narrowing observable range at higher redshift.
If future surveys can empirically determine effects of dust evolution, this would not only remove a major “nuisance parameter” for supernova and cosmology science, but also gain information of intrinsic interest. Namely, we will learn about the cosmic distribution and evolution of host environments of supernovae and thus of star formation.
6 Discussion
The large amount of core-collapse supernovae observed by synoptic surveys will yield a wealth of data and enormous science returns. Here we sketch some of these.
6.1 Survey Impact on the Cosmic Supernova and Star Formation Histories
As we have indicated in the previous section, synoptic surveys will determine cosmic core-collapse supernova rate with high precision out to high redshifts. Moreover, with the large number of supernova counts, and with light curves and host environments known, the total cosmic core-collapse redshift history can be subdivided according to environment and/or supernova type. For example, with photometric data alone one can determine to high accuracy correlations between supernova rate and host galaxy luminosity and Hubble type. One can compare supernova rates in field galaxies versus those in galaxy groups and clusters. Using galaxy morphology one can investigate correlations between supernovae and galaxy mergers. With the addition of spectroscopic information one can also search for correlations with host galaxy metallicity.
The CSNR is also tightly related to the cosmic star-formation rate. Therefore with the high precision CSNR, and assuming an unchanging initial mass function, one can make a similarly precise measure of the cosmic star-formation rate. On the other hand, one can test for environmental and/or redshift variations in the initial mass function, by comparing the supernova rates based on direct survey counts with the star-formation rates determined via UV and other proxies.
In addition to core-collapse explosions, synoptic surveys will of course by design also discover a similarly huge number of Type Ia supernovae. Thus the Type Ia supernova rates can be compared to those for core collapse events. As has been widely noted (e.g., Gal-Yam & Maoz, 2004; Watanabe et al., 1999; Oda & Totani, 2005; Scannapieco & Bildsten, 2005, and references therein) this will yield information about the distribution of time delays between the core-collapse and thermonuclear events. Moreover, one can explore differences in the environmental correlations for the two supernova types (and subtypes).
6.2 Survey Supernovae as Distance Indicators: the Expanding Photosphere Method
Type Ia supernovae have become the premier tool for distance determinations at cosmological scales, thanks to their regular light curves, high peak brightnesses, and relatively less dusty environments. Nevertheless, given the importance of the cosmic distance scale, and the ongoing need for systematic crosschecks and calibration, it is worthwhile to consider other methods. Core-collapse events offer just such a method, via the expanding photosphere/expanding atmosphere method.
This method was originally conceived by Baade (1926) and Wesselink (1946) for study of Cephieds; Kirshner & Kwan (1974) applied the Baade-Wesselink method to supernovae. The key to the technique is to exploit the simple kinematics of a newborn supernova remnant: the freely-expanding photosphere grows in size as . Thus, for purely blackbody emission, the luminosity grows with size (i.e., time) as . With good sampling to measurements time since explosion, and spectroscopic inference of and , one can recover the luminosity. In principle, therefore, one can use the explosion as a standard candle.
In practice, this method has been slow to mature. Until recently, the agreement with independent distance measures has been only good to within a factor (e.g., Vinko & Takats, 2007). The complex (out of local thermodynamic equilibrium) spectra of supernovae has proved difficult to adequately model. However, recently important advances have been made in the radiation transfer modeling of young supernova remnants and its fitting to spectra of local supernovae (Baron et al., 2004; Dessart & Hillier, 2005, 2008). Because of this, the expanding photosphere (or more properly, expanding atmosphere) method now appears to be reaching consistency with other distance measures; this method now shows agreement approaching the level. Similar pecision now seems possiblue using a separate, empirical method (Hamuy & Pinto, 2002) which exploits the observed correlation between luminosity and expansion velocity of Type II-P events. This opens up core-collapse supernovae as alternative distance indicators. Indeed, several group (Nugent et al., 2006; Poznanski et al., 2007; Olivares, 2008) have already applied this method to various collections of Type II-P observations, yielding tight Hubble diagrams out to .
To use this method as it is currently envisioned, follow-up spectroscopy is mandatory for each event (see §6.5), with photometric surveys identifying the candidates. Obviously, for the largest surveys, in practice only a tiny fraction of core-collapse events could be studied in a (separate) spectroscopic campaign, particularly given that the most common core-collapse types are intrinsically dimmer than Type Ia events and thus require longer exposures to obtain spectra. Followup requirements thus are the limiting factor for the use of core-collapse events as distance indicators.
The situation for Type Ia supernovae is better-studied and also potentially more hopeful. Recent work (Poznanski et al., 2007; Kim & Miquel, 2007; Kunz et al., 2006; Blondin & Tonry, 2007; Wang, 2007; Kuznetsova et al., 2008; Sako et al., 2008) suggests that photometric redshifts of Type Ia events near maximum light could be obtained with sufficient precision (give a low-redshift training set) to provide useful dark energy constraints without spectroscopy. Whether photometric-based distances can be derived for core-collapse events with sufficient accuracy remains to be seen. It nevertheless seems to us a worthy object of further study. In this context it is worth noting that DES plans to do followup spectroscopy on of Type Ia events (The Dark Energy Survey Collaboration, 2005). We suggest that at least some modest fraction of this follow-up time be dedicated to core-collapse monitoring.
6.3 Other Science with Cosmic Supernovae
The physics, astrophysics, and cosmology of cosmic core-collapse supernovae is a fertile topic; with our detectability study in hand, a wide variety of problems present themselves. Here we sketch these out; we intend to return to these in future publications.
The huge harvest of core-collapse events will open new windows onto other aspects of supernova physics. For example, the physics of black hole formation in supernovae, and the neutron-star/black hole divide, remain important open questions. Balberg & Shapiro (2001) have estimated the rates of events with observable signatures of black hole formation; LSST should provide a fertile testing ground for these predictions.
The elaboration of the cosmic history and specific sites of high-redshift supernovae will also offer unique new information about supernova “ecology” – i.e., feedback and cycling of energy, mass, and metals into the surrounding environment. For example, large surveys will offer the opportunity to study supernova rates as a function of host galaxy and galaxy clustering, shedding new light onto large-scale star formation and its connection with galaxy evolution. Moreover, DES and other surveys will discover an enormous number of rich galaxy clusters; the occurrence of both Type Ia and core-collapse events in clusters will offer important new insight into the origin of the very high metallicity of intracluster gas (Maoz & Gal-Yam, 2004; Maoz et al., 2005).
Core-collapse supernovae also are the sources, directly or indirectly, of high-energy radiation of various kinds. For example, supernovae act as accelerators of cosmic rays. These in turn interact with interstellar matter to produce high-energy -rays. Pavlidou & Fields (2002) used then-available estimates of the cosmic star-formation rate to show that this -ray signal has a characteristic feature, and makes a significant part of the extragalactic -ray background around GeV. With the successful launch of the high-energy -ray observatory GLAST, this component of the -ray background may for the first time be clearly identified. Regardlessly, a sharper knowledge of the cosmic supernova rate (and thus cosmic-ray injection rate) will work in concert with GLAST observations to probe the history of cosmic rays throughout the universe.
6.4 Comparison with Type Ia Survey Requirements
The characteristic of Type Ia supernovae are in general very similar to the core-collapse supernovae. Hence the observational requirements for their identification in synoptic surveys are also very similar. The rest-frame, full-width at half-maximum timescale for Type Ia supernovae is days. Therefore surveys will need a scan cadence of a few days in order to get a well-sampled light curve. For example, the Pan-STARRS strategy for Type Ia discovery is to sample the light curve every 4 days (Tonry et al., 2003; Tonry, 2003). As we have discussed, this sampling frequency is also suitable for the core-collapse supernovae which the time scale of the light curve also last a few weeks.
6.5 Redshifts and Typing from Photometry and Followup Spectroscopy
Survey supernovae become scientifically useful only when one can establish, at the very least, their redshift and whether they are core collapse or Type Ia. Since followup spectroscopy will not be possible for the large numbers of future events, photometric redshifts will be needed. For events in which a host galaxy is clearly visible, one can use photometric redshifts of the hosts. Here one is helped by the ability of surveys to stack all of the many (non-supernova) exposures to obtain a much deeper image than those with the supernovae. Once the host redshift is know, the supernova type must be determined. Baysean analysis techniques and software (Dahlén & Goobar, 2002; Poznanski et al., 2007) have been developed to distinguish both Type Ia and core-collapse events. These authors find that type discrimination depends crucially on the accuracy with which the redshift is known. For spectroscopic redshifts, their methods is extremely accurate, and for photometric redshifts the method is still quite good, though in this case misclassifications can reach depending on .
Followup spectroscopy on a subset of events will be essential to calibrate the accuracy of the photometric typing (and host redshifts). In particular, spectroscopy will be invaluable in identifying and quantifying catastrophic failures in the typing algorithms; on the basis of these it may be possible to refine the routines. As noted in the previous section, followup is also required for any events one hopes to use in distance determinations.
For events without clear host galaxies and without followup, one must resort to photometric redshifts and typing based on the supernova light curve itself, in whatever bands are available. It is not clear that this can be done with any reliability on an event-by-event basis As Poznanski et al. (2007) emphasize, one might make statistical statements about the types and redshifts of the entire class of “hostless” events. Here spectroscopic followup will be essential, not only for determining the supernova redshift but also the nature of the underlying host.
7 Conclusions and Recommendations for Synopic Surveys
The next ten years will witness a revolution in our observational knowledge of core-collapse supernovae. Synoptic sky surveys will reap an enormous harvest of these events, with tens of thousands discovered in the near future, culminating with of order 100,000 seen annually by LSST. These data will reveal the supernova distribution in space and time over much of cosmic history. The needed observations are naturally a part of the scanning nature of these surveys, and require only that core-collapse events be included in the data analysis pipeline.
The potential science impact of this unprecedented supernova sample is enormous. We have discussed ways in which the photometric supernova data alone will contribute in significant and unique ways to cosmology and astroparticle physics, as well as to studies of core-collapse and supernova evolution themselves. We illustrate one such application by demonstrating how to recover the cosmic supernova rate from the redshift distribution of supernova counts in synoptic surveys. The large datasets ensure that the statistical error will be very low, and the first large surveys will rapidly determine the CSNR to precision exceeding that of current data based on observation of massive-star proxies.
With the addition of spectroscopic followup observations, the survey-identified core-collapse supernovae can be used as distance indicators. Thanks to recent advances in the phenomenology of supernova spectra and the modelling of their expanding atmospheres, the early light curves provide standardizable candles. This expanding photosphere/atmosphere method could provide a cross-check for the cosmic distance scale as inferred from Type Ia supernovae.
To summarize our recommendations for synoptic surveys, in order to capitalize on this potential:
-
1.
Include core-collapse supernovae (all Type II as well as Types Ib and Ic) in the data analysis pipeline.
-
2.
Include a scanning mode in which the depth is as large as possible, in order to maximize the supenova redshift range. Surveys which modes which probe down to could discover many supernovae (both core-collapse and Type Ia) approaching redshift .
-
3.
Adopt scanning cadence of revisits every days, in order to capture core-collapse events at peak brightness, and to obtain a well-sampled lightcurve. This timescale also appropriate for Type Ia events.
-
4.
Allocate some followup spectroscopy to core-collapse events. This will calibrate photometric Type Ia/core-collapse typing and typing among core-collapse subtypes, and will be particularly crucial for probing the nature of events in which a host galaxy is not seen.
We close by re-emphasizing that these recommendations require only modest efforts in analysis, little to no modification of the strategies already in place for Type Ia searches, and some commitment of followup spectroscopy. Thus a small extra investment of resources will reap handsome scientific rewards as we open our eyes to the incessant rise and fall of these beacons marking massive star death throughout the cosmos.
Note: In the final stages of writing this paper we became aware of the work of Young et al. (2008). These authors discuss core collapse rates in sky surveys, with a focus on events in low-metallicity environments. Where it is possible to compare and when we adopt their parameters (particularly ), our analyses seem to be in broad agreement.
Appendix A Appendix: The Supernova/Star-Formation Connection
The star-formation rate and supernova rate for any astrophysical site are intimately related. Moreover, in many applications such as ours the timescales of interest are much longer than the Myr supernova progenitor lifetimes. In this case, the star-formation rate and supernova rates are proportional. This is expressed above in eq. (2). The constant of proportionality can be obtained from the initial mass function . In stellar mass range the number of new stars is proportional to , while the mass of new stars is . Thus the number of supernovae per unit new star mass–i.e., the conversion between star-formation and supernova rates–is
| (A1) |
where is the mass fraction of new stars that will go into supernovae, and is the mean supernova progenitor mass. For illustration, consider a Salpeter IMF over mass range and for the low mass range (Baldry & Glazebrook, 2003, their “Salpeter A” mass function). We also take supernova progenitors to lie in the mass range ). This gives ,, and thus a star-formation/supernova conversion factor . The uncertainty here is significant, probably about a factor of 2.
The cosmic star-formation rate can be estimated from a number of observables tied to massive (i.e., short-lived thus “instantaneous”) star-formation. Proxies often adopted are the UV and/or H luminosity densities (Madau et al., 1996). Of these, UV light has a more direct connection with massive stars, but is also affected more by the dust extinction than the H light (Strigari et al., 2005). Most cosmic star-formation studies find a sharp increase in the rate up to , but there remains a large uncertainty of the star formation rate at higher redshift. In this paper, we adopt the Cole et al. (2001) fitting formula for the cosmic star-formation rate
| (A2) |
where, which are one of the best-fitted parameters according to current observing data found by Hopkins & Beacom (2006). Using the conversion factor of Hopkins & Beacom (2006) and our adopted Hubble constant, this gives a local rate of . The benchmark CC SNe rate rises to a peak around and then slowly declines at high redshift.
To illustrate the impact of different star formation, we also did all calculations with an alternative CSNR. Here we normalize to the current observed, counting-based CSNR (Botticella et al., 2008), and take the shape from the a fitting function of the Hippelein et al. (2003) star formation rate. We also lower the rate by 30% because we want the alternative CSNR to be as much different as the benchmark CSNR as possible and Hopkins & Beacom (2006) suggested that the uncertainty of the normalization of the star formation rate is about 30%. The differences between this and our fiducial rate gives a sense of the current rough but not perfect agreement between the CSNR as inferred indirectly from progenitor light (sometimes reprocessed) and directly from counting.
Appendix B Appendix: Supernova Predictions for Upcoming Synoptic Surveys
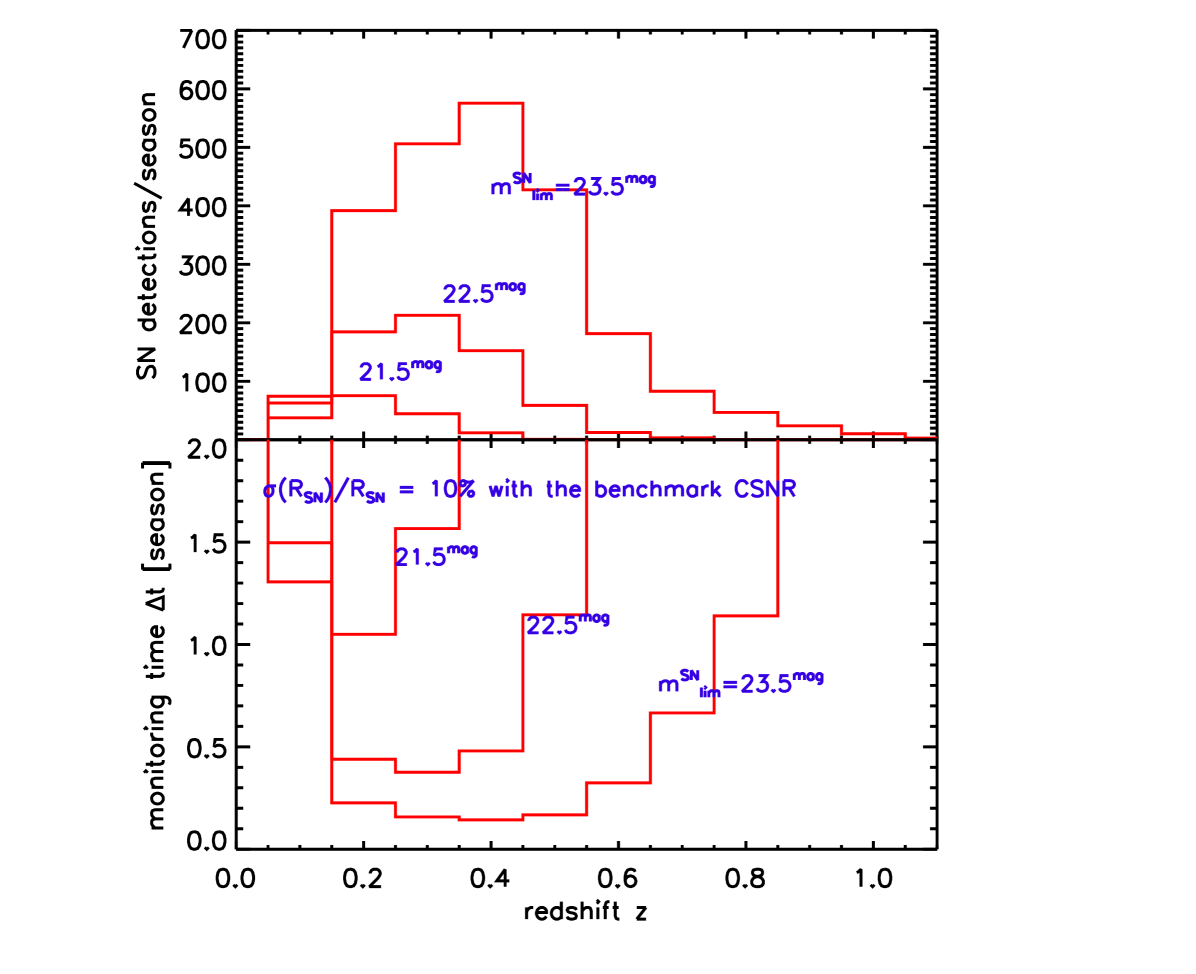

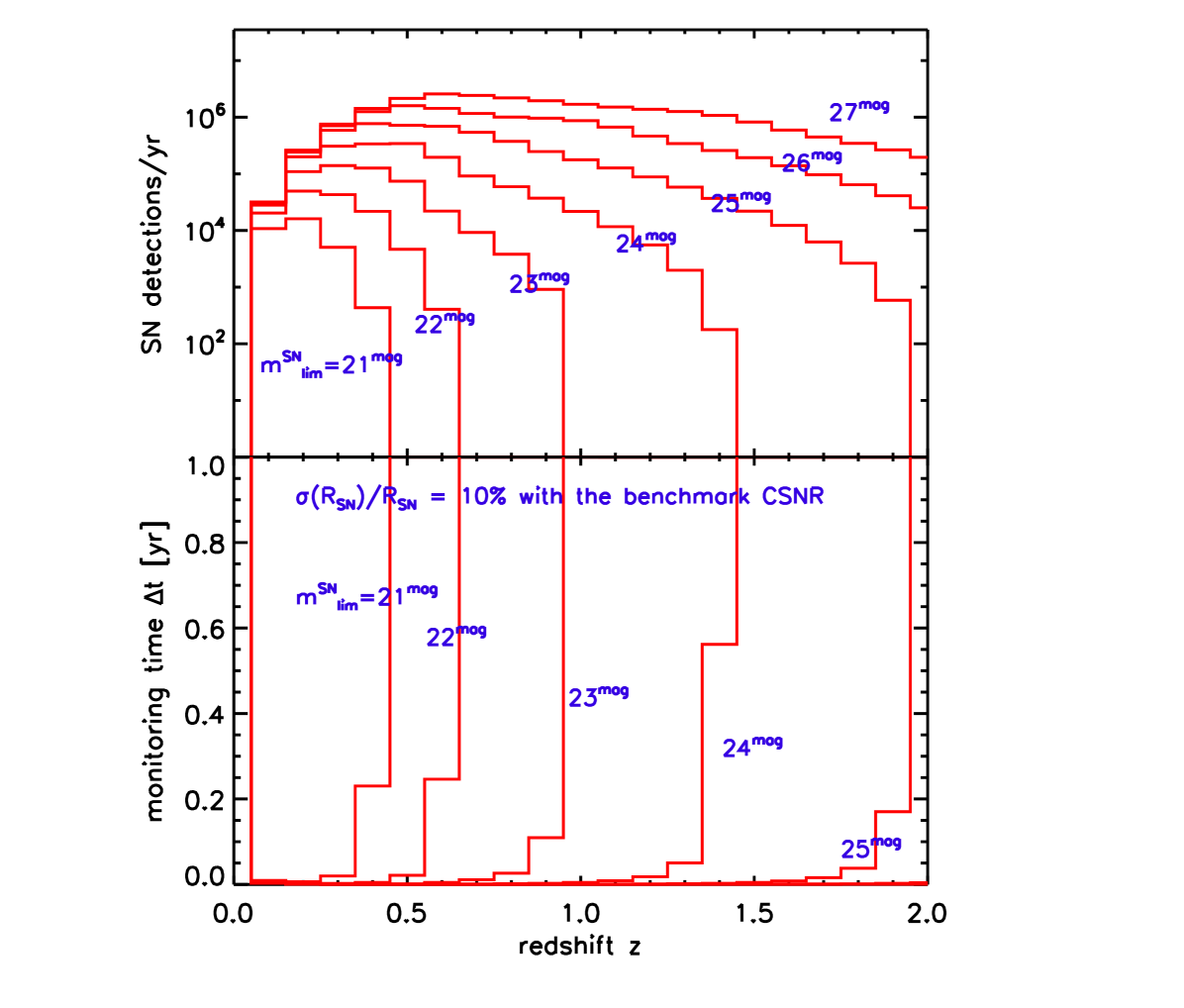
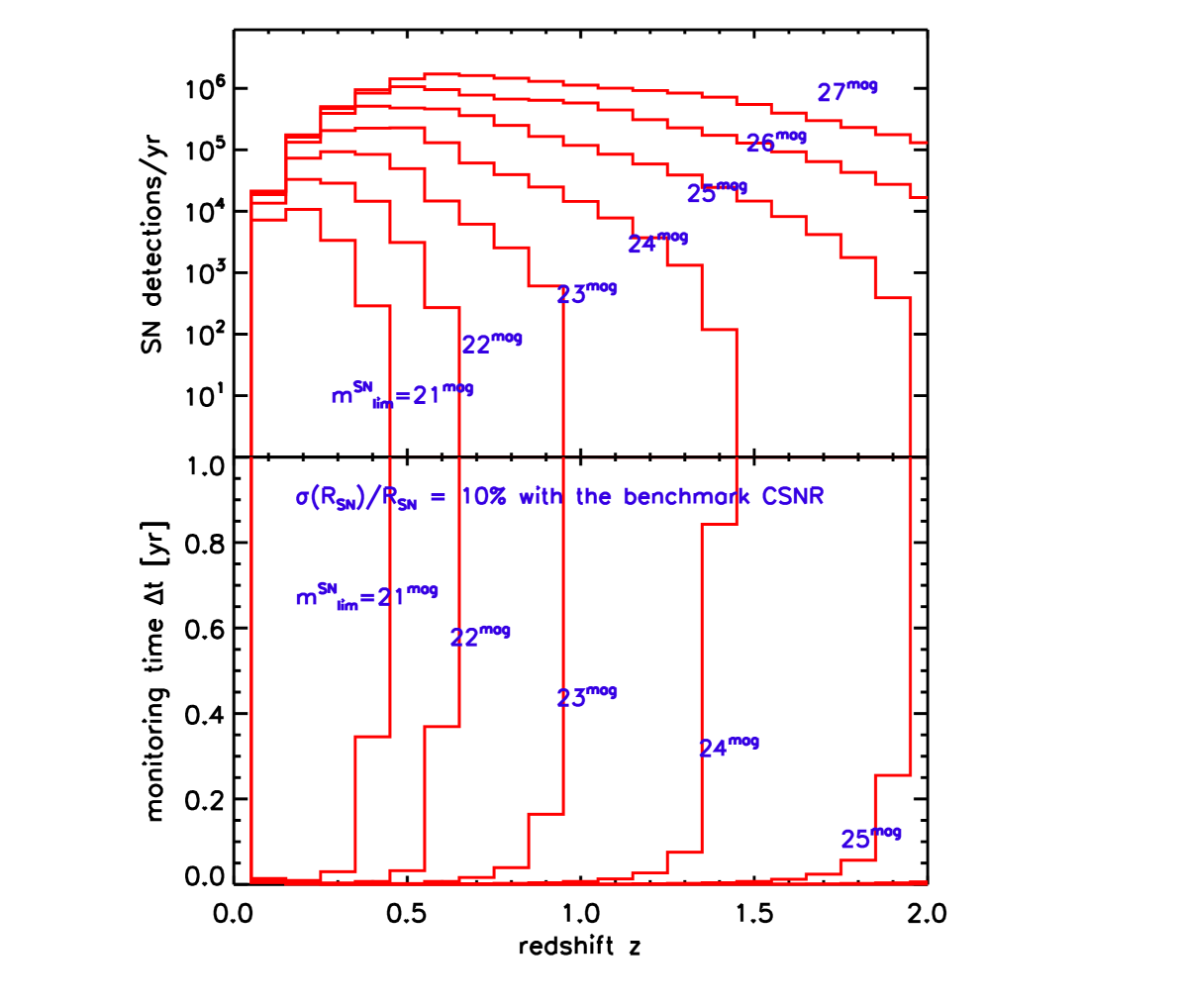
| DES | Pan-STARRS | LSST | ||||
|---|---|---|---|---|---|---|
| [mag] | Total SNe | Redshifts | Total SNe | Redshifts | Total SNe | Redshifts |
| 21 | 0.081 0.18 | 0.007 0.36 | 0.008 0.36 | |||
| 22 | 0.066 0.38 | 0.007 0.56 | 0.008 0.56 | |||
| 23 | 0.064 0.66 | 0.007 0.89 | 0.008 0.89 | |||
| 24 | 0.063 1.10 | 0.007 1.34 | 0.008 1.33 | |||
| 25 | 0.063 1.62 | 0.007 1.88 | 0.008 1.88 | |||
| 26 | 0.063 2.17 | 0.007 2.48 | 0.008 2.47 | |||
| 27 | 0.063 2.68 | 0.007 3.08 | 0.008 3.08 | |||
Figures 7–10 show the supernova forecasts for different surveys. For each we show the expected annual supernova harvest as a function of redshift, with the sky coverage held fixed to the values in Table 1. The count distribution across redshift bins are directly proportional to the differential supernova rate distribution , via eq. (18). Thus the shapes the curves follow those of as seen in Figure 4 an explained in the accompanying discussion.
Figures 7–10 also show the survey scan time required for these data to constrain the cosmic star-formation rate in each redshift bin to within a statistical precision . We have seen (eq. 20) that the precision at each bin is inverse with the counts, . Thus these panels show trends in which monitoring time decreases with the counts per bin. This mirrors the behavior shown in Figure 6 and explained in the surrounding discussion.
Table 3 shows the effect of survey limiting magnitude on redshift range and total supernova harvest in the -band. We see that each unit increase in survey depth yields a large enhancement, in the total supernovae seen. The supernova numbers increase by a factor 4.3 when going from to to factor of 2.0 when going from to . Of course, there is a tradeoff in the needed exposure. For the faintest objects at the highest redshifts, background noise dominates, and monitoring time grows by a factor per magnitude. Thus, including a narrower but deeper survey mode will likely yield fewer supernovae, but if judiciously implemented, this tradeoff may be worth the additional redshift coverage.
Appendix C The -Correction
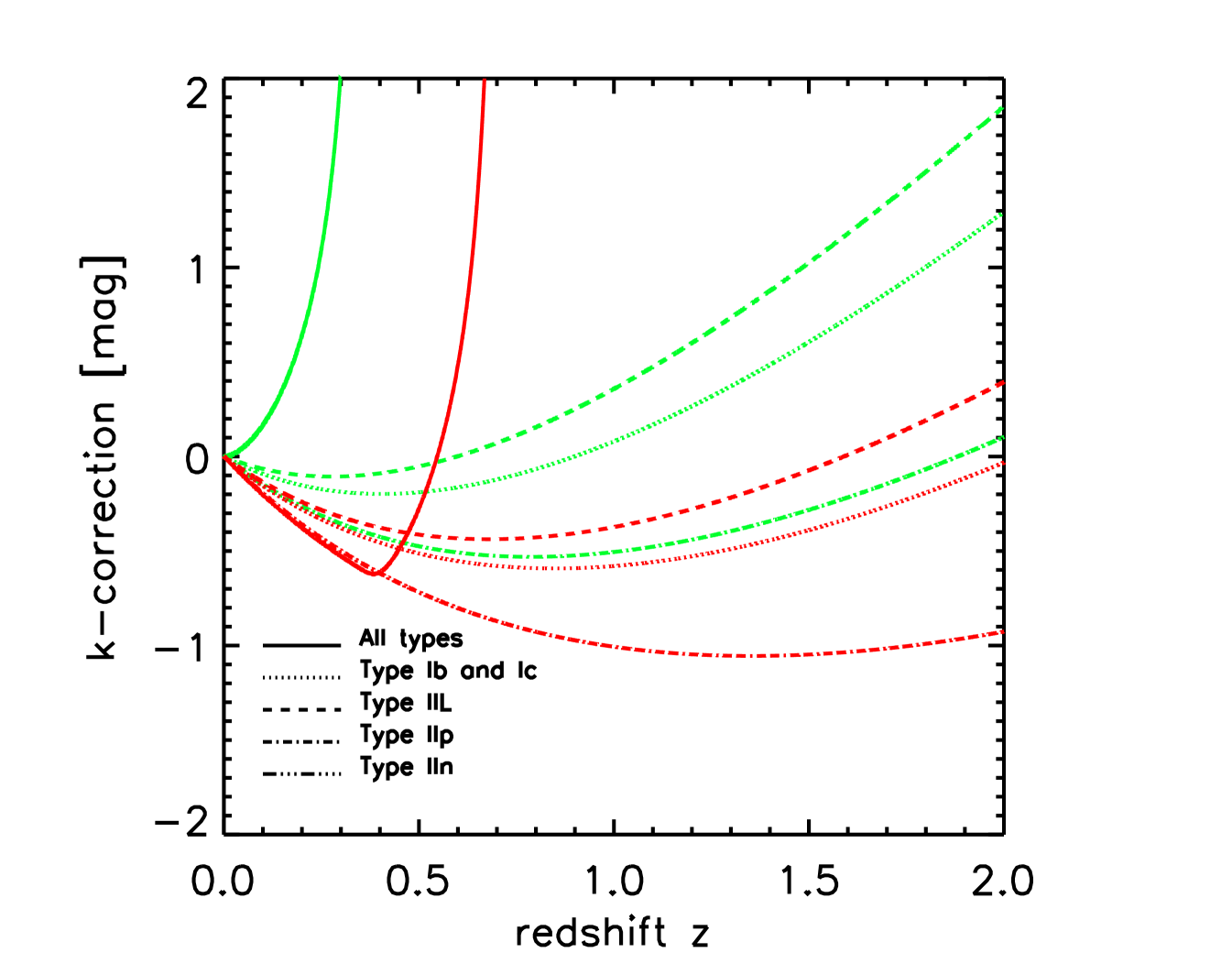
The -correction accounts for redshifting of the supernova spectrum across the passbands in the observer frame. In the context of the Southern inTermediate Redshift ESO Supernova Search, the elegant and instructive analysis of Botticella et al. (2008) determine -corrections for the supernova confirmed and candidate events in their survey. They found that the corrections depend strongly on redshift, light curve phase, and on waveband. In particular, the shifts from observed and bands to rest-frame -band both typically have , i.e, a negative correction, particularly at early times most relevant here; this reflects the blue colors of the early phases. The corrections are at early times (within the first three weeks) usually a shift , with the largest corrections . As seen in eq. (7), a negative correction would reduce the apparent magnitude and thus improve the observability of the supernovae.
In this paper we compute -corrections following the formalism of Kim et al. (1996) in a single band, and add the color correction term (which described as in Section 3.4) to make the corresponding correction when transfer from one band to another. In band , the -correction is
| (C1) |
where is the unobscured, rest-frame spectral distribution of the supernova, and is the sensitivity of filter . We included five types of core collapse supernovae: Ib, Ic, II-L, II-P, IIn. For each spectral type, we adopt a rest-frame spectrum following the prescription of Dahlén & Fransson (1999), who adopt blackbody spectra (sometimes slightly modified) with different temperatures and time evolution. We picked the temperatures which last for about a weak around the peak luminosity and treat them as a constant. Since the surveys we are interested in will have cadence less than a week, this should be a reasonable simplification. For Type Ib and Ic, we choose a 15,000 K blackbody with cutoff at because of UV blanketing. We choose 11,000 K for Type II-L, 10, 000 K for Type II-P, and 14,000 K for Type IIn.
Our resulting -correction appear in Fig. 11, plotted for the and bands which we will see are the optimal for supernova discovery. The huge turnoff of the -correction in Type I-bc is due to the short-wavelength cutoff in its spectrum. A large value is set so that there will be no Type I-bc supernovae observed beyond the cutoff point. Regardless of the turnoff of Type I-bc, for low redshifts the -correction is in the range of to but typically is negative, which is in consistent with Botticella et al. (2008).
References
- Adelberger & Steidel (2000) Adelberger, K. L., & Steidel, C. C. 2000, ApJ, 544, 218
- Astier et al. (2006) Astier, P., et al. 2006, A&A, 447, 31
- Baade (1926) Baade, W. 1926, Astronomische Nachrichten, 228, 359
- Balberg & Shapiro (2001) Balberg, S., & Shapiro, S. L. 2001, ApJ, 556, 944
- Baldry & Glazebrook (2003) Baldry, I. K., & Glazebrook, K. 2003, ApJ, 593, 258
- Baron et al. (2004) Baron, E., Nugent, P. E., Branch, D., & Hauschildt, P. H. 2004, ApJ, 616, L91
- Blondin & Tonry (2007) Blondin, S., & Tonry, J. L. 2007, ApJ, 666, 1024
- Botticella et al. (2008) Botticella, M. T., et al. 2008, A&A, 479, 49
- Cappellaro et al. (1997) Cappellaro, E., Turatto, M., Tsvetkov, D. Y., Bartunov, O. S., Pollas, C., Evans, R., & Hamuy, M. 1997, A&A, 322, 431
- Central Bureau for Astronomical Telegrams (2008) Central Bureau for Astronomical Telegrams http://www.cfa.harvard.edu/iau/cbat.html
- Chen et al. (2007) Chen, H.-W., Prochaska, J. X., & Gnedin, N. Y. 2007, ApJ, 667, L125
- Choi et al. (2006) Choi, P. I., et al. 2006, ApJ, 637, 227
- Cole et al. (2001) Cole, S., et al. 2001, MNRAS, 326, 255
- Cooke (2008) Cooke, J. 2008, ApJ, 677, 137
- The Dark Energy Survey Collaboration (2005) The Dark Energy Survey Collaboration 2005, ArXiv e-prints, arXiv:astro-ph/0510346
- Dahlén & Fransson (1999) Dahlén, T., & Fransson, C. 1999, A&A, 350, 349
- Dahlén & Goobar (2002) Dahlén, T., & Goobar, A. 2002, PASP, 114, 284
- Dessart & Hillier (2005) Dessart, L., & Hillier, D. J. 2005, A&A, 439, 671
- Dessart & Hillier (2008) Dessart, L., & Hillier, D. J. 2008, MNRAS, 383, 57
- Dessart et al. (2008) Dessart, L., et al. 2008, ApJ, 675, 644
- Doggett & Branch (1985) Doggett, J. B., & Branch, D. 1985, AJ, 90, 2303
- Frieman et al. (2008) Frieman, J. A., et al. 2008, AJ, 135, 338
- Fukugita et al. (1996) Fukugita, M., Ichikawa, T., Gunn, J. E., Doi, M., Shimasaku, K., & Schneider, D. P. 1996, AJ, 111, 1748
- Gal-Yam & Maoz (2004) Gal-Yam, A., & Maoz, D. 2004, MNRAS, 347, 942
- Gal-Yam et al. (2002) Gal-Yam, A., Maoz, D., & Sharon, K. 2002, A New Era in Cosmology, 283, 289
- Gezari et al. (2008) Gezari, S., et al. 2008, arXiv:0808.2812
- Gnedin et al. (2008) Gnedin, N. Y., Kravtsov, A. V., & Chen, H.-W. 2008, ApJ, 672, 765
- Hamuy & Pinto (2002) Hamuy, M., & Pinto, P. A. 2002, ApJ, 566, L63
- Hatano et al. (1998) Hatano, K., Branch, D., & Deaton, J. 1998, ApJ, 502, 177
- Hippelein et al. (2003) Hippelein, H., et al. 2003, A&A, 402, 65
- Hopkins & Beacom (2006) Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142
- Hughes et al. (1998) Hughes, D. H., et al. 1998, Nature, 394, 24
- Jewitt (2003) Jewitt, D. 2003, Pan-STARRS Science Goals: Science Overview, URL http://pan-starrs.ifa.hawaii.edu/project/science/precodr.html
- Kim et al. (1996) Kim, A., Goobar, A., & Perlmutter, S. 1996, PASP, 108, 190
- Kim & Lee (2007) Kim, S. S., & Lee, M. G. 2007, PASP, 119, 1449
- Kim & Miquel (2007) Kim, A. G., & Miquel, R. 2007, Astroparticle Physics, 28, 448
- Kirshner & Kwan (1974) Kirshner, R. P., & Kwan, J. 1974, ApJ, 193, 27
- Kuznetsova et al. (2008) Kuznetsova, N., et al. 2008, ApJ, 673, 981
- Kunz et al. (2006) Kunz, M., Bassett, B. A., & Hlozek, R. 2006, ArXiv e-prints, arXiv:astro-ph/0611004
- Le Floc’h et al. (2005) Le Floc’h, E., et al. 2005, ApJ, 632, 169
- Leibundgut & Suntzeff (2003) Leibundgut, B., & Suntzeff, N. B. 2003, Supernovae and Gamma-Ray Bursters, 598, 77
-
The LSST Collaboration (2007)
The Large Synoptic Survey Telescope Collaboration 2007,
Science Requirements Document
http://www.lsst.org/Science/docs/SRD.pdf - Madau et al. (1996) Madau, P., Ferguson, H. C., Dickinson, M. E., Giavalisco, M., Steidel, C. C., & Fruchter, A. 1996, MNRAS, 283, 1388
- Madau et al. (1998) Madau, P., della Valle, M., & Panagia, N. 1998, MNRAS, 297, L17
- Mannucci et al. (2007) Mannucci, F., Della Valle, M., & Panagia, N. 2007, MNRAS, 377, 1229
- Maoz & Gal-Yam (2004) Maoz, D., & Gal-Yam, A. 2004, MNRAS, 347, 951
- Maoz et al. (2005) Maoz, D., Waxman, E., & Loeb, A. 2005, ApJ, 632, 847
- Modjaz et al. (2008) Modjaz, M., et al. 2008, ArXiv e-prints, 805, arXiv:0805.2201
- Nugent et al. (2006) Nugent, P., et al. 2006, ApJ, 645, 841
- Oda & Totani (2005) Oda, T., & Totani, T. 2005, ApJ, 630, 59
- Olivares (2008) Olivares, F. 2008, arXiv:0810.5518
- Pastorello et al. (2006) Pastorello, A., et al. 2006, MNRAS, 370, 1752
- Patat et al. (1993) Patat, F., Barbon, R., Cappellaro, E., & Turatto, M. 1993, A&AS, 98, 443
- Patat et al. (1994) Patat, F., Barbon, R., Cappellaro, E., & Turatto, M. 1994, A&A, 282, 731
- Pavlidou & Fields (2002) Pavlidou, V., & Fields, B. D. 2002, ApJL, 575, L5
- Pérez-González et al. (2003) Pérez-González, P. G., Zamorano, J., Gallego, J., Aragón-Salamanca, A., & Gil de Paz, A. 2003, ApJ, 591, 827
- Perlmutter et al. (1999) Perlmutter, S., et al. 1999, ApJ, 517, 565
- Phillips (1993) Phillips, M. M. 1993, ApJ, 413, L105
- Poznanski et al. (2007) Poznanski, D., Maoz, D., & Gal-Yam, A. 2007, AJ, 134, 1285
- Richardson et al. (2002) Richardson, D., Branch, D., Casebeer, D., Millard, J., Thomas, R. C., & Baron, E. 2002, AJ, 123, 745
- Riess et al. (1996) Riess, A. G., Press, W. H., & Kirshner, R. P. 1996, ApJ, 473, 88
- Riess et al. (1998) Riess, A. G., et al. 1998, AJ, 116, 1009
- Sako et al. (2008) Sako, M., et al. 2008, AJ, 135, 348
- Scannapieco & Bildsten (2005) Scannapieco, E., & Bildsten, L. 2005, ApJ, 629, L85
- Scannapieco et al. (2005) Scannapieco, E., Madau, P., Woosley, S., Heger, A., & Ferrara, A. 2005, ApJ, 633, 1031
- Shaw (1979) Shaw, R. L. 1979, A&A, 76, 188
- Smail et al. (1997) Smail, I., Ivison, R. J., & Blain, A. W. 1997, ApJ, 490, L5
- Spergel et al. (2007) Spergel, D. N., et al. 2007, ApJS, 170, 377
- Strigari et al. (2005) Strigari, L. E., Beacom, J. F., Walker, T. P., & Zhang, P. 2005, Journal of Cosmology and Astro-Particle Physics, 4, 17
- Sullivan et al. (2000) Sullivan, M., Ellis, R., Nugent, P., Smail, I., & Madau, P. 2000, MNRAS, 319, 549
- Suntzeff et al. (2004) Suntzeff, N. B., Smith, R. C.,Hamuy, M., Phillips, M. M., & Tyson, T. 2004, Bulletin of the American Astronomical Society, 36, 1530
- Tonry (2003) Tonry, J. 2003, Pan-STARRS Science Goals: Supernova Science, URL http://pan-starrs.ifa.hawaii.edu/project/science/precodr.html
- Tonry et al. (2003) Tonry, J. L., et al. 2003, ApJ, 594, 1
- Tyson (2002) Tyson, J.A. and the LSST Collaboration, 2002, Proc. SPIE Int.Soc.Opt.Eng. 4836, 10
- Vinko & Takats (2007) Vinko, J., & Takats, K. 2007, ArXiv e-prints, 704, arXiv:0704.0552
- Wang (2007) Wang, Y. 2007, ApJ, 654, L123
- Wang et al. (2004) Wang, Y., Kostov, V., Freese, K., Frieman, J. A., & Gondolo, P. 2004, Journal of Cosmology and Astro-Particle Physics, 12, 3
- Watanabe et al. (1999) Watanabe, K., Hartmann, D. H., Leising, M. D., & The, L.-S. 1999, ApJ, 516, 285
- Wesselink (1946) Wesselink, A. J. 1946, Bull. Astron. Inst. Netherlands, 10, 91
- Wood-Vasey et al. (2007) Wood-Vasey, W. M., et al. 2007, ApJ, 666, 694
- York et al. (2000) York, D. G., et al. 2000, AJ, 120, 1579
- Young et al. (2008) Young, D. R., Smartt, S. J., Mattila, S., Tanvir, N. R., Bersier, D., Chambers, K. C., Kaiser, N., & Tonry, J. L. 2008, ArXiv e-prints, 807, arXiv:0807.3070
- Zheng et al. (2008) Zheng, C., et al. 2008, AJ, 135, 1766