Cosmic Reionization and Early Star-Forming Galaxies: A Joint Analysis of New Constraints from Planck and Hubble Space Telescope

Brant E. Robertson¹¹affiliation: Department of Astronomy, University of Arizona, Tucson, AZ 85721 , Richard S. Ellis²²affiliation: Cahill Center for Astronomy and Astrophysics, California Institute of Technology, MS 249-17, Pasadena, CA 91125 , Steven R. Furlanetto³³affiliation: Department of Physics & Astronomy, University of California, Los Angeles CA 90095 and James S. Dunlop⁴⁴affiliation: Institute for Astronomy, University of Edinburgh, Edinburgh EH9 3HJ, UK Email: brant@email.arizona.edu

Abstract

We discuss new constraints on the epoch of cosmic reionization and test the assumption that most of the ionizing photons responsible arose from high redshift star-forming galaxies. Good progress has been made in charting the end of reionization through spectroscopic studies of $z\simeq$ 6-8 QSOs, gamma-ray bursts and galaxies expected to host Lyman $\alpha$ emission. However, the most stringent constraints on its duration have come from the integrated optical depth, $\tau$ , of Thomson scattering to the cosmic microwave background. Using the latest data on the abundance and luminosity distribution of distant galaxies from Hubble Space Telescope imaging, we simultaneously match the reduced value $\tau=0.066\pm 0.012$ recently reported by the Planck collaboration and the evolving neutrality of the intergalactic medium with a reionization history within $6\lesssim z\lesssim 10$ , thereby reducing the requirement for a significant population of very high redshift ( $z\gg 10$ ) galaxies. Our analysis strengthens the conclusion that star-forming galaxies dominated the reionization process and has important implications for upcoming 21cm experiments and searches for early galaxies with James Webb Space Telescope.

Subject headings:

galaxies: high-redshift

1. Introduction

Cosmic reionization represents an important era for assembling a coherent picture of the evolution of the Universe, and ambitious observational facilities are being constructed to explore the most important redshift range $7<z<20$ . Through the Gunn-Peterson effect in high redshift QSOs and gamma ray bursts (GRBs, e.g., Fan et al., 2006; Bolton et al., 2011; Chornock et al., 2013; McGreer et al., 2015) and the declining visibility of Lyman alpha (Ly $\alpha$ ) emission in high redshift galaxies (Stark et al., 2010; Pentericci et al., 2011, 2014; Schenker et al., 2012, 2014; Treu et al., 2013; Tilvi et al., 2014), observations indicate that reionization ended by redshift $z\simeq 6$ . However, the onset and duration of the reionization process remain less certain. The most convincing constraint is provided by the integrated optical depth, $\tau$ , of Thomson scattering to the cosmic microwave background (CMB). The Wilkinson Microwave Anisotropy Probe (WMAP) delivered a value $\tau=0.088\pm 0.014$ which, in the simplest model, corresponds to ‘instantaneous’ reionization at $z_{\mathrm{reion}}\simeq 10.5\pm 1.1$ (Hinshaw et al., 2013). As a result, the WMAP result has been widely interpreted as implying that reionization began at $z\simeq 15$ or even earlier (Bromm & Yoshida, 2011; Dunlop, 2013).

Important information on the duration of reionization can now be determined from the star formation rate (SFR) history (Madau & Dickinson, 2014, hereafter MD14), since early star-forming galaxies most likely supply the ionizing photons (Robertson et al., 2010, 2013). This conclusion followed the first measures of their abundance over $8<z<10$ from Hubble Space Telescope (HST) Ultra Deep Field (UDF) observations (Beckwith et al., 2006; Koekemoer et al., 2013; Illingworth et al., 2013). With plausible assumptions, $6<z<8$ star-forming galaxies can keep the Universe substantially ionized (Robertson et al., 2013; Finkelstein et al., 2014).

However, to match the WMAP value of $\tau$ , Robertson et al. (2013) also required a significant population of star-forming galaxies beyond a redshift $z\simeq 10$ . As a direct census of $z>10$ galaxies is not currently possible, studies have since focused on the rate of decline in abundance over $8<z<10$ with mixed conclusions (c.f., Oesch et al., 2012, 2013; Ishigaki et al., 2015; McLeod et al., 2014). The requirement for a significant contribution of ionizing photons from $z>10$ galaxies remains an important uncertainty whose resolution is perceived as a major goal for the James Webb Space Telescope (JWST).

The Planck Collaboration et al. (2015) has recently reported a significantly lower value of the optical depth, $\tau=0.066\pm 0.012$ , consistent with a reduced redshift of instantaneous reionization, $z_{\mathrm{reion}}=8.8^{+1.2}_{-1.1}$ . Here we determine the extent to which the Planck result reduces the need for significant star formation in the uncharted epoch at $z>10$ . To demonstrate this, we calculate the contribution of $6<z<10$ star-forming galaxies to the integrated value of $\tau$ , using the latest HST data. We then examine the residual contribution of ionizing photons required from sources beyond $z\simeq$ 10 to match the new value of $\tau$ from Planck, phrasing these constraints in terms of the likely abundance of $z>10$ galaxies that JWST would see in a typical deep exposure.

Throughout we use the AB magnitude system (Oke, 1974), errors represent $1-\sigma$ uncertainties, and all cosmological calculations assume flatness and the most recent Planck cosmological parameters ( $h=0.6774$ , $\Omega_{m}=0.309$ , $\Omega_{b}h^{2}=0.02230$ , $Y_{p}=0.2453$ ; Planck Collaboration et al., 2015).

2. Contribution of $z<10$ Galaxies to Late Reionization

2.1. Cosmic Star Formation History

If Lyman continuum photons from star-forming galaxies dominate the reionization process, an accounting of the evolving SFR density will provide a measure of the time-dependent cosmic ionization rate

\dot{n}_{\mathrm{ion}}=f_{\mathrm{esc}}\xi_{\mathrm{ion}}\rho_{\mathrm{SFR}},

(1)

where $f_{\mathrm{esc}}$ is the fraction of photons produced by stellar populations that escape to ionize the IGM, $\xi_{\mathrm{ion}}$ is the number of Lyman continuum photons per second produced per unit SFR for a typical stellar population, and $\rho_{\mathrm{SFR}}$ is the cosmic SFR density. Following Robertson et al. (2013), we adopt a fiducial escape fraction of $f_{\mathrm{esc}}=0.2$ and, motivated by the rest-frame UV spectral energy distributions of $z\sim 7-8$ galaxies (Dunlop et al., 2013), a fiducial Lyman continuum photon production efficiency of $\log_{10}\xi_{\mathrm{ion}}=53.14~[\mathrm{Lyc}~\mathrm{photons}~\mathrm{s}^{-1}M_{\sun}^{-1}~\mathrm{yr}]$ . Somewhat larger values of $\xi_{\mathrm{ion}}$ may also be acceptable (e.g., Topping & Shull, 2015).

The observed infrared and rest-frame UV luminosity functions (LFs) provide a means to estimate $\rho_{\mathrm{SFR}}$ . We use the recent compilation of IR and UV LFs provided in Table 1 of MD14 and references therein to compute luminosity densities $\rho_{L}$ to a minimum luminosity of $L_{\mathrm{min}}=0.001L_{\star}$ , where $L_{\star}(z)$ is the characteristic luminosity of each relevant LF parameterization (e.g., Schechter or broken power law models)¹¹1We adopt this limit since it corresponds to $M_{\mathrm{max}}\approx-13$ at $z\sim 7$ , which Robertson et al. (2013) found was required to reionize the Universe by $z\sim 6$ . It corresponds to $M_{\mathrm{max}}=M_{\star}+7.5$ .. We supplement the MD14 compilation by including $\rho_{\mathrm{SFR}}$ values computed from the LF determinations at $z\sim 8$ by Schenker et al. (2013), at $z\sim 7-8$ by McLure et al. (2013), and estimates at $z\sim 10$ by Oesch et al. (2014) and Bouwens et al. (2014). We include new HST Frontier Fields LF constraints at $z\sim 7$ by Atek et al. (2014) and at $z\sim 9$ by McLeod et al. (2014), incorporating cosmic variance estimates from Robertson et al. (2014). We also updated the MD14 estimates derived from the Bouwens et al. (2012) LFs at $z\sim 3-8$ with newer measurements by Bouwens et al. (2014). All data were converted to the adopted Planck cosmology.

We adopted the conversion $\rho_{\mathrm{SFR}}=\kappa\rho_{L}$ supplied by MD14 for IR and UV luminosity densities, i.e. $\kappa_{\mathrm{IR}}=1.73\times 10^{-10}~M_{\sun}~\mathrm{yr}^{-1}~L_{\sun}^{-1}$ and $\kappa_{\mathrm{UV}}=2.5\times 10^{-10}~M_{\sun}~\mathrm{yr}~L_{\sun}^{-1}$ respectively, as well as their redshift-dependent dust corrections and a Salpeter initial mass function. Uncertainties on $\rho_{\mathrm{SFR}}$ are computed using faint-end slope uncertainties where available, and otherwise we increased the uncertainties reported by MD14 by the ratio of the luminosity densities integrated to $L=0.03L_{\star}$ and $L=0.001L_{\star}$ . The data points in Figure 1 show the updated SFR densities and uncertainties determined from the IR (dark red) and UV (blue) LFs, each extrapolated to $L_{\mathrm{min}}=0.001L_{\star}$ .

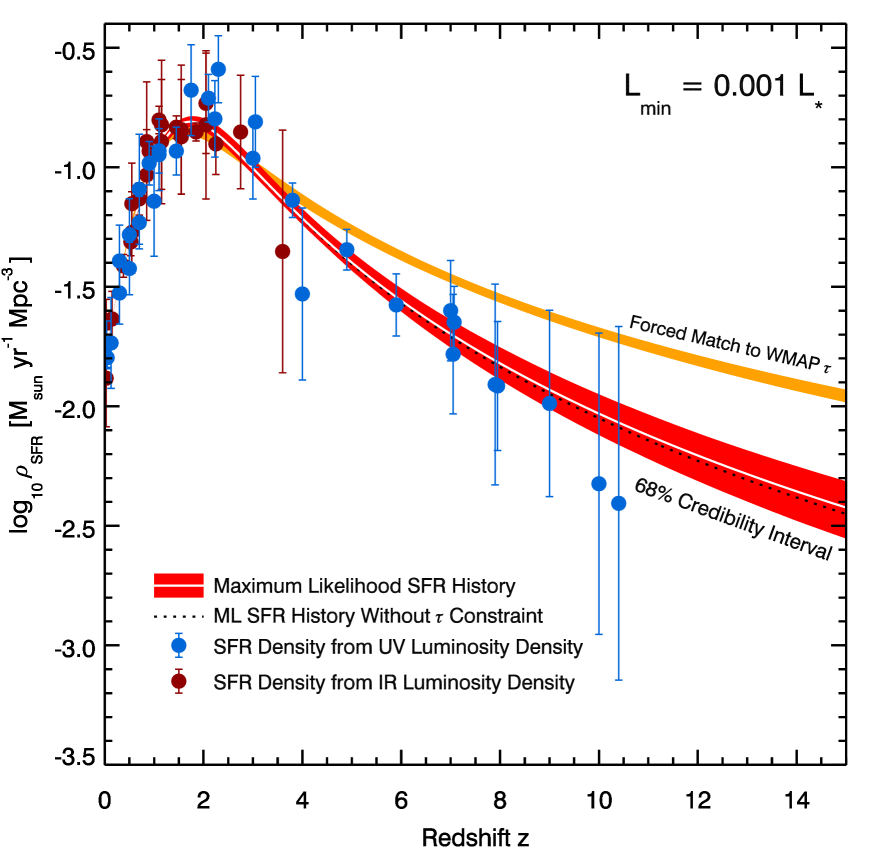
Refer to caption — Figure 1.— Star formation rate density $\rho_{\mathrm{SFR}}$ with redshift. Shown are the SFR densities from Madau & Dickinson (2014) determined from infrared (dark red points) and ultraviolet (blue points) luminosity densities, updated for recent results and extrapolated to a minimum luminosity $L_{\mathrm{min}}=0.001L_{\star}$ . A parameterized model for the evolving SFR density (Equation 2) is fit to the data under the constraint that the Thomson optical depth $\tau$ to electron scattering measured by Planck is reproduced. The maximum likelihood model (white line) and $68\%$ credibility interval on $\rho_{\mathrm{SFR}}$ (red region) are shown. A consistent SFR density history is found even if the Planck $\tau$ constraint is ignored (dotted black line). These inferences can be compared with a model forced to reproduce the previous WMAP $\tau$ (orange region), which requires a much larger $\rho_{\mathrm{SFR}}$ at redshifts $z>5$ .

Since we are interested in the reionization history both up to and beyond the limit of the current observational data, we adopt the four-parameter fitting function from MD14 to model $\rho_{\mathrm{SFR}}(z)$ ,

\rho_{\mathrm{SFR}}(z)=a_{p}\frac{(1+z)^{b_{p}}}{1+[(1+z)/c_{p}]^{d_{p}}}

(2)

and perform a maximum likelihood (ML) determination of the parameter values using Bayesian methods (i.e., Multinest; Feroz et al., 2009) assuming Gaussian errors. If we fit to the data and uncertainties reported by MD14, we recover similar ML values for the parameters of Equation 2. The range of credible SFR histories can then be computed from the marginalized likelihood of $\rho_{\mathrm{SFR}}$ by integrating over the full model parameter likelihoods.

2.2. Thomson Optical Depth

If photons from star forming galaxies drive the reionization process, measures of the Thomson optical depth inferred from the CMB place additional constraints on $\rho_{\mathrm{SFR}}$ . The Thomson optical depth is given by

\tau(z)=c{\langle n_{\mathrm{H}}\rangle}\sigma_{\mathrm{T}}\int_{0}^{z}f_{\mathrm{e}}Q_{\mathrm{H}_{\mathrm{II}}}(z^{\prime})H^{-1}(z^{\prime})(1+z^{\prime})^{2}dz^{\prime}

(3)

where $c$ is the speed of light. The comoving hydrogen density ${\langle n_{\mathrm{H}}\rangle}=X_{p}\Omega_{b}\rho_{c}$ involves the hydrogen mass fraction $X_{p}$ , the baryon density $\Omega_{b}$ , and the critical density $\rho_{c}$ . The Thomson scattering cross section is $\sigma_{T}$ . The number of free electrons per hydrogen nucleus is calculated following Kuhlen & Faucher-Giguère (2012) assuming doubly ionized helium at $z\leq 4$ .

The IGM ionized fraction $Q_{\mathrm{H}_{\mathrm{II}}}(z)$ is computed by evolving the differential equation

\dot{Q}_{\mathrm{H}_{\mathrm{II}}}=\frac{\dot{n}_{\mathrm{ion}}}{{\langle n_{\mathrm{H}}\rangle}}-\frac{Q_{\mathrm{H}_{\mathrm{II}}}}{t_{\mathrm{rec}}}

(4)

where the IGM recombination time

t_{\mathrm{rec}}=[C_{\mathrm{H}_{\mathrm{II}}}\alpha_{\mathrm{B}}(T)(1+Y_{p}/4X_{p}){\langle n_{\mathrm{H}}\rangle}(1+z)^{3}]^{-1}

(5)

is calculated by evaluating the case B recombination coefficient $\alpha_{\mathrm{B}}$ at an IGM temperature $T=20,000$ K and a clumping fraction $C_{\mathrm{H}_{\mathrm{II}}}=3$ (e.g., Pawlik et al., 2009; Shull et al., 2012). We incorporate the Planck Thomson optical depth constraints ( $\tau=0.066\pm 0.012$ , treated as a Gaussian) by computing the reionization history for every value of the $\rho_{\mathrm{SFR}}$ model parameters, evaluating Equation 3, and then calculating the likelihood of the model parameters given the SFR history data and the marginalized Thomson optical depth.

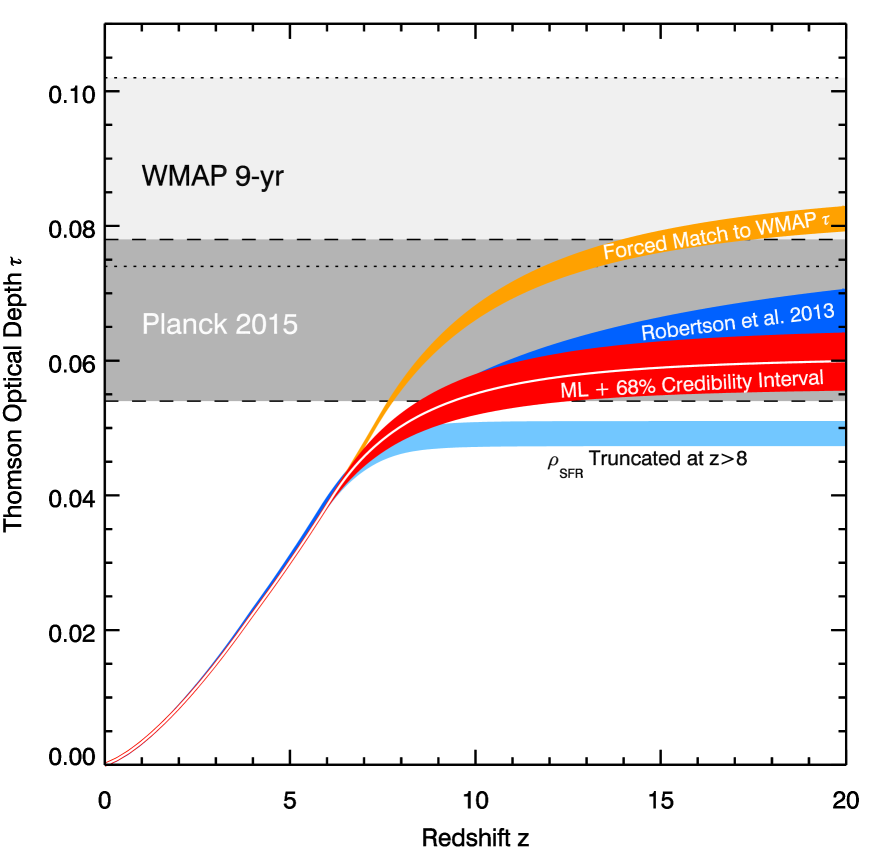
Figure 1 shows the ML and $68\%$ credibility interval (red region) on $\rho_{\mathrm{SFR}}(z)$ given the $\rho_{\mathrm{SFR}}$ constraints and the newly-reported Planck Thomson optical depth. We find the parameters of Equation 2 to be $a_{p}=0.01376\pm 0.001~M_{\sun}~\mathrm{yr}~\mathrm{Mpc}^{-3}$ , $b_{p}=3.26\pm 0.21$ , $c_{p}=2.59\pm 0.14$ , and $d_{p}=5.68\pm 0.19$ . Without the Thomson optical depth constraint, the values change by less than $1\%$ . These inferences can be compared with a SFR history (Figure 1, orange region) forced to match the previous WMAP measurement ( $\tau=0.088\pm 0.014$ ) by upweighting the contribution of the derived $\tau$ value relative to the $\rho_{\mathrm{SFR}}$ data. The model’s ML parameters ( $a_{p}=0.01306$ , $b_{p}=3.66$ , $c_{p}=2.28$ , and $d_{p}=5.29$ ) lie well outside the range of models that reproduce jointly $\rho_{\mathrm{SFR}}(z)$ and the Planck $\tau$ . Fitting to only data at $z>3$ or only independent data points at $z>6$ changes our credibility intervals by $\sim 25\%$ .

We can now address the important question of the redshift-dependent contribution of galaxies to the Planck $\tau=0.066\pm 0.012$ in Figure 2. The red region shows a history which is consistent with the SFR densities shown in Figure 1 given our simple assumptions for the escape fraction $f_{\mathrm{esc}}$ , early stellar populations, and the clumpiness of the IGM. Importantly, the reduction in $\tau$ by Planck (compared to WMAP) largely eliminates the tension between $\rho_{\mathrm{SFR}}(z)$ and $\tau$ that was discussed by many authors, including Robertson et al. (2013). That a SFR history consistent with the $\rho_{\mathrm{SFR}}(z)$ data easily reproduces the Planck $\tau$ strengthens the conclusions of Robertson et al. (2013) that the bulk of the ionizing photons emerged from galaxies. Figure 2 shows that the observed galaxy population at $z<10$ can easily reach the 68% credibility intervals of $\tau$ with plausible assumptions about $f_{\rm esc}$ and $L_{\rm min}$ . As a consequence, the reduced $\tau$ eliminates the need for very high-redshift ( $z\gg 10$ ) star formation (see section 3 below). We note the dust correction used in computing $\rho_{\mathrm{SFR}}$ at $z\sim 6$ permits an equivalently lower $f_{\mathrm{esc}}$ without significant change in the derived $\tau$ . We note that to reach $\tau\gtrsim 0.08$ given the $\rho_{\mathrm{SFR}}(z)$ constraints requires $f_{\mathrm{esc}}\gtrsim 0.3$ or $C_{\mathrm{H}_{\mathrm{II}}}\lesssim 1$ .

Figure 2 also shows $\tau(z)$ computed with the $9-$ year WMAP $\tau$ marginalized likelihood as a constraint on the high-redshift SFR density (blue region; Robertson et al. 2013), which favored a relatively low $\tau\sim 0.07$ . If, instead, the SFR density rapidly declines as $\rho_{\mathrm{SFR}}\propto(1+z)^{-10.9}$ beyond $z\sim 8$ as suggested by, e.g., Oesch et al. (2014), the Planck $\tau$ is not reached (light blue region). Lastly, if we force the model to reproduce the best-fit WMAP $\tau$ (orange region), the increased ionization at high redshifts requires a dramatic increase in the $z>7.5$ SFR (see Figure 1) and poses difficulties in matching other data on the IGM ionization state, as we discuss next.

2.3. Ionization History

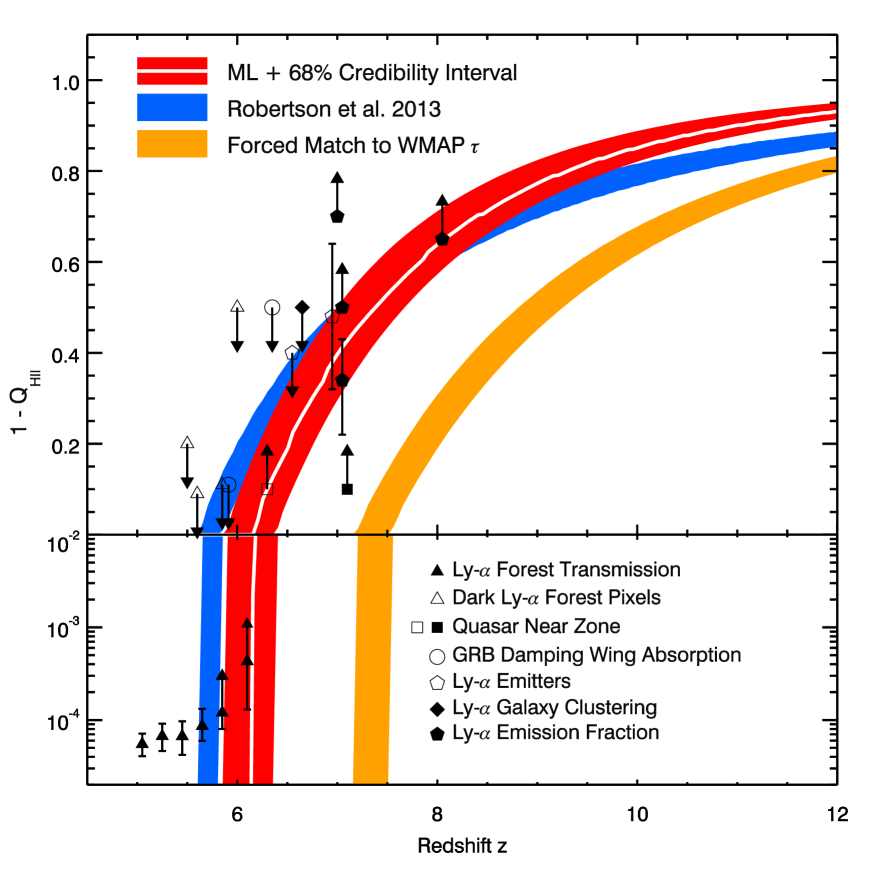
Similarly, we can update our understanding of the evolving ionization fraction $Q_{\mathrm{H}_{\mathrm{II}}}(z)$ computed during the integration of Equation 4. Valuable observational progress in this area made in recent years exploits the fraction of star forming galaxies showing Lyman- $\alpha$ emission (e.g., Stark et al., 2010) now extended to $z\sim 7-8$ from Treu et al. (2013), Pentericci et al. (2014) and Schenker et al. (2014), the Lyman- $\alpha$ damping wing absorption constraints from GRB host galaxies by Chornock et al. (2013), and the number of dark pixels in Lyman- $\alpha$ forest observations of background quasars (McGreer et al., 2015). While most of these results require model-dependent inferences to relate observables to $Q_{\mathrm{H}_{\mathrm{II}}}$ , they collectively give strong support for reionization ending rapidly near $z\simeq$ 6.

Figure 3 shows these constraints, along with the inferred $68\%$ credibility interval (red region; ML model shown in white) on the marginalized distribution of the neutral fraction $1-Q_{\mathrm{H}_{\mathrm{II}}}$ from the SFR histories shown in Figure 1 and the Planck constraints on $\tau$ . Although our model did not use these observations to constrain the computed reionization history, we nonetheless find good agreement²²2The model does not fare well in comparison to Lyman- $\alpha$ forest measurements when $Q_{\mathrm{H}_{\mathrm{II}}}\sim 1$ because of our simplified treatment of the ionization process (see the discussion in Robertson et al., 2013).

Figure 3 also shows the earlier model of Robertson et al. (2013) (blue region) which completes reionization at slightly lower redshift and displays a more prolonged ionization history. This model was in some tension with the WMAP $\tau$ (Figure 2). If we force the model to reproduce the WMAP $\tau$ (orange region), reionization ends by $z\sim 7.5$ , which is quite inconsistent with several observations that indicate neutral gas within IGM over the range $6\lesssim z\lesssim 8$ (Figure 3).

3. Constraints on the Contribution of $z>10$ Galaxies to Early Reionization

By using the parameterized model of MD14 to fit the cosmic SFR histories, and applying a simple analytical model of the reionization process, we have demonstrated that SFR histories consistent with the observed $\rho_{\mathrm{SFR}}(z)$ integrated to $L_{\mathrm{min}}=0.001L_{\star}$ reproduce the observed Planck $\tau$ while simultaneously matching measures of the IGM neutral fraction at redshifts $6\lesssim z\lesssim 8$ . As Figure 1 makes apparent, the parameterized model extends the inferred SFR history to $z>10$ , beyond the reach of current observations. Correspondingly, these galaxies supply a non-zero rate of ionizing photons that enable the Thomson optical depth to slowly increase beyond $z\sim 10$ (see Figure 2). We can therefore ask whether a connection exists between $\rho_{\mathrm{SFR}}(z>10)$ and the observed value of $\tau$ under the assumption that star forming galaxies control the reionization process.

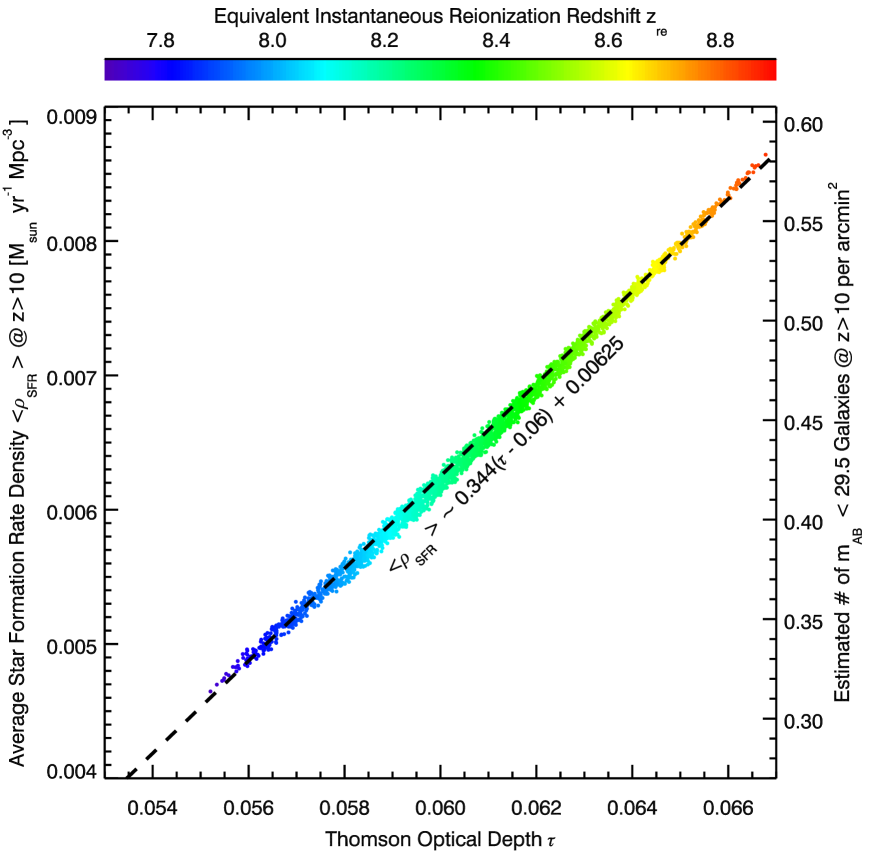
Figure 4 shows samples from the likelihood function of our model parameters given the $\rho_{\mathrm{SFR}}(z)$ and $\tau$ empirical constraints that indicate the mean SFR density ${\langle\rho_{\mathrm{SFR}}\rangle}$ (averaged over $10\lesssim z\lesssim 15$ ) as a function of the total Thomson optical depth $\tau$ . The properties ${\langle\rho_{\mathrm{SFR}}\rangle}$ and $\tau$ are tightly related, such that the linear fit

{\langle\rho_{\mathrm{SFR}}\rangle}\approx 0.344(\tau-0.06)+0.00625~[M_{\sun}~\mathrm{yr}^{-1}~\mathrm{Mpc}^{-3}]

(6)

provides a good description of their connection (dashed line). For reference, the likelihood samples shown in Figure 4 indicate the corresponding redshift of instantaneous reionization $z_{\mathrm{reion}}$ via a color coding.

Given that the SFR density is supplied by galaxies that are luminous in their rest-frame UV, we can also connect the observed $\tau$ to the abundance of star forming galaxies at $z\gtrsim 10$ . This quantity holds great interest for future studies with James Webb Space Telescope, as the potential discovery and verification of distant galaxies beyond $z>10$ has provided a prime motivation for the observatory. The $5$ - $\sigma$ sensitivity of JWST at $2~\mu$ m in a $t=10^{4}$ s exposure is $m_{\mathrm{AB}}\approx 29.5$ .³³3See http://www.stsci.edu/jwst/instruments/nircam/sensitivity/table At $z\sim 10$ , this sensitivity corresponds to a UV absolute magnitude of $M_{\mathrm{UV}}\approx-18$ . Extrapolating the SFR density to $z>10$ and using the shape of the LF at $z\geq 9$ , we estimate that $N\sim 0.5~\mathrm{arcmin}^{-2}$ galaxies at $z>10$ will be present at apparent magnitudes of $m_{\mathrm{AB}}<29.5$ at $\lambda=2~\mu$ m. Deep observations with JWST over $\sim 10~\mathrm{arcmin}^{2}$ may therefore find $\gtrsim 5$ candidates at $z>10$ (see also Behroozi & Silk, 2015). Returning to Figure 1, we can see the impact of the reduced value of $\tau$ by comparing the Planck and WMAP curves beyond $z\simeq 10$ .

4. Discussion

The lower value of the optical depth $\tau$ of Thomson scattering reported by the Planck consortium (2015) strengthens the likelihood that early star-forming galaxies dominated the reionization process, as our model can simultaneously match the observed SFR history (Figure 1) over $6<z<10$ , the integrated value of $\tau$ (Figure 2), and recent constraints on the IGM neutral fraction over $z\simeq 6-8$ (Figure 3).

A state-of-the-art reionization analysis by Choudhury et al. (2014) used the distribution of Lyman $\alpha$ equivalent widths, the IGM photoionization rate, and the mean free path of ionizing photons, to also conclude that reionization likely completed at $z\sim 6$ , with a corresponding $\tau\approx 0.07$ (see also Robertson et al., 2013). With Planck now favoring $\tau\approx 0.066$ and informed by a full accounting of available constraints on the SFR history, we have reached similar conclusions using different empirical inputs.

Our modeling makes some simplifying assumptions, adopting a constant escape fraction $f_{\mathrm{esc}}=0.2$ , IGM clumping factor $C\approx 3$ , and Lyman continuum production efficiency for early stellar populations. In Robertson et al. (2013) we examined these assumptions carefully and tested more complex models, e.g. with evolving escape fraction required to match the IGM photoionization rates at $z<6$ (e.g., Becker & Bolton, 2013). These assumptions influence the computation of $\tau$ and $Q_{\mathrm{H}_{\mathrm{II}}}$ but do not affect the inferred SFR history in Figure 1. Our conclusion that $z\lesssim 10$ galaxies can account for the Planck $\tau$ relies on extrapolating LFs below observed limits and a higher escape fraction than at lower redshift. If galaxies are less efficient ionizers, more $z>10$ star formation would be permitted. However, Robertson et al. (2013) already demonstrated such an ionizing efficiency is required to maintain a highly ionized IGM at $z\sim 7$ (Figure 3).

The “excess” value of $\tau$ above that provided by galaxies at $z<10$ measures $\rho_{\rm SFR}$ at $z>10$ . Equation 6 and the Planck 1- $\sigma$ upper limit on $\tau$ provide an upper limit of $\rho_{\rm SFR}(z>10)\lesssim 0.013\,M_{\odot}$ yr^-1 Mpc^-3. This provides the first empirical limit on models that increase the ionizing efficiency during this epoch e.g. with massive Population III stars and star formation in mini-halos (see Loeb & Furlanetto 2013 for an overview of such models). Our results suggest such models cannot dramatically change the star formation efficiency at the earliest times.

Reionization proceeds relatively quickly as the ionized fraction evolves from $Q_{\mathrm{H}_{\mathrm{II}}}=0.2$ to $Q_{\mathrm{H}_{\mathrm{II}}}=0.9$ in only $400~\mathrm{Myr}$ of cosmic history over $6\lesssim z\lesssim 9$ . This duration is consistent with recent upper limits on the kinetic Sunyaev-Zel’dovich effect (e.g., George et al., 2015). Our results offer extra hope for efforts to make redshifted 21-cm measurements of neutral hydrogen in the IGM, as the experimental foregrounds are weakest at low redshifts (e.g., van Haarlem et al., 2013; Bowman et al., 2013; Pober et al., 2014). Such experiments are essential for testing key assumptions in our analysis (like $f_{\mathrm{esc}}$ and $L_{\rm min}$ ) by observing the reionization process directly. The apparent lateness of reionization suggests that next generation experiments, which hope to reach $z\sim 20$ , can probe even earlier phases of galaxy formation.

We acknowledge useful discussions with George Efstathiou and Martin Haehnelt. This work was supported by Space Telescope Science Institute under award HST-GO-12498.01-A, and the National Science Foundation under Grant No. 1228509. JSD acknowledges the support of the European Research Council via the award of an Advanced Grant, and the contribution of the EC FP7 SPACE project ASTRODEEP (Ref.No: 312725).

References

Atek et al. (2014) Atek, H., et al. 2014, arXiv:1409.0512
Becker & Bolton (2013) Becker, G. D., & Bolton, J. S. 2013, MNRAS, 436, 1023
Beckwith et al. (2006) Beckwith, S. V. W., et al. 2006, AJ, 132, 1729
Behroozi & Silk (2015) Behroozi, P. S., & Silk, J. 2015, ApJ, 799, 32
Bolton et al. (2011) Bolton, J. S., et al. 2011, MNRAS, 416, L70
Bouwens et al. (2014) Bouwens, R. J., et al. 2014, arXiv:1403.4295
Bouwens et al. (2012) —. 2012, ApJ, 752, L5
Bowman et al. (2013) Bowman, J. D., et al. 2013, PASA, 30, 31
Bromm & Yoshida (2011) Bromm, V., & Yoshida, N. 2011, ARA&A, 49, 373
Chornock et al. (2013) Chornock, R., et al. 2013, ApJ, 774, 26
Choudhury et al. (2014) Choudhury, T. R., et al. 2014, arXiv:1412.4790
Dunlop (2013) Dunlop, J. S. 2013, in Astrophysics and Space Science Library, Vol. 396, Astrophysics and Space Science Library, ed. T. Wiklind, B. Mobasher, & V. Bromm, 223
Dunlop et al. (2013) Dunlop, J. S., et al. 2013, MNRAS, 432, 3520
Fan et al. (2006) Fan, X., et al. 2006, AJ, 132, 117
Feroz et al. (2009) Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601
Finkelstein et al. (2014) Finkelstein, S. L., et al. 2014, arXiv:1410.5439
George et al. (2015) George, E. M., et al. 2015, ApJ, 799, 177
Hinshaw et al. (2013) Hinshaw, G., et al. 2013, ApJS, 208, 19
Illingworth et al. (2013) Illingworth, G. D., et al. 2013, ApJS, 209, 6
Ishigaki et al. (2015) Ishigaki, M., et al. 2015, ApJ, 799, 12
Koekemoer et al. (2013) Koekemoer, A. M., et al. 2013, ApJS, 209, 3
Kuhlen & Faucher-Giguère (2012) Kuhlen, M., & Faucher-Giguère, C.-A. 2012, MNRAS, 423, 862
Loeb & Furlanetto (2013) Loeb, A., & Furlanetto, S. R. 2013, The First Galaxies in the Universe (Princeton, NJ: Princeton University Press)
Madau & Dickinson (2014) Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415
McGreer et al. (2015) McGreer, I. D., Mesinger, A., & D’Odorico, V. 2015, MNRAS, 447, 499
McLeod et al. (2014) McLeod, D. J., et al. 2014, arXiv:1412.1472
McLure et al. (2013) McLure, R. J., et al. 2013, MNRAS, 432, 2696
Oesch et al. (2014) Oesch, P. A., et al. 2014, arXiv:1409.1228
Oesch et al. (2013) Oesch, P. A., et al. 2013, ApJ, 773, 75
Oesch et al. (2012) —. 2012, ApJ, 745, 110
Oke (1974) Oke, J. B. 1974, ApJS, 27, 21
Pawlik et al. (2009) Pawlik, A. H., Schaye, J., & van Scherpenzeel, E. 2009, MNRAS, 394, 1812
Pentericci et al. (2011) Pentericci, L., et al. 2011, ApJ, 743, 132
Pentericci et al. (2014) —. 2014, ApJ, 793, 113
Planck Collaboration et al. (2015) Planck Collaboration, et al. 2015, arXiv:1502.01589
Pober et al. (2014) Pober, J. C., et al. 2014, ApJ, 782, 66
Robertson et al. (2010) Robertson, B. E., et al. 2010, Nature, 468, 49
Robertson et al. (2014) Robertson, B. E., Ellis, R. S., Dunlop, J. S., McLure, R. J., Stark, D. P., et al. 2014, ApJ, 796, L27
Robertson et al. (2013) Robertson, B. E., et al. 2013, ApJ, 768, 71
Schenker et al. (2014) Schenker, M. A., et al. 2014, ApJ, 795, 20
Schenker et al. (2013) Schenker, M. A., et al. 2013, ApJ, 768, 196
Schenker et al. (2012) Schenker, M. A., et al. 2012, ApJ, 744, 179
Shull et al. (2012) Shull, J. M., et al. 2012, ApJ, 747, 100
Stark et al. (2010) Stark, D. P., et al. 2010, MNRAS, 408, 1628
Tilvi et al. (2014) Tilvi, V., et al. 2014, ApJ, 794, 5
Topping & Shull (2015) Topping, M. W., & Shull, J. M. 2015, ApJ, 800, 97
Treu et al. (2013) Treu, T., et al. 2013, ApJ, 775, L29
van Haarlem et al. (2013) van Haarlem, M. P., et al. 2013, A&A, 556, A2