Cosmographic constraints on a Gödel-type rotating universe
Abstract
We investigate the possibility of global cosmic rotation using a Gödel-type rotating cosmological model, constrained through a cosmographic analysis of Type Ia supernovae (SNIa) from the Pantheon+ dataset. Employing a Taylor-expanded apparent magnitude–redshift relation derived via the Kristian-Sachs formalism, we analyze low-redshift SNIa data across five redshift bins (up to ). Our results reveal a mild but consistent preference for cosmic rotation, with the dimensionless rotation parameter peaking at for , and a broadly aligned anisotropy axis centered around equatorial coordinates . The inferred Hubble constant remains stable across all bins, while the deceleration parameter trends from near-zero to mildly negative values with increasing redshift. Model comparison using the Akaike Information Criterion (AIC) indicates a statistically significant preference for the rotating model over the standard CDM cosmology at intermediate redshifts. These findings suggest that cosmic rotation, if present, may influence the late-time expansion history of the universe and warrants further investigation beyond the cosmographic regime.
1Department of Physics, Indian Institute of Technology (BHU), Varanasi - 221005, India
2Institute of Theoretical Astrophysics, University of Oslo, Sem Sælands vei 13, 0371 Oslo, Norway
3Russian Academy of Sciences, Nuclear Safety Institute (IBRAE), B. Tulskaya str. 52, 115191 Moscow, Russia
1 Introduction
Rotation is an ubiquitous phenomena in any astronomical setting. Almost all heavenly bodies have some degree of rotation/spin, from the slow rotation of asteroids to the relativistic speeds at the center of galaxies. It is then natural to ponder over the question of whether the universe itself is rotating or not. Could the universe, on the largest scales, be rotating? Or whether the widespread phenomena of rotation is confined to regions where the universe is inhomogeneous? The question of cosmic rotation and its potential role in the structure and evolution of the universe has intrigued physicists for nearly a century. Whittaker [1] and Lemaître [2] contemplated on the nature of a rotating “primeval atom” from which the universe supposedly emerged in relation to the formation of galaxies and large-scale structures.
The study of rotational effects in cosmology started with the work of Lanczos, who modeled the universe as a rigidly rotating dust cylinder with infinite radius [3], and later in the works of George Gamow [4]. However, a more realistic metric with rotation as a solution to Einstein’s field equations was proposed by Gödel in 1949 [5], that is given by the line element,
| (1) |
where ‘’ is a positive number. Gödel’s universe assumes dust as matter with an energy density and a negative cosmological constant ‘’. In this model, the angular velocity parameter ‘’ that quantifies cosmic rotation is given by . This model provided a theoretical framework for studying rotating cosmologies for many years. Earlier model of Lanczos’ was less physical compared to the Gödel’s model [6].
The metric in Eq. (1) is stationary and incorporates non-trivial global properties of rotating space-times. However, one fundamental problem with this solution was the existence of closed time-like curves (CTC) proved by Gödel himself [7]. Gödel attempted to derive completely causal rotating cosmologies in his last work on rotation and presented a generalization of his original stationary model incorporating expansion, but without proof. First explicit solutions were reported in Refs. [8, 9]. Maitra [8] extended the van Stockum’s solution [6] with rotation as well as shear, and also introduced a straightforward condition for determining the absence of closed time-like curves, ensuring that the model avoids causality violations. Later, multiple solutions of rotating models with or without expansion have been developed, each offering unique insights into the role of rotation in cosmology. Theoretical advancements have given rotating cosmologies some serious considerations, including Einstein-Cartan theory that incorporates spin and torsion. Exact rotating solutions in Einstein-Cartan theory of gravity with spin and torsion were described, for example, in Refs. [10, 11, 12, 13, 14, 15, 16, 17, 18, 19].
The discovery of the cosmic microwave background (CMB) and its high degree of isotropy provided a very strong case for isotropic models. However, deviations from a near perfect isotropy are indicative of possible anisotropies present in the early stages of the evolution of our universe. This motivated a class of homogeneous but anisotropic cosmologies known as Bianchi type cosmological models [20, 21, 22]. Gödel’s solution is one such solution within the class of Bianchi type-III cosmological models. Homogeneous but anisotropic rotating cosmologies were verily analyzed earlier in the literature, in which upper limits on the value of cosmic rotation were obtained from data [23, 24, 25, 26, 27, 28]. But, those studies did not separate the effects of vorticity and shear. In Refs. [29, 30], the effects of pure cosmic rotation were delineated from cosmic shear.
Even with the plethora of astrophysical data sets that were accumulated over the years, no completely convincing results were reported. Birch [31, 32, 33] observed an apparent anisotropy in the alignment between the polarization vectors and the major axes of radio sources. He interpreted this observed anisotropy as potential evidence for cosmic rotation. With the advent of precision era in cosmology, primarily driven by CMB observations, the Cosmological principle which is a foundational assumption of modern cosmology was put to test. This lead to finding many instances of isotropy violation in various astronomical and cosmological data sets (see for example Ref. [34]). Such instances of isotropy violation seen in CMB data have come to be known as CMB anomalies [35, 36, 37, 38, 39]. There were many coincidental alignments among various preferred axes seen in these diverse data sets [40]. Besides isotropy violations, the standard concordance model is also riddled with many tensions [41, 42, 43] from observations that challenge it despite its broad success. Apart from providing possible explanation to various signals of anisotropy seen in data, rotating models may also offer mild corrections to the Hubble flow, potentially providing an alternative explanation for dark energy and a possible resolution to the Hubble tension problem (for a review of Hubble tension and various possible (re)solutions see, for example, Ref. [44, 45, 46, 47]).
A study of spins in the intergalactic medium suggests that longest substantially rotating objects in the Universe are likely filaments of matter connecting neighboring galaxy pairs [48]. Another study reported observational evidence that cosmic filaments spin [49]. It was also reported that there is an asymmetry in the distribution of galaxy spin directions (handness) [50, 51, 52]. Further, some spectroscopic surveys indicate that the direction of rotation of a galaxy is coherent with the average motion of its neighbouring galaxies over a scale of 1 Mpc (megaparsec) [53, 54]. It was argued earlier that primordial turbulence or cosmic vorticity could have played a significant role in structure formation, providing a natural origin for galactic angular momentum [55, 56]. The availability of high-resolution CMB data in the last two decades saw a renewed interest in homogeneous but anisotropic cosmologies, including rotating models [57, 58]. Consequently, more stringent limits on cosmic shear and vorticity were derived using CMB [59, 60, 61].
In Sec. 2, we layout the general properties of a rotating and expanding form of Gödel metric given in Eq. (1) and present the relation between apparent magnitude of a luminous source ‘’ vs redshift ‘’ in such a model. In Sec. 3, the data used in constraining the Gödel-like model under study and the methodology to derive constraints on its parameters are described. Finally, we present our results in Sec. 4 and summarize our finding in Sec. 5.
2 Gödel-type rotating cosmological model
In this section we briefly discuss the Gödel-like model that we are going to investigate in this work. First we present an overview of Gödel-type metric with additional details as necessary, followed by a description of the Taylor expanded apparent magnitude vs redshift relation in such a universe. For more details the reader may consult some of the original works and the references therein [29, 62, 63, 64].
2.1 Gödel-type metric
A wide class of homogeneous, sheer-free cosmological models with expansion and rotation were studied in Refs. [29, 62]. These space-time manifolds are completely causal. The cosmic microwave background (CMB) radiation remains isotropic, and rotation does not produce additional astrophysical parallax effects. The general non-stationary form of the original Gödel metric given by Eq. (1) is described by the invariant space-time interval,
| (2) |
where (or simply ‘’) is the time dependent scale factor (same as in FLRW metric) and are constants. We employed natural units in the above equation so that the speed of light is set to unity (). The condition ensures the absence of closed time-like curves in this model. Therefore the metric in Eq. (2) represents a Gödel-type model that features both rotation and expansion. Since the determinant of the metric above is , in terms of geometry, one requires for it to conform with the Lorentzian signature, that is trivially satisfied by the positivity condition on the constants , and as mentioned above.
The magnitude of the global rotation along the -axis (the axis of anisotropy) can be found to be given by,
| (3) |
It is clear that the rotation parameter decreases as the universe expands.
In order to make theoretical predictions and compare them with the observations, one needs to understand how electromagnetic radiation propagates through space-times following the null geodesic path. The geodesic equations as usual follow:
| (4) |
where is the tangent vector to the geodesic curve parameterized by an affine parameter ‘’. These equations describe how light paths evolve in a rotating cosmological background and provide the mathematical basis for understanding observations in such universes.
Next, we describe the luminosity distance (or equivalently the distance modulus) versus the redshift relation that is required to test this model against observations.
2.2 Apparent magnitude versus redshift relation
Owing to spatial homogeneity of this model, we can assign the location of the observer as without loss of generality. Now, the apparent position of a source of radiation as seen by an observer at ‘’ can be denoted by the usual spherical-polar coordinates on the celestial sky.
The observable effects of a rotating model on cosmological scales include the determination of the Hubble parameter , the rotational parameter , and the deceleration parameter . This section will present the potential observational consequences of cosmic rotation within the framework of the Gödel-type universe of Eq. (2).
Observational tests, like those relating apparent magnitude and redshift , angular size with redshift, and other such relations, allows one to probe how astrophysical observables are influenced by a source’s location in the sky with respect to the axis of anisotropy in a rotating cosmological model. To perform cosmological tests with observations from a radiation source such as Type Ia supernova, an important test is comparing the theoretical area distance , which measures the intrinsic area of a source ‘’ subtending a solid angle at the observer’s location ‘’. The area distance ‘’ between ‘’ and ‘’ is given by,
| (5) |
This distance depends both on the direction of observation , and on ‘’ the affine parameter i.e., (or equivalently, the emission time ‘’ of the source that is detected by the observer at time i.e., ).
The relation between luminosity distance ‘’ and the area distance ‘’ is . Further the distance modulus ‘’ is related to the luminosity distance via the apparent magnitude of an astronomical source as,
| (6) |
where ‘’ is the absolute magnitude of a radiating source at a fixed distance of (parsec) from the source.
Rotational effects are most prominent near the rotation axis, where simple expressions can be derived. For arbitrary directions, the formulas become complex and are often simplified using the Kristian-Sachs formalism [65]. This formalism allows one to express geometric and physical quantities of interest as a power series in terms of affine parameter or redshift, enabling one to derive the magnitude-redshift relation. Specifically, we can get a power series expansion for ‘’ in terms of ‘’ as
| (7) |
where ‘’ are coefficients of this Taylor expansion such that for consistency when . This can be inverted to find a relation between ‘’ and ‘’ as,
| (8) |
where the coefficients of expansion ‘’ (as well as ) are functions of and the cosmological parameters , , , etc. Therefore, these expansions capture the angular dependence of the effects of rotation on cosmological observables.
Using this inverted relation for area distance, , in Eq. (6) along with , the apparent magnitude-redshift relation “” in the Gödel-type rotating universe of Eq. (2) can be found to be given by [63, 64],
| (9) |
up to linear order in ‘’. Here ‘’ is dimensionless Hubble parameter at current time in units of km/s/Mpc i.e., . The parameter is also dimensionless and quantifies the magnitude of global rotation today. The constant offset arises as a result of all dimensionful parameters in the luminosity distance vs redshift relation viz., , and ‘’ is the speed of light in km/s. Hereafter we use for brevity.
This expression shows how cosmic rotation could effect the magnitude-redshift relation as compared to the standard FLRW case. We will use this theoretical distance modulus to compare with apparent magnitudes of Type Ia supernovae from observations to derive parameter constraints by performing an MCMC analysis as described in the next section.
3 Type Ia supernova data and Parameter estimation methodology
The Pantheon+ Type Ia supernova (SNIa) dataset111https://github.com/PantheonPlusSH0ES/DataRelease contains 1701 light curves corresponding to approximately 1550 unique spectroscopically confirmed SNIa [66]. The remaining light curves in the dataset pertain to either the same supernova (SN) observed by different surveys or to “SN siblings” that are SNIa found within the same host galaxy. This latest data set includes significant enhancements, such as the addition of new SNIa and corrections for peculiar velocity effects and host galaxy bias in the SNIa covariance matrix.
In order to measure the luminosity distance to these supernovae (SNe), we use Cepheid variable stars, a type of pulsating stars whose intrinsic luminosity is related to their period of variability. This relationship, known as the period-luminosity (P-L) relation, was first discovered by Henrietta Swan Leavitt in 1912 [67, 68] while studying stars in the Magellanic Clouds. Cepheids are bright enough to be observed in relatively nearby galaxies. Distances to them within the Milky Way were first measured using parallax (a geometric method). This provides a way to estimate the absolute brightness (or luminosity) of these stars based solely on their observed period. Next, Cepheids in nearby galaxies - those that also host Type Ia supernovae (SNe Ia) - are observed to link the supernova luminosity scale to absolute distances. This step is crucial because once the absolute magnitudes of SNe are calibrated using Cepheid distances, SNe Ia can then be used to measure much greater cosmological distances. This calibration process allows us to determine the luminosity distance to very distant supernovae in the Hubble flow (of the expanding universe). The Pantheon+ dataset contains Cepheid anchors that were part of the Pantheon+SH0ES analysis [69]. 42 SNe Ia from Cepheid-calibrated host galaxies are included in the analysis, along with 277 Hubble-flow supernovae.
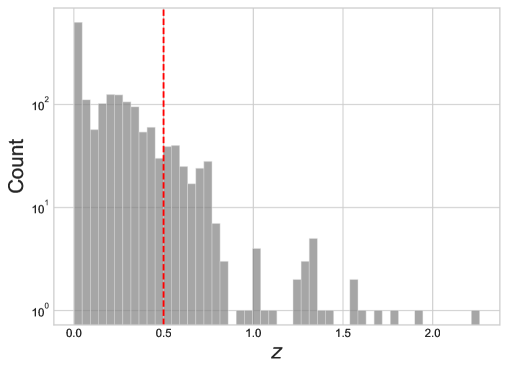
SNIa cosmology relies on comparing the theoretical relationship between redshift () and luminosity distance () or equivalently the distance modulus () that is dependent on various cosmological parameters of our model, with the observed distance modulus () to derive constraints on them. The theoretical and observed distance modulus can be formally expressed as
| (10) |
where ‘’ is the redshift of an SNIa, are the model parameters to be constrained, and ‘’ stands for the distance unit ‘parsec’. Here is the direction of anisotropy i.e., axis of cosmic rotation in equatorial coordinates. Further is the corrected apparent -band magnitude of an SNIa from observations for its correlation with light curve fitting parameters viz., stretch (), color (c) and host mass bias (). The corresponding coefficients , and are global fit parameters along with the absolute -band magnitude ‘’ that are conventionally assumed to be same for all SNIa. ‘’ is notably degenerate with the Hubble parameter (i.e., ), underscoring the importance of using SH0ES Cepheid variables in breaking that degeneracy.
The function, which depends on various fitting parameters , is defined as,
| (11) |
where the goal is to minimize this function to derive the desired constraints. Here, is a column vector with ‘’ elements corresponding to total number of SNe Ia in the dataset. The residual for the -th SNIa is given by,
| (12) |
where,
| (13) |
and denotes the theoretical distance modulus dependent on the model parameters for that -th SNIa, . The above relation (Eq. 12) implies that whenever an SNIa host galaxy also contains a Cepheid, then the theoretical distance modulus is replaced by the well measured value of distance modulus ‘’ to that galaxy obtained using the tight Cepheid period-luminosity relation. This way the degeneracy between the (dimensionless) Hubble parameter ‘’ and the absolute magnitude ‘’ is removed.
Apart from the global fit parameters ‘’ and ‘’ corresponding to stretch and color correction of a supernova light curve, another dimensionless parameter ‘’ captures the dependence of apparent magnitude ‘’ on host-galaxy stellar mass viz., . This host-galaxy stellar mass parameter is defined as a step function depending on its mass as if and if , where denotes 1 solar mass. The values of , , , (as ) and are provided as part of Pantheon+ dataset for each SNIa.
Note that Pantheon+ collaboration also provides for each SNIa. Instead, we use and derive constraints on , and along with cosmological parameters of our model. To account for the correlations among SNIa, which are influenced by both statistical and systematic uncertainties in the light curve fitting, we utilize the full covariance matrix. represents the covariance matrix for supernovae, while denotes the covariance matrix for the SH0ES Cepheid-host distances, both of which are also provided as part of the Pantheon+ data release.
4 Results
This section presents our results from an MCMC likelihood analysis of the Gödel-type rotating cosmological model, discussed in Sec. 2, to probe cosmic rotation. The full set of parameters to be constrained are along with the cosmological parameters that describe the model of our present study. Since the luminosity-distance vs redshift relation given in Eq. (9) is a Taylor expanded relation up to linear order in redshift, , we derive cosmographic constraints on these parameters using low redshift SNIa data up to a maximum of . Specifically we estimate these parameters in five redshift bins ranging from , , , , and . The astrophysical parameters correspond to the SNIa absolute magnitude and coefficients of SNIa light-curve fitting parameters related to stretch, color, and host galaxy properties respectively. Actual cosmological parameters of our model are . All these parameters are constrained using the latest Pantheon+ Type Ia supernova dataset.
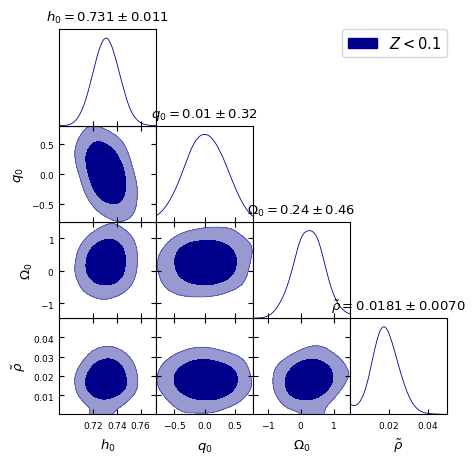
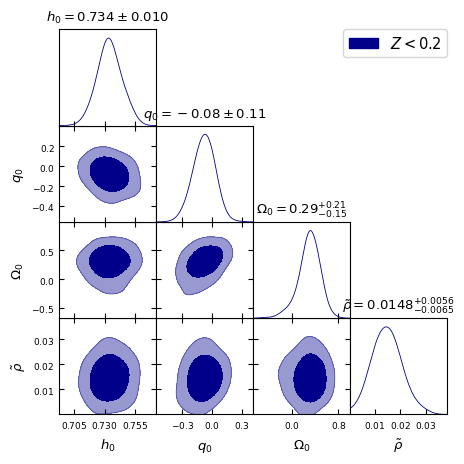
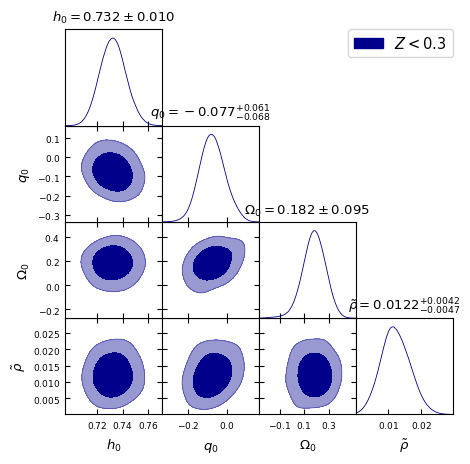
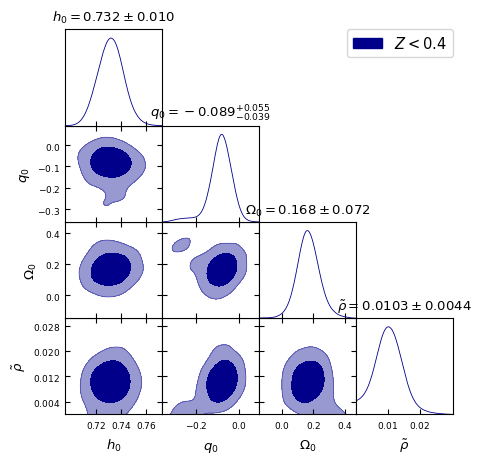
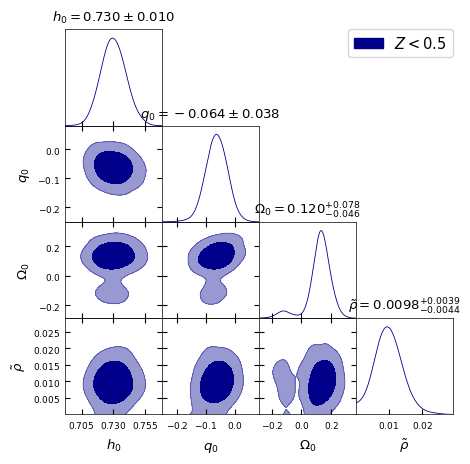
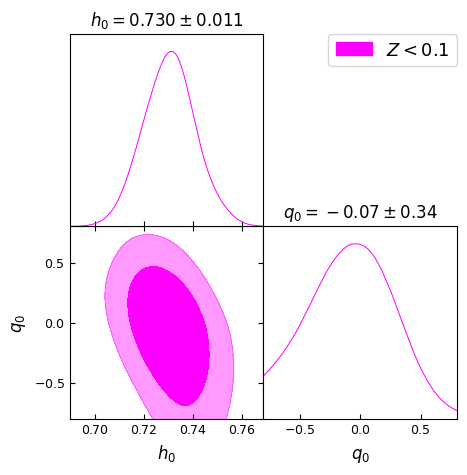
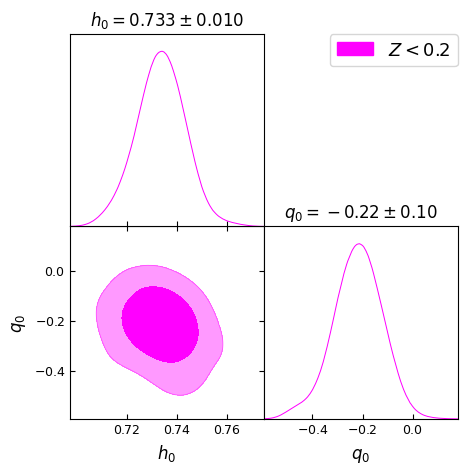
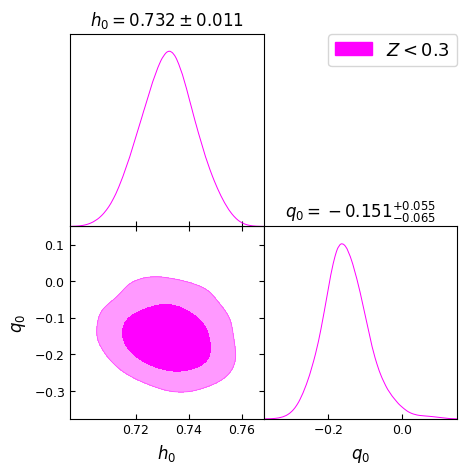
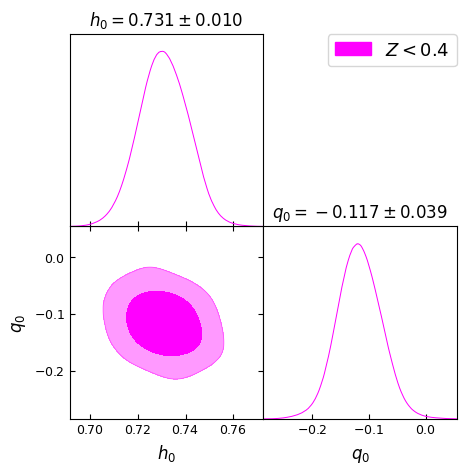
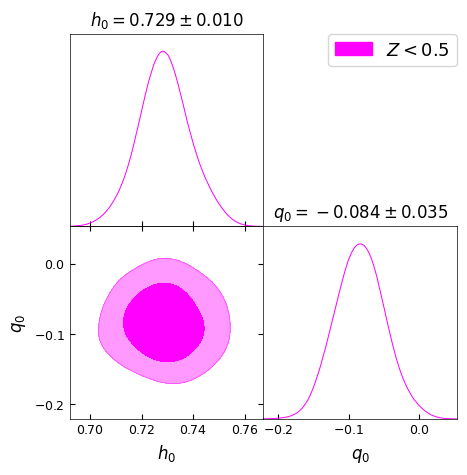
In Fig. [2], we present the 2D contour plots illustrating the and confidence levels (CL) for the model parameters , and from different redshift bins mentioned above. It is important to note that these values should not be directly compared with CDM constraints from SH0ES and Pantheon+ collaborations [69, 70], as the latter were obtained using the full dataset containing SNe Ia upto . Thus, we also perform a similar cosmographic analysis of standard CDM model. These results are presented in Fig. [3] to make appropriate comparison by selected red-shift bins. All the parameter constraints derived from the two models for the chosen redshift bins are tabulated in Table 1.
The Hubble constant ‘’ in the Gödel-type model as well as CDM model remains essentially same across all five redshift bins, with for , , , . These results agree well with the SH0ES determination of (km/s/Mpc) [69]. The agreement suggests two possibilities, that the determination of ‘’ using Pantheon+ SNe Ia compilation is driven by the tighter constraining power of SH0ES subset (that helps breaking the degeneracy between and ) or that the introduction of rotation in the Gödel-type framework may not be affecting the (local) expansion rate significantly.
The maximum likelihood values of the deceleration parameter ‘’, shown in Fig. [2], for the Gödel-type model are , , , , and for the five redshift ranges , , , respectively. A small positive value for at may be due to the limited constraining power of SNe Ia at low redshift or the influence of mild rotational effects on or nature of local matter distribution. It is clear though, from Table 1, that is consistent with ‘zero’ deceleration/acceleration when using SNe Ia upto , given the error bars. However, as we include more number of supernovae with higher redshifts, it tends to take negative values consistent with CDM predictions. Here we note that SH0ES team reported that includes some intermediate redshift SNe also (up to ) in their data from the Pantheon+ sample [69]. In comparison, as shown in Fig. [3], the CDM model with no rotation exhibits consistently negative values, inline with the standard model expectations. We find , , , , and for the same redshift ranges, though is consistent with ‘zero’ given the error bars in the first redshift bin. We observe that these estimates of from CDM model are smaller (more negative) than the values found with Gödel-type model for our Universe. Thus, this may be indicative of the (local) effects of rotation vis-a-vis expansion.

| Parameter | Redshift bins (#SNIa) | ||||
| Gödel-type rotating model | |||||
| CDM | |||||
| Model comparison - AIC | |||||
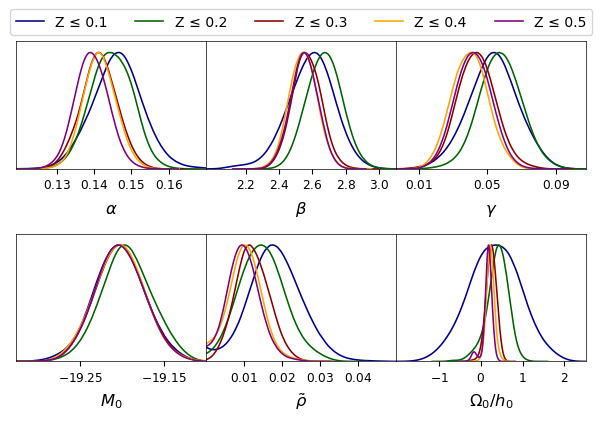
A key parameter in this study corresponding to global rotation, , exhibits a decreasing trend with increasing redshift bin. We obtain for that essentially implies no rotation, that then peaks to for , and thereafter reducing to , , and for , , and , respectively. The trend suggests that the effects of rotation, while uncertain at low redshifts, become more stringent as higher redshift data are included. Another dimensionless parameter ‘’, defined as , that is related to global rotation (see Eq. 3) shows a similar decreasing trend. Constraints derived on both and are presented in Table 1 for different redshift ranges considered. The higher the redshift bin, the smaller the value of assumes. Its values at posterior maxima varies from to from low redshift bin to the highest bin .
This may be indicating two possibilities. On one hand it may be suggesting that we have to go beyond the cosmographic analysis. On the other hand, rotation due to local anisotropic nature of structure could be weakening as we go farther into the Hubble flow. A fuller study of this Gödel-type model, solving the formal luminosity vs redshift relation for any redshift, could provide a resolution to this ambiguity.
The constraints on absolute SNIa magnitude ‘’ remain consistent being from the Gödel-type model as well as the CDM model across all redshift ranges. Its value ranges from to . This also validates the standard candle nature of SNe Ia. Here also it is important to note that we should not compare these values directly with the Panthoen+SH0ES determination of [69] that is estimated from the full data set. The astrophysical nuisance parameters , , and remain almost same across all redshift bins, reinforcing the robustness of SNIa light-curve corrections. Posterior distribution of these nuisance parameters along with and from our MCMC analysis are shown in Fig. [4].
Finally, we plot a derived parameter (), as a 1D contour in Fig. 4 (bottom right panel), that captures the strength of rotation over expansion. The influence of rotation, though modest at , becomes more pronounced for case where . Thereafter rotation to expansion ratio decrease as and for , and respectively, indicating a diminishing impact of rotation as more distant SNe are included. This suggests that cosmic rotation, if present, is more relevant at lower redshifts but becomes negligible on larger scales. Here we note that, since is found to be nearly same () across all redshift ranges, the values of show the same trend as parameter.
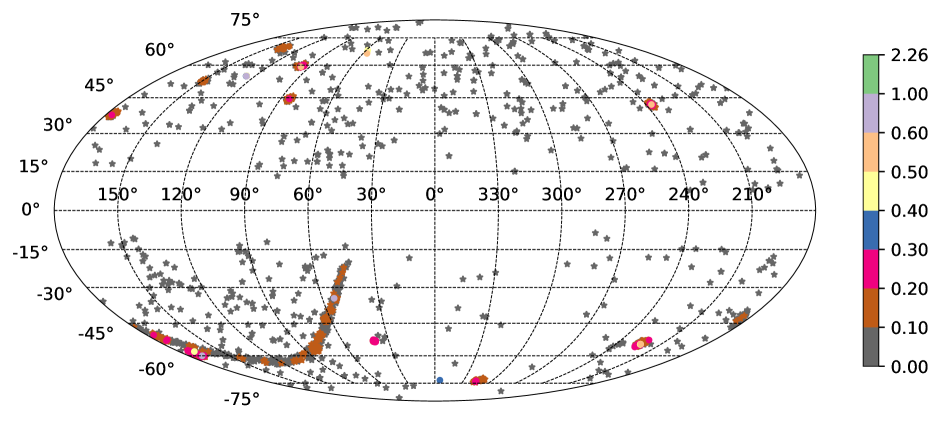
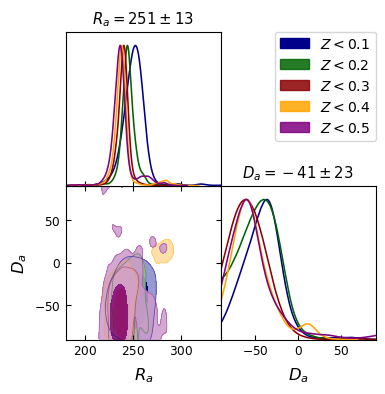
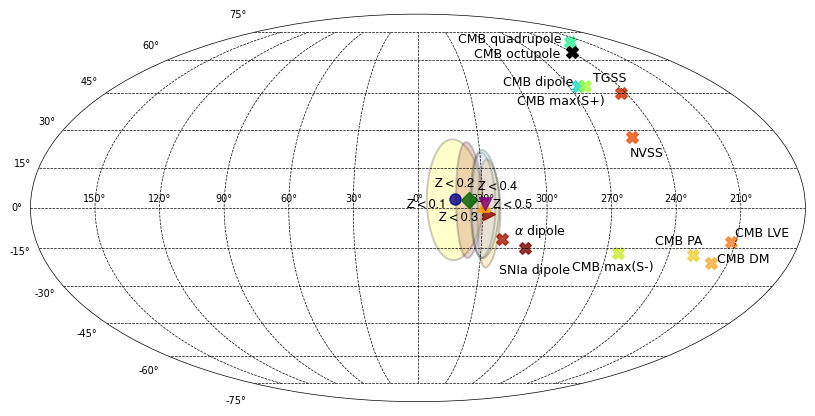
In the end, we present one of the important results of this work viz., constraints on the global axis of anisotropy in our assumed rotating cosmological model. The inferred rotation axes are : for , for , for , for , and for in equatorial coordinates that are also listed in Table 1. To put these anisotropy axes constraints in a broader perspective, these axes from different redshift bins with confidence contours are shown in galactic coordinates along with other anisotropy axes seen in various astronomical and cosmological data sets.
One of the earliest observational constraints on cosmic rotation was reported by Birch in 1982 where a dipole anisotropy in the distribution of observed angle between polarization and position angles of 137 radio sources was interpreted as evidence for cosmic rotation [31]. Birch reported the cosmic rotation axis as in equatorial coordinates. Later, the same was confirmed using ‘indirectional statistics’ by Kendall and Young [76] with a higher significance who reported the axis of rotation to be (using a sample of 134 sources) which is essentially same as that reported by Birch. Using a different sample of 205 sources, Andreasyan reported a cosmic anisotropy in the direction [77]. Considering a subsample of Birch’s data (with 51 sources whose redshifts were known), a global axis of rotation within the present framework of the Gödel-like model was found to be [30].
The present model of our interest given by Eq. (2) was earlier analyzed in Ref. [78] using the gold and silver Type Ia supernovae data sets of Ref. [79]. However, in that study, the rotation term (with the factor ) in Eq. (9) was ignored constraining only the anisotropy axis (of rotation) and the parameter . The gold data set had 157 SNIa and silver data set contained 29 sources. Because of the small sample size, perhaps, they could only find an upper bound on as and , and the axis of anisotropy was found to be and in equatorial coordinates, when using the gold and gold+silver data sets respectively.
Future observations, particularly with additional intermediate and low redshift supernovae, will help refine these constraints and further assess the robustness of the anisotropy signal.
Model comparison through AIC
To qualitatively parameterize a model, one must account for the number of parameters used in model fitting. Since introducing more free parameters in a model usually results in a better fit, we should therefore have a mechanism to either justify or penalize these additional free parameters introduced in a model. To compare different models with different numbers of parameters, it is essential to balance the fit quality against the added complexity. A widely used tool for this is the Akaike Information Criterion (AIC), denoted here as ‘’. Given two models, the preferred model is the one with the minimum AIC value. Note that the AIC value for a model itself cannot define the quality/goodness of fit. It is only the relative AIC values that are used to judge the goodness of fit of one model with respect to another model in describing the data at hand. Based on principles of information theory, ‘’ penalizes model complexity to avoid overfitting while favoring those that effectively/efficiently describe the data [80].
It is defined as,
| (14) |
where ‘’ is the number of parameters, is the maximum likelihood for the given model and is the minimum of the function (Eq. 11) in the parameter space after optimization. The term ‘’ penalizes models with higher complexity. To quantify the relative performance of different models, difference in the values of are computed with respect to a reference model as,
| (15) |
where is the relative AIC value of -th model compared to the reference model. A lower value of indicates that the -th model describes the data better from among all candidate models. Additionally, the probability of each model relative to the reference model is given by [81],
| (16) |
In this study, the flat CDM model serves as the reference, and the values of and the corresponding probabilities are used to evaluate the strength of support for each candidate model. Smaller values indicate stronger evidence for a model, with representing strong support, values in the range suggesting moderate to weak support, and indicating no support [81]. This criterion allows for a quantitative comparison of the likelihood of different models in describing the observed data.
The AIC (), relative AIC () and the relative model probabilities () for our rotating Gödel-type model as well as the standard CDM model for all redshift bins considered are tabulated in Table 1. The interpretation provided by these AIC values [80, 81] shows that the Gödel’s rotating model is either competitive or strongly preferred over the base (reference) flat CDM model for all choices of redshift range considered in this cosmographic analysis. Specifically, for , the rotating model is almost equally ( 1.1 times) probable, while it is 3 , 10, 4.8 and 6.9 times more probable compared to the base model for the redshift cutoffs , and 0.5, respectively.
This result is unexpected and is interesting, since the preference of rotating model over the standard model, particularly at , suggests that the additional kinematic effects introduced by rotation might play a non-negligible role in the late-time expansion history of the universe. Although the statistical evidence favors the rotating model in this analysis, it is important to interpret these results cautiously since the significance of this preference depends on the robustness of the cosmographic expansion employed and the impact of potential systematics in the data. Additional observational constraints, such as those including energy density fractions by deriving the Friedman equations in Gödel type rotating solution, may provide further insights into whether this preference is a genuine physical effect or a statistical anomaly.
5 Conclusions
Rotation is a generic feature arising in any astrophysical setting that is an observational fact as seen in a wide variety of celestial systems. In this study, we explored the possibility of cosmic rotation for our Universe using a Gödel-type metric and observational data from Type Ia supernovae across multiple redshift ranges. We performed a cosmographic analysis of the magnitude vs redshift () relation derived using the Kristian-Sachs formalism. We constrained both cosmological and astrophysical parameters using an MCMC method. Our results indicate interesting deviations from standard CDM constraints for various redshift bins, particularly in the derived parameter , that captures the strength of rotation vs expansion.
The inferred cosmological parameters, particularly the (dimensionless) Hubble constant and the deceleration parameter , are central to understanding the effects of rotation in our analysis. We find that being virtually same for all choices of redshift bins, indicating that the inclusion of rotational degrees of freedom in the Gödel-type model does not significantly alter the overall expansion rate compared to CDM. However, the deceleration parameter exhibits notable variations across redshift bins, with values ranging from at to at . In contrast, for the standard flat CDM model from Pantheon+ SNe Ia constraints [69]. The small positive value at very low redshift and the increasingly negative values at higher redshifts may arise due to statistical limitations in the dataset or subtle rotational effects influencing local expansion. As more high-redshift supernovae are included, approaches the standard CDM expectation, albeit with slightly less negative values than those obtained in a purely isotropic model. This suggests that while rotation does not drastically impact cosmic acceleration, it may introduce small but noticeable deviations from the standard paradigm.
To quantify the relative impact of rotation versus expansion, we analyzed the dimensionless parameter , which provides insight into the strength of cosmic rotation across different redshift bins. Our results indicate that rotational effects are most pronounced at , reaching a maximum value of for the bin. At lower redshifts (), this ratio is relatively small (essentially consistent with zero within error bars). However, as we include higher redshifts, the influence of rotation is found to diminish steadily, with decreasing to for bin. This decline suggests that rotational effects, if present, are confined to relatively local cosmic scales and become negligible when considering more distant supernovae. These results highlight that while rotation may play a role in the cosmic evolution at small redshifts, its contribution becomes increasingly negligible on larger scales, reinforcing the overall isotropy of the universe. The global rotation axis inferred from our model is consistent across all redshift bins, with its mean direction given by .
A related parameter that captures global rotation in this model is . It follows the same trend as and (and hence ). It values decreases steadily from the lowest () to highest () redshift ranges chosen in the present study. Astrophysical parameters viz., , , , and , which characterize supernova magnitude calibration, its light-curve stretch, color and host galaxy properties, are nearly same across different redshift ranges. This reinforces the robustness of the dataset and suggests that systematic effects from supernova standardization are minimal.
The AIC-based model comparison reveals an intriguing preference for the Gödel-type rotating model over the standard flat CDM cosmology, particularly at higher redshifts. While both models remain competitive for , with the candidate model being only marginally more probable, the preference for the rotating model increases significantly at larger redshift cutoffs. Specifically, for , , and , the Gödel-type model is found to be , , and times more probable than CDM model, respectively. This suggests that the additional kinematic effects introduced by cosmic rotation might play a non-negligible role in the late-time expansion history. However, caution is warranted in interpreting these results. The robustness of the cosmographic approach and potential systematics unaccounted for in the data could have a bearing on these findings and further investigation - fully testing this model going beyond the cosmographic expansion - are necessary to determine whether this preference is indicative of a true physical effect or a statistical fluke or a data artifact.
In conclusion, our analysis shows indications for cosmic rotation at intermediate reshifts given that the AIC model assessment metric strongly favours the Gödel-type model over the standard model. Nevertheless it needs further study to derive better constraints on the model to fully understand the ramifications of cosmic rotation more clearly. Future observations from upcoming surveys like Euclid [82] and JWST [83] may provide improved constraints on both the rotation parameter and the anisotropy axis. This could offer new insights into cosmic isotropy and potential deviations that enrich our understanding of the universe’s large-scale structure.
Acknowledgements
AV acknowledges the financial support received through a research fellowship awarded by Council of Scientific & Industrial Research (CSIR), India during this project. We acknowledge National Supercomputing Mission (NSM) for providing computing resources of ‘PARAM Shivay’ at Indian Institute of Technology (BHU), Varanasi, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and Department of Science and Technology (DST), Government of India. DFM thanks the Research Council of Norway for their support and the resources provided by UNINETT Sigma2 – the National Infrastructure for High-Performance Computing and Data Storage in Norway. We acknowledge using Cobaya222https://cobaya.readthedocs.io/en/latest/ [84] - a code for Bayesian analysis in Cosmology, and GetDist333https://getdist.readthedocs.io/en/latest/ [85] - a user friendly GUI for the analysis and plotting of MCMC samples. We also acknowledge the use of SciPy444https://scipy.org/ [86], NumPy555https://numpy.org/ [87], Astropy666http://www.astropy.org [88, 89, 90], and Matplotlib777https://matplotlib.org/ [91].
References
- [1] E.T. Whittaker. Spin in the Universe. Yearbook of Royal Society, Edinburgh:513, 1945.
- [2] G. Lemâıtre. L’hypothèse de l’atome primitif. Acta Pontifica Acad. Sci., 12:25–40, 1948.
- [3] K. Lanczos. Über eine stationäre Kosmologie im Sinne der Einsteinschen Gravitationstheorie. Zeitschrift für Physik, 21:73–110, 1924. [English translation: On a Stationary cosmology in the sense of Einstein’s theory of gravitation, Gen. Rel. Grav. 29 (1997) 361-399].
- [4] G. Gamow. Rotating universe? Nature, 158:549, 1946.
- [5] K. Gödel. An example of a new type of cosmological solutions of Einstein’s field equations of gravitation. Reviews of Modern Physics, 21:447–450, 1949.
- [6] W.J. van Stockum. Gravitational field of a rotating mass as an example of algebraically special metrics. Proceedings of the Royal Society of Edinburgh, 57:135–154, 1936/37.
- [7] K. Gödel. Rotating universes in general relativity theory. In Proceedings of the International Congress of Mathematicians, volume 1, pages 175–181, Cambridge, USA, 1952.
- [8] S. Maitra. Some solutions of Einstein’s field equations. Journal of Mathematical Physics, 7:1025, 1966.
- [9] I. Ozsvath and E. Schücking. An anti-Mach metric. Annals of Physics, 55:166, 1969.
- [10] M. Bedran, V. Vaidya, and M. Som. Stationary cosmological solutions with torsion. Nuovo Cimento B, 87:101–108, 1985.
- [11] L.L. Smalley. Gödel cosmology in Riemann-Cartan space-time with spin density. Physical Review D, 32:3124–3127, 1985.
- [12] L.L. Smalley. Self-consistent Gödel cosmology with spin density in Riemann-Cartan space-time. Physics Letters A, 113:463–466, 1986.
- [13] J. Duarte de Oliveira, A.F.F. Teixeira, and J. Tiomno. Homogeneous cosmos of Weyssenhoff fluid in Einstein-Cartan space. Physical Review D, 34:3661–3665, 1986.
- [14] Yu.N. Obukhov and V.A. Korotky. The Weyssenhoff fluid in Einstein-Cartan theory. Classical and Quantum Gravity, 4:1633–1657, 1987.
- [15] V.N. Pavelkin and V.F. Panov. A study of rotation in cosmology. Sov. Phys. J., 31:541–544, 1989.
- [16] V.A. Korotky and Yu.N. Obukhov. Rotating and expanding cosmology in ECSK-theory. Astrophysics and Space Science, 198:1–12, 1992.
- [17] D. Palle. Imperfect fluid in the Einstein-Cartan gravity. Preprint Dept. Theor. Phys., R. Boskovic Inst., 1995. 6 p.
- [18] D. Palle. On certain relationships between cosmological observables in the Einstein-Cartan gravity. Nuovo Cimento B, 111:671–675, 1996.
- [19] J.E. Åman, J.B. Fonseca-Neto, M.A.H. MacCallum, and M.J. Rebouças. Riemann-Cartan space-times of Gödel type. Classical and Quantum Gravity, 15:1089–1101, 1998.
- [20] G. F. R. Ellis and M. A. H. MacCallum. A class of homogeneous cosmological models. Communications in Mathematical Physics, 12(2):108–141, June 1969.
- [21] M. A. H. MacCallum and G. F. R. Ellis. A class of homogeneous cosmological models: II. Observations. Communications in Mathematical Physics, 19(1):31–64, March 1970.
- [22] M. A. H. MacCallum. A class of homogeneous cosmological models III: Asymptotic behaviour. Communications in Mathematical Physics, 20(1):57–84, March 1971.
- [23] J.D. Barrow, R. Juszkiewicz, and D.H. Sonoda. Structure of the cosmic microwave background. Nature, 305:397–402, 1983.
- [24] J.D. Barrow, R. Juszkiewicz, and D.H. Sonoda. Universal rotation: how large can it be? Monthly Notices of the Royal Astronomical Society, 213:917–943, 1985.
- [25] S.W. Hawking. On the rotation of the universe. Monthly Notices of the Royal Astronomical Society, 142:129–141, 1969.
- [26] C.B. Collins and S.W. Hawking. The rotation and distortion of the universe. Monthly Notices of the Royal Astronomical Society, 162:307–320, 1973.
- [27] A. Kogut, G. Hinshaw, and A.J. Banday. Limits to global rotation and shear from the COBE DMR four year sky maps. Physical Review D, 55:1901–1905, 1997.
- [28] A.M. Wolfe. New limits on the shear and rotation of the universe from the X-ray background. Astrophysical Journal, 159:L61–L67, 1970.
- [29] Yuri N. Obukhov. Gauge Theories of Fundamental Interactions: Proceedings of the XXXII Semester of the S. Banach International Mathematical Center. In M. Pawlowski and R. Raczka, editors, Proceedings of the XXXII Semester of the S. Banach Internat. Math. Center, Warsaw, Poland, 19 Sept-3 Dec 1988, page 341, Singapore, 1990. World Scientific.
- [30] Yu. N. Obukhov. Rotation in cosmology. General Relativity and Gravitation, 24(2):121–128, February 1992.
- [31] P. Birch. Is the Universe rotating? Nature, 298(5873):451–454, July 1982.
- [32] P. Birch. Is there evidence for universal rotation? Birch replies. Nature, 301:736, 1982.
- [33] R.G. Conway, P. Birch, R.J. Davis, L.R. Jones, A.J. Kerr, and D. Stannard. Multi-frequency observations of linear polarization in 94 sources from the 3CR catalogue. I. Observations. Monthly Notices of the Royal Astronomical Society, 202:813–823, 1983.
- [34] Pavan Kumar Aluri, Paolo Cea, Pravabati Chingangbam, Ming-Chung Chu, Roger G. Clowes, Damien Hutsemékers, Joby P. Kochappan, Alexia M. Lopez, Lang Liu, Niels C. M. Martens, C. J. A. P. Martins, Konstantinos Migkas, Eoin Ó Colgáin, Pratyush Pranav, Lior Shamir, Ashok K. Singal, M. M. Sheikh-Jabbari, Jenny Wagner, Shao-Jiang Wang, David L. Wiltshire, Shek Yeung, Lu Yin, and Wen Zhao. Is the observable Universe consistent with the cosmological principle? Classical and Quantum Gravity, 40(9):094001, May 2023.
- [35] C. L. Bennett, R. S. Hill, G. Hinshaw, D. Larson, K. M. Smith, J. Dunkley, B. Gold, M. Halpern, N. Jarosik, A. Kogut, E. Komatsu, M. Limon, S. S. Meyer, M. R. Nolta, N. Odegard, L. Page, D. N. Spergel, G. S. Tucker, J. L. Weiland, E. Wollack, and E. L. Wright. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Are There Cosmic Microwave Background Anomalies? ApJS, 192(2):17, February 2011.
- [36] C. L. Bennett, D. Larson, J. L. Weiland, N. Jarosik, G. Hinshaw, N. Odegard, K. M. Smith, R. S. Hill, B. Gold, M. Halpern, E. Komatsu, M. R. Nolta, L. Page, D. N. Spergel, E. Wollack, J. Dunkley, A. Kogut, M. Limon, S. S. Meyer, G. S. Tucker, and E. L. Wright. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. ApJS, 208(2):20, October 2013.
- [37] P. A. R. Ade et al. Planck 2013 results. XXIII. Isotropy and statistics of the CMB. Astron. Astrophys., 571:A23, 2014.
- [38] P. A. R. Ade et al. Planck 2015 results. XVI. Isotropy and statistics of the CMB. Astron. Astrophys., 594:A16, 2016.
- [39] Y. Akrami et al. Planck 2018 results. VII. Isotropy and Statistics of the CMB. Astron. Astrophys., 641:A7, 2020.
- [40] John P. Ralston and Pankaj Jain. The Virgo Alignment Puzzle in Propagation of Radiation on Cosmological Scales. International Journal of Modern Physics D, 13(9):1857–1877, January 2004.
- [41] Philip Bull et al. Beyond CDM: Problems, solutions, and the road ahead. Phys. Dark Univ., 12:56–99, 2016.
- [42] Elcio Abdalla et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. JHEAp, 34:49–211, 2022.
- [43] L. Perivolaropoulos and F. Skara. Challenges for CDM: An update. New Astron. Rev., 95:101659, December 2022.
- [44] G. Efstathiou. A Lockdown Perspective on the Hubble Tension (with comments from the SH0ES team). arXiv e-prints, page arXiv:2007.10716, July 2020.
- [45] Eleonora Di Valentino, Olga Mena, Supriya Pan, Luca Visinelli, Weiqiang Yang, Alessandro Melchiorri, David F. Mota, Adam G. Riess, and Joseph Silk. In the realm of the Hubble tension-a review of solutions. Classical and Quantum Gravity, 38(15):153001, July 2021.
- [46] Wendy L. Freedman. Measurements of the Hubble Constant: Tensions in Perspective. ApJ, 919(1):16, September 2021.
- [47] Marc Kamionkowski and Adam G. Riess. The Hubble Tension and Early Dark Energy. Annual Review of Nuclear and Particle Science, 73:153–180, September 2023.
- [48] Qianli Xia, Mark C. Neyrinck, Yan-Chuan Cai, and Miguel A. Aragón-Calvo. Intergalactic filaments spin. MNRAS, 506(1):1059–1072, September 2021.
- [49] Stephon Alexander, Christian Capanelli, Elisa G. M. Ferreira, and Evan McDonough. Cosmic filament spin from dark matter vortices. Physics Letters B, 833:137298, October 2022.
- [50] Lior Shamir. Handedness asymmetry of spiral galaxies with shows cosmic parity violation and a dipole axis. Physics Letters B, 715(1):25–29, August 2012.
- [51] Lior Shamir. Large‑scale asymmetry between clockwise and counterclockwise galaxies revisited. Astronomische Nachrichten, 341(3):324–330, March 2020.
- [52] Lior Shamir. Large-Scale Asymmetry in the Distribution of Galaxy Spin Directions—Analysis and Reproduction. Symmetry, 15(9):1704, September 2023.
- [53] Joon Hyeop Lee, Mina Pak, Hye-Ran Lee, and Hyunmi Song. Galaxy Rotation Coherent with the Motions of Neighbors: Discovery of Observational Evidence. ApJ, 872(1):78, February 2019.
- [54] Joon Hyeop Lee, Mina Pak, Hyunmi Song, Hye-Ran Lee, Suk Kim, and Hyunjin Jeong. Mysterious Coherence in Several-megaparsec Scales between Galaxy Rotation and Neighbor Motion. ApJ, 884(2):104, October 2019.
- [55] Joseph Silk and Susan Ames. Primordial Turbulence and the FORMAT10N of Galaxies. ApJ, 178:77–94, November 1972.
- [56] Arthur D. Chernin. Shocks and vorticity in cosmic hydrodynamics. Vistas in Astronomy, 40(2):257–301, January 1996.
- [57] Andrew Pontzen. Rogues’ gallery: The full freedom of the Bianchi CMB anomalies. Phys. Rev. D, 79(10):103518, May 2009.
- [58] Rockhee Sung and Peter Coles. Temperature and polarization patterns in anisotropic cosmologies. J. Cosmology Astropart. Phys, 2011(6):036, June 2011.
- [59] T. R. Jaffe, A. J. Banday, H. K. Eriksen, K. M. Górski, and F. K. Hansen. Evidence of Vorticity and Shear at Large Angular Scales in the WMAP Data: A Violation of Cosmological Isotropy? ApJ, 629(1):L1–L4, August 2005.
- [60] T. R. Jaffe, S. Hervik, A. J. Banday, and K. M. Górski. On the Viability of Bianchi Type VIIh Models with Dark Energy. ApJ, 644(2):701–708, June 2006.
- [61] Daniela Saadeh, Stephen M. Feeney, Andrew Pontzen, Hiranya V. Peiris, and Jason D. McEwen. A framework for testing isotropy with the cosmic microwave background. MNRAS, 462(2):1802–1811, October 2016.
- [62] V. A. Korotkij and Yu. N. Obukhov. Kinematic analysis of cosmological models with rotation. Soviet Journal of Experimental and Theoretical Physics, 72(1):11–15, January 1991. [ZhETF 99 (1991) 22, in Russian].
- [63] Vladimir A. Korotky and Yuri N. Obukhov. On Cosmic Rotation. In P. Pronin and G. Sardanashvily, editors, Gravity Particles and Space-time, pages 421–439. World Scientific, Singapore, January 1996.
- [64] Yuri N. Obukhov. On physical foundations and observational effects of cosmic rotation. In M. Scherfner, T. Chrobok, and M. Shefaat, editors, Colloquium on Cosmic Rotation, page 23. Wissenschaft und Technik Verlag, Berlin, January 2000.
- [65] J. Kristian and R. K. Sachs. Observations in Cosmology. ApJ, 143:379, February 1966.
- [66] Dan Scolnic et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J., 938(2):113, 2022.
- [67] Henrietta S. Leavitt. 1777 variables in the Magellanic Clouds. Harvard Obs. Annals, 60:87–108, 1908.
- [68] Henrietta S. Leavitt and Edward C. Pickering. Periods of 25 Variable Stars in the Small Magellanic Cloud. Harvard College Observatory Circular, 173:1–3, March 1912.
- [69] Adam G. Riess et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s-1 Mpc-1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett., 934(1):L7, 2022.
- [70] Dillon Brout et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J., 938(2):110, 2022.
- [71] N. Aghanim et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron. Astrophys., 641:A1, 2020.
- [72] Y. Akrami, Y. Fantaye, A. Shafieloo, H. K. Eriksen, F. K. Hansen, A. J. Banday, and K. M. Górski. Power Asymmetry in WMAP and Planck Temperature Sky Maps as Measured by a Local Variance Estimator. ApJ, 784(2):L42, April 2014.
- [73] Carlos A. P. Bengaly, Roy Maartens, and Mario G. Santos. Probing the Cosmological Principle in the counts of radio galaxies at different frequencies. J. Cosmology Astropart. Phys, 2018(4):031, April 2018.
- [74] I. Antoniou and L. Perivolaropoulos. Searching for a cosmological preferred axis: Union2 data analysis and comparison with other probes. J. Cosmology Astropart. Phys, 2010(12):012, December 2010.
- [75] Antonio Mariano and Leandros Perivolaropoulos. Is there correlation between fine structure and dark energy cosmic dipoles? Phys. Rev. D, 86(8):083517, October 2012.
- [76] D. G. Kendall and G. A. Young. Indirectional statistics and the significance of an asymmetry discovered by Birch. MNRAS, 207:637–647, April 1984.
- [77] R. R. Andreasyan. The problem of the existence of large-scale anisotropy in metagalactic space. Astrophysics, 24(2):213–220, March 1986.
- [78] Pankaj Jain, Moninder S. Modgil, and John P. Ralston. Search for Global Metric Anisotropy in Type 1a Supernova Data. Modern Physics Letters A, 22(16):1153–1165, January 2007.
- [79] Adam G. Riess et al. Type Ia Supernova Discoveries at from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. ApJ, 607(2):665–687, June 2004.
- [80] H. Akaike. A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, 19:716–723, January 1974.
- [81] K. P. Burnham and D. R. Anderson. Multimodel inference: Understanding AIC and BIC in model selection. Sociological Methods and Research, 33(2):261–304, November 2004.
- [82] Y. Mellier et al. Euclid. I. Overview of the Euclid mission. Astron. Astrophys., 697:A1, 2025.
- [83] Jonathan P. Gardner et al. The James Webb Space Telescope Mission. PASP, 135(1048):068001, June 2023.
- [84] Jesús Torrado and Antony Lewis. Cobaya: code for Bayesian analysis of hierarchical physical models. J. Cosmology Astropart. Phys, 2021(5):057, May 2021.
- [85] Antony Lewis. GetDist: a Python package for analysing Monte Carlo samples. arXiv e-prints, page arXiv:1910.13970, October 2019.
- [86] Pauli Virtanen et al. SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python. Nature Meth., 17:261, 2020.
- [87] Charles R. Harris et al. Array programming with NumPy. Nature, 585(7825):357–362, 2020.
- [88] Thomas P. Robitaille et al. Astropy: A Community Python Package for Astronomy. Astron. Astrophys., 558:A33, 2013.
- [89] A. M. Price-Whelan et al. The Astropy Project: Building an Open-science Project and Status of the v2.0 Core Package. Astron. J., 156(3):123, 2018.
- [90] Adrian M. Price-Whelan et al. The Astropy Project: Sustaining and Growing a Community-oriented Open-source Project and the Latest Major Release (v5.0) of the Core Package*. Astrophys. J., 935(2):167, 2022.
- [91] J. D. Hunter. Matplotlib: A 2d graphics environment. Computing in Science & Engineering, 9(3):90–95, 2007.